1 Introduction

In all over the world, enthused researchers have recently exposed countless attention in scrutinizing the heat transfer phenomenon as a wave instead of diffusion because of its abundant engineering solicitations like cooling of energy invention, magnetic pills pursuing, biomedical applications and atomic vessels for cooling resolutions. The heat transfer is an extensive phenomenon in the nature which subsists owing to dissimilarity of temperature between entities or inside the similar body. For the former two spans, Fourier law of heat transfer [1] has been the only benchmark to estimate the heat transfer amount. The crucial downside of this law termed Paradox of heat conduction was to raise parabolic energy equation which designates that any distraction in the start will transmit all through the material. Cattaneo [2] intersected this obstacle by inserting relaxation time to heat flux. Moreover, this array was enhanced by Christov [3] by changing the material invariant sort of Maxwell–Cattaneo law by exhausting the Oldroyd’s upper convective derivative. Hayat et al. [4] reported the performance of Cattaneo–Christov heat flux theory in variable thicked surface with variable conductivity. Ali and Sandeep [5] addressed the characteristics of an enhanced heat conduction relation on radiative magneto Casson-ferrofluid numerically. An Oldroyd-B fluid in the rotating frame by utilizing a developed heat conduction and mass diffusion relations was studied by Khan et al. [6]. They investigated that for rotation parameter both the primary and secondary velocities decline. Mustafa et al. [7] explored the aspects of thermal conductivity which is time dependent and non-Fourier heat flux concept in rotating structure of Maxwell fluid. They described that owing to insertion of elastic properties the hydrodynamic boundary layer befits thinner. Additional present-day endeavors in this aptitude are reported in references [8,9,10,11,12].

The growths of chemical species in the world arise through both heterogeneous/homogeneous responses. Recently, the technologists and engineers exhibit their thoughtful curiosity on analyzing new catalytic progressions functional at high temperature. Deprived of the exploitation of a catalyst, numerous reactions progress are very leisurely or insignificant. Heterogeneous/homogeneous responses are very compact which comprise the reduction and fabrication of reacting species at diverse amounts on the catalyst surfaces and within the liquids. A homogeneous reaction ensues where reactions and catalyst function in the similar phase; however, the heterogeneous reaction proceeds a limited area. Moreover, there are frequent chemically retorting structures containing both heterogeneous/homogeneous responses such as catalysis, organic systems and ignition. In addition, the significance of chemical species is more apparent in diverse industrial solicitations such as nutrition indulgence, fog materialization and diffusion, design of chemical dispensation apparatus, hydrometallurgical diligence, temperature distribution and vapor over cultivated lands and fruit tree plantations. Chaudhary and Merkin [13] investigated the features of heterogeneous/homogeneous reactions on viscous fluid with the stagnation point flow. Later on, for the study of the viscous liquid subject to heterogeneous/homogeneous reactions an isothermal model was suggested by Merkin [14]. Xu [15] studied the impact of chemical reactions in the stagnation region for heat fluid flow. He achieved multiple elucidations numerically with the aid of hysteresis bifurcations. Hayat et al. [16] scrutinized the chemical reactions on flow of a nanofluid with variable thicknesses. They investigated that the heat transfer amount decreases for Reynolds number. They noted that because of surface reaction this mechanism is dominant. The aspects of chemical species on generalized Burgers liquids were reported by Khan et al. [17]. Numerically the characteristics of convectively heated Riga plate on Williamson nanofluid by utilizing chemical reaction were explored by Ramzan et al. [18]. They detected that both Brownian motion and chemical reaction parameters are diminishing function of concentration field. Some additional current endeavors in this capacity are raised to references ([19,20,21,22,23,24]).

The analysis of liquid flow and heat transfer features of nonlinear materials has attracted the hurrying curiosity of the current researchers owing to the circumstance that most of nonlinear materials have more profuse scientifically and industrial solicitations instead of Newtonian materials [25,26,27,28]. The polymeric liquids, honey solutions, energy slurries, splatters, paper invention, oil retrieval and an assortment of soils are numerous specimens of nonlinear materials. It is quite awkward to increase a solitary constitutive correlation that foresees the assets of these constituents because the nature of these resources is very multifaceted and intricate. For instance, the heat transport properties on nonlinear materials axisymmetric channel via parameterized perturbation technique was analyzed by Ashorynejad et al. [29] An Oldroyd-B fluid by using nanoparticles with combined stratification was examined by Waqas et al. [30]. They establish that the temperature and mass stratification decline the temperature and concentration fields. The impact of the heat sink/source on unsteady radiative flow of Williamson liquid was reported by Khan and Hamid [31]. In their exploration, they initiated that the heat transfer enhances for higher thermal radiation and temperature ratio parameter. Sandeep [32] observed the influence of aligned magnetic field on nanoliquid with graphene nanoparticles. He noticed that aligned magnetic field normalizes the local Nusselt number; however, the thermal conductivity of water increases for intensifying values of volume fraction of nanoparticles. Additionally, to envision their sufficient performance numerous constitutive interactions have been established for non-Newtonian liquids [33,34,35,36,37,38,39,40,41].

Stimulated by all the aforesaid fiction and countless prospective developed and industrial anxieties, the notable concern of this scrutiny is sightseeing the notion of an improved heat conduction and chemical species on an Oldroyd-B fluid flow caused by a stretched cylinder. Additionally, variable thermal conductivity is presented for the heat transfer purpose. Apposite alteration changes the PDEs into nonlinear ODEs which are then elucidated analytically by means of homotopic scheme. Moreover, the flow structures are scrutinized for assorted scheming parameters graphically and conferred in detail.

2 Mathematical formulations

The mathematical framing of the current flow analysis is in the following three subdivisions.

2.1 Flow equation

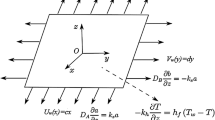
We consider the steady 2D axisymmetric flow of an Oldroyd-B fluid influenced by a stretched cylinder of radius \(R\). The cylinder is stretching with velocity \(\tfrac{{U_{0} z}}{l},\) along \(z\)-direction, where \((U_{0} ,\,l)\) is the reference velocity and characteristic length, respectively. Let the cylindrical polar coordinates \((r,\,z)\) be engaged in such a way that \(z\)-axis is adjacent to the axis of the cylinder and \(r\)-axis is restrained near the radial direction (as depicted in Fig. 1). The continuity and momentum equations of the flow analysis are as follows [42, 43]:

Fig. 1
figure 1

Schematic diagram

Full size image
$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0,$$
(1)
$$\begin{aligned} & u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z} + \lambda_{1} \left[ {w^{2} \frac{{\partial^{2} w}}{{\partial z^{2} }} + u^{2} \frac{{\partial^{2} w}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} w}}{\partial r\partial z}} \right] = \nu \left[ {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r}} \right]\, \\ & + \,\nu \lambda_{2} \left[ {\tfrac{u}{{r^{2} }}\tfrac{\partial w}{\partial r} - \tfrac{1}{r}\tfrac{\partial w}{\partial r}\tfrac{\partial w}{\partial z} - \tfrac{2}{r}\tfrac{\partial u}{\partial r}\tfrac{\partial w}{\partial r} + \tfrac{w}{r}\tfrac{{\partial^{2} w}}{\partial r\partial z} - \tfrac{\partial w}{\partial r}\tfrac{{\partial^{2} w}}{\partial r\partial z} - 2\tfrac{\partial w}{\partial r}\tfrac{{\partial^{2} u}}{{\partial r^{2} }} + \tfrac{u}{r}\tfrac{{\partial^{2} w}}{{\partial r^{2} }} - \tfrac{\partial w}{\partial z}\tfrac{{\partial^{2} w}}{{\partial r^{2} }} + w\tfrac{{\partial^{3} w}}{{\partial r^{2} \partial z}} + u\tfrac{{\partial^{3} w}}{{\partial r^{3} }}} \right], \\ \end{aligned}$$
(2)

subject to boundary conditions

$$w(R,z) = W(z) = \frac{{U_{0} z}}{l},\quad u(R,z) = 0,$$
(3)
$$w \to 0,\quad {\text{as}}\quad r \to \infty .$$
(4)

Here, \((u,\,w)\) are the velocity components in \(r\)- and \(z\)-directions, respectively, \(\nu\) the kinematic viscosity and \(\lambda_{i}\) \((i = 1,\,2)\) the thermal relaxation and retardation times.

Considering the conversions

$$u = - \frac{R}{r}\sqrt {\frac{{U_{0} \nu }}{l}} f(\eta ),\, \, w = \frac{{U_{0} z}}{l}f^{\prime}(\eta ),\, \, \eta = \sqrt {\frac{{U_{0} }}{\nu l}} \left( {\frac{{r^{2} - R^{2} }}{2R}} \right),$$
(5)

Equation (1) is satisfied automatically, and Eqs. (2)–(4) yield

$$\begin{aligned} & (1 + 2\alpha \eta )f^{\prime \prime \prime } + 2\alpha f^{\prime \prime } + ff^{\prime \prime } - f^{\prime 2} + 2\beta_{1} f^{\prime } ff^{\prime \prime } - \beta_{1} f^{2} f^{\prime \prime \prime } - \frac{{\alpha \beta_{1} }}{(1 + 2\alpha \eta )}f^{2} f^{\prime \prime } \\ & + \,(1 + 2\alpha \eta )\beta_{2} (f^{\prime \prime 2} - ff^{iv} ) - 4\alpha \beta_{2} ff^{\prime \prime \prime } = 0, \\ \end{aligned}$$
(6)
$$f(0) = 0,\, \, f^{\prime } (0) = 1,\, \, f^{\prime } (\infty ) = 0.$$
(7)

Here, \(\alpha \left( { = \tfrac{1}{R}\sqrt {\tfrac{\nu l}{{U_{0} }}} } \right)\) is the curvature parameter and \(\beta_{i} \left( { = \tfrac{{\lambda_{i} U_{0} }}{l}} \right)\) \((i = 1,\,2)\) the Deborah numbers.

2.2 Energy equation

The equation of energy for this circumstance is

$$\left( {\rho c} \right)_{p} \left( {u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z}} \right) = - {\mathbf{\nabla }} \cdot {\mathbf{q}},$$
(8)

where \(T\) is the liquid temperature, \((\rho_{p} ,\,c_{p} )\) the liquid density and specific heat at constant pressure, respectively, and \({\mathbf{q}}\) the heat flux. In the vision of Cattaneo–Christov, the heat flux satisfies

$${\mathbf{q + }}\delta_{E} \left( {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{V}} \cdot {\mathbf{\nabla q - q}} \cdot {\mathbf{\nabla V + }}({\mathbf{\nabla }} \cdot {\mathbf{V}}){\mathbf{q}}} \right) = - K(T){\mathbf{\nabla }}T,$$
(9)

where \(\delta_{E}\) is the thermal relaxation time of heat flux and \(K(T)\) the thermal conductivity which is temperature dependent.

For incompressibility condition, the above equation yields

$${\mathbf{q + }}\delta_{E} \left( {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{V}} \cdot {\mathbf{\nabla q - q}} \cdot {\mathbf{\nabla V}}} \right) = - K(T){\mathbf{\nabla }}T.$$
(10)

By eliminating \({\mathbf{q}}\) from Eqs. (8) and (10), we finally have

$$u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} + \delta_{E} \left[ {\begin{array}{*{20}c} {w^{2} \tfrac{{\partial^{2} T}}{{\partial z^{2} }} + u^{2} \tfrac{{\partial^{2} T}}{{\partial r^{2} }} + 2uw\tfrac{{\partial^{2} T}}{\partial z\partial r}} \\ {\left( {w\tfrac{\partial w}{\partial z} + u\tfrac{\partial u}{\partial r}} \right)\,\tfrac{\partial T}{\partial z} + \left( {w\tfrac{\partial u}{\partial z} + u\tfrac{\partial u}{\partial r}} \right)\,\tfrac{\partial T}{\partial r}} \\ \end{array} } \right] = \frac{1}{{\left( {\rho c} \right)_{p} r}}\frac{\partial }{\partial r}\left[ {K(T)r\frac{\partial T}{\partial r}} \right],$$
(11)

with boundary conditions

$$T = T_{w} {\text{ at }}r = R{\text{ and }}T \to T_{\infty } ,\,{\text{ as }}r \to \infty .$$
(12)

Here, \((T_{w} ,\,T_{\infty } )\) are the wall and ambient temperatures, respectively, and \(K(T)\) the temperature-dependent thermal conductivity, which is defined as

$$K(T) = k_{\infty } \left[ {1 + \varepsilon \left( {\frac{{T - T_{\infty } }}{\Delta T}} \right)} \right],$$
(13)

where \(\left( {k_{\infty } ,\,\varepsilon } \right)\) are the thermal conductivity and small scale parameter, respectively, and \(\Delta T\) the difference between the liquid temperature of stretched surface and far away from the surface of cylinder.

The non-dimensional temperature of Oldroyd-B liquid is defined by the following relation:

$$\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}.$$
(14)

Substituting Eqs. (13) and (14) in  Eqs. (11) and (12) we have

$$(1 + 2\alpha \eta )\theta^{{\prime \prime }} + 2\alpha \theta^{{\prime }} + (1 + 2\alpha \eta )(\theta \theta^{{\prime \prime }} + \theta^{\prime 2} )\varepsilon + 2\alpha \varepsilon \theta \theta^{\prime } - \mathop {\Pr }\limits \gamma (ff^{\prime } \theta^{\prime } + \gamma f^{2} \theta^{{\prime \prime }} ),$$
(15)
$$\theta (0) = 1\;\;\;{\text{and }}\;\theta (\infty ) = 0.$$
(16)

Here, \(\gamma \left( { = \tfrac{{\delta_{E} U_{0} }}{l}} \right)\) is the thermal relaxation factor and \(\Pr \left( { = \tfrac{\nu }{{\alpha_{1} }}} \right)\) the Prandtl number.

2.3 Relation for the chemical species

The interaction between heterogeneous and homogeneous responses consists of chemical reactants \(\left( {G,\,H} \right)\) which have the concentrations \(\left( {g,\,h} \right)\) and rate constants \(\left( {k_{c} ,\,k_{s} } \right)\). Also, the isothermal response heterogeneous (surface) of the first order is of the form

$$G + 2H \to 3H,\,{\text{ rate}} = k_{c} gh^{2} ,$$
(17)
$$G \to H,\,{\text{ rate}} = k_{s} g.$$
(18)

Moreover, an assumption is made that both the reactions are isothermal and distant from the sheet at the ambient fluid; for reactant \(G\), there is a uniform concentration \(g_{0}\) while there is no autocatalyst \(H.\)

Under these attentions, the equations of chemical species with boundary conditions are

$$u\frac{\partial g}{\partial r} + w\frac{\partial g}{\partial z} = D_{G} \left( {\frac{1}{r}\frac{\partial g}{\partial r} + \frac{{\partial^{2} g}}{{\partial r^{2} }}} \right) - k_{c} gh^{2} ,$$
(19)
$$u\frac{\partial h}{\partial r} + w\frac{\partial h}{\partial z} = D_{H} \left( {\frac{1}{r}\frac{\partial h}{\partial r} + \frac{{\partial^{2} h}}{{\partial r^{2} }}} \right) + k_{c} gh^{2} ,$$
(20)
$$D_{G} \frac{1}{r}\frac{\partial g}{\partial r} = k_{s} g,\, \, D_{H} \frac{1}{r}\frac{\partial h}{\partial r} = - k_{s} g \, at \, r = R,$$
(21)
$$g \to g_{0} ,\quad h \to 0{\text{ as }}r \to \infty ,$$
(22)

where \((D_{G} ,\,D_{H} )\) are the coefficients of diffusion species \(G\) and \(H,\) respectively.

Under the following conversions

$$g = g_{0} l(\eta ), \, h = h_{0} m(\eta ),$$
(23)

Transformations of Eqs. (19)–(22) yield

$$\frac{(1 + 2\alpha \eta )}{Sc}l^{{\prime \prime }} + fl^{\prime } - k_{1} lm^{2} = 0,$$
(24)
$$\frac{{\lambda^{ * } (1 + 2\alpha \eta )}}{Sc}m^{{\prime \prime }} + fm^{\prime } + k_{1} lm^{2} = 0,$$
(25)
$$l^{\prime } (0) = k_{2} l(0),\, \, \lambda^{ * } m^{\prime } (0) = - k_{2} l(0),\,$$
(26)
$$l \to 1,\, \, m \to 0 \, as \, \eta \to \infty .$$
(27)

In the above equations, \(\lambda^{ * } \left( { = \tfrac{{D_{H} }}{{D_{G} }}} \right)\) is the ratio of the diffusion coefficient, \((k_{2} ,\,k_{1} )\) the measures of the strength of heterogeneous–homogeneous processes and \(Sc\left( { = \tfrac{\nu }{{D_{G} }}} \right)\) the Schmidt number.

According to assumption, the diffusion coefficients \(D_{G}\) and \(D_{H}\) are taken to be equivalent, i.e., \(\lambda^{ * } = 1,\) and we obtained

$$l(\eta ) + m(\eta ) = 1.$$
(28)

Thus, we have the following equation with boundary conditions

$$\frac{(1 + 2\alpha \eta )}{Sc}l^{{\prime \prime }} + fl^{\prime } - k_{1} (1 - l)^{2} l = 0,$$
(29)
$$l^{\prime } (0) = k_{2} l(0),\, \, l \to 1{\text{ as }}\eta \to \infty .$$
(30)

3 Physical interpretation

This crucial section is envisioned to visualize the stimulus of essential somatic parameters on velocity, temperature and concentration fields via homotopic approach. For this purpose, graph is portrayed and conferred in detail. Furthermore, Table 1 shows \(- f^{{\prime \prime }} (0)\) in limiting sense. This table contributes the assessment of up-to-date outcomes with the present prose with excellent agreement.

Table 1 An assessment value of \(- f^{{\prime \prime }} (0)\) for numerous values of \(\;\beta_{1}\) in limiting cases when \(\alpha = \beta_{2} = 0\)
Full size table

3.1 Velocity field

Figure 2a, b is plotted to clarify the features of Deborah numbers \(\beta_{1}\) and \(\beta_{2}\) on the velocity field. From these sketches, we noted that the liquid velocity displays the conflicting tendency for \(\beta_{1}\) and \(\beta_{2}\). The higher values of \(\beta_{1}\) specify that the stress relaxation is unhurried as related to the timescale scrutiny. This means that the liquid exhibits solid-like reaction when subjected to the applied stress, and hence, the liquid velocity declines for \(\beta_{1}\). It is also famed that the retardation time raises to the time required for the buildup of shear stress in a liquid. Therefore, it can be portrayed that the timescales are perceived throughout the start-up investigations that are not clarified by relaxation time. This shows that the liquid flow parallel to the sheet accelerates with an augmentation in liquid retardation time and hence the liquid velocity rises for \(\beta_{2}\). In addition, we can also detect that the thickness of the momentum boundary layer is higher for the case flow over a cylinder when associated flow over a flat plate.

Fig. 2
figure 2

Impact of Deborah numbers \(\beta_{1}\) and \(\beta_{2}\) on velocity field

Full size image

3.2 Temperature field

Figure 3a, b scrutinizes the impact of Deborah number \(\beta_{2}\) and temperature-dependent thermal conductivity \(\varepsilon\) on the temperature field. Increasing values of \(\beta_{2}\) and \(\varepsilon\) decline the temperature field for \(\beta_{2}\), while it enhances for \(\varepsilon\). It can be established that the depth of heat penetration decreases when liquid retardation time intensified which illustrates the reduction in liquid temperature for \(\beta_{2}\). Moreover, the thermal conductivity of liquid boosts up when we increase \(\varepsilon\). The higher thermal conductivity infers thicker the penetration depth and lesser the wall temperature gradient. Because of this circumstance, the liquid temperature of Oldroyd-B liquid is intensified.

Fig. 3
figure 3

Impact of Deborah numbers \(\beta_{2}\) and thermal conductivity parameter \(\varepsilon\) on temperature field

Full size image

The impact of progressive values of Prandtl number Pr and thermal relaxation time parameter \(\gamma\) is shown in Fig. 4a, b. Declining tendency of both the parameters for amassed values of Pr and \(\gamma\) is being noticed from these statistics. As an outcome, for advanced values of Prandtl number Pr we initiate a thinner thickness of the thermal boundary layer with better quality wall slope of temperature. Hence, the temperature field decreases. From Fig. 4b, similar outcomes are being identified for higher values of \(\gamma\). When we enlarges \(\gamma\), a non-conducting behavior of particles appears, which is liable to decline in the temperature field for both \(\alpha = 0\) (sheet) and \(\alpha \ne 0\) (cylinder).

Fig. 4
figure 4

Impact of Prandtl number Pr and thermal relaxation parameter \(\gamma\) on temperature field

Full size image

3.3 Concentration field

Figure 5a, b shows the stimulus of homogeneous–heterogeneous parameters \((k_{1} ,\,k_{2} )\) on concentration field for both cylinder and sheet cases. For escalation in these parameters exhibits conflicting drift on concentration field. It is exposed that the concentration decreases as the strength \(k_{1}\) of homogeneous response increases. It is also known that the concentration field is a diminishing function of the asset of heterogeneous response \(k_{2}\). Physically, the reactants are consumed through the homogeneous response which causes a decrease in the concentration field.

Fig. 5
figure 5

Impact of homogeneous response parameter \(k_{1}\) and heterogeneous response parameter \(k_{2}\) on concentration field

Full size image

Figure 6 shows the impact of higher value of Schmidt number \(Sc\) on concentration field. Augmenting behavior of concentration field is being detected for the progressive values of \(Sc\) on Oldroyd-B liquid. This is owing to the point that Schmidt number \(Sc\) is the proportion of momentum diffusivity to mass diffusivity and as an outcome advanced values of Schmidt number \(Sc\) resemble the lesser mass diffusivity. Hence, the concentration field decreases.

Fig. 6
figure 6

Impact of Schmidt number \(Sc\) on concentration field

Full size image

4 Concluding remarks

The analytical elucidations have been executed for the exploration of an Oldroyd-B liquid in the manifestation of Cattaneo–Christov heat conduction relation and chemical reactions. The temperature-dependent thermal conductivity is also presented. The current investigation demonstrated the following noteworthy facts:

  • It can be inferred that the liquid velocity exhibits conflicting tendency for augmented values of Deborah numbers \(\beta_{1}\) and \(\beta_{2}\).

  • The liquid temperature declines with increasing values of the thermal relaxation parameter \(\gamma\), while analogous impact is being noticed for the thermal conductivity parameter \(\varepsilon\).

  • The Schmidt number \(Sc\) and heterogeneous reaction parameter \(k_{2}\) enhances the concentration field, but the tendency of homogeneous reaction parameter \(k_{1}\) is quite reversed for the concentration of Oldroyd-B liquid.