1 Introduction

In today’s world, the ever-increasing consumption of energy demands preservation in its transportation and utilization. More specifically, nanotechnology is proved to be the best mean of heat transportation and preservation among the thermal sources. Thermo-physical properties of working liquid have a great impact on the efficiency of thermal systems. Nanofluids (NFs) are obtained by mixing solid nanoparticles (NPs) in the base liquids (BLs) which have considerably greater thermo-physical properties as compared with base liquids (BLs). The achieved NFs have distinct chemical and physical features than traditional BLs. Furthermore, NFs have vital role in the improvement of cooling rate with superior thermal efficiency. Khan and Khan [1] considered rheological properties of NPs for Oldroyd-B fluid with heat sink-source. Sheikholeslam et al. [2] studied the aspects of NPs for CuO–water NFs with Lorentz forces. Khan and Khan [3, 4] reported characteristics of non-Newtonian fluid in the presence of NPs. Waqas et al. [5] deliberated characteristics of non-Newtonian fluid with appliance of NPs. Khan et al. [6] analytically analyzed properties of 3D Burgers nanofluid (NF) by considering revised heat flux relation. Khan and Khan [7] investigated appliance of NPs for Burgers NFs in the presence of heat sink-source. Hayat et al. [8] analyzed Lorentz forces and porosity aspects to investigate appliance of NFs for exponentially stretched surface. Ahmad et al. [9] numerically analyzed features time-dependent Sisko NF. Khan et al. [10] described gyrotactic microorganisms for Burgers NF with appliance of NPs. Waqas et al. [11] numerically conveyed characteristics of Williamson fluid accounting Brownian moment and thermophoresis aspects. Khan et al. [12] scrutinized radiation and Lorentz force aspects on 3D Carreau NF utilizing zero flux relation at stretched surface. Waqas et al. [13] reported properties of heat sink-source and stratified flow for Oldroyd-B NF. Sohail et al. [14] considered properties of convectively heated surface for time-dependent second grade NF in the presence of Lorentz force and zero mass flux relation. Khan et al. [15] analytically investigated properties of NPs for generalized Burgers fluid with chemical phenomenon. Animasaun et al. [16] reported the appliance of thermoelectric and Lorentz force for CuO–water NF. Recent analysis on NFs subjected to distinct flow aspects is reported in Refs. [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

The bonding between the chemical components is loosening by catalysis. The catalytic reactions occur in both homogeneous/heterogeneous reactions. In homogeneous catalytic reaction system, both the catalytic materials lie in the same phase space like (gas, liquid or solid). However, in the heterogeneous process, the catalytic material lies in different phase space. Nowadays, there are wide applications of catalysts in industrial processes. More common examples that are in the agricultural and industrial process are fog formation, production of polymer, etc., when we need to start a binary chemical process, we require the minimum amount of energy, i.e., activation energy. The binary chemical process is a reaction process that occurs in two steps. Basically, the binary chemical reactions are common in both vapor and liquid deposition process. The mass transportation with chemical reaction and activation energy has industrial applications such as an oil reservoir, chemical engineering, oil emulsion, coating of metallic objects and glasses, manufacturing of electronic devices. Khan et al. [43, 44] reported properties of chemical process for non-Newtonian fluids. Mahanthesh et al. [45] considered aspects of Lorentz’s force and chemical processes for NF utilizing vertical plate. Characteristics of chemical processes and modified heat flux relation were deliberated by Sohail et al. [46]. Hayat et al. [47] described features of Lorentz’s force and chemical reactive species for third grade fluid. Irfan et al. [48] considered characteristics of variable conductivity and heat sink-source for non-Newtonian fluid with chemical processes. Khan et al. [49] characterized entropy generation and activation energy (AE) aspects for NF. Khan et al. [50] reported properties of AE and radiation for 3D flow of cross-NF with chemical processes. Waqas et al. [51] numerically analyzed properties of Darcy–Forchheimer and activation energy for NF in cylindrical surface. Khan et al. [52] reported appliance of chemical processes and radiative flow for cross-fluid.

Main objective of the present attempt is to examine aspects of infinite shear rate viscosity and entropy generation for magneto-mixed convective flow of cross-nanomaterial toward a stretched surface. Colloidal analysis for cross-fluid is scrutinized by considering Buongiorno relation. Transportation of heat-mass analysis is studied by utilizing activation energy and Brownian moment aspects. More specifically, aspects of viscous dissipation are considered here. System of PDE’s is transformed to one and then solved by implementing MATLAB tool bvp4c. Important physical quantities are discussed through tables and graphs.

2 Problem structure

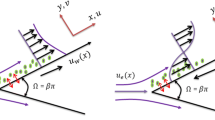
Here, characteristics of infinite hear rate viscosity and entropy optimization rate in mixed convective flow of cross-nanofluid are analyzed. Viscous dissipation activation energy aspects effects are accounted in mathematical formulation. More specifically, colloidal analysis of cross-nanofluid is permeated through Lorentz’s force aspects. Characteristics of thermophoresis and Brownian movement are accounted here. Governing equations for considered flow are

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = & \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] + \upsilon \left( {1 - \beta^{ * } } \right)\frac{\partial u}{\partial y}\frac{\partial }{\partial y}\left[ {\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] \\ & \quad - \frac{{\sigma^{ * } B_{0}^{2} }}{{\rho_{f} }}u + g\left[ {A_{1} \left( {T - T_{\infty } } \right) + A_{2} \left( {C - C_{\infty } } \right)} \right], \\ \end{aligned}$$
(2)
$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = & \frac{v}{{c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] + \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} \\ & \quad + \tau D_{\text{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} - \frac{1}{{(\rho c)_{f} }}\frac{{16\sigma^{ * * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}, \\ \end{aligned}$$
(3)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{\text{r}}^{2} \left( {C - C_{\infty } } \right)\left( {\frac{T}{{T_{\infty } }}} \right)^{m} \exp \left( { - \frac{{E_{\text{a}} }}{\kappa T}} \right),$$
(4)

with constraints

$$\begin{aligned} u = & U_{w} = cx ,\quad v = 0, - k\frac{\partial T}{\partial y} = h_{f} (T_{f} - T), \\ D_{\text{B}} \frac{\partial C}{\partial y} = & h_{\phi } (C - C_{\phi } )\quad {\text{at }}y = 0, \\ \end{aligned}$$
(5)
$$u \to 0 ,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \quad {\text{as }}y \to \infty .$$
(6)

Considering the following transformations

$$\begin{aligned} \eta = & y\sqrt {\frac{c}{v}} ,\quad v = - \sqrt {cv} f(\eta ),\quad u = cxf^{\prime } (\eta ) \\ \theta \left( \eta \right) = & \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\quad \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\phi } - C_{\infty } }}. \, \\ \end{aligned}$$
(7)

Conservation law of mass is verified identically, and remaining flow expressions become

$$\begin{aligned} & \left[ {\beta^{ * } \left\{ {1 + \left( {Wef^{\prime \prime } } \right)^{n} } \right\}^{2} + \left( {1 - \beta^{ * } } \right)\,\left\{ {1 + \left( {1 - n} \right)\,\left( {Wef^{\prime \prime } } \right)^{n} } \right\}} \right]f^{\prime \prime \prime } \\ & \quad - \left[ {1 + \left( {Wef^{\prime \prime } } \right)^{n} } \right]^{2} \left[ {f^{\prime 2} + ff^{\prime \prime } + \lambda \left( {\theta + Nr\phi } \right)} \right] = 0, \\ \end{aligned}$$
(8)
$$\left( {1 + \frac{4}{3}R} \right)\theta^{\prime \prime } + \mathop {Pr}\limits \left[ {f\theta^{\prime } + Nb\theta^{\prime } \phi^{\prime } + Nt\theta^{\prime 2} + Ecf^{\prime \prime 2} \beta^{ * } + \left( {1 - \beta^{ * } } \right)\frac{{Ecf^{\prime \prime 2} }}{{1 + \left( {Wef^{\prime \prime } } \right)^{n} }}} \right] = 0,$$
(9)
$$\phi^{\prime \prime } + Sc\left[ {f\phi^{\prime } + \frac{Nt}{Nb}\theta^{\prime \prime } - \sigma \left( {1 + \delta \theta } \right)^{m} \phi \exp \left( { - \frac{E}{1 + \delta \theta }} \right)} \right] = 0,$$
(10)
$$f\left( 0 \right) = 0,\quad f^{\prime } \left( 0 \right) - 1 = 0,\quad f^{\prime } \left( \infty \right) \to 0,$$
(11)
$$\left( 0 \right) = - \gamma_{1} [1 - \theta \left( 0 \right)],\quad \theta \left( \infty \right) \to 0,$$
(12)
$$\phi^{{^{\prime } }} \left( 0 \right) = - \gamma_{2} [1 - \phi \left( 0 \right)]\quad \phi \left( \infty \right) \to 0.$$
(13)

Non-dimensional form of variables occurring in Eqs. (8)–(13) is given below

$$\begin{aligned} M = & \frac{{\sigma^{ * } B_{0}^{2} }}{{\rho_{f} c}},\quad Nr = \frac{{gA_{2} \left( {C_{w} - C_{\infty } } \right)}}{{gA_{1} \left( {T_{w} - T_{\infty } } \right)}} = \frac{{Gr_{x}^{ * } }}{{Gr_{x} }},\quad \lambda = \frac{{gA_{1} \left( {T_{w} - T_{\infty } } \right)}}{{c^{2} x}} = \frac{{G_{rx} }}{{Re_{x}^{2} }}, \\ \mathop {Pr}\limits = & \frac{\nu }{\alpha },\quad R = \frac{{4\sigma^{ * * } T_{\infty }^{3} }}{{k_{f} m^{ * } }},\quad Nb = \frac{{\tau D_{B} \left( {C_{w} - C_{\infty } } \right)}}{\upsilon },\quad Nt = \frac{{\tau D_{\text{T}} \left( {T_{w} - T_{\infty } } \right)}}{{\nu T_{\infty } }},\quad \sigma = \frac{{kr^{2} }}{c}, \\ Ec = & \frac{{c^{2} x^{2} }}{{c_{p} \left( {T_{w} - T_{\infty } } \right)}},\quad We = \frac{\varGamma cx}{\nu },\quad Sc = \frac{\nu }{{D_{B} }},\quad E = \frac{{E_{\text{a}} }}{{\kappa T_{\infty } }},\quad \delta = \frac{{T_{w} - T_{\infty } }}{{T_{\infty } }},\quad \beta^{ * } = \frac{{\mu_{\infty } }}{{\mu_{0} }}. \\ \end{aligned}$$
(14)

3 Quantities of physical interest

In this section, we express surface drag force \(\left( {C_{fx} } \right)\) and heat/mass transfer rates \(\left( {Nu_{x} ,Sh_{x} } \right)\) in dimensional forms

$$C_{fx} = \frac{{\tau_{\text{w}} }}{{\rho U_{w}^{2} }},$$
(15)
$$Nu_{x} = \frac{{xq_{\text{w}} }}{{k\left( {T_{w} - T_{\infty } } \right)}},$$
(16)
$$Sh_{x} = \frac{{xj_{w} }}{{D_{\text{B}} \left( {C_{w} - C_{\infty } } \right)}},$$
(17)

where

$$\tau_{\text{w}} = \mu \frac{\partial u}{\partial y}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right],$$
(18)
$$q_{\text{w}} = - k\frac{\partial T}{\partial y},J_{\text{w}} = - D_{\text{B}} \frac{\partial C}{\partial y}.$$
(19)

From Eq. (15) to (17), one obtains

$$C_{fx} Re_{x}^{1/2} = \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + \left( {Wef^{\prime \prime } \left( 0 \right)} \right)^{n} }}} \right]\,f^{\prime \prime } \left( 0 \right),$$
(20)
$$Nu_{x} Re_{x}^{ - 1/2} = - \left[ {1 + \frac{4}{3}R} \right]\theta^{\prime } \left( 0 \right),Sh_{x} Re_{x}^{ - 1/2} = - \phi^{\prime } \left( 0 \right).$$
(21)

Where \(Re_{x} = \tfrac{{xU_{w} }}{\nu }.\)

4 Entropy generation

Here, dimensional form of entropy generation is expressed as

$$\begin{aligned} S_{G} = & \frac{{k_{f} }}{{T_{\infty }^{2} }}\left[ {1 + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k_{f} k^{ * } }}} \right]\left( {\frac{\partial T}{\partial y}} \right)^{2} + \frac{\mu }{{T_{\infty } }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right] \\ & \quad + \frac{{\sigma^{ * } B_{0}^{2} u^{2} }}{{T_{\infty } }} + \frac{{R_{D} }}{{C_{\infty } }}\left( {\frac{\partial C}{\partial y}} \right)^{2} + \frac{{R_{\text{D}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}} \right). \\ \end{aligned}$$
(22)

In dimensionless, one has

$$N_{\text{G}} = \alpha_{1} \left[ {1 + \frac{4}{3}R} \right]\theta^{\prime 2} + Br\left[ {\beta^{ * } + \frac{{\left( {1 - \beta^{ * } } \right)}}{{1 + \left( {Wef^{\prime \prime } } \right)^{n} }}} \right]\,f^{\prime \prime 2} + MBrf^{\prime 2} + \frac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{\prime 2} + L\theta^{\prime } \phi^{\prime } ,$$
(23)

where

$$Br = \frac{{\mu U_{w}^{2} }}{\kappa \;\Delta \;T},\quad \alpha_{1} = \frac{\Delta \;C}{{C_{\infty } }},\quad \alpha_{2} = \frac{\Delta \;T}{{T_{\infty } }},\quad N_{\text{G}} = \frac{{\nu T_{\infty } S_{G} }}{\kappa c\;\Delta \;T},\quad L = \frac{{R_{\text{D}} \left( {C_{w} - C} \right)}}{{k_{f} }}.$$
(24)

Mathematically, \(Be\) is defined as

$$Be = \frac{{{\text{Entropy}}\;{\text{generation}}\;{\text{subject}}\;{\text{to}}\;{\text{heat}}\;{\text{and}}\;{\text{mass}}\;{\text{transfer}}}}{{{\text{Total}}\;{\text{entropy}}\;{\text{generation}}}},$$
(25)
$$Be = \frac{{\alpha_{1} \,\theta^{\prime 2} + + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{\prime 2} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} }}{{\alpha_{1} \,\theta^{\prime 2} + Br\left[ {\beta^{ * } + \tfrac{{1 - \beta^{ * } }}{{1 + \left( {Wef^{\prime \prime } } \right)^{n} }}} \right]\,f^{\prime \prime 2} + MBrf^{\prime 2} + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{\prime 2} + L\theta^{\prime } \phi^{\prime } }}.$$
(26)

5 Graphical consequences and physical argument

Here, our objective is to analyze the consequences of sundry non-dimensional variables on velocity, temperature, concentration, surface drag force, entropy optimization rate, Bejan number and heat/mass transfer rate. System of nonhomogeneous ODEs Eq. (8)–(10), (23) and (26) subjected to conditions given in Eq. (11)–(13) is solved by using MATLAB tool bvp4c.

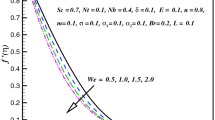
Figure 1 captures influence of \(We\) on \(f^{\prime } (\eta )\). Here, we noticed that for larger values of \(We\) the \(f^{\prime } (\eta )\) is decreased. Figure 2 depicts outcomes of \(Nr\) on velocity profile (\(f^{\prime } (\eta )\)). Clearly, \(f^{\prime } (\eta )\) enhances against \(Nr\). Figure 3 disclosed the effect of \(\lambda\) on velocity profile (\(f^{\prime } (\eta )\)). Here, one can note that \(f^{\prime } (\eta )\) is raised against \(\lambda\). In fact, buoyancy forces rise for larger \(\lambda\) due to which velocity of cross-liquid intensifies. Variation of velocity profile (\(f^{\prime } (\eta )\)) through magnetic parameter \(M\) is examined in Fig. 4. Obviously, \(f^{\prime } (\eta )\) decreased by \(M\). Lorentz force has direct relation with magnetic parameter \(M\). Thus, for higher values of \(M\), the Lorentz force enhances and consequently more resistance decays the fluid motion. Figure 5 shows aspects of \(\beta^{ * }\) on \(f^{\prime } (\eta )\). For higher estimation of \(\beta^{ * }\), the velocity of cross-nanofluid intensifies.

Fig. 1
figure 1

\(f^{\prime } (\eta )\) via \(We\)

Full size image
Fig. 2
figure 2

\(f^{\prime } (\eta )\) via \(Nr\)

Full size image
Fig. 3
figure 3

\(f^{\prime } (\eta )\) via \(\lambda\)

Full size image
Fig. 4
figure 4

\(f^{\prime } (\eta )\) via M

Full size image
Fig. 5
figure 5

\(f^{\prime } (\eta )\) via \(\beta^{ \cdot }\)

Full size image

Behaviors of \(Ec\) (Eckert number), Pr (Prandtl number), \(Nt\) (thermophoresis parameter) \(R\) (radiation parameter) and \(\beta^{ * }\) (ratio of the infinite shear rate viscosity to the zero shear rate viscosity) on \(\theta (\eta )\) are sketched in Figs. 6, 7, 8, 9 and 10. Figure 6 addresses the \(Ec\) impact on \(\theta (\eta )\). Clearly, cross-nanoliquid thermal field remarkably enhances via \(Ec\). In fact, \(Ec\) is the ratio between KE (kinetic energy) and enthalpy difference. Consequently, larger \(Ec\) generates more resistance in liquid motion and therefore \(\theta (\eta )\) intensifies. Figure 7 shows the behaviors of \(Pr\) on \(\theta (\eta )\). It is perceived that \(\theta (\eta )\) declined for lager Pr. Physically, thermal diffusivity deteriorates for large Pr and consequently, \(\theta (\eta )\) decreases. Aspects of \(Nt\) on \(\theta (\eta )\) are shown in Fig. 8. An increase in \(Nt\) leads to an enhancement in \(\theta (\eta )\). Physically, reason behind this trend of \(Nt\) is the gap between reference and surface temperature. For larger \(Nt\), this gap rises and consequently the kinetic energy of nanoparticles enhances. So, \(\theta (\eta )\) intensifies. \(\theta (\eta )\) is raised against \(R\). These features are reported in Fig. 9. Effect of \(\gamma_{1}\) on \(\theta (\eta )\) is depicted in Fig. 10. It can be seen from Fig. 10 that \(\theta (\eta )\) intensifies via \(\gamma_{1}\). Physical reason behind this trend of γ is that less resistance is faced by the thermal wall which causes an enhancement in convective heat transfer to the fluid.

Fig. 6
figure 6

\(\theta (\eta )\) via \(Ec\)

Full size image
Fig. 7
figure 7

\(\theta (\eta )\) via \(Pr\)

Full size image
Fig. 8
figure 8

\(\theta (\eta )\) via \(Nt\)

Full size image
Fig. 9
figure 9

\(\theta (\eta )\) via \(R\)

Full size image
Fig. 10
figure 10

\(\theta (\eta )\) via \(\gamma_{1}\)

Full size image

Rheological properties of \(Sc\) (Schmidt number), \(\gamma_{2}\) (concentration Biot number), \(\sigma\) (dimensionless reaction rate), \(N_{\text{t}}\) (thermophoresis parameter), \(N_{\text{b}}\) (Brownian motion parameter) on concentration \(\phi (\eta )\) are explored in Figs. 11, 12, 13, 14 and 15. Figure 11 captures influence of \(\gamma_{2}\) on \(\phi (\eta )\). Here, we noted that for larger values of \(\gamma_{2}\) the \(\phi (\eta )\) is augmented. Figure 12 describes the influence of \(\sigma\) on \(\phi (\eta )\). Concentration \(\phi (\eta )\) deteriorates via \(\sigma\). Figures 13 and 14 demonstrate the behavior of \(N_{\text{t}}\) and \(N_{\text{b}}\) on concentration \(\phi (\eta )\). Concentration of cross-nanoliquid \(\phi (\eta )\) is enhanced with larger \(N_{\text{t}}\), while \(\phi (\eta )\) declines for greater \(N_{\text{b}}\). In fact, when we rise \(N_{\text{t}}\) gap of temperature between surface and at infinity intensifies due to which nanofluid moves from higher temperature to lower temperature. Consequently, \(\phi (\eta )\) intensifies. Effects of \(Sc\) on \(\phi (\eta )\) are reported in Fig. 15. Clearly, \(\phi (\eta )\) deteriorates via larger \(Sc\).

Fig. 11
figure 11

\(\phi (\eta )\) via \(\gamma_{2}\)

Full size image
Fig. 12
figure 12

\(\phi (\eta )\) via \(\sigma\)

Full size image
Fig. 13
figure 13

\(\phi (\eta )\) via \(Nt\)

Full size image
Fig. 14
figure 14

\(\phi (\eta )\) via \(N_{b}\)

Full size image
Fig. 15
figure 15

\(\phi (\eta )\) via \(Sc\)

Full size image

Variations of \(N_{\text{G}}\) (entropy generation) and Bejan number \(\left( {Be} \right)\) through \(Br\) (Brinkman number), \(L\) (diffusive variable), \(M\) (magnetic parameter), \(\alpha_{1}\) (dimensionless concentration ratio variable), \(\alpha_{2}\)(dimensionless temperature ratio variable) and \(R\) (thermal radiation parameter) are presented through Figs. 16, 17, 18, 19, 20, 21, 22, 23, 24. Figures 16 and 17 examined the characteristics of \(Br\) on \(N_{\text{G}}\) and \(Be\). Clearly, \(N_{\text{G}}\) are boosted via larger \(Be\), while \(Be\) declines for greater \(Be\). Physically, greater \(Br\) provides low thermal conduction to nanofluid and consequently, \(N_{\text{G}}\) intensifies for larger \(Br\). Outcomes of \(L\) (diffusive variable) on \(N_{\text{G}}\) are disclosed in Fig. 18. \(N_{\text{G}}\) declines for higher values of \(L\). Figures 19 and 20 depict outcomes of \(M\) (magnetic parameter) on \(N_{\text{G}}\) (entropy generation) and \(Be\) (Bejan number). Clearly, \(N_{\text{G}}\) boosts against \(M\), while \(Be\) deteriorates for \(M\). Greater estimation of \(M\) (magnetic parameter) offers more resistance to the motion of fluid in system and therefore, heat in the system intensifies. Consequently, entropy rate rises. Impact of \(\alpha_{1}\) (dimensionless concentration ratio variable) and \(\alpha_{2}\)(dimensionless temperature ratio variable) on entropy rate \(N_{\text{G}}\) is presented in Figs. 21 and 22. Here, \(N_{\text{G}}\) is an increasing function of \(\alpha_{1}\) and \(\alpha_{2}\). Figures 23 and 24 report the impact of \(R\) (thermal radiation parameter) on \(N_{\text{G}}\) and \(Be\). Clearly, \(N_{\text{G}}\) shows rising trend for \(R\), while opposite trend is detected for \(Be\). In fact, rise in \(R\) produces greater inertial force, so viscous force deteriorates and therefore the entropy rate intensifies.

Fig. 16
figure 16

\(N_{\text{G}} (\eta )\) via \(Br\)

Full size image
Fig. 17
figure 17

\(Be(\eta )\) via \(Br\)

Full size image
Fig. 18
figure 18

\(N_{\text{G}} (\eta )\) via \(L\)

Full size image
Fig. 19
figure 19

\(N_{\text{G}} (\eta )\) via M

Full size image
Fig. 20
figure 20

\(Be(\eta )\) via M

Full size image
Fig. 21
figure 21

\(N_{\text{G}} (\eta )\) via \(\alpha_{1}\)

Full size image
Fig. 22
figure 22

\(N_{\text{G}} (\eta )\) via \(\alpha_{2}\)

Full size image
Fig. 23
figure 23

\(N_{\text{G}} (\eta )\) via \(R\)

Full size image
Fig. 24
figure 24

\(Be(\eta )\) via \(R\)

Full size image

Features for \(n\) (Power law index), \(M\) (magnetic parameter), \(Ec\) (Eckert number), \(Pr\)(Prandtl number), \(N_{r}\) (buoyancy ratio parameter), \(N_{\text{t}}\) (thermophoresis parameter) \(R\) (radiation parameter) and \(\beta^{ * }\) (ratio of the infinite shear rate viscosity to the zero shear rate viscosity) on skin friction \(\left( {Re^{1/2} C_{fx} } \right)\) Nusselt and number \(\left( {Nu_{x} Re_{x}^{ - 1/2} } \right)\) are computed in Tables 1 and 2. Here, we observed that surface drag force boosts via larger \(We\) and \(M\), whereas it declines for larger \(\lambda ,\) \(n\) and \(\beta^{ * }\). Table 2 is prepared to point out aspects of numerous physical parameters on \(\left( {Nu_{x} Re_{x}^{ - 1/2} } \right)\). It is scrutinized that transportation rate of heat intensifies via larger \(Pr\), whereas it decays for larger \(Ec,\)\(N_{\text{t}}\) and \(N_{\text{b}}\).

Table 1 Surface drag force \(\left( {Re^{1/2} C_{fx} } \right)\) via different estimation of physical parameters
Full size table
Table 2 Computational outcomes for rate of heat transfer (\(Re^{ - 1/2} Nu\))
Full size table

6 Concluding remarks

We have the following significant observations.

  • Lorentz’s force for cross-nanoliquid is used as resistive force which controls the liquid motion.

  • Velocity is increasing function of \(\beta^{*}\).

  • Temperature \(\theta (\eta )\) intensifies via \(N_{\text{t}}\) and \(N_{\text{b}}\), while it is reduced with Pr.

  • Enhancement in \(\phi (\eta )\) (Concentration) occurs for augmented values of \(E\) (activation energy).

  • \(N_{\text{G}}\) (rate of entropy generation) boosts for larger \(Br\) (Brinkman number), \(M\) (magnetic parameter), \(\alpha_{1}\) (dimensionless concentration ratio variable), \(\alpha_{2}\)(dimensionless temperature ratio variable) and \(R\) (thermal radiation parameter); however, it decayed via larger \(L\) (diffusive variable).

  • Bejan number \(\left( {Be} \right)\) rises for greater estimation of \(R\) (thermal radiation parameter), while it deteriorates for \(Br\) (Brinkman number).