Behavior of stratifications and convective phenomena in mixed convection flow of 3D Carreau nanofluid with radiative heat flux

Abstract

Nanoliquids, the engineered liquids with isolated effectual nanoparticles have disclosed a surprising thermo-physical effects and added functionalities and therefore have supported an extensive sort of essential applications. In particular, nanoliquids have displayed pointedly improved aptitude of heat transfer as equated to traditional functioning liquids. The notable intention of current scrutiny is to explore the features of combined convective and stratification phenomena by utilizing Brownian and thermophoresis nanoparticles on 3D mixed convection flow of magnetite Carreau fluid influenced by a bidirectional stretching surface. The heat transport phenomenon is also betrothed in the manifestation of thermal radiation and the heat sink/source. By means of suitable conversions the nonlinear PDEs transformed into nonlinear ODEs. To identify the behavior of numerous somatic parameters, numerically bvp4c tactic has been worked to elucidate the governing ODEs. The graphical depiction is delineated and tables are organized for diverse physical parameters on Carreau nanofluid. It is scrutinized that the impact of magnetic parameter on both the velocity components is analogous and diminishes both the velocities for shear thinning/thickening liquids. Moreover, the present exploration reports that the mixed convection and thermal stratification parameters decline the liquid temperature and allied thickness of the thermal boundary layer for both shear thickening/thinning liquids.

1 Introduction

Energy disaster instigated by the hurried world population and engineering progression in addition to the rapid expansion of the society intensifies gradually and might develop a humanitarian disaster in worldwide. Solar energy has been demanded as the energy of our forthcoming, but approaches with many experiments to overcome, for instance, the high cost and the low proficiency. Solar thermal structure, which usually has a fascinating plate with liquid running inside the pipes, is a communal approach of consuming solar energy. Its competence is partial by not only how competently the solar energy is caught by the fascinating plate, but also how effectually the fascinated energy is transported to the running liquid. Solar energy is the utmost essential renewable cause of energy to produce heat and electrical energy. Countless solar constructed thermal structures are used for producing water distillation, heating of water from solar radiation, electricity and structures air-conditioning. Moreover, the enhancing process of heat transfer in solar energy structures is solitary of the utmost crucial subjects to attain an enhanced enactment of these structures with dense strategies. This might be attained by means of functioning liquids with boosted thermo-physical chattels. One of the operative approaches is to substitute the functioning liquid with nanoliquids as an innovative approach to develop the heat transfer features of the liquid.

In current spans, the rapid expansion in engineering and thermal industrial progressions necessitates additional dense and proficient heat transport structures. In these structures, fluids are utilized as cooling instrument. Owing to lesser in thermal conductivity, these liquids critically disturb the amount of heat transport or cooling progression. It was a thought-provoking assignment to heighten the liquid thermal conductivity for scientists and investigators. Here originates the notion of nanofluids. Nanofluids are as innovative novelty, which was first proposed by Choi [1]. The deferral of nonmetallic and metallic nanoparticles in base liquids like aquatic and paraffin is known as nanofluid. They exhibit boosted thermo-physical assets, equated to base liquids. The manifestation of nanomaterials in the base liquids provides an enhanced flow of fraternization and sophisticated thermal conductivity equated to purify liquids. There are numerous norms with nanotechnology in industrial-related diligences. This innovative expertise is frequently exploited in the creation of nanochips, chilling of microchip technology, lorries apparatus, exchange making, medication distribution, etc. Additionally, the thermal assets of nanoliquids are the assets which are very essential to nanofluids enactment. These are the liquid thermal conductivity, viscosity, specific heat and heat transfer coefficient, respectively. Thermal recital of solar collectors is essentially being contingent on how thermal assets perform in diverse functioning circumstances. Some of the current reports in these trends can be quantified via refs. [2,3,4,5,6,7,8,9,10,11,12]. The impact of thermal energy and melting heat on radiative flow of carbon–water nanofluid was scrutinized numerically by Hayat et al. [13] by seeing the stagnation point effect. Irfan et al. [14] explored numerically the properties of shear thinning/thickening liquids on 3D Carreau nanofluid flow with the influence of heat sink/source and temperature-dependent thermal conductivity. They inspected that the tendency of unsteadiness and thermal conductivity parameters were quite conflicted for both shear thickening/thinning liquids on temperature and concentration fields. The heat transport phenomenon on unsteady Carreau magneto nanofluid towards the cone packed with alloy nanomaterials was discussed Raju et al. [15]. They reported that the heat transfer amount heightened for the viscous variation parameter. Recently, Hayat et al. [16] investigated fluid flow of magneto nanoliquid subject to nonlinear stretched surface. They analyzed that the pressure and velocity fields decline for power law index. The convective and activation energy phenomena on the flow of nanofluid with the properties of chemical reaction were explored by Zeeshan et al. [17]. The behavior of variable conductivity in Eyring and Carreau fluids with nickel and dust nanoparticles was scrutinized by Upadhya et al. [18].

Recently, the mixed convection transport of non-Newtonian liquids via thermal and solute stratifications is a subject of abundant scrutiny owing to their widespread manifestation in the engineering and industrial progressions. The heat dismissal into the atmosphere, for instance, streams, oceans and ponds, and thermal energy-storing structures like astrophysical pools are the numerous specimens of such solicitations. Stratification of liquid is a deposition or establishment of layers that happens because of temperature changes, concentration variation or owing to the manifestation of diverse liquids. It is fascinating to scrutinize the impact of double stratification when both heat and mass transfer are existing instantaneously. Moreover, in the manifestation of gravity the density dissimilarities have a strategic role in the mixing of heterogeneous liquid and dynamics. For instance, thermal stratification in pools can condense the fraternization of oxygen to the lowest water to become anxious through the achievement of organic progressions. Similarly, the scrutiny of thermal stratification is essential for the solar industry as greater energy competence can be attained with enhanced stratification. The mixed convection thermally stratified flow along a stretched cylinder was scrutinized by Mukhopadhyay and Ishak [19]. The stimulus of chemically reacting flow and mixed convective on nanoliquid toward the moving surface was analyzed by Mahantesh et al. [20]. Imtiaz et al. [21] considered the effects of mixed convection and convective phenomena on Casson nanofluid due to stretched cylinder. They examined that for larger Casson liquid and magnetic parameters decline the liquid flow. Waqas et al. [22] explored the mutual effects of thermal and mass stratification on mixed convection Oldroyd-B nanoliquid. They reported that the higher thermal and solutal stratified causes decline the temperature and concentration field, respectively. Moreover, current endeavors on mixed convection as well as double stratifications via diverse thoughtfulness can be referred through refs. [23,24,25,26].

In numerous applications, non-Newtonian materials have sizeable worth throughout the earliest limited spans. In these materials, there is no linear correlation between stress tensor and deformation. The remarkable features of these liquids are their advanced apparent viscosities; therefore, laminar flow circumstances intensify considerably compared to Newtonian liquids. The applications correlated to biological progressions, geophysics and genetic disciplines comprise non-Newtonian ingredients. These materials, for instance, bubbles, colloidal and deferral elucidations, adhesives, stone undercoat and soap suds are nonlinear materials. Numerous researchers have functioned with diverse non-Newtonian liquids which can be seen in refs. [27,28,29,30,31,32,33,34].

In this scrutiny, numerical elucidations are established for 3D radiative flow of a magnetite Carreau nanofluid subject to combined phenomena of convective and stratification influenced by stretching surface. The impact of the heat sink/source is also considered. A compatible conversion changed the PDEs into ODEs and then elucidated numerically by bvp4c to scrutinize the features of physical parameters. Graphs are structured and tables are established and conferred it details.

2 Physical model and constitutive relation

2.1 Rheological models

This study scrutinized Carreau fluid model which is a generalized Newtonian liquid that describes the properties of shear thinning/thickening liquids. The Cauchy stress tensor for the Carreau fluid model is stated as [35,36,37,38]:

$${\mathbf{S}}^{ * } {\mathbf{ = - }}p{\mathbf{I + }}\mu (\mathop \gamma \limits^{ \cdot } ){\mathbf{A}}_{1} ,$$

(1)

with

$$\mu (\dot{\gamma }) = \mu_{\infty } + (\mu_{0} - \mu_{\infty } )[1 + (\varGamma \dot{\gamma })^{2} ]^{{\tfrac{n - 1}{2}}} ,$$

(2)

where $(p$, ${\mathbf{I}}$, $\varGamma ,$ $n,$ $\mu_{0,}$ $\mu_{\infty } )$ are the pressure, identity tensor, material time constant, power law index, zero-shear rate and infinity shear rate viscosities, respectively.

Furthermore, the shear rate and first Rivlin–Ericksen tensor $A_{1}$ is defined as:

$$\dot{\gamma } = \sqrt {\frac{1}{2}tr({\mathbf{A}}_{1}^{2} )} ,\quad {\mathbf{A}}_{1} = {\mathbf{\nabla V}} + ({\mathbf{\nabla V}})^{T} .$$

(3)

We consider the most useful conditions, i.e., $\mu_{0} > > \mu_{\infty }$ and $\mu_{\infty } = 0$. Thus, in view of Eqs. (2), (1) reduces to following form  we have

$${\mathbf{S}}^{ * } {\mathbf{ = - }}p{\mathbf{I + }}\mu_{0} [1 + (\varGamma \dot{\gamma })^{2} ]^{{\tfrac{n - 1}{2}}} {\mathbf{A}}_{1} .$$

(4)

Furthermore, for $n > 1$ this model describes the effects of shear thickening fluid, while for $0 < n < 1$ the effects of shear thinning fluid are attained.

For incompressible 3D fluid flow, the velocity, temperature, concentration and the Cauchy stress tensor are assumed to be:

$${\mathbf{V}} = [u(x,y,z),\;v(x,y,z),\;w(x,y,z)],\quad T = T(x,y,z),\quad C = C(x,y,z),\quad {\mathbf{S}}^{ * } {\mathbf{ = S}}^{ * } (x,y,z).$$

(5)

Here $(u,\,v,\,w)$ are the velocity components in x-, y- and z-directions.

2.2 Governing equations

The constitutive equations for incompressible 3D time-independent flow of Carreau fluid [37] in vectorial form are represented as:

$${\text{div}}\;{\mathbf{V}} = 0,$$

(6)

$$\rho_{{f}} ({\mathbf{V}} \cdot {\mathbf{\nabla }}) = {\mathbf{\nabla }} \cdot {\mathbf{S}}^{ * } ,$$

(7)

where $\rho_{{f}}$ is the fluid density.

Utilizing Eq. (5) in Eqs. (6) and (7), having in mind Eqs. (3) and (4), a lengthy but forthright scheme gives the following boundary layer equation as follows:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,$$

(8)

$$\begin{aligned} & u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = - \frac{1}{{\rho_{f} }}\frac{\partial p}{\partial x} + \nu \frac{{\partial^{2} u}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ & \quad + \,\nu \left( {\frac{\partial u}{\partial z}} \right)\frac{\partial }{\partial z}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{^{{\tfrac{n - 1}{2}}} }} , \\ \end{aligned}$$

(9)

$$\begin{aligned} & u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = - \frac{1}{{\rho_{{f}} }}\frac{\partial p}{\partial y} + \nu \frac{{\partial^{2} v}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ & \quad + {\kern 1pt} \,\nu \left( {\frac{\partial v}{\partial z}} \right)\frac{\partial }{\partial z}\left[ {1 + \varGamma^{2} \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} , \\ \end{aligned}$$

(10)

$$0 = - \frac{1}{{\rho_{{f}} }}\frac{\partial p}{\partial z},$$

(11)

where $\nu$ is the kinematic viscosity.

3 Problem Formulation

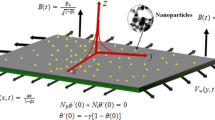
We scrutinize the steady 3D mixed convection flow of a Carreau magnetite nanofluid over a bidirectional stretched surface. The influence of combined stratification and convective conditions is engaged in heat and mass transfer phenomena. Additionally, thermal radiation and the heat sink/source are deliberated. The Brownian motion and thermophoresis nanoparticles are also betrothed in this study. The flow is persuaded by stretching the surface in two nearby x- and y-directions with linear velocity $(u,v) = (ax,by)$, respectively, where a, b > 0 and the fluid overcomes the region z > 0. Furthermore, it is also supposed that the electric and magnetic fields are negligible when we equated with applied magnetic field (as depicted in Fig. 1). This notion is only effective when the magnetic Reynolds number is small.

Fig. 1

Flow configuration

Under these attentions, the governing problem of magnetite Carreau nanofluid is:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,$$

(12)

$$\begin{aligned} & u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = \nu \frac{{\partial^{2} u}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ & \quad + \,\nu (n - 1)\varGamma^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} \\ & \quad - \frac{{\sigma B_{0}^{2} }}{{\rho_{{f}} }}u + g[\beta_{T} (T - T_{\infty } ) + \beta_{C} (C - C_{\infty } )], \\ \end{aligned}$$

(13)

$$\begin{aligned} & u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = \nu \frac{{\partial^{2} v}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ & \quad + \,\nu (n - 1)\varGamma^{2} \left( {\frac{\partial v}{\partial z}} \right)^{2} \frac{{\partial^{2} v}}{{\partial z^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} - \frac{{\sigma B_{0}^{2} }}{{\rho_{{f}} }}v, \\ \end{aligned}$$

(14)

$$\begin{aligned} & u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = \alpha_{1} \frac{{\partial^{2} T}}{{\partial z^{2} }} + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial z}\frac{\partial T}{\partial z} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right] \\ & \quad - \frac{1}{{(\rho c)_{{f}} }}\frac{{\partial q_{r} }}{\partial z} + \frac{{Q_{0} }}{{(\rho c)_{{f}} }}(T - T_{\infty } ), \\ \end{aligned}$$

(15)

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} + w\frac{\partial C}{\partial z} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }}.$$

(16)

Subject to the boundary conditions:

$$\begin{aligned} & u = U_{w} (x) = ax,\;v = V_{w} (y) = {\text{by}},\;w = 0, \\ & \quad - k\frac{\partial T}{\partial z} = h_{{f}} [T_{{f}} - T],\; - D_{\text{B}} \frac{\partial C}{\partial z} = h_{m} [C_{f} - C]\;{\text{at}}\;z = 0, \\ \end{aligned}$$

(17)

$$u \to 0,\;v \to 0,\;T \to T_{\infty } ,\;C \to C_{\infty } \;{\text{as}}\;z \to \infty .$$

(18)

Where $B_{0}$ is the strength of magnetic field, $\sigma$ the electrical conductivity, $g$ the gravitational acceleration, $\left( {\beta_{\text{T}} ,\beta_{\text{C}} } \right)$ the coefficients of thermal and concentration expansion, respectively, (T, C) the nanoliquid temperature and volume friction, $\alpha_{1}$ the thermal diffusivity of liquid, $k$ thermal conductivity of fluid, $(\rho_{{f}} ,c_{{f}} )$ the liquid density and specific heat, respectively, $\;\tau$ the ratio of effective heat capacity of nanoparticles to heat capacity of the base liquid, $Q_{0}$ the heat sink/source coefficient, $(D_{\text{B}} ,D_{\text{T}} )$ the Brownian and thermal diffusion coefficients, respectively. Furthermore, $(h_{f} ,h_{m} )$ are the variable wall heat and variable wall mass transfer coefficients, respectively, $(T_{{f}} ,C_{{f}} ) = (T_{0} + {\text{d}}x,C_{0} + ex)$ the heated liquid temperature and concentration, respectively, $(T_{\infty } ,C_{\infty } ) = (T_{0} + d_{1} x,C_{0} + e_{1} x)$ the ambient temperature and concentration, respectively, in which $(T_{0} ,\,C_{0} )$ the reference temperature and concentration, respectively, $(d,\,d_{1} ,\,e,\,e_{1} )$ the dimensionless constants and $q_{r}$ the radiative heat flux which is defined as

$$q_{r} = \frac{{ - 16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{\partial T}{\partial z},$$

(19)

in which $(\sigma^{ * } ,k^{ * } )$ are the Stefan–Boltzmann constant and mean absorption coefficient, respectively.

3.1 Appropriate conversions

$$\begin{aligned} & u = axf^{\prime}(\eta ),\;v = ayg^{\prime}(\eta ),\;w = - \sqrt {a\nu } [f(\eta ) + g(\eta )], \\ & \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{{f}} - T_{0} }},\;\varphi = \frac{{C - C_{\infty } }}{{C_{{f}} - C_{0} }}\;, \eta = z\sqrt {\frac{a}{\nu }} . \\ \end{aligned}$$

(20)

In vision of above conversions, Eq. (12) is satisfied automatically and Eqs. (13–18) are reduced to the following ODEs:

$$f^{\prime\prime\prime}\left[ {1 + We_{1}^{2} f^{\prime \prime 2} } \right]^{{\tfrac{n - 3}{2}}} \left[ {1 + nWe_{1}^{2} f^{\prime \prime 2} } \right] - f^{\prime 2} + f^{\prime\prime}(f + g) - M^{2} f^{\prime} + \lambda^{ * } (\theta + N^{ * } \varphi ) = 0,$$

(21)

$$g^{\prime\prime\prime}\left[ {1 + We_{2}^{2} g^{\prime \prime 2} } \right]^{{\tfrac{n - 3}{2}}} \left[ {1 + nWe_{2}^{2} g^{\prime \prime 2} } \right] - g^{\prime 2} + g^{\prime\prime}(f + g) - M^{2} g^{\prime} = 0,$$

(22)

$$\left( {1 + \frac{4}{3}R} \right)\theta^{\prime\prime} + \mathop {Pr}\limits (f + g)\theta^{\prime} - \mathop {Pr}\limits f^{\prime}\theta - \mathop {Pr}\limits S_{1} f^{\prime} + \mathop {Pr}\limits \left[ {N_{b} \theta^{\prime}\varphi^{\prime} + N_{t} \theta^{\prime 2} + \delta \theta } \right] = 0,$$

(23)

$$\varphi^{\prime\prime} + \mathop {Pr}\limits Le(f + g)\varphi^{\prime} - \mathop {Pr}\limits Lef^{\prime}\varphi - \mathop {Pr}\limits LeS_{2} f^{\prime} + \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\,\theta^{\prime\prime} = 0,$$

(24)

$$\begin{aligned} f(0) & = 0,\;g(0) = 0,\; \, f^{\prime}(0) = 1,\;g^{\prime}(0) = \alpha , \\ \theta^{\prime}(0) & = - \gamma_{1} (1 - S_{1} - \theta (0))\;, \varphi^{\prime}(0) = - \gamma_{2} (1 - S_{2} - \varphi (0)), \\ \end{aligned}$$

(25)

$$\, f^{\prime} \to 0,\; \, g^{\prime} \to 0,\;\theta \to 0\;, \varphi \to 0\;{\text{as}}\;\eta \to \infty .$$

(26)

Here $\left( {We_{1} ,\,We_{2} } \right)\,\left( { = \sqrt {\tfrac{{\varGamma^{2} aU_{w}^{2} }}{\nu }} ,\,\sqrt {\tfrac{{\varGamma^{2} aV_{w}^{2} }}{\nu }} } \right)$ are the local Weissenberg numbers, $M\left( { = \sqrt {\tfrac{{\sigma B_{0}^{2} }}{{a\rho_{{f}} }}} } \right)$ the magnetic parameter, $\lambda^{ * } \left( { = \tfrac{{g\beta_{{T}} d}}{{a^{2} }}} \right)$ the mixed convection parameter, $N^{ * } \left( { = \tfrac{{\beta_{{C}} .e}}{{\beta_{{T}} d}}} \right)$ the buoyancy ratio parameter, $R_{d} \left( { = \tfrac{{4\sigma^{ * } T_{\infty }^{3} }}{{3kk^{ * } }}} \right)$ the thermal radiation parameter, $N_{b} \left( { = \tfrac{{\tau D_{\text{B}} (C_{{f}} - C_{0} )}}{\nu }} \right)$ the Brownian motion parameter, $N_{t} \left( { = \tfrac{{D_{\text{T}} (T_{{f}} - T_{0} )}}{{\nu T_{0 } }}} \right)$ the thermophoresis parameter, $Pr\left( { = \tfrac{\nu }{{\alpha_{1} }}} \right)$ the Prandtl number, $\delta \left( { = \tfrac{{Q_{0} }}{{a(\rho c)_{{f}} }}} \right)$ the heat source $(\delta > 0)$ and heat sink $(\delta < 0)$ parameter, $Le( = \tfrac{{\alpha_{1} }}{{D_{\text{B}} }})$ the Lewis number, $\alpha \left( { = \tfrac{b}{a}} \right)$ the ratio of stretching rates parameter, $\left( {\gamma_{1} ,\gamma_{2} } \right)\;\left( { = \tfrac{{h_{{f}} }}{k}\sqrt {\tfrac{\nu }{a }} ,\;\tfrac{{h_{m} }}{{D_{{B}} }}\sqrt {\tfrac{\nu }{a }} } \right)$ the thermal and concentration Biot numbers, respectively and $\left( {S_{1} ,\,S_{2} } \right)\,\left( { = \tfrac{{d_{1} }}{d},\,\tfrac{{e_{1} }}{e}} \right)$ the thermal and mass stratification parameters, respectively.

4 Physical quantities

From the industrial and engineering point of view, the essential quantities of physical interest are the skin friction, heat and transfer coefficients which may be defined by the subsequent expression:

$$C_{{fx}} = \frac{{\tau_{{xz}} }}{{\tfrac{1}{2}\rho_{f} U_{w}^{2} }} ,\quad C_{{fy}} = \frac{{\tau_{{yz}} }}{{\tfrac{1}{2}\rho_{{f}} U_{w}^{2} }},$$

(27)

$$Nu_{x} = \left( { - \frac{x}{{\left( {T_{{f}} - T_{\infty } } \right)}} + \frac{{xq_{r} }}{{k\left( {T_{{f}} - T_{\infty } } \right)}}} \right)\left. {\frac{\partial T}{\partial z}} \right|_{z = 0} ,\quad Sh_{x} = - \frac{x}{{\left( {C_{{f}} - C_{\infty } } \right)}}\left. {\frac{\partial C}{\partial z}} \right|_{z = 0} .$$

(28)

The above quantity is in the dimensionless forms:

$$\frac{1}{2}C_{{fx}} Re_{x}^{{\tfrac{1}{2}}} = f^{\prime\prime}(0)\left[ {1 + We_{1}^{2} f^{\prime \prime 2} (0)} \right]^{{\tfrac{n - 1}{2}}} ,\;\frac{1}{2}\left( {\frac{{U_{w} }}{{V_{w} }}} \right)C_{{fy}} Re_{x}^{{\tfrac{1}{2}}} = g^{\prime\prime}(0)\left[ {1 + We_{2}^{2} g^{\prime \prime 2} (0)} \right]^{{\tfrac{n - 1}{2}}} ,$$

(29)

$$Re_{x}^{{ - \tfrac{1}{2}}} Nu_{x} = \frac{{ - \left( {1 + \tfrac{4R}{3}} \right)\theta^{\prime}\left( 0 \right)}}{{1 - S_{1} }},\quad Re_{x}^{{ - \tfrac{1}{2}}} Sh_{x} = - \left( {\frac{1}{{1 - S_{2} }}} \right)\varphi^{\prime}(0),$$

(30)

in which $Re_{x} = \tfrac{{ax^{2} }}{\nu }$ is local Reynolds number.

5 Computational scheme

The nonlinear ODEs (21–24) with boundary conditions (25) and (26) are elucidated numerically via bvp4c scheme. Numerical elucidations of these equations are acquired by switching the governing problem into first-order differential structure.

$$f = y_{1} ,\;f^{\prime} = y_{2} ,\;f^{\prime\prime} = y_{3} ,\; \, f^{\prime\prime\prime} = yy_{1} ,$$

(31)

$$g = y_{4} ,\;g^{\prime} = y_{5} ,\;g^{\prime\prime} = y_{6} ,\;g^{\prime\prime\prime} = yy_{2} ,$$

(32)

$$\theta = y_{7} ,\;\theta^{\prime} = y_{8} ,\;\theta^{\prime\prime} = yy_{3} ,$$

(33)

$$\varphi = y_{9} ,\;\varphi^{\prime} = y_{10} ,\;\varphi^{\prime\prime} = yy_{4} ,$$

(34)

$$yy_{1} = \frac{{ - (y_{1} + y_{4} )y_{3} + y_{2}^{2} + M^{2} y_{2} - \lambda^{ * } (y_{7} + N^{ * } y_{9} )}}{{\varLambda_{1} }},\quad \varLambda_{1} = \left( {1 + nWe_{1}^{2} y_{3}^{2} } \right)*\left( {1 + We_{1}^{2} y_{3}^{2} } \right)^{{^{{\tfrac{n - 3}{2}}} }} ,$$

(35)

$$yy_{2} = \frac{{ - (y_{1} + y_{4} )y_{6} + y_{5}^{2} + M^{2} y_{5} }}{{\varLambda_{2} }},\quad \varLambda_{2} = \left( {1 + nWe_{2}^{2} y_{6}^{2} } \right)*\left( {1 + We_{2}^{2} y_{6}^{2} } \right)^{{^{{\tfrac{n - 3}{2}}} }} ,$$

(36)

$$yy_{3} = \frac{{ - Pr(y_{1} + y_{4} )y_{8} + Pr\,y_{2} y_{7} + Pr\,S_{1} y_{2} - Pr\,N_{b} y_{8} y_{10} - Pr\,N_{t} y_{8}^{2} - Pr\,\delta y_{7} }}{{\varLambda_{3} }},\quad \varLambda_{3} = \left( {1 + \frac{4R}{3}} \right),$$

(37)

$$yy_{4} = - Le\mathop {Pr}\limits (y_{1} + y_{4} )y_{10} + \mathop {Pr}\limits Ley_{2} y_{9} + \mathop {Pr}\limits LeS_{2} y_{2} y_{9} - \frac{{N_{t} }}{{N_{b} }}yy_{3,}$$

(38)

$$y_{1} \left( 0 \right) = 0,\;y_{2} \left( 0 \right) = 1,\;y_{2} \left( \infty \right) = 0,$$

(39)

$$y_{4} \left( 0 \right) = 0,\;y_{5} \left( 0 \right) = \alpha ,\;y_{5} \left( \infty \right) = 0,$$

(40)

$$y_{8} \left( 0 \right) + \gamma_{1} \left( {1 - S_{1} - y_{7} \left( 0 \right)} \right) = 0,\;y_{7} \left( \infty \right) = 0,$$

(41)

$$y_{10} \left( 0 \right) + \gamma_{2} \left( {1 - S_{2} - y_{9} \left( 0 \right)} \right) = 0,\;y_{9} \left( \infty \right) = 0.$$

(42)

6 Analysis of results

The notable objective here is to disclose the properties of numerous parameters on mixed convection stratified flow of magnetite Carreau nanofluid subject to convective phenomena. The heat transport mechanism is also considered in manifestation of the heat sink/source and thermal radiation. For this persistence, graphs are planned and tables are structured for diverse parameters and discussed in facts. Additionally, the range of scheming parameters in existent study is taken to be $0 \le M \le 1.5,$ $0 \le \lambda^{ * } \le 2.0,$ $0.1 \le N^{ * } \le 1.8,$ $0.7 \le \gamma_{1} \le 1.3,$ $0 \le S_{1} \le 0.3,$ $0.1 \le N_{b} \le 1.0,$ $0.4 \le N_{t} \le 1.6,$ $0 \le R \le 1.2,$ $0.6 \le \gamma_{2} \le 1.5,$ $0 \le S_{2} \le 0.5.$

6.1 Impact of $M$ on $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$

To envision the impact of magnetic parameter $M$ on velocity fields $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$ for both shear thinning/thickening cases, Fig. 2a–d is strategized. It is noted that both the liquid velocities decline for enhancing the values of $M$ for shear thinning/thickening cases. This occurs because of the circumstance that the outcomes of strong magnetic field contribute resistance to flow in both the x- and y-directions which intensify the Lorentz force in z-direction. Therefore, the flow in both the directions decay the liquid velocities.

Fig. 2

a–d Impact of $M$ on $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$

6.2 Impact of $\lambda^{ * }$ and $N^{ * }$ on $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$

The stimulus of growing value of mixed convection parameter $\lambda^{ * }$ and buoyancy ratio parameter $N^{ * }$ on velocity fields for $(n < 1)$ and $(n > 1)$ is schemed in Figs. 3a–d and 4a–d. It is noteworthy to note that when we heighten the value of these parameters the liquid velocity $f^{\prime}(\eta )$ increases for both (n = 0.5 and n = 1.5). Physically, augmented values of mixed convection parameter $\lambda^{ * }$ reason a forceful buoyancy force which clues the escalation of velocity field $f^{\prime}(\eta )$. Similarly, the concentration buoyancy strength boosts up for the increase in buoyancy ratio parameter $N^{ * }$ which consequence the declinse of the velocity field $g^{\prime}(\eta )$. Moreover, it is reported that both the velocity fields decay for augmenting values of $\lambda^{ * }$ and $N^{ * }$ for both $(n < 1)$ and $(n > 1)$ as displayed in Figs. 3c, d and 4c, d. Hence, we can say from these strategies that the impact of these flow parameters is entirely conflicting for velocity field $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$.

Fig. 3

a–d Impact of $\lambda^{ * }$ on $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$

Fig. 4

a–d Impact of $N^{ * }$ on $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$

6.3 Impact of $\lambda^{ * }$ and $N^{ * }$ on $\theta (\eta )$

Figures 5a, b and 6a, b are intended to visualize the enactment of mixed convection parameter $\lambda^{ * }$ and buoyancy ratio parameter $N^{ * }$ for shear thickening/thinning cases on nanoliquid temperature field. From these structures, it is scrutinized that both the $\lambda^{ * }$ and $N^{ * }$ are retreating functions of temperature distribution. For higher value of $\lambda^{ * }$ and $N^{ * }$ display thinner thickness of the thermal boundary layer and temperature of Carreau nanofluid. The enhancing value of mixed convection parameter $\lambda^{ * }$ relate to stronger buoyancy force because mixed convection parameter depends on buoyancy force. Hence, this stronger buoyancy force is the reason for the decline in temperature and its allied thickness of the boundary layer. Furthermore, analogous enactment is being detected for the progressive value of buoyancy ratio parameter $N^{ * }$.

Fig. 5

a, b Impact of $\lambda^{ * }$ on $\theta (\eta ).$

Fig. 6

a, b Impact of $N^{ * }$ on $\theta (\eta ).$

6.4 Impact of $\gamma_{1}$ and $S_{1}$ on $\theta (\eta )$

Figures 7a, b and 8a, b expose the tendency of thermal Biot number $\gamma_{1}$ and stratification parameter $S_{1}$, respectively, for $(n = 0.5$ and 1.5) on Carreau liquid temperature field. Here we scrutinized that quite conflicting tendency is being famed for growing value of $\gamma_{1}$ and $S_{1}$. When we intensify the values of thermal Biot number $\gamma_{1}$, the temperature field enhances; however, the temperature of Carreau fluid is declining function of thermal stratification parameter $S_{1}$. Physically, enlarging the values of thermal Biot number $\gamma_{1}$ rises the heat transfer amount which is responsible to enhance the temperature profile. Moreover, our scrutiny explores that the difference between the sheet and ambient liquid temperature decreases for larger values of $S_{1}$. Consequently, the thickness of the thermal boundary layer and temperature field decays for $S_{1}$ as shown in Fig. 8a, b.

Fig. 7

a, b Impact of $\gamma_{1}$ on $\theta (\eta )$

Fig. 8

a, b Impact of $S_{1}$ on $\theta (\eta )$

6.5 Impact of $N_{b}$ and $N_{t}$ on $\theta (\eta )$

The nanoparticles display a strategic role for the enhancement of heat transfer features in Carreau fluid. For this persistence, Figs. 9a, b and 10a, b are designed for both $(n < 1$ and $n > 1)$. We scrutinized from these drafts that $N_{b}$ and $N_{t}$ both are boosting the liquid temperature and thermal thickness of the boundary layer. Intensification in $N_{b}$ enriching the accidental gesture of liquid particles and additional heat is formed which rises the temperature field. In Fig. 9a, b, it is reported that the higher $N_{t}$ also enhances the liquid temperature. As thermophoresis is a mechanism wherein minor elements are dragged away from the hot to cold surface. Therefore, an enormous quantity of nanoparticles is transferred away from the intense surface which increases the temperature of the liquid.

Fig. 9

a, b Impact of $N_{b}$ on $\theta (\eta )$

Fig. 10

a, b Impact of the $N_{t}$ on $\theta (\eta )$

6.6 Impact of $R$ on $\theta (\eta )$

The characteristics of thermal radiation for $(n = 0.5$ and 1.5) is exposed in Fig. 11a, b on nanoliquid temperature field. There is an augmentation in both the liquid temperature and thermal thickness of boundary layer for the advance value of $R$. Increase in $R$ heightens the heat flux from the sheet which contributes to rise in the liquid temperature. Moreover, we can also say that the coefficient of mean absorption decays for enhancing values of $R$ which intensifies the temperature field.

Fig. 11

a, b Impact of $R$ on $\theta (\eta )$

6.7 Impact of $\gamma_{2}$ and $S_{2}$ on $\varphi (\eta )$

An intensification in nanoparticles concentration Biot number $\gamma_{2}$ and stratification parameter $S_{2}$ for shear thinning/thickening parameters is exposed in Figs. 12a, b and 13a, b. These graphs spectacle opposing behavior for higher value of these parameters. Increase in mass Biot number $\gamma_{2}$ enhances the concentration of nanoliquid; however, it declines for mass stratification parameter $S_{2}$. The higher values of $\gamma_{2}$ relate to sophisticated mass transfer coefficient and thus, the concentration field rises. On the other hand, it is inspected that when we enhances $S_{2}$, the difference between surface and reference nanoparticles reduces and the results in the declines of concentration field.

Fig. 12

a, b Impact $\gamma_{2}$ on $\varphi (\eta )$

Fig. 13

a, b Impact of $S_{2}$ on $\varphi (\eta )$

6.8 Tables of local skin friction coefficients, local Nusselt and Sherwood numbers

Tables 1 and 2 are established to show the tendency of the involved parameters on the local skin friction coefficients $\left( {\tfrac{1}{2}C_{{fx}} Re_{x}^{{\tfrac{1}{2}}} ,\tfrac{1}{2}\left( {\tfrac{{U_{w} }}{{V_{w} }}} \right)C_{{fy}} Re_{x}^{{\tfrac{1}{2}}} } \right)$, local Nusselt number $\left( {Re_{x}^{{ - \tfrac{1}{2}}} Nu_{x} } \right)$ and local Sherwood number $\left( {Re_{x}^{{ - \tfrac{1}{2}}} Sh_{x} } \right)$ for both shear thinning/thickening liquids. In Table 1, it is fascinating to note that by increasing the values of $M,$ $S_{1}$ and $S_{2}$ the skin friction coefficient $\left( {\tfrac{1}{2}C_{{fx}} Re_{x}^{{\tfrac{1}{2}}} } \right)$ rises while it declines for enhancing values of $\lambda^{ * } ,$ $N^{ * } ,$ $\gamma_{1}$ and $\gamma_{2}$ for both $(n < 1)$ and $(n > 1)$. It is also noted that the skin friction coefficient $\left( {\tfrac{1}{2}\left( {\tfrac{{U_{w} }}{{V_{w} }}} \right)C_{{fy}} Re_{x}^{{\tfrac{1}{2}}} } \right)$ enhance for $M,$ $\lambda^{ * } ,$ $N^{ * }$, $\gamma_{1}$ and $\gamma_{2}$, whereas conflicting behavior is being identified for $S_{1}$ and $S_{2}$. In Table 2, the rate of heat transfer is intensify for $\lambda^{ * } ,$ $N^{ * } ,$ $\gamma_{1} ,$ $S_{1}$ and $S_{2}$ and decline for $M$ and $\gamma_{2} .$ Moreover, the mass transfer rate for shear thinning/thickening liquids diminished for progressive values of $\lambda^{ * } ,$ $N^{ * }$ and $S_{1}$ while augmented for $M,$ $\gamma_{1}$ and $\gamma_{2} .$

Table 1 Numerical outcomes of skin friction coefficients when $We_{1} = We_{2} = Pr = 1.5,$ $\delta = 0.1,$ $N_{t} = 0.2,$ $\alpha = N_{b} = 0.3,$ $R = 0.5,$ and $Le = 1.0$ are fixed

Table 2 Numerical outcomes of local Nusselt and Sherwood numbers when $We_{1} = We_{2} = \Pr = 1.5,$ $\delta = 0.1,$ $N_{t} = 0.2,$ $\alpha = N_{b} = 0.3,$ $R = 0.5,$ and $Le = 1.0$ are fixed

6.9 Authentication with former upshots

For the endorsement of numerical upshots of $- f^{\prime\prime}(0)$ and $- g^{\prime\prime}(0)$ with former related prose for diverse values of $\alpha ,$ Tables 3 and 4 are organized. It is reported that intensifying values of $\alpha$ heighten $- f^{\prime\prime}(0)$ and $- g^{\prime\prime}(0).$ From these tables, a noteworthy agreement is being noted with earlier studies.

Table 3 An assessment table of $- f^{\prime\prime}(0)$ in limiting sense when $We_{1} = We_{2} = M = \lambda^{ * } = N^{ * } = 0$ and $n = 1$ are fixed

Table 4 An assessment table of $- g^{\prime\prime}(0)$ in limiting sense when $We_{1} = We_{2} = M = \lambda^{ * } = N^{ * } = 0$ and $n = 1$ are fixed

7 Main findings

Here we disclosed the properties of combined convective and stratification phenomena on 3D mixed convection flow of Carreau magnetite nanofluid with the impact of thermal radiation and the heat sink/source. The planned vision of this study is enumerated below:

• Both the liquid velocities $f^{\prime}(\eta )$ and $g^{\prime}(\eta )$ declined for higher magnetic parameter $M$, but the influence of mixed convection parameter $\lambda^{ * }$ was absolutely conflicting on velocity fields for both $(n < 1)$ and $(n > 1)$.

• The temperature field intensified for thermal Biot number $\gamma_{1}$ and thermal radiation parameter $R$, while it decayed for thermal stratification parameter $S_{1}$ for both shear thinning/thickening instances.

• The progressive values of mixed convection parameter $\lambda^{ * }$ diminished the liquid temperature and its allied thickness of the boundary layer, whereas it enhanced for Brownian motion $N_{b}$ and thermophoresis parameter $N_{t}$.

• Quite opposite tend was being noted for advance values of mass stratification $S_{2}$ and mass Biot number $\gamma_{2}$ for both cases $(n = 0.5)$ and $(n = 1.5)$ on concentration field.