1 Introduction

Many chemical reactions with real-life applications may be very slow without the influence of a catalyst. Many chemical systems have simultaneous homogeneous and heterogeneous reactions: e.g. photosynthesis in plants, where carbon dioxide and water are converted to food, aerobic cellular respiration process, combustion and chemical reactions in batteries are common examples of electrochemistry. Khan et al [1] analysed the effects of single-step chemical reaction processes on the three-dimensional flow of Burgers fluid. Khan et al [2] inspected the impact of elementary step chemical reactions on the generalised Burgers fluid. Mustafa et al [3] examined the characteristics of activation energy and single-step chemical reactions. Khan et al [4] discussed the impact of constructive / distructive chemical reactions on radiative heat transfer of three-dimensional flow.

Mostly, chemical reactions are complex in nature, the complexity of a complex reaction can be resolved if we know the intrinsic details of the reaction mechanism. Now, to analyse the complexity of multistep reaction mechanisms, the graphical representation of the involved species (nodes) is commonly used. Two types of nodes take part in graphs: the first one represents the components and the second one represents the forward and reverse reactions. Mathematical graph theory has wide applications in chemical engineering and chemistry, in electrical diagrams and the representation of a railway network, and mechanism of complex chemical reactions is the most common feature of graph theory. In 1956, King and Altman [5] first used graph methods to represent the enzyme-catalysed reactions. Bipartite graphs for representing the complex reaction mechanism have been proposed by Hudyaeu and Vol’pert [6].

The idea of modelling the chemical kinetics is used to transform the physical reality to a mathematical description. A homogeneous reacting system modelled by ordinary differential equations is considered. In the case of a high-dimensional problem, these models are inappropriate for efficient simulation, and stiffness arises if they involve multiple time-scales. To overcome these problems, model reductions are applied. The reduced model contains all the essential information to still describe the system accurately, which is the goal of the model reduction technique in chemical kinetics. Several techniques are used for finding the slow invariant manifold (SIM). A quasi-steady-state approximation which depends on the concentration of some of the active reagents (such as substrate–enzyme complex and radicals) and computational singular perturbation method determines the result of the analytical perturbation method and it is suitable for the stiff system. Lumping, sensitivity and time-scale analysis are the most common modern model reduction techniques while computational singular perturbation and intrinsic low-dimensional manifold (ILDM) are common in the time-scale analysis. The SIM is the subset of the phase space towards all the solutions of the system that come and stay after fast time-scale events are equilibrated. Gorban and Karlin [7] gave the idea of the method of the invariant manifold while Chiavazzo et al [8] showed that the quasi-equilibrium manifold (QEM), spectral quasi-equilibrium manifold (SQEM), method of the invariant grid (MIG), computational singular perturbation are all based on SIM.

Another approach, which was originally proposed by Keck and Gillespie [9] and then developed and used with considerable success by Keck and other researchers, is the rate-controlled constrained-equilibrium (RCCE) method. This method depends on the essential assumptions and the second law of thermodynamics that the slow reaction in a complex reacting system imposes constraints on its composition, which controls the rate at which it approaches the chemical equilibrium, while the system equilibrated by fast reaction is subjected to the constraints imposed by the slow reaction. Keck [10] has delivered a brief theory on RCCE for a chemical reaction in complex systems. Ren et al [11] discussed the dimension reduction persistence to describe reactive systems flow and applied different reduction techniques such as ILDMs and RCCE to reduce a complete system to some required species without losing essential information.

Many detailed reaction mechanisms, homogeneous or inhomogeneous (having many chemical species, elementary reactions), describe a reactive flow. Consequently, the numerical calculation of the reactive flow of complete detailed (homogeneous or inhomogeneous) mechanisms is complicated. To reduce the computational burden imposed by the direct use of a detailed mechanism, we need well-recognised methodologies. From several types of such methodologies for calculating chemically reactive flow, the dimension reduction by using slow manifold is an effective approach for reducing the complexity and computational burden. To describe the inhomogeneous reactive flow, Ren and Pope [12] discussed the chemistry-based manifold by using the reduction technique (a good approximation technique but not purely the invariant) ILDM. Different approaches, namely the Mass–Pope approach, the close-parallel approach and the approximate slow invariant manifold (ASIM) approach for ILDM to combine the transport-chemistry coupling in the reduced description was discussed by Ren and Pope [13]. They also provided a brief overview of the reduced description of inhomogeneous reactive flow through the slow manifold and applied the close-parallel assumption for validation. Ren et al [14] developed another dimension reduction method, the invariant constrained-equilibrium edge pre-image curve (ICE-PIC), and Ren et al [15] demonstrated the application of ICE-PIC for both homogeneous and inhomogeneous reacting systems. For inhomogeneous case, the ICE-PIC method is implemented in two ways: first, one without transport coupling and the second with transport coupling.

Furthermore, different model reduction techniques are applied to a number of chemical reaction mechanisms by different researchers [8, 16,17,18,19,20,21,22,23,24,25,26]. Constales et al [27] analysed the augmentation and reduction of the chemical composition of chemical species. Shahzad and Sultan [28] discussed the behaviour of the involved chemical species in a chemical reaction mechanism in two dimensions and three dimensions and then compared the behaviours.

For the construction of the low-dimensional approximation, we make use of intrinsic multiple time-scales. Reinhardt et al [29] explained that the fast-transient dynamical model is assumed to be relaxed within the reduced model if the long-term behaviour of the system is to be studied. This task is done by replacing the original system of differential equations with one of the lower-dimensional systems without losing too much of key information about the long-term system dynamics.

In the current research, we focus on the construction of C-matrix for two-step reaction mechanism to obtain the key / non-key components (low dimension), Horiuti matrix and overall reaction. Moreover, for the dimension reduction process, different reduction techniques are discussed here. We use three reduction techniques, QEM, SQEM and ILDM, in this study and the efficiency and accuracy of solution curves obtained through these three reduction techniques are compared graphically as well as in tabular form. The refinement method is applied to obtain more accurate results using MATLAB.

2 Problem formulation: A two-step reaction mechanism

Consider that the two-step reversible chemical reaction has five chemical species. In the first step, \(H_2 \) reacts with Z and forms an intermediate \(H_2 Z\). In a next step, \(H_2 Z\) reacts with the species B and gives the product \(\textit{BH}_2 \):

$$\begin{aligned} \begin{aligned}&H_2 +Z\mathop {\rightleftarrows }\limits ^{k_1^\pm }H_2 Z, \\&H_2 Z+B\mathop {\rightleftarrows }\limits ^{k_2^\pm } H_2 B+Z. \\ \end{aligned} \end{aligned}$$
(1)

Graphically, it is shown in figure 1.

Fig. 1
figure 1

Graphical representation of two-step reaction mechanism [30].

Full size image

In figure 1, Z and \(H_2 Z\) are intermediate species while \(H_2 \) and B are reactants and \(\textit{BH}_2 \) is the product species.

Trees and nodes: Considering the intermediates as node points, the line shows edges, while the positive and negative signs represent the forward and backward directions, respectively.

$$\begin{aligned} {\begin{array}{lll} {\hbox {Forward:}} &{} {Z\xleftarrow {+2} H_2 Z,} &{}\quad {H_2 Z\xleftarrow {+1} Z,} \\ {\hbox {Backward:}} &{} {Z\xleftarrow {-1} H_2 Z,} &{}\quad {H_2 Z\xleftarrow {-2} Z.} \\ \end{array}} \end{aligned}$$

To understand the behaviour of complex chemical reaction mechanisms, linear algebraic analysis is one of the key factors and the matrices operation plays a vital role, i.e. C-matrix. The C-matrix comprises the stoichiometric, molecular and Horiuti matrices.

The stoichiometric matrix deals with the key and non-key components and reactions of any mechanism. Thus, each row represents a reaction and a column represents a component, i.e. the example concerns reactions of (1) are

$$\begin{aligned} \begin{array}{c|ccccc} &{}\quad H_2 &{}\quad Z&{}\quad B&{}\quad H_2 Z&{}\quad {\textit{BH}}_2 \\ \hline W_1 &{}\quad -\,1&{}\quad -\,1&{}\quad 0&{}\quad 1&{}\quad 0\\ \\ W_2 &{}\quad 0&{}\quad 1&{}\quad -\,1&{}\quad -\,1&{}\quad 1\\ \end{array} \end{aligned}$$
(2)

Augmenting the above form with identity matrix we obtain

$$\begin{aligned} \begin{array}{c|ccccc|cc} &{}\quad H_2 &{}\quad Z&{}\quad B&{}\quad H_2 Z&{}\quad {\textit{BH}}_2 &{}\quad W_1 &{}\quad W_2 \\ \hline W_1 &{}\quad -1&{}\quad -1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0\\ &{}&{}&{}&{}&{}&{}&{}\\ W_2 &{}\quad 0&{}\quad 1&{}\quad -1&{}\quad -1&{}\quad 1&{}\quad 0&{}\quad 1\\ \end{array} \end{aligned}$$
(3)

Applying RREF, we get the stoichiometric C-matrix as

$$\begin{aligned} \begin{array}{c|ccccc|cc} &{}\quad H_2 &{}\quad Z&{}\quad B&{}\quad H_2 Z&{}\quad BH_2 &{}\quad W_1 &{}\quad W_2\\ \hline W_1 &{}\quad \mathbf{1}&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad -1&{}\quad -1&{}\quad -1\\ &{}&{}&{}&{}&{}&{}&{}\\ W_2 &{}\quad 0&{}\quad \mathbf{1}&{}\quad -1&{}\quad -1&{}\quad 1&{}\qquad 0&{}\qquad 1\\ \end{array} \end{aligned}$$
(4)

The first two columns are pivot columns and thus \(H_2 \) and Z are key components and the rest are dependent components. There is no one dependent reaction as in the augmented block there is no pivot element. Thus, \(W_1\) and \(W_2 \) are independent reactions:

$$\begin{aligned} \begin{aligned}&\eta _{\mathrm{Reaction}} = \eta _{\mathrm{Key\, component}} +\eta _{\mathrm{Dependent \, reaction}} , \\&\eta _{\mathrm{Key \, component}} =\eta _{\mathrm{Indepedent \, reaction}} . \\ \end{aligned} \end{aligned}$$
(5)

Similarly, molecular matrix deals with the key and non-key elements and components, each row represents a different component, and each column a different element, i.e. the involved components are \(H_2 , Z, H_2 Z, B\) and \(\textit{BH}_2 \):

$$\begin{aligned} \begin{array}{c|ccc} &{}\quad H&{}\quad Z&{}\quad B \\ \hline H_2 &{}\quad 2&{}\quad 0&{}\quad 0\\ Z&{}\quad 0&{}\quad 1&{}\quad 0\\ B&{}\quad 0&{}\quad 0&{}\quad 1\\ H_2 Z&{}\quad 2&{}\quad 1&{}\quad 0 \\ \textit{BH}_2 &{}\quad 2&{}\quad 0&{}\quad 1\\ \end{array} \end{aligned}$$
(6)

The augmented molecular matrix is along with the identity matrix, i.e.

$$\begin{aligned}&\begin{array}{ccc|ccccc} H&{}\quad Z&{}\quad B&{}\quad H_2 &{}\quad Z&{}\quad B&{}\quad H_2 Z&{}\quad BH_2 \\ \hline \mathbf{1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -1/2&{}\quad 0&{}\quad 1/2\\ 0&{}\quad \mathbf{1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad -1\\ 0&{}\quad 0&{}\quad \mathbf{1}&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \mathbf{1}&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad -1\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \mathbf{1}&{}\quad -1&{}\quad -1&{}\quad 1\\ \end{array} \end{aligned}$$
(7)
$$\begin{aligned}&\eta _{\mathrm{Component}} =\eta _{\text {Key component}} +\eta _{\text {Key element}} . \end{aligned}$$
(8)

There are two key components, and the dependent components can be expressed as

$$\begin{aligned} \begin{aligned}&\eta _B =-\frac{1}{2}\eta _{H_t } +\eta _{Z_t } +\eta _B +\eta _{H_2 } , \\&\eta _{H_2 Z} =\eta _Z , \\&\eta _{\textit{BH}_2 } =\frac{1}{2}\eta _{H_t } -\eta _{Z_t } -\eta _{H_2 } . \\ \end{aligned} \end{aligned}$$
(9)

The orthogonality condition between the stoichiometric matrix \(\Gamma \) and the molecular matrix M also holds, i.e. \(M\Gamma =0\), i.e.

$$\begin{aligned} M\cdot \Gamma= & {} \left[ {\begin{array}{ccccc} 2 &{}\quad 0 &{}\quad 0 &{}\quad 2 &{}\quad 2 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ \end{array}} \right] \left[ {\begin{array}{rr} -1&{}\quad 0 \\ -1&{}\quad 1 \\ 0&{}\quad -1 \\ 1&{}\quad -1 \\ 0&{}\quad 1 \\ \end{array}} \right] \nonumber \\= & {} \left[ {\begin{array}{cc} 0 &{}\quad 0 \\ 0&{}\quad 0 \\ 0&{}\quad 0 \\ \end{array}} \right] . \end{aligned}$$
(10)

Horuiti matrix deals with the global reaction. For the analysis of overall reaction to wipe out the intermediates using RREF of augmented stoichiometry matrix, intermediates must be listed first:

$$\begin{aligned} \left[ {{\begin{array}{ccccc} Z&{}\quad {H_2 Z}&{}\quad {H_2 }&{}\quad B&{}\quad {\textit{BH}_2 } \\ {-1}&{}\quad {1}&{}\quad {-1}&{}\quad 0&{}\quad 0 \\ 1&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 1 \\ \end{array} }} \right] . \end{aligned}$$
(11)

The augmented matrix along with the unit matrix gives

$$\begin{aligned} \left[ {{\begin{array}{ccccccc} Z&{}\quad {H_2 Z}&{}\quad {H_2 }&{}\quad B&{}\quad {\textit{BH}_2 }&{}\quad {R_1 }&{}\quad {R_2 } \\ {-1}&{}\quad 1&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 1&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 1&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$
(12)

and RREF implies

(13)

From the above matrix (13), the second row gives an overall reaction. The Horiuti numbers are the elements of \(R_{1}\) and \(R_{2}\) in the second row, i.e. \(-1\) and \(-1\). In the matrix form called Horiuti matrix, i.e.

$$\begin{aligned} \sigma =\left[ {\begin{array}{l} -1 \\ -1 \\ \end{array}} \right] . \end{aligned}$$
(14)

Now, we shall model the overall problem according to the available components, elements and reactions.

2.1 Mathematical formulation of invariant manifold

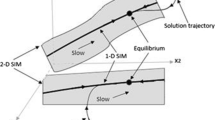
In the phase space, the trajectory of the species during relaxation reveals that they quickly move towards the lower-dimensional manifold, and then once they reach the slow manifold, they do not leave it anymore, proceeding slowly along it towards equilibrium.

Let us consider the following initial parameters for (1):

$$\begin{aligned}&d_1 =H_2 ,\quad d_2 =Z,\quad d_3 =H_2 Z,\\&d_4 =A,\quad d_5 =AH_2 , \\&d_1^{\mathrm{eq}} = 0.5,\quad d_2^{\mathrm{eq}} =0.1,\quad d_3^{\mathrm{eq}} =0.1,\quad d_4^{\mathrm{eq}} =0.4,\\&d_5^{\mathrm{eq}} =0.1, \quad k_1^+ =10,\quad k_2^+ =5. \end{aligned}$$

The rate of reaction for reversible reaction mechanism \(W=W^{+}-W^{-}\) (law of mass action) is given as

$$\begin{aligned} \begin{aligned}&W_1 =W_1^+ -W_1^- =k_1^+ d_1 d_2 -k_1^- d_3 , \\&W_2 =W_2^+ -W_2^- =k_2^+ d_3 d_4 -k_2^- d_5 d_2 . \\ \end{aligned} \end{aligned}$$
(15)

The kinetic equations are the sum of the product of a stoichiometric matrix and rate equations, generally:

$$\begin{aligned} \dot{d}=\sum _{x=1}^r {\Gamma W_x (d)} . \end{aligned}$$
(16)

The system of kinetic equations given by (16) is

$$\begin{aligned} \left[ {\begin{array}{l} \dot{d}_1\\ \dot{d}_2 \\ \dot{d}_3 \\ \dot{d}_4 \\ {\dot{d}_5}\\ \end{array}} \right] =\left[ {\begin{array}{l} k_1^- d_3 -k_1^+ d_1 d_2 \\ k_1^- d_3 -k_2^- d_2 d_5 -k_1^+ d_1 d_2 +k_2^+ d_3 d_4 \\ k_2^+ d_2 d_5 -k_1^- d_3 +k_1^+ d_1 d_2 -k_2^+ d_3 d_4 \\ k_2^- d_2 d_5 -k_2^+ d_3 d_4 \\ k_2^+ d_3 d_4 -k_2^- d_2 d_5 \\ \end{array}} \right] . \end{aligned}$$
(17)

Now, let us apply the following model reduction techniques, i.e. QEM, SQEM and ILDM, on the above system (17). For details of these methods, we refer the readers to [7, 8, 19, 22,23,24,25,26].

In QEM a reduced descripted form \(\xi _{1\ldots r} \) having dimension \(r<(n-1)\) yields such points in a phase space which minimises the Lyapunov function G:

$$\begin{aligned}&(v_1 ,x)=\xi _1 ,\quad (v_2 ,x)=\xi _2 ,\ldots (v_r ,x)=\xi _r , \end{aligned}$$
(18)
$$\begin{aligned}&G=\sum _{i=1}^5 {d_i \left( {\ln \left( {\frac{d_i }{d_i^{\mathrm{eq}} }} \right) -1} \right) } ,\quad \frac{\partial G(x,y)}{\partial y}=0,\nonumber \\&\frac{\partial ^{2}G(x,y)}{\partial ^{2}y}>0. \end{aligned}$$
(19)

Here v are the n-dimensional vectors. The solution of the variational problem \(G\rightarrow \min \) along with (18) and (19) gives QEM, while, if the selection of n-dimensional vectors is a left-slowest eigenvector \(v_{\mathrm{s}}^{\mathrm{l}}\), then the governing method will be SQEM.

Similarly, in ILDM, each point in a state space of the system can easily be divided into two subgroups, based on their eigenstates, i.e. slow and fast subspaces:

$$\begin{aligned}&\max \left\{ {\hbox {re } \lambda _{x_i }, i=1\ldots n_\mathrm{f} } \right\} \nonumber \\&\quad \le \kappa<\min \left\{ {\hbox {re } \lambda _{x_i } , i=n_{\mathrm{f}+1} \ldots n} \right\} \hbox { for } \kappa <0 \end{aligned}$$
(20)

and \(\hbox {re }\lambda _{x_i } \) represent the real fast and slow variations at each point \(d_i \). Equation (20) allows us to distinguish between fast \(n_\mathrm{f}\) and slow \(n_\mathrm{s} =n-n_\mathrm{f}\) subspaces at each point.

Fig. 2
figure 2

Phase flow of the solution trajectories in its reduced form \(d_1 \) and \(d_4 \) near the equilibrium point (a) and 1D solution curve obtained through QEM (b).

Full size image

To start measuring the initial manifold, the best available point is equilibrium \(d^{\mathrm{eq}}\), after that the next point can be measured as

$$\begin{aligned} r=d^{p}\pm hb \end{aligned}$$
(21)

in both the directions to get the one-dimensional (1D)-ILDM. \(d^{p}\) is the previous point h representing a small constant value and b is the slowest eigenvector extracted from E:

$$\begin{aligned} E=\left[ {{\begin{array}{lll} |&{} &{} | \\ {v_1 }&{} \cdots &{} {v_n } \\ |&{} &{} | \\ \end{array} }} \right] , \end{aligned}$$
(22)

where \(v_1 ,\ldots ,v_n \) are column vectors representing the eigenvectors of Jacobian J; \(J=\partial C_K /\partial d_i \).

To avoid any possibilities of moving along the fast direction, we can take them to be in orthogonal direction. But, usually, these vectors are not orthogonal. Therefore, with the help of Gram–Schmidt orthogonalisation method, we apply the Schur decomposition method over J, measured at each point in a phase space.

Theorem

(Schur decomposition). For any \(n\times n\) matrix A with entries from C, there is some orthonormal basis B of C and some upper-triangular matrix R with entries in C.

Thus, a matrix we obtain with an orthonormal basis Q (usually called transition matrix) evolves both the fast and slow eigenvectors \(Q^{f}:V_{x_i} ,i=1\ldots n_\mathrm{f} , Q^{s}:V_{x_i} ,i=n_{\mathrm{f}+1} \ldots n\). Then according to the definition of Maas and Pope, ILDM implies

$$\begin{aligned} Q_{f} \cdot C_K^\mathrm{R} (d)=0. \end{aligned}$$
(23)

where \(C_K^\mathrm{R} (d)\) is the reduced system to be solved and \(Q_{f}\) are \(1\ldots n_\mathrm{f}\) rows of \(Q^{-1}\)(inverse) matrix \((n_\mathrm{f} \times n)\) appropriate to the transpose of Schur matrix and vanishes a big part of the Jacobian matrix matching to the fast time-scale. This will allow us to move along slow time-scales. System (21) further leads to the implication functions which need proper care while solving the system.

Fig. 3
figure 3

QEM solution curve along with the solution trajectories (a) and first and the second refinements of the QEM curve (initial approximation) using the MIG at each grid point (b).

Full size image
Fig. 4
figure 4

ILDM approximation along with equilibrium point (a) and (b) shows SQEM approximation along with equilibrium point.

Full size image

A classified nature of this method allows us to measure the higher-dimensional manifold. For this purpose, 1D-ILDM may be considered in its discretised form. Then each point of subdivision is considered as a starting point to advance the method in both the forward and backward directions. Rest of the procedure is like the procedure adopted for computing 1D-ILDM except for the addition of one more progress variable.

3 Results and discussions

Usually, the transformed system of differential equations is high dimensional and the exact solutions of these equations, in general, look impossible. Consequently, we implement the numerical techniques to find the solutions by setting their initial estimated parameters.

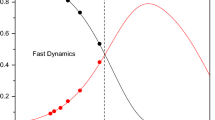
Figure 2a shows the behaviour of the species (in its reduced form) near the equilibrium point where all the initial trajectories starting from different points approaching the equilibrium point. Figure 2b shows the QEM approximation starting from the equilibrium point to both the directions.

Figure 3a shows the difference between the approximate curve and the invariant region, thus QEM approximation needs to be refined. Refinements are carried out using the method of invariant grids [8] shown in figure 3b, and this figure shows that after the second refinement the solution curve lies over the invariant region.

Similarly, the initial approximations started from equilibrium point in both the directions (forward and backward) given by ILDM and SQEM are shown in figures 4a and 4b, respectively.

Fig. 5
figure 5

Comparison of QEM, SQEM and ILDM approximations along with the behaviour of their species near equilibrium.

Full size image

To investigate the efficiency of the reduction method, all the solution curves are compared in figure 5, and it is clear from this figure that the solution curve obtained through ILDM lies over the invariant region. Thus, this technique gives more accurate results than the SQEM and QEM.

Fig. 6
figure 6

Steady-state behaviour of the involved species \(H_2, A\) and \(AH_2\) in the overall reaction mechanism after passing different transition periods.

Full size image

However, in Horuiti setting, it is difficult to measure the short-lived intermediates in terms of long-lived components. Therefore, we find a relationship between the long-lived components that do not involve intermediates at all. In the present case, we have which is an overall reaction. Now the behaviour of the involved species is given in figure 6.

The refined results are shown in table 1. Furthermore, the results obtained using different techniques are compared in table 2.

Table 1 First and second refinement of QEM grid points.
Full size table
Table 2 Difference between ILDM and QEM points and ILDM and SQEM points.
Full size table

4 Conclusion

In this research paper, three model reduction techniques are applied to get the invariants (solution curves) of a complex chemical problem. After getting the reduced model with the help of the C-matrix, results are compared graphically and in a tabulated form. The following conclusions can be drawn:

  • C-matrix relies on the three basic matrices of chemical reactions.

  • C-matrix provides the main information of any reaction mechanism with respect to key elements, key components, independent reactions and global reactions.

  • Model reduction techniques applied to the key species are provided by the C-matrix.

  • The overall reaction is investigated by using the Horiuti matrix.

  • Trees and nodes are defined for the chemical reaction mechanism.

  • QEM solution is refined by applying MIG and after the second refinement, the actual result was obtained.

  • Comparison of MRT implies that the ILDM gives better results than the QEM and SQEM.