1 Introduction

The nature of real world is governed by various nonlinear complex phenomena which are the main concerns of the scholars and researchers. Based on intricate phenomena arise in various branches of science, there have been modeled numerous nonlinear evolution equations among which Schrödinger types are remarkable for their significance (Kilbas et al. 2006; Wazwaz 2002; Miller and Ross 1993; Oldham and Spanier 1974). Nonlinear Schrödinger models as well numerous other nonlinear models have been studied by many researchers with various techniques such as the semi-inverse variational principle has been employed to study log law, power law and cubic nonlinearity of the resonant nonlinear Schrödinger’s equation (Biswas 2013); a higher-order Schrödinger equation with variable coefficients has been examined by the Hirota bilinear method for the periodic attenuating oscillation of solitons (Liu et al. 2019); some researchers have adopted exp-function method to explain in detail the soliton natures arise in the dimensionless coupled nonlinear Schrödinger equations, cubic-quartic nonlinear Schrödinger equation, and the chiral nonlinear Schrödinger’s models (Ekici et al. 2017; Yildirim et al. 2020; Ebadi et al. 2012); the nonlinear Schrödinger equation with parabolic law nonlinearity and an improved nonlinear Schrödinger equation have been investigated for optical solitons by using the ansatz method (Zhou et al. 2015; Savescu et al. 2013); the extended Fan-sub equation method has been utilized to analyze quadratic-cubic and dual-power laws nonlinearity of a couple of nonlinear Schrödinger equations, the ultra-short pulses providing by the Hamiltonian amplitude equation, and the separation phase connecting to the convective-diffusive Cahn–Hilliard equation (Younas and Ren 2021; Younas et al. 2022a, 2022b); the Schrödinger equation relating to cubic optical solitons, the Kraenkel-Manna-Merle system expressing the motion of nonlinear ultra-short wave pulse and the generalized Korteweg-de-Vries-Zakharov-Kuznetsov model arise in plasma physics have been studied through the \({\Phi }^{6}\)-model expansion method (Younas et al. 2021, 2022c, 2022d); the new extended direct algebraic method has been adopted to investigate wave solutions of the three-dimensional Wazwaz-Benjamin-Bona-Mahony equation, and the doubly dispersive equation (Younas and Ren 2022; Younas et al. 2022e); the \(\left( {G^{\prime}/G,1/G^{\prime}} \right)\)-expansion and \(\left( {1/G^{\prime}} \right)\)-expansion techniques have been used to examine (1 + 1)-dimensional Schrödinger equation (Kaplan et al. 2016); the pure-cubic complex Ginzburg-Landau equation having nonlinear refractive index has been studied by applying the new mapping method and the addendum to Kudryashov’s approach (Zayed et al 2021a); a nonlinear Schrödinger model has been studied by implementing extended Fan sub-equation scheme (Cheema and Younis 2016); \((m+{G}^{^{\prime}}/G)\)-expansion and exp-\(\varphi (\xi )\)-expansion tools have been employed to study the cubic-quartic and resonant nonlinear Schrödinger equation for optical soliton solutions (Gao et al. 2020); the fractional order (2 + 1)-dimensional Schrödinger model has been investigated by employing \(({G}^{^{\prime}}/G)\)-expansion approach (Li et al. 2019); the variational iteration method has been adopted to investigate optical solitons of Schrödinger model in normal dispersive regimes (Wazwaz and Kaur 2019); coupled of Schrödinger equations has been explored by operating improved tanh and rational \(({G}^{^{\prime}}/G)\)-expansion schemes to construct diverse optical solitons (Islam et al. 2022a, 2022b); new F-expansion tool has been employed to explore wave solutions of Schrödinger equations (Pandir and Duzgun 2019; Biswas et al. 2019); various F-expansion and extended trial equation procedures have been applied to examine analytic solutions of the (2 + 1)-dimensional Schrödinger model (Rizvi et al. 2017); the cubic Schrödinger equation has been inspected by homotopy analysis method (Hemida et al. 2012) and worth stating further studies (Younis et al. 2018; Liu et al. 2017; Chowdhury et al. 2021; Ismael et al. 2021; Zayed et al. 2021a; Rizvi et al. 2021; Salam et al. 2016; Lu et al. 2017; Malik et al. 2021a; Islam et al. 2022c; Gu et al. 2022; Osman et al. 2022; Biswas et al. 2017).

This present investigation deals with the generalized third-order nonlinear Schrödinger equation

$$i\left( {\phi_{t} + \phi_{xxx} } \right) + \left| \phi \right|^{2} \left( {b\phi + ic\phi_{x} } \right) + id\left( {\left| \phi \right|^{2} } \right)_{x} \phi = 0,$$
(1.1)

where \(\phi\) represents complex function depending on temporal variable \(t\) and spatial variable \(x\); the cubic nonlinearity is affected by \(b\) while the dispersive terms are affected by \(c\) and \(d\). Earlier, this complex governing model has been investigated to seek for accurate wave solutions by the researchers such as Lu et al. have studied Eq. (1.1) by employing exp \((-\Upsilon (\xi ))\)-expansion and extended simple equation methods which provided analytical wave solutions (Lu et al. 2019); the same model has been examined by Nasreen et al. for exact solutions via the Riccati mapping method (Nasreen et al. 2019); the exp-function and unified procedures have been imposed to construct and analyse the wave solutions of the mentioned equation by Hosseini et al. (Hosseini et al. 2020); Malik et al. have utilized the Lie symmetry analysis and different methods, and discovered different optical soliton solutions (Malik et al. 2021b); the novel homotopy perturbation method has been applied to study the stated governing equation by Zhao et al. (2022); Jacobi elliptic function solutions of the mentioned model have been assembled by Wang et al. (2014).

Subsequently, improved auxiliary equation and enhanced rational \(({G}^{^{\prime}}/G)\)-expansion schemes are putted forward to pursue suitable analytic solutions of the governing equation stated in Eq. (1.1). Soliton theory has attracted profound awareness in investigational studies for being effective research extent subjective to telecommunication, engineering, mathematical physics, and several other problems occur in nonlinear sciences. At present, optical solitons have taken great importance from researchers and scholars because of their extensive roles to analyse related complicated phenomena. Optical solitons are special type of solitary waves which endure unaffected during the propagation in long distance. Solitons are supportive in wide-ranging sense in the machinery of signal-based fiber-optic amplifiers, optical pulse compressors, communication links, and some others. We pay our devotion to comprise assorted solitons associated with optical fibers. Accordingly, this investigation adopts the advised methods fruitfully and collects profuse appropriate wave solutions which might be noticeable first time in the literature.

2 Elucidation of advised schemes

Take the evolution equation involving nonlinearity as

$${\Psi }\left( {u,u_{x} ,u_{y} ,u_{t} , \ldots ,u_{xy} ,u_{xt} ,u_{yt} , \ldots ,u_{xx} ,u_{yy} ,u_{tt} , \ldots } \right) = 0,\;\;0 < \alpha \le 1$$
(2.1)

Commencing the new wave variable

$$u = u\left( \xi \right),\;\;\xi = \xi \left( {x,y,t, \ldots } \right)$$
(2.2)

Transforms Eq. (2.1) into the ODE

$${\Omega }\left( {u, u^{\prime}, u^{\prime\prime}, u^{\prime\prime\prime}, \ldots \ldots \ldots } \right) = 0$$
(2.3)

One may integrate Eq. (2.3) as much possible and consider the constant of integration as zero for pursuing soliton solutions. The major dealings of the recommended schemes are stated bellow:

2.1 Improved auxiliary equation technique

The expected solution of Eq. (2.1) is specified as follows (Islam et al. 2021a, b):

$$u\left( \xi \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{s} e_{i} a^{i\psi \left( \xi \right)} }}{{\mathop \sum \nolimits_{i = 0}^{s} f_{i} a^{i\psi \left( \xi \right)} }}$$
(2.4)

where \(e_{i} ^{\prime}s\) and \(f_{i} ^{\prime}s\) are free parameters; one of \(e_{n}\) and \(f_{n}\) is different from zero; \(s\) is decided by using balancing theme for Eq. (2.3) and \(\psi \left( \xi \right)\) satisfies the equation

$$\psi^{\prime}\left( \xi \right) = \frac{1}{\ln a}\left\{ {pa^{ - \psi \left( \xi \right)} + q + ra^{\psi \left( \xi \right)} } \right\}$$
(2.5)

The solutions of Eq. (2.5) are well-known (Akbar et al. 2019). Gripping the calculated value of \(s\), Eq. (2.4) alongside its required differential coefficient and Eq. (2.5) pushes Eq. (2.3) to be a polynomial in \({a}^{\psi (\xi )}\). Set polynomial’s coefficients to zero and unravel them for involved arbitrary constants with the support of the software Maple. Incorporating the solutions of Eq. (2.5) and the found parameter’s values in Eq. (2.4) delivers the expected solitary wave solutions of Eq. (2.1).

2.2 Enhanced rational \(({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})\)-expansion scheme

The desired solution is itemized as (Islam et al. 2021b)

$$u\left( \xi \right) = \frac{{e_{0} + \mathop \sum \nolimits_{i = 1}^{s} e_{i} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{i} + f_{i} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{ - i} }}{{g_{0} + \mathop \sum \nolimits_{i = 1}^{s} g_{i} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{i} + h_{i} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{ - i} }}$$
(2.6)

where \(s\) is picked out as in previous scheme and \(({\mathrm{G}}^{\mathrm{^{\prime}}}(\upxi )/\mathrm{G}(\upxi ))\) satisfies

$${\mathrm{GG}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}=\mathrm{\varepsilon G}{\mathrm{G}}^{\mathrm{^{\prime}}}+\upepsilon {\mathrm{G}}^{2}+\eta {\mathrm{G}}^{\mathrm{^{\prime}}2}$$
(2.7)

where \(\upvarepsilon ,\upepsilon\) and \(\eta\) are free constraints. The Cole-Hopf transformation \({\uppsi }\left( {\upxi } \right) = {\text{G}}^{\prime}\left( {\upxi } \right)/{\text{G}}\left( {\upxi } \right)\) diminishes Eq. (2.7) to be

$${\uppsi }^{\mathrm{^{\prime}}}\left(\upxi \right)=\upepsilon +\mathrm{\varepsilon \psi }\left(\upxi \right)+\left(\eta -1\right){\uppsi }^{2}(\upxi )$$
(2.8)

Equation (2.8) offers several solutions (Zhu 2008). Equation (2.3) alongside Eqs. (2.6) and (2.8) yields a polynomial in \(({G}^{^{\prime}}\left(\xi \right)/G\left(\xi \right))\). Adjust same terms of to zero for algebraic equations. Find out the essential parameter’s values from these equations by computer software Maple. Implanting these values in Eq. (2.6) yields appropriate analytic solutions to Eq. (2.1). Thereupon, we derive the proper solitary wave solutions of the generalized third-order Schrödinger model as follows:

3 Formation of solutions

In this portion, the generalized third-order nonlinear Schrödinger equation is resolved by means of two proficient techniques like improved auxiliary equation approach and enhanced rational \(({G}^{^{\prime}}/G)\)-expansion procedure. We introduce the transformation,

$$\phi \left( {x,t} \right) = u\left( \xi \right)e^{{i\varphi \left( {x,t} \right)}} ,\;\;\varphi \left( {x,t} \right) = ax + \sigma t + \theta ,\;\;\xi = \kappa x + wt$$
(3.1)

The adaptation of the transformation (3.1) in Eq. (1.1) leaves

$$3a\kappa^{2} u ^{\prime\prime} + \left( {\sigma - a^{3} } \right)u + \left( {ac - b} \right)u^{3} = 0$$
(3.2)
$$\kappa^{3} u^{\prime\prime\prime}+ \left( {w - 3\kappa a^{2} } \right)u^{\prime} + \kappa \left( {c + 2d} \right)u^{2} u^{\prime} = 0$$
(3.3)

Integrating Eq. (3.3) and setting integral parameter as zero yields

$$3\kappa^{3} u^{\prime\prime} + 3\left( {w - 3\kappa a^{2} } \right)u + \kappa \left( {c + 2d} \right)u^{3} = 0$$
(3.4)

Equation (3.2) coincides with Eq. (3.4) and hence becomes

$$3\kappa^{2} u^{\prime\prime} + \left( {3w - 9a^{2} \kappa } \right)u + \left( {c + 2d} \right)u^{3} = 0$$
(3.5)

under the conditions \(b=-2ad\), \(\sigma =\frac{3aw-8{a}^{3}\kappa }{\kappa }\). Applying homogeneous balance principle to Eq. (3.5) provides \(s=1\). Now, we adopt the suggested techniques.

3.1 Outcomes via improved auxiliary equation technique

The balancing number forces Eq. (2.1) to be

$$u(\xi )=\frac{{e}_{0}+{e}_{1}{a}^{\psi (\xi )}}{{f}_{0}+{f}_{1}{a}^{\psi (\xi )}}$$
(3.1.1)

Equation (3.2) alongside Eqs. (3.1.1) and (2.1) turns into a polynomial in \({a}^{\psi (\xi )}\). Equating similar terms of the polynomial to zero and resolving them by computer package Maple, the following outcomes are collected:

$${\text{Case 1}}:\quad e_{0} = \pm \frac{{\kappa \left( {2pf_{1} - qf_{0} } \right)\sqrt { - 6\kappa } }}{{2\sqrt {c + 2d} }},\quad e_{1} = \pm \frac{{\kappa \left( {qf_{1} - 2rf_{0} } \right)\sqrt { - 6\kappa } }}{{2\sqrt {c + 2d} }},\quad w = \frac{\kappa }{2}\left\{ {6a^{2} + \kappa^{2} \left( {q^{2} - 4pr} \right)} \right\}$$
(3.1.2)
$${\text{Case 2}}:\quad e_{0} = \pm \frac{{f_{1} \kappa \left( {4pr - q^{2} } \right)\sqrt { - 6\kappa } }}{{4r\sqrt {c + 2d} }},\quad e_{1} = 0,\quad f_{0} = \frac{{qf_{1} }}{2r},\quad w = \frac{\kappa }{2}\left\{ {6a^{2} + \kappa^{2} \left( {q^{2} - 4pr} \right)} \right\}$$
(3.1.3)
$${\text{Case 3}}:\quad e_{0} = \mp \frac{{3\kappa^{2} qf_{0} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = \pm \frac{{f_{0} rk\sqrt { - 6\kappa } }}{{\sqrt {c + 2d} }},\quad f_{1} = 0,\quad w = \frac{\kappa }{2}\left\{ {6a^{2} + \kappa^{2} \left( {q^{2} - 4pr} \right)} \right\}$$
(3.1.4)

Merging Eqs. (3.1.2)–(3.1.4) and Eq. (3.1.1) yield three expressions for traveling wave solutions as follows:

$${\phi }_{1}\left(x,t\right)=\frac{\kappa {e}^{i\varphi (x,t)}\sqrt{-6\kappa }\{\pm \left(2p{f}_{1}-q{f}_{0}\right)\pm \left(q{f}_{1}-2r{f}_{0}\right){a}^{f\left(\xi \right)}\}}{2\sqrt{c+2d}\{{f}_{0}+{f}_{1}{a}^{f\left(\xi \right)}\}}$$
(3.1.5)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

$${\phi }_{2}\left(x,t\right)=\frac{\pm {e}^{i\varphi (x,t)}\kappa (4pr-{q}^{2})\sqrt{-6\kappa }}{2\sqrt{c+2d}\{q+2r{a}^{f\left(\xi \right)}\}}$$
(3.1.6)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

$$\phi_{3} \left( {x,t} \right) = \frac{{3e^{{i\varphi \left( {x,t} \right)}} \kappa^{2} \left\{ { \mp q \mp 2ra^{f\left( \xi \right)} } \right\}}}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }}$$
(3.1.7)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

We derive the families of solitary wave solutions only for the expressions (3.1.5) and (3.1.6) to avoid the anonymity of the readers. Moreover, for the simplicity, some achieved solutions are ignored to record here.

Group 1 Combining Eq. (3.1.5) with the outcomes of Eq. (2.5) provide twenty-eight wave solutions. Some are given as bellow:

The agreements \({q}^{2}-4pr<0\) and \(r\ne 0\) yield

$${{\phi }_{1}}_{2}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2r\left(2p{f}_{1}-q{f}_{0}\right)-\left(q{f}_{1}-2r{f}_{0}\right)\{q+\sqrt{4pr-{q}^{2}}\mathrm{cot}(\sqrt{4pr-{q}^{2}}\xi /2)\}\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2r{f}_{0}-{f}_{1}\{q+\sqrt{4pr-{q}^{2}}\mathrm{cot}(\sqrt{4pr-{q}^{2}}\xi /2)\}\}}$$
(3.1.8)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

According to the conditions \({q}^{2}-4pr>0\) and \(r\ne 0\), the solution is

$${{\phi }_{1}}_{3}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2r\left(2p{f}_{1}-q{f}_{0}\right)-\left(q{f}_{1}-2r{f}_{0}\right)\{q+\sqrt{{q}^{2}-4pr}\mathrm{tanh}(\sqrt{{q}^{2}-4pr}\xi /2)\}\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2r{f}_{0}-{f}_{1}\{q+\sqrt{{q}^{2}-4pr}\mathrm{tanh}(\sqrt{{q}^{2}-4pr}\xi /2)\}\}}$$
(3.1.9)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

Under the assumption \({q}^{2}+4{p}^{2}<0\), \(r\ne 0\) and \(r=-p\), we obtain

$${{\phi }_{1}}_{5}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p\left(2p{f}_{1}-q{f}_{0}\right)+\left(q{f}_{1}+2p{f}_{0}\right)(q-\sqrt{-{q}^{2}-4{p}^{2}}\mathrm{tan}(\sqrt{-{q}^{2}-4{p}^{2}}\xi /2))\}}{2{e}^{-i\varphi \left(x,t\right)}\sqrt{c+2d}\{2p{f}_{0}+{f}_{1}(q-\sqrt{-{q}^{2}-4{p}^{2}}\mathrm{tan}(\sqrt{-{q}^{2}-4{p}^{2}}\xi /2))\}}$$
(3.1.10)
$${{\phi }_{1}}_{6}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p\left(2p{f}_{1}-q{f}_{0}\right)+\left(q{f}_{1}+2p{f}_{0}\right)(q+\sqrt{-{q}^{2}-4{p}^{2}}\mathrm{cot}(\sqrt{-{q}^{2}-4{p}^{2}}\xi /2))\}}{2{e}^{-i\varphi \left(x,t\right)}\sqrt{c+2d}\{2p{f}_{0}+{f}_{1}(q+\sqrt{-{q}^{2}-4{p}^{2}}\mathrm{cot}(\sqrt{-{q}^{2}-4{p}^{2}}\xi /2))\}}$$
(3.1.11)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}+4{p}^{2})\}\).

When \({q}^{2}+4{p}^{2}>0\), \(r\ne 0\) and \(r=-p\),

$${{\phi }_{1}}_{8}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p\left(2p{f}_{1}-q{f}_{0}\right)+\left(q{f}_{1}+2p{f}_{0}\right)(q+\sqrt{{q}^{2}+4{p}^{2}}\mathrm{coth}(\sqrt{{q}^{2}+4{p}^{2}}\xi /2))\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2p{f}_{0}+{f}_{1}(q+\sqrt{{q}^{2}+4{p}^{2}}\mathrm{coth}(\sqrt{{q}^{2}+4{p}^{2}}\xi /2))\}}$$
(3.1.12)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}+4{p}^{2})\}\).

The postulates \({q}^{2}-4{p}^{2}<0\) and \(r=p\) gives the solutions

$${{\phi }_{1}}_{9}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p\left(2p{f}_{1}-q{f}_{0}\right)-\left(q{f}_{1}-2p{f}_{0}\right)(q-\sqrt{-{q}^{2}+4{p}^{2}}\mathrm{tan}(\sqrt{-{q}^{2}+4{p}^{2}}\xi /2))\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2p{f}_{0}+{f}_{1}(q-\sqrt{-{q}^{2}+4{p}^{2}}\mathrm{tan}(\sqrt{-{q}^{2}+4{p}^{2}}\xi /2))\}}$$
(3.1.13)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4{p}^{2})\}\).

If we agree \({q}^{2}-4{p}^{2}>0\) and \(r=p\), then the found solution is

$${{\phi }_{1}}_{11}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p\left(2p{f}_{1}-q{f}_{0}\right)-\left(q{f}_{1}-2p{f}_{0}\right)(q+\sqrt{{q}^{2}-4{p}^{2}}\mathrm{tanh}(\sqrt{{q}^{2}-4{p}^{2}}\xi /2))\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2p{f}_{0}-{f}_{1}(q+\sqrt{{q}^{2}-4{p}^{2}}\mathrm{tanh}(\sqrt{{q}^{2}-4{p}^{2}}\xi /2))\}}$$
(3.1.14)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4{p}^{2})\}\).

For the conditions \(rp<0\), \(q=0\) and \(r\ne 0\), we attain

$${{\phi }_{1}}_{15}\left(x,t\right)=\frac{\pm 2\kappa \sqrt{-6\kappa }\{p{f}_{1}+r{f}_{0}\sqrt{-p/r}coth(\sqrt{-rp} \xi )\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}-{f}_{1}\sqrt{-p/r}coth(\sqrt{-rp} \xi )\}}$$
(3.1.15)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}-4pr{\kappa }^{2}\}\).

According to the supposition \(q=0\) and \(p=-r\), we construct

$${{\phi }_{1}}_{16}\left(x,t\right)=\frac{\mp r\kappa \sqrt{-6\kappa }\{{f}_{1}\left({e}^{-2r\xi }-1\right)+{f}_{0}({e}^{-2r\xi }+1)\}}{{e}^{-i\varphi \left(x,t\right)}\sqrt{c+2d}\{{f}_{0}({e}^{-2r\xi }-1)+{f}_{1}({e}^{-2r\xi }+1)\}}$$
(3.1.16)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+4{r}^{2}{\kappa }^{2}\}\).

If \(p=r=0\), then

$${{\phi }_{1}}_{18}\left(x,t\right)=\frac{\mp q\kappa \sqrt{-6\kappa }\{{f}_{0}-{f}_{1}(\mathrm{cosh}\left(q\xi \right)+\mathrm{sinh}(q\xi ))\}}{2{e}^{-i\varphi \left(x,t\right)}\sqrt{c+2d}\{{f}_{0}+{f}_{1}(\mathrm{cosh}\left(q\xi \right)+\mathrm{sinh}(q\xi ))\}}$$
(3.1.17)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

When \(p=q=K\) and \(r=0\),

$${{\phi }_{1}}_{19}\left(x,t\right)=\frac{\pm K\kappa \sqrt{-6\kappa }\{\left(2{f}_{1}-{f}_{0}\right)+{f}_{1}({e}^{K\xi }-1)\}}{{e}^{-i\varphi (x,t)}2\sqrt{c+2d}\{{f}_{0}+{f}_{1}({e}^{K\xi }-1)\}}$$
(3.1.18)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({K}^{2}-4Kr)\}\).

The agreements \(q=r=K\) and \(p=0\) provide

$${{\phi }_{1}}_{20}\left(x,t\right)=\frac{\mp K\kappa \sqrt{-6\kappa }\{{f}_{0}\left(1-{e}^{K\xi }\right)-\left({f}_{1}-2{f}_{0}\right){e}^{K\xi }\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}(1-{e}^{K\xi })+{f}_{1}{e}^{K\xi }\}}$$
(3.1.19)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{K}^{2}\}\).

For \(q=p+r\),

$${{\phi }_{1}}_{21}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{\left(2p{f}_{1}-\left(p+r\right){f}_{0}\right)\left(1-{re}^{\left(p-r\right)\xi }\right)-\left((p+r){f}_{1}-2r{f}_{0}\right)(1-p{e}^{(p-r)\xi })\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}\left(1-{re}^{\left(p-r\right)\xi }\right)-{f}_{1}(1-p{e}^{(p-r)\xi })\}}$$
(3.1.20)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{(p-r)}^{2}\}\).

When \(p=0\),

$${{\phi }_{1}}_{23}\left(x,t\right)=\frac{\mp \kappa \sqrt{-6\kappa }\{q{f}_{0}\left(1-{re}^{q\xi }\right)-\left(q{f}_{1}-2r{f}_{0}\right)q{e}^{q\xi }\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}(1-{re}^{q\xi })+{f}_{1}q{e}^{q\xi }\}}$$
(3.1.21)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

According to the postulate \(r=q=p\ne 0\), we gain

$${{\phi }_{1}}_{24}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2\left(2p{f}_{1}-q{f}_{0}\right)+\left(q{f}_{1}-2r{f}_{0}\right)(\sqrt{3}\mathrm{tan}(\sqrt{3}p\xi /2)-1)\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{2{f}_{0}+{f}_{1}(\sqrt{3}\mathrm{tan}(\sqrt{3}p\xi /2)-1)\}}$$
(3.1.22)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

For \(p=q=0\),

$${{\phi }_{1}}_{26}\left(x,t\right)=\frac{\pm {f}_{0}\kappa {e}^{i\varphi (x,t)}\sqrt{-6\kappa }}{\xi \sqrt{c+2d}\{{f}_{0}-{f}_{1}/r\xi \}}$$
(3.1.23)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{6{a}^{2}\kappa }{2}\).

According to \(r=p\) and \(q=0\), the solution is

$${{\phi }_{1}}_{27}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{2p{f}_{1}-2p{f}_{0}\mathrm{tan}(p\xi )\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}+{f}_{1}\mathrm{tan}(p\xi )\}}$$
(3.1.24)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}-4{p}^{2}{\kappa }^{2}\}\).

Under the agreement \(r=0\), the solution is obtained as

$${{\phi }_{1}}_{28}\left(x,t\right)=\frac{\pm \kappa \sqrt{-6\kappa }\{\left(2p{f}_{1}-q{f}_{0}\right)+q{f}_{1}({e}^{q\xi }-m/n)\}}{2{e}^{-i\varphi (x,t)}\sqrt{c+2d}\{{f}_{0}+{f}_{1}({e}^{q\xi }-m/n)\}}$$
(3.1.25)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

Group 2 Merging Eq. (3.1.6) together with the solutions of Eq. (2.5) delivers twenty-five wave solutions among which some are as follows:

According to the assumption \({q}^{2}-4pr<0\) and \(r\ne 0\), we obtain the solution

$${{\phi }_{2}}_{1}\left(x,t\right)=\frac{\pm {e}^{i\varphi (x,t)}\kappa \sqrt{-6\kappa (4pr-{q}^{2})}}{2\sqrt{(c+2d)(4pr-{q}^{2})} \mathrm{tan}(\sqrt{4pr-{q}^{2}}\xi /2)}$$
(3.1.26)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

The conditions \({q}^{2}-4pr>0\) and \(r\ne 0\) provide

$${{\phi }_{2}}_{4}\left(x,t\right)=\frac{\pm {e}^{i\varphi (x,t)}\kappa \sqrt{-6\kappa ({q}^{2}-4pr)}}{2\sqrt{(c+2d)({q}^{2}-4pr)}\mathrm{ coth}(\sqrt{{q}^{2}-4pr}\xi /2)}$$
(3.1.27)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

When \({q}^{2}+4{p}^{2}<0\), \(r\ne 0\) and \(r=-p\),

$${{\phi }_{2}}_{6}\left(x,t\right)=\frac{\pm {e}^{i\varphi \left(x,t\right)}\kappa \sqrt{6\kappa (4{p}^{2}+{q}^{2})}}{2\sqrt{(c+2d) }\mathrm{ cot}(\sqrt{-{q}^{2}-4{p}^{2}}\xi /2)}$$
(3.1.28)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}+4{p}^{2})\}\).

Under the assumption \({q}^{2}+4{p}^{2}>0\), \(r\ne 0\) and \(r=-p\), the obtained solution is

$${{\phi }_{2}}_{8}\left(x,t\right)=\frac{\pm {e}^{i\varphi \left(x,t\right)}\kappa \sqrt{-6\kappa ({q}^{2}+4{p}^{2})}}{2\sqrt{c+2d} \mathrm{coth}(\sqrt{{q}^{2}+4{p}^{2}}\xi /2)}$$
(3.1.29)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}+4{p}^{2})\}\).

Imposing \({q}^{2}-4{p}^{2}<0\) and \(r=p\) yield

$${{\phi }_{2}}_{9}\left(x,t\right)=\frac{\pm {e}^{i\varphi \left(x,t\right)}\kappa \sqrt{-6\kappa (4{p}^{2}-{q}^{2})}}{2\sqrt{c+2d} \mathrm{tan}(\sqrt{-{q}^{2}+4{p}^{2}}\xi /2)}$$
(3.1.30)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4{p}^{2})\}\).

The assumption \({q}^{2}-4{p}^{2}>0\) and \(r=p\) give

$${{\phi }_{2}}_{12}\left(x,t\right)=\frac{\pm {e}^{i\varphi \left(x,t\right)}\kappa \sqrt{-6\kappa ({q}^{2}-4{p}^{2})}}{2\sqrt{c+2d} \mathrm{coth}(\sqrt{{q}^{2}-4{p}^{2}}\xi /2)}$$
(3.1.31)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4{p}^{2})\}\).

When \(rp<0\), \(q=0\) and \(r\ne 0\),

$${{\phi }_{2}}_{13}\left(x,t\right)=\mp \frac{\kappa p{e}^{i\varphi (x,t)}\sqrt{6\kappa r}}{\sqrt{p(c+2d)} tanh(\sqrt{-rp} \xi )}$$
(3.1.32)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}-4pr{\kappa }^{2}\}\).

If \(q=0\) and \(p=-r\), the solution is

$${{\phi }_{2}}_{16}\left(x,t\right)=\frac{\mp \kappa r{e}^{i\varphi \left(x,t\right)}\sqrt{-6\kappa } (1-{e}^{2r\xi })}{\sqrt{c+2d} (1+{e}^{2r\xi })}$$
(3.1.33)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+4{\kappa }^{2}{r}^{2}\}\).

According to \(p=r=0\), we acquire

$${{\phi }_{2}}_{17}\left(x,t\right)=\frac{\mp \kappa q{e}^{i\varphi (x,t)}\sqrt{-6\kappa }}{2\sqrt{c+2d}}$$
(3.1.34)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

The agreements \(p=q=K\) and \(r=0\) offer

$${{\phi }_{2}}_{18}\left(x,t\right)=\frac{\mp \kappa K{e}^{i\varphi (x,t)}\sqrt{-6\kappa }}{2\sqrt{c+2d}}$$
(3.1.35)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{K}^{2}\}\).

When \(q=r=K\) and \(p=0\), the solution is

$${{\phi }_{2}}_{19}\left(x,t\right)=\frac{\mp \kappa K{e}^{i\varphi \left(x,t\right)}\sqrt{-6\kappa } (1-{e}^{K\xi })}{2\sqrt{c+2d} (1+{e}^{K\xi })}$$
(3.1.36)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{K}^{2}\}\).

According to the condition \(q=-(p+r)\), the solution is attained as

$${{\phi }_{2}}_{21}\left(x,t\right)=\frac{\pm {e}^{i\varphi \left(x,t\right)}\kappa {\left(p-r\right)}^{2}\sqrt{-6\kappa } (r-{e}^{(p-r)\xi })}{2\sqrt{c+2d}\{\left(p+r\right)(r-{e}^{\left(p-r\right)\xi })-2r(p-{e}^{(p-r)\xi })\}}$$
(3.1.37)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{\left(p-r\right)}^{2}\}\).

When \(p=0\),

$$\phi_{222} \left( {x,t} \right) = \frac{{ \mp e^{{i\varphi \left( {x,t} \right)}} \kappa q^{2} \sqrt { - 6\kappa } \left( {1 - re^{q\xi } } \right)}}{{2\sqrt {c + 2d} \left\{ {q\left( {1 - re^{q\xi } } \right) + 2rqe^{q\xi } } \right\}}}$$
(3.1.38)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

Under the condition \(r=q=p\ne 0\), the delivered solution is

$$\phi_{223} \left( {x,t} \right) = \frac{{ \pm e^{{i\varphi \left( {x,t} \right)}} \kappa \left( {4pr - q^{2} } \right)\sqrt { - 6\kappa } }}{{2\sqrt {c + 2d} \{ q - r + \sqrt 3 r\tan \left( {\sqrt 3 p\xi /2} \right)}}$$
(3.1.39)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}({q}^{2}-4pr)\}\).

The agreement \(r=0\) offers the wave solution

$$\phi_{225} \left( {x,t} \right) = \frac{{ \mp \kappa qe^{{i\varphi \left( {x,t} \right)}} \sqrt { - 6\kappa } }}{{2\sqrt {c + 2d} }}$$
(3.1.40)

where \(\varphi \left(x,t\right)=ax+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\) and \(w=\frac{\kappa }{2}\{6{a}^{2}+{\kappa }^{2}{q}^{2}\}\).

3.2 Outcomes via enhanced rational \(({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})\)-expansion approach

The balancing number forces Eq. (2.1) to be

$$u\left( \xi \right) = \frac{{e_{0} + e_{1} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right) + f_{1} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{ - 1} }}{{g_{0} + g_{1} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right) + h_{1} \left( {G^{\prime}\left( \xi \right)/G\left( \xi \right)} \right)^{ - 1} }}$$
(3.2.1)

Incorporating Eq. (3.2.1) alongside Eq. (2.2) in Eq. (3.2) yields a polynomial in \(({G}^{^{\prime}}(\xi )/G(\xi ))\). Set each coefficient of the found polynomial to zero and solve them for the required results by using Maple software:

$${\text{Case 1}}:\quad e_{0} = \mp \frac{{6\kappa^{2} \varepsilon g_{0} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = \pm \frac{{g_{0} \kappa \left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{c + 2d},\quad f_{1} = \mp \frac{{6\kappa^{2} g_{0} \in }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad h_{1} = \frac{{g_{0} \varepsilon }}{{2\left( {\eta - 1} \right)}},\quad g_{1} = 0,\quad a = \pm \frac{{\sqrt {3\kappa \left\{ {\kappa^{3} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) + w} \right\}} }}{3\kappa }$$
(3.2.2)
$${\text{Case 2}}:\quad e_{0} = \mp \frac{{\kappa \left\{ {\varepsilon g_{0} - 2h_{1} \left( {\eta - 1} \right)} \right\}\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{{2\left( {c + 2d} \right)}},\quad e_{1} = 0,\quad f_{1} = \pm \frac{{\kappa \left( {\varepsilon h_{1} - 2 \in g_{0} } \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{{2\left( {c + 2d} \right)}},\quad g_{1} = 0,\quad w = \frac{\kappa }{2}\left\{ {\kappa^{2} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) + 6a^{2} } \right\}$$
(3.2.3)
$${\text{Case 3}}:\quad e_{0} = \mp \frac{{6\kappa^{2} \varepsilon g_{0} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = \pm \frac{{g_{0} \kappa \left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{c + 2d},\quad f_{1} = \mp \frac{{3\kappa^{2} g_{0} \left( {\varepsilon^{2} - 2 \in \eta + 2 \in } \right)}}{{\left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad h_{1} = \frac{{g_{0} \varepsilon }}{{2\left( {\eta - 1} \right)}},\quad g_{1} = 0,\quad a = \pm \frac{{\sqrt { - 3\kappa \left\{ {\kappa^{3} \left( {2\varepsilon^{2} - 8 \in \eta + 8 \in } \right) - w} \right\}} }}{3\kappa }$$
(3.2.4)
$${\text{Case 4}}:\quad e_{0} = \mp \frac{{3\kappa^{2} \varepsilon g_{0} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = 0,\quad f_{1} = \pm \frac{{g_{0} \in \kappa \sqrt { - 6\kappa \left( {c + 2d} \right)} }}{c + 2d},\quad h_{1} = g_{1} = 0,\quad w = \frac{\kappa }{2}\left\{ {\kappa^{2} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) + 6a^{2} } \right\}$$
(3.2.5)
$${\text{Case 5}}:\quad e_{0} = \mp \frac{{3\kappa^{2} \left\{ {\varepsilon g_{0} + 2h_{1} \left( {\eta - 1} \right)} \right\}}}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = \pm \frac{{g_{0} \kappa \left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{c + 2d},\quad f_{1} = \mp \frac{{3\kappa^{2} \varepsilon h_{1} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad g_{1} = 0,\quad w = \frac{\kappa }{2}\left\{ {\kappa^{2} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) + 6a^{2} } \right\}$$
(3.2.6)
$${\text{Case 6}}:\quad e_{0} = \pm \frac{{h_{1} \kappa \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{{4 \in \left( {c + 2d} \right)}},\quad g_{0} = \frac{{\varepsilon h_{1} }}{2 \in },\quad e_{1} = f_{1} = g_{1} = 0,\quad w = \frac{\kappa }{2}\left\{ {\kappa^{2} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) + 6a^{2} } \right\}$$
(3.2.7)
$${\text{Case 7}}:e_{0} = \quad \mp \frac{{6\kappa^{2} \varepsilon g_{0} }}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad e_{1} = \pm \frac{{g_{0} \kappa \left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }}{c + 2d},\quad f_{1} = \mp \frac{{3\kappa^{2} \varepsilon^{2} g_{0} }}{{2\left( {\eta - 1} \right)\sqrt { - 6\kappa \left( {c + 2d} \right)} }},\quad h_{1} = \frac{{g_{0} \varepsilon }}{{2\left( {\eta - 1} \right)}},\quad g_{1} = 0,\quad a = \pm \frac{{\sqrt { - 6\kappa \left\{ {\kappa^{3} \left( {\varepsilon^{2} - 4 \in \eta + 4 \in } \right) - 2w} \right\}} }}{6\kappa }$$
(3.2.8)

The req uired above cases deliver huge wave solutions in appropriate form. For simplicity, we state the outcomes only for case 1. Using Eqs. (3.2.2) and (3.2.1) yields the assumed expression for traveling wave solutions:

$$\phi \left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \mp (\eta -1)({G}^{^{\prime}}(\xi )/G(\xi ))\mp \epsilon /({G}^{^{\prime}}(\xi )/G(\xi ))\}}{\sqrt{-6\kappa (c+2d)}\{1+\varepsilon /\{2(\eta -1)({G}^{^{\prime}}(\xi )/G(\xi ))\}\}}$$
(3.2.9)

where \(\varphi \left(x,t\right)=\pm \frac{\sqrt{3\kappa \{{\kappa }^{3}\left({\varepsilon }^{2}-4\epsilon \eta +4\epsilon \right)+w\}}}{3\kappa }x+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\).

Type 1 Under the postulates \(\Upsilon ={\upvarepsilon }^{2}-4\upepsilon \left(\eta -1\right)>0\mathrm{ and \varepsilon }\left(\eta -1\right)\ne 0 (\mathrm{or \epsilon }(\eta -1)\ne 0)\), twelve solitary wave solutions are originated among which a few are as follows:

$${\phi }_{1}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \pm (\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{tanh}(\sqrt{\Upsilon }\upxi /2)\}/2)\pm 2\epsilon (\eta -1)/\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{tanh}(\sqrt{\Upsilon }\upxi /2)\}\}}{\sqrt{-6\kappa (c+2d)}\{1-\varepsilon /\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{tanh}(\sqrt{\Upsilon }\upxi /2)\}\}}$$
(3.2.10)
$${\phi }_{2}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \pm (\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{coth}(\sqrt{\Upsilon }\upxi /2)\}/2)\pm 2\upepsilon \left(\eta -1\right)/\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{coth}(\sqrt{\Upsilon }\upxi /2)\}\}}{\sqrt{-6\kappa (c+2d)}\{1-\varepsilon /\{\upvarepsilon +\sqrt{\Upsilon }\mathrm{coth}(\sqrt{\Upsilon }\upxi /2)\}\}}$$
(3.2.11)
$${\phi }_{4}\left(x,t\right)=\frac{\begin{array}{c}6{\kappa }^{2}{e}^{i\varphi \left(x,t\right)}\{\mp \varepsilon \pm \frac{\upvarepsilon +\sqrt{\Upsilon }(\mathrm{coth}\left(\sqrt{\Upsilon }\upxi \right)\pm \mathrm{csch}\left(\sqrt{\Upsilon }\upxi \right))}{2}\\ \pm 2\epsilon \left(\eta -1\right)/\{\varepsilon +\sqrt{\Upsilon }(\mathrm{coth}(\sqrt{\Upsilon }\upxi )\pm csch(\sqrt{\Upsilon }\xi ))\}\}\end{array}}{\sqrt{-6\kappa (c+2d)}\{1-\varepsilon /\{\upvarepsilon +\sqrt{\Upsilon }(\mathrm{coth}(\sqrt{\Upsilon }\upxi )\pm \mathrm{csch}(\sqrt{\Upsilon }\upxi ))\}\}}$$
(3.2.12)
$${\phi }_{7}\left(x,t\right)=\frac{\begin{array}{c}6{\kappa }^{2}{e}^{i\varphi \left(x,t\right)}\{\mp \varepsilon \mp \{-\varepsilon -\frac{\sqrt{\left({\mathrm{c}}_{1}^{2}+{\mathrm{c}}_{2}^{2}\right)\Upsilon }+{\mathrm{c}}_{1}\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi )}{{\mathrm{c}}_{1}\mathrm{sinh}(\sqrt{\Upsilon }\upxi )+{\mathrm{c}}_{2}}\}/2\\ \mp 2\epsilon (\eta -1)/\{-\varepsilon -\frac{\sqrt{\left({\mathrm{c}}_{1}^{2}+{\mathrm{c}}_{2}^{2}\right)\Upsilon }+{\mathrm{c}}_{1}\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi )}{{\mathrm{c}}_{1}\mathrm{sinh}(\sqrt{\Upsilon }\upxi )+{\mathrm{c}}_{2}}\}\}\end{array}}{\sqrt{-6\kappa (c+2d)}\{1+\varepsilon /\{-\upvarepsilon -\frac{\sqrt{\left({\mathrm{c}}_{1}^{2}+{\mathrm{c}}_{2}^{2}\right)\Upsilon }+{\mathrm{c}}_{1}\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi )}{{\mathrm{c}}_{1}\mathrm{sinh}(\sqrt{\Upsilon }\upxi )+{\mathrm{c}}_{2}}\}\}}$$
(3.2.13)

where \({\mathrm{c}}_{1}\) and \({c}_{2}\) are non-zero real parameters.

$${\phi }_{8}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \mp \frac{2\upepsilon (\eta -1)\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2)}{\sqrt{\Upsilon }\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)-\mathrm{\varepsilon cosh}(\sqrt{\Upsilon }\upxi /2)}\mp \frac{\sqrt{\Upsilon }\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)-\mathrm{\varepsilon cosh}(\sqrt{\Upsilon }\upxi /2)}{2\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2)}\}}{\sqrt{-6\kappa (c+2d)}\{1+\frac{\varepsilon (\sqrt{\Upsilon }\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)-\mathrm{\varepsilon cosh}(\sqrt{\Upsilon }\upxi /2))}{4\epsilon (\eta -1)\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2)}\}}$$
(3.2.14)
$${\phi }_{9}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \pm \frac{2\upepsilon (\eta -1)\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)}{\mathrm{\varepsilon sinh}(\sqrt{\Upsilon }\upxi /2)-\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2)}\pm \frac{\mathrm{\varepsilon sinh}(\sqrt{\Upsilon }\upxi /2)-\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2)}{2\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)}\}}{\sqrt{-6\kappa (c+2d)}\{1-\frac{\varepsilon (\mathrm{\varepsilon sinh}(\sqrt{\Upsilon }\upxi /2)-\sqrt{\Upsilon }\mathrm{cosh}(\sqrt{\Upsilon }\upxi /2))}{4\epsilon (\eta -1)\mathrm{sinh}(\sqrt{\Upsilon }\upxi /2)}\}}$$
(3.2.15)

where \(\varphi \left(x,t\right)=\pm \frac{\sqrt{3\kappa \{{\kappa }^{3}\left({\varepsilon }^{2}-4\epsilon \eta +4\epsilon \right)+w\}}}{3\kappa }x+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\).

Type 2 According to the conditions \({{\Upsilon} ={\upvarepsilon} }^{2}-4{\upepsilon} \left(\eta -1\right)<0 \; {{\rm and} \;{\varepsilon} }\left(\eta -1\right)\ne 0 ({\rm{or}} {\epsilon }(\eta -1)\ne 0)\), we might produce twelve wave solutions. But few solutions are recorded here for simplicity as follows:

$${\phi }_{13}\left(x,t\right)=\frac{6{\kappa }^{2}\{\mp \varepsilon \mp \{-\upvarepsilon +\sqrt{-\Upsilon }\mathrm{tan}(\sqrt{-\Upsilon }\upxi /2)\}/2\mp 2\epsilon (\eta -1)/\{-\upvarepsilon +\sqrt{-\Upsilon }\mathrm{tan}(\sqrt{-\Upsilon }\upxi /2)\}\}}{{e}^{-i\varphi \left(x,t\right)}\sqrt{-6\kappa (c+2d)}\{1+\varepsilon /\{-\upvarepsilon +\sqrt{-\Upsilon }\mathrm{tan}(\sqrt{-\Upsilon }\upxi /2)\}\}}$$
(3.2.16)
$${\phi }_{14}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \pm \{\upvarepsilon +\sqrt{-\Upsilon }\mathrm{cot}(\sqrt{-\Upsilon }\upxi /2)\}\pm 2\epsilon (\eta -1)/\{\upvarepsilon +\sqrt{-\Upsilon }\mathrm{cot}(\sqrt{-\Upsilon }\upxi /2)\}\}}{\sqrt{-6\kappa (c+2d)}\{1-\varepsilon /\{\upvarepsilon +\sqrt{-\Upsilon }\mathrm{cot}(\sqrt{-\Upsilon }\upxi /2)\}\}}$$
(3.2.17)
$$\phi _{{19}} \left( {x,t} \right) = \frac{\begin{gathered} \hfill 6\kappa ^{2} e^{{i\varphi \left( {x,t} \right)}} \left\{ { \mp \varepsilon \mp \left\{ { - \varepsilon - \frac{{ \pm \sqrt { - \Upsilon \left( {{\rm{c}}_{1}^{2} - {\rm{c}}_{2}^{2} } \right)} + {\rm{c}}_{1} \sqrt { - \Upsilon } \cos \left( {\sqrt { - \Upsilon } {{\upxi }}} \right)}}{{{\rm{c}}_{1} \sin \left( {\sqrt { - \Upsilon } {{\upxi }}} \right) + {\rm{c}}_{2} }}} \right\}/2} \right. \\ \hfill \left. { \mp 2 \in \left( {\eta - 1} \right)/\left\{ { - {{\upvarepsilon }} - \frac{{ \pm \sqrt { - \Upsilon \left( {{\rm{c}}_{1}^{2} - {\rm{c}}_{2}^{2} } \right)} + {\rm{c}}_{1} \sqrt { - \Upsilon } \cos \left( {\sqrt { - \Upsilon } {{\upxi }}} \right)}}{{{\rm{c}}_{1} \sin \left( {\sqrt { - \Upsilon } {{\upxi }}} \right) + {\rm{c}}_{2} }}} \right\}} \right\} \\ \end{gathered} }{{\sqrt { - 6\kappa \left( {c + 2d} \right)} \left\{ {1 + \varepsilon /\left\{ { - {{\upvarepsilon }} - \frac{{ \pm \sqrt { - \Upsilon \left( {{\rm{c}}_{1}^{2} - {\rm{c}}_{2}^{2} } \right)} + {\rm{c}}_{1} \sqrt { - \Upsilon } \cos \left( {\sqrt { - \Upsilon } {{\upxi }}} \right)}}{{{\rm{c}}_{1} \sin \left( {\sqrt { - \Upsilon } {{\upxi }}} \right) + {\rm{c}}_{2} }}} \right\}} \right\}}}$$
(3.2.18)

where \({c}_{1}\) and \({c}_{2}\) are non-zero real parameters satisfying \({\mathrm{c}}_{1}^{2}-{\mathrm{c}}_{2}^{2}>0\).

$$\phi _{{20}} \left( {x,t} \right) = \frac{{6\kappa ^{2} e^{{i\varphi \left( {x,t} \right)}} \left\{ { \mp \varepsilon \pm \frac{{2 \in \left( {\eta - 1} \right)\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)}}{{\sqrt { - \Upsilon } \sin \left( {\sqrt { - \Upsilon } {\upxi }/2} \right) + {{\upvarepsilon }}\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)}} \pm \frac{{\sqrt { - \Upsilon } \sin \left( {\sqrt { - \Upsilon } {\upxi }/2} \right) + {{\upvarepsilon }}\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)}}{{2\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)}}} \right\}}}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} \left\{ {1 - \frac{{\varepsilon \left( {\sqrt { - \Upsilon } \sin \left( {\sqrt { - \Upsilon } {\upxi }/2} \right) + {{\upvarepsilon }}\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)} \right)}}{{4 \in \left( {\eta - 1} \right)\cos \left( {\sqrt { - \Upsilon } {\upxi }/2} \right)}}} \right\}}}$$
(3.2.19)
$${\phi }_{21}\left(x,t\right)=\frac{6{\kappa }^{2}\{\mp \varepsilon \mp \frac{2\upepsilon (\eta -1)\mathrm{sin}(\sqrt{-\Upsilon }\upxi /2)}{-\mathrm{\varepsilon sin}(\sqrt{-\Upsilon }\upxi /2)+\sqrt{-\Upsilon }\mathrm{cos}(\sqrt{-\Upsilon }\upxi /2)}\mp \frac{-\mathrm{\varepsilon sin}(\sqrt{-\Upsilon }\upxi /2)+\sqrt{-\Upsilon }\mathrm{cos}(\sqrt{-\Upsilon }\upxi /2)}{2\mathrm{sin}(\sqrt{-\Upsilon }\upxi /2)}\}}{{e}^{-i\varphi (x,t)}\sqrt{-6\kappa (c+2d)}\{1+\frac{\varepsilon (-\mathrm{\varepsilon sin}(\sqrt{-\Upsilon }\upxi /2)+\sqrt{-\Upsilon }\mathrm{cos}(\sqrt{-\Upsilon }\upxi /2))}{4\epsilon (\eta -1)\mathrm{sin}(\sqrt{-\Upsilon }\upxi /2)}\}}$$
(3.2.20)

where \(\varphi \left(x,t\right)=\pm \frac{\sqrt{3\kappa \{{\kappa }^{3}\left({\varepsilon }^{2}-4\epsilon \eta +4\epsilon \right)+w\}}}{3\kappa }x+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\).

Type 3 For the agreements \(\upepsilon =0\mathrm{ and \varepsilon }(\eta -1)\ne 0\), we obtain the wave solutions

$$\phi _{{25}} \left( {x,t} \right) = \frac{{6\kappa ^{2} e^{{i\varphi \left( {x,t} \right)}} \left\{ { \mp \varepsilon \pm \frac{{{{\upvarepsilon {\rm{d}}}}_{1} }}{{{\rm{d}}_{1} + \cosh \left( {{{\upvarepsilon \upxi }}} \right) - \sinh \left( {{\upvarepsilon \upxi }} \right)}} \pm \frac{{ \in \left( {\eta - 1} \right)\left[ {{\rm{d}} + \cosh \left( {{\upvarepsilon \upxi }} \right) - \sinh \left( {{\upvarepsilon \upxi }} \right)} \right]}}{{{ {\upvarepsilon {\rm {d}}}}_{1} }}} \right\}}}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} \left\{ {1 - \left\{ {{\rm{d}}_{1} + \cosh \left( {{{\upvarepsilon \upxi }}} \right) - \sinh \left( {{{\upvarepsilon \upxi }}} \right)} \right\}/2d_{1} } \right\}}}$$
(3.2.21)
$$\phi _{{26}} \left( {x,t} \right) = \frac{{6\kappa ^{2} e^{{i\varphi (x,t)}} \left\{ { \mp \varepsilon \pm \frac{{{{\upvarepsilon }}[\cosh \left( {{{\upvarepsilon \upxi }}} \right) + \sinh \left( {{{\upvarepsilon \upxi }}} \right)]}}{{{\rm{d}}_{1} + \cosh \left( {{\upvarepsilon \upxi }} \right) + \sinh \left( {{\upvarepsilon \upxi }} \right)}} \pm \frac{{ \in (\eta - 1)[{\rm{d}}_{1} + \cosh \left( {{\upvarepsilon \upxi }} \right) + \sinh \left( {{\upvarepsilon \upxi }} \right)]}}{{{{\upvarepsilon }}[\cosh \left( {{\upvarepsilon \upxi }} \right) + \sinh \left( {{\upvarepsilon \upxi }} \right)]}}} \right\}}}{{\sqrt { - 6\kappa (c + 2d)} \{ 1 - \{ {\rm{d}}_{1} + \cosh \left( {{\upvarepsilon \upxi }} \right) + \sinh \left( {{\upvarepsilon \upxi }} \right)\} /2[\cosh \left( {{\upvarepsilon \upxi }} \right) + \sinh \left( {{\upvarepsilon \upxi }} \right)]\} }}$$
(3.2.22)

where \({\mathrm{d}}_{1}\) is an arbitrary constant and \(\varphi \left(x,t\right)=\pm \frac{\sqrt{3\kappa \{{\kappa }^{3}{\varepsilon }^{2}+w\}}}{3\kappa }x+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\).

Type 4 Under the assumption \(\eta -1\ne 0\mathrm{ and \epsilon }=\upvarepsilon =0\), the wave solution is found as

$${\phi }_{27}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{i\varphi (x,t)}\{\mp \varepsilon \pm \frac{\eta -1}{\left(\eta -1\right)\upxi +{\mathrm{c}}_{3}}\pm \epsilon \{\left(\eta -1\right)\upxi +{\mathrm{c}}_{3}\}\}}{\sqrt{-6\kappa (c+2d)}\{1-\frac{\varepsilon \{\left(\eta -1\right)\upxi +{\mathrm{c}}_{3}\}}{2(\eta -1)}\}}$$
(3.2.23)

where \({\mathrm{c}}_{3}\) is an arbitrary constant and \(\varphi \left(x,t\right)=\pm \frac{\sqrt{3\kappa w}}{3\kappa }x+\frac{3aw-8{a}^{3}\kappa }{\kappa }t+\theta\), \(\xi =\kappa x+wt\).

4 Results discussion and graphical appearances

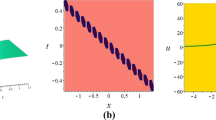
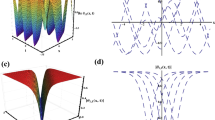
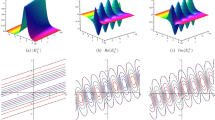
The above created outcomes to the generalized third-order Schrödinger model have been compared with the available results in the literature and claimed to be diverse and novel with the distinct wave characteristics (Lu et al. 2019; Nasreen et al. 2019; Hosseini et al. 2020; Malik et al. 2021b; Zhao et al. 2022; Wang et al. 2014). At this theme, some of the solutions are described graphically for their physical attendance which stands for different type of solitons, like, kink shape soliton, singular kink shape soliton, bell shape soliton, anti-bell shape soliton, periodic soliton, anti-periodic soliton, compacton, peakon, anti-peakon etc. The sketch of solution (3.1.8) is in anti-kink shape soliton: 3D and contour are displayed in Fig. 1a, b with particular values \(c=d=\theta =q=r={f}_{1}=1\), \(a={f}_{0}=0\) and \(\kappa =p=-1\) within the interval \(-4\le x,t\le 4\) while plotting 2D profile in Fig. 1c along with the values of \(t=0\). Compacton soliton obtained from solution (3.1.10): Fig. 2a, b constituted for 3D, contour are drawn with the fixed values of \(c={f}_{0}={f}_{1}=1\), \(\kappa =q=p=-1\), \(a=\theta =0\), \(d=1.25\) in the range \(-0.2\le x\le 0.2\) and \(-0.1\le t\le 0.1\) while Fig. 2c represents 2D figure along with \(t=0\). Yield of the solution (3.1.11) is in periodic form: 3D, contour are established in Fig. 3a, b alongside the values \(c=p={f}_{1}=1\), \(\kappa =q={f}_{0}=-1\), \(a=\theta =0\), \(d=1.25\) within \(-3.5\le x\le 3.5\) and \(-0.5\le t\le 0.5\) whereas 2D graph placed in Fig. 3c for \(t=0\). Soliton of the solution (3.1.14) is in periodic form: Fig. 4a, b portrayed for 3D, contour are drawn together with the fixed values \(\kappa =c=d=\theta =q=p={f}_{0}=1\), \(a={f}_{1}=0.001\) in the interval \(-4\le x\le 8\) and \(-4\le t\le 4\) in which Fig. 4c displayed 2D plot with \(t=0\). The solution (3.1.16) bounces anti-kink shape soliton: Fig. 5a, b exposing 3D, contour are ornamented by denoting the values \(c=d=\theta ={f}_{1}=1\), \(\kappa =r=-1\) and \(a={f}_{0}=0\) within the range \(-2.5\le x,t\le 2.5\) and 2D plot designated in Fig. 5c for \(t=0\). Diagram of solution (3.1.23) is in singular kink shape soliton: 3D, contour are sketched by conveying the particular values of unknown parameters \(\kappa =c=d=\theta ={f}_{0}={f}_{1}=r=1\) and \(a=0.01\) in the duration \(-5\le x,t\le 5\) indicating in Fig. 6a, b where 2D profile displayed in Fig. 6c is found for \(t=0\). Peakon soliton attained for the solution (3.1.27): Fig. 7a, b existing for 3D, contour that are outlined by using fixed values of arbitrary constants \(c=d=\theta =r=1\), \(\kappa =-1\), \(a=0\), \(q=2\) and \(p=0.5\) within the interval \(-4\le x,t\le 4\) in which 2D graph exhibited in Fig. 7c with \(t=0\). Graph of a cuspon gifted from the solution (3.1.28): Fig. 8a, b are decorated by giving the unknown parameter’s values \(c=d=\theta =q=1\), \(\kappa =-1\), \(a=0\), \(p=0.79\) in association with the range \(-4\le x\le 4\) and \(-0.25\le t\le 0.25\) placed for 3D, contour while 2D plot in Fig. 8c is obtained for \(t=0\). Output is in anti-peakon soliton for the solution (3.1.38): Fig. 9a, b sited for 3D, contour are traced by assigning arbitrary constrictions as \(\kappa =1.199\), \(a=-0.019\), \(c=\theta =1\), \(d=1.5\), \(q=1.05\) and \(r=1.19\) within \(-5\le x,t\le 5\) whereas 2D graph in Fig. 9c is appeared with \(t=0\). Attained soliton is in anti-periodic form of solution (3.1.39): Fig. 10a, b representing 3D, contour are portrayed with the values \(c=d=\theta =q=1\), \(\kappa =r=-1\), \(p=0.25\) and \(a=0\) in the interval \(-15\le x,t\le 30\) in which 2D plot are pictured in Fig. 10c for \(t=0\). The singular kink shape soliton obtained from solution (3.2.12): 3D, contour found in Fig. 11a, b for the particular values of \(\epsilon =c=d=w=1\), \(\kappa =-1\), \(a=0.1\), \(\theta =0\), \(\varepsilon =3\) and \(\eta =2\) within the range \(-0.2\le x\le 0.213\) while 2D figure presenting in Fig. 11c along with \(t=0\). Outline of the solution (3.2.13) is in anti-bell shape soliton: 3D, contour are recognized in Fig. 12a, b with the values \(\varepsilon =c=d=w=A=B=1\), \(\epsilon =0.25\), \(\eta =-2\), \(\kappa =-1\) and \(a=\theta =0\) in the interval \(-9\le x\le 9\) where 2D graph positioned in Fig. 12c for \(t=0\).

Fig. 1
figure 1

The sketch of solution (3.1.8) represents anti-kink type soliton for the values of \(c=d=\theta =q=r={f}_{1}=1\), \(a={f}_{0}=0\) and \(\kappa =p=-1\) within the interval \(-4\le x,t\le 4\) while plotting 2D for \(t=0\)

Full size image
Fig. 2
figure 2

Compacton soliton obtained from solution (3.1.10) under \(c={f}_{0}={f}_{1}=1\), \(\kappa =q=p=-1\), \(a=\theta =0\), \(d=1.25\) within \(-0.2\le x\le 0.2\) and \(-0.1\le t\le 0.1\) and 2D figure represents with \(t=0\)

Full size image
Fig. 3
figure 3

Yield of the solution (3.1.11) is in periodic form for the values \(c=p={f}_{1}=1\), \(\kappa =q={f}_{0}=-1\), \(a=\theta =0\), \(d=1.25\) in \(-3.5\le x\le 3.5\) and \(-0.5\le t\le 0.5\) whereas 2D graph for \(t=0\)

Full size image
Fig. 4
figure 4

Soliton of the solution (3.1.14) is periodic type under the values \(\kappa =c=d=\theta =q=p={f}_{0}=1\), \(a={f}_{1}=0.001\) in the range \(-4\le x\le 8\) and \(-4\le t\le 4\) in which 2D plot displayed with \(t=0\)

Full size image
Fig. 5
figure 5

Eq. (3.1.16) bounces anti-kink type soliton for \(c=d=\theta ={f}_{1}=1\), \(\kappa =r=-1\) and \(a={f}_{0}=0\) in association with \(-2.5\le x,t\le 2.5\) and 2D plot nominated for \(t=0\)

Full size image
Fig. 6
figure 6

Diagram of (3.1.23) is singular kink shape soliton under \(\kappa =c=d=\theta ={f}_{0}={f}_{1}=r=1\) and \(a=0.01\) within \(-5\le x,t\le 5\) whereas 2D profile for \(t=0\)

Full size image
Fig. 7
figure 7

Peakon soliton attained for the solution (3.1.27) after fixing the values \(c=d=\theta =r=1\), \(\kappa =-1\), \(a=0\), \(q=2\) and \(p=0.5\) in \(-4\le x,t\le 4\) while 2D graph exhibited by using \(t=0\)

Full size image
Fig. 8
figure 8

Cuspon gifted from (3.1.28) for \(c=d=\theta =q=1\), \(\kappa =-1\), \(a=0\), \(p=0.79\) in \(-4\le x\le 4\) and \(-0.25\le t\le 0.25\) placed for 3D and contour while 2D plot with \(t=0\)

Full size image
Fig. 9
figure 9

Output is in anti-peakon for (3.1.38) under \(\kappa =1.199\), \(a=-0.019\), \(c=\theta =1\), \(d=1.5\), \(q=1.05\) and \(r=1.19\) within \(-5\le x,t\le 5\) while 2D plot for \(t=0\)

Full size image
Fig. 10
figure 10

Attained soliton is in anti-periodic form for (3.1.39) with \(c=d=\theta =q=1\), \(\kappa =r=-1\), \(p=0.25\) and \(a=0\) in \(-15\le x,t\le 30\) in which 2D plot for \(t=0\)

Full size image
Fig. 11
figure 11

Singular kink type soliton of (3.2.12) for \(\epsilon =c=d=w=1\), \(\kappa =-1\), \(a=0.1\), \(\theta =0\), \(\varepsilon =3\) and \(\eta =2\) in the interval \(-0.2\le x\le 0.213\) while 2D figure is portrayed for \(t=0\)

Full size image
Fig. 12
figure 12

The solution (3.2.13) represents anti-bell shape soliton for the values \(\varepsilon =c=d=w=A=B=1\), \(\epsilon =0.25\), \(\eta =-2\), \(\kappa =-1\) and \(a=\theta =0\) in \(-9\le x\le 9\) whereas 2D graph in Fig. 12c under \(t=0\)

Full size image

5 Conclusions

The purpose to construct impressive analytic wave solutions of the considered generalized third-order Schrödinger model by implementing two efficient procedures namely, improved auxiliary equation and enhanced rational \(({G}^{^{\prime}}/G)\)-expansion methods has been accomplished effectively. The abundant achieved solutions involving many free parameters expose distinct dynamic behaviors of nonlinear waves arise in optical fibers which might be helpful to explain respective phenomena in detail. The novel wave structures of the achieved solutions have been made visible graphically in 3D, 2D and contour sketches such as cuspon, compacton, peakon, kink, bell, periodic and so on. A comparable analysis of the acquired outcomes with those of earlier studies has claimed the significance of the present work. The resulting outcomes are impressive, innovative and potentially effective in realizing the transition of energy and diffusion procedures in mathematical simulations of numerous fields like applied physics, ultra-short pulses, transmission system, optical fibre etc. The expanded results with the adaptation of the recommended schemes have confirmed the importance of the study to influence the researchers and scholars for further work in this area as a continuation.