1 Introduction

The nonlinear Schrödinger equations (NLSEs) in partial differential equations (PDEs) arise in many fields of engineering and applied sciences such as quantum mechanics, optics, fluid dynamics, plasma physics, elastic media, molecular biology, magnetostatic spin waves, optical fibres and many more [1,2,3,4,5,6,7]. In dynamical systems, the promulgation of solitons in fibre optics is one of the many fascinating and gorgeous fields of research in these days. In fibre optics, a majority of such systems is usually depicted in time domain and through the field promulgation at various frequencies. The dynamical systems are mostly complex PDEs in nonlinear form [6,7,8,9,10,11]. Several researchers have focussed their attention in the field of optical fibre communication systems. Furthermore, the introduction of fibre amplifiers, nonlinear effects in optical fibre and optical solitons for data transmitting through loss of optical fibres hundreds of kilometres, even submarines, are the sign of comprehensive developments in this period. Lately, moving discrete breathers were linked to embedded solitons as well.

Breathers and solitons are the two basic classes of solutions of the NLSE. These analytical solutions can explain a range of nonlinear complex phenomena and have attracted a lot of attention from the scientific community. Solitons play a main role in the study of dynamics theory of nonlinear waves for more than 50 years. Particularly, the NLSE plays a vital role in sustaining the propagation of non-spreading electromagnetic pulses, by the so-called self-focussing phenomena in nonlinear media [12]. Taking into account nonlinearity and dispersion, Hasegawa and Tappert [13] derived the Schrödinger equation for applications in optical fibre. After this amazing progress, the rapid development in the Schrödinger equation-based soliton theory started taking place in other research fields such as oceanography [14], plasma physics [15], molecular biology [16], meteorology [17], geology [18] and nonlinear field theory [19].

Once the NLSEs are developed, the search for exact solutions in different forms has been done intensely and generally in different aspects. For constructing travelling wave solutions in various forms, several efficient and powerful methods such as F-expansion method [7], Jacobi elliptic function technique [10], semi-inverse variational principle [20], direct algebraic technique [21], Kudryashov method [22], simple equation method (SEM) [23], Darboux transformation [24], similarity transformations method [25], rational expansion scheme [26], expansion method [27], auxiliary equation technique [28], exp-function method [29], spectral collection scheme [30] and many more [31,32,33,34,35,36,37,38] have been developed. The dynamical behaviour of the NLSEs was studied by researchers in [39, 40]. The analytical studies of the model of longitudinal wave motion in solitary wave form in magneto-electro-elastic round sticks were done using the expansion technique [41]. Furthermore, it was employed to get analytical results of the Drinfel’d–Sokolov–Wilson equation and the Painleve integrable Burger equation. Khan et al [42] constructed the analytical solitons of the modified Korteweg–de Vries (KdV) equation by utilising the extension of the expansion scheme. Castro López et al [43] obtained the analytical matter–wave solutions to a generalised Gross–Pitaevskii equation with several new time- and space-varying nonlinearity coefficients and external fields.

The non-Kerr media discernment was shown to be an enormously exciting field of study in the modulational instability (MI) to study the propagation of an optical pulse in NLSE [44]. The MI signifies nonlinear interaction among a strong carrier wave and small periodic perturbation, and occurs in the promulgation of waves, plasmas and different biological systems. Furthermore, it governs the configuration of the periodic train of picosecond pulse, or supercontinuum generation, optical short optical bursts of light and a category of exotic effects in nonlinear optical fibres.

In this paper, the SEM [45] and exp\((-\Phi (\xi ))\)-expansion method [46] are applied on the generalised third-order NLSE to construct different kinds of new soliton solutions. MI is used to argue the stability of achieved analytical solutions, which confirms that all the solutions achieved are stable.

The rest of paper is arranged as follows: the model is described in §2. The use of extended SEM and exp\((-\Phi (\xi ))\)-expansion method is given in §3. In §4, the stability of the solutions is investigated using MI. The discussion of the results of the attained solutions is presented in §5. Conclusion is given in §6.

2 Governing equation

The generalised third-order NLSE has the following form:

$$\begin{aligned}&\mathrm {i} \left( \frac{\partial u}{\partial t} + \frac{\partial ^3 u}{\partial x^3}\right) + |u|^2 \left( \beta _1 u + \mathrm {i} \beta _2 \frac{\partial u}{\partial x} \right) \nonumber \\&\quad + \mathrm {i} \beta _3 \frac{\partial ( |u|^2) }{\partial x} u =0, \end{aligned}$$
(1)

where the values of parameters \(\beta _1, \beta _2\) and \(\beta _3\) are real and the function u(x, t) is complex. Equation (1) has been utilised to model ultrashort pulses in optical fibers. Usually, the above equation also has the term of second-order derivative. However, once the derivative expression of third order is included, the derivative term of the second order can be removed via a gauge transformation. If \( \beta _1= \beta _3 =0\), then eq. (1) is described as the modified KdV or Hirota equation in complex form, which is integrable by the inverse scattering transform technique.

3 Soliton solutions of the generalised third-order NLSE

3.1 Soliton solutions by extended SEM

Assume the solutions in the travelling wave form of eq. (1) as

$$\begin{aligned}&u(x,t)=\Psi (\xi ) \mathrm{e}^{\mathrm{i} P},~~ \Psi (\xi ) = \sum _{i=-M}^{M} b_i \phi ^{i}(\xi ),~~ \nonumber \\&\xi = k x + \omega t, ~~P=\delta x + \lambda t + \theta , \end{aligned}$$
(2)
$$\begin{aligned}&\phi '(\xi )= h_0 + h_1 \phi (\xi ) + h_2 \phi ^2 (\xi ) + h_3 \phi ^3(\xi ), \end{aligned}$$
(3)

where the amplitude component of the wave profile is \(\Psi (\xi )\), phase factor is P, k and \(\delta \) represent the frequencies of solitons, \(\omega \) and \(\lambda \) represent the wave numbers and \(\theta \) is the phase constant. The arbitrary constants are \(h_0, h_1, h_2\) and \(h_3\). The constant M is determined later, which is a positive integer. Substituting eq. (2) into eq. (1) and splitting into real and imaginary parts give

$$\begin{aligned}&3 \delta k^2 \Psi '' + ( \lambda - \delta ^3 ) \Psi + \left( \beta _2 \delta - \beta _1\right) \Psi ^3 = 0, \end{aligned}$$
(4)
$$\begin{aligned}&k^3 \Psi ^{(3)} + ( \omega -3 \delta ^2 k ) \Psi ' + k \left( \beta _2 + 2 \beta _3\right) \Psi ^2 \Psi ' = 0. \end{aligned}$$
(5)

Integrating eq. (5) and taking the integration constant as zero, we have

$$\begin{aligned} k^3 \Psi '' + ( \omega -3 \delta ^2 k ) \Psi + \frac{k}{3} \left( \beta _2 + 2 \beta _3\right) \Psi ^3 = 0. \end{aligned}$$
(6)

Equations (4) and (6) are similar, and thus we obtain the following relation among the coefficients as

$$\begin{aligned} \beta _1 = -2 \beta _3 \delta ,\quad \lambda = \frac{3 \delta \omega -8 \delta ^3 k}{k}. \end{aligned}$$
(7)

Utilise the homogeneous balancing principle in eq. (4) and assume the solution of eq. (4) as

$$\begin{aligned} \Psi (\xi )=\frac{b_{-2}}{\phi ^2(\xi )} + \frac{b_{-1}}{\phi (\xi )} + b_0 + b_1 \phi (\xi ) + b_2 \phi ^2 (\xi ).\nonumber \\ \end{aligned}$$
(8)

Substituting eq. (8) into eq. (4) and making the coefficients to zero of various powers of \(\phi ^i(\xi )\), we obtained a systems of equations in parameters \( b_{-2}, b_{-1}, b_0,\) \( b_1, b_2, h_0, h_1, h_2, h_3,\) \(k, \nu , \omega , \delta , \lambda \) and \(\theta \). This algebraic system of equations is resolved by utilising Mathematica. The following cases of solutions are obtained.

Case 1:   \(h_{0}=h_{2}=0\) and \(\beta _2 + 2 \beta _3 < 0\)

$$\begin{aligned}&b_{-2} = b_{-1} = 0,\quad b_0 = \pm \frac{\sqrt{6} h_1 k}{\sqrt{-\beta _2-2 \beta _3}},\quad b_1 = 0,~\nonumber \\&b_2 = \pm \frac{2 \sqrt{6} h_3 k}{\sqrt{-\beta _2-2 \beta _3}},\quad \omega =2 h_1^2 k^3+3 \delta ^2 k. \end{aligned}$$
(9)

The analytical solutions in solitons and solitary wave form of eq. (1) from solutions (9) are as follows:

$$\begin{aligned} u_{11}(\xi )&= \mp \frac{\sqrt{6} h_1 k (h_3 \mathrm{e}^{2 h_1 \xi }+1)}{\sqrt{-\beta _2-2 \beta _3} \left( h_3 \mathrm{e}^{2 h_1 \xi }-1\right) } \mathrm{e}^{\mathrm{i}P} ,\quad h_1 > 0, \end{aligned}$$
(10)
$$\begin{aligned} u_{12}(\xi )&= \pm \frac{\sqrt{6} h_1 k}{\sqrt{-\beta _2-2 \beta _3}} \left( 1 - \frac{2 h_3}{\mathrm{e}^{-2 h_1 \xi }+h_3}\right) \mathrm{e}^{\mathrm{i} P },\nonumber \\&\qquad h_1 < 0, \end{aligned}$$
(11)

Case 2: \(h_{1}=h_{3}=0\) and \(\beta _2 + 2 \beta _3 < 0 \)

$$\begin{aligned}&b_{-2} = 0,\quad b_{-1} =\pm \frac{\sqrt{6} h_0 k}{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&b_0 = b_1 = b_2 = 0,\quad \omega = 3 \delta ^2 k-2 h_0 h_2 k^3, \end{aligned}$$
(12)
$$\begin{aligned}&b_{-2} = b_{-1} = b_0 = 0,\quad b_1 = \pm \frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&b_2 = 0,\quad \omega = 3 \delta ^2 k-2 h_0 h_2 k^3, \end{aligned}$$
(13)
$$\begin{aligned}&b_{-2} = 0,\quad b_{-1} = \mp \frac{\sqrt{6} h_0 k}{\sqrt{-\beta _2-2 \beta _3}},\quad b_0 = 0,\quad b_2 = 0,\nonumber \\&b_1 = \mp \frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\quad \omega = 4 h_0 h_2 k^3+3 \delta ^2 k, \end{aligned}$$
(14)
$$\begin{aligned}&b_{-1} = \pm \frac{\sqrt{6} h_0 k}{\sqrt{-\beta _2-2 \beta _3}},\quad b_1 = \mp \frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&b_{-2} = 0,\quad b_0 = 0,\quad b_2 = 0,\quad \omega = 3 \delta ^2 k-8 h_0 h_2 k^3.\nonumber \\ \end{aligned}$$
(15)

The solitary wave solutions of eq. (1) are obtained from solution (12) as

$$\begin{aligned} u_{21}(\xi )= & {} \pm \frac{\sqrt{6 h_0 h_2} k \cot (\sqrt{h_0 h_2} \xi )}{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P }, \nonumber \\&h_0 h_2 >0, \end{aligned}$$
(16)
$$\begin{aligned} u_{22}(\xi )= & {} \pm \frac{\sqrt{- 6 h_0 h_2} k \coth (\sqrt{-h_0 h_2} \xi )}{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P }, \nonumber \\&h_0 h_2 <0. \end{aligned}$$
(17)

More solitary wave solutions from solution (13) of eq. (1) are obtained as

$$\begin{aligned} u_{23}(\xi )= & {} \pm \frac{\sqrt{6 h_0 h_2} k \tan (\sqrt{h_0 h_2} \xi )}{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P },\quad h_0 h_2 >0,\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} u_{24}(\xi )= & {} \mp \frac{\sqrt{- 6 h_0 h_2} k \tanh (\sqrt{-h_0 h_2} \xi )}{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P }, \nonumber \\&h_0 h_2 <0. \end{aligned}$$
(19)

One can also get more new analytical results of eq. (1) from (14) and (15) in the same way.

Case 3: \(h_0 = h_3 = 0\),

$$\begin{aligned}&b_{-2} = 0,\quad b_0 = \frac{\sqrt{3} h_1 k}{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) }},\nonumber \\&b_1 = \frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\quad b_{-1} =b_2 = 0,\nonumber \\&\omega = \frac{k (6 \delta ^2+h_1^2 k^2)}{2}, \quad b_{-2} = 0,\end{aligned}$$
(20)
$$\begin{aligned}&b_0 = -\frac{\sqrt{3} h_1 k}{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) }},\quad b_1 = -\frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&b_{-1} =b_2 = 0,\quad \omega = \frac{k (6 \delta ^2+h_1^2 k^2)}{2}. \end{aligned}$$
(21)

We achieved the following solutions in the form of solitons and solitary wave of eq. (1) from solution (20) as

$$\begin{aligned}&u_{31}(\xi )=-\frac{\sqrt{3} h_1 k \left( h_2 \mathrm{e}^{h_1 \xi }+1\right) }{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) } \left( h_2 \mathrm{e}^{h_1 \xi }-1\right) } \mathrm{e}^{\mathrm{i}P },\nonumber \\&\qquad \qquad \,\,\, h_1>0,\end{aligned}$$
(22)
$$\begin{aligned}&u_{32}(\xi ) =-\frac{\sqrt{3} h_1 k \left( h_2 \mathrm{e}^{h_1 \xi }-1\right) }{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) } \left( h_2 \mathrm{e}^{h_1 \xi }+1\right) } \mathrm{e}^{\mathrm{i}P },\nonumber \\&\qquad \qquad \,\,\, h_1<0. \end{aligned}$$
(23)

In a similar way, we can also get more exact solutions of eq. (1) from solution (21).

Case 4: \(h_{3}=0\)

$$\begin{aligned}&b_{-2} = 0,\quad b_{-1} =\mp \frac{\sqrt{6} h_0 k}{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&b_0 = \mp \frac{\sqrt{3} h_1 k}{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) }},\quad b_1 = b_2 =0,\nonumber \\&\omega = \frac{h_1^2 k^3-4 h_0 h_2 k^3+6 \delta ^2 k}{2},\end{aligned}$$
(24)
$$\begin{aligned}&b_{-2} = 0, \quad b_0 = \pm \frac{\sqrt{3} h_1 k}{\sqrt{-2 \left( \beta _2 + 2 \beta _3\right) }},\nonumber \\&b_{1} =\pm \frac{\sqrt{6} h_2 k}{\sqrt{-\beta _2-2 \beta _3}},\quad b_{-1} = b_2 =0,\nonumber \\&\omega = \frac{h_1^2 k^3-4 h_0 h_2 k^3+6 \delta ^2 k}{2}. \end{aligned}$$
(25)

We obtain the solutions in soliton form of eq. (1) from solutions (24) and (25) as

$$\begin{aligned}&u_{41}(\xi )\nonumber \\&\;= \mp \frac{\sqrt{3} k \left( h_1-\frac{4 h_0 h_2}{h_1-\sqrt{4 h_0 h_2-h_1^2} \tan \left( \frac{\sqrt{4 h_0 h_2-h_1^2}}{2} \xi \right) }\right) }{\sqrt{-2\left( \beta _2 + 2 \beta _3\right) }} \mathrm{e}^{\mathrm{i}P },\nonumber \\&\quad \,\,\, 4 h_0 h_2 > h_1^2, \end{aligned}$$
(26)
$$\begin{aligned}&u_{42}(\xi )\nonumber \\&\;=\pm \frac{\sqrt{6 h_0 h_2-\frac{3 h_1^2}{2}} k \tan \left( \frac{\sqrt{4 h_0 h_2-h_1^2}}{2} \xi \right) }{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P },\nonumber \\&\quad \,\,\, 4 h_0 h_2 > h_1^2. \end{aligned}$$
(27)
Fig. 1
figure 1

Solitary waves and soliton in various forms of Case 1 solutions are plotted.

Full size image
Fig. 2
figure 2

Periodic solitary wave and bright soliton in different forms of Case 2 solutions are plotted.

Full size image
Fig. 3
figure 3

Dark and periodic solitary waves in various forms are plotted for Cases 3 and 4 solutions.

Full size image

3.2 Soliton solutions by exp\((-\phi (\xi ))\)-expansion method

Assuming the solutions in the travelling wave form of eq. (1) as

$$\begin{aligned}&u(x,t)=\Psi (\xi ) \mathrm{e}^{\mathrm{i} P},\quad \Psi (\xi ) = \sum _{l=0}^N B_i(\exp (-\phi (\xi ) )^i,\nonumber \\&\xi = k x + \omega t,\quad P=\delta x + \lambda t + \theta , \end{aligned}$$
(28)
$$\begin{aligned}&\phi '(\xi )= \exp (-\phi (\xi ))+\mu \exp (\phi (\xi ))+\rho . \end{aligned}$$
(29)

The arbitrary constants are \(B_i, \mu \) and \(\rho \). The constant N is determined later, which is a positive integer. Substitute eq. (28) into eq. (1) and split into parts as

$$\begin{aligned}&3 \delta k^2 \Psi '' + ( \lambda - \delta ^3 ) \Psi + \left( \beta _2 \delta - \beta _1\right) \Psi ^3 = 0, \end{aligned}$$
(30)
$$\begin{aligned}&k^3 \Psi ^{(3)} + ( \omega -3 \delta ^2 k ) \Psi ' + k \left( \beta _2 + 2 \beta _3\right) \Psi ^2 \Psi ' = 0 \end{aligned}$$
(31)

and integrate eq. (31) and take the integration constant as zero, we have

$$\begin{aligned} k^3 \Psi '' + ( \omega -3 \delta ^2 k ) \Psi + \frac{k}{3} \left( \beta _2 + 2 \beta _3\right) \Psi ^3 = 0. \end{aligned}$$
(32)

Equations (30) and (32) are similar, and hence we get the relation among the coefficients as

$$\begin{aligned} \beta _1 = -2 \beta _3 \delta ,\quad \lambda = \frac{3 \delta \omega -8 \delta ^3 k}{k}. \end{aligned}$$
(33)

Utilising the homogeneous balancing principle in eq. (30), assuming that eq. (4) has solutions as

$$\begin{aligned} \Psi (\xi )= B_0 + B_1(\exp (-\phi (\xi )), \end{aligned}$$
(34)

substituting eq. (34) along with eq. (29) into eq. (30) and taking coefficients as zero for various powers of \(\exp (-\phi (\xi ))^l\), we obtained a system of equations in parameters \( B_{0}, B_{1}, \mu , \rho \), \(k, \nu , \omega , \delta , \lambda \) and \(\theta \). These algebraic systems of equations are resolved utilising Mathematica. The following sets of solutions are obtained:

Set 1:

$$\begin{aligned}&B_0 = \frac{\sqrt{3} k \rho }{\sqrt{2(-\beta _2-2 \beta _3)}},~\quad B_1 = \frac{\sqrt{6} k }{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&\delta =\mp \frac{\sqrt{2 \omega -k^3 \rho ^2 + 4 k^3 \mu }}{\sqrt{6} \sqrt{k}}. \end{aligned}$$
(35)

Set 2:

$$\begin{aligned}&B_0 = - \frac{\sqrt{3} k \rho }{\sqrt{2(-\beta _2-2 \beta _3)}},\quad B_1 = -\frac{\sqrt{6} k }{\sqrt{-\beta _2-2 \beta _3}},\nonumber \\&\delta =\pm \frac{\sqrt{2 \omega -k^3 \rho ^2 + 4 k^3 \mu }}{\sqrt{6} \sqrt{k}}. \end{aligned}$$
(36)

The analytical solutions in the form of solitons and solitary wave of eq. (1) from solutions (35) are given as follows:

$$\begin{aligned}&u_{1}(\xi )=\frac{\sqrt{\frac{3}{2}} k \left( \rho -\frac{4 \mu }{\sqrt{\rho ^2-4 \mu } \tanh \left( \frac{1}{2} (c +\xi ) \sqrt{\rho ^2-4 \mu }\right) +\rho }\right) }{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P },\nonumber \\&\qquad \qquad \,\,\,\mu \ne 0,~ \rho ^2-4 \mu > 0, \end{aligned}$$
(37)
$$\begin{aligned}&u_{2}(\xi )= \frac{\sqrt{\frac{3}{2}} k \left( \frac{4 \mu }{\sqrt{4 \mu -\rho ^2} \tan \left( \frac{1}{2} (c+\xi ) \sqrt{4 \mu -\rho ^2}\right) +\rho }+\rho \right) }{\sqrt{-\beta _2-2 \beta _3}} \mathrm{e}^{\mathrm{i}P },\nonumber \\ ~~&\qquad \qquad \,\,\,\mu \ne 0,~ \rho ^2-4 \mu < 0, \end{aligned}$$
(38)
$$\begin{aligned}&u_{3}(\xi )= \frac{\sqrt{\frac{3}{2}} k \rho \left( \mathrm{e}^{\rho (c+\xi )} +1\right) }{\sqrt{-\beta _2-2 \beta _3} \left( \mathrm{e}^{\rho (c+\xi )}-1\right) } \mathrm{e}^{\mathrm{i}P },~~\mu = 0, \nonumber \\ ~~&\qquad \qquad \,\,\,\rho \ne 0,~~ \rho ^2-4 \mu > 0, \end{aligned}$$
(39)
$$\begin{aligned}&u_{4}(\xi )= \frac{\sqrt{\frac{3}{2}} k \rho }{\sqrt{-\beta _2-2 \beta _3} (c \rho +\xi \rho +1)} \mathrm{e}^{\mathrm{i}P },\nonumber \\ ~~&\qquad \qquad \,\,\,\mu \ne 0,~~ \rho \ne 0,~~ \rho ^2-4 \mu = 0, \end{aligned}$$
(40)
$$\begin{aligned}&u_{5}(\xi )= \frac{\sqrt{\frac{3}{2}} k (c \rho +\xi \rho +2)}{\sqrt{-\beta _2-2 \beta _3} (c+\xi )} \mathrm{e}^{\mathrm{i}P }, \end{aligned}$$
(41)
$$\begin{aligned} ~~&\qquad \qquad \,\,\,\mu = 0,~~ \rho = 0,~~ \rho ^2-4 \mu = 0. \end{aligned}$$
(42)

One can get more soliton solutions from Set 2.

4 Modulation instability

Numerous higher-order nonlinear models illustrate an instability, which leads to investigate steady-state modulation as a consequence of interface between the dispersive and nonlinear effects. To establish MI of higher order NLSE (1) by utilising the linear stability analysis [5, 6, 21] to analyse how the time dependent and weak perturbation build up along the promulgation distance. The solution in the steady state of third-order NLSE is as follows:

$$\begin{aligned} u(x,t)= ( \sqrt{P}+\psi (x,t)) \mathrm{e}^{ \mathrm {i} \varphi (t) },~~ \varphi (t)= P \alpha \epsilon t. \end{aligned}$$
(43)

In the above equation, P is the optical power in the normalised form. The perturbation \(\psi (x,t)\) is investigated by utilising linear stability analysis. Substituting eq. (43) into eq. (1) and linearising, we get

$$\begin{aligned}&\mathrm {i} \left( \frac{\partial \psi }{\partial t} + \beta _2 P \frac{\partial \psi }{\partial x}\right) +\mathrm {i} \beta _3 P \left( \frac{\partial \psi }{\partial t} + \frac{\partial \psi ^{*} }{\partial t} \right) + \mathrm {i} \frac{\partial ^3 \psi }{\partial x^3} \nonumber \\&\quad + \beta _1 P \left( 2 \psi + \psi ^* \right) - P \alpha \epsilon \psi = 0, \end{aligned}$$
(44)

where \(*\) signifies the complex conjugate. Assume the solution of eq. (44) as

$$\begin{aligned} \psi (x,t)=\gamma _1 \mathrm{e}^{ \mathrm {i} \left( k x - \omega t \right) } + \gamma _2 \mathrm{e}^{ -\mathrm {i} \left( k x - \omega t \right) }, \end{aligned}$$
(45)

where \(\omega \) and k are the normalised frequency and wave number of \(\psi (x,t)\). The dispersion relation \(\omega = \omega (k)\) of a constant coefficient linear evolution equation specifies how the time oscillations \(\mathrm{e}^{\mathrm{i} k x}\) are linked to the oscillations of spatial \(\mathrm{e}^{\mathrm{i}\omega t}\) of \(\omega \). Substituting eq. (45) into eq. (44), we obtain the relation as follows:

$$\begin{aligned} \omega =&P k\left( \beta _2+\beta _3\right) -k^3 \nonumber \\&\pm P \sqrt{\alpha ^2 \epsilon ^2-4 \alpha \beta _1 \epsilon +3 \beta _1^2+\beta _3^2 k^2}. \end{aligned}$$
(46)

Relation (46) reveals the steady-state stability which depend on self-phase modulation, wave number \(\omega \) and stimulated Raman scattering. When \(\alpha ^2 \epsilon ^2-4 \alpha \beta _1 \epsilon +3 \beta _1^2+\beta _3^2 k^2 \ge 0 \), i.e. \(\omega \) is real for every k, the steady state is stable along the small perturbation. It becomes unstable when \(\alpha ^2 \epsilon ^2-4 \alpha \beta _1 \epsilon +3 \beta _1^2+\beta _3^2 k^2 < 0 \), i.e. \(\omega \) is imaginary as the perturbation develops exponentially. One can simply observe MI when \( \alpha ^2 \epsilon ^2-4 \alpha \beta _1 \epsilon +3 \beta _1^2+\beta _3^2 k^2 < 0\). Under these circumstances, the growth rate of MI gain spectrum f(k) can be expressed as

$$\begin{aligned} f(k) = 2 \,\mathrm {Im}(k) = 2 P \sqrt{\alpha ^2 \epsilon ^2-4 \alpha \beta _1 \epsilon +3 \beta _1^2+\beta _3^2 k^2}. \end{aligned}$$
(47)
Fig. 4
figure 4

Graph of the dispersion relation \( \omega = \omega (k )\).

Full size image

5 Results and discussion

The analytical solutions achieved in various forms using the current scheme are different from the constructed solutions of other researchers using the existing techniques. Equation (3) presents some particular kind of solutions such as rational and trigonometric functions by granting special values of parameter. Pelinovsky and Yang [47] constructed the embedded soliton solutions of eq. (1). Hence, the solutions obtained by us are new and have not been constructed in the literature.

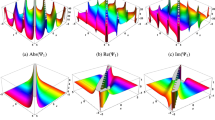
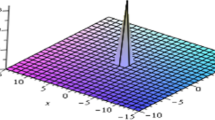
Figure 1 shows the solitary waves of exact solutions in various forms plotted for Case 1. Figures 1a and 1c evaluate the solitary wave and dark soliton of solutions (10) and (11) when \(\beta _2 = 1, \beta _3 = -2, h_1 = 0.5, h_3 = 1, k = 0.5, \delta = 1, \theta = -1\) and \(\beta _2 = 1, \beta _3 = -2, h_1 = - 0.5, h_3 = 1, k = 0.5, \delta = 1, \theta = -1\), respectively, and figures 1b and 1d evaluate the contour plots for the same parameters of the same solutions.

Figure 2 shows the evaluation of solitary waves in different forms plotted for Case 2. Figures 2a and 2c manipulate the periodic solitary waves and bright soliton of solutions (16) and (19) when \(\beta _2 = 1, \beta _3 = -2, h_0 = - 0.5, h_2 = - 1, k = 0.5, \delta = 1, \theta = -1\) and \(\beta _2 = 1, \beta _3 = -2, h_0 = 0.5, h_2 = - 1, k = 0.5, \delta = 1, \theta = -1\), respectively, and figures 2b and 2d evaluate the contour plots for the same parameters of the same solutions.

Figure 3 shows the evaluation of the solitary waves in different shapes for Cases 3 and 4 solutions. Figures 3a and 3c show the dark solitary and periodic solitary wave of solutions (23) and (26) when \(\beta _2 = 1, \beta _3 = -2, h_1 = - 0.5, h_2 = 1, k = 0.5, \delta = 1, \theta = -1\) and \(\beta _2 = 1, \beta _3 = -2, h_0 = 1.5, h_1 = 0.5, h_2 = 1, k = 0.5, \delta = 1, \theta = 1\), respectively, and figures 3b and 3d show the significance of the contour plots for the same parameters of the same solutions. Graph of the dispersion relation \( \omega = \omega (k)\) is shown in figure 4.

6 Conclusion

In this paper, we have investigated the solitons, solitary wave solutions and MI of the generalised third-order NLSE. The extended simple equation technique and exp\((-\Phi (\xi ))\)-expansion method are utilised successfully to construct analytical solutions in different forms such as solitons, solitary waves, periodic solutions and so on. In optical fibres, this model has been utilised to form ultrashort pulses. The achieved analytical solutions are of meticulous curiosity for their prospective applications in various fields such as ultrashort pulses, optical fibre, applied physics, transmission system, etc. The exact expression for the MI gain has been obtained by using the MI analysis that reveals to be sensitive of the septic nonlinearity. A few results are presented graphically. Among the constructed solutions, many exact solutions are new and may be useful for mathematicians, physicists and scientists from other fields to investigate more nonlinear complex physical phenomena. The obtained results and computational work confirm the power and efficiency of the present scheme.