1 Introduction

The study of solitary wave propagation generated by a specific type of nonlinear evolution equations (NLEEs), has garnered significant interest within the scientific community in recent years (Ali et al. 2023; El-Ganaini and Al-Amr 2022; Kumar and El-Ganaini 2020; Akram et al. 2023; Faisal et al. 2023; Muhammad et al. 2023). These NLEEs, which explain the dynamical behavior and composition of such waves, present a significant challenge in fields such as nuclear physics, plasma physics, signal processing, optical communication systems, laser optics, and others (El-Ganaini and Kumar 2020; Osman et al. 2018; Bulut et al. 2018; Abdel-Gawad et al. 2016; Mirzazadeh 2015; Manafian et al. 2017; Ahmad et al. 2023; Feng et al. 2022; Kai-Da et al. 2021; Zhao et al. 2020; Zhang et al. 2023; Guo et al. 2023a, b; Meng et al. 2023; Bai et al. 2021; Li et al. 2018; Jin and Wang 2016; Zhang et al. 2022; Chen et al. 2021; Chen 2022; Yong Zhang et al. 2020). Additionally, many NLEEs also demonstrate the propagation of solitons in fiber optics (Savaissou et al. 2020; Liu et al. 2020; Inc et al. 2020; Vahidi et al. 2021; Sajid and Akram 2020, 2019; Biswas 2003; Osman and Behzad 2018; Bhrawy et al. 2014; Savescu et al. ; Triki et al. 2012; Biswas 2001; Saha et al. 2009; Arnous et al. 2017; Mirzazadeh et al. 2015; Ahmad et al. 2023).

Solitons a2016re light pulses that travel through optical fibers and are typically described using the nonlinear Schrödinger equation (NLSE), which covers fundamental wave effects like group velocity dispersion (GVD) and self-phase modulation (SPM) (Hasegawa and Tappert 1973a, b; Agrawal 2001). Solitons result from the delicate balance between GVD and SPM in the material (Hao et al. 2005). Their robust and stable quality makes them an ideal choice for communication as signal carriers at remote sites. However, in various applications, such as time-resolved infrared spectroscopic techniques, ultrahigh-bitrate optical communication systems, ultrafast physical processes, and optoelectronic sampling, ultrashort femtosecond (fs) pulses are required, leading to the occurrence of various higher-order effects in the optical material (Agrawal 2001; Goyal et al. 2011).

Third-order dispersion plays a crucial role in the propagation of short pulses with widths of nearly 50 fs, while fourth-order dispersion becomes imperative when dealing with pulses shorter than 10 fs (Fernández-Dıaz and Palacios 2000; Palacios 2003; Piché et al. 1996). In such cases, wave structures can be explained using the higher-order NLSE, which considers the effects of various physical phenomena on the propagation and regeneration of short pulses. Understanding the propagation of ultra-short light pulses through inhomogeneous optical fibers with higher-order dispersive effects is essential for designing practical optical systems, maintaining signal quality in optical communications, and advancing fields such as quantum optics and nonlinear optics.

In this paper, we employ the Sardar subequation method (Rezazadeh et al. 2020a, b) to unveil exact solutions of the generalized NLSE in the presence of second, third, and fourth-order dispersion terms (Blow and Wood 1989; Shagalov 1998; Cavalcanti et al. 1991; Kruglov and Harvey 2018; Kruglov 2020; Triki and Kruglov 2020; Demiray 2020; Karpman 1998; Karpman and Shagalov 1999). The solutions derived through this technique complement those obtained by other methods, such as the trail equation method, the functional variable method, and the first integral method. We specifically consider the NLSE combined with the \(\nu\)-time derivative for \(\nu \in (0,~1]\).

Considering the NLSE with second, third, and fourth-order dispersion terms is crucial for accurately modeling pulse propagation in optical fiber, especially in modern communication systems and applications involving ultra-short pulses and advanced modulation formats. It facilitates the design, optimization, and control of optical systems in the presence of higher-order dispersion effects, serving as a fundamental tool for researchers working on advanced optical systems. This provides a foundation for the study and development of techniques to control and manipulate optical pulses.

Fractional calculus is often employed to model complex and anomalous behaviors that cannot be adequately described by integer-order calculus. Conformable derivatives provide a more effective tool for modeling these complex phenomena, especially in fields like mathematical biology, fluid dynamics, heat conduction, quantum physics, signal processing, engineering, electromagnetic theory, optical fiber communication, plasma physics, and viscoelastic materials. Conformable derivatives offer a more flexible approach to fractional calculus by generalizing the traditional Riemann-Liouville and Caputo derivatives, making them applicable to a broader range of functions and systems. This increased applicability allows for a broader class of nonlinear fractional partial differential equations (FPDEs) to be addressed using conformable derivatives. The conformable fractional calculus can often simplify the complexity of FPDEs, leading to more manageable equations that admit exact solutions, which can be particularly valuable in both theoretical and practical applications (Ahmad and Mustafa 2023; Özkan et al. 2023; Akar and Özkan 2023; Özkan and Akar 2022; Ahmad et al. 2023; Ali et al. 2023).

1.1 Properties of \(\nu\)-time derivative

Conformable fractional derivatives offer a more manageable approach and adhere to certain standard characteristics, such as the chain rule, which is lacking in traditional fractional derivatives. However, a notable drawback of this derivative arises: the fractional derivative of any differentiable function at point zero lacks physical significance and cannot currently be interpreted in a physical context. To overcome this limitation, an enhanced version of the conformable derivative has been introduced. This modified derivative is contingent on the interval over which the function is subjected to differentiation (Özkan and Özkan 2021; Özkan and Mehmet 2022).

Atangana et al. (2014) introduced the definition of \(\nu\)-time derivative and later some properties possessed by this derivative are given in Atangana et al. (2016, 2015). The suggested \(\nu\)-derivative possesses numerous features that have found utility in simulating various physical phenomena, addressing shortcomings associated with traditional fractional derivatives.

Definition. Let \(h(\tau )\) be a function defined for all \(\tau > 0\), then the \(\nu\)-time derivative of \(h(\tau )\) is given by

$$\begin{aligned} D^{\nu }_{\tau }( h(\tau ))=\lim _{c\rightarrow 0}\frac{h\left( \tau +c \left( \tau + \frac{1}{ \Gamma \left( \nu \right) } \right) ^{1-\nu }\right) -h(\tau )}{c},\quad \nu \in (0, 1]. \end{aligned}$$

Theorem. Let \(h(\tau )\) and \(n(\tau )\) be \(\nu\)-differentiable functions for all \(\tau > 0\) and \(\nu \in (0, 1]\), then

$$\begin{aligned}{} & {} D^{\nu }_{\tau } (p h(\tau )+q n(\tau ))=pD^{\nu }_{\tau }(h(\tau ))+qD^{\nu }_{\tau }(n(\tau )), \quad \forall p,~q\in {\mathbb {R}},\\{} & {} D^{\nu }_{\tau } (h(\tau )n(\tau ))=h(\tau )D^{\nu }_{\tau }(n(\tau ))+n(\tau )D^{\nu }_{\tau }(h(\tau )),\\{} & {} D^{\nu }_{\tau } \left( \frac{h(\tau )}{n(\tau )}\right) =\frac{n(\tau )D^{\nu }_{\tau }(h(\tau ))-h(\tau )D^{\nu }_{\tau }(n(\tau ))}{(n(\tau ))^{2}}\cdot \end{aligned}$$

1.2 Governing model

The generalized NLSE for the pulse envelope \({E}(z, \tau )\) with \(\nu\)-time derivative has the form (Blow and Wood 1989; Shagalov 1998; Cavalcanti et al. 1991; Kruglov and Harvey 2018; Kruglov 2020; Triki and Kruglov 2020; Demiray 2020; Karpman 1998; Karpman and Shagalov 1999)

$$\begin{aligned} i \frac{\partial {E}}{\partial {z}}-\alpha \frac{\partial ^{2\nu }{E}}{\partial {\tau ^{2\nu }}}-i \sigma \frac{\partial ^{3\nu }{E}}{\partial {\tau ^{3\nu }}}+ \epsilon \frac{\partial ^{4\nu }{E}}{\partial {\tau ^{4\nu }}}+\gamma |{E}|^{2}{E}=0, \end{aligned}$$
(1)

where z is the longitudinal coordinate, \(\tau =t-\beta _{1}z\) is the retarded time, \(\alpha =\frac{\beta _{2}}{2},~\sigma =\frac{\beta _{3}}{6},~\epsilon =\frac{\beta _{4}}{24}\), and \(\gamma\) represents the nonlinear parameter. The parameters \(\beta _{k}=\left( \frac{d^{k}\beta }{d\mu ^{k}}\right) _{\mu =\mu _{0}}\) are the k-order dispersion of the optical fiber and \(\beta (\mu )\) is the propagation constant depending on the optical frequency.

This equation has been extensively studied in literature due to its significance from a variety of perspectives. In Shagalov (1998), the effect of the third and fourth order dispersive terms on the SPM instability was investigated. Particularly, the SPM instability phenomenon of Eq. (1) was presented in the domain of the minimum GVD in Cavalcanti et al. (1991). The exact solitary wave solution with \({{\,\textrm{sech}\,}}^{2}\) form have been analyzed in Kruglov and Harvey (2018) for the Eq. (1) including the dispersion effects of second, third, and fourth-order. The solitary wave solution and periodic solutions of the Eq. (1) with the higher order dispersion effects have been obtained in Kruglov (2020) governing the pulses propagation in optical fibers. In Triki and Kruglov (2020), the exact self-similar dipole soliton solutions of Eq. (1) in highly dispersive optical fiber media have been derived. In Demiray (2020), the optical soliton solutions of Eq. (1) with beta time derivative have been presented by employing the modified exp\((-\Omega (\xi ))\)-expansion function method and generalized Kudryashov method. Some more exact solutions of Eq. (1) have been reported in Roy et al. (2009); Zhu (2007); Inc et al. (2017).

2 Description of the method

In this section, we summarize the Sardar subequation method that was firstly formulated by Rezazadeh et al. (2020a, 2020b). Consider a \(\nu\)-derivative NLEE for \(\varrho =\varrho (z,~\tau )\) to be in the form

$$\begin{aligned} \Omega (\varrho , \varrho _{z}, \varrho ^{(\nu )}_{\tau }, \varrho ^{(2\nu )}_{\tau \tau },\ldots )=0, \end{aligned}$$
(2)

where \(\Omega\) is a polynomial of \(\varrho (z,~\tau )\) and its highest order partial derivatives, as well as the nonlinear terms.

We use the wave transformation

$$\begin{aligned} \varrho (z,~\tau )=\varrho (\xi ), \xi =z-{\frac{\lambda \,}{\nu }} \left( \tau + \frac{1}{ \Gamma \left( \nu \right) } \right) ^{\nu }, \end{aligned}$$
(3)

where \(\lambda\) is for wave speed and Eq. (2) can be converted into the nonlinear ordinary differential equation (NLODE) given as

$$\begin{aligned} \Upsilon (\varrho , \varrho ^{\prime }, \varrho ^{\prime \prime }, \varrho ^{\prime \prime \prime },\ldots )=0, \end{aligned}$$
(4)

where prime denotes the derivatives with respect to \(\xi\).

We suppose that Eq. (4) has the solution of the form:

$$\begin{aligned} \varrho (\xi )= \sum _{i=0}^{L} \psi _{i}\Phi ^{i}(\xi ), \end{aligned}$$
(5)

where \(\psi _{i}~(i=0,1,\ldots ,L)\) are arbitrary constants to be obtained. The value of L will be calculated by balancing the highest order derivative of \(\varrho\) and the highest order nonlinear term in Eq. (4), while \(\Phi (\xi )\) is the solution of the NLODE:

$$\begin{aligned} \Phi ^{'^2}(\xi )= & {} \rho + {a}\Phi ^{2}(\xi )+ {b}\Phi ^{4}(\xi ), \end{aligned}$$
(6)

where \(\rho ,~{a}\) and b are the real constants. Furthermore, Eq. (6) has the following solutions:

Case 1. If \({a}>0\) and \(\rho =0\), then

$$\begin{aligned} \Phi ^{\pm }_{1}(\xi )= & {} \pm \sqrt{-\frac{pqa}{b}}{{\,\textrm{sech}\,}}_{pq}(\sqrt{a}\xi ), \quad b<0, \\ \Phi ^{\pm }_{2}(\xi )= & {} \pm \sqrt{\frac{pqa}{b}}{{\,\textrm{csch}\,}}_{pq}(\sqrt{a}\xi ), \quad b>0, \end{aligned}$$

where

$$\begin{aligned} {{\,\textrm{sech}\,}}_{pq}(\xi )=\frac{2}{p{{{{\,\textrm{e}\,}}}^{\xi }}+q{{{{\,\textrm{e}\,}}}^{-\xi }}},\quad {{\,\textrm{csch}\,}}_{pq}(\xi )=\frac{2}{p{{{{\,\textrm{e}\,}}}^{\xi }}-q{{{{\,\textrm{e}\,}}}^{-\xi }}}\cdot \end{aligned}$$

Case 2. If \({a}<0,~b>0\) and \(\rho =0\), then

$$\begin{aligned} \Phi ^{\pm }_{3}(\xi )= & {} \pm \sqrt{-\frac{pqa}{b}}\sec _{pq}(\sqrt{-a}\xi ), \\ \Phi ^{\pm }_{4}(\xi )= & {} \pm \sqrt{-\frac{pqa}{b}}\csc _{pq}(\sqrt{-a}\xi ), \end{aligned}$$

where

$$\begin{aligned} \sec _{pq}(\xi )&=\frac{2}{p{{{{\,\textrm{e}\,}}}^{i\xi }}+q{{{{\,\textrm{e}\,}}}^{-i\xi }}},\quad \csc _{pq}(\xi )=\frac{2i}{p{{{{\,\textrm{e}\,}}}^{i\xi }}-q{{{{\,\textrm{e}\,}}}^{-i\xi }}}\cdot \end{aligned}$$

Case 3. If \({a}<0,~b>0\) and \(\rho =\frac{{a}^{2}}{4b}\), then

$$\begin{aligned} \Phi ^{\pm }_{5}(\xi )= & {} \pm \sqrt{-\frac{a}{2b}}\tanh _{pq}\left( \sqrt{-\frac{a}{2}}\xi \right) , \\ \Phi ^{\pm }_{6}(\xi )= & {} \pm \sqrt{-\frac{a}{2b}}\coth _{pq}\left( \sqrt{-\frac{a}{2}}\xi \right) , \\ \Phi ^{\pm }_{7}(\xi )= & {} \pm \sqrt{-\frac{a}{2b}}\left( \tanh _{pq}\left( \sqrt{-2a}\xi \right) \pm i \sqrt{pq}{{\,\textrm{sech}\,}}_{pq}\left( \sqrt{-2a}\xi \right) \right) , \\ \Phi ^{\pm }_{8}(\xi )= & {} \pm \sqrt{-\frac{a}{2b}}\left( \coth _{pq}\left( \sqrt{-2a}\xi \right) \pm \sqrt{pq}{{\,\textrm{csch}\,}}_{pq}\left( \sqrt{-2a}\xi \right) \right) , \\ \Phi ^{\pm }_{9}(\xi )= & {} \pm \sqrt{-\frac{a}{8b}}\left( \tanh _{pq}\left( \sqrt{-\frac{a}{8}}\xi \right) + \coth _{pq}\left( \sqrt{-\frac{a}{8}}\xi \right) \right) , \end{aligned}$$

where

$$\begin{aligned} \tanh _{pq}(\xi )&=\frac{p{{{{\,\textrm{e}\,}}}^{\xi }}-q{{{{\,\textrm{e}\,}}}^{-\xi }}}{p{{{{\,\textrm{e}\,}}}^{\xi }}+q{{{{\,\textrm{e}\,}}}^{-\xi }}},\quad \coth _{pq}(\xi )=\frac{p{{{{\,\textrm{e}\,}}}^{\xi }}+q{{{{\,\textrm{e}\,}}}^{-\xi }}}{p{{{{\,\textrm{e}\,}}}^{\xi }}-q{{{{\,\textrm{e}\,}}}^{-\xi }}}\cdot \end{aligned}$$

Case 4. If \({a}>0,~b>0\) and \(\rho =\frac{{a}^{2}}{4b}\), then

$$\begin{aligned} \Phi ^{\pm }_{10}(\xi )= & {} \pm \sqrt{\frac{a}{2b}}\tan _{pq}\left( \sqrt{\frac{a}{2}}\xi \right) , \\ \Phi ^{\pm }_{11}(\xi )= & {} \pm \sqrt{\frac{a}{2b}}\cot _{pq}\left( \sqrt{\frac{a}{2}}\xi \right) ,\\ \Phi ^{\pm }_{12}(\xi )= & {} \pm \sqrt{\frac{a}{2b}}\left( \tan _{pq}\left( \sqrt{2a}\xi \right) \pm \sqrt{pq}\sec _{pq}\left( \sqrt{2a}\xi \right) \right) , \\ \Phi ^{\pm }_{13}(\xi )= & {} \pm \sqrt{\frac{a}{2b}}\left( \cot _{pq}\left( \sqrt{2a}\xi \right) \pm \sqrt{pq}\csc _{pq}\left( \sqrt{2a}\xi \right) \right) ,\\ \Phi ^{\pm }_{14}(\xi )= & {} \pm \sqrt{\frac{a}{8b}}\left( \tan _{pq}\left( \sqrt{\frac{a}{8}}\xi \right) + \cot {pq}\left( \sqrt{\frac{a}{8}}\xi \right) \right) , \end{aligned}$$

where

$$\begin{aligned} \tan _{pq}(\xi )&=-i\frac{p{{{{\,\textrm{e}\,}}}^{i\xi }}-q{{{{\,\textrm{e}\,}}}^{-i\xi }}}{p{{{{\,\textrm{e}\,}}}^{i\xi }}+q{{{{\,\textrm{e}\,}}}^{-i\xi }}},\quad \cot _{pq}(\xi )=i\frac{p{{{{\,\textrm{e}\,}}}^{i\xi }}+q{{{{\,\textrm{e}\,}}}^{-i\xi }}}{p{{{{\,\textrm{e}\,}}}^{i\xi }}-q{{{{\,\textrm{e}\,}}}^{-i\xi }}}\cdot \end{aligned}$$

Substituting Eq. (5) along with Eq. (6) into (4) and setting the coefficients of all powers of \(\Phi ^{i}(\eta )\) to zero leads to a set of algebraic equations in terms of \(a, ~b,~\rho ,~\lambda ,~\psi _{i}(i=0,~1,~2,\ldots ,~L)\). Identifying the values of all parameters, and then substituting these parameters along with the solutions of Eq. (6) into Eq. (5), a series of exact solutions of Eq. (2) are recovered.

Fig. 1
figure 1

3D-plots and contour plots of \(|{E}^{+}_{1}|,Re({E}^{+}_{1})~\) and \(Im({E}^{+}_{1})\) for \(\sigma =-1,~\alpha =1,~\epsilon =0.25,~\lambda =0.1,~\omega =-1.05,~\kappa =1,~\gamma =-2,~ p=0.1,~q=0.2\) and \(\nu =1\)

Full size image
Fig. 2
figure 2

3D-plots and contour plots of \(|{E}^{+}_{3}|,Re({E}^{+}_{3})~\) and \(Im({E}^{+}_{3})\) for \(\sigma =1.4,~\alpha =0.5,~\epsilon =0.25,~\lambda =\omega =\kappa =1,~\gamma =-2,~ p=1,~q=0.1\) and \(\nu =1\)

Full size image

3 Application of the Sardar subequation method

We use the wave transformation

$$\begin{aligned}{} & {} {E}(z, \tau )=u(\xi )e^{{i}{\phi }(z, \tau )}, \quad \xi =z-{\frac{\lambda \,}{\nu }} \left( \tau + \frac{1}{ \Gamma \left( \nu \right) } \right) ^{\nu },\nonumber \\{} & {} \phi =-\kappa z+{\frac{\omega \,}{\nu }} \left( \tau + \frac{1}{ \Gamma \left( \nu \right) } \right) ^{\nu }+\eta _{{0}}, \end{aligned}$$
(7)

where \(\kappa ,~\omega\) and \(\eta _{{0}}\) represent the soliton frequency, soliton wave number and the phase constant, respectively. Substituting Eq. (7) into (1) and separating the real and imaginary parts, we obtain the following equations:

$$\begin{aligned}{} & {} \epsilon \,{\lambda }^{4} {u}''''+ {\lambda }^{2}\left( 3\,\sigma \, \omega -\alpha \,-6\,\epsilon \,{\omega }^{2} \right) {u}''+ \left( \kappa +\alpha \,{\omega }^{2}-\sigma \,{ \omega }^{3}+\epsilon \,{\omega }^{4} \right) {u}+\gamma \,{u}^{3} =0, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \left( \sigma \,-4\,\epsilon \,\omega \right) \lambda ^{3} {u}''+ \left( 1+2\,\omega \lambda \alpha -3\sigma \lambda {\omega }^{2}+4\epsilon \lambda {\omega }^{3} \right) {u} =0. \end{aligned}$$
(9)

Using Eq. (9), we obtain

$$\begin{aligned} {u}''''= -\frac{\left( 1+2\,\omega \lambda \alpha -3\sigma \lambda {\omega }^{2}+4\epsilon \lambda {\omega }^{3} \right) }{\left( \sigma \,-4\,\epsilon \,\omega \right) \lambda ^{3}}{u}'' \cdot \end{aligned}$$
(10)

Substituting Eq. (10) into (8), we get

$$\begin{aligned} {A}\, {u}''+ \left( \sigma \,-4\,\epsilon \,\omega \right) {B}\,{u}+\gamma \,\left( \sigma \,-4\,\epsilon \,\omega \right) {u}^{3} =0, \end{aligned}$$
(11)

where,

$$\begin{aligned} {A}= & {} -\lambda \,\epsilon +2\,\epsilon \,\alpha \,\omega \,{\lambda }^{2}-15\, \epsilon \,\sigma \,{\omega }^{2}{\lambda }^{2}+20\,{\epsilon }^{2}{\omega } ^{3}{\lambda }^{2}+3\,{\lambda }^{2}{\sigma }^{2}\omega -{\lambda }^{2} \alpha \,\sigma \\ B= & {} \kappa +\alpha \,{\omega }^{2}-\sigma \,{ \omega }^{3}+\epsilon \,{\omega }^{4}. \end{aligned}$$

Balancing \({u}''\) and \({u}^{3}\) in Eq. (11) gives \(L=1\). Hence, Eq. (11) has the solution in the form, as

$$\begin{aligned} u(\xi )=\psi _{0}+\psi _{1}\Phi (\xi ), \end{aligned}$$
(12)

where \(\psi _{0}\) and \(\psi _{1}\) are the constants, such that \(\psi _{1}\ne 0\). Using Eq. (12) along Eq. (6) into Eq. (11) and equating the coefficients of all powers of \(\Phi ^{i}(\xi ),\quad i=0,~1,\ldots ,3\) to zero, the system of algebraic equations can be derived, as

$$\begin{aligned} \begin{aligned} \Phi ^{3}(\xi ):~&2\,A\psi _{{1}}b+\gamma \,\sigma \,{\psi _{{1}}}^{3}-4\,\gamma \,\epsilon \, \omega \,{\psi _{{1}}}^{3} =0, \\ \Phi ^{2}(\xi ):~&3\,\gamma \,\sigma \,\psi _{{0}}{\psi _{{1}}}^{2}-12\,\gamma \,\epsilon \, \omega \,\psi _{{0}}{\psi _{{1}}}^{2} =0, \\ \Phi ^{1}(\xi ):~&-4\,B\epsilon \,\omega \,\psi _{{1}}+B\sigma \,\psi _{{1}}+A\psi _{{1}}a+3\, \gamma \,\sigma \,{\psi _{{0}}}^{2}\psi _{{1}}-12\,\gamma \,\epsilon \, \omega \,{\psi _{{0}}}^{2}\psi _{{1}} =0, \\ \Phi ^{0}(\xi ):~&-4\,B\epsilon \,\omega \,\psi _{{0}}+B\sigma \,\psi _{{0}}+\gamma \,\sigma \, {\psi _{{0}}}^{3}-4\,\gamma \,\epsilon \,\omega \,{\psi _{{0}}}^{3} =0. \end{aligned} \end{aligned}$$

Solving the resulting system, we obtain

$$\begin{aligned} \begin{aligned}&\psi _{{0}}=0,~\psi _{{1}}=\sqrt{-{\frac{2\,Ab}{\gamma \,(\sigma -4\,\epsilon \, \omega )}}},\quad a={\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}} \end{aligned} \end{aligned}$$
(13)

Therefore, we provide the exact solutions of Eq. (1) as the following special cases:

Fig. 3
figure 3

3D-plots and contour plots of \(|{E}^{+}_{5}|,Re({E}^{+}_{5})~\) and \(Im({E}^{+}_{5})\) for \(\sigma =\alpha =1,~\epsilon =-0.7,~\lambda =1.5,~\omega =-1,~\kappa =1,~\gamma =-2,~ p=0.1,~q=0.2\) and \(\nu =1\)

Full size image
Fig. 4
figure 4

3D-plots and contour plots of \(|{E}^{+}_{7}|,Re({E}^{+}_{7})~\) and \(Im({E}^{+}_{7})\) for \(\sigma =1,~\alpha =1.5,~\epsilon =-2,~\lambda =1,~\omega =-1,~\kappa =3,~\gamma =-2,~ p=1,~q=0.1\) and \(\nu =1\)

Full size image

Case 1: If \(\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}>0\) and \(\rho =0\), then

$$\begin{aligned}{} & {} {E}^{\pm }_{1}(z, \tau )= \pm \sqrt{-{\frac{2\,pq B}{\gamma }}} {{{\,\textrm{sech}\,}}_{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} {E}^{\pm }_{2}(z, \tau )= \pm \sqrt{{\frac{2\,pq B}{\gamma }}} {{{\,\textrm{csch}\,}}_{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(15)

where,

$$\begin{aligned} {A}=-\lambda \,\epsilon +2\,\epsilon \,\alpha \,\omega \,{\lambda }^{2}-15\, \epsilon \,\sigma \,{\omega }^{2}{\lambda }^{2}+20\,{\epsilon }^{2}{\omega } ^{3}{\lambda }^{2}+3\,{\lambda }^{2}{\sigma }^{2}\omega -{\lambda }^{2} \alpha \,\sigma \end{aligned}$$

and

$$\begin{aligned} {B}=\kappa +\alpha \,{\omega }^{2}-\sigma \,{ \omega }^{3}+\epsilon \,{\omega }^{4}. \end{aligned}$$
Fig. 5
figure 5

3D-plots and contour plots of \(|{E}^{+}_{9}|,Re({E}^{+}_{9})~\) and \(Im({E}^{+}_{9})\) for \(\sigma =1,~\alpha =1,~\epsilon =-1,~\lambda =1,~\omega =-1,~\kappa =1,~\gamma =-2,~ p=0.2,~q=0.1\) and \(\nu =1\)

Full size image
Fig. 6
figure 6

3D-plots and contour plots of \(|{E}^{+}_{10}|,Re({E}^{+}_{10})~\) and \(Im({E}^{+}_{10})\) for \(\sigma =1,~\alpha =1.5,~\epsilon =2,~\lambda =1,~\omega =-1,~\kappa =3,~\gamma =2,~ p=0.9,~q=0.2\) and \(\nu =1\)

Full size image
Fig. 7
figure 7

3D-plots and contour plots of \(|{E}^{+}_{12}|,Re({E}^{+}_{12})~\) and \(Im({E}^{+}_{12})\) for \(\sigma =1,~\alpha =1.5,~\epsilon =2,~\lambda =1,~\omega =-1,~\kappa =1,~\gamma =2,~ p=0.1,~q=0.9\) and \(\nu =1\)

Full size image
Fig. 8
figure 8

3D-plots and contour plots of \(|{E}^{+}_{14}|,Re({E}^{+}_{14})~\) and \(Im({E}^{+}_{14})\) for \(\sigma =1,~\alpha =1.5,~\epsilon =2,~\lambda =-1,~\omega =-0.2,~\kappa =1,~\gamma =2,~ p=1,~q=0.1\) and \(\nu =1\)

Full size image

Case 2: If \(\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}<0\) and \(\rho =0\), then

$$\begin{aligned}{} & {} {E}^{\pm }_{3}(z, \tau )= \pm \sqrt{-{\frac{2\,pq B}{\gamma }}} {\sec _{pq}}\nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} {E}^{\pm }_{4}(z, \tau )= \pm \sqrt{-{\frac{2\,pq B}{\gamma }}} {\csc _{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}\cdot \end{aligned}$$
(17)

Case 3: If \(\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}<0\) and \(\rho =\frac{{a}^{2}}{4b}\), then

$$\begin{aligned}{} & {} {E}^{\pm }_{5}(z, \tau )=\pm \sqrt{-{\frac{ B}{\gamma }}} {\tanh _{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( \sigma -4\,\epsilon \,\omega \right) }{2\,A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \quad {E}^{\pm }_{6}(z, \tau )=\pm \sqrt{-{\frac{ B}{\gamma }}} {\coth _{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( \sigma -4\,\epsilon \,\omega \right) }{2\,A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} {E}^{\pm }_{7}(z, \tau )= \pm \sqrt{-{\frac{ B}{\gamma }}} \Bigg ({\tanh _{pq}} \left( \sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad \pm \, {i}\sqrt{p\,q\,}{{{\,\textrm{sech}\,}}_{pq}} \left( \sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} {E}^{\pm }_{8}(z, \tau )= \pm \sqrt{-{\frac{ B}{\gamma }}} \Bigg ({\coth _{pq}} \left( \sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad \pm \, \sqrt{p\,q\,}{{{\,\textrm{csch}\,}}_{pq}} \left( \sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} {E}^{\pm }_{9}(z, \tau )= \pm \frac{1}{2}\sqrt{-{\frac{ B}{\gamma }}} \Bigg ({\tanh _{pq}} \left( \frac{1}{4}\sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad +\, {\coth _{pq}} \left( \frac{1}{4} \sqrt{{\frac{2\,B \left( \sigma -4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}\cdot \end{aligned}$$
(22)

Case 4: If \(\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}>0\) and \(\rho =\frac{{a}^{2}}{4b}\), then

$$\begin{aligned}{} & {} {E}^{\pm }_{10}(z, \tau )=\pm \sqrt{{\frac{ B}{\gamma }}} {\tan _{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{2\,A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(23)
$$\begin{aligned}{} & {} {E}^{\pm }_{11}(z, \tau )=\pm \sqrt{{\frac{ B}{\gamma }}} {\cot _{pq}} \nonumber \\{} & {} \quad \left( \sqrt{{\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{2\,A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} {E}^{\pm }_{12}(z, \tau )= \pm \sqrt{{\frac{ B}{\gamma }}} \Bigg ({\tan _{pq}}\left( \sqrt{{\frac{2\,B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad \pm \, \sqrt{p\,q\,}{\sec _{pq}} \left( \sqrt{{\frac{2\,B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} {E}^{\pm }_{13}(z, \tau )= \pm \sqrt{{\frac{ B}{\gamma }}} \Bigg ({\cot _{pq}} \left( \sqrt{{\frac{2\,B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad \pm \, \sqrt{p\,q\,}{\csc _{pq}} \left( \sqrt{{\frac{2\,B \left( - \sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} {E}^{\pm }_{14}(z, \tau )= \pm \frac{1}{2}\sqrt{{\frac{ B}{\gamma }}} \Bigg ({\tan _{pq}} \left( \frac{1}{4}\sqrt{{\frac{2\,B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \nonumber \\{} & {} \quad +\, {\cot _{pq}} \left( \frac{1}{4} \sqrt{{\frac{2\,B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}}}\left( z-{\frac{\lambda \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }\right) \right) \Bigg ) {\textrm{e}^{i\left( -\kappa z+{\frac{\omega \,}{\nu }} \Big ( \tau + \frac{1}{ \Gamma \left( \nu \right) } \Big ) ^{\nu }+\eta _{{0}}\right) }}\cdot \end{aligned}$$
(27)

4 Graphical interpretation

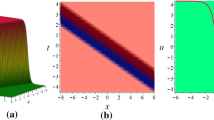
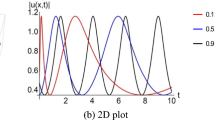
In this section, we analyze the dynamical nature of some of the solutions that are obtained for the optical pulse envelope \(E(z,~ \tau )\) with \(\nu\)-time derivative. We can observe from the results obtained in this paper that all orders of dispersion lead to the generation of optical soliton solutions in the considered model. Consequently, our findings may have practical implications for utilizing optical solitons in optical fiber media with dispersion effects up to the fourth order. Additionally, we identify several new exact solutions by comparing the results of this paper to those in Triki and Kruglov (2020), Demiray (2020). Figures 1, 2, 3, 4, 5, 6, 7 and 8) represent the 3D–plots and contour plots of \(|{E}^{+}_{i}|,Re({E}^{+}_{i})~\) and \(Im({E}^{+}_{i})\), \((i=1,~3,~5,~7,~9,~10,~12,~14)\).

The dynamical behavior of soliton solutions calculated for the generalized NLSE (1) is depicted in the cases 1–4, subject to the existence criteria for the parameter a. For instance, we illustrate the solutions \(|{E}^{+}_{1}|\), \(Re({E}^{+}_{1})~\) and \(Im({E}^{+}_{1})\) in Fig. 1a–f with the parameter values \(\sigma =-1,~\alpha =1,~\epsilon =0.25,~\lambda =0.1,~\omega =-1.05,~\kappa =1\). These values also satisfy the restrictive condition \(a={\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}} > 0\) as indicated in the case 1. Furthermore, we determine the values of A and B using the relations \({A}=-\lambda \,\epsilon +2\,\epsilon \,\alpha \,\omega \,{\lambda }^{2}-15\, \epsilon \,\sigma \,{\omega }^{2}{\lambda }^{2}+20\,{\epsilon }^{2}{\omega } ^{3}{\lambda }^{2}+3\,{\lambda }^{2}{\sigma }^{2}\omega -{\lambda }^{2} \alpha \,\sigma\) and \({B}=\kappa +\alpha \,{\omega }^{2}-\sigma \,{ \omega }^{3}+\epsilon \,{\omega }^{4}.\) Fig. 1a represents the bright soliton solution \(|{E}^{+}_{1}|\), while the periodic wave solutions \(Re({E}^{+}_{1})\) and \(Im({E}^{+}_{1})\) are depicted in Fig. 1b, c, respectively. Similarly, we obtain the solutions \(|{E}^{+}_{3}|\), \(Re({E}^{+}_{3})\) and \(Im({E}^{+}_{3})\) in Fig. 2a–f with the parameter values \(\sigma =1.4,~\alpha =0.5,~\epsilon =0.25,~\lambda =\omega =\kappa =1\) satisfying the constraint condition \(a={\frac{B \left( -\sigma +4\,\epsilon \,\omega \right) }{A}} < 0\) as indicated in case 2. In Fig. 2a–f, the soliton solutions \(|{E}^{+}_{3}|\), \(Re({E}^{+}_{3})\) and \(Im({E}^{+}_{3})\) occur periodically along the propagation distance. In this regard, Fig. 3a represents the kink-type wave profile of solution \(|{E}^{+}_{5}|\), while Fig. 3b, c reveal the solutions \(Re({E}^{+}_{5})\) and \(Im({E}^{+}_{5})\), respectively. Fig. 4a depicts the dark soliton solution \(|{E}^{+}_{7}|\), whereas Fig. 4b, c reveal the periodic dark-bright wave solutions \(Re({E}^{+}_{7})\) and \(Im({E}^{+}_{7})\), respectively. Furthermore, we obtain the bright-singular, singular and periodic solitary wave structures in Figs. 5, 6, 7 and 8 revealed by the solutions \({E}^{+}_{9}\), \({E}^{+}_{10}\), \({E}^{+}_{12}\) and \({E}^{+}_{14}\).

5 Conclusion

In this paper, we have investigated the exact solutions of the NLSE (1) for the pulse envelope \({E}(z,\tau )\) with \(\nu\)-time derivative governing the effects of dispersion up to fourth order using the Sardar subequation method. We have successfully retrieved bright, dark-bright, kink, dark, bright-singular, and periodic solitary wave solutions of the NLSE (1). Additionally, we have presented graphical interpretations that demonstrate the potential application of the proposed method for suitable choices of parameters. In this study, it is vital to take into account the integration of conformal derivatives, as it significantly enhances the precision of describing soliton propagation through high-order dispersive optical fibers. In the future, this approach will be utilized to study the soliton solutions of the high-order NLSE with third and fourth-order dispersion and the cubic-quintic nonlinear terms.