New fascination of solitons and other wave solutions of a nonlinear model depicting ultra-short pulses in optical fibers

Abstract

Nonlinear models arise in numerous branches of science have become the core fascination of the scholars and scientists to illustrate the complexity of the real-life phenomena involved in the nature world. This paper is conducted to extract solitons and other solitary wave solutions of the generalized nonlinear Schrodinger model of order three through two influenced techniques namely, rational $({G}^{\prime}/G)$-expansion and improved tanh tools. The considered model governs wide ranging applications in numerous fields like short-ultra pulses in optical fibers. A heap of hyperbolic, rational, and trigonometric function solutions is successfully constructed by means of the suggested schemes in a decent manner. A few of the acquired outcomes are characterized graphically in 3D profiles, contour shapes and 2D outlines to describe the dynamical behavior. Contour plots describe the density of nonlinearity and 2D sketches make clear the dynamic nature of pulse propagation. A comparable experiment of the constructed results with the prevailing outcomes in literature establishes the novelty and diversity of our achieved solutions and hence confirms the high performance of the used tools as before.

1 Introduction

The universe survives by fighting with various nonlinear substances. These nonlinear convoluted phenomena have been demonstrated with the assistance of nonlinear partial differential equations arise in solid state physics, plasma physics, chemical physics, circuit analysis, fluid mechanics, optical fiber, population ecology, meteorology, aerospace industry, oceanography geochemistry, and numerous branches of nonlinear science (Wazwaz, 2002; Miller and Ross 1993; Kilbas et al. 2006; Oldham and Spanier 1974). Among these nonlinear models the Schrodinger equations have been attracted the scholars due to their significant roles in understanding and describing the underlying behavior of the logarithm law, Kerr law media, polynomial law, saturable law, power law, triple-power law, and dual-power law etc. (Rizvi et al. 2017; Pandir and Duzgun 2019; Malik et al. 2021a; Ismael et al. 2021; Liu et al. 2017; Salam et al. 2016; Islam et al. 2021a; Zayed et al. 2021). Numerous analytical as well as numerical techniques have been derived by knowledge hunters to construct wave solutions of nonlinear partial models. The nonlinear Schrodinger equations have been investigated by using the tools available in literature. As for instant, the extended simple equation method (Lu et al. 2017; Rabie et al. 2021), trial solution and Q-function schemes (Arnous et al. 2017), $({G}^{\prime}/G)$-expansion scheme (Younis et al. 2015a), the ansatz scheme (Younis et al. 2015b), the improved auxiliary equation technique (Islam et al. 2021b), various modifications of the sinh-Gordon techniques (Sulaiman et al. 2019, 2018; Younas et al. 2022a; Sulaiman and Bulut 2019a, 2019b; Sulaiman 2020), the Kudryashov tool (Salahshour et al. 2021), the Hirota approach (Yu et al. 2019), the $({G}^{\prime}/{G}^{2})$-expansion function method (Sulaiman et al. 2022; Younas et al. 2022b), the new extended hyperbolic function and various tanh schemes (Asjad et al. 2021; Ozisik et al. 2022), the Riccati-Bernoulli sub-ODE technique (Ozdemir et al. 2022), the sine–Gordon expansion method (Bulut et al. 2019), the generalized exponential rational function process (Gunay 2021), the extended trial function (Biswas et al. 2020), the modified Khater and modified Jacobian expansion methods (Alshahrani et al. 2021), the modified auxiliary equation, the direct algebraic, and the generalized Kudryashov tools (Khater et al. 2021; Younas et al. 2022c; Younas and Ren 2022), the extended Fan-sub equation method (Younas and Ren 2021; Younas et al. 2022d), the transformed rational function $V$-expansion method (Jhangeer et al. 2021), the extended rational sine–cosine / sinh-cosh, and the modified direct algebraic approaches (Bilal et al. 2021), the ${\Phi }^{6}$-model expansion method (Younas et al. 2021, 2022e, 2022f) etc.

This present work deals with the generalized third-order nonlinear Schrodinger model

$$i\left( {\phi_{t} + \phi_{xxx} } \right) + \left| \phi \right|^{2} \left( {b\phi + ic\phi_{x} } \right) + id\left( {\left| \phi \right|^{2} } \right)_{x} \phi = 0,$$

(1.1)

where $\phi$ is a complex function of time-variable $t$ and space-variable $x$; $b$ effects the cubic nonlinearity; $c$ and $d$ effect the dispersive terms. Earlier, this complex model have been taken into account to seek for closed form solutions by the researchers such as Lu et al. have studied Eq. (1.1) by using extended simple equation tool and exp $(-\Phi (\xi ))$-expansion technique which provided analytical wave solutions (Lu et al. 2019); the same model has been investigated by Nasreen et al. for exact solutions via the Riccati mapping method (Nasreen et al. 2019); the exp_a-function and unified methods have been utilized to assemble and analyse the solutions of the mentioned model by Hosseini et al. (Hosseini et al. 2020); Malik et al. have employed Lie symmetry analysis, and new extended generalized and new generalized Kudryashov methods providing different optical soliton solutions (Malik et al. 2021b). Consequently, improved tanh and rational $({G}^{\prime}/G)$-expansion schemes are put forward to pursue diverse solitons and other solitary wave solutions of the governing equation shown in Eq. (1.1).

Soliton theory has fascinated deep concentration in investigational surveys for being effective research area subjective to mathematical physics, engineering, telecommunication, and many other problems arise in nonlinear sciences. Currently, optical solitons have taken great importance from scholars due to their substantial roles to analyse relevant intricate phenomena. Optical solitons are special type of solitary waves which remain unchanged during the propagation in long distance. Solitons are helpful in extensive range in the mechanism of signal-based fiber-optic amplifiers, optical pulse compressors, communication links, and several others. We pay our attention to construct diverse solitons related to optical fibers. Subsequently, this exploration adopts the advised techniques successfully and accumulates superabundant accurate wave solutions which might be visible first time in the literature.

2 Explanation of the methods

We suppose the nonlinear evolution equation.

$$\Omega \left(u,{u}_{x},{u}_{y},{u}_{t},\dots ,{u}_{xy},{u}_{xt},{u}_{yt},\dots ,{u}_{xx},{u}_{yy},{u}_{tt}, \dots \right)=0, \quad 0<\alpha \le 1$$

(2.1)

Initiating new type wave variable.

$$u=U\left(\phi \right) \phi =\phi (x,y,t,\dots )$$

(2.2)

converts Eq. (2.2) into ODE of a single variable $\phi$ as.

$$\Xi \left( {U,U^{\prime} ,U^{\prime\prime} ,{\text{U}}^{\prime \prime \prime} , \ldots \ldots \ldots { = 0}} \right) \,$$

(2.3)

One may integrate above equation and consider the integral constant zero as seeking for soliton solutions. The major dealings of the recommended procedures are stated bellow:

2.1 Improved tanh technique

This competent tool defines the solution of Eq. (2.1) as

$$U(\sigma )=\frac{{\iota }_{0}+\sum_{i=1}^{e}({\iota }_{i}{\Phi }^{i}(\sigma )+{\tau }_{i}{\Phi }^{-i}(\sigma ))}{{\epsilon }_{0}+\sum_{i=1}^{e}({\epsilon }_{i}{\Phi }^{i}(\sigma )+{\varepsilon }_{i}{\Phi }^{-i}(\sigma ))}$$

(`)

whose unknown constants are determined hereafter (Islam and Akter 2021; Islam et al. 2021c). The value of $e$ is evaluated by applying the homogeneous theme to Eq. (2.3). The function $\Phi =\Phi \left(\sigma \right)$ satisfies

$${\Phi }^{\prime}\left(\sigma \right)=\delta +{\Phi }^{2}(\sigma )$$

(2.1.2)

where $\delta$ is an arbitrary parameter. Equation (2.1.2) has the solutions

$$(i)\,\Phi \left(\sigma \right)=-\sqrt{-\delta }\mathrm{tanh}\left(\sqrt{-\delta }\sigma \right)\mathrm{ or \Phi }\left(\sigma \right)=-\sqrt{-\delta }\mathrm{coth}\left(\sqrt{-\delta }\sigma \right),\delta <0$$

(2.1.3)

$$(ii)\,\Phi \left(\sigma \right)=-\frac{1}{\sigma },\delta =0$$

(2.1.4)

$$(iii)\,\Phi \left(\sigma \right)=\sqrt{\delta }\mathrm{tan}\left(\sqrt{\delta }\sigma \right) \mathrm{or \Phi }\left(\sigma \right)=-\sqrt{\delta }\mathrm{cot}\left(\sqrt{\delta }\sigma \right),\delta >0$$

(2.1.5)

A polynomial in $\Phi \left(\sigma \right)$ is produced after inserting Eq. (2.1.1) and its necessary derivatives in Eq. (2.3). Assign like terms to zero and solve them by Maple for the arbitrary parameters appeared in Eq. (2.1.1) and $\delta$. Inserting the found outcomes in Eq. (2.1.1) and thereupon the solutions of Eq. (2.1.2) provide the closed form solitary wave solutions for Eq. (2.1).

2.2 Rational $({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})$-expansion approach

The solution of Eq. (2.1) due to this competent approach is stated to be the form.

$$U\left(\sigma \right)=\frac{\sum_{i=0}^{e}{\iota }_{i}{({G}^{\prime}\left(\sigma \right)/G\left(\sigma \right))}^{i}}{\sum_{i=0}^{e}{\tau }_{i}{\left({G}^{\prime}\left(\sigma \right)/G\left(\sigma \right)\right)}^{i}}$$

(2.2.1)

where $\iota_{i} \prime {\text{s}}$ and $\tau_{i} \prime {\text{s}}$ are free constants to be fixed next; $e$ is valued after making homogenous balance of required terms in (2.3) (Islam et al. 2018; Akbar et al. 2019). The function $G\left(\sigma \right)$ satisfies.

$${G}^{\prime\prime}\left(\sigma \right)+g{G}^{\prime}\left(\sigma \right)+hG\left(\sigma \right)=0$$

(2.2.2)

whose solutions are

$$\frac{{G}^{\prime}(\sigma )}{G(\sigma )}=\frac{\left\{-g+\sqrt{{g}^{2}-4h}\mathrm{tanh}\left(0.5\sqrt{{g}^{2}-4h}\sigma \right)\right\}}{2}{g}^{2}-4h>0$$

(2.2.3)

$$\frac{{G}^{\prime}(\sigma )}{G(\sigma )}=\{-g+\sqrt{{g}^{2}-4h}\mathrm{coth}(0.5\sqrt{{g}^{2}-4h}\sigma )\}/2{g}^{2}-4h>0$$

(2.2.4)

$$\frac{{G}^{\prime}(\sigma )}{G(\sigma )}=\frac{1}{\sigma }-\frac{g}{2} {g}^{2}-4h=0$$

(2.2.5)

$$\frac{{G}^{\prime}(\sigma )}{G(\sigma )}=\{-g-\sqrt{4h-{g}^{2}}\mathrm{tan}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2 {g}^{2}-4h<0$$

(2.2.6)

$$\frac{{G}^{\prime}(\sigma )}{G(\sigma )}=\{-g+\sqrt{4h-{g}^{2}}\mathrm{cot}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2{g}^{2}-4h<0$$

(2.2.7)

A polynomial in $(G\prime (\sigma ){\text{/G}}(\sigma ))$ is found by inserting Eq. (2.2.1) and its various derivatives into Eq. (2.3). A group of overdetermined algebraic equations is formed after assigning the like terms of the polynomial. Solving this system by computational software Maple provides the values of engaged parameters. Equation (2.2.1) alongside the parameter’s values and the solutions of Eq. (2.2.2) delivers the preferred solutions for Eq. (2.1).

3 Presentation of wave solutions

In this section, the governing Schrodinger model is unraveled by employing two proficient tools such as improved tanh and rational $({G}^{\prime}/G)$-expansion techniques. We announce the transformation.

$$\phi \left(x,t\right)=u\left(\sigma \right){e}^{iv(x,t)}v\left(x,t\right)=ax+\lambda t+\theta \sigma =\kappa x+\omega t$$

(3.1)

The adaptation of the transformation (3.1) in Eq. (1.1) leaves

$$3a\kappa^{2} u^{\prime \prime} { + }\left( {\lambda {\text{ - a}}^{{3}} } \right){\text{u + }}\left( {\text{ac - b}} \right){\text{u}}^{{3}} { = 0}$$

(3.2)

$${\kappa }^{3}{u}^{{\prime \prime \prime}}+\left(\omega -3\kappa {a}^{2}\right){u}^{\prime}+\kappa \left(c+2d\right){u}^{2}{u}^{\prime}=0$$

(3.3)

Integrating Eq. (3.3) yields.

$$3{\kappa}^{3} {u}^{\prime \prime}+3\left(\omega -3\kappa {a}^{2}\right)u+\kappa \left(c+2d\right){u}^{3}=0$$

(3.4)

where integral constant is ignored. Equation (3.2) coincides with Eq. (3.4) and hence becomes.

$$3{\kappa }^{2}{u}^{\prime \prime}+\left(3\omega -9{a}^{2}\kappa \right)u+\left(c+2d\right){u}^{3}=0$$

(3.5)

under the conditions $b=-2ad$ $\lambda =\frac{3a\omega -8{a}^{3}\kappa }{\kappa }$ Utilizing homogeneous theme to Eq. (3.5) provides $e=1$. Now, we adopt the suggested techniques.

3.1 Solutions through improved tanh approach

The balancing number forces Eq. (2.1.1) to be.

$$u(\sigma )=\frac{{\iota }_{0}+{\iota }_{1}\Phi \left(\sigma \right)+{\tau }_{1}{\Phi }^{-1}(\sigma )}{{\epsilon }_{0}+{\epsilon }_{1}\Phi \left(\sigma \right)+{\varepsilon }_{1}{\Phi }^{-1}(\sigma )}$$

(3.1.1)

Equation (3.2) along with Eqs. (3.1.1), (2.1.1) turns into a polynomial in $\Phi \left( \sigma \right)$. Equating similar terms of the polynomial and resolving them by computer package Maple, the outcomes are collected as bellow:

$\mathrm{Case}\, 1: {\iota }_{0}=\pm \frac{\kappa {\varepsilon }_{1}\sqrt{6}}{\sqrt{-(c+2d)}},\,{\iota }_{1}={\tau }_{1}={\epsilon }_{0}={\epsilon }_{1}=0,\,\delta =\frac{3{a}^{2}\kappa -\omega }{2{\kappa }^{3}}$

$\mathrm{Case}\, 2: {\iota }_{0}={\iota }_{1}=0,\,{\epsilon }_{0}=\pm \frac{\kappa {\tau }_{1}\sqrt{-6\kappa (c+2d)}}{3(3{a}^{2}\kappa -\omega )} {\epsilon }_{1}={\varepsilon }_{1}=0,\,\delta =\frac{3{a}^{2}\kappa -\omega }{2{\kappa }^{3}}$

$\mathrm{Case}\, 3:{\iota}_{1}=0,\,{\tau }_{1}=\pm \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{-6\kappa (c+2d)}},\,{ \epsilon }_{1}=0,\,{\varepsilon }_{1}=\pm \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}},\,\delta =\frac{3{a}^{2}\kappa -\omega }{2{\kappa }^{3}}$

${\mathrm{Case}} \,4: {\iota}_{0}=0,\,{\tau }_{1}=\pm \frac{{\iota }_{1}(\omega -3{a}^{2}\kappa )}{4{\kappa }^{3}},\,{\epsilon }_{0}=\pm \frac{{\iota }_{1}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}},\,{\epsilon }_{1}={\varepsilon }_{1}=0,\, \delta =\frac{\omega -3{a}^{2}\kappa }{4{\kappa }^{3}}$

${\mathrm{Case}} \,5: {\iota }_{0}=0,\,{\tau }_{1}=\pm \frac{{\iota }_{1}(\omega -3{a}^{2}\kappa )}{8{\kappa }^{3}},\,{\epsilon }_{0}=\pm \frac{{\iota }_{1}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}},\,{\epsilon }_{1}={\varepsilon }_{1}=0,\,\delta =\frac{3{a}^{2}\kappa -\omega }{8{\kappa }^{3}}$

${\mathrm{Case}} \,6: {\iota}_{0}=\mp \frac{\kappa {\varepsilon }_{1}\sqrt{6\kappa }}{\sqrt{-\left(c+2d\right)}},\,{\tau }_{1}=0,\,{\epsilon }_{0}=\pm \frac{{\iota }_{1}\sqrt{-6\kappa \left(c+2d\right)}}{6{\kappa }^{2}},\,{\epsilon }_{1}=0,\,\delta =\frac{3{a}^{2}\kappa -\omega }{2{\kappa }^{3}}$

Merging these cases in Eq. (3.1.1) and then the results (2.1.3)–(2.1.5) deliver the accepted accurate traveling wave solutions as follows:

Solution group 1: Inserting case 1 in solution Eq. (3.1.1) and consequently in Eq. (3.1) provides.

$$\phi \left(x,t\right)=\pm \kappa {e}^{iv(x,t)}\sqrt{-6/(c+2d)}\Phi (\sigma )$$

(3.1.2)

Equation (3.1.2) with the support (2.1.3)–(2.1.5) give the solutions

$${\phi }_{1}\left(x,t\right)=\mp \kappa {e}^{iv\left(x,t\right)}\sqrt{6\delta /\left(c+2d\right)}\mathrm{tanh}\left(\sqrt{-\delta} \sigma \right),\,\delta <0$$

(3.1.3)

$${\phi }_{2}\left(x,t\right)=\mp \kappa {e}^{iv\left(x,t\right)}\sqrt{6\delta /\left(c+2d\right)}\mathrm{coth}\left(\sqrt{-\delta }\sigma \right),\,\delta <0$$

(3.1.4)

$${\phi }_{3}\left(x,t\right)=\mp \frac{\kappa {e}^{iv\left(x,t\right)}\sqrt{-6/\left(c+2d\right)}}{\sigma},\,\delta =0$$

(3.1.5)

$${\phi }_{4}\left(x,t\right)=\pm \kappa {e}^{iv\left(x,t\right)}\sqrt{-6\delta /\left(c+2d\right)}\mathrm{tan}\left(\sqrt{\delta }\sigma \right),\,\delta >0$$

(3.1.6)

$${\phi }_{5}\left(x,t\right)=\mp \kappa {e}^{iv\left(x,t\right)}\sqrt{-6\delta /\left(c+2d\right)}\mathrm{cot}\left(\sqrt{\delta }\sigma \right),\,\delta >0$$

(3.1.7)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t$

Solution group 2: Inserting case 2 in solution Eq. (3.1.1) and hence in Eq. (3.1) provides.

$$\phi \left(x,t\right)=\frac{3(3{a}^{2}\kappa -\omega ){e}^{iv(x,t)}}{\pm \kappa \sqrt{-6\kappa (c+2d)}\Phi (\sigma )}$$

(3.1.8)

Equation (3.1.8) together with (2.1.3)–(2.1.5) offer the solutions

$${\phi }_{6}\left(x,t\right)=\frac{3(3{a}^{2}\kappa -\omega ){e}^{iv(x,t)}}{\mp \kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{tanh}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.9)

$${\phi }_{7}\left(x,t\right)=\frac{3(3{a}^{2}\kappa -\omega ){e}^{iv(x,t)}}{\mp \kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{coth}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.10)

$${\phi }_{8}\left(x,t\right)=\frac{3(3{a}^{2}\kappa -\omega ){e}^{iv(x,t)}}{\pm \kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{tan}(\sqrt{\delta }\sigma )},\,\delta >0$$

(3.1.11)

$${\phi }_{9}\left(x,t\right)=\frac{3(3{a}^{2}\kappa -\omega ){e}^{iv(x,t)}}{\mp \kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{cot}(\sqrt{\delta }\sigma )},\,\delta >0$$

(3.1.12)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t$

Solution group 3: Inserting case 3 in solution Eq. (3.1.1) and hence in Eq. (3.1) provides.

$$\phi \left(x,t\right)=\frac{{\iota }_{0}\pm \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{-6\kappa (c+2d)}\Phi (\sigma )}}{{\epsilon }_{0}\pm \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}\Phi (\sigma )}}{e}^{iv(x,t)}$$

(3.1.13)

Equation (3.1.13) alongside (2.1.3)–(2.1.5) present the solutions

$${\phi }_{10}\left(x,t\right)={e}^{iv(x,t)}\times \frac{{\iota }_{0}\mp \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{tanh}(\sqrt{-\delta }\sigma )}}{{\epsilon }_{0}\mp \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}\sqrt{-\delta }\mathrm{tanh}(\sqrt{-\delta }\sigma )}},\,\delta <0$$

(3.1.14)

$${\phi }_{11}\left(x,t\right)={e}^{iv(x,t)}\times \frac{{\iota }_{0}\mp \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{coth}(\sqrt{-\delta }\sigma )}}{{\epsilon }_{0}\mp \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}\sqrt{-\delta }\mathrm{coth}(\sqrt{-\delta }\sigma )}},\,\delta <0$$

(3.1.15)

$${\phi }_{12}\left(x,t\right)=\frac{6{\kappa }^{2}{\iota }_{0}{e}^{iv(x,t)}}{6{\kappa }^{2}{\epsilon }_{0}\mp {\iota }_{0}\sigma \sqrt{-6\kappa (c+2d)}},\,\delta =0$$

(3.1.16)

$${\phi }_{13}\left(x,t\right)={e}^{iv(x,t)}\times \frac{{\iota }_{0}\pm \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{tan}(\sqrt{\delta }\sigma )}}{{\epsilon }_{0}\pm \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}\sqrt{\delta }\mathrm{tan}(\sqrt{\delta }\sigma ) }},\,\delta >0$$

(3.1.17)

$${\phi }_{14}\left(x,t\right)={e}^{iv(x,t)}\times \frac{{\iota }_{0}\mp \frac{3{\epsilon }_{0}(\omega -3{a}^{2}\kappa )}{\kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{cot}(\sqrt{\delta }\sigma )}}{{\epsilon }_{0}\mp \frac{{\iota }_{0}\sqrt{-6\kappa (c+2d)}}{6{\kappa }^{2}\sqrt{\delta }\mathrm{cot}(\sqrt{\delta }\sigma )}},\,\delta >0$$

(3.1.18)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t$

Solution group 4: Inserting case 4 in solution Eq. (3.1.1) and hence in Eq. (3.1) provides

$$\phi \left(x,t\right)=\frac{3{e}^{iv(x,t)}\{4{\kappa }^{3}{\Phi }^{2}(\sigma )\pm (\omega -3{a}^{2}\kappa )\}}{\pm 2\kappa \sqrt{-6\kappa (c+2d)}\Phi (\sigma )}$$

(3.1.19)

Equation (3.1.19) with the assistance (2.1.3)–(2.1.5) create the solutions

$${\phi }_{15}\left(x,t\right)=\frac{3{e}^{iv(x,t)}\{4{\kappa }^{3}\{-\delta {\mathrm{tanh}}^{2}(\sqrt{-\delta }\sigma )\}\pm (\omega -3{a}^{2}\kappa )\}}{\mp 2\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{tanh}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.20)

$${\phi }_{16}\left(x,t\right)=\frac{3{e}^{iv(x,t)}\{4{\kappa }^{3}\{-\delta {\mathrm{coth}}^{2}(\sqrt{-\delta }\sigma )\}\pm (\omega -3{a}^{2}\kappa )\}}{\mp 2\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{coth}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.21)

$${\phi }_{17}\left(x,t\right)=\frac{6{{\kappa }^{2}e}^{iv(x,t)}}{\mp \sigma \sqrt{-6\kappa (c+2d)}},\,\delta =0$$

(3.1.22)

$${\phi }_{18}\left(x,t\right)=\frac{3{e}^{iv(x,t)}\{4{\kappa }^{3}\{\delta {\mathrm{tan}}^{2}(\sqrt{\delta }\sigma )\}\pm (\omega -3{a}^{2}\kappa )\}}{\pm 2\kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{tan}(\sqrt{\delta }\sigma )},\,\delta >0$$

(3.1.23)

$${\phi }_{19}\left(x,t\right)=\frac{3{e}^{iv(x,t)}\{4{\kappa }^{3}\{\delta {\mathrm{cot}}^{2}(\sqrt{\delta }\sigma )\}\pm (\omega -3{a}^{2}\kappa )\}}{\mp 2\kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{cot}(\sqrt{\delta }\sigma )},\,\delta >0$$

(3.1.24)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta ,\sigma =\kappa x+\omega t$.

Solution group 5: Inserting case 5 in solution Eq. (3.1.1) and hence in Eq. (3.1) provides

$$\phi \left(x,t\right)=\pm \frac{3{e}^{iv(x,t)}\{8{\kappa }^{3}{\Phi }^{2}\left(\sigma \right)\pm \left(\omega -3{a}^{2}\kappa \right)\}}{4\kappa \sqrt{-6\kappa (c+2d)}\Phi (\sigma )}$$

(3.1.25)

Equation (3.1.25) including (2.1.3)–(2.1.5) provide the solutions

$${\phi }_{20}\left(x,t\right)=\pm \frac{3{e}^{iv(x,t)}\{8{\kappa }^{3}\left\{\delta {\mathrm{tanh}}^{2}(\sqrt{-\delta }\sigma )\right\}\mp (\omega -3{a}^{2}\kappa )\}}{4\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{tanh}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.26)

$${\phi }_{21}\left(x,t\right)=\pm \frac{3{e}^{iv(x,t)}\{8{\kappa }^{3}\left\{\delta {\mathrm{coth}}^{2}(\sqrt{-\delta }\sigma )\right\}\mp (\omega -3{a}^{2}\kappa )\}}{4\kappa \sqrt{6\delta \kappa (c+2d)}\mathrm{coth}(\sqrt{-\delta }\sigma )},\,\delta <0$$

(3.1.27)

$${\phi }_{22}\left(x,t\right)=\mp \frac{6{\kappa }^{2}{e}^{iv\left(x,t\right)}}{\sigma \sqrt{-6\kappa \left(c+2d\right)}},\,\delta =0$$

(3.1.28)

$${\phi }_{23}\left(x,t\right)=\pm \frac{3{e}^{iv(x,t)}\{8{\kappa }^{3}\delta {\mathrm{tan}}^{2}\left(\sqrt{\delta }\sigma \right)\pm (\omega -3{a}^{2}\kappa )\}}{4\kappa \sqrt{-6\delta \kappa (c+2d)}\mathrm{tan}(\sqrt{\delta }\sigma )},\,\delta >0$$

(3.1.29)

$${\phi }_{24}\left(x,t\right)=\mp \frac{3{e}^{iv\left(x,t\right)}\left\{8{\kappa }^{3}\delta {\mathrm{cot}}^{2}\left(\sqrt{\delta }\sigma \right)\pm \left(\omega -3{a}^{2}\kappa \right)\right\}}{4\kappa \sqrt{-6\delta \kappa \left(c+2d\right)}\mathrm{cot}\left(\sqrt{\delta }\sigma \right)},\,\delta >0$$

(3.1.30)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t$

Solution group 6: Inserting case 6 in solution Eq. (3.1.1) and hence in Eq. (3.1) provides.

$$\phi \left(x,t\right)=\frac{6{\kappa }^{2}{e}^{iv(x,t)}\Phi (\sigma )\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }+{\iota }_{1}\sqrt{-(c+2d)}\Phi \left(\sigma \right)\}}{\pm {\iota }_{1}(c+2d)\sqrt{6\kappa }\Phi (\sigma )+6{\kappa }^{2}{\varepsilon }_{1}\sqrt{-(c+2d)}}$$

(3.1.31)

Equation (3.1.31) combining with (2.1.3)–(2.1.5) deliver the solutions

$${\phi }_{25}\left(x,t\right)=\frac{-6{\kappa }^{2}{e}^{iv\left(x,t\right)}\sqrt{-\delta }\mathrm{tanh}(\sqrt{-\delta }\sigma )\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }-{\iota }_{1}\sqrt{\delta \left(c+2d\right)}\mathrm{tanh}(\sqrt{-\delta }\sigma )\}}{\mp {\iota }_{1}\left(c+2d\right)\sqrt{-6\delta \kappa }\mathrm{tanh}(\sqrt{-\delta }\sigma )+6{\kappa }^{2}{\varepsilon }_{1}\sqrt{-(c+2d)}},\,\delta <0$$

(3.1.32)

$${\phi }_{26}\left(x,t\right)=\frac{-6{\kappa }^{2}{e}^{iv\left(x,t\right)}\sqrt{-\delta }\mathrm{coth}(\sqrt{-\delta }\sigma )\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }-{\iota }_{1}\sqrt{\delta \left(c+2d\right)}\mathrm{coth}(\sqrt{-\delta }\sigma )\}}{\mp {\iota }_{1}\left(c+2d\right)\sqrt{-6\delta \kappa }\mathrm{coth}(\sqrt{-\delta }\sigma )+6{\kappa }^{2}{\varepsilon }_{1}\sqrt{-(c+2d)}},\,\delta <0$$

(3.1.33)

$${\phi }_{27}\left(x,t\right)=\frac{-6{\kappa }^{2}{e}^{iv(x,t)}\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }-{\iota }_{1}\sqrt{-\left(c+2d\right)}(1/\sigma )\}}{\mp {\iota }_{1}\left(c+2d\right)\sqrt{6\kappa }+6{\kappa }^{2}{\varepsilon }_{1}\sigma \sqrt{-(c+2d)}},\,\delta =0$$

(3.1.34)

$${\phi }_{28}\left(x,t\right)=\frac{6{\kappa }^{2}{e}^{iv(x,t)}\sqrt{\delta }\mathrm{tan}(\sqrt{\delta }\sigma )\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }+{\iota }_{1}\sqrt{-\delta \left(c+2d\right)}\mathrm{tan}(\sqrt{\delta }\sigma )\}}{\pm {\iota }_{1}\left(c+2d\right)\sqrt{6\delta \kappa }\mathrm{tan}(\sqrt{\delta }\sigma )+6{\kappa }^{2}{\varepsilon }_{1}\sqrt{-(c+2d)}},\,\delta >0$$

(3.1.35)

$${\phi }_{29}\left(x,t\right)=\frac{-6{\kappa }^{2}{e}^{iv\left(x,t\right)}\sqrt{\delta }\mathrm{cot}(\sqrt{\delta }\sigma )\{\mp \kappa {\varepsilon }_{1}\sqrt{6\kappa }-{\iota }_{1}\sqrt{-\delta \left(c+2d\right)}\mathrm{cot}(\sqrt{\delta }\sigma )\}}{\mp {\iota }_{1}\left(c+2d\right)\sqrt{6\delta \kappa }\mathrm{cot}(\sqrt{\delta }\sigma )+6{\kappa }^{2}{\varepsilon }_{1}\sqrt{-(c+2d)}},\,\delta >0$$

(3.1.36)

where $v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta ,\sigma =\kappa x+\omega t$

3.2 Solutions via rational $({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})$-expansion scheme

The balancing number forces Eq. (2.2.1) to be

$$u\left(\sigma \right)=\frac{{\iota }_{0}+{\iota }_{1}({\mathrm{G}}^{\mathrm{^{\prime}}}\left(\sigma \right)/G(\sigma ))}{{\tau }_{0}+{\tau }_{1}({\mathrm{G}}^{\mathrm{^{\prime}}}\left(\sigma \right)/G(\sigma ))}$$

(3.2.1)

Inserting Eq. (3.2.1) alongside Eq. (2.2.2) into Eq. (3.2) yields a polynomial in $({\mathrm{G}}^{\mathrm{^{\prime}}}\left(\phi \right)/G(\phi ))$. Set each coefficient of the polynomial to zero and solve them for the following outcomes by using Maple:

$\mathrm{Case}\, 1: {\iota }_{0}=\pm \frac{\kappa (2\mu {\tau }_{1}-\rho {\tau }_{0})\sqrt{3\kappa }}{\sqrt{-(2c+4d)}},\,{\iota }_{1}=\pm \frac{\kappa (\rho {\tau }_{1}-2{\tau }_{0})\sqrt{3\kappa }}{\sqrt{-(2c+4d)}},\,\omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$

${ \mathrm{Case}} \,2: {\iota }_{0}=\mp \frac{\kappa {\tau }_{1}\left({\rho }^{2}-4\mu \right)\sqrt{3\kappa }}{2\sqrt{-\left(2c+4d\right)}},\,{\iota }_{1}=0,\,{\tau }_{0}=\frac{\rho {\tau }_{1}}{2},\,\omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$

$\mathrm{Case} \,3: {\iota }_{0}=\mp \frac{3{\kappa }^{2}\rho {\tau }_{0}}{\sqrt{-6\kappa \left(c+2d\right)}},\,{\iota }_{1}=\pm \frac{6{\kappa }^{2}{\tau }_{0}}{\sqrt{-6\kappa (c+2d)}},\,{\tau }_{1}=0,\,\omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$

Combining the above cases with Eq. (3.2.1) and the solutions (2.2.3)–(2.2.7) of (2.2.2) delivers the following wave solutions families:

Solution family 1: The solution (3.2.1) due to the case 1 and Eq. (3.1) attains

$$\phi \left(x,t\right)=\kappa {e}^{iv(x,t)}\sqrt{\frac{3\kappa }{-(2c+4d)}}\frac{\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})({\mathrm{G}}^{\mathrm{^{\prime}}}\left(\sigma \right)/G(\sigma ))\}}{{\tau }_{0}+{\tau }_{1}({\mathrm{G}}^{\mathrm{^{\prime}}}\left(\sigma \right)/G(\sigma ))}$$

(3.2.2)

Equation (3.2.2) with the help of (2.2.3)–(2.2.7) create the solutions

$${\phi }_{1}\left(x,t\right)=\frac{\kappa \sqrt{-3\kappa /(2c+4d)}\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})(\{-g+\sqrt{{g}^{2}-4h}\mathrm{tanh}(0.5\sqrt{{g}^{2}-4h}\sigma )\}/2)\}}{{e}^{-iv(x,t)}\{{\tau }_{0}+{\tau }_{1}(\{-g+\sqrt{{g}^{2}-4h}\mathrm{tanh}(0.5\sqrt{{g}^{2}-4h}\sigma )\}/2)\}}{g}^{2}-4h>0$$

(3.2.3)

$${\phi }_{2}\left(x,t\right)=\frac{\kappa \sqrt{-3\kappa /(2c+4d)}\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})(\{-g+\sqrt{{g}^{2}-4h}\mathrm{coth}(0.5\sqrt{{g}^{2}-4h}\sigma )\}/2)\}}{{e}^{-iv(x,t)}\{{\tau }_{0}+{\tau }_{1}(\{-g+\sqrt{{g}^{2}-4h}\mathrm{coth}(0.5\sqrt{{g}^{2}-4h}\sigma )\}/2)\}}{g}^{2}-4h>0$$

(3.2.4)

$${\phi }_{3}\left(x,t\right)=\frac{\kappa {e}^{iv(x,t)}\sqrt{-3\kappa /(2c+4d)}\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})(\frac{1}{\sigma }-\frac{g}{2})\}}{{\tau }_{0}+{\tau }_{1}(\frac{1}{\sigma }-\frac{g}{2})}{g}^{2}-4h=0$$

(3.2.5)

$${\phi }_{4}\left(x,t\right)=\frac{\kappa \sqrt{-3\kappa /(2c+4d)}\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})(\{-g-\sqrt{4h-{g}^{2}}\mathrm{tan}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2)\}}{{e}^{-iv(x,t)}\{{\tau }_{0}+{\tau }_{1}(\{-g-\sqrt{4h-{g}^{2}}\mathrm{tan}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2)\}}{g}^{2}-4h<0$$

(3.2.6)

$${\phi }_{5}\left(x,t\right)=\frac{\kappa \sqrt{-3\kappa /(2c+4d)}\{\pm (2\mu {\tau }_{1}-\rho {\tau }_{0})\pm (\rho {\tau }_{1}-2{\tau }_{0})(\{-g+\sqrt{4h-{g}^{2}}\mathrm{cot}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2)\}}{{e}^{-iv(x,t)}\{{\tau }_{0}+{\tau }_{1}(\{-g+\sqrt{4h-{g}^{2}}\mathrm{cot}(0.5\sqrt{4h-{g}^{2}}\sigma )\}/2)\}}{g}^{2}-4h<0$$

(3.2.7)

$\mathrm{where }v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t\omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$

Solution family 2: The solution (3.2.1) due to the case 2 and Eq. (3.1) attains.

$$\phi \left( {x,t} \right) = \mp \frac{{\kappa \left( {\rho^{2} - 4\mu } \right)e^{{iv\left( {x,t} \right)}} \sqrt { - 3\kappa /\left( {2c + 4d} \right)} }}{{\rho + 2\left( {G^{\prime}\left( \sigma \right)/G\left( \sigma \right)} \right)}}$$

(3.2.8)

Equation (3.2.8) merging with (2.2.3)–(2.2.7) give the solutions

$${\phi }_{6}\left(x,t\right)=\mp \frac{\kappa \left({\rho }^{2}-4\mu \right){e}^{iv\left(x,t\right)}\sqrt{-3\kappa /\left(2c+4d\right)}}{\rho -g+\sqrt{{g}^{2}-4h}\mathrm{tanh}\left(0.5\sqrt{{g}^{2}-4h}\sigma \right)},\,{g}^{2}-4h>0$$

(3.2.9)

$${\phi }_{7}\left(x,t\right)=\mp \frac{\kappa \left({\rho }^{2}-4\mu \right){e}^{iv\left(x,t\right)}\sqrt{-3\kappa /\left(2c+4d\right)}}{\rho -g+\sqrt{{g}^{2}-4h}\mathrm{coth}\left(0.5\sqrt{{g}^{2}-4h}\sigma \right)},\,{g}^{2}-4h>0$$

(3.2.10)

$${\phi }_{8}\left(x,t\right)=\mp \frac{\kappa \left({\rho }^{2}-4\mu \right){e}^{iv\left(x,t\right)}\sqrt{-3\kappa /\left(2c+4d\right)}}{\rho +\frac{2}{\sigma }-g},\,{g}^{2}-4h=0$$

(3.2.11)

$${\phi }_{9}\left(x,t\right)=\mp \frac{\kappa \left({\rho }^{2}-4\mu \right){e}^{iv\left(x,t\right)}\sqrt{-3\kappa /\left(2c+4d\right)}}{\rho -g-\sqrt{4h-{g}^{2}}\mathrm{tan}\left(0.5\sqrt{4h-{g}^{2}}\sigma \right)},\,{g}^{2}-4h<0$$

(3.2.12)

$${\phi }_{10}\left(x,t\right)=\mp \frac{\kappa \left({\rho }^{2}-4\mu \right){e}^{iv\left(x,t\right)}\sqrt{-3\kappa /\left(2c+4d\right)}}{\rho -g+\sqrt{4h-{g}^{2}}\mathrm{cot}\left(0.5\sqrt{4h-{g}^{2}}\sigma \right)},\,{g}^{2}-4h<0$$

(3.2.13)

$\mathrm{where }v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta ,\sigma =\kappa x+\omega t,\omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$.

Solution family 3: The solution (3.2.1) due to the case 3 and Eq. (3.1) attains.

$$\phi \left( {x,t} \right) = \frac{{3\kappa^{2} e^{{iv\left( {x,t} \right)}} \left\{ { \mp \rho \pm 2\left( {G^{\prime } \left( \sigma \right)/G\left( \sigma \right)} \right)} \right\}}}{{\sqrt { - 6\kappa \left( {c + 2d} \right)} }}$$

(3.2.14)

Equation (3.2.14) together with (2.2.3)–(2.2.7) offer the solutions

$${\phi }_{11}\left(x,t\right)=\frac{3{\kappa }^{2}{e}^{iv(x,t)}\{\mp \rho \pm \{-g+\sqrt{{g}^{2}-4h}\mathrm{tanh}(0.5\sqrt{{g}^{2}-4h}\sigma )\}\}}{\sqrt{-6\kappa (c+2d)}},\, {g}^{2}-4h>0$$

(3.2.15)

$${\phi }_{12}\left(x,t\right)=\frac{3{\kappa }^{2}{e}^{iv(x,t)}\{\mp \rho \pm \{-g+\sqrt{{g}^{2}-4h}\mathrm{coth}(0.5\sqrt{{g}^{2}-4h}\sigma )\}\}}{\sqrt{-6\kappa (c+2d)}},\, {g}^{2}-4h>0$$

(3.2.16)

$${\phi }_{13}\left(x,t\right)=\frac{3{\kappa }^{2}{e}^{iv(x,t)}\{\mp \rho \pm (\frac{2}{\sigma }-g)\}}{\sqrt{-6\kappa (c+2d)}},\,{g}^{2}-4h=0$$

(3.2.17)

$${\phi }_{14}\left(x,t\right)=\frac{3{\kappa }^{2}{e}^{iv(x,t)}\{\mp \rho \pm \{-g-\sqrt{4h-{g}^{2}}\mathrm{tan}(0.5\sqrt{4h-{g}^{2}}\sigma )\}\}}{\sqrt{-6\kappa (c+2d)}},\, {g}^{2}-4h<0$$

(3.2.18)

$${\phi }_{15}\left(x,t\right)=\frac{3{\kappa }^{2}{e}^{iv(x,t)}\{\mp \rho \pm \{-g+\sqrt{4h-{g}^{2}}\mathrm{cot}(0.5\sqrt{4h-{g}^{2}}\sigma )\}\}}{\sqrt{-6\kappa (c+2d)}},\,{g}^{2}-4h<0$$

(3.2.19)

$\mathrm{where }v\left(x,t\right)=ax+\frac{3a\omega -8{a}^{3}\kappa }{\kappa }t+\theta \sigma =\kappa x+\omega t \omega =\frac{\kappa ({\kappa }^{2}{\rho }^{2}-4{\kappa }^{2}\mu +6{a}^{2})}{2}$

Remarks:

The above constructed wave solutions to the generalized third-order nonlinear Schrodinger model have been compared with the available findings in the literature and claimed to be diverse and novel with the distinct wave characteristics (Lu et al. 2019; Nasreen et al. 2019; Hosseini et al. 2020; Malik et al. 2021b).

4 Graphical appearances of acquired solutions

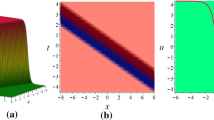
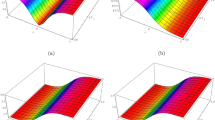
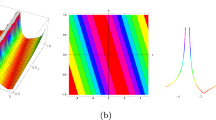
In this section, some of the received solutions are portrayed graphically for physical appearances which stand for dissimilar forms of solitons such as kink shape, anti-kink type, singular kink sort, bell shape, anti-bell shape, peakon, cuspon, periodic type, singular periodic form, compacton etc. The wave outlines in three dimensional, two dimensional and contour formats are figured out to make clear the diverse wave patterns. Sketch of (3.1.5) represents singular kink sort soliton: Fig. 1a, b stand for 3D, contour are drawn with the particular values $\kappa = c = \theta = 1, a = 0.001, \omega = 3, d = - 1,$ in $- 1.5 \le x,t \le 1.5$ while Fig. 1c is plotted for 2D profile alongside $t = 0$. Periodic shape of (3.1.6): Fig. 2a, b constituted for 3D, contour are drawn by assigning the values $\kappa = c = \theta = 1, d = \omega = - 1, a = 0.001$ in the interval $- 2.25 \le x,t \le 2.25$ while Fig. 2c stands for 2D plot with $t = 0$. Outline of (3.1.7) is periodic: Fig. 3a, b established for 3D and contour are painted with the parameter’s values $\kappa = c = \theta = 1, d = \omega = - 1$, $a = 0.001$ within $- 5 \le x,t \le 5$ whereas Fig. 3c is retained for 2D display in connection with $t = 0$. Anti-bell form soliton of (3.1.9): Fig. 4a, b achieved for 3D and contour are accomplished with the attached values $\kappa = c = \omega = \theta = 1, d = - 1$, $a = 0.01$ in the range $- 5 \le x,t \le 5$, and Fig. 4c is exposed for 2D sketch with $t = 0$. The soliton of the solution (3.1.12) is in periodic form: Fig. 5a, b exhibiting 3D and contour are rendered by signifying the parameters as $\kappa = c = \theta = 1, d = \omega = - 1, a = 0.005$ in the range $- 12 \le x,t \le 10$ and 2D plot is given in Fig. 5c at $t = 0$. Outline of (3.1.14) compacton: Fig. 6a, b keep for 3D and contour are plotted by allocating the values $\kappa = a = c = \theta = \iota_{0} = \varepsilon_{0} = 1, d = - 1$, $\omega = 3.001$ in the interval $- 0.5 \le x,t \le 0.5$ while Fig. 6c is displayed for 2D shape at $t = 0$. Soliton for (3.1.21) is kink variety: Fig. 7a, b offered for 3D and contour are delineated by using particular values $\kappa = c = \theta = 1, d = \omega = - 1, a = 0.001$ within the duration $- 8 \le x,t \le 5$ and 2D plot exhibits in Fig. 7c for $t = 0$. Outline is in singular kink shape of (3.1.27): Fig. 8a, b executed for 3D and contour are painted by offering the values of free parameters $\kappa = c = \theta = \omega = 1, d = - 1, a = 0.005$ in the interval $- 0.2 \le x,t \le 0.2$ and 2D plot is represented in Fig. 8c alongside $t = 0$. kink shape soliton of (3.2.9): Fig. 9a, b placed for 3D and contour are traced by assigning free constants as $g = 2.25, h = \kappa = c = \mu = \rho = \theta = 1, d = - 1, a = 0.001$ within the range $- 10 \le x,t \le 1.5$ while $t = 0$ is gives 2D profile in Fig. 9c. Singular periodic outline for solution (3.2.10): Fig. 10a, b presenting 3D and contour are drawn with the values $g = 2.25, h = \kappa = c = \mu = \rho = \theta = 1, d = - 1, a = 0.001$ in the interval $- 10 \le x,t \le 1$ where 2D plot are visualized in Fig. 10c for $t = 0$.

Fig. 1

Sketch of (3.1.5) is singular kink sort for $\kappa =c=\theta =1$, $a=0.001$, $\omega =3$, $d=-1$ within the interval $-1.5\le x,t\le 1.5$ where c signifies 2D profile for $t=0$

Fig. 2

Output is in periodic form of solution (c) under $\kappa =c=\theta =1$, $d=\omega =-1$, $a=0.001$ in the range $-2.25\le x,t\le 2.25$ and 2D plot established in c with $t=0$

Fig. 3

Outline of (3.1.7) is periodic for $\kappa =c=\theta =1$, $d=\omega =-1$, $a=0.001$ in the interval $-5\le x,t\le 5$ while c is 2D at $t=0$

Fig. 4

Sketch of (3.1.9) is anti-bell sort under $\kappa =c=\omega =\theta =1$, $d=-1$, $a=0.01$ in association within $-5\le x,t\le 5$ and c displayed 2D plot when $t=0$

Fig. 5

The periodic form of (3.1.12) for $\kappa =c=\theta =1$, $d=\omega =-1$, $a=0.005$ in the range $-12\le x,t\le 10$ and in c 2D plot are described for $t=0$

Fig. 6

Diagram of the solution (3.1.14) is in compacton soliton under $\kappa =a=c=\theta ={\iota }_{0}={\epsilon }_{0}=1$, $d=-1$, $\omega =3.001$ in $-0.5\le x,t\le 0.5$ while c exhibited 2D plot at $t=0$

Fig. 7

Kink type soliton of (3.1.21) under $\kappa =c=\theta =1$, $d=\omega =-1$, $a=0.001$ along with the interval $-8\le x,t\le 5$ where c presents 2D graph at $t=0$

Fig. 8

Outline of (3.1.27) is singular kink for $\kappa =c=\theta =\omega =1$, $d=-1$, $a=0.005$ in the range $-0.2\le x,t\le 0.2$ and 2D plot exhibit in c together with $t=0$

Fig. 9

kink shape soliton of (3.2.9) for $g=2.25$, $h=\kappa =c=\mu =\rho =\theta =1$, $d=-1$, $a=0.001$ in the interval $-10\le x,t\le 1.5$ while in c 2D is at $t=0$

Fig. 10

Singular periodic form for (3.2.10) under $g=2.25$, $h=\kappa =c=\mu =\rho =\theta =1$, $d=-1$, $a=0.001$ within the interval $-10\le x,t\le 1$ in which 2D plot is depicted in c at $t=0$

5 Conclusions

The exploration has been seemed to be a consequent study to reveal the importance of relevant research. A lot of closed form analytic wave solutions of the generalized third-order nonlinear Schrodinger model has successfully been constructed by adopting the competent improved tanh and rational $({G}^{^{\prime}}/G)$-expansion approaches. The wave solutions found in the form of rational, trigonometric, and hyperbolic functions have been depicted in several contour, three dimensional, and two-dimensional sketches for their physical appearances. As a result, we have celebrated kink type, singular kink sort, anti-kink form, bell shape, anti-bell form, singular bell mode, periodic, singular periodic and compacton profiles of the well-furnished obtained solutions. The solutions have been constructed in mathematical expressions and thereupon converted them into numerical form after assigning particular values to the involved parameters to illustrate dynamical attitude of waves. The comparable analysis of the constructed solutions and existing results in literature has brought out the significance of this study which claims to be awakening of new dimensions in research area. The observation of efficiency and conciseness of the adopted techniques to extract accurate solutions of the considered model might claim further research to the relevant field.