Introduction

In the last decades, nonlinear partial differential equations (NLPDEs) have a remarkable importance to the study of nonlinear physical phenomena such as hydrodynamics, biology, structual mechanics, fluid mechanics, circuit analysis, plasma physics, quantum electronics, optical fiber, solid state physics and so on. To figure out the mechanisms of these intricate physical complex phenomena which can be discussed by NLPDEs, it is necessary to investigate their solutions and features. NLPDEs have become one of the outstanding area for the community of researchers in modern era because of its comprehensive uses in nonlinear sciences. For understanding and study complicated phenomena, it is key to obtain more exact solutions of NLPDEs [1,2,3,4,5,6,7,8].

The concept of soliton or solitary waves is a phenomenon that has attracted the attention of people of all ages. When there is a disturbance in the phenomenon, waves are formed. Soliton interactions occur when two or more solitons come near enough to interact. Soliton waves have risen to prominence among all the waves found in nature due to their fundamental properties that are rarely found in other waves. Due to dispersive effects, the velocity of soliton waves varies with wavelength and is significantly different from the velocity of energy propagation. Moreover, linear effects of soliton waves can be shown dominantly in breaking roll waves on the seashore. Wave spreading effects, also known as dispersive effects, and wave focusing effects, also known as nonlinear effects, have shown a moderate balance in generating waves with a permanent shape. Furthermore, the optical solitons are one of the most significant domains of research in the branch of nonlinear optics. Particularly, the investigation of dispersive optical solitons is getting a lot of consideration in the present days. This tendency is actually continuing, there are numerous new outcomes that are constantly being published in the context of given model. However many efforts are still required in this area of research from the point of view of new optical soliton solutions and also from point of view of their applications. Besides, the exact solutions are necessary for observing the physical properties of mathematical modeled problems. Mathematical techniques are being established in a variety of ways. In fact, these have become a more enticing issue for researchers to attain accurate solutions through capable computing software that eliminates complex and time-consuming algebraic computations. Numerous computational approaches have been established for nonlinear physical models. Last few decades, many scholars have developed several efficient and reliable methodologies to recover exact solutions in the forms of traveling waves or solitary waves, etc. [6, 9,10,11,12,13,14,15,16,17,18,19,20,21,22]. The Biswas–Arshed equation (BAE) which is an extended model derived from the Schrodinger equation also plays an important role in nonlinear optical fiber. Therefore, the extraction of optical soliton solutions of BAE is an important topic that carries relevant benefits in the area of telecommunications. BAE has most marvellous characteristics of neglecting the self-phase modulation, group velocity dispersion (GVD) negligibly small as well as the presence of second and third temporal spatial dispersion in the model to compensate the low GVD. Recently, the different algorithms [23,24,25,26,27,28,29,30,31,32,33,34] have been implemented to Biswas-Arshed equation which yields fruitful results in nonlinear sciences.

The BAE with Kerr law nonlinearity [35] is given below:

$$\begin{aligned}&i \phi _{t}+ a_{1} \phi _{xx}+ a_{2} \phi _{xt}+i(b_{1}\phi _{xxx}+b_{2}\phi _{xxt})\nonumber \\&\quad =i[\lambda (|\phi |^{2}\phi )_{x}+\mu (|\phi |^{2})_{x}\phi +\theta |\phi |^{2}\phi _{x}],~~~~~~~~~i=\sqrt{-1}, \end{aligned}$$
(1)

where the independent variables x and t that indicate spatio-temporal components respectively, and dependent variable \(\phi (x, t)\) is complex-valued wave profile. The first term characterizes temporal evolution whereas the symbols \(a_{1}\) and \(a_{2}\) denote the coefficients of GVD and spatio-temporal dispersion (STD). Moreover, the coefficients \(b_{2}\) and \(b_{1}\) represent third order STD and third order dispersion (3OD). On the right-hand side \(\lambda \) is the effect of self-steepening to eliminate the formulation of shock waves, while \(\mu \) and \(\theta \) provide the effect of nonlinear dispersion. Thus these compensatory effects of dispersion and nonlinearity provides the necessary balance to sustain soliton propagation.

After reviewing the literature, it is examined that the studied model is not solved yet by the proposed techniques. By provoking this, the utmost focus of this work is to retrieve optical and other soliton solutions of a given model by employing powerful mathematical tools, namely the extended sinh-Gordon equation expansion method (ShGEEM) and (\(\frac{G^{\prime }}{G^2}\))-expansion function method [36, 37]. The basic feature of these techniques are to establish some elementary relationships between NLPDEs and others simple NLODEs. It has been examined that with the aid of simple solutions and solvable ODEs, different kinds of traveling wave solutions of some complicated NLPDEs can be easily constructed. This is the key concept of above techniques. The primary benefit of applying techniques are that we have achieved in a single move, to gather various types of new soliton solutions and provide us a guideline that how to organize these solutions.

The outline of this manuscript is devised as follows: In Sect. 2, mathematical analysis is discussed. In Sect. 3, extraction of optical solitons is presented. In Sect. 4, physical description is drawn and in Sect. 5 concluding remarks is revealed.

Mathematical Analysis

For solving the above equation, we begin with the hypothesis \(\phi (x,t)=\Phi (\varrho )e^{ i\psi },~\text{ where }~\varrho =x-\vartheta t~~\text{ and }~~ \psi = -k x + \varpi t +\theta _{0}\). Here \(\theta _{0},\varpi \) and k are parameters, which are the phase constant, frequency and wave number respectively. Inserting above complex wave transformation into Eq. (1) and decomposing into real and imaginary components respectively, the real part implies

$$\begin{aligned}&(a_{1}- a_{2}\vartheta +3 b_{1}k-2b_{2}\vartheta k-\varpi b_{2}) \Phi '' - (\lambda +\theta )k \Phi ^3 \nonumber \\&\quad - (\varpi +a_{1}k^2+b_{1}k^3-a_{2}\varpi k-b_{2}\varpi k^2)\Phi =0. \end{aligned}$$
(2)

The imaginary component yields

$$\begin{aligned}&(b_{1}-b_{2}\vartheta ) \Phi ''' - (3\lambda +2\mu +\theta ) \Phi ^2\Phi '+ (b_{2}\vartheta k^2+2b_{2}\varpi k\nonumber \\&\quad -3 b_{1} k^2-\vartheta -2 a_1 k+a_2\vartheta k+a_{2}\varpi )\Phi ' =0. \end{aligned}$$
(3)

Integrating Eq. (3) by taking the integration constant zero, we attain

$$\begin{aligned}&3(b_{1}-b_{2}\vartheta ) \Phi '' - (3\lambda +2\mu +\theta ) \Phi ^3+ 3(b_{2}\vartheta k^2+2b_{2}\varpi k\nonumber \\&\quad -3 b_{1} k^2-\vartheta -2 a_1 k+a_2\vartheta k+a_{2}\varpi )\Phi =0. \end{aligned}$$
(4)

The same function \(\Phi (\varrho )\) satisfies both Eqs. (2) and (4) under the constraint relation given below

$$\begin{aligned}&\frac{a_{1}-a_{2}\vartheta +3b_{1}k-2b_{2}\vartheta k-\varpi b_{2}}{3(b_{1}-b_{2}\vartheta )}=\frac{(\lambda +\theta )k}{3\lambda +2\mu +\theta }\nonumber \\&\quad =\frac{- (\varpi +a_{1}k^2+b_{1}k^3-a_{2}\varpi k-b_{2}\varpi k^2) }{3(b_{2}\vartheta k^2+2b_{2}\varpi k-3 b_{1} k^2-\vartheta -2 a_1 k+a_2\vartheta k+a_{2}\varpi )} , \end{aligned}$$
(5)

where

$$\begin{aligned} a_1&=\frac{-1}{4 k^2 ( \mu -\theta )^2}\bigg [-4 a_2 \theta ^2 k^2 \vartheta -6 a_2 \theta \lambda k^2 \vartheta +2 a_2 \theta k^2 \mu \vartheta +6 a_2 \lambda k^2 \mu \vartheta \nonumber \\&\quad +\,2 a_2 k^2 \mu ^2 \vartheta +6 a_2 \theta \lambda k \varpi +6 a_2 \theta k \mu \varpi -\,6 a_2 \lambda k \mu \varpi -6 a_2 k \mu ^2 \varpi +4 b_2 \theta ^2 k^3 \vartheta ~~\nonumber \\&\quad -8 b_2 \theta k^3 \mu \vartheta +4 b_2 k^3 \mu ^2 \vartheta -4 b_2 \theta ^2 k^2 \varpi +\,8 b_2 \theta k^2 \mu \varpi -4 b_2 k^2 \mu ^2 \varpi +3 \theta \lambda \varpi \nonumber \\&\quad +\,3 \theta \mu \varpi +9 \lambda ^2 \varpi -9 \theta \lambda k \vartheta -9 \theta k \mu \vartheta -\,9 \lambda ^2 k \vartheta -9 \lambda k \mu \vartheta +15 \lambda \mu \varpi +6 \mu ^2 \varpi \bigg ], \end{aligned}$$
(6)
$$\begin{aligned} b_1&=\frac{1}{8 k^3 (\mu -\theta )^2}\bigg [-2 a_2 \theta ^2 k^2 \vartheta -6 a_2 \theta \lambda k^2 \vartheta -2 a_2 \theta k^2 \mu \vartheta +6 a_2 \lambda k^2 \mu \vartheta +4 a_2 k^2 \mu ^2 \vartheta \nonumber \\&\quad +\,2 a_2 \theta ^2 k \varpi +6 a_2 \theta \lambda k \varpi +\,2 a_2 \theta k \mu \varpi -6 a_2 \lambda k \mu \varpi -4 a_2 k \mu ^2 \varpi +8 b_2 \theta ^2 k^3 \vartheta \nonumber \\&\quad -16 b_2 \theta k^3 \mu \vartheta +8 b_2 k^3 \mu ^2 \vartheta +\,\theta ^2 \varpi +6 \theta \lambda \varpi +4 \theta \mu \varpi \nonumber \\&\quad r +9 \lambda ^2 \varpi -3 \theta ^2 k \vartheta -12 \theta \lambda k \vartheta -6 \theta k \mu \vartheta -9 \lambda ^2 k \vartheta -\,6 \lambda k \mu \vartheta +12 \lambda \mu \varpi +4 \mu ^2 \varpi \bigg ]. \end{aligned}$$
(7)

In the next sections, the Eq. (2) will be studied with extended ShGEEM and (\(\frac{G^{\prime }}{G^2}\))-expansion function methods for the sake of various kinds of optical soliton and other solutions.

Extraction of Optical Solitons

Extended ShGEEM

Now, first we investigate Eq. (2) using extended ShGEEM. Assume the following trial solutions generated from the sinh-Gordon equation by Xian-Lin and Jia-Shi [36].

$$\begin{aligned} \phi _{xt}=\rho \sinh (\phi ), \end{aligned}$$
(8)

where \(\rho \) is a nonzero constant.

Employing the traveling wave transformation

$$\begin{aligned} \phi (x,t)=\Phi (\varrho ),\;\;\; \varrho =\tau (x-\vartheta t). \end{aligned}$$
(9)

Equation (8) turns into the following ODE:

$$\begin{aligned} \Phi ^{''}=-\frac{\rho }{\tau ^{2}\vartheta }\sinh (\Phi ), \end{aligned}$$
(10)

where \(\tau \) and \(\vartheta \) are the wave number and velocity respectively.

Integrating Eq. (10), we have

$$\begin{aligned} \Big (\frac{\Phi ^{'}}{2}\Big )^{2}=-\frac{\rho }{\tau ^{2}\vartheta }\sinh ^{2}\Big (\frac{\Phi }{2}\Big )+h, \end{aligned}$$
(11)

where h is the integration constant. Setting \(-\frac{\rho }{\tau ^{2}c}=d\) and , Eq. (11) becomes

(12)

For different values of parameters d and h, Eq. (12) contains the following set of solutions:

Set-I When \(h=0\), \(d=1\), Eq. (12) becomes

(13)

After simplifying Eq. (13), the following solutions are achieved:

(14)

and

(15)

where \(i=\sqrt{-1}\).

Set-II When \(d=1\), \(h=1\), Eq. (12) converts

(16)

Simplifying Eq. (16), the following solutions are obtained:

(17)

and

(18)

Hence, we have the following as trial solutions to a given nonlinear evolution equation:

(19)
$$\begin{aligned} \Phi (\varrho )=\sum _{j=1}^{n}\bigg (\pm \delta _{j}\;i\;\;\text{ sech }(\varrho )\pm \beta _{j}\tanh (\varrho )\bigg )^{j}+\beta _{0}, \end{aligned}$$
(20)
$$\begin{aligned} \Phi (\varrho )=\sum _{j=1}^{n}\bigg (\pm \delta _{j}\;i\;\text{ csch }(\varrho )\pm \beta _{j}\coth (\varrho )\bigg )^{j}+\beta _{0}, \end{aligned}$$
(21)
$$\begin{aligned} \Phi (\varrho )=\sum _{j=1}^{n}\bigg (\pm \delta _{j}\sec (\varrho )+\beta _{j}\tan (\varrho )\bigg )^{j}+\beta _{0}, \end{aligned}$$
(22)

and

$$\begin{aligned} \Phi (\varrho )=\sum _{j=1}^{n}\bigg (\pm \delta _{j}\;\text{ csc }(\varrho )-\beta _{j}\;\cot (\varrho )\bigg )^{j}+\beta _{0}, \end{aligned}$$
(23)

where \(i=\sqrt{-1}\), and or . For details, see [36].

By using balance rule, we get \(n=1\). For \(n=1\), Eqs. (19)–(23) change to

(24)
$$\begin{aligned} \Phi (\varrho )=\pm \delta _{1}\;i\;\text{ sech }(\varrho )\pm \beta _{1}\tanh (\varrho )+\beta _{0},~~~~~~~~~~~~~ \end{aligned}$$
(25)
$$\begin{aligned} \Phi (\varrho )=\pm \delta _{1}\;i\;\text{ csch }(\varrho )\pm \beta _{1}\coth (\varrho )+\beta _{0},~~~~~~~~~~~~~ \end{aligned}$$
(26)
$$\begin{aligned} \Phi (\varrho )=\pm \delta _{1}\sec (\varrho )+\beta _{1}\tan (\varrho )+\beta _{0},~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(27)

and

$$\begin{aligned} \Phi (\varrho )=\pm \delta _{1}\;\text{ csc }(\varrho )-\beta _{1}\;\cot (\varrho )+\beta _{0}.~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(28)

On inserting Eq. (24) and its second derivative along with and/or into Eq. (2), yields polynomials in hyperbolic functions. By equating the coefficients of powers of these hyperbolic functions to zero we get the clusters of algebraic expressions. The attained algebraic expressions provide the values of the involved coefficients. Substituting the values of the coefficients into Eqs. (25)–(28) provides the solutions to Eq. (2). The following algebraic equations are obtained as:

On solving the above algebraic equations with the aid of Mathematica we recover following results:

Result-1:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=\pm \frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}},\;\delta _{1}=0,\;\; ~~~~~\\ \vartheta =\frac{a_1 \left( k^2+2\right) +a_2 (-k) \varpi -b_2 \left( k^2+2\right) \varpi +b_1 k \left( k^2+6\right) +\varpi }{2 \left( a_2+2 b_2 k\right) }.~ \end{aligned}$$

Result-2:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=0,\;\delta _{1}=\pm \frac{\sqrt{2} \sqrt{k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi }}{\sqrt{k (\theta +\lambda )}},\;\; \\ \vartheta =-\frac{a_1 \left( k^2-1\right) +a_2 (-k) \varpi -b_2 \left( k^2-1\right) \varpi +b_1 k \left( k^2-3\right) +\varpi }{a_2+2 b_2 k}. \end{aligned}$$

Result-3:

$$\begin{aligned}&\beta _0=0,~\beta _1=-\frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}},\\&\quad \delta _1=\frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}},\\&\vartheta =\frac{a_1 \left( 2 k^2+1\right) -2 a_2 k \varpi -b_2 \left( 2 k^2+1\right) \varpi +b_1 k \left( 2 k^2+3\right) +2 \varpi }{a_2+2 b_2 k}. \end{aligned}$$

For Result-1:

\(\mathbf {\bullet }\)  The optical dark soliton solution

$$\begin{aligned} \phi _{1,1}(x, t)=\pm \frac{\sqrt{k \left( a_2 \varpi {-}k \left( a_1{+}b_1 k{-}b_2 \varpi \right) \right) {-}\varpi }}{\sqrt{k (\theta {+}\lambda )}}\tanh [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}.\quad \end{aligned}$$
(29)

\(\mathbf {\bullet }\)  The singular soliton solution

$$\begin{aligned} \phi _{1,2}(x, t)=\pm \frac{\sqrt{k \left( a_2 \varpi {-}k \left( a_1{+}b_1 k{-}b_2 \varpi \right) \right) {-}\varpi }}{\sqrt{k (\theta {+}\lambda )}}\coth [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}.\quad \end{aligned}$$
(30)

\(\mathbf {\bullet }\)  The singular periodic wave solutions

$$\begin{aligned} \phi _{1,3}(x, t)=\pm \frac{\sqrt{k \left( a_2 \varpi {-}k \left( a_1{+}b_1 k{-}b_2 \varpi \right) \right) {-}\varpi }}{\sqrt{k (\theta {+}\lambda )}}\tan [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}.\quad \end{aligned}$$
(31)

and

$$\begin{aligned} \phi _{1,4}(x, t)=\mp \frac{\sqrt{k \left( a_2 \varpi {-}k \left( a_1{+}b_1 k{-}b_2 \varpi \right) \right) {-}\varpi }}{\sqrt{k (\theta {+}\lambda )}}\cot [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}.\quad \end{aligned}$$
(32)

Here \(k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi >0\) and \(k(\theta +\lambda )>0\) for valid solutions.

For Result-2:

  • The optical bright soliton solution

    $$\begin{aligned} \phi _{2,1}(x, t)= & {} \pm \frac{\sqrt{2} \sqrt{k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\;i\text{ sech }[x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (33)

  • The singular soliton solution

    $$\begin{aligned} \phi _{2,2}(x, t)= & {} \pm \frac{\sqrt{2} \sqrt{k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\;i\text{ csch }[x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (34)

  • The singular periodic wave solutions

    $$\begin{aligned} \phi _{2,3}(x, t)= & {} \pm \frac{\sqrt{2} \sqrt{k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\sec [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}.~ \end{aligned}$$
    (35)

    and

    $$\begin{aligned} \phi _{2,4}(x, t)= & {} \pm \frac{\sqrt{2} \sqrt{k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\csc [x-\vartheta t]e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (36)

    Here \(k \left( -\varpi \left( a_2+b_2 k\right) +a_1 k+b_1 k^2\right) +\varpi >0\) and \(k(\theta +\lambda )>0\) for valid solutions.

For Result-3:

  • The mixed dark-bright soliton solution

    $$\begin{aligned} \phi _{3,1}(x, t)= & {} \frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}} \nonumber \\&\quad \times \bigg (i\;\text{ sech }[x-\vartheta t]-\tanh [x-\vartheta t]\bigg ) \mathrm {e}^{ i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (37)

  • The mixed singular soliton solution

    $$\begin{aligned} \phi _{3,2}(x, t)= & {} \frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}} \nonumber \\&\quad \times \bigg (i\;\text{ csch }[x-\vartheta t]-\coth [x-\vartheta t]\bigg ) \mathrm {e}^{ i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (38)

  • The singular periodic wave solutions

    $$\begin{aligned} \phi _{3,3}(x, t)=\frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}}\times \nonumber \\ \bigg (\text{ sec }[x-\vartheta t]-\tan [x-\vartheta t]\bigg ) \mathrm {e}^{ i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (39)

    and

    $$\begin{aligned} \phi _{3,4}(x, t)=\frac{\sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k (\theta +\lambda )}}\times \nonumber \\ \bigg (\text{ csc }[x-\vartheta t]+\cot [x-\vartheta t]\bigg ) \mathrm {e}^{ i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (40)

    Here \(k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi >0\) and \(k(\theta +\lambda )>0\), for valid solutions.

(\(\frac{G^{\prime }}{G^2}\))-Expansion Function Method

Suppose that the solution of Eq. (2) can be expressed by a polynomial in \((\frac{G^{\prime }}{G^2})\)-expansion method as follows

$$\begin{aligned} \Phi (\varrho )=a_{0}+\sum _{n=1}^N\Bigg ( \alpha _n\bigg (\frac{G^{\prime }}{G^2}\bigg )^n+ \beta _n\bigg (\frac{G^{\prime }}{G^2}\bigg )^{-n}\Bigg ),~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(41)

where \(G = G(\varrho )\) holds

with \(\varphi \ne 0\), \(\eta \ne 1\) being integers. The unknown constants \( a_{0}, \alpha _{n}, \beta _{n} ( n=1, 2, 3, \ldots , N)\) must be found.

Step 3. The general solution of \((\frac{G^{\prime }}{G^2})\) has three possibilities as enumerated below:

Case-1: Trigonometric function solutions:

If we take  \(\eta ~\varphi > 0,\)  then 

$$\begin{aligned} \bigg (\frac{G^\prime }{G^2}\bigg )=\sqrt{\frac{\eta }{\varphi }}\bigg (\frac{E\cos \sqrt{\eta \varphi }\varrho +F\sin \sqrt{\eta \varphi }\varrho }{{F\cos \sqrt{\eta \varphi }\varrho -E\sin \sqrt{\eta \varphi }\varrho }}\bigg ). \end{aligned}$$
(42)

Case-2: Hyperbolic function solutions:

If we have \(\eta ~\varphi < 0\), then

$$\begin{aligned} \bigg (\frac{G^\prime }{G^2}\bigg )=-\frac{\sqrt{|\eta \varphi |}}{\varphi }\bigg (\frac{E\sinh (2\sqrt{|\eta \varphi |}\varrho )+E\cosh (2\sqrt{|\eta \varphi |}\varrho )+F}{{E\sinh (2\sqrt{|\eta \varphi |}\varrho )+Ecosh(2\sqrt{|\eta \varphi |}\varrho )-F}}\bigg ). \end{aligned}$$
(43)

Case-3: Rational function solutions:

When \(\eta =0\), \(\varphi \ne 0\) then rational solution can be written as

$$\begin{aligned} \bigg (\frac{G^\prime }{G^2}\bigg )=\bigg (-\frac{E}{\varphi (E~\varrho +F)}\bigg ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(44)

where E and F are constants.

By balancing principle in Eq. (2) yields, \(n=1\). So the solution of Eq. (2) is written as:

$$\begin{aligned} \Phi (\varrho )=\beta _{0}+\beta _{1} \bigg (\frac{G^{\prime }}{G^{2}}\bigg )+\delta _{1} \bigg (\frac{G^{\prime }}{G^{2}}\bigg )^{-1}, \end{aligned}$$
(45)

where \(\beta _{0}, \beta _{1}\) and \(\delta _{1} \) are constants. On inserting Eq. (45) and its second derivative along with \(\big (\frac{G^{\prime }}{G^2}\big )^{\prime }=\eta +\varphi \big (\frac{G^{\prime }}{G^2}\big )^{2}\) into Eq. (2), we attain a system of algebraic expression. By equating the coefficients of powers of \(\big (\frac{G^{\prime }}{G^2}\big )\) to zero we get the clusters of algebraic expressions:

After solving the above equations with the aid of Mathematica we get following results:

Result-1

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=\pm \frac{i \sqrt{\varphi } \sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{\eta k (\theta +\lambda )}},\;\delta _{1}=0,~~~~~~~~~~~~~\;\; \\ \vartheta =-\frac{a_1 \left( k^2-2 \eta \varphi \right) +a_2 (-k) \varpi -b_2 \varpi \left( k^2-2 \eta \varphi \right) +b_1 k \left( k^2-6 \eta \varphi \right) +\varpi }{2 \eta \varphi \left( a_2+2 b_2 k\right) }. \end{aligned}$$

Result-2

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=0,\;\delta _{1}=\pm \frac{i \sqrt{\eta } \sqrt{k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi }}{\sqrt{k \varphi (\theta +\lambda )}},~~~~~~~~~~~~~\;\; \\ \vartheta =-\frac{a_1 \left( k^2-2 \eta \varphi \right) +a_2 (-k) \varpi -b_2 \varpi \left( k^2-2 \eta \varphi \right) +b_1 k \left( k^2-6 \eta \varphi \right) +\varpi }{2 \eta \varphi \left( a_2+2 b_2 k\right) }. \end{aligned}$$

Result-3

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=\pm \frac{\sqrt{\varphi \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{\sqrt{2} \sqrt{\eta k (\theta +\lambda )}},\;~~~~~~~~~~~~~~~~~~~~~~~~~\\ \delta _{1}=\pm \frac{\sqrt{\eta \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{\sqrt{2} \sqrt{k \varphi (\theta +\lambda )}},\;\;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ \vartheta =\frac{a_1 \left( 4 \eta \varphi +k^2\right) +a_2 (-k) \varpi -b_2 \varpi \left( 4 \eta \varphi +k^2\right) +b_1 k \left( 12 \eta \varphi +k^2\right) +\varpi }{4 \eta \varphi \left( a_2+2 b_2 k\right) }.~~ \end{aligned}$$

For Result-1:

For \(\eta \varphi >0\)

  • Trigonometric solution:

    $$\begin{aligned} \phi _{1,1}(x, t)= & {} \mp \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{ k (\theta +\lambda )}}\nonumber \\&\times \bigg (\frac{E\text{ cos }(\sqrt{\eta \varphi }~\varrho )+F \text{ sin }(\sqrt{\eta \varphi }~\varrho )}{F \text{ cos }(\sqrt{\eta \varphi }\varrho )-E \text{ sin }(\sqrt{\eta \varphi }~\varrho )}\bigg )\times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (46)

    For \(\eta \varphi <0\)

  • Hyperbolic solution:

    $$\begin{aligned} \phi _{1,2}(x, t)= & {} \pm \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{ k (\theta +\lambda )}}\nonumber \\&\times \bigg (\frac{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )+F}{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )-F}\bigg )\times e^{i(-k x + \varpi t +\theta _{0})}.\qquad \end{aligned}$$
    (47)

    On setting \(E=F\), we establish singular soliton solution as:

    $$\begin{aligned} \phi _{1,2}(x, t)= & {} \pm \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{ k (\theta +\lambda )}} \nonumber \\&\quad \times \coth \left( \sqrt{ |\eta \varphi | }~ \varrho \right) \times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (48)

    Here \(k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi <0\) and \(k(\theta +\lambda )>0\) for valid solutions.

For Result-2:

For \(\eta \varphi >0\)

  • Trigonometric solution:

    $$\begin{aligned} \phi _{2,1}(x, t)= & {} \mp \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\times \bigg (\frac{E \text{ cos }(\sqrt{\eta \varphi }~\varrho )+F \text{ sin }(\sqrt{\eta \varphi }~\varrho )}{F \text{ cos }(\sqrt{\eta \varphi }~\varrho )-E \text{ sin }(\sqrt{\eta \varphi }~\varrho )}\bigg )^{-1}\times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (49)

    For \(\eta \varphi <0\)

  • Hyperbolic solution:

    $$\begin{aligned} \phi _{2,2}(x, t)= & {} \pm \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{k (\theta +\lambda )}}\nonumber \\&\times \bigg (\frac{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho +E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )+F}{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )-F}\bigg )^{-1}\nonumber \\&\times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (50)

    On setting \(E=F\), we retrieve dark soliton solution as:

    $$\begin{aligned} \phi _{2,2}(x, t)&=\pm \frac{ \sqrt{\varpi -k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) }}{\sqrt{k (\theta +\lambda )}} \nonumber \\&\quad \times \tanh (\sqrt{ |\eta \varphi | }~ \varrho )\times e^{i(-k x + \varpi t +\theta _{0})}.~~~~~~~~~~ \end{aligned}$$
    (51)

    Here \(k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi <0\) and \(k(\theta +\lambda )>0\) for valid solutions.

For Result-3:

Fig. 1
figure 1

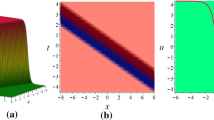
The 3D and 2D behaviour of optical dark soliton solution of Eq. (29) with parameters \(a_1=b_2=k=1~~b_1=\varpi =\theta =2,~~\theta _0=0.5,~~\lambda =a_2=3,~~\text{ and }~~\vartheta =0.7~\)

Full size image
Fig. 2
figure 2

The 3D and 2D physical behavior of singular optical soliton solution of Eq. (30) with parameters \(a_1=b_2=k=1,~~b_1=\varpi =\theta =2,~~\theta _0=0.5,~~\lambda =a_2=3,~~\text{ and }~~\vartheta =0.7~\)

Full size image
Fig. 3
figure 3

The 3D and 2D physical behavior of bright optical soliton solution of Eq. (33) with parameters \(a_1=b_2=k=1,~~b_1=\varpi =\theta =2,~~\theta _0=0.5,~~\lambda =a_2=3,~~\text{ and }~~\vartheta =0.7~\)

Full size image
Fig. 4
figure 4

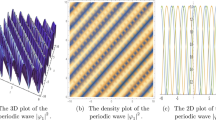
The 3D and 2D physical behavior of periodic wave optical solution of Eq. (39) with parameters \(a_1=\lambda =k=2,~~b_2=\varpi =a_2 =1,~~\theta _0=0,~~\theta =b_1=3,~~\text{ and }~~\vartheta =1.6~\)

Full size image

For \(\eta \varphi >0\)

  • Trigonometric solution:

    $$\begin{aligned} \phi _{3,1}(x, t)=\pm \frac{\sqrt{ \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{\sqrt{2} \sqrt{ k (\theta +\lambda )}}\nonumber \\ \times \bigg (\bigg (\frac{E \text{ cos }(\sqrt{\eta \varphi }~\varrho )+F \text{ sin }(\sqrt{\eta \varphi }~\varrho )}{F \text{ cos }(\sqrt{\eta \varphi }~\varrho )-E \text{ sin }(\sqrt{\eta \varphi }~\varrho )}\bigg )\nonumber \\ -\bigg (\frac{E \text{ cos }(\sqrt{\eta \varphi }~\varrho )+F \text{ sin }(\sqrt{\eta \varphi }~\varrho )}{F \text{ cos }(\sqrt{\eta \varphi }~\varrho )-E \text{ sin }(\sqrt{\eta \varphi }~\varrho )}\bigg )^{-1}\bigg )\nonumber \\ \times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (52)

    On setting, \(E=F\), we attain periodic traveling wave solution as:

    $$\begin{aligned} \phi _{3,1}(x, t)=\pm \frac{\sqrt{2 \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{ \sqrt{ k (\theta +\lambda )}}\times \tan (2\sqrt{ \eta \varphi }~ \varrho )\nonumber \\ \times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (53)

    For \(\eta \varphi <0\)

  • Hyperbolic solution:

    $$\begin{aligned} \phi _{3,2}(x, t)= & {} \mp \frac{\sqrt{ \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{\sqrt{2} \sqrt{ k (\theta +\lambda )}}\nonumber \\&\times \bigg (\frac{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )+F}{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )-F}\bigg )\nonumber \\&- \bigg (\frac{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )+F}{E \text{ sinh }(2\sqrt{|\eta \varphi |}~\varrho )+E \text{ cosh }(2\sqrt{|\eta \varphi |}~\varrho )-F}\bigg )^{-1}\bigg )\nonumber \\&\times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (54)

    On setting \(E=F\), we secure combine dark-singular soliton solution as:

    $$\begin{aligned} \phi _{3,2}(x, t)= & {} \pm \frac{\sqrt{ \left( k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi \right) }}{\sqrt{2} \sqrt{ k (\theta +\lambda )}}\nonumber \\&\times \bigg (\tanh (\sqrt{ |\eta \varphi | }~\varrho ) -\coth (\sqrt{ |\eta \varphi | }~\varrho )\bigg )\nonumber \\&\times e^{i(-k x + \varpi t +\theta _{0})}. \end{aligned}$$
    (55)

    Here \(k \left( a_2 \varpi -k \left( a_1+b_1 k-b_2 \varpi \right) \right) -\varpi >0\) and \(k(\theta +\lambda )>0\) for valid solutions.

Physical Description

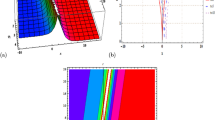
This section deals the graphical view of some solution of the said model along with suitable parametric values. The solutions of the BAE have importance for discussing the various kinds of optical soliton solutions in nonlinear optics. By utilizing the above said methods, optical solitary wave solutions are earned and depicted into distinct physical behaviors in the shape of solitary wave, trigonometric, hyperbolic, periodic, singular wave and their combo form solutions. We analyze that the reported solutions in this work are novel and fresh and to the best of our knowledge these achievements have not been submitted in the previous findings. Moreover, the physical behaviors of some earned solutions are plotted in 3D and 2D graphs by selecting different values for parameters. These results have some other physical meanings; for example, the hyperbolic tangent arises in the calculation of magnetic moment and rapidity of special relativity, the hyperbolic secant arises in the profile of a laminar jet and hyperbolic cotangent arises in the Langevin function for magnetic polarization [38]. Moreover, dark optical soliton describes the solitary waves with lower intensity than the background, whereas bright soliton characterizes the solitary waves whose peak intensity is larger than the background and the singular optical soliton is a solitary wave with discontinuous derivatives; examples of such solitary waves include compactions, which have finite (compact) support, and peakons, whose peaks have a discontinuous first derivative [39, 40]. The graphical view of some physical behavior to the dark, singular, bright, and periodic wave optical soliton solutions can be seen in Figs. 1, 2, 3 and 4. We anticipate that our recovered results will provide us with an essential tool for a better understanding of the waves that occur in diverse nonlinear regions. The following figures are given below

Conclusion

In this research work, we have constructed the dynamics of optical solitary wave solutions in nonlinear optics system which is modelled by BAE incorporating with group velocity dispersion and self-steepening effect. The diverse solitary waves in single and combined form like dark, bright, singular, complex, and combo optical solutions to the governing model are retrieved by the mean of extended ShGEEM and (\(\frac{G^{\prime }}{G^2}\))-expansion function method. Moreover, the singular periodic wave, the hyperbolic as well as trigonometric functions solutions are extracted. The calculations also reveals us the importance of these methods to find the analytic solutions in a more general way. By selecting suitable parametric values, the dynamics of the evaluated results are exemplified by sketching their 3D and 2D profiles. We have plotted some of our obtained solutions in Figs. 1, 2, 3 and 4, which show the solitary wave profiles of these solutions. The earned solitary wave solutions discuss the physical features of this model. The achievements of this study are imperative in the field of nonlinear fiber optics since these soliton solutions will be necessary to execute in the telecommunications industry.