Partially coherent vortex cosh-Gaussian beam and its paraxial propagation

Abstract

In this work, the propagation properties of a partially coherent vortex cosh-Gaussian beam (PCvChGB) have been investigated. Within the framework of the extended Huygens–Fresnel diffraction integral, an analytical formula for a PCvChGB propagating in a paraxial ABCD optical system is derived. Based on the obtained formula, the influences of the spatial coherence, decentered parameter and vortex charge on the propagation properties of a PCvChGB in free space are illustrated numerically and analyzed. The obtained results could be beneficial for applications of PCvChG beams in optical communications, remote sensing and atom optics.

1 Introduction

In the last few years, various beam models have been introduced to describe the optical field of laser output and many of them have attracted great attention for their applications in different domains such as remote sensing, imaging, free-space optical communication, and atom optics. Especially, the vortex hollow dark beams, i.e., the beams with hole-intensity in the centre region and twisted wave-front phase, have been extensively investigated (Allen et al. 1992; Kuga et al. 1997; Paterson et al. 2001; Ponomarenko 2001; Cai et al. 2003; Bishop et al. 2004; Wang et al. 2004, 2012; Torok and Munro 2004; Gao et al. 2011; Zhu et al. 2016; Rubinsztein-Dunlop et al. 2017; Zhou and Zhou 2014; Anguiano-Morales et al. 2015; Yaalou et al. 2019a, 2019b; Hricha et al. 2020a). Up to now, the spreading properties of various hollow vortex models have been examined, such as those of Laguerre-Gaussian beams (Lukin et al. 2012), hollow vortex Gaussian beams (Zhou et al. 2013), Lorentz-Gauss vortex beams (Ni and Zhou 2013), four-petal Gaussian vortex beams (Guo et al. 2014), vortex Hermite-Gaussian beams (Kotlyar et al. 2015), flat-topped vortex hollow beams (Liu et al. 2015), vortex Airy beams (Yu et al. 2016), cosh-Airy vortex beams (Li et al. 2018), higher-order Laguerre-Gaussian beams (Liang et al. 2019), and so on. Recently, we have introduced the so-called vortex cosh-Gaussian beam (vChGB), the beam is the extended form of the hollow vortex Gaussian beam in the rectangular symmetry (Hricha et al. 2020b). By the appropriate choice of the vChGB parameters, namely the decentered parameter b and the vortex charge M, the beam profile in the initial plane can be either a hollow vortex Gaussian-like or a four-petal vortex Gaussian-like. In near-field, the profile of the vChGB is preserved upon propagation, and the stability range depends strongly on the parameter b, while in far-field, the vChGB evolves into a multi-spot structure. Many works on the propagation properties of vChGB in various optical media have been performed (Hricha et al. 2021a, 2021b, 2021c, 2021d), however one can notice that all the previous papers have been limited to the fully coherent vChGB. In general conditions, the light beams are more or less coherent (Mandel and Wolf 1995), and the fully coherence is the ideal state in the strict sense. Therefore, in the present paper we will introduce a new model for a partially coherent vChGB basing on the Schell-model source correlation function. Here after, the obtained beam will be referred to as PCvChGB. The remainder of the paper is structured as follows: in the forthcoming section, we present a theoretical analysis for the paraxial propagation of a PCvChGB based on the extended Huygens-Fresnel diffraction integral. In Sect. 3, numerical examples are presented to discuss the influences of the initial spatial coherence length and beam parameters on the propagation properties of a PCvChGB in free space. Finally, the main results are outlined in the conclusion part.

2 Propagation of a PCvChGB through a paraxial ABCD optical system

For a coherent vChGB propagating along the z-axis, the electric field at z = 0 is defined in the Cartesian coordinate system as Hricha et al. (2020b)

$$E\left( {\vec{r}_{0} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega_{0} }}} \right)\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\left( {x_{0} + iy_{0} } \right)^{M} ,$$

(1)

where $\vec{r}_{0} {\kern 1pt} = {\kern 1pt} \left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)$ is the position vector at the plane z = 0. $\omega_{0}$ is the waist radius of the Gaussian part, b is the decentered parameter associated with the cosh part, and M is the topological charge of the vortex.

Based on the theory of coherence, the cross-spectral density of a PCvChGB generated by a Gaussian Schell-model source at the source plane z = 0 can be expressed as Mandel and Wolf (1995)

$$W\left( {\vec{r}_{01} ,\vec{r}_{02} ,z = 0} \right) = E\left( {\vec{r}_{01} ,0} \right)E * \left( {\vec{r}_{02} ,0} \right)\;\;g\left( {\vec{r}_{01} - \vec{r}_{02} ,z = 0} \right),$$

(2)

where $g\left( {\vec{r}_{01} - \vec{r}_{02} ,z = 0} \right)$ is the spectral degree of coherence of the Gaussian Schell-model source at the initial plane z = 0

$$g\left( {\vec{r}_{01} - \vec{r}_{02} ,z = 0} \right) = \exp \left( { - \frac{{\left( {\vec{r}_{01} - \vec{r}_{02} } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right),$$

(3)

with $\sigma_{0}$ is the spatial coherence length, and the asterisk denotes the complex conjugation.

The PCvChGB considered above can be realized in practice by using a preliminary cosh-Gaussian source. This latter can be generated, for example, by combining a group of virtual sources (Zhang et al. 2007). From a cosh-Gaussian beam, one can produce its corresponding Schell model version (i.e., partially coherent cosh-Gaussian beam) by using a conventional method, which in principle consists of two steps (see Zeng et al. 2019, and Refs therein):

First, one can generate a partially coherent cosh-Gaussian beam (PCChGB) from the cosh-Gaussian excitation by the help of a rotating ground–glass disk (RGGD) or a liquid crystal light modulator (SLM), and so on. Secondly, a vortex phase can be embedded in the PCChGB by means of a spiral phase plate (SPP), SLM or a digital mirror device (DMD) to generate the partially coherent cosh-Gauss vortex beam.

Within the paraxial approximation and based on the extended Huygens–Fresnel diffraction integral, a PCvChGB propagating in a paraxial ABCD optical system at the output plane z can be written as Mandel and Wolf (1995), Zhang et al. (2007), Zeng et al. (2019), Collins (1970)

$$W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = \left( {\frac{k}{2\pi B}} \right)^{2} \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {W\left( {\vec{r}_{01} ,\vec{r}_{02} ,z = 0} \right)\exp \left[ {\frac{ik}{{2B}}\left\{ {A\left( {\vec{r}_{02}^{2} - \vec{r}_{01}^{2} } \right) - 2\left( {\vec{r}_{02} \vec{r}_{2} - \vec{r}_{01} \vec{r}_{1} } \right) + D\left( {\vec{r}_{2}^{2} - \vec{r}_{1}^{2} } \right)} \right\}} \right]dr_{01} dr_{02} } } ,$$

(4)

where $\vec{r}_{1} {\kern 1pt} = \left( {x_{1} {\kern 1pt} ,y_{1} {\kern 1pt} } \right)$ and $\vec{r}_{2} {\kern 1pt} = \left( {x_{2} {\kern 1pt} ,y_{2} {\kern 1pt} } \right)$ are the position vectors at the output plane z. $\vec{r}_{0i} {\kern 1pt} = \left( {x_{0i} {\kern 1pt} ,y_{0i} {\kern 1pt} } \right)$ and $d\vec{r}_{0i} {\kern 1pt} = dx_{0i} dy_{0i}$ (with i = 1 or 2) are the position vector and surface element in the initial plane z = 0, respectively. A, B, and D are the matrix elements of the optical system, and $k = \frac{2\pi }{\lambda }$ is the wave number with λ is the wavelength in vacuum.

Substituting from Eqs. (2–3) into Eq. (4), then recalling the following expansions (Gradshteyn and Ryzhik 1994)

$$\left( {x + iy} \right)^{M} = \sum\limits_{l = 0}^{M} {C_{l}^{M} } x^{l} \left( {iy} \right)^{M - l} ,$$

(4a)

where

$$C_{l}^{M} = \frac{M!}{{l!\left( {M - l} \right){\kern 1pt} !}},$$

(4b)

the cross-spectral density of a PCvChGB can be expressed as

$$W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = \left( {\frac{k}{2\pi B}} \right)^{2} \exp \left\{ {\frac{ikD}{{2B}}\left( {\vec{r}_{2}^{2} - \vec{r}_{1}^{2} } \right)} \right\}\sum\limits_{l = 0}^{M} {\sum\limits_{n = 0}^{M} {C_{l}^{M} C_{n}^{M} \left( { - i} \right)^{l - n} } } U_{l,n} \left( {x_{1} ,x_{2} } \right)U_{M - l,M - n} \left( {y_{1} ,y_{2} } \right),$$

(5)

where $U_{l,n} \left( {s_{1} ,s_{2} } \right)$ is a typical integral expression given by

$$\begin{aligned} U_{l,n} \left( {s_{1} ,s_{2} } \right) = & \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \cosh \left( {\frac{{bs_{01} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha^{ * } s_{01}^{2} + \frac{{iks_{1} }}{B}s_{01} } \right\}} \\ & \;\; \times \left[ {\int\limits_{ - \infty }^{ + \infty } {s_{02}^{n} \cosh \left( {\frac{{bs_{02} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha s_{02}^{2} + \left( {\frac{{s_{01} }}{{\sigma_{0}^{2} }} - \frac{{iks_{2} }}{B}} \right)s_{02} } \right\}ds_{02} } } \right]ds_{01} , \\ \end{aligned}$$

(5a)

where s represents either x or y (hereafter), and

$$\alpha = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }} - \frac{ikA}{{2B}}.$$

(5b)

Using the definition of the cosh (.) function, and recalling the following integral formula (Belafhal et al. 2020)

$$\int\limits_{ - \infty }^{ + \infty } {x^{n} \exp \left( { - px^{2} + 2qx} \right)} dx = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),$$

(6)

where $H_{n} \left( {.{\kern 1pt} {\kern 1pt} } \right)$ is the Hermite polynomial of nth-order, Eq. (5a) can be expressed as

$$U_{l,n} \left( {s_{1} ,s_{2} } \right) = \frac{1}{4}\sqrt {\frac{\pi }{\alpha }} \left( {\frac{1}{2i\sqrt \alpha }} \right)^{n} \left[ {F^{ + } \left( {s_{1} ,s_{2} } \right) + F^{ - } \left( {s_{1} ,s_{2} } \right) + G^{ + } \left( {s_{1} ,s_{2} } \right) + G^{ - } \left( {s_{1} ,s_{2} } \right)} \right]{\kern 1pt} ,$$

(7)

where

$$F^{ \pm } \left( {s_{1} ,s_{2} } \right) = \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} + \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \exp \left\{ {\frac{{q_{ \pm }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right\}H_{n} \left( {\frac{{iq_{ \pm } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right)ds_{01} ,$$

(7a)

and

$$G^{ \pm } \left( {s_{1} ,s_{2} } \right) = \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} - \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \exp \left\{ {\frac{{q_{ \pm }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right\}H_{n} \left( {\frac{{iq_{ \pm } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right)ds_{01} ,$$

(7b)

with

$$q_{ \pm } \left( {s_{01} ,s_{2} } \right) = \frac{{s_{01} }}{{2\sigma_{0}^{2} }} - \frac{{iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}.$$

(7c)

Now, by using the addition formula of the Hermite polynomials with its presentation for physics (Magnus et al. 1966)

$$H_{n} \left( {x + y} \right) = \sum\limits_{j = 0}^{n} {C_{j}^{n} \left( {2x} \right)^{j} } H_{n - j} \left( y \right),$$

(8)

and after carrying out some tedious calculation (see the appendix), the cross-spectral density can be expressed as

$$\begin{aligned} W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = & \frac{1}{16}\frac{1}{\alpha \eta }\left( \frac{k}{2z} \right)^{2} \left( {\frac{1}{2i\sqrt \alpha }} \right)^{M} \exp \left\{ {\frac{ikD}{{2B}}\left( {x_{2}^{2} - x_{1}^{2} + y_{2}^{2} - y_{1}^{2} } \right)} \right\} \\ & \;\; \times \sum\limits_{l = 0}^{M} {\sum\limits_{n = 0}^{M} {C_{l}^{M} C_{n}^{M} \left( i \right)^{n - l} {\rm P}_{l,n} \left( {x_{1} ,x_{2} } \right){\rm P}_{M - l,M - n} \left( {y_{1} ,y_{2} } \right)} } , \\ \end{aligned}$$

(9)

where

$$\begin{aligned} {\rm P}_{l,n} \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{h} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + h} H_{n - h} \left( {\frac{i}{2\sqrt \alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)} \right) \\ & \;\; \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{1s}^{ + } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{2s}^{ + } }}{\sqrt \eta }} \right)} \right] \\ & \;\; + \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{t = 0}^{n} {C_{t}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{t} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + t} H_{n - t} \left( {\frac{ - i}{{2\sqrt \alpha }}\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)} \right) \\ & \;\; \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{1s}^{ - } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{2s}^{ - } }}{\sqrt \eta }} \right)} \right]{\kern 1pt} , \\ \end{aligned}$$

(9a)

with

$$\eta = \alpha^{ * } - \frac{1}{{4\alpha \sigma_{0}^{4} }},$$

(9b)

$$q_{1s}^{ \pm } = \left( {\frac{{iks_{1} }}{2B} + \frac{b}{{2\omega_{0} }}} \right) + \frac{1}{{4\alpha \sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{B} \pm \frac{b}{{\omega_{0} }}} \right),$$

(9c)

and

$$q_{2s}^{ \pm } = \left( {\frac{{iks_{1} }}{2B} - \frac{b}{{2\omega_{0} }}} \right) + \frac{1}{{4\alpha \sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{B} \pm \frac{b}{{\omega_{0} }}} \right).$$

(9d)

Equation (9) is the analytical expression for the cross-spectral density of a PCvChGB propagating in an arbitrary paraxial ABCD optical system, and it will be convenient for analyzing the evolution of the spreading properties of a PCvChGB through a paraxial optical system. In the limit case when $\sigma_{0} \to \infty$ (i.e., for the fully coherence state), Eq. (9) will give the propagation expression of the fully coherent vChGB in a paraxial optical system. The obtained result is consistent with Eq. (8a) of Ref. Hricha et al. (2020b). It is worth noting that in the two special cases b = 0 and M = 0, Eq. (9) will lead to the propagation equations of a partially coherent vortex Gaussian and standard ChGB beams, respectively. The intensity and spatial complex degree of coherence at two points $\vec{r}_{1} = \left( {x_{1} ,y_{1} } \right)$ and $\vec{r}_{2} = \left( {x_{2} ,y_{2} } \right)$ for a PCvChGB propagating through a paraxial optical system in the output plane z can be obtained directly from Eq. (9), respectively, as Mandel and Wolf (1995)

$$I\left( {\vec{r},z} \right) = W\left( {\vec{r},\vec{r},z} \right),$$

(10)

and

$$\mu \left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = \frac{{W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right)}}{{\left[ {W\left( {\vec{r}_{1} ,\vec{r}_{1} {\kern 1pt} ,z} \right)W\left( {\vec{r}_{2} ,\vec{r}_{2} ,z} \right)} \right]^{1/2} }}.$$

(11)

3 Numerical results and analysis

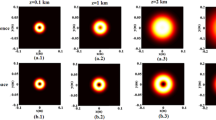
In this section, the evolution of the average intensity distributions of a PCvChGB upon propagation in free space is investigated by numerical calculation of Eq. (10) by taking A = D = 1 and B = z. As the incident PCvChGB can have two typical profile configurations depending on the value of b, the numerical simulations are then performed for the beam in each configuration. In the following numerical calculations, the parameters used are set as λ = 800 nm, ω₀ = 1 mm, and ${\kern 1pt} z_{r} = {{\pi \omega_{0}^{2} } \mathord{\left/ {\vphantom {{\pi \omega_{0}^{2} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }$ denotes the Rayleigh length and is taken as scale factor for propagation distances. Figures 1 and 2 illustrate the evolution of the average intensity distribution of a PCvChGB with M = 1 at four propagation distances (z/z_r = 0.1, 0.5z_r, 2z_r and 10z_r) and for different values of the initial coherence length $\sigma_{0}$ (which is used here after in its normalized form ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$). In the small b configuration (see Fig. 1), the PCvChGB with a low coherence length turns from a ring shape into a solid beam with Gaussian distribution at a short propagation distance ($z < {\kern 1pt} z_{r}$), and the beam keeps the Gaussian shape unchanged upon further propagation. The transition speed for the change of the beam profile from ring shape to Gaussian one is faster as the initial coherence length is smaller.

Fig. 1

The average intensity distribution of partially coherent PCvChGB propagating through free space at four propagation distance z (z = 0.1z_r, 0.5z_r, 2 z_r and z = 10 z_r) and for different values of ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$ with $\lambda = 800\,\,{\text{nm}}$, M = 1 and b = 0.1

Fig. 2

The same as Fig. 1 except b = 4

In the large b configuration (see Fig. 2), one can see that when the value of ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$ is moderate (i.e., ${{0.4 \le \sigma_{0} } \mathord{\left/ {\vphantom {{0.4 \le \sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} \le 2$) the beam is four-petal like at lower propagation distances ($z \le 0.5{\kern 1pt} z_{r}$), but at a sufficiently large propagation distance (i.e., $z = 10\,{\kern 1pt} z_{r}$) the initial beam changes to the Gaussian one. One can also see that the speed of beam change becomes faster as the coherence length decreases.

When the coherence length is sufficiently large, i.e. ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 10$, the partially coherent vChGB behaves like a fully coherent one (see the columns on the right in Fig. 1), which is consistent with the results of Hricha et al. (2020b).

It is worth noting from the illustrations above that the beam spreading is stronger as the initial coherence length is smaller. In addition, one can see that after reaching a maximum value, the intensity of the central peak of the beam decreases gradually and the overall beam size spreads as the propagation distance augments due to the diffraction phenomena.

To show more details about the evolution of beam upon propagation, the intensity distributions are illustrated by curves along the x-direction in Figs. 3 and 4. One can easily see that for a fixed propagation distance z, the beam spot size as well as the bright central region of the beam becomes larger as the initial coherence length decreases.

Fig. 3

The normalized intensity in x-direction partially coherent PCvChGB in free space for three values of the propagation distance z with M = 1, b = 0.1, and a ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 0.4$, b ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 0.8$, c ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 1$, d ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 2$

Fig. 4

The normalized intensity in x-direction of PCvChGB in free space for three propagation distances z (z = 0.1zr, 0.5zr, 2zr), with M = 1, b = 4, and a ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 0.4$, b ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 0.8$, c ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 1$, d ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 2$

Figures 5, 6 display the evolution intensity distribution of a PCvChGB with a fixed value of the initial coherence length (${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }} = 1$) for different values of the topological charge (M = 1, 2, 3 and 4). In the small b case (see Fig. 5), it is clearly seen that a PCvChGB with large vortex charge M is more stable during propagation than the one with small M. While for the large b case (Fig. 6), the intensity profile gradually changes upon propagation and transformed into Gaussian profile-like in far-field for all values of M. One can also see that the rising speed of the central intensity increases as M is decreased. In far-field the bright center region is wider and the beam shape becomes squarer when the vortex charge M is larger (see Fig. 7).

Fig. 5

The average intensity distribution of a PCvChGB propagating in free space for four values M, with ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} = 1}}} \right. \kern-\nulldelimiterspace} {\omega_{0} = 1}}$, $\lambda = 800\,\,{\text{nm}}$ and b = 0.1

Fig. 6

The average intensity distribution of a PCvChGB propagating in free space for M = 1, 2, 3 and 4, ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} = 1}}} \right. \kern-\nulldelimiterspace} {\omega_{0} = 1}}$ and with b = 4

Fig. 7

Modulus of spatial degree of coherence of PCvChGB with b = 0.1 propagating in free space for the different ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$, at a M = 1, b M = 2, with $\lambda = 800\,\,{\text{nm}}$

To evaluate quantitatively the effect of the initial coherence length on the evolution of spatial degree of coherence for a PCvChGB propagating in free space, we calculated numerically $\left| \mu \right|$ at two reference points based on Eq. (11). Three values of $\sigma_{0}$(${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$ = 2, 5 and 10) are considered, and the results are shown in Figs. 7, 8. It is worth noting that the typical points used here (i.e. $\left( {0,0} \right)$ and $\left( {0.2,0} \right)$ mm) are located at the origin and near the propagation axis, respectively. They belong to the paraxial zone which is of practical interest. For a relevant analysis, the distance between the two points is taken of order of magnitude of the coherence length of the initial beam. One can easily see from the plots that the spatial degree of coherence of PCvChGB first quickly increases in near-field, and keeps increasing with slower rate as the propagation distance increases, and finally tends to the sutured value 1. The influence of the initial coherence length gradually disappears as the propagation distance augments. In addition, one can note that for a given propagation distance, the beam with the larger ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$ or larger M has smaller $\left| \mu \right|$.

Fig. 8

Modulus of spatial degree of coherence of PCvChGB with b = 4 propagating in free space for the different ${{\sigma_{0} } \mathord{\left/ {\vphantom {{\sigma_{0} } {\omega_{0} }}} \right. \kern-\nulldelimiterspace} {\omega_{0} }}$, at a M = 1, b: M = 2, with $\lambda = 800\,\,{\text{nm}}$

4 Conclusion

The propagation properties of a PCvChGB through a paraxial optical system have been investigated theoretically. The analytical expression for the cross spectral density of PCvChGB propagating through a paraxial optical system is derived based on the extended Huygens–Fresnel diffraction integral and the coherence theory. Numerical examples illustrating the influences of the initial spatial coherence and beam parameters on the propagation properties of the beam in free space are presented. It is found that the intensity distribution and spatial degree of coherence of a PCvChGB propagating in free space is closely related to the initial spatial coherence, the decentered parameter b and the vortex charge M. The results drawn in the paper can improve the applications of hollow beams in remote sensing, atom optics, and optical communication.

Appendix

The derivation process of Eq. (9) is presented in detail in following.

The cross-spectral density of a PCvChGB propagating in free space is given by Mandel and Wolf (1995), Collins (1970)

$$W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = \left( {\frac{k}{2\pi B}} \right)^{2} \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {W\left( {\vec{r}_{01} ,\vec{r}_{02} ,z = 0} \right)\exp \left[ {\frac{ik}{{2B}}\left\{ {A\left( {\vec{r}_{02}^{2} - \vec{r}_{01}^{2} } \right) - 2\left( {\vec{r}_{02} \vec{r}_{2} - \vec{r}_{01} \vec{r}_{1} } \right) + D\left( {\vec{r}_{2}^{2} - \vec{r}_{1}^{2} } \right)} \right\}} \right]dr_{01} dr_{02} } } .$$

(A1)

Recalling the following expansions (Gradshteyn and Ryzhik 1994)

$$\left( {x + iy} \right)^{M} = \sum\limits_{l = 0}^{M} {C_{l}^{M} } x^{l} \left( {iy} \right)^{M - l} ,$$

(A2)

where

$$C_{l}^{M} = {\kern 1pt} \frac{M!}{{l!\left( {M - l} \right){\kern 1pt} !}},$$

(A3)

the cross-spectral density can be rearranged as

$$W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = \left( {\frac{k}{2\pi B}} \right)^{2} \exp \left\{ {\frac{ikD}{{2B}}\left( {\vec{r}_{2}^{2} - \vec{r}_{1}^{2} } \right)} \right\}\sum\limits_{l = 0}^{M} {C_{l}^{M} \left( i \right)^{M - l} \sum\limits_{n = 0}^{M} {C_{n}^{M} \left( { - i} \right)^{M - n} } {\kern 1pt} } U_{l,n} \left( {x_{1} ,x_{2} } \right)U_{M - l,M - n} \left( {y_{1} ,y_{2} } \right),$$

(A4)

where $U_{l,n} \left( {s_{1} ,s_{2} } \right)$ is the typical integral expression given by

$$\begin{aligned} U_{l,n} \left( {s_{1} ,s_{2} } \right) = & \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \cosh \left( {\frac{{b\,s_{01} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha^{ * } s_{01}^{2} + \frac{{ik\,s_{1} }}{B}s_{01} } \right\}} \\ & \;\; \times \left[ {\int\limits_{ - \infty }^{ + \infty } {s_{02}^{n} \cosh \,\left( {\frac{{b\,s_{02} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha \,s_{02}^{2} + \left( {\frac{{s_{01} }}{{\sigma_{0}^{2} }} - \frac{{ik\,s_{2} }}{B}} \right)\,s_{02} } \right\}ds_{02} ,} } \right]\,ds_{01} , \\ \end{aligned}$$

(A5)

where s represents either x or y (hereafter), and

$$\alpha = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }} - \frac{ikA}{{2B}}.$$

(A6)

Using the definition of the cosh (.) function

$$\cosh \left( x \right) = \frac{{e^{x} + e^{ - x} }}{2},$$

and recalling the following integral equation (Belafhal et al. 2020)

$$\int\limits_{ - \infty }^{ + \infty } {x^{n} \exp \left( { - px^{2} + 2qx} \right)} dx = \sqrt {\frac{\pi }{p}} \,\exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),$$

(A7)

where $H_{n} \left( {.{\kern 1pt} {\kern 1pt} } \right)$ is the Hermite polynomial of nth-order, Eq. (A5) can be expressed as

$$\begin{aligned} U_{l,n} \left( {s_{1} ,s_{2} } \right) = & \frac{1}{2}\sqrt {\frac{\pi }{\alpha }} \left( {\frac{1}{2i\sqrt \alpha }} \right)^{n} \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \cosh \left( {\frac{{b\,s_{01} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha^{ * } s_{01}^{2} + \frac{{ik\,s_{1} }}{B}s_{01} } \right\}} \\ & \;\; \times \left[ {\exp \left( {\frac{{q_{ + }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right)H_{n} \left( {\frac{{iq_{ + } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right) + \exp \left( {\frac{{q_{ - }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right)H_{n} \left( {\frac{{iq_{ - } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right)} \right]\,ds_{01} , \\ \end{aligned}$$

(A8)

where

$$q_{ \pm } \left( {s_{01} ,s_{2} } \right) = \frac{{s_{01} }}{{2\sigma_{0}^{2} }} - \frac{{iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }},$$

(A9)

then Eq. (A8) can be written as

$$U_{l,n} \left( {s_{1} ,s_{2} } \right) = \frac{1}{4}\sqrt {\frac{\pi }{\alpha }{\kern 1pt} {\kern 1pt} } \left( {\frac{1}{2i\sqrt \alpha }} \right)^{n} \left[ {F^{ + } \left( {s_{1} ,s_{2} } \right) + F^{ - } \left( {s_{1} ,s_{2} } \right) + G^{ + } \left( {s_{1} ,s_{2} } \right) + G^{ - } \left( {s_{1} ,s_{2} } \right)} \right]{\kern 1pt} ,$$

(A10)

where

$$F^{ \pm } \left( {s_{1} ,s_{2} } \right) = \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} + \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \exp \left\{ {\frac{{q_{ \pm }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right\}H_{n} \left( {\frac{{iq_{ \pm } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right)ds_{01} ,$$

(A11)

and

$$G^{ \pm } \left( {s_{1} ,s_{2} } \right) = \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} - \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \exp \left\{ {\frac{{q_{ \pm }^{2} \left( {s_{01} ,s_{2} } \right)}}{\alpha }} \right\}H_{n} \left( {\frac{{iq_{ \pm } \left( {s_{01} ,s_{2} } \right)}}{\sqrt \alpha }} \right)ds_{01} {\kern 1pt} .$$

(A12)

Eqs. (A11) and (A12) can also be developed as

$$\begin{aligned} F^{ \pm } \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} + \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \\ & \;\;\exp \left\{ {\frac{1}{\alpha }\left( {\frac{{s_{01}^{2} }}{{4\sigma_{0}^{2} }} + \frac{1}{{\sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)s_{01} } \right)} \right\}H_{n} \left( {\frac{i}{{2\sigma_{0}^{2} \sqrt \alpha }}s_{01} + \frac{i}{\sqrt \alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)} \right)ds_{01} , \\ \end{aligned}$$

(A13)

and

$$\begin{aligned} G^{ \pm } \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l} \exp \left\{ { - \alpha^{ * } s_{01}^{2} + \left( {\frac{{iks_{1} }}{B} - \frac{b}{{\omega_{0} }}} \right)s_{01} } \right\}} \\ & \;\;\;\exp \left\{ {\frac{1}{\alpha }\left( {\frac{{s_{01}^{2} }}{{4\sigma_{0}^{2} }} + \frac{1}{{\sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)s_{01} } \right)} \right\}H_{n} \left( {\frac{i}{{2\sigma_{0}^{2} \sqrt \alpha }}s_{01} + \frac{i}{\sqrt \alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)} \right)ds_{01} . \\ \end{aligned}$$

(A14)

Now, by using the following addition formula of the Hermite polynomials (Magnus et al. 1966)

$$H_{n} \left( {x + y} \right) = \sum\limits_{j = 0}^{n} {C_{j}^{n} \left( {2x} \right)^{j} } H_{n - j} \left( y \right),$$

(A15)

we find the expressions of Eqs. (A13) and (A14)

$$\begin{aligned} F^{ \pm } \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} } \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)^{h} H_{n - h} \left( {\frac{i}{\sqrt \alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)} \right) \\ & \;\;\;\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + h} \exp \left\{ { - \eta s_{01}^{2} + 2q_{1s}^{ \pm } s_{01} } \right\}} ds_{01} , \\ \end{aligned}$$

(A16)

and

$$\begin{aligned} G^{ \pm } \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} } \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)^{h} H_{n - h} \left( {\frac{i}{\sqrt \alpha }\left( {\frac{{ - iks_{2} }}{2B} \pm \frac{b}{{2\omega_{0} }}} \right)} \right) \\ & \;\;\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + h} \exp \left\{ { - \eta s_{01}^{2} + 2q_{2s}^{ \pm } s_{01} } \right\}} ds_{01} , \\ \end{aligned}$$

(A17)

and then Eq. (A10) can be written as

$$U_{l,n} \left( {s_{1} ,s_{2} } \right) = \frac{1}{4}\sqrt {\frac{\pi }{\alpha }{\kern 1pt} {\kern 1pt} } \left( {\frac{1}{2i\sqrt \alpha }} \right)^{n} \left[ \begin{gathered} \left\{ \begin{gathered} \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{ - iks_{2} }}{2B} + \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} } \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)^{h} H_{n - h} \left( {\frac{i}{\sqrt \alpha }\left( {\frac{{ - iks_{2} }}{2B} + \frac{b}{{2\omega_{0} }}} \right)} \right) \hfill \\ \times \left( {\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + h} \exp \left\{ { - \eta s_{01}^{2} + 2q_{1s}^{ + } s_{01} } \right\}} ds_{01} + \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + h} \exp \left\{ { - \eta s_{01}^{2} + 2q_{2s}^{ + } s_{01} } \right\}} ds_{01} } \right) \hfill \\ \end{gathered} \right\} \hfill \\ + \left\{ \begin{gathered} \exp \left\{ {\frac{1}{\alpha }\left( {\frac{{iks_{2} }}{2B} + \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{t = 0}^{n} {C_{t}^{n} } \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)^{t} H_{n - t} \left( {\frac{ - i}{{\sqrt \alpha }}\left( {\frac{{iks_{2} }}{2B} + \frac{b}{{2\omega_{0} }}} \right)} \right) \hfill \\ \times \left( {\int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + t} \exp \left\{ { - \eta s_{01}^{2} + 2q_{1s}^{ - } s_{01} } \right\}} ds_{01} + \int\limits_{ - \infty }^{ + \infty } {s_{01}^{l + t} \exp \left\{ { - \eta s_{01}^{2} + 2q_{2s}^{ - } s_{01} } \right\}} ds_{01} } \right) \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} \right]{\kern 1pt} ,$$

(A18)

By applying again the integral Eq. (A7), we get

$$\begin{aligned} U_{l,n} \left( {s_{1} ,s_{2} } \right) = & \frac{1}{4}\sqrt {\frac{\pi }{\alpha }{\kern 1pt} {\kern 1pt} } \sqrt {\frac{\pi }{\eta }{\kern 1pt} {\kern 1pt} } \left( {\frac{1}{2i\sqrt \alpha }} \right)^{n} \exp \left\{ {\frac{ikD}{{2B}}\left( {s_{2}^{2} - s_{1}^{2} } \right)} \right\} \\ & \;\;\;\;\left\{ \begin{gathered} \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{h} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + h} H_{n - h} \left( {\frac{i}{2\sqrt \alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{1s}^{ + } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{2s}^{ + } }}{\sqrt \eta }} \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{t = 0}^{n} {C_{t}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{t} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + t} H_{n - t} \left( {\frac{ - i}{{2\sqrt \alpha }}\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{1s}^{ - } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{2s}^{ - } }}{\sqrt \eta }} \right)} \right] \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(A19)

with

$$\eta = \alpha^{ * } - \frac{1}{{4\alpha \sigma_{0}^{4} }},$$

(A20)

$$q_{1s}^{ \pm } = \left( {\frac{{iks_{1} }}{2B} + \frac{b}{{2\omega_{0} }}} \right) + \frac{1}{{4\alpha \sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{B} \pm \frac{b}{{\omega_{0} }}} \right),$$

(A21)

and

$$q_{2s}^{ \pm } = \left( {\frac{{iks_{1} }}{2B} - \frac{b}{{2\omega_{0} }}} \right) + \frac{1}{{4\alpha \sigma_{0}^{2} }}\left( {\frac{{ - iks_{2} }}{B} \pm \frac{b}{{\omega_{0} }}} \right).$$

(A22)

After the substitution of Eq. (A18) into Eq. (A4), the cross-spectral density of a PCvChGB propagating through a paraxial optical system is obtained as

$$\begin{aligned} W\left( {\vec{r}_{1} ,\vec{r}_{2} ,z} \right) = & \frac{1}{16}\frac{1}{\alpha \eta }\left( \frac{k}{2z} \right)^{2} \left( {\frac{1}{2i\sqrt \alpha }} \right)^{M} \exp \left\{ {\frac{ikD}{{2B}}\left( {x_{2}^{2} - x_{1}^{2} + y_{2}^{2} - y_{1}^{2} } \right)} \right\} \\ & \;\; \times \sum\limits_{l = 0}^{M} {\sum\limits_{n = 0}^{M} {C_{l}^{M} C_{n}^{M} \left( i \right)^{n - l} {\rm P}_{l,n} \left( {x_{1} ,x_{2} } \right)\,{\rm P}_{M - l,M - n} \left( {y_{1} ,y_{2} } \right)} } , \\ \end{aligned}$$

(A23)

where

$$\begin{aligned} {\rm P}_{l,n} \left( {s_{1} ,s_{2} } \right) = & \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{h = 0}^{n} {C_{h}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{h} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + h} H_{n - h} \left( {\frac{i}{2\sqrt \alpha }\left( {\frac{b}{{\omega_{0} }} - \frac{{iks_{2} }}{B}} \right)} \right) \\ & \;\; \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{1s}^{ + } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ + } } \right)^{2} }}{\eta }} \right\}H_{l + h} \left( {\frac{{iq_{2s}^{ + } }}{\sqrt \eta }} \right)} \right] \\ & \;\; + \exp \left\{ {\frac{1}{4\alpha }\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)^{2} } \right\}\sum\limits_{t = 0}^{n} {C_{t}^{n} \left( {\frac{i}{{\sigma_{0}^{2} \sqrt \alpha }}} \right)}^{t} \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + t} H_{n - t} \left( {\frac{ - i}{{2\sqrt \alpha }}\left( {\frac{b}{{\omega_{0} }} + \frac{{iks_{2} }}{B}} \right)} \right) \\ & \;\; \times \left[ {\exp \left\{ {\frac{{\left( {q_{1s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{1s}^{ - } }}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2s}^{ - } } \right)^{2} }}{\eta }} \right\}H_{l + t} \left( {\frac{{iq_{2s}^{ - } }}{\sqrt \eta }} \right)} \right]{\kern 1pt} . \\ \end{aligned}$$

(A24)