1 Introduction

Nonlinear partial differential equations (NLPDEs) play a pivotal role in describing a wide array of complex phenomena across various scientific disciplines, physics, biology, and engineering [1,2,3,4,5,6,7,8,9]. Their significance lies in capturing intricate behaviors that linear equations often fail to model adequately. In the field of NLPDEs, the Hirota bilinear equation stands out as a particularly intriguing and challenging problem. This equation, embedded in a (2 + 1)-dimensional framework, has attracted considerable attention due to its relevance in understanding nonlinear wave interactions and soliton dynamics. While several existing methods have been employed to tackle nonlinear PDEs, such as: exp-function method [10], Hirota bilinear method [11,12,13], New extended direct algebraic method [14], the tan-cot method [15], the inverse \(\left( \frac{G'}{G}\right) \)-expansion method [16], solitary wave ansatz method [17], the unified solver method [18], the improved \(tan(\frac{\phi (\xi )}{2})\)-expansion method [19], the generalized Riccati equation mapping method [20], Sine-Gordan equation expansion method [21], the Darboux transformations methods [22], the Weierstrass elliptic function method [23], Lie symmetry method [24], Sardar sub-equation method [25,26,27], and many more [28,29,30,31,32]. In this work, we focus on using the multivariate generalized exponential rational integral function to extract the solutions of the (2 + 1)-D Hirota bilinear problem [33]:

$$\begin{aligned}&R_{yt}+c_1 \Big (R_{xxxy}+3R_{xx}\int R_y\,dx+3RR_{xy}\nonumber \\&\quad +6R_xR_y\Big ) +c_2R_{yy}=0, \end{aligned}$$
(1)

where \(c_i\)’s \((1\le i\le 2)\) are arbitrary constants. The Hirota bilinear equation uses in the study of nonlinear wave interactions and soliton dynamics. Its relevance extends to various scientific disciplines, including physics, plasma physics, and nonlinear optics. Soliton solutions of the Hirota bilinear equation are known for their stability and ability to maintain their shape during propagation, making them crucial in describing certain physical phenomena. In recent years many researchers have worked on this equation, which are as follows: In their study, Hua et al. [34] explored two categories of interaction solutions: lump-kink and lump-soliton. These were achieved by combining two positive quadratic functions with either an exponential function or two positive quadratic functions with a hyperbolic cosine function in the bilinear equation. Lu and Ma [35] have discussed the lump solutions and the rogue waves for the Hirota bilinear equation in the context of positive quadratic function solutions. They have presented the sufficient and necessary conditions for analyticity and rational localization of the lumps. Mandal et al. [36] explored an extended version of the generalized (2 + 1)-dimensional Hirota bilinear equation, unveiling nonlinear wave phenomena in diverse fields such as shallow water, oceanography, and nonlinear optics. Their investigation encompassed a thorough examination of integrability aspects, employing the Bell polynomial form to establish the Hirota bilinear form and Bäcklund transformations. The utilization of the Cole-Hopf transformation facilitated the derivation of Lax pairs through the direct linearization of the coupled system involving binary Bell polynomials. Furthermore, the study unveiled an array of infinite conservation laws derived from the two-field condition inherent in the generalized (2 + 1)-dimensional Hirota bilinear equation. Mandal et al. also presented expressions for one-soliton, two-soliton, and three-soliton solutions emanating from the Hirota bilinear equation.

This article is structured into multiple sections, each devoted to exploring how the multivariate generalized exponential rational integral function is applied to the (2 + 1)-D Hirota bilinear equation, elucidating the consequential results. The first section provides a historical overview of the Hirota bilinear equation, offering insights into its origins and development. The second section focuses on the key steps of the proposed method for investigating nonlinear partial differential equations. In the third section, we apply the MGERIF method to the Hirota bilinear equation, obtaining various families of solutions. The fourth section discusses the physical interpretation of the solutions for different parameter choices. Finally, the fifth section briefly concludes our work.

2 Multivariate generalized exponential rational integral function approach

This section introduces an innovative and highly efficient approach referred to as the multivariate generalized exponential rational integral function method. The MGERIF method stands out for its exceptional capability to yield novel and analytical solutions to nonlinear partial differential equations (NLPDEs). This distinctive approach is elucidated with the foundational support of the generalized exponential rational function (GERF) [37, 38] method. The significance of MGERIF lies in its ability to tackle NLPDEs, providing a powerful tool for addressing complex mathematical problems.

  • In general NLPDEs can be written as

    $$\begin{aligned} P(R,R_{x},R_{y},R_{t},R_{xx},R_{xt},...)=0, \end{aligned}$$
    (2)

    where \(R=R(x,y,t)\) is a solution of Eq. (2) with the independent variables x,y and t.

  • To reduce the Eq. (2), we consider the transformation

    $$\begin{aligned}&R=R(x,y,t)=S(\vartheta ),\nonumber \\&\vartheta =a _1x+a _2y+a _3 t+a _4, \end{aligned}$$
    (3)

    where \(a_1, a_2, a_3,\) and \(a_4\) are arbitrary constants. Making use of transformation (3) into (2), then the reduced nonlinear ordinary differential equation (NLODE) can be recast as

    $$\begin{aligned} P(S(\vartheta ), S'(\vartheta ), S''(\vartheta ),...)=0, \end{aligned}$$
    (4)

    with \(S'=\frac{dS}{d\vartheta },~S''=\frac{d^2S}{d\vartheta ^2},~\cdots \) etc.

  • To simplify the NLODE (4), we propose a solution of the form

    $$\begin{aligned} S(\vartheta )&={\mathcal {H}}_0+\sum _{i=1}^{N}{\mathcal {H}}_{i}\left( \underbrace{\int \int \cdots \int }_{i} U(\vartheta ) \, d\vartheta \, d\vartheta \cdots \, d\vartheta \right) ^{i}\nonumber \\&\quad +\sum _{i=1}^{N}{\mathcal {P}}_{i}\left( \underbrace{\int \int \cdots \int }_{i} U(\vartheta ) \, d\vartheta \, d\vartheta \cdots \, d\vartheta \right) ^{-i}. \end{aligned}$$
    (5)

    Here, \(U(\vartheta )\), which appears in the solution, is defined as

    $$\begin{aligned} U(\vartheta )=\frac{k_1 e^{m_1\vartheta }+k_2 e^{m_2\vartheta }}{k_3 e^{m_3\vartheta }+k_4 e^{m_4\vartheta }}. \end{aligned}$$
    (6)

  • In order to satisfy Eq. (1), it is crucial to determine the appropriate values for arbitrary parameters such as \(k_j, m_j\), \((1 \le j \le 4)\), \({\mathcal {H}}_0\), \({\mathcal {H}}_i\) and \({\mathcal {P}}_i\) \((1 \le i \le N)\) to be determined in such a way Eq. (1) satisfies.

  • Additionally, the value of N, which represent the order of the method, is determined by applying the homogeneous balancing principle to both the highest order derivative term and the nonlinear term within NLODE (4).

  • Placing (5) into (4) with (6), we arrive at an algebraic equation \(Q(\Theta _1,\Theta _2,\Theta _3,\Theta _4)=0.\) Here, \(\Theta _j=e^{m_j\vartheta },\) for \(1\le j \le 4.\) Thereafter, we are making each of the coefficient of function in Q to zero.

  • After applying mathematical simplifications through software like Mathematica, we can determine the specific values of the variables \({\mathcal {H}}_0\), \({\mathcal {H}}_i\) and \({\mathcal {P}}_i\) \((1 \le i \le N)\). Once these values are determined, we can substitute them into Eqs. (5) and (6), allowing us to obtain exact soliton solutions for the Eq. (4).

3 Remark:

The introduce method offers a systematic and effective approach for obtaining exact soliton solutions to NLPDEs of the form given in Eq. (2). By employing a transformation and subsequent reducing the NLPDE to a nonlinear ODE in terms of a new variable, the method allows for the systematic simplification of the problem. The proposed solution structure in Eq. (5), involving a series expansion with integrals of a specific function \(U(\vartheta )\), provides a flexible framework to capture the complex dynamics of the underlying equation.

4 Applications of MGERIF method

In this section, we employ the MGERIF method to derive analytic wave solutions for the Hirota Bilinear equation. To initiate this process, we utilize a wave transformation for the Eq. (1), expressed as:

$$\begin{aligned} R(x,y,t)=S(\vartheta ),~~ \text{ with }~~ \vartheta =a _1x+a _2y+a _3 t+a_4. \end{aligned}$$
(7)

This translation transforms the Hirota Bilinear equation into the following equation:

$$\begin{aligned}&a_2 a_1^3 c_1 S^{(4)}(\vartheta )+6 a_2 a_1 c_1 S(\vartheta ) S''(\vartheta )+a_2^2 c_2 S''(\vartheta )\nonumber \\&\quad +6 a_2 a_1 c_1 S'(\vartheta )^2+a_2 a_3 S''(\vartheta )=0. \end{aligned}$$
(8)

By carefully balancing the terms involving \(S^{(4)}\) and \(SS''\) in Eq. (8), we determine that \(N=2\). Consequently, the trial solution is given by

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_0+{\mathcal {H}}_1 \left( \int U(\vartheta ) \, d\vartheta \right) \nonumber \\&\quad +{\mathcal {H}}_2 \left( \int \int U(\vartheta )d\vartheta d\vartheta \right) ^2\nonumber \\&\quad +\frac{{\mathcal {P}}_1}{\int U(\vartheta ) \, d\vartheta }+\frac{{\mathcal {P}}_2}{\left( \int \int U(\vartheta )d\vartheta d\vartheta \right) ^2}. \end{aligned}$$
(9)

Substituting this trial solution into (8) and applying the MGERIF technique with computational software such as Mathematica, we obtain a set of solutions for the Hirota Bilinear equation.

5 1. The familiar sine representation:

Setting the parameters to \([k_1,k_2,k_3,k_4]=[1,-1,i,i]\) and \({[m_1,m_2,m_3,m_4]=[i,-i,0,0]}\), Eq. (6) transforms into the standard form of the sine function

$$\begin{aligned} U(\vartheta )=\sin (\vartheta ). \end{aligned}$$
(10)

After incorporating Eq. (10) into Eq. (9), we are able to establish the expression for \(S(\vartheta )\):

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_2 \sin ^2(\vartheta )-{\mathcal {H}}_1 \cos (\vartheta )+{\mathcal {H}}_0\nonumber \\&\quad +{\mathcal {P}}_2 \csc ^2(\vartheta )-{\mathcal {P}}_1 \sec (\vartheta ). \end{aligned}$$
(11)

Case 1.1:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2=0;\\&{\mathcal {P}}_1=0;{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Substituting the specified constants into Eq. (11), allows us to derive the solution to Eq. (8) as

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_0-{\mathcal {H}}_1 \cos (\vartheta ). \end{aligned}$$
(12)

Hence, using Eq. (12) within the expression (7), allows us to determine the exact invariant solution to the Hirota bilinear equaion

$$\begin{aligned} R(x,y,t)={\mathcal {H}}_0-{\mathcal {H}}_1 \cos \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) . \end{aligned}$$
(13)

Case 1.2:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;\\&{\mathcal {P}}_1\ne 0;{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Substituting the specified constants into Eq. (11), allows us to derive the solution to Eq. (8) as

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_2 \sin ^2(\vartheta )-{\mathcal {H}}_1 \cos (\vartheta )+{\mathcal {H}}_0-{\mathcal {P}}_1 \sec (\vartheta ). \end{aligned}$$
(14)

Hence, using Eq. (14) within the expression (7), allows us to determine the exact invariant solution to the Hirota bilinear equaion

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_2 \sin ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad -{\mathcal {H}}_1 \cos \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad -{\mathcal {P}}_1 \sec \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(15)
Fig. 1
figure 1

Visualization of Eq. (15): real, imaginary and absolute components

Full size image

Case 1.3:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;{\mathcal {P}}_2\ne 0;\\&a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Substituting the specified constants into Eq. (11), allows us to derive the solution to Eq. (8) as

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_2 \sin ^2(\vartheta )-{\mathcal {H}}_1 \cos (\vartheta )+{\mathcal {H}}_0\nonumber \\&\quad +{\mathcal {P}}_2 \csc ^2(\vartheta )-{\mathcal {P}}_1 \sec (\vartheta ). \end{aligned}$$
(16)

Hence, using Eq. (16) within the expression (7), allows us to determine the exact invariant solution to the Hirota bilinear equaion

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_2 \sin ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad -{\mathcal {H}}_1 \cos \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {P}}_2 \csc ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad -{\mathcal {P}}_1 \sec \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(17)
Fig. 2
figure 2

Visualization of Eq. (17): real, imaginary and absolute components

Full size image

Case 1.4:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1=0;{\mathcal {P}}_2=0;\\&a_1=0;a_3=-a_2 c_2. \end{aligned}$$

Substituting the specified constants into Eq. (11), allows us to derive the solution to Eq. (8) as

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_2 \sin ^2(\vartheta )-{\mathcal {H}}_1 \cos (\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(18)

Hence, using Eq. (18) within the expression (7), allows us to determine the exact invariant solution to the Hirota bilinear equaion

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_2 \sin ^2\left( -a_2 c_2 t+a_2 y+a_4\right) \nonumber \\&\quad -{\mathcal {H}}_1 \cos \left( -a_2 c_2 t+a_2 y+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(19)

6 2. The familiar cosine representation:

Setting the parameters to \([k_1,k_2,k_3,k_4]=[1,1,1,1]\) and \({[m_1,m_2,m_3,m_4]=[i,-i,0,0]}\), Eq. (6) transforms into the standard form of the cosine function

$$\begin{aligned} U(\vartheta )=\cos (\vartheta ). \end{aligned}$$
(20)

By plugging in Eq. (20) into Eq. (9), we can determine the specific form for \(S(\vartheta )\):

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_1 \sin (\vartheta )+{\mathcal {H}}_2 \cos ^2(\vartheta )+{\mathcal {H}}_0\nonumber \\&\quad +{\mathcal {P}}_1 \csc (\vartheta )+{\mathcal {P}}_2 \sec ^2(\vartheta ). \end{aligned}$$
(21)

Case 2.1:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

The solution to Eq. (8) can be obtained by inserting these given constants into Eq. (11):

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \sin (\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(22)

Hence, from Eq. (22) in the context of expression (7), we obtain

$$\begin{aligned} R(x,y,t)={\mathcal {H}}_1 \sin \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(23)

Case 2.2:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

The solution to Eq. (8) can be obtained by inserting these given constants into Eq. (11):

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \sin (\vartheta )+{\mathcal {H}}_2 \cos ^2(\vartheta )+{\mathcal {H}}_0+{\mathcal {P}}_1 \csc (\vartheta ). \end{aligned}$$
(24)

Hence, from Eq. (24) in the context of expression (7), we obtain

$$\begin{aligned} R (x,y,t)&={\mathcal {H}}_1 \sin \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {H}}_2 \cos ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\ {}&\quad +{\mathcal {P}}_1 \csc \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(25)
Fig. 3
figure 3

Visualization of Eq. (25): real, imaginary and absolute components

Full size image

Case 2.3:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2\ne 0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

The solution to Eq. (8) can be obtained by inserting these given constants into Eq. (11):

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_1 \sin (\vartheta )+{\mathcal {H}}_2 \cos ^2(\vartheta )\nonumber \\&\quad +{\mathcal {H}}_0+{\mathcal {P}}_1 \csc (\vartheta )+{\mathcal {P}}_2 \sec ^2(\vartheta ). \end{aligned}$$
(26)

Hence, from Eq. (26) in the context of expression (7), we obtain

$$\begin{aligned} R (x,y,t)&={\mathcal {H}}_1 \sin \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {H}}_2 \cos ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {P}}_1 \csc \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {P}}_2 \sec ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(27)
Fig. 4
figure 4

Visualization of Eq. (27): real, imaginary and absolute components

Full size image

Case 2.4:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_1=0;a_3=-a_2 c_2. \end{aligned}$$

The solution to Eq. (8) can be obtained by inserting these given constants into Eq. (11):

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \sin (\vartheta )+{\mathcal {H}}_2 \cos ^2(\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(28)

Hence, from Eq. (28) in the context of expression (7), we obtain

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_1 \sin \left( -a_2 c_2 t+a_2 y+a_4\right) \nonumber \\&\quad +{\mathcal {H}}_2 \cos ^2\left( -a_2 c_2 t+a_2 y+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(29)

7 3. The familiar exponential representation:

Setting the parameters to \([k_1,k_2,k_3,k_4]=[2,2,2,2]\) and \([m_1,m_2,m_3,m_4]=[2/5,2/5,0,0]\), Eq. (6) transforms into the standard form of the exponential function

$$\begin{aligned} U(\vartheta )=\exp \left( \frac{2 \vartheta }{5}\right) . \end{aligned}$$
(30)

By replacing Eq. (30) with Eq. (9), the structure of \(S(\vartheta )\) can be deduced as:

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_0+\frac{5}{2} \exp \left( {\frac{2 \vartheta }{5}}\right) {\mathcal {H}}_1+\frac{625}{16} \exp \left( {\frac{4 \vartheta }{5}}\right) {\mathcal {H}}_2 \nonumber \\&\quad +\frac{2}{5} \exp \left( {-\frac{2 \vartheta }{5}}\right) {\mathcal {P}}_1+\frac{16}{625} \exp \left( {-\frac{4 \vartheta }{5}}\right) {\mathcal {P}}_2. \end{aligned}$$
(31)

Case 3.1:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (31), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )=\frac{5}{2} \exp \left( {\frac{2 \vartheta }{5}}\right) {\mathcal {H}}_1+{\mathcal {H}}_0. \end{aligned}$$
(32)

Equations (32) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned} R(x,y,t)&=\frac{5}{2} {\mathcal {H}}_1 \exp \Bigg (\frac{2}{5} \big (a_1 x+a_2 y\nonumber \\&\quad -a_2 c_2 t+a_4\big )\Bigg )+{\mathcal {H}}_0. \end{aligned}$$
(33)

Case 3.2:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (31), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_0+\frac{5}{2} \exp \left( {\frac{2 \vartheta }{5}}\right) {\mathcal {H}}_1+\frac{625}{16} \exp \left( {\frac{4\vartheta }{5}}\right) {\mathcal {H}}_2 \nonumber \\&\quad +\frac{2}{5} \exp \left( -{\frac{2 \vartheta }{5}}\right) {\mathcal {P}}_1. \end{aligned}$$
(34)

Equations (34) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned}&R (x,y,t)\nonumber \\&\quad =\frac{2}{5} {\mathcal {P}}_1 \exp \left( \frac{-2}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\qquad +\frac{5}{2} {\mathcal {H}}_1 \exp \left( {\frac{2}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) }\right) \nonumber \\&\qquad +\frac{625}{16} {\mathcal {H}}_2 \exp \left( {\frac{4}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) }\right) \nonumber \\&\qquad +{\mathcal {H}}_0. \end{aligned}$$
(35)

Case 3.3:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2\ne 0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (31), we can deduce a solution for Eq. (8) as

$$\begin{aligned}&S(\vartheta )\nonumber \\&\quad ={\mathcal {H}}_0+\frac{5}{2} \exp \left( {\frac{2 \vartheta }{5}}\right) {\mathcal {H}}_1+\frac{625}{16} \exp \left( {\frac{4\vartheta }{5}}\right) {\mathcal {H}}_2\nonumber \\&\qquad +\frac{2}{5} \exp \left( -{\frac{2 \vartheta }{5}}\right) {\mathcal {P}}_1+\frac{16}{625} \exp \left( -{\frac{4\vartheta }{5}}\right) {\mathcal {P}}_2. \end{aligned}$$
(36)

Equations (36) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned}&R (x,y,t)\nonumber \\&\quad =\frac{2}{5} {\mathcal {P}}_1 \exp \left( \frac{-2}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\qquad +\frac{16}{625} {\mathcal {P}}_2 \exp \left( \frac{-4}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\qquad +\frac{5}{2} {\mathcal {H}}_1 \exp \left( {\frac{2}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) }\right) \nonumber \\&\qquad +\frac{625}{16} {\mathcal {H}}_2 \exp \left( {\frac{4}{5} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) }\right) +{\mathcal {H}}_0. \end{aligned}$$
(37)

Case 3.4:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0; {\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_1=0;a_3=-a_2 c_2. \end{aligned}$$

Utilizing the provided set of constant in Eq. (31), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )=\frac{5}{2} \exp \left( {\frac{2 \vartheta }{5}}\right) {\mathcal {H}}_1+\frac{625}{16} \exp \left( {\frac{4 \vartheta }{5}}\right) {\mathcal {H}}_2+{\mathcal {H}}_0. \end{aligned}$$
(38)

Equations (38) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned} R(x,y,t)&=\frac{5}{2} {\mathcal {H}}_1 \exp \left( {\frac{2}{5} \left( -a_2 c_2 t+a_2 y+a_4\right) }\right) \nonumber \\&\quad +\frac{625}{16} {\mathcal {H}}_2 \exp \left( {\frac{4}{5} \left( -a_2 c_2 t+a_2 y+a_4\right) }\right) \nonumber \\&\quad +{\mathcal {H}}_0. \end{aligned}$$
(39)

8 4. The familiar cosine hyperbolic representation:

Setting the parameters to \([k_1,k_2,k_3,k_4]=[i,i,i,i]\) and \([m_1,m_2,m_3,m_4]=[1,-1,0,0]\), Eq. (6) transforms into the standard form of the cosine hyperbolic function

$$\begin{aligned} U(\vartheta )=\cosh (\vartheta ). \end{aligned}$$
(40)

Plugging Eq. (40) into Eq. (9), we can derive the expression for \(S(\vartheta )\) as:

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_1 \sinh (\vartheta )+{\mathcal {H}}_2 \cosh ^2(\vartheta )\nonumber \\&\quad +{\mathcal {H}}_0+{\mathcal {P}}_1 \text {csch}(\vartheta )+{\mathcal {P}}_2 \text {sech}^2(\vartheta ). \end{aligned}$$
(41)

Case 4.1:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

By inserting the given constants into Eq. (41), we can derive the solution of Eq. (8) as:

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \sinh (\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(42)

Therefore, the soliton solution for the Hirota Bilinear equation can be found through Eqs. (42) and (7):

$$\begin{aligned} R(x,y,t)={\mathcal {H}}_1 \sinh \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(43)

Case 4.2:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

By inserting the given constants into Eq. (41), we can derive the solution of Eq. (8) as:

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_0+{\mathcal {H}}_1 \sinh (\vartheta )+{\mathcal {H}}_2 \cosh ^2(\vartheta )\nonumber \\&\quad +{\mathcal {P}}_1 \text {csch}(\vartheta ). \end{aligned}$$
(44)

Therefore, the soliton solution for the Hirota Bilinear equation can be found through Eqs. (44) and (7):

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_1 \sinh \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\ {}&\quad +{\mathcal {H}}_2 \cosh ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\ {}&\quad +{\mathcal {P}}_1 \text {csch}\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(45)

Case 4.3:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2\ne 0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

By inserting the given constants into Eq. (41), we can derive the solution of Eq. (8) as:

$$\begin{aligned} S(\vartheta )&={\mathcal {H}}_1 \sinh (\vartheta )+{\mathcal {H}}_2 \cosh ^2(\vartheta )\nonumber \\&\quad +{\mathcal {P}}_1 \text {csch}(\vartheta )+{\mathcal {P}}_2 \text {sech}^2(\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(46)

Therefore, the soliton solution for the Hirota Bilinear equation can be found through Eqs. (46) and (7):

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_1 \sinh \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {H}}_2 \cosh ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {P}}_1 \text {csch}\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {P}}_2 \text {sech}^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(47)
Fig. 5
figure 5

Visualization of Eq. (47): real, imaginary and absolute components

Full size image

Case 4.4:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_1=0;a_3=-a_2 c_2. \end{aligned}$$

By inserting the given constants into Eq. (41), we can derive the solution of Eq. (8) as:

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \sinh (\vartheta )+{\mathcal {H}}_2 \cosh ^2(\vartheta )+{\mathcal {H}}_0. \end{aligned}$$
(48)

Therefore, the soliton solution for the Hirota Bilinear equation can be found through Eqs. (48) and (7):

$$\begin{aligned} R(x,y,t)&={\mathcal {H}}_1 \sinh \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \nonumber \\&\quad +{\mathcal {H}}_2 \cosh ^2\left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) +{\mathcal {H}}_0. \end{aligned}$$
(49)

9 5. The familiar sine hyperbolic representation:

Setting the parameters to \([k_1,k_2,k_3,k_4]=[2i,-2i,4i,4i]\) and \([m_1,m_2,m_3,m_4]=[1/2,-1/2,0,0]\), Eq. (6) transforms into the standard form of the sine hyperbolic function

$$\begin{aligned} U(\vartheta )=\frac{1}{2}{\sinh }(\vartheta /2 ). \end{aligned}$$
(50)

Upon inserting Eq. (50) into Eq. (9), the expression for \(S(\vartheta )\) becomes:

$$\begin{aligned} S(\vartheta )&=4 {\mathcal {H}}_2 \sinh ^2\left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_1 \cosh \left( \frac{\vartheta }{2}\right) \nonumber \\&\quad +{\mathcal {H}}_0+\frac{1}{4} {\mathcal {P}}_2 \text {csch}^2\left( \frac{\vartheta }{2}\right) +{\mathcal {P}}_1 \text {sech}\left( \frac{\vartheta }{2}\right) . \end{aligned}$$
(51)

Case 5.1:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (51), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )={\mathcal {H}}_1 \cosh \left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_0. \end{aligned}$$
(52)

Equations (52) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned}&R(x,y,t)\nonumber \\&\quad ={\mathcal {H}}_1 \cosh \left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) +{\mathcal {H}}_0. \end{aligned}$$
(53)

Case 5.2:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0;\\&{\mathcal {P}}_2=0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (51), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )&=4 {\mathcal {H}}_2 \sinh ^2\left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_1 \cosh \left( \frac{\vartheta }{2}\right) \nonumber \\&\quad +{\mathcal {H}}_0+{\mathcal {P}}_1 \text {sech}\left( \frac{\vartheta }{2}\right) . \end{aligned}$$
(54)

Equations (54) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned}&R(x,y,t)\nonumber \\&\quad =4 {\mathcal {H}}_2 \sinh ^2\left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\quad \quad +{\mathcal {H}}_1 \cosh \left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\quad \quad +{\mathcal {P}}_1 \text {sech}\left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) +{\mathcal {H}}_0. \end{aligned}$$
(55)

Case 5.3:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1\ne 0; \\&{\mathcal {P}}_2\ne 0;a_3=-a_2 c_2;c_1=0. \end{aligned}$$

Utilizing the provided set of constant in Eq. (51), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )&=4 {\mathcal {H}}_2 \sinh ^2\left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_1 \cosh \left( \frac{\vartheta }{2}\right) \nonumber \\&\quad +{\mathcal {H}}_0+\frac{1}{4} {\mathcal {P}}_2 \text {csch}^2\left( \frac{\vartheta }{2}\right) +{\mathcal {P}}_1 \text {sech}\left( \frac{\vartheta }{2}\right) . \end{aligned}$$
(56)

Equations (56) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned}&R(x,y,t)\nonumber \\&\quad =4 {\mathcal {H}}_2 \sinh ^2\left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\quad \quad +{\mathcal {H}}_1 \cosh \left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\quad \quad +\frac{1}{4} {\mathcal {P}}_2 \text {csch}^2\left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) \nonumber \\&\quad \quad +{\mathcal {P}}_1 \text {sech}\left( \frac{1}{2} \left( a_1 x+a_2 y-a_2 c_2 t+a_4\right) \right) +{\mathcal {H}}_0. \end{aligned}$$
(57)

Case 5.4:

$$\begin{aligned}&{\mathcal {H}}_0\ne 0;{\mathcal {H}}_1\ne 0;{\mathcal {H}}_2\ne 0;{\mathcal {P}}_1=0;\\&{\mathcal {P}}_2=0;a_1=0;a_3=-a_2 c_2. \end{aligned}$$

Utilizing the provided set of constant in Eq. (51), we can deduce a solution for Eq. (8) as

$$\begin{aligned} S(\vartheta )=4 {\mathcal {H}}_2 \sinh ^2\left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_1 \cosh \left( \frac{\vartheta }{2}\right) +{\mathcal {H}}_0. \end{aligned}$$
(58)

Equations (58) and (7) yield the soliton solution for the Hirota Bilinear equation:

$$\begin{aligned} R(x,y,t)&=4 {\mathcal {H}}_2 \sinh ^2\left( \frac{1}{2} \left( -a_2 c_2 t+a_2 y+a_4\right) \right) \nonumber \\&\quad +{\mathcal {H}}_1 \cosh \left( \frac{1}{2} \left( -a_2 c_2 t+a_2 y+a_4\right) \right) \nonumber \\&\quad +{\mathcal {H}}_0. \end{aligned}$$
(59)

10 Physical discussion

To deepen our comprehension of the obtained solutions, we have provided visual representation through 3D plots and corresponding contour plots. These graphical illustrations offer insights into the behavior of the solutions, showcasing their variations based on carefully chosen parameters.

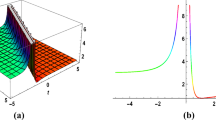
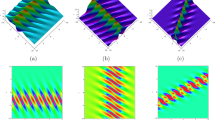
  • In Fig. 1, we depict the lumps corresponding to the real and imaginary components of the solution (15) for the choice of parameters (a)–(d) \(a_1=2;a_2=i;a_4=1;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=0.2 i;\) at \(t=0.1\) (b)–(e) \(a_1=2;a_2=i;a_4=3;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=2;\) at \(t=0.1\) respectively, while the absolute part represents the multi-solitons for (c)–(f) \(a_1=2;a_2=5 i;a_4=3 i;c_2=3;{\mathcal {H}}_0=0.25;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=2 i;\) at \(t=0.02\).

  • The real and imaginary parts of the solution (17) are visualized as lumps in Fig. (2). The absolute part exhibits the multi-soliton profile with different parameter configurations: (a)–(d) \(a_1=2;a_2=2 i;a_4=1;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=2;{\mathcal {P}}_2=2 i;\) at \(t=0.01\) (b)–(e) \(a_1=2;a_2=2 i;a_4=1;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=2;{\mathcal {P}}_2=1;\) at \(t=0.01\) and (c)–(f) \(a_1=3 i;a_2=2;a_4=i;c_2=0.5;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=2 i;{\mathcal {P}}_2=2;\) at \(t=0.03\).

  • The lumps corresponding to the real and imaginary parts of the solution (25) are shown in Fig. (3). The absolute part presents a soliton profile with different parameter values: (a)–(d) \(a_1=2;a_2=i;a_4=0.3;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3 i;\) at \(t=1\) (b)–(e) \(a_1=2;a_2=i;a_4=0.3;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3;\) at \(t=2\) and (c)–(f) \(a_1=2;a_2=i;a_4=0.3;c_2=2 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3;\) at \(t=2\). Here in this figure, we have study the behavior of the solution for full plot range and with no plot range that represent the different dynamics.

  • In Fig. (4), we observe the lumps representing the real and imaginary parts of the solution (27). The absolute part demonstrates a multi-soliton profile for the following parameter choices: (a)–(d) \(a_1=2.2;a_2=3 i;a_4=1.25;c_2=3 i;{\mathcal {H}}_0=0.02;{\mathcal {H}}_1=0.023;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3 i;{\mathcal {P}}_2=2 i;\) at \(t=0.01\) (b)-(e) \(a_1=2;a_2=3 i;a_4=0.4 i;c_2=5;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=7 i;{\mathcal {P}}_2=2 i;\) at \(t=0.03\) and (c)-(f) \(a_1=2;a_2=3 i;a_4=0.4 i;c_2=5 i;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=7;{\mathcal {P}}_2=2 i;\) at \(t=0.3\).

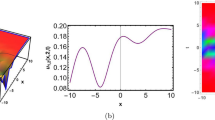
  • Figure (5) displays the lumps for the real component and interaction of lumps and peakon for the imaginary component of the solution (49). The absolute part shows a multi-soliton profile under the parameter configurations: (a)–(d) \(a_1=2;a_2=2 i;a_4=0.02;c_2=3;{\mathcal {H}}_0=2;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3 i;{\mathcal {P}}_2=2.1 i;\) at \(t=1.5\) (b)–(e) \(a_1=2;a_2=2 i;a_4=0.7;c_2=5;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3 i;{\mathcal {P}}_2=2.1 i;\) at \(t=1.5\) and (c)–(f) \(a_1=2;a_2=2 i;a_4=0.7;c_2=5;{\mathcal {H}}_0=0;{\mathcal {H}}_1=0;{\mathcal {H}}_2=0;{\mathcal {P}}_1=3 i;{\mathcal {P}}_2=2.1 i;\) at \(t=1.5\).

11 Conclusion

In conclusion, we have presented a novel method for solving NLPDEs, specifically focusing on the (2 + 1)-dimension Hirota bilinear equation. We have designated the approach as the multivariate generalized exponential rational integral function. We applied this method to the Hirota bilinear equation, demonstrating its effectiveness in finding solutions. The obtained solutions were visualized through 3D and contour plots, providing a comprehensive understanding of the behavior of the solutions. Overall, our proposed method offers a systematic and powerful approach to tackle NLPDEs, particularly showcasing its applicability to the Hirota bilinear equation. The accuracy and efficiency of our method were verified through computational software Mathematica, validating its potential as a valuable tool in the domain of nonlinear differential equations. Future work could involve extending the proposed method to other classes of nonlinear partial differential equations, exploring its applicability and efficiency in diverse mathematical contexts. Additionally, further research could focus on developing numerical techniques for real-time simulations and exploring potential applications in physical systems or interdisciplinary fields. Validating the method on a broader range of benchmark problems and comparing its performance with existing approaches would contribute to establishing its robustness and versatility.