Introduction

The evolution of optical solitons has become much important and valuable in the area of engineering and applied sciences. There are many methods that have been effectively implemented to study the dynamics behavior of optical solitons. In recent years, several efficient methods including tanh-coth method [1, 2], extended tanh method [3, 4], Hirota’s direct method [5, 6], extended direct algebraic method [7, 8], sine-cosine method [9, 10], exp\([-\phi (\xi )]\)-expansion method [11, 12], extended trial approach method [13, 14], a new auxiliary equation method [15, 16], generalized Bernoulli sub-ODE method [17, 18], Jacobi elliptic ansatz method [19, 20], sub equation method [21, 22], functional variable method [23, 24], Kudryashov’s method [25], generalized tanh method [26], generalized unified method (GUM) [27, 28], modified Kudryashov method and improved Riccati sub-equation method [29, 30], hyperbolic and exponential ansatz methods [31], \(\mathrm{exp}_a\)-function methods [32], ansatz method [33], unified and \((G'/G)\)-expansion method [34], \((G'/G,1/G)\)-expansion method [35], generalized Kudryashov technique [36], Lie symmetry analysis method [37], theory of Picard-Lindelof [38], Adomian decomposition method [39], sine-Gordon expansion method (SGEM) and ansatz approach [40], a suitable ansatz and Hirota bilinear approach [41], the invariant subspace method [42], Hirota’s bilinear form [43], projective Riccati equation and the modified F-Expansion methods [44] and many more have been established for efficient solutions of NLEEs .

These methods have significant position in several fields of engineering and science such as nonlinear fibers optics, shallow water wave propagation, fluid mechanics, plasma physics, computer science, solid-state physics, biology, heat, quantum mechanics, etc. Recently, a lot of work has been done on of cubic-quartic (CQ) optical solitons using different techniques [45,46,47,48,49,50,51]. Before this, it was only the idea of pure quartic solitons [52, 53]. A few results are found in literature to discuss CQ solitons in birefringent fibers [54, 55]. Therefore, our work is a follow-up to the previously reported results. In this paper, we implement the new EDAM [56,57,58] to secure CQ optical soliton solutions in birefringent fibers having two types of nonlinear refractive index. First is parabolic law and second is non-local law.

The remaining part of paper is organized as: In “Parabolic Law” section, the solutions of parabolic law by new EDAM are presented. The solutions of the nonlocal law are derived in “Non-local Law” section. Conclusion of the paper is given in “Results and Discussion” section.

Parabolic Law

The CQ-NLSE equation in birefringent fibers with parabolic law [54, 55] is

$$\begin{aligned}&\iota v_t+\iota a_1 v_{xxx}+b_1 v_{xxxx}+(c_1 ~|v|^2+d_1~|u|^2)v+(e_1|v|^4+g_1|v|^2|u|^2+h_1|u|^4)v=0,\nonumber \\&\iota u_t+\iota a_2 u_{xxx}+b_2 u_{xxxx}+(c_2 ~|u|^2+d_2~|v|^2)u+(e_2|u|^4+g_2|u|^2|v|^2+h_2|v|^4)u=0,\nonumber \\ \end{aligned}$$
(1)

with constants \(c_j,~ e_j\) and \(d_j,~ g_j,~ h_j\), \((j=1, 2)\) which represent SPM and XPM, respectively. Also, the effect of four-wave mixing (4WM) is rejected.

$$\begin{aligned} v(x,t)= & {} U_1(\xi )e^{\iota \phi _1(x,t)},\nonumber \\ u(x,t)= & {} U_2(\xi )e^{\iota \phi _2(x,t)}. \end{aligned}$$
(2)

In (2), \(U_j(\xi )\) is the amplitude component and the velocity is

$$\begin{aligned} \xi =u(x-ct), \end{aligned}$$
(3)

while the phase component is as

$$\begin{aligned} \phi _j(x,t)=-k_j x+\omega _j t+\theta _j, \end{aligned}$$
(4)

where the parameters \(~ \theta _j,~k_j,~ w_j\) correspond to the wave number, frequency and phase constant. If (2) is inserted into (1), we get the equation

$$\begin{aligned} b_jU_j^{(4)}+(3 a_j k_j-6 b_j k_j^2)U''_j-(w_j+a_j k_j^3-b_j k_j^4)U_j\nonumber \\ +(c_j+d_j)U_j^3+(e_j+g_j+h_j)U_j^5=0, \end{aligned}$$
(5)

which emerged from the real equation along with \(U_{{\tilde{j}}}=U_j\).

Application of the New EDAM

In this section, we apply the new EDAM [56,57,58] to find the exact solutions of CQ-NLSE equation in birefringent fibers with parabolic law. Consider (5) has a solution of following form

$$\begin{aligned} U_j(\xi )=\sum ^{N}_{i=0}F_i \Phi ^i(\xi ), \end{aligned}$$
(6)

where \(F_i~(0\le i\le N)\) are constants. Utilizing balancing principal in (5), presents \(N=1\), so (6) reduces to

$$\begin{aligned} U_j=F_0+F_1\Phi (\xi ), \end{aligned}$$
(7)

where \(F_0\) and \(F_1\) are constants to be found. Substituting (7) into (5) and setting the coefficients of each polynomial of \(\Phi (\xi )\) to zero, we obtain a set of algebraic equations in \(F_0, ~F_1,~\Theta , ~\omega ~, e~,and ~c\).

Solving the system of equations, we obtain

$$\begin{aligned}&F_0=F_0,~~~F_1=F_1,\nonumber \\&\Theta =\frac{2\varsigma ~ F_0}{F_1},\nonumber \\&e_j=g_j-h_j-\frac{24~ b_j~ \varsigma ^4 ln(A)^4}{F_1^4},\nonumber \\&c_j=\frac{40~ b_j~ \varsigma ^4 ln(A)^4~ F_0^2-F_1^2(2 \varsigma ^2 ln(A)^2(3k_j(a_j-2b_j~k_j)+20~ b_j~\alpha \varsigma ln(A)^2)+d_j~F_1^2)}{F_1^4},\nonumber \\&\omega _j= \frac{1}{F_1^4}(16~ b_j ~\varsigma ^4 ln(A)^4 ~F_0^2-2 \varsigma ^2 ln(A)^2(3k_j(a_j-2b_j~k_j)+16 b_j~\alpha \varsigma ln(A)^2)F_0^2~F_1^2\nonumber \\&\quad +(k_j^3(-a_j+b_j~k_j)+6k_j(a_j-2~b_j~k_j)~\alpha ~\varsigma ln(A)^2+16b_j~\alpha ^2~\varsigma ^2~ln(A)^4)~F_1^4). \end{aligned}$$
(8)

From Eqns. (3), (4), (5) and (8) we acquire following novel families of exact traveling wave solutions of the model.

Family 1: When \( \Theta ^2-4\alpha \varsigma < 0\) and \(\varsigma \ne 0\), then the solutions are as follows

$$\begin{aligned} v_1(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times e^{\iota (-k_1x+\omega _1 t+\theta _1)},\nonumber \\ u_1(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_2(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_2(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_3(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&sec_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_3(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad sec_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_4(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }cot_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csc_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_4(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }cot_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csc_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_5(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma }}{4})\xi )-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4})\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}).\nonumber \\ u_5(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma }}{4})\xi )-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$
(9)

Family 2: When \( \Theta ^2-4\alpha \varsigma > 0\) and \(\varsigma \ne 0\), then the solutions are as follows

$$\begin{aligned} v_6(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}), \nonumber \\ u_6(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg ) \nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_7(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_7(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \end{aligned}$$
(10)
$$\begin{aligned} v_8(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \iota \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad sech_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_8(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \iota \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad sech_A(\sqrt{ (\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \nonumber \\ v_9(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } coth_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csch_A(\sqrt{(\Theta ^2-4 \alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_9(x,t)= & {} F_0+F_1\bigg ({2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } coth_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csch_A(\sqrt{ (\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \nonumber \\ v_{10}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma }}{4})\xi )-\frac{\sqrt{ (\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4})\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}).\nonumber \\ u_{10}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tanh_A(\frac{\sqrt{\Theta ^2-4\alpha \varsigma }}{4})\xi )-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad coth_A(\frac{(\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4})\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$
(11)

Family 3:When \(\alpha \varsigma >0 ~ and~ \Theta =0\), then the solutions are as follows

$$\begin{aligned} v_{11}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }} tan_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1t+\theta _1)}),\nonumber \\ u_{11}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }} tan_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{12}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{12}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{13}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }}tan_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}sec_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{13}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }}tan_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}sec_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{14}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{14}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1t+\theta _2)}),\nonumber \\ v_{15}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(\sqrt{\frac{\alpha }{\varsigma }}tan_{A}(\frac{\sqrt{\alpha \varsigma }}{2}\xi )-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\frac{\sqrt{\alpha \varsigma }}{2})\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}).\nonumber \\ u_{15}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(\sqrt{\frac{\alpha }{\varsigma }}tan_A(\frac{\sqrt{\alpha \varsigma }}{2}\xi ) -\sqrt{\frac{\alpha }{\varsigma }}cot_A(\frac{\sqrt{\alpha \varsigma }}{2})\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$
(12)

Family 4:When \(\alpha \varsigma <0 ~ and ~\Theta =0\), then the solutions are as follows

$$\begin{aligned} v_{16}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{16}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{17}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}coth_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{17}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}coth_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{18}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}cot_A(2\sqrt{-\alpha \varsigma }\xi )\pm \iota \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{-\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1t+\theta _1)}),\nonumber \\ u_{18}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \iota \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{-\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{19}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}cot_A(2\sqrt{-\alpha \varsigma }\xi ) \pm \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{-\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\nonumber \\ u_{19}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}cot_A(2\sqrt{-\alpha \varsigma }\xi )\pm \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{-\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\nonumber \\ v_{20}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )+\sqrt{-\frac{\alpha }{\varsigma }} coth_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}).\nonumber \\ u_{20}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )+\sqrt{-\frac{\alpha }{\varsigma }} coth_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$
(13)

Family 5:When \(\Theta =0 ~ and~ \varsigma =\alpha \), then the solutions are as follows

$$\begin{aligned} v_{21}(x,t)= & {} F_0+F_1\bigg (tan_A(\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1t+\theta _1)}), \\ u_{21}(x,t)= & {} F_0+F_1\bigg (tan_A(\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \\ v_{22}(x,t)= & {} F_0+F_1\bigg (-cot_A(\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}), \\ u_{22}(x,t)= & {} F_0+F_1\bigg (-cot_A(\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \\ v_{23}(x,t)= & {} F_0+F_1\bigg (tan_A(2\alpha \xi )\pm \sqrt{pq}~sec_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}), \\ u_{23}(x,t)= & {} F_0+F_1\bigg (tan_A(2\alpha \xi )\pm \sqrt{pq}~sec_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{24}(x,t)= & {} F_0+F_1\bigg (-cot_A(2\alpha \xi )\pm \sqrt{pq}~csc_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\\ u_{24}(x,t)= & {} F_0+F_1\bigg (-cot_A(2\alpha \xi )\pm \sqrt{pq}~csc_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{25}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(tan_A(\frac{\alpha }{2}\xi )-cot_A(\frac{\alpha }{2}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1}).\\ u_{25}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(tan_A(\frac{\alpha }{2}\xi )-cot_A(\frac{\alpha }{2}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 6:When \(\Theta =0 ~ and~ \varsigma =-\alpha \) then the solutions are as follows

$$\begin{aligned} v_{26}(x,t)= & {} F_0+F_1\bigg (-tanh_A(\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1}),\\ u_{26}(x,t)= & {} F_0+F_1\bigg (-tanh_A(\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{27}(x,t)= & {} F_0+F_1\bigg (-coth_A(\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1}),\\ u_{27}(x,t)= & {} F_0+F_1\bigg (-coth_A(\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{28}(x,t)= & {} F_0+F_1\bigg (-tanh_A(2\alpha \xi )\pm \iota \sqrt{pq}~sech_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\\ u_{28}(x,t)= & {} F_0+F_1\bigg (-tanh_A(2\alpha \xi )\pm \iota \sqrt{pq}~sech_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{29}(x,t)= & {} F_0+F_1\bigg (-coth_A(2\alpha \xi )\pm \sqrt{pq}~csch_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}),\\ u_{29}(x,t)= & {} F_0+F_1\bigg (-coth_A(2\alpha \xi )\pm \sqrt{pq}~csch_A(2\alpha \xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}),\\ v_{30}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(tanh_A(\frac{\alpha }{2}\xi )+coth_A(\frac{\alpha }{2}\xi )\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}).\\ u_{30}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(tanh_A(\frac{\alpha }{2}\xi )+coth_A(\frac{\alpha }{2}\xi )\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 7:When \(\Theta ^2=4\alpha \varsigma \),

$$\begin{aligned} v_{31}(x,t)= & {} F_0+F_1\bigg (\frac{-2\alpha (\Theta \xi ln(A)+2)}{\Theta ^2\xi ln (A)}\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}). \\ u_{31}(x,t)= & {} F_0+F_1\bigg (\frac{-2\alpha (\Theta \xi ln (A)+2)}{\Theta ^2\xi ln (A)}\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 8:When \(\Theta =k,~\alpha =mk ~(m\ne 0 )~and ~\varsigma =0\), then the solutions are as follows

$$\begin{aligned} v_{32}(x,t)= & {} F_0+F_1\bigg (A^{k\xi }-m\bigg )\times (e^{\iota (-k_1x+\omega _2 t+\theta _1)}). \\ u_{32}(x,t)= & {} F_0+F_1\bigg (A^{k\xi }-m\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 9:When \(\Theta =\varsigma =0\),

$$\begin{aligned} v_{33}(x,t)= & {} F_0+F_1\bigg (\alpha \xi ln (A)\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}). \\ u_{33}(x,t)= & {} F_0+F_1\bigg (\alpha \xi ln (A))\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 10:When \(\Theta =\alpha =0\),

$$\begin{aligned} v_{34}(x,t)= & {} F_0+F_1 \bigg (\frac{-1}{\varsigma \xi ln (A)}\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}). \\ u_{34}(x,t)= & {} F_0+F_1 \bigg (\frac{-1}{\varsigma \xi ln (A)}\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 11::When \(\alpha =0~ and~ \Theta \ne 0\),

$$\begin{aligned} v_{35}(x,t)= & {} F_0+F_1\bigg (-\frac{p\Theta }{\varsigma (cosh_A(\Theta \xi )-sinh_A(\Theta \xi +p))}\bigg ) \times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}), \\ u_{35}(x,t)= & {} F_0+F_1\bigg (-\frac{p\Theta }{\varsigma (cosh_A(\Theta \xi )-sinh_A(\Theta \xi +p))}\bigg ) \times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}), \\ v_{36}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta (sinh_A(\Theta \xi )+cosh_A(\Theta \xi ))}{\varsigma (sinh_A(\Theta \xi )+cosh_A(\Theta \xi +q))}\bigg ) \times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}). \\ u_{36}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta (sinh_A(\Theta \xi )+cosh_A(\Theta \xi ))}{\varsigma (sinh_A(\Theta \xi )+cosh_A(\Theta \xi +q))}\bigg ) \times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Family 12:When \(\Theta =k,~\varsigma =mk, ~(m\ne 0)~ and~\alpha =0\),

$$\begin{aligned} v_{37}(x,t)= & {} F_0+F_1\bigg (\frac{pA^{k\xi }}{q-\mp A^{k\xi }}\bigg )\times (e^{\iota (-k_1x+\omega _1 t+\theta _1)}). \\ u_{37}(x,t)= & {} F_0+F_1g\big (\frac{pA^{k\xi }}{q-\mp A^{k\xi }}\bigg )\times (e^{\iota (-k_2x+\omega _2 t+\theta _2)}). \end{aligned}$$

Remark

For (\(j=1,2\)),

$$\begin{aligned} \omega _j= & {} \frac{1}{F_1^4}(16~ b_j ~\varsigma ^4 ln(A)^4 ~F_0^2-2 \varsigma ^2 ln(A)^2(3k_j(a_j-2b_j~k_j)+16 b_j~\alpha \varsigma ln(A)^2)F_0^2~F_1^2\\&\quad +(k_j^3(-a_j+b_j~k_j)+6k_j(a_j-2~b_j~k_j)~\alpha ~\varsigma ln(A)^2+16b_j~\alpha ^2~\varsigma ^2~ln(A)^4)~F_1^4). \end{aligned}$$

Non-local Law

The CQ-NLSE equation in birefringent fibers with non-local nonlinearity [54, 55] is

$$\begin{aligned}&\iota v_t+\iota a_1 v_{xxx}+b_1 v_{xxxx}+(c_1 ~(|v|^2)_{xx}+d_1~(|u|^2)_{xx})v=0,\nonumber \\&\iota u_t+\iota a_2 u_{xxx}+b_2 u_{xxxx}+(c_2 ~(|u|^2)_{xx}+d_2~(|v|^2)_{xx})u=0, \end{aligned}$$
(14)

with constants \(c_j\) and \(d_j\) which represent SPM and XPM.

If Eq. (2) is used into Eq. (14), we get

$$\begin{aligned}&b_jU_j^{(4)}+(3a_jk_j-6b_jk_j^2)U''_j-(w_j+a_jk_j^3-b_jk_j^4)U_j\nonumber \\&\quad +2(c_j+d_j)U_j(U'_j)^2+2(c_j+d_j)U_j^2U''_j=0, \end{aligned}$$
(15)

which comes out from the real part equation along with \(U_{{\tilde{j}}}=U_j\).

Application of the New EDAM

Here, we apply the new EDAM method [56,57,58] to find the exact solutions of CQ-NLSE equation in birefringent fibers with non-local law. Consider (15) has a solution of following form

$$\begin{aligned} U_j(\xi )=\sum ^{N}_{i=0}F_i \Phi ^i(\xi ), \end{aligned}$$
(16)

where \(F_i~(0\le i\le N)\) are constants.

Utilizing balancing rule in Eq. (15), yields \(N=1\), so Eq. (16) reduces to

$$\begin{aligned} U_j=F_0+F_1\Phi (\xi ), \end{aligned}$$
(17)

Where \(F_0\) and \(F_1\) are constants to be found. Substituting Eq. (17) into Eq. (15) and collecting all terms of same order of \(\Phi (\xi )\) together. Comparing the coefficient of each polynomial of \(\Phi (\xi )\) to zero, yield a set of algebraic equations in \(F_0,~F_1,~\alpha ~,~\varsigma ~,b,~c~and~\omega \).

Solving the system of equations, gives

$$\begin{aligned}&F_0=F_0,~~~~F_1=F_1, \nonumber \\&\alpha =\frac{\Theta ~F_0}{F_1},~~~\varsigma =\frac{\Theta ~ F_1}{2~F_0}, \nonumber \\&b_j=\frac{3 a_j ~k_j}{6k_j^2-\Theta ^2 ln(A)^2}, \nonumber \\&c_j=\frac{-3 a_j~k_j~ \Theta ^2 ln(A)^2+(-6 d_j~ k_j^2+d_j~\Theta ^2 ln(A)^2)F_0^2}{(6k_j^2-\Theta ^2 ln(A)^2) F_0^2},\nonumber \\&\omega _j=\frac{a_j ~k_j^2(3(-2+k_j)k_j^2+\Theta ^2 ln(A)^2)}{6k_j^2-\Theta ^2 ln(A)^2}. \end{aligned}$$
(18)

The following families of solutions of Eq. (14) corresponding to Eqs. (15), (16), (17) and (18) are attained.

Family 1: When \( \Theta ^2-4\alpha \varsigma < 0\) and \(\varsigma \ne 0\), then the solutions are as follows

$$\begin{aligned} v_1(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_1(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_2(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_2(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma } cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_3(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad sec_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_3(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tan_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad sec_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_4(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }cot_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csc_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_4(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }cot_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\pm \frac{\sqrt{-pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csc_A(\sqrt{-(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_5(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma }}{4})\xi )-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4})\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\nonumber \\ u_5(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }+\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tan_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma }}{4}\xi )-\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad cot_A(\frac{\sqrt{-(\Theta ^2-4\alpha \varsigma )}}{4}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$
(19)

Family 2: When \( \Theta ^2-4\alpha \varsigma > 0.\) and \(\varsigma \ne 0\), then the solutions are as follows

$$\begin{aligned} v_6(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_6(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_7(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_7(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_8(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \iota \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&sech_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_8(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }tanh_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \iota \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&sech_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_9(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csch_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_9(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }coth_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi ) \pm \frac{\sqrt{pq(\Theta ^2-4\alpha \varsigma )}}{2\varsigma }\nonumber \\&\quad csch_A(\sqrt{(\Theta ^2-4\alpha \varsigma )}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{10}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4}\xi )-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4}\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{10}(x,t)= & {} F_0+F_1\bigg (-\frac{\Theta }{2\varsigma }-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }tanh_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4}\xi )-\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4\varsigma }\nonumber \\&\quad coth_A(\frac{\sqrt{(\Theta ^2-4\alpha \varsigma )}}{4}\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 3:When \(\alpha \varsigma >0 ~ and~ \Theta =0\), then the solutions are as follows pagination

$$\begin{aligned} v_{11}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }} tan_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{11}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }} tan_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{12}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{12}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\sqrt{\alpha \varsigma }\xi )\bigg )\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{13}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }}tan_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{ pq\frac{{\alpha }}{\varsigma }}sec_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\quad \times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{13}(x,t)= & {} F_0+F_1\bigg (\sqrt{\frac{\alpha }{\varsigma }}tan_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{ pq\frac{{\alpha }}{\varsigma }}sec_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{14}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\quad \times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{14}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{15}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(\sqrt{\frac{\alpha }{\varsigma }}tan_A(\frac{\sqrt{\alpha \varsigma }}{2}\xi )-\sqrt{\frac{\alpha }{\varsigma }}cot_A(\frac{\sqrt{\alpha \varsigma }}{2})\xi )\bigg ) \nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\nonumber \\ u_{15}(x,t)= & {} F_0+F_1\bigg (\frac{1}{2}(\sqrt{\frac{\alpha }{\varsigma }}tan_A(\frac{\sqrt{\alpha \varsigma }}{2}\xi ) -\sqrt{\frac{\alpha }{\varsigma }}cot_A(\frac{\sqrt{\alpha \varsigma }}{2})\xi )\bigg ) \nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 4:When \(\alpha \varsigma <0 ~ and ~\Theta =0\), then the solutions are as follows

$$\begin{aligned} v_{16}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{16}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{17}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}coth_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{17}(x,t)= & {} F_0+F_1\bigg (-\sqrt{-\frac{\alpha }{\varsigma }}coth_A(\sqrt{-\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{18}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \iota \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{18}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi \pm \iota \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{19}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi \pm \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{19}(x,t)= & {} F_0+F_1\bigg (-\sqrt{\frac{\alpha }{\varsigma }}cot_A(2\sqrt{\alpha \varsigma }\xi )\pm \sqrt{-pq\frac{{\alpha }}{\varsigma }}csc_A(2\sqrt{\alpha \varsigma }\xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{20}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )+\sqrt{-\frac{\alpha }{\varsigma }} coth_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{20}(x,t)= & {} F_0+F_1\bigg (-\frac{1}{2}(\sqrt{-\frac{\alpha }{\varsigma }}tanh_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )+\sqrt{-\frac{\alpha }{\varsigma }} coth_A(\frac{\sqrt{-\alpha \varsigma }}{2}\xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 5:When \(\Theta =0 ~ and~ \varsigma =\alpha \), then the solutions are as follows

$$\begin{aligned} v_{21}(x,t)=&F_0+F_1\bigg (tan_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_{21}(x,t)= & {} F_0+F_1\bigg (tan_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_{22}(x,t)= & {} F_0+F_1\bigg (-cot_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_{22}(x,t)= & {} F_0+F_1\bigg (-cot_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_{23}(x,t)= & {} F_0+F_1\bigg (tan_A(2\alpha \xi )\pm \sqrt{pq}sec_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_{23}(x,t)=&F_0+F_1\bigg (tan_A(2\alpha \xi )\pm \sqrt{pq}sec_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \nonumber \\ v_{24}(x,t)= & {} F_0+F_1\bigg (-cot_A(2\alpha \xi )\pm \sqrt{pq}csc_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_{24}(x,t)= & {} F_0+F_1\bigg (-cot_A(2\alpha \xi )\pm \sqrt{pq}csc_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \nonumber \\ v_{25}(x,t)=&F_0+F_1\bigg (\frac{1}{2}(tan_A(\frac{\alpha }{2}\xi )-cot_A(\frac{\alpha }{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}). \nonumber \\ u_{25}(x,t)=&F_0+F_1\bigg (\frac{1}{2}(tan_A(\frac{\alpha }{2}\xi )-cot_A(\frac{\alpha }{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$
(20)
Fig. 1
figure 1

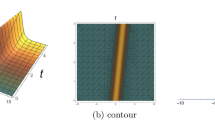
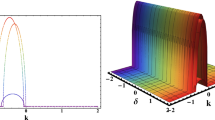
a 3D surface of (9) with \(\alpha =0.60\),  \(\Theta =0.90\),  \(\varsigma =0.70\),  \(w_1=0.7\),    \(p=2\),  \(q=3\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2,~ \nu =0.35\). a-1 2D graph. a-2 Contour graph

Full size image
Fig. 2
figure 2

b 3D surface of (10) with \(\alpha =0.25\),  \(\Theta =0.90\),  \(\varsigma =0.35\),  \(w_1=0.7\),    \(p=2\),  \(q=3\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2\). b-1 2D graph. b-2 Contour graph

Full size image
Fig. 3
figure 3

c 3D surface of (11) with \(\alpha =0.25\),  \(\Theta =0.90\),  \(\varsigma =0.35\),  \(w_1=0.7\),    \(p=2\),  \(q=3\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2 \). c-1 2D graph. c-2 Contour graph

Full size image
Fig. 4
figure 4

d 3D surface of (12) with \(\alpha =0.60\),  \(\Theta =0\),  \(\varsigma =0.70\),  \(A=0.85\),    \(p=1\),  \(q=2\),  \(k=0.4\),  \(\omega =0.5\) and  \(\theta =2.5 \). d-1 2D graph. d-2 Contour graph

Full size image
Fig. 5
figure 5

e 3D surface of (13) with \(\alpha =0.60\),  \(\Theta =0\),  \(\varsigma =-0.70\),  \(w_1=0.7\),    \(p=1\),  \(q=2\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2 \). e-1 2D graph. e-2 Contour graph

Full size image
Fig. 6
figure 6

f 3D graph of (19) with \(\alpha =0.60\),  \(\Theta =0.90\),  \(\varsigma =0.70\),  \(w_1=0.7\),    \(p=2\),  \(q=3\),  \(k=0.5\),  \(c=0.45\),  \(\theta =2~and~~ \nu =0.35 \). f-1 2D graph. f-2 Contour graph

Full size image
Fig. 7
figure 7

g 3D surface of (20) with \(\alpha =0\),  \(\Theta =70\),  \(\varsigma =0.60\),  \(w_1=0.7\),    \(p=2\),  \(q=3\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2 \). g-1 2D graph. g-2 Contour graph

Full size image
Fig. 8
figure 8

h 3D surface of (21) with \(\alpha =0.0\),  \(\Theta =0.90\),  \(\varsigma =0.70\),  \(w_1=0.7\),    \(p=1\),  \(q=2\),  \(k=0.5\),  \(c=0.45\) and  \(\theta =2 \). h-1 2D graph. h-2 Contour graph

Full size image
Fig. 9
figure 9

i 3D surface of (22) with \(\alpha =0\),  \(\Theta =0.65\),  \(\varsigma =0.65\),  \(A=0.85\),    \(p=3\),  \(q=5\),  \(k=2\),  \(\omega =0.6\),  \(\theta =2\), and  \(m=2\). i-1 2D graph. i-2 Contour graph

Full size image

Family 6:When \(\Theta =0 ~ and~ \varsigma =-\alpha \) then the solutions are as follows

$$\begin{aligned} v_{26}(x,t)=&F_0+F_1\bigg (-tanh_A(\alpha \xi )\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{26}(x,t)=&F_0+F_1\bigg (-tanh_A(\alpha \xi )\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{27}(x,t)=&F_0+F_1\bigg (-coth_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}), \\ u_{27}(x,t)=&F_0+F_1\bigg (-coth_A(\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{28}(x,t)=&F_0+F_1\bigg (-tanh_A(2\alpha \xi )\pm \iota \sqrt{pq}sech_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{28}(x,t)=&F_0+F_1\bigg (-tanh_A(2\alpha \xi )\pm \iota \sqrt{pq}sech_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\\ v_{29}(x,t)=&F_0+F_1\bigg (-coth_A(2\alpha \xi )\pm \sqrt{pq}csch_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\\ u_{29}(x,t)=&F_0+F_1\bigg (-coth_A(2\alpha \xi )\pm \sqrt{pq}csch_A(2\alpha \xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}), \\ v_{30}(x,t)=&F_0+F_1\bigg (-\frac{1}{2}(tanh_A(\frac{\alpha }{2}\xi )+coth_A(\frac{\alpha }{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}). \\ u_{30}(x,t)=&F_0+F_1\bigg (-\frac{1}{2}(tanh_A(\frac{\alpha }{2}\xi )+coth_A(\frac{\alpha }{2}\xi )\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 7:When \(\Theta ^2=4\alpha \varsigma \),

$$\begin{aligned} v_{31}(x,t)=&F_0+F_1\bigg (\frac{-2\alpha (\Theta \xi ln (A)+2)}{\Theta ^2\xi ln (A)}\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{31}(x,t)=&F_0+F_1\bigg (\frac{-2\alpha (\Theta \xi ln (A)+2)}{\Theta ^2\xi ln (A)}\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 8:When \(\Theta =k,~\alpha =mk ~(m\ne 0)~and ~\varsigma =0\), then the solution is

$$\begin{aligned} v_{32}(x,t)=&F_0+F_1\bigg (A^{k\xi }-m\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{32}(x,t)=&F_0+F_1\bigg (A^{k\xi }-m\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 9:When \(\Theta =\varsigma =0\),

$$\begin{aligned} v_{33}(x,t)=&F_0+F_1\bigg (\alpha \xi ln (A)\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{33}(x,t)=&F_0+F_1\bigg (\alpha \xi ln (A)\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 10:When \(\Theta =\alpha =0\),

$$\begin{aligned} v_{34}(x,t)=&F_0+F_1 \bigg (\frac{-1}{\varsigma \xi ln (A)}\bigg )\\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\\ u_{34}(x,t)=&F_0+F_1 \bigg (\frac{-1}{\varsigma \xi ln (A)}\bigg )\\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$

Family 11:When \(\Theta =\alpha =0\),

$$\begin{aligned} v_{35}(x,t)=&F_0+F_1\bigg (-\frac{p\Theta }{\varsigma (cosh_A(\Theta \xi )-sinh_A(\Theta \xi +p))}\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}),\nonumber \\ u_{35}(x,t)=&F_0+F_1\bigg (-\frac{p\Theta }{\varsigma (cosh_A(\Theta \xi )-sinh_A(\Theta \xi +p))}\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}),\nonumber \\ v_{36}(x,t)=&F_0+F_1\bigg (-\frac{\Theta (sinh_A(\Theta \xi )+cosh_A(\Theta \xi ))}{\varsigma (sinh_A(\Theta \xi )+cosh_A(\Theta \xi +q))}\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\nonumber \\ u_{36}(x,t)=&F_0+F_1\bigg (-\frac{\Theta (sinh_A(\Theta \xi )+cosh_A(\Theta \xi ))}{\varsigma (sinh_A(\Theta \xi )+cosh_A(\Theta \xi +q))}\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$
(21)

Family 12:When \(\Theta =k,~\varsigma =mk, ~(m\ne 0)~ and~\alpha =0\),

$$\begin{aligned} v_{37}(x,t)=&F_0+F_1\bigg (\frac{pA^{k\xi }}{q-\mp A^{k\xi }}\bigg )\nonumber \\&\times (e^{\iota (-k_1x+\frac{a_1 k_1^2(3(-2+k_1)k_1^2+\Theta ^2 ln(A)^2)}{(6k_1^2-\Theta ^2 ln(A)^2)} t+\theta _1)}).\nonumber \\ u_{37}(x,t)=&F_0+F_1\bigg (\frac{pA^{k\xi }}{q-\mp A^{k\xi }}\bigg )\nonumber \\&\times (e^{\iota (-k_2x+\frac{a_2 k_2^2(3(-2+k_2)k_2^2+\Theta ^2 ln(A)^2)}{(6k_2^2-\Theta ^2 ln(A)^2)} t+\theta _2)}). \end{aligned}$$
(22)

Results and Discussion

In this paper, we effectively gained new exact traveling wave solutions for parabolic law and non-local law nonlinearities using the extended direct algebraic method (EDAM). These solutions also contain the hyperbolic and trigonometric function solutions. For physical interpretation the 3-d, 2-d and contour plots of some of these soliton solutions are added. This technique is considered as latest in this field and it is not applied to this models previously. These constructed solutions discover their application in communication to convey information because solitons have the capability to spread over long distances without reduction and without changing their forms. We present the graphs of some solutions for Eqs. (9), (10), (11), (12), (13), (19), (20), (21) and (22). In this paper, we only added particular figures to avoid overfilling the document. Figures 1, 2, 3, 4, 5, 6, 7, 8 and 9 investigate 3-d, 2-d and contour plots of the some acquired solutions with the help of involved free parameters. Figures 1, 4 and 6 display the solutions given by (9), (12) and (19) which are periodic singular solitons. Figures 2, 5 and 8 display the solutions given by (10), (13) and (21) which are dark solitons. While Figs. 3, 7 and 9 present the solutions given by (11), (20) and (22) which are combined dark-bight, combined periodic-singular and singular solitons, respectively. It is clear that the profile of all constructed solitons does not change throughout their propagation.

Conclusion

In this paper, we constructed optical solitons solutions of parabolic law and non-local law nonlinearities in birefringent fibers with aid of new EDAM. The acquired results are in the form of singular, periodic singular, dark, bright, combined-dark bright and combined bright-singular solitons solutions as well as trigonometric and hyperbolic functions solutions. These results are novel, correct and may have much impact on several fields of nonlinear sciences such as pulse propagation, optical fibers, engineering, physics, applied mathematics etc. It is observed that the method is capable, reliable and fruitful to retrieve the exact solutions of NLPDEs in an extensive range.