1 Introduction

The theory of solitary waves and solitons has emerged as a fundamental aspect of nonlinear dynamics, finding profound applications in a wide array of scientific disciplines, including plasma physics, fluid mechanics, particle physics, condensed matter physics, and photonics, among others. In recent decades, researchers have directed their attention toward investigating the behavior of nonlinear Schrödinger (NLS) equations, which serve as essential models for understanding nonlinear phenomena in various physical systems. To gain deeper insights into the dynamics of NLS equations, numerous integration tools have been proposed by scholars and researchers. Some of these integration methods include the Bell polynomial method [1], Painlevé test [2], Kudryashov’s simplest Equation method [3], Exp-function method [4], Hirota bilinear method [5,6,7,8], modifed rational sine–cosine and sinh–cosh functions [9, 10], Extended Sinh-Gordon equation method [11], Extended rational sin–cos method [12], Darboux transformation method [13], F-expansion method [14], the generalized exponential rational function method [3], Kudryashov-expansion method [15], Lie symmetry method [16,17,18], Backlund transformation [19], test function [20, 21], the new modified generalized exponential rational function method [22], the generalized Riccati equation mapping method [23], Wronskian solutions [24], Riccati projective equation method [25], the extended trial equation scheme [26], Solitary Wave Ansatze [27], right–left-moving wave solutions [28], two-stage epidemic model with a dynamic control strategy [29], extended tanh-coth expansion method [30], and other mathematical approaches [31]. To provide a comprehensive understanding of the soliton theory, the focus of this study lies in investigating the (2+1)-dimensional nonlinear Heisenberg ferromagnetic spin chain (HFSC) equation [32]:

$$\begin{aligned}&i \frac{\partial R(x,y,t)}{\partial t}+\alpha \frac{\partial ^2R(x,y,t)}{\partial x\, \partial x}+\beta \frac{\partial ^2R(x,y,t)}{\partial y\, \partial y}\nonumber \\&\quad +\gamma \frac{\partial ^2R(x,y,t)}{\partial x\, \partial y}-\lambda R(x,y,t) \left| R(x,y,t)\right| ^2=0, \end{aligned}$$
(1)

where \(\alpha = \delta ^4 (J+J_2), \beta =\delta ^4 (J_1+J_2), \gamma =2\delta ^4 J_2,\) and \(\lambda =2\delta ^4\,M.\) In this context, J, \(J_1\), and \(J_2\) stand for the unchanging coefficients of bilinear exchange interactions within a two-dimensional space. The variable M symbolizes the interaction arising from the anisotropy of the crystal field, while \(\delta \) represents the lattice parameter. This equation plays a crucial role in the study of magnetic materials and condensed matter physics, offering valuable insights into the behavior of spins in two-dimensional systems with ferromagnetic interactions. The exploration of this equation is expected to reveal intricate soliton dynamics and collective phenomena, offering valuable insights into the behavior of spins.

In recent years, the HFSC equation has acquired significant attention from researchers exploring diverse methodologies. Some notable studies have contributed to our understanding of this equation: Latha and Vasanthi [32] explored the behavior of spins in (2+1)-dimensional Heisenberg ferromagnetic spin chains. They used the coherent state ansatz and the Holstein–Primakoff representation of spin operators. They looked at how the equation can be solved, creating solutions called multisolitons using the Darboux transformation. Liu [33] offered an explicit formulation for rogue wave solutions in the context of the (2+1)-dimensional nonlinear Schrödinger equation. Employing the bilinear method, they expressed these solutions using Gram determinants. Hashemi [34] focused on the HFSC equation’s solutions incorporating conformable time fractional derivatives. Through the utilization of the simplest equation method and Nucci’s method with conformable fractional derivatives, they derived a range of solutions, including bright and dark solitons. Bashar and Islam [35] extended the modified simple equation and the improved F-expansion method to determine exact solutions of the HFSC equation. Their approach resulted in the construction of traveling wave solutions characterized by hyperbolic, trigonometric, and rational functions, all of which were parameterized. Guan et al. [36] used a mathematical approach called the complete discrimination system for polynomial method to solve the HFSC equation. They also used computer simulations to show how the equation works in different situations. Du et al. [37] directed their attention toward the spin dynamics of nonlinear localized waves within the HFSC equation. By using a technique that nonlinearizes the spectral problem, they obtained values for the spectral parameter and periodic eigenfunction associated with the Lax pair linked to the Jacobian elliptic function of the third kind. Utilizing the Darboux transformation, they generated semirational solutions based on seed solutions expressed using the Jacobian elliptic function.

Soliton solutions obtained through the “Inverse (G’/G)-Expansion Method” have wide-ranging applications across various fields. These solitons are significant in nonlinear optics, where they maintain their shape and speed during propagation, enabling long-distance communication without distortion. Additionally, they find application in plasma physics, where solitons play a crucial role in understanding wave phenomena and energy transport in plasma environments. Moreover, their relevance extends to condensed matter physics, aiding in the study of localized excitations and magnetic behavior in spin chains and other condensed matter systems.

The study of nonlinear partial differential equations has led to the discovery of fascinating wave phenomena, including lump solitons, breather waves, periodic solitons, interactions of lumps with solitary waves, and bubbly solitary waves. These intriguing wave behaviors have captured the attention of researchers across various scientific disciplines, from engineering to physics and mathematics. Lump solitons exhibit localized, compact wave structures that maintain their shape during propagation, while breather waves display periodic oscillations of amplitude and shape. Periodic solitons, on the other hand, manifest as repeating wave patterns with stable spatial periodicity. The interaction of lumps with solitary waves showcases intricate wave dynamics, and bubbly solitary waves represent an intricate combination of solitary waves and bubble-like structures. Understanding and characterizing these distinct wave phenomena hold immense significance in advancing our knowledge of nonlinear wave dynamics and their applications in the natural world and engineered systems.

This article is organized into several sections to comprehensively explore the application of the Inverse \((G'/G)\)-expansion method to the HFSC equation and its implications. In Sect. 1, we delve into the historical background of the HFSC equation, providing an insightful context for its significance in the field of nonlinear wave equations. In Sect. 2, we present a detailed algorithm of our novel proposed “Inverse \((G'/G)\)-expansion method,” outlining its systematic approach for obtaining exact solutions to nonlinear partial differential equations. Moving on to Sect. 3, we demonstrate the successful implementation of the Inverse \((G'/G)\)-expansion method on the HFSC equation, leading to the discovery of new and novel analytic solutions. These solutions are thoroughly examined and analyzed via graphical representations, offering a clear visualization of their unique wave behaviors. In Sect. 4, we establish a connection between our mathematical findings and real-world applications by discussing the implications of specific solutions, particularly those represented by Eqs. (6) and (7). By linking our research to well-known physical phenomena, we enrich the practical significance of our results. Furthermore, in Sect. 5, we explore the visual behavior of the obtained solutions under various parameter choices, elucidating the impact of different parameter values on wave dynamics. This graphical analysis allows for a more profound understanding of the complexities involved in nonlinear wave phenomena. Finally, in Sect. 6, we culminate our research study by presenting a comprehensive conclusion. We summarize the key findings of the Inverse \((G'/G)\)-expansion method’s successful application to the HFSC equation and discuss its potential implications for further advancements in the study of nonlinear wave dynamics. The organization of this article ensures a thorough exploration of our research, providing valuable insights for researchers in various scientific disciplines.

2 Novel methodology: Inverse \(\left( \frac{G'}{G}\right) \)-expansion method

In this section, we outline the fundamental steps of the proposed Inverse \(\left( \frac{G'}{G}\right) \)-expansion method, which is a powerful approach for finding exact solutions to nonlinear partial differential equations (NLPDEs) in various fields, including engineering, physics, and mathematics. This method combines the generalized exponential rational function (GERF) method and the \((G'/G)\)-expansion method. It is based on the concept that the nonlinear traveling wave solutions of NLPDEs can be expressed as a polynomial in \(\left( \frac{G'}{G}\right) \), where G satisfies the Riccati equation. Here is how the method works:

  • Consider the nonlinear partial differential equation (NLPDE):

    $$\begin{aligned} P(R,R_x,R_y,R_t,R_{xx},R_{yy},R_{tt},R_{xt},\dots ) = 0, \end{aligned}$$
    (2)

    where \(R=R(x,y,t)\) is the wave amplitude and P is a polynomial function containing various partial derivatives of R with respect to its independent variables.

  • Assume a traveling wave solution of the form:

    $$\begin{aligned} R(x,y,t) = S(\eta ) \exp (i\mu ), \end{aligned}$$
    (3)

    where \(\eta = a_1 x + a_2 y + a_3 t\) and \(\mu = b_1 x + b_2 y + b_3 t\).

  • Substituting the assumed solution into the NLPDE, it reduces to an ordinary differential equation (ODE) for the function \(S(\eta )\):

    $$\begin{aligned} N(S(\eta ),S'(\eta ),S''(\eta ),\dots ) = 0, \end{aligned}$$
    (4)

    where \(S'=\mathrm{{d}}\frac{S}{d\eta },S''=\frac{d^2S}{d\eta ^2}\), and so on.

  • To solve this ODE (4), we propose a trial solution \(S(\eta )\) as a series expansion in \(\left( \frac{G'(\eta )}{G(\eta )}\right) \):

    $$\begin{aligned} S(\eta ) = M_0 + \sum _{i=1}^{N}M_i~\left( \frac{G'(\eta )}{G(\eta )}\right) ^i + \sum _{i=1}^{N}N_i~\left( \frac{G'(\eta )}{G(\eta )}\right) ^{-i}, \end{aligned}$$
    (5)

    where \(M_i, N_i~(0 \le i \le N)\) represents the arbitrary constants to be determined later, and \(G(\eta )\) satisfies the Riccati equation:

    $$\begin{aligned} G'(\eta ) = p G(\eta ) + q G(\eta )^2 + r, \end{aligned}$$
    (6)

    where p, q, and r are arbitrary constants.

  • By substituting the trial solution \(S(\eta )\) into the ODE (4) and balancing the highest-order derivative term with the nonlinear term, a system of algebraic equations for the arbitrary constants \(M_i\), \(N_i\), p, q, and r is obtained. Solving the system of algebraic equations yields the values of the arbitrary constants, which, in turn, provide the exact solutions to the original NLPDE.

  • By following these steps, the modified \(\left( \frac{G'}{G}\right) \)-expansion method offers a systematic and efficient approach for finding exact solutions to a wide range of NLPDEs, making it a valuable tool for researchers in various scientific and engineering disciplines.

2.1 Remark

The name “Inverse \((G'/G)\)-Expansion method” emphasizes the uniqueness and novelty of the constructed method, highlighting its dual-sided nature in incorporating both positive and negative powers of \((G'/G)\) in the trial solution (5).

3 Application of the Inverse \(\left( \frac{G'}{G}\right) \)-expansion method

In this section, we apply the newly proposed Inverse \((\frac{G'}{G})\)-expansion method to simplify the HFSC Eq. (1). To begin, we introduce a transformation given by

$$\begin{aligned}&R(x,y,t)=S(\eta )\exp (i \mu ) ,~~ \text{ with }~~ \nonumber \\&\eta =a_1 x+a_2 y+a_3 t, \mu =b_1 x+b_2 y+b_3 t. \end{aligned}$$
(7)

Upon using the transformation, the HFSC Eq. (1) reduces into following equation,

$$\begin{aligned}&\left( \alpha a_1^2+a_2^2 \beta +a_2 a_1 \gamma \right) S''(\eta )+i \left( b_1 \left( 2 \alpha a_1+a_2 \gamma \right) \right. \nonumber \\&\quad \left. +b_2 \left( 2 a_2 \beta +a_1 \gamma \right) +a_3\right) S'(\eta )\nonumber \\&\quad -\left( \alpha b_1^2+\beta b_2^2+b_2 b_1 \gamma +b_3\right) S(\eta ) -\lambda S(\eta )^3=0. \end{aligned}$$
(8)

The above Eq.(8) reduces to two separate equations, one for the real part and the other for the imaginary part. The real part equation is represented by

$$\begin{aligned}&\left( \alpha a_1^2 + a_2^2 \beta + a_2 a_1 \gamma \right) S''(\eta ) \nonumber \\&\quad - \left( \alpha b_1^2 + \beta b_2^2 + b_2 b_1 \gamma + b_3\right) S(\eta ) - \lambda S(\eta )^3 = 0, \end{aligned}$$
(9)

where \(\alpha \), \(\beta \), \(\gamma \), and \(\lambda \) are constants related to the HFSC equation. The imaginary part equation is represented by

$$\begin{aligned} \left( b_1 \left( 2 \alpha a_1 + a_2 \gamma \right) + b_2 \left( 2 a_2 \beta + a_1 \gamma \right) + a_3\right) S'(\eta ) = 0. \end{aligned}$$
(10)

From Eq. (10), we deduce the relationship for \(a_3\):

$$\begin{aligned} a_3 = -2 \alpha a_1 b_1 - 2 a_2 \beta b_2 - a_2 b_1 \gamma - a_1 b_2 \gamma . \end{aligned}$$
(11)

Next, we employ the homogeneous balancing principle on the terms \(S''(\eta )\) and \(S(\eta )^3\) in Eq. (9) to determine the value of the parameter N. Through this process, we find that \(N = 1\), which means that our trial solution will take the form

$$\begin{aligned} S(\eta ) = M_0 + M_1\frac{G'(\eta )}{G(\eta )} + N_1\left( \frac{G'(\eta )}{G(\eta )}\right) ^{-1}. \end{aligned}$$
(12)

Incorporating the expression labeled as Eq. (12) along with (11) into the framework of Eq. (9), and subsequently equating the factor associated with \(G(\eta )\) to zero, leads to the formulation of a set of algebraic equations. By solving this system, we get some set of constraints, which play a crucial role in determining the specific form of the exact solutions to the HFSC equation. These constraints ensure that the trial solution (12) and the transformation (7) are compatible with the HFSC equation, leading to valid solutions for the given problem. Next, in the analytic solutions section, we will apply these constraints to obtain and visualize the exact solutions of the HFSC equation using the Inverse \((\frac{G'}{G})\)-expansion method.

3.1 Analytic solutions

3.2 Solution set 1

$$\begin{aligned} M_0\ne & {} 0;M_1\ne 0;N_1\ne 0; \\ b_3= & {} \frac{\left( a_2 b_1-a_1 b_2\right) \left( a_2 \beta b_2-\alpha a_1 b_1\right) }{a_1 a_2};\\ \gamma= & {} \frac{-\alpha a_1^2-a_2^2 \beta }{a_1 a_2};\lambda =0. \end{aligned}$$

From Eq. (12), we obtained the following solutions for ODE given by Eq. (9):

3.3 Case (i): Exploring solutions when \(\Delta =p^2-4 \text {rq}> 0\) and \(pq \ne 0.\)

We obtain the solutions of the ODE (9) as

$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{M_1 \left( \Delta \right) \text {sech}^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) }{2 \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) } +\frac{2 N_1 \cosh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} S(\eta )=M_0-\frac{M_1 \left( \Delta \right) \text {csch}^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) }{2 \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) } -\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{M_1 \sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }{\sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p}\nonumber \\{} & {} + \frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{M_1 \sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }{\sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p}\nonumber \\{} & {} + \frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }. \end{aligned}$$
(16)

Therefore, the solutions of the HFSC equation under the transformation (7) are given by

$$\begin{aligned} R(x,y,t)= & {} e^{i\mu } \left( \frac{\Delta M_1 \text {sech}^2\left( \frac{\sqrt{\Delta } \eta }{2}\right) }{2 \left( \sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta } \eta }{2}\right) +p\right) }+M_0+\frac{2 N_1 \cosh ^2\left( \frac{\sqrt{\Delta } \eta }{2}\right) \left( \sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta } \eta }{2}\right) +p\right) }{\Delta }\right) , \end{aligned}$$
(17)
$$\begin{aligned} R(x,y,t)= & {} e^{i\mu } \left( M_0-\frac{M_1 \left( \Delta \right) \text {csch}^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) }{2 \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }-\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }\right) , \end{aligned}$$
(18)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( M_0+\frac{M_1 \sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }{\sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p}+\right) \end{aligned}$$
(19)
$$\begin{aligned}{} & {} +e^{i \mu }{\left( \frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }\right) }, \end{aligned}$$
(20)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( M_0+\frac{M_1 \sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }{\sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p}\right) \end{aligned}$$
(21)
$$\begin{aligned}{} & {} +e^{i \mu }\left( \frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }\right) , \end{aligned}$$
(22)

where \(\eta =a_1 \left( x-\alpha b_1 t\right) +a_2 \left( y-\beta b_2 t\right) +\frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}\) and \(\mu =b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) -\alpha b_1^2 t+b_2 \left( y-\beta b_2 t\right) .\)

3.4 Case (ii): Exploring solutions when \(r = 0\) and \(pq \ne 0.\)

Subsequently, the solutions of the differential equation (9) can be written in the following manner

$$\begin{aligned}&S(\eta )=M_0-\frac{M_1 (p \sinh (\eta p)-p \cosh (\eta p))}{\zeta _0-\sinh (\eta p)+\cosh (\eta p)}\nonumber \\&-\frac{N_1 \left( \zeta _0-\sinh (\eta p)+\cosh (\eta p)\right) }{p \sinh (\eta p)-p \cosh (\eta p)}, \end{aligned}$$
(23)
$$\begin{aligned}&S(\eta )=M_0+\frac{c M_1 p}{\zeta _0+e^{\eta p}}+\frac{N_1 \left( \zeta _0+e^{\eta p}\right) }{\zeta _0 p}. \end{aligned}$$
(24)

Therefore, the solutions for the HFSC equation are as follows:

$$\begin{aligned} R(x,y,t)=&\exp \left( i \left( b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) \right. \right. \nonumber \\&\left. \left. +\alpha b_1^2 (-t)+b_2 \left( y-\beta b_2 t\right) \right) \right) \nonumber \\&\left( -\frac{M_1 (p \sinh (\eta p)-p \cosh (\eta p))}{\zeta _0-\sinh (\eta p)+\cosh (\eta p)}\right. \nonumber \\&\left. +M_0-\frac{N_1 \left( \zeta _0-\sinh (\eta p)+\cosh (\eta p)\right) }{p \sinh (\eta p)-p \cosh (\eta p)}\right) , \end{aligned}$$
(25)
$$\begin{aligned} R(x,y,t)=&\exp \left( i \left( b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) \right. \right. \nonumber \\&\left. \left. +\alpha b_1^2 (-t)+b_2 \left( y-\beta b_2 t\right) \right) \right) \nonumber \\&\left( \frac{\zeta _0 M_1 p}{\zeta _0+e^{\eta p}}+M_0+\frac{N_1 \left( \zeta _0+e^{\eta p}\right) }{\zeta _0 p}\right) , \end{aligned}$$
(26)

where \(\eta =\frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}+a_1 \left( x-\alpha b_1 t\right) +a_2 \left( y \right. \)\( \left. -\beta b_2 t\right) .\)

3.5 Case (iii): Exploring solutions when \(\Delta =p^2-4 \text {rq}<0\), and \(rq\ne 0\).

We obtain the solutions of the ODE (9) as

$$\begin{aligned} S(\eta )= & {} M_0+\frac{\sqrt{-\Delta } M_1 \left( \frac{1}{4} \sqrt{-\Delta } \csc ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) +\frac{1}{4} \sqrt{-\Delta } \sec ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) }{\sqrt{-\Delta } \left( \tan \left( \frac{\sqrt{-\Delta } \eta }{4}\right) -\cot \left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) -2 p}\nonumber \\{} & {} +\frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \frac{\sqrt{-\Delta } \eta }{4}\right) -\cot \left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) -2 p\right) }{\sqrt{-\Delta } \left( \frac{1}{4} \sqrt{-\Delta } \csc ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) +\frac{1}{4} \sqrt{-\Delta } \sec ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) }, \end{aligned}$$
(27)
$$\begin{aligned} S(\eta )= & {} M_0+\frac{\Delta M_1 \text {sech}^2\left( \frac{\sqrt{\Delta } \eta }{2}\right) }{2 p-2 \sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta } \eta }{2}\right) }+\frac{N_1 \left( -\sqrt{\Delta } \sinh \left( \sqrt{\Delta } \eta \right) +p \cosh \left( \sqrt{\Delta } \eta \right) +p\right) }{\Delta }, \end{aligned}$$
(28)
$$\begin{aligned} S(\eta )= & {} M_0+\frac{2 N_1 \left( \sin \left( \sqrt{-\Delta } \eta \right) -1\right) \left( -\sin \left( \sqrt{-\Delta } \eta \right) \left( p^2-2 q r\right) +\sqrt{-\Delta } p \cos \left( \sqrt{-\Delta } \eta \right) +2 q r\right) -\Delta ^2 M_1}{\Delta \left( p \left( \sin \left( \sqrt{-\Delta } \eta \right) -1\right) -\sqrt{-\Delta } \cos \left( \sqrt{-\Delta } \eta \right) \right) }.\nonumber \\ \end{aligned}$$
(29)

Therefore, the required solutions of the considered equation under the transformation (7) are

$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( M_0+\frac{\sqrt{-\Delta } M_1 \left( \frac{1}{4} \sqrt{-\Delta } \csc ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) +\frac{1}{4} \sqrt{-\Delta } \sec ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) }{\sqrt{-\Delta } \left( \tan \left( \frac{\sqrt{-\Delta } \eta }{4}\right) -\cot \left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) -2 p}\right) \nonumber \\{} & {} +e^{i\mu }\left( \frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \frac{\sqrt{-\Delta } \eta }{4}\right) -\cot \left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) -2 p\right) }{\sqrt{-\Delta } \left( \frac{1}{4} \sqrt{-\Delta } \csc ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) +\frac{1}{4} \sqrt{-\Delta } \sec ^2\left( \frac{\sqrt{-\Delta } \eta }{4}\right) \right) }\right) , \end{aligned}$$
(30)
$$\begin{aligned} R(x,y,t)= & {} e^{i\mu }\left( M_0+\frac{\Delta M_1 \text {sech}^2\left( \frac{\sqrt{\Delta } \eta }{2}\right) }{2 p-2 \sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta } \eta }{2}\right) }+\frac{N_1 \left( -\sqrt{\Delta } \sinh \left( \sqrt{\Delta } \eta \right) +p \cosh \left( \sqrt{\Delta } \eta \right) +p\right) }{\Delta }\right) , \end{aligned}$$
(31)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( \frac{2 N_1 \left( \sin \left( \sqrt{-\Delta } \eta \right) -1\right) \left( -\sin \left( \sqrt{-\Delta } \eta \right) \left( p^2-2 q r\right) +\sqrt{-\Delta } p \cos \left( \sqrt{-\Delta } \eta \right) +2 q r\right) -\Delta ^2 M_1}{\Delta \left( p \left( \sin \left( \sqrt{-\Delta } \eta \right) -1\right) -\sqrt{-\Delta } \cos \left( \sqrt{-\Delta } \eta \right) \right) }+M_0\right) ,\nonumber \\ \end{aligned}$$
(32)

where \(\eta =\frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}+a_1 \left( x-\alpha b_1 t\right) +a_2 \left( y-\beta b_2 t\right) \) and \(\mu =b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) +\alpha b_1^2 (-t)+b_2 \left( y-\beta b_2 t\right) \)

3.6 Solution set 2

$$\begin{aligned} M_0= & {} -\frac{N_1 p}{p^2-4 q r};M_1=0;\nonumber \\ b_3= & {} \alpha a_1^2 \left( p^2-4 q r\right) +a_2^2 \beta \left( p^2-4 q r\right) \nonumber \\{} & {} +a_2 a_1 \gamma \left( p^2-4 q r\right) \nonumber \\{} & {} -b_1 \left( \alpha b_1+b_2 \gamma \right) -\beta b_2^2 ;\lambda =0. \end{aligned}$$
(33)

Now, from Eq. (12), we acquired the following solutions of the ODE(9):

3.7 Case (i): Exploring solutions when \(\Delta =p^2-4 \text {rq}> 0\) and \(pq\ne 0.\)

We obtain the solutions of the ODE (9) as

$$\begin{aligned} S(\eta )= & {} \frac{2 N_1 \cosh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }-\frac{N_1 p}{\Delta }, \end{aligned}$$
(34)
$$\begin{aligned} S(\eta )= & {} -\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }-\frac{N_1 p}{\Delta }, \end{aligned}$$
(35)
$$\begin{aligned} S(\eta )= & {} \frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }-\frac{N_1 p}{\Delta }, \end{aligned}$$
(36)
$$\begin{aligned} S(\eta )= & {} \frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }-\frac{N_1 p}{\Delta }. \end{aligned}$$
(37)

Therefore, the solutions of the HFSC equation under the transformation (7) are given by

$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( \frac{2 N_1 \cosh ^2\left( \frac{1}{2} \sqrt{\Delta } \eta \right) \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \sqrt{\Delta } \eta \right) +p\right) }{\Delta }-\frac{N_1 p}{\Delta }\right) , \end{aligned}$$
(38)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( -\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \sqrt{\Delta } \eta \right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \sqrt{\Delta } \eta \right) +p\right) }{\Delta }-\frac{N_1 p}{\Delta }\right) , \end{aligned}$$
(39)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( \frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \sqrt{\Delta } \eta \right) +\text {csch}\left( \sqrt{\Delta } \eta \right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \sqrt{\Delta } \eta \right) \text {csch}\left( \sqrt{\Delta } \eta \right) -\sqrt{\Delta } \text {csch}^2\left( \sqrt{\Delta } \eta \right) \right) }-\frac{N_1 p}{\Delta }\right) , \end{aligned}$$
(40)
$$\begin{aligned} R(x,y,t)= & {} e^{i \mu } \left( \frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \sqrt{-\Delta } \eta \right) -\sec \left( \sqrt{-\Delta } \eta \right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \sqrt{-\Delta } \eta \right) -\sqrt{-\Delta } \tan \left( \sqrt{-\Delta } \eta \right) \sec \left( \sqrt{-\Delta } \eta \right) \right) }-\frac{N_1 p}{\Delta }\right) , \end{aligned}$$
(41)

where \(\eta =t \left( -2 \alpha a_1 b_1-2 a_2 \beta b_2-a_2 b_1 \gamma -a_1 b_2 \gamma \right) +a_1 x+a_2 y\) and \(\mu =b_1 x+b_2 y +t b_ 3.\)

3.8 Case (ii): Exploring solutions when \( r=0\), and \(pq\ne 0\).

Subsequently, the solutions to the ODE (9) can be written in the following manner

$$\begin{aligned}{} & {} S(\eta )=-\frac{N_1 \left( \zeta _0-\sinh (\eta p)+\cosh (\eta p)\right) }{p \sinh (\eta p)-p \cosh (\eta p)}-\frac{N_1}{p},\nonumber \\ \end{aligned}$$
(42)
$$\begin{aligned}{} & {} S(\eta )=\frac{N_1 e^{\eta p}}{\zeta _0 p}. \end{aligned}$$
(43)

Therefore, the solutions for the HFSC equation are as follows:

$$\begin{aligned} R(x,y,t)= & {} e^{i \left( b_1x+b_2y+b_3t\right) } \left( -\frac{N_1 \left( -\sinh \left( p \left( a_1x+a_2y+a_3t\right) \right) +\cosh \left( p \left( a_1x+a_2y+a_3t\right) \right) +\zeta _0\right) }{p \sinh \left( p \left( a_1x+a_2y+a_3t\right) \right) -p \cosh \left( p \left( a_1x+a_2y+a_3t\right) \right) }-\frac{N_1}{p}\right) , \end{aligned}$$
(44)
$$\begin{aligned} R(x,y,t)= & {} \frac{N_1}{\zeta _0 p} \exp \left( p \left( a_1x+a_2y+a_3t\right) +i \left( t \left( \alpha a_1^2 p^2+a_2^2 \beta p^2+a_1 a_2 \gamma p^2-b_1 \left( \alpha b_1+b_2 \gamma \right) -\beta b_2^2\right) +b_1 x+b_2 y\right) \right) . \end{aligned}$$
(45)

3.9 Case (iii): Exploring solutions when \(\Delta =p^2-4 \text {rq}<0\), and \(rq\ne 0\).

We obtain the solutions of the ODE (9) as

$$\begin{aligned} S(\eta )=&\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \eta \sqrt{-\Delta }\right) -p \cos \left( \eta \sqrt{-\Delta }\right) \right) }{\Delta },\end{aligned}$$
(46)
$$\begin{aligned} S(\eta )=&\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \eta \sqrt{-\Delta }\right) +p \cos \left( \eta \sqrt{-\Delta }\right) \right) }{\Delta }, \end{aligned}$$
(47)
$$\begin{aligned} S(\eta )=&\frac{N_1 \left( \sqrt{-\Delta } \cos \left( \eta \sqrt{-\Delta }\right) -p \sin \left( \eta \sqrt{-\Delta }\right) \right) }{\Delta }. \end{aligned}$$
(48)

Therefore, the required solutions of the considered equation under the transformation (7) are

$$\begin{aligned} R(x,y,t)= & {} \frac{N_1}{\Delta }e^{i \left( b_3 t+b_1 x+b_2 y\right) } \nonumber \\{} & {} \left( \sqrt{-\Delta } \sin \left( \sqrt{-\Delta } \left( a_3 t+a_1 x+a_2 y\right) \right) \right. \nonumber \\{} & {} \left. -p \cos \left( \sqrt{-\Delta } \left( a_3 t+a_1 x+a_2 y\right) \right) \right) , \nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned} R(x,y,t)= & {} \frac{N_1}{\Delta } e^{i \left( b_3 t+b_1 x+b_2 y\right) }\left( \sqrt{-\Delta } \sin \right. \nonumber \\{} & {} \left. \left( \sqrt{-\Delta } \left( a_3 t+a_1 x+a_2 y\right) \right) +p \cos \right. \nonumber \\{} & {} \left. \left( \sqrt{-\Delta } \left( a_3 t{+}a_1 x{+}a_2 y\right) \right) \right) , \end{aligned}$$
(50)
$$\begin{aligned} R(x,y,t)= & {} \frac{N_1}{\Delta } e^{i \left( b_3 t+b_1 x+b_2 y\right) }\left( \sqrt{-\Delta } \cos \right. \nonumber \\{} & {} \left. \left( \sqrt{-\Delta } \left( a_3 t+a_1 x+a_2 y\right) \right) -p \sin \right. \nonumber \\{} & {} \left. \left( \sqrt{{-}\Delta } \left( a_3 t{+}a_1 x{+}a_2 y\right) \right) \right) . \end{aligned}$$
(51)

3.10 Solution set 3.

$$\begin{aligned} M_0\ne & {} 0; M_1=0; N_1\ne 0;\nonumber \\ b_3= & {} \frac{\left( a_2 b_1-a_1 b_2\right) \left( a_2 \beta b_2-\alpha a_1 b_1\right) }{a_1 a_2};\nonumber \\ \gamma= & {} \frac{-\alpha a_1^2-a_2^2 \beta }{a_1 a_2};\lambda =0. \end{aligned}$$
(52)

Now, from Eq. (12), we acquired the following solutions of the ODE(9):

3.11 Case (i): Exploring solutions when \(\Delta =p^2-4 \text {rq}> 0\) and \(pq\ne 0.\)

We obtain the solutions of the ODE (9) as

$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{2 N_1 \cosh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }, \end{aligned}$$
(53)
$$\begin{aligned}{} & {} S(\eta )=M_0-\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Delta }\right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \eta \sqrt{\Delta }\right) +p\right) }{\Delta }, \end{aligned}$$
(54)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \eta \sqrt{\Delta }\right) +\text {csch}\left( \eta \sqrt{\Delta }\right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \eta \sqrt{\Delta }\right) \text {csch}\left( \eta \sqrt{\Delta }\right) -\sqrt{\Delta } \text {csch}^2\left( \eta \sqrt{\Delta }\right) \right) }, \end{aligned}$$
(55)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \eta \sqrt{-\Delta }\right) -\sec \left( \eta \sqrt{-\Delta }\right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \eta \sqrt{-\Delta }\right) -\sqrt{-\Delta } \tan \left( \eta \sqrt{-\Delta }\right) \sec \left( \eta \sqrt{-\Delta }\right) \right) }. \end{aligned}$$
(56)

Therefore, the solutions of the HFSC equation under the transformation (7) are given by

$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{2 N_1 \cosh ^2\left( \frac{1}{2} \sqrt{\Delta }\eta \right) \left( \sqrt{\Delta } \tanh \left( \frac{1}{2} \sqrt{\Delta }\eta \right) +p\right) }{\Delta }\right) , \end{aligned}$$
(57)
$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu }\left( M_0-\frac{2 N_1 \sinh ^2\left( \frac{1}{2} \sqrt{\Delta } \eta \right) \left( \sqrt{\Delta } \coth \left( \frac{1}{2} \sqrt{\Delta } \eta \right) +p\right) }{\Delta }\right) , \end{aligned}$$
(58)
$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{N_1 \left( \sqrt{\Delta } \left( \coth \left( \sqrt{\Delta } \eta \right) +\text {csch}\left( \sqrt{\Delta } \eta \right) \right) +p\right) }{\sqrt{\Delta } \left( \left( -\sqrt{\Delta }\right) \coth \left( \sqrt{\Delta } \eta \right) \text {csch}\left( \sqrt{\Delta } \eta \right) -\sqrt{\Delta } \text {csch}^2\left( \sqrt{\Delta } \eta \right) \right) }\right) , \end{aligned}$$
(59)
$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{N_1 \left( \sqrt{-\Delta } \left( \tan \left( \sqrt{-\Delta } \eta \right) -\sec \left( \sqrt{-\Delta } \eta \right) \right) -p\right) }{\sqrt{-\Delta } \left( \sqrt{-\Delta } \sec ^2\left( \sqrt{-\Delta } \eta \right) -\sqrt{-\Delta } \tan \left( \sqrt{-\Delta } \eta \right) \sec \left( \sqrt{-\Delta } \eta \right) \right) }\right) , \end{aligned}$$
(60)

where \(\eta =\frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}+a_1 \left( x-\alpha b_1 t\right) +a_2 \left( y-\beta b_2 t\right) \) and \(\mu =b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) +\alpha b_1^2 (-t)+b_2 \left( y-\beta b_2 t\right) .\)

3.12 Case (ii): Exploring solutions when \( r=0\) and pq not equal 0.

Then, the solutions of the ODE (9) can be determined as

$$\begin{aligned}{} & {} S(\eta )=M_0-\frac{N_1 \left( \zeta _0-\sinh (\eta p)+\cosh (\eta p)\right) }{p \sinh (\eta p)-p \cosh (\eta p)}, \nonumber \\ \end{aligned}$$
(61)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( \zeta _0+e^{\eta p}\right) }{\zeta _0 p}. \end{aligned}$$
(62)

Therefore, the solutions for the HFSC equation are as follows:

$$\begin{aligned} R(x,y,t)= & {} \frac{1}{p}\exp \left( -i \left( -b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) \right. \right. \nonumber \\{} & {} \left. \left. +\alpha b_1^2 t+b_2 \left( \beta b_2 t-y\right) \right) \right) \nonumber \\{} & {} \left( N_1 \left( \zeta _0 \exp \left( p \left( \frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}+a_1\right. \right. \right. \right. \nonumber \\{} & {} \left. \left. \left. \left. \left( x-\alpha b_1 t\right) +a_2 \left( y-\beta b_2 t\right) \right) \right) {+}1\right) {+}M_0 p\right) ,\nonumber \\ \end{aligned}$$
(63)
$$\begin{aligned} R(x,y,t)= & {} \frac{1}{p \zeta _0}\exp \left( i \left( b_1 \left( \frac{\alpha a_1 b_2 t}{a_2}+\frac{a_2 \beta b_2 t}{a_1}+x\right) \right. \right. \nonumber \\{} & {} \left. \left. +\alpha b_1^2 (-t)+b_2 \left( y-\beta b_2 t\right) \right) \right) \nonumber \\{} & {} \left( N_1 \left( \exp \left( p \left( \frac{\alpha a_1^2 b_2 t}{a_2}+\frac{a_2^2 \beta b_1 t}{a_1}+a_1 \right. \right. \right. \right. \nonumber \\{} & {} \left. \left. \left. \left. \left( x-\alpha b_1 t\right) +a_2 \left( y-\beta b_2 t\right) \right) \right) {+}\zeta _0\right) +\zeta _0 M_0 p\right) .\nonumber \\ \end{aligned}$$
(64)

3.13 Case (iii): Exploring solutions when \(\Delta =p^2-4 \text {rq}<0\), provided \(rq\ne 0\).

We obtain the solutions of the ODE (9) as

$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \eta \sqrt{-\Delta }\right) +p \left( -\cos \left( \eta \sqrt{-\Delta }\right) \right) +p\right) }{\Delta }, \end{aligned}$$
(65)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \eta \sqrt{-\Delta }\right) +p \cos \left( \eta \sqrt{-\Delta }\right) +p\right) }{\Delta }, \end{aligned}$$
(66)
$$\begin{aligned}{} & {} S(\eta )=M_0+\frac{N_1 \left( p \left( -\sin \left( \eta \sqrt{-\Delta }\right) \right) +\sqrt{-\Delta } \cos \left( \eta \sqrt{-\Delta }\right) +p\right) }{\Delta }. \end{aligned}$$
(67)

Therefore, the required solutions of the considered equation under the transformation (7) are

$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \sqrt{-\Delta } \eta \right) +p \left( -\cos \left( \sqrt{-\Delta } \eta \right) \right) +p\right) }{\Delta }+\right) , \end{aligned}$$
(68)
$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{N_1 \left( \sqrt{-\Delta } \sin \left( \sqrt{-\Delta } \eta \right) +p \cos \left( \sqrt{-\Delta } \eta \right) +p\right) }{\Delta }\right) , \end{aligned}$$
(69)
$$\begin{aligned}{} & {} R(x,y,t)=e^{i\mu } \left( M_0+\frac{N_1 \left( p \left( -\sin \left( \sqrt{-\Delta } \eta \right) \right) +\sqrt{-\Delta } \cos \left( \sqrt{-\Delta } \eta \right) +p\right) }{\Delta }\right) , \end{aligned}$$
(70)

where \(\eta =t \left( -\frac{b_1 \left( -\alpha a_1^2-a_2^2 \beta \right) }{a_1}-\frac{b_2 \left( -\alpha a_1^2-a_2^2 \beta \right) }{a_2}\right. \)\( \left. -2 \alpha a_1 b_1-2 a_2 \beta b_2\right) +a_1 x+a_2 y\), and \(\mu = \frac{t \left( a_2 b_1-a_1 b_2\right) \left( a_2 \beta b_2-\alpha a_1 b_1\right) }{a_1 a_2}+b_1 x+b_2 y.\)

Fig. 1
figure 1

Visualization of solution (17): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots

Full size image

4 Bridging the gap: connecting mathematical visualization with real-world phenomena

In the fast-paced and ever-changing technological world of today, developing innovative solutions marks only the initial phase. The true measure of success lies in effectively connecting these solutions to real-world applications, where their potential can be translated into real effects on society. This article investigates into the vital process of bridging the gap between theoretical solutions and practical implementation, shedding light on key strategies and essential considerations for achieving success. Here, we are connecting our obtained solutions with the real-world applications. In Fig.(6), we have discussed the three components of the solution (57) in the combination of 3D graphics, contour graphics, and 2D graphics. From the graphics, we depict the solitary waves from solution. To relate these graphics with real world, we have presented a graphics of “Transverse wave in a Rope,” “Waves on ocean surface,” and “Waves in the depth of ocean” that directly shows the connection between the analytical solution (57) and the real-world application.

In Fig. (7), we present an exploration of the graphical behavior of solution (63). This insightful analysis showcases the bubbly solitary waves and their fascinating characteristics, all made possible through a careful selection of relevant parameters. By presenting this visual representation, we bridge the gap between theoretical findings and real-world applications. To reinforce the practical relevance of our mathematical insights, we have thoughtfully included a captivating image of bubbly solitary waves observed in the vast expanse of the ocean. This picture shows how our mathematical model and the real world are strongly connected. In this context, Fig. (7)b vividly illustrates the presence of an elliptical wave in the ocean, serving as a direct link between the contour plot showcased in Fig. (7)a, while Fig. (7)c intriguingly portrays a bubbly solitary wave in the ocean, seamlessly connecting to the three-dimensional representation highlighted in Fig. (7)a. In doing so, we aim to not only enrich our theoretical understanding but also demonstrate how the study of mathematical solutions can unlock a deeper appreciation of the incredible phenomena that occur naturally around us. This combination of theories and real-world experiences is incredibly helpful. It helps us understand things better and encourages us to discover and use these ideas in different areas of science and engineering.

Fig. 2
figure 2

Visualization of solution (18): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots

Full size image

5 Graphical overview and interpretations

In this section, we look into the behavior of the solutions obtained from the HFSC equation and present our findings graphically. To gain a comprehensive understanding of these solutions, it is essential to explore their graphical representations while carefully selecting appropriate constants within a specific range of values. Since the HFSC equation is the Schrödinger equation, we focus on three crucial aspects: the real part, the imaginary part, and the absolute value of the attained solutions.

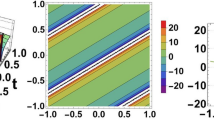
In Fig. (1), we examine the 3D and contour patterns of the solution (17) for \(p=2;q=0.1;r=0.1;\) \(a_1=19 i;a_2=0.3;a_3=0.3;b_1=0.3;b_2=1.2;\alpha =0.2 i;\beta =1.2;M_0=0.02;M_1=0.06;N_1=0.5;\) where \(x\in [0.071,0.1], y\in [-1,1]\), \(x\in [0.07,0.1], y\in [-1,0.8]\), and \(x\in [-0.2,0.2], y\in [-2,2.5]\), respectively, while 2D graphics are discussed for \(x\in [-0.2,0.2]\). Through these visualizations, we gain insights into the nature of lump solitons and their interaction with solitary waves.

In Fig. (2), we explore the 3D and contour behaviors of the real and imaginary components of solution (18) for \(p=4;q=0.1;r=0.1\) \(a_1=9 i;a_2=0.3;a_3=0.3;b_1=0.3;b_2=1.2;b_3=0.5;\alpha =0.2 i;\beta =1.2;M_0=0.02;M_1=0.06;N_1=0.5\) where \(x\in [-0.02,0.02], y\in [-1.5,1]\), \(x\in [0.02,0.02], y\in [-1,0.5]\), respectively, and consider the absolute part for \(p=4;q=0.1;r=0.1\) \(a_1=19 i;a_2=0.3;a_3=0.3;b_1=0.3;b_2=1.2;b_3=0.5;\alpha =0.2 i;\beta =1.2;M_0=0.02;M_1=0.06;N_1=0.5;\) within the range space \(x\in [-0.30,0.20], y\in [-1,2]\). Additionally, we provide 2D representations for \(x\in [-0.15,0.15]\) \(x\in [-0.15,0.15]\) and \(x\in [-0.05,0.05]\), respectively. This graphical representation shows the lump soliton and single soliton.

Fig. 3
figure 3

Visualization of solution (22): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots

Full size image

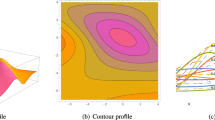
In Fig. (3), we focus on solution (22) for \(p=4;q=0.1;r=0.1;a_1=8 i;a_2=0.5;a_3=0.5;b_1=0.1;b_2=1;b_3=0.5;\alpha =2;\beta =2;M_0=2;M_1=3;N_1=0.1;\) where \(x\in [-0.3,0.3], y\in [-1.5,1.5]\), \(x\in [-0.3,0.3], y\in [-1.5,1.5]\), and \(x\in [-2.5,-1.5], y\in [-1,1]\), respectively, while 2D graphics are discussed for \(x\in [-0.3,0.3]\) \(x\in [-0.3,0.3]\) and \(x\in [-0.5,0.5]\), respectively. The displayed graphics show the presence of lump solitons, breather waves, and periodic solitons in distinct regions, revealing the complexity of their interactions.

In Fig. (4), we analyze the solution (32) for a \(p=4;q=0.1;r=0.1;a_1=29 i;a_2=0.5;a_3=0.5;b_1=0.1;b_2=1;b_3=0.5;\alpha =2;\beta =2;M_0=12;M_1=3;N_1=0.1;\) where \(x\in [-0.11,0.13], y\in [-2.3,2.3]\) (b) \(p=4;q=0.1;r=0.1;a_1=8 i;a_2=0.5;a_3=0.5;b_1=0.1;b_2=1;b_3=0.5;\alpha =2;\beta =2;M_0=2;M_1=3;N_1=0.1;\) where \(x\in [-0.5,0.5], y\in [-2,2]\) (c) \(p=4;q=0.1;r=0.1;a_1=8.01 i;a_2=0.5;a_3=0.5;b_1=0.1;b_2=1;b_3=0.5;\alpha =2;\beta =2;M_0=20;M_1=3;N_1=0.1;\) where \(x\in [-0.5,0.5], y\in [-2,2]\) and corresponding 2D graphics are discussed for \(x\in [-0.11,0.13]\) \(x\in [-0.5,0.5]\) and \(x\in [-0.5,0.5]\), respectively. By this visualization, we depicted the breather waves, lump solitons, and periodic soliton, respectively.

Fig. 4
figure 4

Visualization of solution (32): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots

Full size image
Fig. 5
figure 5

Visualization of solution (44): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots

Full size image
Fig. 6
figure 6

Visualization of solution (57): Exploring Real, Imaginary, and Absolute Components through 3D, Contour, and 2D Plots and showing connection with real-world phenomena

Full size image
Fig. 7
figure 7

Visualization of the real component of solution (63) through 3D plot connecting with bubbly ocean waves

Full size image

In Fig. (5), we present the graphical view of the solution (44) for (a) \(a_1=19 i;a_2=0.03;a_3=0.3;b_1=0.3;b_2=1.2;b_3=0.5;\alpha =0.2 i;\beta =1.2;\zeta _0=1;p=0.2;M_0=4 i;M_1=0.1;N_1=0.05;\) where \(x\in [0.420,0.430], y\in [-4,2]\) (b) \(a_1=19 i;a_2=0.03;a_3=0.3;b_1=0.3;b_2=1.2;b_3=0.5;\alpha =0.2 i;\beta =1.2;\zeta _0=1;p=0.2;M_0=4 i;M_1=0.1;N_1=0.05;\) where \(x\in [0.420,0.430], y\in [-4,2]\) (c) \(a_1=19 i; a_2=0.03; a_3=0.3; M_0=4 i; M_1=0.1; N_1=0.05; p=0.2; b_1=0.3;b_2=1.2;b_3=0.5;\alpha =0.2 i;\beta =1.2;\zeta _0=1;\) where \(x\in [0.40,0.46], y\in [-12,8]\) and corresponding 2D graphics are discussed for \(x\in [0.35,50]\) \(x\in [0.40,0.45]\) and \(x\in [0.40,0.46]\), respectively. By these visualization, we depicted the interaction of solitary wave and lump soliton.

In Fig. (6), our focus turns to the observation of solitary waves within the context of the solution (57) with the choice of parameters \(p=7;q=0.2;r=0.2;a_1=19 i;a_2=0.3;a_3=0.3;b_1=0.3;b_2=0.2;\alpha =0.2 i;\beta =1.2;M_0=0.2;M_1=0.6;N_1=0.5;\) where (a) \(x\in [-0.1,0.1], y\in [-1,1]\) (b) \(x\in [-0.27,0.25], y\in [-1.2,0.01]\) (c) \(x\in [-0.1,0.1], y\in [-1,1]\) and corresponding 2D graphics are discussed for \(x\in [-0.1,0.1]\), \(x\in [-0.27,0.25]\) and \(x\in [-0.1,0.1]\), respectively. By integrating real-world context, we have incorporated relatable visuals into our figures. These include depictions of a transverse wave moving along a rope, waves cresting atop the ocean’s surface, and the oscillations within the ocean depths. These relatable scenarios effectively mirror the patterns observed in our 2D plots, bridging the mathematical findings with the real-world phenomena.

In Fig. (7), we provide a visual depiction of the real part of solution (63). In part (a), where parameters are set as \(a_1=21i\), \(a_2=0.3\), \(a_3=0.3\), \(b_1=0.3\), and \(b_2=1.2\), along with \(\alpha =0.2i\), \(\beta =1.2\), \(M_0=0.02\), \(N_1=0.5\), and \(\zeta _0=0.5\), we explore the behavior within the range of \(x\in [-0.2,0.2]\) and \(y\in [-2,-1]\). This region reveals bubbly wave patterns. The contour visualization of these waves demonstrates a striking reflection of wave patterns, taking an elliptical form. To bridge this mathematical discovery with real-world analogs, we have incorporated an image of elliptical ocean waves in part (b). This image serves as a direct connection to the contour plot, reinforcing the relevance of our findings. In part (c), we have inserted an image of bubbly ocean waves, aligning with the 3D graphics, thereby enhancing our understanding of the dynamics.

6 Conclusion

In conclusion, the proposed Inverse \(\left( \frac{G'}{G}\right) \)-expansion method provides a structured and efficient way to find precise solutions for nonlinear partial differential equations. This method offers a systematic approach for obtaining accurate results. By transforming NLPDEs into ordinary differential equations through this specific technique, we have achieved remarkable success in deriving various exact solitary wave solutions for the HFSC equation. The method’s versatility and applicability extend to diverse fields of study, including engineering, physics, and mathematics, making it a valuable tool for researchers in these domains. Our research has showcased the power of the Inverse \(\left( \frac{G'}{G}\right) \)-expansion method by presenting 3D, 2D, and contour graphics that visually depict the behavior of the obtained solutions. Through careful parameter selection within suitable ranges, we have observed the emergence of diverse wave phenomena, including lump-type, breather-type, periodic, interaction of lumps with solitary waves, and bubbly solitary waves. These findings enrich our understanding of wave dynamics in different scenarios. To further emphasize the relevance of our results to real-world phenomena, we have provided visual comparisons to well-known wave phenomena, such as “Transverse wave in a Rope,” “Wave in the Ocean,” “Wave in ocean on bottom,” and “Bubbly Waves in the Ocean.” These visual connections reinforce the significance of our research and highlight its potential applications in various physical systems.