A generalized (2+1)-dimensional Hirota bilinear equation: integrability, solitons and invariant solutions

Abstract

In this paper, we consider an extended form of generalized $(2+1)$-dimensional Hirota bilinear equation which demonstrates nonlinear wave phenomena in shallow water, oceanography and nonlinear optics. We have successfully studied the integrability characteristic of the nonlinear equation in different aspects. We have applied the Painlevè analysis technique on the equation and found that it is not completely integrable in Painlevè sense. The concept of Bell polynomial form is introduced and the Hirota bilinear form, Bäcklund transformations are obtained. By means of Cole-Hopf transformation, we have derived the Lax pairs by direct linearization of coupled system of binary Bell polynomials. We have also derived infinite conservation laws from two field condition of the generalized $(2+1)$-dimensional Hirota bilinear equation. We have exploited the expressions of one-soliton, two-soliton and three-soliton solutions directly from Hirota bilinear form and demonstrated them pictorially. Further, Lie symmetry approach is applied to analyze the Lie symmetries and vector fields of the considered problem. The symmetry reductions were then obtained using similarity variables and some closed-form solutions such as parabolic wave solutions and kink wave solutions are secured.

1 Introduction

In the recent few decades, researchers are paying more attention to the nonlinear models rather than linear models due to rapid development of science and computer technology. In study of nonlinear models, a lot of integrable systems such as Korteweg de-Vries (KdV) equation, nonlinear Schrödinger equation, Kadomtsev–Petviashvili (KP) equation, modified Korteweg de-Vries (mKdV) equation, Boiti–Leon–Manna–Pempinelli equation, Bogoyavlenskii–Kadomtsev–Petviashvili equation, Camassa–Holm equation [1,2,3,4,5,6,7,8] serves as pioneer physical phenomenon which can be found in real-life situation in different areas of physics and engineering e.g. nonlinear optics [9], Bose–Einstein condensation [10], plasma physics [11], solid state physics [12], string theory [13], fluid mechanics [14], condensed matters [15], propagation of waves in shallow water [16], electro magnetics [17], ferromagnetics [18] and many more. All the equations possess several significant properties such as Hirota bilinear form, Painlevè analysis, Darboux transformations, infinitely many conservation laws, Hamiltonian, bi-Hamiltonian structures, Bäcklund transformations and Lax pair formulation. Among these strategies, Painlevè test [19] can be considered as the ideal one in analyzing the integrability aspect of a nonlinear equation. Weiss [20] checked the integrability characteristic of some well-known nonlinear evolution equations e.g. Burgers equation, KdV equation, mKdV equation, Boussinesq equation, higher-order KdV and KP equations, etc., by using Painlevè test and determined appropriate Lax pairs of those equations. Gibbon et al. [21] investigated the integrability aspect of nonlinear Schrödinger equation and mKdV equation and also shown that Bäcklund transformation deduced from Hirota’s method and Painlevè test are directly related. A. Bekir [22] explicitly presented the Painlevè test for some $(2+1)$-dimensional nonlinear equations and obtained the associated Bäcklund transformation and Hirota bilinear form directly using the Painlevè test. Wazwaz and Liu et al. [23, 24] discussed the integrability aspects of Boiti–Leon–Manna–Pempinelli equation and modified Korteweg-de Vries–Calogero–Bogoyavlenskii–Schiff equation, respectively, through Painlevè analysis and also obtained the exact solutions of those equations. On the other hand, the Hirota bilinear method [25] can be thought least complex and successful method to examine integrability aspect of a nonlinear equation. The Hirota bilinear strategy briefly changes over a nonlinear condition into a bilinear structure through a reliant variable change and yields quasi periodic wave solutions, rational solution, multi soliton solutions and other exact solutions by means of the bilinear structure. Zhang and Liu [26] obtained the multisoliton solution, quasi periodic solution of reverse space and time nonlocal Fokas–Lenells equation from its Hirota bilinear form. Based on Hirota bilinear method, Sheng et al. [27] obtained two-soliton solution, rational solution, semi-rational solution and multiple rational solution of Gardner equation. Li et al. [28] obtained the N-soliton solution, breather wave solution, periodic solution, rogue wave solution and lump solution of extended KP equation via Hirota bilinear form. Ismael et al. [29] derived the one lump, two lump, three lump solution and their interaction phenomena with one-soliton, two-soliton and three-soliton solution of generalized KP equation. Furthermore, the known connection between Hirota bilinear form and a class of P-polynomials (which is a special form of binary Bell polynomials in which all the factors with odd number derivatives are made as zero) introduces the Bell polynomial method proposed by Lambert and Gilson [30,31,32] which ensures the bilinear form of a nonlinear equation in a simpler way. Recently, a systematic combination of binary Bell polynomial and P-polynomial has served as a prominent means of study utilized by number of researchers to obtain the bilinear Bäcklund transformation and corresponding Lax pairs of nonlinear equations. Wang [33] checked the integrability characteristic of Hirota bilinear equation by obtaining its Hirota bilinear form, bilinear Bäcklund transformation and Lax pair with the help of bell polynomial theory. Lump solution and complexiton solution are also derived from Hirota bilinear form. Xu et al. and Zhao et al. [34, 35] implemented bell polynomial theory to obtain Bäcklund transformation, Lax pair and N-soliton solutions of the generalized Nizhnik–Novikov–Veselov equation and Davey–Stewartson system, respectively. An another context of nonlinear integrable system is to enquire the existence of infinite conservation laws. Finally, the way of dealing infinite conservation laws for some nonlinear evolution equations via the means of Bell-polynomial theory is developed by E. Fan [36]. Fan et al. [37] also generalized the classical bell polynomial theory by defining a class of super bell polynomials, which help us to obtain the bilinear Bäcklund transformation, Lax pair, infinite conservation laws systematically of some supersymmetric equations. Using these bell polynomial concept Wazwaz et al. and Wangan et al. [38,39,40] obtained the infinite conservation laws for $(4+1)$-dimensional Boiti–Leon–Manna–Pempinelli equation, higher-order Sawada-Kotera-type equation, higher-order Lax-type equation and $(3+1)$-dimensional generalized breaking soliton equation, respectively. Another elegant concept is the investigation of continuous Lie transformation groups (pioneered by Norwegian mathematician Sophus Lie), which leaves partial differential equations (PDEs) invariant [41,42,43,44]. Lie’s method is widely used to find closed-form similarity solutions to nonlinear PDEs. Using the invariance property, we can reduce the number of independent variables one by one. As a result, the nonlinear PDEs is reduced to an analytically solvable nonlinear ordinary differential equations (ODEs). S. Kumar et al. [45] investigated the exact invariant solutions and the dynamics of soliton solutions to the (2+1)-dimensional generalized Hirota–Satsuma–Ito equations by Lie symmetry analysis and derived different kind of closed form analytical solutions such as parabolic wave solitons, dark-bright solitons, W-shaped solitons, multi-wave structures and curved-shaped parabolic solitons. Rui et al. [46] studied invariant solution and conservation laws of $(2+1)$-dimensional Boussinesq equation by Lie symmetry analysis.

Very recently, Hua et al. [47] proposed a generalized $(2+1)$-dimensional Hirota bilinear equation

$$\begin{aligned}{} & {} u_{yt}+c_{1}\Bigg [u_{xxxy}+3(2u_{x}u_{y}+uu_{xy})\nonumber \\{} & {} \quad +3u_{xx} \int _{-\infty }^{x} u_{y}dx^{\prime }\Bigg ]+c_{2}u_{yy}=0, \end{aligned}$$

(1)

which portraits the study of a generalized model imparting nonlinear dynamical phenomena in shallow water. In Ref. [48], Hua et al. investigated the integrability characteristics of this equation. They have tested Painlevè property and proved that the equation fails to pass the test. After that they obtained the Hirota bilinear form and explored N-soliton solutions. They also exploited the linear superposition principle and Bell polynomial approach to generate resonant solutions, Bäcklund transformation, Lax pair and infinite conservation laws for the equation.

Furthermore, Zhao et al. [49] extended this model to a more generalized form

$$\begin{aligned}{} & {} u_{yt}+c_{1}\Bigg [u_{xxxy}+3(2u_{x}u_{y}+uu_{xy})\nonumber \\{} & {} \quad +3u_{xx} \int _{-\infty }^{x} u_{y}dx^{\prime }\Bigg ]+c_{2}u_{yy}+c_{3}u_{xx}=0, \end{aligned}$$

(2)

which ensures enriched physical meaning in nonlinear waves. The above governing equation can be observed as a $(2+1)$-dimensional generalized nonlinear wave equation endowed with three arbitrary constants $c_1,c_2$ and $c_3$. The authors have successfully obtained N- soliton solution, M-Lump solution, higher-order breather solution and hybrid solution of the Eq. Equation (2) in [49]. We have noticed that the bilinear Bäcklund transformation, Lax pair, infinite conservation laws and Lie symmetry analysis for Eq. (2) have not yet been studied in the literature which instigate us to examine these studies in the present exposition. Our primary focus in this present exposition is to investigate the integrability context of the nonlinear evolution Eq. (2). In this connection, we derive Hirota bilinear form, Lax pair formulation, Bäcklund transformation and infinite conservation laws through Bell polynomials to ensure the integrability aspect. We also derive different form of exact analytic solutions by exploiting Lie symmetry analysis.

The organization of our article is as follows. In Sect. 2, we discuss the Painlevè integrability of Eq. (2). In Sect 3, some fundamental ideas on binary Bell polynomials are analyzed. Sect. 4 is fully devoted on the analysis of Hirota bilinear form, Bäcklund transformation and corresponding Lax pair formulation of Eq. (2) using Bell Polynomial theory. In Sect. 5, an infinite sequence of conservation laws are demonstrated. Moreover, Sect. 6 deals with extracting multi-soliton solutions and illustrating them via corresponding figures. In Sect. 7, analysis of Lie symmetries and vector fields for the problem are shown using Lie symmetry approach. Finally we conclude in Sect. 8.

2 Painlevè analysis

Painlevè analysis [19, 20] can be treated as one of the most complicated but effective tool for checking the integrability aspect of a partial differential equation. A PDE which is single valued about the movable singularity manifold can be observed as a PDE which is integrable in Painlevè sense. In this section, we discuss the Painlevè integrability of Eq. (2) by using Weiss, Tabor, and Carnevale (WTC) method [19]. In the WTC procedure, we are to determine the leading orders Laurent series which enables to identify the powers at which the arbitrary functions can enter into the Laurent series. These are known as resonances and we need to verify the existence of sufficient number of arbitrary functions at the resonance values by not introducing the movable critical manifold. In WTC method, we choose the general solution of PDE in the following ansatz

$$\begin{aligned} v(x,t)=\psi ^{p}(x,t)\sum _{m=1}^{\infty }v_{m}(x,t)\psi ^{m}(x,t) \end{aligned}$$

(3)

where p is negative, $\psi (x, t) = 0$ is the equation of singular manifold and $v_m$ is to be determined by substitution of expansion Eq. (3) in the PDE. In this connection, the PDE takes the form

$$\begin{aligned} \sum _{m=0}^{\infty }E_{m}(v_0,v_1,...v_m,\psi )\psi ^{m+q}=0, \end{aligned}$$

(4)

where q is some negative constant and the values of $E_m$ depends on $\psi$ only by the derivatives of $\psi$. Now we follow the successive steps to discuss the Painlevè analysis. At first, we obtain possible leading orders p by balancing two or more terms of the PDE and conveying that they dominate all other terms. Next, we solve equation $E_0 = 0$ for nonzero values of $v_0$ which may yield several solutions known as branches. After that, we determine the resonance values which clearly provides the values of m for which $v_m$ is undetermined from equation $E_m = 0$. Usually it is in the form

$$\begin{aligned} E_{m}= & {} (m+1) P(m)\psi _{x}^j \psi _{t}^{n-j}u_{m}\nonumber \\{} & {} +Q(v_0,v_1,...v_{m-1},\psi )=0,\,\,\,\forall ~~m>0\,, \end{aligned}$$

(5)

where n denotes the order of the PDE, $0\le j \le n$ and P dictates a polynomial of degree $n-1$. It is to be mentioned that the resonance values are identical with the zeros of P. Finally, we are to examine the compatibility condition of the resonances. If at a resonance value, the direct substitution of the previously obtained value of $v_i, i \le m-1$, the function Q becomes either zero or nonzero, then $v_m$ can be considered arbitrarily and the expansion Eq. (3) does not exist for arbitrary $\psi$. In that case, the resonance is said to be compatible. Now, we exploit the above technique on the equation considered.

We use the following transformation $u=v_{x}$ which converts Eq. (2) into

$$\begin{aligned}{} & {} v_{xyt}+c_1[v_{xxxxy}+3(2v_{xx}v_{xy}+v_{x}v_{xxy}+v_{y}v_{xxx})]\nonumber \\{} & {} \quad +c_2v_{xyy}+c_3v_{xxx}=0. \end{aligned}$$

(6)

We assume that Eq. (2) possesses a solution in the form of Laurent series expansion as follows

$$\begin{aligned} v(x,y,t)=\psi (x,y,t)^\mu \sum _{m=0}^{\infty }v_{m}(x,y,t)\psi ^m(x,y,t),\nonumber \\ \end{aligned}$$

(7)

where $\psi$ and $v_{m}$ are the analytic functions near the singularity manifold $\psi =0$.

Substituting Eq. (7) in Eq. (6) and balancing the most dominant terms, we obtain

$$\begin{aligned} \mu =-1,\,\,\,v_0=2\psi _{x}. \end{aligned}$$

(8)

Furthermore, substituting Eq. (7) into Eq. (6) and equating the coefficient of $\psi ^{j-6}$, we have

$$\begin{aligned}{} & {} c_1(-6+m) (-5+m) (-4+m) (-1+m) \nonumber \\{} & {} \quad (1+m) v_m \psi _{y} \psi _{x}^4=0, \end{aligned}$$

(9)

which yields the resonance values as $m=-1,1,4,5,6$.

The resonance $m=-1$ represents the arbitrariness of the singular manifold $\psi (x,y,t)=0$. The coefficient of $\psi ^{-5}$ is zero, which clearly represents the arbitrariness of $v_1$.

With the help of MATHEMATICA, we collect the coefficients of $\psi ^{-4}$ and $\psi ^{-3}$, respectively, and obtain the explicit values of $v_2$ and $v_3$ as follows

$$\begin{aligned} \begin{aligned} v_2=&\frac{1}{2} \psi _{xy}\psi _{xx}{\psi _{y}}^{-1}{\psi _{x}}^{-2} -\frac{1}{6c_1}\psi _{t}{\psi _{x}}^{-2}\\&-\frac{c_2}{6c_1}{\psi _{y}}^{-1}-\frac{c_3}{6c_1}{\psi _{y}}^{-1}\\&-\frac{1}{2}{\psi _x}^{1}{\psi _y}^{-1}\psi _{xxy}-\frac{1}{6}{\psi _x}^{-2}\psi _{xxx}\\&-\frac{1}{2}{\psi _{y}}^{-1}v_{1,y}-\frac{1}{2}{\psi _{x}}^{-1}v_{1,x} \end{aligned} \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned} v_3=&-\frac{c_2}{8c_1}\psi _{y}{\psi _{x}}^{-4}\psi _{xx} +\frac{1}{8}{\psi _{y}}^{-3}\psi _{yy}{\psi _{x}}^{-2}\\&(\psi _{xy}\psi _{xx} +\psi _{x}\psi _{xxy}) -\frac{c_3}{24 c_1}{\psi _{y}}^{-3}\psi _{yy}\\&-\frac{1}{8} {\psi _{y}}^{-3}\psi _{yy} v_{1,y} +\frac{1}{2}{\psi _{y}}^{-2}{\psi _{x}}^{-3}{\psi _{xy}}^{2}\psi _{xx}\\&-\frac{1}{8}{\psi _{y}}^{-2}{\psi _{x}}^{-2} \left[ \psi _{xyy}\psi _{xx}+4\psi _{xy} \psi _{xxy}+\psi _{x}^2\right. \\&\left. \left\{ 3c_1\psi _{xxyy}-2\psi _{xy}(c_3+3c_1v_{1,y})\right\} \right. \\&\left. +3c_1\psi _{x}^3v_{1,yy}\right] +\frac{1}{24c_1}{\psi _{x}}^{-3}(3\psi _{yt}\psi _{x}^2\\&+3c_2\psi _{yy}\psi _{x}^2-3\psi _{t}\psi _{x}\psi _{xy}\\&+c_3\psi _{x}^2\psi _{xx}+9c_1\psi _{xy} \psi _{xx}^2-9c_1\psi _{x}\psi _{xx}\psi _{xxy}\\&-6c_1\psi _{x}\psi _{xy}\psi _{xxx}\\&+6c_1\psi _{x}^2\psi _{xxxy}+3c_1\psi _{x}^2\psi _{xx}v_{1,y}\\&+6c_1\psi _{x}^3v_{xy})+\frac{1}{24c_1}{\psi _{x}}^{-3}\psi _{y}\\&\left[ -3\psi _{xx}\left\{ \psi _{t}+c_1\psi _{x}^3 +\psi _{x}(\psi _{xt}-2c_2\psi _{xy}\right. \right. \\&\left. \left. +c_1\psi _{xxxx}-6\psi _{xx}v_{1,y}+3\psi _{x}v_{1,xx})\right\} \right] . \end{aligned} \end{aligned}$$

(11)

After simplifying the coefficients of $\psi ^{-2}$ and $\psi ^{-1}$, we found that both becomes zero, which indicates the arbitrariness of $v_4$ and $v_5$. By choosing $\psi (x,y,t)=x+\phi (y,t)$ and using Kruskal ansatz [50] for the resonance value $m=6$, we obtain the compatibility condition as

$$\begin{aligned} \begin{aligned}&-\frac{1}{6c_1}{\phi _{y}}^{-5}\phi _{yy}^2(c_3+3c_1v_{1,y})^2 +\frac{1}{24c_1}{\phi _{y}}^{-4}\\&\quad (c_3+3c_1v_{1,y}) {\text {[}}\phi _{yyy}\{c_3+3c_1v_{1,y}+3\phi _{yy}\\&\quad (5c_1v_{1,yy}+\phi _{yy}(\phi _{t}+3c_1 v_{1,x}))\}\\&\quad +54c_1^2\phi _{yy}^2 v_{1,xxy}]+\frac{1}{24c_1}{\phi _{y}}^{-2} {\text {[}}-c_3\phi _{t}\phi _{yyy}\\&\quad -3c_1\phi _{t}\phi _{yyy}v_{1,y} +\phi _{yt}\phi _{yy}(c_3 +3c_1v_{1,y})\\&\quad +4c_2\phi _{yy}^2(c_3+3c_1v_{1,y})-9c_1^2v_{1,yy}^2\\&\quad -3c_1c_3v_{1,yyy}-9c_1^2v_{1,y}v_{1,yyy}-3c_1c_3\phi _{yyy}v_{1,x}\\&\quad -9c_1^2\phi _{yyy}v_{1,y}v_{1,x}-18c_1^2\phi _{yyy}v_{1,xxy}\\&\quad -3c_1\phi _{yy}\{3\phi _{t}v_{1,yy}+7c_3v_{1,xy}\\&\quad +3c_1(3v_{1,yy}v_{1,x}+7v_{1,y}v_{1,xy}+6v_{1,xxyy})\}]\\&\quad +\frac{1}{8}c_2\phi _{y}^3v_{1,xxx}+\frac{1}{24c_1}\phi _{y}^{-1}\\&\quad {\text {[}}-\phi _{yyt}(c_3+3c_1v_{1,y})-2c_2\phi _{yyy}(c_3+3c_1v_{1,y})\\&\quad +3\phi _{t}\{c_1v_{1,yyy}-\phi _{yy}(\phi _{yt}+c_2\phi _{yy}-c_1v_{1,xy})\}]\\&\quad +\frac{1}{8}{\phi _{y}}^{-1} \{-3c_2\phi _{yy}^2v_{1,x}+3c_3v_{1,xyy}+3c_1(v_{1,yyy}v_{1,x}\\&\quad +4v_{1,yy}v_{1,xy}+3v_{1,y}v_{xyy}\\&\quad +2v_{1,xxyyy})+\phi _{yy}(2v_{1,yt}-c_2v_{1,yy}-3\phi _{yt}v_{1,x}\\&\quad +9c_1v_{1,x}v_{1,xy}+2c_3v_{1,xx}+6c_1v_{1,y}v_{1,xx}\\&\quad +2c_1v_{1,xxxy})\} +\frac{1}{8c_1}\{\phi _{yt}^2+\phi _{yt}(c_2\phi _{yy}\\&\quad +4c_1v_{xy})+\phi _{t}(\phi _{yyt}+c_2\phi _{yyy}-c_1v_{1,xyy})\\&\quad -c_1(2v_{1,yyt}+c_2v_{1,yyy}-3\phi _{yyt}v_{1,x}-3c_2\phi _{yyy}v_{1,x}\\&\quad -5c_2\phi _{yy}v_{1,xy}+12c_1v_{1,xy}^2\\&\quad +9c_1v_{1,x}v_{1,xyy}+6c_1v_{1,yy}v_{1,xx}\\&\quad +3c_3v_{1,xxy}+9c_1v_{1,y}v_{1,xxy}+2c_1v_{1,xxxyy})\}\\&\quad +\frac{1}{24c_1}\phi _{y} {\text {[}}2\phi _{ytt}+7c_2\phi _{yyt}+5c_2^2\phi _{yyy}\\&\quad +3c_1\{96c_1(v_{5,y}+v_{4,xy})+4v_{1,xyt}+3c_2v_{x,yy}\\&\quad -4\phi _{yt}v_{1,xx}-4c_2\phi _{yy}v_{1,xx}-\phi _{t}v_{1,xxy}\\&\quad +c_3v_{1,xxx}+c_1(12v_{1,xy}v_{1,xx}+9v_{1,x}v_{1,xxy}\\&\quad +3v_{1,y}v_{1,xxx}-2v_{1,xxxxy})\}]-\frac{1}{8}\phi _{y}^2[3c_1(32v_{5,x}\\&\quad +v_{1,xx}^2+32v_{4,xx})+2v_{1,xxt}+3c_2v_{xxy}\\&\quad -(\phi _{t}-3c_1v_{1,x})v_{1,xxx}+2c_1v_{1,xxxxx}] \end{aligned} \end{aligned}$$

(12)

which cannot be made equal to zero in case of nontrivial $c_1,c_2$ and $c_3$. Hence we can draw the conclusion that Eq. (2) does not pass the Painlevè test which ensures that Eq. (2) is not integrable in Painlevè sense. It is to be mentioned that Eq. (6) reduces to Eq.(4) of Ref. [47] when $c_3=0$ and all the results related to Painlevè analysis obtained there can be developed from our expressions in that case. This asserts the novelty of the Painlevè analysis method.

3 Bell polynomials

In this section, we briefly demonstrate some fundamental concepts and expressions of Bell polynomials [30, 31]. Let h be a $C^{\infty }$ function of t, then one-dimensional Bell polynomial [30] is defined as

$$\begin{aligned} Y_{nt}(h)= & {} Y_{n}(h_{1},h_{2},..,h_{nt})=e^{-h}{\partial _{t}}^{n}e^{h},\nonumber \\{} & {} \quad \,\,n=1,2,3,...\,. \end{aligned}$$

(13)

A few one-dimensional Bell polynomials can be derived from the above expression as follows

$$\begin{aligned} Y_{t}= & {} h_{t},\,\,Y_{2t}=h_{2t}+{h_{t}}^{2},\,\,Y_{3t}\nonumber \\= & {} h_{3t}+3h_{t}h_{2t}+{h_{t}}^{3},... \,. \end{aligned}$$

(14)

The expressions Eq. (14) are obtained by the formula given by

$$\begin{aligned} Y_{nt}(h)= & {} \sum \frac{n!}{a_{1}!a_{2}!...a_{n}!}\left( \frac{h_{t}}{1!}\right) ^{a_{1}}\nonumber \\{} & {} \left( \frac{h_{2t}}{2!}\right) ^{a_{2}}...\left( \frac{h_{nt}}{n!}\right) ^{a_{n}}, \end{aligned}$$

(15)

where the sum run over all partitions of $n=a_{1}+2{a_{2}}+...+na_{n}$.

We can extend the dimension of the Bell polynomial by assuming that $h=h(t_1,t_2,...,t_s)$ as a $C^{\infty }$ multi-variable function and then the multi-dimensional Bell polynomial can be defined as follows

$$\begin{aligned} Y_{n_{1}t_{1},...,n_{s}t_{s}}(h)\equiv & {} Y_{n_{1},...,n_{s}}(h_{m_{1}t_{1},...,m_{s}t_{s}})\nonumber \\= & {} e^{-h}\partial _{t_{1}}^{n_{1}}...\partial _{t_{s}}^{n_{s}}\,e^{h}, \end{aligned}$$

(16)

where $h_{m_{1}t_{1},...,m_{s}t_{s}}=\partial _{t_{1}}^{m_{1}}...\partial _{t_{s}}^{m_{s}}h,m_{i}=0,1,...,n_{i}\, \text{ and }i=1,2,...,s.$ Here $Y_{n_{1}t_{1},...,n_{s}t_{s}}(h)$ denotes the multi-variable Bell polynomial with respect to $h_{m_{1}t_{1},...,m_{s}t_{s}}$. Specially when $h=h(t,z)$, the associated few lowest order two-dimensional Bell polynomials can be calculated as follows

$$\begin{aligned}&Y_{2t(h)}=h_{2t}+h_t^2,\, Y_{3t(h)}=h_{3t}+3h_{2t}h_{t}+h_{t}^3 , \end{aligned}$$

(17)

$$\begin{aligned}&Y_{t,z}=h_{t,z}+h_{t}h_{z},\,\nonumber \\&Y_{2t,z}(h)=h_{2t,z}+h_{2t}h_{z}+2h_{t,z}h_{t}+h_{t}^{2}h_{z},... \end{aligned}$$

(18)

As per the above Bell polynomials Eq. (16), the multi-dimensional binary Bell polynomials can be characterized as follows

$$\begin{aligned} {\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu ,\omega )=Y_{n_{1}t_{1},...,n_{s}t_{s}}(h), \end{aligned}$$

(19)

where

$$\begin{aligned}{} & {} h_{m_{1}t_{1},...,m_{s}t_{s}}\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll}\nu _{m_{1}t_{1},...,m_{s}t_{s}},\,\,\,m_{1}+...+m_{s} \,\text{ is } \text{ odd, }\\ \omega _{m_{1}t_{1},...,m_{s}t_{s}},\,\,\,m_{1}+...+m_{s} \,\text{ is } \text{ even. }\end{array}\right. } \end{aligned}$$

(20)

According to the above definition, few binary Bell polynomials of lowest order can be calculated as follows

$$\begin{aligned}&{\mathscr {Y}}_{t}(\nu )=\nu _{t}, {\mathscr {Y}}_{2t} (\nu ,\omega )=\omega _{2t}+\nu _{t}^{2},\nonumber \\&{\mathscr {Y}}_{t,z}(\nu ,\omega )=\omega _{t,z}+\nu _{t}\nu _{z},\nonumber \\&{\mathscr {Y}}_{2t,z}(\nu ,\omega )=\nu _{2t,z}+\omega _{2t}\nu _{z}+2\omega _{t,z}\nu _{t}+\nu _{t}^2 \nu _{z}, \nonumber \\&{\mathscr {Y}}_{3t}=\nu _{3t}+3\omega _{2t}\nu _{t}+\nu _{t}^3 ,... \end{aligned}$$

(21)

The binary Bell polynomial and the standard Hirota bilinear expression $D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.g$ can be linked by the following identity

$$\begin{aligned}{} & {} (hg)^{-1}D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.g\nonumber \\{} & {} \quad ={\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu =\ln \,h/g,\,\omega =\ln \,hg), \end{aligned}$$

(22)

where the D- operator is introduced by Hirota [25] as

$$\begin{aligned}{} & {} D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.g =(\partial _{t_{1}}-\partial _{t_{1}^{\prime }})^{n_{1}}... (\partial _{t_{s}}-\partial _{t_{s}^{\prime }})^{n_{s}}\\{} & {} \quad h(t_1,...,t_s).g(t_{1}^{\prime },...t_{s}^{\prime }) |_{t_{1}^{\prime }=t_{1},...,t_{s}^{\prime }=t_{s}}. \end{aligned}$$

In case when $h=g$, the identity Eq. (22) becomes

$$\begin{aligned}{} & {} (h)^{-2}D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.h\nonumber \\{} & {} \quad ={\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu =0,\omega =2\,\ln h)\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll}0, n_{1}+...+n_{s} \,\text{ is } \text{ odd, } \\ {\mathscr {P}}_{n_{1}t_{1},...,n_{s}t_{s}}(p),\,\,\,n_{1}+...+n_{s} \,\text{ is } \text{ even. }\end{array}\right. } \end{aligned}$$

(23)

where ${\mathscr {P}}$-polynomials are the even ordered ${\mathscr {Y}}$-polynomials and first few of them are given as follows

$$\begin{aligned}{} & {} {\mathscr {P}}_{2t}(p) =p_{2t},{\mathscr {P}}_{t,z}=p_{t,z},\nonumber \\{} & {} {\mathscr {P}}_{3t,z}(p)=p_{3t,z}+3p_{t,z}p_{2t}, {\mathscr {P}}_{4t}(p)=p_{4t}+3p_{2t}^{2}.\nonumber \\ \end{aligned}$$

(24)

The binary Bell polynomial ${\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu ,\omega )$ can be written as a linear combination of ${\mathscr {P}}$-polynomials and Bell polynomials $Y_{n_{1}t_{1},...,n_{s}t_{s}}(\nu )$ as

$$\begin{aligned}&(hg)^{-1}D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.g\nonumber \\&\quad ={\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu ,\omega ),\nonumber \\&{ {\textbf {where}}}\,\,\mathbf {{\nu =\ln h/g \,\,{{\textbf {and}}}\, \omega =\ln \,hg}}\nonumber \\&\quad = {\mathscr {Y}}_{n_{1}t_{1},...,n_{s}t_{s}}(\nu ,\nu +p),\,\,\nonumber \\&{{\textbf {where}}}\,\,\mathbf {{\nu =\ln h/g\,\,{{\textbf {and}}}\,\,p=2\ln g}}\nonumber \\&\quad =\sum _{m_{1}=0}^{n_{1}}...\sum _{m_{s}=0}^{n_{s}}\prod _{i=1}^{s}\left( {\begin{array}{c}n_{i}\\ m_{i}\end{array}}\right) \nonumber \\&\qquad {\mathscr {P}}_{m_{1}t_{1},...,m_{s}t_{s}}(p) \,Y_{(n_{1}-m_{1})t_{1},...,(n_{s}-m_{s})t_{s}}(\nu ). \end{aligned}$$

(25)

Under the Hopf-Cole transformation $\nu =\ln \psi$, the Bell polynomial can be written as

$$\begin{aligned} Y_{n_{1}t_{1},...,n_{s}t_{s}}(\nu =\ln \psi )=\frac{\psi _{n_{1}t_{1},...,n_{s}t_{s}}}{\psi }, \end{aligned}$$

(26)

through which Eq. (25) can be reexpressed as

$$\begin{aligned}{} & {} (hg)^{-1}D_{t_{1}}^{n_{1}}...D_{t_{s}}^{n_{s}}h.g\nonumber \\{} & {} \quad =\psi ^{-1}\sum _{m_{1}=0}^{n_{1}}...\sum _{m_{s}=0}^{n_{s}}\prod _{i=1}^{s} \left( {\begin{array}{c}n_{i}\\ m_{i}\end{array}}\right) \nonumber \\{} & {} \qquad {\mathscr {P}}_{m_{1}t_{1},...,m_{s}t_{s}}(p)\,\psi _{(n_{1}-m_{1})t_{1},...,(n_{s}-m_{s})t_{s}}. \end{aligned}$$

(27)

The identity Eq. (27) presents the simplest way to construct the associated Lax pair of corresponding nonlinear evolution equation.

4 Bilinear form, bilinear Bäcklund transformation and Lax pair

In view of deriving the Hirota bilinear form of Eq. (2) via binary Bell polynomial, we introduce a potential field p by setting

$$\begin{aligned} u=p_{xx}. \end{aligned}$$

(28)

Substituting Eq. (28) into Eq. (2) and integrating with respect to x, we have

$$\begin{aligned} E(p)= & {} p_{y,t}+c_{1}(p_{3x,y}+3p_{2x}p_{x,y})\nonumber \\{} & {} +c_{2}p_{2y}+c_{3}p_{2x}=0. \end{aligned}$$

(29)

By using Eq. (24) and considering $c_{1}=c_{2}=c_{3}=1$, Eq. (29) can be rewritten as combination of ${\mathscr {P}}$-polynomial expressions as follows

$$\begin{aligned} E(p)= & {} {\mathscr {P}}_{y,t}(p)+{\mathscr {P}}_{3x,y}(p)\nonumber \\{} & {} +{\mathscr {P}}_{2y}(p)+{\mathscr {P}}_{2x}(p)=0. \end{aligned}$$

(30)

The transformation $p=2~ \ln g$ along with the help of Eq. (23), we have the bilinear form of Eq. (2) in the following form

$$\begin{aligned} (D_{y}D_{t}+D_{x}^{3}D_{y}+D_{y}^{2}+D_{x}^{2})g.g=0. \end{aligned}$$

(31)

We assume that $p=2~\ln g^{\prime }$ be another solution of Eq. (2) in view of obtaining bilinear Bäcklund transformation of (2). Furthermore, introducing two new variables

$$\begin{aligned} \nu =\frac{(p^{\prime }-p)}{2}=\ln \frac{g^{\prime }}{g},\,\,\omega =\frac{(p^{\prime }+p)}{2}=\ln gg^{\prime }, \end{aligned}$$

(32)

the corresponding two field condition can be written as

$$\begin{aligned} { C}(\nu ,\omega )=&E(p^{\prime })-E(p)=2[\nu _{y,t}+\nu _{3x,y}\nonumber \\&+3\omega _{2x}\nu _{x,y}+3\nu _{2x}\omega _{x,y}+\nu _{2y}+\nu _{2x}]=0\, \nonumber \\ =&2\frac{\partial }{\partial y}\left[ {\mathscr {Y}}_{t}(\nu )+{\mathscr {Y}}_{3x}(\nu ,\omega ) +{\mathscr {Y}}_{y}(\nu )\right] \nonumber \\&+6W(\nu ,\omega )=0, \end{aligned}$$

(33)

where $W(\nu ,\omega )\!=\!\text{ Wronskian }\left[ {\mathscr {Y}}_{x,y}(\nu ,\omega )\!+\!\frac{1}{3},{\mathscr {Y}}_{x}(\nu )\right] .$

Taking ${\mathscr {Y}}_{x,y}(\nu ,\omega )+\frac{1}{3}=\alpha {\mathscr {Y}}_{x}(\nu )$, where $\alpha$ is an arbitrary constant, Eq. (33) can be reduced to

$$\begin{aligned} {C} (\nu ,\omega )=2\frac{\partial }{\partial y}\left[ {\mathscr {Y}}_{t}(\nu )+{\mathscr {Y}}_{y}(\nu )+{\mathscr {Y}}_{3x}(\nu ,\omega )\right] =0.\nonumber \\ \end{aligned}$$

(34)

After decoupling the two field condition, we have the following two ${\mathscr {Y}}$-polynomials as follows

$$\begin{aligned}&{\mathscr {Y}}_{x,y}(\nu ,\omega )+\frac{1}{3}-\alpha {\mathscr {Y}}_{x}(\nu )=0,\, \end{aligned}$$

(35a)

$$\begin{aligned}&{\mathscr {Y}}_{t}(\nu )+{\mathscr {Y}}_{y}(\nu )+{\mathscr {Y}}_{3x}(\nu ,\omega )=\beta , \end{aligned}$$

(35b)

where $\beta$ is an arbitrary constant.

Using mixing variable expression Eq. (32) and through the expression Eq. (22), Eq. (35) can be written in the bilinear form as

$$\begin{aligned}&(g^{\prime }\cdot g)^{-1}\left[ D_{x}D_{y}-\alpha D_{x}+\frac{1}{3}\right] (g^{\prime }\cdot g)=0\,\end{aligned}$$

(36a)

$$\begin{aligned}&(g^{\prime }\cdot g)^{-1}[D_{t}+D_{y}+D_{x}^{3}](g^{\prime }\cdot g)=\beta , \end{aligned}$$

(36b)

which is the bilinear Bäcklund transformation of Eq. (2).

Substituting $\omega =\nu +p$ and $\nu =\ln \phi$ into the system of Eq. (35), we have the compatibility of the system of Eq. (35) for $\phi$ as

$$\begin{aligned}&\phi _{x,y}+p_{x,y}\phi +\frac{1}{3}\phi -\alpha \phi _{x}=0\,\end{aligned}$$

(37a)

$$\begin{aligned}&\phi _{t}+\phi _{3x}+3\phi _{x}p_{2x}+\phi _{y}-\phi \beta =0\, . \end{aligned}$$

(37b)

Eliminating $\phi$ from the above equations yields the compatibility condition as

$$\begin{aligned}{} & {} \partial _{x}[p_{y,t}+3p_{3x,y}+3p_{2x}p_{xy}+p_{2y}+p_{2x}]\nonumber \\{} & {} \quad =\partial _{x}[E(p)]=0. \end{aligned}$$

(38)

It follows that Eq. (38) can be considered as the integrability condition for the system of Eq. (37), which is the Lax pair of Eq. (2).

5 Infinite conservation laws

In order to derive the conservation laws for Eq. (2) we rewrite the Bell polynomial type Bäcklund transformation i.e. Equation (35) as follows

$$\begin{aligned}&\omega _{xy}+\nu _{x}\nu _{y}+\frac{1}{3}-\alpha \nu _{x}=0,\,\end{aligned}$$

(39)

$$\begin{aligned}&\nu _{t}+\nu _{3x}+3\nu _{x}\omega _{2x}+\nu _{x}^{3}+\omega _{y}=\beta . \end{aligned}$$

(40)

Introducing new potential function

$$\begin{aligned} \eta = \frac{p^{\prime }-p}{2}, \end{aligned}$$

(41)

we have the following from Eq. (32)

$$\begin{aligned} \eta =\nu _{x},\,\,\,\,\omega _{x}={\partial }_{x}^{-1}u +\eta ,\,\,\,\,\nu _{y}={\partial }_{x}^{-1}(\eta _{y}). \end{aligned}$$

(42)

Substituting Eq. (42) in Eq. (39), we have

$$\begin{aligned} {\partial }_{x}^{-1}u_{y}+\eta _{y}+\eta \left( {\partial }_{x}^{-1}\eta _{y}\right) -\alpha \eta +\frac{1}{3}=0. \end{aligned}$$

(43)

Differentiating Eq. (40) and substituting Eq. (42) in Eq. (40) yields

$$\begin{aligned} \eta _{t}+\partial _{x}[\eta _{xx}+3\eta (u+\eta _{x})+\eta ^{3}]+\eta _{y}=0. \end{aligned}$$

(44)

Substituting the series expansion

$$\begin{aligned} \eta =\sum _{n=1}^{\infty }I_{n}\left( {\partial }_{x}^{-1}u,u,u_{x},u_{y},...\right) \alpha ^{-n} \end{aligned}$$

(45)

into Eq. (43) and equating coefficient of powers of $\alpha$, we obtain the conserved densities formulas as follows

$$\begin{aligned} I_{1}&={\partial }_{x}^{-1}u_{y}+\frac{1}{3},\, \end{aligned}$$

(46)

$$\begin{aligned} I_{2}&=I_{1,y}={\partial }_{x}^{-1}u_{yy}, \end{aligned}$$

(47)

$$\begin{aligned} I_{3}&=I_{2,y}+I_{1}({\partial }_{x}^{-1}I_{1,y})\nonumber \\&={\partial }_{x}^{-1}u_{yyy}+\left( {\partial }_{x}^{-1}u_{y}+\frac{1}{3}\right) ({\partial }_{x}^{-2}u_{yy}), \end{aligned}$$

(48)

$$\begin{aligned} I_{4}&=I_{3,y}+I_{1}({\partial }_{x}^{-1}I_{2,y})+I_{2}({\partial }_{x}^{-1}I_{1,y})\,\nonumber \\&={\partial }_{x}^{-1}u_{yyyy}+({\partial }_{x}^{-1}u_{yy})({\partial }_{x}^{-2}u_{yy})\nonumber \\&\quad +\left( {\partial }_{x}^{-1}u_{y}+\frac{1}{3}\right) ({\partial }_{x}^{-2}u_{yyy})\nonumber \\&\quad +\left( {\partial }_{x}^{-1}u_{y}\frac{1}{3}\right) ({\partial }_{x}^{-2}u_{yyy}) +({\partial }_{x}^{-1}u_{yy})({\partial }_{x}^{-2}u_{yy}), \nonumber \\&\qquad \quad .....\end{aligned}$$

(49)

$$\begin{aligned} I_{n}&=I_{n-1,y}+\sum _{i=1}^{n-1}I_{i}({\partial }_{x}^{-1}I_{n-1-i,y}). \end{aligned}$$

(50)

Again substituting the series expansion of $\eta$ from Eq. (45) into Eq. (44) we have

$$\begin{aligned}{} & {} \sum _{n=1}^{\infty }I_{n,t}\alpha ^{-n}+{\partial }_{x} \left[ \sum _{n=1}^{\infty }I_{n,xx}\alpha ^{-n} +3\left( \sum _{n=1}^{\infty }I_{n}\alpha ^{-n}\right) \right. \nonumber \\{} & {} \quad \left. \left( u+\sum _{n=1}^{\infty }I_{n,x}\alpha ^{-n}\right) +\left( \sum _{n=1}^{\infty }I_{n}\alpha ^{-n}\right) ^{3}\right] \nonumber \\{} & {} \quad +\sum _{n=1}^{\infty }I_{n,y}\alpha ^{-n}=0, \end{aligned}$$

(51)

which successively provides following conservation laws by comparing the coefficient of the different powers of $\alpha$ as below

$$\begin{aligned} {\mathscr {A}}_{n,t}+{\mathscr {B}}_{n,x}+{\mathscr {C}}_{n,y}=0, \end{aligned}$$

(52)

where ${\mathscr {B}}_{n}(n=1,2,...)$ are obtained as follows

$$\begin{aligned}&{\mathscr {B}}_{1}=I_{1,xx}+3uI_{1}, \end{aligned}$$

(53)

$$\begin{aligned}&{\mathscr {B}}_{2}=I_{2,xx}+3(I_{2}u+I_{1}I_{1,x}), \end{aligned}$$

(54)

$$\begin{aligned}&{\mathscr {B}}_{3}=I_{3,xx}+3(I_{3}u+I_{1}I_{2,x}+I_{2}I_{1,x})+I_{1}^{3}, \end{aligned}$$

(55)

$$\begin{aligned} \vdots \nonumber \\&{\mathscr {B}}_{n}=I_{n,xx}+3\sum _{i+j=n}I_{i}I_{j,x}+3I_{n}u\nonumber \\&\quad +\sum _{i+j+k=n}I_{i}I_{j}I_{k},\,\,\,n=1,2,3,... \end{aligned}$$

(56)

Finally, the remaining fluxes ${\mathscr {A}}_{n}$ and ${\mathscr {C}}_{n}$ are given by the recursion formulas Eq. (46)-Eq. (50). It is to be mentioned that the x-derivative of Eq. (52) for $n=1$, i.e. the x-derivative of the first conservation law is Eq. (2) itself.

6 Soliton solutions

6.1 One-soliton solution

We can retrieve the one-soliton solution of Eq. (2) by assuming g in the following form

$$\begin{aligned} g=1+e^{\wp _{1}}, \end{aligned}$$

(57)

where

$$\begin{aligned} \wp _{1}=k_{1}(x+p_{1}y+w_{1}t)+\wp _{1}^{0} \end{aligned}$$

(58)

with $k_{1}$ and $\wp _{1}^{0}$ as arbitrary constants. Substituting Eq. (57) with Eq. (58) in Eq. (31) and equating the coefficients of all exponential function to zero, we have obtained the dispersion relation as

$$\begin{aligned} w_{1}=-\left[ k_{1}^2+\frac{1+p_{1}^{2}}{p_{1}}\right] . \end{aligned}$$

(59)

Finally, substituting Eq. (57) in Eq. (31), we retrieve the one-soliton solution of Eq. (2) as

$$\begin{aligned} u=2[\ln (1+e^{{\wp }_{1}})]_{2x}, \end{aligned}$$

(60)

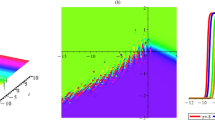
where $\wp _{1}$ and $w_{1}$ are given by Eq. (58) and Eq. (59), respectively. We choose the parametric values as $k_1=1.2, k_2 =1\,\text{ and } \,\wp _{1}^{0}=0$ and obtain the one soliton solution of Eq. (2) as shown in Fig. 1.

Fig. 1

The figures of the solution of the Eq. (2) given by Eq. (60), when $k_1=1.2, p_1 =1\,\text{ and }\, \wp _{1}^{0}=0$, describing one-soliton solution a 3D plot b density plot and c 2D plot at different time

6.2 Two-soliton solution

The two-soliton solution of Eq. (2) can be obtained by assuming g in the following form

$$\begin{aligned} g=1+e^{\wp _{1}}+e^{\wp _{2}}+K_{12}e^{\wp _{1}+\wp _{2}}, \end{aligned}$$

(61)

where

$$\begin{aligned} \wp _{i}=k_{i}(x+p_{i}y+w_{i}t)+\wp _{i}^{0}(i=1,2) \end{aligned}$$

(62)

with $k_{i} \,(i=1,2)$ and $\wp _{i}^{0}\, (i=1,2)$ as arbitrary constants. Substituting Eq. (61) with Eq. (62) in Eq. (34) and equating the coefficients of all exponential function to zero, we have obtained the dispersion relation and $K_{12}$ as follows

$$\begin{aligned}&w_{i}=-\left[ k_{i}^2+\frac{1+p_{i}^{2}}{p_{i}}\right] \, , (i=1,2),\end{aligned}$$

(63)

$$\begin{aligned}&K_{12}=\frac{3p_{1}p_{2}k_{1}k_{2}(k_{1}p_{1}-k_{2}p_{2})(k_{2}-k_{1})-(k_{2}p_{1}-k_{1}p_{2})-(k_{1}-k_{2})^{2}p_{1}p_{2}}{3p_{1}p_{2}k_{1}k_{2}(k_{1}p_{1} +k_{2}p_{2})(k_{1}+k_{2})-(k_{2}p_{1}+k_{1}p_{2})+(k_{1}+k_{2})^{2}p_{1}p_{2}}. \end{aligned}$$

(64)

Furthermore, substituting Eq. (61) in Eq. (31), we obtain the two-soliton solution of the Eq. (2) as

$$\begin{aligned} u=2[\ln (1+e^{\wp _{1}}+e^{\wp _{2}}+K_{12}e^{\wp _{1}+\wp _{2}})]_{2x}, \end{aligned}$$

(65)

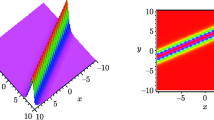
where $\wp _{i}, w_{i}(i=1,2)$ and $K_{12}$ are given by Eq. (62),  Eq. (63) and Eq. (64), respectively. We consider the following parametric values as $k_1=1.5, p_1=1.4, k_2=2.8, p_2=1 \text{ and } \, \wp _{i}^{0}=0~(i=1,2)$ and obtain the two-soliton solution of Eq. (2) as shown in Fig. 2. We also depict the overtaking collisions between two-soliton solutions in Fig. 3.

Fig. 2

The figures of the solution of the Eq. (2) given by Eq. (65), when $k_1=1.5, p_1=1.4, k_2=2.8, p_2=1\,\,\text{ and }\, \wp _{i}^{0}=0,(i=1,2)$ describing two-soliton solution a 3D plot, b density plot and c 2D plot at different time

Fig. 3

Depicting overtaking collisions between two-soliton solutions

6.3 Three-soliton solution

In a similar way, we can find three-soliton solution of Eq. (2) by assuming g in the following form

$$\begin{aligned} g= & {} 1+e^{\wp _{1}}+e^{\wp _{2}}+e^{\wp _{3}}+K_{12}e^{\wp _{1}+\wp _{2}}\nonumber \\{} & {} +K_{13}e^{\wp _{1}+\wp _{3}}+K_{23}e^{\wp _{2}+\wp _{3}}+K_{123}e^{\wp _{1}+\wp _{2}+\wp _{3}},\nonumber \\ \end{aligned}$$

(66)

where

$$\begin{aligned} \wp _{i}=k_{i}(x+p_{i}y+w_{i}t)+\wp _{i}^{0}(i=1,2,3) \end{aligned}$$

(67)

with $k_{i} \,(i=1,2)$ and $\wp _{i}^{0}\, (i=1,2,3)$ as arbitrary constants. Substituting Eq. (66) with Eq. (67) in Eq. (2) and equating the coefficients of all exponential function to zero we have obtained the dispersion relation and $K_{ij}$ as follows

$$\begin{aligned}&w_{i}=-\left[ k_{i}^2+\frac{1+p_{i}^{2}}{p_{i}}\right] \,(i=1,2,3),\end{aligned}$$

(68)

$$\begin{aligned}&K_{ij}=\frac{3p_{i}p_{j}k_{i}k_{j}(k_{i}p_{i}-k_{j}p_{j})(k_{j}-k_{i})-(k_{j}p_{i}-k_{i}p_{j})-(k_{i}-k_{j})^{2}p_{i}p_{j}}{3p_{i}p_{j}k_{i}k_{j}(k_{i}p_{i}+k_{j}p_{j})(k_{i}+k_{j})-(k_{j}p_{i}+k_{i}p_{j})+(k_{i}+k_{j})^{2}p_{i}p_{j}}\,\,(i=1,2,3),\end{aligned}$$

(69)

$$\begin{aligned}&K_{123}=K_{12}K_{13}K_{23}. \end{aligned}$$

(70)

Finally, we substitute Eq. (66) in Eq. (31) and obtain three-soliton solution of Eq. (2) as

$$\begin{aligned} u= & {} 2[\ln (1+e^{\wp _{1}}+e^{\wp _{2}}+e^{\wp _{3}}+K_{12}e^{\wp _{1}+\wp _{2}}\nonumber \\{} & {} +K_{13}e^{\wp _{1} +\wp _{3}}+K_{23}e^{\wp _{2}+\wp _{3}}+K_{123}e^{\wp _{1}+\wp _{2}+\wp _{3}})]_{2x},\nonumber \\ \end{aligned}$$

(71)

where $\wp _{i}, w_{i}(i=1,2,3)$ and $K_{ij}$ are given by Eq. (67), Eq. (68) and Eq. (69), respectively. The following parametric values $k_1=1.5, p_1=.7, k_2=2.3, p_2=1, k_3=2.8, p_3=2.1 \,\text{ and }\,\, \wp _{i}^{0}=0,(i=1,2,3)$ are considered to visualize the two-soliton solution of Eq. (2) in Fig. 4. Also we demonstrate overtaking collisions between three-soliton solutions in Fig. 5.

Fig. 4

The figures of the solution of the Eq. (2) given by Eq. (71), when $k_1=1.5, p_1=.7, k_2=2.3, p_2=1, k_3=2.8, p_3=2.1\,\, \text{ and } \,\wp _{i}^{0}=0,(i=1,2,3)$ describing three-soliton solution (a) 3D plot (b) density plot and (c) 2D plot at different time

Fig. 5

Depicting overtaking collisions between three-soliton solutions

6.4 Graphical illustration

Here we illustrate the pictorial representation of the one, two and three-soliton solutions elaborately using MATHEMATICA software. Figure 1 depicts the 3D plot, density plot and 2D plot of one-soliton solution of the governing Eq. (2), where the parametric values are chosen as $k_1=1.2, p_1=1,\, \text{ and }\, \wp _{i}^{0}=0$. The same illustrations are depicted in Fig. 2 and Fig. 4 in which the 3D plot, contour plot and density plot of two-soliton solution and three-soliton solution of the same Eq. (2) are demonstrated by choosing the parameter values as $k_1=1.5, p_1=1.5, k_2=2.8, p_2=1\, \text{ and }\,\wp _{i}^{0}=0,(i=1,2)$ and $k_1=1.5, p_1=.7, k_2=2.3, p_2=1, k_3=2.8, p_3=2.1 \,\text{ and }\, \wp _{i}^{0}=0,(i=1,2,3)$, respectively. Figure 3 and Fig. 5 demonstrates the motion of two-soliton and three-soliton solutions of the governing equation along the x-line for the time $t\in [-20,20]$, respectively. The remarkable features of the two- and three-soliton solutions can be noted from the plot. The bigger solitary waves appearing behind the smaller waves starts propagating towards the smaller one and make elastic collisions and eventually after the collision, all the waves restore their shapes and the bigger waves continue moving in front of the smaller ones. It can be seen clearly that two-soliton solutions and three-soliton solutions preserve their original shape and size even after the interaction having a phase change only.

7 Lie symmetry analysis

The basic methodology for obtaining the infinitesimal generators of Eq. (6), which is driven from Eq. (1) by the transformation $u = \upsilon _{x}$, has been presented in this section. Consider a one-parameter $(\varrho )$ Lie group of point transformations, which leave Eq. (6) invariant

$$\begin{aligned} \begin{aligned} x^*&=x+\varrho \,\xi (x,y,t,\upsilon )+O(\varrho ^2),\\ y^*&=t+\varrho \,\tau (x,y,t,\upsilon )+O(\varrho ^2),\\ t^*&=t+\varrho \,\phi (x,y,t,\upsilon )+O(\varrho ^2),\\ \upsilon ^*&=\upsilon +\varrho \,\eta (x,y,t,\upsilon )+O(\varrho ^2), \end{aligned} \end{aligned}$$

(72)

where $\xi , \tau , \phi$ and $\eta$ are known as coefficient functions of infinitesimal symmetries relying on x, y, t and $\upsilon$. The infinitesimal generator V, also known as vector field, affiliated with the preceding transformation is shown as

$$\begin{aligned} V = \xi \dfrac{\partial }{\partial x} + \tau \dfrac{\partial }{\partial y} + \phi \dfrac{\partial }{\partial t} + \eta \dfrac{\partial }{\partial \upsilon }. \end{aligned}$$

(73)

If symmetry of Eq. (6) is generated by infinitesimal generator V, then it must satisfy the invariance condition for Eq. (6):

$$\begin{aligned} Pr^{(5)}V(\Delta ) = 0, \end{aligned}$$

(74)

where $\Delta \equiv \upsilon _{xyt} + c_{1} [\upsilon _{xxxxy} + 3(2 \upsilon _{xx}\upsilon _{xy} + \upsilon _{x} \upsilon _{xxy} + \upsilon _{y} \upsilon _{xxx})] + c_{2} \upsilon _{xyy} + c_{3} \upsilon _{xxx}$. Here, $Pr^{(5)}$ represents the fifth-order prolongation, which can be written as

$$\begin{aligned} Pr^{(5)}= & {} V + \eta ^{x}\dfrac{\partial }{\partial \upsilon _{x}} + \eta ^{y}\dfrac{\partial }{\partial \upsilon _{y}} + \eta ^{xx}\dfrac{\partial }{\partial \upsilon _{xx}}\nonumber \\{} & {} + \eta ^{xy}\dfrac{\partial }{\partial \upsilon _{xy}} + \eta ^{xxx}\dfrac{\partial }{\partial \upsilon _{xxx}}\nonumber \\{} & {} + \eta ^{xxy}\dfrac{\partial }{\partial \upsilon _{xxy}} + \eta ^{xyy}\dfrac{\partial }{\partial \upsilon _{xyy}}\nonumber \\{} & {} + \eta ^{txy}\dfrac{\partial }{\partial \upsilon _{txy}} + \eta ^{xxxxy}\dfrac{\partial }{\partial \upsilon _{xxxxy}}, \end{aligned}$$

(75)

where $\eta ^{x}, \eta ^{y}, \eta ^{xx}, \eta ^{xy}, \eta ^{xxx}, \eta ^{xxy}, \eta ^{xyy}, \eta ^{txy}$ and $\eta ^{xxxxy}$ are known as invariant coefficients (for more details see [41, 42]).

By applying the prolongation formula 75 to Eq. (6), a system of determining equations has been obtained. The following infinitesimals are obtained after solving those determining equations:

$$\begin{aligned} \begin{aligned} \xi =&\ \dfrac{F_{1}^{\prime }(t) x}{3} + F_{3}(t), \ \ \ \tau = c_{2} F_{1}(t)\\&+ F_{2}\left( \dfrac{tc_{2}-y}{c_{2}}\right) , \ \ \ \phi = F_{1}(t),\\ \eta =&\ \dfrac{1}{18 c_{1}} \left\{ -6 c_{1} \upsilon F_{1}^{\prime }(t) + x^{2} F_{1}^{\prime \prime }(t) + 6 x F_{3}^{\prime }(t)\right. \\&\left. - 2 c_{3} y F_{1}^{\prime }(t) - 6 c_{3} F_{2}\left( \dfrac{tc_{2}-y}{c_{2}}\right) + 18 c_{1} F_{4}(t) \right\} . \end{aligned} \end{aligned}$$

(76)

Taking $F_{1}(t) = k_{1} t + k_{2}, F_{2}\left( \frac{tc_{2}-y}{c_{2}}\right) = k_{3}, F_{3}(t) = k_{4} t + k_{5}$ and $F_{4}(t) = k_{6}$, the infinitesimals transform to

$$\begin{aligned} \begin{aligned} \xi =&\ \dfrac{k_{1} x}{3} + k_{4} t + k_{5},\\ \tau =&c_{2} (k_{1} t + k_{2}) + k_{3}, \ \ \ \phi = k_{1} t + k_{2},\\ \eta =&\ \dfrac{1}{18 c_{1}} \left\{ -6 k_{1} c_{1} \upsilon + 6 k_{4} x - 2 k_{1} c_{3} y \right. \\&\left. - 6 k_{3} c_{3} + 18 k_{6} c_{1} \right\} . \end{aligned} \end{aligned}$$

(77)

Thus, Lie algebra of symmetries of Eq. (6) can be spanned by the following vector fields:

$$\begin{aligned} \begin{aligned} V_{1}&= \ \dfrac{x}{3} \dfrac{\partial }{\partial x} + c_{2} t \dfrac{\partial }{\partial y} + t \dfrac{\partial }{\partial t} \\&\quad + \dfrac{1}{18 c_{1}} \left\{ -6 c_{1} \upsilon - 2 c_{3} y \right\} \dfrac{\partial }{\partial \upsilon },\\ V_{2}&= \ c_{2} \dfrac{\partial }{\partial y} + \dfrac{\partial }{\partial t}, \ \ \ V_{3} = \dfrac{\partial }{\partial y} - \dfrac{c_{3}}{3 c_{1}} \dfrac{\partial }{\partial \upsilon },\\ V_{4}&= \ t \dfrac{\partial }{\partial x} + \dfrac{x}{3 c_{1}} \dfrac{\partial }{\partial \upsilon }, \ \ \ V_{5} = \dfrac{\partial }{\partial x},\ \ \ V_{6} = \dfrac{\partial }{\partial \upsilon }. \end{aligned} \end{aligned}$$

(78)

Using the similarity variables, now we reduce the governing Eq. (6) into nonlinear ODEs. To do so, we must solve the corresponding characteristic equation

$$\begin{aligned} \frac{dx}{\xi (x,y,t,\upsilon )}= & {} \frac{dy}{\tau (x,y,t,\upsilon )} =\frac{dt}{\phi (x,y,t,\upsilon )}\nonumber \\= & {} \frac{du}{\eta (x,y,t,\upsilon )}, \end{aligned}$$

(79)

where $\xi ,\,\tau ,\, \phi$ and $\eta$ are given by Eq. (76). To solve Lagrange’s Eq. (79), let us take, following cases of vector fields:

• (i) $V_{1}$,

• (ii) $V_{4} + \alpha V_{2}$,

• (iii) $V_{2} + \beta V_{5} + \lambda V_{6}$,

where $\alpha , \ \beta$ and $\lambda$ are arbitrary real numbers.

7.1 The generator $V_{1}$

Along with the generator $V_{1}$, Lagrange’s equation becomes

$$\begin{aligned} \dfrac{dx}{\frac{x}{3}}=\dfrac{dy}{c_{2} t}=\dfrac{dt}{t}=\dfrac{d\upsilon }{-\left[ \frac{\upsilon }{3}+\frac{c_{3} y}{9 c_{1}}\right] }, \end{aligned}$$

(80)

which gives the following similarity variables

$$\begin{aligned} \begin{aligned} X =&\ \dfrac{x}{t^{\frac{1}{3}}},\\ Y =&\ y - c_{2} t,\\ \upsilon (x,y,t) =&\ \dfrac{F(X,Y)}{t^{\frac{1}{3}}} - \dfrac{c_{3}}{12 c_{1}} (4 y - 3 c_{2} t). \end{aligned} \end{aligned}$$

(81)

On plugging Eq. (81) into Eq. (6), we have

$$\begin{aligned}{} & {} -2 F_{XY} + 3 c_{1} (F_{XXXXY}+ 6 F_{XX} F_{XY} + 3 F_{X} F_{XXY}\nonumber \\{} & {} \quad + 3 F_{Y} F_{XXX}) - X F_{XXY} = 0. \end{aligned}$$

(82)

Again, Eq. (82) admits infinitesimals given as

$$\begin{aligned} \begin{aligned} \xi _{X} =&\ d_{2} + d_{3} X,\\ \xi _{Y} =&\ d_{1} S_{1}(Y) + d_{2} S_{2}(Y) + d_{3} S_{3}(Y),\\ \eta _{F} =&\ d_{1} + \dfrac{d_{2} X}{9 c_{1}} + d_{3} \left( \dfrac{X^{2}}{6 c_{1}} - F \right) , \end{aligned} \end{aligned}$$

(83)

where $d_{i}$’s $(1 \le i \le 3)$ are arbitrary constants and $S_{i}$’s $(1 \le i \le 3)$ are arbitrary functions of Y.

7.1.1 $d_{1} \ne 0$, while $d_{2}$ and $d_{3}$ are zero.

In this case, we have the following generator

$$\begin{aligned} V_{11} = S_{1}(Y) \dfrac{\partial }{\partial Y} + \dfrac{\partial }{\partial F}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} G^{\prime \prime \prime } = 0, \end{aligned}$$

(84)

where $(^{\prime })$ represents the derivative with respect to new independent variable $\varphi$, given by

$$\begin{aligned} \varphi = X, \quad F(X,Y) = \int \dfrac{1}{S_{1}(Y)} dY + G(\varphi ). \end{aligned}$$

(85)

The solution of Eq. (84) is

$$\begin{aligned} G(\varphi ) = A_{0} + A_{1} \varphi + A_{2} \varphi ^{2}, \end{aligned}$$

(86)

where $A_{j}$’s $(0 \le j \le 2)$ are arbitrary constants. Inserting the value of $G(\varphi )$ in Eq. (85) and then the resultant in Eq. (81), gives the closed-form solution of Eq. (6) as follow

$$\begin{aligned}{} & {} \upsilon (x,y,t)\nonumber \\{} & {} \quad = \dfrac{1}{t^{\frac{1}{3}}}\left( A_{0} + A_{1} \dfrac{x}{t^{\frac{1}{3}}} + A_{2} \dfrac{x^{2}}{t^{\frac{2}{3}}} + \int \dfrac{1}{S_{1}(Y)} dY \right) \nonumber \\{} & {} \qquad - \dfrac{c_{3}}{12 c_{1}} (4 y - 3 c_{2} t), \end{aligned}$$

(87)

where $Y = y - c_{2} t$.

7.1.2 $d_{2} \ne 0$, while $d_{1}$ and $d_{3}$ are zero.

In this case, we have generator in the form

$$\begin{aligned} V_{12} = \dfrac{\partial }{\partial X} + S_{2}(Y) \dfrac{\partial }{\partial Y} + \dfrac{X}{9 c_{1}} \dfrac{\partial }{\partial F}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} G^{\prime \prime \prime \prime \prime } + 6 \left( G^{\prime \prime }\right) ^{2} + 6 G^{\prime } G^{\prime \prime \prime } = 0,\nonumber \\ \end{aligned}$$

(88)

where

$$\begin{aligned} \varphi = X - \int \dfrac{1}{S_{2}(Y)} dY, \quad F(X,Y) = \dfrac{X^{2}}{18 c_{1}} + G(\varphi ).\nonumber \\ \end{aligned}$$

(89)

The solution of Eq. (88) is

$$\begin{aligned} G(\varphi ) = A_{0} + \dfrac{2 A_{1}}{A_{1} \varphi + A_{2}}. \end{aligned}$$

(90)

Hence, invariant solution of Eq. (6) becomes

$$\begin{aligned}{} & {} \upsilon (x,y,t) \nonumber \\{} & {} \quad = \dfrac{1}{t^{\frac{1}{3}}}\left( A_{0} + \dfrac{x^{2}}{18 c_{1} t^{\frac{2}{3}}}\right. \nonumber \\ {}{} & {} \qquad \left. + \dfrac{2 A_{1}}{A_{1}\left( \dfrac{x}{t^{\frac{1}{3}}} - \int \dfrac{1}{S_{2}(Y)} dY \right) + A_{2}} \right) \nonumber \\{} & {} \qquad - \dfrac{c_{3}}{12 c_{1}} (4 y - 3 c_{2} t),\nonumber \\ \end{aligned}$$

(91)

where $Y = y - c_{2} t$.

7.1.3 $d_{3} \ne 0$, while $d_{1}$ and $d_{2}$ are zero.

This case yields the following generator

$$\begin{aligned} V_{13} = X \dfrac{\partial }{\partial X} + S_{3}(Y) \dfrac{\partial }{\partial Y} + \left( \dfrac{X^{2}}{6 c_{1}} - F \right) \dfrac{\partial }{\partial F}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned}{} & {} G^{\prime \prime \prime \prime \prime } - 10 G^{\prime \prime \prime \prime } + 35 G^{\prime \prime \prime } - 50 G^{\prime \prime } +24 G^{\prime } -51 G^{\prime } G^{\prime \prime } \nonumber \\{} & {} \quad + 21 G G^{\prime \prime } - 36 G G^{\prime } +6 G^{\prime } G^{\prime \prime \prime } - 3 G G^{\prime \prime \prime } \nonumber \\{} & {} \quad + 6 \left( G^{\prime \prime }\right) ^{2} + 57 \left( G^{\prime }\right) ^{2} = 0, \end{aligned}$$

(92)

where

$$\begin{aligned}{} & {} \varphi = \ln (X) - \int \dfrac{1}{S_{3}(Y)} dY, \nonumber \\{} & {} F(X,Y) = \dfrac{X^{2}}{18 c_{1}} + \dfrac{G(\varphi )}{X}. \end{aligned}$$

(93)

The solution of Eq. (92) is

$$\begin{aligned} G(\varphi ) = \dfrac{2}{3} + \dfrac{2 A_{1}}{A_{1} \varphi + A_{2}}. \end{aligned}$$

(94)

Hence, invariant solution of Eq. (6) is

$$\begin{aligned}{} & {} \upsilon (x,y,t) = \dfrac{x^{2}}{18 c_{1} t} \nonumber \\{} & {} \quad + \dfrac{1}{x} \left( \dfrac{2}{3} + \dfrac{2 A_{1}}{A_{1} \left( \ln (x) - \dfrac{1}{3} \ln (t) - \int \dfrac{1}{S_{3}(Y)} dY \right) + A_{2}}\right) \nonumber \\{} & {} \qquad - \dfrac{c_{3}}{12 c_{1}} (4 y - 3 c_{2} t), \end{aligned}$$

(95)

where $Y = y - c_{2} t$.

7.2 The generator $V_{4} + \alpha V_{2}$

Along with the generator $V_{4} + \alpha V_{2}$, Lagrange’s equation becomes

$$\begin{aligned} \dfrac{dx}{t}=\dfrac{dy}{\alpha c_{2}} = \dfrac{dt}{\alpha } = \dfrac{d\upsilon }{\frac{x}{3c_{1}}}, \end{aligned}$$

(96)

which gives the following similarity variables

$$\begin{aligned} \begin{aligned}&M = \ 2 \alpha x - t^{2},\\&N = \ y - c_{2} t,\\&\upsilon (x,y,t) = \ H(M,N) + \dfrac{6 \alpha x t + t^{3}}{18 c_{1} \alpha ^{2}}. \end{aligned} \end{aligned}$$

(97)

Substituting Eq. (97) into Eq. (6), gives

$$\begin{aligned}{} & {} 2 \alpha c_{1} H_{MMMMN}+ 6 c_{1} H_{MM} H_{MN} \nonumber \\{} & {} \quad + 3 c_{1} H_{M} H_{MMN} + 3 c_{1} H_{N} H_{MMM} + c_{3} H_{MMM} = 0.\nonumber \\ \end{aligned}$$

(98)

Again, Eq. (98) admits the infinitesimals given by

$$\begin{aligned} \begin{aligned} \xi _{M} =&\ d_{1} + d_{3} M,\\ \xi _{N} =&\ d_{1} H_{1}(N) + d_{2} H_{2}(N) + d_{3} H_{3}(N),\\ \eta _{H} =&\ - \dfrac{d_{1} c_{3} H_{1}(N)}{3 c_{1}} + d_{2}\left( \dfrac{3 c_{1} - c_{3} H_{2}(N)}{3 c_{1}}\right) \\&+ d_{3} \left( -H - \dfrac{c_{3} (N + H_{3}(N))}{3 c_{1}}\right) , \end{aligned} \end{aligned}$$

(99)

where $d_{i}$’s $(1 \le i \le 3)$ are arbitrary constants and $H_{i}$’s $(1 \le i \le 3)$ are arbitrary functions of Y.

7.2.1 $d_{1} \ne 0$, while $d_{2}$ and $d_{3}$ are zero.

In this case, we have the vector

$$\begin{aligned} V_{21} = \dfrac{\partial }{\partial M} + H_{1}(N) \dfrac{\partial }{\partial N} - \dfrac{c_{3} H_{1}(N)}{3 c_{1}} \dfrac{\partial }{\partial H}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} \alpha J^{\prime \prime \prime \prime \prime } + 3 \left( J^{\prime \prime }\right) ^{2} + 3 J^{\prime } J^{\prime \prime \prime } = 0, \end{aligned}$$

(100)

where $(^{\prime })$ denotes the derivative with respect to new independent variable $\sigma$, given by

$$\begin{aligned}{} & {} \sigma = M - \int \dfrac{1}{H_{1}(N)} dN, \nonumber \\{} & {} H(M,N) = - \dfrac{c_{3} N}{3 c_{1}} + J(\sigma ). \end{aligned}$$

(101)

The solution of Eq. (100) is

$$\begin{aligned} J(\sigma ) = A_{0} + \dfrac{4 \alpha A_{1}}{A_{1} \sigma + A_{2}}. \end{aligned}$$

(102)

Hence, invariant solution of Eq. (6) is

$$\begin{aligned}{} & {} \upsilon (x,y,t) \nonumber \\{} & {} \quad = A_{0} + \dfrac{4 \alpha A_{1}}{A_{1}\left( 2\alpha x - t^{2} - \int \dfrac{1}{H_{1}(N)} dN \right) + A_{2}}\nonumber \\{} & {} \qquad - \dfrac{c_{3} (y - c_{2} t)}{3 c_{1}} + \dfrac{6 \alpha x t + t^{3}}{18 c_{1} \alpha ^{2}}, \end{aligned}$$

(103)

where $N = y - c_{2} t$.

7.2.2 $d_{2} \ne 0$, while $d_{1}$ and $d_{3}$ are zero.

In this case, we have the generator as

$$\begin{aligned} V_{22} = H_{2}(N) \dfrac{\partial }{\partial N} + \left( 1 - \dfrac{c_{3} H_{2}(N)}{3 c_{1}}\right) \dfrac{\partial }{\partial H}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} J^{\prime \prime \prime } = 0, \end{aligned}$$

(104)

where

$$\begin{aligned} \sigma = M, \, H(M,N) = \int \dfrac{3 c_{1} - c_{3} H_{2}(N)}{3 c_{1}H_{2}(N)} dN + J(\sigma ).\nonumber \\ \end{aligned}$$

(105)

The solution of Eq. (104) is

$$\begin{aligned} G(\sigma ) = A_{0} + A_{1} \sigma + A_{2} \sigma ^{2}. \end{aligned}$$

(106)

Hence, invariant solution of Eq. (6) becomes

$$\begin{aligned} \upsilon (x,y,t)= & {} A_{0} + A_{1} \left( 2 \alpha x - t^{2}\right) + A_{2} \left( 2 \alpha x - t^{2}\right) ^{2} \nonumber \\{} & {} + \dfrac{6 \alpha x t + t^{3}}{18 c_{1} \alpha ^{2}} + \int \dfrac{3 c_{1} - c_{3} H_{2}(N)}{3 c_{1}H_{2}(N)} dN,\nonumber \\ \end{aligned}$$

(107)

where $N = y - c_{2} t$.

7.2.3 $d_{3} \ne 0$, while $d_{1}$ and $d_{2}$ are zero.

This case yields the following generator

$$\begin{aligned} V_{23}= & {} M \dfrac{\partial }{\partial M} + H_{3}(N) \dfrac{\partial }{\partial N} \\{} & {} - \left( H + \dfrac{c_{3} (N+H_{3}(N))}{3 c_{1}} \right) \dfrac{\partial }{\partial H}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned}{} & {} 2 \alpha \sigma J^{\prime \prime \prime \prime \prime } + 10 \alpha J^{\prime \prime \prime \prime } + 6 \sigma \left( J^{\prime \prime }\right) ^{2}\nonumber \\{} & {} \quad + 21 J^{\prime } J^{\prime \prime } + 6 \sigma J^{\prime } J^{\prime \prime \prime } + 3 J J^{\prime \prime \prime } = 0, \end{aligned}$$

(108)

where

$$\begin{aligned} \sigma = \dfrac{M}{N}, \quad H(M,N) = - \dfrac{c_{3} N}{3 c_{1}} + \dfrac{J(\sigma )}{N}. \end{aligned}$$

(109)

The solutions of Eq. (108) are

$$\begin{aligned} J(\sigma ) = \dfrac{A_{1}}{\sigma } \qquad \text {and} \qquad J(\sigma ) = \dfrac{ 4 \alpha A_{1}}{A_{1} \sigma + A_{2}}. \end{aligned}$$

(110)

Hence, Eq. (6) has the following closed-form solution

$$\begin{aligned} \upsilon (x,y,t)= & {} - \dfrac{c_{3}(y-c_{2} t)}{3 c_{1} } + \dfrac{A_{1}}{2 \alpha x - t^{2}} \nonumber \\{} & {} + \dfrac{6 \alpha x t + t^{3}}{18 c_{1} \alpha ^{2}}, \end{aligned}$$

(111)

and

$$\begin{aligned} \upsilon (x,y,t)= & {} - \dfrac{c_{3}(y-c_{2} t)}{3 c_{1} } \nonumber \\{} & {} + \dfrac{4 \alpha A_{1}}{A_{1}(2 \alpha x - t^{2}) + A_{2}(y-c_{2} t)} \nonumber \\{} & {} + \dfrac{6 \alpha x t + t^{3}}{18 c_{1} \alpha ^{2}}. \end{aligned}$$

(112)

7.3 The generator $V_{2} + \beta V_{5} + \lambda V_{6}$

Along with the generator $V_{2} + \beta V_{5} + \lambda V_{6}$, Lagrange’s equation turn into

$$\begin{aligned} \dfrac{dx}{\beta }=\dfrac{dy}{c_{2}} = \dfrac{dt}{1} = \dfrac{d\upsilon }{\lambda }, \end{aligned}$$

(113)

which gives the following similarity variables

$$\begin{aligned} \begin{aligned}&P = \ x - \beta t,\\&Q = \ y - c_{2} t,\\&\upsilon (x,y,t) = \ \lambda t + K(P,Q). \end{aligned} \end{aligned}$$

(114)

Substituting Eq. (114) into Eq. (6), gives

$$\begin{aligned}{} & {} c_{1} K_{PPPPQ}+ 6 c_{1} K_{PP} K_{PQ} + 3 c_{1} K_{P} K_{PPQ} \nonumber \\{} & {} \quad + 3 c_{1} K_{Q} K_{PPP} + c_{3} K_{PPP} - \beta K_{PPQ} = 0. \end{aligned}$$

(115)

Again, Eq. (115) admits infinitesimals given as

$$\begin{aligned} \begin{aligned} \xi _{P} =&\ d_{1} + d_{3} P,\\ \xi _{Q} =&\ d_{1} R_{1}(Q) + d_{2} R_{2}(Q) + d_{3} R_{3}(Q),\\ \eta _{K} =&\ - \dfrac{d_{1} c_{3} R_{1}(Q)}{3 c_{1}} + d_{2}\left( \dfrac{3 c_{1} - c_{3} R_{2}(Q)}{3 c_{1}}\right) \\&+ d_{3} \left( -K + \dfrac{2 \beta P}{3 c_{1}} - \dfrac{c_{3} (Q + R_{3}(Q))}{3 c_{1}}\right) . \end{aligned} \end{aligned}$$

(116)

where $d_{i}$’s $(1 \le i \le 3)$ are arbitrary constants and $R_{i}$’s $(1 \le i \le 3)$ are arbitrary functions of Q.

7.3.1 $d_{1} \ne 0$, while $d_{2}$ and $d_{3}$ are zero.

In this case, we have the vector

$$\begin{aligned} V_{31} = \dfrac{\partial }{\partial P} + R_{1}(Q) \dfrac{\partial }{\partial Q} - \dfrac{c_{3} R_{1}(Q)}{3 c_{1}} \dfrac{\partial }{\partial K}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} c_{1} L^{\prime \prime \prime \prime \prime } + 6 c_{1} \left( L^{\prime \prime }\right) ^{2} + 6 c_{1} L^{\prime } L^{\prime \prime \prime } - \beta L^{\prime \prime \prime } = 0, \end{aligned}$$

(117)

where $(^{\prime })$ represents the derivative with respect to new independent variable $\psi$, given by

$$\begin{aligned} \psi= & {} P - \int \dfrac{1}{R_{1}(Q)} dQ, \nonumber \\ K(P,Q)= & {} - \dfrac{c_{3} Q}{3 c_{1}} + L(\psi ). \end{aligned}$$

(118)

The solution of Eq. (117) is

$$\begin{aligned} L(\psi ) = A_{0} + A_{1} \tanh \left( \dfrac{A_{1}}{2} \psi \right) , \end{aligned}$$

(119)

under the constraint $\beta = c_{1} A_{1}^{2}$. Hence, invariant solution of Eq. (6) takes the form

$$\begin{aligned} \upsilon (x,y,t)= & {} A_{0} + A_{1} \tanh \left( \dfrac{A_{1}}{2}\left( x-c_{1} A_{1}^{2} t\right. \right. \nonumber \\{} & {} \left. \left. - \int \dfrac{1}{R_{1}(Q)} dQ\right) \right) +\lambda t - \dfrac{c_{3} (y - c_{2} t)}{3 c_{1}},\nonumber \\ \end{aligned}$$

(120)

where $Q = y - c_{2} t$.

Fig. 6

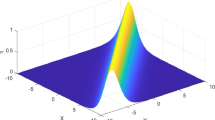
The wave profile for Eq. (87), with $A_{0} = 2, A_{1} = 1.3, A_{2} = 0.8, c_{1} = 2.3, c_{2} = 0.1, c_{3} = 1.22, t = 1$ and $S_{1}(Y) = 1/Y,$ a 3D plot, b contour plot and c 2D plot

Fig. 7

The representation of Eq. (107), while $A_{0} = 2, A_{1} = 1.3, A_{2} = 1.5, c{1} = 1.33, c_{2} = 0.67, c_{3} = 1, \alpha = 1.5, y = 1$ and $H_{2}(N) = 1/\sinh (N),$ a 3D plot, b contour plot and c 2D plot at different time

7.3.2 $d_{2} \ne 0$, while $d_{1}$ and $d_{3}$ are zero.

In this case, we have the generator as

$$\begin{aligned} V_{32} = R_{2}(Q) \dfrac{\partial }{\partial Q} + \left( 1 - \dfrac{c_{3} R_{2}(Q)}{3 c_{1}}\right) \dfrac{\partial }{\partial K}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned} L^{\prime \prime \prime } = 0, \end{aligned}$$

(121)

where

$$\begin{aligned} \psi = P, \quad K(P,Q) = \int \dfrac{3 c_{1} - c_{3} R_{2}(Q)}{3 c_{1}R_{2}(Q)} dQ + L(\psi ).\nonumber \\ \end{aligned}$$

(122)

The solution of Eq. (121) is

$$\begin{aligned} L(\psi ) = A_{0} + A_{1} \psi + A_{2} \psi ^{2}. \end{aligned}$$

(123)

Hence, corresponding solution of Eq. (6) becomes

$$\begin{aligned} \upsilon (x,y,t)= & {} A_{0} + A_{1} \left( x - \beta t\right) + A_{2} \left( x - \beta t\right) ^{2} \nonumber \\{} & {} + \lambda t + \int \dfrac{3 c_{1} - c_{3} R_{2}(Q)}{3 c_{1}R_{2}(Q)} dQ, \end{aligned}$$

(124)

where $Q = y - c_{2} t$.

7.3.3 $d_{3} \ne 0$, while $d_{1}$ and $d_{2}$ are zero.

This case yields the following generator

$$\begin{aligned} V_{33}= & {} P \dfrac{\partial }{\partial P} + R_{3}(Q) \dfrac{\partial }{\partial Q}\\{} & {} + \left( - K + \dfrac{2 \beta P}{3 c_{1}} - \dfrac{c_{3} (Q+R_{3}(Q))}{3 c_{1}} \right) \dfrac{\partial }{\partial K}, \end{aligned}$$

which reduces Eq. (82) into following ODE

$$\begin{aligned}{} & {} \psi L^{\prime \prime \prime \prime \prime } + 5 L^{\prime \prime \prime \prime } + 6 \psi \left( L^{\prime \prime }\right) ^{2} + 21 L^{\prime } L^{\prime \prime } \nonumber \\{} & {} \quad + 6 \psi L^{\prime } L^{\prime \prime \prime } + 3 L L^{\prime \prime \prime } = 0, \end{aligned}$$

(125)

where

$$\begin{aligned} \psi = \dfrac{P}{Q}, \quad K(P,Q) = \dfrac{\beta P - c_{3} Q}{3 c_{1}} + \dfrac{L(\psi )}{Q}. \end{aligned}$$

(126)

We get the solutions of Eq. (125) as

$$\begin{aligned} L(\psi ) = \dfrac{A_{1}}{\psi } \qquad \text {and} \qquad L(\psi ) = \dfrac{2 A_{1}}{A_{1} \psi + A_{2}}. \end{aligned}$$

(127)

Hence, corresponding solutions of Eq. (6) becomes

$$\begin{aligned} \upsilon (x,y,t)= & {} \lambda t + \dfrac{\beta (x- \beta t) - c_{3}(y-c_{2} t)}{3 c_{1} } \nonumber \\{} & {} + \dfrac{A_{1}}{(x- \beta t)}, \end{aligned}$$

(128)

and

$$\begin{aligned} \upsilon (x,y,t)= & {} \lambda t + \dfrac{\beta (x- \beta t) - c_{3}(y-c_{2} t)}{3 c_{1} } \nonumber \\{} & {} + \dfrac{2 A_{1}}{A_{1}(x- \beta t) + A_{2}(y-c_{2}t)}. \end{aligned}$$

(129)

7.4 Graphical illustration

In this section, Fig. 6-Fig. 8 depicts the 3D plot, contour plot and 2D plot of closed-form solutions of Eq. (6). Figure 6 describes the parabolic wave profile for Eq. (87), with arbitrary constants and function which are taken as $A_{0} = 2, A_{1} = 1.3, A_{2} = 0.8, c_{1} = 2.3, c_{2} = 0.1, c_{3} = 1.22, t = 1$ and $S_{1}(Y) = 1/Y$. Figure 7 describes the parabolic wave profile for Eq. (107), with arbitrary constants and function which are taken as $A_{0} = 2, A_{1} = 1.3, A_{2} = 1.5, c_{1} = 1.33, c_{2} = 0.67, c_{3} = 1, \alpha = 1.5, y = 1$ and $H_{2}(N) = 1/\sinh (N)$. While, Fig. 8 describes the kink wave profile for Eq. (120), with arbitrary constants and function which are taken as $A_{0} = 2, A_{1} = 1.5, c_{1} = 3, c_{2} = 1, c_{3} = 0.5, \lambda = 0.1, y = 1$ and $R_{1}(Q) = 1/Q$.

Fig. 8

Wave profile representation of Eq. (120), when $A_{0} = 2, A_{1} = 1.5, c{1} = 3, c_{2} = 1, c_{3} = 0.5, \lambda = 0.1, y = 1$ and $R_{1}(Q) = 1/Q,$ a 3D plot, b contour plot and c 2D plot at different time

8 Conclusions

In this paper, we have carried out an investigation on the integrability characteristic for a generalized $(2+1)$-dimensional nonlinear equation which can be considered as an extended form of generalized $(2+1)$-dimensional Hirota bilinear equation originated from shallow water wave theory. One aspect of our study was to apply the Painlevè analysis on the governing equation and it is found that the equation is not completely integrable in Painlève sense. On the other hand, we have presented some basic ideas on the binary Bell polynomials and derived the Hirota bilinear form of the governing equation by exploiting the concept of P-polynomial. We have also obtained the Bäcklund transformation by utilizing the concepts of decoupling two field condition and linearizing the system of equation. In addition, we pursue the Hopf-Cole transformation and obtained the corresponding Lax pair formulation of the concerned equation. Furthermore, we use the connection between Riccati-type equation and a divergence-type equation and retrieved an infinite sequence of conservation laws. Finally, the multi-soliton solutions of the governing equation have been derived from the bilinear form and the corresponding soliton solutions were demonstrated pictorially via interesting figures. In view of the existence of noteworthy indicators such as Hirota bilinear form, Bäcklund transformation, Lax pair formulation and existence of infinite conservation laws, it can be concluded that this extended form of generalized $(2+1)$-dimensional Hirota bilinear equation is completely integrable. Finally, corresponding to Eq. (6), several exact analytic solutions were established using the Lie group transformation approach. The obtained results are more significant and precise in explaining various physical phenomena, such as nonlinear wave phenomena in shallow water, oceanography and nonlinear optics. In future, our aim would be to apply linear superposition principle to Hirota bilinear form in complex field and extract complex exponential wave function solutions and then complexitons, resonant solitons, etc. Another direction of study would be using long wave limit in the Hirota bilinear form to construct rogue wave solutions and study their interaction with lump solutions, kink solutions, breather solutions, etc.