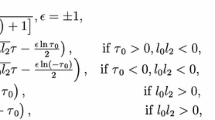1 Introduction

The nature is full of nonlinear phenomena. The interior behaviors of this nonlinearity are modeled for illustration alongside nonlinear partial differential equations (NPDEs) of fractional order as well as integer order (Miller and Ross 1993; Hassani et al. 2020). The fractional-order equations are mostly considered to analyze the intricated characteristic of complex physical phenomena arise in numerous branches of science at a small scale (Gomez-Aguilar et al. 2018; Bonyah et al. 2018). Subsequently, intellectuals and specialists have paid their profound deliberation to explore the approximate and appropriate solutions of the nonlinear evolution equations. Due to the various angle of vision of researchers, a large number of techniques have been created recently to solve these equations. Instantly, the Adomian decomposition method (Helal and Mehana 2006), the variational iteration method (Mohyud-Din et al. 2009), the Backlund transformation method (Jianming et al. 2011), the extended finite difference method (Yokus 2018), the inverse scattering transformation method (Ablowitz and Clarkson 1991), the Bernoulli sub-equation function method (Duran et al. 2021), the extended auxiliary equation method (Seadawy 2017), the sine–cosine method (Al-Mdallal and Syam 2007) the \(\left( {G^{\prime}/G} \right)\)-expansion method (Das and Ghosh 2019), the rational fractional \(\left( {D_{\xi }^{\alpha } G/G} \right)\)-expansion method (Islam and Akter 2020), the modified \(\left( {1/G^{\prime}} \right)\)-expansion method (Duran et al. 2021), the extended tanh method (Islam et al. 2018a).

Let us pour a bottle of cola. We have all witnessed the movement of gas bubbles one by one. We have all witnessed the formation movement of gas bubbles. In other words, a foam form quickly. Bubbles appear in the form of elegant polyhedral cells. This gradual change is shaped by rearrangements after a certain period of time. We can observe the formation of foam initially and then its change in daily life, especially in a certain time interval that begins with the pouring of cola. After this observation, let us examine the concept of foam in the literature. The foam theory was first described by the Belgian physicist Joseph Plateau in the nineteenth century (Plateau 1873). In this theory, the importance of the concept of liquid foam in fluid dynamics is mentioned (Cantat et al. 2013). As a result of experimental studies, especially with the soap layer, the first foundations of mathematical models describing the thin strips in the foam were laid (Kraynik et al. 2003; Weaire and Hutzler 2001). The physical theory of the foam has left its place in applied mathematics, especially with the local examination of the foam surface and the emergence of this model as a non-linear differential equation. In particular, the exact solutions obtained from the fractional foam drainage equation (FFDE) modeling this format are mathematically important. We think that combining these exact solutions with physical theory will add a different perspective to the world of science. Consider the nonlinear space–time FFDE (Shi et al. 2020)

$$ D_{t}^{\alpha } u = \frac{1}{2}uD_{x}^{2\beta } u + 2u^{2} D_{x}^{\beta } u + \left( {D_{x}^{\beta } u} \right)^{2} ,\;\;t > 0, \alpha > 0, \;\;\beta \le 1. $$
(1)

\(u = u\left( {x,t} \right)\) denotes the function representing the Plateau cross-sectional area dependent on the spatial x and temporal t variables (Al-Mdallal et al. 2020). It is also the order of the compatible derivative, which we receive as the fractional derivative operator \(\alpha\) and \(\beta\). In this study, we physically deal with the concept of foam in fluid dynamics. The local pressure gradient and gravity are two forces that play an important role, especially in the liquid in the foam. After a certain period of time, the concept of equilibrium can be defined by the harmony of these two forces. Of these concepts, the pressure gradient is related to the surface tension of the foam. This connection is defined as capillarity in the literature. Equation (1) under consideration is meant to explain the mechanisms of how fluid flows through nodes and channels between foams determined by gravity and capillarity (Weaire et al. 2003). The foam drainage equation, whose solutions we have investigated in this study, also has application areas in different sectors such as beer, packaging, manufacturing and ore separation (Cox et al. 2002; Hoogland et al. 2016).

A remarkable and logistic study have appeared in literature with the space–time FFDE. Akgul et al. (2013) have investigated the space and time FFDE by the improved \(\left( {G^{\prime}/G} \right)\)-expansion method and found only a few analytic solutions; Ege and Misirli (2014) examined the same equation by the modified Kudryashov method which yields two analytic solutions; Islam and Akbar (2018a) have used the generalized \(\left( {G^{\prime}/G} \right)\)-expansion method which provides analytic solutions to the mentioned equation; Pandir and Yildirim (2018) considered the same equation and obtained three solutions by the extended tanh method; Islam et al. (2018b) examined the above equation by the rational \(\left( {G^{\prime}/G} \right)\)-expansion method and gained nine traveling wave solutions; Cevikel (2018) studied the equation by exp-function method and found only one exact solution; Shi et al. (2020) has taken into account the FFDE via Lie-group scaling transformation method and improved the \(\left( {G^{\prime}/G} \right)\)-expansion method; Al-Mdallal et al. (2020) have found numerical solutions to this equation. The generalized \(\left( {G^{\prime}/G} \right)\)-expansion method has been put forward by Islam and Akbar (2018b) to investigate this equation and the exact solutions obtained were defined traveling wave solutions.

In this study, we functionate the work by means of the recently established improved tanh method (Islam and Akter 2021) and modified \(\left( {1/G^{\prime}} \right)\)-expansion method (Yokuş et al. 2021). According to the present results, traveling wave solutions obtained as a result of the proposed approaches differ from the literature in terms of novelty and generality in this study. When the literature is examined (Akgul et al. 2013; Ege and Misirli 2014; Islam and Akbar 2018a, b; Pandir and Yildirim 2018; Islam et al. 2018b; Cevikel 2018; Al-Mdallal et al. 2020), it is emphasized that the solutions obtained for FFDE provide the equation, but it can be seen as a shortcoming that these solutions do not include the discussions about foam in fluid dynamics. One of the most important purposes of this study is to analyze the responses of the solutions for different values of the parameters affecting the wave velocity for the traveling wave solutions to be obtained, supported by simulations. As a result of these analyses, it is thought that it will offer a different perspective on the foam phenomenon through traveling wave solutions.

The conformable fractional derivative is adopted together with a composite wave variable transformation to reduce the considered equations into the differential equations due to a single independent variable. Khalil et al., have announced the conformable fractional derivative as follows (Khalil et al. 2014; Abdeljawad et al. 2019):

The conformable fractional derivative of a function \(u\left( x \right)\) is

$$ D_{x}^{\alpha } \left( {u\left( x \right)} \right) = \mathop {{\text{lim}}}\limits_{\varepsilon \to 0} \frac{{u\left( {x + \varepsilon x^{1 - \alpha } } \right) - u\left( x \right)}}{\varepsilon }, $$
(2)

where \(x > 0\) and \(\alpha\) signifies the order of derivative like \(\alpha \in \left( {0,1} \right]\). The following theorem highlight the qualities of this formulation (Abdeljawad 2015):

Theorem

If \(v\left( x \right)\) and \(u\left( x \right)\) are \(\alpha\)-differentiable at any point \(x > 0\) for \(\alpha \in \left( {0,1} \right]\),

  • \(D_{x}^{\alpha } \left( {x^{n} } \right) = nx^{n - \alpha }\) \(\forall n \in {\varvec{R}}\).

  • \(D_{x}^{\alpha } \left( \lambda \right) = 0\), here \(\lambda\) is arbitrary constant.

  • \(D_{x}^{\alpha } \left( {au\left( x \right) + bv\left( x \right)} \right) = aD_{x}^{\alpha } \left( {u\left( x \right)} \right) + bD_{x}^{\alpha } \left( {v\left( x \right)} \right), \) \(\forall a,b \in {\varvec{R}}\).

  • \(D_{x}^{\alpha } \left( {u\left( x \right)v\left( x \right)} \right) = u\left( x \right)D_{x}^{\alpha } \left( {v\left( x \right)} \right) + v\left( x \right)D_{x}^{\alpha } \left( {u\left( x \right)} \right)\).

  • \(D_{x}^{\alpha } \left( {u\left( x \right)/v\left( x \right)} \right) = \frac{{v\left( x \right)D_{x}^{\alpha } \left( {u\left( x \right)} \right) - u\left( x \right)D_{x}^{\alpha } \left( {v\left( x \right)} \right)}}{{v^{2} \left( x \right)}}\).

  • \(D_{x}^{\alpha } \left( u \right)\left( x \right) = x^{1 - \alpha } \frac{{{\text{d}}u\left( x \right)}}{{{\text{d}}x}}\),

  • \(D_{x}^{\alpha } \left( {u\left( x \right).v\left( x \right)} \right) = x^{1 - \alpha } v^{\prime}\left( t \right)u^{\prime}\left( {v\left( t \right)} \right)\).

2 Modified \((1/G^{\prime}\))-expansion method

This method, which has recently been brought to the literature with a doctoral study (Yokus 2011), has been modified and used to attain the traveling wave solution of NPDEs (Yokuş et al. 2021).

Consider the general form of the fractional NPDE depending on the spatial variable x and the temporal variable t as follows:

$$ T\left( {u, D_{t}^{\alpha } u, \ldots ,D_{{x_{1} }}^{\alpha } u,D_{{x_{1} }}^{2\alpha } u, D_{{x_{1} }}^{\beta } u,D_{{x_{1} }}^{2\beta } u, \ldots , D_{{x_{n} }}^{\alpha } u, D_{{x_{n} }}^{2\alpha } u, \ldots , D_{{x_{1} t}}^{\alpha } u,D_{{x_{1} t}}^{\beta } u, \ldots } \right) = 0, $$
(3)

where \(0 < \alpha \le 1\; {\text{and}} \;0 < \beta \le 1. \)

Let \(u = u\left( {t, x_{1} , x_{2} , \ldots ,x_{n} } \right) = U\left( \xi \right), { }\xi = k\left( {\frac{{x_{1}^{\beta } }}{\beta } + \frac{{x_{2}^{\beta } }}{\beta } + \cdots + \frac{{x_{n}^{\beta } }}{\beta }} \right) + l\frac{{t^{\alpha } }}{\alpha },\)

where \(l\) is the velocity of the wave and k is the wavelength. The values \(\alpha\) and \(\beta\) are the order of the conformable derivative, which we consider as the fractional derivative operator. We may be converted into the following ODE for \(U\left( \xi \right):\)

$$ L\left( {U,U^{\prime},U^{\prime\prime},U^{\prime\prime\prime}, \ldots } \right) = 0. $$
(4)

The solution of Eq. (4) is supposed to have the form

$$ U\left( \xi \right) = a_{0} + \mathop \sum \limits_{i = 1}^{n} a_{i} \left( {\frac{1}{{G^{\prime}}}} \right)^{i} + a_{ - i} \left( {\frac{1}{G^{\prime}}} \right)^{ - i} , $$
(5)

where \(a_{i} , a_{ - i}\), \(i = \left\{ {1,2, \ldots ,n} \right\}\) are scalars, \(G = G\left( \xi \right)\) provides the following second-order IODE

$$ G^{\prime\prime} + \lambda G^{\prime} + \mu = 0,{ }\lambda , \mu \in {\varvec{R}} .{ } $$
(6)

The solution named the expansion method is in the form below

$$ \frac{1}{{G^{\prime}\left[ \xi \right]}} = \frac{1}{{ - \frac{\mu }{\lambda } + A\cos h\left[ {\xi \lambda } \right] - A\sin h\left[ {\xi \lambda } \right]}},$$
(7)

where \(A\) is an integral constant. The desired derivatives of Eq. (5) are computed and entered into Eq. (4), yielding a polynomial with \(\left( {1/G^{\prime}} \right)\). An algebraic system of equations is formed by equating the coefficients of this polynomial to zero. The package software solves the equation, and the default Eq. (4) is substituted in the solution function. Finally, the solutions to Eq. (3) are discovered.

3 Explication of the improved tanh method

This method is an expansion method used to obtain traveling wave solutions of NPDEs in the form of tanh functions (Malfliet 1992). This method has recently been modified and used to obtain a traveling wave solution of the NPDEs (Islam and Akter 2021).

Consider the following NPDE involving \(u\left( {t, x_{1} , x_{2} , \ldots ,x_{n} } \right)\):

$$ F\left( {u, D_{t}^{\alpha } u, \ldots ,D_{{x_{1} }}^{\alpha } u,D_{{x_{1} }}^{2\alpha } u, D_{{x_{1} }}^{\beta } u,D_{{x_{1} }}^{2\beta } u, \ldots , D_{{x_{n} }}^{\alpha } u, D_{{x_{n} }}^{2\alpha } u, \ldots , D_{{x_{1} t}}^{\alpha } u,D_{{x_{1} t}}^{\beta } u, \ldots } \right) = 0. $$
(8)

If the classical wave transform below the Eq. (8) is taken into account,

$$ u = u\left( {t, x_{1} , x_{2} , \ldots ,x_{n} } \right) = U\left( \xi \right), { }\xi = \frac{{x_{1}^{\beta } }}{\beta } + \frac{{x_{2}^{\beta } }}{\beta } + \cdots + \frac{{x_{n}^{\beta } }}{\beta } + \frac{{t^{\alpha } }}{\alpha }, $$
(9)

become the following ODE due to \(\xi\):

$$ R\left( {U, U^{\prime}, U^{\prime\prime}, U^{\prime\prime\prime}, \ldots } \right) = 0. $$
(10)

For the purposes of examining soliton solutions, we could disregard the constant of integration. Equation (8) is supposed to be satisfied by

$$ u\left( \xi \right) = \frac{{a_{0} + \mathop \sum \nolimits_{i = 1}^{n} \left( {a_{i} \phi^{i} \left( \xi \right) + b_{i} \phi^{ - i} \left( \xi \right)} \right)}}{{c_{0} + \mathop \sum \nolimits_{i = 1}^{n} \left( {c_{i} \phi^{i} \left( \xi \right) + d_{i} \phi^{ - i} \left( \xi \right)} \right)}}. $$
(11)

The arbitrary constants that Eq. (11) contains and that will be calculated later are \(a_{0} ,a_{1} , \ldots ,a_{n} , b_{1} ,b_{2} , \ldots ,b_{n}\). \(n\) is a constant determined using the balance principle and taking into consideration the Eq. (10). The Riccati differential equation is provided by the function \(\phi = \phi \left( \xi \right)\)

$$ \phi^{\prime}\left( \xi \right) = \delta + \phi^{2} \left( \xi \right),\;\delta \in {\varvec{R}}\user2{.} $$
(12)

The following are the solutions to Eq. (12):

  1. (i)

    \(\phi \left( \xi \right) = - \sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \xi } \right)\) or \(\phi \left( \xi \right) = - \sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \xi } \right)\), \(\delta < 0\).

  2. (ii)

    \(\phi \left( \xi \right) = - 1/\xi\), \(\delta = 0\).

  3. (iii)

    \(\phi \left( \xi \right) = \sqrt \delta {\text{tan}}\left( {\sqrt \delta \xi } \right)\) or \(\phi \left( \xi \right) = - \sqrt \delta {\text{cot}}\left( {\sqrt \delta \xi } \right)\), \(\delta > 0\).

Equation (10), when combined with Eqs. (11) and (12), yields a polynomial in \(\phi \left( \xi \right)\) whose coefficients are equated to zero and may be solved using any computing software for the values of the obscure arbitrary constants involved in Eq. (11). Insert these values into Eq. (11), which, coupled with the solutions of Eq. (12), yields the solutions of Eq. (8).

4 Construction of solutions of the space–time FFDE using modified \((1/\user2{G^{\prime}}\))-expansion method

Let us consider the methodology of the modified \((1/G^{\prime}\))-expansion method to construct the traveling wave transform of the space–time FFDE. The wave variable transformation

$$ u\left( {x,t} \right) = u\left( \xi \right),\;\xi = \frac{{kx^{\beta } }}{\beta } + \frac{{lt^{\alpha } }}{\alpha }, $$
(13)

translates Eq. (1) into the ODE,

$$ - lu^{\prime} + \frac{1}{2}k^{2} uu^{\prime\prime} + 2ku^{2} u^{\prime} + k^{2} \left( {u^{\prime}} \right)^{2} = 0. $$
(14)

The equilibrium term of Eq. (14) is \(n = 1\), according to the homogeneous balancing principle and the following situation is attained in Eq. (5),

$$ U\left( \xi \right) = a_{0} + a_{1} \left( {\frac{1}{{G^{\prime}\left[ \xi \right]}}} \right) + a_{2} G^{\prime}\left[ \xi \right], a_{2} \ne 0 or a_{1} \ne 0 . $$
(15)

By replacing Eq. (15) into Eq. (14) and the coefficients of Eq. (1) are equal to zero, we can create the following algebraic equation systems.

\({\text{Const}}:l\tau a_{2} + \frac{1}{2}k^{2} \lambda \tau a_{0} a_{2} - 2k\tau a_{0}^{2} a_{2} - k^{2} \lambda^{2} a_{1} a_{2} + k^{2} \tau^{2} a_{2}^{2} - 2k\tau a_{1} a_{2}^{2} = 0\),

\(\frac{1}{{G^{\prime}\left[ \xi \right]}}: - l\lambda a_{1} + \frac{1}{2}k^{2} \lambda^{2} a_{0} a_{1} + 2k\lambda a_{0}^{2} a_{1} - 2k^{2} \lambda \tau a_{1} a_{2} + 2k\lambda a_{1}^{2} a_{2} = 0\),

$$ \frac{1}{{G^{\prime}\left[ \xi \right]^{2} }}: - l\tau a_{1} + \frac{3}{2}k^{2} \lambda \tau a_{0} a_{1} + 2k\tau a_{0}^{2} a_{1} + \frac{3}{2}k^{2} \lambda^{2} a_{1}^{2} + 4k\lambda a_{0} a_{1}^{2} - k^{2} \tau^{2} a_{1} a_{2} + 2k\tau a_{1}^{2} a_{2} = 0, $$
$$ \frac{1}{{G^{\prime}\left[ \xi \right]^{3} }}:\user2{ }k^{2} \tau^{2} a_{0} a_{1} + \frac{7}{2}k^{2} \lambda \tau a_{1}^{2} + 4k\tau a_{0} a_{1}^{2} + 2k\lambda a_{1}^{3} = 0, $$
$$ \frac{1}{{G^{\prime}\left[ \xi \right]^{4} }}{: }2k^{2} \tau^{2} a_{1}^{2} + 2k\tau a_{1}^{3} = 0, $$
$$ G^{\prime}\left[ \xi \right]:\user2{ }l\lambda a_{2} + \frac{1}{2}k^{2} \lambda^{2} a_{0} a_{2} - 2k\lambda a_{0}^{2} a_{2} + \frac{5}{2}k^{2} \lambda \tau a_{2}^{2} - 4k\tau a_{0} a_{2}^{2} - 2k\lambda a_{1} a_{2}^{2} = 0, $$
$$ \begin{gathered} G^{\prime}\left[ \xi \right]^{2} :\user2{ }\frac{3}{2}k^{2} \lambda^{2} a_{2}^{2} - 4k\lambda a_{0} a_{2}^{2} - 2k\tau a_{2}^{3} = 0, \hfill \\ G^{\prime}\left[ \xi \right]^{3} :\user2{ } - 2k\lambda a_{2}^{3} = 0. \hfill \\ \end{gathered} $$
(16)

In Eq. (16), considering \(- 2k\lambda a_{2}^{3} = 0\) formed by the coefficient of the \( G^{\prime}\left[ \xi \right]^{3}\) term, \(a_{2} = 0\) is encountered. In addition, when Eq. (16) is solved by the aid of computer programs, the following case is presented:

Case 1

$$ a_{0} = - \frac{k\lambda }{2}, a_{1} = - k\tau , a_{2} = 0, l = \frac{{k^{3} \lambda^{2} }}{4}, $$
(17)

By substituting values from Eq. (17) into Eq. (15) and obtaining hyperbolic wave solutions for Eq. (1):

$$ u_{1} \left( {x,t} \right) = - \frac{k\lambda }{2} - \frac{k\tau }{{ - \frac{\tau }{\lambda } + A{\text{Cosh}}\left[ {\lambda \left( {\frac{{kx^{\beta } }}{\beta } + \frac{{k^{3} t^{\alpha } \lambda^{2} }}{4\alpha }} \right)\left] { - A{\text{Sinh}}} \right[\lambda \left( {\frac{{kx^{\beta } }}{\beta } + \frac{{k^{3} t^{\alpha } \lambda^{2} }}{4\alpha }} \right)} \right]}} $$
(18)

The exponential form of the solution is as follows:

$$ u_{1} \left( {x,t} \right) = k\lambda \left( {\frac{1}{2} + \frac{A\lambda }{{ - A\lambda + {\text{e}}^{{\frac{{kx^{\beta } \lambda }}{\beta } + \frac{{k^{3} t^{\alpha } \lambda^{3} }}{4\alpha }}} \tau }}} \right). $$
(19)

5 Construction of solutions of the space–time FFDE using Improved tanh method

If we consider Eq. (14), balancing principle to Eq. (14) forces the solution (3.4) to be

$$ u = \frac{{a_{0} + a_{1} \phi \left( \xi \right) + b_{1} \phi^{ - 1} \left( \xi \right)}}{{c_{0} + c_{1} \phi \left( \xi \right) + d_{1} \phi^{ - 1} \left( \xi \right)}} . $$
(20)

Using Eq. (19) and its various derivatives as needed alongside Eq. (12) we find a polynomial in \(\phi \left( \xi \right)\) from Eq. (14). The coefficient of each term of this polynomial is set to zero. Next, a system of equations is constructed and solved to calculate the constants contained in Eq. (19). By substituting the calculated constants in Eq. (19), the solution of Eq. (14) is reached. When the wave transform is operated in reverse, the solution of the Eq. (1) is produced.

Case 1: \(a_{0} = 0\), \(a_{1} = - c_{0} k\), \(b_{1} = \delta kc_{0}\), \(c_{1} = 0\), \(d_{1} = 0\), \(l = - 4k^{3} \delta\).

This case offers

$$ U_{1} \left( \xi \right) = - \frac{{\left( {{\text{tanh}}^{2} \left( {\sqrt { - {\updelta }} {\upxi }} \right) + 1} \right){\delta k}}}{{\sqrt { - {\updelta }} {\text{tanh}}\left( {\sqrt { - {\updelta }} {\upxi }} \right)}},\delta < 0 $$
(21)
$$ U_{2} \left( \xi \right) = - \frac{{\left( {{\text{coth}}^{2} \left( {\sqrt { - {\updelta }} {\upxi }} \right) + 1} \right){\delta k}}}{{\sqrt { - {\updelta }} {\text{coth}}\left( {\sqrt { - {\updelta }} {\upxi }} \right)}},\;\delta < 0 $$
(22)
$$ U_{3} \left( \xi \right) = \frac{{\left( {1 - {\text{tan}}^{2} \left( {\sqrt {\updelta } {\upxi }} \right)} \right)\sqrt {\updelta } {\text{k}}}}{{{\text{tan}}\left( {\sqrt {\updelta } {\upxi }} \right)}},\;\delta > 0 $$
(23)
$$ U_{4} \left( \xi \right) = - \frac{{\left( {1 - {\text{cot}}^{2} \left( {\sqrt {\updelta } {\upxi }} \right)} \right)\sqrt {\updelta } {\text{k}}}}{{{\text{cot}}\left( {\sqrt {\updelta } {\upxi }} \right)}},\;\delta > 0 $$
(24)

where \(\xi = \frac{{k\left( {\alpha x^{\beta } - 4\beta k^{2} \delta t^{\alpha } } \right)}}{\alpha \beta }\).

Case 2: \(a_{0} = - kd_{1}\), \(c_{0} = 0\), \(a_{1} = 0\), \(b_{1} = 0\), \(c_{1} = 0\), \(\delta = - \frac{l}{{k^{3} }}\).

Accordingly,

$$ U_{5} \left( \xi \right) = k\sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \xi } \right),\;\delta < 0 $$
(25)
$$ U_{6} \left( \xi \right) = k\sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \xi } \right),\;\delta < 0 $$
(26)
$$ U_{7} \left( \xi \right) = - k\sqrt \delta {\text{tan}}\left( {\sqrt \delta \xi } \right),\;\delta > 0 $$
(27)
$$ U_{8} \left( \xi \right) = k\sqrt \delta {\text{cot}}\left( {\sqrt \delta \xi } \right),\;\delta > 0 $$
(28)

where \(\xi = \frac{{kx^{\beta } }}{\beta } + \frac{{lt^{\alpha } }}{\alpha }\).

Case 3:\( a_{0} = - kd_{1}\), \(a_{1} = 0\), \(c_{1} = 0\), \(l = - \frac{{k^{2} b_{1} }}{{c_{0} }}\), \(\delta = \frac{{b_{1} }}{{kc_{0} }}\).

Subsequently,

$$ U_{9} \left( \xi \right) = \frac{{kd_{1} \sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \xi } \right) + b_{1} }}{{d_{1} - c_{0} \sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \xi } \right)}},\;\delta < 0 $$
(29)
$$ U_{10} \left( \xi \right) = \frac{{kd_{1} \sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \xi } \right) + b_{1} }}{{d_{1} - c_{0} \sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \xi } \right)}},\;\delta < 0 $$
(30)
$$ U_{11} \left( \xi \right) = \frac{{b_{1} - kd_{1} \sqrt \delta {\text{tan}}\left( {\sqrt \delta \xi } \right)}}{{c_{0} \sqrt \delta {\text{tan}}\left( {\sqrt \delta \xi } \right) + d_{1} }},\;\delta > 0 $$
(31)
$$ U_{12} \left( \xi \right) = \frac{{kd_{1} \sqrt \delta {\text{cot}}\left( {\sqrt \delta \xi } \right) + b_{1} }}{{d_{1} - c_{0} \sqrt \delta {\text{cot}}\left( {\sqrt \delta \xi } \right)}},\;\delta > 0 $$
(32)

where \(\xi = \frac{{k\left( {x^{\beta } c_{0} \alpha - \beta kb_{1} t^{\alpha } } \right)}}{{c_{0} \alpha \beta }}\).

Case 4: \(a_{0} = 0\), \(a_{1} = 0\), \(b_{1} = \delta kc_{0}\), \(c_{1} = 0\), \( d_{1} = 0\), \(l = - k^{3} \delta\).

Afterward,

$$ U_{13} \left( \xi \right) = - \frac{\delta k}{{\sqrt { - \delta } {\text{tanh}}\left( {\sqrt { - \delta } \xi } \right)}},\;\delta < 0 $$
(33)
$$ U_{14} \left( \xi \right) = - \frac{\delta k}{{\sqrt { - \delta } {\text{coth}}\left( {\sqrt { - \delta } \xi } \right)}},\;\delta < 0 $$
(34)
$$ U_{15} \left( \xi \right) = \frac{\sqrt \delta k}{{{\text{tan}}\left( {\sqrt \delta \xi } \right)}},\;\delta > 0 $$
(35)
$$ U_{16} \left( \xi \right) = - \frac{\sqrt \delta k}{{{\text{cot}}\left( {\sqrt \delta \xi } \right)}},\;\delta > 0 $$
(36)

where \(\xi = \frac{{k\left( {\alpha x^{\beta } - k^{2} \beta \delta t^{\alpha } } \right)}}{\alpha \beta }\).

The well-gained traveling wave solutions to the foam drainage equation of fractional order are compared with the earlier results (Akgul et al. 2013; Ege and Misirli 2014; Islam and Akbar 2018a; Pandir and Yildirim 2018; Islam et al. 2018b). It is worth mentioning that the solutions have newly been appeared in this work and might be significant to be a valuable part of the literature.

6 Results and discussion

6.1 Graphical representations

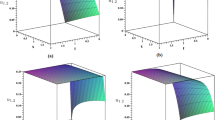
Physical appearances of solutions to NPDEs portray the behavior of underlying structures of natural phenomena. The solutions originated above are taken different 3-D views namely kink type, bell shape, cuspon, compacton and periodic etc. The 3-D graph of the traveling wave solution obtained with the help of the modified (1/G′)-expansion method is presented in Fig. 1 with the help of special values given to arbitrary parameters. Similarly, 3-D graphics of the solutions obtained by the aid of the improved tanh method are presented in Figs. 2, 3, 4, 5, 6, 7. A few among the drown-graphs are as follows:

Fig. 1
figure 1

Outline of solution Eq. (17) for \(\alpha = 0.8, \beta = 0.9\), \(A = \tau = \lambda = - 1\), \(k = 0.5,l = 1\) in \(- 10 \le x \le 10, 0 \le t \le 1\)

Full size image
Fig. 2
figure 2

Outline of Eq. (24) for \(\alpha = 0.8, \beta = 0.9,\delta = 1\), \(k = 0.5\) in \(- 15 \le x \le 15, 0 \le t \le 5\)

Full size image
Fig. 3
figure 3

Plot of Eq. (25) for \(\alpha = 0.8,\beta = 0.9\), \(k = l = 0.5\) in \(- 15 \le x \le 15, 0 \le t \le 1\)

Full size image
Fig. 4
figure 4

Shape of Eq. (31) for \(\delta = 0.1, \alpha = 0.8, \beta = 0.9, c_{0} = 1\), \(k = 1\), \(b_{1} = 0.5\), \(d_{1} = 1\) in \(- 15 \le x \le 15, 0 \le t \le 5\)

Full size image
Fig. 5
figure 5

View of Eq. (32) for \(\alpha = 0.8, \beta = 0.9, d_{1} = 1\), \(k = 1\), \(b_{1} = 0.5\), \(c_{0} = - 0.5\) in \(- 15 \le x \le 15, 0 \le t \le 5\)

Full size image
Fig. 6
figure 6

View of Eq. (33) for \(\alpha = 0.8, \beta = 0.9\), \(k = 0.5, \delta = - 0.1\) in \(- 15 \le x \le 15, 0 \le t \le 5\)

Full size image
Fig. 7
figure 7

Shape of Eq. (36) for \(\alpha = 0.8,\beta = 0.9\), \(k = - 1\), \(\delta = 0.1\) in \(- 15 \le x \le 15, 0 \le t \le 5\)

Full size image

6.1.1 For modified (1/G′)-expansion method

See Fig. 1.

6.1.2 For improved tanh method

See Figs. 2, 3, 4, 5, 6, 7.

6.2 Physical discussions

The FFDE, which has an important place in fluid dynamics and sheds light on the physical liquid foam phenomenon, is discussed. Traveling wave solutions are presented using two different analytical methods to present a different perspective of the liquid foam phenomenon. In this section, first, the advantages and disadvantages of both analytical methods are discussed, and second, the comparison of the obtained traveling wave solutions with the solutions in the literature is given. A physically different perspective is presented to the liquid foam phenomenon by using the third and final solutions.

While some similarities were encountered in terms of the functioning of the two analytical methods, different aspects were also encountered. Similar aspects are reduced to an ordinary differential equation with the help of conventional wave transform. In addition, the use of the balancing principle, the creation of the algebraic equation system and the solution of the equation systems, and the search for the coefficients in the accepted solutions are other similar aspects. The different aspects of both analytical methods are that the traveling wave solutions accepted depending on the basis equation have different forms. It has been observed that the modified \((1/G^{\prime}\))-expansion method is more useful than the improved tanh method in terms of processing complexity. However, the improved tanh method is quantitatively richer in generating traveling wave solutions for Eq. (1). The hyperbolic form of the traveling wave solution produced by the modified \((1/G^{\prime}\))-expansion method is in a different form than the wave solutions produced by the improved tanh method. It is difficult to comment on the superiority of the methods since both analytical methods produce different types of traveling wave solution functions. Because the solutions obtained are very important in terms of different physical meanings as well as providing the equation mathematically.

Second, we can say that the obtained traveling wave solutions are different and more general when analyzed with the solutions in the literature. Traveling wave solutions produced by both analytical methods are different from the solutions presented in the literature with (Akgul et al. 2013; Islam and Akbar 2018a, b; Islam et al. 2018b; Cevikel 2018). In addition, it was concluded that the solutions obtained in the improved tanh method are more general than the solutions presented with Pandir and Yildirim (2018) in the literature. The most important reason for this is the solution function accepted in the operation of the method.

Third, there is no parameter representing a physical phenomenon in Eq. (1), which represents the liquid foam mechanism. Therefore, the parameters representing the wavelength (k) and wave velocity (l), which are physically significant in conventional wave conversion, have been taken into account. Let us discuss the effects of these parameters on the behavior of traveling wave solutions, which play an important role in the transport of energy. If we pay attention to Eq. (17), there is a relation \(l = \frac{{k^{3} \lambda^{2} }}{4}\) between wavelength and wave velocity. Therefore, let us present the following simulation for different values of wavelength affecting wave velocity.

Figure 8, it was observed that there were no distortions in the structure of the solitary wave for small values of wavelength. For k = 1, the wavelength was in the range of [− 0.5, 0.5]. For k = 1.5, the wavelength was in the range of [− 0.8, 0.8]. In addition, for k = 2.5, it is seen that the wavelength is in the range of [− 1.8, 1.2], while small distortions occur in the structure of the solitary wave. Finally, for k = 5.5, it is seen that the wavelength is in the range of [− 2.75, 2.5], and the disturbances in the structure of the wave have become more evident.

Fig. 8
figure 8

Simulation graphs of Eq. (17) for \(\alpha = \beta = 1\), \(A = \tau = \lambda = - 1\)

Full size image

7 Conclusions

The main purpose of this work was to investigate traveling wave solutions in the appropriate form of the time and space fractional nonlinear foam drainage equation by using modified \((1/G^{\prime}\))-expansion method and newly established improved tanh method. Abundant attractive solutions to the recommended equation are successfully constructed by executing the advised methods confirming its high performance. By giving special values to the parameters in the traveling wave solutions produced by both analytical methods, graphs representing the behavior of the wave at any moment were presented with the help of 3D. In addition, the advantages and disadvantages of both analytical methods are given in the results and discussion section. In addition, the traveling wave solutions obtained with the help of the methods were compared with the solutions in the literature. Finally, wave behavior simulation has been performed using the values assigned to the parameters with physical qualities in classical wave transformation, which are shared by the methodology of both methods. Consequently, these methods are competent, concise and creative which might be put forward for further use to search appropriate analytic wave solutions of any other nonlinear fractional partial differential equations relating to nature sciences. The attained solutions are claimed to be novel, motivating and substantial which might be advantageous to describe the underlying constructions of complicated physical phenomena connecting to the real world. In addition, we think that this study will provide important information for researchers interested in the wave transformation of NPDEs.