High-order rogue waves and their dynamics of the Fokas–Lenells equation revisited: a variable separation technique

Abstract

The Fokas–Lenells (FL) equation is an integrable higher-order extension of nonlinear Schrödinger equation. One approach to generating its breather solutions is based on Darboux transformation (DT) and iterations. However, the DT of FL equation contains negative powers of the spectral parameter, which can lead to very complicated expressions when N is large. In this paper, we avoid the negative powers by adopting a variable separation and Taylor expansion technique to solve the Lax pair of FL system. Furthermore, stability of the proposed technique is demonstrated in detail.

1 Introduction

Rogue waves are instantaneous large-amplitude localized waves and have been extensively studied in many fields, including oceanic motion, optics, plasmas and super fluids (see for instance in [1,2,3,4,5,6,7,8,9,10,11,12,13]). The generation of rogue waves is a complex process, involving many factors such as dispersion enhancement of transient wave groups, geometrical focusing, wave-current interaction and modulation instabilities. A much-studied model is the integrable nonlinear Schrödinger (NLS) equation [10] and its breather solutions, especially the Peregrine breather [11]. There are several integrable reductions of the higher-order NLS models, such as the derivative NLS equation and Hirota and Sasa–Satsuma equations [14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Here, we consider the Fokas–Lenells (FL) equation, which is closely linked to the derivative NLS model,

$$\begin{aligned} iq_{xt}-iq_{xx}+2q_x-q_xqq^*+iq=0, \end{aligned}$$

(1)

where q is a complex wave amplitude. It is a higher-order integrable extension of NLS equation [28,29,30,31] and has been invoked in the context of optical fibers [29]. The soliton solutions of the FL equation (1) were exhibited by [28, 29] and some breather solutions by [30, 31].

The soliton solutions (often identified as rogue waves) of NLS equation are usually obtained through Darboux transformations (DTs). That is, the first-order solitons are found from a pre-specified seed solution, and the Nth-order solitons are found through iterations of DT. One key step is to expand the specific solution in terms of the spectral parameter. However, DT of the FL equation contains negative powers of the spectral parameter, which can lead to very complicated expressions when N is large [31]. Here, we adopt a different approach by introducing a parameter matrix and then directly find the Nth-order breathers through a variable separation technique and Taylor series expansion, see [32,33,34,35,36] for use of similar methods for NLS equations.

The rest of the article is organized as follows. Section 2 provides some preliminaries related to FL equation and introduces our variable separation technique. In Sect. 3, we describe the expansion of the eigenfunction and obtain the formula for Nth-order soliton solutions in Sect. 4. In Sect. 5, we confirm the effectiveness of our method and a range of dynamic behaviors of rogue wave solutions are displayed graphically. Section 6 summarizes the stability of the proposed technique guarantees.

2 Variable separation for the eigenfunction $\varPsi$

It is useful to recall that we can extend (1) into an FL system, [30, 31]

$$\begin{aligned}&iq_{xt}-iq_{xx}+2q_x-q_xqr+iq=0, \end{aligned}$$

(2)

$$\begin{aligned}&ir_{xt}-ir_{xx}-2r_x+r_xrq+ir=0. \end{aligned}$$

(3)

Clearly, when $r =q^*$, the FL system (2, 3) reduces to the FL equation (1). The Lax pair of the FL system (2, 3) is

$$\begin{aligned}&\varPsi _x= U\varPsi ,\, U=J\lambda ^2+Q\lambda , \end{aligned}$$

(4)

$$\begin{aligned}&\varPsi _t{=} V\varPsi ,\, V{=}J\lambda ^2+Q\lambda +V_0{+} V_{-1}\lambda ^{-1} +\frac{1}{4}J\lambda ^{-2}.\nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned}&\varPsi =\left( \begin{array}{c} \varphi \\ \phi \end{array} \right) ,\quad J=\left( \begin{array}{cc} -i&{}0\\ 0&{}i \end{array} \right) ,\quad Q=\left( \begin{array}{cc} 0&{}q_x\\ r_x&{}0 \end{array} \right) ,\\&V_0{=}\left( \begin{array}{cc} i-\frac{1}{2}iqr&{}0\\ 0&{}-i+\frac{1}{2}iqr \end{array} \right) ,\,\,\, V_{-1}{=}\left( \begin{array}{cc} 0&{}\frac{1}{2}iq\\ -\frac{1}{2}ir&{}0 \end{array} \right) . \end{aligned}$$

Here, $\lambda$ is the complex spectral parameter. $\varPsi (x,t)=(\varphi ,\phi )^T$ is a two-dimensional vector, the eigenfunction corresponding to $\lambda$. Applying the expression

$$\begin{aligned} U_t-V_x+UV-VU=0 \end{aligned}$$

to Eqs. (4) and (5) yields the FL system (2, 3).

Now, we present a variable separation for the eigenfunction $\varPsi$. First, note that the FL equation (1) has a periodic seed solution

$$\begin{aligned} q=c\exp \left\{ axi+\left( \frac{(a+1)^2}{a}-c^2\right) ti\right\} . \end{aligned}$$

(6)

For any $\lambda$, we expand $\varPsi$ as

$$\begin{aligned}&\varPsi =\begin{pmatrix} \varphi (x,t)\\ \phi (x,t) \end{pmatrix}=AFGZ, \end{aligned}$$

(7)

$$\begin{aligned}&F=\exp (i\varLambda x),\quad G=\exp (i\varOmega t), \end{aligned}$$

(8)

$$\begin{aligned}&A=\left( \begin{array}{cc} 1&{}0\\ 0&{}e^{\pm i\zeta }. \end{array} \right) . \end{aligned}$$

(9)

Here, we assume that in matrix A, $\zeta$ is linearly composed of x and t, i.e., $\zeta =kx+\tilde{c}t$, where k and $\tilde{c}$ are two constants. Similarly, Z is a two-dimensional constant vector. Next, suppose that the matrices $\varLambda , \varOmega$ satisfy the commutator relationship,

$$\begin{aligned}{}[\varLambda ,\varOmega ]=\varLambda \varOmega -\varOmega \varLambda =0. \end{aligned}$$

(10)

Plugging equation (7) into the Lax equations (4, 5) yields

$$\begin{aligned} A_x+iA\varLambda -UA=0,\quad A_t+iA\varOmega -VA=0. \end{aligned}$$

Hence, we solve that

$$\begin{aligned}&A{=}\left( \begin{array}{cc} 1&{}0\\ 0&{}e^{-i(ax+\frac{(a+1)^2}{a}t-c^2t)} \end{array} \right) ,\, \varLambda {=}\left( \begin{array}{cc} -\lambda ^2&{}ac\lambda \\ -ac\lambda &{}\lambda ^2+a \end{array} \right) ,\nonumber \\&\varOmega {=}\left( 1{+}\frac{1}{2a}\lambda ^{-2}\right) \varLambda {+}\left( 1{-}\frac{1}{4}\lambda ^{-2}{+}\frac{1}{2a}-\frac{c^2}{2}\right) .\nonumber \\ \end{aligned}$$

(11)

In order to obtain F, we find the eigenvalues of the matrix $\varLambda$

$$\begin{aligned} a_1=\frac{a+\sqrt{a^2-4(-\lambda ^4+(a^2c^2-a)\lambda ^2)}}{2},\end{aligned}$$

(12)

$$\begin{aligned} a_2=\frac{a-\sqrt{a^2-4(-\lambda ^4+(a^2c^2-a)\lambda ^2)}}{2}, \end{aligned}$$

(13)

$$\begin{aligned} a_1+a_2=a,\quad a_1\cdot a_2=-\lambda ^4-a\lambda ^2+a^2c^2\lambda ^2, \end{aligned}$$

and the eigenvector matrix is

$$\begin{aligned} H=\left( \begin{array}{cc} 1&{}1\\ \frac{\lambda ^2+a_1}{ac\lambda }&{}\frac{\lambda ^2+a_2}{ac\lambda } \end{array} \right) , \quad H^{-1}=\left( \begin{array}{cc} \frac{\lambda ^2+a_2}{a_2-a_1}&{}\frac{-ac\lambda }{a_2-a_1}\\ \frac{-\lambda ^2-a_1}{a_2-a_1}&{}\frac{ac\lambda }{a_2-a_1} \end{array} \right) .\nonumber \\ \end{aligned}$$

(14)

To note

$$\begin{aligned} F=\exp {(i\varLambda x)}=H \left( \begin{array}{cc} e^{a_1 ix}&{}0\\ 0&{}e^{a_2 ix} \end{array} \right) H^{-1}. \end{aligned}$$

Let $\eta =\frac{a_1-a_2}{2}$,

$$\begin{aligned} F=e^{\frac{a}{2}ix} \left( \begin{array}{cc} \cos {(\eta x)}-si\sin {(\eta x)}&{}\frac{ac\lambda }{\eta }i\sin {(\eta x)}\\ -\frac{ac\lambda }{\eta }i\sin {(\eta x)}&{}\cos {(\eta x)}+si\sin {(\eta x)} \end{array} \right) , \end{aligned}$$

(15)

where $s= \frac{\lambda ^2+\frac{a}{2}}{\eta }$. Similarly, the combination of (11) and $G=\exp {(i\varOmega t)}$ derives

$$\begin{aligned} G=e^{Kit} \left( \begin{array}{cc} \cos {(\eta \varepsilon t)}-si\sin {(\eta \varepsilon t)}&{}\frac{ac\lambda }{\eta }i\sin {(\eta \varepsilon t)}\\ -\frac{ac\lambda }{\eta }i\sin {(\eta \varepsilon t)}&{}\cos {(\eta \varepsilon t)}+si\sin {(\eta \varepsilon t)} \end{array} \right) , \end{aligned}$$

(16)

with

$$\begin{aligned} \varepsilon =1+\frac{1}{2a}\lambda ^{-2}, \; K=(1+\frac{1}{2a}-\frac{c^2}{2}+\frac{a}{2}). \end{aligned}$$

3 Expansion of eigenfunction $\varPsi$

In this section, we describe the expansion of eigenfunction $\varPsi$. When $a^2+4\lambda ^4-4(a^2c^2-a)\lambda ^2\rightarrow 0$ and $\eta \rightarrow 0$, F and G become rational matrices. To take advantage of this, we choose $\lambda _0$ being one solution to the equation $a^2+4y^4-4(a^2c^2-a)y^2=0$ (concerning y) and set $\lambda = \lambda _0(1+\delta )$. Through the Taylor series expansions,

$$\begin{aligned} F|_{\lambda =\lambda _0(1+\delta )}=e^{\frac{a}{2}ix}\sum \limits _{n=0}^{\infty }F_n\delta ^n, \end{aligned}$$

(17)

where

$$\begin{aligned} F_n= \left( \begin{array}{cc} F_{n11}&{}F_{n12}\\ F_{n21}&{}F_{n22} \end{array} \right) , \end{aligned}$$

(18)

$$\begin{aligned}&F_{n11}=\gamma _n-(\lambda _0^2+\frac{a}{2})i\tau _n-2\lambda _0^2i\tau _{n-1}- \lambda _0^2i\tau _{n-2},\\&F_{n12}=ac\lambda _0i(\tau _n+\tau _{n-1}),\\&F_{n21}=-F_{n12},\\&F_{n22}=\gamma _n+(\lambda _0^2+\frac{a}{2})i\tau _n+2\lambda _0^2i\tau _{n-1}+\lambda _0^2i\tau _{n-2}, \end{aligned}$$

and

$$\begin{aligned}&\gamma _n=\sum \limits _{k=0}^{\lfloor \frac{3}{4}n\rfloor }\sum \limits _{l=0}^{\lfloor \frac{k}{3}\rfloor }\sum \limits _{m=0}^{\lfloor \frac{k-3l}{2}\rfloor }C_{n-k}^{l}C_{n-k-l}^{m}C_{n-k-l-m}^{k-3l-2m}(-1)^{n-k}\\&\quad \quad \; \cdot \; 4^{m}\lambda _0^{2n-2k+2l+2m}(6\lambda _0^2-2a^2c^2+a)^{k-3l-2m}\\&\quad \quad \; \cdot \; (4\lambda _0^2-2a^2c^2+2a)^{n+2l+m-2k}X_{2(n-k)}, \\&\tau _n=\sum \limits _{k=0}^{\lfloor \frac{3}{4}n\rfloor }\sum \limits _{l=0}^{\lfloor \frac{k}{3}\rfloor }\sum \limits _{m=0}^{\lfloor \frac{k-3l}{2}\rfloor }C_{n-k}^{l}C_{n-k-l}^{m}C_{n-k-l-m}^{k-3l-2m}(-1)^{n-k}\\&\quad \quad \; \cdot \; 4^{m}\lambda _0^{2n-2k+2l+2m} (6\lambda _0^2-2a^2c^2+a)^{k-3l-2m}\\&\quad \quad \; \cdot \; (4\lambda _0^2-2a^2c^2+2a)^{n+2l+m-2k}X_{2(n-k)+1}, \\&X_m=\frac{x^m}{m!}. \end{aligned}$$

Similarly, by expanding G,

$$\begin{aligned} G|_{\lambda =\lambda _0(1+\delta )}=e^{(1+\frac{1}{2a}-\frac{c^2}{2}+\frac{a}{2})it}\sum \limits _{n=0}^{\infty }G_n\delta ^n. \end{aligned}$$

(19)

The calculation of $G_n$ is a lengthy calculation, and we only outline some key steps and definitions here. First, note that

$$\begin{aligned} \cos {(\eta \varepsilon t)}{=}\sum \limits _{k=0}^{\infty }(-1)^k \eta ^{2k}\varepsilon ^{2k}T_{2k},\quad T_m=\frac{t^m}{m!} . \end{aligned}$$

If $\eta =\frac{\sqrt{a^2+4\lambda ^4-4(a^2c^2-a)\lambda ^2}}{2}, \; \lambda =\lambda _0(1+\delta ), \; \varepsilon =1+\frac{1}{2a}\lambda ^{-2} \; , \; \hbox {then}$

$$\begin{aligned} \cos {(\eta \varepsilon t)}=\sum \limits _{n=0}^{\infty }(-1)^n\lambda _0^{2n}\delta ^n\alpha \frac{(2a\lambda _0^2(1+\delta )^2+1)^{2n}}{(1+\delta )^{4n}4^na^{2n}\lambda _0^{4n}}T_{2k}, \end{aligned}$$

where

$$\begin{aligned} \alpha {=}(\lambda _0^2\delta ^3{+}4\lambda _0^2\delta ^2{+}(6\lambda _0^2{-}a^2c^2{+}a)\delta {+}(4\lambda _0^2{-}2a^2c^2{+}2a))^n. \end{aligned}$$

Next, let

$$\begin{aligned} \sum \limits _{i=0}^{\infty }\pi _i \delta ^i= & {} (-1)^k\lambda _0^{2k}\delta ^k[\lambda ^2\delta ^3 + 4\lambda _0^2\delta ^2 +4\lambda _0^2-2a^2c^2 \nonumber \\&+ \,(6\lambda ^2-a^2c^2+a)\delta +2a]^k, \nonumber \\ \sum \limits _{j=0}^{\infty }\kappa _j' \delta ^j= & {} [2a\lambda _0^2+1+4a\lambda _0^2\delta +2a\lambda _0^2\delta ^2]^{2k}, \nonumber \\ \sum \limits _{m=0}^{\infty }\upsilon _m' \delta ^m= & {} \left( (\delta +1)^{2k}4^ka^{2k}\lambda _0^{4k} \right) ^{-1}. \nonumber \\ \pi _i= & {} \sum \limits _{l=0}^{\lfloor \frac{i-k}{3}\rfloor }\sum \limits _{m=0}^{\lfloor \frac{i-k-3l}{2}\rfloor }(-1)^kC_{k}^{l}C_{k-l}^{m}C_{k-l-m}^{i-k-3l-2m} \nonumber \\&\cdot \, \lambda _0^{2k+2l+2m}4^m(4\lambda _0^2-2a^2c^2+2a)^{2k+2l+m-i}\nonumber \\&\cdot \, (6\lambda _0^2-a^2c^2+a)^{i-k-3l-2m}, \end{aligned}$$

(20)

$$\begin{aligned} \kappa _j'= & {} \sum \limits _{p=0}^{\lfloor \frac{j}{2}\rfloor }C_{2k+1}^{p}C_{2k+1-p}^{j-2p}2^{2j-3p}a^{j-p}\lambda _0^{2j-2p} \nonumber \\&\cdot \,(2a\lambda _0^2+1)^{2k+p-j}, \end{aligned}$$

(21)

$$\begin{aligned} \upsilon _m'= & {} \frac{(-1)^m}{m!}(4k)_m \left( 2a\lambda _0^2 \right) ^{-2k}, \end{aligned}$$

(22)

where $(k)_n=k(k+1)\cdots (k+n-1),\; n>0, \; (k)_0=1.$ Here, when $i<k$ and $i>4k$, define $\pi _i=0$, and when $j>4k+2$ define $\kappa _j=0$. Next, let

$$\begin{aligned} \alpha _n=\sum \limits _{k=0}^n\sum \limits _{i=0}^n\sum \limits _{j=0}^{n-i}\pi _i\kappa _j'\upsilon _{n-i-j}'T_{2k}. \end{aligned}$$

(23)

Finally, we obtain $G_n$,

$$\begin{aligned} G_n= \left( \begin{array}{cc} G_{n11}&{}G_{n12}\\ G_{n21}&{}G_{n22} \end{array} \right) , \end{aligned}$$

(24)

$$\begin{aligned}&G_{n11}=\alpha _n-(\lambda _0^2+\frac{a}{2})i\beta _n-2\lambda _0^2i\beta _{n-1}-\lambda _0^2i\beta _{n-2}, \\&G_{n12}= G_{n21} = ac\lambda _0i(\beta _n+\beta _{n-1}) ,\\&G_{n22}=\alpha _n+(\lambda _0^2+\frac{a}{2})i\beta _n+2\lambda _0^2i\beta _{n-1}+\lambda _0^2i\beta _{n-2} , \end{aligned}$$

where

$$\begin{aligned}&\beta _n=\sum \limits _{k=0}^n\sum \limits _{i=0}^n\sum \limits _{j=0}^{n-i}\pi _i\kappa _j\upsilon _{n-i-j}T_{2k+1},\quad \alpha _0=1,\\&\kappa _j=\sum \limits _{p=0}^{\lfloor \frac{j}{2}\rfloor }C_{2k}^{p}C_{2k-p}^{j-2p}2^{2j-3p}a^{j-p}\lambda _0^{2j-2p}(2a\lambda _0^2+1)^{2k+1+p-j}, \\&\upsilon _m=\frac{(-1)^m}{m!}(4k+2)_m\cdot \frac{1}{(2a\lambda _0^2)^{2k+1}}. \end{aligned}$$

Then, let

$$\begin{aligned} Z=\sum \limits _{q=0}^{\infty }Z_q\delta ^q, \end{aligned}$$

where $Z_j$ is a complex vector. Thus, we expand $\varPsi$ as

$$\begin{aligned}&\varPsi |_{\lambda =\lambda _0}=e^{Kit+a/2ix}A\sum \limits _{n=0}^{\infty }\varPsi _n\delta ^n,\nonumber \\&\varPsi _n=\left( \begin{array}{c} \varphi _n\\ \phi _n \end{array} \right) =\sum \limits _{s=0}^n\sum \limits _{t=0}^n F_sG_tZ_{n-s-t}. \end{aligned}$$

(25)

In this manner, we have expanded $\varPsi$ around the point $\lambda =\lambda _0$ with only algebraic manipulations. Since the matrix $F_n$ depends only on x and $G_n$ depends only on t, we call this a variable separation method.

It is useful to note that the binomial expansion

$$\begin{aligned} \begin{aligned}&\lambda ^j\varphi (\delta )=(\lambda _0)^j(1+\delta )^j\varphi (\delta )= \sum _{i=0}^{\infty }\varphi [j,i]\delta ^i, \\&\lambda ^j\phi (\delta )=(\lambda _0)^j(1+\delta )^j\phi (\delta )= \sum _{i=0}^{\infty }\phi [j,i]\delta ^i, \end{aligned} \end{aligned}$$

(26)

so that

$$\begin{aligned} \begin{aligned}&\varphi [j,n]=\sum \limits _{s=0}^n(\lambda _0)^jC_j^{n-s}\varphi _s,\\&\phi [j,n]=\sum \limits _{s=0}^n(\lambda _0)^jC_j^{n-s}\phi _s,\quad j>0,\\&\varphi [j,n]=\sum \limits _{s=0}^n(-1)^{n-s}(\lambda _0)^j\frac{(-j)_{n-s}}{(n-s)!}\varphi _s,\quad j<0,\\&\phi [j,n]=\sum \limits _{s=0}^n(-1)^{n-s}(\lambda _0)^j\frac{(-j)_{n-s}}{(n-s)!}\phi _s, \quad j<0. \end{aligned} \end{aligned}$$

(27)

4 Nth order rogue waves

In this section, we examine the Nth-order DT and derive the formula for breather solutions. When $r=q^*$, the FL system (2, 3) reduces to the FL equation (1). Performing this reduction, $r[N]=q[N]^*$ and $\lambda _k^*=\lambda _l$ , which lead to

$$\begin{aligned}&\varphi _k^*=\phi _l,\quad \phi _k^*=\varphi _l,\quad k\ne l.\\&\lambda _{l}=\lambda _{l+1}^*,\; \varPsi _{l}=\left( \begin{array}{c} \varphi _{l}\\ \phi _{l} \end{array} \right) =\left( \begin{array}{c} \phi _{l-1}^*\\ \varphi _{l-1}^* \end{array} \right) , \; l=1,2,\ldots ,n. \end{aligned}$$

Combining (25) and the binomial expansion, we get

$$\begin{aligned} q[N]=q\left( 1+\frac{|E_{N2}|}{|E_{N1}|}\right) , \end{aligned}$$

(28)

where

And W is defined as

$$\begin{aligned} \left[ \begin{array}{ccccc} \varphi [N,0]&{}\phi [N-1,0]&{}\cdots &{}\varphi [-N+2,0]\\ \phi [N,0]^*&{}\varphi [N-1,0]^*&{}\cdots &{}\phi [-N+2,0]^*\\ \vdots &{}\vdots &{} &{}\vdots \\ \varphi [N,N-1]&{}\phi [N-1,N-1]&{}\cdots &{}\varphi [-N+2,N-1]\\ \phi [N,N-1]^*&{}\varphi [N-1,N-1]^*&{}\cdots &{}\phi [-N+2,N-1]^*\\ \end{array} \right] . \end{aligned}$$

Thus, using the seed solution (6), q[N] is an Nth-order breather solution, which has been obtained here using only algebraic and matrix manipulations.

5 Applications with $N =1, 2, 3$

To verify our method, we display the first, second and third breather solutions both numerically and graphically. Fix $a = c = 1$ in the seed solution (6). With

$$\begin{aligned} F_0{=}\left( \begin{array}{cc} 1-\frac{i-1}{2}x&{}\frac{i-1}{2}x\\ \frac{1-i}{2}x&{}1+\frac{i-1}{2}x \end{array} \right) , G_0{=}\left( \begin{array}{cc} 1-it&{}it\\ -it&{}1+it \end{array} \right) . \end{aligned}$$

And combine Eqs. (25, 27),

$$\begin{aligned}&\varPsi _0=\left( \begin{array}{c} \varphi _0\\ \phi _0 \end{array} \right) =F_0G_0Z_0,\\&\varphi [0,0]=\varphi _0,\quad \phi [0,0]=\phi _0,\\&\varphi [1,0]=\frac{1+i}{2}\varphi _0,\quad \phi [1,0]=\frac{1+i}{2}\phi _0,\\&\varphi [-1,0]=(1-i)\varphi _0,\quad \phi [-1,0]=(1-i)\phi _0. \end{aligned}$$

According to (28), we can express q[1] as

$$\begin{aligned} q[1]=\exp {i(x+3t)}\cdot \left( 1+\frac{|E_{12}|}{|E_{11}}|\right) , \end{aligned}$$

where

$$\begin{aligned} |E_{12}|{=}\begin{vmatrix} \varphi [1,0]&-\varphi [-1,0]\\ \phi [1,0]^*&-\phi [-1,0]^*\\ \end{vmatrix},\; |E_{11}|{=}\begin{vmatrix} \varphi [1,0]&\phi [0,0]\\ \phi [1,0]^*&\varphi [0,0]^*\\ \end{vmatrix}. \qquad \qquad \qquad \qquad \end{aligned}$$

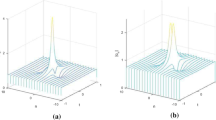
With $Z_0=(1,0)^T$, we plot the solution in Fig. 1. In the limit $x \rightarrow \infty$, $t \rightarrow \infty$, $|q[1]| = 1$. The maximum amplitude of |q[1]| equals 3 and occurs at $t = 0.5$ and $x = -1$. Note that [30] Fig. 2 displays the plot of $|q[1]|^2$, with parameters $a = 1$ and $c = -1$. Hence, the maximum amplitude in their computation is the same as ours, and the performance of the waves is quite similar. The small difference, like the position of the apex, is due to the selection of $Z_0$.

Fig. 1

The image of first-order rogue wave with specific parameters $a = 1, c = 1, Z_0=(1,0)^T$. The maximum amplitude occurs at $t = 0.5$ and $x = -1$

For the second- or third-order rouge waves, we can similarly obtain explicit expressions given fixed parameters. Let $N=2$ and (18, 24) yield,

$$\begin{aligned}&F_1=\left( \begin{array}{cc} -\frac{i-1}{12}x^3+\frac{x^2}{2}+x&{}\frac{i-1}{2}(x+\frac{x^3}{6})\\ -\frac{i-1}{2}(x+\frac{x^3}{6})&{}\frac{i-1}{12}x^3+\frac{x^2}{2}-x \end{array} \right) ,\\&G_1=\left( \begin{array}{cc} -\frac{t^3}{3}-it^2+2t&{}\frac{t^3}{3}-t\\ -\frac{t^3}{3}+t&{}\frac{t^3}{3}-it^2-2t \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned}&\varPsi _1=\left( \begin{array}{c} \varphi _1\\ \phi _1 \end{array} \right) = F_1G_0Z_0+F_0G_1Z_0+F_0G_0Z_1,\\&\varphi [0,1]{=}\varphi _1,\; \phi [0,1]{=}\phi _1,\; \varphi [2,0]{=}\frac{i}{2}\varphi _0,\; \phi [2,0]=\frac{i}{2}\phi _0,\\&\varphi [1,1]=\frac{i+1}{2}(\varphi _0+\varphi _1),\; \phi [1,1]=\frac{i+1}{2}(\phi _0+\phi _1),\\&\varphi [-1,1]=(1-i)(-\varphi _0+\varphi _1),\\&\phi [-1,1]=(1-i)(-\phi _0+\phi _1),\\&\varphi [2,1]=\frac{i}{2}(2\varphi _0+\varphi _1),\; \phi [2,1]=\frac{i}{2}(2\phi _0+\phi _1),\\&\varphi [-2,0]=-2i\varphi _0,\; \phi [-2,0]=-2i\phi _0,\\&\varphi [-2,1]=-2i(-2\varphi _0+\varphi _1),\\&\phi [-2,1]=-2i(-2\phi _0+\phi _1). \end{aligned}$$

Hence, from (28), we have the second-order rogue wave expression

$$\begin{aligned} q[2]=\exp i(x+3t)\cdot (1+\frac{E_{22}}{E_{21}}), \end{aligned}$$

where

$$\begin{aligned}&E_{22}=\begin{vmatrix} \varphi [2,0]&\phi [1,0]&\varphi [0,0]&-\varphi [-2,0]\\ \phi [2,0]^*&\varphi [1,0]^*&\phi [0,0]^*&-\phi [-2,0]^*\\ \varphi [2,1]&\phi [1,1]&\varphi [0,1]&-\varphi [-2,1]\\ \phi [2,1]^*&\varphi [1,1]^*&\phi [0,1]^*&-\phi [-2,1]^*\\ \end{vmatrix},\\&E_{21}=\begin{vmatrix} \varphi [2,0]&\phi [1,0]&\varphi [0,0]&\phi [-1,0]\\ \phi [2,0]^*&\varphi [1,0]^*&\phi [0,0]^*&\varphi [-1,0]^*\\ \varphi [2,1]&\phi [1,1]&\varphi [0,1]&\phi [-1,1]\\ \phi [2,1]^*&\varphi [1,1]^*&\phi [0,1]^*&\varphi [-1,1]^*\\ \end{vmatrix}. \end{aligned}$$

A typical plot of a second-order solution is shown in Fig. 2. Note that when $Z_0=(1,1)^T, Z_1=(0,0)^T$, this reduces to a first-order solution.

Fig. 2

The image of second-order rogue wave with specific parameters $a = 1, c = 1, Z_0=(1,40)^T$, $Z_1=(8000,1)^T$

The third-order rogue wave ($N=3$) can be found in the same way. From Eq. (28), we have

$$\begin{aligned} q[3]=\exp i(x+3t)\cdot (1+\frac{E_{32}}{E_{31}}). \end{aligned}$$

And similarly from (18, 24), we have

$$\begin{aligned} F_2=\left( \begin{array}{cc} F_{2,11} &{} F_{2,12}\\ F_{2,21} &{}F_{2,22} \end{array} \right) , \quad G_2=\left( \begin{array}{cc} G_{2,11} &{} G_{2,12}\\ G_{2,21} &{} G_{2,22} \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} F_{2,11}= & {} \frac{1 - i}{240}x^5 + \frac{1}{24}x^4 + \frac{7-3i}{24}x^3 + \frac{3}{4}x^2 + \frac{1}{2}x,\\ F_{2,12}= & {} \left( \frac{i-1}{240}\right) (x^2+50)x^3,\\ F_{2,21}= & {} -\left( \frac{i-1}{240}\right) (x^2+50)x^3,\\ F_{2,22}= & {} -\frac{1 - i}{240}x^5 + \frac{1}{24}x^4 - \frac{7-3i}{24}x^3 + \frac{3}{4}x^2 - \frac{1}{2}x,\\ G_{2,11}= & {} \frac{1}{30}t(-30+t^4i-5t^3+(-40i+5)t^2\\&+\,(15i+60)t),\\ G_{2,12}= & {} -\frac{1}{30}t(t^4i+(-30i+5)t^2-15i-15),\\ G_{2,21}= & {} \frac{1}{30}t(t^4i+(-30i+5)t^2-15i-15),\\ G_{2,22}= & {} -\frac{1}{30}t(-30+t^4i-5t^3+(-40i+5)t^2\\&+\,(15i+60)t). \end{aligned}$$

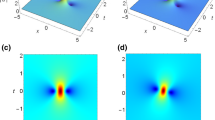
A typical plot is shown in Fig. 3. We select $Z_0 = (1, 2)^T$ , $Z_1=(50,1)^T$, $Z_2=(2000,1)^T$ and draw the plot 3.

Fig. 3

The image of second-order rogue wave with specific parameters $a = 1, c = 1, Z_0=(1,2)^T$, $Z_1=(50,1)^T$, $Z_2=(2000,1)^T$

6 Stability of the proposed technique

In this section, we would like to show that our propose technique would be stable. We give an error tolerance to the seed solution parameter a and c, to limit the residual between the after-perturbation solution and the original one. To clarify, we would let $||\cdot ||$ denote the modulus of a complex number.

At first, we introduce two lemmas. For convenience, in the following discussion, we would focus on one root of $\lambda _0$ (12)

$$\begin{aligned} \lambda _0=\sqrt{\frac{1}{2}(a^2c^2-a + ac\sqrt{a^2c^2-2a})}. \end{aligned}$$

(29)

In the first lemma, we consider the case where if given a tiny perturbation on a, and other parameters remain unchanged, the computation of $\lambda _0$ is stable.

Lemma 1

Assume that c is fixed and $\Vert \lambda _0 \Vert > 0$. For any $\delta > 0$, there exists an $\varepsilon > 0$, such that given $\left| \frac{a-\tilde{a}}{a} \right| < \varepsilon$, $\left\Vert\lambda _0-\tilde{\lambda }_0\right\Vert< \delta$ holds, where $\tilde{\lambda }_0$ is the derivation of $\tilde{a}$ according to (29).

Proof

Fix c and set $\tilde{a}=a(1+\varepsilon _a)$. With the assumption $\Vert \lambda _0 \Vert > 0$, $\varepsilon _a>0$ and $\varepsilon _a\rightarrow 0$, we have

$$\begin{aligned} \left\Vert\lambda _0-\tilde{\lambda }_0 \right\Vert=\sqrt{\frac{1}{2}} \left\Vert\frac{N_1}{D_1} \right\Vert, \end{aligned}$$

where $N_1$ equals

$$\begin{aligned} \left\Vert{a}^2c^2-a+ac\sqrt{a^2c^2-2a}-\tilde{a}^2c^2+\tilde{a}-\tilde{a}c\sqrt{{\tilde{a}}^2c^2-2{\tilde{a}}} \right\Vert, \end{aligned}$$

and $D_1$ equals

$$\begin{aligned} \left\Vert\sqrt{a^2c^2-a+ac\sqrt{a^2c^2-2a}}+\sqrt{{\tilde{a}}^2c^2-{\tilde{a}}+{\tilde{a}}c\sqrt{{\tilde{a}}^2c^2-2{\tilde{a}}}} \right\Vert. \end{aligned}$$

For the numerator $N_1$,

$$\begin{aligned} N_1\le & {} c^2a^2 \left\Vert\varepsilon _a^2 +2\varepsilon _a\right\Vert+ \Vert {a}\Vert \Vert \varepsilon _a\Vert \\&+\left\Vert{ac}\sqrt{a}\right\Vert\left\Vert\sqrt{ac^2-2}-\sqrt{{\tilde{a}}c^2-2}(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert. \end{aligned}$$

Here, we focus on the third term

$$\begin{aligned} \left\Vert\sqrt{ac^2-2}-\sqrt{{\tilde{a}}c^2-2}(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert\end{aligned}$$

and analyze it case by case.

If $ac^2-2 \ge 0$,

$$\begin{aligned}&\left\Vert\sqrt{ac^2-2}-\sqrt{{\tilde{a}}c^2-2}(1+\varepsilon _a)\sqrt{1+\varepsilon _a} \right\Vert\\&\quad =\sqrt{ac^2-2 + a\varepsilon _a c^2}(1+\varepsilon _a)^\frac{3}{2} - \sqrt{ac^2-2}(1+\varepsilon _a)^\frac{3}{2}\\&\qquad + \sqrt{ac^2 - 2}((1+\varepsilon _a)^\frac{3}{2} - 1),\\&\quad \le (1+\varepsilon _a)^\frac{3}{2}(\sqrt{ac^2 - 2 + a\varepsilon _a c^2}-\sqrt{ac^2-2})\\&\qquad + \sqrt{ac^2 - 2}((1+\varepsilon _a)^\frac{3}{2} - 1). \end{aligned}$$

If $ac^2 - 2 < 0$, we can find $\varepsilon _a$ small enough so that $ac^2-2+\varepsilon _ac^2 < 0$.

$$\begin{aligned}&\left\Vert\sqrt{ac^2-2}-\sqrt{{\tilde{a}}c^2-2}(1+\varepsilon _a)^\frac{3}{2}\right\Vert\\&\quad = \left\Vert\sqrt{2-ac^2}i-\sqrt{2-ac^2-a\varepsilon _ac^2}(1+\varepsilon _a)^\frac{3}{2}i\right\Vert, \\&\quad =\left\Vert\sqrt{2-ac^2}-\sqrt{2-ac^2-a\varepsilon _ac^2}(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert, \\&\quad \le \left\Vert\sqrt{2-ac^2}-\sqrt{2-ac^2}(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert\\&\qquad + \left\Vert\sqrt{2-ac^2}-\sqrt{2-ac^2-a\varepsilon _ac^2}\right\Vert\left\Vert(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert, \\&\quad =\left\Vert\sqrt{2-ac^2}\right\Vert\left\Vert(1+\varepsilon _a)^{\frac{3}{2}} - 1\right\Vert\\&\qquad + \left\Vert\frac{\varepsilon _a c^2}{\sqrt{2-ac^2}+\sqrt{2-ac^2-\varepsilon _ac^2}} \right\Vert, \left\Vert(1+\varepsilon _a)^{\frac{3}{2}}\right\Vert. \end{aligned}$$

When it comes to the denominator, we can choose the perturbation $\varepsilon _a$ wisely to make sure $|| D_1 ||$ is bigger than some positive constant $K_0$, which helps us to reach the conclusion

$$\begin{aligned} \left\Vert\lambda _0-\tilde{\lambda }_0 \right\Vert\le \frac{K_a}{K_0}\varepsilon _a = K_1\varepsilon _a, \end{aligned}$$

where $K_1 \sim O(1)$. $\square$

This completes the proof.

In the second lemma, we discuss the cases where perturbations on both a and c.

Lemma 2

Assume $\Vert \lambda _0 \Vert > 0$. For any $\delta > 0$, there exists an $\varepsilon > 0$, such that if given $\left| \frac{a-\tilde{a}}{a} \right| < \varepsilon$ and $\left| \frac{c-\tilde{c}}{c} \right| < \varepsilon$, we will also have $\left\Vert\lambda _0-\tilde{\lambda }_0 \right\Vert< \delta$.

Proof

Now we assume $\tilde{a}=(1+\varepsilon _0)a$, $\tilde{c}=(1+\varepsilon _0)c$, $\varepsilon _0>0$, $\varepsilon _0\rightarrow 0$. Similarly,

$$\begin{aligned} \left\Vert\lambda _0-\tilde{\lambda }_0 \right\Vert=\sqrt{\frac{1}{2}} \left\Vert\frac{N_2}{D_2} \right\Vert, \end{aligned}$$

where $N_2$ equals

$$\begin{aligned} \left\| a^2c^2-a+ac\sqrt{a^2c^2-2a}-\tilde{a}^2\tilde{c}^2+\tilde{a}-\tilde{a}\tilde{c}\sqrt{{\tilde{a}}^2\tilde{c}^2-2\tilde{a}}\right\| \end{aligned}$$

and $D_2$ equals

$$\begin{aligned}&\Big \Vert \sqrt{a^2c^2-a+ac\sqrt{a^2c^2-2a}}\\&\quad +\,\sqrt{{\tilde{a}}^2{\tilde{c}}^2-{\tilde{a}}+{\tilde{a}}{\tilde{c}}\sqrt{{\tilde{a}}^2{\tilde{c}}^2-2{\tilde{a}}}} \Big \Vert . \end{aligned}$$

For the numerator $N_2$,

$$\begin{aligned}&N_2 \nonumber \\\le & {} \Big \Vert {a}^2c^2-a+ac\sqrt{a^2c^2-2a}-\tilde{a}^2c^2+ \tilde{a}\nonumber \\- & {} \tilde{a}c\sqrt{\tilde{a}^2c^2-2\tilde{a}})\Big \Vert +\Big \Vert \tilde{a}^2c^2-\tilde{a}+\tilde{a}c\sqrt{\tilde{a}^2c^2-2\tilde{a}}\nonumber \\- & {} (\tilde{a}^2\tilde{c}^2-\tilde{a}+\tilde{a}\tilde{c}\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}})\Big \Vert , \nonumber \\\le & {} K_a\varepsilon _0+\tilde{a}^2c^2\Vert \varepsilon _0^2+2\varepsilon _0\Vert , \nonumber \\&+\Vert \tilde{a}c\Vert \left\Vert\sqrt{\tilde{a}^2c^2-2\tilde{a}}-(1+\varepsilon _0)\sqrt{\tilde{a}^2c^2(1+\varepsilon _0)^2-2\tilde{a}} \right\Vert.\nonumber \\ \end{aligned}$$

(30)

Similarly, we will focus on the last term. If $a^2c^2-2a > 0$, we can choose $\varepsilon _0$ small enough to let $\tilde{a}^2c^2-2\tilde{a}>0$ and $\tilde{a}^2\tilde{c}^2-2\tilde{a}>0$, which results in

$$\begin{aligned}&\left\Vert\sqrt{\tilde{a}^2c^2-2\tilde{a}}-(1+\varepsilon _0)\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}}\right\Vert\\\le & {} \left\Vert\varepsilon _0\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}} \right\Vert+ \left\Vert\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}}-\sqrt{\tilde{a}^2c^2-2\tilde{a}}\right\Vert, \\= & {} \Vert \varepsilon _0 \Vert \left\Vert\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}} \right\Vert+ \left\Vert\frac{\tilde{a}^2(\tilde{c}^2-c^2)}{\sqrt{\tilde{a}^2\tilde{c}^2-2\tilde{a}}+\sqrt{\tilde{a}^2\tilde{c}^2-2a}}\right\Vert. \end{aligned}$$

If $ac^2-2a<0$, search an $\varepsilon _0$ so that $\tilde{a}^2\tilde{c}^2-2\tilde{a}<0$ and $\tilde{a}^2c^2-2\tilde{a}<0$.

$$\begin{aligned}&\left\Vert\sqrt{{\tilde{a}}^2c^2-2{\tilde{a}}}-(1+\varepsilon _0)\sqrt{{\tilde{a}}^2{\tilde{c}}^2-2{\tilde{a}}} \right\Vert\\= & {} \left\Vert\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2}-(1+\varepsilon _0)\sqrt{2{\tilde{a}}-{\tilde{a}}^2{\tilde{c}}^2} \right\Vert,\\\le & {} \left\Vert\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2}-(1+\varepsilon _0)\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2}\right\Vert\\&+\Vert {1}+\varepsilon _0\Vert \left\Vert\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2}-\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2-O(\varepsilon _0)}\right\Vert, \\= & {} \Vert \varepsilon _0 \Vert \left\Vert\sqrt{2{\tilde{a}}-{\tilde{a}}^2c}\right\Vert\\&+\Vert {1}+\varepsilon _0\Vert \left\Vert{O(\varepsilon _0)} (\sqrt{2{\tilde{a}} - {\tilde{a}}^2c}+\sqrt{2{\tilde{a}}-{\tilde{a}}^2c^2-O(\varepsilon _0)})^{-1} \right\Vert. \end{aligned}$$

Similar to what we have done in the last proof, we can search for some small $\varepsilon _0$ to control the denominator. Therefore,

$$\begin{aligned} \Vert \lambda _0-\tilde{\lambda _0}\Vert \le K\varepsilon _0, \end{aligned}$$

(31)

where K is a constant. $\square$

Using these two lemmas, we can then prove the theorem as follows:

Theorem 1

Assume $\Vert \lambda _0 \Vert > 0$ and $|E_{N1}| > 0$. For any $\delta > 0$, there always exists an $\varepsilon > 0$, s.t. given $\left| \frac{a-\tilde{a}}{a} \right| < \varepsilon$ and $\left| \frac{c-\tilde{c}}{c} \right| < \varepsilon$, we will have $\left\Vert{q[N]}-\tilde{q}[N]\right\Vert< \delta$, where $\tilde{q}[N]$ is the derivation of $\tilde{a}$ and $\tilde{c}$ according to (28).

Proof

Recall that in (18)

$$\begin{aligned} F_n= \left( \begin{array}{cc} F_{n11}&{}F_{n12}\\ F_{n21}&{}F_{n22} \end{array} \right) . \end{aligned}$$

We now perform perturbations on a and c as discussed above. In order to present $\tilde{\lambda }$ in a similar pattern like $\tilde{a}$ and $\tilde{c}$, using the result of Lemma 1 and Lemma 2, we can redefine $\lambda$ from the expression (31) so that

$$\begin{aligned} \tilde{\lambda }_0=\lambda _0(1+\varepsilon ), \end{aligned}$$

From (19), we can derive that

$$\begin{aligned} \gamma _n=\lambda ^{\frac{n}{2}}(C_{\gamma }+O(\lambda )), \end{aligned}$$

where $C_{\gamma }$ is in O(1) order. Hence,

$$\begin{aligned} \widetilde{\gamma }_n=\lambda _0^{\frac{n}{2}}(1+\varepsilon )^{\frac{n}{2}}(C_{\gamma } +O(\lambda ))=\gamma _n+O(\varepsilon ). \end{aligned}$$

Similarly,

$$\begin{aligned} \widetilde{\tau }_n=\tau _n+O(\varepsilon ). \end{aligned}$$

Thus, $\widetilde{F}_n=F_n+\varDelta F$, where all the elements of $\varDelta F$ are in $O(\varepsilon )$ order.

From the expressions of $\pi _i$, $\kappa _j'$, $\upsilon _m'$, $\beta _n$, $\kappa _j$, $\upsilon _m$ ((20)-(25))

$$\begin{aligned}&\widetilde{\pi _i}=\widetilde{\lambda }_0^{2k} O(1),\\&\widetilde{\kappa }'_j=\sum \limits _{p=0}^{\frac{j}{2}}\widetilde{\lambda }_0^{2j-2p} \tilde{a}^{\lceil \frac{j}{2}\rceil }O(1),\\&\widetilde{\kappa }_j=\sum \limits _{p=0}^{\frac{j}{2}}\widetilde{\lambda }_0^{2j-2p} \tilde{a}^{\lceil \frac{j}{2}\rceil }O(1),\\&\widetilde{\upsilon }_m'=\frac{(-1)^m}{m!}(4k)_m\frac{1}{2^{2k}\tilde{a}^{2k}\widetilde{\lambda }_0^{4k}},\\&\widetilde{\upsilon }_m=\frac{(-1)^m}{m!}(4k+2)_m\frac{1}{2^{2k+1}\tilde{a}^{2k+1}\widetilde{\lambda }_0^{4k+2}}. \end{aligned}$$

Thus, from (23) and (25)

$$\begin{aligned} \alpha _n=\left\{ \begin{array}{rl} \frac{1}{\lambda ^{2k-1}} O(1), \ &{}j\ \mathrm{is}\ \mathrm{odd} \\ \frac{1}{\lambda ^{2k}}O(1), \ &{}j\ \mathrm{is}\ \mathrm{even} \\ \end{array} \right. , \end{aligned}$$

(32)

$$\begin{aligned} \beta _n=\left\{ \begin{array}{rl} \frac{1}{\lambda ^{2k+1}}O(1), \ &{}j\ \mathrm{is}\ \mathrm{odd} \\ \frac{1}{\lambda ^{2k+2}}O(1), \ &{}j\ \mathrm{is}\ \mathrm{even}\\ \end{array} \right. , \end{aligned}$$

(33)

where $\tilde{a}$ is reduced from both the numerator and denominator.

What we have done in the steps above is to extract the factors which contain high-order $\lambda _0$. From $G_n$’s expression (24), we notice that the term $\lambda$ or $\lambda ^2$ is multiplied by terms $\beta _n,$$\beta _{n-1}$ and $\beta _{n-2}$. Since we have proved that $\tilde{\lambda }_0 \rightarrow \lambda _0$ and $\lambda _0$ is not a singular point, we can come to the conclusion $\widetilde{G}_n \thickapprox G_n$. Thus,

$$\begin{aligned} \widetilde{\varPsi }_n&=\sum \sum \widetilde{F}_sG_tZ_{n-s-t} \\&=\sum \sum (F_s+O(\varepsilon ))G_tZ_{n-s-t}=\varPsi _n+O(\varepsilon ), \end{aligned}$$

which implies

$$\begin{aligned} \left( \begin{array}{c} \widetilde{\varphi }_n\\ \widetilde{\phi }_n \end{array} \right) = \left( \begin{array}{c} \varphi _n +O(\varepsilon )\\ \phi _n +O(\varepsilon ) \end{array} \right) . \end{aligned}$$

From what is shown in (27), we can then derive that

$$\begin{aligned} \begin{aligned}&\widetilde{\varphi }[j,n] = \varphi [j,n] +O(\varepsilon ),\\&\widetilde{\phi }[j,n] = \phi [j,n] +O(\varepsilon ). \end{aligned} \end{aligned}$$

Expression (28) shows q[N] can be derived form $E_{N1}$ and $E_{N2}$, whose elements are all $\varphi [j,n]$ and $\phi [j,n]$. Leibniz formula shows that the determinant of a matrix can be written as the linear combination of all its elements. Therefore, we can conclude that

$$\begin{aligned} \begin{aligned}&\widetilde{E}_{N1} = E_{N1} + O(\varepsilon ),\\&\widetilde{E}_{N2} = E_{N1} + O(\varepsilon ). \end{aligned} \end{aligned}$$

Finally, we have the stability of our algorithm. $\square$

7 Conclusion

In this paper, we expand the Lax pair of Fokas–Lenells equation with a variable separation method and obtain Nth rogue wave expression. Compared to the more usual expansion methods [30, 31], our method has several advantages. In particular, it is relatively easy to compute expressions and plot figures. Moreover, it is quite convenient for adjusting the parameters through selecting different $Z_n$’s. The flexibility would hugely improve the efficiency in simulation and computation when the initial seed solution is given.

Similar to that in [30, 31], we are inspired by the efficiency and structure of Darboux transformation to generate Nth-order solutions. The novel features presented by DT and the FL system are quite different from those generated from standard integrable systems like the AKNS and the KN systems. As shown in Figs. 1, 2 and 3, we obtain similar plots as in [30, 31]. The maximum amplitudes in the examples are about three times to those when $x \rightarrow \infty$ and $t \rightarrow \infty$. We expect that our work may spark some research interests in generation of rogue waves and serve as a time saver applied to many much-studied methods.