1 Introduction

Rogue wave was founded in many fields, such as nonlinear optics, fluid mechanics, and even finance [1,2,3]. A mass of nonlinear evolution equations including the NLS equation, Kundu–Eckhaus equation, Hirota equation, Sasa–Satuma equation, nonlinear wave equation and so on, can describe the RW phenomena [4,5,6,7,8,9,10]. As a basic model that describes optical soliton propagation in Kerr media, the NLS equation contains multi-soliton solutions, breather solutions, and RW solutions [5, 11,12,13]. However, in the regime of ultra-short pulses, the NLS equation is inappropriate to accurately describe the phenomena, and higher-order nonlinear dispersion terms must be taken into account [6,7,8,9, 14]. In discrete integrable system, the RW solutions of the AL equation, coupled discrete NLS equation and discrete Hirota equation are also discussed based on generalized Darboux transformation (DT) and Hirota bilinear method [15,16,17,18]. There are great differences on RWs between the continuous integrable system and discrete integrable system. Ohta and Yang point out that the RWs can exist in the defocusing Ablowitz–Ladik equation [17].

As we know, the higher-order NLS equation named as the Lakshmanan–Porsezian–Daniel (LPD) equation [19]

$$\begin{aligned} \begin{aligned}&iq_t+q_{xx}+2|q|^{2}q\\&\quad +\gamma \left( q_{xxxx}+8|q|^2q_{xx}+6q^*q^2_x+4q|q_x|^2 \right. \\&\quad \left. +2q^2q^*_{xx}+6|q|^4q\right) =0. \end{aligned} \end{aligned}$$
(1)

is the third member of the NLS hierarchy. Here q is a varying wave packet envelope, \(q^*\) denotes the complex conjugate q, and \(\gamma \) is a real parameter and stands for the strength of higher-order linear and nonlinear effects. Equation (1) can also describe the dynamics of higher-order alpha-helical proteins with nearest and next nearest neighbour interactions [20, 21]. This equation has attracted great attentions. In Refs. [19, 22], Authors establish the relation between higher-order NLS equation and one-dimensional Heisenberg ferromagnetic chains when higher order spin-spin exchange interactions (biquadratic type) and the effect of discreteness are considered. The integrability of Eq. (1) including its singularity structure, construction of Lax pair and Bäcklund transformation have been discussed in detail in Ref. [22]. The one soliton solution of Eq. (1) has been constructed [20] by using Hirota method. Multisoliton solutions using DT is presented in [23]. Rogue waves for the three-coupled fourth-order NLS system is studied in [24]. Besides, Eq. (1) can be regarded as a special case for an integrable three-parameter fifth-order nonlinear Schrödinger equation [25, 26]. Rational solutions, breather solutions, rogue wave and modulation instability of this integrable three-parameter fifth-order nonlinear Schrödinger equation are analytically studied based on DT and robust inverse scattering transform [27, 28]. The corresponding rational solutions and breather solutions of Eq. (1) can be obtained under certain constraints.

In this article, we focus on the following spatial discretization [20] of integrable higher-order NLS equation (1)

$$\begin{aligned} \begin{aligned}&iq_{n,t}+\frac{\gamma }{h^4}(1+|q_n|^2)\left( (1+|q_{n-1}|^2)q_{n-2}\right. \\&\left. \quad +(1+|q_{n+1}|^2)q_{n+2}-4q_{n-1}-4q_{n+1}\right. \\&\quad \left. +q^*_n(q^2_{n+1}+q^2_{n-1})\right. \\&\left. \quad + q_n(q^*_{n-1}q_{n+1}+q_{n-1}q^*_{n+1})+6q_n\right) \\&\quad +\frac{1}{h^2}\left( (1+|q_n|^2)(q_{n+1}+q_{n-1})-2 q_n\right) =0, \end{aligned} \end{aligned}$$
(2)

Equation (2) can govern the discrete \(\alpha \)-helical protein chain model with several higher-order excitations and interactions. Under the transformation

$$\begin{aligned} q_n(t)=hq(nh,t)\triangleq h q(x,t), \end{aligned}$$
(3)

the higher-order integrable discrete NLS equation (2) yields the integrable fourth-order NLS equation (1). Reference [20] investigates the integrability of Eq. (2) including Hamiltonian, discrete Lax pair, discrete soliton and gauge equivalence. However, as we know, there is little work on rogue wave solutions and breather solutions of this higher-order integrable discrete NLS equation (2). This is the main motivation for us to investigate the higher-order RWs of the discrete integrable NLS equation (2) with higher-order excitations in this paper. Moreover, it is very meaningful to study other integrable properties of the higher-order integrable discrete NLS equation (2). We shall give an insight into the continuous limit theory of higher-order integrable discrete NLS equation (2) including discrete DT, discrete rational solutions, discrete breather solutions and gauge equivalence in the future. The paper is organized as follows. In Sect. 2, by using the modified discrete Lax pairs, we apply the generalized (1,N-1)-fold Darboux transformation [5, 15] to construct higher-order discrete RW solutions of Eq. (2). The dynamical behaviors of these discrete RWs are discussed in Sect. 3, which exhibits interesting wave structures. Finally, in Sect. 4 the modulation instability of continuous-wave states of the higher-order discrete NLS equation (2) is investigated.

2 Lax pair and generalized discrete DT

The higher-order discrete NLS equation (2) admits the following discrete modified Lax pair

$$\begin{aligned} \begin{aligned} E\varphi _{n}&=U_n\varphi _n,\\ \varphi _{n,t}&=V_n\varphi _n, \end{aligned} \end{aligned}$$
(4)

where the shift operator E is defined as \(E\varphi _{n}=\varphi _{n+1}\), \(\varphi _n=(\varphi _{n,1},\varphi _{n,2})^T\) is the vector eigenfunction. The matrices \(U_n\) and \(V_n\) with spectral parameter \(\lambda \) take the forms

$$\begin{aligned} \begin{aligned} U_n=&\left( \begin{array}{cc} \lambda &{} q_n \lambda ^{-1}\\ - q^*_n \lambda &{} \lambda ^{-1} \\ \end{array}\right) ,\\ V_n=&\frac{i\gamma }{h^4}\left( \begin{array}{cc} A_n(\lambda ,\lambda ^{-1},q_n) &{} B_n(\lambda ,\lambda ^{-1},q_n) \\ B_n(\lambda ^{-1},\lambda ,q^*_n) &{} -A_n(\lambda ^{-1},\lambda ,q^*_n)\\ \end{array}\right) \\&\quad +\frac{i}{h^2} \left( \begin{array}{cc} C_n(\lambda ,\lambda ^{-1},q_n) &{} D_n(\lambda ,\lambda ^{-1},q_n) \\ D_n(\lambda ^{-1},\lambda ,q^*_n) &{} -C_n(\lambda ^{-1},\lambda ,q^*_n)\\ \end{array}\right) , \end{aligned} \end{aligned}$$
(5)

in which

$$\begin{aligned} \begin{aligned}&A_n(\lambda ,\lambda ^{-1},q_n)=\frac{\lambda ^4+\lambda ^{-4}}{2}\\&\qquad +\lambda ^2( q_nq^*_{n-1}-2)+\lambda ^{-2}( q^*_nq_{n-1}-2) -4 q_nq^*_{n-1}\\&\qquad +q_n^2q^{*2}_{n-1}+(1+|q_{n-1}|^2)q_nq^*_{n-2}\\&\qquad +(1+|q_{n}|^2)q_{n+1}q^*_{n-1}+3,\\&B_n(\lambda ,\lambda ^{-1},q_n)=\lambda ^2q_n-\lambda ^{-4}q_{n-1}\\&\qquad +(1+|q_n|^2)q_{n+1}+ q_n^2q^*_{n-1}-4q_n\\&\qquad -\lambda ^{-2}\left( (1+|q_{n-1}|^2)q_{n-2}+ q^*_nq^2_{n-1}-4q_{n-1}\right) ,\\&C_n(\lambda ,\lambda ^{-1},q_n)\\&\quad =\lambda ^2-1-(\lambda -\lambda ^{-1})+q_nq_{n-1}^*,\\&D_n(\lambda ,\lambda ^{-1},q_n)\\&\quad =q_n-q_{n-1}\lambda ^{-2}. \end{aligned} \end{aligned}$$

One can directly verify that the discrete zero curvature condition \(U_{n,t}=(EV_{n})U_n-U_nV_n\) of the linear spectral equations (4) yields the generalized integrable discrete NLS equation (2).

Following the idea in [29], the Darboux transformation of the higher-order discrete NLS equation (2) can be obtained. Under the gauge transformation

$$\begin{aligned} \psi _{n}^{[1]}=T_n[N](\lambda )\psi _{n}, \end{aligned}$$
(6)

with

$$\begin{aligned} \begin{aligned} T_n[N]=\left( \begin{array}{ll} \lambda ^N+\sum \limits _{k=1}^{N}T^{(N-2k)}_{n,1}\lambda ^{N-2k} &{} \sum \limits _{k=1}^{N}T^{(N-2k+1)}_{n,2}\lambda ^{N-2k} \\ (-1)^{N+1}\sum \limits _{k=1}^{N}T^{(N-2k+1)*}_{n,2}\lambda ^{-N+2k} &{} (-1)^N(\lambda ^{-N}+\sum \limits _{k=1}^{N}T^{(N-2k)*}_{n,1}\lambda ^{-N+2k}) \\ \end{array}\right) , \end{aligned} \end{aligned}$$

where \(T^{(N-2k)}_{n,1}\) and \(T^{(N-2k+1)}_{n,2}\) can be determined by

$$\begin{aligned} \begin{aligned}&\left( \lambda _j^N+\sum \limits _{k=1}^{N}T^{(N-2k)}_{n,1}\lambda _j^{N-2k}\right) \varphi _{n,1}^{(j)}\\&\quad +\left( \sum \limits _{k=1}^{N}T^{(N-2k+1)}_{n,2}\lambda ^{N-2k} \right) \varphi _{n,2}^{(j)}=0,\\&\left( (\lambda ^*_j)^{-N}+\sum \limits _{k=1}^{N}T^{(N-2k)}_{n,1}(\lambda ^*_j)^{-N+2k}\right) \varphi _{n,2}^{(j)*}\\&\quad -\left( \sum \limits _{k=1}^{N}T^{(N-2k+1)}_{n,2}(\lambda ^*_j)^{-N+2k} \right) \varphi _{n,1}^{(j)*}=0. \end{aligned} \end{aligned}$$
(7)

The linear spectral problem (4) changes to new one as

$$\begin{aligned} E{\tilde{\psi }}_{n}={\tilde{U}}_n\psi _{n}, ~~~~\frac{\mathrm{d}{\tilde{\psi }}_{n}}{\mathrm{d}t}={\tilde{V}}_n\psi _{n}, \end{aligned}$$
(8)

and the matrices \({\tilde{U}}_n\) and \({\tilde{U}}_n\) satisfy

$$\begin{aligned} {\tilde{U}}_n= & {} T_{n+1}[N]U_{n}(T_{n}[N])^{-1},\\ {\tilde{U}}_n= & {} (T_{n,t}[N]+T_{n}[N]V_{n})(T_{n}[N])^{-1}, \end{aligned}$$

The relation between potential \({\tilde{q}}_n[N]\) and potential \(q_n\) is

$$\begin{aligned} {\tilde{q}}_n[N]=-q_nT^{(-N)}_{n+1,1}-T^{(-N+1)}_{n+1,2}, \end{aligned}$$
(9)

where

$$\begin{aligned} T^{(-N)}_{n,1}=-\frac{\Omega _1[N]}{\Omega [N]},\quad T^{(-N+1)}_{n,2}=-\frac{\Omega _2[N]}{\Omega [N]}, \end{aligned}$$
(10)

with

$$\begin{aligned} \Omega [N]= \left| \begin{array}{lllllll} \lambda _1^{-N}\varphi _{n,1}^{(1)} &{} \lambda _1^{-N}\varphi _{n,2}^{(1)} &{} \lambda _1^{-N+2}\varphi _{n,1}^{(1)} &{} \lambda _1^{-N+2}\varphi _{n,2}^{(1)} &{} \cdot \cdot \cdot &{} \lambda _1^{N-2}\varphi _{n,1}^{(1)} &{} \lambda _1^{N-2}\varphi _{n,2}^{(1)}\\ \lambda _2^{-N}\varphi _{n,1}^{(2)} &{} \lambda _2^{-N}\varphi _{n,2}^{(2)} &{} \lambda _2^{-N+2}\varphi _{n,1}^{(2)} &{} \lambda _2^{-N+2}\varphi _{n,2}^{(2)} &{}\cdot \cdot \cdot &{} \lambda _2^{N-2}\varphi _{n,1}^{(2)} &{} \lambda _2^{N-2}\varphi _{n,2}^{(2)}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \lambda _N^{-N}\varphi _{n,1}^{(N)} &{} \lambda _N^{-N}\varphi _{n,2}^{(N)} &{} \lambda _N^{-N+2}\varphi _{n,1}^{(N)} &{} \lambda _N^{-N+2}\varphi _{n,2}^{(N)} &{}\cdot \cdot \cdot &{} \lambda _N^{N-2}\varphi _{n,1}^{(N)} &{} \lambda _N^{N-2}\varphi _{n,2}^{(N)}\\ (\lambda _1^*)^N \varphi _{n,2}^{(1)*} &{} -(\lambda _1^*)^{N} \varphi _{n,1}^{(1)*} &{} (\lambda _1^*)^{N-2} \varphi _{n,2}^{(1)*} &{} -(\lambda _1^*)^{N-2} \varphi _{n,1}^{(1)*} &{} \cdot \cdot \cdot &{} (\lambda _1^*)^{-N+2} \varphi _{n,2}^{(1)*} &{} -(\lambda _1^*)^{-N+2} \varphi _{n,1}^{(1)*}\\ (\lambda _2^*)^N \varphi _{n,2}^{(2)*} &{} -(\lambda _2^*)^{N} \varphi _{n,1}^{(2)*} &{} (\lambda _2^*)^{N-2} \varphi _{n,2}^{(2)*} &{} -(\lambda _2^*)^{N-2} \varphi _{n,1}^{(2)*} &{} \cdot \cdot \cdot &{} (\lambda _2^*)^{-N+2} \varphi _{n,2}^{(2)*} &{} -(\lambda _2^*)^{-N+2} \varphi _{n,1}^{(2)*}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ (\lambda _N^*)^N \varphi _{n,2}^{(N)*} &{} -(\lambda _N^*)^{N} \varphi _{n,1}^{(N)*} &{} (\lambda _N^*)^{N-2} \varphi _{n,2}^{(N)*} &{} -(\lambda _N^*)^{N-2} \varphi _{n,1}^{(N)*} &{} \cdot \cdot \cdot &{} (\lambda _N^*)^{-N+2} \varphi _{n,2}^{(N)*} &{} -(\lambda _N^*)^{-N+2} \varphi _{n,1}^{(N)*}\\ \end{array}\right| \end{aligned}$$

It is noted that the expression of \(\Omega _1[N]\) and \(\Omega _2[N]\) can be derived by substituting \((\lambda _1^N\varphi _{n,1}^{(1)},\lambda _2^{N}\varphi _{n,1}^{(2)}, \cdot \cdot \cdot ,\lambda _N^N\varphi _{n,1}^{(N)},\) \((\lambda _1^*)^{-N} \varphi _{n,2}^{(1)*}, (\lambda _2^*)^{-N} \varphi _{n,2}^{(2)*},\cdot \cdot \cdot ,(\lambda _N^*)^{-N} \varphi _{n,2}^{(N)*})^\text {T}\) for the first and second column in \(\Omega [N]\), respectively.

Next, we will construct the generalized \((1,N-1)\)-fold DT for higher-order discrete NLS equation (2). The generalized \((1,N-1)\)-fold DT links to single spectral parameter \(\lambda =\lambda _{1}\) and the order N-1 of the highest-order derivatives for the eigenfunctions. Using the similar method in Ref. [5, 18], we get a generalized \((1,N-1)\)-fold DT for higher-order discrete NLS equation (2). Especially, we consider the following eigenfunction solution of the Lax pair (4) with seed solution \(q_0(n,t)=c e^{i\phi t}\)

$$\begin{aligned} \varphi (\lambda )= \left( \begin{array}{l} (C_{1}\chi _{1}^{-}e^{n\ln \nu _{1}^{-}+\mu _{1}^{-}t}+C_{2} \chi _{1}^{+}e^{n\ln \nu _{1}^{+}+\mu _{1}^{+}t})e^{i\phi t+\Phi (\epsilon ^{2})} \\ (C_{1}e^{n\ln \nu _{1}^{-}+\mu _{1}^{-}t}+C_{2}e^{n\ln \nu _{1}^{+}+\mu _{1}^{+}t})e^{-i\phi t+\Phi (\epsilon ^{2})} \end{array} \right) ,\nonumber '\\ \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned} \phi&=\frac{2c^2(3c^2\gamma +h^2)}{h^4},\\ \Phi (\epsilon ^{2})&= \sqrt{(\lambda ^{2}-1)-4\lambda ^{2}c^{2}}\sum \limits _{k=1}^{N}(d_{k}+if_{k})\epsilon ^{2k},\\ \chi _{1}^{\pm }&=\frac{1-\lambda ^2\mp \sqrt{\lambda ^4-2(1+2c^2)\lambda ^2+1}}{2c\lambda ^{2}},\\ \nu _{1}^{\pm }&=\lambda +\frac{c}{\lambda \chi _{1}^{\pm }}, \\ \mu _{1}^{\pm }&=\frac{i(\lambda ^{2}-1)\left( h^{2}\lambda ^{2}(\lambda -1)^2\pm (\gamma \lambda ^4+(h^2+2(c^2-1)\gamma ) \lambda ^2+\gamma )\sqrt{\lambda ^4-2(2c^2+1)\lambda ^2+1}\right) }{2h^4\lambda ^4}, \end{aligned} \end{aligned}$$

with \(C_{j}~(j=1,2)\) are arbitrary complex parameters (i.e.,\(C_{1}=1,C_{2}=0\)), \(d_{k},f_{k}\) are free real and \(\epsilon \) is small parameter. We fix the spectral parameter \(\lambda =\lambda _{1}+\epsilon ^{2}\) with \(\lambda _{1}=\sqrt{1+c^2}\pm c\) in Eq. (11) and expand eigenfunction \(\varphi (\lambda )\) into the Taylor series at \(\epsilon =0\), then we obtain

$$\begin{aligned} \begin{aligned}&(\lambda _{1}+\epsilon ^{2})^{j}\phi _{1}(\lambda _{1}+\epsilon ^{2})= \lambda _{1}^{j}\phi _{1}+\phi _{1}[j,1]\epsilon ^{2}\\&\quad +\cdots +\phi _{1}[j,N]\epsilon ^{2N}+\cdots ,\\&(\lambda _{1}+\epsilon ^{2})^{j}\psi _{1}(\lambda _{1}+\epsilon ^{2})= \lambda _{1}^{j}\psi _{1}+\psi _{1}[j,1]\epsilon ^{2}\\&\quad +\cdots +\psi _{1}[j,N]\epsilon ^{2N}+\cdots , \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} \begin{aligned} \phi _{1}[j,l]&=\frac{1}{(2l)!}\frac{\partial ^{2l}}{\partial \epsilon ^{2l}}[(\lambda _{1}+\epsilon ^2)^{j}\phi _{1}(\lambda _{1}+\epsilon ^2)]|_{\epsilon =0},\\ \psi _{1}[j,l]&=\frac{1}{(2l)!}\frac{\partial ^{2l}}{\partial \epsilon ^{2l}}[(\lambda _{1}+\epsilon ^2)^{j}\psi _{1}(\lambda _{1}+\epsilon ^2)]|_{\epsilon =0},\\ j&=-N,-N+1,\ldots ,0,1,\ldots ,N\\&\quad -1,N;l=1,2,\ldots . \end{aligned} \end{aligned}$$

Then we obtain a generalized DT for the higher-order discrete NLS equation (2)

$$\begin{aligned} q_{n}[N]=-q_{0}f_{n+1}^{(-N)}-g_{n+1}^{(-N+1)}, \end{aligned}$$
(13)

where

$$\begin{aligned} f_{n}^{(-N)}=-\frac{\bigtriangleup _{1}^{[N]}}{\bigtriangleup ^{[N]}},~~~g_{n}^{(-N+1)}=-\frac{\bigtriangleup _{2}^{[N]}}{\bigtriangleup ^{[N]}}, \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \bigtriangleup ^{[N]}={ \left| \begin{array}{llllllll} \lambda ^{-N-1}\phi _{1} &{} \phi _{1}[-N-1,1] &{} \cdots &{} \phi _{1}[-N-1,N] &{} \lambda ^{*{N+1}}\psi _{1}^{*} &{} \psi _{1}[N+1,1]^{*} &{} \cdots &{} \psi _{1}[N+1,N]^{*} \\ \lambda ^{-N-1}\psi _{1} &{} \psi _{1}[-N-1,1] &{} \cdots &{} \psi _{1}[-N-1,N] &{} -\lambda ^{*{N+1}}\phi _{1}^{*} &{} -\phi _{1}[N+1,1]^{*} &{} \cdots &{} -\phi _{1}[N+1,N]^{*} \\ \lambda ^{-N+1}\phi _{1} &{} \phi _{1}[-N+1,1] &{} \cdots &{} \phi _{1}[-N+1,N] &{} \lambda ^{*{N-1}}\psi _{1}^{*} &{} \psi _{1}[N-1,1]^{*} &{} \cdots &{} \psi _{1}[N-1,N]^{*} \\ \lambda ^{-N+1}\psi _{1} &{} \psi _{1}[-N+1,1] &{} \cdots &{} \psi _{1}[-N+1,N] &{} -\lambda ^{*{N-1}}\phi _{1}^{*} &{} -\phi _{1}[N-1,1]^{*} &{} \cdots &{} -\phi _{1}[N-1,N]^{*} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \lambda ^{N-1}\phi _{1} &{} \phi _{1}[N-1,1] &{} \cdots &{} \phi _{1}[N-1,N] &{} \lambda ^{*{-N+1}}\psi _{1}^{*} &{} \psi _{1}[-N+1,1]^{*} &{} \cdots &{} \psi _{1}[-N+1,N]^{*} \\ \lambda ^{N-1}\psi _{1} &{} \psi _{1}[N-1,1] &{} \cdots &{} \psi _{1}[N-1,N] &{} -\lambda ^{*{-N+1}}\phi _{1}^{*} &{} -\phi _{1}[-N+1,1]^{*} &{} \cdots &{} -\phi _{1}[-N+1,N]^{*} \\ \end{array} \right| .} \end{aligned} \end{aligned}$$

The matrix \(\bigtriangleup _{1}^{[N]}\) and \(\bigtriangleup _{2}^{[N]}\) are described by \(\bigtriangleup ^{[N]}\) respectively, but the first row and the second row in the \(\bigtriangleup ^{[N]}\) are changed to \((\lambda ^{N+1}\phi _{1},\ldots ,\phi _{1}[N+1,N],\lambda ^{*{-N-1}}\psi _{1}^{*},\ldots , \psi _{1}[-N-1,N]^{*})\), respectively.

3 RW solutions and dynamic behaviors

Case 1: one-order RW solutions

As \(N=1\), the solution (13) reduces

$$\begin{aligned} q_{n}[1]=-q_{0}f_{n+1}^{(-1)}-g_{n+1}^{(0)}, \end{aligned}$$
(14)

with

$$\begin{aligned} \Delta ^{[1]}=\left| \begin{array}{llll} \lambda ^{-2}\phi _{1} &{} \phi _{1}[-2,1] &{} \lambda ^{*{2}}\psi _{1}^{*} &{} \psi _{1}[2,1]^{*} \\ \lambda ^{-2}\psi _{1} &{} \psi _{1}[-2,1] &{} -\lambda ^{*{2}}\phi _{1}^{*} &{} -\phi _{1}[2,1]^{*} \\ \phi _{1} &{} \phi _{1}[0,1] &{} \psi _{1}^{*} &{} \psi _{1}[0,1]^{*} \\ \psi _{1} &{} \psi _{1}[0,1] &{} -\phi _{1}^{*} &{} -\phi _{1}[0,1]^{*} \\ \end{array} \right| . \end{aligned}$$

For convenient, choose \(h=1,c=\frac{3}{4}\) corresponding to \(\lambda _{1}=\frac{1}{2}\) then we obtain the first-order RW solution of Eq. (2) is

$$\begin{aligned}&q_{n}[1]=-\frac{3}{4}e^{\frac{9}{128}i(16+27\gamma )t}\nonumber \\&\quad \frac{12288n(3n-2)+225t(8+27\gamma )(9t(8+27\gamma )-128i)-81920}{12288n(3n-2)+5(4096+405t^2(8+27\gamma )^{2})}.\nonumber \\ \end{aligned}$$
(15)

Note that \(q_{n+n_{0}}[1]\) is a solution with arbitrary real number shift \(n_{0}\) and the translational property also satisfies the following higher-order RW solutions. Next we illustrate the property of first-order RW solution (15).

By analyzing the explicit formula of \(q_{n+n_{0}}[1]\), we find that the parameter \(\gamma \) produces no effect in the amplitude of the first-order RW solution (15). The maximum amplitude of \(|q_{\mathrm{n}}[1]|\) is \(\frac{63}{16}\) at point \((n_{1},t_{1})=(0,0)\) with the shift \(n_{0}=\frac{1}{3}\), which is an on-site RW (see Fig. 1a). The minima amplitude attains 0 at two sites \((n_{2},t_{2})=(-1,0),(n_{3},t_{3})=(1,0)\) with the shift \(n_{0}=\frac{4-\sqrt{21}}{3},\frac{\sqrt{21}-2}{3}\) respectively. Moreover, we find that the lower peak amplitude of the first-order RW can reach at two adjacent lattice sites when \(n_{0}=\frac{5}{6}\), which is called inter-site RW (see Fig.1b). Through detailed calculation, we find that the higher-order discrete NLS equation (2) has the identical amplitude but different center points with the same background wave plane comparing with the fundamental RW solution in the AL equation [17].

Fig. 1
figure 1

First-order RW solution (15) with \(\gamma =1\): a on-site RW (\(n_{0}=1/3\)); b inter-site RW (\(n_{0}=5/6\))

Full size image

Next, we consider the effect of higher-order term \(\gamma \) and spectrum parameter \(\lambda \) on RWs. Figure 2a, b, c show that the first-order RWs become narrower with the increase of nonlinear term parameter \(\gamma \) but the peak does not changed. When \(\gamma \rightarrow \infty \), the first-order RWs can concentrate the energy. On the conversely, when \(\gamma \rightarrow 0\), Eq. (2) reduces to the AL equation, and the RWs approach the fundamental RWs of the AL equation. Altering the parameter \(\lambda \), we see that the amplitudes of the fist-order RWs increase with the spectrum \(\lambda \) increase (see Fig. 2d, e).

Fig. 2
figure 2

First-order RWs (15) with \(n_{0}=1/3\) and the different parameter \(\gamma \): a \(\gamma =1/5\); b \(\gamma =2\); c \(\gamma =10\) and plots with different parameter \(\lambda \): d \(\lambda =2/3\),the shift \(n_{0}=4/5\), e \(\lambda =1+\sqrt{2}\),the shift \(n_{0}=(1-\sqrt{2})/2\), f \(\lambda =4\),the shift \(n_{0}=-1/15\)

Full size image

The numerical simulation with random noise is an effective method to test the stability of the system [30, 31]. In what follows, we study the dynamical behaviors of the first-order RW solutions by numerical simulation with the initial conditions and perturbation for Eq. (2). Figure 3a is the exact first-order RW solution (15). Figure 3b, c are the profiles of the numerical simulation, which exhibit the time evolution of the RWs with initial condition and the perturbation of the initial solution with 2% amplitude as random noise at \(t\in (-1,1)\), respectively. The corresponding results show that the numerical simulations of the first-order RW solution can well agree with the exact RW solution (15) besides a little weak oscillation near the edges with the perturbation case.

Fig. 3
figure 3

The first-order RW solutions (15). a Exact solution, b numerical simulations using exact solutions (15) with \(t=-1\). c numerical simulations by adding random noise with amplitude 2% as the initial condition

Full size image

Case 2: second-order RW solutions

Formula (13) with \(N=2\) yields

$$\begin{aligned} q_{n}[2]=-q_{0}f_{n+1}^{(-2)}-g_{n+1}^{(-1)}, \end{aligned}$$
(16)

where

$$\begin{aligned} f_{n}^{(-2)}=-\frac{D_{1}^{[2]}}{D^{[2]}}, ~~~g_{n}^{(-1)}=-\frac{D_{2}^{[2]}}{D^{[2]}}, \end{aligned}$$

with

$$\begin{aligned} \Delta ^{[2]}=\left| \begin{array}{cccccc} \lambda ^{-3}\phi _{1} &{} \phi _{1}[-3,1] &{} \phi _{1}[-3,2] &{} \lambda ^{*3}\psi _{1}^{*} &{} \psi _{1}[3,1]^{*} &{} \psi _{1}[3,2]^{*} \\ \lambda ^{-3}\psi _{1} &{} \psi _{1}[-3,1] &{} \psi _{1}[-3,2] &{} -\lambda ^{*3}\phi _{1}^{*} &{} -\phi _{1}[3,1]^{*} &{} -\phi _{1}[3,2]^{*} \\ \lambda ^{-1}\phi _{1} &{} \phi _{1}[-1,1] &{} \phi _{1}[-1,2] &{} \lambda ^{*}\psi _{1}^{*} &{} \psi _{1}[1,1]^{*} &{} \psi _{1}[1,2]^{*} \\ \lambda ^{-1}\psi _{-1} &{} \psi _{1}[-1,1] &{} \psi _{1}[-1,2] &{} -\lambda ^{*}\phi _{1}^{*} &{} -\phi _{1}[1,1]^{*} &{} -\phi _{1}[1,2]^{*} \\ \lambda \phi _{1} &{} \phi _{1}[1,1] &{} \phi _{1}[1,2] &{} \lambda ^{*-1}\psi _{1}^{*} &{} \psi _{1}[-1,1]^{*} &{} \psi _{1}[-1,2]^{*} \\ \lambda \psi _{1} &{} \psi _{1}[1,1] &{} \psi _{1}[1,2] &{} -\lambda ^{*-1}\phi _{1}^{*} &{} -\phi _{1}[-1,1]^{*} &{} -\phi _{1}[-1,2]^{*} \\ \end{array} \right| , \end{aligned}$$

and \(\Delta _{1}^{[2]}\) and \(\Delta _{2}^{[2]}\) are described by \(\Delta ^{[2]}\), but the first row and the second row are replace by

\((\lambda _{1}^{3}\phi _{1},\phi _{1}[3,1],\phi _{1}[3,2], \lambda _{1}^{*-3}\psi _{1}^{*},\psi _{1}[-3,1]^{*},\psi _{1}[-3,2]^{*})\) in the \(\Delta ^{[2]}\), respectively.

If we choose \(c=3/4\),\(\lambda =2\),\(h=\gamma =1\), the exact second-order RW solutions can be expressed as

$$\begin{aligned} q_{n}[2]=-\frac{3}{4}e^{\frac{387}{128}it} \frac{A_{2}(n,t)}{B_{2}(n,t)}\Big |_{n\rightarrow n+n_{0}} \end{aligned}$$
(17)

where \(B_{2}(n,t),A_{2}(n,t)\) are obtained through mathematica software:

$$\begin{aligned}&B_{2}(n,t)=68719476736(1600+3n(1280+3n(497\\&\quad +3n(136 +3n(26+n(8+n))))))+849346560000(23465\\&\quad +21n(-2056+3n(-96+7n(16+3n))))t^2\\&\quad +1200225600000000(670+21n(8+3n))t^4\\&\quad +1696058545166015625t^6+1061683200\\&(25t(4096(-125+21n(8+3n))-5788125t^2)d_{1}\\&\quad +3276800d_{1}^{2}+64e_{1}(4096n(1+n)(3+n)\\&\quad -275625(4+3n)t^2+51200e_{1})),\\&A_{2}(n,t)=68719476736 (100+3n(-1520+3n(-428\\&\quad +n(8+3n(53+3n(8+n))))))-2415919104000i(-4880\\&\quad +3n(-1336+3n(-6+7n(16+3n))))t\\&\quad +2548039680000(-29220+7n(-4856+3n(-446\\&\quad +7n(16+3n))))t^2-975421440000000i\\&(275+21n(8+3n))t^3+1200225600000000(-205\\&\quad +21n(8+3n))t^4-2067576131250000000it^{5}\\&\quad +1696058545166015625t^6+589824000(\\&\quad -262144i(20+3n(8+3n))+184320(50+21n(8\\&\quad +3n))t+158760000it^2-260465625t^3)d_{1}\\&\quad +3478923509760000d_{1}^{2}\\&\quad +7549747200e_{1}(4096(100+3n(34+3n(4+n)))\\&\quad +1008000i(4+3n)t\\&\quad -2480625(4+3n)t^2+460800e_{1}). \end{aligned}$$
Fig. 4
figure 4

The second-order discrete RW solutions (17) with \(c=3/4\), \(\lambda \)=2, \(h=\gamma =1\). a \(d_{1}=f_{1}=0\), \(n_{0}=0\); b \(d_{1}=10,~f_{1}=0\), \(n_{0}=-5/6\); c \(d_{1}=0,~f_{1}=10\), \(n_{0}=2/3\)

Full size image

We see that the parameters \(d_{1}\) and \(f_{1}\) control the strong and weak interaction of the second-order RW (17).

\(\bullet \) For the case \(d_{1}=f_{1}=0\), the strong interaction happens that the RWs have four minimum points and five local maximum including a biggest peak at the center of the wave packets (see Fig. 4a).

\(\bullet \) For the case \(d_{1}\ne 0\) or \(f_{1}\ne 0\), the second-order RWs split into three first-order RWs, whose centers become a rotating triangle, and the whole profiles have three local maximum and six minimum points (see Fig. 4b, c).

Moreover, adjusting the parameters freely, we find that the area of the triangle increases with the increase of the parameters \(|d_{1}|\) or \(|f_{1}|\) and \(|f_{1}|\) can control the rotation of the triangle RWs.

Next, we give the dynamical property for the second-order RWs by the numerical simulation. Figure 5a, d are exact second-order RW solutions with different parameters \(d_{1}\) and \(e_{1}\). Figure 5b, c show that the numerical simulation of the strong interaction (i.e.,\(d_{1}=0,f_{1}=0\)) can well agree with the exact solution except for weak oscillations at \(t>0.4\) (see Fig. 5c). For the weak interaction case (i.e.,\(d_{1}=10,f_{1}=0\)), we find that the wave propagation can also match the exact solution well. However, if we add the random noise (2%) to the initial solution, the weak interaction displays serious oscillations after time exceeds 0.2, which may be due to the main energy distribution [17].

Fig. 5
figure 5

The second-order RW solutions (17). Exact solutions with a \(d_{1}=f_{1}=0\) and d \(d_{1}=10,=f_{1}=0\). b and e the numerical simulation using exact solutions (17) at \(t=-1\) as initial conditions. d and f numerical simulations by adding random noise with amplitude 2% to the exact solutions (17) as initial conditions

Full size image

Case 3: third-order RW solutions

When \(N=3\), by the formula (13) and take the special spectral parameters \(\lambda =\frac{7}{4}\) with \(c=\frac{33}{56}\), then the third-order discrete RW solution is obtained as

$$\begin{aligned} {q}_{n}[3]=-q_{0}f_{n+1}^{(-3)}-g_{n+1}^{(-2)}, \end{aligned}$$
(18)

where

$$\begin{aligned} f_{n}^{(-3)}=-\frac{\Delta _{1}^{[3]}}{\Delta ^{[3]}},~~~g_{n}^{(-2)} =-\frac{\Delta _{2}^{[3]}}{\Delta ^{[3]}}, \end{aligned}$$

with

$$\begin{aligned} \Delta ^{[3]}=\left| \begin{array}{cccccccc} \phi _{1}[-4,0] &{} \phi _{1}[-4,1] &{} \phi _{1}[-4,2] &{} \phi _{1}[-4,3] &{} \psi _{1}[4,0]^{*} &{} \psi _{1}[4,1]^{*} &{} \psi _{1}[4,2]^{*} &{} \psi _{1}[4,3]^{*} \\ \psi _{1}[-4,0] &{} \psi _{1}[-4,1] &{} \psi _{1}[-4,2] &{} \psi _{1}[-4,3] &{} -\phi _{1}[4,0]^{*} &{} -\phi _{1}[4,1]^{*} &{} -\phi _{1}[4,2]^{*} &{} -\phi _{1}[4,3]^{*} \\ \phi _{1}[-2,0] &{} \phi _{1}[-2,1] &{} \phi _{1}[-2,2] &{} \phi _{1}[-2,3] &{} \psi _{1}[2,0]^{*} &{} \psi _{1}[2,1]^{*} &{} \psi _{1}[2,2]^{*} &{} \psi _{1}[2,3]^{*} \\ \psi _{1}[-2,0] &{} \psi _{1}[-2,1] &{} \psi _{1}[-2,2] &{} \psi _{1}[-2,3] &{} -\phi _{1}[2,0]^{*} &{} -\phi _{1}[2,1]^{*} &{} -\phi _{1}[2,2]^{*} &{} -\phi _{1}[2,3]^{*} \\ \phi _{1}[0,0] &{} \phi _{1}[0,1] &{} \phi _{1}[0,2] &{} \phi _{1}[0,3] &{} \psi _{1}[0,0]^{*} &{} \psi _{1}[0,1]^{*} &{} \psi _{1}[0,2]^{*} &{} \psi _{1}[0,3]^{*} \\ \psi _{1}[0,0] &{} \psi _{1}[0,1] &{} \psi _{1}[0,2] &{} \psi _{1}[0,3] &{} -\phi _{1}[0,0]^{*} &{} -\phi _{1}[0,1]^{*} &{} -\phi _{1}[0,2]^{*} &{} -\phi _{1}[0,3]^{*} \\ \phi _{1}[2,0] &{} \phi _{1}[2,1] &{} \phi _{1}[2,2] &{} \phi _{1}[2,3] &{} \psi _{1}[-2,0]^{*} &{} \psi _{1}[-2,1]^{*} &{} \psi _{1}[-2,2]^{*} &{} \psi _{1}[-2,3]^{*} \\ \psi _{1}[2,0] &{} \psi _{1}[2,1] &{} \psi _{1}[2,2] &{} \psi _{1}[2,3] &{} -\phi _{1}[-2,0]^{*} &{} -\phi _{1}[-2,1]^{*} &{} -\phi _{1}[-2,2]^{*} &{} -\phi _{1}[-2,3]^{*} \\ \end{array} \right| , \end{aligned}$$

and \(\Delta _{1}^{[3]}\) and \(\Delta _{2}^{[3]}\) change to \(\Delta ^{[3]}\) but the first row and second row in the \(\Delta ^{[3]}\) are replaced by \((\phi _{1}[4,0],\phi _{1}[4,1], \phi _{1}[4,2],\phi _{1}[4,3],\psi _{1}[-4,0]^{*}, \psi _{1}[-4,1]^{*},\psi _{1}[-4,2]^{*},\psi _{1}[-4,3]^{*})\), respectively. The exact expression of three-order RW solution is so clumsy that we omit it here.

We just give its structural analysis corresponding to the four different parameters \((d_{1,2},f_{1,2})\).

\(\bullet \) For the case \(d_{1,2}=f_{1,2}=0\), the strong intera—-ction is displayed in Fig. 6a.

The weak interaction happens when \(d_{1}\ne 0\) or \(d_{2}\ne 0\), \(f_{1,2}=0\).

\(\bullet \) For the case \(d_1=10,d_2=f_{1,2}=0\), the third-order RWs split into six first-order RWs, which form a triangular pattern (see Fig. 6b);

\(\bullet \) For the case \(d_2=10,d_1=f_{1,2}=0\), the third-order RWs also split into six first-order RWs, which array to a rotating pentagon pattern with a first-order RWs located at the center (see Fig. 6c).

Now we study the dynamical behaviors for the third-order RWs (18) by the numerical simulation. Here, we only consider the strong-interaction case (see Fig. 6a) and weak interaction case (see Fig. 6b). Figure 7a, b show that the strong-interactions of third-order RWs almost agree with the exact solution (18). If a small noise adds to the exact solution (18) in strong-interaction case, the wave propagation behaves well except a small bulge around the edges (see Fig. 7c) but the amplitude is obviously lower than the one’s of the exact solution and numerical simulation case (see Fig. 7a, b). On the other hand, no matter what we add a noise or not to the initial condition, the wave propagations of weak interaction of third-order RWs display strong oscillations (see Fig. 7d–f). We infer that the dispersed energy of the third-order RWs can more easily lead to the disorder than the strong interaction case.

Fig. 6
figure 6

Third-order discrete RW solutions with \(h=\gamma =1\) a strong interaction \(d_{1,2}=f_{1,2}=0\), \(n_{0}=0\); b a triangular pattern with \(d_{1}=10,d_{2}=0,f_{1,2}=0\), \(n_{0}=-1/2\); c a pentagon pattern with \(d_{1}=0,d_{2}=10,f_{1,2}=0\), \(n_{0}=-1/3\)

Full size image

4 Modulation instability of continuous-wave states

Many studies [32,33,34,35] have shown that the modulational instability (MI) associated with the growth of perturbations on a plane wave background can result in the RWs. We consider the continuous-wave solution of Eq. (2) with \(q_0(n,t)=c e^{i\phi t}\), where the real amplitude \(c\ne 0\). We perturb this solution

$$\begin{aligned} q_{n}(t)=\left( 1+\frac{\varepsilon }{c}{\hat{q}}_{n}(t)\right) q_0(n,t), \end{aligned}$$
(19)

where \(\varepsilon \) is an infinitesimal amplitude and \({\hat{q}}_{n}(t)\) is a perturbation solution. Substituting (19) into Eq. (2) yields a complex linearized equation

$$\begin{aligned} \begin{aligned}&i{\hat{q}}_{n,t}+\gamma (1+c^2)^2{\hat{q}}_{n-2}+(1+c^2+4\gamma (c^2-1)){\hat{q}}_{n-1}\\&\quad +(2\gamma (c^2+1)(c^2-3)-2){\hat{q}}_{n}+\gamma (c^2+1)^2{\hat{q}}_{n+2}\\&\quad +(c^2+1)(4\gamma (c^2-1)+1){\hat{q}}_{n+1}+2c^2\gamma (1+c^2){\hat{q}}^{*}_{n-1}\\&\quad +2c^2(1-2\gamma +4c\gamma ){\hat{q}}^{*}_{n}+2c^2\gamma (1+c^2){\hat{q}}^{*}_{n+1}=0. \end{aligned} \end{aligned}$$
(20)

We consider the perturbation with real and imaginary parts \({\hat{q}}_{n}=q_{1,n}(t)+iq_{2,n}(t)\), which changes the complex linearized equation can change into two real equations

$$\begin{aligned} \begin{aligned}&\gamma (1+c^2)^2q_{1,n-2}+(1+c^2)(1-4\gamma +6\gamma c^2)q_{1,n-1}\\&\quad +2(-1+c^2+\gamma (3-4c^2+5c^4))q_{1,n}\\&\quad +(1+c^2)\gamma (-4+6c^2))q_{1,n+1}\\&\quad +(1+c^2)^2q_{1,n+2}-q_{2,n,t}=0,\\&(1+c^2)[\gamma (1+c^2)q_{2,n-2}+(1+2\gamma (c^2-2))q_{2,n-1}\\&\quad -2(1+3\gamma (c^2-1))q_{2,n}\\&\quad +(1+2\gamma (c^2-2))q_{2,n+1}\\&\quad +\gamma (1+c^2)q_{2,n+2}]+q_{1,n,t}=0. \end{aligned} \end{aligned}$$
(21)

Assume that real equation (21) exists the following complex solution

$$\begin{aligned} (q_{1,n}(t),q_{2,n}(t))=(q_{1,n}^{(0)},q_{2,n}^{(0)})e^{gt+ikn}, \end{aligned}$$
(22)

where g is the MI gain k is an arbitrary real wavenumber and \(q_{1,n}^{(0)},q_{2,n}^{(0)}\) are constant amplitudes of the perturbation eigenmode. Substituting (22) into Eq. (21) yields the MI dispersion equation in the form of the determinant

$$\begin{aligned} \left| \begin{array}{ll} -g &{}\quad 2(c^2-1+(c^2+1)\cos k)(1+2\gamma (2c^2-1)+2\gamma (c^2+1)\cos k) \\ -4(c^2+1)(1+2\gamma (c^2-1)+2\gamma (c^2+1)\cos k)\sin ^{2}\frac{k}{2} &{}\quad g \\ \end{array} \right| =0, \end{aligned}$$
(23)
Fig. 7
figure 7

The third-order RW solutions (18). The exact solution a \(d_{1,2}=f_{1,2}=0\) and d \(d_{1}=10,d_{2}=f_{1,2}=0\) (left); b and e simulated simulation using exact solutions (18) as the initial conditions (middle); c and f numerical simulations by adding random noise with amplitude 2% to the exact solutions (18) as initial conditions (right)

Full size image
Fig. 8
figure 8

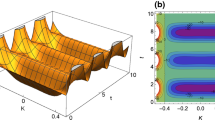
Gain spectra of the MI for different CW amplitude c and higher order parameter \(\gamma \). a Different amplitude with \(c=2\) (blue solid), \(c=3\) (red dashed), and \(c=4\) (green dotted-dashed); b Different parameter with \(\gamma =1\) (blue solid), \(\gamma =2\) (red dashed), and \(\gamma =3\) (green dotted-dashed)

Full size image

which gives an explicit dispersion relation

$$\begin{aligned}&g^2=8 (1 + c^2)\left( c^2-1+(c^2+1)\cos k\right) \nonumber \\&\quad \left( 1+2\gamma (2 c^2-1)+2\gamma (1+c^2)\cos k\right) ^2 \sin ^2\frac{k}{2}.\nonumber \\ \end{aligned}$$
(24)

We point out here the MI takes place when expression (24) is positive. The MI condition \(g^2>0\) holds as

$$\begin{aligned}&\cos k>\frac{1-c^2}{1+c^2},\\&\cos k\ne -\frac{1+2\gamma (2c^2-1)}{2\gamma (1+c^2)}, and\\&k\ne 2m\pi ,m\in Z. \end{aligned}$$

Figure 8 shows that the growth rate g(k) becomes larger and larger as the amplitude c increases, meanwhile, for the fixed amplitude \(c=2\), \(g_{\max }(k)\) also gets larger with the increase of parameter \(\gamma \).

5 Conclusions

In this paper, we have studied a higher-order integrable discrete NLS equation by the generalized discrete \((1,N-1)\)-fold Darboux transformation. The discrete higher-order RW solutions are given by determinants. We have analytically studied the dynamical behaviors of discrete RW solutions, which exhibits abundant patterns including on-site, inter-site, the rotating triangle and pentagon structures. Comparing with the discrete NLS equation, the first-order RWs of integrable higher-order discrete NLS equation have the identical peaks but different center points with the same plane-wave amplitude. We also find that the nonlinear term parameter \(\gamma \) can control energy density of the RWs. By means of numerical simulation with the time evolutions of the RW solutions, we reveal that the strong interaction RWs are more stable on the wave propagation than the weak interaction case. Finally, the modulation instability condition of the background wave solutions are given.