Two-dimensional localized Peregrine solution and breather excited in a variable-coefficient nonlinear Schrödinger equation with partial nonlocality

Abstract

Hierarchies of Peregrine solution and breather solution are derived in a (2+1)-dimensional variable-coefficient nonlinear Schrödinger equation with partial nonlocality. Based on these solutions, we study the control of the excitation of Peregrine solution and breather solution in different planes. In particular, the localized Peregrine solution and breather solution are firstly reported in two-dimensional space. It is expected that our analysis and results may give new insight into higher-dimensional localized rogue waves in nonlocal media.

1 Introduction

Localized structures based on different nonlinear evolution equations were intensively studied [1,2,3,4,5,6]. Peregrine solution and breather solution based on the nonlinear Schrödinger equation (NLSE) have become important prototypes to describe rogue wave motions in different fields of physics and ocean engineering [10,11,12,13]. Localized structures based on quintic and cubic-quintic NLSEs were extensively discussed [7,8,9]. Rogue waves are also called as freak waves, monster waves, killer waves. One of important characteristics of rogue waves is their unpredictability that “waves that appear from nowhere and disappear without a trace” [14].

In ocean, rogue waves exhibit harmful aspects, and they destroy ships and marine structures [15, 16]. Many mainstream media such as Nature News, BBC News, Reuters, ScienceDaily, Physicsworld, Financial Express. have reported their extreme hazards in different sea areas. However, rogue waves can occur in other media than water. In particular, optical rogue waves allow study of the phenomenon in the laboratory. In optics, scientists excite rogue waves in the useful fields, e.g., harnessing and control of optical rogue waves in supercontinuum generation [17, 18].

Relative to a reference frame co-moving with the optical pulse, the basic nonlinear model describing the rogue wave phenomenon is the focusing NLSE

$$\begin{aligned} \text {i}U_T+ U_\mathrm{XX}+2|U|^2U=0. \end{aligned}$$

(1)

Based on this model, the theoretical study for rogue wave began with the pioneering work of Akhmediev’s group [14, 19,20,21,22]. By means of the Darboux transformation, hierarchies of Peregrine solution and breather solution for NLSE have been reported to describe rogue waves [14, 19,20,21,22].

Considering the concept of nonautonomous solitons [23], nonautonomous Peregrine solution and breather solution and the related control of excitation have been discussed [24,25,26]. Moreover, nonautonomous Peregrine solution and breather solution in higher-dimensional case have also been studied [27,28,29]. However, all higher-dimensional Peregrine solution and breather structures in previous literatures [27,28,29] are not completely localized in space (such as x-y space).

In this paper, we consider the propagation of localized Peregrine solution and breather structures in a medium with partially nonlocal inhomogeneous nonlinearities by the following (2+1)-dimensional NLSE

$$\begin{aligned} \text {i}u_t+ \beta (t)u_\mathrm{xx}+\chi (t) u\int _{-\infty }^{+\infty }|u|^2\mathrm{d}y=0, \end{aligned}$$

(2)

with the normalized complex field envelope u(t, x, y), diffraction coefficient $\beta (t)$ and nonlinear coefficient $\chi (t)$. Here the subscripts denote the derivation to the corresponding variables. In this case, x-direction is localized, however, y-direction is nonlocal because the quantity at point y is related to other vicinal points. Equation (2) is a nonlinear differential–integral equation, and it is a variable-coefficient extension of the (2+1)-dimensional equation [30, 31]. As reported in [30], Eq. (2) can be considered as the vector NLSE with infinitely many components. When $\beta$ and $\chi$ are both constant, the Gram-type determinant solution and localized soliton interactions were studied [30]. More physical interpretation of Eq. (2) can also be found in Refs. [30, 31].

2 Similarity reduction between nonlocal equation (2) and local equation (1)

Inserting the transformation

$$\begin{aligned} u(t,x,y)=&\rho (y,t)U[X(x,t),T(t)] \nonumber \\&\quad \times \,\exp {[\text {i}\phi (t,x,y)]}, \end{aligned}$$

(3)

into Eq. (2), when function U[X(x, t), T(t)] satisfies Eq. (1), we obtain the following set of equation

$$\begin{aligned}&\rho _t+\beta \rho \phi _\mathrm{xx}=0, X_t+\beta X_x\phi _x=0,\nonumber \\&\quad \phi _t +\beta \phi _x^2=0, T_t-2\beta X_x^2=0, X_\mathrm{xx}=0, \end{aligned}$$

(4)

$$\begin{aligned}&\int _{-\infty }^{+\infty } \rho ^2 \mathrm{d}y=2T_t/\chi . \end{aligned}$$

(5)

After some algebra from Eqs. (4) and (5), we obtain the result: If $\beta (t)$ and $\chi (t)$ satisfy the relation

$$\begin{aligned} \chi (t)=-\frac{2}{w_0^2}\beta (t)\varPi (t), \end{aligned}$$

(6)

then the amplitude, accumulated time, similarity variable and phase read

$$\begin{aligned}&\rho (y,t)=A(y)\Omega (t), T(t)=\frac{\Omega (t)\varPi (t)}{w_0^2},\nonumber \\&X(x,t)=\frac{x}{w(t)},\nonumber \\&\phi (t,x,y)=-\frac{s_0\Omega (t)}{4}x^2+\varphi (y), \end{aligned}$$

(7)

and function A(y) satisfies

$$\begin{aligned} \int _{-\infty }^{+\infty }|A(y)|^2\mathrm{d}y=1, \end{aligned}$$

(8)

with the width $w(t)=\frac{w_0}{\Omega (t)}$, the accumulated diffraction $\varPi (t)=\int ^t_0\beta (\tau )\text {d}\tau$, chirp function $\Omega (t)=[1-s_0\varPi (t)]^{-1}$ and initial constants $w_0, s_0$ and free function $\varphi (y)$.

The normalization condition (8) for A(y) hints that many types of function A(y) can be selected. Function A(y) can be the hyperbolic secant function as $A(y)=\text {sech}(y)/\pi$. Moreover, function A(y) can also be the Hermite–Gaussian function

$$\begin{aligned} A(y)=\frac{1}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}, \end{aligned}$$

(9)

with the Hermite polynomial $H_n(\omega y)$ and nonnegative integer n.

Therefore, if $\beta (t)$ and $\chi (t)$ satisfy the relation (6), via the transformation (3) with (7), nonlocal equation (2) is reduced to the local equation (1).

3 Hierarchy of Peregrine solution

According to the modified Darboux transformation (DT) technique in Ref. [19] and choosing the plane-wave solution $u_0=\exp (2\text {i}T)$ as seed solution, from the one-to-one correspondence (3), we have the first-order rational solution (Peregrine solution)

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\left[ -1+\frac{G_1+\text {i}K_1}{D_1}\right] \nonumber \\&\quad \times \,\exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\quad \left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(10)

where $G_1=4,K_1=16T_s,D_1=1+4X_s^2+16T_s^2$ with $T_s=T-T_0$ and $X_s=X-vT_s$, and T and X are given in the expression (7).

Using solution (10) as the seed solution in DT technique, we obtain the second-order rational solution

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\left[ 1+\frac{G_2+\text {i}K_2}{D_2}\right] \nonumber \\&\times \,\exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(11)

where

$$\begin{aligned} G_2= & {} 36-15360T_s^4-3456T_s^2-192X_s^4\\&-288X_s^2-4608T_s^2X_s^2,\\ K_2= & {} T_s(720-12288T_s^4-1536T_s^2-768X_s^4\\&+1152X_s^2-6144T_s^2X_s^2),\\ D_2= & {} 9+4096T_s^6+6912T_s^4+1584T_s^2+64X_s^6\\&+48X_s^4+108X_s^2+3072T_s^4X_s^2\\&+768T_s^2X_s^4-1152T_s^2X_s^2 \end{aligned}$$

with $T_s=T-T_0$ and $X_s=X-vT_s$, and T and X are given in the expression (7).

Similarly, using solution (11) as the seed solution in DT technique, we obtain the third-order rational solution

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\left[ -1+\frac{G_3+\text {i}K_3}{D_3}\right] \nonumber \\&\times \exp \,\left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(12)

where $G_3=24576\,{X_s}^{10}+ \left( 92160+ 1474560\,{T_s}^{2} \right) {X_s}^{8}+ ( -1474560\,{T_s}^{2}+322560$ $+19660800\,{T_s}^{4}) {X_s}^{6}+ (-172800+2764800\,{T_s}^{2} -14745600\,{T_s}^{4}+110100480\,{T_s}^{6} ) {X_s}^{4}+ ( -64800- 20736000\,{T_s}^{2}+165888000\,{T_s}^{4}+165150720\,{T_s}^{6}+283115520\,{T_s}^{8} ) {X_s}^{2}+276824064\,{T_s}^{ 10}+778567680\,{T_s }^{8}+215285760\,{T_s}^{6}-47001600\,{T_s}^{4}-777600\,{T_s}^{2}+16200,$ $K_3=98304\,{X_s}^{10}T_s+ \left( -368640\,T_s + 1966080\,{T_s}^{3}\right) {X_s}^{8}+ (-921600\,T_s-13762560\,{T_s}^{3}$ $+15728640\,{T_s}^{5}) {X_s}^{6}+ ( -2073600\,T_s-11059200\,{T_s}^ {3}-82575360\,{T_s}^{5}+62914560\,{T_s}^{7}) {X_s}^{4}+ ( 1814400\,T_s-38707200\,{T_s}^{3}+168099840{ T_s}^{5}-94371840\,{T_s}^{7}+125829120\,{T_s}^{9}) {X_s}^{2}+100663296\,{T_s}^{11}+157286400\,{T_s}^{9}-342097920\,{T_s}^{7}-236666880 \,{T_s}^{5}-3801600\,{T_s}^{3}+ 453600\,T_s,$ $D_3=4096\,{X_s}^{12}+ ( 6144+98304\,{T_s}^{2}) {X_s}^{10}+ (34560 -368640\,{T_s}^{2}+983040\,{T_s}^{4} ) {X_s}^{8}+ (149760+552960\,{T_s}^{2}-2949120\,{T_s}^{4}+ 5242880\,{T_s}^{6} ) {X_s}^{6}+ ( 54000+3456000\,{T_s}^{2}- 5529600\,{T_s}^{4}+3932160\,{T_s}^{6}+15728640\,{T_s}^{8} ) {X_s}^{4}+ ( 48600-2332800\,{T_s}^{2}+80179200\,{T_s}^{4}+221184000\,{T_s}^ {6}+70778880\,{T_s}^{8} + 25165824\,{T_s}^{10}) {X_s}^{2}+16777216\,{T_s}^{12}+132120576\,{T_s}^{10}+244776960\,{T_s}^{8}+62668800\, {T_s}^{6}+36806400\,{T_s}^{4}+1490400\,{T_s}^ {2}+2025$ with $T_s=T-T_0$ and $X_s=X-vT_s$, and T and X are given in the expression (7).

Therefore, along this procedure, for any m-order, we can write the solution of Eq. (2) as follows

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\times \,\left[ (-1)^m+\frac{G_m+\text {i}K_m}{D_m}\right] \nonumber \\&\times \,\exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(13)

where $G_m, K_m$ and $D_m$ are polynomials in the two variables T and X. For the limit of length, we do not list these expressions here.

4 Hierarchy of breather solution

According to the modified DT technique in Ref. [22] and choosing the plane-wave solution $u_0=\exp (2\text {i}T)$ as seed solution, from the one-to-one correspondence (3), we derive the first-order breather solution

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\times \,\left[ -1+\frac{L_1+\text {i}M_1}{N_1}\right] \nonumber \\&\times \,\exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(14)

where $L_1=2\kappa _1^2\cosh \delta _1(T-T_1),M_1=4\kappa _1\nu _1\sinh \delta _1(T-T_1),N_1=4[\cosh \delta _1(T-T_1) -\nu _1\cos \kappa _1(X-X_1)]$ with $\nu _1=\text {Im}(\lambda _1)$ and $\delta _1=\nu _1\kappa _1.$ Here T and X are given in the expression (7). When $0<\nu _1<1$, this solution (14) describe breather, and when $\nu _1>1$ ($\kappa _1$ is imaginary), this solution (14) describes KM soliton. Specifically, if $\nu _1\rightarrow 1$, this solution (14) can degenerate into the first-order rational solution (11) via the l’Hôpital’s rule.

When we consider the second-order solution, two independent frequencies of modulation, $\kappa _1$ and $\kappa _2$, are combined in the solution via the next step of the DT. Along the procedure in Ref. [22], we derive the second-order breather solution

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\times \,\left[ 1+\frac{L_2+\text {i}M_2}{N_2}\right] \nonumber \\&\times \,\exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\,\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(15)

where $L_2=-\kappa _{12}[\kappa _1^2\delta _2\cosh (\delta _1T_{s1})\cos (\kappa _2X_{s2})/\kappa _2-\kappa _2^2\delta _1\cosh (\delta _2T_{s2}) \cos (\kappa _1X_{s1})/\kappa _1 -\kappa _{12}\cosh (\delta _1T_{s1}) \cosh (\delta _2T_{s2})],$ $M_2=-2\kappa _{12}[\delta _1\delta _2\sinh (\delta _1T_{s1})\cos (\kappa _2X_{s2})/\kappa _2- \delta _2\delta _1\sinh (\delta _2T_{s2})\cos (\kappa _1X_{s1})/\kappa _1-\delta _1\sinh (\delta _1T_{s1})\cosh (\delta _2T_{s2}) +\delta _2\cosh (\delta _1T_{s1})\sinh (\delta _2T_{s2})],$ $N_2=2(\kappa _1^2+\kappa _2^2)\delta _1\delta _2\cos (\kappa _1X_{s1})\cos (\kappa _2X_{s2}) /(\kappa _1\kappa _2)-(2\kappa _1^2-\kappa _1^2\kappa _2^2+2\kappa _2^2)\cosh (\delta _1T_{s1})$ $\cosh (\delta _2T_{s2}) +4\delta _1\delta _2[\sin (\kappa _1X_{s1})\sin (\kappa _2X_{s2}) +\sinh (\delta _1T_{s1})\sinh (\delta _2T_{s2})]$ $-2\kappa _{12} [\delta _1\cos (\kappa _1X_{s1})\cosh (\delta _2T_{s2})/\kappa _1-\delta _2\cos (\kappa _2X_{s2})\cosh (\delta _1T_{s1})/\kappa _2]$ with $T_{sj}=2(T-T_{j}),X_{sj}=X-X_{j},\delta _j=\kappa _j\sqrt{4-\kappa _j^2}/2,\kappa _{12}=\kappa _1^2-\kappa _2^2,\kappa _j=2\sqrt{1+\lambda _j^2},j=1,2$. Here $\kappa$ is the modulation frequency, $T_j$ and $X_{j}$ determine the center of solution in t-x coordinates, and T and X are given in the expression (7).

When the values of $\text {Im}(\lambda _1)$ and $\text {Im}(\lambda _2)$ are both between 0 and 1, this solution (15) describes two breathers. When the values of $\text {Im}(\lambda _1)$ and $\text {Im}(\lambda _2)$ are both bigger than 1, this solution (15) describes two Kuznetsov-Ma solitons. For the values of $\text {Im}(\lambda _1)$ and $\text {Im}(\lambda _2)$, if one of them is bigger than 1, and another is between 0 and 1, a breather and a Kuznetsov-Ma soliton can be constructed together.

Especially, if $\kappa _1\ne 0$ and $\kappa _2\rightarrow 0$, solution (15) describes a breather or a Kuznetsov-Ma soliton with a Peregrine solution. In this case, expressions of $L_2,M_2$ and $N_2$ in solution (15) has the form

$$\begin{aligned} L_2= & {} \kappa \{\kappa [\kappa ^2(4T_{s2}^2+4X_{s2}^2+1)-8]\nonumber \\&\times \,\cosh (\delta T_{s1})+8 \delta \cos (\kappa X_{s1})\}/8,\nonumber \\ M_2= & {} \kappa \{8T_{s2}[\delta \cos (\kappa X_{s1})-\kappa \cosh (\delta T_{s1})]\nonumber \\&+\,\delta \kappa (4T_{s2}^2+4X_{s2}^2+1) \sinh (\delta T_{s1})\}/4,\nonumber \\ N_2= & {} -\{\delta [\kappa ^2(4T_{s2}^2+4X_{s2}^2+1)-16]\nonumber \\&\times \,\cos (\kappa X_{s1})+\kappa ([\kappa ^2(4T_{s2}^2+4X_{s2}^2-3)+16] \nonumber \\&\times \,\cosh (\delta T_{s1}) \nonumber \\&-\,16\delta [T_{s2}\sinh (\delta T_{s1})\nonumber \\&+\,X_{s2}\sin (\kappa X_{s1})])\}/(4\kappa ) \end{aligned}$$

(16)

with $T_{sj}=2(T-T_{j}),X_{sj}=X-X_{j},\delta =\kappa \sqrt{4-\kappa ^2}/2,\kappa =2\sqrt{1+\lambda _1^2},j=1,2$. When $0<\text {Im}(\lambda _1)<1$ and $\text {Im}(\lambda _1)>1$ in solution (16), we can obtain the Peregrine solution combined by a breather and Kuznetsov-Ma soliton, respectively.

Similarly, along the procedure in Ref. [22], we derive m-order solution

$$\begin{aligned} u(t,x,y)= & {} \frac{\Omega (t)}{\sqrt{n!2^n\sqrt{\pi }}}H_n(\omega y)e^{-\omega ^2 y^2/2}\nonumber \\&\times \left[ (-1)^m+\frac{L_m+\text {i}M_m}{N_m}\right] \nonumber \\&\times \exp \left\{ \text {i}[(2-v^2)T_s+vX\right. \nonumber \\&\left. -\frac{s_0\Omega (t)}{4}x^2+\varphi (y)]\right\} , \end{aligned}$$

(17)

where $L_m,M_m$ and $N_m$ are polynomials in the two variables T and X. For the limit of length, we do not list these expressions here.

5 Controllable behaviors of localized structures

The controllable behaviors of localized structures are studied in the following soliton control system [32, 33]

$$\begin{aligned} \beta (t)=\beta _{0}\exp (-\sigma t), \end{aligned}$$

(18)

which is the exponentially modulated control system. Parameter $\beta _{0}$ describes the initial diffraction. This system is a typical diffraction decreasing system (DDS) for $\sigma >0$. Moreover, if $\sigma =0$, Eq.(18) is a constant diffraction system.

Fig. 1

Complete excitation of Peregrine solution in DDS at a x-t plane with $y=3$ and b–f x-y space with b, c $n=0,t=8$, d $n=0,t=100$, e $n=1,t=8$, and f $n=2,t=100$. Parameters are chosen as $w_0=0.5,\beta _0=0.1,\sigma =0.05,s_0=0.02,v=0.2,T_0=5,\omega =1$

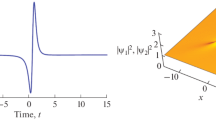
At first, we reconsider the excitation of Peregrine solution (10) in the framework of the focusing NLSE (1). As reported in Ref. [19], Peregrine solution reaches its maximum at center point ($X_0=0,T_0$). Along T-axis, Peregrine solution is excited from a continuous-wave background (emerging at $T\approx T_0$) and disappears soon.

Fig. 2

Peak excitation of Peregrine solution in DDS at a x-t plane with $y=3$ and b–f x-y space with b $n=0,t=10$, c $n=0,t=100$, d $n=1,t=10$, e $n=2,t=100$, and f $n=3,t=100$. Parameters are chosen as $w_0=0.5,\beta _0=0.1,\sigma =0.162,s_0=0.02,v=0.2,T_0=5,\omega =1$

Note that the accumulated time T and similarity variable X are not real time t and real spatial variable x in our study, respectively. From the expression $T(t)=\frac{\Omega (t)\varPi (t)}{w_0^2}$ in Eq. (7), we know that the value of T(t) is not free, and it is limited to a certain range. In the DDS, $T(t)=\frac{\beta _0[1-\exp (-\sigma t)]}{w_0^2\{\sigma -s_0\beta _0[1-\exp (-\sigma t)]\}}$, which indicates that $T(t)\rightarrow T_m\equiv \frac{\beta _0}{w_0^2[\sigma -s_0\beta _0]}$ as real time $t\rightarrow \infty$.

Fig. 3

Initial excitation of Peregrine solution in DDS at a x-t plane with $y=3$ and b–f $x-y$ space with b $n=0,t=10$, c $n=0,t=100$, d $n=1,t=10$, e $n=2,t=100$, and f $n=4,t=100$. Parameters are chosen as $w_0=0.5,\beta _0=0.1,\sigma =0.4,s_0=0.02,v=0.2,T_0=5,\omega =1$

Therefore, the relation between $T_0$ and $T_m$ is crucial to determine the degree of excitation. As reported in our previous study [24, 25, 27], if $T_m>T_0$, Peregrine solution is completely and quickly excited; if $T_m=T_0$, Peregrine solution is excited to peak and maintain this shape a long time; if $T_m<T_0$, Peregrine solution is only excited to initial shape. Note that here we discuss the control for the excitation of two-dimensional localized Peregrine solution, which is hardly studied to the best of our knowledge, and different from two-dimensional line rogue waves reported in [27,28,29].

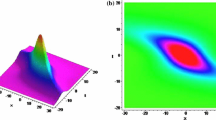
Figure 1 shows the complete excitation of Peregrine solution with $T_m=16.67>T_0=5$. Figure 1a exhibits the complete excitation of Peregrine solution at the range of $5<t<11$ in the x-t plane. In x-y space, the combined structure is made up of the Hermite–Gaussian structure in y-component and Peregrine solution. During the stage of complete excitation, the combined structure in x-y space appear a localized structure at the range of $-0.5<x<0.5$ in Fig. 1b when $n=0$. Corresponding to Fig. 1b, the detailed structures in x-direction (when $y=0$) and y-direction (when $x=0$) are shown in Fig. 1c. When $t>11$, there is a constant plane in the x-t plane, and thus only the Gaussian structure is shown in x-y space in Fig. 1d. For $n=1$, when $t=8$, two localized wave packets [like structures in Fig. 1c] appear in the x-t plane in Fig. 1e. When $t=100$, there is a constant plane in the x-t plane, and thus only the Hermite–Gaussian structure is shown in x-y space. For other values of n, if $t>11$, there are only the Hermite–Gaussian structures in x-y space. Figure 1f is another example of the Hermite–Gaussian structure in x-y space when $n=2$.

Fig. 4

Complete excitation of superposed breather in DDS at a x-t plane with $y=3$ and x-y space with b $n=0,t=7$, c $n=0,t=100$; peak excitation of superposed breather in DDS at d x-t plane with $y=3$ and x-y space with e $n=0,t=100$, f $n=5,t=100$; initial excitation of superposed breather in DDS at g x-t plane with $y=3$ and x-y space with h $n=0,t=100$, i $n=6,t=100$. Parameters are chosen as $\kappa _1=0.4,\kappa _2=1.4,w_0=0.5,\beta _0=0.1,s_0=0.02,v=0.2,$ $T_1=T_2=5,\omega =1$ with a–c $\sigma =0.05$, d–f $\sigma =0.162$ and g–i $\sigma =0.4$

If $T_m=T_0=5$, the peak excitation of Peregrine solution can maintain a long time with a self-similar propagating behavior in Fig. 2a, where its amplitude and width self-similarly change after a short propagation time from the initial condition. Corresponding to the initial stage of excitation in Fig. 2a, a wave packet is embedded in a line Gaussian structure in x-y space in Fig. 2b at $t=10$ when $n=0$. Corresponding to the peak stage of excitation in Fig. 2a, the combined structure in x-y space appear localized structure [like structure in Fig. 1c] at the range of $-0.5<x<0.5$ in Fig. 2c when $t=100$. Similarly, for other values of n, if $t>11$, there are all localized structures [like structures in Fig. 1c] in x-y space, and the number of localized structures is decided by $n+1$ for n-th order of Hermite polynomial. Figure 2d–f demonstrates these localized structures [like structures in Fig. 1c] for different n.

If $T_m=2.01<T_0=5$, the excitation of Peregrine solution is restrained and only excited to initial shape in Fig. 3a because the threshold of exciting Peregrine solution is never reached. This structure looks like a bright optical similariton and separated bright similariton pairs [34] with very small amplitudes propagating stably on a non-zero background. In x-y space, no localized structures appear. From Fig. 3b ($t=10$) to Fig. 3c ($t=100$), only a small packet is superimposed on a line Gaussian structure when $n=0$. For other values of n, only small packets are also superimposed on the line Hermite–Gaussian structures. Some examples are shown in Fig. 3d–f.

For other order rational solutions, when $T_m>T_0$, $T_m=T_0$ and $T_m<T_0$, complete excitation, peak excitation and initial excitation will happen. These cases are similar to Peregrine solution in Figs. 1–3. For the limit of length, we omit the related plots.

Fig. 5

Numerical rerun of Peregrine solution (10) in Figs. 1c, 2d and 3e at time $t=100$. An added 5% white noise is added to the initial values. The parameters are the same as those in the corresponding analytical plots

In the following, we consider the control of the excitation of superposed breather. Solution (15) can describe two arrays of separated breathers. Each breathers are composed of Peregrine solution-like structures. In each arrays, the numbers of Peregrine solution-like structures are decided by the ratio of $\kappa _1$ and $\kappa _2$. When two arrays of separated breathers share the same origin, we can construct superposed breathers. Similarly to these excitations of Peregrine solution in Figs. 1–3, when $T_m>T_1=T_2$, $T_m=T_1=T_2$ and $T_m<T_1=T_2$, complete excitation, peak excitation and initial excitation of superposed breather will occur.

Here we choose $\kappa _1=0.2$ and $\kappa _2=1.4$, namely, the number of Peregrine solution-like structures in two array is 1 : 7. When they share the same origin, two Peregrine solution-like structures with the same value of x form a parallel Peregrine solution-like pair, and three Peregrine solution-like structures triangularly laying out become a second-order rational solution.

If $T_{m}$ is remarkably bigger than $T_1=T_2$, the full superposed breather is excited completely. Figure 4a shows the complete excitation at the range of $0<t<17$ in the x-t plane. In x-y space, the combined structure is made up of the Hermite–Gaussian structure in y-direction and breather in x-direction. During the stage of complete excitation, in x-y space, the combined structure appears a breather in x-direction with Gaussian structures in y-direction in Fig. 4b when $n=0$. When $t>17$, there is a constant plane in the x-t plane, and thus only the Gaussian structure is shown in x-y space in Fig. 4c. For other values of n, $(n+1)$-arrays of breathers appear at the range of $0<t<17$, and the Hermite–Gaussian structure appears at $t>17$ in x-y space.

If $T_{m}=T_1=T_2$, in x-t plane, the peak excitation of superposed breather can maintain a long time with self-similar propagating behaviors (see Fig. 4d). The amplitude and width of sustained breather self-similarly change after a short propagation time from the initial condition. Corresponding to the initial stage of excitation in Fig. 4d, the combined structure in x-y space appears a breather in Fig. 4e when $t=100$. Similarly, for other values of n, if $t>11$, there are $(n+1)$-arrays of breathers in x-y space. For example, Fig. 4f displays six arrays of breathers in x-y space when $n=5$.

If $T_{m}<T_1=T_2$, the threshold of exciting superposed breather is never reached, its excitation is restrained an d only initial part is excited in the x-t plane (see Fig. 4g), which looks like a periodic wave with very small amplitudes propagating stably with the time. In x-y space, only some small packets are superimposed on the line Hermite–Gaussian structures. Figure 4h, demonstrate two examples when $n=0$ and $n=6$, respectively.

At last, we discuss the stability of these Peregrine solutions with different controllable excitations. We study analytical solutions evolving with time when they are disturbed from their analytically given forms. We perform the direct numerical simulation (the split-step Fourier technique) with initial white noise for Eq. (2) with initial fields coming from solution (10) in some cases. Figure 5 displays the numerical rerun of Peregrine solution (10) in Figs. 1c, 2d and 3e at time $t=100$. From Fig. 5a, one can find that Peregrine solution with complete excitation for $n=1$ stably evolves with time in both x and y directions, and the white noise hardly influences the evolution of Peregrine solution. In Fig. 5b, the white noise has a stronger influence on Peregrine solution with peak excitation for $n=2$, especially two sides of Peregrine solution in x-direction. From Fig. 5c, Peregrine solution with initial excitation for $n=3$ is unstable and broken down the initial shape after evolving time $t=100$, and at last turns into noise especially for its shape in x-direction. Compared these Peregrine solutions in Fig. 5a–c, the stability attenuates with the add of n.

6 Conclusions

In conclusion, we obtain hierarchies of Peregrine solution and breather solution excited in a (2+1)-dimensional variable-coefficient NLSE with partial nonlocality. Based on these solutions, we study the control of the excitation of Peregrine solution and breather solution in different planes. If $T_m>T_0 (\text {or} T_1=T_2)$, Peregrine solution or breather solution is completely and quickly excited; if $T_m=T_0 (\text {or} T_1=T_2)$, Peregrine solution or breather solution is excited to peak and maintain this shape a long time; if $T_m<T_0 (\text {or} T_1=T_2)$, Peregrine solution or breather solution is only excited to initial shape. In particular, we report firstly the localized Peregrine solution and breather solution in two-dimensional space. Numerical rerun for analytical solution indicates that the stability of Peregrine solution attenuates with the add of n. It is expected that our analysis and results may give new insight into higher-dimensional localized rogue waves in nonlocal media.