Baseband modulation instability, rogue waves and state transitions in a deformed Fokas–Lenells equation

Abstract

We study a deformed Fokas–Lenells equation which is related to the integrable derivative nonlinear Schrödinger hierarchy with higher-order nonholonomic constraint. The baseband modulation instability as an origin of rogue waves is displayed. The explicit rogue wave solutions are obtained via the Darboux transformation. Typical rogue wave patterns such as the standard rogue wave, dark rogue wave and twisted rogue wave pair in three different components of the deformed Fokas–Lenells equation are presented. Besides, the state transitions between rogue waves and solitons are analytically found when the modulation instability growth rate tends to zero in the zero-frequency perturbation region. The explicit soliton solutions under the special parameter condition are given. The anti-dark and W-shaped solitons in their respective components are shown.

1 Introduction

A generalized nonlinear Schrödinger (NLS) equation

$$\begin{aligned} iu_{t}-\nu u_{tx}+\gamma u_{xx}+\sigma |u|^2(u+i\nu u_{x})=0,\ \sigma =\pm 1, \end{aligned}$$

(1)

the so-called Fokas–Lenells (FL) equation, was first proposed by Fokas through the bi-Hamiltonian method [1] and then derived by Lenells in single-mode optical fibers when certain higher-order nonlinear effects are taken into account [2]. In Eq. (1), $\gamma$ and $\nu$ are two nonzero real parameters that can be assigned to have the same sign as a result of the transformation $x\rightarrow -x$, and u(x, t) represents the complex field envelope. The relationship between Eq. (1) and the NLS equation is the same as the relationship between the Camassa–Holm equation and the Korteweg–de Vries equation in view of the bi-Hamiltonian point [2,3,4]. When $\nu =0$, Eq. (1) degenerates to the NLS equation.

As mentioned before, one can assume $\gamma /\nu >0$, then the gauge transformation $u\rightarrow \sqrt{\gamma /\nu ^3}\exp (ix/\nu )u$ converts Eq. (1) into the following equation [4]

$$\begin{aligned} iu_{xt}-\dfrac{i\gamma }{\nu }u_{xx}+\dfrac{2\gamma }{\nu ^2}u_{x} +\dfrac{\gamma }{\nu ^3}\sigma |u|^2u_{x}+\dfrac{i\gamma }{\nu ^3}u=0. \end{aligned}$$

For simplicity, by setting $\nu =\gamma =\sigma =1$ we have

$$\begin{aligned} iu_{xt}-iu_{xx}+2u_{x}+|u|^2u_{x}+iu=0, \end{aligned}$$

(2)

which admits a Lax pair that ensures that one can solve the initial value problem for it via the inverse scattering transform [4]. Recent developments for Eqs. (2) or (1) concentrate on finding its soliton solutions, breather solutions and rogue wave solutions by means of the dressing method [5], the Hirota’ direct method [6], the Darboux transformation (DT) method [7,8,9] and the complex envelope function method [10]. More recently, the two-component integrable generalization of Eq. (2) and its explicit soliton solutions and rogue wave solutions have been researched with the aid of the Riemann–Hilbert method and the DT method [11,12,13,14].

The nonholonomic deformation of the classical integrable system has been extensively investigated during the past decades [15, 16]. On the one hand, such deformations can be viewed as a perturbation of the original integrable system with certain differential constraint on the perturbing function without spoiling the system integrability and thus can be used to obtain some novel integrable equations such as the sixth-order KdV equation [15], the multiple self-induced transparency system [16, 17] and the aforementioned FL equation. On the other hand, this new class of deformed integrable equations actually possesses some interesting features, such as the solitons with shape changing and accelerating motion [16] and the breather/rogue wave-to-soliton transitions [17,18,19,20,21]. Moreover, they are applicable in very different physical fields, from shallow water wave to optical fiber communication and so on [16]. In this paper, we consider a deformed FL equation which takes a normalized form as

$$\begin{aligned}&iu_{xt}-iu_{xx}+2u_{x}+|u|^2u_{x}+iu+2gu_{x}+2w=0, \end{aligned}$$

(3a)

$$\begin{aligned}&g_{x}=i(u_{x}w^{*}-u^{*}_{x}w),\end{aligned}$$

(3b)

$$\begin{aligned}&w_{x}=(i|u|^2u_{x}-u). \end{aligned}$$

(3c)

Equation (3) was derived by Kundu when studying the nonholonomic deformation of the integrable derivative nonlinear Schrödinger hierarchy [22]. It is clearly seen that the first part of Eq. (3a) is exactly identical to the standard FL equation with the complex field envelope u(x, t), which, however, is deformed by the perturbing real function g(x, t) and complex function w(x, t) with nonholonomic constraints (3b) and (3c). Here, asterisk means complex conjugation. In Ref. [22], the integrability such as the Lax pair and the simple soliton solutions for Eq. (3) have been obtained.

In the past few years, the study of rogue waves has become a hot issue of numerous theoretical and experimental researches [23, 24]. Briefly, a wave can belong to the rogue wave category when the following two significant features are satisfied: (i) Its wave height is at least twice than the significant wave height [25]; (ii) it comes seemingly from nowhere and disappear without trace [26]. A landmark formal description of a single rogue wave in mathematics is the Peregrine soliton [27], which is a rational quadratic polynomial solution of the NLS equation with nonzero plane wave background, and characterized by a doubly localized wave packet that reaches a climax of 3 over the background and eventually decays and vanishes back into the background. Meanwhile, some classical methods such as the DT method [28,29,30,31,32,33], the Hirota’ direct method [34,35,36] and the symmetry reduction method [37,38,39] have been modified to derive the more abundant rational solutions and the corresponding interaction solutions. However, considering the various physical contexts, rogue wave solutions in several nonlinear models beyond the NLS description such as the Hirota equation [40, 41], the Sasa–Satsuma (SS) equation [42, 43], the coupled NLS equations (Manakov system) [44, 45] and the coupled Hirota equations [46, 47] have been investigated. In addition, it has been recently demonstrated that the baseband modulational instability (MI) where the MI gain band contains a limiting case of zero-frequency perturbation can lead to rogue wave generation [48, 49], which fundamentally reveals the mechanism of generating rogue waves.

In this paper, we focus on studying rogue waves and state transitions in Eq. (3) by using the MI analysis method and the DT method. The arrangement of our paper is as follows. In Sect. 2, we pay attention to the standard linear instability analysis of the plane wave solutions and exhibit the baseband MI to reveal the existence of rogue waves. In Sect. 3, we derive the explicit rogue wave solutions and show the standard, dark and twisted rogue wave pair [43] structures in three different components of the deformed FL equation. In Sect. 4, we obtain the parameter condition for the state transitions between rogue waves and solitons and then present the explicit soliton solutions and show the anti-dark and W-shaped solitons in their respective components.

2 Baseband MI and existence of rogue waves

For our studies, we begin with the plane wave solutions of Eq. (3)

$$\begin{aligned}&u[0]=ae^{i\theta },\ g[0]=g_{0},\ w[0]=ia(a^2+1/q)\hbox {e}^{i\theta },\nonumber \\&\theta =qx+\nu t, \end{aligned}$$

(4)

where

$$\begin{aligned} \nu =[q^3+(a^2+2g_{0}+2)q^2+(2a^2+1)q+2]/q^2, \end{aligned}$$

in which a, q and $g_{0}$ are three real constants, which stand for the background and frequency of the complex field envelope u, and the initial excitation of the perturbing real function g, respectively. In order to derive the MI growth rate, we introduce the following perturbed backgrounds

$$\begin{aligned}&u=ae^{i\theta }(1+p_{1}),\ g=g_{0}+p_{2}, \\&w=ia(a^2+1/q)\hbox {e}^{i\theta }(1+p_{3}), \end{aligned}$$

where $p_{j}(x,t)$ ($j=1,2,3$) are the small perturbed functions and satisfy the linearized deformed FL equation

$$\begin{aligned} \begin{aligned}&q^2p_{1xt}-q^2p_{1xx}+i(2qa^2-q^3+q+2)p_{1x}\\&\quad +iq^3p_{1t}+(q^3a^2-2q^2a^2-2q)p_{1}\\&\quad +q^3a^2p_{1}^{*}+2q^3p_{2}+2(q^2a^2+q)p_{3}=0,\\&q p_{2x}-(qa^4+a^2)p_{1x}-(qa^4+a^2)p^{*}_{1x}\\&\quad -i(q^2a^4+qa^2)p_{1}+i(q^2a^4+qa^2)p_{1}^{*}\\&\quad +i(q^2a^4+qa^2)p_{3}-i(q^2a^4+qa^2)p_{3}^{*}=0,\\&i(qa^2+1)p_{3x}-iqa^2p_{1x}+(2q^2a^2+q)p_{1}\\&\quad +q^2a^2 p_{1}^{*}-(q^2 a^2+q)p_{3}=0. \end{aligned} \end{aligned}$$

Substituting

$$\begin{aligned} \begin{aligned} p_{1}&=f_{1}\hbox {e}^{i\kappa [x-\varOmega t]}+f_{2}^{*}\hbox {e}^{-i\kappa [x-\varOmega ^{*} t]},\\ p_{2}&=f_{3}\hbox {e}^{i\kappa [x-\varOmega t]}+f_{3}^{*}\hbox {e}^{-i\kappa [x-\varOmega ^{*} t]},\\ p_{3}&=f_{4}\hbox {e}^{i\kappa [x-\varOmega t]}+f_{5}^{*}\hbox {e}^{-i\kappa [x-\varOmega ^{*} t]} \end{aligned} \end{aligned}$$

into the linearized deformed FL equation, where $f_{j}$ ($j=1,2,\cdots ,5$) are the small Fourier amplitudes, $\kappa$ denotes the perturbation frequency and $\varOmega$ represents the complex propagation parameter of perturbations, we obtain a algebraic equation $D(f_{1},f_{2},f_{3},f_{4},f_{5})^{\mathrm{T}}=0$, here $D=(D_{ij})_{1\le i,j\le 5}$ is a $5\times 5$ matrix that reads

$$\begin{aligned} \begin{aligned} D_{11}&=q^2(\varOmega +1)\kappa ^2+[q^3\varOmega -2(q a^2+1)\\&\quad +\,q^3-q]\kappa -q [2(q a^2+1)-q^2 a^2],\\ D_{12}&=q^3a^2,\ D_{13}=2q^3, \ D_{14}=2q(qa^2+1),\\ D_{15}&=0,\\ D_{21}&=q^3a^2, \ D_{23}=2q^3, \ D_{24}=0, \\ D_{25}&=2q(qa^2+1), \\ D_{22}&=q^2 (\varOmega +1) \kappa ^2+[2(q a^2+1)-q^3\varOmega \\&\quad -\,q^3+q]\kappa -q [2(q a^2+1)-q^2 a^2],\\ D_{31}&=-i[a^2 (q a^2 +1)\kappa +q a^2 (q a^2 +1)],\\ D_{32}&=-i[a^2(q a^2+1)\kappa -qa^2(q a^2+1)],\\ D_{33}&=iq\kappa ,\ D_{34}=iqa^2(qa^2+1),\\ D_{35}&=-iqa^2(qa^2+1),\\ D_{41}&=qa^2\kappa +q(2q a^2+1),\ D_{42}=q^2 a^2,\ D_{43}=0,\\ D_{44}&=-(q a^2+1)\kappa -q(q a^2+1),\ D_{45}=0,\\ D_{51}&=q^2 a^2,\ D_{52}=-qa^2\kappa +q(2q a^2+1),\ D_{53}=0,\\ D_{54}&=0,\ D_{55}=(q a^2+1)\kappa -q(q a^2+1). \end{aligned} \end{aligned}$$

Solving $\det (D)=0$, we obtain the MI growth rate

$$\begin{aligned} \begin{aligned} G&=\kappa \left| \hbox {Im}\{\varOmega \}\right| \\&=\dfrac{\kappa \sqrt{-a^{2}q^{3}(qa^2+2)-\kappa ^2}}{(q^2-\kappa ^2)^2q^2}\\&\quad \left| (2qa^2+q+2)\kappa ^2-(6a^2q+q+6)q^2\right| . \end{aligned} \end{aligned}$$

(5)

Fig. 1

a Rogue wave existence condition on the (a, q) plane given by Eq. (7); b MI map of $\ln (G)$ on the $(\kappa ,q)$ plane given by Eq. (5) for $a=1$

At this point, it can be immediately found that the MI exists if and only if

$$\begin{aligned} |\kappa |<\sqrt{-q(qa^2+2)}|q||a| \end{aligned}$$

(6)

is satisfied. Further, turning to the baseband MI theory [48], the limit of $\kappa =0$ requires that $-q(qa^2+2)>0,$ viz.

$$\begin{aligned} -\dfrac{2}{a^2}<q<0, \end{aligned}$$

(7)

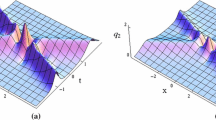
which is just the parameter condition for the existence of rogue waves and is shown in Fig. 1a. We further plot the MI map which is defined by $\ln (G)$, see Fig. 1b. It is clearly seen that there is a stability region (the dashed red line) in the MI map where the corresponding MI growth rate is equal to zero. In the rest of this paper, we will show that, for the deformed FL equation, the state transitions between rogue waves and solitons just arise from the attenuation of the MI growth rate in the zero-frequency perturbation region, while for the standard FL equation, this kind of state transitions cannot happen.

3 Rogue waves

In this section, we apply the DT method to derive the rogue wave solutions for Eq. (3). To this end, we first present the Lax pair of Eq. (3)

$$\begin{aligned} \varPhi _{x}&=U\varPhi , \end{aligned}$$

(8a)

$$\begin{aligned} \varPhi _{t}&=V\varPhi , \end{aligned}$$

(8b)

where

$$\begin{aligned} \begin{aligned} U&=-\dfrac{i}{\zeta ^2}\sigma _{3}+\dfrac{1}{\zeta }U_{0x},\\ V&=\dfrac{i}{4}\zeta ^4\sigma _{3} -\dfrac{1}{2}i\zeta ^3U_{0}\sigma _{3}-\dfrac{i}{4}\zeta ^2(\sigma _{3}-2U_{0}^2\sigma _{3})\\&\quad +\dfrac{1}{2}\zeta (i\sigma _{3}U_{0}+2\widetilde{U}_{0}) +\dfrac{i}{2}(2g+|u|^2+2)I\\&\quad +\dfrac{1}{\zeta }U_{0x}-\dfrac{i}{\zeta ^2}\sigma _{3}, \end{aligned} \end{aligned}$$

in which

$$\begin{aligned} \sigma _{3}=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right) ,\ U_{0}=\left( \begin{array}{cc} 0 &{} u \\ -u^{*} &{} 0 \\ \end{array} \right) ,\ \widetilde{U}_{0}=\left( \begin{array}{cc} 0 &{} w \\ -w^{*} &{} 0 \\ \end{array} \right) \end{aligned}$$

and I is the $2\times 2$ identity matrix. The compatibility condition $U_{t}-V_{x}+[U,V]=0$ of Eqs. (8a) and (8b) can immediately give rise to Eq. (3). Notice that the matrices $U(x,t;\zeta )$ and $V(x,t;\zeta )$ obey the symmetry relations

$$\begin{aligned}&U(x,t;-\zeta )=\sigma _{3}U(x,t;\zeta )\sigma _{3},\\&V(x,t;-\zeta )=\sigma _{3}V(x,t;\zeta )\sigma _{3}, \end{aligned}$$

and

$$\begin{aligned}&U^{\dag }(x,t;\zeta )=-U(x,t;\zeta ^{*}),\\&V^{\dag }(x,t;\zeta )=-V(x,t;\zeta ^{*}), \end{aligned}$$

which indicate that

$$\begin{aligned}&\varPhi (x,t;-\zeta )=\sigma _{3}\varPhi (x,t;\zeta )\sigma _{3},\\&\varPhi (x,t;\zeta )\varPhi ^{\dag }(x,t;\zeta ^{*})=I. \end{aligned}$$

Therefore, the Darboux matrix [28,29,30,31,32] for the linear spectral problem (8) is subordinated to the symmetry relations

$$\begin{aligned}&T(x,t;-\zeta )=\sigma _{3}T(x,t;\zeta )\sigma _{3},\\&T^{-1}(x,t;\zeta )=T^{\dag }(x,t;\zeta ^{*}). \end{aligned}$$

Here, $\dag$ stands for the Hermite conjugation. We thus can assume the Darboux matrix be of the form

$$\begin{aligned} T=I+\dfrac{A}{\zeta -\zeta _{1}^{*}}-\dfrac{\sigma _{3}A\sigma _{3}}{\zeta +\zeta _{1}^{*}} \end{aligned}$$

and

$$\begin{aligned} T^{-1}=I+\dfrac{A^{\dag }}{\zeta -\zeta _{1}} -\dfrac{\sigma _{3}A^{\dag }\sigma _{3}}{\zeta +\zeta _{1}}, \end{aligned}$$

where A is a $2\times 2$ matrix that needs to be determined. Then, by letting $\varPhi _{1}=(\psi _{1},\varphi _{1})$ be a special solution of the spectral problem (8) at $\zeta =\zeta _{1}$, $u=u[0]$, $g=g[0]$, $w=w[0]$ and using the identities

$$\begin{aligned} T|_{\zeta =\zeta _{1}}\varPhi _{1}=0,\ \varPhi _{1}^{\dag }T^{-1}|_{\zeta =\zeta _{1}^{*}}=0, \end{aligned}$$

one obtains

$$\begin{aligned} A=\left( \begin{array}{cc} \dfrac{1}{\alpha -\beta } &{} 0 \\ 0 &{} \dfrac{1}{\alpha +\beta } \\ \end{array} \right) \varPhi _{1}\varPhi _{1}^{\dag }, \end{aligned}$$

where

$$\begin{aligned} \alpha =\dfrac{\varPhi _{1}^{\dag }\sigma _{3}\varPhi _{1}}{\zeta _{1}+\zeta _{1}^{*}},\ \beta =\dfrac{\varPhi _{1}^{\dag }\varPhi _{1}}{\zeta _{1}-\zeta _{1}^{*}}. \end{aligned}$$

Further, the transformation for the complex field envelope u can be given by

$$\begin{aligned} T_{x}+TU=U[1]T,\ U[1]=U[1](u[1],g[1],w[1]), \end{aligned}$$

that is,

$$\begin{aligned} u[1]=u[0]+2\psi _{1}\varphi _{1}^{*}/\left( \dfrac{\varPhi _{1}^{\dag }\sigma _{3}\varPhi _{1}}{\zeta _{1}+\zeta _{1}^{*}} -\dfrac{\varPhi _{1}^{\dag }\varPhi _{1}}{\zeta _{1}-\zeta _{1}^{*}}\right) . \end{aligned}$$

(9)

Moreover, since the new potential u[1] is obtained, one can successively present the new perturbing functions w[1] and g[1] through the differential and/or integral calculations of u[1] in Eq. (3c) and (3b), namely

$$\begin{aligned} w[1]=\int \left( i|u[1]|^2u[1]_{x}-u[1]\right) \hbox {d}x \end{aligned}$$

(10)

and

$$\begin{aligned} g[1]=\int i\left( u[1]_{x}w[1]^{*}-u[1]^{*}_{x}w[1]\right) \hbox {d}x. \end{aligned}$$

(11)

After that, by taking account of the parameter condition (7), we set $a=1$, $q=-1/3$ and $g_{0}=1$ in the plane wave solutions (4). Then, by suitably choosing the spectral parameter be $\zeta =\zeta _{1}=-\sqrt{5}-i$, we can obtain a special solution of the linear spectral problem (8)

$$\begin{aligned} \begin{aligned} \psi _{1}&=\dfrac{2\sqrt{2}(\sqrt{5}x-20\sqrt{5}t-6+ix+178it-3\sqrt{5}i)}{(\sqrt{5}+i)^3},\\ \varphi _{1}&=\dfrac{2\sqrt{2}i(-\sqrt{5}x+20\sqrt{5}t-6-ix-178it-3\sqrt{5}i)}{(\sqrt{5}+i)^3}. \end{aligned} \end{aligned}$$

Substituting them into Eqs. (9)–(11) leads to the explicit rogue wave solutions of Eq. (3)

$$\begin{aligned} u[1]_\mathrm{r}&=-\left[ 1+\dfrac{12(106it-2ix-9)}{D_{1}}\right] \hbox {e}^{-\frac{i(x-41t)}{3}}, \end{aligned}$$

(12)

$$\begin{aligned} g[1]_\mathrm{r}&=1-\dfrac{216(2x^2-1400tx-29428t^2+81)}{F_{1}},\end{aligned}$$

(13)

$$\begin{aligned} w[1]_\mathrm{r}&=2i\dfrac{G_{1}}{D_{1}^2}\hbox {e}^{-\frac{i(x-41t)}{3}}, \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{aligned} D_{1}&=2x^2+52tx+11228t^2+27+6ix+276it,\\ F_{1}&=4x^4+208tx^3+47616t^2x^2\\&\quad +144x^2+1167712t^3x\\&\quad +6120tx+126067984t^4+682488t^2+729,\\ G_{1}&=4x^4+208tx^3+47616t^2x^2\\&\quad +288x^2+1167712t^3x\\&\quad +5112tx+126067984t^4-2491272t^2+729\\&\quad +i(3024tx^2-24x^3-39888t^2x-1620x\\&\quad +20479872t^3-138672t). \end{aligned} \end{aligned}$$

Here, one can exactly check the validity of the above solutions (12)–(14) by putting them into the original equations.

Fig. 2

a, b Evolution and density plots of the standard rogue wave for $|u[1]_\mathrm{r}|$ of Eq. (12)

Fig. 3

a, b Evolution and density plots of the dark rogue wave for $g[1]_\mathrm{r}$ of Eq. (13)

Fig. 4

a, b Evolution and density plots of the twisted rogue wave pair for $|w[1]_\mathrm{r}|$ of Eq. (14)

Figure 2 displays the standard rogue wave structure in the u component. It is seen that there are one peak and two valleys around the center: The maximum amplitude of the peak is 3 and is localized at (0, 0), and the minimum amplitude of the two valleys is zero and appears at $(\pm \,4.4325,\pm \,0.0515)$. Figure 3 shows the dark rogue wave structure in the real g component: The minimum amplitude of the dark rogue wave is -23 and occurs at (0, 0), and the maximum amplitude of that is 6.5390 and arrives at $(\pm \,2.6576,\pm \,0.0597)$. In addition, the twisted rogue wave pair (first reported in the SS equation, see Ref. [43]) which consists of two standard rogue waves distributing with antisymmetric shape is exhibited in Fig. 4. The twisted rogue wave pair has two peaks and four zero-amplitude valleys, the maximum of it is 6.4703 and is reached at $(\pm \,1.3365,\pm \,0.0143)$, and the coordinates of the four zero-amplitude points read $(\pm \,2.9782,\pm \,0.0940)$ and $(\pm \,1.6556,\mp 0.0238)$. Furthermore, one can compute that as $x\rightarrow \infty$, $t\rightarrow \infty$, $|u[1]_{\mathrm{r}}|\rightarrow 1$, $g[1]_{\mathrm{r}}\rightarrow 1$ and $|w[1]_{\mathrm{r}}|\rightarrow 2$.

Fig. 5

a Stability curve given by Eq. (15) in the perturbation frequency region $|\kappa |<\sqrt{-q(qa^2+2)}|q||a|$ for $a=1$; b MI map of $\ln (G)$ on the $(\kappa ,q)$ plane given by Eq. (17) for $a=1$

4 State transitions

In this section, we return to the stability curve shown in Fig. 1b which is given by

$$\begin{aligned} \kappa =\pm |q|\sqrt{\dfrac{(6a^2+1)q+6}{(2a^2+1)q+2}} \end{aligned}$$

(15)

when letting the MI growth rate tend to zero in the perturbation frequency region $|\kappa |<\sqrt{-q(qa^2+2)}|q||a|$. Then, by focusing our interest on the stability curve in the limit $\kappa \rightarrow 0$, we have

$$\begin{aligned} q=q_{\mathrm{s}}=-\dfrac{6}{6a^2+1}. \end{aligned}$$

(16)

At this point, it is worthwhile to remark that, as $q\rightarrow q_{\mathrm{s}}$, the state transitions between rogue waves and solitons can occur in the deformed FL equation. However, it should be noted that the kind of state transitions cannot happen in the standard FL equation, since for the plane wave solution of Eq. (2)

$$\begin{aligned} u=a\exp \{i[qx+(q^2+qa^2+2q+1)/qt]\}, \end{aligned}$$

we can also get the corresponding MI growth rate by using the standard linear instability analysis method, i.e.,

$$\begin{aligned} G=\kappa |\hbox {Im}\{\varOmega \}|=\dfrac{\kappa \sqrt{-a^{2}q^{3}(qa^2+2)-\kappa ^2}}{|q(q^2-\kappa ^2)|}, \end{aligned}$$

(17)

but, in this circumstance, we cannot obtain the stability curve representation in the perturbation frequency region $|\kappa |<\sqrt{-q(qa^2+2)}|q||a|$ by letting the MI growth rate tend to zero. Therefore, the key point of $q=q_{\mathrm{s}}$ cannot be solved in Eq. (17) that is related to the standard FL equation. At this point, we can find that, although the parameter conditions for the existence of rogue waves of the deformed FL equation and the standard FL equation are same, namely $-2/a^2<q<0$, the MI characteristics for these two equations are different and hence lead to much richer types of nonlinear waves in the deformed FL equation. We display in Fig. 5a the stability curve in the perturbation frequency region $|\kappa |<\sqrt{-q(qa^2+2)}|q||a|$ and in Fig. 5b the MI map (17) that is related to the standard FL equation for $a=1$. It is calculated that the key point is $q=q_{\mathrm{s}}=-6/7$ for $a=1$, and moreover, it is obviously seen that there is not a stability region in this MI map, hence justifying the impossibility of the state transitions between rogue waves and solitons in the standard FL equation.

Fig. 6

a, b Evolution and density plots of the anti-dark soliton for $|u[1]_\mathrm{s}|$ of Eq. (18)

Fig. 7

a, b Evolution and density plots of the W-shaped soliton for $g[1]_\mathrm{s}$ of Eq. (19)

Fig. 8

a, b Evolution and density plots of the anti-dark soliton for $|w[1]_\mathrm{s}|$ of Eq. (20)

At this time, we set $a=1$, $q=q_{\mathrm{s}}=-6/7$ and $g_{0}=1$ in the plane wave solutions (4) and select a particular spectral parameter be $\zeta =\zeta _{1}=-2\sqrt{3}/3-i$, and then, we can put forward the following special solution of the linear spectral problem (8)

$$\begin{aligned} \begin{aligned} \psi _{1}&=\dfrac{\sqrt{2}(216\sqrt{3}x-470\sqrt{3}t-63+324ix -705it-252\sqrt{3}i)}{6(2\sqrt{3}+3i)^3},\\ \varphi _{1}&=\dfrac{\sqrt{2}(-216\sqrt{3}x+470\sqrt{3}t-63-324ix +705it-252\sqrt{3}i)}{6(2\sqrt{3}+3i)^3}. \end{aligned} \end{aligned}$$

Using Eqs. (9)–(11), we have the explicit soliton solutions

$$\begin{aligned} u[1]_\mathrm{s}&=-\left[ 1+\dfrac{252(470it-216ix-147)}{D_{2}}\right] \nonumber \\&\quad \hbox {e}^{-\frac{2i(27x-106t)}{63}}, \end{aligned}$$

(18)

$$\begin{aligned} g[1]_\mathrm{s}&=1\nonumber \\&\quad -\dfrac{7056(186624x^2-812160tx+883600t^2-64827)}{F_{2}},\end{aligned}$$

(19)

$$\begin{aligned} w[1]_\mathrm{s}&=\dfrac{i}{6}\dfrac{ G_{2}}{D_{2}^2}\hbox {e}^{-\frac{2i(27x-106t)}{63}}, \end{aligned}$$

(20)

where

$$\begin{aligned} D_{2}= & {} 11664x^2-50760tx\\&+55225t^2+9261+13608ix\\&-29610it,\\ F_{2}= & {} 136048896x^4-1184129280tx^3\\&+3864866400t^2x^2\\&+401218272x^2-5606442000t^3x\\&-1746042480tx\\&+3049800625t^4+1899629550t^2\\&+85766121,\\ G_{2}= & {} 3049800625t^4-5606442000t^3x\\&+3864866400t^2x^2\\&-1184129280tx^3+136048896x^4\\&+8621395650t^2\\&-7924346640tx+1820913696x^2\\&+3859475445\\&+i(2072226240tx^2-317447424x^3\\&-4509010800t^2x\\&+4284805392x+3270424500t^3\\&-9323419140t). \end{aligned}$$

The validity of solutions (18)–(20) can be straightly tested by putting them into the deformed FL equation.

Figure 6 shows the anti-dark soliton in the u component; the maximum amplitude of the hump is 3 and occurs at $t=108x/235$. Figure 7 displays the W-shaped soliton in the g component; the maximum amplitude of the hump is 19 / 3 and appears at $t=108x/235$, while the minimum amplitude of the two valleys is − 0.5342 and arrives at $t=108x/235\pm 21\sqrt{147+21\sqrt{721}}/940$. Moreover, as shown in Fig. 8, the soliton can also exhibit the anti-dark structure in the w component; the maximum amplitude of the hump is 7.5 and is reached at $t=108x/235$. We calculate that, as $x\rightarrow \infty$, $t\rightarrow \infty$, $|u[1]_{\mathrm{s}}|\rightarrow 1$, $g[1]_{\mathrm{s}}\rightarrow 1$ and $|w[1]_{\mathrm{s}}|\rightarrow 1/6$. At last, we conclude the results as follows:

Model/component	u	g	w
Deformed FL equation	$\begin{array}{c} \text {Standard RW} \rightarrow \\ \text {Anti-dark soliton} \end{array}$	$\begin{array}{l} \text {Dark RW} \rightarrow \\ \text {W-shaped soliton} \end{array}$	$\begin{array}{c} \text {Twisted RW pair} \rightarrow \\ \text {Anti-dark soliton} \end{array}$
Standard FL equation	Standard RW	–	–

5 Conclusion

In summary, we investigated a deformed FL equation which contains two effective perturbing functions compared with the standard FL equation. The standard linear instability analysis of the plane wave solutions was performed. The baseband modulation instability as an origin of rogue waves was then confirmed. Moreover, the explicit rogue wave solutions were presented by means of the DT method. It was shown that diverse rogue wave structures such as the standard rogue wave, dark rogue wave and twisted rogue wave pairs in three different components of the deformed FL equation were displayed. Further, the intriguing state transitions between rogue waves and solitons were analytically established by letting the MI growth rate tend to zero in the zero-frequency perturbation region. The explicit soliton solutions were obtained in choice of the special parameter $q=q_{\mathrm{s}}$, and then, the anti-dark and W-shaped solitons in their respective components were exhibited. It is important to note that this kind of state transitions cannot happen in the standard FL equation that does not have the critical perturbing functions, and hence demonstrates the nontriviality and significance of this deformed FL equation. We anticipate that our results may help to understand the complicated rogue wave phenomena in oceanography, nonlinear optics and so on.