Lumps and rogue waves of generalized Nizhnik–Novikov–Veselov equation

Abstract

We investigate the generalized $(2+1)$ Nizhnik–Novikov–Veselov equation and construct its linear eigenvalue problem in the coordinate space from the results of singularity structure analysis thereby dispelling the notion of weak Lax pair. We then exploit the Lax pair employing Darboux transformation and generate lumps and rogue waves. The dynamics of lumps and rogue waves is then investigated.

1 Introduction

The identification of dromions [1, 2] in the Davey–Stewartson I (DSI) equation which has given a fillip to the investigation of $(2+1)$ dimensional integrable nonlinear partial differential equations (pdes) [3] has virtually triggered a renewed interest toward other localized structures like lumps [4], breathers [5] etc. Recent identification of rogue waves [6, 7] in nonlinear pdes which appear from nowhere has once again prompted a deeper investigation of integrable $(2+1)$ nonlinear pdes in an effort to unearth similar structures in them. It should also be mentioned that even though the integrability of $(2+1)$ dimensional nonlinear pdes has been well established in terms of the abundance of localized solutions, there exists no systematic approach to unearth other signatures of integrability like Lax pair [4], Bäcklund transformation [8], Hamiltonian Structures [9], conservation laws [10] etc. In this connection, Boiti et al. [11, 12] had pointed out that $(2+1)$ dimensional nonlinear pdes like Nizhnik–Novikov–Veselov (NNV) equation [13] admits only weak Lax pair in the subspace of coordinate space. In other words, the lax operators commute at least on the functional subspace of the eigenfunction and they should be compatible at least for one eigenvalue. Even though the concept of weak lax pair has yielded several $(2+1)$ integrable nonlinear pdes and facilitated their investigation from the viewpoint of localized coherent structures [14, 15], a closer look at the investigation of integrable $(2+1)$ nonlinear pdes may yield other richer structures and would enable us to get a deeper understanding of integrability.

The Painlevé property [16] has been proved to be a powerful test for identifying the integrability as well as a good basis for the determination of many of the properties derived of the integrability of a given pde [4]. In this paper, we investigate the $(2+1)$ dimensional generalized Nizhnik–Novikov–Veselov equation [14] and generate the Lax pair in the coordinate space employing the singular manifold method [17] based on the Painlevé analysis. We then exploit the Lax pair employing Darboux transformation approach, and construct lumps and rogue waves. We then discuss their dynamics.

The present paper is structured as follows: in Sect. 2, we drive the linear eigenvalue problem of the NNV equation by using the results of Painlevé analysis. We then exploit the Lax pair and employ Darboux transformation in Sect. 3, to derive lumps in Sect. 4 and rogue waves in Sect. 5. After studying the dynamics of lumps and rogue waves, the results are summarized at the end.

2 Singular manifold method for the Nizhnik–Novikov–Veselov equation

The generalized Nizhnik–Novikov–Veselov (NNV) equation is a symmetric generalization of the KdV equation to $(2+1)$ dimensions and is given by

$$\begin{aligned}&u_t + au_{xxx}+bu_{yyy}+c~u_x+d~u_y-3~a(uv)_x \nonumber \\&\quad -\,3~b (uw)_y = 0 \end{aligned}$$

(1)

$$\begin{aligned}&u_x = v_y \end{aligned}$$

(2)

$$\begin{aligned}&u_y =w_x \end{aligned}$$

(3)

where a, b, c and d are parameters. This equation, which is also known to be completely integrable, has been investigated in [14, 15] where exponentially localized solutions have been generated and their dynamics has been investigated. Introducing the following change of variables,

$$\begin{aligned} u= -2~ m_{xy},~~ v= \frac{c}{3~a} -2~ m_{xx} ,~~ w =\frac{d}{3 ~b} - 2~ m_{yy}\nonumber \\ \end{aligned}$$

(4)

Equations (1)–(3) get converted to the following equation:

$$\begin{aligned}&m_{xyt} +a~(m_{xxxy} +6~ m_{xx} m_{xy})_x +b~(m_{yyyx}\nonumber \\&\quad +\,\,6 ~m_{yy} m_{xy})_y =0 \end{aligned}$$

(5)

According to the singular manifold method [17, 18], the truncated Painlevé expansion for m should be

$$\begin{aligned} m^{[1]} = m^{[0]} + \ln (\phi _1) \end{aligned}$$

(6)

where $m^{[1]}$ and $m^{[0]}$ are both solutions of Eq. (5) and $\phi _1$ is the singular manifold for the seed solution $m^{[0]}$. Furthermore, Eq. (6) also implies an iterative method of constructing solutions where the super index [0] denotes a seed solution and [1] the iterated one. Substitution of Eq. (6) into (5) yields an expression in negatives powers of $\phi _1$. Equation (5) is symmetric under the interchange of (x, a) and (y, b) and hence it is reasonable to suggest the ansatz,

$$\begin{aligned} \phi _{1,t} = a~G_a(x,y,t) +b~ G_b(x,y,t) \end{aligned}$$

(7)

such that the terms in a and b cancel independently. Substituting Eq. (7) into the expression in negatives powers of $\phi _1$, we obtain two polynomials(one for the terms in a and other for the terms in b) in negative powers of $\phi _1$. If we require all the coefficients of these polynomials to be zero, we obtain the following expressions after some algebraic manipulations [using Maple]. The result can be summarized as follows:

$$\begin{aligned} G_a= & {} -\phi _{1,xxx} - 6 ~\phi _{1,x} m^{[0]}_{xx},\nonumber \\ G_b= & {} -\phi _{1,yyy} - 6~ \phi _{1,y} m^{[0]}_{yy} \end{aligned}$$

(8)

The rest of the terms can be independently integrated as,

$$\begin{aligned}&\frac{\phi _{1,xy} +2 ~\phi _1 m^{[0]}_{xy} }{\phi _{1,x} } + K_2(y) \nonumber \\&\quad +\,K_1(y) \int \left( \frac{\phi _1}{\phi _{1,x}}\right) ^2 \mathrm{d}x = 0 \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\phi _{1,xy} +2 ~\phi _1 m^{[0]}_{xy} }{\phi _{1,y} } + H_2(x) \nonumber \\&\quad +\,H_1(x) \int \left( \frac{\phi _1}{\phi _{1,y}}\right) ^2 \mathrm{d}y = 0 \end{aligned}$$

(10)

where $H_i (x)$ and $K_i (y)$ are arbitrary functions. Comparison of Eqs. (9), (10) yields (with $H_1 = H_2= K_1 = K_2 = 0$) and therefore,

$$\begin{aligned} \phi _{1,xy} +2~ \phi _1 m^{[0]}_{xy} =0 \end{aligned}$$

(11)

and the combination of Eqs. (7) and (8) yields,

$$\begin{aligned}&\phi _{1,t} + a ~\left( \phi _{1,xxx} + 6 ~\phi _{1,x} m^{[0]}_{xx}\right) \nonumber \\&\quad +\,\, b~ \left( \phi _{1,yyy} + 6~ \phi _{1,y} m^{[0]}_{yy}\right) =0 \end{aligned}$$

(12)

Equations (11) and (12) constitute the Lax pair for the NNV Eq. (5). The above Lax pair is in sharp contrast to the notion of weak Lax pair postulated by Boiti et al. [11, 12] in the subspace of coordinate space.

3 Darboux transformations

The truncated expansion given by Eq. (6) can be considered as an iterative method [4, 18] such that an iterated solution $m^{[1]}$ can be obtained from the seed solution $m^{[0]}$, if we know a solution $\phi _1$ for the Lax pair of this seed solution. This means that if we denote $\phi _{1,2}$ as the eigenfunction for the iterated solution $m^{[1]}$, it should satisfy the following Lax pair,

$$\begin{aligned}&(\phi _{1,2})_{xy} +2 ~\phi _{1,2} m^{[1]}_{xy} =0 \end{aligned}$$

(13)

$$\begin{aligned}&(\phi _{1,2})_{t}+a \left[ (\phi _{1,2})_{xxx} +6 (\phi _{1,2})_{x} m^{[1]}_{xx}\right] \nonumber \\&\quad +\,b \left[ (\phi _{1,2})_{yyy} +6 (\phi _{1,2})_{y} m^{[1]}_{yy}\right] =0 \end{aligned}$$

(14)

The Lax pair can also be considered as a nonlinear system between the fields and eigenfunction together [4, 18]. It means that the truncated Painlevé expansion given by Eq. (6) should be combined in Eqs. (13), (14) with a similar expansion for the eigenfunction such as,

$$\begin{aligned} \phi _{1,2} = \phi _2 -\frac{\Delta _{1,2}}{\phi _1} \end{aligned}$$

(15)

where $\phi _i$, (i=1,2) are eigenfunctions for the seed solution $m^{[0]}$ and therefore,

$$\begin{aligned}&\phi _{i,xy} +2~ \phi _i m^{[0]}_{xy} =0 \end{aligned}$$

(16)

$$\begin{aligned}&\phi _{i,t}+a~\left( \phi _{i,xxx} +6 ~\phi _{i,x} m^{[0]}_{xx}\right) \nonumber \\&\quad +\,b~\left( \phi _{i,yyy} +6~ \phi _{i,y} m^{[0]}_{yy}\right) =0 \end{aligned}$$

(17)

Substitution of Eqs. (6) and (15) into Eqs. (13), (14) yields $\Delta _{i,j}$ as the exact derivative

$$\begin{aligned} \mathrm{d}\Delta _{i,j}= & {} 2~ \phi _j ~\phi _{i,x} \mathrm{d}x + 2 ~ \phi _{j,y} \phi _{i} \mathrm{d}y\nonumber \\&+\,2 a \left( \phi _{j,x} \phi _{i,xx} - \phi _{i,x} \phi _{j,xx} -\phi _j \phi _{i,xxx} \right. \nonumber \\&\left. -6 ~m^{[0]}_{xx} \phi _j \phi _{i,x}\right) dt \nonumber \\&+\,2~ b~ \left( \phi _{i,y} \phi _{j,yy}-\phi _{j,y} \phi _{i,yy} -\phi _i \phi _{j,yyy}\right. \nonumber \\&\quad \left. -\,6 ~m^{[0]}_{yy} \phi _{i} \phi _{j,y}\right) dt \end{aligned}$$

(18)

where

$$\begin{aligned} \Delta _{i,j} =2 ~\phi _i \phi _j -\Delta _{j,i} \end{aligned}$$

(19)

The Painlevé expansion given by Eqs. (6) and (15) can be also considered as a binary Darboux transformation that relates the Lax pairs given by Eqs. (13), (14) and Eqs. (16), (17).

3.1 Iterated solution

In the previous section, we have introduced a singular manifold $\phi _{1,2}$ which allows us to iterate Eq. (6) again in the following form: $m^{[2]} = m^{[1]} +\ln (\phi _{1,2}) = m^{[0]} +\ln (\tau _{1,2})$, where $\tau _{1,2}$ is the $\tau$- function defined as,

$$\begin{aligned} \tau _{1,2} =\phi _{1,2}~ \phi _1 =\phi _1~ \phi _2 - \Delta _{1,2} \end{aligned}$$

(20)

From Eq. (19), $\Delta _{1,2} = 2 ~\phi _1~ \phi _2 - \Delta _{2,1}$. If $\tau ^2_{12} = det(\Delta _{i,j})$  where $i,j = 1,2$. Therefore, we can construct the solution $m^{[2]}$ for the second iteration with just the knowledge of two eigenfunctions $\phi _1$ and $\phi _2$ for the seed solution $m^{[0]}$.

4 Lumps

In this section, we obtain lumps for the generalized NNV Eq. (5).

4.1 Seed solution and eigenfunction

We consider a seed solution of the form,

$$\begin{aligned} m^{[0]} =q_0 xy \end{aligned}$$

(21)

where $q_0$ is an arbitrary constant. Solutions of Eqs. (16), (17) can be obtained through the following form,

$$\begin{aligned} \phi _i(k_i)= & {} \mathrm{exp}^{k_i(x+J(k_i))} P^n(k_i) ,~~ J(k_i) \nonumber \\= & {} -2 \frac{q_0 }{k_i^2} y +\left( -a k^2_i +\frac{8bq_0^3}{k_i^4}\right) t \end{aligned}$$

(22)

$$\begin{aligned} P^n(k_i)= & {} \sum ^{n}_{j=0} a_j(k_i) \psi (k_i)^j ,~~ \psi (k_i) \nonumber \\= & {} k_i^2 \left( x+ \frac{2 q_0 }{k_i^2} y-3\left( a k_i^2 +\frac{8bq_0^3}{k_i^4}\right) t\right) \end{aligned}$$

(23)

such that $P^n(k_i)$ is a polynomial in x of degree n whose coefficients $a_i$ can be obtained by substituting Eqs. (22), (23) into Eqs. (16), (17). We obtain after some algebraic calculation,

$$\begin{aligned} \frac{\partial a_j}{\partial y}= & {} -k_i (j+1) \frac{\partial a_{j+1}}{\partial y} \nonumber \\&-\,2 q_0 k_i (j+1)(j+2) a_{j+2} \end{aligned}$$

(24)

$$\begin{aligned} \frac{\partial a_j}{\partial t}= & {} (j+1) \left( b k_i \frac{\partial ^3 a_{j+1}}{\partial y^3} -12 b q_0 \frac{\partial ^2 a_{j+1}}{\partial y^2} \right. \nonumber \\&\left. + \frac{36 b q^2_0}{k_i} \frac{ \partial a_{j+1}}{\partial y}\right) \nonumber \\&+\, (j+1)(j+2) \left( 2 b q_0 k_i \frac{\partial ^2 a_{j+2}}{\partial y^2} \right. \nonumber \\&\left. - \,24 b q_0^2 \frac{\partial a_{j+2}}{\partial y} -\frac{3}{k_i}\left( ak_i^6-16bq_0^3\right) a_{j+2}\right) \nonumber \\&-(j+1)(j+2)(j+3)(a k_i^6 + 8 b q_0^3) a_{j+3}\nonumber \\ \end{aligned}$$

(25)

where we can set $a_n=1$, $a_{n-1}=0$. From the above, it is obvious that there are an infinite number of possible eigenfunctions characterized by an integer n and a wave number $k_i$.

4.2 Case-I: $n=1$

The simplest case can be obtained by taking $n=1$, in which case the eigenfunction given by Eqs. (22), (23) is of the following form,

$$\begin{aligned} \phi _{i}(k_{i})= & {} \mathrm{exp}^{k_{i} (x+J(k_{i}))} \psi (k_{i}), \nonumber \\ J(k_{i})= & {} \frac{-2 q_0 y}{k^2_{i}} +\left( -a k^2_{i} +\frac{8 b q_0^3}{k^4_{i}}\right) t \end{aligned}$$

(26)

$$\begin{aligned} \psi (k_{i})= & {} k^2_{i}\left( x+\frac{2 q_0 y}{k^2_{i}} -3\left( a k^2_{i} +\frac{8 b q^3_0}{k^4_i}\right) t\right) \end{aligned}$$

(27)

According to Eq. (18), we can calculate $\Delta _{i,j}$ as,

$$\begin{aligned} \Delta _{i,j}= & {} \frac{2 k_i}{k_i+k_j} \left[ \left( \psi (k_i)+ \frac{k_i k_j}{k_i+k_j}\right) \left( \psi (k_j)\right. \right. \nonumber \\&\left. \left. -\frac{k^2_j}{k_i+k_j}\right) +\frac{k^2_i k^2_j}{(k_i+k_j)^2}\right] \nonumber \\&\mathrm{exp}^{k_i(x+J(k_i))+k_j(x+J(k_j))} \end{aligned}$$

(28)

It is important to note that, $2 \phi _i \phi _j =\Delta _{i,j}+ \Delta _{j,i}$

4.3 $\tau - function$

A second iteration provides,

$$\begin{aligned} m^{[2]} = m^{[0]} +\ln (\tau _{1,2}) \end{aligned}$$

(29)

Substituting Eq. (21) into (29), we obtain,

$$\begin{aligned} m^{[2]} = q_0 x y +\ln (\tau _{1,2}) \end{aligned}$$

From Eq. (4), we have

$$\begin{aligned} u^{[2]} =-2 m^{[2]}_{x,y}= -2\left( q_0 +\left( \frac{(\tau _{1,2})_x}{\tau _{1,2}}\right) _y\right) \end{aligned}$$

where  $\tau _{1,2} = \phi _1 \phi _2 -\Delta _{1,2} = \frac{1}{2} \left( \Delta _{2,1} -\Delta _{1,2}\right)$, which after simplification can be written as,

$$\begin{aligned} \tau _{1,2}= & {} - \frac{k_1 - k_2}{k_1 +k_2} \mathrm{exp}^{k_{1} (x+J(k_{1}))+k_2(x+J(k_{2}))} \varOmega _{1,2}\nonumber \\ \varOmega _{1,2}= & {} (\psi (k_1)+g(k_1,k_2))(\psi (k_2)\nonumber \\&+\,g(k_2,k_1))+d(k_1,k_2) \end{aligned}$$

(30)

where $g(k_i,k_j)$, $d(k_i,k_j)$ are

$$\begin{aligned} g(k_i,k_j) = \frac{2 k_j k_i^2}{k_i^2-k_j^2} ,~~ d(k_i,k_j)=\frac{2 k_i^2 k_j^2(k_i^2+k_j^2)}{(k_i^2-k_j^2)^2}\nonumber \\ \end{aligned}$$

(31)

and therefore  $u^{[2]} = -2\left( q_0 +\left( \frac{(\varOmega _{1,2})_x}{\varOmega _{1,2}}\right) _y\right)$.  In order to have real expressions, we set $k_2$ as the complex conjugate of $k_1$ which means

$$\begin{aligned} k_1=A + i B,~~ k_2 = A - i B \end{aligned}$$

(32)

Using Eq. (32) in (30), we obtain

$$\begin{aligned} \varOmega _{1,2}= & {} \left[ (A^2-B^2)x +2q_0 y +\left( 3a(6A^2 B^2 -A^4\right. \right. \nonumber \\&\left. \left. -B^4)-24 q_0^3\frac{A^2-B^2}{(A^2+B^2)^2}\right) t+\frac{A^2+B^2}{2A}\right] ^2 \nonumber \\&+ \left[ 2A B x+12 A B \left( -a(A^2-B^2)\right. \right. \nonumber \\&\left. \left. +\frac{4 b q_0^3}{(A^2+B^2)^2}\right) t - \frac{A^2+B^2}{2 B}\right] ^2 \nonumber \\&+(B^2-A^2)\left[ \frac{A^2+B^2}{2AB}\right] ^2 \end{aligned}$$

(33)

which for $B^2 > A^2$ has no zeros which means that Eq. (33) does not have singularities. Actually, it is possible to define a Galilean transformation of the following form,

$$\begin{aligned} x= & {} X + X_0 +v_x t,~~ y = Y +Y_0 +v_y t,\nonumber \\ X_0= & {} \frac{A^2+B^2}{4 A B^2},~~ Y_0 = -\frac{(A^2+B^2)^2}{8 q_0 A B^2},\nonumber \\ v_x= & {} \left[ 6a(A^2-B^2)-\frac{24 b q_0^3}{(A^2+B^2)^2}\right] , \nonumber \\ v_y= & {} \frac{1}{q_0} \left[ -\frac{3a}{2} (A^2+B^2)^2+24 b q_0^3 \frac{(A^2-B^2)}{(A^2+B^2)^2}\right] \nonumber \\ \end{aligned}$$

(34)

such that in the new coordinates, $\varOmega _{1,2}$ reads as the static solution

$$\begin{aligned} \varOmega _{1,2}= & {} \left[ (A^2-B^2) X + 2 q_0 Y \right] ^2 +\left[ 2 A B X\right] ^2 \nonumber \\&+\,(B^2-A^2)\left[ \frac{A^2+B^2}{2AB}\right] ^2 \end{aligned}$$

(35)

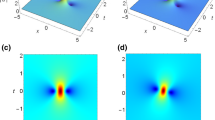
Similarly, one can define $v^{[2]}$ and $w^{[2]}$. The lump solution for $u^{[2]}$ is represented in Fig. 1. It is interesting to note that one gets a similar lump profile for $v^{[2]}$ and $w^{[2]}$.

Fig. 1

Lump for $n=1$ when $q_0 =0.3$, $A=0.5$, $B=1$

4.4 Case-II: $n=2$

Substituting $n=2$ into Eqs. (22), (23), we have

$$\begin{aligned} \phi _{i}(k_{i})= & {} \mathrm{exp}^{k_{i} (x+J(k_{i}))} \left( \psi (k_{i})^2+ a_0 (k_{i})\right) , \nonumber \\ J(k_{i})= & {} \frac{-2 q_0 y}{k^2_{i}} +\left( -a k^2_{i} +\frac{8 b q_0^3}{k^4_{i}}\right) t,\nonumber \\ \psi (k_{i})= & {} k^2_{i} \left( x+\frac{2 q_0 y}{k^2_{i}} -3\left( a k^2_{i} +\frac{8 b q^3_0}{k^4_i}\right) t\right) \end{aligned}$$

(36)

From Eqs. (24), (25),

$$\begin{aligned} a_0 (k_i) =-4 q_0 k_i y -\frac{6}{k_i} \left( a k_i^6 -16 b q_0^3 \right) t \end{aligned}$$

(37)

We can calculate the matrix $\Delta _{i,j}$ through the integration of Eq. (18) as,

$$\begin{aligned}&\Delta _{i,j} \left( \frac{k_1+k_2}{2 k_1}\right) \mathrm{exp}^{ -k_i(x+J(k_i))-k_j(x+J(k_j))}\nonumber \\&\quad =\psi (k_1)^2 \psi (k_2)^2 -\frac{2 k_2^2 }{k_1+k_2}\psi (k_1)^2 \psi (k_2)\nonumber \\&\qquad +\frac{2 k_1 k_2}{k_1 +k_2} \psi (k_1) \psi (k_2)^2\nonumber \\&\qquad +\left( a_0(k_2) +\frac{2 k_2^4}{(k_1+k_2)^2}\right) \psi (k_1)^2\nonumber \\&\qquad +\left( a_0(k_1) -\frac{2 k_2 k_1^3}{(k_1+k_2)^2}\right) \psi (k_2)^2 +\frac{2 k_1 k_2}{k_1+k_2} \left( a_0(k_2)\right. \nonumber \\&\qquad \left. + \frac{2 k_2^3 (k_2-2 k_1)}{(k_1+k_2)^2}\right) \psi (k_1)\nonumber \\&\qquad - \frac{2 k_2^2}{k_1+k_2}\left( a_0(k_1) +\frac{2 k_1^3 (k_1 -2 k_2)}{(k_1+k_2)^2}\right) \psi (k_2)\nonumber \\&\qquad +\, a_0(k_1) a_0(k_2) +\frac{2 k_2}{(k_1+k_2)^2}\left( k_2^3 a_0(k_1)- k_1^3 a_0(k_2)\right) \nonumber \\&\qquad +\frac{4 k_2^2k_1 (k_1-k_2)}{(k_1+k_2)^2} \psi (k_1) \psi (k_2)+\frac{12 k_1^3 k_2^4(k_1-k_2)}{(k_1+k_2)^4} \end{aligned}$$

(38)

4.5 $\tau - function$

A second iteration provides,   $m^{[2]} = q_0 x y + \ln (\tau _{1,2})$

$$\begin{aligned} u^{[2]}= & {} -2(m_{x,y}^{[2]})=-2\left( q_0 +\left( \frac{(\tau _{1,2})_x}{\tau _{1,2}}\right) _y \right) \end{aligned}$$

(39)

where $\tau _{1,2} = \phi _1 \phi _2 -\Delta _{1,2} = \frac{1}{2} \left( \Delta _{2,1} -\Delta _{1,2}\right)$, which after simplification can be written as,

$$\begin{aligned} \tau _{1,2}= & {} -\frac{k_1 - k_2}{k_1 +k_2} \mathrm{exp}^{k_{1} (x+J(k_{1}))+k_2(x+J(k_{2}))} \varOmega _{1,2},\nonumber \\ \varOmega _{1,2}= & {} \left[ (\psi (k_1)+g(k_1,k_2)) ^2 +a_0(k_1)\right. \nonumber \\&\left. -\frac{k_1}{k_2} g(k_1,k_2)^2\right] \left[ (\psi (k_2)+g(k_2,k_1))^2\right. \nonumber \\&\left. +\,a_0(k_2)-\frac{k_2}{k_1} g(k_2,k_1)^2)\right] \nonumber \\&+\,4 d(k_1,k_2)\left[ (\psi (k_1)-c(k_1,k_2))(\psi (k_2)\right. \nonumber \\&\left. -\,c(k_2,k_1))\right] +p(k_1,k_2) \end{aligned}$$

(40)

where $g(k_i,k_j)$, $d(k_i,k_j)$ are defined in Eq. (31) and

$$\begin{aligned} c(k_i,k_j)= & {} k_i^2 \frac{k_i^2 -k_i k_j +2 k_j^2}{(k_i+k_j) (k_i^2+k_j^2)}, \\ p(k_i,k_j)= & {} \frac{8 k_i^4 k_j^4 (k_i^2+k_j^2+k_ik_j)}{(k_i^2+k_j^2) (k_i+k_j)^4} \end{aligned}$$

Since $c(k_i,k_j)$, $p(k_i,k_j)$ are constants, we have   $u^{[2]} = -2\left( q_0 +\left( \frac{(\varOmega _{1,2})_x}{\varOmega _{1,2}}\right) _y\right)$. If we select $k_1=A + i B$, $k_2 = A- i B$, we obtain the real expression for $\varOmega _{1,2}$ as

$$\begin{aligned} \varOmega _{1,2}= & {} \left[ \left( A^2 -B^2)X +2 q_0 Y\right) ^2 - 4 A^2 B^2 X^2 - 4 A q_0 Y\right. \nonumber \\&\left. +\,\,8 A^2 B^2 h_1 t +\frac{(3 A^2 -B^2)(A^4-B^4)}{4 A^2 B^2} \right] ^2\nonumber \\&+\,\left[ 4(A^2-B^2)A B X^2 +8 q_0 A B X Y -4 q_0 B Y\right. \nonumber \\&\left. -\,\,8 A^2 B^2 h_2 t +\frac{(3 A^2 -B^2)(A^2+B^2)}{2 A B} \right] ^2\nonumber \\&+\,\,(B^2-A^2) \left[ \frac{A^2+B^2}{2AB}\right] ^2 \left[ (A^2-B^2)X\right. \nonumber \\&\left. +\,\,2 q_0 Y -\frac{2 A^4 -A^2 B^2 -B^4}{2A(A^2-B^2)}\right] ^2\nonumber \\&+\,\,(B^2-A^2) \left[ \frac{A^2+B^2}{2AB}\right] ^2 \left[ 2 A B X \right. \nonumber \\&\left. +\,\frac{A^4- A^2 B^2 +2 B^4}{2 B (A^2 -B^2)}\right] ^2\nonumber \\&+ \,\frac{B^2-3 A^2}{B^2 - A^2}\left[ \frac{(A^2+B^2)^2}{2 A^2}\right] ^2 \end{aligned}$$

(41)

where $h_1$ and $h_2$ are constants defined by

$$\begin{aligned} h_1= & {} \frac{3}{A(A^2 + B^2)^2}\left[ 8 b q_0^3 \right. \nonumber \\&\left. +\,a \left( 3 A^6 -B^6 +5 A^4 B^2 +A^2 B^4 \right) \right] ,\nonumber \\ h_2= & {} \frac{3}{B(A^2+B^2)} \left[ 8 b q_0^3 \right. \nonumber \\&\left. -\,a\left( 3 B^6 -A^6 +5 B^4 A^2 +B^2 A^4\right) \right] \end{aligned}$$

(42)

and X, Y are the coordinates defined in Eq. (34). From Eq. (41), it is easy to see that $\varOmega _{1,2}$ does not have zeros when $B^2 > 3 A^2$. If we wish to study the behavior of the solution when $t\rightarrow \pm \infty$, we need to perform the transformation,   $X = X_{\infty } \pm \sqrt{c t}$, $Y = Y_{\infty } \pm z \sqrt{c t}$ and fix c and z to cancel the higher powers in t of Eq. (41). The result is

$$\begin{aligned}&c^2 - 2 h_1 c -h_2^2=0 \Rightarrow c=h_1\pm \sqrt{h_1^2+h_2^2},\\&z =\frac{B^2-A^2}{2 q_0}+ \frac{A B h_2}{q_0 c} \end{aligned}$$

In this case, at $t\rightarrow \pm \infty$, $\varOmega _{1,2}$ behaves as

$$\begin{aligned}&\varOmega _{1,2} \sim \left[ \left( 2 h_2 (A^2-B^2) -4 A B c\right) X_\infty \right. \nonumber \\&\quad \left. +\,4 q_0 h_2 Y_\infty -2 A h_2 +\left( \frac{A^2-B^2}{B}\right) c\right] ^2 \left[ \left( 4 A B h_2\right. \right. \nonumber \\&\quad \left. +\,2(A^2-B^2)c\right) X_\infty +4 q_0 c Y_\infty -2 B h_2 \nonumber \\&\quad \left. +\left( \frac{A^2-B^2}{A}\right) c\right] ^2\nonumber \\&\quad +(h_2^2+c^2)(B^2-A^2)\left[ \frac{A^2+B^2}{2AB}\right] ^2 \end{aligned}$$

(43)

which corresponds to a static lump. Let us consider the two possible solutions of Eq. (43) separately.

$\bullet$ At $t\longrightarrow -\infty$

$$\begin{aligned} c_-= & {} -\sqrt{h_1^2+h_2^2} +h_1 < 0\Rightarrow c_-t>0, \\ z_-= & {} \frac{B^2 - A^2}{2 q_0} -\frac{A B h_2}{q_0 (\sqrt{h_1^2+h_2^2}+h_1)} \end{aligned}$$

There are two lumps approaching along the line,  $X = X_{-\infty } \pm \sqrt{c_- t}$,  $Y = Y_{-\infty } \pm z_-\sqrt{c_- t}$,  $Y-Y_{-\infty } = \tan (\theta _-) (X-X_{-\infty })$

$$\begin{aligned} tg(\theta _-)= & {} z_- = \frac{B^2-A^2}{2 q_0 }-\frac{A B h_2}{q_0 \left( -\sqrt{h_1^2 +h_2^2}+h_1\right) } \end{aligned}$$

$\bullet$ At $t\longrightarrow \infty$

$$\begin{aligned} c_+ = \sqrt{h_1^2+h_2^2} +h_1> 0\Rightarrow c_+t>0 \end{aligned}$$

There are again two lumps moving away along the line,  $X = X_{+\infty } \pm \sqrt{c_+ t}$,  $Y = Y_{+\infty } \pm z_+\sqrt{c_+ t}$,  $Y-Y_{+\infty } = \tan (\theta _+) (X-X_{+\infty })$ and therefore,

$$\begin{aligned} \tan (\theta _+) = z_+ = \frac{B^2-A^2}{2 q_0} -\frac{A B h_2}{q_0 \left( \sqrt{h_1^2 +h_2^2}+h_1\right) } \end{aligned}$$

The scattering angle between the lumps is given by,

$$\begin{aligned} \tan (\theta )= & {} \tan (\theta _+ -\theta _-)\\= & {} \frac{8 q_0 A B \sqrt{h_1^2+h_2^2}}{4 q_0^2 h_2 +4 A B h_1 (A^2 -B^2) +h_2 (A^4 -6 A^2 B^2 +B^4)} \end{aligned}$$

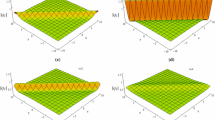
Similarly, one can define $v^{[2]}$ and $w^{[2]}$. The lump solution for $u^{[2]}$ is shown in Fig. 2. It is again interesting to note that one gets the same lump profile for $v^{[2]}$ and $w^{[2]}$. From Fig. 2, one understands that there is only a rotation of lumps without any interaction (or exchange of energy). Figure 2b shows the coalesced state of two lump solution, wherein the two lumps just pass through each other.

Fig. 2

Lump for $n=2$, when $q_0=0.5$, $a=1$, $b=66$, $A=0.5$, $B=1$. a $t<0$, b $t=0$ and c $t>0$

4.6 Two lump solution

As we have seen in the previous section, the one lump solution is obtained through the second iteration. It obviously means that for the two lump solution, we need to go to the fourth iteration. If we start with the singular manifold $\phi _1$, we can generalize Eqs. (15) and (19) as:

$$\begin{aligned} \phi _{1,j} =\phi _j -\frac{\Delta _{1,j}}{\phi _{1}},~~ \Delta _{i,j} = \Delta (\phi _i,\phi _j) \end{aligned}$$

From the fourth iteration, we have

$$\begin{aligned} \phi _{1,i,j,k}= & {} \phi _{1,i,k} - \frac{\Delta _{1,i,j,k}}{\phi _{1,i,j}}, \\ \Delta _{1,i,j,k}= & {} \Delta (\phi _{1,i,j} , \phi _{1,i,k}) =\Delta _{i,j,k}- \frac{\Delta _{1,j,i} \Delta _{1,i,k}}{\phi _{1,i}^2} \end{aligned}$$

The solution becomes

$$\begin{aligned} m^{[4]}= & {} m^{[3]}+\ln (\phi _{1,2,3,4}) = m^{[2]} +\ln (\phi _{1,2,3}) \\&+\ln (\phi _{1,2,3,4}) \\= & {} m^{[1]} +\ln (\phi _{1,2})+\ln (\phi _{1,2,3})+\ln (\phi _{1,2,3,4})\\= & {} m^{[0]} +\ln (\phi _{1})+\ln (\phi _{1,2}) \\&+\ln (\phi _{1,2,3}) +\ln (\phi _{1,2,3,4}) \end{aligned}$$

which reads

$$\begin{aligned} m^{[4]} =m^{[0]}+ \ln (\tau _{1,2,3,4}) \end{aligned}$$

(44)

where $\tau _{1,2,3,4} = \phi _{1,2,3,4} \phi _{1,2, 3} \phi _{1,2} \phi _1$. With the previous definition, we can construct the $\tau$ function for the fourth iteration from the eigenfunctions of the seed solution $m^{[0]}$ in the following form:

$$\begin{aligned} \tau _{1,2,3,4}= & {} \frac{1}{4} (\Delta _{2,1} -\Delta _{1,2})(\Delta _{4,3} - \Delta _{3,4})\\&-\frac{1}{4} (\Delta _{4,2} -\Delta _{2,4})(\Delta _{3,1} - \Delta _{1,3}) \\&+ \frac{1}{4} (\Delta _{4,1} -\Delta _{1,4})(\Delta _{3,2} - \Delta _{2,3}) \end{aligned}$$

where we have used, $\phi _i\phi _j =\frac{1}{2} (\Delta _{j,i}+\Delta _{i,j})$. One can write $\tau _{1,2,3,4}$ in a more compact form as: $\tau ^2_{1,2,3,4} = det(\Delta _{i,j}), \, {\text {if}} \,\,i,j = 1..4$. We shall consider the simplest case in which we have the seed solutions with $n=1$.

4.6.1 Solution for two lumps with $n=1$

The simplest case can be obtained by taking $n=1$. The eigenfunction given by Eqs. (22), (23) again taking the form given by Eqs. (26), (27). We can calculate the matrix $\Delta _{i,j}$ again taking the form given by Eq. (28). We have,

$$\begin{aligned} u^{[2]} = -2\left( q_0 +\left( \frac{(\tau _{1,2,3,4})_x}{\tau _{1,2,3,4}}\right) _y\right) \end{aligned}$$

(45)

and we choose

$$\begin{aligned} k_1= & {} A_1 +i B_1,~~ k_2 = k_1^* = A_1 - i B_1, \\ k_3= & {} A_2 + i B_2,~~ k_4 = k_3^* = A_2- i B_2 \end{aligned}$$

It is convenient to define a center of mass coordinate system as

$$\begin{aligned} x= & {} X_{cm} +\frac{1}{2} (v_x^1 + v_x^2) t, \nonumber \\ y= & {} Y_{cm} +\frac{1}{2} (v_y^1+ v_y^2) t \end{aligned}$$

(46)

where $(v_x^i,v_y^i)$ are the individual velocities of each soliton (see Eq. (34))

$$\begin{aligned} v_x^i= & {} \left( 6a(A^2_i-B^2_i)-\frac{24 b q_0^3}{(A^2_i+B^2_i)^2}\right) ,\nonumber \\ v_y^i= & {} \frac{1}{q_0} \left( \frac{-3a}{2} \left( A^2_i+B^2_i\right) ^2+24 b q_0^3 \frac{(A^2_i-B^2_i)}{(A^2_i+B^2_i)^2}\right) \nonumber \\ \end{aligned}$$

(47)

Using the change of variables given in Eqs. (46), (47) in Eq. (27), we have

$$\begin{aligned} \psi (k_1)= & {} k_1^2 (X_{cm} -V_x t)+2q_0 (Y_{cm} -V_y t), \\ \psi (k_2)= & {} k_2^2 (X_{cm} -V_x t)+2q_0 (Y_{cm} -V_y t),\\ \psi (k_3)= & {} k_3^2 (X_{cm} +V_x t)+2q_0 (Y_{cm} +V_y t), \\ \psi (k_4)= & {} k_4^2 (X_{cm} +V_x t)+2q_0 (Y_{cm} +V_y t) \end{aligned}$$

where, $V_x = \frac{1}{2} (v_x^1 -v_x^2),~~ V_y= \frac{1}{2} (v_y^1 -v_y^2)$.   In the center of mass system, the solution asymptotically yields two lumps that move with equal and opposite velocities. To clarify this point, we can consider the asymptotic behavior of each lump

Fig. 3

Two Lump solution for $n=1$, when $a=1$, $b=0.2$, $q_0=0.5$, $A_1=0.5$, $B_1=1$, $A_2=0.5$, $B_2=\frac{4}{3}$. a $t<0$, b $t=0$ and c $t>0$

$\bullet$ Let us define

$$\begin{aligned} X_{cm} = X_1 - X_{0}^1 +V_x t,~~ Y_{cm} = Y_1 - Y_{0}^1 +V_y t \end{aligned}$$

which (the tedious calculation has been made with MAPLE) allows us to write the limit of the $\tau$-function when $t\rightarrow \pm \infty$ as the static lump

$$\begin{aligned}&\tau _{1,2,3,4} \sim \left[ (A_1^2-B_1^2) X_1 + 2 q_0 Y_1 \right] ^2 \\&\quad +\left[ 2 A_1 B_1 X_1\right] ^2 + (B_1^2-A_1^2)\left[ \frac{ (A_1^2+B_1^2)}{2 A_1 B_1}\right] ^2 \end{aligned}$$

where

$$\begin{aligned} X_0^1= & {} -\frac{A_1^2+B_1^2}{4 A_1 B_1^2}\\&-\frac{4 A_2 \left[ (A^2_2+B^2_2)^3+(A^2_2-3B^2_2)(A_1^2+B_1^2)^2+2(A^2_2+B^2_2)^2(B_1^2-A^2_1)\right] }{[(A_1+A_2)^2+(B_1-B_2)^2][(A_1-A_2)^2+(B_1-B_2)^2][(A_1+A_2)^2+(B_1+B_2)^2][(A_1-A_2)^2+(B_1+B_2)^2]}\\ q_0Y_0^1= & {} \frac{A_1^2+B_1^2}{8 A_1 B_1^2} \\&-\frac{2 A_2(A_1^2+B_1^2)^2[(A^2_1+B^2_1)^2+(A^2_2-3B^2_2)(A^2_2+B^2_2) +2 (A_2^2+B^2_2) (B_1^2-A_1^2)]}{[(A_1+A_2)^2+(B_1-B_2)^2][(A_1-A_2)^2+(B_1-B_2)^2][(A_1+A_2)^2+(B_1+B_2)^2][(A_1-A_2)^2+(B_1+B_2)^2]} \end{aligned}$$

$\bullet$ If we now define

$$\begin{aligned} X_{cm} = X_2 - X_{0}^2 -V_x t,~~ Y_{cm} = Y_2 - Y_{0}^2 -V_y t \end{aligned}$$

the limit of the $\tau$-function when $t\rightarrow \pm \infty$ as the static lump becomes

$$\begin{aligned} \tau _{1,2,3,4}\sim & {} \left[ (A_2^2-B_2^2) X_2 + 2 q_0 Y_2\right] ^2 +\left[ 2 A_2 B_2 X_2\right] ^2 \\&\quad +(B_2^2-A_2^2)\left[ \frac{(A_2^2+B_2^2)}{2 A_2 B_2}\right] ^2 \end{aligned}$$

where

$$\begin{aligned} X_0^2= & {} -\frac{A_2^2+B_2^2}{4 A_2 B_2^2} \\&- \frac{4 A_1 \left[ (A_1^2+B_1^2)^3+(A_1^2-3B_1^2)(A_2^2+B_2^2)^2+2(A_1^2+B_1^2)^2(B_2^2-A_2^2)\right] }{[(A_1+A_2)^2+(B_1-B_2)^2][(A_1-A_2)^2+(B_1-B_2)^2][(A_1+A_2)^2+(B_1+B_2)^2][(A_1-A_2)^2+(B_1+B_2)^2]}\\ q_0Y_0^2= & {} \frac{A_2^2+B_2^2}{8 A_2 B_2^2}\\&-\frac{2 A_1(A_2^2+B_2^2)^2[(A^2_2+B^2_2)^2+(A^2_1-3B^2_1)(A^2_1+B^2_1) +2 (A_1^2+B_1^2) (B_2^2-A_2^2)]}{[(A_1+A_2)^2+(B_1-B_2)^2][(A_1-A_2)^2+(B_1-B_2)^2][(A_1+A_2)^2+(B_1+B_2)^2][(A_1-A_2)^2+(B_1+B_2)^2]} \end{aligned}$$

In this system of reference, the asymptotic behavior of the solution for $t \longrightarrow \pm \infty$ corresponds to two lumps moving with equal and opposite velocities along parallel lines as shown in Fig. 3a, c, Fig. 3b again represents the coalesced state of two lump solution where again the lumps which seem to merge move away in opposite directions later. Similarly, one can define $v^{[2]}$ and $w^{[2]}$.

5 Rogue waves

In the section, we will focus on the construction of rogue waves for Eq. (5).

5.1 Solution

Taking the easiest choice of the variable m(x, y, t) as,

$$\begin{aligned} m = A(x,t) +B(y,t) \end{aligned}$$

(48)

where A and B are arbitrary functions in the indicated variables, we now substitute equation Eq. (48) in Eq. (4) to obtain

$$\begin{aligned} u^{[0]}= & {} -2 m^{[0]}_{xy} = 0 \end{aligned}$$

(49)

$$\begin{aligned} v^{[0]}= & {} \frac{c}{3 a} - 2 m^{[0]}_{xx} = \frac{c}{3a} -2 A_{xx} = v(x,t) \end{aligned}$$

(50)

$$\begin{aligned} w^{[0]}= & {} \frac{d}{3b} -2 m^{[0]}_{yy} = \frac{d}{3b} - 2 B_{yy} =w(y,t) \end{aligned}$$

(51)

One possibility is to choose

$$\begin{aligned} \phi _1 = F(x,t),~ \phi _2 = G(y,t) \end{aligned}$$

(52)

where F(x, t) and G(y, t) are again arbitrary functions. Substituting Eqs. (48) and (52) in Eqs. (13), (14), we have

$$\begin{aligned} F_t + G_t =-a\left( F_{xxx} + 6 F_{x} A_{xx}\right) -b\left( G_{yyy} +6 G_y B_{yy}\right) \end{aligned}$$

where

$$\begin{aligned} A_{xx} = - \frac{F_t + a F_{xxx}}{6 a F_x},~~ B_{yy} = -\frac{G_t + b G_{yyy}}{6 b G_y} \end{aligned}$$

From Eq. (19), we have  $\Delta _{1,2} = 2 F(x,t) G(y,t)+c_0$,  where $c_0$ is an arbitrary constant. Hence, Eq. (20) now yields

$$\begin{aligned} \tau _{1,2} = - \left( F(x,t) G(y,t) + c_0 \right) \end{aligned}$$

Now, the solution for $u^{[2]}$, $v^{[2]}$ and $w^{[2]}$, can be written as,

$$\begin{aligned} m^{[2]}= & {} m^{[0]} + \ln (\tau _{1,2}) \\ u^{[2]}= & {} - 2 m^{[2]}_{xy} \\= & {} -2 \left( m^{[0]}+\ln \left( -\left( F(x,t) G(y,t) +c_0 \right) \right) \right) _{xy} \\ v^{[2]}= & {} \frac{c}{3 a} - 2 m^{[2]}_{xx} =\frac{c}{3 a} \\&-2 \left( m^{[0]}+\ln \left( - \left( F(x,t) G(y,t) +c_0 \right) \right) \right) _{xx} \\ w^{[2]}= & {} \frac{d}{3 b} - 2 m^{[2]}_{yy} = \frac{d}{3 b}\\&-2 \left( m^{[0]}+\ln \left( \left( - (F(x,t) G(y,t) +c_0\right) \right) \right) _{yy} \end{aligned}$$

where

$$\begin{aligned} F= & {} f(x,t) + \frac{c_3}{c_4},~~ G= g(y,t) +\frac{c_2}{c_4}, \\ c_0= & {} \frac{c_1}{c_4} - \frac{c_2 c_3}{c_4^2} \end{aligned}$$

5.2 Case-I

To construct a single rogue wave, we choose

$$\begin{aligned} f(x,t) = \frac{1}{1+t^2 +(x-1)^2},~~ g(y,t) = 2 y^2 \end{aligned}$$

Rogue waves for $u^{[2]}$, $v^{[2]}$ and $w^{[2]}$ are shown in Fig. 4. The time evolution of the rogue waves indicates their unstable nature.

Fig. 4

Rogue waves for $u^{[2]}$, $v^{[2]}$ and $w^{[2]}$ with $c_1 = 0.06$,  $c_2 = 0.01$,  $c_3 = 0.01$,  $c_4 = 0.1$,  $a =1$, $b = 1$, $c =1$, $d = 1$ at $t=0$

Fig. 5

Multi rogue waves for $u^{[2]}$, $v^{[2]}$ and $w^{[2]}$ with $c_1 = 0.06$,  $c_2 = 0.01$,  $c_3 = 0.1$,  $c_4 = 0.1$,  $a =15,~ b = 10, ~c =10, ~d = 10$, $k= 0.01$ at $t=0$

5.3 Case-II

To obtain a multi rogue waves, we choose,

$$\begin{aligned} f(x,t)= & {} \cos (x)+ \sin (x), \\ g(y,t)= & {} \frac{1}{(1+(y-1)^2+ k t^2)^2} \end{aligned}$$

Multi rogue waves for $u^{[2]}$, $v^{[2]}$ and $w^{[2]}$ are shown in Fig. 5.

6 Discussion

In this paper, we have analyzed the generalized NNV equation (GNNV) and derived its Lax pair in the coordinate space destroying the myth of weak Lax pair. We have then generated lumps and rogue waves of the GNNV equation and studied their dynamics. The lumps do not interact and they merely pass through each other or move away from each other, while the rogue waves generated are found to retain their unstable nature. We believe that a deeper investigation may unearth other elusive localized solutions.