1 Introduction

The past decades have witnessed a constant growth in the number of studies on the existence, stability, and robustness of solitons (or more properly solitary waves) and their applications in diverse areas, such as optical fibers, matter waves (Bose–Einstein condensates), and water waves [1,2,3,4,5,6,7,8,9]. Finding exact solutions to nonlinear partial differential equations (PDEs) describing the evolution of localized waveforms is a significant subject in nonlinear science [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Many nonlinear evolution equations that model the realistic physical problems are variable-coefficient nonlinear PDEs [34,35,36,37,38,39,40,41,42,43]. They describe a plethora of physical effects in fluid dynamics, condensed matter physics, plasma physics, optics and photonics (especially in nonlinear fiber optics [44,45,46,47,48,49,50]). Solitons propagating in optical fibers may be adequately described by variable-coefficient nonlinear Schrödinger (VCNLS) equations, see book [2] and Refs. [44, 50]. To increase the transmission rate, ultrashort (picosecond or subpicosecond) pulses are often used as data carriers, for which the higher-order dispersion (HOD) cannot be ignored. Therefore, finding analytical families of soliton solutions of nonlinear PDEs that incorporate higher-order terms, especially finding exact solutions of higher-order variable-coefficient NLS-type equations, is of great importance from both theoretical and experimental point of view [51,52,53,54].

Recently, many works addressed soliton solutions for the higher-order VCNLS equations, using various methods, such as the Darboux transformation and Hirota bilinear method [55,56,57,58,59]. In particular, breather solutions for a higher-order VCNLS equation have been found by means of the Darboux transformation [60], producing the effect of HOD on the obtained solutions, and the analysis of a sixth-order VCNLS equation [61] has yielded one- and two-soliton solutions with the help of the Hirota bilinear method, showing that HOD significantly affects velocities and amplitudes of the solitons. Further, a method to realize the transition between nonautonomous breathers and the nonautonomous multi-peak solitons for a VCNLS equation with HOD has been proposed in [62]. Recently, first- and second-order rogue-wave solutions for a fourth-order VCNLS equation have been obtained in Ref. [63], and effects of group velocity dispersion (GVD) and fourth-order dispersion (FOD) on rogue waves have been revealed.

In this paper, we investigate the following fifth-order VCNLS equation [64]:

$$\begin{aligned}&iu_{x}+\beta (x)\left( \frac{1}{2}u_{tt}+u|u|^{2}\right) -\,i\alpha (x)\left( u_{ttt}+6|u|^{2}u_{t}\right) \nonumber \\&\quad +\,\gamma (x)\left( u_{tttt}+6u^{*}u_{t}^{2}+4u|u_{t}|^{2} \right. \nonumber \\&\quad \left. +\,8|u|^{2}u_{tt}+2u^{2}u_{tt}^{*}+\,6u|u|^{4}\right) \nonumber \\&\quad -\,i\delta (x)\left( u_{ttttt}+10|u|^{2}u_{ttt}+30|u|^{4}u_{t}+10uu_{t}u_{tt}^{*} \right. \nonumber \\&\quad \left. +\,10uu_{t}^{*}u_{tt}+20u^{*}u_{t}u_{tt}+10u_{t}^{2}u_{t}^{*}\right) =0, \end{aligned}$$
(1)

which may be used as an integrable model to describe the propagation of ultrashort pulses in inhomogeneous optical fibers. Here u(x, t) is a complex function representing the envelope of the optical pulse, x is the normalized transmission distance, and t is the retarded time, the asterisk standing for the complex conjugate. Physically, real parameters \(\beta (x)\), \(\alpha (x)\), \(\gamma (x)\), and \(\delta (x)\) represent GVD, third-order dispersion (TOD), FOD, and the fifth-order dispersion, respectively. Equation (1) with constant coefficients has been proved to be completely integrable by using the Lax pair and Darboux transformations [64]. However, possible integrability of Eq. (1) with x-dependent coefficients \(\alpha (x)\), \(\beta (x)\), \(\gamma (x)\) and \(\delta (x)\) has not been studied before. In the present work, analytical one- and two-soliton solutions to Eq. (1) are derived by means of the Hirota bilinear method for some particular choices of these coefficient functions, such as the one give by Eqs. (15) and (16). A comprehensive analysis of integrability conditions for the x-dependent coefficients of Eq. (1) should be a subject of a separate work.

Based on the obtained solutions, we present different scenarios of soliton interactions and reshaping, by adjusting parameters of the governing model. In particular, we will demonstrate a possibility to have pulse widths of two interacting solitons changing after the collision, without a change in their amplitudes. In addition, we demonstrate that the state of two interacting solitons can be changed, after a certain propagation distance, from a bound state to a pair of separating solitons with different amplitudes and widths. Also, an interesting effect revealed by the exact solutions is that a spatiotemporal pulse train can be compressed in the course of the propagation.

The rest of the paper is arranged as follows. The bilinear form and one- and two-soliton solutions of Eq. (1) are derived in Sect. 2 via the Hirota method. In Sect. 3, the use of the model’s parameters for shaping one-soliton states and control of two-soliton interactions is illustrated graphically, using the obtained exact one- and two-soliton solutions. Finally, conclusions are formulated in Sect. 4.

2 Bilinear forms and solutions of Eq. (1)

In this section, bilinear forms and one- and two-soliton analytical solutions of Eq. (1) are given, using the Hirota bilinear method [65, 66].

2.1 Bilinear forms

To transform Eq. (1) into the Hirota bilinear form, we introduce a dependent-variable transformation,

$$\begin{aligned} u(x,t)=\frac{g(x,t)}{f(x,t)}, \end{aligned}$$

where g(x, t) is a complex differentiable function, while f(x, t) is a real one. Then Eq. (1) can be transformed into

$$\begin{aligned}&i\frac{D_{x}g\cdot f}{f^{2}}+\beta (x)\left( \frac{D_{t}^{2}g\cdot f}{2f^{2}}-\frac{g}{2f}\frac{D_{t}^{2}f\cdot f}{f^{2}}+\frac{g}{f}\frac{|g|^{2}}{f^{2}}\right) \nonumber \\&\quad -\,i\alpha (x)\left( \frac{D_{t}^{3}g\cdot f}{f^{2}}-3\frac{D_{t}g\cdot f}{f^{2}} \times \frac{D_{t}^{2}f\cdot f}{f^{2}}\right. \nonumber \\&\quad +\left. 6\frac{|g|^{2}}{f^{2}}\frac{D_{t}g\cdot f}{f^{2}}\right) \nonumber \\&\quad +\,\gamma (x)\left[ \frac{D_{t}^{4}g\cdot f}{f^{2}}-\frac{g}{f}\frac{D_{t}^{4}f\cdot f}{f^{2}}+6\frac{g}{f}\left( \frac{D_{t}^{2}f\cdot f}{f^{2}}\right) ^{2}\right. \nonumber \\&\left. \quad -\,6\frac{D_{t}^{2}g\cdot f}{f^{2}}\frac{D_{t}^{2}f\cdot f}{f^{2}}+6\frac{g^{*}}{f}\left( \frac{D_{t}g\cdot f}{f^{2}}\right) ^{2}\right. \nonumber \\&\left. \quad +\,4\frac{g}{f}\frac{D_{t}g\cdot f}{f^{2}}\frac{D_{t}g^{*}\cdot f}{f^{2}} \right. \nonumber \\&\left. \quad +\,8\frac{|g|^{2}}{f^{2}}\left( \frac{D_{t}^{2}g\cdot f}{f^{2}}-\frac{g}{f}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) \right. \nonumber \\&\left. \quad +\,2\frac{g^{2}}{f^{2}}\left( \frac{D_{t}^{2}g^{*}\cdot f}{f^{2}}-\frac{g^{*}}{f}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) +6\frac{g}{f}\frac{|g|^{4}}{f^{4}}\right] \nonumber \\&\quad -\,i\delta (x)\left[ \frac{D_{t}^{5}g\cdot f}{f^{2}}-10\frac{D_{t}^{3}g\cdot f}{f^{2}}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right. \nonumber \\&\left. \quad -\,5\frac{D_{t}g\cdot f}{f^{2}}\frac{D_{t}^{4}f\cdot f}{f^{2}}+30\frac{D_{t}g\cdot f}{f^{2}}\left( \frac{D_{t}^{2}f\cdot f}{f^{2}}\right) ^{2}\right. \nonumber \\&\left. \quad +\,10\frac{|g|^{2}}{f^{2}}\left( \frac{D_{t}^{3}g\cdot f}{f^{2}}-3\frac{D_{t}g\cdot f}{f^{2}}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) \right. \nonumber \\&\left. \quad +\,30\frac{|g|^{4}}{f^{4}}\frac{D_{t}g\cdot f}{f^{2}}+10\frac{g}{f}\frac{D_{t}g\cdot f}{f^{2}}\left( \frac{D_{t}^{2}g^{*}\cdot f}{f^{2}}\right. \right. \nonumber \\&\left. \quad \left. -\,\frac{g^{*}}{f}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) +10\frac{g}{f}\frac{D_{t}g^{*}\cdot f}{f^{2}}\left( \frac{D_{t}^{2}g\cdot f}{f^{2}}\right. \right. \nonumber \\&\left. \quad \left. -\,\frac{g}{f}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) +20\frac{g^{*}}{f}\frac{D_{t}g\cdot f}{f^{2}}\left( \frac{D_{t}^{2}g\cdot f}{f^{2}}\right. \right. \nonumber \\&\left. \quad \left. -\,\,\frac{g}{f}\frac{D_{t}^{2}f\cdot f}{f^{2}}\right) +10\left( \frac{D_{t}g\cdot f}{f^{2}}\right) ^{2}\frac{D_{t}g^{*}\cdot f}{f^{2}}\right] =0,\nonumber \\ \end{aligned}$$
(2)

where the Hitota bilinear operators \(D_{x}^{m}\) and \(D_{x}^{n}\) are defined by [65, 66]

$$\begin{aligned}&D_{x}^{m}D_{t}^{n}g(x,t)\cdot f(x,t) =\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{\prime }} \right) ^{m}\nonumber \\&\quad \times \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t^{\prime }}\right) ^{n}g(x,t)f(x^{\prime },t^{\prime })\bigg |_{x^{\prime }=x,t^{\prime }=t}. \end{aligned}$$
(3)

Setting \(D_{t}^{2}f\cdot f=2|g|^{2}\), and according to the properties of the Hirota bilinear D-operator:

$$\begin{aligned} {\frac{D_{t}^{4}f\cdot f}{f^{2}}=\left( \frac{D_{t}^{2}f\cdot f}{f^{2}}\right) _{tt}+3\left( \frac{D_{t}^{2}f\cdot f}{f^{2}}\right) ^{2},} \end{aligned}$$
(4)

Eq. (2) can be simplified as

$$\begin{aligned}&\frac{\Big [iD_{x}+\frac{\beta (x)}{2}D_{t}^{2}-i\alpha (x)D_{t}^{3}+\gamma (x)D_{t}^{4}-i\delta (x)D_{t}^{5}\Big ]g\cdot f }{f^{2}}\nonumber \\&\quad -\,\frac{3\gamma (x)g^{*}\left( D_{t}^{2}g\cdot g\right) }{f^{3}}\nonumber \\&\quad -\,i\frac{5\delta (x)g_{t}^{*}\left( D_{t}^{2}g\cdot g\right) }{f^{3}}-i\frac{10\delta (x)g^{*}\left( D_{t}g\cdot g_{tt}\right) }{f^{3}}\nonumber \\&\quad -\,i\frac{5\delta (x)g^{*}\left( D_{t}^{2}g\cdot g\right) f_{t}}{f^{4}}=0. \end{aligned}$$
(5)

Introducing two complex auxiliary functions \(r=r(x,t)\) and \(s=s(x,t)\), the bilinear relations for Eq. (1) can be derived as

$$\begin{aligned}&D_{t}^{2}f\cdot f=2|g|^{2}, \end{aligned}$$
(6a)
$$\begin{aligned}&D_{t}^{2}g\cdot g=sf, \end{aligned}$$
(6b)
$$\begin{aligned}&2D_{t}g\cdot g_{tt}+sf_{t}=rf, \end{aligned}$$
(6c)
$$\begin{aligned}&\left[ iD_{x}+\frac{\beta (x)}{2}D_{t}^{2}-i\alpha (x)D_{t}^{3}+\gamma (x)D_{t}^{4}-i\delta (x)D_{t}^{5}\right] g\cdot f \nonumber \\&\quad -3\gamma (x)g^{*}s-i5\delta (x)g_{t}^{*}s=i5\delta (x)g^{*}r, \end{aligned}$$
(6d)

where the Hitota bilinear operators \(D_{x}^{m}\) and \(D_{x}^{n}\) are defined by [65, 66]

$$\begin{aligned}&D_{x}^{m}D_{t}^{n}g(x,t)\cdot f(x,t) =\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{\prime }} \right) ^{m}\nonumber \\&\quad \times \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t^{\prime }}\right) ^{n}g(x,t)f(x^{\prime },t^{\prime })\bigg |_{x^{\prime }=x,t^{\prime }=t}. \end{aligned}$$
(7)

Equation (6) can be solved by expanding functions g(x, t), f(x, t), r(x, t), and s(x, t) in powers of a formal small parameter \( \varepsilon \):

$$\begin{aligned}&g(x,t)=\varepsilon g_{1}(x,t)+\varepsilon ^{3}g_{3}(x,t)+\varepsilon ^{5}g_{5}(x,t)+\cdots , \end{aligned}$$
(8a)
$$\begin{aligned}&f(x,t)=1+\varepsilon ^{2}f_{2}(x,t)+\varepsilon ^{4}f_{4}(x,t)\nonumber \\&\quad +\varepsilon ^{6}f_{6}(x,t)+\cdots , \end{aligned}$$
(8b)
$$\begin{aligned}&r(x,t)=r_{0}(x,t)+\varepsilon ^{2}r_{2}(x,t)+\varepsilon ^{4}r_{4}(x,t)\nonumber \\&\quad +\varepsilon ^{6}r_{6}(x,t)+\cdots , \end{aligned}$$
(8c)
$$\begin{aligned}&s(x,t)=s_{0}(x,t)+\varepsilon ^{2}s_{2}(x,t)+\varepsilon ^{4}s_{4}(x,t)\nonumber \\&\quad +\varepsilon ^{6}s_{6}(x,t)+\cdots , \end{aligned}$$
(8d)

where \(g_{m}(x,t)\) \((m=1,3,5,\ldots )\), \(r_{n}(x,t)\), and \(s_{n}(x,t)\) \( (n=0,2,4,6,\ldots )\) are complex functions and \(f_{l}(x,t)\) \((l=2,4,6,\ldots )\) are real ones.

2.2 One-soliton solutions

To obtain the one-soliton solution for Eq. (1), we assume \( g(x,t)=\varepsilon g_{1}(x,t)\), \(f(x,t)=1+\varepsilon ^{2}f_{2}(x,t)\), \( r(x,t)=r_{0}(x,t)\), \(s(x,t)=s_{0}(x,t)\). The expressions of \(g_{1}(x,t)\) and \(f_{2}(x,t)\) are assumed to be

$$\begin{aligned} g_{1}(x,t)= & {} e^{\theta }, \nonumber \\ f_{2}(x,t)= & {} \sigma (x)e^{\theta +\theta ^{*}}. \end{aligned}$$
(9)

Here \(\theta =k(x)+wt+d\), where k(x) is a complex function, and w and d are complex constants. Then, we substitute expression (9) into Eq. (6). After some calculations, the constraints on the parameters can be obtained as follows:

$$\begin{aligned} k(x)= & {} \int \left[ \frac{i}{2}w^{2}\beta (x)+w^{3}\alpha (x)\right. \nonumber \\&\left. +\,iw^{4}\gamma (x)+w^{5}\delta (x) \right] dx, \nonumber \\ r_{0}(x,t)= & {} s_{0}(x,t)=0,\quad \sigma (x)=\frac{1}{(w+w^{*})^{2}}.\nonumber \\ \end{aligned}$$
(10)

Without loss of generality, we set \(\varepsilon =1\), and the analytic one-soliton solution for Eq. (1) can be written as

$$\begin{aligned} u(x,t)=\frac{g_{1}(x,t)}{1+f_{2}(x,t)}. \end{aligned}$$
(11)
Fig. 1
figure 1

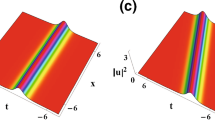
One-soliton shaping based on the solution (11) with parameters: \(w=1\), \(d=2\), \(\beta (x)=\gamma (x)=\delta (x)=x\). a \(\alpha (x)=\tan (x)\); b \(\alpha (x)=\tan (0.69x)\); c \(\alpha (x)=\tan (1.3x)\); d \(\alpha (x)=\tan (0.6x)\). In this figure and similar ones presented below, values of \(|u|^{2}\) are shown by means of the vertical axis, which seems as a back-tilted left square bracket,[

Full size image
Fig. 2
figure 2

One-soliton shaping based on the solution (11) with parameters: \(w=1\), \(d=2\), \(\beta (x)=\sin (x)\), \(\gamma (x)=\sin (x)\), \(\delta (x)=\tan (x)\). a \(\alpha (x)=\sin (x)\); b \(\alpha (x)=\sin (0.69x)\); c \(\alpha (x)=\sin (0.52x)\); d \(\alpha (x)=\sin (0.42x)\)

Full size image

2.3 Two-soliton solution

To obtain the two-soliton solution of Eq. (1), we assume \( g(x,t)=\varepsilon g_{1}(x,t)+\varepsilon ^{3}g_{3}(x,t)\), \( f(x,t)=1+\varepsilon ^{2}f_{2}(x,t)+\varepsilon ^{4}f_{4}(x,t)\), \(r(x,t)=r_{0}(x,t)+\varepsilon ^{2}r_{2}(x,t)\) and \(s(x,t)=s_{0}(x,t)\) +\(\varepsilon ^{2}s_{2}(x,t)\), while the expressions for \(g_{1}(x,t)\), \( g_{3}(x,t)\), \(f_{2}(x,t)\), and \(f_{4}(x,t)\) are taken as

$$\begin{aligned} g_{1}(x,t)= & {} e^{\theta _{1}}+e^{\theta _{2}}, \nonumber \\ g_{3}(x,t)= & {} \rho _{1}(x)e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}}+\rho _{2}(x)e^{\theta _{1}+\theta _{2}+\theta _{2}^{*}}, \nonumber \\ f_{2}(x,t)= & {} \varphi _{1}(x)e^{\theta _{1}+\theta _{1}^{*}}+\varphi _{2}(x)e^{\theta _{1}+\theta _{2}^{*}} \nonumber \\&+\,\varphi _{3}(x)e^{\theta _{2}+\theta _{1}^{*}}+\varphi _{4}(x)e^{\theta _{2}+\theta _{2}^{*}}, \nonumber \\ f_{4}(x,t)= & {} \psi (x)e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}+\theta _{2}^{*}}. \end{aligned}$$
(12)

Here \(\theta _{j}(x,t)=k_{j}(x)+w_{j}t+d_{j}\) \((j=1,2)\), where \(k_{j}(x)\) are complex functions, and \(w_{j}\) and \(d_{j}\) are complex constants. Then, we substitute expression (12) into Eq. (6). After some calculations, the expressions for the parameters can be obtained as follows:

$$\begin{aligned} k_{1}(x)= & {} \int \left[ \frac{i}{2}w_{1}^{2}\beta (x)+w_{1}^{3}\alpha (x)+iw_{1}^{4}\gamma (x)\right. \nonumber \\&\left. +\,w_{1}^{5}\delta (x)\right] dx, \nonumber \\ k_{2}(x)= & {} \int \left[ \frac{i}{2}w_{2}^{2}\beta (x)+w_{2}^{3}\alpha (x)+iw_{2}^{4}\gamma (x)\right. \nonumber \\&\left. +\,w_{2}^{5}\delta (x)\right] dx, \nonumber \\ r_{0}(x,t)= & {} s_{0}(x,t)=0, \quad r_{2}(x,t)=\zeta (x)e^{\theta _{1}+\theta _{2}}, \nonumber \\ s_{2}(x,t)= & {} \xi (x)e^{\theta _{1}+\theta _{2}}, \quad \ \ \xi (x)=2(w_{1}-w_{2})^{2}, \nonumber \\ \zeta (x)= & {} -2(w_{1}-w_{2})^{2}(w_{1}+w_{2}), \nonumber \\ \varphi _{1}(x)= & {} \frac{1}{\left( w_{1}+w_{1}^{*}\right) ^{2}}, \quad \ \ \varphi _{2}(x)=\frac{1}{\left( w_{1}+w_{2}^{*}\right) ^{2}}, \nonumber \\ \varphi _{3}(x)= & {} \frac{1}{\left( w_{2}+w_{1}^{*}\right) ^{2}}, \quad \ \ \varphi _{4}(x)=\frac{1}{\left( w_{2}+w_{2}^{*}\right) ^{2}}, \nonumber \\ \rho _{1}(x)= & {} \frac{\varphi _{1}(x)\varphi _{3}(x)\xi (x)}{2},\quad \nonumber \\ \rho _{2}(x)= & {} \frac{\varphi _{2}(x)\varphi _{4}(x)\xi (x)}{2}, \nonumber \\ \psi (x)= & {} \frac{\varphi _{1}(x)\varphi _{2}(x)\varphi _{3}(x)\varphi _{4}(x)|\xi (x)|^{2}}{4}. \end{aligned}$$
(13)

We set \(\varepsilon =1\), and the analytic two-soliton solution for Eq. (1) can be written as

$$\begin{aligned} u(x,t)=\frac{g_{1}(x,t)+g_{3}(x,t)}{1+f_{2}(x,t)+f_{4}(x,t)}. \end{aligned}$$
(14)

3 Discussion

In this section, we will consider the effect of relevant model parameters on shaping of one-soliton states and control of the two-soliton interaction, and subsequent reshaping of the solitons after the collision. The obtained results will be illustrated graphically by using both three-dimensional plots and two-dimensional contour plots of the corresponding waveforms.

To investigate the effect of HOD on the reshaping of the fundamental soliton, we fix the coefficients of GVD, FOD, and fifth-order dispersion and only vary the value of TOD to show the change of the shape of the soliton in the course of the propagation, as displayed in Figs. 1 and 2. When the variable (x-dependent) TOD is taken as

$$\begin{aligned} \alpha (x)=\tan (Cx), \end{aligned}$$
(15)

with real constant C, and a linear function of x is chosen for coefficients of the inhomogeneous GVD, FOD, and fifth-order dispersion, i.e., we consider

$$\begin{aligned} \beta (x)=\gamma (x)=\delta (x)=x, \end{aligned}$$
(16)

the reshaping of the fundamental soliton is shown in Fig. 1a for \(C=1\). It is clearly seen in Fig. 1a that the soliton trajectory in the (x, t) plane is a parabola-like one in this specific case. In the course of the soliton propagation, it shrinks to the narrowest state along the negative direction of t, and a phase flip occurs. Then, the width of the soliton expands, leading to the generation of left-right symmetric grooves in the course of the propagation. Further, the distance between two adjacent phase flips increases along the negative direction of t, while the amplitude of the soliton remains almost unchanged before and after the phase flip. If we adjust coefficient C in Eq. (15), the frequency of the soliton phase-flipping can be reduced without changing the soliton’s amplitude, as shown in Fig. 1b. Furthermore, the amplitude of the soliton can be changed discontinuously by changing the same coefficient. As shown in Fig. 1c and d, the soliton’s amplitudes, corresponding to the two sides of the phase flip, are quite different. These propagation scenarios show that both the width and amplitude of the soliton can be controlled by appropriately adjusting the HOD effects.

Fig. 3
figure 3

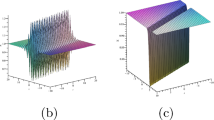
The interaction of two solitons based on the solution (14) with parameters \(d_{1}=d_{2}=0\), \(\beta (x) =\alpha (x) = \gamma (x) =1\), \(\delta (x)=\tanh (x)\). a \(w_{1}=0.6-0.34i\), \( w_{2}\) \(=0.72+0.72i\); b \(w_{1}=-0.88+0.016i\), \(w_{2}=-0.73+0.56i\); c The same as in (b), except for \(\beta (x) =\alpha (x) =\gamma (x) =-1\)

Full size image
Fig. 4
figure 4

Contour plots displayed in panels a, b, and c correspond to the three-dimensional plots in Fig. 3a, b, and c, respectively

Full size image
Fig. 5
figure 5

The interaction of two solitons based on solution (14) with parameters \(\delta (x)=\tanh (x)\), \(d_{1}=d_{2}=0\). a \(\beta (x) =-0.56\), \(\alpha (x) =0.56\), \(\gamma (x) =0.31\), \( w_{1}=\) \(-0.75-0.8i\), \(w_{2}=-0.84-0.063i\); b The same as in (a), but with \(\beta (x) =-1.75\), \(\alpha (x) =0.22\), \(\gamma (x) =-0.095\); c The same as in (a), but \(\beta (x) =0.66\), \(\alpha (x) =1\), \( \gamma (x) =1\), \(w_{1}=0.7+0.094i\), \(w_{2}=0.91+0.031i\)

Full size image
Fig. 6
figure 6

Contour plots displayed in panels a, b, and c correspond to the three-dimensional plots in Fig. 5a, b, and c, respectively

Full size image

When we choose function \(\tan (x)\) as the parameter of the fifth-order dispersion, and select the function \(\sin (Cx)\) as the variable GVD, TOD, and FOD coefficients, the soliton performs periodic oscillations along x, as displayed in Fig. 2a, with its width changing periodically in the course of the propagation. C is a real constant. In this case, we only vary the TOD coefficient, to observe its effect on the soliton transmission. As Fig. 2b–d shows, the periodic oscillations of the soliton can be controlled by adjusting coefficient C in \(\sin (Cx)\) for the inhomogeneous TOD. It is also found that the variation of TOD affects the overall shape of the oscillations. Naturally, the oscillation intensity increases with the decrease of C.

In the above discussion of the reshaping of the fundamental soliton, we assumed that all HOD coefficients are functions of variable x. In contrast to that, in the analysis of two-soliton interactions, presented below, we assume that the GVD, TOD, and FOD coefficients are constant, while the fifth-order dispersion coefficient \(\delta \) remains a function of x. As shown in Fig. 3a, widths of the two solitons change after the interaction, namely, one soliton expands while the other one gets compressed. Furthermore, amplitudes of the interacting solitons remain unchanged while their propagation directions in the \(\left( x,t\right) \) plane change after the collision. By appropriately modifying the values of complex constants \( w_{1}\) and \(w_{2}\), a noteworthy interaction scenario occurs, in which both solitons are compressed simultaneously after the collision, as shown in Fig. 3b. Besides that, we show that phases of the two solitons can be reversed when the values of \(\beta (x)\), \(\alpha (x)\), and \(\gamma (x)\) are replaced by \(-\beta (x)\), \(-\alpha (x)\), and \(-\gamma (x)\), as shown in Fig. 3c. These three generic scenarios of the two-soliton interaction are additionally illustrated by the corresponding contour plots in Fig. 4.

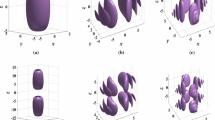
Figure 5 shows another interesting interaction effect, namely, that a complex of two interacting solitons can transform from a bound state to a state in which the solitons are well separated. The three panels in Fig. 5 show that the two solitons attract and repel each other periodically, generating a kind of a bound state. However, after propagating steadily for a certain distance, the solitons suddenly separate from each other and then propagate in different directions. These results may be used to design optical switches and to realize an optical path control. The interaction between two bound solitons and their subsequent separation are observed more clearly in Fig. 6, which shows contour plots corresponding to the interaction scenarios displayed in Fig. 5.

Fig. 7
figure 7

The interaction of two solitons based on the solution (14) with parameters \(\delta (x)=\tanh (x)\), \(w_{1}=0.75+0.31i\) , \(w_{2}=-0.56-0.61i\). a \(\beta (x) =0.92\), \(\alpha (x) =0.99\), \( \gamma (x) =1\); b \(\beta (x) =-1.44\), \(\alpha (x) =-1.51\), \( \gamma (x)=-1.2\)

Full size image
Fig. 8
figure 8

Contour plots displayed in panels a and b correspond to the three-dimensional plots in Fig. 8a and b, respectively

Full size image
Fig. 9
figure 9

The evolution of the soliton train based on solution (14) with parameters: \(\delta (x)=\tanh (x)\), \(d_{1}=d_{2}=0\), \( w_{1}=0.75+0.54i\), \(w_{2}=0.73-0.855i\). a \(\beta (x) =1.8\), \(\alpha (x) =1.8\), \(\gamma (x)=1.79\); b \(\beta (x) =\alpha (x) = \gamma (x) =1\)

Full size image
Fig. 10
figure 10

Contour plots displayed in panels a and b correspond to the three-dimensional plots in Fig. 9a and b, respectively

Full size image

Apart from the bound-state soliton complex, another type of soliton–soliton interactions is displayed in Fig. 7. In Fig. 7a, fusion of two colliding solitons into a train of identical spatiotemporal pulses with equal separations between them is shown. The amplitudes of the emerging pulses are, obviously, much larger than the input amplitudes of the two colliding solitons. This effect may be used in specific applications in nonlinear fiber optics and high-power fiber lasers. Moreover, phases of two pulses can be flipped by replacing \(\beta (x)\), \(\alpha (x)\), and \(\gamma (x)\) by \( -\beta (x)\), \(-\alpha (x)\), and \(-\gamma (x)\), as shown in Fig. 7b. The formation of the spatiotemporal pulse train as the result of the collision can be observed more clearly in Fig. 8, which shows the corresponding contour plots.

Finally, Fig. 9 shows another noteworthy effect, in which the spatiotemporal pulse train compresses itself after propagating a certain distance. As shown in Fig. 9a, the spatiotemporal train propagates stably after performing the self-compression, maintaining identical shapes of the individual pulses and equal distances between them. However, the propagation direction of the compressed train changes in the \(\left( x,t\right) \) plane. We also note that, changing only the coefficients of dispersion terms in the underlying model one can adjust both the width of the spatiotemporal train and its propagation direction, keeping the self-compression property, as shown in Fig. 9b. In Fig. 10, contour plots additionally illustrate the dynamical scenarios from Fig. 9.

4 Conclusions

In this work, analytical one- and two-soliton solutions for the fifth-order nonlinear Schrödinger equation (1) with variable coefficients have been obtained by means of the Hirota bilinear method. Several generic scenarios of one-soliton shaping and two-soliton interaction and reshaping have been put forward based on exact one- and two-soliton solutions (11) and (14). According to the one-soliton solution (11), parabola-like and periodic oscillation patterns of the evolution of fundamental solitons have been presented in Figs. 1 and 2. The results show that both the amplitude and period of the soliton’s oscillations can be controlled by changing the variable TOD coefficient \(\alpha (x)\), which may help to apply dispersion management to solitons propagating in fibers with inhomogeneous higher-order dispersion. Using the two-soliton solution (14), we have found a scenario where one of the two interacting solitons widens, while the width of the other soliton is compressed, see Fig. 3a. For other sets of the model’s parameters we have found that, after the interaction, the two solitons are compressed, see Fig. 3b. The analysis has also revealed an interesting effect, in which the complex composed of two interacting solitons can transform from a bound state into a pair of separating solitons, see Fig. 5. Further, in Fig. 7 we display the fusion of two colliding solitons into a train of identical spatiotemporal pulses with equal separations between them. In the latter case, the amplitude of the emerging train is much larger than amplitudes of the two input solitons. Also, a simple method to realize the soliton phase reversal has been proposed, see Figs. 3c, 4c, 7b, and 8b. Lastly, the exact solution demonstrates that the spatiotemporal pulse train can strongly compress itself, as shown in Figs. 9 and 10. The results reported in this work may be useful to the design of optical switches and path controllers, and for performing pulse compression in fiber laser systems.