Lax pair, rogue-wave and soliton solutions for a variable-coefficient generalized nonlinear Schrödinger equation in an optical fiber, fluid or plasma

Abstract

In this paper, a variable-coefficient generalized nonlinear Schrödinger equation, which can be used to describe the nonlinear phenomena in the optical fiber, fluid or plasma, is investigated. Lax pair, higher-order rogue-wave and multi-soliton solutions, Darboux transformation and generalized Darboux transformation are obtained. Wave propagation and interaction are analyzed: (1) The Hirota and Lakshmanan–Porsezian–Daniel coefficients affect the propagation velocity and path of each one soliton; three types of soliton interaction have been attained: the bound state, one bell-shape soliton’s catching up with the other and two bell-shape soliton head-on interaction. Multi-soliton interaction is elastic. (2) The Hirota and Lakshmanan–Porsezian–Daniel coefficients affect the propagation direction of the first-step rogue waves and interaction range of the higher-order rogue waves.

1 Introduction

Some of the nonlinear evolution equations with soliton or rogue-wave solutions have been studied (Agrawal 1995; Hesegawa and Kodama 1995), such as the nonlinear Schrödinger-type (Chabchoub et al. 2011; Solli et al. 2007; Hirota 1973; Sun et al. 2015a, b; Xie et al. 2015a) and Lakshmanan–Porsezian–Daniel (LPD) (Lakshmanan et al. 1988; Porsezian et al. 1992; Porsezian 1997; Jia et al. 2015) equations. Those equations can be used to describe the nonlinear phenomena in nonlinear optics, fluid mechanics, plasma physics, biophysics and star formation (Ablowitz and Clarkson 1991; Jia et al. 2015; Agrawal 1995; Hirota 1973; Lakshmanan et al. 1988; Porsezian et al. 1992; Porsezian 1997; Hesegawa and Kodama 1995; Chabchoub et al. 2011; Solli et al. 2007). A rogue wave is thought of as an isolated “huge” wave with the amplitude “much larger” than the average wave crests around it in optics (Solli et al. 2007), ocean (Akhmediev et al. 1987), and also seen in the Bose-Einstein condensates and superfluids (Akhmediev et al. 2009; Ankiewicz et al. 2010). A soliton is a solitary wave which preserves its velocity and shape after the interaction (Ablowitz and Clarkson 1991), i.e., the soliton can be considered as a quasi-particle (Benes et al. 2006; Christov and Christov 2008).

However, in the practical situations, the nonlinear phenomena are so complicated that the higher-order terms, such as the third-order dispersion, self-steepening and other nonlinear effects, need to be taken into account (Porsezian and Nakkeeran 1995; Ankiewicz et al. 2009). In this paper, we will work on a variable-coefficient generalized nonlinear Schrödinger equation:

$$\begin{aligned}&-i \alpha (x) \psi _{ttt}-6 i \alpha (x) \psi _{t} \psi \psi ^*+4 \gamma (x) \psi _{t} \psi \psi ^*_{t}+8 \gamma (x) \psi _{tt} \psi \psi ^*+6 \gamma (x) \psi _{t}^2\psi ^* \\ &\quad +6 \gamma (x) \psi ^3(\psi ^*)^2+2 \gamma (x) \psi ^2\psi ^*_{tt}+\gamma (x) \psi _{tttt}+\psi ^2\psi ^*+\frac{1}{2} \psi _{tt}+i \psi _x=0, \end{aligned}$$

(1)

where $\psi$ is a function of the scaled temporal coordinate t and spatial coordinate x, the Hirota coefficient, $\alpha (x)$, and LPD coefficient, $\gamma (x)$, are both the real functions of x. In the nonlinear fibre, fluid or plasma, special cases of Eq. (1) are seen as follows:

• (a) When $\alpha (x)=\gamma (x)=0,$ Eq. (1) degenerates into the nonlinear Schrödinger equation, which describes the solitons and rogue waves in the nonlinear fiber (Solli et al. 2007), water tank (Chabchoub et al. 2011) or Bose-Einstein Condensate (Wen et al. 2011).

• (b) When $\alpha (x)=0$ and $\gamma (x)=\hbox{constant}$, Eq. (1) degenerates into the LPD equation, which can be used to describe the nonlinear spin excitations in one-dimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole-dipole interaction (Palacios and Fernández-Díaz 2000; Daniel et al. 1999).

• (c) When $\gamma (x)=0$ and $\alpha (x)=\hbox{constant}$, Eq. (1) degenerates into the Hirota equation (Hirota 1973), which can be considered as a combination of the nonlinear Schrödinger equation and modified Korteweg-de Vries equation (Hirota 1973). Modified Korteweg-de Vries equation can describe the interfacial waves in the two-layer liquid with gradually varying depth, Alfvén waves in the interaction-less plasma and acoustic waves in the an-harmonic lattice (Ames 1967).

• (d) When $\gamma (x)=\hbox{constant}$ and $\alpha (x)=\hbox{constant}$, Eq. (1) degenerates into an extended nonlinear Schrödinger equation with higher-order odd and even terms with independent coefficients, soliton solutions of which have been attained by virtue of the Darboux transformation (DT) (Ankiewicz and Akhmediev 2014).

To our knowledge, Lax pair, soliton and rogue-wave solutions, DT and generalized DT of Eq. (1) have not been obtained. With the aid of symbolic computation (Zhen et al. 2015a, b; Xie et al. 2015b), in Sect. 2, Lax pair, multi-soliton solutions and DT for Eq. (1) will be attained. In Sect. 3, higher-order rogue-wave solutions and generalized DT of Eq. (1) will be obtained. In Sect. 4, wave propagation and interaction will be discussed. Section 5 will be the conclusions.

2 Lax pair, DT and soliton solutions of Eq. (1)

2.1 Lax pair of Eq. (1)

With the Ablowitz-Kaup-Newell-Segur procedure (Ablowitz et al. 1973), Lax pair of Eq. (1) have the forms

$$\begin{aligned} \overrightarrow{R}_t=L\overrightarrow{R},\qquad \overrightarrow{R}_x=B\overrightarrow{R}, \end{aligned}$$

(2)

where $\overrightarrow{R}=(r_1,~r_2)^T$ is a vector function while $r_1$ and $r_2$ are both the functions of x and t, T denotes the transpose of a vector/matrix, and matrices L and B have the forms of

$$\begin{aligned} L&=\left[ \begin{array}{cc} i \lambda &{}\quad i \psi ^* \\ i \psi &{}\quad -i \lambda \\ \end{array} \right] ,\qquad B=\begin{bmatrix} B_{11}&\quad B_{12}\\ B_{21}&\quad -B_{11} \end{bmatrix},\\ B_{11}&=i \lambda ^2-4 i \lambda ^3 \alpha (x)-8 i \lambda ^4 \gamma (x)-\frac{1}{2} i \psi \psi ^*+2 i \lambda \alpha (x) \psi \psi ^*+4 i \lambda ^2 \gamma (x) \psi \psi ^*\\ &\,-3 i \gamma (x) \psi ^2 (\psi ^*)^2-\alpha (x) \psi ^*\psi _{t}-2 \lambda \gamma (x) \psi ^*\psi _{t}+\alpha (x) \psi \psi ^*_{t}+2 \lambda \gamma (x) \psi \psi ^*_{t}\\ &\,+i \gamma (x) \psi _{t}\psi ^*_{t}-i \gamma (x) \psi ^*\psi _{tt}-i \gamma (x) \psi \psi ^*_{tt}, \\ B_{12}&=i \lambda \psi ^*-4 i \lambda ^2 \alpha (x) \psi ^*-8 i \lambda ^3 \gamma (x) \psi ^*+2 i \alpha (x) \psi (\psi ^*)^2+4 i \lambda \gamma (x) \psi (\psi ^*)^2\\ &\,+\frac{1}{2} \psi ^*_{t}-2 \lambda \alpha (x) \psi ^*_{t} -4 \lambda ^2 \gamma (x) \psi ^*_{t}+6 \gamma (x) \psi \psi ^* \psi ^*_{t} +i \alpha (x) \psi ^*_{tt}+2 i \lambda \gamma (x) \psi ^*_{tt}\\ &\,+\gamma (x) \psi ^*_{ttt}, \\ B_{21}&=i \lambda \psi -4 i \lambda ^2 \alpha (x) \psi -8 i \lambda ^3 \gamma (x) \psi +2 i \alpha (x) \psi ^2 \psi ^*+4 i \lambda \gamma (x) \psi ^2 \psi ^*-\frac{1}{2} \psi _t\\ &\,+2 \lambda \alpha (x) \psi _t+4 \lambda ^2 \gamma (x) \psi _t-6 \gamma (x) \psi \psi ^* \psi _t+i \alpha (x) \psi _{\mathrm {tt}}+2 i \lambda \gamma (x) \psi _{\mathrm {tt}}-\gamma (x) \psi _{\mathrm {ttt}}, \end{aligned}$$

where complex parameter $\lambda$ is independent of x and t. The compatibility condition $B_t-L_x+BL-LB=0$ leads to Eq. (1).

2.2 DT of Eq. (1)

We assume that $\psi ^{[0]}$ is a solution of Eq. (1). By virtue of Lax Pair (2), DT matrix $M^{[1]}$ has the form of

$$\begin{aligned} M^{[1]}&=\begin{bmatrix} \lambda&\quad 0\\ 0&\quad \lambda \end{bmatrix}- \begin{bmatrix} \phi _{11}(\lambda _1)&\quad \phi _{12}^*(\lambda _1)\\ \phi _{12}(\lambda _1)&\quad -\phi _{11}^*(\lambda _1) \end{bmatrix} \begin{bmatrix} \lambda _1&\quad 0\\ 0&\quad \lambda _1^* \end{bmatrix} \begin{bmatrix} \phi _{11}(\lambda _1)&\quad \phi _{12}^*(\lambda _1)\\ \phi _{12}(\lambda _1)&\quad -\phi _{11}^*(\lambda _1) \end{bmatrix}^{-1}, \end{aligned}$$

(3)

where $[\phi _{11}(\lambda _1),\,\phi _{12}(\lambda _1)]^T$ is a solution of Lax Pair (2) at $\lambda =\lambda _1$ and $\psi =\psi ^{[0]}$, while $\phi _{11}$ and $\phi _{12}$ are both the functions of x and t, $\lambda _1$ is a complex parameter independent of x and t, while $(H^{[1]})^{-1}$ is the inverse matrix of $H^{[1]}$ and the sign $^{[k]}\ (k=1,2,3,\ldots ,N)$ with N as a positive integer means that the matrix/function is engendered from the k-th DT. Therefore, the first-order solutions of Eq. (1) can be given as

$$\begin{aligned} \psi ^{[1]}=\psi ^{[0]}-\frac{2(\lambda _1-\lambda _1^*)\phi _{12}(\lambda _1) \phi ^*_{11}(\lambda _1)}{\phi _{11}(\lambda _1) \phi ^*_{11}(\lambda _1)+\phi _{12}(\lambda _1)\phi ^*_{12}(\lambda _1)}. \end{aligned}$$

(4)

Iterating the DT N times, we can give the Nth-iterated potential transformation

$$\begin{aligned} \psi ^{[N]}=\psi ^{[0]}-2\sum _{k=1}^N\frac{(\lambda _k-\lambda _k^*) \phi _{k2}(\lambda _k)\phi ^*_{k1}(\lambda _k)}{\phi _{k1}(\lambda _k) \phi ^*_{k1}(\lambda _k)+\phi _{k2}(\lambda _k)\phi ^*_{k2}(\lambda _k)}, \end{aligned}$$

(5)

with $\lambda _k'$s as the different complex parameters and

$$\begin{aligned} \phi _{m+1j}(\lambda _{m+1})= & {} (\lambda _{m+1}-\lambda _m^*)\phi _{mj}(\lambda _{m+1}) -\frac{A_m(\lambda _m-\lambda _m^*)\phi _{mj}(\lambda _m)}{\phi _{m1}(\lambda _m) \phi ^*_{m1}(\lambda _m)+\phi _{m2}(\lambda _m)\phi ^*_{m2}(\lambda _m)}, \\ A_m= & {} \phi _{m1}(\lambda _{m+1})\phi _{m1}^*(\lambda _m)+\phi _{m2}(\lambda _{m+1})\phi _{m2}^*(\lambda _m), \\ j= & {} 1,2,m=1,2,\cdots , N-1, \end{aligned}$$

(6)

where $[\phi _{k1}(\lambda _k),~\phi _{k2}(\lambda _k)]^T$ is a solution of Lax Pair (2) at $\lambda =\lambda _k$ and $\psi =\psi ^{[k-1]}$ while $\phi _{k1}(\lambda _k)$ and $\phi _{k2}(\lambda _k)$ are both the functions of x and t.

2.3 Soliton solutions of Eq. (1)

By virtue of Expression (5), we can obtain the soliton solutions for Eq. (1). For the one-soliton solutions $\psi ^{[1]}$, we take $\psi ^{[0]}=0$ as the seed solution of Eq. (1), then, the solution $[\phi _{11}(\lambda _1),~\phi _{12}(\lambda _1)]^T$ of Lax Pair (2) at $\lambda =\lambda _1$ and $\psi =\psi ^{[0]}$ is

$$\begin{aligned} \phi _{11}(\lambda _1)&=e^{i t \lambda _1 -i \lambda _1 ^2 \int _1^x \left[ 4 \lambda _1 \alpha (x)+8 \lambda _1 ^2 \gamma (x)-1\right] \, dx},\end{aligned}$$

(7a)

$$\begin{aligned} \phi _{12}(\lambda _1)&=e^{-i t \lambda _1 +i \lambda _1 ^2\int _1^x \left[ 4 \lambda _1 \alpha (x)+8 \lambda _1 ^2 \gamma (x)-1\right] \, dx}. \end{aligned}$$

(7b)

Substituting Expressions (7) into Expression (4), we can obtain the one-solition solutions for Eq. (1).

We take $N=2$ in Expression (5) and substitute Expressions (7) into Expressions (5) and (6), we can attain the two-solition solutions for Eq. (1). If we continue such process, the N-soliton solutions of Eq. (1) can be obtained.

3 Rogue-wave solutions and generalized DT of Eq. (1)

In this section, we will get the rogue-wave solutions for Eq. (1). To get the non-zero seed solutions of Eq. (1), we need to take $\alpha (x)$ and $\gamma (x)$ as the constants by virtue of the method of undetermined coefficients (Akhmediev et al. 2009; Ankiewicz et al. 2010). Thus, we will rewrite $\alpha (x)$ and $\gamma (x)$ as $\alpha$ and $\gamma$ correspondingly in this part.

3.1 Generalized DT of Eq. (1)

By virtue of DT (3), the generalized DT for Eq. (1) will be obtained. Guo et al. has assumed that ${\widetilde{\psi }}$ is a solution of Eq. (1) and

$$\begin{aligned} \overrightarrow{\Theta }(\zeta _1+\varepsilon ) \end{aligned}$$

(8)

is a solution for Lax Pair (2) at $\psi ={\widetilde{\psi }}$ and $\lambda =\zeta _1+\varepsilon$, where $\zeta _1$ and $\varepsilon$ are both the parameters independent of x and t. Expanding $\overrightarrow{\Theta }$ at $\zeta _1,$ we have

$$\begin{aligned} \overrightarrow{\Theta }(\zeta _1+\varepsilon )=\overrightarrow{\Xi }_0+\overrightarrow{\Xi }_1\varepsilon +\overrightarrow{\Xi }_2\varepsilon ^2+ \cdots , \end{aligned}$$

(9)

where $\overrightarrow{\Xi }_l=\frac{1}{l!}\frac{\partial ^l}{\partial \zeta ^l}\overrightarrow{\Theta }(\zeta )| _{\zeta =\zeta _1}\,(l=0,1,2,\cdots ).$ It can be shown that $\overrightarrow{\Xi }_0$ is a solution of Lax Pair (2) at $\psi ={\widetilde{\psi }}$ and $\lambda =\zeta _1$.

By virtue of DT (3), the generalized DT matrix ${{\mathcal {M}}}^{[1]}$ of the first-step generalized DT for Eq. (1) is

$$\begin{aligned} {{\mathcal {M}}}^{[1]}= \begin{bmatrix} \lambda&\quad 0\\ 0&\quad \lambda \end{bmatrix} -\begin{bmatrix} \varphi _{11}&\quad (\varphi _{12})^*\\ \varphi _{12}&\quad -(\varphi _{11})^* \end{bmatrix} \begin{bmatrix} \zeta _1&\quad 0\\ 0&\quad \zeta ^*_1 \end{bmatrix} \begin{bmatrix} \varphi _{11}&\quad (\varphi _{12})^*\\ \varphi _{12}&\quad -(\varphi _{11})^* \end{bmatrix}^{-1} \end{aligned}$$

(10)

where $(\varphi _{11},\,\varphi _{12})^T=\overrightarrow{\Xi }_0$, while $\varphi _{11}$ and $\varphi _{12}$ are both the functions of x and t. Thus, the first-order solutions ${\widetilde{\psi }}^{[1]}$ for Eq. (1) are

$$\begin{aligned} {\widetilde{\psi }}^{[1]}={\widetilde{\psi }}-\frac{2(\zeta _1-\zeta _1^*) \varphi _{12}(\varphi _{11})^*}{\varphi _{11} (\varphi _{11})^*+\varphi _{12}(\varphi _{12})^*}. \end{aligned}$$

(11)

As the second-step generalized DT, using DT (10) for Expression (9) and taking the limit process, we have

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{\big (\mathcal{M}^{[1]}|_{\lambda =\zeta _1+\varepsilon }\big )\overrightarrow{\Theta }}{\varepsilon }= &\, \lim _{\varepsilon \rightarrow 0}\frac{\big (\varepsilon +{{\mathcal {M}}}^{[1]}|_{\lambda =\zeta _1}\big )\overrightarrow{\Theta }}{\varepsilon } \\ = &\, \overrightarrow{\Xi }_0+\mathcal{M}^{[1]}|_{\lambda =\zeta _1}\overrightarrow{\Xi }_1=(\varphi _{21},\,\varphi _{22})^T, \end{aligned}$$

(12)

and find a solution $(\varphi _{21},\,\varphi _{22})^T$ for Lax Pair (2) at $\psi ={\widetilde{\psi }}^{[1]}$ and $\lambda =\zeta _1$, while $\varphi _{21}$ and $\varphi _{22}$ are both the functions of x and t. Thus, we can obtain the second-step generalized DT matrix ${{\mathcal {M}}}^{[2]}$ as

$$\begin{aligned} {{\mathcal {M}}}^{[2]}= \begin{bmatrix} \lambda&0\\ 0&\lambda \end{bmatrix} -\begin{bmatrix} \varphi _{21}&\quad (\varphi _{22})^*\\ \varphi _{22}&\quad -(\varphi _{21})^* \end{bmatrix} \begin{bmatrix} \zeta _1&\quad 0\\ 0&\quad \zeta ^*_1 \end{bmatrix} \begin{bmatrix} \varphi _{21}&\quad (\varphi _{22})^*\\ \varphi _{22}&\quad -(\varphi _{21})^* \end{bmatrix}^{-1}, \end{aligned}$$

(13)

which allows us to find the second-order solutions ${\widetilde{\psi }}^{[2]}$ of Eq. (1) as

$$\begin{aligned}&{\widetilde{\psi }}^{[2]}={\widetilde{\psi }}^{[1]}-\frac{2(\zeta _1-\zeta _1^*) \varphi _{22}(\varphi _{21})^*}{\varphi _{21} (\varphi _{21})^*+\varphi _{22}(\varphi _{22})^*}. \end{aligned}$$

(14)

Similarly, for the third-step generalized DT, we have

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0}\frac{\big ({{\mathcal {M}}}^{[2]}|_{\lambda =\zeta _1+\varepsilon }\big )\big ({{\mathcal {M}}}^{[1]}|_{\lambda =\zeta _1+\varepsilon }\big )\overrightarrow{\Theta }}{\varepsilon ^2} \\ &\quad =\lim _{\varepsilon \rightarrow 0}\frac{\big (\varepsilon +{{\mathcal {M}}}^{[2]}|_{\lambda =\zeta _1}\big )\big (\varepsilon +{{\mathcal {M}}}^{[1]}|_{\lambda =\zeta _1}\big )\overrightarrow{\Theta }}{\varepsilon ^2} \\ &\quad =\overrightarrow{\Xi }_0+({{\mathcal {M}}}^{[2]}|_{\lambda =\zeta _1}+{{\mathcal {M}}}^{[1]}|_{\lambda =\zeta _1})\overrightarrow{\Xi }_1+{{\mathcal {M}}}^{[2]}|_{\lambda =\zeta _1}{{\mathcal {M}}}^{[1]}|_{\lambda =\zeta _1}\overrightarrow{\Xi }_2 \\ &\quad =(\varphi _{31},\,\varphi _{32})^T. \end{aligned}$$

(15)

Thus, we find a solution $(\varphi _{31},\,\varphi _{32})^T$ for Lax Pair (2) at $\psi ={\widetilde{\psi }}^{[2]}$ and $\lambda =\zeta _1,$ while $\varphi _{31}$ and $\varphi _{32}$ are both the functions of x and t. That allows us to find the third-order solutions ${\widetilde{\psi }}^{[3]}$ of Eq. (1) as

$$\begin{aligned} {\widetilde{\psi }}^{[3]}={\widetilde{\psi }}^{[2]}-\frac{2(\zeta _1-\zeta _1^*) \varphi _{32}(\varphi _{31})^*}{\varphi _{31} (\varphi _{31})^*+\varphi _{32}(\varphi _{32})^*}. \end{aligned}$$

(16)

If we continue such a process, the fourth- and fifth-step generalized DTs for Eq. (1) might be obtained.

3.2 Rogue-wave solutions of Eq. (1)

In order to obtain the rogue-wave solutions of Eq. (1), we need to take the plane waves $\psi =\frac{1}{\sqrt{\gamma }}e^{\frac{7ix}{\gamma }}$ as the seed solutions for Eq. (1) via the method of undetermined coefficients. Then, the solution $\overrightarrow{\Theta }(x,t;h)$ for Lax Pair (2) at $\psi =\frac{1}{\sqrt{\gamma }}e^{\frac{7ix}{\gamma }}$ and $\lambda =\frac{ih}{\sqrt{\gamma }}$ is

$$\begin{aligned} \overrightarrow{\Theta }(x,t;h)=\begin{bmatrix}i \left (e^\eta \sqrt{\frac{h-\sqrt{h^2-1}}{h^2-1}}-e^{-\eta }\sqrt{\frac{h+\sqrt{h^2-1}}{h^2-1}}\right )e^{-\frac{7ix}{2\gamma }}\\ \left (e^\eta \sqrt{\frac{h+\sqrt{h^2-1}}{h^2-1}}-e^{-\eta }\sqrt{\frac{h-\sqrt{h^2-1}}{h^2-1}}\right )e^{\frac{7ix}{2\gamma }} \end{bmatrix}, \end{aligned}$$

(17)

where

$$\begin{aligned} \eta =\frac{\sqrt{h^2-1} \left[ \left( 2+4 h^2\right) \alpha +i h \left( 5+8 h^2\right) \sqrt{\gamma }\right] }{\gamma ^{3/2}} \left[ x+\frac{ t\gamma }{\left( 2+4 h^2\right) \alpha +i h \left( 5+8 h^2\right) \sqrt{\gamma }}\right] , \end{aligned}$$

and h is a parameter independent of x and t. Expanding the vector function $\overrightarrow{\Theta }(x,t;h)$ at $h=1$, we take $h=1+\tau ^2$, where $\tau$ is a parameter independent of x and t, we have

$$\begin{aligned} \overrightarrow{\Theta }(x,t;\tau )=\overrightarrow{\Xi }_0+\overrightarrow{\Xi }_1\tau ^2+\overrightarrow{\Xi }_2\tau ^4\cdots , \end{aligned}$$

(18)

where

$$\begin{aligned}&\overrightarrow{\Xi }_0= \begin{bmatrix} i e^{-\frac{7 i x}{2 \gamma }} \left( 2\frac{ 6 x \alpha +13 i x \sqrt{\gamma }+t \gamma }{\gamma ^{3/2}}-1\right) \\ e^{\frac{7 i x}{2 \gamma }} \left( 2\frac{ 6 x \alpha +13 i x \sqrt{\gamma }+t \gamma }{\gamma ^{3/2}}+1\right) \end{bmatrix}, \qquad \overrightarrow{\Xi }_1= \begin{bmatrix} \widehat{{\widehat{\theta }}}_1{[1]} \\ {\widehat{\theta }}_1{[1]} \end{bmatrix}, \end{aligned}$$

(19)

with

$$\begin{aligned} \widehat{{\widehat{\theta }}}_1{[1]}&=\frac{1}{12 \gamma ^{9/2}}i e^{-\frac{7 i x}{2 \gamma }} \left \{8 x^3 \big (6 \alpha +13 i \sqrt{\gamma } \big )^3+12 x^2 \big (2 t-\sqrt{\gamma }\big ) \big (6 \alpha +13 i \sqrt{\gamma }\big )^2 \gamma \right. \\ &\quad +\,6 x \gamma ^2 \big [4 t^2 \big (6 \alpha +13 i \sqrt{\gamma }\big )-4 t \big (6 \alpha \sqrt{\gamma } +13 i \gamma \big )+38 \alpha \gamma +129 i \gamma ^{3/2}\Big ]\\ &\quad \left.+\,\gamma ^3 \big (8 t^3-12 t^2 \sqrt{\gamma }+6 t \gamma +3 \gamma ^{3/2}\big )\right \},\\ {\widehat{\theta }}_1{[1]}&=\frac{1}{12 \gamma ^{9/2}}e^{\frac{7 i x}{2 \gamma }} \Big \{8 x^3 \big (6 \alpha +13 i \sqrt{\gamma }\big )^3+12 x^2 \big (6 \alpha +13 i \sqrt{\gamma }\big )^2 \big (2 t+\sqrt{\gamma }\big ) \gamma \\ &\quad +\,\gamma ^3 \big (8 t^3+12 t^2 \sqrt{\gamma }+6 t \gamma -3 \gamma ^{3/2}\big )+6 x \gamma ^2 \big [4 t^2 \big (6 \alpha +13 i \sqrt{\gamma }\big )+4 t \big (6 \alpha \sqrt{\gamma }\\ &\quad +\,13 i \gamma \big )+38 \alpha \gamma +129 i \gamma ^{3/2}\big ]\Big \}. \end{aligned}$$

By virtue of Expressions (11) and (19), we can obtain the first-order rogue-wave solutions as

$$\psi^{[1]}=-\frac{e^{\frac{7 i x}{\gamma }} \big[8 x (6t \alpha -13 i \gamma ) \gamma +\big(4 t^2-3 \gamma \big) \gamma^2+4 x^2 \big(36 \alpha ^2+169 \gamma \big)\big]}{\sqrt{\gamma }\big[48 t x \alpha \gamma +\gamma ^2 \big(4 t^2+\gamma \big)+4 x^2\big(36 \alpha ^2+169 \gamma \big)\big]}$$

(20)

By virtue of Expressions (14), (16), (18) and (19), we can obtain the second-order rogue-wave solutions $\psi ^{[2]}$ and third-order rogue-wave solutions $\psi ^{[3]}$, which are exhibited in the “Appendix”.

If we continue such a process, the fourth- and fifth-order rogue-wave solutions for Eq. (1) might be obtained.

Fig. 1

One-soliton solutions for $|\psi |$ via Expression (4) with the parameters $\lambda _1 =1+i$ and a of $\alpha (x)=\frac{\cos ^24x}{4},~\gamma (x)=\frac{\sin 4x}{4}$; b of $\alpha (x)=-\frac{\cos ^24x}{4},~\gamma (x)=\frac{\sin 4x}{4};$ c of $\alpha (x)=\frac{\cos ^24x}{2},~\gamma (x)=\frac{\sin 4x}{4}$

4 Wave interaction and propagation

4.1 Solitons’ propagation and interaction

Figure 1 displays that the coefficients affect the propagation of one soliton: Propagation velocity of the one soliton in Fig. 1b is larger than that in Fig. 1a; Propagation path of the one soliton in Fig. 1a, c are both S-shaped curves, while it is not in Fig. 1b. All of the above phenomena caused by the sign of $\alpha (x)$. Figure 1c shows an example of the stationary solition for Eq. (1). Besides, the solitons in Fig. 1 have the same shapes as the bright solitons described by the nonlinear Schrödinger equation, which has been used to characterized the propagation and interaction of the optical solitons (Hasegawa 2003).

Fig. 2

One-soliton solutions for $|\psi |$ via Expression (4) with the parameters $\lambda _1 =1+0.9i$ and a of $\alpha (x)=\frac{\cos ^22x}{4},~\gamma (x)=\frac{\sin 2x}{4}$; b of $\alpha (x)=\frac{\cos ^24x}{4},~\gamma (x)=\frac{\sin 2x}{4}$; c of $\alpha (x)=\frac{\cos ^24x}{4},~\gamma (x)=\frac{\sin 2x}{2}$

Figure 2 displays that the propagation path of each soliton has the double periodic properties: one period caused by $\alpha (x)$ is shown in Figure 2a, b while the other period caused by $\gamma (x)$ is exhibited in Fig. 2b, c.

Fig. 3

Two-soliton interaction for $|\psi |$ via Expression (5) with the parameters $N=2$ and a of $\alpha (x)=\frac{\cos ^2x}{2},~\gamma (x)=\frac{\sin x}{2},~\lambda _1=0.8+0.9i,~\lambda _2=0.2-0.5i$; b of $\alpha (x)=-\frac{\cos ^2x}{2},~\gamma (x)=\frac{\sin x}{2},~\lambda _1=0.5+0.4i,~\lambda _2=0.2-0.5i$; c of $\alpha (x)=\frac{3\cos ^2x}{2},~\gamma (x)=-\frac{\sin 2x}{3},~\lambda _1=0.5+0.4i,~\lambda _2=0.2-0.5i$

For the interactions, Fig. 3a represents the bound state of the two solitons, where the solitons do not diverge (Zakharov and Shabat 1972); Fig. 3b shows that the one bell-shape soliton catches up with the other one; Fig. 3c exhibits the two-bell-shape-soliton head-on interaction.

Fig. 4

Two-soliton interaction for $|\psi |$ via Expression (5) with the parameters $N=2,~\alpha (x)=\frac{1}{2},~\gamma (x)=\frac{1}{3}$ and a of $\lambda _1=0.8+0.5i,~\lambda _2 =-0.8+0.5i$; b of $\lambda _1=0.4+0.5i,~\lambda _2 =-0.4+0.5i$

Figure 4 displays that the real parts of $\lambda _1$ and $\lambda _2$ affect the interaction of the two solitions, i.e., Fig. 4a shows that the one soliton catchs up the other one and exceeds it, while Fig. 4b exhibits the two solitons’ head-on interaction, during which the amplitude and velocity of each soliton remain unvaried after the interaction. The two-soliton interaction is elastic, i.e., the amplitude and velocity of each soliton remain unvaried after the interaction.

Fig. 5

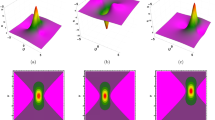
The first-order rogue-wave solutions for $|\psi |$ via Expression (20) with the parameters (a) of $\alpha =-3,~\gamma =5.3$; b of $\alpha =3,~\gamma =5.3$; c of $\alpha =3,~\gamma =1.9$

4.2 Rogue waves’ propagation and interaction

Figure 5a shows that the propagation direction of the first-order rogue waves is consistent with the positive x axis. Figure 5b exhibits that the propagation direction of the first-order rogue waves is consistent with the negative x axis. Wave crest in Fig. 5c is higher than that in Fig. 5a, b. Besides, shapes of the rogue waves in Fig. 5 are similar to those of the rogue waves detected in the high-speed pulse trains via the pulse-resolved filtering of long wavelengths (Solli et al. 2007). Figure 5 displays that the Hirota coefficient, $\alpha$, and LPD coefficient, $\gamma$, do not affect the shapes of the first-order rogue waves.

Fig. 6

The second-order rogue-wave interaction for $|\psi |$ as shown in the “Appendix” with the parameters a of $\alpha =2,~\gamma =5.3$; b of $\alpha =-2,~\gamma =5.3$; c of $\alpha =2,~\gamma =2.3$

Figure 6 shows the two-rogue-wave head-on interaction. Interaction range of the second-order rogue waves in Fig. 6c is smaller than those of the others.

Fig. 7

The third-order rogue-wave interaction for $|\psi |$ as shown in the “Appendix” with the parameters a of $\alpha =-2,~\gamma =4.3$; b of $\alpha =2,~\gamma =4.3$; c of $\alpha =2,~\gamma =2.3$

Figure 7 shows the third-order rogue-wave interaction, the behaviors of which are similar to those of the second-order rogue waves in Fig. 6.

5 Conclusions

In this paper, a variable-coefficient generalized nonlinear Schrödinger equation, Eq. (1), has been investigated. Our main results are exhibited as follows:

• (a) Lax Pair (2), The First-Order Rogue Waves (20), second- and third-order rogue waves shown in the “Appendix” and Multi-Soliton Solutions (5), DT (3), The First–Step Generalized DT (10) and The Second-Step Generalized DT (13) have been obtained.

• (b) Solitons’ propagation and interaction have been analyzed: Figure 1 has displayed that the propagation velocity of the one soliton in Fig. 1b is larger than that in Fig. 1a, because of the sign of the Hirota coefficient $\alpha (x).$ Figure 1c has shown an example of the stationary solition for Eq. (1). Shapes of the solitons in Fig. 1 are alike except for Fig. 1b due to the sign of $\alpha (x).$ Besides, the solitons in Fig. 1 have the same shapes as the bright solitons described by the nonlinear Schrödinger equation, which has been used to characterized the propagation and interaction of the optical solitons (Hasegawa 2003). Figure 2 has displayed that the propagation path of each one soliton has the double periodic properties: one period caused by $\alpha (x)$ is shown in Fig. 2a, b, while the other period caused by the LPD coefficient, $\gamma (x)$, is exhibited in Fig. 2b, c. For the soliton interaction, Fig. 3a has represented the bound state of the two solitons, where the solitons do not diverge; Fig. 3b has shown that the one bell-shape soliton catches up with the other one; Fig. 3c has exhibited the two-bell-shape-soliton head-on interaction. Fig. 4a has shown that the one soliton catches up the other one and exceeds it, while Fig. 4b has exhibited the two solitons’ head-on interaction, during which the amplitude and velocity of each soliton remain unvaried after the interaction.

• (c) Rogue waves’ propagation and interaction have been analyzed: Figure 5a has shown that the propagation direction of the first-order rogue waves is consistent with the positive x axis; Fig. 5b has exhibited that the propagation direction of the first-order rogue waves is consistent with the negative x axis; Wave crest in Fig. 5c is higher than those in Fig. 5a, b. Besides, shapes of the rogue waves in Figs. 5 are similar to those of the rogue waves detected in the high-speed pulse trains via the pulse-resolved filtering of long wavelengths (Solli et al. 2007). Figure 5 has displayed that the Hirota coefficient, $\alpha$, and LPD coefficient, $\gamma$, do not affect the shapes of the first-order rogue waves. For the rogue-wave interaction, Fig. 6 has presented the two-rogue-wave head-on interaction: Interaction range of the second-order rogue waves in Fig. 6c is smaller than those of the others. Figure 7 has shown the third-order rogue-wave interaction, the behaviors of which are similar to those of the second-order rogue waves in Fig. 6.

Appendix

The second-order rogue-wave solutions of Eq. (1):

$$\begin{aligned} \psi ^{[2]}= & {} \big (e^{\frac{7 i x}{\gamma }} \big (384 x^5 (6 t \alpha -13 i \gamma ) \gamma \big (36 \alpha ^2+169 \gamma \big )^2+64 x^6 \big (36 \alpha ^2+169 \gamma \big )^3+24 x \gamma ^5 \\ &\,\big (96 t^5 \alpha -208 i t^4 \gamma -208 t^3 \alpha \gamma +696 i t^2 \gamma ^2-234 t \alpha \gamma ^2+291 i \gamma ^3\big )+\gamma ^6 \\ &\,\big (64 t^6-144 t^4 \gamma -180 t^2 \gamma ^2+45 \gamma ^3\big )-12 x^2 \gamma ^4 \big (9984 i t^3 \alpha \gamma -6720 i t \alpha \gamma ^2 \\ &-\,16 t^4 \big (180 \alpha ^2+169 \gamma \big )+15 \gamma ^2 \big (100 \alpha ^2+401 \gamma \big )+24 t^2 \gamma \big (204 \alpha ^2+1261 \gamma \big )\big ) \\ &+\,192 x^3 \gamma ^3 \big ({-}52 i t^2 \gamma \big (108 \alpha ^2+169 \gamma \big )-6 t \alpha \gamma \big (252 \alpha ^2+3107 \gamma \big )-i \gamma ^2 \\ &\, \big (612 \alpha ^2+10309 \gamma \big )+24 t^3 \big (60 \alpha ^3+169 \alpha \gamma \big )\big )-48 x^4 \gamma ^2 \big (2496 i t \alpha \gamma \big (36 \alpha ^2+169 \gamma \big ) \\ &-\,4 t^2 \big (6480 \alpha ^4+36504 \alpha ^2 \gamma +28561 \gamma ^2\big )+\gamma \big (10800 \alpha ^4+175032 \alpha ^2 \gamma \\ &+\,173563 \gamma ^2\big )\big )\big )\big )/\big (\sqrt{\gamma } \big (2304 t x^5 \alpha \gamma \big (36 \alpha ^2+169 \gamma \big )^2+64 x^6 \big (36 \alpha ^2+169 \gamma \big )^3 \\ &+\,48 t x \alpha \gamma ^5 \big (48 t^4-8 t^2 \gamma +51 \gamma ^2\big )+\gamma ^6 \big (64 t^6+48 t^4 \gamma +108 t^2 \gamma ^2+9 \gamma ^3\big ) \\ &+\,1152 t x^3 \alpha \gamma ^3 \big (4 t^2 \big (60 \alpha ^2+169 \gamma \big )-\gamma \big (108 \alpha ^2+1079 \gamma \big )\big )\\&+12 x^2 \gamma ^4 \big ({-}360 t^2 \gamma \big (4 \alpha ^2+39 \gamma \big )+16 t^4 \big (180 \alpha ^2+169 \gamma \big )+3 \gamma ^2 \big (556 \alpha ^2+5379 \gamma \big )\big ) \\ &+\,48 x^4 \gamma ^2 \big (4 t^2 \big (6480 \alpha ^4+36504 \alpha ^2 \gamma +28561 \gamma ^2\big )+13 \gamma \big ({-}432 \alpha ^4-2232 \alpha ^2 \gamma \\ &+\,30589 \gamma ^2\big )\big )\big )\big ), \end{aligned}$$

The third-order rogue-wave solutions of Eq. (1):

$$\begin{aligned} \psi ^{[3]}= & {} -\big (e^{\frac{7 i x}{\gamma }} \big (49152 x^{11} (6 t \alpha -13 i \gamma ) \gamma \big (36 \alpha ^2+169 \gamma \big )^5+4096 x^{12} \big (36 \alpha ^2+169 \gamma \big )^6 \\ &+\,\gamma ^{12} \big (4096 t^{12}-18432 t^{10} \gamma -57600 t^8 \gamma ^2-172800 t^6 \gamma ^3+226800 t^4 \gamma ^4 \\ &+\,113400 t^2 \gamma ^5-14175 \gamma ^6\big )+48 x \gamma ^{11} \big (6144 t^{11} \alpha -13312 i t^{10} \gamma -33280 t^9 \alpha \gamma \\ &+\,111360 i t^8 \gamma ^2-57600 t^7 \alpha \gamma ^2+1920 i t^6 \gamma ^3-187200 t^5 \alpha \gamma ^3+165600 i t^4 \gamma ^4 \\ &+\,286200 t^3 \alpha \gamma ^4-936900 i t^2 \gamma ^5+141750 t \alpha \gamma ^5-137025 i \gamma ^6\big )+24 x^2 \gamma ^{10} \\ &\, \big ({-}1597440 i t^9 \alpha \gamma +10690560 i t^7 \alpha \gamma ^2-5760 t^6 \big (356 \alpha ^2-4545 \gamma \big ) \gamma ^2 \\ &+\,10828800 i t^5 \alpha \gamma ^3-7200 t^4 \big (1596 \alpha ^2-1993 \gamma \big ) \gamma ^3+34675200 i t^3 \alpha \gamma ^4 \\ &-\,14536800 i t \alpha \gamma ^5+675 \big (1116 \alpha ^2-8837 \gamma \big ) \gamma ^5+1024 t^{10} \big (396 \alpha ^2+169 \gamma \big ) \\ &-\,3840 t^8 \gamma \big (612 \alpha ^2+1261 \gamma \big )+2700 t^2 \gamma ^4 \big (3700 \alpha ^2+33247 \gamma \big )\big )+960 x^3 \\ &\,\gamma ^9 \big ({-}576 t^5 \alpha \big (684 \alpha ^2-30817 \gamma \big ) \gamma ^2+720 i t^2 \big (13620 \alpha ^2-6893 \gamma \big ) \gamma ^4 \\ &-\,3328 i t^8 \gamma \big (324 \alpha ^2+169 \gamma \big )-4608 t^7 \alpha \gamma \big (252 \alpha ^2+1261 \gamma \big )+15930 t \alpha \gamma ^4 \\ &\,\big (156 \alpha ^2+2231 \gamma \big )-1440 t^3 \alpha \gamma ^3 \big (2732 \alpha ^2+9741 \gamma \big )+1440 i t^4 \gamma ^3 \\ &\,\big (3108 \alpha ^2+10933 \gamma \big )+256 i t^6 \gamma ^2 \big (21924 \alpha ^2+31603 \gamma \big )+45 i \gamma ^5 \\ &\,\big (11676 \alpha ^2+748199 \gamma \big )+1536 t^9 \big (132 \alpha ^3+169 \alpha \gamma \big )\big )-6144 x^{10} \gamma ^2 \\ &\,\big (36 \alpha ^2+169 \gamma \big )^3 \big (6240 i t \alpha \gamma \big (36 \alpha ^2+169 \gamma \big )-4 t^2 \big (14256 \alpha ^4+73008 \alpha ^2 \gamma \\ &+\,28561 \gamma ^2\big )+\gamma \big (21168 \alpha ^4+382824 \alpha ^2 \gamma +305383 \gamma ^2\big )\big )+240 x^4 \gamma ^8 \\ &\,\big (15360 i t^3 \alpha \big (2700 \alpha ^2-1651 \gamma \big ) \gamma ^3-638976 i t^7 \alpha \gamma \big (108 \alpha ^2+169 \gamma \big ) \\ &+\,34560 i t \alpha \gamma ^4 \big (6940 \alpha ^2+36839 \gamma \big )+12288 i t^5 \alpha \gamma ^2 \big (21924 \alpha ^2+86021 \gamma \big ) \\ &+\,256 t^8 \big (42768 \alpha ^4+109512 \alpha ^2 \gamma +28561 \gamma ^2\big )-1792 t^6 \gamma \big (32400 \alpha ^4 \\ &+\,272376 \alpha ^2 \gamma +134017 \gamma ^2\big )+480 t^4 \gamma ^2 \big ({-}3888 \alpha ^4+1687176 \alpha ^2 \gamma \\ &+\,164437 \gamma ^2\big )-720 t^2 \gamma ^3 \big (141552 \alpha ^4+1348968 \alpha ^2 \gamma +1587599 \gamma ^2\big ) \\ &+\,45 \gamma ^4 \big (970320 \alpha ^4+19226664 \alpha ^2 \gamma +42713269 \gamma ^2\big )\big )-61440 x^9 \gamma ^3 \\ &\,\big (36 \alpha ^2+169 \gamma \big )^2 \big (52 i t^2 \gamma \big (11664 \alpha ^4+60840 \alpha ^2 \gamma +28561 \gamma ^2\big )+6 t \alpha \gamma \\ &\,\big (19440 \alpha ^4+362232 \alpha ^2 \gamma +656903 \gamma ^2\big )+i \gamma ^2 \big ({-}112752 \alpha ^4-961272 \alpha ^2 \gamma \\ &+\,5969249 \gamma ^2\big )-24 t^3 \big (4752 \alpha ^5+28392 \alpha ^3 \gamma +28561 \alpha \gamma ^2\big )\big )+1536 x^5 \gamma ^7 \\ &\,\big ({-}4160 i t^6 \gamma \big (27216 \alpha ^4+85176 \alpha ^2 \gamma +28561 \gamma ^2\big )+600 t^3 \alpha \gamma ^2 \big (14256 \alpha ^4 \\ &+\,1350216 \alpha ^2 \gamma +1161199 \gamma ^2\big )+720 i t^4 \gamma ^2 \big (438480 \alpha ^4+3089320 \alpha ^2 \gamma \\ &+\,1627977 \gamma ^2\big )-450 t \alpha \gamma ^3 \big (106704 \alpha ^4+1771944 \alpha ^2 \gamma +4105049 \gamma ^2\big ) \\ &-\,96 t^5 \alpha \gamma \big (789264 \alpha ^4+9533160 \alpha ^2 \gamma +13500565 \gamma ^2\big )-180 i t^2 \gamma ^3 \big (684720 \alpha ^4 \\ &+\,10797800 \alpha ^2 \gamma +42206567 \gamma ^2\big )+45 i \gamma ^4 \big (2545200 \alpha ^4+41227640 \alpha ^2 \gamma \\ &+\,154878191 \gamma ^2\big )+384 t^7 \big (42768 \alpha ^5+182520 \alpha ^3 \gamma +142805 \alpha \gamma ^2\big )\big )-256 x^6 \gamma ^6 \\ &\,\big (179712 i t^5 \alpha \gamma \big (27216 \alpha ^4+141960 \alpha ^2 \gamma +142805 \gamma ^2\big )-11520 i t^3 \alpha \gamma ^2 \\ &\,\big (789264 \alpha ^4+8213400 \alpha ^2 \gamma +11681449 \gamma ^2\big )+12960 i t \alpha \gamma ^3 \big (396144 \alpha ^4 \\ &+\,6663800 \alpha ^2 \gamma +29182751 \gamma ^2\big )-64 t^6 \big (10777536 \alpha ^6+68992560 \alpha ^4 \gamma \\ &+\,107960580 \alpha ^2 \gamma ^2+24134045 \gamma ^3\big )+720 t^4 \gamma \big (3592512 \alpha ^6+57198960 \alpha ^4 \gamma \\ & +\,155152140 \alpha ^2 \gamma ^2+55322657 \gamma ^3\big )-180 t^2 \gamma ^2 \big (2099520 \alpha ^6+108714960 \alpha ^4 \gamma \\ & +\,301817100 \alpha ^2 \gamma ^2+848461627 \gamma ^3\big )+135 \gamma ^3 \big (2376000 \alpha ^6+66895920 \alpha ^4 \gamma \\ & +\,480320620 \alpha ^2 \gamma ^2+2572161917 \gamma ^3\big )\big )+6144 x^7 \gamma ^5 \big ({-}15 i \gamma ^3 \big (26827200 \alpha ^6 \\ & +\,500020560 \alpha ^4 \gamma +2244182772 \alpha ^2 \gamma ^2-191958481 \gamma ^3\big )-1040 i t^4 \gamma \big (979776 \alpha ^6 \\ & +\,7665840 \alpha ^4 \gamma +15422940 \alpha ^2 \gamma ^2+4826809 \gamma ^3\big )+120 i t^2 \gamma ^2 \big (9471168 \alpha ^6 \\ & +\,128859120 \alpha ^4 \gamma +313599780 \alpha ^2 \gamma ^2+62748517 \gamma ^3\big )+270 t \alpha \gamma ^2 \big (171072 \alpha ^6 \\ & +\,7562160 \alpha ^4 \gamma +40799980 \alpha ^2 \gamma ^2+135293457 \gamma ^3\big )-80 t^3 \alpha \gamma \big (5178816 \alpha ^6 \\ & +\,102958128 \alpha ^4 \gamma +444892500 \alpha ^2 \gamma ^2+459289441 \gamma ^3\big )+96 t^5 \big (1539648 \alpha ^7 \\ & +\,13798512 \alpha ^5 \gamma +35986860 \alpha ^3 \gamma ^2+24134045 \alpha \gamma ^3\big )\big )+3840 x^8 \gamma ^4 \\ &\, \big ({-}39936 i t^3 \alpha \gamma \big (36 \alpha ^2+169 \gamma \big )^2 \big (108 \alpha ^2+169 \gamma \big )+16 t^4 \big (36 \alpha ^2+169 \gamma \big )^2 \big (42768 \alpha ^4 \\ & +\,109512 \alpha ^2 \gamma +28561 \gamma ^2\big )+768 i t \alpha \gamma ^2 \big (4059072 \alpha ^6+65926224 \alpha ^4 \gamma \\ & +\,206667396 \alpha ^2 \gamma ^2-62748517 \gamma ^3\big )+3 \gamma ^2 \big (27433728 \alpha ^8+1302448896 \alpha ^6 \gamma \\ &+\,9723935520 \alpha ^4 \gamma ^2+3364714288 \alpha ^2 \gamma ^3-245264645717 \gamma ^4\big )-72 t^2 \gamma \\ &\, \big (22954752 \alpha ^8+549110016 \alpha ^6 \gamma +3394628640 \alpha ^4 \gamma ^2+6730799504 \alpha ^2 \gamma ^3 \\ & +\,2447192163 \gamma ^4\big )\big )\big )\big )/\big (\sqrt{\gamma } \big (294912 t x^{11} \alpha \gamma \big (36 \alpha ^2+169 \gamma \big )^5+4096 x^{12} \\ &\, \big (36 \alpha ^2+169 \gamma \big )^6+96 t x \alpha \gamma ^{11} \big (3072 t^{10}-1280 t^8 \gamma +17280 t^6 \gamma ^2+73440 t^4 \gamma ^3 \\ & -\,15300 t^2 \gamma ^4+19575 \gamma ^5\big )+\gamma ^{12} \big (4096 t^{12}+6144 t^{10} \gamma +34560 t^8 \gamma ^2+149760 t^6 \gamma ^3 \\ & +\,54000 t^4 \gamma ^4+48600 t^2 \gamma ^5+2025 \gamma ^6\big )+24 x^2 \gamma ^{10} \big (21600 t^4 \big (316 \alpha ^2-561 \gamma \big ) \gamma ^3 \\ & -\,172800 t^8 \gamma \big (4 \alpha ^2+13 \gamma \big )+1024 t^{10} \big (396 \alpha ^2+169 \gamma \big )+1920 t^6 \gamma ^2 \big (948 \alpha ^2+5627 \gamma \big ) \\ & -\,2700 t^2 \gamma ^4 \big (972 \alpha ^2+10993 \gamma \big )+675 \gamma ^5 \big (1996 \alpha ^2+30607 \gamma \big )\big )+5760 t x^3 \alpha \gamma ^9 \\ &\, \big ({-}6912 t^6 \gamma \big (12 \alpha ^2+65 \gamma \big )+256 t^8 \big (132 \alpha ^2+169 \gamma \big )+240 t^2 \gamma ^3 \big (1732 \alpha ^2+3359 \gamma \big ) \\ & +\,288 t^4 \gamma ^2 \big (444 \alpha ^2+4067 \gamma \big )-45 \gamma ^4 \big (3148 \alpha ^2+59907 \gamma \big )\big )+368640 t x^9 \alpha \gamma ^3 \\ &\, \big (36 \alpha ^2+169 \gamma \big )^2 \big (4 t^2 \big (4752 \alpha ^4+28392 \alpha ^2 \gamma +28561 \gamma ^2\big )+\gamma \big ({-}14256 \alpha ^4 \\ & -\,118872 \alpha ^2 \gamma +371293 \gamma ^2\big )\big )+6144 x^{10} \gamma ^2 \big (36 \alpha ^2+169 \gamma \big )^3 \big (4 t^2 \big (14256 \alpha ^4 \\ & +\,73008 \alpha ^2 \gamma +28561 \gamma ^2\big )+\gamma \big ({-}15984 \alpha ^4-90792 \alpha ^2 \gamma +951301 \gamma ^2\big )\big ) \\ &+\,9216 t x^5 \alpha \gamma ^7 \big (20 t^2 \gamma ^2 \big (289008 \alpha ^4+3943080 \alpha ^2 \gamma -5354765 \gamma ^2\big )+64 t^6 \\ &\, \big (42768 \alpha ^4+182520 \alpha ^2 \gamma +142805 \gamma ^2\big )-16 t^4 \gamma \big (462672 \alpha ^4+4422600 \alpha ^2 \gamma \\ & +\,4932265 \gamma ^2\big )+45 \gamma ^3 \big (204048 \alpha ^4+3111560 \alpha ^2 \gamma +19527885 \gamma ^2\big )\big )+240 x^4 \gamma ^8 \\ &\, \big (1440 t^4 \gamma ^2 \big (22896 \alpha ^4+245400 \alpha ^2 \gamma -396305 \gamma ^2\big )-3328 t^6 \gamma \big (9072 \alpha ^4+68040 \alpha ^2 \gamma \\ & +\,28223 \gamma ^2\big )+256 t^8 \big (42768 \alpha ^4+109512 \alpha ^2 \gamma +28561 \gamma ^2\big )+720 t^2 \gamma ^3 \big (115920 \alpha ^4 \\ & +\,1071864 \alpha ^2 \gamma +5490797 \gamma ^2\big )+45 \gamma ^4 \big ({-}82608 \alpha ^4-316248 \alpha ^2 \gamma +35623589 \gamma ^2\big )\big ) \\ & +\,256 x^6 \gamma ^6 \big (45 \gamma ^3 \big (12094272 \alpha ^6+213073200 \alpha ^4 \gamma +1200264780 \alpha ^2 \gamma ^2-143365235 \gamma ^3\big ) \\ &+\,64 t^6 \big (10777536 \alpha ^6+68992560 \alpha ^4 \gamma +107960580 \alpha ^2 \gamma ^2+24134045 \gamma ^3\big )-240 t^4 \gamma \\ &\, \big (6858432 \alpha ^6+79606800 \alpha ^4 \gamma +156997620 \alpha ^2 \gamma ^2+30817319 \gamma ^3\big )+540 t^2 \gamma ^2 \\ &\,\big (1570752 \alpha ^6+31071600 \alpha ^4 \gamma +76350820 \alpha ^2 \gamma ^2+372920977 \gamma ^3\big )\big )+12288 t x^7 \alpha \gamma ^5 \\ &\,\big ({-}200 t^2 \gamma \big (699840 \alpha ^6+9552816 \alpha ^4 \gamma +27286740 \alpha ^2 \gamma ^2+10767497 \gamma ^3\big )+48 t^4 \\ &\,\big (1539648 \alpha ^6+13798512 \alpha ^4 \gamma +35986860 \alpha ^2 \gamma ^2+24134045 \gamma ^3\big )+15 \gamma ^2 \big (2659392 \alpha ^6 \\ &+\,79785648 \alpha ^4 \gamma +623457900 \alpha ^2 \gamma ^2+3109750241 \gamma ^3\big )\big )+3840 x^8 \gamma ^4 \\ &\,\big (16 t^4 \big (36 \alpha ^2+169 \gamma \big )^2 \big (42768 \alpha ^4+109512 \alpha ^2 \gamma +28561 \gamma ^2\big )-72 t^2 \gamma \big (16236288 \alpha ^8 \\ &+\,254741760 \alpha ^6 \gamma +926958240 \alpha ^4 \gamma ^2+243568208 \alpha ^2 \gamma ^3-815730721 \gamma ^4\big )+3 \gamma ^2 \\ &\,\big (40870656 \alpha ^8+1826489088 \alpha ^6 \gamma +23770674720 \alpha ^4 \gamma ^2+146083802800 \alpha ^2 \gamma ^3 \\ &+\,162851708851 \gamma ^4\big )\big )\big )\big ). \end{aligned}$$