Solitons and dromion-like structures in an inhomogeneous optical fiber

Abstract

In this paper, a generalized higher-order variable-coefficient nonlinear Schrödinger equation is studied, which describes the propagation of subpicosecond or femtosecond pulses in an inhomogeneous optical fiber. We derive a set of the integrable constraints on the variable coefficients. Under those constraints, via the symbolic computation and modified Hirota method, bilinear equations, one-, two-,three-soliton solutions and dromion-like structures are obtained. Properties and interactions for the solitons are studied: (a) effects on the solitons resulting from the wave number k, third-order dispersion $\delta _1(z)$, group velocity dispersion $\alpha (z)$, gain/loss $\varGamma _2(z)$ and group-velocity-related $\gamma (z)$ are discussed analytically and graphically where z is the normalized propagation distance along the fiber; (b) bound state with different values of $\alpha (z)$, $\delta _1(z)$, $\gamma (z)$ and $\varGamma _2(z)$ are presented where some periodic or quasiperiodic formulae are derived. Interactions between the two solitons and between the bound states and a single soliton are, respectively, discussed; and (c) single, double and triple dromion-like structures with different values of $\alpha (z)$, $\delta _1(z)$, $\gamma (z)$ are also presented, distortions of which are found to be determined by those variable coefficients.

1 Introduction

Soliton study has been seen in fluids [1–8], plasmas [9–11], Bose–Einstein condensations [12–15], biophysics [16, 17] and fiber communication systems [18–21]. In order to derive the soliton solutions for nonlinear evolution equations, the Hirota’s bilinear method has been reported, which plays an important role in soliton theory [22, 23]. As application of the Horita’s bilinear method, many analytical solutions for some nonlinear evolution equations have been constructed [24–31]. Furthermore, the Hirota’s bilinear method has been generalized [32] and a refined invariant subspace method has been systematically presented and analyzed for solving nonlinear equations [33, 34]. Nonlinear Schrödinger (NLS) equation with the group velocity dispersion (GVD) and self-phase modulation (SPM) [35, 36],

$$\begin{aligned} i\varOmega _x+\frac{1}{2}\varOmega |\varOmega |^2+\varOmega _{\tau \tau }=0, \end{aligned}$$

(1)

is a model for the propagation and interaction of optical solitons in the picosecond domain, where x and $\tau$, respectively, are the normalized propagation distance along the fiber and the retarded time, $\varOmega (x,\tau )$ is the slowly varying envelope of the electric field, and the subscripts represent the partial derivatives. Optical solitons in a dielectric fiber have been regarded as an alternative data bit carrier to the next generation of ultrafast optical telecommunication systems [37, 38]. A systematic study for Eq. (1) has been reported in [39]. For the inhomogeneous optical fiber, the subpicosecond or femtosecond soliton pulses can be governed by the following higher-order variable-coefficient NLS equation [40–42]:

$$\begin{aligned}&iu_z+\alpha (z)u_{tt}+\beta (z)u|u|^2+i\gamma (z)u_t\nonumber \\&\quad \; +\,i\delta _1(z)u_{ttt}+i\delta _2(z)(u|u|^2)_t+i\delta _3(z)u(|u|^2)_t\nonumber \\&\quad \; +\,[\varGamma _1(z)+i\varGamma _2(z)]u=0, \end{aligned}$$

(2)

where z and t are the normalized propagation distance along the fiber and retarded time, u(z, t) represents the complex envelope of the electric field in the comoving frame, all of the variable coefficients are the real functions of z, $\alpha (z)$ and $\beta (z)$ denote the GVD and SPM, respectively, the term proportional to $\gamma (z)$ results from the group velocity, $\varGamma _1(z)$ is the frequency shift parameter, $\varGamma _2(z)$ is the linear gain/loss, $\delta _1(z)$ denotes the third-order dispersion (TOD), $\delta _2(z)$ is the self-steepening (SS), and $\delta _3(z)$ is related to the delayed nonlinear response effect.

In general, Eq. (2) is not integrable [43–45]. Two sets of the integrable constraints for Eq. (2) via the Painlevé analysis have been reported [41], one of which, $\alpha (z)=-3\beta (z)\delta _1(z)/\delta _3(z)$ and $\delta _3(z)=q_1\delta _1(z)e^{2\int (\varGamma _2(z)\mathrm{d}z)}$ where $q_1$ is a constant, is similar to that shown in Refs. [45–47]. Under the other set, $\alpha (z)=-3q_2\delta _1(z)/(2c_3)$ and $\delta _3(z)=q_3\delta _1(z)e^{2\int (\varGamma _2(z)\mathrm{d}z)}$ where $q_2\ne 0$ and $q_3\ne 0$ are a couple of constants, the $2\times 2$ Lax pair has been transformed to a $3\times 3$ linear eigenvalue problem with some soliton solutions obtained via the Darboux transformation [41, 48]. Anti-dark solitons for Eq. (2) have been constructed [42].

Special cases of Eq. (2) in the optical fibers have been seen: (a) When $\alpha (z)=d_0(z)/2$, $\beta (z)=h_0(z)$, $\delta _1(z)=b_0(z)/6$, $\delta _2(z)=-l_0(z)$, $\delta _3(z)=-ik_0(z)$ and $\gamma (z)=\varGamma _1(z)=\varGamma _2(z)=0$, Eq. (2) can be reduced to a perturbed NLS equation which describes the long distance propagation for the very short optical solitons in a nonlinear optical fiber, where $d_0(z)$ and $b_0(z)$ are the second-order and third-order dispersion profiles between the amplifiers, and $h_0(z)$, $k_0(z)$ and $l_0(z)$ are chosen to incorporate both the exponential factor due to the linear loss and the lumped amplification [49]; (b) Eq. (2) can be reduced to a higher-order NLS equation with $\alpha (z)=\alpha _1$, $\beta (z)=\alpha _2$, $\delta _1(z)=-\alpha _3$, $\delta _2(z)=-\alpha _4$, $\delta _3(z)=-\alpha _5$ and $\gamma (z)=\varGamma _1(z)=\varGamma _2(z)=0$, which governs the femtosecond light pulses in an optical fiber, where $\alpha _1$, $\alpha _2$, $\alpha _3$, $\alpha _4$ and $\alpha _5$ are all the real parameters with some soliton solutions for the higher-order NLS equation that have been constructed via a scaling transformation [50, 51]; (c) when $\alpha (z)=1/2$, $\beta (z)=1$, $\delta _1(z)=\alpha _3$, $\delta _2(z)=\alpha _1$, $\delta _3(z)=\alpha _2-\alpha _1$ and $\gamma (z)=\varGamma _1(z)=\varGamma _2(z)=0$, Eq. (2) can be reduced to a extended third-order cubic NLS equation which describes the slow evolution of the wave envelope in nonlinear dispersive system, and soliton solutions have been derived based on the Galilean transformation and generalized Galilean invariance [52]; and (d) under the Hirota conditions $\alpha (z)\delta _2(z)=3\beta (z)\delta _1(z)$ and $\delta _2(z)=-\delta _3(z)$, Eq. (2) can be reduced to a variable-coefficient Hirota equation [45–47], analytic multi-soliton solutions for which have been obtained via the bilinear method [46] and Darboux transformation [47], respectively.

Dromion structures have been investigated in the (2+1)- or higher- dimensional partial differential equations (PDEs) [53–58], which have hardly been obtained in the $(1+1)$-dimensional PDEs [59]. For instance, dromion solutions for the $(2+1)$- and $(3+1)$-dimensional Korteweg-de Vries equations have been reported [53, 54], respectively. Dromion solutions for the Davey–Stewartson (DS) have been obtained explicitly [55] and numerically [56]. Dromion solutions for the noncommutative DS equations have been derived via the Darboux transformation [57]. Dromions for the $(2+1)$-dimensional NLS equation with nonlinearity coefficients have been constructed via the Hirota’s bilinear method [58]. Dromion-like structures for the variable-coefficient Ginzburg–Landau equation have been studied [59]. Lump solitons, which is a kind of dromion-like solutions, for the KP and the generalized KP and BKP equations have been constructed [60]

However, to our knowledge, for Eq. (2), interactions between/among the subpicosecond or femtosecond solitons and dromion-like structures based on the analytic soliton solutions have not been discussed. In this paper, we will devote to obtain the soliton solutions and dromion-like structures via the Hirota’s bilinear method and to discuss the interactions between/among the subpicosecond or femtosecond solitons. In Sect. 2, we will derive the variable-coefficient bilinear equations for Eq. (2) via symbolic computation. In Sect. 3, one-, two- and three-soliton solutions for Eq. (2) will be obtained, interactions between/among the two and three solitons will be discussed with different values of variable coefficients, and bound states and dromion-like structures will be presented. Our conclusions will be given in Sect. 4.

2 Bilinear equations and integrable constraints for Eq. (2)

With the dependent-variable transformation [45]

$$\begin{aligned} u(z,t)=A(z)g(z,t)/f(z,t), \end{aligned}$$

(3)

Eq. (2) can be transformed into

$$\begin{aligned}&iA(z)\frac{D_z g \cdot f}{f^2}+iA(z)_z\frac{g}{f}+\alpha (z)A(z)\nonumber \\&\quad \times \left( \frac{D_t^2 g \cdot f}{f^2}-\frac{g}{f}\frac{D_t^2 f \cdot f}{f^2}\right) +\,\beta (z)A(z)^3\frac{g^2g^*}{f^3} \nonumber \\&\quad +i\gamma (z)\frac{D_tg\cdot f}{f^2}+iA(z)\delta _1(z)\nonumber \\&\quad \times \left( \frac{D_t^3 g \cdot f}{f^2}-\,3\frac{D_t g \cdot f}{f^2}\frac{D_t^2 f \cdot f}{f^2}\right) \nonumber \\&\quad +i\delta _2(z)A(z)^3\left( \frac{g^2D_tg^*\cdot f}{f^4}+\frac{2gg^*D_tg\cdot f}{f^4}\right) \nonumber \\&\quad +i\delta _3(z)A(z)^3\left( \frac{g^2D_tg^*\cdot f+gg^*D_tg\cdot f}{f^4}\right) \nonumber \\&\quad +A(z)\left[ \varGamma _1(z)+i\varGamma _2(z)\right] g/f=0, \end{aligned}$$

(4)

where f(z, t) and A(z) are the real functions, g(z, t) is a complex one, the asterisk denotes the complex conjugate, $D_z$ and $D_t$ are the Hirota’s bilinear derivative operators defined by [61]

$$\begin{aligned}&D_z^mD_t^n\Phi (z,t)\cdot \Psi (z,t)\equiv \left( \frac{\partial }{\partial z}-\frac{\partial }{\partial z^{\prime }}\right) ^{m}\nonumber \\&\quad \times \left( \frac{\partial }{\partial t} -\frac{\partial }{\partial t^{\prime }}\right) ^{n}\Phi (z,t) \Psi (z^{\prime },t^{\prime })|_{z^{\prime }=z,t^{\prime }=t} , \end{aligned}$$

(5)

where $z^{\prime }$ and $t^{\prime }$ are the formal variables, $\Phi (z,t)$ and $\Psi (z,t)$ are the differentiable functions of z and t, m and n are the nonnegative integers. Assuming that $D_t^2 f\cdot f=\kappa gg^*$, where $\kappa$ is a positive constant, we can transform Eq. (4) into

$$\begin{aligned} \begin{aligned}&\frac{A(z)\left[ iD_z+\alpha (z)D_t^2+i\gamma (z)D_t+i\delta _1(z)D_t^3 +\varGamma _1(z)\right] g\cdot f}{f^2}\\&\quad +\,\frac{ig[A(z)\varGamma _2(z)+A(z)_z]}{f}+\frac{A(z)g}{f^4}\left\{ |g|^2f\left[ A(z)^2\beta (z)\right. \right. \\&\left. \quad -\,\kappa \alpha (z)\right] +iA(z)^2g\left[ \delta _2(z) +\delta _3(z)\right] D_tg^*\cdot f\\&\left. \quad +\,g^*D_tg\cdot f\left[ 3\kappa \delta _1(z) -A(z)^2(2\delta _1(z)+\delta _3(z))\right] \right\} =0. \end{aligned} \end{aligned}$$

(6)

Splitting Eq. (6) [45, 62] yields

$$\begin{aligned}&\left[ iD_z+\alpha (z)D_t^2+i\gamma (z)D_t+i\delta _1(z)D_t^3 +\varGamma _1(z)\right. \nonumber \\&\left. \quad +\,iA(z)\varGamma _2(z)+iA(z)_z\right] g\cdot f=0, \end{aligned}$$

(7a)

$$\begin{aligned}&A(z)^2\beta (z)-\kappa \alpha (z)=0, \end{aligned}$$

(7b)

$$\begin{aligned}&\delta _2(z)+\delta _3(z)=0, \end{aligned}$$

(7c)

$$\begin{aligned}&3\kappa \delta _1(z)-A(z)^2\left[ 2\delta _2(z)+\delta _3(z)\right] =0. \end{aligned}$$

(7d)

For Eq. 6, we can choose $iA(z)\varGamma _2(z)+iA(z)_z=0$ which leads to $A(z)=e^{-\int \varGamma _2(z)\mathrm{d}z}$. From Eq. 7b–d, we get the constraints

$$\begin{aligned} \begin{aligned} \beta (z)&=\kappa \alpha (z)e^{2\int \varGamma _2(z)\mathrm{d}z},~\delta _3(z)=-\delta _2(z),\\ \delta _2(z)&=3\kappa \delta _1(z)e^{2\int \varGamma _2(z)\mathrm{d}z}, \end{aligned} \end{aligned}$$

(8)

which are similar to the Hirota conditions [45–47]. Under Constraints (8), the variable-coefficient bilinear equations are derived as

$$\begin{aligned}&D_t^2 f\cdot f=\kappa gg^*,\nonumber \\&\quad \left[ iD_z +\alpha (z)D_t^2 +i\gamma (z) D_t +i\delta _1(z)D_t^3+\varGamma _1(z)\right] g\nonumber \\&\quad \cdot f=0. \end{aligned}$$

(9)

3 Soliton solutions for Eq. (2) under Constraints (8)

In this part, we will derive the soliton solutions for Eq. (2) by expanding f and g as

$$\begin{aligned} \begin{aligned} f&=1+\epsilon f_1+\epsilon ^2 f_2+\epsilon ^3 f_3\cdots ,\\ g&=g_0(1+\epsilon g_1+\epsilon ^2 g_2+\epsilon ^3 g_3)\ldots , \end{aligned} \end{aligned}$$

(10)

with $\epsilon$ as a formal expansion parameter, $g_{i}^{\prime }$s ($i\!=\!$1,2,3...) are the complex functions of z and t, and $f_{k}^{\prime }$s ($k=$1,2,3...) are the real ones. The solutions can be constructed by substituting Expressions (10) into Bilinear Equation (9) and collecting terms proportional to the same powers of $\epsilon$.

3.1 One-soliton solutions for Eq. (2) under Constraints (8)

Truncating Expressions (10) as

$$\begin{aligned} \begin{aligned}&g=\epsilon g_1,\quad f=1+\epsilon ^2f_2, \end{aligned} \end{aligned}$$

(11)

substituting Expressions (11) into Bilinear Equations (9) and setting $\epsilon =1$, we can obtain the one-soliton solutions for Eq. (2) under Constraints (8) as

$$\begin{aligned} u=A(z)\frac{g_1}{1+f_2} \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned}&g_1=e^{\eta },\quad f_2=Be^{\eta +\eta ^*},\quad B=\frac{\kappa }{2(k+k^*)^2},\\&\eta =k t\!+\!\int \left[ ik^2\alpha (z)\!+\!i\varGamma _1(z)\!-\!k\gamma (z)\!-\!k^3\delta _1(z)\right] \,\mathrm{d}z+\!\phi \end{aligned} \end{aligned}$$

with k being a complex constant, and $\phi$ is a real one. Taking $k=k_R+k_Ii$, where the subscripts R and I denote the real and imaginary parts, respectively, we obtain the intensity of the optical pulse as

$$\begin{aligned} |u|^2=\text {e}^{-2\int \varGamma _2(z)\mathrm{d}z}\frac{2k_R^2}{\kappa }\text {sech}^2\left( \eta _{R} +\frac{1}{2}\ln \frac{\kappa }{8k_R^2}\right) , \end{aligned}$$

(13)

with

$$\begin{aligned} \begin{aligned} \eta _R&=k_Rt-k_R\int \left[ 2k_I\alpha (z)+\gamma (z)+(k_R^2 \right. \\&\left. \quad -\,3k_I^2)\delta _1(z)\right] \mathrm{d}z. \end{aligned} \end{aligned}$$

(14)

To derive the velocity for a soliton, we can track a point of the soliton where the intensity keeps unchanged, from which a characteristic line equation can be written as

$$\begin{aligned} \begin{aligned}&k_Rt-k_R\int \left[ 2k_I\alpha (z)+\gamma (z)+(k_R^2\right. \\&\left. \quad -\,3k_I^2)\delta _1(z)\right] \mathrm{d}z+\frac{1}{2}\ln \frac{\kappa }{8k_R^2}=\text {constant}. \end{aligned} \end{aligned}$$

(15)

Differentiating Eq. (15) with respect to z, we obtain

$$\begin{aligned} \frac{\mathrm{d}t}{\mathrm{d}z}-\left[ (k_R^2-3k_I^2)\delta _1(z)+2k_I\alpha (z)+\gamma (z)\right] =0, \end{aligned}$$

(16)

from which we derive the velocity for the soliton as

$$\begin{aligned} v=\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{1}{(k_R^2-3k_I^2)\delta _1(z)+2k_I\alpha (z)+\gamma (z)}. \end{aligned}$$

(17)

Fig. 1

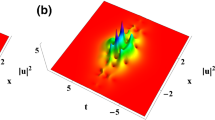
One solitons via Solutions (12), with the parameters as $k=1/4+i/3,\, \kappa =2,\, \varGamma _1(z)=z,\, \varGamma _2(z)=1/10,\, \phi =0\,:\, \mathbf a \, \alpha (z)=z/2,\, \gamma (z)=z/4,\, \delta _1(z)=z/3;\, \mathbf b \, \alpha (z)=z^2/10,\, \gamma (z)=z^2/20,\, \delta _1(z)=z^2/15;\, \mathbf c \, \alpha (z)=3\text {sin}(z/2),\, \gamma (z)=3\text {sin}(z/2), \, \delta _1(z)=3\text {cos}(z/2)$

From the intensities of one-soliton solutions (12), we find that the soliton amplitude is related to the real part of the wave number, k, and that the velocity of the soliton is determined by the TOD $\delta _1(z)$, GVD $\alpha (z)$ and $\gamma _1(z)$ resulting from the group velocity. Linear gain/loss term, $\varGamma _2(z)$, can directly affect the soliton amplitude. Soliton width is related to the TOD, GVD, $\gamma _1(z)$ and wave number k. We present some figures with different values of the variable coefficients to illustrate those properties. In Fig. 1, we find that the variable coefficients, $\alpha (z)$, $\delta _1(z)$ and $\gamma (z)$, can influence the structure, amplitude and velocity of the soliton: Velocity and amplitude change all the time along the z-axis; when $\alpha (z)=z/2$, $\delta _1(z)=z/3$ and $\gamma (z)=z/4$, we obtain a parabolic soliton via Solutions (12), as shown in Fig. 1a; when $\alpha (z)=z^2/10$, $\delta _1(z)=z^2/15$ and $\gamma (z)=z^2/20$, we plot a cubic soliton via Solutions (12), as seen in Fig. 1b. In Fig. 1c, when $\alpha (z)=3\text {sin}(z/2)$, $\delta _1(z)=3\text {cos}(z/2)$ and $\gamma (z)=3\text {sin}(z/2)$, we present a periodical oscillating soliton via Solutions (12). Further, influence of $\varGamma _2(z)$ can be seen when we compare Figs. (1) and (2): When $\varGamma _2(z)=1/10$, we derive that $\text {e}^{-2\int \varGamma _2(z)\mathrm{d}z}=\text {e}^{-z/5}$ which leads to the soliton amplitude compressed along the z-axis, as seen in Fig. 1. As $\varGamma _2(z)=z/50$, we can derive that $\text {e}^{-2\int \varGamma _2(z)\mathrm{d}z}=-\text {e}^{z^2/50}$ which leads to the soliton amplitude compressed along the z-axis on both directions, as shown in Fig. 2.

Fig. 2

The same as Fig. 1 except that $\varGamma _2(z)=z/50$

3.2 Two-soliton solutions for Eq. (2) under Constraints (8)

In order to obtain the two-soliton solutions, we truncate Expressions (10) as

$$\begin{aligned} g=\epsilon g_1+\epsilon ^3g_3,\quad f=1+\epsilon ^2f_2+\epsilon ^4f_4. \end{aligned}$$

(18)

Substituting Expressions (18) into Bilinear Equations (9) and setting $\epsilon =1$, we obtain the two-soliton solutions for Eq. (2) under Constraints (8) as

$$\begin{aligned} u=A(z)\frac{g_1+g_3}{1+f_2+f_4}, \end{aligned}$$

(19)

where

$$\begin{aligned} g_1= & {} e^{\eta _1}+e^{\eta _2},\\&g_3=A_{123}e^{\eta _1+\eta _2+\eta _1^*} +A_{124}e^{\eta _1+\eta _2+\eta _2^*},\\ f_2= & {} A_{13}e^{\eta _1+\eta _1^*}+A_{23}e^{\eta _2+\eta _1^*}\\&+\,A_{14}e^{\eta _1+\eta _2^*}+A_{24}e^{\eta _2+\eta _2^*},\\ f_4= & {} A_{1234}e^{\eta _1+\eta _2+\eta _1^*+\eta _2^*},\eta _m=k_mt\\&+\,w_m(z)+\phi _m,\\ w_m(z)= & {} \int \left[ ik_m^2\alpha (z)-k_m\gamma (z)-k_m^3\delta _1(z)\right] \mathrm{d}z,\\ A_{m,n+2}= & {} \kappa /2(k_m+k_n^*)^2,~~~(m=1,2),~~~(n=1,2),\\ A_{12}= & {} 2(k_1-k_2)^2/\kappa ,~~~A_{34}=2(k_1^*-k_2^*)^2/\kappa ,\\ A_{123}= & {} A_{12}A_{13}A_{23}, A_{124}=A_{12}A_{14}A_{24},\\ A_{1234}= & {} A_{123}A_{14}A_{24}A_{34}, \end{aligned}$$

with $k_1$ and $k_2$ being the complex constants, and $\phi _m^{\prime }$s as the real ones. Via symbolic computation and Solutions (19), intensity of the two-soliton solutions can be written as

$$\begin{aligned} |u|^2= & {} \text {e}^{\int [-2\varGamma _2(z)]\mathrm{d}z}\nonumber \\&\frac{|\xi _1|^2 +|\xi _2|^2+2\chi }{[C_0+2re^{\eta _{1R}+\eta _{2R}}\cos (\eta _{1I}-\eta _{2I}+\varphi )]^2}, \end{aligned}$$

(20)

where

(21)

it is obvious that periods exist in the two-soliton solutions.

Interactions between the two solitons are presented in Figs. 3 and 4: When $\alpha (z)=\delta _1(z)=\gamma (z)=z/2$, interaction between a parabolic and static soliton can be seen in Fig. 3a, where the intensity approaches to zero quickly along the z-axis; When $\alpha (z)=\delta _1(z)=\gamma (z)=z^2/5$, interaction between the cubic and static solitons is obtained in Fig. 3b; when $\alpha (z)=\delta _1(z)=\gamma (z)=3\text {sin}(z/2)$, interaction between the periodic and static solitons is presented in Fig. 3c. Although the intensities of the two solitons in Fig. 3 decay exponentially along the z-axis, attenuation degree of which in Fig. 3c is much weaker than that in Fig. 3a, b. Compared with Fig. 3, if we take $\varGamma _2(z)=z/10$, interaction features between the two solitons in this case are similar to those in Fig. 3 except that the intensities decrease along the z- axis in both directions, as presented in Fig. 4.

Fig. 3

Interactions between the two solitons via Solutions (19), with the parameters as $k_1=1/3+(1+\sqrt{13/3})i/3,\,k_2=1/4+i/5,\,\kappa =4, \,\varGamma _1(z)=z,\,\varGamma _2(z)=1/10,\,\phi _1=\phi _2=0\,:\, \mathbf a \,\alpha (z)=\gamma (z)=\delta _1(z)=z/2;\, \mathbf b \,\alpha (z)=\gamma (z)=\delta _1(z)=z^2/5;\, \mathbf c \,\alpha (z)=\gamma (z)=\delta _1(z)=3\text {sin}(z/2)$

Fig. 4

The same as Fig. 3 except that $\varGamma _2(z)=z/10$, $\kappa =2$

Bound-state solitons can be obtained with certain parameters: For a bound-state soliton, we choose two static solitons to satisfy the limitation that the two solitons have the same velocity and to derive an explicit relation between a and b from Eq. (17) as $b=(\alpha (z)\pm \sqrt{\alpha (z)^2+3\delta _1(z)\gamma (z) +3a^2\delta _1(z)^2})/(3\delta _1(z))$. Because b is a constant in the soliton solution, we need to introduce a set of the constraints among the variable coefficients as $\alpha (z)=c_1\gamma (z)=c_2\delta _1(z)$, with $c_1$ and $c_2$ being two real constants. For the sake of brevity, we can take $\alpha (z)=\gamma (z)=\delta _1(z)$, i.e., $c_1=c_2=1$, the relation between a and b can be rewritten as $b=(1\pm \sqrt{4+3a^2})/3$. For the two solitons propagating with the same velocity, we have $b_\rho =(1\pm \sqrt{4+3\rho ^2})/3, (\rho =1,2)$ so as to derive that $\eta _{2I} -\eta _{1I}=(b_2-b_1)t+\varGamma \int \alpha (z)\mathrm{d}z$, where $\varGamma =8\Bigg (\sqrt{4+3a_1^2}+3a_1^2\sqrt{4+3a_1^2}-\sqrt{4+3a_2^2} -3a_2^2\sqrt{4+3a_2^2}\Bigg )$.

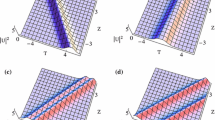
Studies on the bound-state solitons can be carried out for different variable coefficients: (a) Setting $\varGamma \int \alpha (z)\mathrm{d}z=2n\pi$ and $\alpha (z)=\zeta z$, with $\zeta$ being a real constant, we can obtain $|\varGamma |\zeta z_n^2/2=2n\pi \,(n=1,2,3 \ldots )$, which leads to $z_n=2\sqrt{n}\sqrt{\pi /|\varGamma |\zeta }$, from which the quasiperiodic formulae along the z-axis can be expressed as $T_n=2(\sqrt{n}-\sqrt{n-1})\sqrt{\pi /|\varGamma |\zeta }.$ In this case, when we choose the variable coefficients as $\alpha (z)=\gamma (z)=\delta _1(z)=2z$, the two-soliton solutions evolve into a quasiperiodic bound state, as shown in Fig. 5a. Quasiperiodic attractions and repulsions lead to the redistribution of the energy between the two solitons. Furthermore, we can calculate the quasi-periods of the bound state. Using the parameters given in Fig. 5a, we obtain the periods $T_1=7.834$, $T_2=3.245$ and $T_3=2.450$. Meanwhile, we can derive the ratio among the quasi-periods, which is $T_1:T_2:T_3 \dots =1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})\cdots$; (b) if $\alpha (z)=\zeta z^2$, with $\zeta$ being a real constant, we can obtain $|\varGamma |\zeta z_n^3/3=2n\pi \,(n=1,2,3 \ldots )$, which leads to $z_n=\root 3 \of {n}\root 3 \of {6\pi /|(\varGamma |\zeta )}\,$, from which the quasiperiodic formulae along the z-axis can be expressed as $T_n=(\root 3 \of {n}-\root 3 \of {n-1})\root 3 \of {6\pi /|(\varGamma |\zeta )}.$ As shown in Fig. 5b, where $\alpha (z)=\gamma (z)=\delta _1(z)=z^2/5$, we present a bound state which is similar to that in Fig. 5a. Using the parameters given in Fig. 5, we derive the periods of the bound state ($T_1=9.728$, $T_2=2.528$ and $T_3=1.774$); and (c) setting $\alpha (z)=\zeta \text {cos}(\varpi z)$, where $\zeta$ and $\varpi$ are both the real constants, we obtain $|\varGamma |\zeta \text {sin}(\varpi z_n)/\varpi =2n\pi (n=1,2,3\ldots )$. Due to the fact that $\text {cos}(\varpi z)$ is a periodic function, $2\pi /\varpi$ is one of the periods. In addition, the quasiperiodic formulae can be expressed as $T_n=\arcsin (2\pi \varpi \frac{n}{\varGamma \zeta })/\varpi -\arcsin (2\pi \varpi \frac{n-1}{\varGamma \zeta })/\varpi .$ With the parameters given in Fig. 5c, the periods can also be derived.

Fig. 5

Bound states via Solutions (19), with the parameters as $k_1=1/3+(1+\sqrt{13/3})i/3,\, k_2=1/4+(1+\sqrt{67}/4)i/3,\,\kappa =2, \,\varGamma _1(z)=z,\,\varGamma _2(z)=1/12,\,\phi _1=\phi _2=0\,:\, \mathbf a \,\alpha (z)=\gamma (z)=\delta _1(z)=2z;\, \mathbf b \,\alpha (z)=\gamma (z)=\delta _1(z)=z^2/5;\, \mathbf c \,\alpha (z)=\gamma (z)=\delta _1(z)=10\text {sin}(z/5)$

Fig. 6

The same as Fig. 5a except that $\mathbf a \,\phi _1=-5/2,\,\phi _2=5/2;\,\mathbf b \,\phi _1=-1/2,\,\phi _2=1/2;\, \mathbf c \,\phi _1=1/2,\,\phi _2=-1/2$

As shown in Fig. 6a, when $\phi _1=-5/2$ and $\phi _2=5/2\,$ which are related to the initial position, we plot two static solitons which are parallel to the z-axis. The two solitons propagate along the z-axis in the optical fiber with a constant separation between them. After we set $\phi _1=-1/2$ and $\phi _2=1/2\,$, an interaction between the two parallel solitons is obtained, as seen in Fig. 6b. When we change the parameters to $\phi _1=0$ and $\phi _2=0\,$, the bound is achieved, as depicted in Fig. 5a. When $\phi _1=1/2$ and $\phi _2=-1/2\,$, an interaction similar to that in Fig. 6b between the two solitons is presented, as seen in Fig. 6c. From the above, we find that the parameters $\phi _1$ and $\phi _2$ related to the initial positions can influence the separation and interaction between the two solitons.

3.3 Three-soliton solutions for Eq. (2) under Constraints (8)

To derive the three-soliton solutions for Eq. (2) under Constraints (8), we truncate Expressions (10) as

$$\begin{aligned} \begin{aligned} g&=\epsilon g_1+\epsilon ^3g_3+\epsilon ^5g_5,\\ f&=1+\epsilon ^2f_2+\epsilon ^4f_4+\epsilon ^6f_6, \end{aligned} \end{aligned}$$

(22)

substituting Eq. (22) into Bilinear Equations (9) and setting $\epsilon =1$, we can derive the three-soliton solutions for Eq. (2) as

$$\begin{aligned} \begin{aligned}&u=\frac{g_1+g_3+g_5}{1+f_2+f_4+f_6}, \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned} g_1= & {} e^{\eta _1}+e^{\eta _2}+e^{\eta _3},~g_3=A_{124}e^{\eta _1+\eta _2+\eta _1^*}\\&+\,A_{125}e^{\eta _1+\eta _2+\eta _2^*}+A_{126}e^{\eta _1+\eta _2+\eta _3^*}\\&+\,A_{134}e^{\eta _1+\eta _3+\eta _1^*}\\&+\,A_{135}e^{\eta _1+\eta _3+\eta _2^*}+A_{136}e^{\eta _1+\eta _3+\eta _3^*}\\&+\,A_{234}e^{\eta _2+\eta _3+\eta _1^*}\\&+\,A_{235}e^{\eta _2+\eta _3+\eta _2^*}+A_{236}e^{\eta _2+\eta _3+\eta _3^*}, \end{aligned}$$

$$\begin{aligned} g_5= & {} A_{12345}e^{\eta _1+\eta _2+\eta _3+\eta _1^*+\eta _2^*}\\&+\,A_{12346}e^{\eta _1+\eta _2+\eta _3+\eta _1^*+\eta _3^*}\\&+\,A_{12356}e^{\eta _1+\eta _2+\eta _3+\eta _2^*+\eta _3^*}, \end{aligned}$$

$$\begin{aligned} f_2= & {} A_{14}e^{\eta _1+\eta _1^*}+A_{24}e^{\eta _2+\eta _1^*}\\&+\,A_{34}e^{\eta _3+\eta _1^*}+A_{15}e^{\eta _1+\eta _2^*}+A_{25}e^{\eta _2+\eta _2^*}\\&+\,A_{35}e^{\eta _3+\eta _2^*}\\&+\,A_{16}e^{\eta _1+\eta _3^*}+A_{26}e^{\eta _2+\eta _3^*}+A_{36}e^{\eta _3+\eta _3^*}, \end{aligned}$$

$$\begin{aligned} f_4= & {} A_{1245}e^{\eta _1+\eta _2+\eta _1^*+\eta _2^*}+A_{1246}e^{\eta _1+\eta _2+\eta _1^*+\eta _3^*}\\&+\,A_{1256}e^{\eta _1+\eta _2+\eta _2^*+\eta _3^*}+A_{1345}e^{\eta _1+\eta _3+\eta _1^*+\eta _2^*}\\&+\,A_{1346}e^{\eta _1+\eta _3+\eta _1^*+\eta _3^*}+A_{1356}e^{\eta _1+\eta _3+\eta _2^*+\eta _3^*}\\&+\,A_{2345}e^{\eta _2+\eta _3+\eta _1^*+\eta _2^*}+A_{2346}e^{\eta _2+\eta _3+\eta _2^*+\eta _3^*}\\&+\,A_{2356}e^{\eta _2+\eta _3+\eta _2^*+\eta _3^*}, \end{aligned}$$

$$\begin{aligned} f_6= & {} A_{123456}e^{\eta _1+\eta _2+\eta _3+\eta _1^*+\eta _2^*+\eta _3^*}, \end{aligned}$$

$$\begin{aligned} \eta _p= & {} k_pt+w_p(z)+\phi _p, \end{aligned}$$

$$\begin{aligned} w_p(z)= & {} \int \left[ i\alpha (z)k_p^2-\gamma (z)k_p-\delta _1(z)k_p^3\right] {d}z, \end{aligned}$$

$$\begin{aligned} A_{p,q+3}= & {} \frac{\kappa }{2(k_p+k_q^*)^2},~(p=1,2,3),~(q=1,2,3), \end{aligned}$$

$$\begin{aligned} A_{12}= & {} \frac{2(k_1-k_2)^2}{\kappa },A_{13}=\frac{2(k_1-k_3)^2}{\kappa }, \end{aligned}$$

$$\begin{aligned} A_{23}= & {} \frac{2(k_2-k_3)^2}{\kappa },A_{45}=\frac{2(k_1^*-k_2^*)^2}{\kappa }, \end{aligned}$$

$$\begin{aligned} A_{46}= & {} \frac{2(k_1^*-k_3^*)^2}{\kappa },A_{56}=\frac{2(k_2^*-k_3^*)^2}{\kappa }, \end{aligned}$$

$$\begin{aligned} A_{m_1m_2m_3}= & {} A_{m_1m_2}A_{m_2m_3}A_{m_1m_3},(m_1\ne m_2\ne m_3),\\ A_{n_1n_2n_3n_4}= & {} A_{n_1n_2}A_{n_1n_3}A_{n_1n_4}A_{n_2n_3}A_{n_2n_4}A_{n_3n_4},\\&(n_1\ne n_2\ne n_3\ne n_4), \end{aligned}$$

$$\begin{aligned}&A_{12345}=A_{123}A_{145}A_{24}A_{25}A_{34}A_{35},\\&A_{12346}=A_{123}A_{146}A_{24}A_{26}A_{34}A_{36},\\&A_{12356}=A_{123}A_{156}A_{25}A_{26}A_{35}A_{36},\\&A_{123456}=A_{123}A_{145}A_{246}A_{356}A_{16}A_{25}A_{34}, \end{aligned}$$

with $r_1$, $r_2$ and $r_3$ being the complex constants.

Fig. 7

Interactions among the three solitons via Solutions (23), with the parameters as $k_1=1/2+i/3,\,k_2=1/3+i/4,\,k_3=1/4+i/5,\,\kappa =8,\,\phi _1=\phi _2=0, \,\varGamma _1(z)=z,\,\varGamma _2(z)=1/8\,:\, \mathbf a \,\alpha (z)=z/2,\,\gamma (z)=z/4,\,\delta _1(z)=z/3;\, \mathbf b \,\alpha (z)=z^2/10,\,\gamma (z)=z^2/20,\,\delta _1(z)=z^2/15;\, \mathbf c \,\alpha (z)=2\text {sin}(z/2),\,\gamma (z)=2\text {cos}(z/2), \,\delta _1(z)=2\text {sin}(z/2)$

Fig. 8

Interactions between the bound state and a single soliton via Solutions (23), with the parameters as $k_1=1/3+(1+\sqrt{13/3})i/3,\, k_2=1/4+(1+\sqrt{67}/4)i/3,\,k_3=1/4+i/3,\,\kappa =4,\,\phi _1 =\phi _2=\phi _3=0,\,\varGamma _1(z)=z,\,\varGamma _2(z)=1/12\,:\, \mathbf a \,\alpha (z)=\gamma (z)=\delta _1(z)=2z;\, \mathbf b \,\alpha (z)=\gamma (z)=\delta _1(z)=z^2/5;\, \mathbf c \,\alpha (z)=\gamma (z)=\delta _1(z)=3\text {sin}(z/3)$

Fig. 9

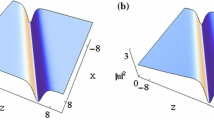
Single dromion-like structures via Solutions (12), with the parameters as $k=1/4+i/3,\,\kappa =1/5,\,\varGamma _1(z)=z,\,\varGamma _2(z)=z/3,\,\phi =0\,:\, \mathbf a \,\alpha (z)=z/2,\,\gamma (z)=z/4,\,\delta _1(z)=z/3;\, \mathbf b \,\alpha (z)=z^2/10,\,\gamma (z)=z^2/20,\,\delta _1(z)=z^2/15;\, \mathbf c \,\alpha (z)=3\text {sin}(z/2),\,\gamma (z)=3\text {sin}(z/2), \,\delta _1(z)=3\text {cos}(z/2)$

Figure 7 presents the interactions among the three solitons for Eq. (2). As seen in Fig. 7a, b, separations among them decrease along the optical fiber. The gain/loss term, $\gamma _2(z)$, leads to the exponential decay for the intensity of solitons. Three parallel solitons propagate along the z-axis periodically, as shown in Fig. 7c, which is similar to that in Fig. 6a. As the three solitons are the representative example of the multi-solitons, discussing some interactions among them might be used for the future development of the optical fiber, and we consider the interaction between the bound state and a single soliton: As presented in Fig. 8a, we plot the interaction between the bound state and a parabolic soliton, from which we note that the interaction does not affect the structure and velocity of any of them except for a constant phase shift in the interaction area. In Fig. 8b, we can see the cubic soliton passes through the bound state and propagates along the z- axis and a constant phase shift is formed as well. Interaction between the bound state and a periodical oscillating soliton is plotted in Fig. 8c.

Fig. 10

Double dromion-like structures via Solutions (12), with the parameters as $k_1=1/3+i/4,~k_2=1/4+i/5,~\kappa =1/5,~\varGamma _1(z)=z, ~\varGamma _2(z)=z/3,~\phi _1=\phi _2=2\,:~ \mathbf a ~\alpha (z)=\gamma (z)=\delta _1(z)=z/2;~ \mathbf b ~\alpha (z)=\gamma (z)=\delta _1(z)=z^2/5;~ \mathbf c ~\alpha (z)=\gamma (z)=\delta _1(z)=3\text {sin}(z/2)$

Fig. 11

Triple dromion-like structures via Solutions (23), with the parameters as $k_1=1/2+i/3,~k_2=1/3+i/4,~k_3=1/4+i/5,~\kappa =1/3, ~\phi _1=\phi _2=\phi _3=0,~\varGamma _1(z)=z,~\varGamma _2(z)=z/3\,:~ \mathbf a ~\alpha (z)=z/2,~\gamma (z)=z/4,~\delta _1(z)=z/3;~ \mathbf b ~\alpha (z)=z^2/10,~\gamma (z)=z^2/20,~\delta _1(z)=z^2/15;~ \mathbf c ~\alpha (z)=2\text {sin}(z/2),~\gamma (z)=2\text {cos}(z/2), ~\delta _1(z)=2\text {sin}(z/2)$

3.4 Dromion-like structures for Eq. (2) under Constraints (8)

As shown in Fig. 9, we present the single dromion-like structures with different values of variable coefficients for Eq. (2) under Constraints (8) and find that the variable coefficients related to Eq. (2) can influence the dromion-like structures. For the two-soliton solutions, we present the double dromion-like structures, as presented in Fig. 10: In Fig. 10a, the double dromion-like structures do not interact, from which we find that the distance between them can be influenced by the parameters related to the initial positions. Seen in Fig. 10b is the double dromion-like structure which evolves from the two cubic solitons. The double dromion-like structure in Fig. 10c is from the two periodically oscillating solitons, the distortion degree of which is much more serious than that in Fig. 10a, b. Triple dromion-like structures are shown in Fig. 11: There are three lumps in all of the figures, and the maximum values of the optical solitons are the same. The distortion of the figures is determined by the variable coefficients $\alpha (t)$ and $\gamma _1(t)$.

4 Conclusions

In this paper, with symbolic computation and modified Hirota method, Eq. (2), a higher-order variable-coefficient NLS equation for the propagation of subpicosecond and femtosecond pulses in an inhomogeneous optical fiber, has been investigated. Under integrable Constraints (8), Bilinear Equations (9) have been derived and one-, two- and three-soliton solutions have been obtained, i.e., Solutions (12), (19) and (23). Soliton amplitude has been found to be related to the real part of the wave number, $k_R$. Velocity of the soliton has been seen to be determined by the TOD $\delta _1(z)$, GVD $\alpha (z)$ and the group-velocity-related $\gamma _1(z)$. Linear gain/loss term, $\varGamma _2(z)$, has been found to lead to the soliton amplitude exponential decay along the z-axis. Soliton width has been seen to be determined by the TOD, GVD, $\gamma _1(z)$ and wave number $k_R$. Other results of the paper are summarized as follows:

• 1. The one-, two- and three-soliton solutions for Eq. (2) under Constraints (8) with different values of $\alpha (z)$, $\delta _1(z)$, $\gamma _1(z)$ and $\varGamma _2(z)$ have been discussed graphically: As seen in Figs. 1 and 2, we have presented the parabolic, cubic and periodically oscillating solitons with different values of $\alpha (z)$, $\gamma _1(z)$ and $\varGamma _2(z)$. In Figs. 3 and 4, interactions between the two solitons have been obtained.

• 2. For the two- and three-soliton solutions, we have presented the interactions and bound states with different values of $\alpha (z)$, $\delta _1(z)$, $\gamma _1(z)$ and $\varGamma _2(z)$: In Fig. 5, we have discussed the bound state evolving from the two solitons with certain parameters, and periods or quasi-periods have been calculated for each case, respectively. Separations and interactions between the two solitons influenced by the parameters $\phi _1$ and $\phi _2$ which are related to the initial positions have been analyzed, as seen in Fig. 6. Interactions among the three solitons have been shown in Fig. 7. Interactions between the bound state and a single soliton have been obtained in Fig. 8.

• 3. Dromion-like structures for Eq. (2) have been depicted in Figs. 9, 10 and 11: In Fig. 9, single dromion-like structures with different values of $\alpha (z)$, $\delta _1(z)$ and $\gamma _1(z)$ have been plotted. In Fig. 10, double dromion-like structures have been presented. Triple dromion-like structures have been addressed in Fig. 11: There are three lumps in all of the figures with different values of $\alpha (z)$, $\delta _1(z)$, $\gamma _1(z)$ and $\varGamma _2(z)$, and the distortions of the three solitons have been found to be determined by variable coefficients.