Memory-dependent response of the thermoelastic two-dimensional functionally graded rectangular plate

Abstract

This article uses a memory-dependent derivative (MDD) — which may be better than a fractional derivative — to develop a novel heat conduction problem in a functionally graded material (FGM) layer with a distinct exponential gradient model. A theoretical framework is designed for a functionally graded plate (FGP) incorporating the fractional heat conduction theory that incorporates single-phase-lag (SPL) and two-temperature discrepancy factors to capture the thermoelastic response and the memory-dependent effect. Then, the modified model is used to investigate the thermoelastic response of an FGP subjected to thermal shock at the left surface of the plate, keeping other faces at zero temperature. The temperature change is determined using the integral transform technique, and the solution is obtained in the Laplace transform domain. The transient temperature response in the time domain is evaluated through numerical inversion of the Laplace transform to generate numerical data. The general solutions of the governing equation of stress function are obtained by utilizing material attributes represented by the exponential-law index. The transient responses, namely temperature, displacement, and stress, are graphically depicted. FGP is composed of partially stabilized zirconia (PSZ) particles, and the austenitic stainless steel (SUS304) matrix was used in the analysis. The use of FGM requires careful compositional choices to prevent thermal stresses from being generated in the FGP. The study compares temperature distributions using non-Fourier and classical Fourier models, revealing wave-like phenomena in fractional heat transfer, which are undetected in classical Fourier heat conduction.

1 Introduction

Functionally graded materials (FGMs) are heterogeneous materials with continuous variations in properties along specific axes. They are renowned for their excellent mechanical toughness and heat resistance, making them widely used in advanced industries like aerospace and aviation. Many investigations have been conducted in related fields to better understand the mechanical properties of FGMs at extremely high temperatures. These studies have employed functionally graded layers (Byrd and Birman 2010; Zhou et al. 2011; Wang et al. 2018; Ma and Chen 2011; Ohmichi et al. 2016), cylinders and spheres (Tarn and Wang 2004; Zhao et al. 2007; Hosseini et al. 2007; Asgari and Akhlaghi 2009; Nezhad et al. 2011; Daneshjou et al. 2015), and three-dimensional (Ootao and Tanigawa 2005; Kim and Noda 2001; Li and Wen 2014; Yu et al. 2016) models. The research investigation was performed using techniques such as analytical methods (Delale and Erdogan 1983; Eischen 1987; Erdogan 1995; Bao and Wang 1995; Erdogan and Wu 1997; Choi et al. 1998; Cai and Bao 1998; Long and Delale 2005; Ding et al. 2010), numerical simulations (Santare and Lambros 2000; Kim and Paulino 2002; Comi and Mariani 2007), and experimental methods (Butcher et al. 1998; Abanto-Bueno and Lambros 2006). However, the extensive use of laser heating technology has led to significant interest in studying high-rate heat transfer.

Heat conduction analysis needs to be revised due to the infinite speed at which thermal disturbances propagate in the traditional Fourier law. Several other heat conduction models or generalized heat conduction theories have been proposed to overcome this disadvantage, such as the hyperbolic heat conduction model (Lord and Shulman 1967) and the dual-phase-lag heat conduction model (Tzou 1995a,b). Torabi and Saedodin (2011) examined hyperbolic heat conduction with a heat flux boundary condition. Askarizadeh and Ahmadikia (2016) examined the impact of non-Fourier thermal conduction on convective straight fins with a constant cross-section under periodic boundary conditions. They proposed an exact analytical solution for the dual-phase-lag heat conduction. Rahideh et al. (2012) simulated heat conduction in composite materials and FGMs. They specifically focused on a multilayered FGM medium that experiences heat generation. The simulation utilized non-Fourier heat transfer equations and accounted for finite heat-wave speed. Babaei and Chen (2010) addressed the problem of transient hyperbolic heat conduction in a functionally graded hollow cylinder of infinite length. Keles and Conker (2011) proposed a hyperbolic heat conduction problem in FGM cylinders and spheres with varied material characteristics. Akbarzadeh and Chen (2012, 2013) examined the transient heat conduction in a functionally graded medium using the dual-phase-lag theory. Peng et al. (2018) employed the hyperbolic heat-moisture coupling model to explore the impact of phase delays between heat flux and moisture flux on the transient hygrothermal response in an elastic cylinder. The fractional calculus, which is an extension of the conventional integer order calculus, has been developed to investigate many problems in science and technology, such as thermoelastic difficulties (Podlubny 1998; Ortigueira 2011). Povstenko (2004) introduced a quasi-static uncoupled theory of thermoelasticity that relies on a time-fractional equation. This equation combined aspects of both heat conduction and wave equations and was also examined by Fujita (1990). In addition, Sherief et al. (2010) and Youssef (2010) expanded the Cattaneo heat conduction equation into fractional versions, respectively. Ezzat (2011, 2011) formulated a novel model for the equation of fractional heat conduction by employing the recently constructed Taylor series expansion of time-fractional order, as proposed by Jumarie (2010). Ezzat et al. (2018, 2016, 2013, 2023, 2019) work on fractional calculus applications to thermoelasticity, including the introduction of new models of the fractional heat conduction equation. The study examined the transient thermal stresses caused by a crack in a hollow elastic cylinder using the fractional thermoelasticity theory and the superposition method (Zhang and Li 2017). Zhang et al. (2018) examined the issue of thermal shock in an elastic half-space with a penny-shaped crack close to the surface. Their investigation was based on a fractional thermoelasticity theory. Ma and He (2016) conducted a study on the fractional order theory of thermoelasticity, examining the transient thermo-piezoelectric reaction of a functionally graded piezoelectric rod under dynamic heat. Recently, Zhang et al. (2019) investigated the problem of FGMs based on the fractional order generalized fractional heat conduction with heat flow phase-lag, examining two typical scenarios of convective heat or temperature movement at boundaries using the Laplace transform method. From the study mentioned above articles, it is evident that most literature pertains to classical, hyperbolic, or phase-lag thermoelasticity theories. However, various authors suggest different formulas.; that is, the thermoelastic theories are not unique in their form.

Over the past decade, fractional calculus has gained significant attention due to its applications in physics and various engineering fields. Wang and Li (2011) presented the memory-dependent derivative (MDD) concept has been introduced as an integral version of a common derivative, including a kernel function across a sliding interval. This definition accurately represents the memory effect, where the previous state influences the pace of instantaneous change. The MDD is more intuitive for understanding the physical significance and has more expressive power than the fractional one. Several seminal studies may be reviewed in the literature by Ezzat et al. (2014, 2016, 2017) and Sur et al. (2024, 2023a, 2023b, 2023, 2024, 2024) after the development of the MDD philosophy. It is widely understood that time-fractional-order thermoelasticity can be applied to depict memory-dependent derivative (MDD) behaviours. Therefore, the study of thermoelasticity within the framework of the memory-dependent two-temperature theory holds significant importance. As far as the author is aware, there is no existing analysis for a transient thermal conduction problem of a two-dimensional functionally graded plate with a memory-dependent derivative, and this may be due to the extreme difficulty of using the analytical approach.

The purpose of this paper is to modify the conventional Fourier law of heat conduction and establish analytical solutions to two-dimensional problems to capture the thermoelastic response using fractional-order single-phase-lag (FOSPL) by introducing a temperature discrepancy factor in the context of memory-dependent effect. The resulting non-dimensional equations are applied to a specific problem of an FGP subjected to thermal shock on the boundary, which is traction-free. An integral transform approach is introduced to obtain the exact solutions in the Laplace transform domain for different forms of kernel function. The Laplace transforms are inverted using the modified Durbin’s numerical inversion method. The innovative theory is analyzed using graphical representations, with FGMs as representative composite materials due to their exceptional heat resistance in non-isothermal conditions. The presence of a memory-dependent derivative also enhances the exceptional predictive capability exhibited. In conclusion, the definition of MDD is more intuitive as compared to the fractional derivative. Some parametric results are established to display the influences of the fractional-order parameter, the phase-lag parameter and the exponential-law index on the considered physical quantities.

The subsequent sections of this paper is organized as follows: The modified mathematical model for the governing equations with FOSPL and two-temperature theory via MDD effect is described in Sect. 2. The practical statement of heat conduction and thermoelastic field is the topic of discussion in Sect. 3. An overview of the formation of analytical solutions for the temperature distribution and the stress that is associated with it is given in Sect. 3. The numerical results are provided, and parametric studies are undertaken in Sect. 4. The findings that were presented are included in Sect. 5.

2 Mathematical model

The generalized fractional single phase-lag (FSPL) heat transfer model (Ezzat and Karamany 2011):

$$ q(x,y,t)\left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}\frac{\partial ^{\alpha}}{\partial t^{\alpha}} \right ) = - \nabla T(x,y,t,k), 0 < \alpha \le 1 $$

(1)

where the fractional derivative (Sherief et al. 2010) is

$$ \frac{\partial ^{\alpha} f(t)}{\partial t^{\alpha}} = \left \{ \textstyle\begin{array}{l} f(t) - f(0), \alpha \to 0 \\ I^{\alpha - 1}\frac{\partial ^{\alpha} f(t)}{\partial t^{\alpha}}, 0 < \alpha < 1 \\ \frac{\partial f(t)}{\partial t}, \alpha = 1 \end{array}\displaystyle \right . $$

(2)

and

$$ I^{\alpha} = \frac{1}{\Gamma (\alpha )}\int _{0}^{t} (t - \tau )^{\alpha - 1} f(\tau )d\tau , \alpha > 0 $$

(3)

As the variable $\alpha \to 1$, Eq. (1) simplifies to the widely recognized Cattaneo law. Kimmich (2002) states that the time-fractional diffusion equation, with fractional-order $\alpha$ describes various diffusion cases where $0 < \alpha < 1$ correspond to weak diffusion, $\alpha = 1$, it correspond to normal diffusion, $1 < \alpha < 2$ corresponds to strong diffusion, and $\alpha = 2$, it corresponds to ballistic diffusion.

Consider the energy balance while considering heat flux

$$ \rho (x) c(x)\frac{\partial}{\partial t} T(x,y,t,k) = - \nabla q(x,y,t) $$

(4)

Chen and Gurtin (1968) proposed dividing real materials into simple and non-simple categories by considering two temperatures, that is, conductive and thermodynamic, and the two temperatures are related by

$$ \Phi (x,y,t,k) = (1 - b \nabla ^{2}) T(x,y,t,k), b > 0 $$

(5)

The material parameter $b$ is a crucial distinction between the two-temperature and classical theories. As a limiting case, $b \to 0$, $\Phi \to T$ give rise to the classical Fourier theory. Combing Eqs. (1), (4), and (5), and multiplying ($1 - b \nabla ^{2}$) and neglecting differential coefficients of order higher than $\nabla ^{2}$, and using $\nabla ^{2} \approx (1/\kappa ) (\partial /\partial t)$, one obtains

$$ \left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}\frac{\partial ^{\alpha}}{\partial t^{\alpha}} \right )\rho (x) c(x) \frac{\partial}{\partial t}\left ( 1 - \frac{b}{\kappa (x)} \frac{\partial}{\partial t} \right )T(x,y,t) = \nabla ^{2}T(x,y,t,k) $$

(6)

Wang and Li (2011) introduced the concept of ‘memory-dependent derivatives’ as a captivating and distinct alternative to fractional order derivatives, which accurately capture the influence of memory. The Caputo and Mainardi (1971) fractional derivative was transformed into an integral representation of a first-order ordinary derivative using the kernel function. The MDD for the first order of a function $f(t)$ can be expressed as an integral using a kernel function over a sliding interval, mathematically as

$$ D_{\omega} f(t) = (1/\omega )\int _{t - \tau}^{t} K(t - \xi )f'(\xi )d\xi $$

(7)

The selection of the kernel function $K(t - \xi )$ and the time-delay parameter $\omega > 0$ is flexible and can be selected freely, as

$$ K(t - \xi ) = 1 - \frac{2g}{\omega} (t - \xi ) + \frac{e^{2}}{\omega ^{2}}(t - \xi )^{2} = \left \{ \textstyle\begin{array}{l} 1; \text{if} e = 0,g = 0 \\ 1 - (t - \xi )/\omega ; \text{if} e = 0, g = 0.5 \\ \left ( 1 - (t - \xi )/\omega \right )^{2}; \text{if} e = 1,g = 1 \end{array}\displaystyle \right . $$

(8)

where $\omega > 0$ is the delay time; $e$ and $g$ are constants, respectively. The kernel can be considered the degree of the past effect on the present. Moreover, if $K \equiv 1$,

$$ D_{\omega} f(t) = \frac{1}{\omega} \int _{t - \omega}^{t} f'(\xi )d\xi = \frac{f(t) - f(t - \omega )}{\omega} \to f'(t)\quad \text{as} \omega \to 0 $$

(9)

and it is noted that an ordinary function $d/dt$ is obtained if the limiting case of $D_{\omega}$ is taken as $K = 1$ and $\omega \to 0$ (Mondal et al. 2021). The right-hand side of Eq. (7) can be interpreted as the mean of $f'(\xi )$ over the previous interval [$t - \omega$, $t$], with varying weights. From an applications perspective, memory significantly impacts at $0 \le K(t - \xi ) < 1$ for $\xi \in [t - \omega ,t]$, resulting in memory-dependent derivatives that are often smaller in magnitude compared to the common derivatives $f'(t)$. The possibility of this situation depends on implementing the concept of MDD, as fractional derivatives are insufficient when the lower-end value greatly varies from the top-end value in the definition of fractional order derivatives. The modified partial differential equation of Eq. (6), which expresses memory-dependent characteristics, can presented as:

$$ e^{ - \gamma x}\left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}D_{\omega}^{\alpha} \right ) \rho (x) c(x)\frac{\partial}{\partial t}\left ( 1 - \frac{b}{\kappa (x)} \frac{\partial}{\partial t} \right )T(x,y,t) = \nabla ^{2}T(x,y,t,k) $$

(10)

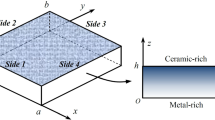
In a layered FGM, the characteristics of the material vary depending on its location. However, in practical applications, FGMs are typically engineered to have material properties that change in a specified direction for specific reasons. For instance, combining ceramics with metals can result in materials that can withstand high temperatures and minimize thermal stresses. Ceramics with lower heat conductivity and thermal expansion coefficient are matched by metals, which possess stronger toughness and better heat conductivity. Therefore, for the sake of simplicity, it is logical to assume in this document that the material properties are only dependent on spatial variable $x$ and exhibit an exponential gradient pattern (Noda and Jin 1993) as follows:

$$ \rho (x) = \rho _{0}e^{\beta _{1}x},c(x) = c_{0}e^{\beta _{2}x},k(x) = k_{0}e^{\delta x} $$

(11)

where $\rho _{0}(\rho _{h})$, $c_{0}(c_{h})$, $k_{0}(k_{h})$ are the corresponding values that vary through the way $x$ axis, and gradient indices are defined by

$$ \beta _{1} = \frac{1}{h}\ln \frac{\rho _{h}}{\rho _{0}},\beta _{1} = \frac{1}{h}\ln \frac{c_{h}}{c_{0}},\delta = \frac{1}{h}\ln \frac{k_{h}}{k_{0}} $$

(12)

where $\gamma = \beta _{1} + \beta _{2} - \delta$ is the graded parameter. The limiting case $\gamma = 0$ means that the thermal conductivity and the volumetric heat capacity have the same exponential law and correspond to a homogenous plate. Under the assumption of the exponential gradient (11), Eq. (10) can be written as

$$ e^{ - \gamma x}\left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}\frac{\partial ^{\alpha}}{\partial t^{\alpha}} \right ) \rho (x) c(x)\frac{\partial}{\partial t}\left ( 1 - \frac{b}{\kappa (x)} \frac{\partial}{\partial t} \right )T(x,y,t) = \nabla ^{2}T(x,y,t,k) $$

(13)

By adjusting the values of fractional order $\alpha$, and phase-lag $\tau _{q}$ one can derive the limiting cases of the two-temperature FSPL heat conduction, Eq. (10) as

• if we put $\tau _{q} = 0$, it reduces to classical thermoelasticity (CTE).

• when $\tau _{q} \ge 0$ and $\alpha = 1$, it reduces to hyperbolic thermoelasticity (HTE) (Lord and Shulman 1967).

• If $\alpha ! = 1$ and $\tau _{q}^{\alpha} \ge 0$, it reduces to Sherief’s fractional model (SFTE) (Sherief et al. 2010)

• Eq. (13) is yielded to Ezzat’s fractional model (EFTE) when $\tau _{q}^{\alpha} \ge 0$ (Ezzat and Karamany 2011)

Thus, Eq. (10) expresses the partial differential heat conduction in the context of the memory-dependent two-temperature theory the authors are curious about.

3 Statement of the problem

Let us consider an FGM plate with a thickness $a$ and a width $h$ occupying the space $D: - h/2 \le x \le h/2$, $0 \le y \le a$ as shown in Fig. 1. In this case, the thermal shock $T_{0}H(t)$ is applied on the left face surface ($x = h/2$), and the temperature on the other face surface ($x = - h/2$) is kept at zero. Both the top and lower faces are adiabatic. The heat conductivity, Young’s modulus, and the coefficient of the linear thermal expansion may be described using exponential functions that depend on their position.

Fig. 1

FGP subjected to a thermal shock and boundary conditions

When a material property changes along $x$-axis, a two-dimensional transient heat conduction equation based on Eq. (13) is given by

$$ e^{ - \gamma x}\left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}D_{\omega}^{\alpha} \right ) \rho (x) c(x)\frac{\partial}{\partial t}\left ( 1 - \frac{b}{\kappa (x)} \frac{\partial}{\partial t} \right )T = \left ( \frac{\partial}{\partial x}k(x)\frac{\partial}{\partial x} + \frac{\partial}{\partial y}k(x)\frac{\partial}{\partial y} \right )T $$

(14)

As an example, we have examined the specific boundary condition influenced by thermal shock on one side of a plate using FGP varying according to an exponential law and its thermoelastic response with a memory effect is studied.

3.1 Single-phase lag two-temperature thermal field

By referring to the dimensionless variables

$$ \textstyle\begin{array}{l} (x^{ *},y^{ *} ) = (x,y)/h, (t^{ *},\tau _{q}^{\alpha *},D_{\omega}^{\alpha *} ) = (t,\tau _{q}^{\alpha},D_{\omega}^{\alpha} )k_{0}/\rho _{0}c_{0}h^{2}, \\ (T^{ *},\Phi ^{ *} ) = (T,\Phi )/T_{0}, (\beta _{1}^{*},\beta _{2}^{*},\delta ^{ *},\gamma ^{ *} ) = (\beta _{1},\beta _{2},\delta ,\gamma )h, \\ (u^{ *},v^{ *} ) = (u,v)/\rho _{0}c_{0}h^{2},\sigma _{ij}^{ *} = \sigma _{ij}/\rho _{0}c_{0}h^{2} \end{array} $$

(15)

Here and in the following, the asterisk * of the dimensionless variables is omitted for simplicity for later stages. The dimensionless two-dimensional transient heat conduction equation of Eq. (14) is given by

$$ e^{ - \gamma x}\left ( 1 + \frac{\tau _{q}^{\alpha}}{\alpha !}D_{\omega}^{\alpha} \right ) \frac{1}{\kappa (x)}\frac{\partial}{\partial t}\left ( 1 - \frac{b}{\kappa (x)} \frac{\partial}{\partial t} \right )T = \frac{\partial ^{2}T}{\partial x^{2}} + \frac{k'(x)}{k(x)}\frac{\partial T}{\partial x} + \frac{\partial ^{2}T}{\partial y^{2}} $$

(16)

subjected to mechanical conditions

$$ \sigma _{xy}(x,0,t) = \sigma _{yy}(x,0,t) = v(x,0,t) = 0, - h/2 < x < h/2 $$

(17)

and initial and associated thermal boundary conditions

$$ \Phi (x,y,0) = T(x,y,0) = 0, \frac{\partial}{\partial t} T(x,y,0) = 0 $$

(18)

$$ T( - h/2,y,t) = 0, T(h/2,y,t) = T_{0}H(t) $$

(19)

3.2 Thermoelastic field

The equilibrium equation (in the absence of body forces) for the plane problem:

$$ \frac{\partial \sigma _{xx}}{\partial x} + \frac{\partial \sigma _{yx}}{\partial y} = 0, \frac{\partial \sigma _{xy}}{\partial x} + \frac{\partial \sigma _{yy}}{\partial y} = 0 $$

(20)

The strain-displacement relations and compatibility equation have the form

$$ \varepsilon _{xx} = \frac{\partial u}{\partial x},\varepsilon _{yy} = \frac{\partial v}{\partial y}, \varepsilon _{xy} = \frac{1}{2}\left ( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right ) $$

(21)

$$ \frac{\partial ^{2}\varepsilon _{xx}}{\partial y^{2}} + \frac{\partial ^{2}\varepsilon _{yy}}{\partial x^{2}} = 2\frac{\partial ^{2}\varepsilon _{xy}}{\partial x\partial y} $$

(22)

The constitutive equations are

$$ \textstyle\begin{array}{l} \varepsilon _{xx} = (\sigma _{xx} - \upsilon \sigma _{yy})/E^{e} + \alpha _{t}^{e}T, \\ \varepsilon _{yy} = (\sigma _{yy} - \upsilon \sigma _{xx})/E^{e} + \alpha _{t}^{e}T, \\ \varepsilon _{yy} = E^{e}\sigma _{xx}/(1 + \upsilon ^{e}) \end{array} $$

(23)

where

$$ \textstyle\begin{array}{l} E^{e} = E, \upsilon ^{e} = \upsilon ,\alpha _{t}^{e} = \alpha _{t} \text{for} \mathrm{plane} \mathrm{stress} \\ E^{e} = E/(1 - \upsilon ^{2}), \upsilon ^{e} = \upsilon /(1 - \upsilon ),\alpha _{t}^{e} = (1 + \upsilon )\alpha _{t} \text{for} \mathrm{plane} \mathrm{strain} \end{array} $$

(24)

while the material properties depend on the position.

The stress components in terms of stress function $\chi$ are obtained as

$$ \sigma _{xx} = \frac{\partial ^{2}\chi}{\partial y^{2}},\qquad \sigma _{xy} = \frac{\partial ^{2}\chi}{\partial x \partial y},\qquad \sigma _{yy} = \frac{\partial ^{2}\chi}{\partial x^{2}} $$

(25)

The basic equation governing the temperature and the stress function in the FGM plate can be obtained by substituting Eqs. (25) into the compatibility condition (22) through the constitutive law (23), as

$$\begin{aligned} \nabla ^{2}\left ( \frac{1}{E^{e}}\nabla ^{2}\chi + \alpha _{t}T \right ) =& \frac{\partial ^{2}}{\partial x^{2}}\left ( \frac{1 + \upsilon ^{e}}{E^{e}}\frac{\partial ^{2}\chi}{\partial y^{2}} \right ) + \frac{\partial ^{2}}{\partial y^{2}}\left ( \frac{1 + \upsilon ^{e}}{E^{e}}\frac{\partial ^{2}\chi}{\partial x^{2}} \right ) \\ &{} - 2\frac{\partial ^{2}}{\partial x\partial y}\left ( \frac{1 + \upsilon ^{e}}{E^{e}}\frac{\partial ^{2}\chi}{\partial x\partial y} \right ) \end{aligned}$$

(26)

It is supposed that the material possesses the exponential gradient pattern (Noda and Jin 1993):

$$ E^{e}(x) = E_{0}e^{\beta _{3}x},\alpha _{t}^{e}(x) = \alpha _{0}e^{\beta _{4}x} $$

(27)

where $E_{0}(E_{h})$, $\alpha _{0}(\alpha _{h})$ are the corresponding values that vary through the way $x$- axis, and $\beta _{3}( < 0),\beta _{4}$ are gradient indices defined by

$$ \beta _{3} = \frac{1}{h}\ln \frac{E_{h}}{E_{0}},\beta _{4} = \frac{1}{h}\ln \frac{\alpha _{h}}{\alpha _{0}} $$

(28)

Substituting Eq. (27) into Eqs. (26) and using Eq. (15), one obtains the following dimensionless forms

$$ \nabla ^{2}\nabla ^{2}\chi - 2\beta _{3}\frac{\partial \nabla ^{2}\chi}{\partial y} + \beta _{3}^{2}\left [ \nabla ^{2}\chi - (1 + \upsilon )\frac{\partial ^{2}\chi}{\partial x^{2}} \right ] + e^{(\beta _{3} + \beta _{4})x}\left ( \nabla ^{2}T + 2\beta _{4}\frac{\partial T}{\partial x} + \beta _{4}^{2}T \right ) = 0 $$

(29)

The traction-free boundary conditions as

$$ \sigma _{xx} = \sigma _{xy} = 0\quad \mathrm{at} x = \pm h/2 $$

(30)

$$ \int _{ - h/2}^{ h/2} \sigma _{yy}dy = \int _{ - h/2}^{ h/2} \sigma _{yy}ydy = 0\quad \mathrm{at} y = 0, a $$

(31)

Equations (1)-(34) constitute the mathematical formulation of the problem.

4 Solution of the problem

4.1 Solution of the heat conduction problem

Employing the Laplace transform defined by

$$ \bar{f}(r,s) = \mathcal{L}[f(r,t)] = \int _{0}^{\infty} e^{ - st} f(r,t)dt, \operatorname{Re} (s) \ge d > 0 $$

(32)

By utilizing the convolution theorem, it becomes possible to employ the Laplace transform to the higher-order memory-derivative $D_{\omega}^{p}$, satisfying the property

$$ \mathcal{L} [\omega D_{\omega}^{p}f(x,t)] = \mathcal{L} [\int _{t - \omega}^{t} K(t - \xi ) f^{p}(x,\xi )d\xi ] = s^{p - 1}G(s,\omega )\mathcal{L} [f(x,t)] $$

(33)

where $p \in \mathbb{\mathrm{R}}$ and

$$ G(s,\omega ) = (1 - e^{ - s\omega} )\left ( 1 - \frac{2f}{s\omega} + \frac{2e^{2}}{s^{2}\omega ^{2}} \right ) - \left ( e^{2} - 2f + \frac{2e^{2}}{s\omega} \right )e^{ - s\omega} $$

(34)

Using Eqs. (11), (18), and applying Laplace transforms to the governing Eqs. (16), and (19), we obtain the transformed equation; one obtains

$$ e^{ - \gamma x}q^{2}\bar{T} = \frac{\partial ^{2}\bar{T}}{\partial x^{2}} + \frac{\partial ^{2}\bar{T}}{\partial y^{2}} + \gamma \frac{\partial \bar{T}}{\partial x} $$

(35)

$$ \bar{T}( - h/2,y,s) = 0, \bar{T}(h/2,y,s) = T_{0}/s $$

(36)

where

$$ q^{2} = \left ( 1 + \frac{1}{\alpha !}G(s,\omega ) \right ) \frac{s}{\kappa _{0}}\left ( 1 - \frac{b}{\kappa _{0}} s \right ) $$

(37)

We bring in a finite sine-Fourier integral transform in the interval $0 < y \le \bar{a}$, stated as

$$ \mathfrak{F}_{s}\{ g(z)\} = \tilde{g}(n) = \int _{0}^{\bar{a}} g(z) \sin (\vartheta _{n}z) dz; 0 \le z \le \bar{a},\vartheta _{n} = n\pi /\bar{h}, n = 1,2,3... $$

(38)

together with its inverse transform

$$ \mathfrak{F}_{s}^{ - 1}\{ \tilde{g}(n)\} = g(z) = (2/\bar{a})\sum _{n = 1}^{\infty} g(n)\sin (\vartheta _{n}z) $$

(39)

and the orthogonal property as

$$ \mathfrak{F}_{s}\{ \partial ^{2}g(z)/\partial z^{2}\} = \vartheta _{n} [g(0) - ( - 1)^{n}g(\bar{a})] - \vartheta _{n}^{2} \tilde{g}(n) $$

(40)

Applying the sine-Fourier transform as defined in Eq. (39) to the governing Eqs. (35), one obtains the transformed equation as

$$ \frac{\partial ^{2}\bar{\bar{T}}}{\partial x^{2}} + \gamma \frac{\partial \bar{\bar{T}}}{\partial x} - (e^{ - \gamma x}q^{2} + \vartheta _{n}^{2})\bar{\bar{T}} = 0 $$

(41)

$$ \bar{\bar{T}}( - h/2,n,s) = 0, \bar{\bar{T}}(h/2,n,s) = T_{0}/s $$

(42)

Taking the transformation of variables as

$$ \xi = (2q/\gamma )e^{ - \gamma x/2} $$

(43)

and taking

$$ \bar{\bar{T}}(x,n,s) = \xi \bar{\bar{\theta}} (\xi ,n,s) $$

(44)

Considering Eqs. (43)-(44) into (41)-(42), one obtains

$$ \frac{\partial ^{2}\bar{\bar{\theta}}}{\partial \xi ^{2}} + \frac{1}{\xi} \frac{\partial \bar{\bar{\theta}}}{\partial \xi} - \left ( 1 + \frac{\eta ^{2}}{\xi ^{2}} \right )\bar{\bar{T}} = 0 $$

(45)

$$ \bar{\bar{\theta}} ( - h/2,n,s) = 0, \bar{\bar{\theta}} (h/2,n,s) = \theta _{0}/s $$

(46)

The general solution of Eq. (18) with the aid of modified Bessel functions

$$ \bar{\bar{\theta}} = C_{1}I_{\eta} (\xi ) + C_{2}K_{\eta} (\xi ) $$

(47)

where $\eta ^{2} = 1 + (2\vartheta _{n}/\gamma )^{2}$, and $C_{i}$ ($i = 1,2$) are two parameters independent of $\xi$, which can be determined by two boundary conditions (46) as

$$ C_{1} = \frac{\theta _{0}K_{\eta} ( - h/2)}{s [I_{\eta} (h/2)K_{\eta} ( - h/2) - I_{\eta} ( - h/2)K_{\eta} (h/2)]} $$

(48)

$$ C_{2} = \frac{\theta _{0}I_{\eta} ( - h/2)}{s [I_{\eta} (h/2)K_{\eta} ( - h/2) - I_{\eta} ( - h/2)K_{\eta} (h/2)]} $$

(49)

From Eqs. (44) and (48)-(49), we obtain the solution for Eq. (41)

$$ \bar{\bar{T}}(x,n,s) = \frac{\theta _{0}[K_{\eta} ( - h/2)I_{\eta} (\xi ) + I_{\eta} ( - h/2)K_{\eta} (\xi )]\xi}{s [I_{\eta} (h/2)K_{\eta} ( - h/2) - I_{\eta} ( - h/2)K_{\eta} (h/2)]} $$

(50)

and then using Eq. (39), the temperature Eq. (50) in the Laplace domain as

$$ \begin{aligned} \bar{T}(x,y,s) ={}& \sum _{n = 1}^{\infty} \frac{\theta _{0}[K_{\eta} ( - h/2)I_{\eta} ((2q/\gamma )e^{ - \gamma x/2}) + I_{\eta} ( - h/2)K_{\eta} ((2q/\gamma )e^{ - \gamma x/2})]}{s [I_{\eta} (h/2)K_{\eta} ( - h/2) - I_{\eta} ( - h/2)K_{\eta} (h/2)]} \\ &{}\times (2q/\gamma )(2/a)e^{ - \gamma x/2}\sin (\vartheta _{n}y) \end{aligned} $$

(51)

Equation (51) depicts the temperature at each instant and all positions of the plate with a finite height in the Laplace domain.

4.2 Solution of thermal stress

Using temperature is given by Eq. (51), Eq. (29) reduces to

$$ \textstyle\begin{array}{l} \nabla ^{4}\chi - 2\beta _{3}\frac{\partial \nabla ^{2}\chi}{\partial y} + \beta _{3}^{2}\nabla ^{2}\chi - (1 + \upsilon )\beta _{3}^{2}\frac{\partial ^{2}\chi}{\partial x^{2}} = \\ \frac{\left \langle \textstyle\begin{array}{c} [ - \gamma ^{2}\beta _{4}^{2}K_{\eta} (h/2)I_{\eta} ((2q/\gamma )e^{ - \gamma x/2}) + I_{\eta} ( - h/2)K_{\eta} ((2q/\gamma )e^{ - \gamma x/2})] \\ \times [e^{\gamma x}(\gamma - 2\beta _{4}) - \gamma ^{2}\beta _{4}^{2}] + [K_{\eta} (h/2)I_{\eta} ((2q/\gamma )e^{ - \gamma x/2}\beta _{4}) \\ + I_{\eta} ( - h/2)K_{\eta} ((2q/\gamma )e^{ - \gamma x/2}\beta _{4})] [e^{\gamma x/2}\gamma (5\gamma - 4\beta _{4})\beta _{4}] \end{array}\displaystyle \right \rangle}{a\pi s [I_{\eta} ( - h/2) - I_{\eta} (h/2)]^{2}} \\ \times \theta _{0} \beta _{4}(2q/\gamma )(2/a)e^{(\beta _{3} + \beta _{4})x - 3\gamma x/2}\sin (h\pi /2)\sin (\vartheta _{n}y) \end{array} $$

(52)

The general solution can be expressed as the sum of the complementary and particular solutions as $\chi = \chi _{c} + \chi _{p}$. The separation of variables can get the complementary part $\chi _{c}$ (Ohmichi and Noda 2006) of Eq. (52)

$$ \left ( \textstyle\begin{array}{c} 1 \\ x \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} 1 \\ y \\ \beta _{3} \\ ye^{\beta _{3}y} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} 1 \\ x \\ x^{2} \\ x^{3} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} 1 \\ e^{\beta _{3}y} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} 1 \\ x \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{c} e^{\beta _{3}\sqrt{\upsilon} /2} \\ e^{ - \beta _{3}\sqrt{\upsilon} /2} \end{array}\displaystyle \right ) e^{\Upsilon _{i}x}e^{\wp y} e^{\Psi x}e^{\Delta _{i}y} i = 1,2,3,4 $$

(53)

in which $\beta _{3} \ne 0$ and $\Upsilon _{i}$ is root of the characteristic equation

$$ \Upsilon ^{4} + (2\wp ^{2} - 2\beta _{3}\wp - \upsilon \beta _{3}^{2})\Upsilon ^{2} + \wp ^{2}(\wp - \beta _{3})^{2} = 0 $$

(54)

and $\Delta _{i}$ is root of the characteristic equation

$$ \Delta ^{4} - 2\beta _{3}\Delta ^{3} + (\beta _{3}^{2} + 2\Psi ^{2})\Delta ^{2} - 2\beta _{3}\Psi ^{2}\Delta + \Psi ^{2}(\Psi ^{2} - \upsilon \beta _{3}^{2}) = 0 $$

(55)

and $p_{ni}$ is root of the characteristic equation

$$ p_{n}^{4} - 2\beta _{3}p_{n}^{3} + (\beta _{3}^{2} - 2\beta _{n}^{2})p_{n}^{2} + 2\beta _{3}\beta _{n}^{2}p_{n} + \beta _{n}^{2}(\beta _{n}^{2} + \upsilon \beta _{3}^{2}) = 0 $$

(56)

Therefore, the complementary solution $\chi _{c}$ of the equation

$$ \begin{aligned} \chi _{c} ={}& A_{0} + B_{0}y + C_{0}e^{\beta _{3}y} + D_{0}ye^{\beta _{3}y} \\ &{}+ \sum _{n = 1}^{\infty} (A_{n}e^{p_{n1}y} + B_{n}e^{p_{n2}y} + C_{n}e^{p_{n3}y} + D_{n}e^{p_{n4}y} )\cos \vartheta _{n}x \end{aligned} $$

(57)

The particular integral $\chi _{p}$ is given by

$$ \chi _{p} = \frac{4\theta _{0} \beta _{4}^{2}q\sin (h\pi /2)K_{\eta} (h/2)}{a^{2}\pi s [I_{\eta} ( - h/2) - I_{\eta} (h/2)]^{2}}\sum _{m = 0}^{\infty} \frac{A^{2m + \eta} e^{\Omega x}\sin (\vartheta _{n}y)}{m!\Gamma (m + \eta + 1)} [\Lambda _{1} + \Lambda _{2}e^{ - \gamma x} + \Lambda _{3}e^{ - \gamma x/2}] $$

(58)

where

$$ \textstyle\begin{array}{l} \Lambda _{1} = \frac{ - \gamma \beta _{4}(\gamma - 2\beta _{4})}{\Omega ^{4} - 2\beta _{3} \Omega ^{3} + \beta _{3}^{2} \Omega ^{2}}, \Lambda _{2} = \frac{\gamma ^{3}\beta _{4}^{3}}{(\Omega - \gamma )^{4} - 2\beta _{3} (\Omega - \gamma )^{3} + \beta _{3}^{2} (\Omega - \gamma )^{2}}, \\ \Lambda _{3} = \frac{(5\gamma - 4\beta _{4})\beta _{4}^{2m + \eta}}{(\Omega - \gamma /2)^{4} - 2\beta _{3} (\Omega - \gamma /2)^{3} + \beta _{3}^{2} (\Omega - \gamma /2)^{2}}, \\ \Omega = 2k + \eta + \beta _{3} + \beta _{4} - \gamma /2 \end{array} $$

(59)

Thermal stresses can be obtained from Eq. (57)-(58) and (25)

$$ \begin{aligned} \sigma _{xx} ={}& (C_{0}\beta _{3}^{2} + D_{0}\beta _{3}^{2}y + 2D_{0}\beta _{3})e^{\beta _{3}y} \\ &{}+ \sum _{n = 1}^{\infty} (A_{n}p_{n1}^{2} e^{p_{n1}y} + B_{n}p_{n2}^{2} e^{p_{n2}y} + C_{n}p_{n3}^{2}e^{p_{n3}y} + D_{n}p_{n4}^{2}e^{p_{n4}y} )\cos \vartheta _{n}x \\ &{}- \vartheta _{n}^{2}\frac{4\theta _{0} \beta _{4}^{2}q\sin (h\pi /2)K_{\eta} (h/2)}{a^{2}\pi s [I_{\eta} ( - h/2) - I_{\eta} (h/2)]^{2}}\sum _{m = 0}^{\infty} \frac{A^{2m + \eta} e^{\Omega x}\sin (\vartheta _{n}y)}{m!\Gamma (m + \eta + 1)} \\ &{}\times [\Lambda _{1} + \Lambda _{2}e^{ - \gamma x} + \Lambda _{3}e^{ - \gamma x/2}] \end{aligned} $$

(60)

$$ \begin{aligned} \sigma _{xy} ={}& - \sum _{n = 1}^{\infty} (A_{n}p_{n1}e^{p_{n1}y} + B_{n}p_{n2}e^{p_{n2}y} + C_{n}p_{n3}e^{p_{n3}y} + D_{n}p_{n4}e^{p_{n4}y} )\vartheta _{n}\sin \vartheta _{n}x \\ &{}+ \frac{4\theta _{0} \beta _{4}^{2}q\sin (h\pi /2)K_{\eta} (h/2)}{a^{2}\pi s [I_{\eta} ( - h/2) - I_{\eta} (h/2)]^{2}}\sum _{m = 0}^{\infty} \frac{A^{2m + \eta} e^{\Omega x}\beta \cos (\vartheta _{n}y)}{m!\Gamma (m + \eta + 1)} \\ &{}\times [\Omega \Lambda _{1} + \Lambda _{2}(\Omega - \gamma )e^{ - \gamma x} + \Lambda _{3}(\Omega - \gamma /2)e^{ - \gamma x/2}] \end{aligned} $$

(61)

$$ \begin{aligned} \sigma _{yy} ={}& - \sum _{n = 1}^{\infty} (A_{n}e^{p_{n1}y} + B_{n}e^{p_{n2}y} + C_{n}e^{p_{n3}y} + D_{n}e^{p_{n4}y} )\beta _{n}^{2}\cos \vartheta _{n}x \\ &{}+ \frac{4\theta _{0} \beta _{4}^{2}q\sin (h\pi /2)K_{\eta} (h/2)}{a^{2}\pi s [I_{\eta} ( - h/2) - I_{\eta} (h/2)]^{2}}\sum _{m = 0}^{\infty} \frac{A^{2m + \eta} e^{\Omega x}\sin (\vartheta _{n}y)}{m!\Gamma (m + \eta + 1)} \\ &{}\times [\Omega ^{2}\Lambda _{1} + \Lambda _{2}(\Omega - \gamma )^{2}e^{ - \gamma x} + \Lambda _{3}(\Omega - \gamma /2)^{2}e^{ - \gamma x/2}] \end{aligned} $$

(62)

The unknown constants $A_{n}$, $B_{n}$, $C_{n}$, $D_{n}$ can be obtained from Eqs. (60)-(61) and (30); and $C_{0}$, $D_{0}$ can be obtained from Eqs. (62) and (31). The lengthy calculation has been omitted for conciseness, but it should still be considered for numerical calculations.

5 Inversion of the transformed functions

The inversion formula for Laplace transform for Eq. (32) can be written as

$$ f(x,y,t) = \mathcal{L}^{ - 1}[f(x,y,t)] = \frac{1}{2\pi i}\int _{d - i\infty}^{d + i\infty} e^{st} \bar{f}(x,y,s)ds $$

(63)

Taking $s = d + iz$ in Eq. (63), one obtains

$$ f(x,y,t) = \frac{e^{d t}}{2\pi} \int _{ - \infty}^{\infty} e^{i t z} \bar{f}(x,y,d + iz)dz $$

(64)

Now, taking Fourier series expansion of the function $h(x,y,t) = e^{ - d t} f(x,y,t)$ in the interval [$0,2L$], one obtains the approximate formula (Durbin 1974) summed up to a finite number $N_{0}$ of terms as

$$ \begin{aligned} f_{N}(x,y,t)& = \frac{e^{d t}}{L}\left \{ \frac{\bar{f}(x,y,d)}{2} + \operatorname{Re} \sum _{k = 1}^{N} [e^{i\wp} \bar{f}(x,y,d + i\wp )] \right \} + E_{r} \\ &= \frac{1}{2}C_{0} + \sum _{k = 1}^{N} C_{k} + E_{r} \end{aligned} $$

(65)

where $\wp = k\pi /L$, $N_{0}$ is a finite integer, $d$ parameter has a value of 5 $\leq \ dt\ \leq$ 10, and $E_{r}$ is discretization error is added to produce the total approximate error, and

$$ C_{k} = \frac{\exp (dt)}{T}\left \{ \exp \left [ ik\pi t/T\overline{f}\left ( x,d + i\frac{k\pi t}{T} \right ) \right ] \right \} $$

(66)

The “Korrektur” method allows a reduction of the discretization error without enlarging the truncation error. Therefore, using Eq. (65) can be expressed as

$$ f_{N}(x,y,t) = f_{N}(x,y,t) - e^{ - 2d L}f_{N'}(x,y,2L + t), N < N' $$

(67)

we shall now describe the $\varepsilon$-algorithm that is used to accelerate the convergence of the series in Eq. (65). Let $N = 2q + 1$, where $q$ is a natural number and let $S_{m} = \sum _{k = 1}^{m} C_{k}$ be the sequence of partial sums of series in (65). We define the $\varepsilon$-sequence by $\varepsilon _{0,m} = 0,\ldots\varepsilon _{1,m} = S_{m}$ and $\varepsilon _{p + 1,m} = \varepsilon _{p - 1,m + 1} + 1/(\varepsilon _{p,m + 1} - \varepsilon _{p,m})$, $p = 1,2,3$,.... It can be shown (Honig and Hirdes 1984) that the sequence $\varepsilon _{1,1}, \varepsilon _{3,1},\varepsilon _{5,1},\ldots\varepsilon _{N,1}$ converges to $f(x,y,t) + E_{r} - C_{0}/2$ faster than the sequence of partial sums $s_{m}$ ($m = 1,2,3,\ldots$). The actual procedure used to invert the Laplace transform consists of using Eq. (79) together with the $\varepsilon$-algorithm. The actual procedure used to invert the Laplace transform consists of using Eq. (66). The values of $d = 7.5$ and $L$ are chosen according to the criterion outlined in Durbin (1974).

6 Numerical results and discussion

This section conducts numerical computations to demonstrate the impact of phase delays of heat flux, fractional order, temperature discrepancy factor, and material attributes on the transient temperature field and its associated stress under memory-dependent derivatives. For numerical calculations, the following physical parameters were considered: $h = 1$, $a = 1$, and the reference temperature as 150⁰C. The thermomechanical properties composed of partially stabilized zirconia (PSZ), and austenitic stainless steel (SUS304) are given in Table 1.

Table 1 Thermo-mechanical properties of PSZ and SUS 304

In this session, numerical calculations were conducted to analyze the impact of heating on the plate. The results of these calculations are shown in the following figures using the MATHEMATICA program.

Figure 2 illustrates the spatial arrangement of the temperature distribution at different dimensionless time intervals using the MDD kernel function. At the beginning, the dimensionless temperature change is zero on the initial surface, as anticipated. However, the $x$-axis along the far end surface has a greater magnitude in dimensionless temperature. The temperature change in the FGM layer is time-dependent and observed with propagation characteristics of wave-like phenomena. For instance, the temperature up to position $x = 0.5$ remains constant or slightly gradual change for $t = 0.2$ and 0.8, respectively. It suggests that thermal waves do not propagate to these positions within such short time intervals. However, when the value of $x$ exceeds 0.5, the temperature shift can be observed over the entire FGM layer.

Fig. 2

Temperature profile when $\alpha = 0.8$, $\tau _{q} = 0.3$, $b = 0.8$, $\delta = - 1$, $\gamma = 1$

Figure 3 illustrates the impact of the FGM parameter $\gamma$ along the $y$-axis on the temperature distributions represented by Eq. (51) with $x = 0.5$. The temperatures slightly fall along the $y$-axis in proportion to the $\gamma$, since the heat flow from the boundary $x = 1$ also rises with the parameter $\gamma$. Table 2 displays the disparity in temperature distributions between homogeneous materials (HM) and functionally graded materials (FGM) along the $y$-axis, as shown by Eq. (51). For $\gamma = 1.2$, the thermal conductivities of FGM are greater than those of HM. As a result, the heat input of FGM from the boundary $x = 0.5$ is bigger than that of HM.

Fig. 3

Temperature profile when x = 0.5, $\alpha = 0.8$, $\tau _{q} = 0.3$, $b = 0.8$, $\delta = - 1$

Table 2 Comparison of temperature profile at x = 0.5 along the x-axis

Following Akbarzadeh and Chen (2013), Ortigueira (2011), fixing $\alpha = 1$ in Eq. (16), the heat flux propagation velocity can be obtained as $V = \sqrt{1/\tau _{q}D_{\omega}}$. As the kernel function in Eq. (34) is 1 and taking $\tau _{q} = 0.0146$, one obtains $V = \{ 68.49\}^{1/2}$. The dimensionless propagation distance $\Delta x = Vt = \{ 68.49\}^{1/2}(0.06) = 0.5$, is in agreement with the numerical prediction, as shown in Fig. 4. It is reflected that if the time is taken as $t = 0.05$, then the hyperbolic temperature increases with the increase in position is less than $\Delta x = 0.5$. By setting $\eta =1$ in Eq. (45), we observe that the above modified Bessel equation is mathematically equivalent to the one described in reference Zhou et al. (2011). To verify the validity of the numerical inversion of the Laplace transform, an exact solution for the classical Fourier heat conduction with kernel $K(t - \xi ) = 1$ was obtained. The exact temperature, denoted as Texact, is provided in reference Zhou et al. (2011), as shown in Figure 6. The temperature Tnum may be determined using Eq. (51). The error ratio is defined as (Tnum - Texact)/Texact × 100 [%]. The error ratio reaches its highest value of 0.611 when $x$ is equal to 0.8 and $y$ is equal to 0.2. Figures 5 and 7 show the effects of gradient indices $\gamma$ and $\delta$ on the distribution of temperature fields, respectively. From Fig. 5, it can be seen that with a fixed fractional order $\alpha$ with gradient indices $\gamma$ varying from −1 to 1, the wave-like behaviour of the fractional heat conduction model becomes more evident. Therefore, the fractional heat conduction model can capture not only the essence of hyperbolic heat conduction but also the diffusion characteristic of classical Fourier heat conduction, irrespective of MDD kernels. Figure 7 also shows a wave-like distribution with gradient indices $\delta$ varying from −2 to 2 for different MDD kernel functions. Initially it is noticed that the temperature rises slightly, then decrease till to attain minimum value and then increases exponentially with the increase of x until finished.

Fig. 4

Temperature when $\alpha = 0.8$, $\tau _{q} = 0.0146$, $b = 0.6$, $\delta = - 1$, $\gamma = 1$

Fig. 5

Effect of gradient index $\gamma$ when x = 0.75, $\alpha = 0.8$, $\tau _{q} = 0.3$, and $\delta = - 1$

Fig. 6

Exact Vs numerical inversion Laplace transform-based temperature

Fig. 7

Temperature for various gradient indices $\delta$ when $\alpha = 0.8$, $\tau _{q} = 0.3$, $\lambda = 1$

The through-the-length variation of the longitudinal normal stress $\sigma _{xx}$, the transverse shear stress $\sigma _{xy}$, and the transverse normal stress $\sigma _{yy}$ change significantly along the $x$-axis. For example, in Fig. 8, at $x = 0.4 \sim 0.5$, the magnitude of the longitudinal stress $\sigma _{xx}$ is maximum at a point throughout the length due to high tensile area during the fixed value of $\alpha = 0.8$, $\tau _{q} = 0.0146$, $b = 0.6$, $\delta = -$ 1, $\gamma = 1$. Figures 8 and 10 show that the normal stress $\sigma _{xx}$ and shear stress $\sigma _{xy}$ have zero temperature at both ends, thus satisfying Eq. (30). Similar comments apply to the transverse shear stress $\sigma _{xy}$ whose value is about 33% less than that of the longitudinal normal stress $\sigma _{xx}$. The through-the-width variation of the normal stress $\sigma _{yy}$ is a non-linear sinusoidal nature since material properties and the temperature change vary through the thickness, as illustrated in Fig. 9.

Fig. 8

Normal stress $\sigma _{xx}$ when $\alpha = 0.8$, $\tau _{q} = 0.0146$, $b = 0.6$, $\delta = - 1$, $\gamma = 1$

Fig. 9

Normal stress $\sigma _{yy}$ when $\alpha = 0.8$, $\tau _{q} = 0.0146$, $b = 0.6$, $\delta = - 1$, $\gamma = 1$

Fig. 10

Shear stress $\sigma _{xy}$ when $\alpha = 0.8$, $\tau _{q} = 0.0146$, $b = 0.6$, $\delta = - 1$, $\gamma = 1$

7 Conclusion

The study develops a comprehensive thermal uncoupled model for memory-dependent differential, examining thermal flow under rapid temperature increase with a two-dimensional FG plate. Appropriately selecting the volumetric ratio of ceramics and metal components can greatly lower the heat stresses in the plate. An increase in the coefficient of linear thermal expansion reduces both maximum and lowest thermal stresses, while an increase in Young’s modulus increases both. Using appropriate compositional materials can minimize thermal stresses, potentially reaching negligible levels. The numerical results yield several inferences:

• Memory-dependent derivatives’ non-Fourier effects significantly impact thermal field response history and distribution, with energy dissipation potentially causing temperature decrease without heat transfer.

• Revised categorization system for materials based on memory-dependent derivative parameters evaluates heat conduction capacity, considering thermoelasticity with two temperatures.

• The phase-lag heat and temperature gradient significantly impact thermal field variables in memory-dependent derivatives time. The temperature change rate increase is influenced by the fractional order and relaxation time during the process. Thus, different theories like CTE, HTE, SFTE, and EFTE models can be derived.

• The PSZ/SUS304 FGP material experiences the maximum compressive stress on the heating surface. It experiences a maximum tensile stress, which is lower than the maximum compressive stress. The maximum stresses occur along the normal stress $\sigma _{yy}$, whereas they are less in normal stress $\sigma _{xx}$ and shear stress $\sigma _{xy}$.

The study suggests that future research could effectively utilize micro- and nano-functionally graded resonators with different compositional materials like ZrO2/Ti-6Al-4V, ZrO2/Ti-6Al-4V and ZrO2/SUS304.

Appendix A: The kernel function

In this context, Laplace transform of Eq. (8)

$$ G(s,\omega ) = = \left \{ \textstyle\begin{array}{l} 1 - e^{ - s\omega}; \kappa (t - \xi ) = 1 \\ 1 - \frac{1 - e^{ - s\omega}}{s}; \kappa (t - \xi ) = 1 - (t - \xi ) \\ \left ( 1 - \frac{2}{s\omega} \right ) + \frac{2(1 - e^{ - s\omega} )}{s^{2}\omega ^{2}}; \kappa (t - \xi ) = \left ( 1 - \frac{t - \xi}{\omega} \right )^{2} \end{array}\displaystyle \right . $$

(A.1)