Transient heat conduction in functionally graded thick hollow cylinders by analytical method

Abstract

In this article, transient heat conduction in a cylindrical shell of functionally graded material is studied by using analytical method. The shell is assumed to be in axisymmetry conditions. The material properties are considered to be nonlinear with a power law distribution through the thickness. The temperature distribution is derived analytically by using the Bessel functions. To verify the proposed method the obtained numerical results are compared with the published results. The comparisons of temperature distribution between various time and material properties are presented.

1 Introduction

Functionally graded materials (FGMs) are new kind of materials. These materials are spatial composite within which the mechanical properties vary continuously in the macroscopic sense from one surface to the other. These materials are expected to be used for thermal applications and high rate temperature loading. An important and useful aspect in this case is the determination of transient temperature distribution. Analytical and computational studies of appointing stresses and displacements in cylindrical shell made of FGM have been carried out by some of researchers as following.

Temperature and stress distributions were determined in a stress-relief-type plate of FGMs with steady state and transient temperature distributions by Awaji [1]. A multi-layered material model was employed to solve the transient temperature field in an FGM strip with continuous and piecewise differentiable material properties by Jin [2]. He obtained a closed form asymptotic solution of the temperature field for short times, by using an asymptotic analysis and an integration technique and the Laplace transform. A general analysis of one dimensional steady state thermal stresses in a thick hollow cylinder under axisymmetry and nonaxisymmetry loads was developed by Jabbari et al. [3,4].

A local boundary integral equation method with the moving least squares approximation of physical fields was applied to transient heat conduction analysis in functionally graded materials by Sladek et al. [5]. They solved the initial boundary value problem in the Laplace transform domain with a subsequent numerical Laplace inversion to obtain time-dependent solutions. Tarn et al. [6] have studied the end effects of steady state heat conduction in a hollow or solid circular cylinder of FGM under 2D thermal loads with arbitrary end conditions. They evaluated the decay length that characterizes the end effects on thermal field by using matrix algebra and eigen function expansion. The sensivity analysis of heat conduction for functionally graded materials and the steady state, transient problem treated with the direct method and the adjoint method were presented by Chen et al. [7]. The precise time integration method is employed to solve the transient problem by them. Transient temperature field and associated thermal stresses in functionally graded materials have been determined by using a finite element-finite difference method (FEM/FDM) by Wang et al. [8]. Thermal shock fracture of a FGM plate and the thermal shock resistance of FGMs were analyzed by them. A finite element/finite difference method (FEM/FDM) was developed also to solve the time-dependent temperature field in non-homogeneous materials such as functionally graded materials by Wang et al. [9].

This paper presents an analytical solution for transient temperature distribution in functionally graded thick hollow cylinders.

2 Temperature field

To determine the temperature distribution in functionally graded thick hollow cylinder with inner and outer radii a and b, the following boundary and initial conditions for the temperature field are considered. The inner surface of shell is considered to be made of a ceramic material. The boundary conditions are:

$$k\frac{\partial T}{\partial r} + hT = 0 \quad \hbox{at}\ r = a$$

(1)

$$\frac{\partial T}{\partial r} = 0 \quad \hbox{at} \ r = b$$

(2)

where k is the thermal conductivity and h is the heat transfer coefficient and T is defined by:

$$T{\left(r,t\right)} = \theta {\left(r,t\right)} - \theta _{1}$$

(3)

where θ(r,t) is the temperature of shell body and θ ₁ is the temperature of fluid that flows in the cylinder. The initial condition for temperature field is:

$$T{\left(r,0\right)} = T_{0}$$

(4)

where T ₀ is a constant temperature. The heat transfer equation in functionally graded hollow cylinder for plane strain and axisymmetry case is:

$$\frac{1}{r}\frac{\partial}{\partial r}{\left({k\cdot r\cdot \frac{\partial T}{\partial r}}\right)} = \rho c\frac{\partial T}{\partial t}$$

(5)

where ρ is the density and c is the specific heat. We used the following nondimensional variables for temperature field.

$$\bar{T} = \frac{T}{T_{0}},\quad \bar{r} = \frac{r}{a},\quad \bar{t} = \frac{th}{\rho c_{\rm c}\cdot a},\quad \bar{\rho}\bar{c} = \frac{\rho c}{\rho c_{\rm c}},\quad \bar{k} = \frac{k}{ah}$$

Where ρ c _c is the standard value (the density and specific heat of inner surface ceramic material). Using these terms, the heat transfer and boundary conditions equations can be written as follows:

$$\frac{1}{\bar{r}}\frac{\partial}{\partial \bar{r}}{\left({\bar{k}\cdot \bar{r}\cdot \frac{\partial \bar{T}}{\partial \bar{r}}} \right)} = \bar {\rho}\bar{c}\frac{\partial \bar{T}}{\partial \bar{t}}$$

(6)

$$\bar{k}\frac{\partial \bar{T}}{\partial \bar{r}} + \bar{T} = 0\quad at\ \bar{r} = 1$$

(7)

$$\frac{\partial \bar{T}}{\partial \bar{r}} = 0\quad at\ \bar{r} = b/a$$

(8)

$$\bar{T}{\left(r,0\right)} = 1$$

(9)

It is assumed that the thermal conductivity $\bar{k}$ and $\bar{\rho}\bar{c}$ are the power functions of r as:

$$\bar{k} = k_{0} \bar{r}^{m_{1}}$$

(10)

$$\bar{\rho}\bar{c} = \rho c_{0} \bar{r}^{m_{2}}$$

(11)

In the above equations k ₀, ρ c ₀, m ₁, m ₂ are the material constants and ρ c ₀  =  1 for the ceramic material. With introducing Eqs. 10 and 11 in Eq. 6 the following equation is obtained:

$$k_{0} \bar{r}^{m} \frac{\partial ^{2} \bar{T}}{\partial \bar{r}^{2}} + k_{0} {\left( m_{1} + 1\right)}\bar{r}^{m - 1} \frac{\partial \bar{T}}{\partial \bar{r}} = \rho c_{0} \frac{\partial \bar{T}}{\partial \bar{t}}$$

(12)

where:

$$m = m_{1} - m_{2}$$

(13)

To solve the partial differential Equation (12), by using the separation of variables method, the following solution is assumed:

$$\bar{T}{\left( \bar{r},\bar{t} \right)} = R{\left(\bar{r} \right)}\cdot g{\left(\bar{t}\right)}$$

(14)

Substituting Eq. 14 into Eq. 12 yields:

$$k_{0} \bar{r}^{m} \frac{\partial ^{2} R}{\partial r^{2}}\cdot g + k_{0} {\left( {m_{1} + 1} \right)}\bar{r}^{m - 1}\frac{\partial R}{\partial r}\cdot g = \rho c_{0} \frac{\partial g}{\partial t}\cdot R$$

(15)

or,

$$\frac{k_{0} \bar{r}^{m} \frac{\partial ^{2} R}{\partial \bar{r}^{2}} + k_{0} {\left({m_{1} + 1} \right)}\bar{r}^{m - 1} \frac{\partial R}{\partial \bar{r}}}{R} = \frac{\rho c_{0} \frac{\partial g}{\partial \bar{t}}}{g} = - \lambda^{2}$$

(16)

In the above equations, λ is a constant value. From Eq. 16, two ordinary differential equations are obtained as follows:

$$\rho c_{0} \frac{\partial g}{\partial \bar{t}} + \lambda ^{2} g = 0$$

(17)

$$k_{0} \bar{r}^{m} \frac{\partial ^{2} R}{\partial \bar{r}^{2}} + k_{0} {\left(m_{1} + 1\right)}\bar{r}^{m - 1} \frac{\partial R}{\partial \bar{r}} + \lambda ^{2} R = 0$$

(18)

Solutions of Eqs. 17 and 18 are:

$$g(\bar{t}) = A_{1} {\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}}$$

(19)

$$R{\left(\bar{r}\right)} = \bar{r}^{- \frac{m_{1}}{2}}{\left\{{B_{1} J_{n} {\left({\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2} Y_{n} {\left({\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}}$$

(20)

where:

$$n = \frac{m_{1}}{m - 2}$$

(21)

$$\gamma = \frac{2\lambda}{{\sqrt {k_{0}}}{\left( {m - 2} \right)}}$$

(22)

Thus the temperature distribution is:

$$\bar{T}{\left({\bar{r},\bar{t}} \right)} = {\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}}\cdot \bar{r}^{- \frac{m_{1}}{2}} {\left\{{B_{1} J_{n} {\left({\gamma \bar{r}^{\frac{2 - m}{2}}}\right)} + B_{2} Y_{n} {\left({\gamma \bar{r}^{\frac{{2 - m}}{2}}} \right)}} \right\}}$$

(23)

By using Eqs. 23 and 10, the boundary condition (7) is rewritten as the follows:

$$\begin{aligned} \,& k_{0} \bar{r}^{m_{1}} {\left[ {{\rm e}^{- \frac{\lambda ^{2} }{\rho c_{0}}\bar{t}} {\left({-\frac{m_{1}}{2}} \right)}\bar{r}^{- \frac{m_{1}}{2} - 1} {\left\{{B_{1} J_{n} {\left(\gamma \bar{r}^{\frac{2 - m}{2}} \right)} + B_{2} Y_{n} {\left(\gamma \bar{r}^{\frac{2 - m}{2}} \right)}} \right\}}} \right]} \\ \,&\quad + k_{0} \bar{r}^{m_{1}} {\left[ {{\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}}\cdot \bar{r}^{- \frac{m_{1}}{2}} \gamma {\left( {\frac{2 - m}{2}} \right)}\bar{r}^{- \frac{m}{2}} {\left\{{B_{1} {J}^{\prime}_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2} {Y}^{\prime}_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}}} \right]} \\ \,&\quad + {\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}} \cdot \bar{r}^{- \frac{m_{1}}{2}} {\left\{{B_{1} J_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2} Y_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}} = 0\\ \end{aligned}$$

(24)

where $\bar{r} = 1,$ thus:

$$\frac{B_{2}}{B_{1}} = \frac{f_{2}}{f_{1}}$$

(25)

where

$$f_{1} = {\left( {(1)^{- \frac{m_{1}}{2}} - \frac{m_{1} }{2}k_{0} (1)^{\frac{m_{1}}{2} - 1}} \right)}Y_{n} {\left( {\gamma (1)^{\frac{2 - m}{2}}} \right)} + {\left({\frac{2 - m}{2}} \right)}\gamma k_{0} (1)^{\frac{m_{2}}{2}} \cdot {Y}^{\prime}_{n} {\left( {\gamma (1)^{\frac{2 - m}{2}}} \right)}$$

(26)

$$f_{2} = {\left( {(1)^{- \frac{m_{1}}{2}} - \frac{m_{1} }{2}k_{0} (1)^{\frac{m_{1}}{2} - 1}} \right)}J_{n} {\left( {\gamma (1)^{\frac{2 - m}{2}}} \right)} + {\left( {\frac{2 - m}{2}} \right)}\gamma k_{0} (1)^{\frac{m_{2}}{2}} \cdot {J}^{\prime}_{n} {\left({\gamma (1)^{\frac{2 - m}{2}}} \right)}$$

(27)

and the boundary condition (8) is written as:

$$\begin{aligned} \frac{\partial \bar{T}}{\partial \bar{r}} &= {\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}} {\left({- \frac{m_{1}}{2}} \right)}\bar{r}^{- \frac{{m_{1}}}{2} - 1} {\left\{{B_{1} J_{n} {\left( {\gamma \bar{r}^{\frac{{2 - m}}{2}}}\right)} + B_{2} Y_{n} {\left( {\gamma \bar{r}^{\frac{{2 - m}}{2}}}\right)}} \right\}} \\ & + {\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}}\cdot \bar{r}^{- \frac{m_{1}}{2}} \gamma {\left( {\frac{2 - m}{2}} \right)}\bar{r}^{- \frac{m}{2}} {\left\{{B_{1} {J}^{\prime}_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2} {Y}^{\prime}_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}} = 0 \\ \end{aligned}$$

(28)

where $\bar{r} = b/a,$ thus:

$$\frac{B_{2}}{B_{1}} = \frac{f_{4}}{f_{3}}$$

(29)

where

$$f_{3} = {\left({\frac{2 - m}{2}} \right)}\gamma (b/a)^{\frac{m_{2} - 2m_{1}}{2}}\cdot {Y}^{\prime}_{n} {\left( {\gamma (b/a)^{\frac{2 - m}{2}}} \right)} - \frac{m_{1}}{2} (b/a)^{- \frac{m_{1}}{2} - 1}\cdot Y_{n} {\left( {\gamma (b/a)^{\frac{2 - m}{2}}} \right)}$$

(30)

$$ f_{4} = {\left( {\frac{2 - m}{2}} \right)}\gamma (b/a)^{\frac{m_{2} - 2m_{1}}{2}}\cdot {J}^{\prime}_{n} {\left({\gamma (b/a)^{\frac{2 - m}{2}}} \right)} - \frac{m_{1}}{2}(b/a)^{- \frac{m_{1}}{2} - 1}\cdot J_{n} {\left( {\gamma (b/a)^{\frac{2 - m}{2}}} \right)} $$

(31)

and

$${J}^{\prime}_{n} {\left({\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} = \frac{\rm d}{\hbox{d}\eta}{\left[{J_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right]} $$

(32)

$${Y}^{\prime}_{n} {\left( {\gamma \bar{r}^{\frac{2 - m}{2}}} \right)} = \frac{\rm d}{\hbox{d}\eta}{\left[ {Y_{n} {\left({\gamma \bar{r}^{\frac{2 - m}{2}}} \right)}} \right]} $$

(33)

where $\eta = \gamma \bar{r}^{\frac{2 - m}{2}}.$ The right-hand side of both Eqs. 25 and 29 shall be equal.

$$\frac{f_{2}}{f_{1}} = \frac{f_{4}}{f_{3}}$$

(34)

The eigenvalue γ can be obtained from Eq. 35 as the follows:

$$f_{1}\cdot f_{4} - f_{3}\cdot f_{2} = 0$$

(35)

The Eq. 35 can be solved by using numerical methods, such as Newton–Rophson method and using MATLAB software. The boundary condition (7) can be derived by using Eqs. 26 and 27 as follows:

$${\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}} (B_{2}\cdot f_{1} - B_{1}\cdot f_{2}) = 0$$

(36)

The coefficient B ₁ replaces by Eq. 29 and then:

$${\rm e}^{- \frac{\lambda ^{2}}{\rho c_{0}}\bar{t}} (B_{2}\cdot f_{1} - B_{2} \frac{f_{3}}{f_{4}}\cdot f_{2})= {\rm e}^{- \frac{\lambda ^{2} }{\rho c_{0}}}\bar{t} \frac{B_{2}}{f_{4}}(f_{1}\cdot f_{4} - f_{3}\cdot f_{2}) = 0$$

(37)

It means that the boundary condition (7) is satisfied for each eigenvalues. By using similar method, the boundary condition (8) can be satisfied. There are infinite numbers of roots for Eq. 35 thus Eq. 23 can be written:

$$\bar{T}{\left( {\bar{r},\bar{t}} \right)} = {\sum\limits_{i = 1}^\infty {{\rm e}^{- \frac{\lambda _{i} ^{2}}{\rho c_{0} }\bar{t}}\cdot \bar{r}^{- \frac{m_{1}}{2}} {\left\{{B_{1i} J_{n} {\left({\gamma _{i} \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2i} Y_{n} {\left( {\gamma _{i} \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}}}} $$

(38)

where γ _i (eigen values) are the roots of Eq. 35 and i = 1,..., ∞. To determine of the value of B _1i and B _2i , we consider N numbers of eigenvalues. By using the initial conditions at t = 0, Eq. 38 can be satisfied.

$$1 = {\sum\limits_{i = 1}^\infty {\bar{r}^{- \frac{m_{1}}{2}} {\left\{{B_{1i} J_{n} {\left({\gamma _{i} \bar{r}^{\frac{2 - m}{2}}} \right)} + B_{2i} Y_{n} {\left({\gamma _{i} \bar{r}^{\frac{2 - m}{2}}} \right)}} \right\}}}}$$

(39)

For 2N values of r between 1 and b/a, the Eq. 39 can be calculated and 2N equations will derive. These derived equations can be written in matrix form as follows:

$${\left[ {\begin{array}{*{20}c} {k{\left( {1,1} \right)}} & . & . & . & {k{\left(1,2N\right)}} \\ . & . & & & . \\ . & & . & & . \\ . & & & . & . \\ {k{\left(2N,1\right)}} & . & . & . & {k{\left(2N,2N\right)}} \\ \end{array}} \right]}{\left\{ {\begin{array}{*{20}c} {B_{11}} \\ {B_{21}} \\ . \\ {B_{1N}} \\ {B_{2N}} \\ \end{array}} \right\}} = {\left\{{\begin{array}{*{20}c} {1} \\ . \\ . \\ . \\ 1 \\ \end{array}} \right\}}$$

(40)

The components of k matrix are:

$$k{\left(i,2j - 1\right)} = \bar{r}_{i}^{- \frac{m_{1} }{2}}\cdot J_{n} {\left( {\gamma _{j}\cdot \bar{r}_{i}^{\frac{2 - m}{2}}} \right)}$$

(41)

$$k{\left(i,2j\right)} = \bar{r}_{i}^{- \frac{m_{1}}{2}}\cdot Y_{n} {\left({\gamma _{j}\cdot \bar{r}_{i}^{\frac{2 - m}{2}}} \right)} \quad {j}=1,\ldots, N\ \hbox{and}\ i=1,\ldots, 2N$$

(42)

The B _1i and B _2i coefficients are determined from Eq. 40 as:

$${\left\{{\begin{array}{*{20}c} {B_{11}} \\ {B_{21}} \\ . \\ {B_{1N}} \\ {B_{2N}} \\ \end{array}} \right\}} = {\left[ k \right]}^{-1} {\left\{{\begin{array}{*{20}c} {1} \\ . \\ . \\ . \\ 1 \\ \end{array}} \right\}} $$

(43)

To achieve high precision results, the number of eigenvalues in Eq. 38 should be increased.

3 Numerical results and discussion

To verify the proposed method, the functionally graded hollow cylinder with b/a = 1.1 where a and b are inner and outer radii, is considered. Suppose that the inner surface is made of graphite/epoxy with thermal conductivity of k = 0.72 W/m K. This shell is a thin hollow cylinder.

For t=0 and m ₁ = 0 (homogeneous material), the first six eigenvalues are obtained by using the boundary conditions (flux-prescribed at inner and outer surfaces) in Ref. [6]. For simplicity of analysis the power law coefficients for m ₁ and m ₂ are considered to be the same. These eigenvalues are compared with the results presented in Ref. [6]. This comparison is shown in Table 1.The results for various m ₁ and b/a = 1.1 are in good agreement with those obtained according to Ref. [6]. Consider the functionally graded thick hollow cylinder with inner radius a and outer radius b. The boundary and initial conditions are defined in Eqs. 7, 8 and 9. Suppose that the inner surface is made of alumina (ceramic). The alumina specifications are k _c  = 46 W/m K, c _c  = 0.76 kJ/kg K, ρ _c  = 3,800 kg/m³, and inner radius a is 0.25 m.

Table 1 The first six eigenvalues for thin hollow cylinder (b/a = 1.1)

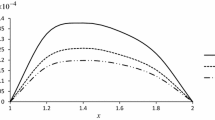
The convection coefficient and temperature of the fluid flowing within hollow cylinder are h = 4,600 W/m² K and θ ₁ = 200° C. The first five eigenvalues of the functionally graded thick hollow cylinder for various values of power index m ₁ and b/a and infinite length are given in Tables 2 and 3. It can be seen that the eigenvalues for various power law exponents are increased as the value of b/a is decreased. By using the proposed method, the behavior of a shell subjected to a transient thermal loading can be shown. Figure 1 shows the radial distribution of temperature for $\bar{t}=0.5$ and b/a = 1.5 and various values of power law exponents. It is evident that the errors decrease as the numbers of eigenvalues are increased. The effects of eigenvalue numbers on the accuracy of the solution are shown in Fig. 2. The accuracy of the results can be improved, by increasing the number of applied eigenvalues. For large values of power exponents, one can see higher rates of heat transfer. Histories of the temperature distribution across the thickness of the shell are illustrated in Fig. 3. Figures 4 and 5 show the radial distribution of temperature and histories of temperature distribution across thickness of shell for b/a = 2. It can be seen from the Figs. 3 and 5 that for small values of b/a, the shell reaches the steady-state temperature profile faster than the case with larger values of b/a. By decreasing the value of b/a, the behavior of the shell approaches to the behavior of a shell made of homogeneous material. The comparison of the present method and a numerical method (using MATLAB software) for m ₁ = m ₂ = 0.5 and b/a = 2, for different times, are illustrated in Fig. 6. The results are in good agreement with obtained results from numerical method (MATLAB software). For m ₁ and m ₂ differing from each other, assume that the outer surface of shell is aluminum with specifications as: k _m  = 204 W/m K, c _m  = 0.896 kJ/kg K, ρ _m  = 2,707 kg/m³

Fig. 1

Radial distribution of temperature for = 0.5 and b/a = 1.5

Fig. 2

The effects of eigenvalue numbers on results

Fig. 3

History of temperature radial distribution for m ₁ = m ₂ = 0.5 and b/a = 1.5

Fig. 4

Radial distribution of temperature for t = 0.5 and b/a = 2

Fig. 5

History of temperature radial distribution for m ₁ = m ₂ = 0.5 and b/a = 2

Fig. 6

The comparison of present results and numerical method

Table 2 The first eight eigenvalues for FGM hollow cylinder (b/a = 1.5)

Table 3 The first eight eigenvalues for FGM hollow cylinder (b/a = 2)

Using Eqs. 10 and 11, the power function exponents m ₁ and m ₂ can be calculated as, m ₁ = 4.018, m ₂ =  −  0.432.The history of temperature distribution across the thickness is shown in Fig. 7.

Fig. 7

History of temperature radial distribution for m ₁ =  4.018, m ₂ =  − 0.432 and b/a = 1.5

4 Conclusion

In this paper, an analytical solution for transient heat conduction of functionally graded thick hollow cylinder is presented in axisymmetry conditions. The material properties through the thickness of the shell are assumed to be nonlinear with a power law distribution. The temperature distribution of functionally graded cylindrical shells are investigated for various power function exponent m ₁ and m ₂. The results of this procedure can be outlined as:

• 1. The trend of the variation of the first eight eigenvalues of functionally graded thick hollow cylinder for various power law exponents and infinite length show that the accuracy of the results can be increased by using more number of eigenvalues.

• 2. The transient temperature distribution in functionally graded thick hollow cylinder is obtained analytically in closed form. This distribution can be useful in determining the thermal stress fields. The optimization of heat conduction can be carried out by using this form of solution.