Effectiveness of nonlinear kernel with memory for a functionally graded solid with size dependency

Abstract

Structures made of graded composites play an important role in various industrial fields, such as aerospace and biomechanics. By incorporating nonlocal stress theory the internal length scale parameter of the nonlocal model provides detailed information on long-range forces of atoms or molecules. This paper investigates the size-dependent modeling of a functionally graded unbounded medium influenced by a heat source and an induced magnetic field on the bounding plane. The heat transport equation is governed by a unified formulation that integrates both the three-phase-lag model and Moore–Gibson–Thompson theory of generalized thermoelasticity, incorporating a memory-dependent derivative with nonlinear and linear kernels. Using nonlocal stress theory, the constitutive equations are addressed. The basic equations are simplified in the transformed domain through the Laplace and Fourier integral transforms. To obtain solutions in the real space-time domain, the Fourier transforms are analytically inverted using residue calculus, with poles of the integrand numerically determined in the complex domain via Laguerre’s method. Subsequently, the numerical inversion of the Laplace transform is performed using a method based on Fourier series expansion. The computational results and corresponding graphical representations reveal significant effects of parameters such as the nonlocality parameter, time-delay parameter, and the influence of the magnetic field. Furthermore, the impact of different kernel functions is examined, demonstrating the superiority of nonlinear kernels over linear kernels within this new theoretical framework.

1 Introduction

The materials characterized by the variation in composition and structure gradually vary over volume, which results in corresponding changes in the properties of the material. These special types of materials are commonly known as functionally graded materials (FGMs). The concept of FGM was first introduced to remove the sharp interface that existed in the traditional composite material and to replace it with the gradually changing interface, which were therein translated into the changing chemical composition of this composite at this interface. Such important characteristics of the FGM motivated the scientific community to make them to be favored in most of the areas in mechanical engineering (Lotfy and Tantawi 2020; Kalkal et al. 2023; Mondal and Sur 2021). Nowadays, there can be a number of applications of FGM addressed in various industries such as aerospace, automobile, biomedical, defense, electrical/electronic, energy, marine, optoelectronics, and thermoelectronics. Thermosensitive materials capable of altering the state are substances that absorb or release significant amounts of energy during melting process, solidification or sublimation. Also note that these materials absorb energy during the heating process when the phase change takes place and in the case where the cooling process energy can be transferred to the environment while returning to the initial phase (Manthena et al. 2017; Abouelregal et al. 2023a, 2024).

The point state is defined as a function of strain at that point, but interatomic regions are ignored entirely in the traditional continuum theories (El-Karamany and Ezzat 2014; Ezzat and Abd-Elaal 2016; Ezzat 2011). Since there can be noted a lack of a well-established scientific assumption that strain is a function of size, researches on traditional continuum mechanics concepts are not good enough for figuring out how micro- and nanostructured materials behave mechanically. As a consequence, scientists came up with revised elasticity models like the couple stress (CS) (Mindlin and Tiersten 1962; Yang et al. 2002), strain gradient (SG) (Lam et al. 2003), general nonlocal (GN) (Fan et al. 2020), and even Eringen’s nonlocal (EN) (Eringen 2002, 1972, 1983) concepts as a way to figure out the problem. The nonlocal theory proposed by Eringen treats a point as reliant on the state of the complete body, and it provides a powerful and accurate framework for investigating nanobeams. Eringen’s hypothesis also takes into account the small-scale parameter, which is not inconsequential when compared to the size of the nanostructured materials.

Over the past few decades, theories of thermoelasticity admitting finite velocity for thermal signals have received a lot of attention to the researchers (Ezzat and Bary 2009; Ezzat et al. 2011, 2018; Ezzat and El-Bary 2016; Ezzat et al. 2014). Lord and Shulman (Lord and Shulman 1967) was the first who presented the first theory of generalized thermoelasticity involving one relaxation time, whereas Green and Lindsay (Green and Lindsay 1972) obtained the second theory of generalized of thermoelasticity with two relaxation times, in contrast to the coupled thermoelasticity theory based on a parabolic heat equation (Biot 1956). Because of the experimental evidences in the support of finiteness of the heat propagation speed, recently, employing the generalized thermoelasticity theories, several remarkable studies have been reported (Sur and Kanoria 2014; Abbas 2007; Abbas and Youssef 2012). One of these modern theories, the so-called three-phase-lag model, was proposed by Roychoudhuri (Roychoudhuri 2007). According to this model,

$$ \left (1+\tau _{q} \frac{\partial}{\partial t}+ \frac{\tau _{q}^{2}}{2}\frac{\partial ^{2}}{\partial t^{2}}\right ) \dot{\mathbf{q}}=-K\left (1+\tau _{T}\frac{\partial}{\partial t} \right ) \nabla \dot{\theta} -K^{\star }\left (1+\tau _{\nu} \frac{\partial}{\partial t}\right ) \nabla \theta , $$

(1)

where $\nabla \theta$ is the temperature gradient at a point $P$ of the material at time $t+\tau _{T}$, $\mathbf{q}$ is the heat flux vector at the point $P$ in time $t+\tau _{q}$, $K$ is the thermal conductivity of the material, and $K^{\star}$ is the conductivity rate parameter (Chakravorty et al. 2017; Sur 2023a). The delay time $\tau _{T}$ is interpreted as that caused by the microstructural interactions and is called the phase lag of the temperature gradient. The other delay time $\tau _{q}$ is interpreted as the relaxation time due to the fast transient effects of thermal inertia and is called the phase lag of the heat flux, and $\tau _{\nu}$ is the phase lag for thermal displacement gradient. Moreover, in recent years, the area of fluid mechanics (Thompson 1972) has gained a lot of interest for the Moore–Gibson–Thompson (MGT) heat conduction law, which is considered by adjoining the energy equation to the equation (Gupta et al. 2022; Chena and Ikehata 2021; Dell’Oro et al. 2016)

$$ \mathbf{q}+\tau _{0} \frac{\partial \mathbf{q}}{\partial t}=-(K \nabla \theta +K^{\star }\nabla \nu ), \;\; \dot{\nu}=\theta , $$

(2)

where $\mathbf{q}$ is the heat flux vector, $\tau _{0}>0$ is the relaxation time, $\nu$ is the thermal displacement, $K$ is the thermal conductivity, and $K^{\star}$ is the conductivity rate parameter (Kumar and Mukhopadhyay 2020; Fernández and Quintanilla 2021). Quintanilla (Quintanilla 2019; Pellicer and Quintanilla 2020) has derived constitutive equations for coupled thermoelasticity theory based on this MGT theory. The uniqueness of the solution and exponential stability of this new theory are also discussed by Quintanilla (Quintanilla 2019; Pellicer and Quintanilla 2020). This new theory can be seen as a fusion of both LS and GN-III (Green and Naghdi 1992a,b, 1993) thermoelasticity theories, and, naturally, it has dragged the interest of the researchers and prompted them to work in this direction (Tiwari 2023; Abouelregal et al. 2023c; Sur 2023a). Under the MGT thermoelasticity theory, Pellicer and Quintanilla (Pellicer and Quintanilla 2020) proved the uniqueness and instability of some thermomechanical problems. The domain of influence results for MGT theory are recently discussed by Jangid and Mukhopadhyay (Jangid and Mukhopadhyay 2020a,b). Recently, Sur (Mondal and Sur 2024) has reported the thermo-hydro-mechanical problem due to the vibration of mining vehicle within porous sea sediments in the context of Moore–Gibson–Thompson theory. Also, Othman et al. (Othman et al. 2023) have studied the influence of memory dependence for a rotating porous solid medium. Further, the theoretical aspects and some practical applicabilities of the MGT theory can be found in (Conti et al. 2020a,b; Bazarra et al. 2021).

Wang and Li (Wang and Li 2011) introduced the first-order memory-dependent derivative (MDD) of a function $f$, defined in an integral form of a common derivative with a kernel function on a slipping interval as follows:

$$ D_{\omega }f(t)=\frac{1}{\omega}\int _{t-\omega}^{t}K(t-\xi )f'(\xi ) d \xi , $$

(3)

where $\omega >0$ is the delay time, and $K(t-\xi )$ is the kernel function, which can be completely customized, e.g., $K(t-\xi )=1$, $1-\frac{t-\xi}{\omega}$, or even $\left (1-\frac{t-\xi}{\omega}\right )^{2}$. The kernel function can be understood as the degree of the past effect on the present. In addition, if $K(t-\xi )\rightarrow 1$, then the common derivative $\frac{d}{dt}$ can be seen as the limit of $D_{\omega}$ as $\omega \rightarrow 0$. Note that the memory effect requires that $0\leqslant K(t-\xi )<1$ for $\xi \in [t-\omega , t)$, so the magnitude of the memory-dependent derivative is usually smaller than that of the common derivative $f'(t)$. The variational principles, reciprocal theorems, and uniqueness of solutions due to memory dependence in a thermodiffusive medium have been proved by El-Karamany and Ezzat (El-Karamany and Ezzat 2016).

Recently, Sur and Kanoria (Sur and Kanoria 2017) proposed the constitutive law for the heat flux under memory-dependent 3P lag model as

$$ \left (1+\tau _{q} D_{\omega}+\frac{\tau _{q}^{2}}{2}D^{2}_{\omega} \right )\dot{q}_{i}= -K\left (1+\tau _{T} D_{\omega}\right ) \dot{\theta}_{,i} -K^{\star}\left (1+\tau _{\nu }D_{\omega}\right ) \theta _{,i}, $$

(4)

where $\omega$ is the delay time.

Further, the heat transport law for MGT theory has been proposed by Sur (Sur 2023b) in the form

$$ \left (1+\tau _{0}D_{\omega}\right )\mathbf{q}=-(K \vec{\nabla} \theta +K^{\star }\vec{\nabla} \nu ), \;\; \dot{\nu}=\theta . $$

(5)

Nowadays, structures made of FGMs play an important role in different industrial fields such as aerospace, biomechanics, etc. Some studies have been carried out by researchers on the static and dynamic behavior of FGM beams and plates. Studies devoted to understanding the static, buckling, free vibration, and also the forced vibration under stationary transient loading of the functionally graded beams, plates, and shells have gained importance in the last decades because of the wide application areas of FGMs. However, in comparison with the extensive research works on the vibration characteristics of homogenous and laminated composite beams and plates under moving load, only limited works can be found in this regard in the open literature for functionally graded structural elements. To the best knowledge of the author, it is quite hard to find out the research works for a functionally graded body in the context of nonlocal stress theory. However, to study the macroscopic interactions, it has a wide range of applications. With these motivations in mind, the present contribution is to represent a viable simulation technique to highlight the thermoelastic interaction for a functionally graded unbounded medium due to the presence of a heat source in the boundary. The graded changes of the medium is justified on taking the exponential variation of inhomogeneity. A heat transport equation for the present problem is considered using some unified parameters assimilating the memory dependence from which the 3P lag model and MGT theories can be achieved as some particular cases. Moreover, the constitutive relation for the present problem is formulated in the context of nonlocal elasticity theory proposed by Eringen. Employing the Laplace and Fourier integral transforms, the basic equations have been solved in the transformed domain. To arrive at the solutions in the real space-time domain, the inversion of the Fourier transform has been carried out analytically, using the residual calculus, where poles of the integrand are obtained numerically in a complex domain by using Laguerre’s method. Thereinafter, the numerical inversion of the Laplace transform has been carried out using the method based on Fourier series expansion (Honig and Hirdes 1984). Through the achieved computational results and the corresponding graphical representations, noteworthy effect of the effective parameters such as the nonlocality parameter, time-delay parameter, and the influence of magnetic field has been reported. Moreover, a significant effect of different choices of the kernel function is indicated. We also note that nonlinear kernel functions are superior compared to linear kernels in the context of this new theory. Excellent predictive capability is also demonstrated due to the influence of reinforcement and inhomogeneity.

2 Basic equations

For a homogeneous and isotropic elastic solid occupying the region of volume $V$ and surface area $\partial V$, the linear theory is expressed as (Eringen 1983)

$$\begin{aligned} &t_{ij,j}+\rho (f_{i}-\ddot{u}_{i})=0, \\ &t_{ij}(\mathbf{x}')=\int \limits _{\mathbf{V}}\alpha (|\mathbf{x}'- \mathbf{x}|, \chi )\sigma _{ij}(\mathbf{x}')dv(\mathbf{x}'), \\ &\sigma _{ij}(\mathbf{x})=\lambda e_{rr}(\mathbf{x}')\delta _{ij}+2\mu e_{ij}( \mathbf{x}'), \\ &e_{ij}(\mathbf{x}')=\displaystyle \frac{1}{2}\left ( \frac{\partial u_{i}(\mathbf{x}')}{\partial x'_{j}}+ \frac{\partial u_{j} (\mathbf{x}')}{\partial x'_{i}}\right ), \end{aligned}$$

(6)

where $t_{ij}$, $\rho$, $f_{i}$, and $u_{i}$ denote the nonlocal stress tensor, mass density, body force, and the displacement component at a reference point $\mathbf{x}$ within the body, respectively, at time $t$. Also, $\sigma _{ij}(\mathbf{x}')$ is the macroscopic (classical) stress tensor at a point $\mathbf{x}'$ in the body at time $t$, $\lambda$ and $\mu$ being the Lamé constants.

We can mention various examples of nonlocal modulus $\alpha$, such as (Eringen 1983)

$$ \alpha (|\mathbf{x}'-\mathbf{x}|, \chi )=\displaystyle \frac{1}{2l\chi}e^{- \frac{|\mathbf{x}'-\mathbf{x}|}{l\chi}}, \;\; \chi = e_{0}a_{0}/l. $$

(7)

Let $\alpha$ be a Green’s function of the linear differential operator (Eringen 1983)

$$ L \alpha (|\mathbf{x}'-\mathbf{x}|, \chi )=\delta (|\mathbf{x}'- \mathbf{x}|). $$

(8)

Suppose the operator $L$ satisfies

$$ (Lt_{ij})_{,j}=Lt_{ij,j}. $$

(9)

Hereinafter, applying $L$ in equation (6)₂ yields

$$ \begin{aligned} Lt_{ij}(\mathbf{x}') & = L\int \limits _{\mathbf{V}}\alpha (|\mathbf{x}'- \mathbf{x}|, \chi )\sigma _{ij}(\mathbf{x}')dv(\mathbf{x}'), \\ & = \int \limits _{\mathbf{V}}L\alpha (|\mathbf{x}'-\mathbf{x}|, \chi ) \sigma _{ij}(\mathbf{x}')dv(\mathbf{x}'), \\ & =\int \limits _{\mathbf{V}}\delta (|\mathbf{x}'-\mathbf{x}|, \chi ) \sigma _{ij}(\mathbf{x}')dv(\mathbf{x}'), \\ & = \sigma _{ij}(x). \end{aligned} $$

(10)

Therefore equation (6)₁ yields

$$ Lt_{ij,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0. $$

(11)

Using equation (9), equation (11) can be further expressed as

$$ (Lt_{ij})_{,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0. $$

(12)

In view of equation (10), equation (11) reduces to

$$ \sigma _{ij,j}+L (\rho f_{i}-\rho \ddot{u}_{i})=0, $$

(13)

where the differential operator $L$ for equation (8) is defined as (Sur 2023c; Das et al. 2024)

$$ L\equiv 1-\chi ^{2} l^{2} \nabla ^{2}. $$

(14)

For the present problem, the constitutive equation is given by

$$ \left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]\sigma _{ij}= 2\mu e_{ij}+ \left [\lambda e -\gamma (\theta -\theta _{0})\right ]\delta _{ij}, \;\; i, j=1, 2, 3, $$

(15)

and the strain-displacement relation is given by

$$ e_{ij}=\frac{1}{2}\left (u_{i,j}+u_{j,i}\right ), $$

(16)

where $u_{i}$ are the displacement components, $e_{ij}$ are the strain components, and $\sigma _{ij}$ are the stress components. Consider the one-dimensional medium $\infty < x<\infty$ influenced by an initial magnetic field $\mathbf{H}$, an induced persisting magnetic field $\mathbf{h}$, and an electric field $\mathbf{E}$ together with the Lorentz Force $\mathbf{F}$. Taking into account linear theory of thermoelasticity, we presume that $\mathbf{h}$ and $\mathbf{E}$ are so small in magnitude that the products can be neglected due to the linearization. Therefore the electromagnetic governing equations are given by (Sur 2023b)

$$ \begin{aligned} &\text{curl}~ \mathbf{h} = \displaystyle \mathbf{J}+\epsilon _{0} \frac{\partial \mathbf{E}}{\partial t}, \\ &\text{curl}~ \mathbf{E} = - \mu _{0} \displaystyle \frac{\partial \mathbf{h}}{\partial t}, \\ &\mathbf{E}= \displaystyle -\mu _{0}\left ( \frac{\partial \mathbf{u}}{\partial t}\times \mathbf{H}\right ), \\ &\text{div} ~\mathbf{h}=0, \end{aligned} $$

(17)

where $\mathbf{J}$ is the electric current density, and $\mu _{0}$ and $\epsilon _{0}$ are the magnetic permeability and electric permittivity in vacuum, respectively. The equation of motion is supplemented with Maxwell’s equations as (Sur 2023b)

$$ \sigma _{ij,j}+\left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]\left ( \mathbf{J}\times \mathbf{H}\right )_{i}=\rho \left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]\ddot{u}_{i}. $$

(18)

Invoking some unified parameters $\chi _{1}$, $\chi _{2}$, $\chi _{3}$, the heat transport equation has been framed upon assimilating the memory-dependent derivative as (Bayones et al. 2021; Ezzat et al. 2012)

$$ \begin{aligned} &\left [K\left (1+\chi _{1} \tau _{T} D_{\omega}\right )\dot{\theta}_{,i} \right ]_{,i}+\left [K^{\star }\left (1+\chi _{2} \tau _{\nu }D_{ \omega}\right )\theta _{,i}\right ]_{,i}\\ &\quad =\left (1+\tau _{q} D_{\omega}+ \chi _{3}\frac{\tau _{q}^{2}}{2}D^{2}_{\omega}\right )\left (\rho c_{ \nu }\ddot{\theta}+\gamma \theta _{0} \ddot{e}-\rho \dot{Q}\right ), \end{aligned} $$

(19)

where $K$ is the thermal conductivity, $K^{\star}$ is the conductivity rate parameter, $\rho$ is the density of the medium, $\gamma =(3\lambda +2\mu )\alpha _{t}$, $\alpha _{t}$ being the coefficient of linear thermal expansion of the material, and the unified parameters can be customized as follows: $\chi _{1}=\chi _{2}=\chi _{3}=1$ corresponds to the 3P lag model, whereas $\chi _{1}=\chi _{2}=\chi _{3}=0$ and $\tau _{q}=\tau _{0}$ yield the MGT model.

For a functionally graded medium, it is assumed that the parameters $\lambda$, $\mu$, $\gamma$, $K$, $K^{\star}$, $\rho$ are no longer constant but varies with the spatial coordinates. As a consequence, $\lambda$, $\mu$, $\gamma$, $K$, $K^{\star}$, and $\rho$ have been replaced by $\lambda _{0} f(\mathbf{x})$, $\mu _{0} f(\mathbf{x})$, $\gamma _{0} f(\mathbf{x})$, $K_{0} f(\mathbf{x})$, $K^{\star}_{0} f(\mathbf{x})$, and $\rho _{0} f(\mathbf{x})$, where $\lambda _{0}$, $\mu _{0}$, $\gamma _{0}$, $K_{0}$, $K^{\star}_{0}$, and $\rho _{0}$ are assumed to be constants, and $f(\mathbf{x})$ is a dimensionless function of the space variable $\mathbf{x}=(x,y,z)$. Then equations (15), (18), and (19) are expressed as

$$ \left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]\sigma _{ij}= f( \mathbf{x})\left [2\mu _{0} e_{ij}+\left \{\lambda _{0} e -\gamma _{0}( \theta -\theta _{0})\right \}\delta _{ij}\right ], \;\; i, j=1, 2, 3, $$

(20)

$$ f(\mathbf{x})\left [2\mu _{0} e_{ij}+\left \{\lambda _{0} e +\gamma _{0}( \theta -\theta _{0})\right \}\delta _{ij}\right ]_{,j}+f(\mathbf{x})_{,j} \left [2\mu _{0} e_{ij}+\left \{\lambda _{0} e +\gamma _{0}(\theta - \theta _{0})\right \}\delta _{ij}\right ] $$

$$ +\left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]f(\vec{x})\left ( \mathbf{J}\times \mathbf{H}\right )_{i}=\rho _{0} f(\mathbf{x}) \left [1-(e_{0}a_{0})^{2} \nabla ^{2}\right ]\ddot{u}_{i}, $$

(21)

$$ \left [K_{0} f(\mathbf{x})\left (1+\chi _{1} \tau _{T} D_{\omega} \right )\dot{\theta}_{,i}\right ]_{,i}+\left [K^{\star}_{0} f( \mathbf{x}) \left (1+\chi _{2} \tau _{\nu }D_{\omega}\right )\theta _{,i} \right ]_{,i} $$

$$ =\left (1+\tau _{q} D_{\omega}+\chi _{3}\frac{\tau _{q}^{2}}{2}D^{2}_{ \omega}\right )\left (\rho _{0} f(\mathbf{x}) c_{\nu }\ddot{\theta}+ \gamma _{0} f(\mathbf{x})\theta _{0} \ddot{e}-\rho _{0} f(\mathbf{x}) \dot{Q}\right ). $$

(22)

3 Formulation of the problem

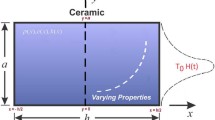
Consider a functionally graded isotropic medium occupying the region $-\infty < x< \infty$ kept at a uniform temperature $\theta _{0}$, in which the medium is influenced by an initial magnetic field $\mathbf{H }$, which is nonhomogeneous with its constituents $(0,0,H_{0}f(\mathbf{x}))$ as depicted in Fig. 1. The induced magnetic field $\mathbf{h}= (0,0,h)$, and the induced electric field $\mathbf{E}=(0,E,0)$. The problem is considered as one-dimensional with all the variables depending on the space coordinate $x$ and time $t$, so that the displacement vector $\mathbf{u}$ and the temperature $\theta$ can be expressed in the form

$$ \begin{aligned} &\mathbf{u}=(u(x,t),0,0), \\ &\theta =\theta (x,t).\end{aligned} $$

(23)

Fig. 1

Geometry of the problem

We assume that material properties depend only on the $x$-coordinate. So the material inhomogeneity can be characterized by the function $f(x)$ instead of $f(\mathbf{x})$.

The supposed magnetic field $\mathbf{h}$ and electric field $\mathbf{E}$ also act upon a one-dimensional medium, which provides (Sur 2023b)

$$ \mathbf{E}=\left (0,\; \; \mu _{0} H_{0} f(\mathbf{x}) \frac{\partial u}{\partial t},\; \; 0\right ), $$

(24)

$$ \mathbf{h}= \left (0, \;\;0, \;\;-H_{0} f(\mathbf{x}) \frac{\partial u}{\partial x}\right ), $$

(25)

$$ \mathbf{J} = \left (0, \;\;-\left (\frac{\partial h}{\partial x}+ \epsilon _{0} \mu _{0} H_{0} f(\mathbf{x}) \frac{\partial ^{2}u}{\partial t^{2}}\right ),\;\; 0\right ). $$

(26)

Therefore, in terms of the Lorentz force $\mathbf{F}$, the equation of motion is given by

$$ \begin{aligned} &f(x)\left [(\lambda _{0}+2\mu _{0}) \frac{\partial ^{2} u}{\partial x^{2}}-\gamma _{0} \frac{\partial \theta}{\partial x}\right ]+\left [(\lambda _{0}+2\mu _{0}) \frac{\partial u}{\partial x}-\gamma _{0}(\theta -\theta _{0})\right ] \frac{\partial f(x)}{\partial x}\\ &\quad = \rho _{0} f(x) R_{M}^{2} \left [1-(e_{0}a_{0})^{2} \frac{\partial ^{2}}{\partial x^{2}}\right ]\ddot{u}. \end{aligned} $$

(27)

The heat conduction equation, in the context of MGT theory and LS theory assimilating the memory responses, can be characterized as

$$ \frac{\partial}{\partial x}\left [K_{0} f(x)\left (1+\chi _{1} \tau _{T} D_{\omega}\right )\frac{\partial \dot{\theta}}{\partial x}\right ]+ \frac{\partial}{\partial x}\left [K^{\star}_{0} f(x) \left (1+\chi _{2} \tau _{\nu }D_{\omega}\right )\frac{\partial \theta}{\partial x} \right ] $$

$$ =\left (1+\tau _{q} D_{\omega}+\chi _{3}\frac{\tau _{q}^{2}}{2}D^{2}_{ \omega}\right )\left (\rho _{0} c_{\nu }\ddot{\theta}+\gamma _{0} \theta _{0} \ddot{e}-\rho _{0} \dot{Q}\right )f(x), $$

(28)

$$ \left [1-(e_{0}a_{0})^{2}\frac{\partial ^{2}}{\partial x^{2}}\right ] \sigma _{xx}= f(x)\left [(\lambda _{0}+2\mu _{0})e_{xx}-\gamma _{0}( \theta -\theta _{0})\right ], $$

(29)

$$ e_{xx}= \frac{\partial u}{\partial x}, $$

(30)

where $R_{H}=\displaystyle H_{0} \sqrt{\frac{\mu _{0}}{\rho _{0}}}$ is the Alfvén velocity, $c=\displaystyle \frac{1}{\left (\mu _{0} \epsilon _{0}\right )^{1/2}}$ is the speed of light in vacuum, and $\displaystyle R_{M}^{2}=1+\frac{R_{H}^{2}}{c^{2}}$.

To simplify equations (27)–(30), we invoke the following dimensionless variables (Sur and Kanoria 2014):

$$ x'=\frac{x}{l}, \hspace{.1in} t'=\frac{vt}{l}, \hspace{.1in} u'=\frac{\lambda _{0}+2\mu _{0}}{l\gamma _{0}\theta _{0}}u, \hspace{.1in} \sigma '= \frac{\sigma}{\gamma _{0} \theta _{0}}, \hspace{.1in} \omega '= \frac{v\omega}{l}, $$

$$ \tau '_{0}= \frac{v\tau _{0}}{l}, \hspace{.1in} \xi =\frac{e_{0}a_{0}}{l}, \hspace{.1in} Q_{0}= \frac{lQ}{\theta _{0} c_{\nu }v}, \hspace{.1in} f'(x')=f(x), \hspace{.1in} e'_{x'x'}=e_{xx}, $$

where $l$ is a standard length, and $v$ is a standard speed. Upon discarding primes, to justify the functionally graded solid, the exponential variation of inhomogeneity is taken into consideration by the function $f(x)=e^{-kx}$, where $k$ is a dimensionless constant. Then equations (27)–(30) yield

$$ \left (1-\xi ^{2}\frac{\partial ^{2}}{\partial x^{2}}\right )\sigma _{xx}= e^{-kx}\left (\frac{\partial u}{\partial x}-\theta \right ), $$

(31)

$$ e_{xx}=\beta _{1}\frac{\partial u}{\partial x}, $$

(32)

$$ \frac{\partial ^{2} u}{\partial x^{2}}- \frac{\partial \theta}{\partial x}-k\left ( \frac{\partial u}{\partial x}-\theta \right )= \frac{R_{M}^{2}}{C_{P}^{2}}\left (1-\xi ^{2} \frac{\partial ^{2}}{\partial x^{2}}\right )\ddot{u}, $$

(33)

$$\begin{aligned} &C_{K}^{2} \left (1+\chi _{1} \tau _{T} D_{\omega}\right ) \frac{\partial ^{2} \dot{\theta}}{\partial x^{2}}+ C_{T}^{2} \left (1+ \chi _{2} \tau _{\nu }D_{\omega}\right ) \frac{\partial ^{2} \theta}{\partial x^{2}}\\ &- kC_{K}^{2} \left (1+ \chi _{1} \tau _{T} D_{\omega}\right ) \frac{\partial \dot{\theta}}{\partial x} -kC_{T}^{2} \left (1+\chi _{2} \tau _{\nu }D_{\omega}\right )\frac{\partial \theta}{\partial x} \end{aligned}$$

$$ =\left (1+\tau _{q} D_{\omega}+\chi _{3}\frac{\tau _{q}^{2}}{2}D^{2}_{ \omega}\right )\left ( \ddot{\theta}+\epsilon _{T} \frac{\partial ^{3} u}{\partial x\partial t^{2}}-Q_{0}\right ), $$

(34)

where

$$\begin{array}{rlrl}& C_P^2=\frac{{\lambda }_0+2{\mu }_0}{{\rho }_0{v}^2},& C_K^2=\frac{K_0}{{\rho }_0{c}_{\nu }lv},& C_T^2=\frac{K_0^{\star }}{{\rho }_0{c}_{\nu }{v}^2},{ϵ}_T=\frac{{\gamma }_0^2{\theta }_0}{{\rho }_0{c}_{\nu }({\lambda }_0+2{\mu }_0)},\\ & {\beta }_1=\frac{{\gamma }_0{\theta }_0}{{\lambda }_0+2{\mu }_0}.\end{array}$$

We presume that the medium is initially at rest while the undisturbed state is maintained at reference temperature. This yields the initial conditions for the problem as

$$ u(x,0)=\dot{u}(x,0)=\theta (x,0)=\dot{\theta}(x,0)=0. $$

The kernel function $K(t-\xi )$ for the heat transport equation can be customized as (Abouelregal and Dargail 2023; Ezzat et al. 2017; Abouelregal 2022; Ezzat et al. 2013; Abouelregal et al. 2023b)

$$ K(t-\xi )=1-\frac{2f}{\omega}(t-\xi )+\frac{e^{2}}{\omega ^{2}}(t- \xi )^{2}=\left \{ \textstyle\begin{array}{l@{\quad}l@{\quad}l} 1 & \text{if} & e =0, f = 0, \\ 1-\frac{(t-\xi )}{\omega} & \text{if} & e=0, \, f=\frac{1}{2}, \\ \left (1-\frac{t-\xi}{\omega}\right )^{2} & \text{if} & e=1,\; f=1, \end{array}\displaystyle \right . $$

where $\omega$ is the delay time, and $e$ and $f$ are constants.

4 Method of solution

Define the Laplace and Fourier integral transforms for a function $g(x,t)$ by

$$ \textstyle\begin{array}{l@{\quad}l} \mathscr{L}\left \{g(x,t)\right \}=\bar{g}(x,p)&=\displaystyle \int \limits _{0}^{\infty}g(x,t)e^{-pt}dt,\;\; \text{Re}(p)>0, \\ \mathscr{F}\left \{\bar{g}(x,p)\right \}=\hat{\bar {g}}(\alpha ,p)&= \displaystyle \frac{1}{\sqrt{2\pi}}\int \limits _{-\infty}^{\infty} \overline{g}(x,p)e^{i\alpha x}dx, \end{array} $$

which satisfy the operational relationship

$$ \mathscr{L}\left [\int \limits _{t-\omega}^{t}K(t-\xi )f'(x,\xi )d \xi \right ]=\bar{f}(x,y,p)G_{\omega}(p), $$

where

$$ G_{\omega}(p)=1-\frac{2f}{\omega}+\frac{2e^{2}}{\omega ^{2}}-e^{-p \omega}\left [(1-2f+e^{2})+ \frac{2(e^{2}-f)}{\omega p}+ \frac{2e^{2}}{\omega ^{2}p^{2}}\right ]. $$

Therefore, applying the Laplace and the Fourier transforms simultaneously, equations (31)–(34) reduce to

$$ (1+\alpha ^{2} \xi ^{2})\hat{\bar{\sigma}}_{xx}(\alpha , p)= -i( \alpha +ik)\hat{\bar{u}}(\alpha +ik, p)-\hat{\bar{\theta}}(\alpha +ik, p), $$

(35)

$$ \hat{\bar{e}}_{xx}(\alpha , p)=i\beta _{1} \alpha \hat{\bar{u}}( \alpha , p), $$

(36)

$$ \left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(1+\alpha ^{2}\xi ^{2})+ \alpha ^{2} -i\alpha k\right ]\hat{\bar{u}}(\alpha , p)=(i\alpha +k) \hat{\bar{\theta}}(\alpha , p), $$

(37)

$$ (i\alpha k +\alpha ^{2})\hat{\bar{\theta}}(\alpha , p)= a_{3} \left [p^{2} \hat{\bar{\theta}}(\alpha , p)- \epsilon _{T} i\alpha p^{2} \hat{\bar{u}}(\alpha , p)-\hat{\bar{Q}}\right ], $$

(38)

where

$$ a_{3}= \frac{1+\frac{\tau _{q}}{\omega}G_{\omega}+ \frac{\tau _{q}^{2}}{2\omega}G_{\omega}^{2} \chi _{3} }{C_{T}^{2}\left (1+\chi _{2} \frac{\tau _{\nu}}{\omega}G_{\omega}\right )+C_{K}^{2} p \left (1+\chi _{1} \frac{\tau _{T}}{\omega}G_{\omega}\right )}. $$

Solving equations (37) and (38), we have

$$ \hat{\bar{u}}(\alpha , p)= \frac{\hat{\bar{Q}}a_{3} (i\alpha +k)}{\mathcal{M}(\alpha )}, $$

(39)

$$ \hat{\bar{\theta}}(\alpha , p)= \frac{\hat{\bar{Q}}a_{3}\left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(1+\alpha ^{2}\xi ^{2})+\alpha ^{2} -i\alpha k\right ] (i\alpha +k)}{\mathcal{M}(\alpha )}, $$

(40)

where

$$ \textstyle\begin{array}{l@{\quad}l} \mathcal{M}(\alpha ) &= \displaystyle \left (1+ \frac{R_{M}^{2} \xi ^{2} p^{2}}{C_{P}^{2}}\right )\alpha ^{4}-\alpha ^{3} \left [2ik+\frac{ik\xi ^{2}R_{M}^{2} p^{2}}{C_{P}^{2}}\right ]\\ &\quad + \displaystyle \alpha ^{2} \left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(\alpha ^{2}+a_{3} \xi ^{2})+a_{3} p^{2} (1+\epsilon _{T})+k^{2}\right ] \\ &\quad -\displaystyle \alpha p^{2}\left [a_{3}(\epsilon _{T}+ik)+ \frac{ikR_{M}^{2}}{C_{P}^{2}}\right ]+ \frac{a_{3} R_{M}^{2} p^{4}}{C_{P}^{2}} \\ &= \mathcal{N}(p)(\alpha -\alpha _{1})(\alpha -\alpha _{2})(\alpha - \alpha _{3})(\alpha -\alpha _{4}), \end{array} $$

and

$$ \mathcal{N}(p)= 1+\frac{R_{M}^{2} \xi ^{2} p^{2}}{C_{P}^{2}}. $$

We assume that the heat source is distributed over the plane $x=0$ in the form

$$ Q=Q_{0} \delta (x)H(t), $$

(41)

where $\delta$ is the Dirac delta function, and $H$ is the Heaviside unit step function. Therefore, applying the Laplace and Fourier integral transforms yields

$$ \hat{\bar{Q}}=\frac{Q_{0}}{\sqrt{2\pi}p}. $$

(42)

Thus the solutions for the thermophysical quantities are defined in the Laplace transform domain as

$$ \bar{u}(x,p)=\frac{1}{2 \pi p}\int \limits _{-\infty}^{\infty } \frac{Q_{0}a_{3} (i\alpha +k)}{\mathcal{M}(\alpha )}\; e^{-i\alpha x} d \alpha , $$

(43)

$$ \bar{\theta}(x,p)=\frac{1}{2 \pi p}\int \limits _{-\infty}^{\infty } \frac{Q_{0}a_{3} \left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(1+\alpha ^{2}\xi ^{2})+\alpha ^{2} -i\alpha k\right ]}{\mathcal{M}(\alpha )} \; e^{-i\alpha x} d \alpha , $$

(44)

$$ \bar{\sigma}_{xx}(x,p)=\frac{1}{2 \pi p}\int \limits _{-\infty}^{ \infty } \frac{Q_{0}a_{3} \left [2\alpha (\alpha +ik)-\frac{R_{M}^{2} p^{2}}{C_{P}^{2}}\left \{1-\xi ^{2} (\alpha +ik)^{2}\right \}\right ]}{\mathcal{M}(\alpha +ik)(1+\alpha ^{2} \xi ^{2})} \; e^{-i\alpha x} d \alpha , $$

(45)

$$ \bar{e}_{xx}(x,p)=-\frac{1}{2 \pi p}\int \limits _{-\infty}^{\infty } \frac{Q_{0}a_{3}\beta _{1} \alpha (ik-\alpha )}{\mathcal{M}(\alpha )} \; e^{-i\alpha x} d \alpha . $$

(46)

Thus, on applying contour integration, the expressions for the displacements, temperature, and stress and strain in the Laplace transform domain take the form

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{u}(x,p) &=& -\displaystyle \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})< 0 }\end{array}\displaystyle }^{4} A_{j} (i \alpha _{j} +k )\; e^{-i\alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x > 0 \\ && \\ & = & \displaystyle \hspace{.1in} \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})>0}\end{array}\displaystyle }^{4} A_{j} (i q_{j} +k) \; e^{-i \alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x< 0, \end{array} $$

(47)

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{\theta}(x,p) &=& -\displaystyle \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})< 0 }\end{array}\displaystyle }^{4} A_{j} \left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(1+\alpha _{j}^{2} \xi ^{2})+\alpha ^{2} -i\alpha _{j} k\right ] \\ &&\\ &&{}\times e^{-i\alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x > 0 \\ && \\ & = & \displaystyle \hspace{.1in} \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})>0}\end{array}\displaystyle }^{4} A_{j} \left [\frac{R_{M}^{2}p^{2}}{C_{P}^{2}}(1+\alpha _{j}^{2} \xi ^{2})+\alpha ^{2} -i\alpha _{j} k\right ] \\ &&\\ &&{}\times e^{-i \alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x< 0, \end{array} $$

(48)

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{\sigma}_{xx}(x,p) &=& -\displaystyle \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(l_{j})< 0 }\end{array}\displaystyle }^{4} B_{j} \left [2l_{j}(l_{j}+ik)-\frac{R_{M}^{2} p^{2}}{C_{P}^{2}} \left \{1-\xi ^{2} (l_{j}+ik)^{2}\right \}\right ] \\ &&\\ &&{}\times e^{-il_{j} x} \hspace{1em} \text{for} \hspace{1em} x > 0 \\ && \\ & = & \displaystyle \hspace{.1in} \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(l_{j})>0}\end{array}\displaystyle }^{4} B_{j} \left [2l_{j}(l_{j}+ik)-\frac{R_{M}^{2} p^{2}}{C_{P}^{2}} \left \{1-\xi ^{2} (l_{j}+ik)^{2}\right \}\right ]\\ &&\\ &&{}\times e^{-i l_{j} x} \hspace{1em} \text{for} \hspace{1em} x< 0, \end{array}\displaystyle \end{aligned}$$

(49)

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{e}_{xx}(x,p) &=& \displaystyle \dfrac{iQ_{0}\beta _{1}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})< 0 }\end{array}\displaystyle }^{4} A_{j} \alpha _{j} \left (ik-\alpha _{j}\right ) \; e^{-i\alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x > 0 \\ && \\ & = & \displaystyle \hspace{.1in} \dfrac{iQ_{0}a_{3} }{p\mathcal{N}(p)} \sum _{ \textstyle\begin{array}{c} j=1 \\ \mathrm{{Im}(\alpha _{j})>0}\end{array}\displaystyle }^{4} A_{j} \alpha _{j} \left (ik-\alpha _{j}\right ) \; e^{-i \alpha _{j} x} \hspace{1em} \text{for} \hspace{1em} x< 0, \end{array} $$

(50)

where $A_{j}$ and $B_{j}$ are given by

$$ A_{j}=\displaystyle \prod _{ \textstyle\begin{array}{c} n=1 \\ n\neq j \end{array}\displaystyle }^{4}\frac{1}{(\alpha _{j}-\alpha _{n})} \hspace{.1in} \text{and} \hspace{.1in} B_{j}=\displaystyle \prod _{ \textstyle\begin{array}{c} n=1 \\ n\neq j \end{array}\displaystyle }^{4}\frac{1}{(l_{j}-l_{n})}, \;j=1,2,3,4. $$

5 Numerical results and discussions

To attain the solution for the thermophysical such as displacement, temperature, thermal stress, and volumetric strain in the real space-time domain, we need to incorporate the inversion of the Laplace transform to equations (47)–(50), respectively. These computations have been carried out numerically using a method based on the Fourier series expansion technique (Honig and Hirdes 1984), as outlined in Appendix A. Moreover, to control the discretization error by the “Korrektur” method, a suitable scheme has also been outlined in Appendix B. The numerical computations have been carried out using the MATLAB 2023 software package. To obtain the roots of the polynomial equations $M(\alpha )$ and $M(\alpha +i k)$ in a complex domain, Laguerre’s method is used. For illustration, a copper material has been used, for which the values of the following material constants are taken (Sur and Kanoria 2014; Ezzat et al. 2012):

$$ \epsilon _{T}=0.0618, \hspace{.1in} \lambda _{0}=7.76\times 10^{10} ~\text{N}/ \text{m}^{2}, \hspace{.1in} \mu _{0}= 3.86\times 10^{10}~\text{N}/ \text{m}^{2}, \hspace{.1in} \alpha _{T}=1.78\times 10^{-5}]~\text{K}^{-1}, $$

$$ \rho =8954~\text{kg}/ \text{m}^{3}, \hspace{.1in} \theta _{0}=293~\text{K}, \hspace{.1in} c_{\nu}=383.1~\text{m}^{2}/ \text{s}^{2} ~\text{K}, $$

and the hypothetical relaxation parameters are taken as

$$ \tau _{q}=0.01, \hspace{.1in} \tau _{0}=0.01, \hspace{.1in} \tau _{\nu}=0.025, \hspace{.1in} \tau _{T}=0.015. $$

Also, the other parameters have been taken as $Q_{0}=1$, $\hspace{.1in} C_{P}=1$, $\hspace{.1in} C_{K}=0.6$, $\hspace{.1in} C_{T}=2$, so the faster wave is the thermal wave. It is already checked that these material constants and the hypothetical parameters satisfy the stability conditions for both 3P lag model and MGT theories. For the 3P lag model, the system will be stable (Quintanilla and Racke 2008) if $K_{0}^{\star }\tau _{q} <\tau _{\nu}^{\star }< \frac{2K_{0}\tau _{T}}{\tau _{q}}$, where $\tau _{\nu}^{\star }= K_{0}+K_{0}^{\star }\tau _{\nu}$. Moreover, the phase lag parameters and the additional material constants have been taken from (Sherief and Abd El-Latief 2013) and satisfy the stability condition for MGT heat conduction (Sur 2023d), so that the solution will be exponentially stable if $\tau _{0}>0$, $K_{0}>0$, $K_{0}^{\star}>0$, and $K_{0}>K_{0}^{\star }\tau$ (Quintanilla 2019, 2020).

Figure 2 represents the effectiveness of different kernel functions on the variation of the thermal stress distribution against the distance $x$ for both the presence and absence of inhomogeneity. The graphical illustration is computed in the context of MGT theory at time $t=0.2$, whereas the delay-time parameter is taken as $\omega =0.01$, and the time-delay parameter is $\xi =0.2$. The following kernel functions are considered for the numerical estimates: $K(t-\xi )=1$, $1-\frac{t-\xi}{\omega}$, and $\left (1-\frac{t-\xi}{\omega}\right )^{2}$. As we see from the figure, the stress-wave reveals a compressive characteristic near the plane $x=0$, where the heat source is active. Also note that the magnitude of the stress is larger for a nonlinear kernel $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$ than that for a constant kernel $K(t-\xi )=1$ compared to a linear kernel function $K(t-\xi )=1-\frac{t-\xi}{\omega}$. Also notice from the figure that $\sigma _{xx}$ attains the maximum magnitude near the plane of applied heat source and, as we traverse at far from the boundary, the stress asymptotically diminishes to zero value for various kernels. We can also validate the phenomena from the analytical expression of $\overline{\sigma}_{xx}$ in equation (49). The dominating factor for this is $e^{-i \alpha _{j} x}$ $(\text{Im}(\alpha _{j})<0 \hspace{.1in} \text{for} \hspace{.1in} x>0)$. Also note that a significant effect of the inhomogeneity can be addressed in the variation of the stress distribution.

Fig. 2

$\sigma _{xx}$ vs. $x$ for MGT theory at $t=0.4$, $\omega =0.01$, $\xi =0.2$

Figures 3 and 4 exhibit the variation of the physical fields to address a comparative study between the MGT and 3P lag models. These comparisons have been carried out for $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )^{2}$ for both presence and absence of inhomogeneity.

Fig. 3

$u$ vs. $x$ for $K(t-\xi )= \left (1-(t-\xi )/\omega \right )^{2}$ at $t=0.4$, $\omega =0.01$, $\xi =0.2$

Fig. 4

$\sigma _{xx}$ vs. $x$ for $K(t-\xi )= \left (1-(t-\xi )/\omega \right )^{2}$ at $t=0.4$, $\omega =0.01$, $\xi =0.2$

Figure 3 demonstrates the variation of the displacement $u$ for both theories at time $t=0.2$ for a nonlocal medium in the presence and absence of inhomogeneity. We see that the displacement increases in magnitude near $0< x<0.25$ and $-0.25< x<0$ to attain the maximum magnitude near $x=\pm 0.25$. However, with the increase of the distance $x$, the displacement $u$ also disappears at far from the boundary. There are two major observations corresponding to the graphical illustration viz. the displacement $u$ attains a higher magnitude for the 3P lag model compared to MGT theory, which is now proposed. Also, the presence of inhomogeneity has a tendency to influence the magnitude of the profile of the displacement $u$ within the medium. This is realistic since the 3P lag model was proposed to consider microstructural effects into the delayed response in time in the macroscopic formulation by taking into account that increase of the lattice temperature is delayed due to photon–electron interactions on the macroscopic level. Therefore, although the high heat flux is produced within the body for a sufficiently small span of time, compared to MGT theory, the 3P lag model has the ability to capture the effects more prominently.

Figure 4 characterizes the distribution of the stress $\sigma _{xx}$ for the same set of parameters as outlined above. Corresponding to this case, a promising result is also achieved due to the presence of inhomogeneity parameter as already mentioned above. Also note that the 3P lag model produces more stress within the body for both the presence and absence of inhomogeneity.

Figure 5 characterizes the effect of the time delay parameter in the distribution of the temperature profile $\theta$ for an inhomogeneous medium in the context of nonlocal stress theory. The kernel of the heat transport is taken as a linear function (i.e., $K(t-\xi )=\left (1-\frac{t-\xi}{\omega}\right )$). The time delay parameter is taken as $\omega =0.001, \; 0.01, \; 0.1$, respectively. It is observed from the figure that $\theta$ attains the maximum magnitude near the plane $x=0$, where the heat source is active, and with the increase of $x$, the magnitude of $\theta$ diminishes to zero value for different choices of $\omega$. Moreover, note that with the increment of the time-delay, the magnitude of the profile of $\theta$ also increases, which is quite plausible. This phenomenon is realistic, since delay-time indicates the time-difference for heat exposure between any two adjacent points within the graded composite. So in the case of heat transfer problems in sufficiently short-time intervals with high heat fluxes, the magnitude of the field quantities produced influences characteristics due to the increment of time delay.

Fig. 5

$\theta$ vs. $x$ for $K(t-\xi )= \left (1-(t-\xi )/\omega \right )^{2}$ at $t=0.4$, $\xi =0.2$

In Figs. 6–8 the contour plots have now been depicted to study the distribution of the physical quantities for a constant kernel $K(t-\xi )=1$ at delay time $\omega =0.01$ in a nonlocal medium i.e., the nonlocal parameter is considered to be $\xi =0.2$. The computations have been captured for $0< t<1$. Significant effectiveness in the distribution of each thermophysical quantities has been revealed from the graphical illustrations.

Fig. 6

Contour plot for displacement distribution

Fig. 7

Contour plot for temperature distribution

Fig. 8

Contour plot for stress distribution

Also, Figs. 9–11 have been plotted to demonstrate the 3D-surface plot of each physical quantity for the above set of time-frames, as already mentioned. Significant variability can be address in variation of each of the thermophysical quantities revealed from the respective graphical illustrations.

Fig. 9

Surface plot for displacement distribution

Fig. 10

Surface plot for temperature distribution

Fig. 11

Surface plot for stress distribution

Figure 12 illustrates the variation of the thermal stress versus the distance $x$ for the inhomogeneous medium in the presence and absence of nonlocal stress theory. Noteworthy difference can be remarked due to the presence of nonlocal stress theory. Note that the presence of nonlocal stress theory influences the stress profile within the body compared to a local medium, which has significant implications for material design and performance in applications involving boundary interactions. The phenomenon is realistic in the sense that for nonlocal theory, the stress at a point is assumed to be a function of volumetric strains at all other points of the continuum. Therefore this new theory consists of more information about the functionally graded material.

Fig. 12

$\sigma _{xx}$ vs $x$ for local and nonlocal media

Figures 13 and 14 have been depicted to study the effectiveness of the induced magnetic field in the variation of displacement profile and temperature distribution for the graded composite. As found from the graphical illustration, noteworthy significant differences can be revealed in the distribution of the displacement $u$ along the length of the graded medium. We see that the absence of magnetic field has the effectiveness to influence the displacement of the functionally graded solid. However, no such effect of magnetic field is found in the variation of temperature profile. The phenomena is realistic, since both the magnetic field and the temperature seem to be mutually independent.

Fig. 13

$u$ vs. $x$ in the presence and absence of a magnetic field

Fig. 14

$\theta$ vs. $x$ in the presence and absence of a magnetic field

Figure 15 is now plotted for a homogeneous medium $(k=0)$ to compare the computed results (COMPUT) of the present problem in the absence of nonlocal $(\xi =0)$, without memory effect and in the absence of magnetic field $(R_{H}=0)$ in the context of the 3P lag model with the estimated results of the existing literature (Ezzat et al. 2012). We see from the variation of the temperature profile $(\theta )$ that the computed and estimated results agree up to a certain level of accuracy. The fact can also be justified from the tabulated values in Table 1.

Fig. 15

Comparative study between computed and estimated results in the absence of memory and magnetic field

Table 1 Comparative study of the temperature ($\theta$) distribution

6 Conclusions

In this work, a magneto-thermoelastic nonlocal heat conduction model has been considered. This novel nonlocal model has been derived on the basis of the concepts investigated by Eringen, in addition to the derivative frame based on memory. The medium is influenced under the effect of a heat source. From the present investigation, the following conclusions can be revealed.

• 1. While incorporating various forms of kernels, significant effects can be noticed for the selected kernel functions. It can be therefore addressed that in the problem of high heat transfer, suitable kernels can be customized according to the necessity of applications for a graded composite.

• 2. The inhomogeneity parameter plays a significant role in the heat transfer problem. The exponential variation can produce significant effects in the variation of each physical field. Therefore, while dealing with the heat transport problem for a graded composite, the inhomogeneity parameter should be taken care of.

• 3. Increase in the magnitude of the delay time also influences the magnitude of each physical field. This is realistic, since in this context the delayed response of the heat transport mechanism also increases.

• 4. Effects of delay time on the physical fields can be understood as an indicator for the classification of the materials. So memory response in heat transport is of growing interest in the field of material science.

• 5. The second-degree term of delay-time for a nonlinear kernel influences the heat transport law more compared to the linear kernel function, which is more effective in the heat transport mechanism.

• 6. For the heat transfer problems, in which some high heat flux is produced for a sufficiently small span of time or even in delayed intervals of memory responses, it is advantageous to formulate the problem based on MGT theory compared to three-phase-lag generalized theory.

Appendices

Appendix A

1.1 A.1 Numerical inversion of the double transform

The expression for $\overline{f}(x,y,p)$, the Laplace transform of $f(x,y,t)$, can be obtained from $\widehat{\overline{f}}(x,q,p)$ by taking its Fourier inversion as follows:

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{f}(x,y,p)&=& \dfrac{1}{\sqrt{2\pi}}\displaystyle \int\limits _{- \infty}^{\infty}e^{i{q}x}\widehat{\overline{f}}(q,y,p)dq, \\ &=&\sqrt{\dfrac{2}{\pi}}\displaystyle \int\limits _{0}^{\infty}[\cos (qx) \widehat{\overline{f}}_{e}(q,y,p)+ i\sin (qx)\widehat{\overline{f}}_{0}(q,y,p)]dq, \end{array} $$

(A.1)

where $\widehat{\overline{f}}_{e}$ and $\widehat{\overline{f}}_{0}$ denote the even and odd parts of $\widehat{\overline{f}}(q,y,p)$, respectively.

To get the solution in space-time domain, we have to apply the Laplace inversion to equation (A.1), which have been done numerically using a method based on the Fourier series expansion technique (Honig and Hirdes 1984). The outline of the numerical inversion method used is given as follows.

Let $\overline{f}(x,y,p)$ be the Laplace transform of a function $f(x,y,t)$. Then the inverse formula for the Laplace transform can be written as

$$ f(x,y,t)=\frac{1}{2\pi{i}}\int\limits _{\gamma -i\infty}^{\gamma +i\infty}e^{pt} \overline{f}(x,y,p)dp, $$

(A.2)

where $\gamma$ is an arbitrary real number greater than the real parts of all the singularities of $\overline{f}(x,y,p)$. Taking $p=\gamma +iw$, the preceding integral takes the form

$$ f(x,y,t)=\frac{e^{\gamma{t}}}{2\pi}\int\limits _{-\infty}^{\infty}e^{itw} \overline{f}(x,y,\gamma +iw)dw. $$

(A.3)

Expanding $e^{-\gamma{t}}f(x,y,t)$ in a Fourier series in the interval $[0,2T]$, we obtain the approximate formula (Honig and Hirdes 1984)

$$ f(x,y,t)=f_{\infty}(x,y,t)+E_{D}, $$

(A.4)

where

$$ f_{\infty}(x,y,t)=\frac{1}{2}c_{0}+\sum _{k=1}^{\infty}c_{k} \hspace{1cm} \text{ for} \;\;\; 0\leqslant{t}\leqslant{2T}, $$

(A.5)

$$ c_{k}=\frac{e^{\gamma{t}}}{T}\Big[e^{\frac{ik\pi{t}}{T}}\overline{f} \left (x,y,\gamma +\frac{ik\pi{t}}{T}\right )\Big], $$

(A.6)

and $E_{D}$ is the discretization error. The error $E_{D}$ can be made arbitrarily small by choosing $\gamma$ large enough (Honig and Hirdes, 1984). Since the infinite series in equation (A.5) can be summed up to a finite number $N$ of terms, the approximate value of $f(x,y,t)$ becomes

$$ f_{N}(x,y,t)=\frac{1}{2}c_{0}+\sum _{k=1}^{N}c_{k} \hspace{1cm} \text{for} \;\;\; 0\leqslant{t}\leqslant{2T}, $$

(A.7)

Using this formula to evaluate $f(x,y,t)$, we introduce the truncation error $E_{T}$ that must be added to the discretization error. Two methods are used to reduce the total error. First, the “Korrecktur” method is used to reduce the discretization error. Next, the $\varepsilon$-algorithm is used to accelerate the convergence. The “Korrecktur” method uses the following formula to evaluate the function $f(x,y,t)$:

$$ f(x,y,t)=f_{\infty}(x,y,t)-e^{-2\gamma{T}}f_{\infty}(x,y,2T+\eta )+E'_{D}, $$

(A.8)

where the discretization error $|E'_{D}|\ll |E_{D}|$. Thus the approximate value of $f(x,y,t)$ becomes

$$ f_{NK}(x,y,t)=f_{N}(x,y,t)-e^{-2\gamma{T}}f_{N}'(x,y,2T+\eta ). $$

(A.9)

We will now describe the $\varepsilon$-algorithm that is used to accelerate the convergence of the series in equation (A.5). Let $N=2q+1$, where $q$ is a natural number, and let $s_{m}=\displaystyle \sum _{k=1}^{m}c_{k}$ be the sequence of partial sums of series (A.7). We define the $\varepsilon$-sequence by

$$ \varepsilon _{0,m}=0, \hspace{1cm} \varepsilon _{1,m}=s_{m}, $$

and

$$ \varepsilon _{l+1,m}=\varepsilon _{l-1,m+1}+ \frac{1}{\varepsilon _{l,m+1}-\varepsilon _{l,m}}, l=1,2,3, \dots \,. $$

It can be shown that the sequence $\varepsilon _{1,1}$, $\varepsilon _{3,1}$, $\varepsilon _{5,1}$,…, $\varepsilon _{N,1}$ converges to $f(x,y,t)+E_{D}-\frac{c_{0}}{2}$ faster than the sequence of partial sums $s_{m},m=1,2,3,\dots$. The actual procedure used to invert the Laplace transform consists of using equation (A.6) together with the $\varepsilon$-algorithm. The values of $\gamma$ and $T$ are chosen according to the criterion outlined in (Honig and Hirdes 1984).

Appendix B

2.1 B.1 Error analysis for the numerical inversion of the Laplace and Fourier transforms

The Laplace transform of a real function $f: \mathbb{R\rightarrow \mathbb{R}}$ with $f(t)=0$ for $t<0$ and its inversion formula are defined as

$$ \textstyle\begin{array}{c@{\quad}c} F(p)& =\mathscr{L}\big[f(t)\big] =\displaystyle \int \limits _{0}^{ \infty }e^{-pt} f(t) dt, \\ f(t) & = \mathscr{L}^{-1}\big[F(p)\big]=\displaystyle \frac{1}{2\pi i }\int \limits _{v-\text{\i} \infty}^{v+\text{\i} \infty} e^{pt}F(p) dp, \end{array} $$

(B.1)

where $p=v+iw$, $v, \; w \in \mathbb{R}$. It is known that $v \in \mathbb{R}$ is chosen arbitrary but greater than the real parts of all the singularities of $F(p)$. The integrals in (B.1) exist for $\text{Re}(p)> a \in \mathbb{R}$ if

(i) $f$ is locally integrable,

(ii) there exist $t_{0} \geqslant 0$ and $k, \; a \in \mathbb{R}$ such that $|f(t)|\leqslant k e^{at}$ for all $t \geqslant t_{0}$,

(iii) for all $t \in (0, \infty )$, there is a neighborhood in which $f$ is of bounded variation.

Applying the inversion formula

$$ f(t) = \displaystyle \frac{e^{vt}}{\pi}\int \limits _{0}^{\infty} \big[\text{Re}\left \{F(p)\right \}\cos (wt)-\text{Im}\left \{F(p) \right \}\sin (wt)\big] dw $$

(B.2)

and a Fourier series expansion of $h(t)=e^{-vt}f(t)$ in the interval $[0, \; 2T]$, we arrive at the following approximation formula:

$$ f(t) = \frac{e^{vt}}{T}\left [-\frac{1}{2}\text{Re}\left \{F(v)\right \}+\sum _{k=0}^{\infty }\text{Re}\left \{F\left (v+i\frac{k \pi}{T} \right )\right \}\times \cos \frac{k \pi}{T}t\right . $$

$$ \left .- \sum _{k=0}^{\infty }\text{Im}\left \{F\left (v+i \frac{k \pi}{T} \right )\right \}\times \sin \frac{k \pi}{T}t\right ]-F1(v,t,T) $$

(B.3)

for $0< t<2T$. Thereafter, the discretization error $F1(v, t, T)$ is defined by

$$ F1(v, t, T)=\sum _{k=1}^{\infty }e^{-2vkT}f(2kT+t). $$

(B.4)

Since there are no singularities of $F(p)$ within the right half-plane, the constants $c>0$, $m \geqslant 0$, and $t_{0} \geqslant 0$ are assumed to be such that

$$ |f(t)|\leqslant ct^{m} \hspace{.1in} \text{for all} ~~ t \geqslant t_{0}. $$

(B.5)

From (B.3) and (B.4) we can address the following estimates of the discretization error (Honig and Hirdes 1984):

$$ \text{For}~~ m=0, ~~ |F1(v,t,T)|\leqslant \frac{c}{e^{2vt}-1}, $$

(B.6)

$$ ~~ |F1(v,t,T)|\leqslant K (2T)^{m} e^{-2vT}\left ( \frac{\alpha _{1}}{2vT}+\frac{\alpha _{2}}{(2vT)^{2}}+\cdots + \frac{\alpha _{m+1}}{(2vT)^{m+1}}\right ), $$

(B.7)

where $K$, $\alpha _{1}$, $\alpha _{2}$, …, $\alpha _{m+1} \in \mathbb{R}$.

We can see from the above estimates that the discretization error can be made sufficiently small on choosing $v$ considerably large. The infinite series in (B.3) can only be summed up to a finite number of terms $N$. The truncation error can also appear, which is given by

$$ \begin{aligned} &FA(N, v, t, T)\\ &\quad = \frac{e^{vt}}{T}\left [\sum _{k=N+1}^{\infty } \text{Re}\left \{ F\left ( v+i \frac{k \pi}{T}\right )\right \}\cos \frac{k \pi}{T}t- \text{Im}\left \{ F\left ( v+i \frac{k \pi}{T} \right )\right \}\sin \frac{k \pi}{T}t\right ]. \end{aligned} $$

(B.8)

Therefore the approximate value of $f(t)$ is given by

$$ f_{N}(t) = \frac{e^{vt}}{T}\left [-\frac{1}{2}\text{Re}\left \{F(v) \right \}+\sum _{k=0}^{N} \text{Re}\left \{F\left (v+i\frac{k \pi}{T} \right )\right \}\times \cos \frac{k \pi}{T}t\right . $$

$$ \left .- \sum _{k=0}^{N} \text{Im}\left \{F\left (v+i\frac{k \pi}{T} \right )\right \}\times \sin \frac{k \pi}{T}t\right ]. $$

(B.9)

From (B.6) and (B.7) it is obvious that the discretization error can be made arbitrarily small if the product $vT$ is sufficiently large.

The “Korrektur” method allows for a reduction of the discretization error without enlarging the truncation error. Therefore, using equation (B.9), equation (B.3) can be expressed as

$$ f(t) = f_{\infty }(t) - F1 (v, t, T). $$

(B.10)

The “Korrektur” method uses the approximation formula given by

$$ f(t) = f_{\infty }(t) - e^{-2vT}f_{\infty }(2T+t)-F2(v,t,T), $$

(B.11)

in which the discretization error $F2(v,t,T)$ is much smaller than $F1(v,t,T)$. From the truncation error stated in equation (B.8), the approximate value of $f(t)$, using the “Korrektur” method, is given by

$$ f_{NK}(t)= f_{N}(t)- e^{-2vT}f_{N_{0}}(2T+t). $$

(B.12)

It must be mentioned that the truncation error of the “Korrektur” method is much smaller than $FA(N, v, t, T)$ for $N=N_{0}$. Therefore we can choose $N_{0}< N$, i.e., only a few additional function evaluations of $F(p)$ are necessary to achieve a considerable reduction of the discretization error.