Nonlinear transient thermo-elastoplastic analysis of temperature-dependent FG plates using an efficient 3D meshless model

Abstract

This paper presents a nonlinear thermo-elastoplastic bending analysis of temperature-dependent functionally graded (FG) plates exposed to a combination of mechanical and thermal loads using an efficient three-dimensional (3D) truly meshless approach based on the local radial point interpolation method (LRPIM). In this model, while using a new radial basis function (RBF), it is well shown that the quality of the LRPIM shape functions is not affected by the shape parameter. The modified rule of mixtures is employed to locally evaluate the effective temperature-dependent parameters of the functionally graded material. To describe the plastic behavior of the FG plate, the von Mises yield criterion, isotropic strain hardening, and the Prandtl-Reuss flow rule are adapted. To demonstrate the high capability and efficiency of the present method, the current results are compared with other existing numerical and analytical results, which shows an excellent agreement. The effect of significant parameters such as material gradient, ceramic volume fraction, plate thickness-to-length ratio, and boundary conditions on the nonlinear bending response of FG plates has also been investigated.

1 Introduction

Functionally graded materials (FGMs) are advanced composites that are made by mixing two or more materials, usually ceramic and metal, in an organized manner so that, to achieve the desired mechanical properties, the constituent volume fractions change with a specific function in one or more directions. The unique mechanical and thermal properties of FGMs, especially in high-temperature environments, have allowed designers to use them extensively in a variety of fields to improve the performance of modern engineering structures. Due to their high practical capabilities, these materials have been adopted as an important component in various industries, e.g., mechanical, aerospace, electronics, marine/naval, nuclear reactors, biomechanical, medical devices, etc. The special capabilities of FGMs, their temperature-dependent properties, and the importance of analyzing practical problems exposed to high operating temperatures have made the study of the thermo-mechanical behavior of FG plates an attractive research area.

Several plate theories have been proposed for the analysis of plates such as the classical plate theory (Dawe et al. 1992; Chen and Li 2014; Panah et al. 2021), the first-order shear deformation plate theory (FSDPT) (Abolghasemi et al. 2016; Izadi et al. 2018; Salehi Kolahi et al. 2021; Noori and Temel 2021), and the higher-order shear deformation plate theory (HSDPT) (Reddy 1984; Shi 2007; Asadi and Fariborz 2012; Nguyen et al. 2015; Dergachova et al. 2020; Wang et al. 2021). Of course, solutions derived from 3D theories, which do not have the limitations of these 2D theories, offer deeper physical insights and more realistic solutions, especially in dealing with thick plates (Xu and Zhou 2009; Alibeigloo and Alizadeh 2015; Vaghefi 2020a, b). 3D bending responses of FG plates have been provided analytically by many researchers. Mian and Spencer (Mian and Spencer 1998) derived an exact solution for the 3D bending of FG and laminated plates with zero surface traction. Using an asymptotic expansion method, Reddy and Cheng (Reddy and Cheng 2001) presented a 3D thermo-mechanical analysis of simply supported rectangular FG plates. Vel and Batra (2002) provided a 3D analytical solution for the thermo-mechanical bending behavior of a simply supported FG plate, by assuming a power–law variation through the thickness. They also developed a 3D exact solution of transient thermal stresses in a simply supported FG plate using the uncoupled quasi-static thermoelasticity theory (Vel and Batra 2003). A 3D exact closed-form solution for simply supported FG plates exposed to transversely distributed load was proposed by Kashtalyan (2004). Zhong and Shang (2008) performed a 3D exact analysis of FG plates with simply supported constraints by considering different models for variation of material properties. Xu and Zhou (2009) derived a 3D exact solution of simply supported FG rectangular plates with variable thickness. Vafakhah and Neya (2019) provided an exact solution for 3D flexural response of thick rectangular FG plates with simply supported constraints using the displacement potential function method. It should be noted that the results obtained from analytical methods can be very good criteria for validating numerical methods and evaluating the accuracy of their results, but it must be admitted that analytical solutions often include simple geometries and certain types of boundary and loading conditions. Therefore, using numerical methods to analyze complex and practical problems is very useful and sometimes unavoidable.

Some 3D numerical analyses have been presented in the literature to investigate the flexural behavior of FG plates. Ramirez et al. (2006) utilized the Ritz method combined with a discrete layer theory for the 3D bending analysis of anisotropic FG plates. Vaghefi et al. (2010) developed a meshless local Petrov–Galerkin (MLPG) model to explore the 3D flexural response of thick FG plates. They extended the MLPG model to predict the elastoplastic deformations of FG plates exposed to thermo-mechanical loads (Vaghefi et al. 2016). Zafarmand and Kadkhodayan (2014) provided a 3D static response of thick FG plates considering the graded finite element method (FEM) combined with the Rayleigh–Ritz energy method. Mojdehi et al. (2011) employed an MLPG approach for 3D static and dynamic analysis of thick FG plates. Nikbakht et al. (2017) presented the 3D bending response of FG plates up to yielding using a layer-wise FEM. According to the above-mentioned literature review, it seems that limited works have been conducted to predict the thermo-plastic behavior of FG plates.

Recently, various meshless methods (Nayroles et al. 1992; Belytschko et al. 1994; Liu et al. 1995; Duarte and Oden 1996; Babuska and Melenk 1997; Lucy 1977; Liu and Liu 2003; Sukumar et al. 1998; Atluri and Zhu 1998; Atluri et al. 1999; Wang and Liu 2000; Onate et al. 2001; Mukherjee 2002; Abbaszadeh and Dehghan 2020) have been used as efficient and powerful computational tools to solve many practical problems that exist in science and engineering. Furthermore, the use of deep neural networks (DNNs) to solve partial differential equations (PDEs) or metamodeling PDE-based systems has been promising (Samaniego et al. 2020; Zhuang et al. 2021; Guo et al. 2019). It is worth noting that many meshless methods do not count as truly meshless methods because they use background mesh to approximate field variables and determine domain integrals. Moreover, the shape functions of these methods often do not satisfy the Kronecker delta function property. Hence, special treatment such as the transformation method (Liew et al. 2004), Lagrange multipliers (Onate et al. 2001), or penalty method (Cho et al. 2008) should be provided to enforce the essential boundary conditions. One of the truly meshless methods is the LRPIM, first introduced by Liu and Gu (2001), Liu et al. (2002). This method uses radial basis functions (RBFs) to approximate field variables and calculates local residual integration on local sub-domains. The shape functions created by RBFs have the properties of the Kronecker delta function and the direct imposition of the essential boundary conditions is one of their most important features (Liu et al. 2005). Besides, the LRPIM analysis does not depend on any cell for integrating and approximating field variables. Until now, the LRPIM has been used for solving various problems, such as vibration analysis of 2D solids (Liu and Gu 2001), 2D dynamic and static analysis of plates (Xia et al. 2009a, b), 2D elastostatic analysis of FGMs (Ebrahimijahan et al. 2022), inverse heat conduction problem (Shivanian and Khodabandehlo 2016), fluid flow problems (Saeedpanah et al. 2011), simulation of the 2D Maxwell equations (Dehghan and Haghjoo-Saniji 2017), sine–Gordon equation (Dehghan and Shokri 2008; Dehghan and Ghesmati 2010), and Klein–Gordon equation (Dehghan and Shokri 2009). However, most of this research is limited to analyzing 2D problems. To the best of the author's knowledge, this is the first time to date that a robust and improved version of the LRPIM has been employed to achieve a 3D thermo-elastoplastic flexural response.

In the present study, an efficient truly meshless method based on the LRPIM is presented and successfully employed for 3D nonlinear transient thermo-elastoplastic bending analysis of temperature-dependent FG plates exposed to a combination of mechanical and thermal loads. In this method, to improve the interpolation process and approximation of the field variable, a new RBF is used that maintains the quality of LRPIM shape functions regardless of the change in the shape parameter. The present study, which presents an uncoupled thermo-elastoplastic analysis, divides the solution process into two main parts: “thermal analysis” and “mechanical analysis”. First, transient heat conduction analysis is performed to achieve the transient temperature distribution, and then the resulting temperature field is applied as a thermal load along with the mechanical load to obtain displacements and stresses in the mechanical analysis. The Prandtl-Reuss flow rule, von Mises yield criterion, and isotropic strain hardening model are adapted to describe the plastic behavior of the FG plate. To locally evaluate the effective elastoplastic parameters, the modified rule of mixtures (Suresh and Mortensen 1998) is used. The material properties, which are assumed to be temperature-dependent, are continuously varying in the thickness direction according to a power-law function in terms of the ceramic and metal volume fractions. To confirm the efficiency and effectiveness of the present method, the necessary comparisons between the results obtained with the existing analytical solutions (3D and quasi-3D) and 3D FEM results have been accomplished. Several numerical examples are provided and some parameters such as material gradients, ceramic volume fraction, plate thickness-to-length ratios and boundary conditions, which can have very significant effects on the results, are investigated. Necessary scrutiny has also been done on the number of nodes required to extract results with good convergence.

2 Problem domain and boundary conditions

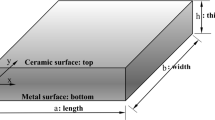
A rectangular FG plate with dimensions ($a \times b \times h$) is considered in the Cartesian coordinate system xyz as shown in Fig. 1. The z-axis is positioned across the thickness and the xy plane ($z = 0$) coincides with the bottom surface of the plate. It is assumed that the bottom surface of the plate varies from metal-rich to ceramic-rich at the top surface. The ceramic volume fraction varies continuously through the thickness according to a power-law function as

$$ V^{c} (z) = V_{{{\text{max}}}}^{{\text{c}}} \left( \frac{z}{h} \right)^{n} ,\,\,\,\,\,0 \le V_{{{\text{max}}}}^{{\text{c}}} \le 1, $$

(1)

and the volume fraction for the metal phase is determined as $V^{{\text{m}}} (z) = 1 - V^{{\text{c}}} (z)$. $V_{{{\text{max}}}}^{{\text{c}}}$ is the maximum volume fraction of ceramic associated with the top surface of the plate, and $n$ is the volume fraction exponent $(n \ge 0)$.

In the present 3D model, the Simply supported (S), Clamped (C), and Free (F) boundary conditions on the side edges of the plate are defined as follows:

$$ S{:}\,\,\left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{{}} = 0,\,\,v = w = 0\,\,\,{\text{on}}\,\,\,x = 0,a} \\ {\sigma_{yy}^{{}} = 0,\,\,u = w = 0\,\,\,{\text{on}}\,\,\,y = 0,b} \\ \end{array} } \right. $$

(2)

$$ C{:}\,\,\,u = v = w = 0\,\,\,\,{\text{on}}\,\,\,x = 0,\,a\,\,\,{\text{and}}\,\,\,y = 0,\,b $$

(3)

$$ F{:}\,\,\left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{{}} = \sigma_{xy}^{{}} = \sigma_{xz}^{{}} = 0\,\,\,{\text{on}}\,\,\,x = 0,a} \\ {\sigma_{yy}^{{}} = \sigma_{yx}^{{}} = \sigma_{yz}^{{}} = 0\,\,\,{\text{on}}\,\,\,y = 0,b} \\ \end{array} } \right. $$

(4)

where u, v and w are displacement components at x, y and z directions, respectively. It is assumed that the plate is initially at a uniform temperature $T_{0} \, = 300\;\,{\text{K}}$ and is completely stress-free. Subsequently, the top surface of the plate is exposed to a combination of thermal and mechanical loads. The thermal load is applied as sinusoidal heat flux Q with the intensity q as follows

$$ Q(x,y,h,t) = q\sin (\pi x/a)\sin (\pi y/b), $$

(5)

and the uniformly distributed mechanical load is imposed as follows

$$ \sigma_{zz}^{{}} (x,y,h,t) = - p,\,\,\sigma_{zx}^{{}} (x,y,h,t) = \sigma_{zy}^{{}} (x,y,h,t) = 0. $$

(6)

Fig. 1

Geometry of rectangular plate considered in the 3D Cartesian coordinate system

3 Effective material properties of the temperature-dependent FG plate

In general, the ceramic constituent is completely brittle and always retains its elastic deformation. While yield in FGMs occurs in its metal constituent when the equivalent stresses are greater than the yield limit. Several homogenization methods for describing the nonlinear behavior of metal-ceramic composite materials and estimating their effective mechanical properties have been proposed in the literature (Budiansky 1965; Hill 1965; Love and Batra 2006; Mori and Tanaka 1973; Vena et al. 2008). One of the simplest and most convenient homogenization techniques is the modified rule of mixtures (Suresh and Mortensen 1998), which predicts the effective material properties of a metal-ceramic composite using the volume fraction of its constituents. Figure 2 shows the stress–strain curve of FGM based on the modified rule of mixtures. Therefore, the effective elastic modulus $E_{{{\text{eff}}}}$, Poisson’s ratio $\nu_{{{\text{eff}}}}$, tangent modulus $H_{{{\text{eff}}}}$, and yield stress $\sigma_{{{\text{y}}\,\,{\text{eff}}}}$ of FGM can be evaluated separately as follows

$$ E_{{{\text{eff}}}}^{{}} (T,z) = {{\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + E^{{\text{m}}} (T)}}E^{{\text{m}}} (T)V^{{\text{m}}} (z) + E^{{\text{c}}} (T)V^{{\text{c}}} (z)} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + E^{{\text{m}}} (T)}}E^{{\text{m}}} (T)V^{{\text{m}}} (z) + E^{{\text{c}}} (T)V^{{\text{c}}} (z)} \right)} {\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + E^{{\text{m}}} (T)}}V^{{\text{m}}} (z) + V^{{\text{c}}} (z)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + E^{{\text{m}}} (T)}}V^{{\text{m}}} (z) + V^{{\text{c}}} (z)} \right)}}, $$

(7)

$$ \nu_{{{\text{eff}}}}^{{}} (T,z) = \nu^{{\text{c}}} (T)V^{{\text{c}}} (z) + \nu^{{\text{m}}} (T)V^{{\text{m}}} (z), $$

(8)

$$ \sigma_{{{\text{y}}\,\,{\text{eff}}}}^{{}} (T,z) = \sigma_{{\text{y}}}^{{\text{m}}} (T)\left( {\frac{{\hat{q} + E^{{\text{m}}} (T)}}{{\hat{q} + E^{{\text{c}}} (T)}}\frac{{E^{{\text{c}}} (T)}}{{E^{{\text{m}}} (T)}}V^{{\text{c}}} (z) + V^{{\text{m}}} (z)} \right), $$

(9)

$$ H_{{{\text{eff}}}}^{{}} (T,z) = {{\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + H^{{\text{m}}} (T)}}H^{{\text{m}}} (T)V^{{\text{m}}} (z) + E^{{\text{c}}} (T)V^{{\text{c}}} (z)} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + H^{{\text{m}}} (T)}}H^{{\text{m}}} (T)V^{{\text{m}}} (z) + E^{{\text{c}}} (T)V^{{\text{c}}} (z)} \right)} {\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + H^{{\text{m}}} (T)}}V^{{\text{m}}} (z) + V^{{\text{c}}} (z)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{\hat{q} + E^{{\text{c}}} (T)}}{{\hat{q} + H^{{\text{m}}} (T)}}V^{{\text{m}}} (z) + V^{{\text{c}}} (z)} \right)}}, $$

(10)

where the superscripts ‘m’ and ‘c’ represent the ceramic phase and metal phase, respectively. $\hat{q}$ is the ratio of stress to strain transfer ($0 \le \hat{q} \le \infty$) and is expressed by the following equation (Williamson et al. 1993):

$$ \hat{q} = \frac{{\left| {\sigma^{{\text{m}}} - \sigma^{{\text{c}}} } \right|}}{{\varepsilon^{{\text{m}}} - \varepsilon^{{\text{c}}} }}, $$

(11)

where σ^m, ε^m, and σ^c, ε^c are the corresponding true stress and strain of the metal and ceramic, respectively. As shown in Fig. 2, $\hat{q}$ is the slope of a correspondence line on the stress–strain curve. In this way, large slopes ($\hat{q} \to \infty$) will be close to the isostrain condition ($\varepsilon^{{\text{m}}} = \varepsilon^{{\text{c}}} = \varepsilon_{{{\text{y}}_{{0}} \;{\text{eff}}}}$), and small slopes ($\hat{q} \to 0$) will create the isostress condition ($\sigma^{{\text{m}}} = \sigma^{{\text{c}}} = \sigma_{{{\text{y}}_{{0}} \;{\text{eff}}}}$); in which $\sigma_{{{\text{y}}_{{0}} \;{\text{eff}}}}$ and $\varepsilon_{{{\text{y}}_{{0}} \;{\text{eff}}}}$ are the FGM flow stress and strain (see Fig. 2). For example, $\hat{q} \to 0$ means that FGM flows plastically when the metal phase is yielded, while $\hat{q} \to \infty$ indicates that the constituent elements deform identically in the loading direction (Williamson et al. 1993). In this study, $\hat{q} = 5\,{\text{GPa}}$ is considered.

Fig. 2

Stress–strain curve of FGMs predicted by the modified rule of mixtures

The effective thermal expansion coefficient $\alpha_{{{\text{eff}}}}$, mass density $\rho_{{{\text{eff}}}}$, specific heat $c_{{{\text{eff}}}}$, and heat conductivity coefficient $\kappa_{{{\text{eff}}}}$ are expressed as Mori and Tanaka (1973), Hatta and Taya (1985), Rosen and Hashin (1970)

$$ \alpha_{{{\text{eff}}}}^{{}} (T,z) = \alpha^{{\text{m}}} (T) + \frac{{\left[ {1/K_{{{\text{eff}}}}^{{}} (T,z) - 1/K^{{\text{m}}} (T)} \right]\left[ {\alpha^{{\text{c}}} (T) - \alpha^{{\text{m}}} (T)} \right]}}{{1/K^{{\text{c}}} (T) - 1/K^{{\text{m}}} (T)}}, $$

(12)

$$ \rho_{{{\text{eff}}}}^{{}} (T,z) = \rho^{{\text{m}}} (T)V^{{\text{m}}} (z) + \rho^{{\text{c}}} (T)V^{{\text{c}}} (z), $$

(13)

$$ c_{{{\text{eff}}}}^{{}} (T,z) = \frac{1}{{\rho_{{{\text{eff}}}}^{{}} (T,z)}}\left( {c_{{}}^{{\text{c}}} (T)\rho^{{\text{c}}} (T)V^{{\text{c}}} (z) + c_{{}}^{{\text{m}}} (T)\rho^{{\text{m}}} (T)V^{{\text{m}}} (z)} \right), $$

(14)

$$ \kappa_{{{\text{eff}}}}^{{}} (T,z) = \kappa^{{\text{m}}} (T) + \frac{{\left( {\kappa^{{\text{c}}} (T) - \kappa^{{\text{m}}} (T)} \right)V^{{\text{c}}} (z)}}{{1 + \left[ {{{\left( {\kappa^{{\text{c}}} {(}T) - \kappa^{{\text{m}}} (T)} \right)} \mathord{\left/ {\vphantom {{\left( {\kappa^{{\text{c}}} {(}T) - \kappa^{{\text{m}}} (T)} \right)} {3\kappa^{{\text{m}}} (T)}}} \right. \kern-\nulldelimiterspace} {3\kappa^{{\text{m}}} (T)}}} \right]V^{{\text{m}}} (z)}}, $$

(15)

where $K_{{{\text{eff}}}}^{{}}$ is the effective bulk’s modulus and $K_{{{\text{eff}}}}^{{}} (T,z) = \tfrac{{E_{{{\text{eff}}}}^{{}} (T,z)}}{{3(1 - 2\nu_{{{\text{eff}}}}^{{}} (T,z))}}$. Although the present formulation can be used to analyze different types of FGMs, in this investigation a mixture of zirconium oxide (${\text{ZrO}}_{{2}}$) and titanium alloy (${\text{Ti - 6Al - 4V}}$) is considered. The temperature-dependent thermo-elastoplastic properties of ${\text{Ti - 6Al - 4V}}$ and ${\text{ZrO}}_{{2}}$, used in the present analysis, are given in Table 1 (Nemat-Alla et al. 2009).

Table 1 Temperature-dependent material properties used in the FGM (Nemat-Alla et al. 2009)

4 Governing equations

4.1 Governing equations of nonlinear heat conduction

When the material properties depend on the position ${\varvec{x}}(x,y,z)$ and the temperature $T({\varvec{x}},t)$, the transient nonlinear heat conduction problem in the 3D domain $\Omega$ with boundary $\Gamma$, for no internal heat source term, is governed by Lewis et al. (2004)

$$ \frac{\partial }{\partial x}\left( {\frac{\partial T}{{\partial x}}\kappa ({\varvec{x}},T)} \right) + \frac{\partial }{\partial y}\left( {\frac{\partial T}{{\partial y}}\kappa ({\varvec{x}},T)} \right) + \frac{\partial }{\partial z}\left( {\frac{\partial T}{{\partial z}}\kappa ({\varvec{x}},T)} \right) = \,\rho ({\varvec{x}},T)\,c({\varvec{x}},T)\,\frac{\partial T}{{\partial t}}\,\,\,\,{\text{in}}\,\Omega , $$

(16)

where $c$ is the specific heat, $\kappa$ is the thermal conductivity, $\rho$ is the density, and $t$ is a temporal variable. The above equation is completed with the following initial and boundary conditions:

$$ T({\varvec{x}},0) - T_{0} = 0\,\,\,\,\,{\text{in}}\,\Omega , $$

(17)

$$ T({\varvec{x}},t) - \overline{T} = 0\,\,\,\,\,{\text{on}}\,\Gamma_{T} , $$

(18)

$$ \left( {\frac{\partial T}{{\partial x}}n_{x} + \frac{\partial T}{{\partial y}}n_{y} + \frac{\partial T}{{\partial z}}n_{z} } \right)\kappa ({\varvec{x}},T) = - \overline{q}\,\,\,\,on\,\Gamma_{q} , $$

(19)

where $T_{0}$ denotes the initial condition, while $\overline{T}$ and $\overline{q}$ are the specified temperature and heat flux on the boundary $\Gamma_{T}$ and $\Gamma_{q}$, respectively. In addition, $n_{x}$, $n_{y}$, and $n_{z}$ are direction cosines.

4.2 Governing equations of thermo-elastoplasticity

The incremental equilibrium equation and boundary conditions in a domain $\Omega$ surrounded by closed boundary $\Gamma$ can be expressed as Hsu (1986)

$$ {\text{d}}\sigma_{ij,j} + {\text{d}}b_{i} = 0\,\,\,\,\,{\text{in}}\,\,\Omega , $$

(20)

$$ {\text{d}}\sigma_{ij} n_{j} - {\text{d}}\overline{t}_{i} \, = 0\,\,\,{\text{on}}\,\Gamma_{t} , $$

(21)

$$ {\text{d}}u_{i} - {\text{d}}\overline{u}_{i} = 0\,\,\,{\text{on}}\,\Gamma_{u} , $$

(22)

where ${\text{d}}\sigma_{ij}$, ${\text{d}}u_{i}$, ${\text{d}}t_{i}$, and ${\text{d}}b_{i}$ denote incremental components of the stress, displacement, traction and body force vector, respectively. ${\text{d}}\overline{u}_{i}$ and ${\text{d}}\overline{t}_{i}$ are the predefined incremental displacement and traction on the boundary $\Gamma_{u}$ and $\Gamma_{t}$, respectively. $n_{i}$ is the unit outward normal vector at $\Gamma$.

In the small strain theory, it is assumed that the total incremental strain vector $\{ d{{\varvec{\upvarepsilon}}}\}$, whose components are defined as ${\text{d}}\varepsilon_{ij} = ({\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}})({\text{d}}u_{i,j} + {\text{d}}u_{j,i} )$, can be additively decomposed into the elastic part $\{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e}}} \}$, thermal part $\{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{{\text{th}}}} \}$, plastic part $\{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{p}}} \}$, and strain vector related to the dependence of material properties on temperature $\{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e,th}}} \}$ according to the relationship (Sluzalec 1992)

$$ \{ {\text{d}}{{\varvec{\upvarepsilon}}}\} = \{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e}}} \} + \{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{{\text{th}}}} \} + \{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e,th}}} \} + \{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{p}}} \} . $$

(23)

In Eq. (23), $\{ d{{\varvec{\upvarepsilon}}}^{th} \}$ and $\{ d{{\varvec{\upvarepsilon}}}^{e,th} \}$ are defined as

$$ \left\{ {{\text{d}}{{\varvec{\upvarepsilon}}}^{{{\text{th}}}} } \right\} = \{ {{\varvec{\upalpha}}}\} {\text{d}}T,\,\,\,\,\,\,\left\{ {{\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e,th}}} } \right\} = \left( {\frac{{\partial [{\varvec{D}}^{e} ]^{ - 1} }}{\partial T}} \right)\{ {{\varvec{\upsigma}}}\} {\text{d}}T, $$

(24)

where $[{\varvec{D}}_{{\text{e}}} ]$ and $\{ {{\varvec{\upalpha}}}\}$ are the elastic stiffness matrix and the vector of the thermal expansion coefficient, respectively (Sadd 2009). The von-Mises yield function, i.e., $F = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\sigma^{\prime}_{ij} \sigma^{\prime}_{ij} - {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}\sigma_{y}^{2}$, and the Prandtl–Reuss model, which consists of an associated flow rule are used for the thermo-elastoplastic analysis. The incremental plastic strain ${\text{d}}{{\varvec{\upvarepsilon}}}^{p}$ is calculated according to the following equation

$$ \left\{ {{\text{d}}{{\varvec{\upvarepsilon}}}^{p} } \right\} = {\text{d}}\lambda \left\{ {\frac{\partial F}{{\partial \sigma }}} \right\} = {\text{d}}\lambda \{ {\varvec{\sigma^{\prime}}}\} , $$

(25)

where $\{ {\varvec{\sigma^{\prime}}}\}$ and ${\text{d}}\lambda$ are the deviatoric stress tensor and the plastic coefficient, respectively. In the case of temperature-dependent isotropic hardening, the yield stress function is represented by $\sigma_{y} = \sigma_{{y_{0} }} (T) + H(T)\overline{\varepsilon }^{{\text{p}}}$, where $\sigma_{{y_{0} }}$, $H$ and $\overline{\varepsilon }^{{\text{p}}}$ are the initial yield stress, strain hardening parameter and equivalent plastic strain, respectively. The plastic coefficient can be obtained by imposing the consistency condition (${\text{d}}F = {\text{d}}F\left( {T,\{ {{\varvec{\upsigma}}}\} ,K} \right) = 0$) as (Hsu 1986)

$$ {\text{d}}\lambda = \frac{{\left\{ {{\varvec{\sigma^{\prime}}}} \right\}^{T} \left[ {{\varvec{D}}^{e} } \right]\left( {\left\{ {{\text{d}}{{\varvec{\upvarepsilon}}}} \right\} - \left\{ {{\text{d}}{{\varvec{\upvarepsilon}}}^{{{\text{th}}}} } \right\} - \{ {\text{d}}{{\varvec{\upvarepsilon}}}^{{\text{e,th}}} \} } \right) + \frac{\partial F}{{\partial T}}{\text{d}} T}}{{\left\{ {{\varvec{\sigma^{\prime}}}} \right\}^{T} \left[ {{\varvec{D}}^{e} } \right]\left\{ {{\varvec{\sigma^{\prime}}}} \right\} - \frac{\partial F}{{\partial \overline{\sigma }}}\frac{{\partial \overline{\sigma }}}{{\partial \overline{\varepsilon }^{{\text{p}}} }}\frac{{\partial \overline{\varepsilon }^{{\text{p}}} }}{\partial K}\left\{ {\frac{\partial K}{{\partial \varepsilon^{{\text{p}}} }}} \right\}^{T} \left\{ {{\varvec{\sigma^{\prime}}}} \right\}}}, $$

(26)

where $\overline{\sigma }$ is the equivalent stress. For hardening materials, K is a function of $\varepsilon^{{\text{p}}}$, and here ${\text{d}}K = \sigma_{ij} {\text{d}}\varepsilon_{ij}^{{\text{p}}}$. The incremental thermo-elastoplastic constitutive equations can be derived from Eqs. (23) to (26) as

$$ \left\{ {d{{\varvec{\upsigma}}}} \right\} = \left[ {{\varvec{D}}^{{{\text{ep}}}} } \right]\left( {\{ {\text{d}}{{\varvec{\upvarepsilon}}}\} - \left\{ {{\text{d}}\,{\tilde{\varvec{\varepsilon }}}^{{\text{th - ep}}} } \right\}} \right),\, $$

(27)

$$ \left\{ {d\,{\tilde{\varvec{\varepsilon }}}^{{\text{th - ep}}} } \right\} = \left\{ {d{{\varvec{\upvarepsilon}}}^{{{\text{th}}}} } \right\} + \left\{ {d{{\varvec{\upvarepsilon}}}^{{\text{e,th}}} } \right\} + \frac{{\left[ {{\varvec{D}}^{{{\text{ep}}}} } \right]^{ - 1} [{\varvec{D}}^{e} ]\{ {\varvec{\sigma^{\prime}}}\} \frac{\partial F}{{\partial T}}{\text{d}}T}}{{\left\{ {{\varvec{\sigma^{\prime}}}} \right\}^{T} \left[ {{\varvec{D}}^{e} } \right]\left\{ {{\varvec{\sigma^{\prime}}}} \right\} - \frac{\partial F}{{\partial \overline{\sigma }}}\frac{{\partial \overline{\sigma }}}{{\partial \overline{\varepsilon }^{{\text{p}}} }}\frac{{\partial \overline{\varepsilon }^{p} }}{\partial K}\left\{ {\frac{\partial K}{{\partial \varepsilon^{{\text{p}}} }}} \right\}^{T} \left\{ {{\varvec{\sigma^{\prime}}}} \right\}}}, $$

(28)

$$ [{\varvec{D}}^{{{\text{ep}}}} ] = [{\varvec{D}}^{{\text{e}}} ] - \frac{{[{\varvec{D}}^{{\text{e}}} ]\{ {\varvec{\sigma^{\prime}}}\} \{ {\varvec{\sigma^{\prime}}}\}^{T} [{\varvec{D}}^{{\text{e}}} ]}}{{\left\{ {{\varvec{\sigma^{\prime}}}} \right\}^{T} \left[ {{\varvec{D}}^{{\text{e}}} } \right]\left\{ {{\varvec{\sigma^{\prime}}}} \right\} - \frac{\partial F}{{\partial \overline{\sigma }}}\frac{{\partial \overline{\sigma }}}{{\partial \overline{\varepsilon }^{{\text{p}}} }}\frac{{\partial \overline{\varepsilon }^{{\text{p}}} }}{\partial K}\left\{ {\frac{\partial K}{{\partial \varepsilon^{{\text{p}}} }}} \right\}^{T} \left\{ {{\varvec{\sigma^{\prime}}}} \right\}}}, $$

(29)

where $[{\varvec{D}}^{{{\text{ep}}}} ]$ and $\{ d\,{\tilde{\varvec{\varepsilon }}}^{{\text{th - ep}}} \}$ are the tangent elastoplastic stiffness matrix and the overall incremental thermo-elastoplastic strain vector, respectively.

5 Efficient LRPIM formulation

The LRPIM is a truly meshless method based on the local weak form in which no cell is required to approximate field variables and numerical integrations (Kazemi et al. 2017). So far, various types of RBFs, which are used to construct LRPIM shape functions, have been employed to achieve good performance in numerical analyses. Usually, the thin plate spline (TPS) (Powell 1994), the Gaussian (EXP) (Agnantiaris et al. 1996) and the multiquadric (MQ) (Hardy 1990) functions have been widely used in many engineering problems. Note that to achieve a desirable performance of the method, shape parameters must be appropriately selected in using RBFs (Wang and Liu 2002). The shape parameters of EXP play a major role in finding solutions with good convergence, and for MQ, the stability of solutions should be evaluated by the fitting parameters (Do and Lee 2018). Hence, choosing the optimal values for the shape parameters is still a difficult task (Do and Lee 2017). Recently, to determine the optimal value of uncertain and important input parameters to achieve desired model outputs, a sensitivity analysis toolbox consisting of a set of Matlab functions was provided by Vu-Bac et al. (2016).

In the next section, a new and efficient RBF is presented to construct LRPIM shape functions in which the qualitative behavior of the shape function is completely independent of shape parameter changes.

5.1 Shape functions

The interpolation function ${\text{f}}^{{\text{h}}} (x,{\text{t}})$, which can be displacement or temperature vector components, is constructed at any point ${\varvec{x}}$ based on a linear combination of polynomial and the RBFs as follows (Liu et al. 2002)

$$ {\text{f}}^{{\text{h}}} (x,{\text{t}}) = \sum\limits_{{{\text{I = }}1}}^{{\text{N}}} {{\text{g}}_{{\text{I}}} (x){\text{a}}_{{\text{I}}} ({\text{t}})} + \sum\limits_{{{\text{j = }}1}}^{{\text{m}}} {{\text{p}}_{{\text{j}}} (x)} {\text{b}}_{{\text{j}}} ({\text{t}}) = \left\{ {g^{{\text{T}}} (x)\,\,\,\,p^{{\text{T}}} (x)} \right\}\left\{ {\begin{array}{*{20}c} {a({\text{t}})} \\ {b({\text{t}})} \\ \end{array} } \right\}\,\,\,\,\forall x \in \Omega_{{\text{x}}} , $$

(30)

where

$$ g^{{\text{T}}} (x) = \{ {\text{g}}_{1} (x),{\text{g}}_{2} (x),...,{\text{g}}_{{\text{N}}} (x)\} , $$

(31)

$$ {\varvec{p}}^{T} ({\varvec{x}}) = \{ 1,x,y,z\} \;{\text{Linear basis}}\;(m = 4), $$

(32)

$$ {\varvec{p}}^{T} ({\varvec{x}}) = \{ 1,x,y,z,x^{2} ,y^{2} ,z^{2} ,xy,yz,zx\} \;{\text{Quadratic basis}}\;(m = 10). $$

(33)

In Eq. (30), ${\text{g}}_{{\text{I}}} (x)$ is the RBF, ${\text{a}}_{{\text{I}}}$ and ${\text{b}}_{{\text{j}}}$ are interpolation constants, and ${\text{N}}$ is the number of scattered nodes in the support domain $\Omega_{{\text{x}}}$. In general, the polynomial term in Eq. (30) is not always necessary because the RBFs are augmented by m polynomial basis functions, and so when m = 0, pure RBFs are used. Although the higher-order polynomial basis usually has better approximation and convergence properties, increasing the computational costs prevent the practical use of such functions (Chowdhury et al. 2017). Therefore, a minimum number of terms of polynomial basis is often used (m = 4 or 10). To obtain a unique approximation function $f$, the following constraint conditions should be imposed

$$ \sum\limits_{{{\text{I = }}1}}^{{\text{N}}} {{\text{p}}_{{\text{j}}} (x_{{\text{I}}} ){\text{a}}_{{\text{I}}} ({\text{t}})} = P^{{\text{T}}} a = 0\,\,\,{\text{with}} \,\,{\text{j = }}1,2, \ldots ,{\text{m}}, $$

(34)

where

$$ P = \left[ {p(x_{1} ),p(x_{2} ), \ldots ,p(x_{{\text{N}}} )} \right]_{{({\text{m}} \times {\text{N}})}}^{{\text{T}}} . $$

(35)

The coefficients ${\text{a}}_{{\text{I}}}$ and ${\text{b}}_{{\text{j}}}$ can be determined by enforcing Eq. (30) to all ${\text{N}}$ scattered nodal points within $\Omega_{{\text{x}}}$, which leads to the following ${\text{N}}$ linear equation

$$ {\text{f}}^{{\text{h}}} (x_{{\text{k}}} ,{\text{t}}) = \sum\limits_{{{\text{I = }}1}}^{{\text{N}}} {{\text{g}}_{{\text{I}}} (x_{{\text{k}}} ){\text{a}}_{{\text{I}}} ({\text{t}})} + \sum\limits_{{{\text{j = }}1}}^{{\text{m}}} {{\text{p}}_{{\text{j}}} (x_{{\text{k}}} )} {\text{b}}_{{\text{j}}} ({\text{t}})\,\,\,{\text{with}} \,\,{\text{k}} = 1,2, \ldots ,{\text{N}}. $$

(36)

Combining Eqs. (34) and (36) gives

$$ \left[ {\begin{array}{*{20}c} G & P \\ {P^{T} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} a \\ b \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} f \\ 0 \\ \end{array} } \right\}\,, $$

(37)

where

$$ f = \{ {\text{f}}_{1} ,{\text{f}}_{2} , \ldots ,{\text{f}}_{{\text{N}}} \}^{{\text{T}}} ,\,\,\,\,G(x) = \left[ {g(x_{1} ),g(x_{2} ), \ldots ,g(x_{{\text{N}}} )} \right]_{{({\text{N}} \times {\text{N}})}}^{{\text{T}}} . $$

(38)

By solving Eq. (37), we obtain

$$ {\text{f}}^{{\text{h}}} (x,{\text{t}}) = \left\{ {g^{{\text{T}}} (x)\,\,\,\,p^{{\text{T}}} (x)} \right\}\left[ {\begin{array}{*{20}c} G & P \\ {P^{{\text{T}}} } & 0 \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} f \\ 0 \\ \end{array} } \right\} = {{\varvec{\Phi}}}(x)f = \sum\limits_{{{\text{I}} = 1}}^{{\text{N}}} {\phi_{{\text{I}}} ({\varvec{x}}){\text{f}}_{{\text{I}}} ({\text{t}})} , $$

(39)

where the LRPIM shape functions can be expressed as

$$ {{\varvec{\Phi}}}({\varvec{x}}) = \{ \phi_{1} ({\varvec{x}}),\phi_{2} ({\varvec{x}}), \ldots ,\phi_{N} ({\varvec{x}})\} . $$

(40)

Here, a new and effective RBF is presented based on the original fourth-order spline function (Liu 2003), in which the qualitative behavior of the shape function is completely independent of the shape parameter and for a one-dimensional domain is expressed as follows

$$ g_{I} (x) = 1 - 6\left( {\frac{{\theta d_{x}^{I} }}{{r_{x}^{I} }}} \right)^{2} + 8\left( {\frac{{\theta d_{x}^{I} }}{{r_{x}^{I} }}} \right)^{3} - 3\left( {\frac{{\theta d_{x}^{I} }}{{r_{x}^{I} }}} \right)^{4} ,\,\,\,\,\,\,\,0 \le \theta d_{x}^{I} \le r_{x}^{I} , $$

(41)

where $\theta$ is the correlation parameter, which will be discussed later. $r_{x}^{I}$ denotes the size of the support domain that is calculated as $r_{x}^{I} = \alpha \overline{d}_{x}^{I}$ in which $\alpha$ is a scaling parameter and $\overline{d}_{x}^{I}$ represents the average of $d_{x}^{I} = \left| {x - x_{I} } \right|$. In order not to complicate the mapping procedure when the global boundary intersects a local sub-domain, in the present study, all integrals are calculated on brick-shaped local sub-domains (Vaghefi et al. 2009). For the 3D domain, the present RBF can be expressed by a simple extension of $g_{I} (x)$ as follows

$$ g_{I} ({\varvec{x}}) = g_{I} (x)\,g_{I} (y)\,g_{I} (z), $$

(42)

where $g_{I} (y)$ and $g_{I} (z)$ are obtained by substituting ${{d_{y}^{I} } \mathord{\left/ {\vphantom {{d_{y}^{I} } {r_{y}^{I} }}} \right. \kern-\nulldelimiterspace} {r_{y}^{I} }}$ and ${{d_{z}^{I} } \mathord{\left/ {\vphantom {{d_{z}^{I} } {r_{z}^{I} }}} \right. \kern-\nulldelimiterspace} {r_{z}^{I} }}$ instead of ${{d_{x}^{I} } \mathord{\left/ {\vphantom {{d_{x}^{I} } {r_{x}^{I} }}} \right. \kern-\nulldelimiterspace} {r_{x}^{I} }}$ in Eq. (41), respectively.

5.2 Discretization of the governing equations

Here, the efficient LRPIM formulation is presented for the 3D thermo-elastoplastic equation.

5.2.1 Discretized form of the 3D nonlinear heat conduction equation

Using Eq. (16), the generalized local weak formulation of the heat conduction equation over an integration local sub-domain $\Omega_{s}^{I}$ with the boundary $\partial \Omega_{s}^{I} = \Gamma_{s}^{I}$ is written as

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I} \left( {\rho ({\varvec{x}},T)c({\varvec{x}},T)\dot{T}({\varvec{x}},t) - [\kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)]_{,i} } \right)\,} {\text{d}}\Omega = 0, $$

(43)

where $\nu_{I}$ is the weight function. By applying the divergence theorem and integration by parts, the following equation can be obtained:

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\left( {\nu_{I} \rho ({\varvec{x}},T)c({\varvec{x}},T)\dot{T}({\varvec{x}},t) + \nu_{I,i} \kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)} \right)} {\text{d}}\Omega - \int_{{\Gamma_{s}^{I} }}^{{}} {\nu_{I} \kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)n_{i} } {\text{d}}\Gamma = 0. $$

(44)

By satisfying the natural boundary conditions, we obtain:

$$ \begin{gathered} \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I} \rho ({\varvec{x}},T)c({\varvec{x}},T)\dot{T}({\varvec{x}},t)} {\text{d}}\Omega + \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I,i} \kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)} {\text{d}}\Omega \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int_{{\Gamma_{si}^{I} }}^{{}} {\nu_{I} \kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)n_{i} } {\text{d}}\Gamma - \int_{{\Gamma_{sT}^{I} }}^{{}} {\nu_{I} \kappa ({\varvec{x}},T)T_{,i} ({\varvec{x}},t)n_{i} } {\text{d}}\Gamma = - \int_{{\Gamma_{sq}^{I} }}^{{}} {\nu_{I} \overline{q}} {\text{d}}\Gamma , \hfill \\ \end{gathered} $$

(45)

in which $\Gamma_{si}^{I}$ is the internal boundary of $\Omega_{s}^{I}$, while $\Gamma_{sT}^{I}$ and $\Gamma_{sq}^{I}$ are the parts of $\Gamma_{s}^{I}$ over which essential and natural boundary conditions are prescribed, respectively. The temperature field function based on Eq. (39), can be written as

$$ {\text{T}}^{{\text{h}}} (x,{\text{t}}) = \sum\limits_{{{\text{J}} = 1}}^{{\text{N}}} {\phi_{{\text{J}}} ({\varvec{x}}){\text{T}}_{{\text{J}}} } ({\text{t}}), $$

(46)

where ${\text{T}}_{{\text{J}}} ({\text{t}})$ is the nodal temperature. Substituting Eq. (46) in Eq. (45), we obtain the nonlinear transient heat conduction equation system as

$$ {\varvec{C(x}},T{\varvec{)\dot{T}}}(t){\varvec{ + }}{\varvec{\hat{K}}}({\varvec{x}},T){\varvec{T}}(t){\varvec{ = q}}{,} $$

(47)

where

$$ C_{IJ} = \int_{{\Omega_{s}^{I} }}^{{}} {\rho ({\varvec{x}},T)c} ({\varvec{x}},T)\phi_{I} ({\varvec{x}})\phi_{J} ({\varvec{x}}){\text{d}}\Omega {,} $$

(48)

$$ \begin{gathered} \hat{K}_{IJ} = \int_{{\Omega_{s}^{I} }}^{{}} {\kappa ({\varvec{x}},T)\phi_{I,i} ({\varvec{x}})\phi_{J,i} ({\varvec{x}})\,} {\text{d}}\Omega - \int_{{\Gamma_{si}^{I} }}^{{}} {\kappa ({\varvec{x}},T)\phi_{I} ({\varvec{x}})\phi_{J,i} ({\varvec{x}})n_{i} } \,{\text{d}}\Gamma \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, \quad- \int_{{\Gamma_{sT}^{I} }}^{{}} {\kappa ({\varvec{x}},T)\phi_{I} ({\varvec{x}})\phi_{J,i} ({\varvec{x}})n_{i} } \,{\text{d}}\Gamma , \hfill \\ \end{gathered} $$

(49)

$$ q_{I} = - \int_{{\Gamma_{sq}^{I} }}^{{}} {\overline{q}\phi_{I} ({\varvec{x}})} {\text{d}}\Gamma . $$

(50)

In Eq. (47), ${\hat{\varvec{K}}}$ and ${\varvec{C}}$ are the stiffness and damping matrices, respectively, and ${\varvec{q}}$ is the load vector. To solve the nonlinear heat conduction problem, an iterative method is used at each time step and discretization of the time domain is performed by the Crank-Nicolson method (Reddy 1993). Thus, the equilibrium Eq. (47) for the (t + 1)-th time step is expressed as follows:

$$ {\overline{\varvec{K}}}_{t + 1} {\varvec{T}}_{t + 1} {\varvec{ = \tilde{K}}}_{t} {\varvec{T}}_{t} {\varvec{ + \tilde{q}}}_{{{\text{t}},{\text{t}} + 1}} , $$

(51)

where

$$ {\tilde{\varvec{K}}}_{t} = {\varvec{C}}_{t} {\varvec{ - }}{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\Delta t_{t + 1} {\hat{\varvec{K}}}_{t} , $$

(52)

$$ {\overline{\varvec{K}}}_{t + 1} = {\varvec{C}}_{t + 1} {\varvec{ + }}{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\Delta t_{t + 1} {\hat{\varvec{K}}}_{t + 1} , $$

(53)

$$ {\tilde{\varvec{q}}}_{{{\text{t}},{\text{t}} + 1}} = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\Delta t_{t + 1} ({\varvec{q}}_{t} + {\varvec{q}}_{t + 1} ). $$

(54)

Note that the damping, stiffness, and load matrices at the t-th time step are calculated based on the temperature distribution obtained at the (t-1)-th time step. The matrices should be updated at each iteration until the results reach the expected accuracy.

5.2.2 Discretized form of the thermo-elastoplastic constitutive equation

Using Eq. (20), the generalized local weak formulation of the thermo-elastoplastic equation over an integration local sub-domain $\Omega_{s}^{I}$ is written as

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I} \,(\Delta \sigma_{ij,j} + \Delta b_{i} )} \,{\text{d}}\Omega_{s} = 0. $$

(55)

Using the relation $\nu_{I} \Delta \sigma_{ij,j} = (\nu_{I} \Delta \sigma_{ij} )_{,i} - \nu_{I,j} \Delta \sigma_{ij}$ we have

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\,\nu_{I,j} \Delta \sigma_{ij} } \,{\text{d}}\Omega_{s} - \int_{{\Omega_{s}^{I} }}^{{}} {\,(\nu_{I} \Delta \sigma_{ij} )_{,i} } \,{\text{d}}\Omega_{s} = \int_{{\Omega_{s}^{I} }}^{{}} {\,\nu_{I} \Delta b_{i} } \,{\text{d}}\Omega_{s} . $$

(56)

Applying the divergence theorem, Eq. (56) becomes

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I,j} \Delta \sigma_{ij} } \,{\text{d}}\Omega - \int_{{\Gamma_{s}^{I} }}^{{}} {\nu_{I} \Delta \sigma_{ij} n_{j} } \,{\text{d}}\Gamma = \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I} \Delta b_{i} \,} {\text{d}}\Omega , $$

(57)

where $\Gamma_{s}^{I} = \partial \Omega_{s}^{I}$ is the boundary of the local sub-domain $\Omega_{s}^{I}$. Satisfying natural boundary conditions gives:

$$ \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I,j} \Delta \sigma_{ij} } \,{\text{d}}\Omega - \int_{{\Gamma_{si}^{I} }}^{{}} {\nu_{I} \Delta \sigma_{ij} n_{j} } \,{\text{d}}\Gamma - \int_{{\Gamma_{su}^{I} }}^{{}} {\nu_{I} \Delta \sigma_{ij} n_{j} } \,{\text{d}}\Gamma = \int_{{\Omega_{s}^{I} }}^{{}} {\nu_{I} \Delta b_{i} \,} {\text{d}}\Omega \, + \int_{{\Gamma_{st}^{I} }}^{{}} {\nu_{I} \Delta \overline{t}_{j} } \,{\text{d}}\Gamma , $$

(58)

where $\Gamma_{su}^{I}$ and $\Gamma_{st}^{I}$ are the parts of $\Gamma_{s}^{I}$ over which essential and natural boundary conditions are prescribed, respectively. According to Eqs. (39) and (27), the increment of displacement and stress fields are expressed as

$$ \Delta {\text{u}}^{{\text{h}}} ({\varvec{x}}) = {{\varvec{\Phi}}}(x){{\varvec{\Delta}}}u({\text{t}}) = \sum\limits_{{{\text{J}} = 1}}^{{\text{N}}} {\phi_{{\text{J}}} ({\varvec{x}})\Delta {\text{u}}_{{\text{J}}} } ({\text{t}}), $$

(59)

$$ {\varvec{\Delta \sigma }} = {\varvec{D}}^{ep} ({\varvec{\Delta \varepsilon }} - {\varvec{\Delta \tilde{\varepsilon }}}^{{th{ - }ep}} ) = {\varvec{D}}^{ep} \left( {\sum\limits_{J = 1}^{N} {{\varvec{B}}_{J} {\varvec{\Delta u}}_{J} } - {\varvec{\Delta \tilde{\varepsilon }}}^{{th{ - }ep}} } \right), $$

(60)

where $\Delta {\text{u}}_{{\text{J}}} ({\text{t}})$ is the incremental nodal displacement, and

$$ {\varvec{B}}_{J} = \left[ {\begin{array}{*{20}l} {\phi_{J,x}^{{}} } \hfill & 0 \hfill & 0 \hfill & {\phi_{J,y}^{{}} } \hfill & 0 \hfill & {\phi_{J,z}^{{}} } \hfill \\ 0 \hfill & {\phi_{J,y}^{{}} } \hfill & 0 \hfill & {\phi_{J,x}^{{}} } \hfill & {\phi_{J,z}^{{}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\phi_{J,z}^{{}} } \hfill & 0 \hfill & {\phi_{J,y}^{{}} } \hfill & {\phi_{J,x}^{{}} } \hfill \\ \end{array} } \right]^{T} ,\,\,\,\,{{\varvec{\Delta}}}{\varvec{u}}_{J} = \left\{ {\begin{array}{*{20}c} {\Delta u_{J}^{x} } \\ {\Delta u_{J}^{y} } \\ {\Delta u_{J}^{z} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\Delta u_{J} } \\ {\Delta v_{J} } \\ {\Delta w_{J} } \\ \end{array} } \right\}. $$

(61)

Eventually, by substituting Eq. (60) in Eq. (58), we obtain the discretized incremental thermo-elastoplastic equation system as

$$ \sum\limits_{J = 1}^{M} {{\varvec{K}}_{IJ} {\varvec{\Delta u}}_{J} {\varvec{ = }}{\varvec{\Delta f}}_{I} } \,\,\,{\text{with}}\,\,I = 1,\,2,\,...,\,M, $$

(62)

where

$$ {\varvec{K}}_{IJ} = \int_{{\Omega_{s}^{I} }}^{{}} {{\varvec{B}}_{I} } {\varvec{D}}^{ep} {\varvec{B}}_{J} \,{\text{d}}\Omega - \int_{{\Gamma_{si}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{ND}}^{ep} {\varvec{B}}_{J} {\text{d}}\Gamma } - \int_{{\Gamma_{su}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{ND}}^{ep} {\varvec{B}}_{J} } \,{\text{d}}\Gamma , $$

(63)

$$ \begin{gathered} {\varvec{\Delta f}}_{I} = \int_{{\Omega_{s}^{I} }}^{{}} {{\varvec{B}}_{I} } {\varvec{D}}^{ep} {\varvec{\Delta \tilde{\varepsilon }}}^{{th{ - }ep}} \,{\text{d}}\Omega - \int_{{\Gamma_{si}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{ND}}^{ep} {\varvec{\Delta \tilde{\varepsilon }}}^{{th{ - }ep}} \,{\text{d}}\Gamma } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int_{{\Gamma_{su}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{N}}{\varvec{D}}^{ep} {\varvec{\Delta \tilde{\varepsilon }}}^{{th{ - }ep}} \,{\text{d}}\Gamma } + \int_{{\Omega_{s}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{\Delta b}}\,} {\text{d}}\Omega + \int_{{\Gamma_{st}^{I} }}^{{}} {{{\varvec{\Phi}}}_{I} {\varvec{\Delta \overline{t}}}} \,{\text{d}}\Gamma . \hfill \\ \end{gathered} $$

(64)

${\varvec{K}}$ and ${\varvec{\Delta f}}$ are the elastoplastic stiffness matrix and the incremental load vector, respectively, and M is the total number of nodes. In addition, ${{\varvec{\Phi}}}_{I}$ and ${\varvec{N}}$ are expressed as

$$ {{\varvec{\Phi}}}_{I} = \left[ {\begin{array}{*{20}c} {\phi_{I} } & 0 & 0 \\ 0 & {\phi_{I} } & 0 \\ 0 & 0 & {\phi_{I} } \\ \end{array} } \right],\,\,\,\,{\varvec{N}} = \left[ {\begin{array}{*{20}c} {n_{x} } & 0 & 0 & {n_{y} } & 0 & {n_{z} } \\ 0 & {n_{y} } & 0 & {n_{x} } & {n_{z} } & 0 \\ 0 & 0 & {n_{z} } & 0 & {n_{y} } & {n_{x} } \\ \end{array} } \right]. $$

(65)

In an elastoplastic deformation problem, the incremental form of the discretized system equations within an incremental load can be written as

$$ {\varvec{K}}{\varvec{\Delta u}} - {\varvec{\Delta f}} = {\varvec{f}}^{{{\text{res}}}} , $$

(66)

where ${\varvec{f}}^{{{\text{res}}}}$ is the residual force vector. Using the Newton–Raphson method, a combined incremental and iterative solution procedure is considered to solve the system of nonlinear Eq. (66). The overall solution process is as follows:

• 1. Set as 0 the vectors ${\varvec{u}}$, ${\varvec{f}}$, and ${\varvec{f}}^{{{\text{res}}}}$, for the first load increment.

• 2. Set ${\varvec{\Delta f}}$ equal to the current increment load vector (${\varvec{f}}^{j}$): ${\varvec{\Delta f}} = {\varvec{f}}^{j}$ and ${\varvec{f}} = {\varvec{f}} + {\varvec{\Delta f}}$.

• 3. Solve ${\varvec{\Delta u}} = {\varvec{K}}_{{}}^{ - 1} {\varvec{\Delta f}}$.

• 4. Set ${\varvec{u}}^{j} = {\varvec{u}}^{j - 1} + {\varvec{\Delta u}}$.

• 5. At each integration point, evaluate the incremental stress state ${\varvec{\Delta \sigma }}$, and thus the total stress state according to Eq. (60): ${{\varvec{\upsigma}}}^{j} = {{\varvec{\upsigma}}}^{j - 1} + {\varvec{\Delta \sigma }}$. At each integration point, evaluate ${{\varvec{\upsigma}}}^{j}$ to satisfy the yield criterion, depending on the states of ${{\varvec{\upsigma}}}^{j - 1}$ and ${{\varvec{\upsigma}}}^{j}$ (see Ref. (Moreira et al. 2017)). It is worth noting that, assuming a proportional loading path, the incremental stress and strain resultant relation is valid.

• 6. Evaluate the residual force vector: ${\varvec{f}}^{{{\text{res}}}} = {\varvec{K}}{\varvec{\Delta u}} - {\varvec{\Delta f}}$.

• 7. Check the convergence using the following residual force convergence criteria: $E_{{{\text{res}}}} = ({\varvec{f}}^{{{\text{res}}}} \cdot {\varvec{f}}^{{{\text{res}}}} )^{1/2} \times ({\varvec{f}}^{j} \cdot {\varvec{f}}^{j} )^{ - 1/2}$ < toler, where toler is a specified tolerance.

• 8. If the solution has converged ($E_{{{\text{res}}}}$ < toler), go to step 9; Else continue.

  • 8.1 Set iterative number $i = 1$.

  • 8.2 Set ${\varvec{f}}_{0}^{{{\text{res}}}} = {\varvec{f}}_{{}}^{{{\text{res}}}}$, ${\varvec{u}}_{0}^{j} = {\varvec{u}}^{j}$, and ${{\varvec{\upsigma}}}_{0}^{j} = {{\varvec{\upsigma}}}^{j}$.

  • 8.3 Set ${\varvec{\Delta f}}$ equal to the last residual force vector (${\varvec{f}}_{i - 1}^{{{\text{res}}}}$):${\varvec{\Delta f}} = {\varvec{f}}_{i - 1}^{{{\text{res}}}}$.

  • 8.4 Solve ${\varvec{\Delta u}} = {\varvec{K}}_{{}}^{ - 1} {\varvec{\Delta f}}$.

  • 8.5 Set ${\varvec{u}}_{i}^{j} = {\varvec{u}}_{i - 1}^{j} + {\varvec{\Delta u}}$.

  • 8.6 At each integration point, evaluate the iterative incremental stress state ${\varvec{\Delta \sigma }}$, and the total stress state of the present iteration: ${{\varvec{\upsigma}}}_{i}^{j} = {{\varvec{\upsigma}}}_{i - 1}^{j} + {\varvec{\Delta \sigma }}$. At each integration point, evaluate ${{\varvec{\upsigma}}}_{i}^{j}$ to satisfy the yield criterion.

  • 8.7 Evaluate the residual force vector: ${\varvec{f}}_{i}^{{{\text{res}}}} = {\varvec{K}}{\varvec{\Delta u}} - {\varvec{\Delta f}}$.

  • 8.8 Check the convergence using: $E_{{{\text{res}}}} = ({\varvec{f}}_{i}^{{{\text{res}}}} \cdot {\varvec{f}}_{i}^{{{\text{res}}}} )^{1/2} \times ({\varvec{f}}^{j} \cdot {\varvec{f}}^{j} )^{ - 1/2}$ < toler.

  • 8.9 If $E_{{{\text{res}}}}$ < toler, go to step 9; Else go to step 8.3.

• 9. If this is not the last increment, go to step 2; Else stop.

6 Numerical results and discussion

In this section, first, to prove the efficiency and capability of the present truly meshless method, various numerical examples are analyzed and the results are compared with those obtained from analytical and numerical methods. Subsequently, the nonlinear thermo-elastoplastic bending response of FG plates under a combination of thermal and mechanical loads is presented taking into account the temperature-dependent thermo-mechanical properties. In all analyzes, 216 $(6 \times 6 \times 6)$ Gauss points are considered for the numerical integration on the 3D local sub-domain $\Omega_{s}$ around each node, and 36 $(6 \times 6)$ Gauss points are used at each boundary $\Gamma_{s}^{{}}$.

6.1 Effect of the correlation parameter θ

In this section, it will be proved that the new RBF used maintains the quality of the LRPIM shape functions well, and as a result, the solutions are not affected by the correlation parameter. Consider an SSSS square ${\text{Al/SiC}}$ FG plate under the sinusoidal mechanical load $\sigma_{zz} (x,y,h) = p\sin (\pi x{/}a)sin(\pi y{/}b)$ on the top surface. The constituent materials’ properties are as follows: $E_{{{\text{Al}}}} = 70\,{\text{GPa}}$, $\nu_{{{\text{Al}}}} = 0.3$, $E_{{{\text{SiC}}}} = 427\,{\text{GPa}}$, and $\nu_{{{\text{SiC}}}} = 0.17$. The Mori–Tanaka model (Mori and Tanaka 1973) for estimating the effective material properties, the scaling factor $\alpha = 2.5$, and the nodal distribution $15 \times 15 \times 15$ (3375 nodes) are considered. Table 2 shows the normalized deflections ($\overline{w} = 100E^{m} h^{3} w{/}pa^{4}$) of the plate for $h{/}a = 0.2$, $n = 2$, and different values of the correlation parameter $\theta$. The results are compared with the exact 3D solution given by Vel and Batra (2002). What can be seen is the very good agreement of the present results with the exact solutions, which are completely stable and independent of θ for a wide range of correlation parameters. Therefore, in all subsequent analyzes, the correlation parameter 1 is used.

Table 2 The non-dimensional deflection ($\overline{w} = 100E^{{\text{m}}} h^{3} w{/}pa^{4}$) of an SSSS ${\text{Al/SiC}}$ FG square plate subjected to sinusoidal mechanical load $\sigma_{zz} (x,y,h) = p\sin (\pi x{/}a)sin(\pi y{/}b)$, ($n = 2$, $h{/}a = 0.2$, $V_{{{\text{max}}}}^{{\text{c}}} = 1$)

6.2 Convergence study

Here, a convergence study is performed on the results of the present method to find suitable choices for the scaling parameter $\alpha$ and nodal distribution. To make the necessary comparisons, the exact 3D solution given by Vel and Batra (2002) (discussed in Sect. 6.1) is used. Table 3 presents the normalized deflections $\overline{w} = \tfrac{{100E^{m} h^{3} }}{{pa^{4} }} \times w\,(\tfrac{a}{2},\tfrac{b}{2},h)$ for different values of $\alpha$, while the thickness-to-side ratio $h{/}a = 0.2$ and the regular nodal distribution $15 \times 15 \times 15$ (3375 nodes) are considered. The relative error is calculated as follows:

$$ {\text{Error (\% )}} = \left| {\left( {\frac{{{\text{Present solution}} - \,{\text{Exact solution [21]}}}}{{{\text{Exact solution}}\,[21]}}} \right) \times 100} \right|. $$

Table 3 Effect of scaling parameter $\alpha$ on the normalized central deflection ($\overline{w} = 100E^{m} h^{3} w{/}pa^{4}$) of an SSSS ${\text{Al/SiC}}$ FG square plate subjected to sinusoidal mechanical load $\sigma_{zz} (x,y,h) = p\sin (\pi x{/}a)sin(\pi y{/}b)$, ($n = 2$, $h{/}a = 0.2$, $V_{{{\text{max}}}}^{{\text{c}}} = 1$)

Table 3 clearly shows that the best agreement with the exact solution is obtained for $\alpha = 2.5$, therefore this value has been used in all subsequent analyzes.

In Table 4, seven different regular nodal distributions are used to investigate the convergence of the results. For further scrutiny, this table presents the results of 3D finite element analysis using ABAQUS software, obtained by the author considering 8-node brick elements. It is observed that in the present method with the nodal distribution of $15 \times 15 \times 15$, the results with a convergence rate much higher than the conventional FEM, are adapted to the analytical solution. It can also be seen that conventional finite element results with $45 \times 45 \times 45$ nodes have excellent agreement with the analytical solution. In all subsequent analyzes, the node distributions of $15 \times 15 \times 15$ and $45 \times 45 \times 45$ have been used in the present LRPIM and FEM, respectively.

Table 4 Convergence of the normalized deflection ($\overline{w} = 100E^{m} h^{3} w{/}pa^{4}$) of an SSSS ${\text{Al/SiC}}$ FG square plate under sinusoidal mechanical load $\sigma_{zz} (x,y,h) = p\sin (\pi x{/}a)sin(\pi y{/}b)$, ($n = 2$, $h{/}a = 0.2$, $V_{{{\text{max}}}}^{{\text{c}}} = 1$)

6.3 Example 1: Elastoplastic analysis of cantilever beam subjected to a concentrated force

Consider a cantilever beam with the length L = 8 m, height h = 1 m, and depth t = 8 m, which is under a concentrated force at its free end. Young's modulus E = 10⁵ Pa, Poisson's ratio ν = 0.25, the yield stress σ_y = 25 Pa, and the concentrated force P = 1 N are assumed. The linear hardening model is adopted, with E′ = 0.2E, and the plane stress condition is considered. Figure 3a shows the variation of the beam deflection w along its length for three different types of regular nodal distributions, including 7 × 3, 9 × 4, and 11 × 5 nodes. The relationship between the loading and displacement of the midpoint of the end of the beam is also presented in Fig. 3b. These results are compared with those of the element-free Galerkin method (EFGM) proposed by Peng et al. (2011). According to Fig. 3a and b, it can be seen that the present results with the nodal distribution of 11 × 5 are in very good agreement with the EFGM results.

Fig. 3

a Variation of deflection w along the beam length, and b relationship between the loading and displacement of the midpoint of the end of the beam

Here, the effect of unstructured discretization on the performance of the present LRPIM has been studied to show its versatility. For this purpose, according to Fig. 4, both structured and unstructured discretizations, including 55 nodes, have been used. It can be seen from Fig. 4a and b that the LRPIM results with unstructured discretization, for the deflection w and the load–deflection (P–w) curve, are in good agreement with the EFGM reference solution. According to Fig. 4b, the maximum difference between the structured and unstructured discretization results is 0.6%.

Fig. 4

a Variation of deflection along the beam length, and b load–deflection curve of the midpoint of the end of the beam for structured and unstructured discretizations with 55 nodes

6.4 Example 2: mechanical analysis of FG plates

In this example, the 3D elastic bending response of an SSSS ${\text{Al/Al}}_{2} {\text{O}}_{{3}}$ FG square plate under two types of mechanical loading, including uniformly distributed load (UL), $\sigma_{zz}^{{}} (x,y,h) = p$, and sinusoidal distributed load (SL), $\sigma_{zz}^{{}} (x,y,h) = p\sin (\pi x{/}a)sin(\pi y{/}b)$, are provided and compared with the other available solutions to verify the validity of the meshless approach. The Young’s modulus of the constituent materials are $E_{{{\text{Al}}}} = 70\,{\text{GPa}}$ and $E_{{{\text{Al}}_{2} {\text{O}}_{3} }} = 380\,{\text{GPa}}$, while a constant value of 0.3 is considered for the Poisson’s ratio.

Table 5 presents non-dimensional deflection ($\overline{w} = 10E^{c} h^{3} w{/}pa^{4}$) and non-dimensional stresses ($\overline{\sigma }_{ij} = h\sigma_{ij} {/}pa$) for various values of the power-law exponent n and $h{/}a = 0.1$. For validation, the results are compared with those of the layer-wise FEM obtained by Nikbakht et al. (2017). Also, the results of a new sinusoidal shear deformation plate theory (SSDPT) provided by Thai and Vo (2013) and the hyperbolic shear deformation plate theory (HSDPT) given by Benyousef et al. (2010) are included in Table 5. It is clear that for all values of n, the results of the present method are in perfect agreement with the other authentic theories. Because in homogeneous plates, non-dimensional stresses are independent of Young's modulus, the results for the fully metal and fully ceramic plates are similar.

Table 5 Effects of power-law exponent n and loading on the non-dimensionl deflection and stresses of an SSSS ${\text{Al/Al}}_{2} {\text{O}}_{3}$ FG square plate ($h{/}a = 0.1$, $V_{{{\text{max}}}}^{{\text{c}}} = 1$)

6.5 Thermo-elastoplastic analysis of FG plates

Here, the numerical results of the thermo-elastoplastic bending of the temperature-dependent square ($a = b = 1\,\;{\text{m}}$) ${{\text{Ti - 6Al - 4V}} \mathord{\left/ {\vphantom {{\text{Ti - 6Al - 4V}} {{\text{ZrO}}_{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{ZrO}}_{{2}} }}$ FG plate described in Sect. 2, are presented. In all analyzes, the load $p = 20\,{\text{MPa}}$ is applied to the plates $h{/}a = 0.1$ for 1500 s, while $p = 200\,{\text{MPa}}$ is imposed on the plates with $h{/}a = 0.3$ for 3000 s. In all cases, the intensity of sinusoidal heat flux q is considered to be $70\,\;\;kW/m^{2}$.

6.5.1 Effect of power-law exponent n

The through-the-thickness results of the temperature and deflection of the SSSS FG plates are respectively portrayed in Figs. 5 and 6 for two thickness-to-side ratios of $h{/}a = 0.1$ and 0.3. Here, $V_{{{\text{max}}}}^{{\text{c}}} = 0.9$, the time step size $\Delta t = 10\,{\text{s}}$, and five different power-law exponent n, including 0.2, 0.5, 1, 2 and 5 are considered. It is clear that for all values of n and $h{/}a$, the maximum values of deflection and temperature occur at the top surface of the plates, and as n increases, these values decrease. Similar diagrams for the normal stresses $\sigma_{xx}$ and $\sigma_{zz}$, and shear stress $\sigma_{xz}$ are depicted in Figs. 7, 8, and 9, respectively. According to Fig. 7, the maximum tensile and compressive stresses occur at the lower and upper surfaces of the plate, respectively. The through-the-thickness variation of $\sigma_{xx}$ is nonlinear and there is no coincidence between the neutral surface and the mid-plane. Figure 6 shows that with increasing n, $\sigma_{zz}$ decreases while its value at $z = 0$ is always zero. Also, as expected, the zero shear stress conditions at the upper and lower surfaces of the plate are met (see Fig. 9).

Fig. 5

Effect of power-law exponent $n$ on temperature $T(0.5a,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 6

Effect of power-law exponent $n$ on deflection $w(0.5a,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 7

Effect of power-law exponent $n$ on in-plane normal stress $\sigma_{xx} (0.5a,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 8

Effect of power-law exponent $n$ on transverse normal stress $\sigma_{zz} (0.5a,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 9

Effect of power-law exponent $n$ on shear stress $\sigma_{xz} (0,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Figure 10 shows the effect of exponent n on equivalent stress $\overline{\sigma }$ for two thickness-to-side ratios of $h{/}a = 0.1$ and 0.3. Figure 11 depicts the effect of this coefficient on the equivalent stress–strain ($\overline{\sigma } - \overline{\varepsilon }$) curve. It is observed that increasing the coefficient n reduces the equivalent strain. Due to the use of the temperature-dependent material properties in the analysis, it is evident that the stress–strain curve is nonlinear even in the elastic region.

Fig. 10

Effect of power-law exponent $n$ on equivalent stress $\overline{\sigma }(0.5a,0.5b,z)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 11

Effect of power-law exponent $n$ on $\overline{\sigma } - \overline{\varepsilon }$ curve at the point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

The equivalent plastic strain–time ($\overline{\varepsilon }^{p} - t$) curve of FG plates for different values of n is depicted in Fig. 12. It is seen that for both ratios $h{/}a$, the equivalent plastic strain decreases with increasing n, while it increases with time. The contour plots of the temperature, deflection, equivalent stress, and equivalent plastic strain at the top surface of the FG plate with $n = 0.2$ and $h{/}a = 0.1$ are depicted in Fig. 13a. Similar results for $n = 1$ and 5 are presented in Fig. 13b and c, respectively. It is observed that as n increases, the temperature and equivalent plastic strain decrease while deflection and equivalent stress increase. However, regardless of the value of n, the maximum value of all the parameters occurs in the center of the plates.

Fig. 12

Effect of power-law exponent $n$ on $\overline{\varepsilon }^{p} - t$ curve at the point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of the SSSS FG plate with a $h{/}a = 0.1$, and b $h{/}a = 0.3$; $\left( {V_{{{\text{max}}}}^{{\text{c}}} = 0.9} \right)$

Fig. 13

Contour plot of $T$, $w$, $\overline{\sigma }$ and $\overline{\varepsilon }^{p}$ at the top surface of the SSSS FG plate for a $n = 0.2$, b $n = 1$, and c) $n = 5$; ($h{/}a = 0.1,\,\,V_{{{\text{max}}}}^{{\text{c}}} = 0.9,\,\,t = 1500\;{\text{s}}$)

The effect of the time step size ∆t on the through-the-thickness distribution of the deflection w and normal stress σ_xx of the SSSS square FG plates with h/a = 0.3 and n = 1 is shown in Fig. 14. Four different time step sizes, i.e., ∆t = 5, 10, 20, and 50 s are considered. The present results are compared with the FEM solutions obtained by the author with the fine mesh (see Sect. 6.2). According to Fig. 14, the maximum relative error of σ_xx for the time step sizes of 50, 20, 10, and 5 s is 5.3%, 3.1%, 1.0%, and 0.8%, respectively. As can be seen, the accuracy of the results obtained by the time step of 10 s is still acceptable, so the time step size is set to 10 s.

Fig. 14

Effect of time step size on, a deflection $w\,(0.5a,0.5b,z)$, and b in-plane normal stress $\sigma_{xx} (0.5a,0.5b,z)$ of the SSSS FG plate with $h{/}a = 0.3$; ($V_{{{\text{max}}}}^{{\text{c}}} = 0.9,\,n = 1$)

6.5.2 Effect of maximum volume fraction of ceramic ( $V_{{{\text{max}}}}^{{\text{c}}}$)

Here, five different values of $V_{{{\text{max}}}}^{{\text{c}}}$, i.e., 0, 0.25, 0.5, 0.75, and 0.9 are considered to investigate its effect on the bending response of the SSSS FG plates with $n = 1$ and $h{/}a = 0.3$. Figures 15a and b show the distributions of the temperature and the deflection through the thickness of the plates, respectively. It is observed that the maximum temperature and deflection occur at $z = h$ (ceramic-rich surface), while these values increase with increasing $V_{{{\text{max}}}}^{{\text{c}}}$. Similar diagrams for studying the effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on the stresses $\sigma_{xx}$ and $\sigma_{xz}$ are depicted in Fig. 16a and b, respectively. Figure 16(a) shows that with increasing $V_{{{\text{max}}}}^{{\text{c}}}$, $\sigma_{xx}$ decreases at $z = h$.

Fig. 15

Effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on a temperature $T(0.5a,0.5b,z)$, and b deflection $w(0.5a,0.5b,z)$ of the SSSS FG plate with $h{/}a = 0.3$ and $n = 1$

Fig. 16

Effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on a in-plane normal stress $\sigma_{xx} (0.5a,0.5b,z)$, and b shear stress $\sigma_{xz} (0,0.5b,z)$ of the SSSS FG plate with $h{/}a = 0.3$ and $n = 1$

Figure 17a and b illustrate the effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on the through-the-thickness distributions of the stress $\sigma_{zz}$ and $\overline{\sigma }$, respectively. Also, the $\overline{\sigma } - \overline{\varepsilon }$ and $\overline{\varepsilon }^{p} - t$ curves for different values of $V_{{{\text{max}}}}^{{\text{c}}}$ are displayed in Fig. 18a and b, respectively. It can be seen from Fig. 18 that with increasing $V_{{{\text{max}}}}^{{\text{c}}}$, the equivalent strain $\overline{\varepsilon }$ and equivalent plastic strain $\overline{\varepsilon }^{p}$ increase.

Fig. 17

Effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on a transverse normal stress $\sigma_{zz} (0.5a,0.5b,z)$, and b equivalent stress $\overline{\sigma }(0,0.5b,z)$ of the SSSS FG plate with $h{/}a = 0.3$ and $n = 1$

Fig. 18

Effect of $V_{{{\text{max}}}}^{{\text{c}}}$ on a $\overline{\sigma } - \overline{\varepsilon }$ curve, and b $\overline{\varepsilon }^{p} - t$ curve, at the point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of the SSSS FG plate with $h{/}a = 0.3$ and $n = 1$

6.5.3 Effect of boundary conditions

Numerical results of the FG plates considering the SSSS and CCCC boundary conditions with $h{/}a = 0.1$ and various values of n and $V_{{{\text{max}}}}^{{\text{c}}}$ are given in Table 6. For a more complete comparison, the FEM results obtained by the author are also included in this table. It can be seen that the results of the present method are in excellent agreement with the FEM solutions obtained with the fine mesh. According to Table 6 and regardless of the type of boundary conditions, increasing n increases the deflection and decreases the temperature and equivalent plastic strain. However, increasing $V_{{{\text{max}}}}^{{\text{c}}}$ decreases the deflection and increases the temperature and equivalent plastic strain. Similar results are obtained for the FG plates with $h{/}a = 0.3$ in Table 7, where the agreement between the results of the present method and FEM is quite evident.

Table 6 Numerical results at point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of SSSS and CCCC square ${{{\text{Ti}}{ - }{\text{6Al}}{ - }{\text{4V}}} \mathord{\left/ {\vphantom {{{\text{Ti}}{ - }{\text{6Al}}{ - }{\text{4V}}} {{\text{ZrO}}_{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{ZrO}}_{{2}} }}$ FG plates with $h{/}a = 0.1$, ($t = 1500s$)

Table 7 Numerical results at point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of SSSS and CCCC square ${{{\text{Ti}} - {\text{6Al}} - {\text{4V}}} \mathord{\left/ {\vphantom {{{\text{Ti}} - {\text{6Al}} - {\text{4V}}} {{\text{ZrO}}_{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{ZrO}}_{{2}} }}$ FG plates with $h{/}a = 0.3$, ($t = 3000s$)

Table 8 presents the numerical results of the FG plates considering nine different types of boundary conditions including CCCC, CFCF, CCCF, CCCS, SCSC, SSSC, SFSF, SSSF, and SSSS, with $n = 1$, $V_{{{\text{max}}}}^{{\text{c}}} = 0.9$, and $h{/}a = 0.1$. The results are provided three times of 500, 1000 and 1500 s along with the FEM solutions. Similar results are given in Table 9 for $h{/}a = \,0.3$ at times 1000, 2000, and 3000 s. It can be seen from Table 9 that for all the types of boundary conditions, the equivalent stress and deflection of the thick plates decrease over time while their equivalent plastic strain increases.

Table 8 Effect of boundary conditions on numerical results at point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of ${{{\text{Ti}} - {\text{6Al}} - {\text{4V}}} \mathord{\left/ {\vphantom {{{\text{Ti}} - {\text{6Al}} - {\text{4V}}} {{\text{ZrO}}_{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{ZrO}}_{{2}} }}$ FG square plates with $h{/}a = 0.1$, ($n = 1$, $V_{{{\text{max}}}}^{{\text{c}}} = 0.9$)

Table 9 Effect of boundary conditions on numerical results at point $({0}{\text{.5}}a{,0}{\text{.5}}b{,}h)$ of ${{\text{Ti - 6Al - 4V}} \mathord{\left/ {\vphantom {{\text{Ti - 6Al - 4V}} {{\text{ZrO}}_{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{ZrO}}_{{2}} }}$ FG square plates with $h{/}a = 0.3$, ($n = 1$, $V_{{{\text{max}}}}^{{\text{c}}} = 0.9$)

7 Conclusions

For the first time, an efficient truly meshless approach based on the LRPIM was presented to explore the 3D nonlinear thermo-elastoplastic bending behavior of temperature-dependent FG plates exposed to a combination of mechanical and thermal loads. To obtain the effective temperature-dependent elastoplastic parameters of the FGM, the modified rule of mixtures were used. The von Mises yield criterion, isotropic strain hardening, and the Prandtl-Reuss flow rule were adapted to describe the plastic behavior of FG plates.

In the present model, whose new RBFs are based on the quartic spline function, it is well demonstrated that the quality of the LRPIM shape functions is completely independent of the shape parameter. It was observed that the results of the proposed LRPIM model agree well with other available numerical and analytical solutions so that for a wide range of correlation parameters from $\theta = - 100$ to 10,000, they are independent of θ and completely stable. Therefore, the present approach can be very useful in designing FG plates used in high-temperature gradient conditions. Numerical results confirmed that the proposed method, with the same number of nodes, can predict the thermo-elastoplastic bending response of FG plates much more accurately than the conventional FEM with a higher convergence rate. Detailed parametric studies demonstrated that the effect of parameters such as the material gradient, ceramic volume fraction, plate thickness-to-length ratio, and boundary condition on the flexural behavior of FG plates is significant.