1 Introduction

Functionally graded materials (FGMs) are new advanced composite materials intentionally designed so that they possess desirable properties for specific applications, especially for performance under thermal environment. In the theory of elasticity, FGMs are mostly treated as nonhomogeneous materials with material constants varying continuously along one spatial direction. In the past two decades, a number of investigations have dealt with the unsteady thermoelastic problems for the basic structural components of FGMs. Obata and Noda [1, 2] proposed an analytical method of one-dimensional unsteady thermal stresses in a FGM plate by using the perturbation method. Araki et al. [3, 4] and Sugano et al. [5, 6] derived the analytical solution of the temperature distribution in a multilayered material under pulse or stepwise heating. Tanigawa et al. [7–9] analyzed the one-dimensional transient thermal stresses of a FGM plate and a FGM cylinder using a laminated composite model, and discussed the temperature dependence of material properties. Awaji et al. [10, 11] also proposed techniques for analyzing one-dimensional transient temperature distribution in a FGM plate and a hollow FGM cylinder. Kim and Noda [12] researched the unsteady thermal stresses in an infinite hollow cylinder of FGM by using a Green’s function approach. Abd-All et al. [13] studied the transient thermal stresses in a spherically orthotropic nonhomogeneous solid continuum with a spherical cavity by using an integral transform technique. Wang and Mai [14, 15] obtained transient temperature fields and associated thermal stresses in some common elements (such as plate, shell and sphere) of FGMs by using a finite element/finite difference (FE/FD) method, with temperature-dependent material properties taken into consideration.

However, most investigations concentrated on the thermo-mechanical behaviors of unidirectional FGM plate, hollow FGM cylinder and sphere under specified surface temperature or specified surface heat flux boundary conditions. The investigations on the transient temperature fields and associated thermal stresses in FGM solid components with various shapes under the convective boundary conditions have been very few [16], notwithstanding their significance in the evaluation of the thermal shock resistance of FGM components. To this end, this paper presents an approach to the calculations of the one-dimensional transient temperature fields in an infinite FGM plate with planar symmetric material properties, an infinite FGM solid cylinder with axially symmetric material properties and a FGM solid sphere with spherically symmetric material properties under the convective boundary conditions. The thermo-physical properties of the three FGM solids are expressed as power functions of the spatial coordinate along the gradient direction. The separation-of-variables method and the variable substitution method are used to derive the analytical formulae of the transient temperature fields for the three FGM solids. With the proposed model, the calculation precision can be improved as compared with those obtained by using finite element method (FEM). The paper also provides a valuable basis for the investigation of the thermal shock resistance for FGMs with various shapes.

As numerical examples, an infinite FGM plate, an infinite FGM solid cylinder and a FGM solid sphere composed of Al2O3 and TiC are considered so as to investigate the influence of the shape of FGM component on the transient temperature distributions. Furthermore, the results are compared with those obtained for the homogeneous components with the same geometries under the same thermal loading condition to reveal the effects of the distributions of thermo-physical properties on the transient temperature fields.

2 Analytical development

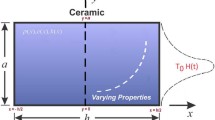
Consider an infinite FGM plate of thickness 2b with symmetrical structure, an infinite FGM solid cylinder of diameter 2b and a FGM solid sphere of diameter 2b as shown in Fig. 1a–c. A Cartesian coordinate system (x, y, z) (with the x–y plane lying on the middle of the plate), a cylindrical coordinate system (r, θ, z) (with the z-axis lying on the axis of the cylinder) and a spherical coordinate system (r, θ, ϕ) (with the origin at the center of the sphere) are established for the FGM plate, the FGM solid cylinder and the FGM solid sphere, respectively. The thermo-physical properties of the FGM plate, the FGM cylinder and the FGM sphere are continuously varied in the thickness direction z (with the x–y plane being the symmetry plane), the radial direction r and the radial direction r, respectively.

Fig. 1
figure 1

FGM components. a Infinite FGM plate, b infinite FGM solid cylinder and c FGM solid sphere

Full size image

It is assumed that initially the three FGM components are at a uniform temperature T 0, and at time t=0 the top and bottom faces of the plate (at z=±b), the surface of the cylinder (at r=b) and the surface of the sphere (at r=b) are suddenly exposed to a convective medium of temperature T s. And the coefficient of heat transfer h is assumed to be a constant. Heat flows within the FGM solids induce one-dimensional transient temperature distributions, with planar symmetric temperature field in the infinite FGM plate, axially symmetric temperature field in the infinite FGM cylinder and spherically symmetric temperature field in the infinite FGM sphere.

By not taking into account the temperature dependence of thermal conductivity λ, specific heat c, specific gravity ρ and other properties of the material, the one-dimensional heat conduction equation, the initial and boundary conditions for solid FGM components of these three shapes can be unified as follows:

$$\rho {\left( \xi \right)} \cdot c{\left( \xi \right)} \cdot \frac{{\partial T}}{{\partial t}} = \frac{1}{{\xi ^{m}}} \cdot \frac{\partial}{{\partial \xi}}{\left[{\xi ^{m} \cdot \lambda {\left( \xi \right)} \cdot \frac{{\partial T}}{{\partial \xi}}} \right]}$$
(1)
$$T{\left( {\xi, 0} \right)} = T_{0} $$
(2)
$$\left. {\frac{{\partial T}}{{\partial \xi}}} \right|_{{\xi = 0}} = 0$$
(3a)
$$\left. {- \lambda {\left( b \right)}\frac{{\partial T}}{{\partial \xi}}} \right|_{{\xi = b}} = h{\left( {T - T_{{\text{s}}}} \right)}$$
(3b)

where T is temperature, t is time, ξ is the coordinate variable in the gradient direction (ξ=z and m=0, for infinite FGM plate; ξ=r and m=1, for infinite FGM cylinder; ξ=r and m=2, for FGM sphere).

For the purpose of simplicity, the following dimensionless variables are introduced:

$$\left. \begin{array}{*{20}l} \bar{\xi } = \xi/b \\ \tau = \kappa (b)t/b^{2} \\ V{\left({\bar{\xi}, \tau } \right)} = \frac{{T{\left( {\xi ,t} \right)} - T_{{\text{s}}} }}{{T_{{\text{0}}} - T_{{\text{s}}} }} = \frac{{T{\left( {\xi ,t} \right)} - T_{{\text{s}}} }}{{\Delta T}}\\ \bar{c}{\left({\bar{\xi }} \right)} = {c (\xi)} /c (b)\\ \bar{\rho }{\left({\bar{\xi }} \right)} = \rho {(\xi)} / \rho (b) \\ \bar{\lambda }{\left({\bar{\xi }} \right)} = {\lambda (\xi)}/ \lambda (b)\\ \end{array} \right\}$$
(4)

where c(b), ρ(b), λ(b) and κ(b) are the specific heat, the specific gravity, the thermal conductivity and the thermal diffusivity of the FGM component surface (ξ=b).

Hence, Eqs. 1, 2, 3a and 3b have the following dimensionless forms:

$$\bar{\rho}{\left( {\bar{\xi}} \right)} \cdot \bar{c}{\left( {\bar{\xi}} \right)} \cdot \frac{{\partial V}}{{\partial \tau}} = \frac{1}{{\bar{\xi}^{m}}} \cdot \frac{\partial}{{\partial \bar{\xi}}}{\left[{\bar{\xi}^{m} \cdot \bar{\lambda}{\left( {\bar{\xi}} \right)} \cdot \frac{{\partial V}}{{\partial \bar{\xi}}}} \right]}$$
(5)
$$V{\left( {\bar{\xi},0} \right)} = 1$$
(6)
$$\left. {\frac{{\partial V}}{{\partial \bar{\xi}}}} \right|_{{\bar{\xi} = 0}} = 0$$
(7a)
$$\left. {- \frac{{\partial V}}{{\partial \bar{\xi}}}} \right|_{{\bar{\xi} = 1}} = B \cdot V{\left( {1,\tau} \right)}$$
(7b)

where B=h·b/λ (b) is the Biot number of the surface.

To solve the dimensionless heat conduction equation (5), we use the separation-of-variables method by asking:

$$V(\bar{\xi},\tau) = W(\bar{\xi}) \cdot U{\left( \tau \right)}$$
(8)

Eq. 5 can be transferred into:

$$\frac{{\frac{{{\text{d}}U{\left( \tau \right)}}}{{{\text{d}}\tau}}}}{{U{\left( \tau \right)}}} = \frac{{\bar{\lambda}{\left( {\bar{\xi}} \right)}}}{{\bar{\rho}{\left( {\bar{\xi}} \right)}\bar{c}{\left( {\bar{\xi}} \right)}}} \cdot \frac{{\frac{{{\text{d}}^{{\text{2}}} W{\left( {\bar{\xi}} \right)}}}{{{\text{d}}\bar{\xi}^{2}}}}}{{W{\left( {\bar{\xi}} \right)}}} + \frac{{\frac{{\text{d}}}{{{\text{d}}\bar{\xi}}}{\left[{\bar{\xi}^{m} \bar{\lambda}{\left( {\bar{\xi}} \right)}} \right]}}}{{\bar{\xi}^{m} \bar{\rho}(\bar{\xi})\bar{c}(\bar{\xi})}} \cdot \frac{{\frac{{{\text{d}}W{\left( {\bar{\xi}} \right)}}}{{{\text{d}}\bar{\xi}}}}}{{W{\left( {\bar{\xi}} \right)}}} = - \mu ^{{\text{2}}} $$
(9)

where μ > 0 and μ2 is a constant. Eq. 9 can be decomposed into the following two differential equations:

$$\frac{{{\text{d}}U{\left( \tau \right)}}}{{{\text{d}}\tau}} + \mu ^{2} U(\tau) = 0$$
(10a)

and

$$\frac{{{\text{d}}^{2} W{\left( {\bar{\xi}} \right)}}}{{{\text{d}}\bar{\xi}^{2}}} + \frac{{\frac{\partial}{{\partial \bar{\xi}}}{\left[{\bar{\xi}^{m} \bar{\lambda}{\left( {\bar{\xi}} \right)}} \right]}}}{{\bar{\xi}^{m} \bar{\lambda}{\left( {\bar{\xi}} \right)}}} \cdot \frac{{{\text{d}}W{\left( {\bar{\xi}} \right)}}}{{{\text{d}}\bar{\xi}}} + \mu ^{2} \frac{{\bar{\rho}{\left( {\bar{\xi}} \right)}\bar{c}{\left( {\bar{\xi}} \right)}}}{{\bar{\lambda}{\left( {\bar{\xi}} \right)}}} \cdot W{\left( {\bar{\xi}} \right)} = 0$$
(10b)

The solution to Eq. 10a is:

$$U(\tau) = A{\text{exp}}{\left( {- \mu ^{{\text{2}}} \tau} \right)}$$
(11)

where the coefficient A is a constant which can be omitted.

To solve Eq. 10b, we assume the dimensionless thermal conductivity and the dimensionless thermal diffusivity to be described with a power law as:

$$ \left. \begin{array}{*{20}l} \bar{\lambda}{\left( {\bar{\xi}} \right)} = \bar{\lambda}{\left( 1 \right)} \cdot \exp {\left[{n_{\lambda} {\left({1 - \bar{\xi}} \right)}} \right]} & n_{\lambda} = \ln {\left[{\frac{{\bar{\lambda}{\left(0\right)}}} {{\bar{\lambda}{\left( 1 \right)}}}} \right]} \\ \bar{\kappa}{\left( {\bar{\xi}} \right)} = \frac{{\bar{\lambda}{\left({\bar{\xi}} \right)}}} {{\bar{c}{\left( {\bar{\xi}}\right)}\bar{\rho}{\left( {\bar{\xi}} \right)}}} = \bar{\kappa}{\left(1\right)} \cdot \exp {\left[{n_{\kappa} {\left( {1 - \bar{\xi}} \right)}}\right]}& n_{\kappa} = \ln {\left[{\frac{{\bar{\kappa}{\left( 0 \right)}}} {{\bar{\kappa}{\left(1\right)}}}} \right]} \\ \end{array} \right\} 0 \leq \bar{\xi} \leq 1 $$
(12)

where \(\bar{\lambda}(1) = 1,\) \(\bar{\kappa}(1) = 1\) (referring to Eqs. 4)

By using the method of variable substitution, the solution to the second order differential equation (10b) with variable coefficients can be obtained and the dimensionless transient temperature fields for the three FGM components can be expressed respectively as (the details are omitted here for brevity):

$$V{\left( {\bar{z},\tau} \right)} = {\sum\limits_{l = 1}^\infty {D_{l}}}\cos {\left[{\mu _{l} {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - {\text{2}}n_{\lambda}}}{2}\bar{z}}} {\sum\limits_{n = 0}^\infty {\frac{{n_{\lambda} ^{n} \bar{z}^{{n + 1}}}}{{{\left( {n + 1} \right)} \cdot n!}}}}} \right]}{\text{e}}^{{- \mu _{l} ^{2} \tau}}\quad \hbox{(FGM plate)}$$
(13a)
$$V{\left( {\bar{r},\tau} \right)} = {\sum\limits_{l = 1}^\infty {D_{l}}}\cos {\left[{\mu _{l} \bar{r}{\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - {\text{2}}n_{\lambda}}}{2}\bar{r}}} {\left( {\ln {\left| {n_{\lambda} \bar{r}} \right|} + {\sum\limits_{n = 1}^\infty {\frac{{\left( {n_{\lambda} \bar{r}} \right)}^{n}}{{n \cdot n!}}}}} \right)}} \right]}{\text{e}}^{{- \mu _{l} ^{2} \tau}} \quad \hbox{(FGM cylinder)}$$
(13b)
$$V{\left( {\bar{r},\tau} \right)} = {\sum\limits_{l = 1}^\infty {D_{l}}}\cos {\left[{\mu _{l} \bar{r}^{2} {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - {\text{2}}n_{\lambda}}}{2}\bar{r}}} {\left( {n_{\lambda} \ln {\left| {n_{\lambda} \bar{r}} \right|} - \frac{1}{{\bar{r}}} + {\sum\limits_{n = 2}^\infty {\frac{{n_{\lambda} ^{n} \bar{r}^{{n - 1}}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right)}} \right]}{\text{e}}^{{- \mu _{l} ^{2} \tau}}\quad \hbox{(FGM sphere)} $$
(13c)

where the discrete values μ l and D l are the roots of Eqs. 14a, 14b, 14c, 15a, 15b and 15c, respectively.

$$\mu {\left[{\frac{{n_{\kappa} - {\text{2}}n_{\lambda}}}{{\text{2}}}{\sum\limits_{n = 0}^\infty {\frac{{n_{\lambda} ^{n}}}{{{\left( {n + 1} \right)} \cdot n!}}}} + {\sum\limits_{n = 0}^\infty {\frac{{n_{\lambda} ^{n}}}{{n!}}}}} \right]} \cdot \tan {\left( {\mu {\text{e}}^{{- n_{\lambda}}} {\sum\limits_{n = 0}^\infty {\frac{{n_{\lambda} ^{n}}}{{{\left( {n + 1} \right)} \cdot n!}}}}} \right)} = B{\text{e}}^{{n_{\lambda}}} \quad \hbox{(FGM plate)}$$
(14a)
$$\mu {\left[{\frac{{n_{\kappa} + {\text{2}} - {\text{2}}n_{\lambda}}}{{\text{2}}}{\left( {\ln {\left| {n_{\lambda}} \right|} + {\sum\limits_{n = 1}^\infty {\frac{{n_{\lambda} ^{n}}}{{n \cdot n!}}}}} \right)} + {\text{1}} + {\sum\limits_{n = 1}^\infty {\frac{{n_{\lambda} ^{n}}}{{n!}}}}} \right]}\cdot \tan {\left[{\mu {\text{e}}^{{- n_{\lambda}}} {\left( {\ln {\left| {n_{\lambda}} \right|} + {\sum\limits_{n = 1}^\infty {\frac{{n_{\lambda} ^{n}}}{{n \cdot n!}}}}} \right)}} \right]} = B{\text{e}}^{{n_{\lambda}}} \quad \hbox{(FGM cylinder)}$$
(14b)
$$\begin{aligned} \,&\mu {\left[{\frac{{n_{\kappa} - {\text{2}}n_{\lambda}}}{{\text{2}}}{\left( {n_{\lambda} \ln {\left| {n_{\lambda}} \right|} - 1 + {\sum\limits_{n = 2}^\infty {\frac{{n_{\lambda} ^{n}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right)} + 2n_{\lambda} {\text{ln}}{\left| {n_{\lambda}} \right|} + n_{\lambda} - {\text{1}} + {\sum\limits_{n = 2}^\infty {\frac{{{\left( {n + 1} \right)}n_{\lambda} ^{n}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right]}\\ &\,\quad \cdot \tan {\left[{\mu {\text{e}}^{{- n_{\lambda}}} {\left( {n_{\lambda} \ln {\left| {n_{\lambda}} \right|} - 1 + {\sum\limits_{n = 2}^\infty {\frac{{n_{\lambda} ^{n}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right)}} \right]} = B{\text{e}}^{{n_{\lambda}}} \quad \hbox{(FGM sphere)}\\ \end{aligned}$$
(14c)
$$D = \frac{{\int_0^1 {\cos {\left[{\mu {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{z}}} {\sum\nolimits_{n = 0}^\infty {\frac{{n_{\lambda} ^{n} \bar{z}^{{n + 1}}}}{{{\left( {n + 1} \right)} \cdot n!}}}}} \right]}}}{\text{d}}\bar{z}}{{{\int_0^1 {\cos ^{2} {\left[{\mu {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{z}}} {\sum\nolimits_{n = 0}^\infty {\frac{n_{\lambda} ^{n} \bar{z}^{{n + 1}}}{{\left( {n + 1} \right)} \cdot n!}}}} \right]}}}{\text{d}}\bar{z}}}\quad \hbox{(FGM plate)}$$
(15a)
$$D = \frac{{{\int_0^1 {\cos {\left[{\mu \bar{r}{\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{r}}} {\left( {\ln {\left| {n_{\lambda} \bar{r}} \right|} + {\sum\nolimits_{n = 1}^\infty {\frac{{{\left( {n_{\lambda} \bar{r}} \right)}^{n}}}{{n \cdot n!}}}}} \right)}} \right]}}}{\text{d}}\bar{r}}}{{{\int_0^1 {\cos ^{2} {\left[{\mu \bar{r}{\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{r}}} {\left( {\ln {\left| {n_{\lambda} \bar{r}} \right|} + {\sum\nolimits_{n = 1}^\infty {\frac{{{\left( {n_{\lambda} \bar{r}} \right)}^{n}}}{{n \cdot n!}}}}} \right)}} \right]}}}{\text{d}}\bar{r}}}\quad \hbox{(FGM cylinder)}$$
(15b)
$$D = \frac{{{\int_0^1 {\cos {\left[{\mu \bar{r}^{2} {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{r}}} {\left( {n_{\lambda} \ln {\left| {n_{\lambda} \bar{r}} \right|} - \frac{1}{{\bar{r}}} + {\sum\nolimits_{n = 2}^\infty {\frac{{n_{\lambda} ^{n} \bar{r}^{{n - 1}}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right)}} \right]}}}{\text{d}}\bar{r}}}{{{\int_0^1 {\cos ^{2} {\left[{\mu \bar{r}^{2} {\text{e}}^{{- \frac{{n_{\kappa}}}{2}}} {\text{e}}^{{\frac{{n_{\kappa} - 2n_{\lambda}}}{2}\bar{r}}} {\left( {n_{\lambda} \ln {\left| {n_{\lambda} \bar{r}} \right|} - \frac{1}{{\bar{r}}} + {\sum\nolimits_{n = 2}^\infty {\frac{{n_{\lambda} ^{n} \bar{r}^{{n - 1}}}}{{{\left( {n - 1} \right)} \cdot n!}}}}} \right)}} \right]}}}{\text{d}}\bar{r}}}\quad \hbox{(FGM sphere)}$$
(15c)

In the previous work of the author [16], the dimensionless transient temperature field in an infinite FGM plate with symmetrical structure was derived by using the perturbation method, which is expressed as:

$$V{\left( {\eta, \tau} \right)} = 2{\sum\limits_{n = 1}^\infty {\frac{{{\left( {\omega ^{2}_{n} + B^{2} \zeta ^{2}} \right)}\sin \omega _{n} \cos {\left(\omega _{n} \eta/\zeta \right)}}}{{\omega _{n} {\left( {\omega ^{2}_{n} + B^{2} \zeta ^{2} + B\zeta} \right)}}}}}{\text{e}}^{{- {\left( {{\omega _{n}}/\zeta} \right)}^{2} \tau}}$$
(16)

where B is the Biot number of the surface, η is an introduced variable, which was defined as:

$$\begin{aligned} \eta &= {\int\limits_0^{\bar{z}} {\frac{1}{{{\sqrt {\bar{\kappa}{\left( {\bar{z}} \right)}}}}}{\text{d}}\bar{z}}}\\ \zeta &= {\int\limits_0^1 {\frac{1}{{{\sqrt {\bar{\kappa}{\left( {\bar{z}} \right)}}}}}{\text{d}}\bar{z}}}\\ \end{aligned}$$

The discrete values ω n are the roots of the following transcendental equation:

$$\omega \cdot \tan \omega = B\zeta\quad n=1, 2, 3,\ldots$$
(17)

3 Numerical results and discussion

An infinite FGM plate, an infinite FGM solid cylinder and a FGM solid sphere composed of Al2O3 and TiC are considered for the numerical calculations. They have the material properties of TiC at the surface \((\bar{z} = \pm 1{\text{ for FGM plate, }}\bar{r} = 1{\text{ for FGM cylinder and FGM sphere) }}\)and those of Al2O3 at the center \((\bar{z} = 0{\text{ for FGM plate, }}\bar{r} = 0{\text{ for FGM cylinder and FGM sphere).}}\)Data of the physical properties of Al2O3 and TiC are listed in Table 1. The exponents n κ and n λ (referring to Eq. 12) are 0.2986 and 0.4055, respectively for the three FGM solid components. Considering the computation capacity and computation time, only the first 12 roots of Eqs. 14a, 14b and 14c are used in the calculations. By comparison, the calculations of the transient temperature fields in an infinite homogeneous plate, an infinite homogeneous cylinder and a homogeneous sphere are also conducted by using the well-established theories.

Table 1 Data of the physical properties of Al2O3 and TiC
Full size table

Figure 2 depicts the dimensionless temperature distributions in the three FGM components as a function of dimensionless coordinate \(\bar{\xi}\) \((\bar{\xi} = \bar{z}{\text{ for FGM plate, }}\bar{\xi} = \bar{r}{\text{ for FGM cylinder and FGM sphere)}}\) at different dimensionless times when Biot number B=2. The same results are obtained by using the perturbation method [16] for the dimensionless temperature distributions in the FGM plate, validating the current solution. It can be seen clearly from Fig. 2 that the dimensionless temperature \(V{\left({\bar{\xi},\tau} \right)}\) of the FGM plate at any dimensionless coordinate \(\bar{\xi}\) and any dimensionless time τ is always higher than that of the FGM cylinder. Whereas the dimensionless temperature \(V{\left( {\bar{\xi},\tau} \right)}\) of the FGM sphere at any dimensionless coordinate \(\bar{\xi}\) and any dimensionless time τ is always lower than that of the FGM cylinder. In case of a cold shock (T 0>T s, e.g., quenching), the cooling speed of the FGM sphere is the highest, while the cooling speed of the FGM plate is the lowest.

Fig. 2
figure 2

Dimensionless temperature distributions in the FGM components as a function of dimensionless coordinate \(\bar{\xi}\) at different dimensionless times when B=2

Full size image

Figure 3 shows the dimensionless temperature distributions in the three homogeneous components when Biot number B=2. By comparing Fig. 2 with Fig. 3, it can be concluded consequently that the transient temperature distributions in the FGM components have similar shape effect to that of homogeneous components. It can also be seen from Figs. 2 and 3 that the dimensionless temperature\(V{\left({\bar{\xi},\tau} \right)} \) of a FGM component at any dimensionless coordinate \( \bar{\xi}\) and any dimensionless time τ is always lower than that of the corresponding homogeneous component with the same shape, i.e., the rate of heat transfer in a FGM component is higher than that in a homogeneous component with the same shape and same size under the same thermal loading condition. The higher heat transfer rate of FGM components than those of homogeneous components should obviously be attributed to the distributions of their thermo-physical properties along the gradient direction: The thermal diffusivity κ (=λ /(cρ)) of the center (Al2O3) is higher than that of the surface (TiC), with the exponent n κ being positive (referring to Eq. 12 and Table 1).

Fig. 3
figure 3

Dimensionless temperature distributions in the homogeneous components as a function of dimensionless coordinate \(\bar{\xi}\) at different dimensionless times when B=2

Full size image

On the basis of the present work, the transient thermal stresses in FGM components especially the maximum thermal stress attained at the surface (if taking cold shock as an example) and its time of occurrence can be obtained. And consequently, the thermal shock resistance of FGM components can be evaluated that has been demonstrated by the previous work of the author [16], despite the technological difficulties in the fabrication of FGM solid cylinders and FGM solid spheres with continuously radial composition transition.

4 Conclusions

In this paper, the one-dimensional transient temperature fields in an infinite FGM plate with planar symmetric material properties, an infinite FGM solid cylinder with axially symmetric material properties and a FGM solid sphere with spherically symmetric material properties under the convective boundary conditions are determined by using the separation-of-variables method and the variable substitution method. Numerical calculations conducted for the three FGM components composed of Al2O3 and TiC show that the transient temperature fields of the FGM components have similar shape effect to that of homogeneous components. In case of a cold shock, the cooling speed of the FGM sphere is the highest, while the cooling speed of the FGM plate is the lowest. The present work would be valuable for the investigation of the thermal shock resistance of FGMs with various shapes.