Stability of a (2G) Coated, Thin-Film YBaCuO 123 Superconductor: Intermediate Summary

Abstract

This paper summarises results obtained with stability calculations of thin films and multi-filamentary superconductors. In a series of papers, all the contributions have been published in this journal. We now extend our previous investigations to the temporal aspect of the internal heat transfer and to the material homogeneity problem. Within multi-component heat transfer (solid conduction, radiation), the standard theory of radiative transfer in a coated, thin-film, YBaCuO3 123 superconductor correctly treats the energetic aspects of radiation propagation; this is the actual core of stability models. But a rigorous solution of the temporal aspect still is missing. It is the study of this aspect that would provide a new access to the physics of superconductor stability, in particular if after a disturbance the system is already close to a phase transition. A matrix formulation, using a combination of Monte Carlo and radiative transfer calculations, is suggested to circumvent the temporal solid conduction/radiative transfer problem in multi-component heat flow. As an important result, quench is not an event that proceeds instantaneously. Instead, it is a process the speed of which decreases the more, the closer the superconductor temperature approaches critical temperature until the residual number of electron pairs becomes too small to support critical current. The stability of superconductors and thermal fluctuations might reflect a common background: the relaxation time of the density of electron pairs after disturbances.

1 Survey: Superconductor Stability Models

Standard, analytic stability models of how to avoid quench of superconductors are thoroughly described by Wilson [1], Dresner [2] and Seeger [3] and in a large number of other contributions; see citations to original literature in these three references. When applied to superconductor magnet design and operation, the success of these stability models is impressive and uncontested.

But the traditional models, without modifications, assume worst-case scenarios and stationary conditions, while quench of superconductors proceeds on very small timescales. Since critical current density, J_Crit(x, y, t), in the superconductor (x, y-) cross section strongly depends on temperature, thorough analysis of temperature fields, T(x, y, t) and their short-time, transient development after disturbances becomes mandatory. This is important if superconductor temperature, or the other critical superconductor parameters, during or after a disturbance, approach their critical values.

This situation, the superconductor already close to critical temperature, is the central focus of the present paper.

In the literature, attempts have been made to adapt traditional stability models, like the adiabatic model, to dynamic situations, for example by

• Inclusion of a constant maximum ratio of transport to critical current (thereby modifying the distribution of screening currents and internal magnetic field pattern, both a very rough approximation)

• Introduction of realistic heat transfer coefficients (in the literature, these coefficients frequently are considered as independent of the temperature difference to the coolant, an assumption that may lead to serious errors)

• Filling factors; compare Eq. (7.27) with Eq. (7.7) in [1]

Though questionable from the physics behind, these modifications all are very practical for technical design and applications; their derivation in some cases is highly sophisticated and of best analytic quality.

However, traditional stability models even then are applicable without complications to only situations clearly before the system approaches the phase transition, a situation that the models shall help to avoid. But quench belongs to life of a magnet.

Although numerical simulations of the stability problem request increased computational efforts, they are more flexible (easier to adapt to practical situations) and provide deeper insight into the physics of superconductor stability. A first, successful numerical simulation of superconductor stability was presented by Flik and Tien [4] when they applied a finite differences method.

Numerical methods in general are suitable to describe local critical current density distribution and percolation of the transport current; take into account microscopic conductor/matrix composition, interfacial contacts, local disturbances and local heat transfer to the coolant; and, most importantly for superconductor stability, identify local hot spots arising under transport current exceeding critical current density in the conductor cross section. Numerical methods are suitable to also check superconductor stability with respect to the homogeneity of the material, an aspect that is rarely taken into consideration in stability calculations.

Analytical models cannot provide this information, and time-resolved analysis is hardly possible with standard stability models. Numerical methods obviously are the most flexible tool that presently is available in the stability analysis of superconductors.

In a series of papers [5,6,7,8,9,10,11,12,13], all published in this journal, we have investigated the stability of YBaCuO and BSCCO superconductors against quench by means of finite element simulations of transient temperature fields. While the calculations initially were focused on single, isolated disturbances, the calculations were extended to disturbances arising from flux flow losses. These arise if in a magnetic field transport current density, J_Transp, exceeds critical current density, J_Crit, with the superconductor temperature below its critical value. Flux flow losses in AC applications may be periodic. This loss component would be no longer isolated, point-like, but may arise within the total superconductor volume.

The present paper is intended to continue with the verification of numerical tools and of the results obtained in the previous stability calculations and to take further steps to extend the applicability of the tools with respect to the homogeneity of material properties.

Discussion of the accuracy of stability calculations in [13, 14] was focused on the potential of the applied numerical procedures and their applicability. However, applicability does not mean “completeness” of a theory. In the present paper, it is investigated whether the so-called additive approximation, and radiative transfer in general, not only is applicable to superconductors but also constitutes a complete theory. This discussion is missing in the literature but is closely connected to the temporal problem of heat transfer.

Local and extended, transient and continuous disturbances are responsible for non-uniform and transient superconductor temperature fields. Since critical current density strongly depends on temperature, analysis of transient temperature fields thus is important for conductor design and operation and for investigation of their stability against quench. The numerical investigations reported in [5,6,7,8,9,10,11,12,13], therefore, are not just academic: By the temperature dependency of J_Crit, they have tight connections to technical problems.

As before, we will not present design calculations in this paper. It is the variety of numerical results obtained so far that shall be described and the applied tools and possible modifications suggested for further superconductor stability research.

In superconductor solids, radiation transport is negligible. But the situation may change substantially in thin films and, in general, near the phase transition, the most critical situation of the stability problem.

1.1 Stability Studied with Numerical Simulations

When inspecting the physics behind superconductor stability, there are besides the traditional, preferentially thermal (energetic) aspects at least four more problems the solution of which can be obtained only with numerical simulations (items i to iv):

• (i) The superconductor stability problem cannot be modelled adequately by assuming constant and uniform conductor temperature, after any kind of disturbance (flux flow and Ohmic losses, flux jump, hysteretic and coupling losses, release of stored mechanical tension energy, absorption of particle radiation and fluctuations of the cooling power). A comprehensive catalogue of disturbances is listed in [1]).

The same applies to “thermal fluctuations” at superconducting/normal-conducting interfaces. We cannot expect material homogeneity and uniform temperature distributions near these interfaces.

• (ii) Understanding of superconductor stability is tightly coupled to understanding the phase transition.

• (iii) Modelling may become very complex, if not impossible, if relaxation of the electron system, after a transient disturbance, takes too long to establish a new thermodynamic equilibrium, in relation to the time steps in an analytical or numerical analysis; see Fig. 1 of the present paper.

• (iv) We have a twofold problem with timescales: The first is almost trivial and results from the time lag, Δt_Lag, arising from more than only one internal heat transfer mechanism that contributes to total heat flow: We have solid conduction plus radiation in thin films and within the filaments of multi-filamentary superconductors [11,12,13]. The time lag then results from the different propagation velocity by which a disturbance (like just a local temperature variation), in parallel under both transport mechanisms, proceeds in the superconductor.

Fig. 1

Relaxation time (the time needed to obtain thermodynamic, quasi-equilibrium in tiny volumes, V_C, at the centroids of turns 96 (light-green, lilac, orange and blue diamonds, respectively) and 100 (red diamonds) of a coil of coated, thin-film YBaCuO 123 superconductor (in total 100 turns), after a thermal disturbance (flux flow losses) originating from transport current density locally exceeding critical current density. The light-green, lilac, orange and blue diamonds refer to element temperature calculated in the finite element simulation; dark-green circles are calculated for an arbitrary sequence of element temperatures. Differences of the calculated relaxation times originate solely from the random distances between two electrons in the volumes, V_C. As soon as the element temperature exceeds 91.925 K, coupling of all electrons in this thin-film superconductor to a new dynamic equilibrium can no longer be completed within the integration times, here 1 or 50 μs, in the finite element procedure, indicated as length of process time intervals (lilac horizontal dashed lines) in this figure. The figure is copied from [1]

A time lag becomes the more important the more closely, locally or extended in its total volume, the superconductor approaches its critical parameters. Electric/magnetic properties and the specific heat of the superconductor materials diverge during this approach.

The second problem is less obvious. It manifests itself in a “cloud”, i.e. in a great number of “images” that in the solid arise from disturbances and their propagation in the superconductor: Assume an “event”, like a temperature variation, occurring anywhere in the conductor. It initiates emission of thermal radiation. These signals (mid-IR photons), when absorbed/remitted or scattered to other positions, induce local temperature variations, the images of the original event. The “cloud” thus results from redistribution, spatial or temporal, of thermal energy by the radiative transport channel. Compare Fig. 2a, b.

Fig. 2

a A mid-IR beam (or a raditive thermal wave) originally emitted at (z = 0, t = 0) that propagates through a non-transparent medium (schematic, not to scale; in case of the wave, the arrows indicate the normal to its surfaces). The medium may be identified with a superconductor. Emission of the beam results from a disturbance (dark-grey solid circle), an event like a heat pulse, temperature fluctuation or a local quench. At the positions 1 to 6, black solid symbols indicate physical obstacles to radiation (absorption/remission or scattering centres). The beam during its interaction (events) with the obstacles splits into corresponding parts according to local values of albedo and extinction properties of the material. Thermal remission is assumed to be isotropic (dashed red circles with radii, r_ij). In this schematic presentation, thermally remitted beams (thick red arrows) in this figure run in parallel to scattered intensity (thick blue arrows); in reality, the directions are quite different (depend on the angular Planck radiation distribution and the scattering phase function). Directions of the original beam and its scattered parts all are at random angles from the surface of each of the obstacles. Lengths of the arrows are at least the mean free path, l_m, of photons between two successive radiation/solid interactions. Images on the time axis, t, of the events are illustrated by means of mapping functions (compare text for their definition). A “cloud” of images resulting from a single original event is schematically indicated by the open circles in Fig. 2b. b The cloud of images, i′, i″, i″ (open circles, as multiples generated by mapping functions, f [e(t₀)]), from a single original event e(t₀), the dark-grey, solid circle. The event is defined as a disturbance in a superconductor like a temperature variation (schematic, not to scale). Images i′ and i″ will be received, from a transport process, by an observer at different positions, z′ and z″, at the same time, t₁, after the start of the experiment. If, on the other hand, position z of the images would be the same, z₁ = z₂, the observer will recognize the images at different times. Since the number of different transport properties (like random fluctuations of propagation velocity, radiation/solid particle interactions, local values of extinction coefficients and albedo Ω) in principle can be arbitrarily large, the number of images that originate from the same individual event, e(s,t), can be very large, too. In non-transparent objects, there is accordingly no unique (bijective) correlation between events, e(s,t), and their images, i [e(s,t)], at any time, t. With solid conduction heat flow and radiation propagation in parallel, the propagation velocity of the signal (thermal radiative wave front; blue and red, dashed vertical front lines, respectively) is much larger under solely scattering interactions (albedo Ω = 1) in relation to conductive heat flow. Existence of the cloud under multiple scattering is confirmed in Figs. 11 to 13a, b and Section 5.2

The cloud reflects statistical uncertainties of the propagation of the mid-IR radiation through the superconductor: These comprise a temporal component, Δt_Fluct, and a spatial value, ΔL_Fluct. Both uncertainties to the most part result from radiation scattering.

The temporal value, Δt_Fluct, indicates how images of a single event or of a series of events, when counted on a timescale (if it exists), scatter around a mean value. The uncertainty Δt_Fluct, is not identical to the time lag Δt_Lag.

The spatial value, ΔL_Fluct, reflects the geometrical dimension of the cloud. The cloud is a virtual volume created within the superconductor. Each transport mechanism creates its own cloud. In parallel to Δt_Lag, it is this volume that is responsible for, and quantifies, uncertainties of the temperature fields. The cloud volume reflects a large variety of “obstacles”, e.g. to propagation of radiation in the solid, like local materials and optical in-homogeneities. For the solid conduction part, dimension of the cloud reflects e.g. interfacial thermal (contact) resistances between neighbouring particles in a grain structure.

Existence of the uncertainties Δt_Fluct and ΔL_Fluct apparently never has been investigated (or they have simply been assumed as completely negligible). We will show (Section 5) that at least ΔL_Fluct has significant impacts on stability analysis.

The point is, any single, isolated event, by the different transport channels and by the “obstacles”, may produce a large variety of images. Beyond time lag, the uncertainties Δt_Fluct and ΔL_Fluct, in their ultimate consequences, may question the existence of uniquely defined, physical timescales within the cloud volumes and thus in part or in the total volume of the superconductor. As has been shown, and is simply the corollary of radiative and multi-component heat transfer, this is the case in non-transparent media. Superconductors may be non-transparent to mid-IR radiation.

The question then is whether a rigorously time-resolved, analytical or numerical treatment of the stability problem under Δt_Lag, Δt_Fluct and ΔL_Fluct remains possible at all. We will explain this problem in more detail in Section 5 of the present paper.

To approach these situations, in particular if the superconductor is already close to a phase transition, and to support the investigation of the stability problem under these conditions, a microscopic stability model was presented in [6]. Characteristic (relaxation or life-) times, τ_El, of thermally excited electron states were numerically estimated from their decay rates using a sequence of contributions,

• (a) From a formal analogy to an aspect of the nucleon-nucleon, pion-mediated Yukawa interaction

• (b) From the Racah problem, which means the expansion of an anti-symmetric N-particle wave function from a N-1 parent state, with summations of individual decay widths to obtain the total lifetime, τ_El, of the excited electron system, and

• (c) From uncertainty and (d) Pauli principles

Stability analysis is an inter-disciplinary challenge. Also, the analysis of thermal fluctuations could be supported by this model (but this will be the subject of a following paper).

Another approach comprises the application of statistical variations of the superconductor critical parameters T_Crit, B_Crit and J_Crit (B_Crit is the upper critical field, B_Crit,2, of a type II superconductor) and of the anisotropy factor χ of the thermal diffusivity in crystallographic ab-plane vs. c-axis directions. The statistical treatment of the critical parameters is described in Fig. 19 of the Appendix 2 of the present paper. Random variations ΔT_Crit, ΔB_Crit, ΔJ_Crit and Δχ of these parameters are within 1 K, 5 T, 1% and 0.5 of their absolute values: T_Crit, B_Crit,₂, J_Crit and χ amount to 92 K (in zero field), 240 Tesla (at T = 0), 3 10¹⁰ A/m² and 10 (both at T = 77 K), respectively. Examples for the statistical variations and the correlation of these variations with breakdown of the critical current are shown in Figures 3, 6 and 7 in [11].

This approach is made to account for experimental uncertainties of the values of superconductor critical parameters. Also shortcuts resulting from industrial conductor manufacture or handling can be treated by this statistical method.

These methods (statistical distribution of superconductor electrical and magnetic parameters and the microscopic stability model) will be extended in this paper to also random distributions of thermal material parameters (in a first step, the solid conductivity, λ_Cond). This is studied with a coated, thin-film conductor that serves for winding a coil of 100 turns.

These statistical approaches to the “ideal” values of T_Crit, B_Crit, J_Crit, χ and λ_Cond shall help to put the results of the laborious numerical stability calculations on stable grounds. Real (ideal) values of these parameters never will become available with absolute zero uncertainty.

A numerical model to estimate local flux flow resistivity and corresponding local AC losses in superconductors was presented in [9]. This model is intended to replace the standard but questionable estimate of flux flow resistivity, ρ_FF = ρ_NC B/B_Crit,2, which is found in traditional volumes on superconductivity. The ratio of magnetic inductions, B and B_Crit,2 simply multiplies the normal conduction resistance of the superconductor, ρ_NC. This estimate can be improved, at least with respect to grain structure and its interfacial resistances.

1.2 Superconductor Transparency

Large extinction coefficients of mid-IR radiation of YBaCuO and BSCCO were obtained from application of rigorous scattering theory [12]. Superconductor solids trivially are non-transparent to mid-IR radiation, but this may be also the case even with superconductor thin films.

Clarification of the situation is important and by no means academic: finite element calculations of superconductor stability performed with the highest possible spatial and time resolutions might allow to catch the superconductor “on the last meters” (when its temperature is milli-Kelvin just below critical temperature) from quenching. This works only if the mid-IR optical properties are known with sufficient accuracy.

While in standard optical experiments, transmission of mid-IR through superconductor solids or films is almost zero, this does not mean that there is no radiation within the superconductor volume; there is at least thermal radiation, by absorption/remission that locally contributes to total, internal heat transfer, and there is scattered radiation; all these contributions are taken into account by the Equation of Radiative Transfer; see later Eq. (4a) and Eq. (4b).

1.3 Results Obtained with Numerical Simulations (Intermediate Summary)

All results reported in [5,6,7,8,9,10,11,12,13] are not design calculations. It is the physics of stability, at situations close to the phase transition, that was approached in these studies. Overall results are the following:

• Under disturbances, we cannot expect uniform temperature distribution within the superconductor. This concerns also multi-filament superconductors: Temperature neither is uniform in the total superconductor/matrix cross section (this is almost trivial) nor, surprisingly, is it uniform within the filaments; compare Figures 5a,b in [10] and 2 and 3a,b in [14].

• Heat transfer to a coolant has locally to be modelled, separately, at all positions of the solid/liquid interface and with heat transfer coefficients that depend on the temperature difference between solid and liquid. This becomes important when a local temperature fluctuation extends to times t > 10 ms.

• Increase of local superconductor temperature, dT(x, y, t)/dt, under disturbances can be enormous, within short periods by rates up to 10⁸ K/s.

• Regions in the conductor cross section where zero-loss current transport is possible, at least during short time intervals, may exist in parallel to flux flow and Ohmic resistances; distribution and extension of these regions are time dependent. There is, accordingly, no permanent, sharp separation between resistive and inductive current limiting.

• Stability is not uniform, neither within the cross section at a certain length co-ordinate of the conductor nor over its total volume.

• Quench always starts locally.

• Current transport in a superconductor under any disturbance is not like laminar flow but percolates through the conductor cross section

• Time lag can become substantial, with respect to superconductor stability, in calculated temperature fields and stability functions in multi-component heat transfer (compare Fig. 3 of this paper); this may have serious consequences for superconductor safety.

• The lifetime of residual electron pairs is finite and increases the more the closer the conductor temperature approaches its critical value; compare Figures 9a,b to 11 in [14]; this means stability analysis and simulation, by analytical or numerical simulations, runs into severe problems when T → T_Crit.

• At situations very close the phase transition, and because of the increased lifetime of residual of electron pairs, their decay cannot be not complete; it is tempting to assume this might contribute to the existence of thermal fluctuations.

• A time lag in multi-component internal heat transfer would be correlated to different, competing heat transfer mechanisms and their propagation velocity (and quench under this condition cannot occur simultaneously at all conductor positions). But a principal, parallel problem is made visible by the already mentioned cloud of images (Fig. 2a, b of the present paper) that may exist within a single transport channel, here the radiative heat transfer mechanism.

• For a physical time to uniquely exist, the system must be transparent to radiation at any wavelength. This is trivial, but it in turn means that within superconductors at local positions (clouds), even in the case of thin films, physical time, because of non-transparency against mid-IR radiation, cannot be defined uniquely. The consequence of this finding culminates in the surprising, strange, urgently to be discussed but apparently inevitable conclusion originating from solely, standard radiative transfer: In systems with strong absorption and scattering and near the phase transition, time itself is not transparent.

Fig. 3

Stability function, Φ(t), for a periodic, point-like disturbance of DC transport in a 1G multi-filamentary superconductor, a filament of 200 μm radius, under diffusive, solid conduction plus radiation and solid/liquid (initially conductive later convective) heat transfer. Materials properties are of YBaCuO 123, but filaments of this type, and with strongly reduced diameter) would preferentially be prepared from BSCCO. The disturbance, Q(t) = 2 Q₀ sin(2π ω t) + Q₀ [W], with Q₀ = 0.0125 W, is incident on the target positioned at the centre of the filament (red spot in the inset, axial co-ordinate z = 0). Results are calculated by the finite element method, with the crystallographic c-axis (weak electrical conductivity and solid thermal diffusivity) oriented parallel to the z-axis of the co-ordinate system. The results obtained under solid conduction plus radiation and solely solid conduction (solid and open diamonds, respectively) apply to increasing distances (planes), z, from the target plane. The thick solid, coloured circles, introduced at t = 36, 67 and 106 ms, serve to identify a time lag of about 30 and 39 ms, at the planes z = 325 and 525 μm, respectively, by which it is predicted the conductor, at these co-ordinates, would react later, to a disturbance when simulating solely conduction in comparison to conduction plus radiation; see the positions, under constant Φ = 0.27 or 0.4, on the time axis (and the descriptions in the text). Without its present modifications, the figure was presented in [7], Figure 10a

The last two items are explained in items (a) to (f) in [12], Sect. 2.2.1, that in sharp contrast define transparency in the usual optical sense. They are explained also in Sect. 6 of the same reference and in Section 3.3 of the present paper. The conclusions do not collide with relativity principles, do not introduce “new physics”, they are strict corollaries of radiative transfer. In Section 5, we will try to calculate the dimension of the cloud of images by a Monte Carlo simulation.

1.4 Organisation of the Present Paper

Sections 2 and 3 reflect multi-component heat transfer, in particular radiative transfer, under a new viewpoint: “completeness”. What is a “complete” theory? Section 4 for this purpose considers the most important aspects of radiative transfer parallel to conduction heat flow in superconductors.

Sections 4.5 and 6 are focused on how uncertainties in superconductor material properties (electrical and thermal) have impacts on stability functions. This is the problem of homogeneity of superconductor material properties.

Stability calculations are based on mapping of the calculated temperature field onto the field of critical current density. The temperature field therefore must be obtained, as precise as possible, from a complete, solid conduction plus radiative transfer theory. To successfully understand the complications inherent to the radiative transfer mechanism (Section 4), we in Section 7 contrast the traditional, radiative transfer (continuum) theory and its approximation (the radiative diffusion model) by a totally unconventional, abstract counterpart: quantum-mechanical entanglement. It is the most sensitive comparison that can be imagined.

In Section 7, also the entropy concept provides an alternative access to improve understanding of the completeness problem in multi-component heat transfer.

2 The Additive Approximation, a Complete Theory?

Most part of the results listed in the preceding section relies on the “Additive Approximation” of heat transfer, an approximation that applies a diffusion model of all contributing heat flow components. Applicability of this model in superconductors and in thin films has been confirmed only very recently [12,13,14]. In short, in a non-transparent object, the integro-differential Equation of Radiative Transfer (see later, Section 4, Eqs. 4a and 4b) reduces to a differential equation, by which also the radiative flux, ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ can be written in terms of a “radiative conductivity”, λ_Rad.

We have ${\dot{\mathbf{q}}}_{\mathrm{Rad}}=-{\lambda}_{\mathrm{Rad}}$ dT/ds, like in the standard Fourier conduction law:

$$ \dot{\mathbf{q}}=-{\lambda}_{\mathrm{Cond}}\ \mathbf{\operatorname{grad}}\ T. $$

Derivation of the diffusion model of radiative transfer is explained in standard volumes [15,16,17,18].

The additive approximation reads

$$ {\lambda}_{\mathrm{Total}}={\lambda}_{\mathrm{Cond}}+{\lambda}_{\mathrm{Rad}} $$

(1)

if there is only solid conduction and radiative heat flow.

At a first glance, this relation looks trivial (as an algebraic relation, it is just the sum of two components). However, this simple equation was subject to controversial debates in the literature of the 1980s (an apparently existing “thickness effect” was imagined when measuring the thermal conductivity of partly transparent thermal insulations).

Heat fluxes ${\dot{\mathbf{q}}}_{\mathrm{Cond}}$ and ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$, if they depend on temperature, usually are coupled to each other by the temperature profile in the object. But heat fluxes are increasingly decoupled, if optical thickness, τ, of the system approaches τ → ∞. The point is, in the additive approximation, each of the components of λ_Total can be estimated independently of the other modes of heat transfer. One can also say: If the different components are not coupled by temperature profiles in the superconductor (or in any other object).

It is important to investigate whether the additive approximation not only is fulfilled (and applicable) in superconductors but, more generally, whether this approximation also satisfies another criterion, namely being “a complete theory”.

What is a “complete theory”? Predictions on stability of superconductors rely on knowledge, precision and uniqueness of the temperature fields within the conductor and must strictly and uniquely be correlated to their origins like “disturbances” of superconductor states. A theory that fulfils this criterion without any exception will in the following be called a “complete theory”.

More thoroughly, the question whether a physical theory is complete or not has been discussed in a historical paper by Einstein, Rosen and Podolsky (EPR) in the quantum-mechanical literature [19]; this paper is known under the heading “Entanglement”.

The authors of the EPR paper certainly had only quantum-mechanical systems in mind when they requested “every element of physical reality must have a counterpart in physical theory”; otherwise, the theory would be incomplete.

This request might collide with the microscopic reality of total, multi-component heat transfer: Both time lag, Δt_Lag and in parallel, existence of the uncertainties Δt_Fluct and ΔL_Fluct (the dimensions of the cloud of images) in non-transparent objects are non-zero quantities. Both collide with uniquely defined timescales. In transparent objects, this would require Δt_Lag, Δt_Fluct and ΔL_Fluct to be absolutely zero. Otherwise, namely in non-transparent objects, the theory cannot be complete.

Entanglement is illustrated later in Fig. 4 and will be used as a sharp contrast to standard theory of radiative transfer in Section 7, to contribute to its understanding.

Fig. 4

Entanglement in a two-particle system. As an example, the figure schematically shows the (rare) decay of the η-meson into a muon pair. Dashed circles denote decay products (muons); each of the muons is of spin 1/2; spin correlation is to a spin-singlet state, S = (S_x, S_y, S_z). Let the decay occur at time t₀ = 0, and suppose observers O1 and O2 at t > 0 measure S_z, the spin z-components (red arrows) of the separated particles 1 or 2. If O1 does not perform measurements, O2 will find S_z of particle 2 (moving to the left) positive or negative, each with probability 1/2. But as soon as O1, at any t > t₀, measures S_z of particle 1 (moving to the right), and if he finds S_z+, observer O2, simultaneously and with probability 1, will find S_z− regardless of the distance between particles 1 and 2

3 Timescales

3.1 Time Lag in the Stability Function

Transient temperature fields and stability functions in our previous papers [5,6,7,8,9,10,11,12,13,14] were obtained from finite element calculations to solve Fourier’s differential equation or from a combined Monte Carlo/finite element method. After thermal excitation of a target, the Monte Carlo simulation was used to generate, by absorption of the bundles emitted from a target, a random distribution of radiative heat sources within the superconductor filament or thin film.

An initial temperature distribution is equivalent to a distribution of instantaneous, initial heat sources (like radiative); see Carslaw and Jaeger [20]. Conversely, once radiative sources are determined, like in a Monte Carlo simulation, this distribution is equivalent to an initial temperature distribution in the sample. Then, it makes sense to treat the whole, solid conduction parallel to radiation thermalisation problem as a conduction process. For this purpose, all internal heat transfer channels must be of the diffusion type.

When the transient temperature distribution during a disturbance has become available, the stability function, Φ, can be calculated from the obtained, stationary or transient temperature distributions, T(x, y, t), in the superconductor: The calculated field T(x, y, t) in this procedure is mapped onto the field J_Crit(x, y, t) of critical current density.

The stability function, Φ, a tool that is frequently applied in stability analysis, apparently originates from [4], there without taking into account the presence of magnetic fields and with only a constant heat transfer coefficient for the contact to the coolant (this has been improved in our previous papers).

The stability functions answer the question up to which conductor temperature, in an integral view taken over the total conductor cross section, would allow zero-loss current transport.

In the more complete form, Φ includes the dependence on magnetic field (magnetic flux density, B) of the critical current density. This is because under flux flow losses there is no zero-loss current transport, like under Ohmic resistance. Accordingly, we have

$$ 0\le \Phi (t)=1-\left\{\int {J}_{\mathrm{Crit}}\left[T\left(x,y,t\right),B\left(x,y,t\right)\right]\ \mathrm{d}A\right\}/\left\{\int {J}_{\mathrm{Crit}}\left[T\left(x,y,{t}_0\right),B\left(x,y,{t}_0\right)\right]\ \mathrm{d}A\right\}\le 1 $$

(2a)

This is approximated by

$$ 0\le \Phi (t)=1-\left\{{\Sigma J}_{\mathrm{Crit}}\left[T\left(x,y,t\right),B\left(x,y,t\right)\right]\Delta A\right\}/\left\{{\Sigma J}_{\mathrm{Crit}}\left[T\left(x,y,{t}_0\right),B\left(x,y,{t}_0\right)\right]\Delta A\right\}\le 1 $$

(2b)

with the summations taken over all superconductor finite elements with their individual cross sections, ΔA.

The method is explained in detail in Appendix 2 to this paper.

If T(x, y, t) approaches T_Crit (when neglecting the dependency of J_Crit on B), the critical current density, J_Crit(x, y, t), becomes very small, which means Φ(t) → 1, and zero-loss current transport through the total superconductor cross section, A,

$$ {I}_{\mathrm{Transp}}(t)={J}_{\mathrm{Crit}}\left[\left(x,y,T=77\ \mathrm{K}\right]\ \mathrm{A}\ \right[1\hbox{--} \Phi (t)\Big] $$

(3a)

then is hardly possible.

In Eq. (3a), J_Crit(x, y, T = 77 K) = J_Crit(x, y, t₀) is assumed as uniform (apart from fluctuations, ΔJ_Crit, compare Fig. 19), with t₀ the time when the simulation is started.

If T(x, y, t₀) and J_Crit(x, y, t₀) are not uniform at t₀, Eq. (3a) transforms into

$$ {I}_{\mathrm{Transp}}(t)=\left\{{\Sigma J}_{\mathrm{Crit}}\left[T\left(x,y,{t}_0\right),B\left(x,y,{t}_0\right)\right]\ \Delta A\right\}\left[1\hbox{--} \Phi (t)\right] $$

(3b)

Calculation of Φ(t) by Eqs. (2a) and (2b) provides an integral view of the temperature distribution and, when Φ(t) > 0, indicates that anywhere, at unknown positions in the conductor cross section or volume superconductor temperature might have approached or exceeded critical temperature.

The exact position is not available from Φ(t). This information can be achieved either from experiments (that would be very difficult to perform) or from numerical simulations. The value Φ → 1 indicates that a critical situation within the superconductor immediately might come up, and actions have to be taken to avoid a catastrophic failure.

The benefits of the stability function become obvious already in situations still safely apart from the ultimate catastrophe: As an example, Fig. 3 (with slight modifications copied from [7]) shows results for Φ obtained for a thin filament of cylindrical cross section.

After subsequent compaction by mechanical/thermal treatment, the filament radius will strongly be reduced and conductor length elongated. Dozens or hundreds of such ceramic superconductor filaments may be bundled into a cable within an appropriate matrix material (Cu or CuNi) to a “first-generation (1G)” superconductor. BSCCO materials presently are given preference against YBaCO for this filamentary conductor concept, but this is not the problem.

The results shown in Fig. 3 apply to DC (constant transport current) under a periodic disturbance. At constant depth position, z, in the superconductor (cylindrical filament, compare the co-ordinate axis in the inset in Fig. 3), the simulation for all values of Φ predicts a non-zero time lag, Δt_Lag, between the cases “solid conduction plus radiation” (solid diamonds) and “only solid conduction” in the filament (open symbols).

Compare along the time axis, and at constant Φ, the curves with the solid and open diamonds, respectively. The simulations performed with the standard simulation procedure (finite element calculation with solely solid conduction, open symbols) predict that under a disturbance the Φ would be reached later in comparison to the more exact, combined Monte Carlo/finite element prediction including solid conduction plus radiation. This means the conductor in practice would experience the quench earlier (probably local, in first stages) than predicted by the standard method (only solid conduction, the procedure applied in standard stability calculations). For Φ = 0.4 const, for example, the time lag, at z = 325 μm obtained between the thick solid, dark-green circles, amounts to 30 ms. This is more than one cycle in a 50-Hz technical application.

Again with Φ = 0.4 constant, the superconductor arrives at this value at times differing by in total 69 (30 + 39) ms between the two (depth) positions z = 325 and 525 μm (solid plus radiative conduction: compare the solid, light-green and turquoise diamonds; the black, dashed curve is used just to guide the eye). We have zero-loss current transport (under 60% of critical current) only after a time lag of 69 ms between these two positions.

The different values of the stability function observed at different depth z of the wire also indicate that the current distribution most probably is not uniform. This means that current percolates through the conductor cross section. For Φ = const, the integral over the transport current is constant, too, but it is not clear at all that the distribution of the current would be uniform. Quench always starts locally, under any disturbance.

In order to safely predict maximum zero-loss current transport through the whole conductor length, the minimum of the stability functions, Φ = Φ(z), among all co-ordinates, z, has to be identified. But this is a theoretical issue. Instead, its maximum is decisive for safety of the conductor in that it limits the transport current to the maximum allowable amount.

As a consequence of Fig. 3, there is no uniform stability criterion over the length of a superconducting wire or cable: At a given cross section or length position in the superconductor, zero-loss current transport may be possible, but at different positions, this is not necessarily (or no longer) fulfilled, and a quench, first rising locally, could be the consequence.

This conclusion is confirmed in Fig. 5a, b with the stability function calculated for a coil that applies a second-generation (2G) thin-film YBaCuO 123 coated superconductor. A sudden increase of transport current to a fault (Fig. 5a) is responsible for flux flow losses in turns 1 to 100 beginning at t = 3 ms and for the mixture of zero loss, flux flow and Ohmic resistances in Fig. 5b.

Fig. 5

a Stability function, Φ(t), obtained for solid conduction plus radiation (and solid/liquid heat transfer at the solid/coolant contacts) in the thin film, YBaCuO 123 superconductor. Thickness and width of the thin film is 2 μm and 6 mm, respectively. Results are shown for turns 96 to 100 (Figure 1 of [11]) of a coil prepared using the coated conductor. The calculations assume a sudden increase of transport current above its nominal value beginning at t = 3 ms; flux flow resistances then are responsible for thermal losses that locally increase conductor temperature. All curves in this and in the following figures apply the same (“standard”) uncertainties ΔT_Crit, ΔB_Crit,₂, ΔJ_Crit and the anisotropy factor, Δr (within ± 1 K, ± 5 Tesla, ± 1% and ± 0.5, respectively) of the electrical/magnetic critical parameters T_Crit, B_Crit,₂ and J_Crit (92 K, 240 Tesla and 3 10¹⁰ A/m² at T = 77 K) and of the anisotropy factor (r = 10, again at T = 77 K) of the thermal diffusivity, as in previous papers (see text and Fig. 19 for explanation of the uncertainties). Uncertainties of solid thermal conductivity, λ_Cond, and of critical current density, J_Crit, in the following tests are superimposed onto the results achieved with the “standard” set (see captions of the corresponding figures). In the present figure, coloured curves are obtained with no random fluctuations of λ_Cond, and of J_Crit, but the black crosses instead apply to a ± 5% random variation of λ_Cond, at randomly selected positions within turn 98. b Temperature distribution (nodal values) in turn 98 of the coil shown in Figure 1 of [11] at t = 4.2 ms after a sudden increase of transport current. The curves in this and in the following Figures apply “standard” uncertainties of the electrical/magnetic critical parameters of T_Crit, B_Crit, J_Crit and of the anisotropy factor, r, of the thermal diffusivity (see Caption to Figure 5a) onto which additional uncertainties of solid thermal conductivity, λ_Cond, and of critical current density, J_Crit, are superimposed (compare text and the corresponding Figure Captions). Outside the superconductor thin film, temperature of the layers immediately below and above the film, in turns 95...97 and 99 to 100 still are close to the start value (77 K) of the simulation, due to the small thermal diffusivity of the superconductor material in c-axis direction

Up to t = 4.0 ms, there is almost no limitation of zero-loss current transport. Close inspection shows that this remains possible up to t = 4.2 ms in turns 97 to 100, but in turn 96 (the innermost of the curves in this figure, solid red diamonds), zero-loss current transport is finished at already 4.1 ms.

This constraint must be observed strictly regardless whether 100% zero-loss current transport might be realised at any other circumferential positions of turns 97 to 100 or in any other turn. This is another example to demonstrate that quench does not start uniformly in the conductor volume even if the disturbance results from uniformly distributed flux flow losses.

3.2 Contributions by Solid Conduction and Radiation to Conductor Temperature After a Disturbance

Let a different disturbance, a heat pulse, be deposited on the surface of a thin film in a coated, thin-film superconductor, here under zero transport current. The situation is described in Fig. 6, part a, item (2), the red circle in the inset. Under this condition, the temperature peak seen in Fig. 7 at small co-ordinates, z, for the case “solid conduction plus radiation” is due to (i) strong anisotropic forward scattering, (ii) large extinction coefficients against mid-IR radiation (see Figures 15 and 20a in [12], the latter in comparison with Figure 20b of the same reference), (iii) strongly anisotropic solid conductivity, (iv) the short duration of the pulse (its thermalisation to stagnation temperature is not completed before 1 μs), and (v) different transit times.

Fig. 6

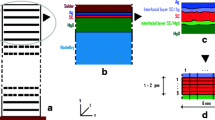
Numerical simulation scheme for the YBaCuO 123 superconductor (schematic, not to scale). The figure shows a overall design of the second-generation (2G), thin-film, coated superconductor and b the co-ordinate system for the finite element and Monte Carlo simulations; part a is copied from Figure 2 in [7]; the original of a is from Freyhardt (2004) lecture notes. Part c is explained below and in more detail in Section 6. a Current transport is almost entirely within the x,z-cross section, i.e. parallel to the (x,y)- (the crystallographic ab-) plane; crystallographic c-axis of the YBaCuO material accordingly is (anti-) parallel to the z-axis of the co-ordinate system. The vertical, dashed-dotted line denotes the axis of symmetry (x = 0). The target indicates the position of local heat sources within the conductor cross section (item 1), or (item 2, the red circle), the heat source is located on the upper surface of the superconductor thin film. Thickness of the YBaCuO film is D = 2 μm, with its width of 6 mm. Protective coatings (not shown in the figure) are used for thermal/mechanical stabilisation of the conductor and as bias for temporarily current sharing if transport current exceeds critical current of the film. b Individual radiation beam (dashed, light-blue line, or a thermal wave) selected of a set of in total (in the Monte Carlo language) M ≤ 10⁵ bundles emitted into the depth (z > 0) of the superconductor thin film. The scheme defines area elements, k(i, j), used for both Monte Carlo and finite element simulations. Volume elements (concentric rings) are generated by rotating the area elements against the symmetry axis, r (x = 0, thick, dashed-dotted line). Scattering angles are denoted by φ. c Two superconductor boundary layers (schematic, each of 0.1 μm thickness) with random values of the solid thermal conductivity, λ_Cond, assigned to the finite elements. The total conductivity is applied in the additive approximation, λ_Total = λ_Cond + λ_Rad (Eq. 1). Random values of λ_Cond are indicated by the different colours of the elements. Solid/solid interfaces 1 and 2 (between layers i = 1 and 2) separate materials of random conductivity, while solid/solid interface 2 (between i = 2 and 3) denotes gradual transition from random to regular (uniform, red colour) conductivity

Fig. 7

Superconductor temperature distribution (nodal values, at t = 8 ns) in the plane z = 0 of the YBaCuO 123 superconductor thin film. Results are shown at increasing vertical co-ordinates (depth of the thin film), z, when a rectangular heat pulse of total Q = M 1.25 10⁻¹² Ws, using M = 1, is incident on the target (z = 0; its position is indicated by the red circle in Fig. 6, part a, direction 2). Total duration of the pulse is 8 ns. Results apply to constant boundary temperature conditions and conduction plus radiation heat transfer. Penetration depth of the radiation is parallel to the axial direction of its co-ordinate system. The combined Monte Carlo/finite element method (compare text, Sections 4.5 and 5) is applied under the Additive Approximation, Eq. (1). In steps of 0.1 μm, the figure shows temperature between 0 ≤ z ≤ 2 μm and within 0 ≤ x ≤ 1.2 μm (of in total x ≤ 5 μm extension in the simulations) of the thin film. Axial (z-) direction is (anti-) parallel to the crystallographic c-axis of the superconductor material. The figure covers only one half of the total x,y-plane

Like in Fig. 3, results of all following calculations confirm the clear differences in the conductor temperature seen between the cases “solid conduction plus radiation” and “solely solid conduction” and under variation of the above items (i) to (v). It is therefore important to describe heat transfer in superconductors by taking into account all contributing components (solid conduction, radiation, heat transfer to the coolant if the simulations extend to t > 10 ms) and not restrict the stability calculation to solid conduction only.

In summary of these first sections, the numerical method, though laborious, is most flexible and comparatively simply applicable.

3.3 Mapping Functions to Create Timescales

Traditional heat transfer assumes that signals arising at given conductor positions and time from excitations of any particular type (here: conduction or radiation) by transport channels arrive simultaneously at any other positions in the conductor. From the mathematical aspect, this is because Fourier’s differential equation contains a sole (exactly one) time variable. From the physics behind, however, signals arriving by conduction and radiation cannot be recognised at the same time at a given co-ordinate in the object (this is just the time lag).

The situation is still more complicated. There are not only differences of the transit times between signals belonging to separate (different) categories “solid conduction” and “radiation” but also within the single category “conduction heat transfer” and “radiative transfer”.

In the category, “radiative transfer”, photons propagate on randomly distributed paths from their source (the event, like a temperature variation) to their images (received by a detector). Different transit lengths or transit times (the spatial and time distribution of the images, i.e. the dimension of the corresponding clouds) are observed if the radiative transit occurs by absorption/remission or by only scattering. The difference becomes important in particular under strong scattering contributions to radiation heat transfer.

In a previous paper [12], we have described the possible correlation of events, e(s, ζ), like a temperature variation occurring at a positon, s, at an instant, ζ, with corresponding images of this variation in transparent and non-transparent media. The correlation was realised by means of mapping functions. This method shall help to find a solution of the temporal problem in multi-component heat transfer. Only its most important aspects shall be repeated here.

Let an event e_i(s_i, ζ_i) occur in R³ at a position, s_i. All positions (end points of vectors, s_i) shall be assigned real numbers. Real numbers are an extension of rational numbers; rational plus irrational numbers constitute the body of real numbers. Mapping functions create images, f[e_i(s_i, ζ_i)], of this event or of an arbitrarily large number of events, e_i(s_i, ζ_i), again in R³. Only if images, f[e_i(s_i, ζ_i)], of all events exist, regardless of their number, if the medium is transparent and if the images are “dense”, we can speak of uniquely defined physical time scales.

“Dense” means: Like the set of real numbers in the space R³. In the mathematical sense, there is, between two arbitrarily selected, real numbers (elements of the set R³) an infinitely large number of other elements of the same set, with infinitely small differences between two, strictly speaking: between any of these. In contrast to rational numbers, real numbers have special topological properties that allow them to be associated with e.g. length or area of very diversely structured objects. If the elements of a timescale really were rational numbers, irrational or transcendent numbers like 2^1/2, π, e and others would be excluded. But length of a path of a radiation beam, when defining “elements” of the “cloud” in Fig. 2b, may well depend on π.

The analogy between the above-mentioned images and the elements of the set R³ ends when a physically observable, non-zero difference between any of the elements of the timescale (the images) no longer can be identified. An absolutely lower physical limit of the differences between the images, if it exists, cannot be explained from solely standard Radiative Transfer Theory but must take into account that the images in reality are wave packets the extensions of which are subject to the uncertainty principle.

Physical timescales, t, exist only under these conditions (unlimited number of events, dense images thereof). While mapping functions, f[e_i(s_i, ζ_i)], in transparent objects are bijective, and the images thus are logically ordered (by their succession) and dense, this cannot be fulfilled in non-transparent objects.

Accordingly, physical timescales, the scales themselves, are not uniquely defined. Timescales to exist need a dense and ordered sequence of images.

It is also this lack that causes radiative transfer to be incomplete. Strictly speaking, this concerns heat transfer in general, and becomes the more important the more scattering and other heat transfer mechanisms contribute to the transfer problem.

Standard radiative transfer, and thus also heat transfer in general, presently accounts for energetic aspects, not of the temporal aspect of heat flow. The temporal aspect in radiative transfer will now be considered.

4 Radiative Transfer in Superconductors

Radiative transfer has thoroughly been treated in traditional volumes like Chandrasekhar [16], Sparrow and Cess [17] or, more application-related, by Siegel and Howell [21] and also in a large variety of highly qualified papers; we mention here only the work of Viskanta and Grosh, and Yuen [20, 22, 23]. There is also the plethora of investigations of radiative transfer in atmospheric physics and in astronomy.

But the temporal aspect in radiative transfer has been given less attention. In Sect. 21.6 of [21] and citations therein, only radiation propagation under absorption/remission (no other modes of heat transfer) is considered in the time-dependent equation of radiative transfer. There is just a short notice in a paper by Klemens [24], but P. G. Klemens without any doubt was aware of the problem. There are a few papers that explicitly consider this aspect in measurements of the thermal diffusivity of thin films by laser flash and related techniques but there the focus is on limitation of length of the initial, incident laser pulse in relation to the transit time of the initiated, conductive heat flow; both must not interfere.

4.1 Conservation of Energy

Let a beam or a temperature wave front (Fig. 2a, b, schematic) originally emitted at (z = 0, t = 0) propagate through a non-transparent medium. In the literature, radiative transfer (RT) calculations usually apply constant values of Albedo of single scattering, Ω, and constant (scattering) anisotropy factor, m_S. Few publications consider wavelength or temperature-dependent extinction coefficients, albedo and anisotropy factor.

But even slight variations of geometry, composition and index of refraction of an absorbing/remitting and scattering object that frequently are observed in real particulate media, and the corresponding variations of the scattering parameter, x = π d/Λ (with d the diameter of the object, Λ the wavelength), lead to strong variations of the absorption and scattering cross sections and of the scattering phase functions. Compare Bohren and Huffmann [25], Chap. 8, or Figure 20.10 in Siegel and Howell [21] for the scattering phase function, or other traditional references like the volumes by van de Hulst [26] and Kerker [27], in all these volumes mostly for visible wavelengths. But the same rules apply to the mid-IR spectrum.

We will account for such variations (Sections 4.5 and 6) by assuming random fluctuations of refractive index and albedo around their theoretical or widely accepted, experimental mean values. In the present paper, the mean values are obtained by application of rigorous scattering theory to YBaCuO 123 and to BSCCO 2212 and 2223 [12] (the fluctuations are the same as explained in our previous papers).

Thin-film superconductor material (probably all solid superconductors) can be understood as a particulate medium, not a particulate medium in the common, solid materials but in the radiative sense: It is sufficient that local variations of optical properties and density can be described as a quasi-particulate, cell structure in space; compare Figures 6a,b and 7a–c in [12]. We thus do not need a detailed description of the properties of solid/solid contacts, cracks or pinholes or other material irregularities and their distribution in the object.

For modelling the radiation/solid particle interactions, the cells can be divided into cylindrical substructures (compare [12], Figure 13), and since the mid-IR wavelength is large against these substructures, the material can be assumed a macroscopic continuum with respect to interaction with, and propagation of, radiation. With the small radiation parameters, x = πd/Λ, in the order 10⁻², this enormously simplifies the radiative transfer problem.

Sample geometry, finite element mesh and paths of absorbed/remitted or solely scattered beams are schematically indicated in Fig. 6, part b. The different lengths of the principal axes of the ellipses schematically indicate forward scattering, a condition fulfilled in the YBaCuO 123 superconductor under mid-IR radiation. This is because the dimension of the obstacles, the quasi-particulate cells and their sub-structures, in the radiative sense are comparable to or larger than the thermal mid-IR wavelength (27 to 32 μm, within 77 to 92 K; in the literature, this is called the region of “Mie scattering”).

4.2 Standard Radiative Transfer Theory

The theory of radiative transfer and the radiative diffusion model are explained in [15,16,17,18]. Applications to thin films, single fibres and multi-filamentary superconductors have been described previously [5,6,7,8,9,10,11,12,13,14]; details will not be repeated here. In short, heat transfer including radiation requests the simultaneous solutions of

• The equation of radiative transfer (the ERT)

• The equation of conservation of energy (the “energy equation”)

• (a) Structure of the ERT

Omitting for simplicity the wavelength index, Λ, the ERT within the object under study reads, see e.g. Eq. (20.56) in [21].

$$ di\hbox{'}\left(\tau \right)/ d\tau =-i\hbox{'}\left(\tau \right)+\left[\left(1-\varOmega \right)\ i{\hbox{'}}_{\mathrm{BB}}\left(\tau \right)+\varOmega /\left(4\pi \right)\int \Psi\ \left({\omega}_{\mathrm{i}},\omega, \tau \right)\ i\hbox{'}\left(\tau \right)\ d\omega \right] $$

(4a)

with i′ the directional intensity; τ the optical thickness; dτ = E ds, E the extinction coefficient, E = A + S, with A and S the absorption and scattering coefficients, and ds a differential of the radiation path length; i′_BB the directional, black body (BB) intensity; Ω = S/E the Albedo of single scattering; and Ψ the scattering phase function. The quantities ω_i (incident radiation) and ω indicate solid angles.

But is it really black body radiation, with its spectral and directional intensity, that is emitted from a superconductor? Can we successfully apply an emission coefficient to modify i′_BB in order to approach the superconductor materials, specific radiative properties? These questions come up also in the diffusion approximation to Eq. (4a): Its derivation and the T⁴-dependence of the hemispherical emission (and the radiative conductivity with its T³-dependence) reflect the Planck radiation function.

The diffusion approximation to Eq. (4a) applies experimentally determined, complex refractive index (available in the literature as spectral values) and the absorption and scattering coefficients calculated from application of rigorous scattering (Mie) theory, as explained in [12]. It is the obtained success that justifies this procedure when the same calculation scheme previously was applied to a large variety of ceramic and glass particulates: Surprisingly, good coincidence of calculated and experimental values was obtained when extinction coefficients calculated using rigorous scattering theory were compared with values derived from heat transfer experiments interpreted in terms of the diffusion model and from spectroscopy.

The scattering phase function, Ψ, in Eq. (4a) either is measured or again is calculated from application of rigorous scattering (Mie) theory. This yields the scattering coefficients, S, taking account the grain structure of YBaCuO 123. The scattering integral is to be taken over the unit sphere; scattering in thermal transport problems usually is understood as elastic scattering. For details of the calculations, see again [12]. The result for YBaCuO 123 is shown in Fig. 8a of the present paper.

Fig. 8

a Scattering phase function, Ψ, calculated from a total set of bundles (M = 10⁵) in the Monte Carlo simulation and with random values R(θ) in Eq. (16). The phase function is represented by the number of bundles, n(θ), scattered under angles, θ, within the conductor against surface normal of the concentric rings (generated by rotation of the plane elements, Fig. 6, part b). Results apply to the 2-μm thin-film YBaCuO 123 superconductor and are given for different values of the (scattering) anisotropy factor, m_S, at mid positions within Δθ = 10 deg intervals. As before, the larger the values of m_S, the more bundles are concentrated at small (forward) scattering angles. When m_S = 162 (light-grey diamonds), the bundles are sharply focussed to θ < 10 deg. b Mean value, μ_m = cos(φ)_m of the random, individual cos(φ) values obtained for individual bundles of the total set M = 10⁵. Results are calculated using the scattering phase function in a

The terms in the square brackets in Eqs. (4a) and (4b), the source function, result from absorption/remission and scattering within the object. If the source function is omitted, Eqs. (4a) and (4b) reduce to the well-known Lambert-Beer’s law that describes attenuation of directional intensity, i′, which means transmission of a beam goes to zero if the optical thickness, τ, is large.

Solutions for i′(τ) obtained from Eqs. (4a) and (4b) provide the spatial distribution of the total (absorbed/remitted plus scattered) radiation field. For coupling of the radiation field to the temperature field in the same object, which means to the “energy equation”, Eq. (5), the radiation has to be restricted to only the absorbed/remitted part of the radiation. Accordingly, we need solutions of

$$ di^{\prime}\left(\tau \right)/ d\tau =-i^{\prime}\left(\tau \right)+\left[\left(1-\varOmega \right)\ i{\prime}_{\mathrm{BB}}\left(\tau \right)\right] $$

(4b)

for Ω < 1. When this intensity (i.e. the corresponding radiative flux, see below) is inserted into the energy equation, it delivers the temperature field, T(x, y, t), in the superconductor.

Any variation of the temperature field is reflected by variations of a large number of variables, not only critical current density but specific heat, index of refraction, critical lower and upper magnetic fields, penetration depths, optical properties and others. Exact determination of superconductor temperature accordingly is complicated, and in many cases the radiative transfer problem cannot be solved at all.

• (b) Conservation of energy accordingly requests

$$ {\rho c}_{\mathrm{p}}\partial T/\partial t=\mathbf{\operatorname{div}}\left({\dot{\mathbf{q}}}_{\mathrm{Cond}}+{\dot{\mathbf{q}}}_{\mathrm{Rad}}\right) $$

(5)

to be solved. In Eq. (5), ${\dot{\mathbf{q}}}_{\mathrm{Cond}}$ + ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ denote heat flux vectors due to conduction and radiation, respectively. Like the ERT in Eqs. (4a) and (4b), this again is the standard formulation. Radiative sources, internal to the object or located outside, will be considered below.

Under stationary conditions, ∂T/∂t = 0, and again neglecting the wavelength index (and also a temperature dependency of the absorption coefficient, A), we have in each volume element of the object

$$ {\displaystyle \begin{array}{c}\mathbf{\operatorname{div}}\left({\dot{\mathbf{q}}}_{\mathrm{Rad}}\right)=4\ A\ \sigma\ {n}^2{T}^4-\mathrm{A}\int \mathrm{i}\hbox{'}\Psi \mathrm{d}\upomega \\ {}\kern4.66em =-\mathbf{\operatorname{div}}\left({\dot{\mathbf{q}}}_{\mathrm{Cond}}\right)\end{array}} $$

(6)

with σ the Stephan-Boltzmann constant and n the refractive index. For derivation of Eq. (6), see again [21]. It is again assumed that emission from the volume element is by black body radiation. With superconductors, this is largely correct (and, as mentioned above, has been confirmed in radiative transfer calculations with other ceramic substances). But if there is emission of radiation from coatings contacting the superconductor thin film, the situation is different; see later.

Both heat fluxes, ${\dot{\mathbf{q}}}_{\mathrm{Cond}}$ and ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ (with ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ including solely absorbed/remitted, not scattered, radiation), depend on temperature. They therefore are coupled to each other by the calculated transient temperature, Eq. (5), within the object.

The conduction component, ${\dot{\mathbf{q}}}_{\mathrm{Cond}}$, is given by Fourier’s conduction law. The term ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ is obtained from the integral taken over all solid angles of the directional intensity i′(τ),

$$ {\dot{\mathbf{q}}}_{\mathrm{Rad}}=\int i\hbox{'}\Psi\ d\omega $$

(7)

If there is only black body radiation, i′ is to be replaced by i′_BB, not including any contributions from scattering. If there is also scattering, Eqs. (4a), (4b), (5) and (7) have to be modified (e.g. by the matrix formulation suggested later in this paper, Section 4.4).

Sources located within the thin film, if any, not necessarily are constant but in superconductors may oscillate like flux flow or Ohmic losses under alternating transport currents or under variations of magnetic fields.

In standard theory of radiative transfer, the spectral distribution emitted within the superconductor either is of the black body type, for all internal sources and, if so, it only then can be integrated into (local) terms (1 − Ω)i′_BB(τ) in Eqs. (4a) and (4b). Or the black body radiation as mentioned has to be replaced by an approximation that takes into account different (directional) intensity and angular distributions of the emitted radiation.

A different solution has to be found if radiation is generated outside the superconductor, like in metallic coatings (stabilisers) of the superconductor thin film in which heat pulses arising from excess current and the Ohmic resistances of this material may be generated (excess current is the current that exceeds critical current, like during a fault; we then have current sharing between superconductor and stabiliser).

While solutions, exact or as approximations, can be found for all these radiative transfer aspects, the real problem in Eqs. (4a) and (4b) is that the variation of the directional intensity, di′(τ)/dτ, with optical thickness assumes that both absorbed/remitted and scattered radiation, after a differential path length (or over macroscopic distances), simultaneously arrive at given positions dτ or τ = ∫ E ds. This is the completeness problem of radiative transfer since it is not clear that the assumption is fulfilled. This will be demonstrated by Monte Carlo simulations of path lengths and transit times for different contributions of absorption/remission and scattering. The results demonstrate (Section 5) that the problem is substantial.

4.3 How to Find Solutions of the ERT in Superconductors

Radiation emitted by stabiliser coatings deposited on superconductor thin films has to be taken into the transfer calculations until a fault current is switched off. But emission from metallic surfaces is not of the black body spectral type; intensity and distribution with wavelength and angular dependence are strongly different; compare Figures 4.5 (dielectrics), 4.7 and 4.8 (metals) in [21]. In this case, the situation can be compared with experiments to determine the thermal diffusivity of thin films of partly transparent or of non-transparent materials, like SiO₂, Al₂O₃, AlN or ZrO₂, as will be discussed in the following.

4.3.1 The Parker and Jenkins Approach to Thin Films

In standard experiments to determine the thermal diffusivity of thin films, short laser pulses (or pulses from other sources) are directed onto the film surface, and transient temperature evolution at its front or rear side is measured with precision. Heat transfer within the thin film then is considered as by conduction only (as we will see immediately, this is not necessarily fulfilled).

The analysis appears to be straightforward: A series expansion of the temperature on the front or rear sample side is applied to solve the 1D or 2D Fourier’s differential equations under a transient heat source (the pulse). Uniform temperature at either sample side, and vanishing penetration depth of the beam, also are standard assumptions. Compare the frequently cited paper by Parker and Jenkins [28].

But if, for example, a 1-mm ZrO₂ pellet is irradiated at the sample front side with a 1-J laser pulse during 8 ns, quite a practical situation in such experiments, and if the cross section of the beam is finite, numerical (finite element) simulation shows that temperature at the rear surface is not uniform, contrary to the 1D assumption made in [28]. The real situation is shown in Figure 6b,c in [29], which indicates application of 1D heat transfer in thin films means a considerable risk.

To avoid direct penetration of the radiation pulse (and continue with the “solely conduction” assumption), it was suggested in the 1980s to prepare thin opaque coatings onto the sample. As opaque coatings of thickness, ζ, black paint or plasma sprayed or otherwise deposited TiO₂ layers are candidates. From a practical viewpoint, this method to determine thermal diffusivity of thin films, as an alternative to the original, Parker and Jenkins approach, seems plausible; such coatings can easily be prepared, but the analysis now becomes definitely more complicated:

For measurement of thermal diffusivity, by comparison of RT theory predictions with experiment, and for description of RT through the total thickness of the thin film (including its coating), a term (1 − R)A_ζ i′(τ = 0, t) exp(− τ_ζ) occasionally is added to the ERT, with the factor (1 − R) the part of the impinging radiation that is not reflected. A_ζ denotes the absorption coefficient of the coating. The radiation pulse quickly decays since the coating is prepared as non-transparent to the incoming wavelength; the decay at this wavelength is described by the exponential factor, exp(− τ_ζ), Beer’s law, with τ_ζ = (A_ζ + S_ζ)ζ the optical thickness.

The idea accordingly is that radiation transport within the thin black, surface coating disappears at the co-ordinate x = ζ, and the temperature can be coupled at this co-ordinate to solely conduction heat transfer in the proper, semi-transparent or non-transparent ZrO₂ film. This is a risky procedure.

4.3.2 The Thin-Film Superconductor as a Parallel to the Parker and Jenkins Approach

In thin-film superconductors, with reference to the physics of RT, we roughly can distinguish three layers generated during film preparation (Fig. 9a): We have thin boundary layers each of about 100 to 150 nm thickness that in the simulations account for irregularities of the material properties arising from substrate, superconductor thin film and stabiliser. The solid/solid contacts can be modelled with random variations of electric and thermal transport parameters within the thin boundary layers against the superconductor thin film core.

Fig. 9

a Cross section of the 2-μm superconductor thin film (schematic) with microscopic, superconductor boundary (interfacial) layers (light blue) of about 0.1 to 0.15 μm thickness and the (proper) superconductor core (dark blue). Orientation of the z-axis in the co-ordinate system in Fig. 6 (part a and b) is parallel to the arrows (directional intensities, dI′). The superconductor to the right is in solid/solid contact to a metallic coating (dark grey) that is used as a stabilizer against quench for current sharing. On the left, it is in contact to the substrate (not shown). Differential volumes dV, dV′ and dV″ (from left to right, size strongly exaggerated) are taken as examples among a total of up to N_El = 10⁵ finite elements (area or volume elements). During each interaction within any dV’, a beam arriving a these volume elements is split into absorbed/remitted and scattered parts, as indicated by the local Albedo, Ω. Remitted radiation proceeds with a speed much smaller, by orders of magnitude, than scattered radiation. Transit time t_Trans in Fig. 13a applies to the residual scattered radiation. b Hemispherical spectral emissive power, e_λb (solid blue circles, schematic), of black body radiation into vacuum. The e_λb are calculated using the Planck formula applied to temperature that increases with time in the superconductor under a short time disturbance (the temperature evolution is shown in part 3 of Fig. 14). The dashed, horizontal red line indicates the e_λb that would be emitted at T = T_Crit = 92 K const. Times θ₁, θ₂,...θ_J, θ_K,...and their sub-divisions t₁, t₂,...t_j, t_j+1, t_j+2...t_N, t_N+1,...t_k−1, t_k of each of the intervals θ_J, θ_K indicate the intervals within which solution of the ERT, Eqs. (4a) and (4b), and the energy equation, Eq. (5), shall be calculated by application of the matrix, Eqs. (9a), (9b), (10a) and (10b)

But complications arise in both applications, the Parker and Jenkins experiment with its improvement (the black coating) and the quasi-layered superconductor thin film:

• (i) While insertion of the term (1 − R)A_ζi′(τ = 0,t) exp(− τ_ζ) describes attenuation of the incoming radiation at this wavelength, the attenuation by absorption, within the coating or, respectively, within the thin boundary layers of the superconductor, invariably initiates remission. We now have to account in both ZrO₂ or superconductor thin films for the full black body spectrum, not only for just one wavelength (the wavelength of the incoming beam).

This finding is contrary to our intention: If there is absorption of an external radiation source in the thin, 100- to 150-nm surface layers, the actual, 1.8-μm superconductor thin-film material, at specific wavelengths, might be semi-transparent in parts of the mid-IR wavelength spectrum. Heat transfer within the thin film then is not only by conduction but also by radiation.

• (ii) The absorption and scattering coefficients, A_ζ and S_ζ, in the thin surface layers can be strongly different from the coefficients A and S within the 1.8-μm superconductor thin film.

It is not clear that the outer layers, ζ, of the superconductor after deposition should have much stronger absorption properties (to become non-transparent at all wavelengths) than the interior of the 1.8-μm thin film; rather, the contrary is to be expected: With thin (e.g. 100 to 150 nm) evaporated or sputtered thin films, or if they are prepared by chemical vapour deposition, homogeneity is not guaranteed, and extinction coefficients are smaller. Application of the Parker and Jenkins method and its solution to the present superconductor problem thus is not possible.

While this appears to be clear from physical and material aspects, more difficulties concerning the solutions of the ERT and of the energy equation are of mathematical origin.

Though it has frequently been reported in the literature, it is obviously not helpful (and even is meaningless) to simply add to the ERT a term containing exp(− τ_ζ,λ), to account for absorption in thin surface layers (like those in Fig. 9a) if the optical properties of which are different from those of the proper thin-film body. Equations like

$$ di{\hbox{'}}_{\varLambda}\left({\tau}_{\varLambda}\right)/{d\tau}_{\varLambda }=-i{\hbox{'}}_{\varLambda}\left({\tau}_{\varLambda}\right)+\left[\left(1-{\varOmega}_{\varLambda}\right)\ i{\hbox{'}}_{b,\varLambda}\left({\tau}_{\varLambda}\right)+{\varOmega}_{\varLambda }/\left(4\pi \right)\int \varPhi\ \left({\omega}_i,\omega, {\tau}_{\varLambda}\right)\ i{\hbox{'}}_{\varLambda}\left({\tau}_{\varLambda}\right)\ d\omega \right]+\left\{\left(1-{R}_{\zeta\ \varLambda,}\right)\ {A}_{\zeta, \varLambda }i{\hbox{'}}_{\varLambda}\left({\tau}_{\zeta \varLambda}\right)\ \exp \left(-{\tau}_{\zeta, \varLambda}\right)\right\} $$

(8)

in which the term enclosed in curly brackets is not constant, cannot be integrated analytically.

Instead, a procedure substantially different from the standard radiation transport theory and from the Parker and Jenkins approach has to be found.

In a first step, this is provided by a Monte Carlo approach to the exact solution of Eqs. (4a) and (4b), if a solution exists at all. This step has been realised in our previous contributions. But the procedure leads to a central problem of radiation heat transfer, the time dependence of the solution when scattering becomes important.

Scattering becomes important if the albedo Ω is large. We have shown in [12] that the albedo of the YBaCuO 123 superconductor exceeds Ω = 0.8 (decreases from about 0.94 to 0.8 within the temperature range between 92 and 91 K, respectively). Near the phase transition, scattering clearly exceeds absorption/remission.

4.3.3 Complications Arising from Scattering

The ERT is absolutely logical formulated and correctly treats the energetic aspect of the radiation transport problem in RT within objects of arbitrary optical thickness. But the temporal aspect of RT becomes a problem, not only when other heat transfer modes exist in parallel to radiation. It is a problem within the theory of RT: In case Ω < 1, the integration of scattered radiation into the source function, I′(τ), in Eqs. (4a) and (4b) assumes that residual, remitted and scattered radiation all are simultaneously incident onto the volume element, dV.

This is clear from the integrated, i.e. common, solution scheme of Eqs. (4a), (4b) and (5). Solutions are performed on a common timescale since the ERT contains one and only one time variable.

A radiation detector positioned in the volume dV (Fig. 9a), if it is not in solid/solid contact to the material, would receive radiation signals at the co-ordinate z from different radiation sources: By emission from the surrounding solid material in dV (when it is heated by conduction between dV′ and dV), and by absorbed/remitted and scattered radiation both originating from position z′ in dV′.

Scattered radiation directed from any volume element dV″ or dV′ onto the element dV (Fig. 9a) propagates by the velocity of light, while absorption/remission (and the parallel conduction heat flow) proceeds with finite, much smaller diffusion-like velocity.

If the material is non-transparent, an observer, if he is positioned within the volume dV (Fig. 9a), cannot distinguish between radiation emitted (from dV) and absorbed/remitted and scattered (from dV′ and dV″) volume elements, neither by consideration of angular distributions nor by measurement of transit times that remitted and scattered radiation need to travel from dV′ and dV″ to dV, or by differentiation between wavelengths of both remitted and scattered radiation. It is solely by mid-IR wavelength that all radiation arrives at dV (elastic scattering excludes any wavelength shift).

4.4 A series of ERTs and energy equations

As a way out of the problem, we suggest a matrix the elements of which are of the ERT and energy equation type. For this purpose, Eqs. (4a), (4b) and (5) are applied to formulate a series of ERTs and, correspondingly, a series of energy equations each of which is defined in separate time intervals, Δθ_K,J that are adjusted to the different transit times and corresponding values of the albedo. The intervals are between times θ₁, θ₂, θ₃, ... as schematically shown in Fig. 9b, like Δθ_K,j = Δθ_2,1 = θ₂ − θ₁, all within the three regions that cover the surface layers and the proper core of the superconductor thin film.

The series consists of equations

$$ di{\hbox{'}}_{i,\varLambda}\left({\tau}_{\varLambda}\right)/{d\tau}_{\varLambda }=-i{\hbox{'}}_{i,\varLambda}\left({\tau}_{\varLambda}\right)+{\varOmega}_{\varLambda }/\left(4\pi \right)\int \varPsi\ \left({\omega}_i,\omega, {\tau}_{\varLambda}\right)\ i{\hbox{'}}_i{,}_{\varLambda}\left({\tau}_{\varLambda}\right)\ d\omega $$

(9a)

for the case Ω = 1 and

$$ di{\prime}_{j,\varLambda}\left({\tau}_{\varLambda}\right)/{d\tau}_{\varLambda }=-i{\prime}_{j,\varLambda}\left({\tau}_{\varLambda}\right)+i{\prime}_{BB,j,\varLambda}\left({\tau}_{\varLambda}\right) $$

(9b)

for Ω=0 and of Eq. (4a) in case we have 0 < Ω_Λ < 1, all formulated at appropriate times t_i, t_j, and wavelengths, Λ. The t_i, t_j belong to those time intervals within which absorption/remission and scattering or only absorption/remission, respectively, contribute to radiative transfer. The same applies to the corresponding set of energy equations,

$$ \rho\ {c}_{\mathrm{p}}\partial T\ \left({t}_i\right)/\partial t=\mathbf{\operatorname{div}}\left[{\dot{\mathbf{q}}}_{\mathrm{Cond}}\left({t}_i\right)\right] $$

(10a)

for the case Ω = 1 and

$$ \rho\ {c}_{\mathrm{p}}\partial T\ \left({t}_j\right)/\partial t=\mathbf{\operatorname{div}}\left[{\dot{\mathbf{q}}}_{\mathrm{Cond}}\left({t}_j\right)+{\dot{\mathbf{q}}}_{\mathrm{Rad},\mathrm{BB}}\left({t}_j\right)\right] $$

(10b)

again for Ω = 0 and (Eq. 5) for 0 < Ω < 1.

The matrix thus is split into two sets (intervals) that correspond to different source functions, transit times, different radiation propagation mechanisms, wavelengths, and energy equations. With its specification of transit time intervals (t_i, t_j) within which Eqs. (9a), (10a) shall be applied, the procedure has some similarity to the telegraph equation. By a time-loop, the method separates “fast” from “slow” transport phenomena in combined solid conduction and radiation heat transfer. By this method, the problem resulting from the different transit times of conduction and radiation, from dV′ or dV″ to dV in Fig. 9a, can be circumvented.

In this scheme, boundary conditions (intensity, temperature) applied within the intervals replace modelling exponential decay of radiation absorbed and remitted in the surface layers and in the core of the superconductor.

The matrix concept, Eqs. (9a), (9b), (10a) and (10b), to solve the combined solid conduction/radiation transport problem at every instant, t_i, t_j, of course is laborious. But if the object under study is non-transparent, modelling of radiative transfer drastically simplifies to diffusion solutions, and the concept reveals an ideal condition for application of Monte Carlo (for radiative contributions) combined with finite element (for conduction heat flow) simulations.

We have applied the combined Monte Carlo/finite element calculations first to thin ceramic films to remotely determine their thermal diffusivity [29]. Though laborious, tests of the matrix concept were promising, here without phase transitions and applied to 10 to 15 intervals. When the same calculations are applied to the superconductors, the matrix concept delivers also the number of interactions, N, during transit path (Fig. 11) and length L of transit path and of transit time t_Trans (Fig. 13a) and their standard deviations, σ (Fig. 10b), all from the Monte Carlo simulation. The results indicate the dimension of the cloud of statistical uncertainties during propagation of mid-IR radiation through the superconductor, see Sect. 5.

Fig. 10

a Conductor temperature, T(x, y, t), nodal values (light-green solid circles), at the centre of the target (x = 0, z = 0). The results are calculated for adiabatic conditions and conduction plus radiation (diffusive) heat transfer. Temperature is plotted vs. time after start of single, isolated disturbances. A rectangular heat pulse of total Q = M 1.25 10⁻¹² Ws, using the factor M indicated in the figure, is incident on the target at t ≥ 0, with total duration of 8 ns. The results are part of Fig. 7 when M = 1. The curves again apply uncertainties of the electrical/magnetic critical parameters of T_Crit, B_Crit, J_Crit and of the anisotropy factor, r (these are the “standard” uncertainties in the simulations; compare text and caption of Fig. 19 in Appendix 2). Solid circles are obtained without fluctuation of the solid thermal conductivity, λ_Cond. In contrast, fluctuations Δλ_Cond = ± 5% (constant) of λ_Cond yield the coloured diamonds. b Stability function, Φ(t), calculated from Eqs. (2a) and (2b) using the superconductor temperature distribution, T(x, y, t), in the (x, y)-conductor plane in Fig. 10a. Results are calculated for adiabatic conditions and conduction plus radiation (diffusive) heat transfer. The stability function is shown for only level i = 1 (Fig. 6, part c, the coloured elements). The c-axis component of the critical current density is oriented perpendicular to the (dominating) current flow direction through the (x,z)-conductor cross section. As a rough estimate, J_Crit,c ≈ J_Crit,ab/10 has been applied in the simulations (r = 10); compare text for the selection of the z-direction. Identification of the curves and of the uncertainties is the same as in Fig. 10a. The light-green, solid circles are obtained without fluctuation of the solid thermal conductivity. In contrast, coloured diamonds in this figure result from ± 5% fluctuation of λ_Cond. For the magnitude of the heat pulses, see caption to Fig. 10a. The stability function in the elements of layer i = 1 is small for all M. With M = 10 (red diamonds), theoretically, about 96% of the critical transport current (of density J_Crit,c) would be predicted as zero-loss current in this (the z) direction. The percentage of zero-loss current transport in the (standard) ab-plane is much smaller

Besides statistical fluctuations of λ_Cond, a random distribution of the values of the Albedo scattered around its mean value obtained from rigorous scattering theory, has been applied.

Fig. 11

Number N of interactions per bundle (arithmetic mean values, obtained in the Monte Carlo simulations). During each interaction, part of the radiation is absorbed, while the beam proceeds with the residual, scattered part. The N are shown for bundles along their transition paths, L, through the 2-μm YBaCuO 123 superconductor thin film. Results (solid black diamonds) are plotted against radiation temperature (see text for explanation). The results apply to the optical properties of the thin film using extinction coefficients E₁ = E₃ = 3.417 10⁶ and E₂ = 1.409 10⁷ 1/m, respectively (the values are taken from [12]; indices 1 and 3 apply to the 0.1-μm surface layers, the index 2 to the 1.8-μm core of the thin film). Albedo Ω = 0.912 const and different values of the (scattering) anisotropy factor m_S1 = m_S3 = 2, m_S2 = 6 in layers 1, 2 and 3 are used in the simulations (the m_S = 6 value indicates moderately forward, m_S = 2 approximately isotropic scattering). The calculations are performed with a set of in total M = 10⁵ bundles. For comparison, the dashed lines indicate results obtained with hypothetical values of the albedo Ω = 1 (pure scattering) and Ω = 0.001 (almost complete absorption/remission). The case Ω = 1 reflects the number of interactions that approximately would be observed in a BSCCO 2212, strongly scattering superconductor thin film of same thickness

Fig. 12

Check of the impact of the (scattering) anisotropy factor, m_S, on the number N of interactions (absorption/remission, scattering) per bundle that it experiences on its transit path through the 2-μm YBaCuO 123 superconductor thin film. The diagram shows results for the first 100 (of in total M = 5 10⁴) bundles. Mean values of N can be identified from the small dashed lines visible within the light-blue circles

Results of these calculations, the corresponding stability functions, and comparison of the results obtained when only the "standard" uncertainties (of T_Crit, B_Crit, J_Crit and of the anisotropy factor, r) are applied, are shown in Fig. 7a,b.

4.5 Application of the Combined Monte Carlo/Finite Element Method

Stability functions shall be calculated in the following for again the coated thin-film, YBaCuO 123 superconductor. All thermal and optical parameters are taken from previous papers, and the radiation propagation scheme in the Monte Carlo simulation is explained in Fig. 6, part b. Against Fig. 6a, the finite element scheme has been reduced by extracting the superconductor thin-film cross section (plus its contact layers to substrate and stabiliser) from the complete, original scheme applied in [11], the 100 turns coil.

Figure 10a shows nodal temperature vs. time calculated in the centre of the target (solid, light-green circles), z = 0. Results are obtained under single, local disturbances, here the deposition of a rectangular heat pulse of in total Q = M 1.25 10⁻¹² Ws incident onto the target surface at t ≥ 0 during in total 8 ns, with 1 ≤ M ≤ 10.

An example for the physical background of the rectangular pulse is a sudden release of mechanical (strain) energy and its transformation to thermal energy in the superconductor, at any length position. For a multi-filamentary superconductor, the rough estimate of Q has been reported previously, Sect. 3.3 in [7] (in the same reference, we also considered the absorption of particle radiation in the YBaCuO thin film). The present estimate for the YBaCuO thin-film sample in principle follows the same procedure and yields Q between 10⁻¹² and 10⁻¹¹ Ws, with a large number of elements during one conductor displacement under a circular (r = 1 μm) target surface.

Distribution of the incident pulse to the heat flow components ${\dot{\mathbf{q}}}_{\mathrm{Cond}}$ and ${\dot{\mathbf{q}}}_{\mathrm{Rad}}$ is not constant but results from the temperature-dependent (coupled) transport mechanisms, under conservation of energy (Eqs. 5, (10a) and (10b). The stability functions, Φ(t), are calculated using Eqs. (2a) and (2b) with the relation between critical current density and temperature,

$$ {J}_{\mathrm{Crit}}\left(T,B\right)={J}_{\mathrm{Crit}}(T)/\left({B}_0+B(t)\right) $$

(11a)

$$ {J}_{\mathrm{Crit}}(T)={J}_{\mathrm{Crit},0}{\left[1\hbox{--} T/{T}_{\mathrm{Crit}}\right]}^n $$

(11b)

with the exponent n = 2 (compare [5] and the original literature cited therein). Results are shown in Fig. 10b. Values of B₀ (constant) and B(t) = B(x, y, t) are taken from previous papers.

In standard calculations of zero-loss current transport, the cross section A in Eq. (3a) usually is the superconductor part of the total conductor cross section (wire, thin-film or multi-filamentary conductors) assuming uniform material properties. The calculations in the present paper shall be extended to incorporate also fluctuations of superconductor electric/magnetic and thermal parameters (here, the solid conductivity, λ_Cond), separately and independently and different in each of the elements (not uniform in the total superconductor cross section).

However, the finite element code (Ansys) accepts a maximum number of only 100 elements that can be modified in this sense. The analysis thus has to be performed with the limited number of modified elements (100) taken as the statistical sample of the much larger population (1000) given by all superconductor elements.

A first result has been shown in Fig. 5a. There, the stability curve (black crosses) obtained with random fluctuations of the solid conductivity, λ_Cond, of ± 5% of the experimental value, at random positions in the total conductor cross section, is almost identical with the coloured curves (diamonds) with only the standard uncertainties of the electrical/magnetic critical parameters T_Crit, B_Crit and J_Crit and of the anisotropy parameter, χ (all these are schematically described in Fig. 19).

In general, a significant temperature rise is observed only at small (x- and z-) co-ordinates (Figs. 7 and 10a) while the temperature outside this region remains close to the start temperature; this results, besides reasons mentioned above, from the small, solid conduction thermal diffusivity of the YBaCuO 123 material (between 10⁻⁶ and 10⁻⁵ m²/s) in this range of temperature (the upper curve in Figure 5 of [7]).

The expected stability function (obtained by the integral over the (x, z-) cross section of the target), therefore, would be small, a favourable result for zero-loss current transport, but as mentioned does not negate the existence of hot spots existing elsewhere in the total conductor cross section.

The conclusion from this first homogeneity study is as follows: For current transport in the ab-plane (item 1 in the inset of Fig. 6, part a), on the statistical level given by (a) maximum 100 modified elements of 1000 in the superconductor cross section of turn 98, (b) the ± 5% uncertainty of λ_Cond, (c) the (standard) variations of the electric/magnetic superconductor critical parameters (as indicated in Fig. 19 of Appendix 2) and (d) the position A or B where the disturbance is applied (a sudden heat pulse), the thus initiated uncertainties have almost no impacts on the stability functions provided the strength of the disturbance (here the total heat pulses, Q) is kept constant. This conclusion is confirmed in the other test in Fig. 5a where flux flow losses after a sudden increase of transport current to a fault are responsible for the strong temperature increase.

However, temperature distributions definitely depend on the positions A or B or others. It would be interesting to check the situation with a larger number of randomly distributed elements.

A significant difference exists between the simulations in Figs. 3 and 5a, b and Fig. 10a, b in the following study:

While the direction of transport current is parallel to the symmetry axis of the wire (Fig. 3) or parallel to the z-direction, the current in the crystallographic ab-plane in Fig. 10a, b flows through the rectangular (x,z)-cross section (item 2 in the inset of Fig. 6, part a) and thus is perpendicular to the symmetry axis, r, of the target and to the column of all finite elements below. Transport current thus runs against concentric, approximately axis-symmetrical “cones” (current tangentially hits the cones) that all are of different temperature and thus of different J_Crit.

For orientation of transport current again in the ab-plane, numerical treatment to obtain the stability function is a problem of spherical geometry. Its solution, though very detailed, is straightforward but would be beyond the scope of this paper.

Instead, calculation of the stability function is performed for c-axis oriented critical current density. The component J_Crit,c < < J_Crit,ab then is parallel to the z-axis of the co-ordinate system.

This enormously simplifies the simulations but is sufficient to investigate the impacts on the stability problem if we again assign random values of critical superconductor parameters like J_Crit and of the solid thermal conductivity, λ_Cond, to the elements. The random value distribution will be applied to levels 1 and 2; the levels are defined in Fig. 6, part c. Results of these simulations will be shown later, Fig. 15a,b.

Fig. 13

a Total lengths (average values), L, per bundle of transition path and of transit time, t_Trans (solid black and red diamonds, respectively) in the 2-μm thin-film YBaCuO 123 superconductor using extinction coefficients for dependent and independent scattering, m_S-factors and albedo of the thin, 0.1-μm boundary layers and of the 1.8-μm core of the thin-film superconductor, respectively (all data are from [12]). During each interaction, part of the radiation is absorbed, while the beam proceeds with the residual, scattered part. Both lengths apply to this residual scattered radiation. The Monte Carlo simulation applies M = 5 10⁴ bundles. b Standard deviations of the results obtained for the lengths L and t_Trans in a

Experimental uncertainties, or just manufacturing shortcuts, may again be responsible for random fluctuations, not only of electrical/magnetic critical parameters but also of the solid thermal conductivity and its impacts on the stability function, Φ, now obtained with the z-component of J_Crit. The results (coloured diamonds, fluctuations within ± 5%) are already contained in Fig. 10a, b and again are almost identical. The same applies to Fig. 15a,b (see later) with even stronger fluctuations. All these results confirm the curves in Fig, 10a,b and, later, Fig. 15a,b.

5 Transit Time from Monte Carlo Simulations

The results of the following Monte Carlo simulations quantitatively demonstrate the completeness problem in radiative transfer and allow to estimate the dimensions of the cloud of the images in Fig. 2b.

Transit times have to be calculated under combined solid conductive and radiative transfer propagation mechanisms. The uncertainties, Δt_Lag and both Δt_Fluct and ΔL_Fluct (both indicating the dimensions, in time and length, respectively, of the cloud of images), will be extracted from the results achieved with the Monte Carlo simulation.

We will start with a signal propagating solely by radiation. The transit time, t_Trans, of this signal that it needs to travel from z = 0 to a position z > 0 (here the opposite boundary, z = D, in Fig. 6, part b) in a non-transparent object follows a zigzag path through the object.

If, on the other hand, the signal propagates only by solid conduction, the path, on the microscopic level, is zigzag, too, but with less fluctuations against the (major) direction (here prescribed by the local temperature gradients). Transit time in this case follows from the solution of Fourier’s differential (conduction) equation.

If simultaneously both heat transfer mechanisms are present, a solution for the transit time, from separate calculation of the transit time of both mechanisms, exists only in non-transparent media, as is clear from the preceding sections of this paper: Either component of heat transfer can be treated as if the other is not present.

Under competing heat transfer mechanisms, the total transit time of the combined conduction/radiation heat transfer problem equals the smaller transit time among all the existing heat transfer channels. Trivially, this is not the sum up of the components. Again trivial, one might assume that radiation arrives first, but this is correct only for solely scattering interactions. The situation may be different in case of absorption/remission and scattering if these mechanisms would be mixed along the transition path, in a series of statistically determined, sequential interactions.

For an order of magnitude estimate, transit times instead from Monte Carlo simulations can be obtained also when using an analytical relation between thermal diffusivity and length of the path, L, that excitations have to travel. In case of solely thermal conduction, the transit time, t, derived from Fourier’s differential equation in plane co-ordinates, compare e.g. Eq. 4.3–26 in [30], is related to L by the approximation for a flat slab,

$$ L=C\ {\left({a}_{\mathrm{Th}}t\right)}^{0.5} $$

(12a)

with the transit time, t = t_Trans, that a signal needs to travel the length, L, within the object if there are no heat sources or sinks. In Eq. (12a), the quantity a_th denotes the (standard) thermal diffusivity,

$$ {a}_{\mathrm{Th}}=\lambda /\left(\rho\ {c}_{\mathrm{p}}\right) $$

(13)

with λ, ρ and c_p the thermal conductivity, the density of the solid material and its specific heat, respectively; C denotes a constant; in plane geometry, C = 3.6.

With a signal propagating solely by radiation, the transit time, t, is given in a non-transparent, absorbing/remitting object (no scattering), in analogy to the familiar Eq. (12a),

$$ L=C\ {\left({a}_{\mathrm{Rad}}t\right)}^{0.5} $$

(12b)

provided the radiative conductivity, λ_Rad, and accordingly the radiative diffusivity, a_Rad = λ_Rad/(ρ c_p), exist; this means if the propagation of the radiative signal is solely by diffusion, with accordingly a large absorption coefficient, A = E, to fulfil this condition.

Equation (12b) must be applied only for the absorption/remission part. But if albedo Ω < 1, scattering is not excluded, and the interaction may statistically change at each radiation obstacle from absorption/remission to scattering and vice versa. Application of Eq. (12b) then is not possible. If we keep Ω < 1 constant (no statistical variations), the result from Eq. (12b) yields an upper limit for the transit time. The solution for t_Trans then can be found only from Monte Carlo simulations.

The radiative conductivity, λ_Rad, reads, with a correction to anisotropic scattering by the factor Ω μ_m [31],

$$ {\lambda}_{\mathrm{Rad}}=16\ \sigma\ {n}^2{T}^3/\left[E\ \left(1-\varOmega\ {\mu}_{\mathrm{m}}\right)\right] $$

(14)

For the scattering phase function, Ψ, and the mean value, μ_m, of cos(φ), with φ the scattering angle, see Fig. 8a, b. The factor Ω μ_m in the denominator of Eq. (14) reduces the extinction coefficient to an effective value, which means the radiative contribution may significantly be increased, the diffusivity a_Rad accordingly increased and the transit time, t_Trans, reduced.

With z = 2 μm total conductor thickness, the radiative diffusivity amounts to a_Rad = 3.12 10⁻⁷ and 3.973 10⁻⁷ m²/s of core and 0.1 μm boundary layers, respectively, at temperature close to T_Crit. In case the signal would proceed parallel to the surface normal, we get from this analytical method a total transit time of about 8 10⁻⁷ s. Because of multiple absorption/remission events, the real transit time substantially will be longer. The reader will easily verify that then the transit time might get into conflict with the result obtained if the mechanism is solely by solid conduction (see below).

Results from the Monte Carlo simulation provide the number N of interactions, a mean value per bundle, of the thin superconductor film (Fig. 11). The total length, L, of the transit path (again per bundle, no solid conduction) is given in Fig. 13a (the upper curve).

The length, L, is defined by the sum of all individual (statistical) mean free path lengths during the series of interactions. Summing up is stopped when either the radiation beam (the bundle) is completely absorbed or when it has left the thin film at z = 0 (backward scattering) or at z = 2 μm.

Mean values of N in the thin film are between 25 and 60, with approximately constant l_m, the mean free path of a photon (the mean free path is inversely proportional to the extinction coefficient, E). The total length, L, of the transit path primarily reflects the number N of interactions.

By its definition, optical thickness, dτ = E ds, uses the integral taken over the thickness, D, of the sample (taken normal to parallel boundaries). But the photons are scattered off the surface normal to a zigzag path, which means the number N as well as the length L increase with increasing albedo, Ω. Total length L of the transit path thus strongly (by a multiple of 3 to 4) exceeds the D = 2 μm thickness of the thin film.

The observed large number, N, of interactions is another proof that application of the diffusion model of RT is justified even for the thin-film superconductor. If its extinction coefficient E is large, or l_m is small, this is just the origin of the large N.

The optical thickness, τ = E D = D/l_m, of the film equals N, which means τ is large, namely the said 25 to 60 steps, that strongly exceeds the (approximate) limit τ = 15 above which, by experience, the angular distributions of radiation escaping from the slab become isotropic (in the long run approach the theoretical cos(φ)-distribution; compare Fig. 16 in Section 6.3 and Figs. 17 and 18 in Appendix 2).

Note in Fig. 11 the clear dependency of the number N on the albedo Ω: With increasing absorption/remission (Ω → 0), the number of interactions decreases strongly. This is because bundles are the more extinguished, the smaller the albedo (the larger the absorption coefficient, A = (1 − Ω) E, of the material).

The lower curve in Fig. 13a predicts transit times in the order of 10⁻¹⁴ s. The naive estimate, t_Trans = D/c, with c the velocity of light, approximately yields 1/3 of the Monte Carlo value. This is yet in accordance with the ratio of total lengths, L, of transit paths: Instead of the straight 2 μm (sample thickness), the photons in reality, because of the zigzag path, travel a distance that is longer by the multiple of 3 to 4 (6 to 8 μm, the upper curve in Fig. 13a).

Signals proceeding by solely solid conduction in the 2-μm thin film roughly need t ≈ 10⁻⁷ s.

All these results demonstrate the completeness problem of the ERT (Eq. 4a): Radiation under absorption/remission and scattering cannot arrive simultaneously at positions after differential or macroscopic path lengths, dτ or τ, respectively.

5.1 Dimensions of the Cloud of Images Generated by Single Events

Figure 13b shows standard deviations of path length, σ_L, and of transit time, σ_t; the results are obtained from the data reported in Fig. 13a.

The standard deviation, σ_L, of the path length in Fig. 13b is almost as large as the value of L itself and increases the more the temperature approaches the critical value. The large σ_L not necessarily indicates that the bundles would have left the thin film; there is enough scattering of the bundles to keep most of them within the object.

This observation allows to estimate the uncertainty, ΔL_Fluct, which means the spatial dimension, r_L, of the cloud in Fig. 2b: In the non-transparent object, images of the same event (here the emission of single bundles from the target in the Monte Carlo simulation) are scattered to occupy (end) positions, identified by the path length L, within the superconductor real volume.

The statistical uncertainty of L (its standard deviation from the mean value in Fig. 13a) thus defines a virtual, spatial volume of 3 ≤ r_L ≤ 13 μm in the temperature range given in Fig. 13b. This is the radiative dimension of the (spatial) cloud (Fig. 2b) within which the position of the images (i.e. the correlation with the underlying events) cannot be identified with certainty. In turn, an observer positioned within this volume would not be able to identify individual events, like positions on the target from which the bundles were emitted, or position of a local quench occurring outside the cloud volume, as origins of the images that create the cloud.

The standard deviation, σ_t, of the radiative temporal dimension of the cloud is small, below 2 10⁻¹⁴ s. With a temperature increase dT/dt of up to 10⁸ K/s near the "hot spots" in the conductor cross section, the temperature variation within this period would be below 10⁻⁶ K (whereas the uncertainty of calculated conductor temperature is much larger). At positions outside the hot spot, i. e. in the region that has to be protected against quench, the dT/dt are smaller, by orders of magnitude. But in analogy to the virtual radiative spatial uncertainty volume, there is a non-zero, virtual radiative temporal uncertainty volume within which the position of the images on a common timescale cannot be identified. In the ultimate consequence, this means a common physical timescale, within the temporal volume, cannot exist, cannot uniquely be created from the images located within this volume.

The results shown in Fig. 13a, b are correct if the relaxation time of the superconductor electron system is not too long to allow creation and completion of new thermodynamic equilibrium states during propagation of the heat pulse or of any other disturbance (this is the implicit assumption made in calculation of the curves in this figure; this concerns also Eqs. 12a, (12b) and (14)).

In summary of this subsection, Figs. 11 to 13a, b not only confirm the existence of a time lag and yield estimates of the cloud dimensions. Existence of a corresponding conductive cloud of uncertainties will be investigated in a later paper. Also, from the calculated N and L, it is again concluded that the diffusion model is applicable to the RT in the thin YBaCuO 123 film.

5.2 Comparison with Relaxation Time

How long does it take the electron system to achieve, after a disturbance, a new thermodynamic equilibrium? Figure 1 shows relaxation time in the YBaCuO 123 thin-film superconductors applied in a coil of in total 100 turns [11]. The relaxation time has been calculated using the microscopic stability model that incorporates the four items mentioned in Section 1.1.

As soon as element temperature exceeds 91.925 K, coupling of all electrons in this thin-film superconductor to a new dynamic equilibrium of electron pairs can no longer be completed within the integration times, here 1 or 50 μs in the finite element procedure, indicated as the length of process time intervals (lilac horizontal dashed lines) in Fig. 1. This conflict between physics (relaxation time) and simulation (the integration step length in the FE procedure) may prevent numerical (and also analytical) investigations of superconductor stability near the phase transition: Too long integration steps prevent convergence of the solution scheme. See Sect. 6 in [14].

In addition, Fig. 1 shows that quench is not an event that proceeds instantaneously and that it does no occur simultaneously at several positions. Instead, it is a process the speed of which decreases the more, the closer the superconductor temperature approaches critical temperature. Reduction of electron pair density then becomes slower and slower, with correspondingly extended in time zero-loss current transport.

6 Random Variations of Thin-Film Properties, Impact on Stability and on Thermal Fluctuations

We have to differentiate between two physically different situations that may arise at superconducting/normal-conducting interfaces:

The first is the well-known phenomenon of thermal fluctuations. At the interfaces, within the same superconductor material (not necessarily at superconductor/normal conductor material contacts), swarms of electron pairs are statistically created and may exist above critical temperature. Superconducting/normal-conducting interfaces within the superconductor result from non-uniform temperature distributions under any kind of disturbance or from magnetic flux density above B_Crit,2. Existence of such swarms within the normal conduction region may have substantial impact on its current transport properties.

The second situation is simply due to the existence of different materials in the total conductor cross section. After disturbances, zero loss, flux flow and Ohmic resistances may co-exist (Fig. 9a of the present paper) as well as within single filaments (Figures 2 and 3a,b in [14]).

Simulation of current conductor stability, in this situation, has its focus on variations of material properties at interfaces between the two different material regions.

6.1 Thermal Fluctuations

Thermal fluctuations are considered as the cause for the increase of electrical conductivity in the normal-conducting region of a low-T_Crit superconductor; see the references to the literature given in Chap. 4.8 of [32].

The additional conductance, σ′(T), depends on the temperature difference T − T_Crit (see Eqs. 4-97 to 4-100 in [32]). The striking, smooth course of the curves σ′(T) vs. T in these figures suggest that T_Crit is a constant. The conductance, σ′(T), is believed to exist only temporarily and only locally, in small regions, ξ. There, electron pairs create the more an almost perfect electrical conductivity the closer temperature of this local system, from T > T_Crit, approaches the phase transition.

Where does the increase of the electrical conductivity come from? Equilibrium concentration of electron pairs in the normal-conducting phase should be zero. Yet let us tentatively assume that at T > T_Crit, the increase of electrical conductivity relies on large, non-zero deviations from (the properly) zero equilibrium electron pair concentration. This is because the correspondingly very small probability for its fluctuation at constant T > T_Crit to occur might be overcompensated if local values of dT(x, y, t)/dt, i.e. of temperature variations, would be very large. We indeed have dT/dt exceeding 10⁸ K/s at hot spots, under disturbances, as has been shown in the simulations. The same applies if there are large temperature gradients, grad [T(x, y, t)], like the gradients in the order of 10⁷ K/m shown in Figure 6b of [14]. Both temperature variations could strongly contribute to short-time existence of electron pairs even at T > T_Crit.

It then appears as if the explanation of superconductor stability against quench near critical temperature and the explanation of the increase of electrical conductivity, σ′(T), are correlated with the lifetime of electron pairs.

The lifetime of electron pairs (the relaxation time) is shown in Fig. 1. If the temperature very closely approaches critical temperature, the lifetime of residual electron pairs increases strongly. At local positions, under a fluctuation T > T_Crit, their existence then might be responsible for the additional, overall electrical conductivity, and explanation of stability of superconductors and of the increased electrical conductivity under thermal fluctuations then might go back to a common background:

To clarify the situation, it would be necessary to measure a time dependence, if it exists, of the conductivity, σ′(T), over long periods of time.

6.2 Results for Superconductor/Normal Conductor Interfaces

The impact of fluctuations of these parameters in elements all located inside the core of the thin film has already been simulated in Section 4.5. We now investigate stability with respect to fluctuations of electrical and thermal parameters within the 0.1-μm boundary layers of the thin-film YBaCuO superconductor. The boundary layers are indicated in Fig. 6, part c (the coloured elements).

In Fig. 14a (part of Figure 1 in [11]), the thin-film superconductor and the interfaces were considered as homogeneous, with uniform thermal material properties. But this was a tentative approach that can be improved in the following.

Fig. 14

a Conductor geometry in the superconductor (SC) coil of 100 turns investigated previously; the figure (not to scale) is part of the overall simulation scheme of Figure 1 in [11]). Left: layers in the immediate neighbourhood of the superconductor, the YBaCuO 123 thin film. Right (detail of the left diagram): very thin (interfacial SC/Ag and SC/MgO layers, non-zero volumes of 0.1 μm thickness) instead of zero-volume, shell elements in the FE model are used between SC film and Ag (metallisation) and between SC and MgO (buffer layer). Surface roughness is highly exaggerated. b Part (1) and (2): nodal temperature in turns 96 and 100 of the coil consisting of in total 100 windings. Conductor architecture is indicated in Figure 1 of [11]. Superconductor thin-film thickness is 2 μm; width is 6 mm; thickness and width of Ag elements are the same. Crystallographic c-axis of the YBaCuO layers is vertical to the planes in this figure. The anisotropy factor, r = D_ab/D_c, of the thermal diffusivity is 10. White dashed lines are part of the finite element mesh; narrowly spaced, double lines indicate electrical insulation between the turns. Results are shown at time t = 4.15 (1) and 4.2 ms (2), after the start of the disturbance (flux flow losses; transport current exceeding critical current density). Symbols “MX” and “MN” denote maximum and minimum temperature within the conductor cross section. The large diversity of the local temperature indicates that zero-loss, flux flow and Ohmic resistances regimes in parallel exist in the conductor cross section. Part (3): element temperature (centroid; arithmetic mean of nodal temperature) calculated with ratio I_Transp/I_Crit = 1 but with different r = D_ab/D_c. When r = 10 constant, the figure (copied from Figure 5b in [11]) also illustrates the impact of thickness and of thermal diffusivity of the interfacial layers (IFL) on superconductor temperature: black open circles refer to d_IFL = 40 nm (standard) and λ = 100 W/(m K), as rough estimate made for the SC/Ag interfacial composite; red symbols denote d_IFL = 1 μm and λ = 1 W/(m K), as an extreme case, and the light-green symbols are obtained with the same (increased) IFL thickness and 100 W/(m K), respectively. The red solid circles illustrate that the interfacial layers thermally insulate the superconductor thin films, and superconductor temperature accordingly increases. The fast increase of element temperature during 4.1 ≤ t ≤ 4.15 ms is the higher, the larger r while its sudden decay results from current limiting by the generated Ohmic resistances

Elements of finite volume again are used but with random variations of the materials and transport properties all defined separately in each of the previously mentioned maximum 100 elements (the limit set by the FE program). We do not apply 1D finite element surface shell elements because variations of material properties over element thickness then would not be possible.

This step is the first to fill life into the previously reported attempt to model interfaces between superconductor and stabilisator (metallic layers) by tiny, non-zero volumes [11].

We define in the boundary layers the values of T_Crit, B_Crit, J_Crit and of the thermal parameters, as in [11] and in previous papers, again as random material variables scattered around mean values. In the second step, temperature and temperature variations, dT/dt, obtained in the simulations represent an entity Χ the elements of which all are statistically scattered.

Variations dT/dt in the present paper refer to 0.1 × 0.1 μm², i.e. non-zero finite element cross sections. These cross sections incorporate a large number of ξ_ab ξ_c ≈ 0.0016 × 0.0003 μm² cells using unit cell dimensions of the YBaCuO 123 superconductor. As a large multiple of the elementary cells, the 0.1 × 0.1 μm finite elements can be considered as representative.

Figure 15a shows nodal temperature, T(x, y, t) (coloured, solid diamonds), resulting from random variations of the solid conductivity, λ_Cond, against its experimental (zero fluctuation) values (light-green solid circles).

Fig. 15

a Nodal temperature, T(x, y, t) (coloured diamonds), obtained at z = 0 in the centre of the target at constant incident power (a rectangular heat pulse of in total Q = M 1.25 10⁻¹² Ws, using M = 5, applied at t ≥ 0 onto the circular target, item 2 in Fig. 6, part a, duration 8 ns). Results are shown for the levels i = 1 to 5; for identification, see b. Temperature (again under adiabatic conditions) is obtained for conduction plus radiation (diffusive) heat transfer and random fluctuations, Δλ_Cond, within ± 15% in the elements of level 1 and within 5% in level 2, of the solid thermal conductivity, λ_Cond. Results are compared against zero fluctuation (“ideal”) values of λ_Cond and of T_Crit and with the uncertainties of the other (the “standard”) critical superconductor parameters (light-green, solid circles). The fluctuations possibly interfere with random fluctuations, ΔJ_Crit, within ± 1%, of the critical current density, J_Crit. b Stability function, Φ(t), calculated from Eqs. (2a) and (2b) and like in Fig. 10b using the c-axis component of J_Crit. A rectangular heat pulse of in total Q = M 1.25 10⁻¹² Ws, using M = 5, is incident on the target (z = 0, starting at t ≥ 0) during in total 8 ns. Results using the temperature distribution in a are shown for the levels i = 1 to 5 of the finite element scheme; compare Fig. 6, part b, and for adiabatic conditions and conduction plus radiation (diffusive) heat transfer. The calculations assume random fluctuations, Δλ_Cond, within ± 15 in the elements of level 1 and within ± 5% in level 2, of the solid thermal conductivity, λ_Cond (solid diamonds). Open circles denote fluctuation of ± 5% of λ_Cond in the elements of both levels i = 1 and 2. The fluctuations possibly interfere with those arising from random fluctuations, ΔJ_Crit, within ± 1% of critical current density, J_Crit (the uncertainty ΔJ_Crit of the “standard set”)

Quality of coatings depends strongly on substrate quality and relies on initial growth of the thin films. Roughness has to be filled up before halfway regular structures and tight, clean solid/solid contacts can be created. But fill-up is never complete; there is a considerable, non-zero porosity near the solid/solid contacts. This porosity can roughly be estimated using e. g. the traditional Russell cell model to obtain an effective value of the solid conductivity (we have used this cell model previously in [9] in the suggested, new flux flow resistance model). Imperfect surfaces also allow diffusion of foreign atoms and non-stoichiometric species into the depth of the conductor.

Therefore, irregularities of also the optical parameters in the following have been taken into account by assigning random fluctuations to the extinction coefficient, to albedo, scattering anisotropy factor and refractive index and by application of specific values of the density in the boundary layers and proper thin-film, core material.

6.3 Experimental Data Used in the Simulations

Optical properties of thin films, with thickness substantially below 0.1 μm, are frequently reported from transmission experiments. But hardly no exact experimental values of the highly anisotropic thermal transport properties of thin-film or filamentary superconductors, at cryogenic temperature, are available in the literature.

Measurements of the thermal conductivity of YBaCuO thin-film and of BSCCO multi-filamentary superconductors were performed in a co-operation between ABB Corporate Research and the University of Wuerzburg [33] using three different experimental concepts: Depth-sensitive, non-stationary 3ω measurements (Cahill, 1987), thin-film, stationary thermal resistance measurements in z-direction (Swartz and Pohl, 1987) and a dynamic Angström technique for the measurement of the conductivity in lateral sample direction.

The results obtained for the thermal conductivity and the anisotropy ratio (up to r = 95 at 70 K) in the BSCCO 2223 compound have already been applied in previous stability calculations; see Figure 8 in [9]. For YBaCuO samples, the accuracy of the reported results of this study was better than 10%, a small experimental error in view of the anisotropic transport properties of the thin film.

Accuracy of the thermal conductivity measurements of porous ceramic or glass, powder or fibre substances in general depends very sensitively on parasitic thermal losses; the experimental errors hardly ever are below 10%, even if in standard, stationary experiments with macroscopic samples more than only one guard ring is applied (the samples may act as “thermal mirrors”).

The method would be efficient if it can be shown that the final temperature distributions and stability functions depend only weakly on the assumed irregularities. Small differences seen in the temperature distributions trivially would result in small differences in the stability functions but there are possibly existing, destructive interferences of the impacts that the separate (parallel) variations of e.g. the thermal (λ_Cond) and electrical (J_Crit) parameters might generate.

This assumption is confirmed: The differences of nodal temperature, T(x, y, t), calculated in Fig. 15a with variations of ± 5% of the solid conductivity, λ_Cond, against the (true) zero fluctuation values within the 0.1-μm layer are small. If the fluctuation is within ± 5 or ± 10%, the differences are positive or negative but there are only minute variations of conductor temperature. In an extreme case, the variation of T(x, y, t) amounts to almost − 2.5 K for the fluctuation of the solid conductivity within ± 15%. While this no longer can be neglected in view of the exponential dependence of J_Crit on temperature, the stability functions even then remain almost unchanged provided the incident heat pulse is the same.

6.4 Stability Functions

The stability function, by its definition, should increase with increasing conductor temperature. This can safely be verified only if conductor temperature increases within more or less the whole conductor cross section. By constraints set by the finite element program (100 area elements of in total 1000), the simulation again had to be restricted to variations of the parameters in only the first two levels (the “levels” are indicated by the coloured diamonds in Fig. 6c, counted from below).

The area elements in the two levels, i = 1 and 2, may be considered as the statistical sample of a much larger population. With its dimension (10% of the total population), the result obtained suggests that a similar result, with high probability, would be obtained if the sample is much larger or the analysis could be extended to even 100% of the number of elements.

Accordingly, we have applied random fluctuations of λ_Cond in level 1, i = 1, within ± 15%. This is the level within which the first superconductor layers are deposited directly on the substrate (the corresponding elements are directly contacting the elements of the substrate material, with comparatively large variations of materials, thin-film quality).

In level 2, i = 2, the fluctuation of λ_Cond is expected to become smaller (within ± 5%, that reflect the experimental results from [33]). The corresponding elements gradually converge to the proper λ_Cond of the superconductor thin film core.

Comparison shows that there is hardly any difference between Figs. 10b and 15b if the results obtained with fluctuations of λ_Cond and J_Crit are compared for the same incident heat pulse and with elements of the same levels, i. But this observation is just what is desired for verification of numerical procedures: The results reported in the previous papers, e.g. [11], most likely are confirmed, on a statistical sample/population basis, by this comparison.

In summary, the results shown in Figs. 5a and 10b (total superconductor cross section) and in Fig. 15b (though performed with only levels 1 and 2, as boundary layers) have demonstrated only very weak dependence of the stability function on fluctuations of electrical/magnetic and material parameters. Yet an extension of these investigations to larger samples of randomly selected elements, in which each individually is subject to random parameter fluctuations, would be desirable, in particular to investigate the impact of probably existing interferences if more than only two parameter variations (instead of only of J_Crit and λ_Cond) are considered.

7 Contrasting Radiative Transfer by Quantum Mechanical Entanglement and Entropy

To continue with our attempts to understand superconductor transport properties near the phase transition, a further check of the reliability of the applied simulation models is advisable. For this purpose, a thought-experiment shall be made. It uses a concept that is strongly different from standard physical propagation theory. In particular, it is in total contrast to the numerical models used in this paper.

7.1 Entanglement

Consider the two particle system indicated in Fig. 4, and let its total angular momentum be zero before decay. If after the decay the angular momentum is measured with particle 1, the conjugate quantity, the angular momentum of particle 2, becomes determined with certainty. This observation is not very exciting, it just denotes conservation of angular momentum. But the quantum-mechanical description of this situation leads to a paradox:

If observer O1 does not perform measurements, observer O2 will find the component S_z of particle 2 (moving to the left in Fig. 4) positive or negative, each with probability 1/2. But as soon as O1 measures the S_z of particle 1 (moving to the right) at a time t₀ = 0, and if he, for example, in this measurement finds the plus component, S_z+, observer O2, simultaneously and with certainty, will find the minus component, S_z−, regardless of the distance between particles 1 and 2 and at any time t > t₀.

It is as if particle 2 immediately “knows” that a measurement at particle 1 has been performed. The two particles and their response to experiments (the physical reality) are said to be entangled. “Immediately” means, there is no transport mechanism by which information would become available to observer 2 of particle 2 before he has started his own measurement.

This situation either is the result of an interaction between particles 1 and 2 that proceeds instantly, which means: by infinitely large velocity (provided it is a transport process at all). This explanation would be in conflict with relativity. Or the result (the information on the results of the measurements) is already encoded in particles 1 and 2, by hidden parameters. Since the first explanation can be excluded, and since quantum mechanics does not allow hidden parameter, quantum mechanics would be incomplete.

Causality to exist requests the sequence of cause and effect to be ordered logically, which means both must not occur at exactly the same time. Causality thus cannot be violated in the EPR experiment.

Suggested solutions to solve this paradox still are under controversial debates.

7.2 Entropy, Entanglement, Radiative Transfer, Superconductors—Differences and Parallels

Entropy of the superconductor increases at the superconducting/normal-conducting phase transition, due to the loss of order of the electron system.

Entropy flow in the EPR experiment, at the decay of the “parent” particle, concerns information available about decay and fly-apart of particles 1 and 2. Starting from the pure quantum system (the parent particle), if the separated states of all subsystems (here particles 1 and 2) cannot or shall not be measured, a reduced density matrix can be constructed by tracing over the allowed states of the unobserved subsystems [34]. This yields the entanglement entropy, the von Neumann entropy of the reduced density matrix and reflects the loss of information originally present in the entangled state from quantum correlations.

Entropy flow, dS/dt, under thermal conduction through a flat slab of total thickness, D, at two different positions within the slab, runs parallel to thermal conduction flow [35].

$$ dS\left(z=\zeta \right)/ dt- dS\left(z=\zeta -\delta \right)/ dt=\left[ dT/\left({T}_1{T}_2\right)\right]\ {\dot{q}}_{\mathrm{Cond}} $$

(15)

with δ ≤ D. Because of conservation of energy, the position, ζ, is arbitrary. The rule is heat flow, like ${\dot{q}}_{\mathrm{Cond}}$, is an energy flow that is accompanied by an entropy flow.

Under stationary conditions, ${\dot{q}}_{\mathrm{Cond}}$ = − λ_Cond dT/dx = const. If λ_Cond is small, this gets the temperature difference dT = T₁ − T₂ between z = ζ and z = ζ − δ large (with T₁, T₂ the boundary temperatures of the layer, δ). As a consequence, T₂ is small against T₁. With dT sufficiently large, T₂ small and ${\dot{q}}_{\mathrm{Cond}}$ = const, entropy production in the traditional conduction process becomes large.

Entropy production in thermal conduction is not a constant (and never is zero), but depends on temperature differences. While heat flow is conserved under stationary conditions, this is not the case with entropy.

If radiative transfer can be written as a conduction process, i.e. in a non-transparent object (τ = E D → ∞), radiative flow reads ${\dot{q}}_{\mathrm{Rad}}$ = − λ_Rad dT/dx, provided the radiative conductivity, λ_Rad, exists (it exists if τ is very large and albedo Ω > 0). Both energy flow by conduction and radiation, under this condition (non-transparency), and also entropy flow, are diffusion-like processes.

While elastically scattered radiation does not change the temperature of the scattering obstacles, yet there is a flow of entropy since the spatial distribution of radiation becomes more and more uniformly distributed (approach the ideal cos(φ)-distribution; compare Figs. 16, 17 and 18), and its origin (hemispherical or directional radiation sources, single, point-like or distributed) becomes more and more hidden and thus undeterminable.

Contrary to the rule mentioned above, there is an energy, but not a heat flow parallel to the entropy flow. A heat flow cannot be assigned to pure elastic scattering, yet a corresponding entropy flow exists.

If in the EPR experiment no measurement with particle 1 is performed, the situation can be interpreted as a parallel to the RT situation: Before, in the EPR picture, the measurement of S_z with particle 1 is done, the angular momentum of particle 1 (and of particle 2) is undetermined, like the angular distribution of scattered radiation becomes the more uniform (and its origin the more unknown and undeterminable), the larger the optical thickness.

The space in the EPR picture when no measurement of angular momentum is performed apparently has a property that, in analogy to radiative transfer, can be identified as being quasi-totally “non-transparent”. This changes suddenly once angular momentum or other physical variables are measured; the space then suddenly becomes totally transparent (though corresponding mapping functions would not be bijective). But time lag, Δt_Lag, and uncertainty, Δt_Fluct, are zero.

In superconductors, when an electron pair is excited during an interaction that is strong enough to destroy electron/electron pairing, the decay products (separated but not uncoupled electrons), must find final (allowed) states within the solid. This re-organisation process takes the more time the more states are already occupied. Results obtained from the microscopic stability model suggest that time diverges the more the system approaches the phase transition (Fig. 1).

This process, to arrive at a new equilibrium state, possibly cannot be completed. The situation therefore is completely different from entanglement:

In a superconductor, the process to obtain the new equilibrium proceeds gradually, perhaps with no final completion. Since its optical properties rely on the electron system, the change from non-transparency to transparency, made visible by a transport process in the superconductor, again proceeds gradually.

In entanglement, changes occur suddenly to completion. There is, contrary to the superconductor, no “final” state to which the system in a process would converge.

7.3 Is Radiative Transfer a Complete Theory?

Within radiative transfer, entropy flow related to the radiation transport process is maximum. It becomes most important if the object is non-transparent. But entropy flow cannot be divided into components related to mixtures of absorption/remission and scattering contributions. Obviously, these are tightly related to each other, by the statistical ratio, Ω, of scattering to total radiation extinction.

Entropy from its definition is a unique integral quantity. In the system “superconductor”, there is no entropy that separately might integrate both components (solid conduction and radiation) to a total entropy, by assuming both entropy components could be defined as if the other is not present.

If Ω < 1, we can in Eqs. (1) and (5) assign an entropy flow parallel to each of the conduction components (both coupled by the temperature profiles). But both equations do not consider scattering contributions, since these are not coupled to temperature. This is, from the radiative flow aspect, exact (it fulfils conservation of thermal energy, provided Ω < 1). In entropy flow, however, scattering cannot be neglected; scattering might provide the overwhelming part of total radiative flow. This obviously is a conflict between radiative transfer and entropy flow.

In conclusion, with entropy from its definition being a unique integral quantity,

• The entropy principle is a complete theory. This is because entropy is defined for all transport processes (conductive, radiative in non-transparent media, regardless whether radiative flow proceeds by absorption/remission or by scattering). Entropy itself is a production and a transport process. In its temporal aspect, there are no constraints that might be set on entropy in one transport mechanism against the other. Entropy, as a transport process, can be assigned a differentiable flow, but the flow is not restricted to a flow of energy that is requested to proceed in parallel to thermal flow (and otherwise would be zero).

• Standard radiative transfer theory is not complete: First, it suffers from substantially different transit times that result from different absorption/remission and scattering properties and from the parallel existence of other heat transfer mechanisms; all these proceed with different propagation speeds. In particular, it cannot integrate temporal aspects of propagation by scattering in relation to conduction heat flow. Second, by its definition, it cannot couple (elastic) scattering to temperature fields (elastic scattering is usually assumed in thermal transport problems). While scattering is contained in the source function in Eq. (4a), scattering is not coupled by the energy equation (Eq. 4b) to temperature development (while conduction heat flow is).

• Entanglement takes a position between entropy and radiative transfer, but with no similarity to either. In entanglement, changes of the physical interpretation of the situation, after an experiment like in Fig. 4, occur suddenly and proceed instantaneously to completion. Contrary to the superconductor, there is no “final” state to which the system in a differentiable process would converge. While entropy can be assigned to also entanglement, there is no flow of entropy (nor an underlying transport process at all). The temporal propagation problem accordingly does not exist in entanglement, at least not in the situation described in Fig. 4.

8 Summary

The following conclusions are the extension of the 13 items listed in Section 1.3 (the intermediate summary).

• (i) The diffusion model of radiative transfer again is confirmed as a valuable tool for the calculation of multi-component heat transfer in superconductors. This is the actual core of superconductor stability investigations. Verification of the tool is provided by results numerically obtained for transit times and angular distributions of radiation leaving a superconductor, thin-film sample.

• (ii) Whereas stability functions depend on statistical fluctuations of superconductor electrical/magnetic critical parameters (as was shown in previous papers), dependence on thermal material parameters (here the solid conductivity) apparently is only weak, when assuming fluctuations either within the superconductor (in its boundary layers to substrates or stabilizers) or in thin films. But interferences of the results under fluctuations of electrical/magnetic and thermal material properties presently cannot be excluded.

• (iii) Mid-IR radiation scattering is highly involved in the stability of superconductors.

• (iv) Relaxation time to obtain new equilibrium states after a disturbance may increase to very large values. As a consequence, an important result is that quench is not an event that proceeds instantaneously. Instead, it is a process the speed of which decreases the more, the closer the superconductor temperature approaches critical temperature until the residual number of electron pairs becomes too small to support critical current.

• (v) Stability of superconductors and thermal fluctuations may reflect a common background, the time dependence of the density of electron pairs after disturbances. If both phenomena would be correlated, electrical conductivity, σ′(T), observed during thermal fluctuations at temperature exceeding, but very close to T_Crit, might depend on time, when measured over long periods. These aspects will be investigated in a subsequent paper.

• (vi) By Monte Carlo simulations of transit times, we have confirmed the existence and, apparently for the first time, quantified the dimensions of a cloud of images that result from events like local temperature variations in a thin film object. Existence of this cloud, in particular in strongly scattering objects, stresses the importance to integrate the temporal problem into existing theory of radiative heat transfer. Far from critical states, dimensions of the cloud are of little importance for stability but become the more important the closer the system approaches its critical states.

Appendices

Appendix 1. Monte Carlo approximation

The Monte Carlo approach considers a large number M of beams that after emission experience a total N of interactions on their transit path of total length, L, through an object. Each beam shall be emitted from any position within the target, at z = 0 (Fig. 6, part b) and under arbitrary angles, θ, against the surface normal. Its transit time can be calculated for arbitrary events of absorption/remission and scattering interactions. In the Monte Carlo language, beams are called “bundles”. For more descriptions of Monte Carlo simulations applied to radiative heat transfer, see Chap. 11 in [21] or, in short, Chap. 18 in [29].

Monte Carlo and finite element simulations have to be performed in appropriately chosen time steps.

The part Ω (the albedo) and its impact on transit time is responsible for the energy remaining from the bundle after absorption/remission processes; this part again is scattered and the transit time accordingly has to be simulated by the Monte Carlo approach. Also propagation of purely scattered radiation (Ω = 1) can be described as a diffusion-like process because of a multiple of scattering interactions, but a radiative conductivity cannot exist in this case (we do not have absorption/remission and thus no radiative equilibrium within the object).

For the Monte Carlo method, the scattering angle, θ, under elastic scattering can be defined as a random variable by

$$ \theta =\operatorname{arccos}\ \left[1-R\left(\theta \right)/{m}_{\mathrm{S}}\right] $$

(16)

in which R(θ) denotes the probability to find a bundle emitted or scattered at particular angle θ from the total set 0 ≤ θ ≤ π. Large m_S indicate strong forward scattering; compare the spider diagram in Figure A1 in [29]. In the same reference (Fig. 7), it has already been shown that the angular distributions of scattered radiation in ceramic samples approach the better the theoretical cos(φ)-distribution (when bundles leave the rear sample surface) the larger the extinction coefficient and the larger the number of bundles.

The effect of variations of the extinction coefficient on the distribution of the scattered bundles is shown in Fig. 18. Convergence of the solid symbols to the theoretical cos(φ) curve locally becomes weak due to interferences of the results obtained in the three optically different layers (Fig. 9a). But the overall result confirms applicability of the diffusion model.

The angular distribution of scattered bundles leaving the thin-film sample at the rear position, D = 2 μm, is presented in Figs. 16, 17 and 18. The total thickness of the film is divided into three sections. Results in Fig. 16 are obtained assuming m_S-factors and albedo identical in each of the layers. In all cases, the solid symbols approach the theoretical cos(φ)-distribution (open circles).

As a more realistic case, values m_S different in each layer are applied in Fig. 17, and Fig. 18 shows results obtained with different extinction coefficients in the thin surface layers and the core of the thin film.

If not just single, individual bundles but the total set of M = 10⁵ bundles is applied, and if m_S is large, all M bundles are sharply focussed to small forward angles, Fig. 8a.

The scattering phase function, Ψ(μ), is obtained from counting the number of bundles, n(θ), that as a result of the Monte Carlo simulation are scattered into intervals in steps of Δθ = 10 deg (with the angle θ vs. surface normal between 0 and 90 deg) and for different values of the (scattering) anisotropy parameter m_S. We have Ψ(μ) = n(θ)/M, with μ = cos(θ) given by the midpoints in the intervals.

Figure 8b shows the mean value, μ_m = cos(θ)_m, to be used in the radiative conductivity, Eqs. (12a) and (12b). It is calculated from

$$ {\mu}_{\mathrm{m}}=1/2\int \varPsi \left(\mu \right)\ \mu\ d\mu $$

(17)

as the weighted mean of the individual cos(θ), with the weights provided by the scattering phase function in Fig. 8a.

Appendix 2. Calculation of the Stability Function

If the critical current density, J_Crit, in a superconductor depends only on temperature (neglecting its dependence on magnetic field), and when assuming uniform temperature in the total superconductor cross section, its critical current density is uniform, too.

If at a time t > t₀ losses (like Ohmic) come up in the superconductor, its temperature increases from T(t₀) to T(t). We then write the stability function, Φ(t), as

$$ \varPhi (t)=1-{J}_{\mathrm{Crit}}\ \left[T\left(t>{t}_0\right)\right]\ A/{J}_{\mathrm{Crit}}\ \left[T\left({t}_0\right)\right]\ A $$

(18)

with A the total conductor cross section. This can be rewritten as

$$ \varPhi (t)=\left\{{J}_{\mathrm{Crit}}\ \left[T\left({t}_0\right)\right]\ A-{J}_{\mathrm{Crit}}\ \left[T\left(t>{t}_0\right)\right]\ A\ \right\}/{J}_{\mathrm{Crit}}\ \left[T\left({t}_0\right)\right]\ A $$

Because of the dependency of J_Crit on T, we have J_Crit [T(t₀)] > J_Crit [T(t > t₀)].

Recalling that any current in a superconductor flows with critical current density, the stability function in this simple case accordingly reads

$$ \varPhi (t)=\left\{{I}_{\mathrm{Crit}}\ \left[T\left({t}_0\right)\right]\kern0.37em -{I}_{\mathrm{Crit}}\ \left[T\left(t>{t}_0\right)\right]\right\}/{I}_{\mathrm{Crit}}\ \left[T\left({t}_0\right)\right] $$

In other words, Φ(t) under losses (strictly speaking: under any kind of source functions) is the ratio of zero-loss transport current at time t > t₀ to the critical current at the start temperature, t₀. Without losses, T(t) remains constant, I_Crit [T(t₀)] = I_Crit [T(t > t₀)] and Φ(t) = 0.

In this simple case, we have assumed that transport current, I, would occupy the total superconductor cross section. This is not necessarily the case: Since I flows with critical current density, part of the conductor cross section might be sufficient to carry the (full) transport current. In the remaining part of A, I_Crit might be very small, which means there is a non-zero current distribution in all parts of the cross section (the transport current circumvents those parts of the cross section that are resistive). Regions with zero resistances, flux flow and Ohmic resistances thus may exist in parallel. Current transport (its distribution in the cross section) is an optimisation problem.

But in real situations, superconductor temperature is not uniform, and critical current density and critical temperature depend on time (since losses depend on time like in AC applications). If we again assume that critical current density depends on only temperature (again neglecting the dependence on the magnetic field), we need the temperature distribution, T(x, y, t), in the conductor cross section to obtain the distribution of critical current density, J_Crit(x, y, t). The temperature distribution results from local (Ohmic or other) losses or from boundary conditions like cooling. The obtained temperature field, T(x, y, t), accordingly is mapped onto the field of critical current density, J_Crit(x, y, t). This mapping is not bijective.

There are well-known relations between J_Crit and T that apply approximations to experimental data. If at any local position, temperature exceeds critical temperature, T_Crit, the critical current density at this position is zero, with corresponding variations of the stability function.

If the dependency of J_Crit also on the magnetic field (flux density, B) is considered, the stability function reads, in analogy to Eq. (16),

$$ \varPhi (t)=1-\left\{\int {J}_{\mathrm{Crit}}\ \left[T\left(x,y,t\right),B\left(x,y,t\right)\right]\ dA\right\}/\left\{\int {J}_{\mathrm{Crit}}\ \left[T\left(x,y,{t}_0\right),B\left(x,y,{t}_0\right)\right]\ dA\right\} $$

Solutions of this equation cannot be found with analytical methods but have to be obtained numerically.

The first step is calculation of the temperature field T(x, y, t) by e.g. finite differences or finite element (FE) methods to solve Fourier’s differential equation. For this purpose, the total conductor cross section, A, is divided into a large number (a set) of geometrical, i.e. area elements, ΔA_i. The ΔA_i not necessarily would be of equal size.

The division of A into the set ΔA_i has to be made fine enough to approximate the continuous variation of the field T(x, y, t) by a discrete distribution T_i (ΔA_i, t). The finite element solution delivers local, discrete nodal values (temperature at the corners of e.g. a plane area element) from which the element temperature, T_i (ΔA_i), is obtained as the arithmetic mean, or solutions are provided at the centroid of the elements.

The set T_i (ΔA_i, t) replaces the continuous distribution, T(x, y, t). Roughly speaking, the finer the division of A into the set ΔA_i, the more exact is the finally obtained solution (but the longer is the computation time). The T_i (ΔA_i, t) are obtained under convergence criteria in standard FE computer programs. In our previous papers, you will find information on the finite element mesh, the solution (integration) procedures, convergence criteria and, occasionally, enormous computation times with standard, 4-core PC under Windows 7.

The next step is calculation of the field J_Crit,i (ΔA_i). Relations like J_Crit(T) = J_Crit(T₀) (1 − T/T_Crit)ⁿ are frequently reported in the literature, with J_Crit(T₀) the value at t = t₀ and with the exponent n as a material specific property. In applications of high-temperature superconductors, we for example find n = 2. But J_Crit(T₀) is not the same in each of the area elements; it fluctuates against a mean value (like in Fig. 19) because of experimental uncertainties, or from tolerances in conductor manufacturing and handling.

We accordingly have J_Crit,i(T₀) given as random values in the corresponding ΔA_i, usually with i ≤ N a very large number. The same applies to critical temperature, T_Crit,i and the lower and upper critical magnetic field, B_Crit,1,2,i, and to the anisotropy ratio, r. Random variations ΔT_Crit, ΔB_Crit,₂ and ΔJ_Crit of the electrical/magnetic critical parameters against the conventional values of YBaCuO 123 in the present paper (92 K, 240 Tesla at T = 0 and 3 10¹⁰ A/m² at T = 77 K) are within ± 1 K, ± 5 Tesla and ± 1%, respectively.

The anisotropy ratio, r, of thermal diffusivity and of J_Crit is taken into account in directions parallel to the crystallographic ab-plane against the c-axis, respectively. In the present paper, we have applied r = 10 constant, from experimental tests, with fluctuations Δr of ± 0.5.

Once J_Crit,i(T₀) and J_Crit,i(T₀) are available, the critical current density has to be transformed to its magnetic field dependence, J_Crit,i [x, y, t, B(t)]. We consider each of the area elements, ΔA_i, as tiny conductors. The field dependence is taken into account using standard relations (found in tables in volumes on electrotechnical problems) for calculation of the magnetic field of conductors of simple geometry (self-fields and fields from neighbouring conductors that are added to obtain the local field for each ΔA_i). Insertion of B(x, y, t) yields J_Crit [x, y, t, B(x, y, t)] of the superconductor, as indicated in Eqs. (11a) and (11b).

The stability function (area element index i omitted) then reads

$$ \varPhi (t)=1-\left\{\Sigma {J}_{\mathrm{Crit}}\ \left[T\left(x,y,t\right),B\left(x,y,t\right)\right]\Delta A\right\}/\left\{\Sigma {J}_{\mathrm{Crit}}\ \left[T\left(x,y,{t}_0\right),B\left(x,y,{t}_0\right)\right]\Delta A\right\}, $$

with the summations taken over all ΔA_i (the x,y-co-ordinates are the centroids of the area elements, ΔA_i).

In most stability calculations and application of high-temperature superconductors, it is only current flow parallel to the ab-plane that is relevant for superconductor technical applications and their stability. An example for the stability function also in c-axis direction is reported in the present paper.

Calculation of the T_i (ΔA_i), in each of the area elements ΔA_i, takes into account magnitude and distribution of losses that may depend on time (like in an AC application), experimental values of the thermal diffusivity of the superconductor material, and boundary conditions.

The thermal diffusivity of YBaCuO 123 in the ab-plane is shown in Figure 5 of [7].

Calculation of the J_Crit,i (ΔA_i) applies penetration depth of the magnetic field, with B estimated using standard relations for single conductors of given (ΔA_i) cross sections; with these results, the Meissner effect is checked in each of the ΔA_i. For this purpose, critical temperature, T_Crit,_i in each of the ΔA_i is taken not as constant but in dependence of local magnetic induction, B_i.

For the estimate of B, the transport current distribution in the conductor cross section has to be known. It is obtained from the electric resistances that result separately for each of the area elements ΔA_i. This takes into account Ohmic and flux flow resistances, the former in dependence of temperature and with experimental values of the specific resistance, the latter from comparison of J_Crit vs. J_Transport as described in the standard literature or using a new flux flow resistance model described in [9, 11]. Once the resistances are obtained, the elements ΔA_i as mentioned are considered as tiny current-conducting transport channels all directed in parallel along the length of the conductor. Current distribution then follows from the distribution of the individual resistances of the ΔA_i in an iterative procedure and from application of Kirchhoff’s law.

An interesting practical problem is to calculate the stability function in case there is current-sharing, but this is beyond the scope of the present paper.

All electric/magnetic and thermal material parameters are considered as dependent on temperature. Since temperature under losses or from boundary conditions is transient, all obtained results and the calculated stability functions depend on time.

Note that calculation of the stability function does not imply an actual transport current and its actual distribution. The stability function only delivers a criterion to decide whether, and to which extent, zero-loss current transport remains possible under disturbances (here Ohmic and flux flow losses). It is then the task of the designer to decide by this tool which percentage of critical current can be tolerated as transport current in a technical application of superconductivity.

Fig. 16

Angular distribution, n(φ), calculated at z = 2 μm of in total M = 5 10⁴ bundles emerging from x = y = 0, z = 0 (compare Fig. 6, part a and b) that leave the rear surface (thin-film sample of the YBaCuO 123 superconductor). Results are shown vs. angle φ against surface normal of the volume elements (concentric rings generated by rotation of the area elements of Fig. 6, part b) and in dependence of the (scattering) anisotropy factor m_S. The curves (solid diamonds) are indexed as m_S1, m_S2, m_S3 (running from 2 to 18; these are the same m_S that were applied in the spider diagram shown in Fig. A1 in [28]). The m_S factors in this figure are assumed as identical in the inner (index 1) and outer, about 0.1 μm thin boundary layers (3) and in the 1.8-μm-thick central core (2) of the thin film. The same applies to values of the albedo (Ω = 0.912 in the three layers; the value is taken from [11]). Extinction coefficients in the three layers are E₁ = E₃ = 3.417 10⁶ and E₂ = 1.409 10⁷ 1/m, respectively, again from [11]. The solid symbols approach the theoretical cos(φ) distribution (open circles) of the residual beams leaving the sample on the rear surface

Fig. 17

Angular distribution, n(φ), again of M = 5 10⁴ bundles. The curves are calculated as before (albedo, Ω, and extinction coefficients, E, are the same as in Fig. 16), but the m_S values are different in the three layers: m_S1 = 6, m_S2 = 2 and m_S3 = 6 (red diamonds) and m_S1, m_S2, m_S3 = 2, 6, 2 (lilac-brown diamonds, indexed as before). Local deviations of both curves from the theoretical cos(φ) distribution and in particular the dip of the solid red symbols at scattering angles between − 25 and + 25 degrees result from interferences caused by the strongly different optical parameters of the three layers. The overall tendency to approach the theoretical distribution is confirmed also in these cases

Fig. 18

Angular distribution, n(φ), of in total M = 5 10⁴ bundles. The curves are calculated as before (Figs. 16 and 17) using identical m_S values (m_S1 = m_S2 = m_S3 = 6) and the same albedo (Ω = 0.972), but here with a variation of the extinction coefficients: E₁ = E₃ = 3.417 10⁶ and E₂ = 1.409 10⁷ (solid lilac diamonds) and, reversely, E₁ = E₃ = 1.409 10⁷ and E₂ = 3.417 10⁶ 1/m (green diamonds). Indices are as before

Fig. 19

Existence diagram of type II superconductivity (schematic, not to scale; the lower critical magnetic field is not shown). The dashed blue line and the open blue circles in this figure denote the conventional region of existence of superconductivity (the open blue circles accordingly are located on the corresponding axes of the diagram). Random variations of T_Crit(B), J_Crit(B) and J_Crit(T) against this (conventional) region are indicated by small black dots; this applies (schematically) to the existence diagrams of all elements in the finite element scheme. These random variations (taken as standard variations in each of the area elements) ΔT_Crit, ΔB_Crit,₂ and ΔJ_Crit of the electrical/magnetic critical parameters against the conventional values of YBaCuO 123 in the present paper are within ± 1 K, ± 5 Tesla and ± 1%, respectively. For a particular element number, jj, as an example, its region of superconductivity existence is indicated by the coloured quadrants that in this single, special case are (exaggerated) located all within the conventional region (the dashed blue curves). Thick black solid circles indicate for this element the critical values T_Crit, B_Crit, J_Crit that, again exaggerated, are shifted against the conventional values. The figure is copied from [15], here with slight modifications. Reprinted from [15]. With kind permission of Old City Publishing Inc., Philadelphia PA 19123, USA