1 Survey

A superconductor is stable if it does not quench. Quench is initiated by disturbances like insufficient cooling, local release of mechanical energy, absorption of particle radiation or transport currents exceeding the critical current. Quench proceeds on very small timescales. In many cases, quench causes local damage but may even lead to total destruction of a conductor. Quench can be avoided by appropriate design of superconductors (wires, filaments, thin films) using stability models. Stability models yield predictions on permissible conductor geometry like maximum radius of filaments or aspect ratio of thin films, and of maximum zero-loss transport current to which a superconductor may be exposed.

But fast transitions from superconducting to normal conducting state, like in a quench, offer rich potential of self-regulating fault current limiting (FCL), for example in case of short circuits in an electrical distribution system. When simulating current propagation, we accordingly have to consider two mutually exclusive situations: energy losses and quench during nominal conductor operation safely has to be avoided, which means the actual conductor temperature, current density and magnetic field have safely to be kept below their critical values. On the other hand, fault current limiting relies just on overrunning the critical parameters. Simulation of current propagation has to account for both situations.

Attempts to develop FCL and successful realisations of this advanced safety concept have very frequently been reported in the literature and are an important step forward. Summary reports prepared soon after the discovery of high-temperature superconductivity, with reference to FCL projects, can be found in [1, 2]; a more recent description, again with numerous citations to original literature, is given in [3], Chap. 8. Design and successful operation of fault current limiters contribute to a deeper understanding of current transport in general and to short-time, superconductor materials behaviour under extreme current load.

Current limitation can be achieved if at least one of the three critical parameters (temperature TCrit, critical magnetic field BCrit and critical current density JCrit) is exceeded by actual values T, B and J. Roughly speaking, an Ohmic resistive FCL integrated into an electrical circuit immediately after the start of a fault (J > > JCrit) generates flux flow resistances and corresponding losses which quickly raise the conductor temperature to above TCrit; thus, a large obstacle to fault current flow is generated. A flux flow FCL, too, generates flux flow resistance but with the conductor temperature below TCrit (no phase change to normal conduction). Inductive current limiters comprise a primary normal conductor winding and a shielded iron core. Shielding of the core is realised by a secondary superconductor winding (a cylinder positioned between the primary conductor and iron core). Shielding is lost when large fault currents quench the superconductor, which in turn increases the impedance of the primary circuit.

Technically realised FCL are purposefully designed to suppress fault current in a medium voltage grid to tolerable residual values, preferentially to only a very small multiple of nominal current. In the past, there were about ten industrial, FCL projects of resistive and saturated iron core types, and there are about five projects at present.

The major idea of this paper is fourfold: (a) show that there is inhomogeneity of temperature and, as a consequence, of current distribution, critical temperature, current density, magnetic field and also of current limitation (because limitation might occur in only part of the cross section); (b) explain that a distinction between (solely) Ohmic resistive and flux flow resistive current limiting, as is presently done in the literature, becomes highly questionable; (c) introduce random critical parameters as a new method to account for shortages in materials development and manufacture issues; and (d) investigate possibly existing correlations between stability and current limiting.

Current limiters in this paper serve as extreme cases of current propagation. But focus is on the physics behind current propagation. We will describe by numerical methods how fast and to which extent a superconductor bundle reacts to a sudden increase of current load (like in a fault).

Investigations of current propagation and limiting that rely on homogeneous temperature distribution in the conductor cross section have been presented, e.g. in [3–5]; there are more numerous reports that apply the same simplifying assumption. But there are another four shortages of traditional stability models:

  1. (a)

    The models assume instantaneous distribution within the conductor volume, or thermalisation, of a local disturbance.

  2. (b)

    The models do not specify the location and intensity of a disturbance in the conductor.

  3. (c)

    The Stekly, adiabatic or dynamic stability models derive results under quasi-stationary and adiabatic conditions; for a survey, see Wilson [6] or Dresner [7].

  4. (d)

    Flux flow resistive states are not included.

Among these, items (a), (b) and (d) are the most critical ones. To improve the situation, standard stability models have recently been extended by numerical models (Flik and Tien [8], and by the present author). We have investigated the reaction of superconductors under direct current (DC) transport to either

  1. (i)

    Transient disturbances [9]—a single (Dirac) heat pulse locally released in the conductor by absorption of infrared or particle radiation, or by a sudden transformation of mechanical to thermal energy (conductor movement under Lorentz forces)

  2. (ii)

    Periodic disturbances [10, 11]—exposure of a sample to periodic energy pulses that as local disturbances lead to periodic variations of local temperature and corresponding, periodic variations of critical current density and stability functions

Investigations in [8–11] apply the temperature dependency of the critical current density as the sole basis to predict the maximum zero-loss transport current by a stability function (this function is explained later). The investigations have not considered losses that may arise under flux flow resistive states (J > JCrit), with the conductor temperature below the critical temperature.

A very interesting case (iii) accordingly appears when the density of an alternating current (AC) itself initiates periodic disturbances by flux flow losses. The disturbances then are no longer point-like, isolated from each other or of only a very short duration, but may be extended over a considerable part (or total) of the conductor cross section. They also may oscillate and exist over extended periods of time. This case will be studied in this paper.

The paper is organised as follows: In part I, a numerical model will be described to calculate local electrical, magnetic and thermal states of a high-temperature superconductor (HTSC) under disturbances initiated by a transport or a fault current. The simulations are applied to a bundle of several hundred identical conductor filaments all switched in parallel (the selection of a HTSC model conductor material is in detail explained in Appendix A1). The bundle is integrated into an electrical circuit (Fig. 1a) that allows comparison with a similar system described in [4] with same root mean square phase voltage, same conductor cross section and same critical current density. We could in principle take any large- or small-scale electrical grid, like in a laboratory experiment, with an appropriately dimensioned superconducting component; the point is the analysis of this component under high current load.

Fig. 1
figure 1

a Schematic view of an electrical grid. A sudden, strong increase of current load onto a superconductor filament bundle will be simulated, either in a small-scale laboratory experiment or, on large scale, the grid could describe a medium voltage distribution system. The normal conductor serves as an auxiliary variable; its assumed sudden decrease initiates the increase of transport current (not necessarily a fault caused by accidents like short circuit or lightning). b Schematic view, not to scale, showing an axial section of a superconductor filament (polycrystalline material) embedded in a metallic matrix (not shown). Current direction is parallel to longitudinal axis of symmetry. The figure assumes ideal c-axis orientation of grains (light blue; size strongly enlarged) and circumferential direction of the magnetic field (flux density; green circle). The flat grey surface illustrates the finite element scheme of 4-node, plane model elements which are rotated against the longitudinal axis to generate volume elements

Full size image

Figure 1a also incorporates a normal conductor with non-zero resistance (in a large-scale experimental setup, the normal conductor in Fig. 1a might be a conventional transmission line or a standard power cable). The resistance of this conductor, and thus the total resistance of the circuit, is used as an auxiliary variable: Continuous, though fast, reduction of the resistance serves for definition of a sudden strong increase of transport current, a procedure that strongly simplifies numerical calculations and stabilises the achieved solutions.

Part II of the paper reports results for integral conductor states like stability functions, maximum zero-loss currents and current limiting. Part III deals with a possible correlation between stability, current propagation and limitation.

2 Description of Stability, Current Propagation and Limiting Calculations

The numerical concept (meshing, boundary conditions, solution schemes) originates from a finite element method (Reiss and Troitsky [12]) how to obtain thermal diffusivity of opaque, transparent or semitransparent thin films; an analogue of this procedure recently has been applied [9–11] to the investigation of superconductor stability.

2.1 Data Input

Electrical resistances of the superconductor filaments comprise Ohmic, inductive, flux flow, hysteresis and coupling resistances (the filaments shall be embedded in a metallic matrix). Dimensions of the filaments, details of meshing and solution schemes will be reported in Section 2.4.

Strictly speaking, we could take any reasonable superconductor material for stability analysis (reasonable in the sense that it allows numerical, finite element simulations to converge). This requests, for example, that the critical temperature of the conductor is not 10 −6 K or the like, or its anisotropy is not in the order of 10 3. In principle, even an LHe-cooled LTSC could be applied and also any conductor architecture. Results like existence of transient temperature profiles, large temperature gradients, local current distribution and an anticipated correlation between stability and current propagation and suppression, qualitatively were the same. However, the computational problems were much larger, and convergence of the results might be impossible to obtain.

The numerical simulations thus have to be performed with a simple conductor architecture and a HTSC material (as mentioned, a model conductor) of which its electrical/ magnetic and thermal properties shall be available from experiments, over a large range of temperature and, according to experience, its anisotropy to current transport be modest (in the order of 10; this is fulfilled with a YBaCuO solid).

The application of a model conductor, as will be shown, clearly illustrates the problems that would arise in any 1G or 2G conductor under transient current propagation (the problems reflect the list of major ideas of this paper, as given in Section 1): inhomogeneity of temperature and current distribution; inhomogeneity of critical temperature, current density and magnetic field; and inhomogeneity of current limitation.

All parameters of the conductor take into account interactive physical dependencies, like TCrit vs. BCrit1,2, or BCrit1,2 vs. T, and thermal diffusivity vs. T.

Modelling of Ohmic resistance states is straight-forward with data from [13], and modelling of flux flow resistivity to axial current (Fig. 1b) is made according to [14]. The weak-link structure of a polycrystalline conductor constitutes a potential obstacle that is laid upon is constituents; the obstacle not only concerns electrical transport (electron charges) but also magnetic (movement of vortices under flux flow) and thermal transport. Resistance to magnetic transport has to be considered separately in grains and in grain boundaries. A schematic, rather optimistic orientation of plate-like grains and circumferential magnetic field, under axial current, is indicated in Fig. 1b (small, light-blue shells). Flux flow, if any, roughly occurs in radial directions only.

Reference [14] explains that the low temperature, empirical relation between specific resistivity of flux flow, ρ FF, and normal conduction, ρ NC

$$ \mathrm{\rho}_{\text{FF}}=\mathrm{\rho}_{\text{NC}}\mathrm{B/B}_{\mathrm{Crit,2}} $$
(1)

is applicable to also high-temperature superconductors. However, this relation is valid for superconductor solids, and as [15], p. 128, points out, there may be deviations from (1) in type II superconductors (like HTSC) with large values of the Ginzburg-Landau parameter, κ; this accordingly could indicate a problem in the present study but will not be pursued here. Instead, in the present simulations, the overall structure of (1) shall be maintained but modifications applied to account for weak-link behaviour.

References [12] and [14] report strong anisotropy of the resistance against transport of magnetic flux vortices, much larger than anisotropy of resistance to current. In a rough approximation, we have estimated grain and grain boundary volumes and the results used as weights assigned to the anisotropy ratios that were estimated following [14, 16]. A weighted mean accounting for porosity and anisotropy is applied as a pre-factor to (1). Details of the procedure will be reported elsewhere.

The final result, axial resistivity, ρ FF, to current transport, under radial flux flow in the porous, polycrystalline, roughly layered material, is shown in Fig. 2. The resistivity ρ FF is larger than ρ NC, contrary to what would be expected from the standard (1). But (1), in its original form, applies to solids, not to a network of solid particles surrounded by weak-link shells; the comparatively large ρ FF thus does not necessarily indicate strong flux pinning. The resistivity ρ FF is also larger than the constant ρ FF = 10 −6 Ω m used in [4]; it is not at all clear that ρ FF should be constant, independent of temperature.

Fig. 2
figure 2

Specific resistance to transport current under normal conduction (blue diamonds) and to flux flow (green diamonds) in porous YBaCuO, vs. temperature, at magnetic flux densities that exceed the lower critical field, BCrit,1. The large difference results from estimated contributions of grain boundaries (weak links) to flux flow resistance; for more explanations, see text

Full size image

Thermal diffusivity, DT, of a YBaCuO superconductor solid material (with conductivity from [17]) is between 4 10 −6 and 2 10 −6 m 2/s, at temperatures of 77 and 120 K, respectively. The values are the same as previously used [9 - 11]; compare the original literature cited therein. For a periodic disturbance that initiates a local increase of temperature, and when taking a mean value of DT in the expression for the penetration depth δ SC(ω) = C (2 DT/ ω)1/2of a thermal wave ([18], p. 159), we have δ SC(ω) ≈ 1600 μm, with C a constant, for simplicity C = 4.6 for a flat, semi-infinite sample, and ω = 50 Hz. Also, this estimate applies to a solid; it does not take into account the porosity of the conductor. However, a correction to DT using the traditional Russell cell model (see below) does not yield substantial alterations so that δ SC(ω) safely exceeds rFil, the filament radius defined in Section 2.4. Local temperature, T(x,y,t), of all volume elements in the filament thus will very quickly respond to any disturbance that propagates by thermal diffusion through the polycrystalline network but does not, as will be shown, guarantee a homogeneous conductor temperature.

Geometry and orientation of the grains (Fig. 1b) assume an ideal case, a layered distribution of platelets from which the more deviations will have to be expected, the more layers would be generated. To obtain both electrical resistivity and thermal conductivity of porous materials, the traditional Russell cell model is applied to the corresponding solid state data ([19]; an old but flexible model since it is applicable to particulates of rather arbitrary shape). We use porosity, Π = 0.1, of the superconductor material, and for the linear part of the normal state resistivity, ρ NC, the slope d ρ NC/dT = 4.27 10 −9 Ω m/K reported in [14]. For application of Russell’s cell model, it is assumed that the resistivity against current transport in grain boundary volumes is by a factor of at least five larger than within grains. This ratio is a very rough estimate and not identical to, but much smaller than, anisotropy of transport of magnetic flux vortices.

Inductive losses of the filament bundle have been estimated following traditional models (standard electro-technical literature) and do not need specification. Hysteresis and coupling losses are modelled following [6], Chap. 8.2 and 8.3. All losses, if they depend on current, can be transformed into expressions that contain corresponding specific electrical resistances. Corrections to the most important Ohmic and flux flow resistive losses by inductive, hysteresis and coupling counterparts are small.

Electrical and thermal properties of the matrix material are needed for description of current sharing (see the results in Appendix A2, Figs. 14, 15, 16 and 17).

A new concept introduced in this paper is consideration of critical current density, critical temperature, upper critical magnetic field and the weak-link problem overlaid onto flux flow transport as random variables:

No existing superconductor, if manufactured in technically important quantities, shows perfectly homogeneous materials properties. Deviations from ideal conditions must be taken into account that may arise during conductor design and manufacture. Conductor inhomogeneity may turn out, for example, as local deviation from oxygen stoichiometry, or may result from high angle grain boundaries as obstacles against current transport in basal planes, or from tolerances in mechanical working steps, or from weak links, in total a very large number of potential divergences arising in polycrystalline materials. Modelling their impact on current propagation using, like in radiative exchange calculations, cell models (for example, the well-known brick wall model) is too simplifying and could lead to enormous uncertainties. A possible way out of the problem is to treat the most important critical parameters as statistical quantities (random values, with fluctuations around their mean).

We have applied random values like those illustrated in Figs. 12 and 13 (Appendix A1). In this model, critical current density and the other critical parameters of the superconductor and its weak link, anisotropic resistance against flux flow, are different in each of the finite elements (but with the traditional dependency on field and temperature, respectively). Maximum fluctuation is roughly estimated from experience [22]. Application of this model seems plausible (though it introduces additional numerical problems), but general validity of this concept has to be verified in additional studies.

2.2 Overall Calculation Scheme

The overall numerical procedure consists of four steps:

  1. (a)

    Calculation of transient temperature fields by a standard finite element method.

  2. (b)

    Re-calculation of resistances and critical parameters.

  3. (c)

    Determination of the new current distribution; comparison of conductor temperature, magnetic field and current with the corresponding critical ones; and re-calculation of resistances and losses.

  4. (d)

    Specification of a fault (or, more generally, of a sudden, strong increase of current) and return to step (a); we will in the following simply speak of a fault although the simulated strong current increase might not reflect an accident like short circuit or lightning.

In step (a), we use the same data for boiling LN2 as in previous reports [9 - 11]. Close to the interface to the coolant, oscillations of T(x,y,t) against coolant temperature are small; maximum amplitude variation in the present study is within ΔT = 1 K, which means there will be almost no periodic but approximately constant thermal boundary conditions at the solid/liquid interface. After an initial settling period needed for creation of the first nitrogen vapour bubbles (in the order of 5 ms), the static description of boiling heat transfer is applicable (we again take data reported for smooth metallic surfaces; compare the original literature cited in [9 - 11]).

In step (b), the Meissner effect has to be checked separately in each of the finite elements of the numerical calculation scheme. Its property, “zero resistance” at magnetic fields below the lower critical field, cannot be handled reasonably when in a transient numerical analysis current distribution shall be determined from Kirchhoff’s laws. Very small but finite values of the specific resistances (values below 10 −20 Ω m) then have to be assumed.

The resistances obtained in step (b) are the basis to determine the new transient current distribution in step (c). The new distribution not necessarily is the same as obtained in previous time steps; instead, the distribution may fluctuate and the current percolate through the conductor, all in dependence of the actual resistances.

Summation over all re-calculated local currents yields the same total current in the conductor cross section, at all axial positions of the conductor including the metallic matrix.

In step (d), it has been assumed that a strong increase of current is initialized, under the nominal voltage of the circuit, by a sudden but controlled reduction, within 2.5 ms, of the total AC resistance of the grid. As mentioned, this not necessarily indicates really a fault (in a small-scale example of Fig. 1a, a sudden current increase might result from cutting off a large normal resistance from a laboratory circuit); the point is that the method shall generally be applicable, not only to public grids.

For this purpose, divisors, NCut off, beginning at t = 6.5 ms after the start of the simulation, gradually increase from an initial value, NCut off = 1, to their final value at t = 9 ms and then are constant. The N Cut off are used as auxiliary variables. No attempt was made to simulate details of a real short circuit like excursion of over-current and inductive voltage, −L dI/dt, at the position of the fault, temporarily existing arcs, resistances and their lifetimes.

Increase of the total (nominal plus fault) current (absolute value) is illustrated in Fig. 3 for different final NCut off. Note the upturn of all curves (coloured diamonds) during 6.5 ≤ t ≤ 9 ms: Increase of the total current (under nominal voltage) by the reduced resistance to very large values overcompensates its reduction expected from the oscillation of nominal current, ITransp(t) = I0 (sin ω t), during this period.

Fig. 3
figure 3

Absolute value of total (nominal plus fault) current, ITransp(t), within 0 ≤ t ≤ 20 ms (note the logarithmic ordinate scale). The figure shows to which extent the transport current will increase if the (AC) phase resistance, within 6.5 ≤ t ≤ 9 ms, is reduced to 1/ NCut off of its undisturbed value. The length of the normal conductor is 10 5 m, in order to keep the current load onto filaments small. Open black circles denote the undisturbed normal conductor (NCut off = 1). Results are obtained with TCrit, JCrit, BCrit,1 and BCrit,2 identical in each element (not random numbers) and with the same field or temperature dependency, respectively, and constant anisotropy for transport of magnetic flux quanta. The local upturn of the curves is the stronger, the larger NCut off

Full size image

2.3 Solution Scheme

The total simulated period has been split into periods Δt = 10 −4 s. To obtain convergence of the results, the procedure within each period Δt had to be repeated by up to N = 10 iterations of steps (a) to (d) specified in Section 2.2. The large number of iterations reflects the strong non-linearity of almost all involved parameters. Integration time δ t within each Δt is between 10 −14 and 10 −7 s. Convergence is achieved at the end of each sub-step of duration Δt/ N = 10 −5 s. The calculations yield a series of converged, quasi-stationary solutions. This scheme generates convergence because the time interval Δt/N is large in comparison to

  1. (i)

    Characteristic (diffusion) time, τ C, of electrical or magnetic fields and of currents, τ C ≤ 4 \(r_{\text {Fil}}^{\mathrm {2}}\)/(π 2 DC) ([6], p. 143) using for the diffusivity the expression DC = ρ NC/ μ 0, with ρ NC the specific resistivity of the filament material in the normal conducting state, and μ 0 the vacuum constant. We have D C = 0.361 m 2/s. This yields τ C ≤ 10 −7 s.

  2. (ii)

    Time τ Rneeded to establish new equilibrium charge distributions (compare [21], Fig. 2b). This period covers total redistribution of electron pairs to the ground states of the superconductor; this would request also the exchange of charge between neighbouring elements. The estimates yield τ R < 10 −6 s except for temperatures very close to the critical temperature.

No divergences (T < 77 K, or runaway to an extremely high temperature) were finally observed that could result from too large a time step or from too small an element volume in the numerical procedure.

Both estimates (i) and (ii) justify calculation of the transient current distributions in a stepwise numerical procedure to obtain quasi-stationary, discrete intermediate states. If these conditions were not fulfilled, the procedure would have to be altered to a continuous model of current exchange between neighbouring finite elements to allow re-organisation of charge distribution in the whole conductor, too difficult a task to be solved presently.

Computational efforts to fully cover all these procedures were enormous. The solution scheme applied sparse matrix direct solvers (requests a large memory space; alternatives like JCG or ICG iterative solvers were tested but convergence is not guaranteed). The calculation scheme (a) to (d), with in step (a) the embedded finite element core (a commercially available FE code), for simulation of a total period of 10 ms, took a standard PC with 4 GB workspace about 8 to 10 h, under Windows XP or Windows 7. This mainly results from the large number of IF…THEN…ELSE steps to be executed separately in each of the elements, with respect to all potentially allowed superconductor resistance states, and in each iteration cycle.

Nodal temperature results from solution of Fourier’s differential equation. In the present case, 4-node, plane model elements have been applied, with rotation against the axis of symmetry to generate volume elements. Element temperature is the arithmetic mean of nodal temperatures.

2.4 Conductor Geometry and Critical Current Density

Finite element size is Δr = 6 μm radial thickness and 200 μm axial length. The most inner elements are rods of circular cross section, whereas all other elements (superconductor and matrix) are circular shells (annuli of constant width).

Size of filaments in OPIT band-like (1G) conductors usually is about 20×200μm. Current transport and temperature simulations in this fine structure would request too short characteristic and integration times. Instead, modelling of the conductor follows Wilson [6], Fig. 12.9, with a double or multi-stacking technique: We call a “filament” a composite of 1 < N thr ≤ N thr,max very thin, superconductor threads (objects that result from extrusion). Definition of this filamentary composite (threads plus matrix) is for calculation purposes only; its radius is r Fil = 300μm. The conditions set for Δr (radial width of finite elements), ar (aspect ratio), r Fil (filament radius) and Russelss cell model then allow modeling of the interior of one filament as a structural continuum (instead of explicitly modeling fine threads). The calculated results (inhomogeneity of temperature, etc. within one filament) do not depend on the filament (composite) radius r Fil.

All filaments are bundled into a strand of identical filaments. A number N Fil = 354 filaments yields total superconductor (bundle) cross section ASC = 10−4 m 2, the value reported in [4]. The number Nthr of fine threads in the total (strand) cross section, N Fil < N thr ≤ N Fil × N thr,max, and the amount of weak link and metal matrix material are adjusted to yield filament (not strand) porosity ⨅ = 0.1 to be used in Russel’ cell model [19]. The amount 1 - ⨅ in one filament is occupied by the superconductor threads. The relative amount of superconductor material in one strand is much lower, like in LTSC strands.

The filaments are, in principle, of arbitrary length, L Fil > > r Fil. Before the start of the proper simulations, conductor length is limited to LFil = LSC = 500 m; see below for this estimate.

We select one single filament to be simulated; it shall be located close to the periphery of the bundle (close to the solid/liquid interface to the coolant). Thickness of the metal matrix at peripheral positions is about 200 μm (larger than the clearance between filaments located in the interior of the strand).

Assume as a macroscopic example of Fig. 1a that the length of the normal conductor in Fig. 1a is LCu = 12.5 km and the impedance of one phase amounts to 0.38 Ω (same value as in [4]). With the specific resistance of Cu, ρ Cu = 1.8 10 −8 Ω m, and a cross section ACu = 10 −4 m 2 (again the same as in [4]), we have a loss of resistance of ΔRCu = 22.5 Ω if the normal conductor resistance loss were total, NCut off → ∞; this loss shall at least partly be compensated by the superconductor filament bundle. By its length and cross section, the resistance of the normal conductor determines the current load onto the superconductor filaments.

Assume for the moment that filament temperature is homogeneous and above critical temperature, say T = 100 K (T Crit0 = 92 K of YBaCuO), which means the filaments altogether would act as an Ohmic resistance current limiter. The specific resistance of the conductor at this temperature is about ρ SC = 4.5 10 −7 Ω m. Length LSC of the filaments then can be estimated from ΔRCu = ρ SC LSC/ ASC, with the total cross section, ASC, of the bundle of filaments. Using the said ASC = 10 −4 m 2, this yields the above-mentioned L SC of about 500 m. Note that this simple estimate relies on a homogenous conductor temperature, T = 100 K, of all filaments, which, as we will show, is not the reality.

If only part of the filament cross sections would be in Ohmic resistance state (it will be shown below that this is indeed the case), or if the superconductor specific resistance is larger than the ρ SC = 4.5 10 −7 Ω m, a strongly different, smaller LSC could result. The L SC of 500 m is of the same order of magnitude like the LSC = 232 m reported in [4] for design of a flux flow current limiter.

In the following simulations, either number, NFil, of filaments or filament and normal conductor lengths, LSCor LCu, respectively, or the critical current density, JCrit, will be varied:

  1. (a)

    177 ≤ NFil ≤ 881; NFil = 354 yields total conductor cross section ASC = 10 −4 m 2, again the value used in [4]. In these tests, LCu = 10 3 m, ACu = 10 −4 m 2 and LSC = 500 or 5000 m

  2. (b)

    10 2 ≤ LCu ≤ 10 5 m; NFil = 354, L SC = 500 or 5000 m, ACu = 10 −4 m 2kept constant

The LSC = 5000 m will be explained below. In the following cases (i) and (ii), “higher” and “lower” values of JCrit(T,B) are calculated from corresponding random reference values, J Crit0 (the higher JCrit0 are plotted in Fig. 13, Appendix A1).

Cases (i) and (ii) are defined as follows:

  1. (i)

    A mean value of JCrit = 3.75 10 8 A/m 2 at T = 77 K and magnetic field B = 100 mT. In text and figure captions, this value will be called the “higher” JCrit.

  2. (ii)

    In order to replicate the results reported in [4], also a mean value of tentatively JCrit = 10 7 A/m 2 is applied in the calculations (this is the “lower” JCrit taken from [4]).

A field dependence of JCrit was neglected in [4]. Random values of JCrit0 in the present calculations have been adjusted to replicate the 10 7 A/m 2, as a mean value, again at T = 77 K and B = 100 mT. This J Crit is rather small; HTSC filaments with significantly higher JCrit have become available which shall be accounted for by the higher JCrit, case (i).

All calculations apply NCut off = 20 finally obtained at t = 9 ms (and then are kept constant); this limit is applied to interpret the results in a general sense and is not necessarily restricted to faults arising from accidents and in medium voltage grids only.

Except for the superconductor, the phase impedance (0.38 Ω) is the only resistance considered in [4] (they assume that no non-zero Ohmic resistance has survived the short circuit). In the present model, a length LCu = 4.2 10 4 m of the normal conductor is required, under NCut Off = 20, to replicate the absolute value of total phase resistance (the reported 0.38 Ω). When in the following figures length LCu = 4.2 10 4 m of the normal conductor is indicated, it is done so to solely introduce an equivalent resistance of 0.38 Ω into the circuit.

Results obtained with the higher JCrit in the following figures are identified by coloured solid or open symbols or black triangles. Light or dark grey symbols concern results calculated for the design described in [4] using the lower or higher JCrit, respectively.

If there was no temperature dependence of JCrit (but only a dependence on the local magnetic field), the transport current would flow in regions of the conductor cross section where the magnetic field is small, in the present case near the axis of symmetry. But this is not confirmed in reality. Both magnetic field distribution and temperature distribution are responsible, not only for the local JCrit(x,y,t) but also for transport current distribution, J(x,y,t).

With the given filament radius and the calculated filament current, local values of B(x,y,t) as expected are in the order 10 −4 to 100 mT.

Random values of TCrit0 are shown in Fig. 14 (Appendix A1). They have to be converted to field-dependent TCrit(B), which is achieved with the corresponding inverse function derived from BCrit(T) = BCrit0 (1 − (T/ TCrit)2).

Both JCrit0 and TCrit0 are materials properties (randomly distributed in the cross section), while JCrit(T,B) and TCrit(B) are conductor properties because they reflect the actual operational states of the conductor, with the dependency on transient T and B; only these have to be considered in the numerical simulations and for calculation of stability functions.

Accordingly, to determine the transient resistive states of all parts of the conductor, the following relations have to be checked separately in each element:

$$\begin{array}{@{}rcl@{}} &&\mathrm{T}\le \mathrm{T}_{\text{Crit}}(\mathrm{B}), \text{with} \mathrm{T}=\mathrm{T}(\mathrm{x},\mathrm{y},\mathrm{t})~\text{and}\\ &&\mathrm{B}=\mathrm{B}(\mathrm{x},\mathrm{y},\mathrm{t}), \text{and} \end{array} $$
(2a)
$$\begin{array}{@{}rcl@{}} &&\mathrm{J}_{\text{Transp}}\le \mathrm{J}_{\text{Crit}}(\mathrm{T},\mathrm{B}), \text{with}~\mathrm{J}_{\text{Transp}}=\mathrm{J}_{\text{Transp}}(\mathrm{x},\mathrm{y},\mathrm{t}),\\ &&\mathrm{T}=\mathrm{T}(\mathrm{x},\mathrm{y},\mathrm{t})~\text{and}~\mathrm{B}=\mathrm{B}(\mathrm{x},\mathrm{y},\mathrm{t}), \end{array} $$
(2b)

3 Results

3.1 Temperature Fields

Figure 4a shows the calculated temperature field, T(x,y,t), in a section of 3.2 mm axial length of a single superconductor filament. It is not possible to simulate the current propagation problem over the whole length of filaments (for substantial limiting of fault current by flux flow resistances: at least hundreds of metres). Attempts to do so would not be very reasonable: We would immediately be driven back to simplifications like homogeneous conductor temperature and homogeneity of the other properties. If thermal contact between filament and matrix, and between matrix and coolant, remains the same over the whole length of a bundle containing a large number of filaments (an ideal situation but little speaks against it), the simulated short length is justified.

Fig. 4
figure 4

a Temperature field in an axial section (3.2 mm length) of a filament conductor (the diagram is provided by the finite element code). The horizontal bar indicates the range of the calculated temperature. Results are given for t = 9 ms (the end of the increase of NCut off(t)) with LSC = 232 m, LCu = 4.2 10 4 m, NFil = 354 filaments and the lower JCrit values (compare text; mean value JCrit (T = 77 K, B = 100 mT) = 10 7 A/m 2). The calculation applies random values of TCrit, JCrit and BCrit,2 and a divisor, NCut off = 20 (final value obtained at t = 9 ms). b Temperature field; same calculation as in Fig. 4a but with the higher JCrit (compare text; mean value JCrit (T = 77 K, B = 100 mT) = 3.75 10 8 A/m 2). Results are given for t = 9 ms. Note the regular variations of temperature observed at axial distances of about 600 μm that may develop to hot spots; they probably result from application of the random TCrit, JCrit and BCrit,2 in the calculations (these variations are absent in Fig. 5)

Full size image

Results are presented at t = 9 ms after the start of the simulation for LSC = 232 m, LCu = 4.2 10 4 m, NFil = 354, JCrit(T = 77 K, B = 100 mT) = 10 7 A/m 2 (mean value, the lower JCrit that equals the JCrit assumed in [4]). Temperate variation in this case is within only 0.5 K (compare the horizontal bar), in radial or axial directions within this short section. Provisionally, this speaks in favour of current limitation, if any, by flux flow resistance.

The situation changes significantly if instead of JCrit = 10 7 A/m 2 a mean value JCrit = 3.75 10 8 A/m 2 (the higher JCrit) enters the calculations (Fig. 4b). No homogeneous temperature distribution, except within small regions close to and within the metallic matrix, can be identified: Instead, radial variation of conductor temperature amounts to about 7 K. Accordingly, there are regions where T(x,y,t) is below or, close to these regions, above the individual, randomly distributed critical temperatures. Current limitation, if any, thus would intuitively be expected from solely the corresponding local Ohmic resistances. But it is clear that a distinction between solely Ohmic or solely flux flow resistive limiting of current propagation becomes questionable if there are temperature profiles, with temperature variations of this magnitude, in a conductor.

Both Fig. 4a and b alone do not allow to definitely make a decision between possibly existing flux flow or Ohmic resistances current limiting, respectively. Stability functions have to be checked (Section 4.1) whether besides control of temperature fields this additional method could be necessary and sufficient to identify the physical origin of current limitation.

When instead of random values of TCrit, JCrit, BCrit,1 and BCrit,2 a set of variables is used that apart from their individual field or temperature dependency would be identical in each element, we obtain a very regular, stratified temperature distribution (Fig. 5). Accordingly, the variations seen in Fig. 4a, b might be the consequence of using random TCrit, JCrit, BCrit,1 and BCrit,2. Since these were intended to account for deviations from ideal conductor properties, the well-known hot spot problem in first-generation HTSC (prepared by the OPIT method) might be explained by statistical variations of conductor materials quality or from tolerances in production processes.

Fig. 5
figure 5

Temperature field as in Fig. 4a, b; results have been obtained immediately before the start of the disturbance (t = 6.5 ms) using TCrit, JCrit, BCrit,1 and BCrit,2 identical in each element (no random numbers, but with corresponding temperature or field dependency, respectively). Note the homogeneous stratification of the temperature distribution within the superconductor filament

Full size image

An example for excursion of local conductor (element) temperature, T(x,y,t), with time is shown in Fig. 6 for a different number NFil of identical filaments. After the first 3 ms of the simulation (a numerical settling procedure, with fluctuations from numerical instabilities), element temperatures gradually converge to values near critical temperature to obtain quasi-stationary, discrete states (this settling procedure is shorter than the period of time that is needed to generate bubbles at the superconductor/coolant interface, to justify modelling heat transfer to the coolant across a smooth metallic surface under static conditions).

Fig. 6
figure 6

Element temperature, T(x,y,t), calculated at an axial distance of 100 μm from the lower end of the short conductor section at positions close to the superconductor/matrix interface, for different numbers, NFil, of identical filaments switched in parallel, then in series, to the normal conductor. Coloured symbols apply LSC = 5000 m and LCu = 10 3 m and the higher JCrit. Solid black triangles apply LSC = 500, LCu = 10 4 m and the higher JCrit; solid light or dark grey diamonds refer to the flux flow limiter design of [4], with LSC = 232 m, LCu = 4.2 10 4 m and the lower and higher JCrit, respectively. All results have been calculated using a divisor, NCut off = 20 (final value), and random critical variables that are different in each element (but with the same field or temperature dependency)

Full size image

3.2 Phase and Filament Resistances

Figure 7a, b shows how total (AC) phase resistance and total (AC) filament resistance develop with time, for different numbers of filaments and different lengths of filaments and normal conductor, respectively.

Fig. 7
figure 7

a Coincidence of total (AC) phase resistance (open coloured and light and dark grey circles) and total (AC) filament resistance (solid coloured diamonds), for different numbers, NFil, of identical filaments. Coloured diamonds are calculated with LSC = 5000 m, LCu = 10 3 m and the higher JCrit. Solid black triangles apply LSC = 500, LCu = 10 4 m and again the higher JCrit. Solid light or dark grey diamonds and circles refer to the flux flow limiter design of [4], with LSC = 232 m, LCu = 4.2 10 4 m and the lower and higher JCrit, respectively. As before, all results are obtained with the divisor NCut off = 20 (final value) and random, but equally field- or temperature-dependent variables. Coincidence is obtained only between open and solid coloured symbols. In other cases (all observed with short filament lengths), the residual phase resistance is larger than the filament resistance, and no substantial current limitation can be obtained. b Coincidence of total phase resistance calculated as before (Fig. 7a) but for different lengths, LCu, of the normal conductor in the phase (initiating different current loads) and with constant number, NFil = 354, of identical filaments. Coloured solid and open symbols apply to LSC = 5000 m, LCu = 10 2, 10 3 or 10 4 m and the higher JCrit. Coincidence is obtained only with the higher loads (permitted by the smaller LCu) onto the filaments

Full size image

In Fig. 7a, coloured open symbols (the final total resistance of the phase) coincide with total filament resistances if LSC = 5000 m (coloured diamonds). This indicates that only in this case will filament resistances finally become responsible for the residual total resistance of this phase. Such coincidence is not observed for shorter conductor lengths (LSC = 500 m, or for the system described in [4], with LSC = 232 m only). In these cases, the residual phase resistance still is larger than the corresponding filament resistance. No efficient current limitation can be expected if current limiter resistance is much smaller than the total residual phase resistance.

The same calculation is performed (Fig. 7b) with a constant NFil but a different load on the filaments initiated by different lengths LCu that specify current load on the filaments. No coincidence is obtained if LCu ≥ 10 4 m.

In summary of Fig. 7a, b, total phase resistance only then results from overwhelming total filament resistance if their length is at least LSC = 5000 m and if there is a higher current load which requests LCu below 10 4 m (the current load is shown in Fig. 8).

Fig. 8
figure 8

Total (nominal plus fault) current for different numbers, NFil, of identical filaments (solid coloured diamonds) calculated using LSC = 5000 m, LCu = 10 3 m and the higher JCrit. Solid black triangles apply LSC = 500, LCu = 10 4 m and again the higher JCrit. Solid light or dark grey diamonds refer to the flux flow limiter design of [4], with LSC = 232 m, LCu = 4.2 10 4 m and the lower and higher JCrit. Solid lilac circles denote transport current if there is no superconductor and no disturbance (no short circuit or the like) of the normal conductor, while solid yellow circles indicate current with no superconductor but with the disturbance of the normal conductor initiated by the NCut off. The sharp peak of the yellow circles and of the solid black triangles results from the discrete time steps in the simulations. All results have been obtained with random (but equally field- or temperature-dependent) critical variables

Full size image

It is obvious from Fig. 7a, b that the onset of a fault current at t = 6.5 ms is not reflected by a corresponding increase of calculated filament resistances. The fault current does not (or does not sufficiently) trigger a substantial reaction of the filaments. Instead, it is the filament resistance that exists from the beginning of the simulations to which the total phase resistance converges finally. This indicates there might be Ohmic losses over all this period, not only after a fault has been initiated.

Absence of a triggering signal also concerns the design of [4]: When using the lower JCrit, the conductor temperature in Fig. 6 (light grey diamonds) remains very close to 77 K. When instead using, for the same design, the higher JCrit (dark grey diamonds), a substantial increase of conductor temperature is not observed before t ≥ 7.5 ms. Filament resistances generated by concept [4] are too small, at least under the small current load (LCu very large, 4.2 10 4 m, needed to replicate the assumed permanent impedance of 0.38 Ω) to compensate reduction of total phase resistance.

Can substantial current limitation be obtained with concept [4] if the load would be increased? By assuming reduced lengths LCu of the normal conductor below 10 4 m?

The answer can be given from inspection of the solid black triangles in Figs. 6 and 7b: (a) The conductor temperature in Fig. 6 is driven close to or above critical temperature, which means the limiting concept no longer relies on flux flow but mostly on Ohmic resistances, and (b) total filament resistance in Fig. 7b still would be too small to coincide with the total phase resistance.

A second attempt might be more successful: Length LSC of the filaments (232 m in concept [4]) could be increased. But the black triangles in Fig. 6 indicate an increase to LSC = 500 m would not be sufficient while an increase to LSC = 5000 m would early drive conductor temperature out of the flux flow regime (coloured diamonds in Fig. 6). Accordingly, it is not clear that substantial limitation could practically be achieved with flux flow resistive conductor states; a thorough re-design becomes necessary.

Shimizu et al. [4] assume that the FCL instantly, at the very beginning of a fault, generates a resistance (and would also be able to pass a load current immediately after fault clearing). At least the first assumption is questionable (compare again the gradualincrease of element temperature in Fig. 6, solid dark grey diamonds and solid black triangles).

3.3 Residual Total Current

The total phase current (nominal transport plus fault currents), calculated from nominal system voltage and from the total phase resistances (Fig. 7a, b), is shown in Fig. 8. This figure also shows excursion of current if (a) there is no superconductor and no disturbance (no short circuit or the like) of the normal conductor (solid lilac circles) while (b) solid yellow circles indicate a current with no superconductor but with the disturbance of the normal conductor.

In medium voltage distribution systems, traditional power switches (vacuum interrupters) are assessed to 12 to 24 kV, rated current 4000 A and rated short circuit breaking current of 60 kA. The current peak (yellow circles in Fig. 8) is higher, more than 120 kA, but is within range of fault currents that in medium voltage electrical systems may arise (up to 250 kA if there is absolutely no current limitation). Short circuits presently are handled by conventional current (Is) limiters. Without protection, no electrical, medium voltage system could physically withstand this load, even within the shortest periods of time.

Accordingly, it is this extreme case (yellow circles in Fig. 8) to which the results obtained for the total limited current (coloured diamonds) have to be compared. In the other cases (black triangles, light and dark grey diamonds), a comparison has to be made with respect to the corresponding peaked curves.

From comparison of the different curves in Fig. 8, the filaments indeed provide substantial reduction of the total (nominal and fault) current, without runaway of their temperature, but a direct response to the simulated fault circuit, at a specific time t′ after onset of the fault (t ≥ 6.5 ms), cannot be identified. Instead, if we neglect an initial settling period, it seems limitation is achieved by the filaments from the beginning, t = t0, of the simulations. But a limitation is clearly seen and will explicitly be shown later (Fig. 11).

As final conclusions of Section 3, when using a bundle of filaments and a model conductor, the properties of which are not too far away from conductors in technically realised devices, we see that (a) conductor temperature and, accordingly, critical and transport current distribution in these filaments are not homogeneous and (b) efficient fault current limitation, by solely flux flow resistance, is hard to achieve. The amount of current limiting by the filaments is clearly evident, but a sudden increase of filament resistance triggered by onset of a fault cannot be identified.

4 Stability and Correlation with Current Limiting

4.1 Stability Functions

Though it appears current limitation by phase change is observed in Figs. 7a, b and 8, a safe decision upon the real limitation mechanism (Ohmic or from flux flow resistance) cannot be made up to this point.

In this section, we will check whether stability functions, an integral view of critical current density distributions, or stability functions plus temperature fields, could provide this information. If it is clear that current limitation is solely by Ohmic resistances, stability functions reflect temperature distribution, T(x,y,t), in the conductor. For example, oscillating temperature profiles should be reflected by corresponding oscillations of the stability function, as was observed in [10, 11].

Experimental investigations of JCrit of high-temperature superconductors (compare the original literature cited in [9]) proved the relation between critical current density and temperature

$$ \mathrm{J}_{\text{Crit}}(\mathrm{T})=\mathrm{J}_{\mathrm{Crit0}} [1~-~\mathrm{T}/\mathrm{T}_{\text{Crit}}]^{\mathrm{n}} $$
(3a)

is applicable also to these materials if an exponent n = 2 is applied. To take into account the dependence of JCrit on also the local magnetic field (flux flow density, B), we apply as an approximation a standard relation

$$ \mathrm{J}_{\text{Crit}}(\mathrm{T},\mathrm{B})=\mathrm{J}_{\text{Crit}}(\mathrm{T})/(\mathrm{B}_{\mathrm{0}}+\mathrm{B}(\mathrm{t})) $$
(3b)

with local B(t) and B0 a constant.

The stability function, Φ(t), originally assumes critical current density to solely depend on conductor temperature. In this case, there are non-zero contributions to the stability integral

$$ 0~\le {\Phi} (\mathrm{t})=~1~-\smallint \mathrm{J}_{\text{Crit}}(\mathrm{x},\mathrm{y},\mathrm{t}) \text{dA}/ \smallint \mathrm{J}_{\text{Crit}}(\mathrm{x},\mathrm{y},\mathrm{t}_{\mathrm{0}}) \text{dA}~\le ~1 $$
(4a)

only if element temperature T(x,y,t) < TCrit(x,y,t); otherwise, JCrit(x,y,t) is zero. Equation 4a is approximated by

$$ 0~\le {\Phi} (\mathrm{t})=~1~-{\Sigma} \mathrm{J}_{\text{Crit}}(\mathrm{x},\mathrm{y},\mathrm{t}) \text{dA}/ {\Sigma} \mathrm{J}_{\text{Crit}}(\mathrm{x},\mathrm{y},\mathrm{t}_{\mathrm{0}}) \text{dA}~\le ~1 $$
(4b)

The summations are taken over all superconductor elements in planes y= const; the result is summed up over all planes and finally divided by the total number of planes in the conductor. The result is the stability function averaged over conductor volume. The differential dA in (4b) denotes element cross section.

The stability function assumes values 0 ≤ Φ(t) ≤ 1 of which Φ(t) = 0 are the optimum and Φ(t) = 1 the worst case. Time t0 = 0 denotes the start of the present simulation; at this time, all element temperatures are at their original values, T(x,y,t0) = 77 K, and critical current density, JCrit(x,y,t0), is maximum. Its distribution at t0 accordingly is homogeneous, apart from statistical fluctuations caused by the random JCrit0 (the materials property). This situation quickly changes at times t > t0.

In previous stability calculations [8–11], in (4a, 4b), only the dependence of JCrit on temperature was considered; calculations were performed for standard disturbances. These were not induced by a nominal transport or fault current but were of the familiar type, like transformation of mechanical stress energy to thermal energy, absorption of particle radiation or the like. In the present paper, however, we have to apply temperature and field dependence of JCrit for calculation of stability functions because J > JCrit, too, constitutes a disturbance, by flux flow losses. A problem then arises from application of (4a, 4b):

When assuming flux flow resistive conditions, the conductor temperature is below critical temperature, which means integrals or summations in (4a, 4b) might apply values of JCrit(x,y,t) close to JCrit(x,y,t0). Stability function then is small, and maximum zero-loss transport current

$$ \mathrm{I}_{\text{max}}(\mathrm{t})=\mathrm{J}_{\text{Crit}}[\mathrm{T}(\mathrm{x},\mathrm{y},\mathrm{t}=\mathrm{t}_{\mathrm{0}})] [1~-{\Phi} (\mathrm{t})] \mathrm{A}_{\mathrm{SC }} $$
(5)

is close to Imax(t0), with ASC the total conductor cross section.

But flux flow resistances and corresponding losses are not directly correlated with conductor temperature; there is at best a correlation with temperature indirectly by the temperature dependence of normal conduction resistivity, ρ NC, in (1). Only the condition T < TCrit, at all times, t, has to be fulfilled. Thus, flux flow losses are correlated neither with values J Crit nor with Φ. Stability function Φ and maximum zero-loss current, Imax(t), accordingly can reasonably be calculated from (4a, 4b) and (5) only for Ohmic resistance states (as was done in [8–11]) or, approximately, if there are only few elements that show flux flow resistance. If flux flow resistance would strongly contribute to total resistance, the procedure using (4a, 4b) and (5) is no longer applicable.

This is illustrated in Fig. 9 that shows stability functions for a different number of filaments. In all cases, the dependence of (random) JCrit on temperature and magnetic fields has tentatively been applied to (4a, 4b). Under small magnetic fields, as is mostly the case in the present simulations, the difference between JCrit(T) and JCrit(T,B) is small. The obtained Φ thus are very close to 1 since the T(x,y,t) are close to or exceed TCrit(x,y,t). The large Φ indicate that indeed only few elements are at temperatures below TCrit; in other words, an overall phase change to normal Ohmic resistance states has occurred, with little contribution of flux flow to total resistance. The application of (4a, 4b) and (5) thus was justified.

Fig. 9
figure 9

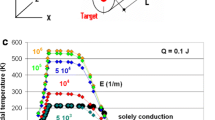
Volume averaged stability functions, within 5 ≤ t ≤ 10 ms, for different numbers, NFil, of identical filaments. Coloured diamonds apply LSC = 5000 m, LCu = 10 3 m and the higher JCrit. Scattering of the data results from the random JCrit0 (the materials properties). Solid dark grey diamonds refer to LSC = 232 m, LCu = 4.2 10 4 m, NFil = 354 (the flux flow limiter design of [4]) and the higher JCrit (this curve reasonably can be calculated only for t > 8 ms; compare text). Results obtained with the same LSC, LCu and NFil, but with the lower JCrit, are not shown (the stability function again cannot be applied; if yet a formal calculation is performed, the stability function at all t ≤ 10 ms, with very small variations amounts on the average to 0.65, the average taken over six planes located at the same axial positions as the JCrit in Figs. 5b and 10)

Full size image

Though it appears at first sight that it is only a theoretical discipline, the following relations shall be checked whether they would provide benefits of practical interest.

(1) Given T(x,y,t) > TCrit(x,y,t), then JCrit = 0 and Φ = 1. This is clear from the previous comments (and is the natural way of operation of an Ohmic resistive FCL). Check whether the reverse (1 ′) of (1) is true:

(1 ′) From Φ close to 1, we cannot uniquely conclude T > TCrit. Given a large transport current, it might create a sufficiently large magnetic field that at sufficiently high temperature, in particular if it is close to critical temperature, exceeds BCrit,2(T) = BCrit,2(x,y,t), with T = T(x,y,t). Accordingly, the reverse relation (1 ′) to (1) “If is close to 1 (which means the JCrit(x,y,t) are close to zero), then T(x,y,t) > TCrit(x,y,t)”, holds only if the magnetic field is small against BCrit,2(x,y,t). In the present simulations, local B(x,y,t) fulfil the condition B(x,y,t) < < BCrit,2 (x,y,t) except for temperatures very close to the critical temperature. This means that under the condition “B(x,y,t) small”, the reverse (1 ′) is true. We have a logically, bijectively connected correlation between stability, critical current density and temperature.

The large Φ observed in Fig. 9 accordingly indicates that element temperature, in a very large fraction of the superconductor volume, is above critical temperature (the result already seen in Fig. 4b). This conclusion is also correct in case of the design in [4], but only for t > 8 ms, and the stability function in Fig. 9 (dark grey diamonds) is plotted for this period only.

The question then is whether a bijective correlation exists also between superconductor stability and current limiting. What can we learn for superconductor safety if such a correlation would not exist?

4.2 Correlation of Stability with Current Limiting

Distribution of critical current density, JCrit(T,B), for the flux flow resistance limiter design [4], calculated with the lower JCrit, is shown in Fig. 10. The almost homogeneous distribution reflects the homogeneous temperature field in Fig. 4a (temperature variation within 0.5 K) and Fig. 6 (light grey diamonds). The stability function, if again tentatively calculated with an extension of (4a, 4b) to also include the dependence of JCrit(x,y,t) on B(x,y,t),

$$\begin{array}{@{}rcl@{}} &&0~\le {\Phi} (\mathrm{t})=~1~-\smallint \mathrm{J}_{\text{Crit}}[\mathrm{T}(\mathrm{x},\mathrm{y},\mathrm{t}), \mathrm{B}(\mathrm{x},\mathrm{y},\mathrm{t})] \text{dA}/ \\&&\smallint \mathrm{J}_{\text{Crit}}[\mathrm{T}(\mathrm{x},\mathrm{y},\mathrm{t}_{\mathrm{0}}), \mathrm{B}(\mathrm{x},\mathrm{y},\mathrm{t}_{\mathrm{0}})] \text{dA}~\le ~1 \end{array} $$
(6)

depends on ratios JCrit(t)/ JCrit(t0), with JCrit(t0) = 10 7 A/m 2 (“tentatively” means before it is clarified that there are only or strongly dominating Ohmic resistance states). Apart from statistical fluctuations, these ratios closely approach unity, and the stability function accordingly should be small.

Fig. 10
figure 10

Distribution of critical current density in a superconductor filament, calculated at t = 9 ms after the start of the simulation (the end of the increase of NCut off(t)) using LCu = 4.2 10 4 m, LSC = 232 m and NFil = 354 (the design reported in [4]) with the lower JCrit. Axial positions (distances from the lower end of the conductor section) indicated by blue, red, dark green, light green, dark yellow and lilac diamonds are 0.1, 0.7, 1.3, 1.9, 2.5 and 3.1 mm, respectively

Full size image

A limitation factor Ψ shall be defined as the ratio between absolutely unlimited total (nominal plus fault) current to total limited current. In Section 4.3, this concerns a comparison between solid yellow circles and solid coloured diamonds, and between black triangles and grey diamonds with the corresponding peaked curves. Note that Fig. 11 shows Ψ in dependence on LCu (Ψ is given for a different current load onto the filaments), not the dependence of Ψ on LSC.

Fig. 11
figure 11

Limitation factor (damping), Ψ, the ratio of total (nominal plus fault) unlimited current to limited current, obtained with NFil = 354 superconducting filaments, all switched in parallel and in series to the normal conductor. Results refer to different lengths, LCu (different current loads onto the filaments), of the normal conductor (coloured diamonds); these are obtained with LSC = 5000 m and the higher JCrit. Solid black triangles apply LSC = 500, LCu = 10 4 m and the higher JCrit. Solid light grey diamonds refer to the flux flow limiter design of [4], with LSC = 232 m, LCu = 4.2 10 4 m and the lower JCrit (application of the higher JCritcoincides with the light grey symbols). Substantial current limitation (Ψ about ≥2) is observed only with the shorter normal conductor lengths (increased load onto the filaments)

Full size image

(2) Given Φ = 1, then JCrit(x,y,t) = 0, and T(x,y, t) > TCrit(x,y,t) and Ψ are accordingly large. Again, this correlation is clear from the previous comments. Check whether the reverse (2 ′) or (2”) is true: Given large Ψ, how large is Φ?

(2 ′) Substantial current limiting, Ψ, can be achieved if the conductor length, LSC, is strongly increased, or the conductor cross section, ASC, is made sufficiently small. All this does not alter JCrit0, a materials property, and accordingly does not alter Φ, if it is tentatively calculated from (6), and for small B(x,y,t). Strong current limiting, Ψ, then either suggests T(x,y,t) > TCrit(x,y,t) that yields JCrit(x,y,t) = 0 and Φ = 1 (a first extreme case) or, under variation of conductor dimension (large LSC, small ASC) and T(x,y,t) < TCrit(x,y,t), it suggests Φ → 0, the other extreme case. This means: Contrary to (1) and (1 ′), a correlation (2) and (2 ′) is not bijective.

Inspection of solely Ψ, if one does not know anything about JCrit(T,B), with T = T(x,y,t) and B = B(x,y,t), also does not allow a decision (2”): It is not clear that the device would be stable against quench. Given large Ψ, how large is Φ? Is the device stable?

(2”) Large Ψ can be obtained with large LSC and small ASC (large conductor resistance). The conductor temperature shall be below but possibly close to TCrit (most of the conductor cross section in flux flow, but a considerable part in Ohmic resistive states). In this case, flux flow resistance or Ohmic losses might quickly drive the temperature beyond this limit (compare the solid dark grey symbols in Fig. 6). Thus, a correlation also between (2) and (2”) is not bijective. This implies little stability of the device. Under practical aspects, serious consequences for conductor safety would arise if temperature and field distribution is not controlled in parallel to the control of Ψ.

Finally, it would be interesting to check whether the propagation velocity of a normal zone in YBaCuO cables as reported in [23], in relation to a propagation of the temperature front, both calculated with a finite element method, can be explained by a similar correlation analysis as presented above, and whether inhomogeneities and current percolation have been observed. This will be investigated in a separate paper.

4.3 Limitation Factors

Limitation factors, Ψ, to fault current can be extracted in Fig. 11 from the ratio between solid yellow circles and coloured diamonds for long conductor lengths, LSC = 5000 m, and for short conductor lengths, LSC = 500 m (solid black triangles) or LSC = 232 m (light grey diamonds, the flux flow limiter design of [4]). A modest limitation is observed: The total unlimited current (solid yellow circles) is reduced by about a factor Ψ ≤ 5 to the total limited current. This result is achieved with the larger conductor lengths. The reduction of unlimited fault current is the higher the larger the load (the fault current) onto the filaments. For the short conductor length, no substantial limitation is observed.

5 Summary

If besides standard disturbances (like release of mechanical energy) the transport current itself constitutes disturbances, the determination of local temperature and of local current distribution becomes mandatory. This is necessary to appropriately handle stability models and for making a step forward to conclude under which resistance states (Ohmic or flux flow) current propagation would be limited.

Temperature profiles observed in this paper, with variations ΔT up to about 7 K, do not allow a clear distinction between Ohmic resistive or flux flow resistive fault current limiting concepts. Though frequently made in the literature, this separation is highly questionable. Ohmic resistive and flux flow resistive states may locally coexist, side by side, but are not very stable in conductor volume.

The magnitude of the nominal plus fault current may fluctuate in the interior and percolate through a polycrystalline, porous conductor by a network of grains and grain boundaries.

Any superconductor, even if perfectly designed and manufactured with highest available precision, over extended lengths in reality never will exhibit perfectly homogeneous materials properties. An attempt has been made in this paper to account for this problem by means of a random variation of the most important conductor materials properties; it is a potentially new method to improve the safety of electrical circuits incorporating superconducting components and reliability of stability predictions, but additional work is required to verify this concept with different superconductor materials and conductor architectures.

Unique (bijective) correlations cannot be found between stability and current limiting if there is flux flow resistivity, which probably constitutes a safety problem for all cases of current propagation when the transport current exceeds critical current density.