The Additive Approximation for Heat Transfer and for Stability Calculations in a Multi-filamentary Superconductor - part A

Abstract

This paper addresses the applicability of the “additive approximation” of total thermal conductivity in heat transfer and in superconductor stability calculations. If cases (a), (b) and (c) denote total (conductive plus radiative), or only conductive or only radiative heat flux, respectively, each flux $\dot{q}$ calculated with Fourier’s conduction law using the corresponding thermal conductivity (λ_a, λ_b, λ_c), the additive approximation would be confirmed if the heat flux difference Δ$\dot{\mathrm{q}}$ = ${\dot{\mathrm{q}}}_{\mathrm{a}}-$${\dot{\mathrm{q}}}_{\mathrm{b}}-$${\dot{\mathrm{q}}}_{\mathrm{c}}$, at any position of an investigated object, and at any time, converges to zero. This is not trivial because of the strong, non-linear temperature dependence of the radiation component. Heat transfer calculations including radiative transfer are presented in this paper, first for simple, homogeneous, thin film test samples and later for a multi-filamentary BSCCO 2223 superconductor. The simulated heat sources either result from a sudden increase of conductor boundary temperature or from flux flow and Ohmic resistances in the superconductor under a disturbance (like transport current exceeding critcal current density). The conductors, though very thin, are non-transparent to mid-IR radiation. Validity of the additive approximation is critical for superconductor stability against quench. Based on the applied numerical scheme, a hypothesis is suggested concerning correlation of the results of the simulation (the “numerical space”) with the experimental situation (the “physical reality”): Non-convergence of the numerical scheme might tightly be correlated with occurrence of a quench in the simulated superconductor.

1 Introduction

This paper addresses the validity of the “additive approximation” of total thermal conductivity in analytic and numerical calculations of heat transfer. Assume that there is more than only one heat transfer mode, like conduction, radiation or convection, all parallel to each other, in any compact or dispersed, solid or liquid medium: Is it then allowed to calculate heat flux with Fourier’s conduction law simply by addition of the corresponding thermal conductivities to a total value? It is not clear that a radiative conductivity would exist in all heat transfer problems; this will be explained later. But if it exists, is it then permissible to apply this conductivity and the additive approximation in analytic or numerical (finite element) simulations of heat transfer in a solid?

At first sight, the problem (why not simply add conductivities?) seems to be trivial. However, verification of the additive approximation turns out to be quite complicated if radiative heat transfer, parallel to conduction, becomes involved. The same problem would come up if there are, all in parallel, other pairs or combinations of heat transfer modes.

Numerous investigations reported in the literature have assumed that the applicability of the additive approximation is justified under the strict condition that the objects, besides being non-transparent, are homogeneous and have simple geometrical (mechanical) structure. See the results reported in traditional volumes like Sparrow and Cess [1], Chap. 9.2, or Siegel and Howell [2], Chap. 19–3, in particular Eq. (19–23). These volumes include citations to original work, frequently to the contributions by Viskanta and Grosh wherein the same assumptions were made.

The number of papers that apply the additive approximation in superconductivity is large, too, but it is not clear that applicability of this approximation always has been checked. It is even not clear that available computer codes (usually black boxes to the users) always would check the pre-condition (large optical thickness, homogeneity) for successful application of this approximation.

There are many objects composed of materials of which their structural and their thermal transport properties are strongly inhomogeneous. But the most critical problem with application of the additive approximation arises when modelling multi-mode heat transfer in thin films. Besides the large variety of thin film applications (electronic devices, protective coatings, photo-voltaic cells), examples are multi-filamentary or thin film, coated superconductors. A challenging example is the BSCCO 2223 superconductor tape. This “first generation” (1G) superconductor consists of filaments of superconductor material embedded in a metallic (Ag) matrix. A cross section of this conductor will be shown later (Figs. 1 and 2a, b in Sect. 2).

Fig. 1

a–c Microstructure of a multi-filamentary superconductor tape showing filaments and grains (schematic, all dimensions are in micrometres; overall tape dimensions are given in Fig. 2a, b for the Long Island Cable Superconductor). The superconductor part of the tape is embedded in a metallic matrix. Part (a) shows a section of the tape with several filaments (black rectangles of 20 to 30-μm thickness and 300- to 400μm width) that are composed of grains (flat, thin plate-like objects, schematic, not to scale). Matrix material (Ag) is schematically indicated by light-green background. Part (b) is an enlarged section of a filament (the uppermost filament in part (a), for identification enclosed in a blue rectangle) showing grains as solid black lines; the light-grey part of the filament cross section is empty. Part (c) The real layer structure of the slightly curved, plate-like grains compressed to almost horizontal orientation in a single filament, a result typically achieved after a series of powder in tube manufacturing steps. Because of the large anisotropy ratio of the grains, they can be considered, from a pure thermal transport aspect, as roughly flat (the better the orientation, the larger the critical current density of the tape). Length of the bar (to the lower-right of the figure, part c) indicates 5 μm. The Ag matrix material is removed from this sample. This figure, already used in [14], is copied from [24]

Fig. 2

a Cross section of the BSCCO 2223/Ag Long Island Cable superconductor tape [3]. A number N = 91 identical filaments is integrated in the total cross section of one multi-filamentary tape, and a large number of tapes is switched in parallel to yield total superconductor cross section (10⁻⁴ m²). Dimensions of filaments and tape in x (horizontal) and y (vertical) directions are as follows: x = 280 μm (filament) and 3.84 mm (total tape width), and y = 20 μm (filament) and 264 μm (total tape thickness), respectively. b Finite element model of the left half of the conductor cross section showing superconductor filaments (black) and matrix material (Ag, light-grey). The thick dashed line denotes axis of symmetry, x = 1.92 mm. Thin white lines indicate details of the finite element, mapped meshing (with a total number of elements N_El between 4032 and 29580). This scheme is the same as used in previous reports [19,20,21]

The BSCCO 2223 superconductor roughly can be considered a thin film (thickness about 250 to 300 μm) but with strongly different geometrical dimensions of its filaments and Ag matrix inter-layers. Not only is the solid thermal conductivity of the BSCCO 2223 material strongly different from the conductivity of the Ag matrix, but its solid conductivity also is highly anisotropic. Calculation of heat transfer within this object (tape) is a challenging task, in particular under transport current and magnetic field. Yet heat flux, temperature and current distributions and conductor stability calculations by the finite element method, in this conductor and its multiples arranged to a cable, have been reported recently by the present author (see later for citations). These papers investigate superconductor stability against quench under disturbances (conductor stability and disturbances will be defined in the next sections). All these simulations have applied the additive approximation. It is thus important to confirm its applicability since the results of the reported stability calculations strongly rely on the validity of this approximation.

The paper is organised as follows: We will first explain the overall modelling problem: Radiative transfer in a particulate, thin-film superconductor and how to determine a radiative conductivity in this material. Then, a short description of superconductor stability is given. The numerical calculations, in the then following sections, apply a multi-step approximation approach: We start with simple heat transfer calculations assuming homogeneous conductor properties and simple disturbances (heat pulses applied to the upper surface of a tape). Subsequently, the proper problem (multi-filamentary cross section, with its strongly inhomogeneous structural and thermal transport properties) will be studied, again under simple disturbances. Finally, realistic, distributed disturbances within the conductor cross section resulting from internal heat sources (thermal losses generated from transport current exceeding critical current, including magnetic field and heat transfer to the coolant) will be applied in the finite element simulations.

2 The Overall Radiative Transfer Problem in a Particulate Superconductor

Figure 1a–c show the microstructure of a multi-filamentary superconductor tape showing filaments and grains (schematic, all dimensions are in micrometres). The tape usually consists of a large number of filaments that are composed of grains (flat, thin plate-like objects). Note the hierarchy, ordered by dimensions: grains, filaments, tapes, cables; deviations from this sequence or other designations occasionally appear in the literature, like a single tape assigned “a conductor” to wind a magnet. Matrix material (Ag) in the tape is schematically indicated by light-green background. The real layer structure of the slightly curved, plate-like grains is shown in part (c) of the figure. The grains are arranged in almost horizontal orientation in a single filament, a result typically achieved after a series of powder in tube manufacturing steps (a standard method in metallurgy).

Because of the large (x,y) anisotropy ratio of the grain solid thermal conductivity, the grains can be considered, from a pure thermal transport aspect, as roughly flat (the better their uniform, horizontal orientation, the larger the critical current density of the tape). The Ag matrix material is removed from the micrograph sample in part (c).

Figure 2a and b show a successful realisation of this powder in tube manufacturing concept, the cross section of a tape of the BSCCO 2223/Ag Long Island Cable superconductor [3]. The multi-filamentary tape of this conductor consists of N = 91 identical filaments (black in Fig. 2a) all embedded in the metallic (Ag) matrix (light-grey) and switched in parallel. Several tapes, again switched in parallel, yield a superconductor cable.

For comparison, the finite element (FE) scheme for calculation of transient temperature fields and heat flux in this tape is roughly shown in Fig. 2b (here using mapped 2D meshing; details of the calculations will be explained later, Sect. 5).

Thickness of filaments and tape is about 20 to 30 and 250 to 300 μm, respectively. Thickness of the grains is very small in relation to thickness of the filaments, compare Fig. 1 part (c).

In the following, we do not model the radiation contribution of the filaments in a Ag-environment (the Ag matrix). Instead, it is the radiative conductivity of the grains within in a filament that has to be modelled to calculate the radiative conductivity of the filaments from the result obtained for the grains.

Likewise, a solid conductivity of the filaments hardly can be measured with sufficient accuracy. Therefore, on the same level within the said hierarchy (grains, filaments, tapes and cables), we apply the conductivity measured with continuous superconductor material to calculate the conductivity of the grains, and from the result the conductivity of the filaments. This has to be done taking into account anisotropy, porosity, orientation of the grains and contact resistances.

In engineering heat transfer problems like heat transfer in packed beds, radiative and solid conductivity can be calculated by the well-known procedures described by Tsotsas and Martin [4], Vortmeyer [5], Wakao and Kato [6]. These and many other references explain cell models applied for these calculations.

For the calculation of a radiative conductivity, cell models of course could be directed onto the superconductor filaments embedded in a continuum. Radiation propagation then would be modelled by geometrically defined radiation exchange factors that take into account particle (filament) size and shape and its surface properties. Classical cell models usually assume a highly symmetric arrangement of constituents in 3D space.

However, neither do we have a continuum transparent to radiation nor are the filaments superconductors per se, or the filaments themselves a homogeneous material. Also, cell models assume that the wavelength of incoming radiation should be small against particle dimensions. Like the tiny ceramic particles in thermal super-insulations (evacuated powders, fibres), grains in the 1G multi-filamentary, high-temperature superconductors (Fig. 1c) are small against wavelength. Their dimensions thus are not very suitable for application of the relations from standard cell models between particle dimension and radiative conductivity (the minute particle dimensions in thermal super-insulations and of the grains in superconductors then might eventually result in zero radiative conductivity).

A better solution is provided by approximation of the grains not as a material but as a radiation continuum, a method well established in thermal super-insulations. There, the analysis is not based on geometrically defined radiation exchange factors and surface properties but on classical radiative transfer methods [7,8,9], and in particular, on radiation as a diffusion process.

The diffusion model [10] can be applied provided the optical thickness of the continuum is large. Large optical thickness indicates that the object under study is non-transparent to incoming radiation.

The diffusion model of radiative transfer applies the mean free path of photons between successive collisions of radiation and IR-optical inhomogeneities like solid particles, variation of refractive index (or bubbles in a liquid). In the present case, i. e. operation of the multi-filamentary, BSCCO 2223 superconductor below its critical temperature (about 108 K), these are mid-IR photons with wavelength of about 30 μm. This is not very small against grain particle (or even filament) dimensions.

The mean free path relies on the extinction properties of the superconductor material (these depend on particle geometry, the ratio of particle radius to incoming wavelength, the refractive index and the clearance between neighbouring particles). The calculations provide also the Albedo of single scattering to come to a decision whether there are overwhelming absorption/remission or scattering (radiation/solid particle) interactions.

Calculation and measurement of extinction cross sections of standard materials (dispersions of solid particles, gases, liquids) have frequently been reported in the literature; besides classical volumes [11, 12], there is a large variety of papers, see e. g. the citations in [13]. But their application to particulate superconductors apparently has never been reported. This application has only very recently been described [14] using three different methods that include application of rigorous scattering theory.

3 Survey: Stability of Superconductors

A superconductor is stable if it does not quench under a disturbance, which means if the correlation of electrons to electron pairs is strong enough to compensate increase of internal energy arising from conductor movement (with immediate transformation of mechanical into thermal energy), fault currents, absorption of radiation or momentary cooling failure. Even a small decrease of local critical current density, from a corresponding local increase of superconductor temperature, can initiate losses, lead to further temperature increase and, as a consequence, to a quench.

Quench proceeds on very small timescales (milliseconds or less) and frequently leads to local damage or even to destruction of the conductor. Quench can be avoided by appropriate design of superconductors (filaments, thin films) using stability models.

Stability models yield predictions on permissible conductor geometry and dimensions. Traditional stability models assume homogeneous superconductor temperature, compare, e. g. [15, 16]. It appears this assumption is approximately fulfilled only in exceptional cases, like in LHe-cooled superconductors, but not in high temperature, multi-filamentary or thin film, coated superconductors. Improved stability calculations accordingly rely on local temperature fields in the superconductor cross sections.

A significant step into this direction was presented by Flik and Tien [17]. This step is important since superconductor critical current density and critical magnetic field strongly depend on conductor temperature. A 3D finite element simulation of temperature, electric field and current density evolution in a current limiter was presented in [18], with analysis of current flow in superconductors and their response to magnetic fields. In each element of our BSCCO 2212 and YBaCuO 123 at typical inhomogeneities like geometrical obstacles to current flow or regions of poor materials quality. These investigations again stress the importance of the temperature distribution within the conductors and the thus resulting non-uniform critical current density and transport current distribution. Fine agreement between simulations and experiment was reported in [18].

However, we in the present paper as well as in previous work [19,20,21] do not present design calculations, e. g. of a current limiter, but focus has been on materials aspect, behaviour of superconductors under transport and fault currents and their response to magnetic fields. In each element of our finite element model, the Meissner effect is simulated. Focus is also on the physics behind quench, i. e. the time scales under which, at superconductor temperature very close to T_Crit, decay of coupled electron states and recombination proceed [22].

4 Numerical Tests of the Additive Approximation

4.1 Survey: the Radiative Diffusion Model

The literature generally believes high-temperature superconductors are materials non-transparent to mid-infrared radiation. This is certainly correct for bulk materials. But recent investigations [16] with multi-filamentary BSCCO 2212 and 2223 and with thin film, coated YBaCuO 123 superconductors have shown that these materials, too, are non-transparent, because of their large extinction coefficients that overcompensate small conductor thickness.

In a non-transparent object, the radiative contribution to total heat transfer trivially is very small; this matter of fact shall strongly be emphasised here. But it has been demonstrated in [19,20,21] that inclusion of radiative transfer may become important in case it is a multi-filamentary or thin film superconductor and the superconductor temperature under a disturbance is already close to its critical value. Thermal fluctuations near critical temperature will not be discussed, however.

With the well-known strong non-linear dependence of superconductor states (electron pair density, current and thermal transport properties, critical current, field penetration) on temperature, then even tiny temperature fluctuations can drive the superconductor locally into flux flow or Ohmic resistive states (flux flow resistive states will be described later). These local resistive states may quickly spread over the total conductor cross section, by conduction and radiation propagation.

Inspection of the results reported in [19,20,21] (or of Fig. 11a of the present paper, see later) shows local conductor temperatures already close to critical temperature, which means even a temperature increase of just 1 K could initiate a local phase transition. Taking into account radiative transfer in thin film or filamentary superconductor material then is indispensable.

Calculation of temperature fields in these materials, if interpreted as a radiative continuum, therefore requires simultaneous solution of (a) the equation of radiative transfer (ERT) and (b) the equation of conservation of energy:

• a. Neglecting for simplicity the wavelength, the ERT without internal and external radiation sources reads (see the above cited volumes on Radiative Transfer)

$$ {\mathrm{di}}^{\prime }/\mathrm{d}\uptau ={i}^{\prime }\ \left(\tau \right)+\left[{i}_{\mathrm{b}}^{\prime}\left(\uptau \right)+\int \Phi \left({\upomega}_{\mathrm{i}},\upomega, \uptau \right)\ {i}^{\prime }\ \left(\uptau \right)\ \mathrm{d}\upomega \right] $$

(1)

with i′ the directional radiation intensity, τ the optical thickness, dτ = E ds, ds the length of an infinitesimal small step in the conductor, E the (local) extinction coefficient of the material, i′_b the black body intensity, Φ the scattering phase function and ω_i (incident radiation) and ω the solid angles. Because of anisotropic (forward, backward) scattering, the integral is to be taken over the total 4π unit sphere.

• b. Conservation of energy requires Eq. (1) to be supplied with solutions of the following:

$$ \rho\ cp\ \partial T/\partial t+\operatorname{div}\ \left({\overset{\cdot }{q}}_{Cond}+{\overset{\cdot }{q}}_{Rad}\right)={\overset{\cdot }{q}}_s $$

(2)

in which the ${\dot{\ \boldsymbol{q}}}_{Cond}$ + ${\dot{\ \boldsymbol{q}}}_{Rad}$ denote heat flux vectors due to conduction and radiation that proceed in parallel to each other, respectively, with ${\dot{\ \boldsymbol{q}}}_{Rad}$ the integral, taken over the solid angles, of the intensity i′. The (local) intensity, i′ = i′ (τ), obtained from solution of Eq. (1), is needed for ${\dot{\ \boldsymbol{q}}}_{Rad}$ in Eq. (2) while, conversely, temperature, T, calculated from Eq. (2) serves for calculation of the (directional) black body intensity, i′_b, in Eq. (1). In a superconductor, the term ${\dot{\mathrm{q}}}_{\mathrm{s}}$ indicates an energy source (for example, internal disturbances like flux flow or Ohmic resistance losses), or a sink (heat transfer to coolant, to a matrix material, metallic protective coatings or to other components that could stabilise the zero-loss current state against disturbances).

Since temperature dependence of ${\dot{\boldsymbol{q}}}_{Cond}$ and ${\dot{\ \boldsymbol{q}}}_{Rad}$ (and also of ${\dot{\mathrm{q}}}_{\mathrm{s}}$) usually is quite different, Eq. (2) is a strongly non-linear integro-differential equation for the temperature field in the object.

Derivation of Eqs. (1) and (2) is described in the standard literature on radiative transfer, see the cited volumes. Among various approximations, a diffusion solution of the radiative transfer problem can be applied if optical thickness of an absorbing object under study is large. In this case, the radiative flux, ${\dot{\ \boldsymbol{q}}}_{Rad}$, can be written in terms of a “radiative conductivity”, λ_Rad. Like in the standard Fourier conduction law,

$$ \dot{\ \mathbf{q}}=-\lambda\ \mathbf{\operatorname{grad}}\ \mathbf{T} $$

(3a)

derivation of the diffusion solution of radiative transfer yields

$$ {\dot{\ \mathbf{q}}}_{\mathrm{Rad}}=-{\lambda}_{\mathrm{Rad}}\ \mathbf{\operatorname{grad}}\ \mathbf{T}=-{\lambda}_{\mathrm{Rad}}\ \mathbf{dT}/\mathbf{ds} $$

(3b)

For details of the derivation of the diffusion solution in general and of Eq. (3b), the reader might perhaps be interested in the original publication [10].

In the continuum radiation transfer model, it is solely this exceptional case, under strict non-transparency, that λ_Rad really exists and is allowed to simply be added to the solid conduction conductivity, λ_Cond, to yield the total thermal conductivity, λ_Total, of the superconductor that formally can be used in the Fourier conduction law. Only in this case, and in the rather unrealistic case that the material is solely scattering (no absorption/remission) are the heat fluxes ${\dot{\boldsymbol{q}}}_{Cond}$ + ${\dot{\ \boldsymbol{q}}}_{Rad}$ uncoupled from each other. If λ_Total would be calculated in this way in transparent samples, conservation of energy could strongly be violated.

In (discrete) cell models, the question is whether a gradient dT/ds really exists since its existence relies on a differentiable temperature profile, T = T(s,t).

In the continuum model, the point is each of the components of λ_Total, in the additive approximation (and solely in this case),

$$ {\lambda}_{\mathrm{Total}}={\lambda}_{\mathrm{Cond}}+{\lambda}_{\mathrm{Rad}} $$

(4)

can be estimated independently of the other modes of heat transfer. The conductivities of the different components are estimated as if the other components would not be present at all. One can also say: if the different components are not coupled by temperature profiles in the superconductor solid.

If ${\dot{\ \boldsymbol{q}}}_{Rad}$ depends on temperature (which it strongly does) and if also ${\dot{\boldsymbol{q}}}_{Cond}$ is a function of temperature, which is the case with almost all existing solid substances, then ${\dot{\boldsymbol{q}}}_{Cond}$ directly responds to the temperature profile, and vice versa.

Even if ${\dot{\boldsymbol{q}}}_{Cond}$ would be constant (independent of temperature), it would still have to respond, now indirectly, to variations of ${\dot{\ \boldsymbol{q}}}_{Rad}$ and thus to variations of temperature.

The literature treats the radiation diffusion problem almost entirely in absorbing media. Problems may come up if the medium has strong radiation scattering properties. Radiative transfer in the medium then splits into absorption/remission and scattering interactions that proceed by strongly different propagation velocity. The grains can be modelled using very small, virtual sub-particles, the extinction cross sections are added, and corrections for dependent scattering are taken into account.

A check of the scattering properties of BSCCO 2212 and 2223 by application of rigorous scattering theory shows [14] that absorption/remission is the much larger radiation transfer process in these materials (while solid conduction dominates). Albedo of single scattering then is close to zero.

4.2 Solid Conductivity and its Anisotropy

The solid thermal conductivity of the proper superconductor grain material used in the finite element (FE) calculations is taken from experiments (Fig. 3). It reflects

• i. The transport properties of the specific crystallography of the superconductor solid material. Transport properties (current, heat) are anisotropic, with large values in the crystallographic ab-planes and much smaller values in the vertical, c-axis directions. Thermal transport in the superconductor material is mostly by phonons. The solid thermal conductivity reflects also

• ii. The powder in tube manufacturing process, like mechanical treatment interleaved with repeated thermal treatment of the superconductor material that results in filaments, embedded in the Ag-matrix. Rolling or hammering and other standard metallurgical methods aligns the grains horizontally (Fig. 1c), and the better the alignment (the crystallographic ab-plains parallel to the horizontal grain axis), the better the current transport properties (in particular the critical current density) of grains and, consequently, of filaments, tapes and cables. Uniform horizontal orientation of all grains strongly improves also thermal transport properties in the same plane. In vertical, c-axis direction, current and thermal transport properties are much smaller because of a large number of electrical resistances (quasi Josephson resistances in the crystals) and interfacial thermal resistances between neighbouring grains.

Fig. 3

Solid and radiative conductivity of BSCCO 2223 used for calculation of temperature distributions and heat fluxes, as explained in Sect. 4. The radiative conductivity is calculated using Eq. (5) and different extinction coefficients, E. Results are plotted vs. radiative temperature, T_Rad. If in an experiment the local temperature, T(x,y,t), is not available, the radiative temperature, T_Rad, can be approximated by expressions like T_Rad = [(T₁⁴ – T₂⁴)/(T₁ – T₂)]^1/3, with T₁ and T₂ the boundary temperature of a slab. The local T_Rad is the better approximated by this expression the smaller the thickness of the slab (or the larger the extinction coefficient or the optical thickness). Data for the solid thermal conductivity of the superconductor material are taken from Gmelin, E.: Thermal Properties of High Temperature Superconductors, in: Narlikar A. V. (Ed.): Studies of High Temperature Superconductors, Vol. 2, Nova Science Publ. (1989) 95–127. The experimentally determined anisotropy ratio of the solid conductivity was reported in Fricke, J., Frank, R., Altmann, H., Wärmetransport in anisotropen supraleitenden Dünnschichtsystemen, Report E 21–0394 - (1994), in: Knaak, W., Klemt, E., Sommer, M., Abeln, A., Reiss, H.: Entwicklung von wechselstromtauglichen Supraleitern mit hohen Übergangstemperaturen für die Energietechnik, Bundesministerium für Forschung und Technologie, Forschungsvorhaben 13 N 5610 A, Abschlußbericht Asea Brown Boveri AG, Forschungszentrum Heidelberg (1994)

All these suppress electrical and thermal currents in the vertical direction. Grains and filaments, and because of their orientation, also tapes are bodies with strongly anisotropic transport properties of current and heat. The situation is similar to the transport properties of graphite.

Because of the large anisotropy ratio of thermal transport property, the grains (though of some curved geometry) can be considered, from a pure thermal transport aspect, as roughly flat provided the mechanical treatment (rolling, hammering in the powder in tube process) leads to almost perfect horizontal orientation.

5 Investigation of the Additive Approximation by Numerical Calculations

5.1 Test Procedure for its Applicability in Coupled Conduction/Radiation Problems

Figure 3 shows the radiative conductivity calculated from the diffusion model

$$ {\lambda}_{\mathrm{Rad}}=16{\mathrm{n}}^2\upsigma\ {\mathrm{T}}^3/3\mathrm{E} $$

(5)

using the extinction coefficient, E, of BSCCO 2223. Approximately, a value E ≥ 10⁶ 1/m is expected for BSCCO 2212 and 2223 from Fig. 19a, b in [14]. In Eq. (5), n denotes the real part of the refractive index of the sample material, and σ is the Stefan-Boltzmann constant.

The radiative conductivity, λ_Rad, as is expected, is much smaller than the solid conductivity, λ_Cond, of this material, even when compared in c-axis direction.

How then can the validity of Eq. (4) be confirmed numerically? We insert into Fourier’s equation the following three different expressions, with indices (a), (b) and (c), of the total conductivity,

• a. The λ_Total of an object (a solid or a completely evacuated, compacted aggregate, like powders or fibres) with its λ_Total expressed by the components solid conduction (λ_Cond) and radiation (λ_Rad), the latter in its diffusion approximation (and if it really exists); this yields, with conduction and radiation resistances switched in parallel,

$$ {\lambda}_{\mathrm{Total}}={\lambda}_{\mathrm{Cond}}+{\lambda}_{\mathrm{Rad}}={\lambda}_{\mathrm{a}}, $$

• b. Solely the component λ_Cond yielding

$$ {\lambda}_{\mathrm{Total}}={\uplambda}_{\mathrm{Cond}}={\lambda}_{\mathrm{b}}, $$

• c. Solely the component λ_Rad (again in its diffusion approximation and if it exists) yielding

$$ {\lambda}_{\mathrm{Total}}={\lambda}_{\mathrm{Rad}}={\lambda}_{\mathrm{c}} $$

The total conductivity, λ_Total, is introduced, separately in each case, into the finite element calculation procedure to solve Fourier’s differential equation for given conductor geometry, boundary conditions and for calculation of the corresponding heat flow densities, ${\dot{\mathbf{q}}}_{\mathrm{a}}$, ${\dot{\mathbf{q}}}_{\mathrm{b}}$ and ${\dot{\mathbf{q}}}_{\mathrm{c}}$, respectively (the same procedure of course can be applied, though not in the same detail, by analytical calculation of the heat flow densities).

The additive approximation then is confirmed if, with increasing optical thickness, τ₀, the heat flux differences Δ$\dot{\mathbf{q}}$ = ${\dot{\mathbf{q}}}_{\mathrm{a}}-$${\dot{\mathbf{q}}}_{\mathrm{b}}-$${\dot{\mathbf{q}}}_{\mathrm{c}}$, at any arbitrary time and at any arbitrary inner position in the object converges to or equals zero. Trivially, this is fulfilled wtih τ₀ → ∞ because then the component λ_Rad disappears completely.

If the object is a superconductor, all thermal transport properties of other than the superconductor components of the tape are kept unchanged in the simulations, but the effect resulting from the cases (a) to (c) on temperature distribution and heat flux in the filaments will become obvious in also the Ag-matrix, see later.

In a superconductor, assumption (c) is hypothetic: There is no real solid material, the thermal transport properties of which would be based solely on radiation (absorption/remission plus scattering). Also the case “pure scattering”, parallel to solid conduction, probably arises in only very rare situations in superconductors (an example has been identified in [14]).

Can Eq. (4) be confirmed also experimentally? This is really the case, compare the results reported in the very recently published 12th Ed. of the German VDI Heat Atlas [23], Chap. K6: See λ_Cond in its Fig. 14b and the comparison of the extinction coefficients in Tab. 6.

5.2 Application to Layered Temperature Distribution

As a first step of the analysis, we for simplicity assume the tape consists of only the BSCCO 2223 material, with no Ag matrix material at all, no interfacial thermal resistances and with no transport current and magnetic field (this conductor hardly would be stable against quench).

As a disturbance, the surface temperature of the tape, within a time interval of Δt = 8 ns, is quickly raised by absorption of a heat pulse directed onto the nodes of the applied FE scheme on its upper boundary, y = 296 μm. Magnitude of the heat pulse, 10¹⁰ to 10¹² W/m², applied to the target surfaces defined below, is chosen to yield within the tape cross section approximately consistent (not diverging) temperatures during the test calculations.

The finite element simulation scheme is indicated in Fig. 2a, b. The same scheme will later be used for calculations with the proper materials composition (superconductor filaments and Ag matrix). Details of the numerical procedure (application of Ansys 16 as the finite element program, selection of element type, key options, time steps of integration, convergence criteria) have been reported previously [19,20,21]. The calculations are restricted to 2D geometry.

In the first set of calculations, the heat pulse is deposited onto all nodes within 0 ≤ x ≤ 1.92 mm (the target; in this case over the total width of the tape). For the extinction coefficient, we apply E = 10⁶ 1/m const including corrections to anisotropic and dependent scattering.

In the calculations for Fig. 4, heat transfer to coolant is not simulated. The calculations cover only very small time intervals. No substantial contribution to upper and lower tape surface temperatures can be expected from solid/liquid heat transfer within the simulated periods (the time needed to generate a gas bubble in LN₂ on the flat surface is in the order of 10 ms, under standard pool boiling conditions). Temperature variation of the target surface and at inner positions of the object thus is due to solely absorption of the pulse and internal thermal transport properties. Boundary temperature at the lower and upper tape surfaces, y = 0 and y = 264 μm, respectively, at time, t = 0, are T = 77 K constant, and adiabatic condition at the lower surface. Specification of the emissivity of the tape surfaces is not needed (in view of the large optical thickness of the sample, see below).

Fig. 4

Transient temperature fields (nodal temperatures), T(x,y,t), calculated using E = 10⁶ 1/m const and solely case (a) λ_Total = λ_Cond + λ_Rad. Both diagrams assume uniform materials composition (only superconductor, no Ag matrix material). Upper diagram: As a disturbance, a heat pulse of 1.08 10¹⁰ W/m² during a period of 8 ns is directed onto all nodes located at 0 ≤ x ≤ 1.92 mm (left half of the upper tape surface, y = 264 μm); the exactly stratified temperatures are shown at time t = 100 ms after start of the disturbance. Lower diagram: Heat pulse of 2.16 10¹⁰ W/m² during 8 ns directed onto a point-like target (all nodes between 1.87 ≤ x ≤ 1.92 mm, again at y = 264 μm); results are shown at time t = 35 ms. In both diagrams, results for simplicity are calculated with no inclusion of heat transfer to a coolant

All these assumptions enormously reduce the numerical problems (convergence of the results) and the calculation time that has been encountered in previous investigations of superconductor stability. We could of course extend the calculations to a 3D scheme; strongly increased computation time but little additional information would be result from this extension.

In case (a), conduction in parallel to radiation, and with the heat pulse deposited onto the total (left-half) upper surface of the tape, the finite element solution trivially yields strictly stratified, layered in parallel to the tape surface, temperature distributions in the conductor cross section (Fig. 4, upper diagram). These reflect the large anisotropy of the BSCCO 2223 solid thermal conductivity (Fig. 3) and the applied boundary conditions (uniform heating of the upper, adiabatic condition at the lower tape surface).

The temperature distribution in case (b), solely conduction, not shown, is very similar to case (a) because of the strong solid conduction contribution to the total conductivity. The fictitious case (c), only radiation, with the then strongly reduced total thermal conductivity, λ_Total = λ_Rad, yields much larger conductor temperature (again not shown). It is clear also that this distribution is strictly (horizontally) stratified.

In all cases, (a) to (c), temperature gradient is positive so that the corresponding heat fluxes, $\dot{q}$, are negative (Fig. 5a).

Fig. 5

a Directional (vertical in Fig. 2a, b) heat flux, ${\dot{q}}_{\mathrm{y}}$, all negative (temperature gradient dT/dy positive), given at vertical nodal positions, y, calculated for the cases (a) λ_Total = λ_Cond + λ_Rad, (b) λ_Total = λ_Cond and (c) λ_Total = λ_Rad, all at E = 10⁶ 1/m, at tape centre, x = 1.92 mm, and all obtained at t = 100 ms. The figure serves for calculation in Fig. 5b of the difference of the heat flux results obtained for the cases (a), (b) and (c) assuming homogeneous tape composition (only superconductor, no matrix material). The applied heat pulse is described in the caption of Fig. 4 (upper diagram, all nodes within 0 ≤ x ≤ 1.92 mm at y = 264 μm). Results are obtained without inclusion of heat transfer to a coolant (adiabatic conditions on the lower tape surface; only the inner nodes are considered). b Deviation Δ$\dot{q}$ from zero of directional (vertical in Fig. 2a, b) heat flux differences when the results, ${\dot{q}}_{\mathrm{y}}$, calculated with (b) λ_Total = λ_Cond and (c) λ_Total = λ_Rad are subtracted from the ${\dot{q}}_{\mathrm{y}}$obtained with (a) λ_Total = λ_Cond + λ_Rad, with extinction coefficients, E = 10³ (tentatively, for a test) and for a realistic E = 10⁶ 1/m. Homogeneous tape composition (superconductor, no matrix material). Again, the applied heat pulse is described in the caption of Fig. 4 (upper diagram, all nodes within 0 ≤ x ≤ 1.92 mm at y = 264 μm). The deviation is calculated as percent of the flux resulting from case (a), at vertical nodal positions, y, and at t = 100 ms. Near the lower surface, results are given for only the inner nodes of the tape. Note the strongly increasing deviation of Δ$\dot{q}$ from zero at y ≥ 200 μm, when E is reduced to 10³ 1/m, a clear indication that the additive approximation no longer can be confirmed

If size of the irradiated target is reduced to a quasi-point-like area (including all nodes at positions 1.87 ≤ x ≤ 1.92 mm, again at y = 264 μm), the strictly horizontally stratified temperature distribution partly gets lost (Fig. 4, lower diagram), again calculated with E = 10⁶ 1/m const; the result is shown for case (a) λ_Total = λ_Cond + λ_Rad.

In this preliminary step, with the assumed homogeneous, materials composition of the tape and because of the approximately stratified temperature distributions, it is sufficient to consider only directional components of the heat fluxes. From these, the differences Δ$\dot{\mathrm{q}}$ = ${\dot{\mathrm{q}}}_{\mathrm{a}}-$${\dot{\mathrm{q}}}_{\mathrm{b}}-$${\dot{\mathrm{q}}}_{\mathrm{c}}$, at the tape centre, x = 1.92 mm, are shown in Fig. 5b (y direction). Using the $\dot{\mathrm{q}}$ of Fig. 6a, b, the differences in x and y-directions are plotted in Fig. 7a, b).

Fig. 6

a Directional vertical heat flux, ${\dot{q}}_{\mathrm{y}}$ (see Fig. 2a, b), again all negative (gradient dT/dy positive), at tape centre and given at vertical nodal positions, y. Same calculation as in Fig. 5a for (a) λ_Total = λ_Cond + λ_Rad, (b) solely λ_Cond and (c) solely λ_Rad, but a heat pulse of 2.16 10¹⁰ W/m² during a period of 8 ns is directed onto only the point-like target (all nodes located at 1.87 ≤ x ≤ 1.92 mm on the upper tape surface, y = 264 μm). All results are obtained with E = 10⁶ 1/m const and at t = 35 ms. b Directional horizontal heat flux, ${\dot{q}}_{\mathrm{x}}$, again all negative (gradient dT/dx positive), at tape centre, at vertical nodal positions, y; same calculation as in Fig. 6a, for (a) λ_Total = λ_Cond + λ_Rad, (b) solely λ_Cond and (c) solely λ_Rad, all with E = 10⁶ 1/m const; results are shown at t = 35 ms.

The extinction coefficient, E = 10⁶ 1/m, is responsible for the large optical thickness, τ. From the ratio of directional radiation intensities, i′(x = D)/i′ (x = 0) = exp (−E D), we at least have τ = E D = 20, so that i′ (x = D)/i′ (x = 0) is in the order of 10⁻⁹. This fulfils the diffusion approximation and explains the very small differences Δ$\dot{q}$ (far below 0.01% of the value ${\dot{q}}_{\mathrm{a}}$Fig. 7a, b). It confirms that application of the additive approximation at least in this simple case is successful (homogeneous material, stratified temperature, strictly in parallel or only slightly curved temperature distributions if there is only the point-like disturbance).

Fig. 7

a Deviation Δ$\dot{q}$ from zero directional (vertical in Fig. 1a) heat flux differences, ${\dot{q}}_{\mathrm{y}}$, calculated using E = 10⁶ 1/m from the results in Fig. 6a. b Deviation Δ$\dot{q}$ from zero directional (horizontal in Fig. 1a) heat flux differences, ${\dot{q}}_{\mathrm{x}}$ calculated using E = 10⁶ 1/m from the results in Fig. 6b

But if the extinction coefficient is reduced to E = 10³ 1/m, which indicates the sample now would be transparent to radiation, τ < 1, the additive approximation fails, compare in Fig. 5b the increase of the light-green diamonds, Δ$\dot{q}$, to about 100% deviation, again given as percentage of the flux resulting from case (a). It should be zero, or at the most be very small, for the additive approximation to be applicable to heat transfer calculations also in this sample.

In the next step, we again assume as a disturbance a heat pulse directed onto the small, quasi-point-like target on the upper tape surface but the internal structure of the tape now is that of the proper multi-filamentary BSCCO 2223/Ag superconductor.

From technical and manufacturing aspects, and because of their improved current limiting properties, thin film, coated YBaCuO 123 superconductors presently are considered more attractive than multi-filamentary BSCCO 2223/Ag tapes. But the results reported so far in this paper apply also to the coated superconductor provided it can be understood as perfectly homogeneous.

Simulation and check of the additive approximation in a multi-filamentary superconductor are the more targeted and challenging task. The calculations for this reason have been confined to the multi-filamentary conductor.

5.3 Single (Dirac-Like) Heat Pulse on a Multi-filamentary Superconductor

Figure 8 shows the temperature distribution, T(x,y), at t = 8.6 ms, for cases (a) and (c), upper and lower diagram, respectively, calculated for E = 10⁶ 1/m. Selection of the time t = 8.6 ms will be explained later, Sect. 5.4.

Fig. 8

Transient temperature fields, T(x,y,t), in the BSCCO 2223 tape; nodal results, calculated using E = 10⁶ 1/m const and for cases (a) λ_Total = λ_Cond + λ_Rad (above) and (c) λ_Total = λ_Rad (below). Contrary to Fig. 4, 5, 6 and 7a, b, the diagrams are calculated using the proper materials composition (superconductor grains and filaments embedded in Ag matrix material). As a first step, disturbance in this simulation results from a heat pulse of 8.64 10¹¹ W/m² during the period of 8 ns applied to all nodes in 1.87 ≤ x ≤ 1.92 mm, y = 264 μm (a point-like target). Results are shown at time t = 8.6 ms for all nodes of the tape (including heat transfer to the coolant)

The disturbance consists of a single heat pulse of 8.64 10¹¹ W/m² applied during the period Δt = 8 ns to all nodes at positions 1.87 ≤ x ≤ 1.92 mm on the upper tape surface (y = 264 μm, the point-like target, as before); this is a rough approximation of a Dirac pulse. Note that the filament temperatures, because of the assumed small (fictitious) thermal conductivity, λ_Total = λ_Rad, of the BSCCO 2223 superconductor, remain below the temperature of the Ag matrix material. Conduction heat transfer from the Ag matrix into the depth of the superconductor filaments therefore is partly blocked.

Because of the strong anisotropy of the solid thermal conductivity, λ_Cond, of BSCCO 2223 (Fig. 3), and since the conductor cross section now involves two materials (ceramic grains and the matrix Ag) with fundamentally different conductivities, we have to calculate the vector heat flux $\dot{\mathbf{q}}$ (instead of the directional ${\dot{q}}_{\mathrm{y}}$ or ${\dot{q}}_{\mathrm{x}}$ in the previous subsection) and the corresponding deviations Δ$\dot{\mathbf{q}}$. Results are shown in Figs. 8 and 9.

Fig. 9

Vector heat flux, $\dot{\mathbf{q}}$, at tape centre, x = 1.92 mm, given at vertical nodal positions, y, for case (a) λ_Total = λ_Cond + λ_Rad, (b) λ_Total = λ_Cond and (c) λ_Total = λ_Rad (red and blue and light-green diamonds, circles and triangles, respectively, as before), all with E = 10⁶ 1/m const and at t = 8.6 ms. The diagram is calculated using the proper materials composition: Superconductor (SC) filaments embedded in Ag matrix material. The applied heat pulse is described in the caption of Fig. 8. Note that all $\dot{\mathbf{q}}$ shown in the Ag sections indicate solely solid conduction (but depend on heat transfer in the SC filaments, by conservation of energy)

As a result, heat flux, $\dot{\mathbf{q}}$, in superconductor and matrix sections is strongly different (Fig. 9). But the Δ$\dot{\mathbf{q}}$ (existing in only the superconductor sections) converge to zero (Fig. 10), as requested.

Fig. 10

Deviation Δ$\dot{\mathbf{q}}$ (flux difference) in the superconductor (SC) sections from zero when vector heat flux results, $\dot{\mathbf{q}}$, calculated with (b) λ_Total = λ_Cond plus (c) λ_Total = λ_Rad are subtracted from the vector heat flux obtained under case (a) (λ_Total = λ_Cond + λ_Rad), all with extinction coefficients, E = 10⁶ 1/m. The diagram is obtained using the proper materials composition (superconductor grains and filaments embedded in Ag matrix material). The disturbance by a heat pulse is described in the caption of Fig. 8. Results are given for all nodes of the tape at x = 1.92 mm (including heat transfer to the coolant). The deviation is shown at vertical nodal positions, y, at time t = 8.6 ms. Deviations from zero in the SC layers (red diamonds) are very small, below 0.01% of the vector heat flux of case (a). It would not be reasonable to calculate deviations Δ$\dot{q}$ (flux differences) in the Ag sections (the $\dot{\mathbf{q}}$ in these sections indicate solely solid conduction)

5.4 Internal Heat Sources in the Multi-filamentary Superconductor

We finally consider the conduction and radiation heat transfer problem if there are only disturbances arising from solely internal heat sources, in the same conductor as before (no longer disturbances arising from the heat pulses described in the previous subsections.) Internal heat sources arise from flux flow or Ohmic resistances.

Flux flow resistances limit current transport when in an experiment transport current density exceeds critical current density; this situation can be understood as a disturbance. Flux flow resistance happens even if conductor temperature is still below its critical temperature. Temperature is a thermodynamic variable: With temperature below its critical value, the conductor is still in the superconducting state.

In the literature, the specific flux flow resistance, ρ_FF, of ceramic superconductors is considered of in the order 10⁻⁷ Ω m. An alternative model to estimate flux flow resistances recently has recently been described in [21]; for BSCCO 2223 it yields ρ_FF < 5.7 10⁻⁷ Ω m at 100 K and under a field B = 1 mT, clearly above the specific resistance of Ag. Losses arising from flux flow resistance increase conductor temperature. If the temperature increases beyond its critical value, the conductor finally is in the Ohmic resistance state, which causes even higher losses.

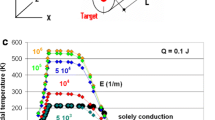
With the internal heat sources arising from flux flow or Ohmic resistances under transport current, Fig. 11a shows transient temperature fields, T(x,y,t), in the multi-filamentary conductor, at t = 7.6, 8.1 and 8.6 ms (from top to bottom) calculated for case (a) λ_Total = λ_Cond + λ_Rad and using E = 10⁶ 1/m const. For case (c) λ_Total = λ_Rad, the temperature distribution is shown in Fig. 11b.

Fig. 11

a Transient temperature fields, T(x,y,t), in the multi-filamentary conductor, at t = 7.6, 8.1 and 8.6 ms (from top to bottom) calculated using E = 10⁶ 1/m const for case (a) λ_Total = λ_Cond + λ_Rad. As a second step, the disturbance in this simulation (contrary to Fig. 8) results from a sudden increase of transport current to a fault (transport current density exceeding critical current density, compare text). No heat pulse is applied to the upper surface of the tape. The diagrams are obtained using the proper materials composition (superconductor filaments embedded in Ag matrix material). Details of the calculations are described in [19,20,21]. Again, only the left half of the total tape width is shown. Results are given for all nodes of the tape at x = 1.92 mm (including heat transfer to the coolant). b Transient temperature field, T(x,y,t), at t = 8.6 ms, for E = 10⁶ 1/m, for case (c) λ_Total = λ_Rad. The diagram is calculated using the proper materials composition (superconductor grains and filaments embedded in Ag matrix material). The disturbance in this simulation like in Fig. 11a results from a sudden increase of transport current to a fault (transport current density exceeding critical current density). No heat pulse is applied to the upper surface of the tape. In comparison with Fig. 11a, the small (only radiative) conductivity (or the corresponding large thermal radiations resistances) strongly increases local temperature in grains and filaments

Note again that we are not satisfied with the overall temperature field in the BSCCO 2223 tape. We need the temperature distribution within the filaments and thus the temperature of the grains. Figure 11a and b accordingly shows that:

• i. Superconductor temperature in the tape cross section is by no means homogeneous but strongly depends on materials composition and thus on position within the tape (also critical and transport current distribution and magnetic field distribution, all not shown in Fig. 11a, b, are responsible for the temperature distribution). Trivially, temperature within the filaments exceeds temperature of the Ag matrix material,

• ii. Also within the filaments, temperature distribution is not homogeneous. This means the superconductor filaments may partly (locally) be in zero-resistance, flux flow resistance or even Ohmic resistive states, within short periods of time.

The results confirm the calculated temperature distributions of multi-filamentary superconductors reported in [19,20,21]. Convergence of the results again is achieved at times up to t = 8.6 ms (2.1 ms after start of the disturbance). At later times, heat losses from the then mostly Ohmic resistances, and the increase of local conductor temperature, are so strong that convergence of the numerical results no longer can be achieved.

This is the consequence of a run-away of local temperatures, a clear indication of the onset of a quench. It first occurs at isolated positions within the conductor cross section but will spread quickly.

It should be the very aim of stability calculations to identify exactly these positions at this critical instant when heat generation rates, at temperature even below critical temperature, can become exorbitant, under only flux flow resistance to transport current.

The disturbance in this case results from nominal transport current increasing to a fault, like in a short-circuit. The simulated increase of the current starts at t = 6.5 ms, within 2.5 ms to its 20-fold nominal value in an electrical grid.

Neither heat capacity of the conductor and matrix material nor heat transfer to a coolant would be able to over-compensate the thermal divergence arising at times later than t = 8.6 ms (in this conductor and under the given load) if there are no highly conductive components (stabilisers) like Cu-layers or shunts in the tape or cable cross sections to which the current could be commuted, and no external safety measures (interruption of transport current by conventional equipment) immediately could be taken.

Note from Fig. 11a (mid-position), the enormous rate of local conductor temperature increases once the disturbance is switched on. The rate, about 3 10³ K/s observed within the period 6.5 ≤ t ≤ 8.1 ms, results from solely flux flow resistance, but finally would increase to more than 10⁵ K/s when critical temperature of the superconductor BSCCO 2223 (T_Crit = 108 K) is exceeded; compare Fig. 16.

Also, the distribution of the vector heat flux, $\dot{\mathbf{q}}$, is not homogeneous (Fig. 12, with the strong variations between superconductor and Ag sections). But the deviations Δ$\dot{\mathbf{q}}$ (Fig. 13) fortunately are very small again (below 0.01%).

Fig. 12

Vector heat flux, $\dot{\mathbf{q}}$, at tape centre, x = 1.92 mm, given at vertical nodal positions, y, for case (a) λ_Total = λ_Cond + λ_Rad, (b) λ_Total = λ_Cond and (c) λ_Total = λ_Rad, all with E = 10⁶ 1/m const and at t = 8.6 ms. Identification of the symbols (red and blue and light-green diamonds, circles and triangles) is the same as in the previous figures. The disturbance in this simulation again results from a sudden increase of transport current to a fault (transport current density exceeding critical current density, no radiation pulse applied onto the upper surface of the tape). Large heat flux values appear only in the Ag sections, but the $\dot{\mathbf{q}}$ in the Ag sections trivially refer to solely solid conduction

Fig. 13

Deviation Δ$\dot{\mathbf{q}}$ (flux difference) in the superconductor (SC) sections from zero when vector heat flux results, $\dot{\mathbf{q}}$, calculated with (b) λ_Total = λ_Cond plus (c) λ_Total = λ_Rad are subtracted from the vector heat flux obtained under case (a) (λ_Total = λ_Cond + λ_Rad, all with extinction coefficients, E = 10⁶ 1/m. The disturbance in this simulation is the same as in Figs. 11a, b and 12 (sudden increase of transport current to a fault). Results are given for all nodes of the tape at x = 1.92 mm (including heat transfer to the coolant). The deviation from zero is shown at vertical nodal positions, y, at time t = 8.6 ms and is again below 0.01% of the results for case (a). Calculation of Δq in the Ag sections again would not be reasonable

This confirms the results of the heat transfer and stability calculations reported in our previous papers and the applicability of the additive approximation.

5.5 Check of the Finite Element Mesh

All available, high-quality finite element computer programs provide options to automatically check design and suggest improvements of the mesh. Yet the check of the mesh by inspection of the results obtained from the simulated transport processes is indispensable.

Figure 14a and b compare details of the transient temperature field, T(x,y,t), reported in Figs. 8 and 11a (lower diagram), both at time t = 8.6 ms. With an external disturbance positioned in the small target on top of the tape, close to the axis of symmetry, with uniform start temperature (T = 77 K at t = 0 on all nodes), and if there are no internal heat sources, heat flow necessarily is in direction into the matrix and from there into the filaments (Fig. 14a).

Fig. 14

a Detail (enlarged) of Fig. 8 (upper diagram, t = 8.6 ms): Heat flow into the filaments resulting from the heat pulse applied to the target area on the upper tape surface close to the axis of symmetry (x = 1.92 mm). No internal heat sources (no transport current, no magnetic field). Because of the small thermal conductivity, λ_Total, of the superconductor, the filament temperatures are below temperature of the matrix material (heat transfer into the depth of the filaments is blocked by the thermal resistance of the ceramic superconductor grains and by interfacial resistances). b Detail (enlarged) of Fig. 11a (lower diagram, t = 8.6 ms): Heat flow out of the filaments (due to flux flow and Ohmic resistance losses). No external heat sources (no pulse onto the tape). Note there are quite inhomogeneous temperature distributions between and, in particular, within the filaments

The situation becomes different when there are internal heat sources. Figure 14 b shows transient temperature field, T(x,y,t), that develops under flux flow and Ohmic resistances under transport current. Since the generated heat losses enormously increase filament temperature, heat flow in this simulation necessarily is from filaments into the matrix material.

Both situations are confirmed by the conductor temperature shown in Fig. 15a and b, respectively; this cannot be achieved if the applied finite element mesh (the same in both situations) is too coarse. With a much finer mesh, computation time would strongly increase but without much gain for the success of the analysis (the calculation for the temperature field shown in Fig. 11b, for example, takes about 12 h, on a standard PC with a 4-core processor and under Windows 7).

Fig. 15

a Temperature profile, T(x = 1.92 mm, y), close to the axis of symmetry, at t = 8.6 ms. Results are shown for the quasi-point-like heat pulse deposited during 8 ns on the top of the tape (no internal heat sources). The figure is extracted from the results shown in Fig. 14a (the detail of Fig. 8, upper diagram). Symbols for cases (a) and (b) are the same as before. Heat flow into the filaments results from the positive temperature gradient in the superconductor (SC) sections (small deviation from strict positive gradient is explained by the large conductivity of the matrix material). b Temperature profile, T(x = 1.92 mm, y), at t = 8.6 ms, close to the axis of symmetry. The disturbance results from flux flow and Ohmic resistance losses (no external heat pulse applied to the tape). The results indicate heat flow out of the filaments. The diagram includes heat transfer to the coolant and is calculated from Fig. 14b (the detail of Fig. 11a, lower diagram). Symbols for cases (a) and (b) are as before. Within the SC sections, at large coordinates, y, there are positive and negative temperature gradients

6 Identification of the Onset of a Quench - A Hypothesis

Figure 16 shows increase of conductor temperature with time, ∂T(x,y,t)/∂t, given for all elements of the multi-filamentary BSCCO 2223 tape (including the Ag elements).

Fig. 16

The self-stimulating effect immediately before quench: The larger the local conductor temperature, the larger its increase with time. The figure shows ∂T(x,y,t)/∂t, calculated using the results of the finite element simulation obtained for 8.1 ≤ t ≤ 8.6 ms after start of the disturbance (transport current density exceeding critical current density). Data are shown for all elements of the multi-filamentary BSCCO 2223 tape (superconductor grains and filaments, and Ag matrix; compare text). Local quench is expected after critical times, beginning at t_Crit = 8.4 ms or at = 8.6 ms, at the latest, at different positions (not explicitly specified in this figure) in the conductor cross sections (red and black diamonds, respectively). Exact positions can be obtained from comparison of this figure with the cross sections shown in Figs. 11a and 2a, b

The larger the local conductor temperature of the BSCCO conductor or of the Ag matrix, the larger its increase with time: At t = 8.4 and 8.6 ms, the variations ∂T(x,y,t)/∂t amount to about 7 10⁴ K/s. At later times, the conductor then in the Ohmic resistance regime, ∂T(x,y,t)/∂t would increase to values above 10⁵ K/s.

The curves in Fig. 16 thus suggest we are observing a kind of self-intensifying effect, locally and immediately before quench: The larger the local conductor temperature, the larger its increase with time, ∂T(x,y,t)/∂t. The second-order derivative, ∂²T(x,y,t)/∂t², too, then positive, would still more definitely indicate divergence of the numerical simulations once conductor temperature has increased to levels close to critical temperature.

The situation probably could be described more precisely when instead of comparing temperatures [T(x,y,t) larger than T_Crit(x,y,t)?] the dynamical aspect, temperature variations, at least the increase ∂T(x,y,t)/∂t but possibly also ∂²T(x,y,t)/∂t², are inspected. There is possibly a correlation of results of the simulation (the “numerical space”) with the experimental space (the “physical reality”). The correlation becomes the better the more precise the predictions of numerical simulations and the temperature measurements.

This suggests the following hypothesis: A superconductor will quench immediately when convergence of the corresponding numerical scheme no longer can be achieved.

But origins of non-convergence in Finite Element calculations can be manifold, like badly defined physical models, too complicated overall geometry, too strongly differing materials properties, poor meshing, inadequate selection of element types, integration time steps, frontal or iterative solvers or of convergence criteria. The “physical reality” of a superconductor then might not be correlated with non-convergence of the numerical results, and vice-versa, and the above mentioned mapping thus not be defined uniquely.

In the present case, the proper Finite Element calculation was used just as an iterative core procedure (step a) that is embedded in a master scheme (steps b to d). The master scheme serves for calculation of local values of critical parameters (current density, magnetic field), of Meissner effect, local resistance, fault states and electrical losses of the conductor, all obtained in each of the Finite Elements and thus in dependence of local temperature obtained in step (a). The whole procedure, steps (a) to (d), then is repeated (steps (b) to (d) are not elements of the Finite Element code).

The solution scheme of the (proper) Finite Element problem (step a) applied sparse matrix direct solvers (requests large memory space; alternatives like JCG or ICG iterative solvers were tested but convergence is not guaranteed). In the present case, 4-node, plane model elements have been applied that allow rotation against axis of symmetry.

The whole simulated period, originally designed to a length of 20 ms, has been split into periods Δt = 10^-4 s. To obtain convergence, the procedure within each period Δt was repeated by up to N = 10 iterations of the steps (a) to (d) because of strong non-linearity in almost all involved parameters. Within each Δt, regular or fault currents were kept constant. Integration time δt within each Δt/N was between 10^-14 and 10^-7 s. Length of the intervals Δt/N is large in comparison to characteristic (diffusion) time, τ_C, of electrical or magnetic fields and of currents, and of time τ_R needed to establish new equilibrium, electron charge distributions.

The procedure is similar to the working steps and the iterative, saw-toothed temperature excursions described in Figures 4 and 7a, b of [19]: We again look, now within the intervals Δt₂ = Δt, for converence values of T(x,y,t). In Figure 4 of this reference, these were indicated by the solid black circles obtained under point-like disturbances, and their existence, as a result of the calculations, was confirmed in Figure 7a, b of the same reference. In the present case, the disturbance results from an AC fault current that is not point-like but in principle may extend to the cross sections of all filaments.

Decision on occurrence or non-occurrence of a quench then is made not with respect to critical loads of given, fixed safety limits, but by divergence of temperature excursion in any of the integration steps j + 1, which means, even if local superconductor temperature in the foregoing step, j, still might be below critical temperature. Convergence is obtained for all regular transport currents (DC, AC). Divergence (non-convergence, first observed as local results) appears when under quickly increasing fault current conductive and radiative distribution of the load, and heat capacity and heat transfer to the coolant, no longer compensate the losses.

The calculations yielded a series of converged, quasi-stationary solutions. With these solutions, onset of a quench is considered as the consequence of diverging values of T(x,y,t) to be expected from ∂T(x,y,t)/∂t or ∂²T(x,y,t)/∂t² also if T(x,y,t) is below, but very close to, T_Crit(x,y,t). This procedure covers flux flow losses; we do not wait in the calculations until T(x,y,t) turns out to really exceed T_Crit(x,y,t), and conductor losses then, almost completely, be caused by Ohmic resistance, the standard (trivial) condition for a quench.

The superconductor stability problem, under fault current, thus appears to be similar to unstable crack propagation in fracture mechanics.

Current distribution in step j not necessarily is the same as obtained in foregoing integration time steps, j - 1; it may fluctuate and the current percolate through the conductor, in response to the actual resistances. Computational efforts to fully cover all these procedures were enormous.

The trend of the temperature excursions, ∂T(x,y,t)/∂, in Fig. 16 is very similar in superconductor filaments and Ag matrix. Temperature measurement in the conductor, by contacting the Ag matrix, thus could more conveniently be realised than at the superconductor surfaces (ceramic materials, surfaces may be rough, irregularly shaped, possibly with chemical impurities, which means contact measurement of superconductor temperature might become too difficult).

7 Summary, Conclusion and Outlook

Finite element calculations of cryogenic temperature distribution and internal heat transfer have been reported for multi-filamentary superconductor samples with artificial homogeneous and, realistically, inhomogeneous materials composition and under thermal disturbances (resistive states initialised by flux flow resistance). The additive approximation of thermal conductivity has been shown to be justified not only for simple geometrical structure of the objects. Even if geometry and materials composition are highly diversified, like in a multi-filamentary superconductor, and with internal heat sources, the additive approximation has been shown to be successfully applicable if the optical thickness of the superconductor conductor materials part is large.

The additive approximation fails if the optical thickness of an investigated object would be small and the diffusion solution of radiative transfer then no longer be applicable.

There is another problem to be investigated within the additive approximation and the radiative transfer diffusion solution, even within radiative transfer in general if there are absorption/remission and scattering obstacles within an irradiated, conducting object. According to Eq. (4), solid conduction and radiation are switched in parallel. This delivers correct results under the energetic viewpoint. But Eq. (4) squeezes both components onto a common time scale. Transit times thus become a series of events registered on this time scale where transit times, when registered, become a series of images. It is not clear if this series will uniquely be ordered [14] since conduction and radiative heat flow, in parallel, proceed at strongly different propagation velocities (different by orders of magnitude).

This problem is not restricted to superconductors: A similar situation arises in laser-flash experiments to determine the thermal diffusivity of thin films. The question again is whether in such experiments the non-transparency condition, of both incoming laser and absorbed/remitted thermal radiation, i. e. in completely different spectral regions, was really fulfilled. Impacts on stability predictions will again be investigated in a subsequent paper. In part B of the present paper, we will try to approach still more closely the "point of no return" of the self-intensifying disturbation (presently identified at about 8.6 ms) and investigate on which timescale break-down of electron pair density has to be expected; this break-down must be correlated with the dynamics of the phase transition.