Abstract
Radiative transfer calculations are presented for multi-filamentary BSCCO 2212 and 2223 and for thin film-coated YBaCuO 123 superconductors. A strictly radiative view allows conductor morphology of these superconductors to be interpreted as particulate or quasi-particulate objects. Problems then arising from non-regular particle shape, missing refractive indices, dependent scattering and superconductor material (diamagnetic) properties are solved in a multi-step, approximation approach. Both types of conductors are shown to be non-transparent to mid-IR radiation. Non-transparency may become critical for superconductor stability. The obtained extinction cross sections converge near the phase transition. A substantial difference of extinction properties between the superconducting and normal conducting state thus cannot be observed. As a first corollary from non-transparency, application of the additive approximation for the total thermal conductivity used in previous numerical calculations of the BSCCO and YBaCuO superconductors is confirmed. Second, within transit time intervals, the length of which depends on optical thickness, no uniform equilibrium conditions of electron pair density within the conductor cross section and near critical temperature are observed. Phase transition does not proceed uniformly, neither spatial nor temporal, and the order (succession on time scales) of local events (temperature variations, quench), in extreme cases, is completely dissolved. As another corollary, non-transparency even makes the existence of uniquely defined, physical time scales doubtful in a superconductor. The obtained results are expected to improve existing stability models and will be of practical value for future materials development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Survey and Organisation of the Paper
Radiative transfer calculations are presented in this paper for multi-filamentary BSCCO 2212 and 2223 and for thin film-coated YBaCuO 123 superconductors. Instead of investigating radiative transfer in superconductor solids, the rationale for this selection of filaments and thin films for a thorough radiative transfer study is their present technological relevance for current transport.
Non-transparency is an extreme aspect of radiative transfer theory. In a simplified picture, any object (solid, liquid or gaseous) is non-transparent if its radiation extinction coefficient is very large. Penetration depth of incident radiation then is small against the size of the object. Non-transparent media are distinguished from their transparent counterparts by a critical optical thickness. The critical optical thickness will be defined later.
We will investigate radiative transfer and non-transparency in the BSCCO and YBaCuO superconductors within the wavelength interval between 27 and 32 μm. This interval is located within the mid-infrared (mid-IR) spectral range. The interval is related to conductor temperature roughly between 108 and 92 K, the critical temperature of BSCCO 2223 and YBaCuO 123, respectively.
When preparing radiative transfer calculations, a decision has to be made whether the objects to be modelled are of continuous or discrete structure with respect to propagation of radiation. A radiation continuum model would assume that the wavelength of impinging radiation is large against the size of the constituents of the object.
Multi-filamentary (first-generation (1G)) BSCCO superconductors can be considered as particulate or granular since their filaments consist of a large number of flat, plate-like superconductor grains. The grains are arranged in parallel along the length of the conductor, and all are embedded in a metallic matrix.
Thin-film YBaCuO superconductors can be interpreted as (quasi-) particulate materials if they include, as seen from the radiative transfer aspect, deviations from ideal, homogeneous film properties, like sudden variations of the refractive index in an otherwise homogeneous medium, or if there are deviations from perfect film morphology, like grains and domains, all with reference to the wavelength of incident radiation (this is, to some extent, an analogue to the disturbance of radiation propagation in liquids by bubbles).
In both cases, the mid-IR wavelength is not always very large against particle size (filaments or thin-film quasi-particulates, respectively). We will later describe these constituents as being composed of very small subparticles of cylindrical shape. This idea allows to model radiation/solid particle interactions by rigorous scattering theory and heat transfer by the principles of radiative transfer. Propagation of radiation then is described in a radiative continuum.
Besides established superconductor properties (zero loss current transport, existence of persistent currents and expulsion of a magnetic field), it is an open question whether there is also a change of the radiative transfer mechanism at the phase transition. The literature generally believes high-temperature superconductors are opaque materials (in this paper, non-transparency and opacity will be used as synonyms). This is correct for bulk superconductors, but there is no proof that filaments and thin films, too, would be non-transparent.
What is the physical background of non-transparency of superconductors? A change of their radiative properties against normal conducting state at the phase transition could be expected from the already existence of an energy gap in the electronic energy states. But in YBaCuO 123, the energy of thermally emitted mid-IR photons (within the range 90 ≤T< 92 K of conductor temperature) is below the gap energy (compare Fig. 26 in the Appendix). Incident photons from this temperature range cannot contribute to break-up of electron pairs and, as a consequence, cannot be held responsible for the possibly existing non-transparency, except for wave numbers, ω > 317 (1/cm).
But there are other potential candidates for radiation extinction in YBaCuO 123: resonant processes (electron inter-band transitions), vibrational excitations, fluctuations near critical temperature (instability of charge density waves), normal modes (coherent oscillations at a characteristic frequency) or contribution by phonons. Besides absorption, scattering can be shown to strongly contribute to non-transparency. Calculation of refractive indices decides whether these processes are within reach of the mid-IR radiation that is emitted by the superconductor materials in the above-mentioned temperature interval.
Measurements of optical properties of thin-film conductors (permittivity, optical resistance, index of refraction) obtained from reflectance and transmittance measurements neither analyse radiative transfer in dependence of local conductor temperature nor do they yield information on multiple and dependent scattering and on interferences in particulate superconductors. This is the task of radiative transfer and of application of rigorous scattering theory to radiation/particle interactions.
Radiative transfer, in general, means propagation of radiation over short distances. In exceptional cases, radiative transfer proceeds like a conductive, diffusion process. On the other hand, if propagation of radiation occurs over extended distances (direct interaction of radiation with neighbouring particles, with sample boundaries or substrates), we speak of radiation exchange. Interaction with substrates by radiation exchange is frequently observed in optical experiments with thin films.
This paper investigates how radiative transfer explains extinction properties (absorption and scattering) of particulate superconductors and to which extent it may have impacts on superconductor stability.
A superconductor is stable if it does not quench, which means if the correlation of electrons to electron pairs is strong enough to completely compensate an increase of internal energy that, for example, may result from thermalisation of a disturbance.
Disturbances comprise conductor movement, with transformation of mechanical into thermal energy, or absorption of particle radiation, fault currents or momentary cooling failure. Disturbances frequently are transient, but there are also permanent disturbances like hysteretic or flux flow losses. Even a small decrease of local critical current density, from a corresponding local increase of superconductor temperature, can initiate losses and lead to further temperature increase and, as a consequence, to a quench. This may happen also under constant transport current.
Quench proceeds on very small time scales (milliseconds or less) and frequently leads to local damage of the conductor. But quench belongs to life of a superconducting magnet, which means measures have to be taken to avoid quench. Quench can be avoided by an appropriate design of superconductors (filaments, thin films) using stability models.
Stability models yield predictions on permissible conductor geometry like maximum radius of filaments or aspect ratio of thin films, or maximum, zero loss transport current. For a description of traditional, analytic stability models, see the standard literature like Wilson [1] or Dresner [2].
As an advance over-analytical stability models, numerical methods have recently been introduced by Flik and Tien [3] and by the present author [4,5,6,7]. Instead of assuming uniform temperature distribution, these methods to predict stability rely on calculation of temperature fields in the superconductor.
This step is important since superconductor critical current density and critical magnetic field strongly depend on local conductor temperature. Under a transport current, it is, in particular, the transient, not only the stationary superconductor temperature field that is needed for stability analysis.
Near the phase transition, already tiny temperature fluctuations can drive the superconductor into normal conducting state. In such situations, inclusion of radiative transfer into heat transfer calculations becomes indispensable although the contribution by radiation to total heat transfer could be small in relation to other heat transfer components.
A superconductor might be non-transparent to radiation and stable against quench, while the opposite situation might be possible as well: if the sample is transparent, stability might be missing and the superconductor also under a weak disturbance would undergo a phase transition. It is not clear that a correlation between non-transparency and superconductor stability might exist. This question, like a variety of related problems, will be investigated in this paper.
The paper is organised as follows: in Section 2, we explain in detail the properties of non-transparent objects. Section 3 describes the general aspects of radiative transfer and its application to superconductors. Section 4 presents the calculations of extinction cross sections by means of three independent models including results from rigorous scattering theory, and Section 5 adds a risk analysis. We investigate whether there is a change of radiative transfer mechanism at the phase transition that could be indicated by a sudden jump of the extinction cross sections.
Finally, Section 6 discusses an interesting corollary from radiative transfer, the question whether physical time and time scales, in general, are uniquely defined in non-transparent superconductors. An answer to this question may have important consequences for the applicability and reliability of all stability models.
At the end of Section 6, a conclusion is made how the stability of superconductors can be improved in future development of materials by a step directly derived from the results of radiative transfer calculations reported in the following.
2 Superconductor Temperature Distributions
2.1 Numerical Calculations
Traditional stability models assume homogeneous superconductor temperature. It appears this assumption is fulfilled only in exceptional cases. Real situations have been analysed by numerical simulations of temperature fields in multi-filamentary BSCCO 2223 and in coated YBaCuO 123 conductor thin films. Results of the calculations, and the position of BSCCO filaments within the tape cross section and positions of YBaCuO thin films in coated conductors, are shown in Figs. 1a, b and 2a, b. From both figures, quench of a superconductor in these conductors occurs neither homogeneously nor simultaneously in all its single cross section or conductor volume elements.
a Nodal temperature in the cross section of a BSCCO 2223 multi-filamentary conductor, calculated by a transient finite element analysis including radiative transfer in the diffusion (additive) approximation. Because of axial symmetry, only the left half of the total conductor cross section needs to be shown (symmetry axis is on the right). Results are reported at t = 1.7 ms, 2.0 ms and 2.1 ms (from top to bottom) after the start of a permanent disturbance (flux flow resistance, by a large fault transport current exceeding critical current). Local temperatures are identified by the corresponding horizontal bars. Symbols MX and MN indicate positions in the cross section where minimum and maximum temperatures are observed. The temperature diagram at the bottom is copied from [5]. b Cross section of the (1G) BSCCO 2223/Ag Long Island superconductor [55] (a tape consisting of about 100 filaments; the figure shows a section of Fig. 1b in [5]). The crystallographic c-axis is perpendicular to the filament planes. The vertical, solid red line schematically indicates the direction of a hypothetical scan of the thermal diffusivity by a thermal wave technique, for detection of a local quench. The distance between the open red circles serves for estimating the transit time that a radiative signal emitted at the centre of the tape by diffusion needs to cross half the tape thickness
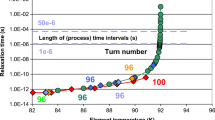
a Nodal temperature calculated in an YBaCuO 123-coated, thin-film conductor, calculated like in Fig. 1a, here at time t = 4.2 ms after the start of a disturbance (again transport current exceeds critical current). The simulation comprises the upper turns 96 to 100 of a superconductor coil. White dashed lines are part of the mesh; narrowly spaced, double white lines indicate the electrical insulation between the turns, and the outer double lines reflect the reinforcement of the casting compound. Superconductor temperature in turn 96 has already increased to about 94 K (exceeds TCrit = 92 K) while in turns 97 to 100, temperature is still close to coolant temperature. The figure is taken from [7]. b Simulation scheme of a coated, thin-film YBaCuO 123 superconductor (schematic, not to scale). The upper diagram in b shows the metallization (Ag), buffer layer (MgO and corresponding interfacial layers) in immediate neighbourhood of the superconductor (SC) thin film (the conductor architecture is typical for a coated conductor). Dimension of the surface roughness is highly exaggerated. The lower diagram in b shows the cross section and meshing of the superconductor thin film. Superconductor layer thickness is 2 μm, its width is 6 mm and the thickness and width of the Ag elements are the same as those of the SC film. The crystallographic c-axis of the YBaCuO layer is parallel to the y-axis of the overall coordinate system. The figure is a section of Fig. 1 in [7]
Experimental confirmation of these numerically simulated results would be most welcome, but its realisation is a laborious task. Experiments recently have been reported, for example, by Solovyov and coworkers [8]; they investigated the spatial distribution of critical current density using separate strips prepared for patterning a coated conductor. From the non-uniform critical current distributions, one may conclude there is also a non-uniform distribution of local conductor temperature, like those in Fig. 2a. But more experimental evidence is needed.
Note in Fig. 1a the enormous rate of local conductor temperature increases once the disturbance is switched on (in this case, a sudden runaway of nominal current to a fault). The rate of about 3 × 103 K/s observed within the period 0 ≤ t ≤ 2 ms results from solely flux flow resistance but later increases to more than 105 K/s when critical temperature is exceeded.
Therefore, transient distribution of critical current density, in general, will be neither constant nor uniform in the conductor cross section. Positions with superconductor temperature above and below critical temperature, after a disturbance, may coexist in the total cross section, at least within short time intervals. Different resistive states in parallel would be responsible for transient current limiting, and quench may occur locally, at different positions and times, after a disturbance. Strong local variations of superconductor temperature invariably lead to non-zero radiative contributions to local heat flow.
The transient temperature profiles have been calculated with a finite element program (ANSYS 16). Finite element methods serve for solution of Fourier differential equation. The calculated temperature fields are mapped onto fields of critical current density and magnetic fields. Details of the simulations (meshing, selection of time steps, convergence) have been reported previously [4,5,6,7].
The solutions apply the additive approximation for the thermal conductivity. The total thermal conductivity λTotal is written as a sum of separately modelled components, λTotal = λCond + λRad, where λCond and λRad are the (competing) contributions by solid conduction and radiation, respectively. The additive approximation cannot be understood without a detailed analysis of radiation propagation (see later Section 3).
Intuitively, one would expect heat transfer might be enforced by radiation transport (large λRad) so that hot spots soon would disappear. But propagation of radiation is blocked in non-transparent objects, which, in turn, means a quench, under a disturbance, is more probable to occur in non-transparent materials.
It is thus important to clarify the situation: are multi-filamentary and coated thin-film superconductors transparent or non-transparent to radiation? Is the additive approximation correct when it was applied in the finite element calculations to obtain Figs. 1a and 2a?
2.2 Transparency vs. Non-transparency
Optical thickness (τ) is defined by the sample’s extinction coefficient (E) and its thickness (D): if E is independent of wavelength and if E is also homogeneous (constant) through the object under study, we have τ = ED (a more rigorous definition of optical thickness is given in Section 3). Optical thickness serves for separation of transparency and non-transparency of a superconductor (Section 2.2.2).
2.2.1 Transparency
A sample is considered as transparent if its optical thickness (τ) is zero or at least extremely small (a situation approximately fulfilled in some dilute gases). If the optical thickness is zero, a beam, if emitted from a directionally emitting radiation source, will not be scattered into directions different from its original direction; also, there are no absorption/remission interactions and interference effects. The case τ = 0 accordingly indicates direct transmission.
A transmission experiment is simulated in Fig. 3. Assume that a strongly focused, directional radiation source (Fig. 3A) is placed in front of an optically transparent sample (for simplicity, the figure is schematically used for explanation of transparent and, later, also of non-transparent samples). The transmission experiment is located in the space R3, at a stationary position, and shall be invariant under translations and rotations. Close to the sample’s rear surface, an observer, C, sensitive to radiation at different wavelengths) shall be positioned exactly on the beam axis.
Upper diagram (schematic) a disk of thickness (D); a radiation source (A, red circle) that emits radiation pulses of directional intensity (\(i^{\prime } )\); a real observer at position (C), in front of the rear surface of a non-transparent, solid slab 0 ≤ x ≤ D; and a virtual observer (B), operating within the slab. Boundaries at x = 0 and x = D are transparent. Arrows and large half-circles (envelopes to the thin, solid arrows) at x = D indicate isotropic intensity (remission and scattering of radiation from this position). For simplicity, the figure is used for transparent (no absorption/remission or scattering events within 0 ≤ x ≤ D) or non-transparent (where photons, under multiple absorption/remission and scattering interactions, indicated by the small circles, travel along statistically defined paths (W1 or W2); compare text). If the sample is non-transparent, there are diffuse radiative boundary layers each located between x = 0 and x1 = 15lm and between x2 = D − 15lm and x = D (dashed, blue lines, schematic; the real observer (C) will not be able to look deeper into the disk). A virtual observer (B) (explained in Section 6) is indicated by the solid black circle. Small circles within the slab indicate scattering or absorption/remission events. Lower diagram: open and closed circles on the dashed horizontal line denote images, f [e(s, \(\xi ^{\prime }\))], of events, e(s, \(\xi ^{\prime } \)), on the different paths (W1 and W2) that the virtual observer books as a sequence of images. The lower horizontal line indicates the (ideal, i.e. dense) time scale (t) experienced as physical time. The origin (t0) of physical time, as indicated on the horizontal dashed line, could be identified only in a transparent material
A completely transparent sample would not contain any material constituents or any variations of optical properties like the refractive index between the planes x = 0 and x = D. If the detector responds exclusively to the original beam, the observer at his position then will be able to differentiate between
-
(a)
Radiation emitted by the source at constant power or wavelength, with the radiation source at different (axial) positions, or
-
(b)
Radiation emitted at variable power or wavelength, but with the radiation source at a fixed, single position
-
(c)
Monochromatic radiation intensity emitted by the source at different power
-
(d)
Radiation intensity emitted at constant power but at different wavelengths
-
(e)
Single, isolated pulses, or series thereof, and periodic radiation sources, all emitted from any (stationary) position or at any wavelength or at any time or frequency
In order to fulfil items (a) to (e), the time interval between any event, like a variation of the source’s emissive properties, and when its image is taken by the detector, must be shorter than the characteristic time of any variation of the source (the event must be stationary within this time interval). We add this condition as item (f) to the above given list (a) to (e).
The observer accordingly will only then almost immediately notice any variation of the emitted signals (wavelength, duration, intensity, position of the source). Limitations are due solely to the velocity of light (and to the time constant of the detector). The same conclusions would apply if emission from the source was isotropic, or if emission comes from a thermal source of infinitely small or of extended, non-zero cross section.
We can put the above items (a) to (f) into mathematical form: transparency can be described by means of mapping functions, f [e(s, ζ)], that create images, e(s, t), of events, e(s, ζ). Events occur in R3 at locations (s). The scale ζ will be explained below.
Images of events comprise space and time coordinates. There is no problem with space coordinates; we can use the same coordinate system (s) to identify the location of events and of their images. Accordingly, space coordinates (s) of events and of their images, f [e(s, ζ)], for simplicity shall be located in the same space R3.
But the situation is different with time coordinates: trivially, when an event takes place, a specific time is intuitively coupled to this event. But signals (ζ), as reported by a clock, do not constitute time in the usual sense but simply describe either single events or a series of discrete events, indicated by mechanical signals or, for example, electronic signals or what is indicated by an hourglass. All these events, by their signals (ζ), have to be booked on proper time scales (t).
Contrary to the discrete structure of the series ζ, and contrary also to mechanically or otherwise booked signals, time scales, in the usual understanding, do not have a discrete structure but are dense (the exact mathematical meaning of “dense” will be explained in Section 6.3).
In addition to items (a) to (f), we must, for a time scale to be unique and unambiguously defined, also request that the time interval between two successive events, e(s, ζ) to be booked as e(s, t), may be arbitrarily small. If this cannot be fulfilled, part of events of a sequence could be lost from registration on the time scale (t), which means a dense set that could be generated by an arbitrarily large number of images of events (from an arbitrary large number of events) cannot be obtained. Both events and their images potentially must be dense.
Images (bookings), e(s, t), of discrete or continuous events, e(s, ζ) (like oscillation of a charge) after signals received from these events, have to be ordered. While ordering on the ζ-scale is provided automatically by operation of a clock, mechanically or otherwise, mapping functions, f [e(s, ζ)], are needed to realise orderly booking on continuous (dense) time scales (t). The f [e(s, ζ)] are needed also to enable differentiations, like ds/dt, while the same procedure, tentatively realised on the scale (ζ), would provide only ratios Δs/Δζ, with both Δs and Δζ of finite size. A time scale accordingly is dense, if an arbitrary variable, v(t), can be differentiated with respect to this time scale (t).
But it is not clear that the order (succession), ζ, of events will be conserved when they are booked on the time scale, t (this restriction has nothing to do with relativity; all events shall take place at fixed space coordinates). While conservation of the order will certainly be provided in case of transparent media, this is not necessarily fulfilled in a non-transparent medium.
Orderly booking on the time scale (t) can be realised by the properties of the mapping functions, f [e(s, ζ)]: to uniquely define transparency, the mapping functions, f [e(s, ζ)], must allow the creation of images in R3 from all events in R3 occurring at any position or instant (and irrespective of their number, limited or infinitely large). The f [e(s, ζ)] also must allow reverse mapping: inverse mapping, e(s, ζ) = f− 1f[e(s, ζ)] = f− 1[e(s, t), must exist for all events and uniquely reproduce from the images, e(s, t), the underlying origins, e(s, ζ), and their original order. In other words, the mapping functions must be bijective, which means they must be injective and surjective, in the usual mathematical sense, and irrespective of the number of images and their origins.
Definition of the mapping function, f [e(s, ζ)], applies to all items, (a) to (e), of the above and their extension, item (f). But what happens if these items cannot be fulfilled? The explanation is that mapping functions, f [e(s, ζ)], in non-transparent media, are not bijective. The mapping functions, f[e(s, ζ)] = e(s, t) and e(s, ζ) = f− 1f[e(s, ζ)] = f− 1[e(s, t)], will again be needed in Section 6.
2.2.2 Non-transparency
Comparison with a critical optical thickness, τCrit, is a simple, numerical means to decide whether a sample is non-transparent. However, from the physical standpoint, which means the impact of non-transparency on propagation of radiation (like spatial distribution of scattered radiation), the difference between transparency and non-transparency is better understood from observations (see Section 2.2.3).
Numerical definition of the critical optical thickness is based on Lambert-Beer’s law: optical thickness, if it exceeds τCrit = 15, reduces incident radiation to almost zero, since the ratio of residual to original, directional intensity, \(i^{\prime }/i^{\prime }_{\mathrm {0}}=\exp (-\tau \)), is below 10− 6 (zero in the sense that a detector would not be able to differentiate between an original signal and its 1/106 residuum). This number is small enough to say there is almost no directly transmitted radiation arriving from the source at the position of a detector. The position is defined by this optical thickness.
The criterion τCrit = 15 appears to be arbitrary. We could also define τCrit = 50 or 100 that causes even stronger damping of incident radiation, but the then-required geometrical thickness (D) under a given extinction coefficient (E) might become larger than the limit set by the dimensions of the objects under study. In the present case, the limit is set by dimensions of grains and filaments and by thickness of thin superconductor films in high-temperature superconductors.
2.2.3 Observations
In non-transparent media, radiation propagation proceeds by a large number of single steps and becomes diffusely distributed. Neither is it possible to safely make decisions on the properties of the radiation source nor can decisions be made on single, internal scattering and absorption/remission processes in the medium (except for a possibly existing diffuse boundary). This applies even if the radiation source would strongly be focussed in the direction of the detector or if the scattering properties of the medium are highly anisotropic.
As an example, the angular distribution of originally N = 5 × 104 rays (“bundles” in the Monte Carlo language), leaving the rear surface of a cylindrical pellet, is shown in Fig. 4. After a multiple of absorption/remission and scattering interactions within the sample, with the radiation source located in front of, or exactly at the front surface, the final distribution, on the rear sample surface, of the emitted or scattered radiation leaving this non-transparent sample is highly isotropic.
Monte Carlo simulation of the distribution of radiation emitted from the rear sample side (x = D) in Fig. 3. Emission from the front sample side is by an extended (not point-like), realistic diffuse radiation source (the same result would be obtained if the radiation is anisotropically emitted, like a beam from a laser, and if optical thickness is large). Data are calculated for a bed of ZrO2 particles using extinction coefficients, E[1/m] = 5 × 103 (olive), 104 (dark blue) and 5 × 104 (red diamonds); the corresponding optical thickness amounts to τ = 5, 10 or 20, respectively. Results are obtained for anisotropic internal scattering (mS = 2, forward scattering) and albedo (of single scattering; Ω = 0.5) (compare the original report). The solid curve indicates the theoretical, diffuse cos(Θ) distribution given by Lambert-Beer’s cosine law. The larger the extinction coefficient, the better is the angular distribution of the bundles represented by a diffusely radiating (rear) surface. The figure is redrawn from [54]
Accordingly, if the observer (C) in Fig. 3 recognises the diffuse distribution of radiation, he will conclude that the object between x = 0 and x< D is non-transparent (provided the plane x = D does not deteriorate the distribution of radiation emerging from the internal positions of the object).
In any non-transparent dispersed medium, constituents like solid single particles or any other obstacles to radiative transfer can be interpreted as pairs of sources and observers: if radiation is emitted as thermal radiation from a particle (A), any particle (B) in Fig. 3 may be considered an “observer” that responds to the incoming radiation from A, for example by scattering.
If the observer (particle B) is located inside the non-transparent medium or within only a diffuse boundary layer, we will call it a “virtual” observer. The difference between transparent and non-transparent media then becomes more obvious:
-
(i)
In the transparent case, distances of virtual observers from a source are completely arbitrary; they see each other, almost instantaneously, and, most importantly, they see any radiation source. Items (a) to (f) are fulfilled.
-
(ii)
In a non-transparent medium, virtual observers at certain positions see only their closest neighbours (the radiation that they scatter or emit in direction of these positions), but they never see a source located at a distance of more than the said τ ≥ 15 mean free paths, and they see even the closest neighbours only after an extended transit time (as will be shown, in most cases not simply given by the velocity of light, which would apply to solely pure scattering interactions, but in reality includes absorption/remission processes that take much longer). Items (a) to (f) thus would be violated.
The description of observations in non-transparent media, and how they can be described by radiative transfer, is difficult because of the presence of also heat transfer contributions other than radiation in real situations. One of the most cited volumes, with emphasis on purely radiative transfer, is by Chandrasekhar [9]. Analytical or numerical handling of radiation propagation, in parallel to also other modes of heat transfer like conduction in solids, is treated in traditional volumes like [10] and [11]. First numerical studies of the overall impact of radiation heat transfer on the stability of a superconductor, in the presence of also conductive heat transfer, have been reported in [12] and [13]. Radiative transfer in solid, non-transparent media has been studied, and a radiative diffusion model has been explained in [14]. The present paper apparently is the first attempt to apply radiative transfer calculations to realistic particulate structures of high-temperature superconductors.
2.2.4 Multi-filamentary Superconductors as Particle Beds
Non-transparent media in many cases are highly dispersed. A schematic division of non-transparent media against their transparent or translucent counterparts is given at the end of this paper (Fig. 25 in the Appendix).
For a medium to be classified as dispersed (a particle “bed”), it is sufficient that the constituents can be distinguished by their solid surfaces or by interfacial layers near their surfaces, against their hosts. Solid particles and the corresponding interfacial layers, as materials’ obstacles, are responsible for local, discrete variations of the index of refraction.
We will use for the radiative transfer calculations the expression “particle bed” not only for these classically (mechanically) dispersed media but also for solid spheres or filaments, or for particles of any other geometry, if they are dispersed in a solid matrix, with mechanical or radiative strictly different properties.
Multi-filamentary superconductors, in this view, constitute a particle bed, too, as they are composed of thin, ceramic superconductor filaments dispersed in a highly conducting, metallic matrix (like Ag, Cu). This aspect (a particle bed constituted by particles in a hosting solid) will become important in connection with calculation of extinction coefficients by application of scattering theory in Section 4).
Particle beds and clouds, in general, and their constituents like ceramic filaments in a multi-filamentary superconductor, do not have sharply defined radiative surfaces but diffuse boundary layers, in contrast to the proper solid surfaces or solid/solid interfaces that can more or less precisely be located (apart from surface roughness, adsorbed species or contaminations).
BSCCO 2223 multi-filamentary superconductors are manufactured as tapes, with thickness of about 250 μm to 300 μm and width of 3–4 mm, each with presently about 100 filaments in their cross section (Fig. 5). In type II LHe-cooled, multi-filamentary superconductors, like NbTi or Nb3Sn, the number of filaments is larger, by orders of magnitude, but again, all filaments are dispersed in a highly conducting, metallic matrix.
Microstructure of a multi-filamentary superconductor showing filaments, domains and grains (schematic, all dimensions are in micrometres). a Grains as flat, plate-like objects (schematic, not to scale; this reflects the finite element meshing scheme used in Fig. 1a, b). Matrix material (Ag) is schematically indicated by light green background. Parts a and b apply to Fig. 6a (and approximately to also the very densely packed flat, thin, plate-like particles in Fig. 6b). b An enlarged section of grains as solid black lines; the light grey part of the filament cross section is empty. c The multilayer scheme to calculate radiative heat transfer (radiative exchange between screens); a sequence of open structures within which the radiative exchange model ((7a), (7b) and (8)) is applied. Direction of an incident beam of intensity (\(i^{\prime } \)) in b, c is indicated schematically by the thin red lines perpendicular to the crystallographic ab-planes of grains and filaments. Additionally, part (c) of the figure shows the series of conductor volumes within which (i) the multi-foil concept (in the voids) and (ii) the treatment of the radiative exchange problem under dependent scattering (in the grains) has to be modelled
The macro-porosity of BSCCO multi-filamentary, (1G) tapes depends on the ratio of superconductor to matrix material cross sections; in BSCCO 2223, this ratio is between 0.3 and 0.5. Filament dimensions in tapes prepared of this material are of about 30 μm thickness and 300 to 400 μm width, with Ag as the matrix material. The filament porosity is much smaller (below 0.1, compare Fig. 6a and b) and depends on the ratio of superconductor material (the grains) to the void cross sections. In Section 4.3, the grain micro-porosity will be estimated in connection with an attempt to model dependent scattering by very small subparticles.
a, b Microstructure of particulate BSCCO superconductors. a Layer structure of slightly curved, plate-like grains in a single BSCCO 2223 conductor filament, a result typical for powder in-tube manufacture steps. Because of the large anisotropy ratio of thermal transport, the grains can be considered, from a pure thermal transport aspect, as roughly flat. Length of the bar (to the lower right of a) indicates 5 μm. The figure is copied from [56] (Ag matrix material is removed). b BSCCO 2212 grains in textured fibres prepared by laser-induced, directional solidification [57]. As a template, Fig. 1 of this reference has been copied for preparation of the present Fig. 6b (insertion of blue curves by the present author, in order to identify domains within which the grains are approximately aligned in parallel). Grains (black lines) are of flat, plate-like geometry, with the thickness of about 0.1–0.3 μm. The grains are much more densely packed than the grains in Fig. 6a. Length of the red bar, to the lower right of Fig. 6b, is 5 μm. The cryogenic radiation screen model (Section 4.2) should be applicable preferentially in this case
Deposited on appropriate (flexible) substrates, together with a variety of thin inter-layers for improving orientation of crystallographic axes, growth rates, for electrical insulation and as protective layers, thin films with thickness in the order of 1 μm to 2 μm are increasingly applied as second-generation (2G) coated conductors for current transport. Their porosity is much smaller.
The thickness of thin-film superconductors (like single layers of YBaCuO 123) that are suitable for laboratory optical spectroscopy is only between 15 and 200 nm.
2.2.5 Selection of Samples for the Radiative Transfer Calculations
Figures 6a, b and 7a–c are selected for the radiative transfer calculations in multi-filamentary and thin-film superconductors, respectively. The figures are taken from the literature; see figure captions for references to the corresponding original work.
a–c Micrographs of thin-film and thick-film YBaCuO conductors used for coated conductor architecture indicating the existence of grains, in the radiative sense, in thin films. The grains are obstacles to radiative transfer. a Surface morphology of an YBCO film with an electrodeposited Ag thin film. The flat irregular structures in the Ag coating are considered as images that result from irregularities of the YBaCuO 123 superconductor film below (deviations from ideal single-crystal lattice geometry, or statistically distributed, polycrystalline manifolds). Length of the thin white bar (right, at the bottom of this figure) is 5 μm. The figure is taken from [58]. Reprinted with permission of the National Renewable Energy Laboratory, from https://www.nrel.gov/docs/fy11osti/49702.pdf, accessed on April 11, 2018. b Scanning tunnelling micrograph of a highly textured, YBaCuO 123 layer deposited by IBAD on a non-textured, flexible metallic substrate. The figure is taken from [59]. c Section of a polycrystalline, thick YBaCuO superconductor, consisting of flat, approximately plate-like particles. Yellow, green and red circles are added by the present author to schematically indicate shadowing (dependent scattering) by neighbouring particles, as obstacles to incident radiation (the blue beam). Compare text. The original figure is taken from [60]. Aspect ratio is about 4 to 6 (Fig. 6 of this reference)
Figure 6a shows grains in a BSCCO 2223 (1G) filament with the typical layer structure of approximately flat, plate-like grains arranged parallel to each other. The layer structure results from powder in-tube manufacturing. In Fig. 6a, the matrix material (Ag) has been removed from the sample.
Figure 6b shows a section of a BSCCO 2212 (again, 1G) fibre produced by laser-induced directional solidification. Its very thin, orthorhombic superconductor grains are densely aligned in domains, with an increased number of solid/solid contacts between neighbouring particles. The crystallographic ab-planes are arranged in the direction of the fibre axis. Yet, there are voids within the BSCCO fibre between grains and within domains, by cracks and other deficiencies that, in Figure 6b, all cause a micro-porosity that is much smaller than the porosity of the (particulate) BSCCO 2223 conductor sample, about 0.01 against the 0.3 to 0.5 of the filaments.
Instead of the particulate structure prepared with BSCCO (Fig. 6a and b), with mechanically, clearly separated solid particles (grains, fibres, domains), Fig. 7a, b shows thin films used for (2G), standard coated conductor architecture while thick films (Fig. 7c) have been suggested as a surrogate (technically alternative, thick YBaCuO 123 conductors). Again, Fig. 7a–c is taken from the literature, with the references to original work given in the figure captions.
A first idea is that thin films do not contain particulates. However, microscopic, particulate structure (grains) of thin films of also a coated conductor and their influence on critical current density has been confirmed in [15]. Compare Figs. 23b and 24a of this reference that describe an hexagonal grain array and a Monte Carlo grain growth model using square elements, the most simply configuration, to describe current percolation in the thin film-coated conductor.
To go one step ahead, separation of a thin film into particulates not necessarily requests, in general, the creation of mechanically defined interfaces. Any variations of local electrical resistance (of whatever type, like a flux flow resistance that arises from a local transport current exceeding critical current density) may induce a particulate structure, in the view of current transport. Likewise, any local variation of an otherwise perfectly homogeneous, radiative continuum, for example a fluctuation of the refractive index, creates, from the radiative transport view, particulate internal structures of a thin film.
Accordingly, whether a thin film or any other object is of particulate structure has to be defined with respect to its transport properties, electrical or radiative or others. Figure 7a shows an example. A thin Ag film is electrodeposited onto the YBaCuO 123-coated conductor in Fig. 7a. Topography of the thin film provides an image (replication) of near-surface grain boundaries or of other disturbances in the regular lattice of the YBaCuO film; the proper YBaCuO film thus appears not to be strictly homogeneous but incorporating specific (as seen from the current transport view) particulate structures. Lateral dimension of the images is between 2 and 15 μm. Because of the YBaCuO film deposition process, the objects should be flat and, from the dimensions of the images, of plate-like particulate geometry. The authors demonstrate that direct Ag plating has not degraded the tape quality; its critical current is more or less the same as that of the bare YBaCuO layer, or when it was sputtered with Ag.
A scanning tunnelling micrograph of a highly textured, YBaCuO 123 layer of 300 nm thickness deposited by ion beam-assisted deposition (IBAD) on a non-textured, flexible metallic substrate is shown in Fig. 7b. A highly textured, Yttrium stabilized zirconia (YSZ) layer was prepared as a buffer. The superconductor film has much larger grains (average size of about 200 nm), with apparently no correlation to the grain structure of the substrate. The micrograph shows the top surface of the superconductor with the grains (ab-planes) formed by island growth.
The sample shown in Fig. 7c is the section of a thick YBaCuO superconductor prepared by bio-mimetic bulk synthesis. According to the authors, the conductor originally was developed to circumvent problems with the manufacture of (2G) coated conductors. The study served to achieve microscopically, morphological control of YBaCuO 123. In this microstructure, platelets on a flat substrate subsequently arrange themselves in preferred (x, y) orientation (the crystallographic ab-planes). The thickness of the platelets is about 1 μm to 3 μm, larger than the thickness of the particles in Fig. 6a and b, and the total sample thickness is much larger than, and contrary to, the presently accepted, standard coated conductor architecture with thin YBaCuO films. Voids between the particles apparently do not contain any material.
All grains, and from the radiative transfer aspect, also all grain-like structures, in Figs. 6a, b and 7a–c, respectively, are obstacles to propagation of radiation.
3 Radiative Transfer Calculations
For a first, provisional estimate, using a filament thickness of 30 μm and an extinction coefficient of at least that of a highly conducting, solid metallic sample, in the order of 107 (1/m) ([16], Table 2.1, the value of Au at visible wavelength and at RT), the optical thickness amounts to τ = 300. This clearly indicates non-transparency.
Assuming the hypothetical thickness of a superconductor thin film of 1 μm to 2 μm, like in a coated conductor, and if again E = 107 (1/m), we still have τ = 10 or 20, respectively. Accordingly, metallic and superconductor films, provided their extinction coefficient is of the same value and their thickness is at least 2 μm, can be considered as non-transparent.
But if thin film thickness is only 15 nm to 100 nm, a standard thickness for optical investigations of superconductors, they safely would be transparent to radiation if their extinction coefficients do not significantly exceed the E = 107 (1/m). Radiative transfer in a substrate then would become visible in the measured reflectance or transmittance spectra, and radiative diffuse boundary layers (Fig. 3) then probably would overlap.
The question thus is whether the extinction coefficients of superconductors are of the same order as those of highly conducting metals, the approximately E = 107 (1/m).
3.1 Optical Thickness and the Equation of Radiative Transfer
In radiative transfer, the mean free path between two successive radiation/solid particle interactions at a wavelength (Λ) is a function of the spectral extinction coefficient, EΛ(s), at a position s. The extinction coefficient serves for the definition of the optical thickness
at the geometrical position, s∗, in relation to s∗ = 0. The extinction coefficient, EΛ(s), need not be a continuous function of position s, which means the number per unit volume of constituents in a medium or their geometry and dimensions, or their optical properties like the refractive index, may locally be different. The path s may be oriented under any angle against surface normal of a sample.
The spectral mean free path (lm,Λ) reads
see Siegel and Howell [17], p. 414.
Equation (1b) defines lm,Λ as a distribution of statistically variable, spectral values. Thus, the mean free path (lm,Λ) only statistically would coincide with centre-to-centre distance or with the clearance between particles in a particle bed.
Both extinction coefficient, EΛ(s), and mean free path, lm,Λ(s), are local values (depending on the space coordinate (s)), in contrast to the optical thickness (τΛ) that integrates the extinction properties of the superconductor material over total sample thickness (this distinction will become important in Section 4.3).
If EΛ does not depend on s, the mean free path reduces to the usual expression lm,Λ = 1/EΛ, and if the medium is grey, we have lm = 1/E.
Individuality of an obstacle, or of a particle/particle phalanx characteristic for radiation exchange cell models, is lost in the statistical expression ((1b) for lm).
3.2 The Additive Approximation
Calculation of temperature profiles, of life importance for stability analysis in filaments and thin films, requires simultaneous solution of (a) the equation of radiative transfer (ERT) and (b) the equation of conservation of energy.
-
(a) Omitting for simplicity the index Λ for the wavelength, the ERT reads
$$\begin{array}{@{}rcl@{}} \mathrm{d}i^{\prime} /d\tau = i^{\prime} (\tau) + [i^{\prime}_{\mathrm{b}}(\tau) + \smallint {\Phi} (\omega_{\mathrm{i}},\omega ,\tau )i\prime (\tau )\mathrm{d}\omega] \end{array} $$(2a)where i′ is the directional intensity, τ is the optical thickness, dτ = Eds, \(i^{\prime }_{\mathrm {b}}\) is the black-body intensity, Φ is the scattering phase function, ωi is the incident radiation and ω is the solid angles. The integral is to be taken over the total 4π sphere.
The terms in brackets in (2a) result from absorption/remission and scattering that are redirected to, and superimposed onto, the residual intensity (i′).
If both terms, \(i^{\prime }_{\mathrm {b}}(\tau \)) and the scattering integral, ∫Φ(ωi, ω, τ)i′(τ)dω, are zero, Eq. (2a) reduces to Lambert-Beer’s law
$$\begin{array}{@{}rcl@{}} \mathrm{d} i^{\prime} (\tau)/d\tau = i^{\prime}(\tau) \end{array} $$(2b)Because of the scattering integral, Eq. (2a) describes radiative non-equilibrium. If in Eq. (2a) solely the scattering integral is zero, there is local thermal equilibrium, at any position within the object.
For details of the solution procedures of (2a), see, for example, Ref. [17] (Chap. 14, 15 and 19–20) or other standard volumes like [9,10,11].
-
(b) Conservation of energy requires (2a) to be solved with solutions of
$$ pc_{\mathrm{p}} \partial T/\partial t+\mathbf{div}\left( {\dot{\mathbf{{q}}}_{\text{Cond}} +\dot{\mathbf{{q}}}_{\text{Rad}} } \right)=\dot{q}_{\mathrm{s}} $$(2c)where \(\dot {\mathbf {{q}}}_{\text {Cond}} +\dot {\mathbf {{q}}}_{\text {Rad}}\) (the dot indicates the derivative dq/dt) denotes the heat flux vectors due to conduction and radiation, respectively, with \(\dot {\mathbf {{q}}}_{\text {Rad}} \) as the integral, over solid angles, of the intensity i′. The directional intensity, i′ = i′(τ), results from the solution of (2a). The term \(\dot {q}_{\mathrm {S}}\) denotes an energy source or a sink. In a superconductor, the energy source is the result of ohmic or flux flow losses or from a quench; a sink is given, for example, by a stabilisator coating or, trivially, by the coolant.
The solution of (2c) provides the transient temperature, T = T(τ, t), which, in turn, is needed for calculation of \(i^{\prime }_{\mathrm {b}}(\tau \)) and thus of i′(τ) in (2a). Both heat fluxes, \(\dot {\mathbf {{q}}}_{\text {Cond}} \) and \(\dot {\mathbf {{q}}}_{\text {Rad}} \) (conductive and radiative flux, W/m2), are coupled to each other by their non-linear temperature dependency and, accordingly, by the calculated temperature profiles.
Among various approximations described in the literature, a diffusion solution of (2a) can be applied if optical thickness is large. In this case, the integro-differential equation, (2a), reduces to a differential equation, in which the radiative flux (\(\dot {\mathbf {{q}}}_{\text {Rad}} \)) can be written in terms of a radiative conductivity (λRad). We have \(\dot {\mathbf {{q}}}_{\text {Rad}} =-\lambda _{\text {Rad}} \mathrm {d}T/\mathrm {d}\mathbf {s}\), just like the standard Fourier conduction law \(\dot {\mathbf {{q}}}=-\lambda \mathbf {grad~}T\). Details of this diffusion model of radiative transfer are explained in [14].
This is solely an exceptional case, under strict non-transparency, that λRadexists and is allowed to simply be added to the solid conduction conductivity (λCond) to yield the total thermal conductivity (λTotal = λCond + λRad). Only in this case are the heat fluxes \(\dot {\mathbf {{q}}}_{\text {Cond}} +\dot {\mathbf {{q}}}_{\text {Rad}} \) uncoupled from each other. If λTotal would be calculated in this way in transparent samples, conservation of energy would be violated.
The point is that each of the components of λTotal, in the additive approximation (and solely in this case), can be estimated independent of the other modes of heat transfer. The conductivities of the different components are estimated as if the other components would not be present at all (one can also say if the different components are not coupled by temperature profiles in the superconductor solid).
If an object is semi-transparent, possibly in only a limited range of wavelengths, corrections to λRad have been suggested in the literature, and in the completely transparent case, propagation of radiation, no longer a step-wise transport process, has to be calculated with radiation exchange factors (compare the collections of such factors in standard volumes on radiative transfer, for example [17], Appendix B).
3.3 Application to Superconductors
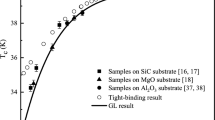
Reflectance of YBaCuO thin films is large, exceeding 90% in the normal conducting state at small frequency (ω < 25 (1/cm)) and in the superconducting state (ω < 600 (1/cm)), compare Figs. 3.5 and 3.6 in Chen [18], of 150-nm-thick, optimum doped samples, respectively. Similar observations were previously reported by Zhang et al. [19] for very thin samples (thickness between 10 and 200 nm, Figs. 4 and 6 in this reference), where reflectance exceeds 90% at wavelengths around 23 μm and 50 μm at T = 300 K, and around 23 μm at 10 K, respectively.
In metals, for comparison, large reflection indicates (and is the origin of) very strong absorption. This conclusion is supported by a thought experiment in [16] (Fig. 2.3, a torsion testing machine). The question is whether this conclusion (strong absorption, as indicated by large reflection) applies also to grains and filaments in multi-filamentary superconductors and to thin films in coated superconductors. This requests the calculation of the albedo of the superconductor (see later Section 4.3).
Thin-film optics (reflectivity, transmission, optical conductivity, refractive indices) has frequently been studied in the literature. Besides [18] and [19], compare also Gao [20], Phelan et al. [21], Zhang et al. [22], Kumar et al. [23] or Tanner and Timusk [24] and numerous references cited therein.
The radiative transfer problem, however, as a transport process within particulate and, in the radiative sense, quasi-particulate, thin-film superconductors, apparently has never been investigated. The optical thin-film studies reported in Refs. [18,19,20,21,22,23,24] have not analysed the interaction of radiation with any microscopic, discrete (grain or domain boundaries) or continuous (variations of refractive index) internal radiation obstacles in the thin films, and they have not considered coupling of radiation with other heat transfer modes (it is also not clear that this lack can fully be compensated with frequently applied, short radiation pulses). Again, this is the task of radiative transfer calculations.
Although there are intensive solid/solid, point or surface contacts in between the grains within a BSCCO filament, the superconductor grains, from the radiative transfer aspect, may be considered as quasi-independent obstacles because in this particle bed, the index of refraction, of any kind of (open or filled) voids between grains, is strongly different from that of the superconducting grains themselves. The same applies to thin films (the voids between the quasi-particulates).
For spherical particles, the radiative transfer problem in a very first step reduces to the well-known problem of light scattering by small particles; it was solved by Mie [25] in his paper. Though Mie derived this solution for diffraction by a single sphere, it also applies to an arbitrary number of randomly distributed spheres (identical by radius and composition) if the distance between each other is large against wavelength.
For cylindrical, dielectric or conducting particles embedded in an electrically non-conducting medium, thorough descriptions of the Mie and Raleigh scattering problems are given by Born and Wolf [26] (pp. 633–664) and by Kerker [27]; compare also the compilation provided by van de Hulst [28] in his book (pp. 326–328).
All these studies are restricted to particles of regular geometry. Computer programs and examples for calculation of spectral extinction cross sections of normal conductors and dielectrics, all for regular particle geometry (spheres and cylinders), can be found in Bohren and Huffman [29]. But in the present case, we do not have regularly shaped particles so that a way to treat flat, plate-like particles has to be found (Section 4.3).
In the following, principles of solely linear optics will be applied (scattering and absorption/remission independent of the radiation intensity). With the extinction coefficient (E) in terms of (dimensionless) extinction cross sections (QExt), given for one individual particle of (regular) geometrical shape, we have for spherical particles (skipping again the index, Λ, the wavelength), the relation
if the particles are homogeneously distributed in a volume and if the clearance between particles is large against wavelength. For cylindrical particles
with uniform orientation of the fibre axes. The star (*) assigned to E and QExt indicates anisotropic scattering.
In (3a) and (3b), d denotes the particle diameter and ρ and ρ0 are the density of the particulate medium (the particle bed, in vacuum) and of the solid materials of which the particles are made from, respectively.
The extinction cross section (QExt) is dimensionless; it indicates the ratio CExt/CGeom between the radiative (effective) extinction cross section (CExt) and the geometrical particle cross section (CGeom) (a value QExt > 1 thus indicates that the radiative extinction cross section, by diffraction and interference effects, is, by this factor, larger than its geometrical counterpart).
If the particles really are not homogeneously distributed in a unit conductor volume, corrections to (3a) and (3b) have to be applied, which means in the cylindrical particle case, a factor has to account for different orientations of cylinder axis to incident radiation. The corrections will depend on the albedo of the particles (whether they predominantly absorb or only scatter radiation).
But the QExt of constituents like single particles (grains) in a multi-filamentary superconductor tape, after final manufacturing steps, cannot be measured directly. The only alternative is to calculate the QExt by application of rigorous scattering theory (Section 4.3; before this is started, the order of magnitude estimates of QExt and E will be made in Sections 4.1 and 4.2).
All items (QExt and E) in (3a) and (3b) depend on wavelength. These have to be averaged following Rosseland [14] to generate mean, wavelength-averaged extinction cross sections, QExt,R of QExt,Λ and of extinction coefficients, ER of EΛ (strictly speaking of absorption coefficients, A), the latter by derivatives ∂eΛb/∂eb of Planck’s black-body radiation law integrated over the corresponding wavelength intervals (ΔΛ); the QExt,R, in turn, modifies the densities, ρSph and ρCyl, to effective values. The procedure is explained in detail in standard volumes on radiative transfer (see, for example, [17], Chap. 15).
By the manufacturing procedure (pressing, rolling, hammering) of the BSCCO tapes, its grains, filaments and domains are of approximately flat, plate-like geometry (Fig. 6a). The same applies to the quasi-particulate structures seen in Fig. 7a–c.
But expressions from rigorous scattering theory, or from approximations thereof, for extinction cross sections (QExt) of flat, plate-like particles are not available. See Bohren and Huffman [29], Chap. 8 (a “potpourri of particles”; the geometry of the superconductor grains, however, is not found in this catalogue). The same applies to Mugnai and Wiscombe [30]: while they successfully calculate scattering and absorption cross sections for a large variety of non-spherical, randomly oriented, rotationally symmetric Chebyshev particles and variations thereof, the particles neither directly reproduce nor at least approach the flat, plate-like geometry of the superconductor grains.
If incoming wavelength is large in relation to (any) particle geometry, the classical Rayleigh-Gans approximation could be another candidate ([28], pp. 85–102). But this approximation applies to particles the refractive index of which is similar to the index of the hosting medium. This is not fulfilled in the present (superconductor/matrix metal) cross sections.
In addition, particles by diffraction could be shadowed by very closely positioned neighbours (which reduces the extinction of radiation to effective values). This is the regime of dependent scattering.
A separation of independent and dependent scattering regimes of spherical dielectric and normal conducting particles has been reported in [31]. Separation of both regimes is given as a function of scattering parameter (x = πd/Λ) and volume fraction (fV). Since clearance (C) in the present case is very small or even zero (by plane or point-wise, multiple solid/solid contacts with neighbouring grains), the ratio C/Λ is clearly below 0.3, where Λ is the wavelength (in the present case, with the maximum of directional emission at about Λ = 30μm).
But the grains shown in Figs. 6a, b and 7a–c not only are not of regular, spherical shape; they also are not made of normal conducting material. It appears this problem is much more serious than the difference between real and regular particle geometry.
Further, if spherical and cylindrical particle distributions are embedded in a continuous phase, its electrical conductivity must be zero to apply solutions for QExt reported by Mie [25] and Kerker [27].
Heat transfer in particulate superconductors, like grains and filaments of the BSCCO type embedded in Ag, or of the quasi-particulate structures in thin films, especially the radiative component, requires a completely new approach.
Radiative transfer in such particulate or quasi-particulate media accordingly involves a threefold problem:
-
(i) Non-regular shape of particle geometry
-
(ii) Total extinction cross section not given just as a multiple of the individual cross sections of the constituents, because of self-interactions and dependent scattering
-
(iii) Derivation of rigorous scattering theory solutions for single, small superconducting, magnetic particles (the grains or thin films); this step primarily addresses the superconductor material problem
In the following, we describe three different models, independent of each other, to calculate extinction coefficients of particulate or quasi-particulate superconductors. The first two models serve only for a first, rough estimate of what finally is to be expected from rigorous scattering theory:
-
(1)
As an explorative method, the first attempt relies on the comparison between the London penetration depth of a magnetic field and the radiation extinction coefficient of a solid. This step (Section 4.1) only indirectly reflects the particulate nature of the superconductors. It is intended as just an order of magnitude estimate. The advantage is that it circumvents the problems associated with particle shape and the ratio of wavelength to particle dimensions.
-
(2)
The second method (Section 4.2) applies a multi-layer, radiation screen model well known in cryogenic engineering. Here, the particulates are interpreted as quasi-2D isothermal surfaces. Particle shape, refractive indices and diamagnetism need not be considered.
-
(3)
The third model (Section 4.3) relies on the application of classical (rigorous) scattering theory. The obtained extinction cross sections together with a diffusion model allow to explicitly calculate radiative transfer in particulate media. This method, however, cannot be realised without consideration of diamagnetic properties and refractive indices of the superconductor.
Calculations in [32] performed for highly normal conducting, metallic cylindrical particles (Ag) yield very large specific extinction coefficients, as shown in Fig. 8. It will be decisive to so see whether the extinction properties of superconducting cylinders (and later also of real particles, not of regular shape) might exceed those made of Ag. For normal conducting particles, the Ag fibres apparently constitute maximum extinction coefficients that can experimentally be realised in the regime of normal conductors.
Specific extinction coefficients (ER*/ρ; the Rosseland mean of spectral EΛ) for anisotropic scattering of thermal radiation by thin Ag cylinders, vs. temperature (T) and particle diameter (d). The results do not include dependent scattering, which means they can be applied to only small particulate density (ρ). The figure is redrawn from its original publication [42]
Only very few information is available on the refractive indices of particulate media. The literature on radiative properties of superconductors preferentially deals with their optical properties (optical conductivity, permittivity, refractive indices), preferentially of thin films but rarely addresses the properties of particulates.
4 Estimation of Extinction Cross Sections in Superconductors
4.1 Comparison of Penetration Depths
One finds that the larger the extinction coefficient (E) of a particulate ceramic medium (non-conductor grains), the smaller the particle diameter (d). We have E ∼ 1/d (see [33], p. 40) and if QExt is considered approximately constant ((3a) and (3b) of the present paper).
But (3a) and (3b) are simply a geometrical relation for deriving extinction coefficients from geometrical and extinction cross sections, E from QExt, and from relative density ((3a) and (3b) thus assume linear optics). Instead, it is the QExt that contains the decisive information on the extinction process. If QExt of superconductor spheres is not too different from the QExt of non-conductors, E ∼ /d also for superconductor particulates. As will be shown in Section 4.3, there is no jump of the extinction cross sections and coefficients at the phase transition so that this assumption appears to be applicable.
Huebener (private communication, July 2018) reports that the Meissner phase experimentally investigated with superconductor powders disappears with smaller particle size. The disappearance of the Meissner phase, at T < TCrit in type I superconductors, can be understood as the disappearance of the London penetration depth (λL). The extinction coefficient thus would be correlated qualitatively to the penetration depth of a magnetic field by E∼1/λL in superconductor particulates. Can this relation be extended to thin-film superconductors?
Most investigations of magnetic field penetration into superconductors deal with static external magnetic fields. The familiar spatial decay law, under stationary conditions, reads
with λL for high-temperature superconductors of λab = 150 nm [35] and to at least λc = 1000 nm (Table 2.7 in [36]). Since λc is large against grain thickness (about 0.3 μm in the c-axis direction, Fig. 6b), all grains in a filament, irrespective of their vertical position, would completely be penetrated by the magnetic field, a hardly realistic interpretation. In the following, the penetration depth, therefore, is understood as that of the filaments, with almost zero porosity.
For describing the penetration of time-dependent magnetic fields, we can estimate the spatial dependence of the field decay if we insert the Maxwell equation, curl E = −dH/dt, into the first London equation, \(\mathbf {E} = \lambda _{\mathrm {L}}^{\mathrm {2}}\)dJ/dt. This yields
see Huebener [34] (p. 6). Using curl H = J, Huebener obtains
from which div grad dH/dt = (1/\(\lambda _{\mathrm {L}}^{\mathrm {2}}\)) dH/dt and its time dependent solution is obtained
In both static and time-dependent magnetic fields, the spatial dependence of the decay of H is the same.
Let us now compare the spatial decay of dH(x)/dt with the decay of directional radiation intensity (i′) given by Lambert-Beer’s law, physically a completely different decay process, but the spatial structure of both decay laws again is the same.
Consider a harmonic, plane electromagnetic wave, with both its electrical and magnetic field vectors, E and H, in phase
In vacuum, the vectors E and H are oriented perpendicular to each other. They are also perpendicular to the wave propagation vector (k). Assume that the wave impinges under right angle onto a flat (x, y) superconductor surface (Fig. 9a). E and H then oscillate in planes parallel to this surface. Conservation of energy is indicated by the Poynting vector, S = E×H.
a Orientation of the vectors of electric and magnetic fields (E and H, respectively) and of propagation vector (k) of a harmonic electromagnetic wave (schematic and in vacuum). The dashed lines (triangle) denotes an example of intermediate x, y-planes all positioned within a flat superconductor and all parallel to superconductor surface. The impact of a complex refractive index of the superconductor on E and H is neglected. b Extinction coefficients, E (1/m), and specific extinction cross sections, QExt, of YBaCuO 123, vs. radiation temperature. The E coefficients are obtained from comparison of the IR radiation penetration depth (1/E), with the London penetration depth (λL) of an external, time-dependent magnetic field. The QExt is given for one cylindrical particle (compare text for explanations). The penetration depth (λL), here the value λab of mid-IR radiation incident perpendicular to the crystallographic ab-plane, is about 150 nm (measured in [35]; screening currents are flowing in this plane)
The Poynting vector represents momentary radiation energy density (time-dependent radiative flux) penetrating in z-direction into the sample; dimension of S is expressed in W/m2. Radiation intensity (i′) of a beam, on the other hand, is described by the radiative energy flux per unit solid angle and per wavelength interval; dimension of i′ is W/(m2/sr/μm). Restriction of the intensity “per solid angle (steradian)” and “per wavelength interval (μm)” is of no importance for comparison of the spatial, directional decay, provided solid angle and wavelength intervals are small. Decay of the radiation intensity thus can be described by decay of its magnetic field vector, H. Both vectors Hexp and Hmid−IR are of the same dimension.
If magnitude of the H field and intensity (i′) are not too large, the superconductor cannot distinguish between an experimentally applied, time dependent magnetic field (Hexp, which means in a standard field penetration experiment) and the radiation field vector (Hrad) in the Poynting vector of an incident beam. This works if field orientations and frequency are the same. Frequency is given by ω = c/Λmid−IR, where c is the velocity of light and Λmid−IR is the wavelength of the incident radiation, in this case the mid-IR wavelength. Under these conditions, the exponents, − x/λL, and − τ = −Ex, are independent of the corresponding magnitudes of magnetic field and of radiation intensity.
The formal identity of relations (a) and (b)
-
(a) The spatial dependence of magnetic field decay in a superconductor flat slab (with field parallel to the surface), dH(x)/dt = dH0/dt exp (− x/λL)
-
(b) The spatial dependence of directional radiation intensity decay (incident under right angle onto the slab at x = 0), i′(τ)/i′(0) = exp(− τ)
then allows the extraction of the extinction coefficient (E) from the identity of the exponents (− x/λL) and (− τ = −Ex), certainly within only small ranges of particle size, temperature and position x. Superconductor temperature should be fairly below critical temperature. This means the exponents should not be too small to assure both decay laws approaching zero field or zero directional intensity within the filament and at approximately identical positions.
This extraction works without explicit, detailed calculation of extinction cross sections (QExt) from particulate properties.
Dependence on temperature of the obtained extinction coefficient is shown in Fig. 9b for YBaCuO 123. The standard BCS expression for the temperature dependence of the penetration depth (λL) has been applied. Near-critical temperature induces a rather strong dependence of E on temperature. The comparison therefore should be restricted to temperature not very close to TCrit.
Results for BSCCO 2212 and 2223, obtained with the same estimate, will be shown later (in Fig. 19a, we have E of about 106 (1/m) from this approach; for comparison, the result with Nb3Sn from the same approach amounts to E = 107 (1/m).
4.2 Multi-layer, Radiation Screen Model
This method interprets the single filaments in a BSCCO 2223 multi-filamentary conductor (Fig. 6a) and the thin BSCCO 2212 grains (Fig. 6b) as consisting of staples (columns) of separate, approximately flat, plate-like thin grains. In a second step, in particular, Fig. 6b suggests comparing the thin grains and their orientation perpendicular to the thermal gradient, with thin, highly reflecting radiation screens, arranged in parallel.
This reflects an engineering concept well known from the evacuated, multi-layer super-insulations in cryogenic applications. There, a number of up to 40 highly reflecting radiation screens (thin metallic or metallised polymer foils) in a narrow, evacuated insulation space either are arranged in parallel to the walls of a rectangular container, or the screens are wound in spirals around a liquid gas storage tank, to reduce radiative heat losses.
While the thin grains in Fig. 6a are slightly bent and the solely geometrical aspect optically little resembles flat screens, the grains in Fig. 6b come closer to the point. In both cases, because of their thermal transport properties, with a high degree of anisotropy of current and thermal transport in the high-temperature superconductor materials, heat transfer in horizontal direction (in the crystallographic ab-planes of the grains of Fig. 6a and b) is much larger than that in vertical (c-axis) direction. The degree of anisotropy in YBaCuO 123 is in the order of 10 to 15, but is particularly large, by more than 1 order of magnitude, in BSCCO 2212 and 2223. From the heat transfer view, the grains at least in Fig. 6b, and their blocking of radiation, therefore can be modelled approximately as flat, thin-film radiation obstacles oriented perpendicular to temperature gradient.
In Fig. 6b, the lateral (x, y) dimension of the grains is between about 300 μm × 400 μm, which is large against grain thickness (about 0.3 μm) and (vertical) clearance between grains (about 10 nm or below). Dimensions in lateral direction are not very important for the present radiation exchange problem as long as the radiation obstacles, i.e. the grains, are arranged as staples and the particles see their closely located neighbours, provided they are of approximately equal geometrical size.
Let εWall and εFoil denote the thermal emissivity of flat walls of a container that houses a multiple N of highly reflecting foils arranged in parallel. Under stationary conditions, the residual net radiative flux, over infinitely extended screens, is given by
see Kaganer [33] (pp. 33–35) for its derivation, with plane shields and with both thermal emissivities (ε) that are very small. In (7a), we have ηWall = εWall/(2 − εWall) and ηFoil = εFoil/(2 − εFoil), as reduced emissivity.
In reality, the lateral clearance between the grains in Fig. 7a and b is large so that radiation will advance through the voids. However, for determination of the extinction coefficients (as it is a local quantity), it is sufficient to
either restrict the analysis to the real lateral dimensions of the grains (which means, we do not consider radiative flow over total insulation surfaces). In Fig. 6b, the lateral dimensions are large against mid-IR wavelength,
or decide for the following that the grains are treated as if they were infinitely extended but with considerable holes between the grains (a quasi-perforation of the screens, like the very small perforations that are usually applied in thermal super-insulations to facilitate evacuation of the space in between).
The second alternative will be applied in the following.
The term \(\dot {{q}}_{\text {Rad,0}} \) in (7a) denotes the radiative heat flux without foils (N = 0)
where T1 and T2 are the temperature of flat hot and cold walls of an evacuated container. The factor σ denotes the Stefan-Boltzmann constant.
If we apply (7a) and (7b) to the staples in Fig. 6a, b, the emissivity (εWall) of the wall would be given by the matrix material (Ag), of which the emissivity, at the wall/grain interfaces, due to the manufacturing process is certainly larger than the emissivity of a clean, polished, optical quality Ag surface (below 0.01).
The emissivity of the grains is much larger, certainly in the order εGrain = 0.9, but hardly can be measured. Below, in Fig. 10a and b, we will test by means of a radiative exchange model how strongly in practice the εGrain would influence the calculated extinction coefficients. All grains approximately have the same (reduced) emissivity, ηFoil = ηGrain, and the size of the opposite surfaces between any pair of grains, in a staple, is approximately constant.
a Schematic description of the two-flux model for radiative transfer. The model considers directional intensities (\(i^{\prime } \)) and hemispherical radiative fluxes (q+ and q−, indicated by the half-spheres) obtained after integration of the \(i^{\prime } \) over solid angle. Anisotropic scattering can be treated with N-flux extensions of this model (the method of discrete ordinates [17], pp. 495–502, or a short summary in [37]). But it would not be realistic to assume strong forward scattering or predominantly forward emission from the metallic screens. b Extinction coefficients, E (1/m), and specific extinction cross sections, QExt, of YBaCuO 123 (dark blue) and BSCCO 2212 (dark yellow symbols), vs. radiation temperature. The extinction coefficients (E) are estimated from comparison of the transmittance of one filament of 30 μm thickness obtained with the cryogenic multi-foil model. Prediction of hemispherical transmittance, in dependence of E, is made with the two-flux model (see text for explanation). The QExt, given for one cylindrical particle, is calculated from the E using the densities of the particle bed and the solid material. All results are calculated with the hemispherical emissivity, εGrain = 0.9 const (a sensitivity test, at constant temperature, with 0.6 ≤ εGrain ≤ 0.99, showed only weak dependence of E on this parameter)
The ratio \(\dot {{q}}_{\text {Rad,0}} /\dot {{q}}_{\text {Rad}} \) is equivalent to hemispherical radiation transmission. This ratio can be simulated by means of the (radiative) two-flux model. This model is a well-known method in radiative transfer (see e.g. [17], pp. 491–494, or a short description in [37]).
The two-flux model is explained in Fig. 10a. Integration of the directional intensities, \(i^{\prime }_{\mathrm {+}}\) and \(i^{\prime }_{\mathrm {-}}\), over the upper and lower half-spheres yields oppositely oriented radiative fluxes, \(\dot {{q}}_{+}\) and \(\dot {{q}}_{-}\). The transmittance through a slab of thickness (x = D) is calculated from the ratio \(\dot {{q}}_{+} (x {=} D)/\dot {{q}}_{+} (x{=}0)\). A reasonable assumption is that scattering is isotropic (it would not be realistic to assume clean, optical surface quality of the grain surfaces). We then obtain for the transmittance
with α = 2E(1 −Ω)1/2, β = [1 − (1 −Ω)1/2]/[1 + (1 −Ω)1/2], and Ω is the albedo of single scattering.
Comparison of the ratio \(\dot {{q}}_{\text {Rad}} /\dot {{q}}_{\text {Rad,0}} \) from (7a) and (7a) of BSCCO 2212 grains (those in Fig. 6b) with (8) yields the extinction coefficient E (the extinction coefficient is contained in the factor α in (8)).
The result is shown in Fig. 10b (both E and QExt) for BSCCO 2212 particles (and for comparison also for YBaCuO), in dependence of radiation temperature. We use the hemispherical emissivity εGrain = 0.9 const of the BSCCO 2212 and YBaCuO 123 grains (dark yellow and dark blue diamonds, respectively). Assuming the same emissivity for both materials, the ratio \(\dot {{q}}_{\text {Rad,0}} /\dot {{q}}_{\text {Rad}} \) depends only on the number of screens. The extinction cross section (QExt) can be obtained by means of (3a) and (3b) from E.
The overall result, strong radiation extinction by superconductor grains and filaments, (E ≥ 1.2 × 107 1/m), does not change substantially if εGrain runs from 0.6 to 0.95. It is expected εGrain strongly exceeds 0.5, because it is a ceramic material, and the surface roughness of the grains certainly is large. A correction for dependent scattering will not be applied: the radiation screen model is an extreme case, namely zero-dependent scattering. But a correction for quasi-perforations (the a large amount of voids between the grains) has to be applied to the results, as shown in Fig. 19b.
With thickness of the staple (the filament) in Fig. 6a of about 30 μm, the extinction coefficients, E, in Fig. 10b are large enough to get the optical thickness, τ ≥ 360, very large against critical optical thickness, τCrit = 15. From this second estimate, we provisionally conclude (before results from Section 4.3 are available) that multi-filaments prepared for current transport from BSCCO 2212 and YBaCuO 123 conductors in the superconducting state will be non-transparent to radiation.
But the approximations, (7a), (7a) and (8), neglect possible penetration of matrix material in the BSCCO conductors into the space between grains. Further, in (7a) and (7a), the grains are treated as if temperature gradients are zero over grain thickness. Possibly existing non-zero temperature gradients across each radiation screen (grain) would modify (7a) and (7a). Accordingly, there are risks arising from application of also this model for an estimate of the extinction coefficient; these risks will be discussed in more detail in Section 5.
4.3 Extinction Cross Sections from Application of Rigorous Scattering Theory
The third method first applies in a first step to single regularly shaped particles. Modifications will be applied later to approach the real (flat, plate-like) geometry of the superconductor grains.
Electromagnetic scattering theory involves the solution of the Maxwell equations at the interface between two media that are characterised by different indices of refraction. The following calculations are confined to only YBaCuO 123 quasi-particulate superconductors (refractive indices for the BSSCO conductors are missing). The applied refractive indices are those of thin films (the extinction coefficient (E) is defined per unit length and thus does not depend on thickness).
4.3.1 Refractive Indices of YBaCuO Thin Films
In the normal conducting state, standard description of the complex permittivity, ε(ω), of YBaCuO thin film includes a two-component model (see e.g. [24]) with a free-carrier, temperature-dependent absorption (Drude) term, a mid-infrared (Lorentz) term and a constant, high-frequency contribution
The Drude parameter describes accelerated free electrons that are subject to an electron scattering rate. The Lorentz term applies to bound electrons, here with a broad, mid-IR absorption band and a damping constant (see below; detailed descriptions are provided in [18,19,20,21,22,23,24]). In the present case, only excitation of vibrational states in the IR spectrum is included in the refractive indices derived from (9a) and (9b).
In the superconducting state, the free-carrier part of ε(ω), using the standard two-fluid model, is split by the fraction (fS) of electrons that are condensed to electron pairs (index S) while the remaining part (1 − fS) remains to be normal conducting. We have the following in the Drude-Lorentz model:
If T → TCrit, fS → 0; this reduces ε(ω) to only the classical Drude and Lorentz terms (apart from the high frequency contribution, εHF, that is usually neglected in the analysis of the mid-IR spectra of superconductors).
If T → TCrit, fS → 0 yields the expression of the ε(ω) for a normal conducting metal or a dielectric. There is no jump of ε(ω) at T = TCrit.
Equations (9a) and (9b) need discussion: a standard assumption is to consider the normal-state resistivity part, the (1 − fS) fraction, as constant, down to zero temperature, which implies also the fS, the fraction of electrons condensed to pairs, is constant. See, for example, [22, 23]; there, the fS fractions are kept fixed, at a few selected, different temperatures, in a multi-parameter fit to experimental reflectance and transmittance data.
In both references, the fS fractions apparently do not include dynamic equilibrium states (these include decay of electron pairs and recombination) and non-equilibrium processes. This is an obvious lack of the procedure since there is a strong temperature dependency of the density (nS), the density of electron pairs, by which the fS fractions are defined, fS = nS(T)/nS(T = 0).
The total set of electrons available for superconductivity, the fraction (fS), after any disturbance that would lead to any temperature variation, has to be re-organised according to the Pauli principle. A numerical model on how to perform this calculation has been suggested in [38] (and meanwhile applied in [7] to a coated superconductor). The model involves decay and recombination of electron pairs after a temperature variation (in this paper, it is, for simplicity, called the “microscopic stability model”).
The model includes the Racah problem, namely the expansion of an anti-symmetric N-particle wave function from an N − 1 parent state. The situation is the analogue to calculation of “coefficients of fractional parentage” in atomic and nuclear physics: if the anti-symmetric, total wave function of a nuclear state incorporating N of nucleons shall be formulated, it can formally be expressed by appropriate coupling of an anti-symmetric wave function of (N − 1) nucleons with a one-particle wave function. The calculations thus have to be performed sequentially, following a chain of events (recombination or decay) that finally yield the new dynamic equilibrium electron state. The Yukawa interaction in this model is taken as a tool to estimate the recombination times.
The more the temperature approaches its critical value, the longer takes it the electronic system to reach a new dynamic equilibrium; this is simply the consequence of the Yukawa interaction and, near TCrit, the strongly increasing number of decay products and, finally, the Pauli principle. Therefore, fractions (fS) in (9b) are not constants but strongly depend on time and temperature. The same applies to ε(ω) and all its components. All these are dynamic variables.
The concentration ratios, fS = nS(T)/nS(T= 0), of electron pairs obtained from this model continuously converge to zero when T→ TCrit. There is no sudden jump to zero of nS(T) when T → TCrit and, consequently, no sudden jump, but a continuous variation, of the ε(ω) from superconducting to values of the normal conducting state. See Fig. 11b.
a Decay rates of electron pairs in YBaCuO at temperature very close to critical temperature. At T = 91.99 K and even more at T = 91.999 K, the system, though in dynamical equilibrium, should increasingly be stable in relation to the state at T = 91.5 K or to any other, earlier state (at still lower temperature) because of the fast decrease of the decay rates with increasing temperature. b Relative density, nS(T)/nS(T= 4K), of electron pairs (fraction (fS) to be used in the permittivity, ε(ω), in (9b)), in dependence of temperature, calculated for comparison of the predictions from the microscopic stability model (dark blue) with results from (8) in [21] (light green diamonds). Dark yellow diamonds indicate the (relative) minimum density of electron pairs that would be necessary to generate a critical current density of 3 × 1010 A/m2 at 77 K in zero magnetic field
The calculation of the nS(T) involves the probability for exciting the electron system. This is proportional to exp[−ΔE(T)/kT], under equilibrium conditions. With the electron density, at temperature close to absolute zero, of about 6 × 1027 1/m3, of which about (1/2)(1/10) would be available for pair formation, and for simplicity, the standard (BCS) temperature dependence of ΔE(T) = 1.74ΔE(T= 0)(1 − T/TCrit)1/2, with binding energy (ΔE) taken as temperature dependent and ΔE(T= 0) = 60 meV, we obtain the nS(T). The final step in the microscopic stability model then is application of the Yukawa interaction and the Pauli principle to obtain the decay rates of YBaCuO, as given in Fig. 11a.
a Real part (n) of the complex refractive index (m = n − ik) of YBaCuO 123, calculated using (9a), (9b), (12a) and (12b); compare text for explanations. Red, blue, and light green diamonds indicate values from [20, 23] and [19], respectively (see also Table 1). The lilac diamonds are for Ag. Black solid and open diamonds are mean values (compare text). b Imaginary part (k) of the complex refractive index of YBaCuO. The same symbols as in a
In order to check the convergence of the nS(T) and of the decay and recombination rates, and assuming thermal fluctuations near the phase transition are absolutely zero, we may allow the conductor temperature numerically and very closely, in the course of the conductor temperatures T(x, y, t) in Figs. 1a and 2a (or during other disturbances), approaching the critical temperature (TCrit= 92 K in YBaCuO 123). Under this condition, checking of convergence can be made at hypothetical conductor temperatures like 91.999 K at which, because of T < TCrit and zero thermal fluctuations, the conductor is still in the solely superconducting state (this applies to all fS < 1).
Presently, assuming zero thermal fluctuations can be accepted only as an approximation (second-order transitions, like superconducting/normal conducting phase transitions at zero magnetic field, invariably imply fluctuations; see Section 5.4.4 in [39]).
Under these conditions, the decay rates are small. Between T = 91.99 K or 91.999 K and 91.5 K, the rates decrease by 7 or 10 orders of magnitude, respectively, which means the (yet) dynamical states at 91.99 K and 91.999 K are almost (and increasingly) stable in relation to the state at T ≤ 91.5.
Calculation of the extinction cross sections (QExt) at T = 91.99 K and at temperature even more close to T = TCrit thus will allow to clearly distinguish between superconductor states before and after a phase transition. This is because the refractive indices of thin YBaCuO films, available at T= 300 K, are not very different from the refractive indices near T = TCrit. Though this assumption, made in [19], appears to be plausible, it should be checked since the suggested extrapolation extends over the enormous range of 200 K.
The calculated concentration ratios, fS = nS(T)/nS(T), are shown in Fig. 11b. The fS fractions reported by Zhang et al. [22] (Table 1) and by Kumar et al. [23] (Table 1) are clearly below these fractions. In [23], the authors obtain fS = 0.35 and 0.25 at T1 = 10 K and T2 = 50 K against the TCrit of about 81 K. But in both [22] and [23], the fS fractions are parameters kept fixed, at rather small values, within a multi-parameter fit onto experimental reflectance and transmittance data. This does not seem very realistic and is definitely contrary to the results (temperature-dependent fS) obtained with the microscopic model and reasonable expectations.
A simple check of this controversy can be made with reference to the wavelength interval (ΔΛ) between incident photon energy and the ΔE of the gap. We do not know the cross sections of radiation/electron pair interactions. But the fraction of black-body radiation within ΔΛ, calculated with the \(F_{\mathrm {0-{\Lambda }}_{T}}\) in [17] (Appendix A), amounts to 18% of the total spectrum. The fractions (fS) should be located within this percentage (the probability (p) that electron pairs would be broken by IR photons is below 1).
One would therefore expect larger fS than that reported in [23], also in view of the large temperature differences of T1 and T2 from TCrit (note the large uncertainty of 20% that the authors assign to the fS fractions). The same argument applies to the 0.7 ≤ fS ≤ 0.85 reported in [22] for T1 between 10 and 45 K.
Yet, both papers (Fig. 1 in [22] and Figs. 4 and 6 in [23]) report good agreement with measured reflectance and transmittance results. A possible explanation is that the (multi-parameter) fits of the reflectance and transmittance data really might not very sensitively depend on the parameters fS (multi-parameter fits, according to all experiences, can be quite arbitrary).
It is interesting to compare the predictions by the microscopic stability model of the fractions (fS) also with the ratio nS(T)/nS(T = 0) = 1 − (T/TCrit)4 reported in (8) of [21] (though it is not clear that this equation was derived for dynamic equilibrium states). The comparison is shown in Fig. 11b. The microscopic stability model predicts the density of electron pairs in a spherical volume of which the radius is calculated in dependence of temperature, while the said (8) in [21] is related to the overall volume of the superconductor (the comparison thus is of only limited significance).
Both predictions (trivially) agree in that the fractions (fS) = nS(T)/nS(T= 0) should converge to zero when T → TCrit (and to 1 when T→ 0); these convergences are confirmed in Fig. 11b. That the fS fractions obtained from the microscopic stability model (dark blue diamonds) are the larger ones is probably due to the dynamic equilibrium decay and recombination processes included in the microscopic stability model (the larger fS also would not contradict fluctuation effects near transition temperature).
When T → TCrit, the strong decrease of the fS in (9b) causes also a strong decrease of the permittivity (ε).
So far, the situation concerns the availability of refractive indices of YBaCuO thin films. The situation becomes definitely worse when refractive indices not of thin films but of particulate, plate-like morphology are needed. The indices reported by Kezuka et al. (Fig. 3 in [40]) in principle could be used in the calculations for a thick YBaCuO conductor. But the refractive indices are not specified by frequency or wavelength (and are not as detailed as those reported in [19]). Values n= 1.692, k= 0.403 and n= 1.629, k= 1.461, in m = n − ik, are much smaller than those measured by Zhang et al. [19] and Kumar et al. [23] with thin films.
The availability of refractive indices also of BSCCO multi-filamentary conductor, with again a flat, plate-like microstructure, is scarce, as before. We again find only few single values, for only its real part, and mostly not specified by frequency or wavelength and temperature. Results reported by Sandilands et al. [41] indicate n = 5.8 for a bulk BSCCO 2212 sample at ω = 2000 1/cm, outside the interesting range of frequency.
Therefore, the main conclusions of this section, to promote radiative transfer calculations, can be summarised as follows:
-
(a) Refractive indices should be calculated by an appropriate model (this model is given by the standard (9a) and (9b))
-
(b) The calculations of the fractions, fS(T), should be supported by a more realistic estimate than presently used in the literature
Finally, using the imaginary part (k) of the refractive index, the extinction (absorption) coefficient E = K = 4πk/Λ (in the Maxwell derivation) of the thin-film superconducting state increases to about 107 1/m in the IR to mid-IR. But a large imaginary part (k) not necessarily indicates strong scattering.
4.3.2 Material Parameter Problems
Before the start of the calculations of QExt, we have to check the following conditions (1a) to (4):
-
(1)
Is the basic requirement, particles in a non-conducting medium, to apply standard derivations of scattering and absorption cross sections fulfilled within the filaments? Strictly speaking, the electrical conductivity (σ) of the hosting material must be zero if the Mie and Kerker results shall be applied. Fortunately, the space between the grains (not between filaments) is empty because the metal Ag, though highly ductile, is too hard to penetrate during the manufacture of filament and tapes into the tiny voids between the grains
-
(2)
Only refractive index of YBaCuO from experiments with thin films is available, at temperature strongly below critical temperature. How can we approach the indices near the phase transition?
-
(3)
The fractions (fS) of the free-electron part of ε(ω) depend on time and temperature and converge against zero at temperature near its critical value. Can this observation (convergence of fS) perhaps be exploited to find an approach how the problem with scattering of IR radiation by superconductors can be modelled?
-
(4)
Solutions to the scattering problem reported in Born and Wolf [26] and Kerker [27] can be applied not only to dielectrics and metals but also to a perfect electrical conductor (not a superconductor). Kerker [27] (Chap. 6.5.2), in particular Fig. 6.13, predicts very large extinction cross sections for very thin cylinders in case the electrical conductivity is infinitely large. Fortunately, this prediction was confirmed, numerically in [42] and experimentally in [43]; see the end of this section. Can we count on the reliability of the procedure in case the conductivity of the base material is that of a superconductor instead of a very clean dielectric or metal?
Three more items complicate condition (4a):
-
(4a)
While a perfect conductor (like a superconductor) under a time-dependent magnetic field generates persistent screening currents, it does not show the Meissner effect. This means if we would apply the refractive indices of an excellent, clean, electrical normal (metallic) conductor (perhaps from measurements with thin films), and the Mie and Kerker [25, 27] solutions or corresponding standard programs (written for normal conducting particles), the result could not be acceptable for the extinction cross sections of superconducting particles.
-
(4b)
If transport current density (J) exceeds critical current density (JCrit) either in the whole conductor cross section or only locally (a situation like in Figs. 1a and 2a), the superconductor gets into flux flow resistive states. As long as T< TCrit, the system still is a superconductor. Flux flow resistivity of BSCCO grains was estimated in the order 10− 7Ω m [6, 7]. Though the superconductor is resistive, this does not mean the Mie and Kerker solutions could be applied as if the material was a classical (weakly resistive) normal conductor.
-
(4c)
With a single plane wave, derivation of the variation of H(x, t) and B(x, t) into time- and space-dependent components in a dielectric or in a metal immediately follows from solely Maxwell equations and their derivatives, like the Fresnel equations. This is different with superconductors: variation of B and H, with exponential decay in time and distance works only if Maxwell and London equations are taken into account. To which extent would this difference request corrections of the Mie and Kerker solutions?
The physics of the interaction between a plane electromagnetic wave with the surface of small superconductor particles has to take into account the following:
-
(j) The distribution of screening currents near the particle surface
-
(jj) The resulting magnetisation (M) of the superconductor, items (j) and (jj) by appropriate boundary conditions
-
(jjj) The Meissner effect, items (j) to (jjj) by inclusion of the London equations into the solution procedure to obtain the screening currents
All these items [(1) to (4), (4a) to (4c), (j) to (jjj)] are elements of a macroscopic, continuum theory level. On the microscopic level, the simultaneous presence of electron pairs and their interaction with incident radiation, and of quasi-particles (that condense to electron pairs at very low temperature) and of normal conducting electrons, has to be considered.
Presently, a solution procedure that satisfactorily would take into account all these items is not available. A way out of the material problem [items (1) to (4), (4a) to (4c), (j) to (jjj)] has to be found.
4.3.3 A Way Out of the Material Parameter Problems
In Fig. 11b, the fractions (fS), under dynamic equilibrium, converge to zero if temperature approaches its critical value. Magnetisation M = −B = μ0H of the superconductor then goes to zero as well.
This conclusion is obvious also if we look at the scattered intensity of incident radiation: in the small particle limit, scattered intensity is composed of two polarised components (I1 and I2). In case of non-magnetic particles, I1 and I2 describe the solely electric dipole radiation, while in case of magnetic materials, a contribution from both electric and magnetic dipoles has to be considered. For spherical particles, Kerker et al. [44] (p. 766) report
In (10a) and (10b), Λ denotes the wavelength, r is the distance to an observer, φ is the angle between the electric vector of the incident wave and the scattering plane, x is the scattering parameter (x = πd/Λ, with d the particle diameter), 𝜃 is the angle between forward and backward scattering directions and ε and μ are the relative dielectric constant and magnetic permeability, respectively.
With χ as the magnetic susceptibility, reduction of μ = 1 + χ to μ very close to 1 (the normal conducting value of μ) reduces (10a) and (10b) to scattering of radiation by normal-conducting particles, which, in turn, goes in line with the convergence of the fraction (fS) to zero.
The calculations accordingly could be performed at temperature very close to TCrit, if the number of residual electron pairs still remains sufficiently large to carry a critical current that as a screening current successfully screens the interior of the superconductor against an external magnetic field. Even a tiny fraction of electrons condensed to electron pairs is sufficient to transport current without losses, in particular screening currents, that all flow with critical current density (JCrit).
If we restrict the interesting temperature interval, within which the calculations shall be performed, to 91.9 ≤ T < TCrit = 92 K for YBaCuO (or to 107.9 ≤ T < TCrit = 108 K for BSCCO), the density of electron pairs still must satisfy a minimum condition to generate the critical current density in dependence of the abscissa (temperature) values in Fig. 11b. The minimum density is obtained from
where JCrit = 3 × 1010A/m2 at 77 K, within this range of conductor temperature; nS(T) is the approximately linear temperature dependence of the density of electron pairs; vFermi is the Fermi velocity; and e is the elementary electrical charge. The nS(T) is obtained from the dark blue diamonds in Fig. 11b, and the Fermi velocity, in YBaCuO at about 4.5 × 105 m/s, is given by
where ξ0 is the coherence length in the ab-plane, ΔE(T = 0) is the energy gap and h denotes Planck’s constant. The density, nS(T), not only must be stable (though in dynamic equilibrium), but the ratio fS = nS(T)/nS(T = 4 K) in Fig. 11b must be at least in the order of 10− 4 of the T = 0 K value; compare the dark yellow diamonds.
Finally, to apply (9a) and (9b) for εDrude and εLorentz, from which refractive indices are calculated, we have the following for normal conduction (and using the nomenclature of [23]):
where ωP is the plasma frequency and ω is the angular frequency at which the calculations are performed. Below critical temperature (1/τ = 0), (12a) reduces to
with \(\omega _{\mathrm {P}}^{\mathrm {2}}=\sigma _{\text {DC}}/(\varepsilon _{\mathrm {0}}\tau )\).
The Lorentz term, under normal conduction, reads
where ωpe is again the plasma frequency, ωe is the centre frequency of the absorption band and γe is the damping constant. Equation (12b) is written for a single oscillator; inclusion of higher-order oscillators has been treated in [18, 20] but is not necessary in the present case.
All frequencies in (12a) and (12b) and thus also the εDrude, εLorentz, the final ε and, as a consequence, all refractive indices depend on temperature.
In the following, for YBaCuO, we have estimated the refractive indices using (10a), (10b), (12a) and (12b) in the interval 90.5 ≤ T ≤ 91.999999 K; the corresponding fractions (fS) at these temperatures are calculated from the microscopic stability model. Values of the DC electrical conductivity, plasma and centre frequencies, electron scattering rates and damping constants are listed in Table 1.
The results for the refractive indices do not sensitively depend on the choice of the Lorentz parameters, but the DC conductivity involved in the Drude component has to be chosen carefully (as recommended, by linear extrapolation to temperatures below TCrit). Radiation temperature is converted to wavelength and frequency by application of Wien’s displacement law (see the note at the beginning of Section 5).
Results for the real (n) and imaginary (k) parts of the refractive index, m = n − ik, are shown in Fig. 12a and b. They are in rough agreement with Fig. 5 in [23] if their measurements would be extrapolated to the 310 ≤ ω ≤ 320 1/cm in the present case.
4.3.4 A Way Out of the Particle Shape Problem
The idea interprets the irregularly formed, flat plate-like grains as being composed of subparticles of regular shape (small cylinders) for which solutions of Maxwell equations are already available. Like a casting mould, the irregular, proper grain geometry in this model serves as a 3D enclosure tightly filled with the regular subparticles (likewise, a thin cylinder can be imagined as a straight chain of spheres of the same small diameter).
The plate-like grains could also be divided into, or filled with, tiny cubicles or spheres small enough that a uniform internal field approximation becomes accurate. This approach (Ku and Shim [45]) is particularly interesting in view of the Meissner effect and because randomly oriented, chain-like agglomerates of small particles have unique scattering characteristics, with the extinction roughly the same when comparing results of agglomerates with the same number of individual spheres.
A disadvantage of the subparticle model arises from dependent scattering, which includes far-field interference and multiple scattering effects. By contrast, independent scattering (the radiation field not influenced by neighbouring particles), and no (far-field) interference of scattered waves, would be an idealistic assumption that can be fulfilled only if the particles are point-like. This is not the case. Dependent scattering is taken into account in the next section.
The advantage of the subparticle model is that the calculation of the QExt of regular particles has frequently been confirmed in the literature.
The plate-like grains of Fig. 7a–c are approximated, in their horizontal (x, y) extensions, either by a series and staples of densely arranged thin cylinders (the subparticles, Fig. 13) or by a 2D dense array of spheres.
Superconducting thin cylinders (view from top, schematic, not to scale) applied for calculation of the effective extinction cross section (QExt) of a grain due to dependent scattering (shadowing of neighbouring particles). The grain, and its total number of thin cylinders (the subparticles, light grey shaded), is enclosed in a red rectangle. The figure illustrates the dependent scattering effect for one cylinder (dark blue shaded, located at a central geometrical position) onto several single, neighbouring particle surfaces (enclosed in a blue rectangle; they are at least partly shadowed by this cylinder). Thickness (in z-direction) of the grain (flat, plate-like particle) is d = 0.3 μm, and horizontal dimensions (lx and ly) are each between about 250 and 300 μm. The large yellow arrow indicates the direction of transport current density, J
In case of cylinders, the direction of incident radiation (z-direction) would preferentially be perpendicular to their axes. The cylinder axes are arranged in parallel to the direction of current flow (y-direction), which means perpendicular to the crystallographic c-axis (z-direction).
Inspection of Figs. 6b and 7a–c suggests fixing the subparticle diameters in this model to about 0.3 μm, the apparent thickness of the thin grains in Fig. 6b.
The small subparticle diameter ensures that the ratio of wavelength to particle dimension is large, the array accordingly is a radiation continuum and the analysis can be realised with the equation of radiative transfer and its solutions.
The first approach (cylinders) also is consistent with the direction of current (Fig. 13) and induced self-fields. On the other hand, the spherical particle alternative has the advantage that the result (corrections of the extinction cross sections imposed by dependent scattering) could be compared with predictions of the Percus-Yevick hard-sphere model (see below). But current flow paths within the grains then would frequently be interrupted (like in the proper weak link problem by quasi-insulating obstacles). The distance between such obstacles (contact resistances with each of the other spheres) is strongly below the spherical particle diameter (0.3 μm), which means a large variety of contact resistances would reduce critical current.
For this reason, preference is given to the thin cylinder, subparticle model (Fig. 13). With the length (lx) of one grain of about 300 μm and its thickness (d) of 0.3 μm, we have N = lx/d, about 1000 cylinders, arranged in parallel. From the ratio of the N cylinder cross sections, ACyl = N(π/4)d2 in one grain, to the total grain cross section (AGrain), we have the grain porosity, πGrain = 1 − ACyl/AGrain = 0.215, or the volume fraction (fV) 0.785. With the wavelength of about 30 μm, this yields the scattering parameter, x = πd/Λ, of about 0.03 (usually an indication of strong absorption and small scattering).
4.3.5 Dependent Scattering
Dependent scattering in the following is included into this analysis by sole calculation of shadowing effects in dependence of the single particle extinction cross sections.
Rigorous calculation of dependent scattering would have to take into account dipole and multi-pole expansions of the scattered amplitudes, excited by incoming electromagnetic waves, in each atom or molecule of all particles of an array of closely arranged grains in a filament. Superimposing all primary and secondary fields emitted from the array would completely be impractical; the number of fields is too large to reasonably handle the corresponding huge set of Maxwell equations.
As an alternative, mixing rules like the Maxwell-Garnett method could be applied, and another alternative is the application of Eq. (16) in [45] to non-magnetic particles of cubicle or of any other cell geometry in combination with adjusted refractive indices (a step very similar to the original Lorentz-Lorenz, the Clausius-Mossotti and the later followed Maxwell-Garnett methods). Like the dipole and multi-pole expansions, mixing rules would consider the radiative transfer problem from an integral view of the particle bed. Again, this appears to be too complicated or would introduce still more uncertainties than listed in the previous sections.
Also, approximations like the equivalent sphere concept are not very attractive (the difference between the real shape of the grains in comparison to a sphere with adjusted diameter and refractive index appears to be too large to yield acceptable solutions with reasonable computational efforts. This applies to also other concepts investigated in [45]. Also, ray tracing and Monte Carlo simulations of radiative transfer in packed beds, though powerful methods in general (compare e.g. Singh and Kaviany [37]), are not very suitable for the solution of the very present radiative transfer problem, again because of practical reasons: the porosity of the grains is too small, and the geometrical shape of the grains is too irregular, to limit the number of bundles to a reasonable computational effort.
With the single-particle QExt of one cylinder, the CExt exceeds the (geometric) particle cross sections (CGeom) by this factor. Assuming, for example, QExt = 7 (odd number, to avoid summations over half-cylinders), the total QExt,total of one grain is not given simply by the number NQExt = 7000. Instead, counting the number of cylinders that fully or only partly contributes to the total overlap of the cross sections and assuming there is no interference of the radiation scattered from neighbouring cylinders, we have QExt,total = 988. This large correction, by dependent scattering, reduces the total radiation extinction within one grain to an effective value, QExt,total/(NQExt) = 0.141, about 1/7 of the naïve estimate QExt,total = NQExt (radiation scattered by one obstacle multiplied with their number (N) yields total scattered radiation only if the obstacles are strictly identical and if the clearance is large against the wavelength).
This reduction applies to each grain in each of the filaments. The calculated radiative flux, because of penetration of radiation into the grains (instead of almost zero penetration into the highly reflecting shields in Section 4.2), is reduced by this factor to an effective value, by an order of magnitude smaller than the proper radiative heat flux (\(\dot {{q}}_{\text {Rad}}\)) through the stack of grains. The effective optical thickness thus reduces from τ to only a fraction, χτ0 = [QExt,total/(NQExt)]τ.
The second attempt (again modelling plate-like grains by small regular particles) applies very small spheres. If again d = 0.3 μm and with the same x, y-dimensions of the platelet as before, we have a dense set of 106 spherical particles in one grain. This yields the porosity πGrain = 1 − ASpheres/AGrain = 0.476.
With its analytic formula, the Percus-Yevick hard-sphere model [31] takes into account the interference of radiation scattered from neighbouring single or multiples of spherical particles. The ratio of the effective extinction cross (QExt,dep sc, under dependent scattering) to its regular value (QExt) of single particles according to this model reads
With the porosity πGrain = 0.476, we have QExt,dep sc/QExt = 0.0123, by an order of magnitude smaller than what would be obtained from simply counting the number of shadowed spheres. This would yield QExt,dep sc/QExt = 0.139, again for QExt = 7.
The large difference, 0.0123 vs. 0.139, can be explained by the interference of scattered radiation from neighbouring spheres. This is a definite manifestation of dependent scattering (far-field interference and multiple scattering).
It is to be expected that similar, but probably less severe corrections from interference effects would apply to the optical thickness for the cylindrical particle model. Unfortunately, there is no such model that, like the Percus-Yevick hard-sphere model, would yield QExt,dep sc/QExt, in dependence solely of its porosity.
The factors, χ = QExt,total/NQExt, apply to radiation incident in z-direction and result from simply the extinction cross sections being larger than their geometrical counterpart.
4.3.6 Extinction Cross Sections of the Irregularly Shaped Particles
Finally, for calculations of extinction cross sections (QExt) and albedo (Ω) of YBaCuO 123, the cylindrical subparticles (Fig. 13) are used as a tool, with the refractive indices from Fig. 12a and b, at the same radiation temperatures, for the particle diameter 0.3 μm.
Results are shown in Fig. 14a and b in dependence of radiation temperature. The same calculation for BSCCO 2212 subparticles is performed with refractive indices obtained from the components of ε(ω) reported in [46].
a Extinction cross section (QExt) of IR and mid-IR radiation interacting with cylindrical YBaCuO 123 and BSCCO 2212 pseudo (sub)-particles (explained in Fig. 13) of 0.3 μm diameter, in dependence of radiation temperature. The results are calculated from (9a), (9b), (12a) and (12b); compare text for explanations. Diamonds (red, blue and light green) are calculated for the YBaCuO conductor using the parameters from [20, 23] and [19], respectively, and the lilac diamonds are for Ag. Full, dark yellow circles are for the BSCCO 2212 superconductor. For YBaCuO, solid black diamonds (average 1) indicate the QExt calculated with the arithmetic mean of each of the Drude and Lorentz parameters (like σDC, ωpe and ωe); open black diamonds (average 2) indicate the arithmetic mean of all QExt obtained with the individual dielectric parameters. Because calculation of the QExt by scattering theory is highly non-linear, both averages (1 and 2) are not necessarily identical. b Albedo of single scattering for the cylindrical YBaCuO 123 pseudo (sub)-particles. For identification of the diamonds and of averages 1 and 2, compare a
Radiation temperature needs a comment. Contrary to the radiation temperature, \(T_{\text {Rad}}=[(T_{\mathrm {1}}^{\mathrm {4}}-T_{\mathrm {2}}^{\mathrm {4}})/(T_{\mathrm {1}}-T_{\mathrm {2}})] ^{\mathrm {1/3}}\), that is a characteristic variable in the radiative diffusion model, with T1 − T2 as the temperature difference taken over a slab of a non-transparent sample, here TRad is the local temperature within the sample (obtained from the temperature difference over a slide of infinitely small thickness). If not otherwise specified, TRad either is used as an input parameter to the radiative transfer calculations or corresponds to the wavelength where the maximum of black-body radiation into vacuum is observed (Wien’s displacement law).
The magnitude of QExt (Fig. 14a) substantially exceeds the corresponding values of Ag particles (Fig. 8). Temperature dependence of extinction cross section and of albedo (Fig. 14b) reflects the strong temperature dependence of the fraction (fS) in Fig. 11b. Absorption dominates in the extinction cross section, at this particle diameter.
The QExt is converted to the extinction coefficients (E) using, in (3b), the densities ρ0 = 5968 and ρ = 4687 kg/m3 (the density (ρ) of the grains is explained in the next subsection). Results are shown in Fig. 15.
Extinction coefficients (E) of YBaCuO 123 and BSCCO 2212 before and after application of the correction resulting from dependent scattering to the QExt. The diamonds and full circles are identified from the caption to Fig. 14a and b
The corrections (χ) for dependent scattering obtained with the cylindrical particle approach are substantial (even though interference effects cannot be included in this simple model). With a polynomial approximation of the curve χ vs. QExt, comparison before and after the application of this correction to the extinction coefficients (E) is shown in Fig. 15, in dependence of radiation temperature (the original QExt is from Fig. 14a).
The total extinction cross sections (QExt) of a grain results from the additive, layer-by-layer, extinction cross sections induced by the cylindrical subparticles. For simplicity, these can be considered arranged as a column of cylinders stapled in z-direction, the direction of incident radiation. The column is described by the same extinction coefficient (E, defined as the decay of radiation per unit length) as only one layer, and the correction factor (χ) of this one layer covers also the reduced radiation extinction generated within the total thickness of a single grain.
So far, the calculations for YBaCuO 123 thin films were performed. Calculations of also the refractive indices of BSCCO 2212 have been performed with the data from [46]. With the reported large, in-plane optical conductivity in the permittivity (ε) of the meta-material (a layered superconductor with strongly anisotropic properties), and the in-plane real part of ε that is strongly negative, the imaginary part of the permittivity increases to very large values at the frequency below 1013 1/s. This results in large imaginary parts (k) of the refractive index m (besides small n). The extinction coefficients become very large, and the albedo converges to Ω = 1, almost pure scattering.
As a concluding remark, it is not clear whether fS → 0 implies also electron/phonon coupling to converge in a similar manner to a fixed rate, or whether there is a corresponding jump of this coupling at the phase transition.
4.4 Optical Thickness of a Single Filament and of a Tape
Results obtained for the extinction coefficients (E) now have to be checked whether, under these conditions, the optical thickness of grains and filaments still exceeds τCrit = 15.
The optical thickness (Fig. 16) of one BSCCO 2212 or 2223 filament, or of any other aggregate of grains if the total thickness is D ≥ 30μm, calculated using the extinction coefficients (E) from Fig. 15 and accounting for dependent scattering, is substantially larger (τ about 100) than the critical optical thickness (τCrit = 15). This applies to also the thick YBaCuO conductor in Fig. 7c.
Optical thickness (τ) of a thick YBaCuO conductor and for BSCCO filaments calculated for independent (above) and dependent (below) scattering. The diamonds and full circles are identified from the caption to Fig. 14a and b
The optical thickness of the grain-like constituents (again as seen under the radiative transfer aspect) in the thin films of Fig. 7a and b of a coated conductor is much smaller: the optical thickness of a bare, 2-μm-thick YBaCuO film, again under dependent scattering, amounts to only about τ = 10. But in coated conductors, there are thin interfacial layers between superconductor and metallisation (Ag) and between superconductor and buffers, plus the Ag layer itself (Fig. 2b). These increase the active thickness of the radiation obstacle to 3–5 μm. Thin films in coated conductors are non-transparent to mid-IR radiation.
The result for the 30-μm-thick BSCCI filaments, or for a thick YBaCuO conductor and for the coated, thin-film YBaCuO conductor, confirms that application of the additive approximation in the finite element calculations of transient temperature distributions (Figs. 1a and 2a) and in corresponding figures of the papers [4,5,6,7, 12, 13] (not all confined to sole superconductivity) was justified, and the radiation contribution to total heat transfer was correctly simulated.
A scan along the vertical, solid red line in Fig. 1b hits a sequence of different, but strongly absorbing, very thin normal conducting and superconducting material layers. With dgrain = 0.3μm, dFilament = 30μm, dAg = 25μm and DTape = 300μm, we have τ = τ1 + τ2 + τ3 + …τN at about 1.2 × 104. The final ratio i′(x)/i′ (0) of directional intensity is practically zero.
For comparison, predictions for the extinction coefficients of cylindrical particles, made of an electrically highly conducting normal metal (not a superconductor), have been confirmed previously [43] using metallised glass fibres. Experimental EΛ∗/ρ obtained for double-sided, coated borosilicate glass fibres is in the order of 5 m2/g, even at T = 300 K (Fig. 17). These are the largest specific extinction coefficients that ever have been reported for a dispersed, solid particulate medium.
Specific extinction coefficients (E*/ρ) of thin, metallised glass fibres (coated with Al). The figure is redrawn from its original publication in [43]
The tendency predicted in Fig. 8 is confirmed (very large extinction coefficients obtained with small particle diameter and at low temperature). Since this is an extreme case of radiation/particle interactions, the agreement supports the calculations reported above of the extinction cross sections of superconducting particles by the same numerical tools as used with the metallised glass fibres.
Since high-temperature superconductor fibres of diameter below 100 nm are not available, glass fibres coated with thin superconductor layers might be a manageable way to also experimentally confirm superconductor grains are non-transparent to thermal radiation. A first attempt was made [32] (Section 6.3) with a low TCrit superconductor evaporated on thin glass fibres, d ≤ 100 nm. In a LHe-cooled magnetometer, the Meissner effect was clearly demonstrated, but transmission measurements at T < TCrit still have to be completed.
The albedo (Ω) of single scattering by metallic and dielectric grains was calculated in [42] again using the computer program written by Bohren and Huffman [29]. Figure 18 shows results of the calculations for Ag cylinders and dielectric fibres, in dependence of particle radius (r). The calculations were performed with spectral, complex indices (m) of refraction of Ag and borosilicate glass, at the wavelength (Λ) = 5μm; the ratio Λ/r of wavelength to particle dimension (r) thus is very large so that again the ensemble of grains in a fibre can be described as a radiation continuum. At very small particle radii, the albedo converges to zero.
Albedo of single scattering by dielectric and metallic, thin cylindrical particles, vs. scattering parameter (x = πd/Λ), with d and Λ as the particle diameter and wavelength, respectively. The dashed curve calculated with the large imaginary part of the refractive index indicates strong absorption in a metal (here, Ag). The figure is redrawn from [42]
The extinction cross sections QExt of both types of normal conducting, cylindrical particles (Ag and glass fibres) thus almost completely rely on absorption: with the extinction coefficient E = S + A, using S and A as the scattering and absorption coefficients (like E of dimension [1/m]), respectively, and Ω → 0 for r → 0, we have, with S = ΩE and A = (1 −Ω)E, the result E = A.
But the albedo of the superconducting cylinders (Fig. 14b) is smaller, with exception of the BSCCO 2212 particles where the albedo (Ω) is almost equal to 1.
4.5 Comparison of the Results Obtained in Sections 4.1 to 4.3
Figure 19a shows the comparison between extinction coefficients (E) obtained for the (quasi-) particulate superconductor YBaCuO 123 and for the particulate BSCCO 2212 and BSCCO 2223 superconductors using the three different approaches in Sections 4.1 to 4.3 (triangles, circles and diamonds, respectively). The extinction coefficients of the three materials, before corrections from dependent scattering are applied, safely exceed E = 106 (1/m).
a Comparison of the results obtained with the three different methods (Sections 4.1 to 4.3) to obtain extinction coefficients, all at temperature close to critical temperature. Diamonds, circles and triangles indicate results from rigorous scattering theory (Section 4.3), the cryogenic screening model (Section 4.2) and the comparison between the penetration depths (Section 4.1), respectively. Results from the screening model are given for constant hemispherical, thermal emissivity (ε = 0.9). Compare text for explanations. Magnetic field (London) penetration depth (λL), perpendicular to the ab-plane (with screening currents in this plane), of BSCCO 2212 and 2223 amounts to λab = 200 nm to 300 nm and 150 nm, respectively; these values are from [36] (Table 2.7), and the dependence of λab on temperature is λab = λab(4 K) [1 − (T/TCrit)4]0.5 (small triangles). For BSCCO 2212, λab = 205 nm, and a linear temperature dependence, λab = λab(0) (1 + αT), as reported in [61] for a single crystal, has been applied (large triangles). b Comparison of the results obtained with the three different methods (Sections 4.1 to 4.3) now including corrections from dependent scattering according to Fig. 13, and for quasi-perforations in the radiation screen model
With corrections due to dependent scattering, the agreement between the extinction coefficients obtained from the three independent methods is further improved (compare Fig. 19b).
For the radiation screen model, a correction is needed for the transmission windows (quasi-perforations) between the grains. The literature reports substantial contributions to radiative flux by radiation windows even if perforation is tiny, in total just 1% or below of the total surface. There is also radiation propagating parallel to the surfaces. In the present case, perforation is large. Inspection of Fig. 6a and comparison with experimental data suggest the effective radiative flux increases strongly, by about 1 order of magnitude (in other words, radiation screens consisting of an array of flat, plate-like particles, even if evacuated, would not be very effective to reduce radiative losses in cryogenic engineering). This yields a corresponding decrease of the effective extinction coefficients calculated in Section 4.2. The final result is shown in Fig. 19b.
The agreement of the results obtained with scattering theory and the cryogenic screening model (blue diamonds and circles, respectively) for YBaCuO 123 is surprisingly good. Even for BSCCO 2212 (light red diamonds and circles), the corresponding deviation is within a factor of about 3 (not catastrophic in view of the complicated approximations and calculation steps).
4.6 Comparison of the Results with Normal Conductors
Extinction coefficients for the normal conducting YBaCuO 123 (quasi-) particulate superconductor are calculated in Fig. 20a, for T = 300 K (blue diamonds). Comparison with the red diamonds and with Fig. 19a and b shows that there is no jump of the extinction coefficients at T = TCrit that would be large enough (exceeding numerical uncertainties of the calculations) to allow a clear distinction of the superconductive and normal conductive states by their radiative transfer properties.
a Comparison of the extinction coefficients (E) of YBaCuO 123 calculated at 92.001 ≤ T ≤ 200 K (red diamonds); results are shown in dependence of wavelength by application of scattering theory and the Drude-Lorentz model to estimate the complex refractive indices as a function of temperature. Blue diamonds are obtained using spectral refractive indices (m = n − ik), for room temperature (RT) as reported in [19]. b Specific extinction coefficients (ER*/ρ, the Rosseland mean of spectral EΛ) for anisotropic scattering of thermal radiation by thin dielectric fibres, vs. temperature (T) and particle diameter (d). The refractive index m = 1.5 − 0.0016i corresponds to glass fibres. Like in Fig. 8, the results do not include dependent scattering, which means they can be applied, without corrections, to only small particulate density (ρ). Assuming a density of ceramic or glass wool (ρ) of about 200 kg/m3, the extinction coefficients (E*) are below 105 (1/m) (the star indicates inclusion of anisotropic scattering). The figure is redrawn from its original publication [42]
The extinction coefficients of superconductors, in normal conducting state, accordingly are not smaller than those in superconducting state (in zero magnetic field, below critical temperature).
For comparison, the extinction coefficients of classical normal conductors, like ceramic or glass fibres, are clearly below these results (Fig. 20b). Only the extinction coefficients of high-density, bulk ceramics, like ZrO2, are in the same order of magnitude as those shown in Fig. 19a.
Figure 20a also confirms that extrapolation of (9a), (9b), (12a) and (12b), the Drude-Lorentz model, together with the input parameters in Table 1, to the temperature range T> TCrit is reasonable: the method yields quite similar results when the spectral refractive indices m = n −ik reported in [19] are taken for the calculation of E in dependence of wavelength.
Very large extinction coefficient and optical thickness in the superconducting state, vs. a hypothetically small optical thickness under normal conduction of the same superconductor (particulate) material, indeed would have confirmed also the perhaps existing, extended correlation between non-transparency, superconducting/normal conducting phase transition and quench of a superconductor. As Fig. 20a shows, this is not the case.
5 Uncertainties, Risks and Discussion of the Conclusions
In this paper, radiative properties of the superconductors are considered at the wavelength (Λmax) where the maximum emissive power of the black body is observed. Contrary to optical experiments, we cannot investigate radiative transfer at just one wavelength. This might be questionable since 3/4 of the whole black-body spectrum is at wavelengths Λ > Λmax. However, the spectral intensity per wavelength interval reduces exponentially at all wavelengths Λ≠Λmax. Possible errors become smaller when Λ deviates more from Λmax. Contributions to the absorption cross sections from short wavelengths and from millimetre and radar wavelengths in the whole black-body spectrum thus are neglected.
5.1 Comparison of Penetration Depths
If the standard temperature dependence of the penetration depth is accepted, the position within the conductor at which exp(−x/λL) becomes close to zero might not coincide with the position where exp(−τ) disappears. Zero-to-zero comparisons, and conclusions drawn thereof, are highly questionable. The comparison can be made with finite penetration depth only. Even then, the equality of the two decay equations expected relies on an equality of exponentials and thus might work in exceptional situations only.
Further, corrections to the extracted extinction coefficients may become necessary since both interactions occur in a solid with its specific refractive index, not in vacuum. To become a (semi-) quantitative method, experiments have to be performed that yield both penetration depths in a variety of superconductor materials.
The extinction coefficients obtained from comparison of penetration depths, 1/E and λL, for the three materials (triangles) in Fig. 19a are much smaller, by about 1 order of magnitude. Deviations apparently are systematic and possibly are the consequence of the method as a whole (refractive index of the superconductor material neglected in (7a) and (7a) and because of uncertainties of the penetration depth (λL) of a magnetic field; literature values indeed show strong uncertainties, and the structure of the samples is not always indicated).
Applicability and practical use of this method certainly need thorough investigations before it can be considered as a, at best, semi-quantitative tool. The difference between the large and small, light red triangles in Fig. 19a results from the measurement of λab using a BSCCO 2212 single crystal that yields the larger values of E.
5.2 Radiation Screen Model
A schematic view of the conductive and radiative thermal resistances (RCond and RRad, respectively) of a column of j ≤ j + 5 of total N grains within a filament is shown in the Appendix (Fig. 24). First, the model neglects the matrix material (Ag); the space between the grains is assumed to be empty. This approximation can be accepted since the Ag hardly penetrates into the voids between two or very few layers of grains, perhaps only at positions near the upper and lower boundaries of the filaments.
Derivation of (7a), (7a) and (8) assumes that in each screen, the temperature of front and back sides of the screen is identical. But both equations assume the screen material was Al or Ni or other highly reflecting and thermally conducting metal. In case of the superconductor material, this is not fulfilled.
In cryogenic multi-screen engineering, this is no problem: if emissivity is very small (or the reflectivity very large), and also the thermal conductivity of the screen material is very large (with Al or Ni as the screen material), incident radiation is strongly damped in the foil material, and the large thermal conductivity of Al or Ni (and the screens evacuated) is responsible for outbalancing any temperature gradients to almost zero. But in case of the superconductor grains, this is not clear. Radiation may penetrate into the grains within the diffuse radiative boundary layers (Fig. 3), and the conductivity of the superconductor is by orders of magnitude smaller than that of Al or Ni. This induces additional thermal resistances against the total thermal radiative flow.
But non-zero temperature gradients across each radiation screen (grain) would increase optical thickness. Optical thickness decreases radiative heat flow, like a large temperature gradient in a solid conducting medium indicates reduced solid thermal conductivity. In turn, because of non-zero temperature gradients over the grains, the optical thickness thus would be larger than estimated from this model.
The large correction applied to the results in Fig. 19a by taking into account transmission windows (the quasi-perforation) is not very surprising. It is well known even tiny disturbances of perfect surface quality of highly reflecting screens can exert catastrophic effects (this applies already to fingerprints resulting from careless handling of the highly reflecting foils).
5.3 Results from Application of Scattering Theory
The method applies extrapolations of permittivity reported in the literature (its parameters and calculation steps), from temperature far below TCrit (in few cases, T≤ 50 K) to values very close to critical temperature (TCrit = 92 K in YBaCuO 123). This possibly constitutes a serious problem since part of these parameters was obtained by the corresponding authors from multi-parameter fitting procedures.
If we instead of temperature intervals consider frequencies (ω) or wavelengths (Λ), there is between T = 50 and 90 K a variation of ω from 175 to 315 1/cm (Λ from 58 to 32 μm). In this range of frequency or wavelengths, a strong variation of the refractive indices (m = n −ik) is not expected (compare Fig. 8 in [19] or Fig. 5 in [23] with the smooth variations of n and k (these were measured at T = 10 K and with ω only below 100 (1/cm), or at T = 300 K with Λ ≤ 100 μm, respectively). But this is rather a plausibility argument, not a proof.
On the other hand, comparison of the extinction coefficients (E) calculated at T> TCrit of YBaCuO 123, in dependence of wavelength (Fig. 20a), shows good agreement between the blue diamonds (obtained with spectral refractive indices m = n −ik reported in [19] for T = 300 K const) and the red diamonds (from application of the Drude-Lorentz model calculated for 92.001 ≤ T ≤ 200 K radiation temperature). This agreement indicates that the risk from the above-mentioned extrapolations of the permittivity is less dramatic; an agreement like in Fig. 20a would not be obtained if application of (9a), (9b), (12a) and (12b) to temperature near TCrit and at T = 300 K is not possible.
The results obtained for the permittivity and, consequently, for the extinction cross sections, the extinction coefficients and the albedo (Figs. 14a, b, 15 and 16) also rely on the convergence of the fractions (fS) to zero if sample temperature becomes close to critical temperature. In order to reduce this risk, the calculations of QExt, E, Ω and τ were performed also with the “average 1” (calculations performed with the arithmetic mean of the parameters listed in Table 1). Agreement of the obtained E with “average 2” (the mean value of the calculated results, Fig. 14a and b), within 5%, again is encouraging.
There is still the uncertainty inherent in the estimate of minimum fraction (fS) of electron pairs that is necessary to generate and retain critical currents, as transport currents or as screening and persistent currents and for magnetisation. But the risk from uncertainty in the fS, in particular the minimum fS, appears to be small since the estimate of the fS is highly conservative.
Measurement of refractive indices at temperature below, but very close to, critical temperature involves enormous difficulties and will hardly ever be performed. Efforts might better be invested to improve the theoretical models for application of the combined Drude and Lorentz models in this critical range of temperature. As a first step in this direction, application of the microscopic stability model, with its calculation of the density nS of electron pairs, is suggested in this paper and might be useful in other simulations.
It is an open question whether algorithms like the time domain finite difference (TDFD) schemes appropriately could be adjusted to include also the London equations and thus yield a solution of the irregular particle shape problem. The desired solution is not trivial and is illustrated, for example, in transformations like f(T, J) = ns(T,0) − ns(T, J))/ns(T,0), that applied Eq. (2c) in [47], where the authors believe the relative dependency of superfluid density (ns) on current density (J) can be used in this equation if “current density, J, be much less than critical current density, Jc”.
This cannot work properly: current in a superconductor always flows with critical current density. The transformation thus has to be based on absolute current, not on current density, which means current distribution in the conductor cross section has to be known first. The procedures could perhaps be improved by a series of iterations.
It is also rather questionable whether the approach reported in [48] can be successful: the authors assume a type I superconductor with zero penetration depth. This simulates a perfect conductor but does not satisfy the Meissner effect. Reference [48], and the literature cited in reference [49], also does not consider the other central problems of the present paper: radiative transfer in superconductor particulate objects.
It appears as if in [49], a parameter (ka) was introduced to replace the fundamental T< TCrit criterion for superconductivity and field shielding. Instead, the parameter ka is allowed to assume continuously varying values, ka ≥ 0 (compare Figs. 2, 3 and 4 of this reference). As a consequence, there would be no complete shielding at which an external magnetic field is suddenly excluded from the superconductor volume as soon as T < TCrit. Field expulsion in type I superconductors cannot be described on the basis of a continuously varying parameter.
6 Physical Time in Non-transparent Objects
6.1 Survey of the Problem
In the previous sections, we have investigated the possible existence of a correlation between non-transparency and stability against quench. The answer was negative. It is a weak anti-correlation or inverse correlation that can be found, at the most: non-transparency of a superconductor may exclude its stability against quench (it, most probably, does not promote stability).
The aim of the present section is to discuss whether a correlation or anti-correlation could be found between non- transparency and existence of physical time in non-transparent superconductors. Presently, it is a mere hypothesis. However, the existence of such a relation would be highly interesting: if it existed, it would, for example, read: “The more a superconductor sample becomes non-transparent, the less can time and space co-ordinates be identified when a quench occurs in the conductor cross section”. The consequence “the less can time and space co-ordinates be identified” would have impacts on detection of a quench.
The temperature profiles in Figs. 1a and 2a clearly show that quench may occur at different positions (x) not uniformly distributed in the conductor cross section. In both figures, there are several positions where local temperature difference to the corresponding TCrit is so small that only little additional energy is needed to increase temperature at these positions above the limit.
The following is a corollary of the results obtained from the radiative transfer calculations in the previous sections.
6.2 Transit Times
In simulations of temperature distribution in a superconductor, the contribution by radiation in the diffusion model usually is small against its solid thermal conductivity. For example, the temperature difference (T1 − T2), taken in Fig. 1a (bottom diagram, in a mid-plane position) over the cross section of a single filament (located at the centre of the tape) amounts to about 18 K (T1 = 116 K, T2 = 98 K). With an extinction coefficient (E) in the order of 107 (1/m), the radiative conductivity (λRad) from the diffusion model amounts to about 5–6 10− 5 W/(m K), less than 0.1% of the solid thermal conductivity of the BSCCO 2223 superconductor (λCond about 0.12 W/(m/K), in c-axis direction and near its critical temperature). The small percentage of the radiation contribution results from non-transparency of the conductor.
Despite its small value, the radiative conductivity has important consequences for temperature profiles, stability functions, zero loss transport currents (compare [12, 13]) and for transit times of signals emitted from, for example, a disturbance in the centre of the filament in direction to its neighbouring filaments. Different transit times between both positions can be distinguished with respect to different heat transport processes (conduction, radiation and interferences thereof).
But if propagation of radiative signals is blocked by non-transparency, events are not only spatially separated (like in Figs. 1a and 2a) but also temporally separated so that events and their images (the response, exemplified as results of measurements) are no longer uniquely correlated.
If there is only some residual radiation (no solid conduction), the difference 𝜃 = ty − tx (the transit time between positions y and x) may become arbitrarily large. Then, events e(y, ty) and e(x, tx), cannot be correlated because ty cannot be correlated with tx by a finite and uniquely known difference (ty − tx). In an extreme case (non-transparency), the difference might not exist at all when tx or ty cannot be indicated. Instead, e(y, ty) and e(x, tx) can be correlated only if ty − tx is very small (like in the sole scattering case where 𝜃 is in the order of 10− 13 s; see below) and if both ty and tx are booked on uniquely and unambiguously defined time scales. In turn, e(y, ty) and e(x, tx) can be correlated only if optical thickness is very small (the transparent case) and if there is no or only very weak solid conduction.
But the correlation between e(y, ty) and e(x, tx) not only would fail because of an undefined difference (ty − tx), the question is whether an uncountably large number of events would completely, uniquely and unambiguously be recognised on a dense time scale (ty) of their images.
In order to be completely, uniquely and unambiguously be recognised, bijective mapping, f[e(s, t)], the result of Section 2 must exist between events at (x, tx) and their images at (y, ty).
6.3 Modelling Physical Time in a 1D Space
Physical time is not identical to psychological time. Orientation of the arrow of physical time becomes possible when the second law of thermodynamics is taken into account. The differentiation between past and future, and the determination of the arrow of physical time, relies on an initial, minimum entropy state [50]. Mathematically, irreversibility thus reduces R to the half-set R+ [51]. But psychological time extends in both orientations to infinity. Both orientations emerge from a finite, non-zero-length presence interval. Physical time postulates zero-length elements, while psychological time does not. Superconductors belong to the favourite circle by which the standard, commonly accepted idea of a universal physical time possibly could be confirmed or questioned.
Physical time does not exist a priori, and it needs events for its definition, like temperature variations or quench of a superconductor or others. The point is time scales cannot exist without events, like space does not exist without bodies.
Physical time (t) usually is added to the 3D Euclidean space (xk,1 ≤ k ≤ 3) as the fourth component (x4 = ict, with c as the speed of light). This 4D structure has been proven suitable for application in transparent space. The situation is different in non-transparent space. Instead of the standard, 4D space-time, we will construct the arrow of physical time in a separate space (Z) to describe this space independent of the properties of the 3D vector space R3 (in a stationary system, there should be no problem).
It is not clear that the separate space (Z) really might fulfil criteria of a vector space. We will provisionally speak of Z as a vector-like time space. Yet, psychological time suggests that Z should be 1D, Z = Z1.
In a purely mathematical sense, physical time may be identified with, or its number of elements imagined as equipotent to, the set (R) of real numbers. If the correlation between events and their images correlation is bijective (as is realised in transparent, but questionable in non-transparent objects), physical time is dense since the set R is dense. Thus, physical time is dense only in transparent media. This understanding of a time scale to be dense does not, and need not, consider the granularity concept of quantum gravitation and the Planck time, tP, about 10− 44 s. Provided t >> tP, images not necessarily but potentially form a (quasi-) continuum on a time scale.
The set R, for t >> tP, is totally ordered: if a1 and a2 are elements of R, one and only one of the following three relations holds: a1 < a2, a1 = a2 or a1 > a2.
All this does not collide with relativity principles as long as we consider only stationary systems. Thus, physical time is dense and totally ordered only in transparent media.
Elements of the Euclidean space R3 as usual are interpreted as vectors that are multiples and linear combinations of a set of basic vectors, rk (1 ≤ k ≤ 3). By analogy, physical time (t) shall be constructed in Z1 as elements (zi) that are multiples and linear combinations in 1D space of a basic element (z), which means zi = αiz. The factor α will be specified below.
A coordinate ti = zi of the image f [ei(si, ζi)] = ei(si, ti) on a physical time scale (t) (if it is uniquely and unambiguously defined) is the distance from an origin z0 of Z1. The existence of a zero element of physical time, z0 = t0 = α0 and z = 0, has to be postulated, without loss of generality, by the difference between two coincident images (elements of Z1); otherwise, it would not be possible to define coincidence in Z1. Accordingly, the difference αz − αz = z0 is zero only in transparent space.
That the 1D space Z1 is dense accordingly can be formulated also with respect to the set of constants (αi) in the images, f [ei(si, ζi)] = ei(si, ti), with ti = z0 + αiz, if the αi belongs to an uncountably infinite set, like the set (R) of real numbers. If this is the case, and with its zero-length element z0, the mathematical structure of Z1 then is close to the theory of one-parameter half-groups [52].
As a result, the space Z1 in transparent space is dense and ordered.
6.4 Images and Probability of Their Existence
Local conductor temperature is extracted from scanning the temperature distributions in Fig. 1a (scan along the vertical, red line in Fig. 1b) and in Fig. 2a (there, temperature is extracted at horizontal position near the symbol MX of the finite element plot, where nodal temperature shows a local maximum). The result (nodal temperature in the BSCCO 2223 and YBaCuO 123) is shown in Fig. 21a and b.
a Nodal temperature, T(y), in the multi-filament (1G) BSCCO 2223 superconductor. Temperature is extracted from Fig. 1a at y-coordinates along the vertical red line in Fig. 1b. Vertical positions (y) are counted from the bottom to the top of the conductor cross section. Thin vertical black lines indicate the positions of the superconductor (SC) filaments within the total tape cross section. b Nodal temperature, T(y), in the thin film (2G)-coated YBaCuO 123 superconductor. Temperature is extracted from Fig. 2a. Vertical positions (y) are counted from the bottom to the top of the thin film cross section. Thin vertical black lines indicate the positions of the SC film within the total winding cross section (winding no. 96 of the simulated coil)
In Fig. 21a, the peak in the temperature distribution within the superconductor (SC) regions results from flux flow and normal conducting losses that overcompensate the much larger thermal conductivity of the Ag matrix into which the five filaments are embedded. In Fig. 21b, the large thermal mass of thick layers below the superconductor thin film (MgO, Hastelloy) is responsible for the approximately linear temperature profile, shortly after the start of the disturbance. Horizontal temperature variations in turn 96 of the simulated coil result from statistical variations of the parameters TCrit, BCrit and JCrit (this is explained in [5,6,7]; we cannot expect exactly identical critical superconductor parameters over extended conductor lengths from industrially manufactured conductors).
With the extracted T(y) shown in Fig. 21b, Fig. 22 shows local values of extinction coefficients, E = E[T(y)], in the thin film-coated YBaCuO 123 superconductor. The extinction coefficients (E) are calculated using their temperature dependence in Fig. 15. That E[T(y)], in contrast to T(y), deviates from linear dependence on temperature is due to the wavelength dependence of the refractive indices used for calculation of the QExt.
Figure 23a shows calculated transit times 𝜃1, 𝜃2 and 𝜃3 for an event like temperature variation or for a beam scattered or emitted at position (x = const, y ≥ 126 μm, the lower boundary of the filament) or for a quench from which signals (energy quanta, thermal disturbances) are emitted. The transit times, 𝜃1, 𝜃2 and 𝜃3, are needed for a signal to arrive at the filament upper boundary (x = const, y = 128 μm), or vice versa, within the YBaCuO 123 superconductor thin film, using the extinction coefficients (E) from Fig. 22.
a Transit time for a beam scattered or emitted at position (x = const, y ≥ 126 μm) that is needed to arrive at the upper boundary (x = const, y = 128 μm), or vice versa within the YBaCuO 123 superconductor thin film, using the extinction coefficients (E) from Fig. 22. In case of pure scattering, the beam proceeds by the velocity of light in the medium of refractive index (n); otherwise, in a non-transparent object, transit time is calculated from 𝜃 = [(Δy/C)2]/aTotal, with the diffusivity (aTotal) to be taken according to the strength of heat transfer components and by application of the additive approximation, if appropriate. b Probability function, p(x), that each beam scattered or emitted at position (x = const, y ≥ 126 μm), on its straight way through the YBaCuO 123 thin film (all x = const), under the right angle hits the upper boundary (x = const, y = 128 μm), or vice versa, within the conductor cross section and using the extinction coefficients, E, from Fig. 22
If transit time depends solely on thermal conduction, the situation may already become critical if local temperature is close to critical temperature; even a temperature increase of only 1 K then could initiate phase transition. In case of solely solid conduction (if there is, hypothetically, no radiation at all in the superconductor), transit time, for example taken over a distance of half-filament thickness in Fig. 1a, is about only 23 μs. Yet, within this short period, the local temperature under the given disturbance, because of the large variation dT/dt, would increase by 2.3 K.
In a real situation (solid conduction plus radiation), there will be at least two, but possibly more images of a single event. The images can be differentiated by the corresponding transit times.
A first image, as an extreme case, may result from pure (elastic) scattering (albedo Ω = 1) and without solid conduction. This can be realised if particles do not, or do only very slightly, contact each other and if, for example, the material is BSCCO 2212, with its Ω = 1 (using the data reported in [46] for calculation of the refractive index; the condition “no solid conduction” of course cannot be fulfilled with this material). This image is generated by propagation of a signal solely by radiation, with the velocity of light in the object.
A second image, the other extreme, would be due to pure absorption/remission (without scattering, Ω = 0, and again without solid conduction). This case happens with superconducting thin cylinders (or with thin Ag cylinders, all described in the previous sections and again with only little solid/solid contacts).
Transit time (𝜃) of a signal arising from any excitation, over a distance (Δy) is obtained from solution of Fourier’s differential equation
for a flat slab and with a as the thermal diffusivity assumed to be constant. In the present case, the diffusivity is calculated using aRad = λRad/(ρcp), with λRad the radiative conductivity (from the diffusion approximation), ρ as the density and cp as the specific heat.
Images also result from the case 0 < Ω < 1, with scattering and absorption/remission in parallel (and still without conduction). Transit time results from the scattering contribution, S = ΩE, and from the remaining absorption/remission part, A = (1 −Ω)E. While the part S again proceeds by the velocity of light in the object, the absorption/remission part is calculated with the radiative diffusivity mentioned above and with scattered radiation in parallel to the absorption/remission part.
More images result from combined conduction plus radiation heat transfer, with 0 ≤ Ω ≤ 1. This is the most realistic case, not restricted to sole radiation. In a non-transparent object, transit time in this case is obtained from 𝜃 = [(Δy/C)2]/aTotal, under the additive approximation, with aTotal as the total thermal diffusivity. In the additive approximation, aTotal is calculated using the total thermal conductivity, λTotal = λCond + λRad, and with density and specific heat as before. Calculation of the transit time by this procedure includes only radiation by absorption/remission. The scattering part again proceeds, in parallel, by the velocity of light and does not contribute to obtain radiative equilibrium.
Heat transfer by combined conduction plus radiation heat transfer, with 0 ≤ Ω ≤ 1, has frequently been studied in the literature. However, in terms of transit time, the case (Ω > 0) in a conductive medium is only occasionally discussed (for example, Klemens [53]; explanations can be found in [42], p. 81): large albedo may create a strong temperature jump (while the temperature field remains differentiable). A temperature jump is only step-by-step degraded by the slow, diffusion-like, radiative absorption/remission transport processes (but degradation may be accelerated by the conduction component). Each of the images of events like a temperature variation thus cannot be constant in time and therefore is not uniquely defined.
The number of images, in principle, may increase to even an arbitrarily large number since there is an arbitrarily large number of combinations of S and A in the extinction coefficient, E = S + A. This means the number of different values of the albedo might be arbitrarily large, too.
A correspondingly similar, but less complicated situation has been investigated in Monte Carlo simulations of radiative transfer in thin-film, normal conductors, by assuming the albedo within certain limits is a random variable [54]. Each random variation of the albedo, at each of the large number of radiation/solid collisions, delivers another total transit time.
The point is while also in the non-transparent object total heat flux is given by the sum of the different contributions, by conservation of energy, and is uniquely defined, the transit time and thus the position of the corresponding images, and their order on the time scales, are not. Even if events are arranged orderly, the order of their images might completely be dissolved.
This has a peculiar consequence: time in non-transparent objects is not transparent. Consequently, there is neither a unique identification of images belonging to the same event nor of events belonging to the same image.
This situation still becomes more difficult if we consider the probability by which signals arrive at a detector, solely by radiation, to generate an image. In a non-transparent object, the original directional intensity of a beam not only is exponentially damped, according to the optical thickness. Because of (1a), the final signals (images taken by a detector) also fluctuate statistically: the mean free path (lm) is not constant. Each path, W1 or W2 in Fig. 3, incorporates a different number of lm, and each of the lm depends on specific, local absorption/remission or scattering interactions that not necessarily would be identical along the paths. The probability to receive a uniform signal thus becomes small.
As a numerical example, Fig. 23b shows the probability (p) in dependence of the position (y) within the YBaCuO 123 thin film, from which a beam of directional intensity is emitted or scattered, under right angles to opposite positions (the x-coordinates kept fixed). The intensity, if scattered, or after absorption remitted, in other directions, will be damped more strongly than shown in Fig. 23b, which further reduces the probability of a signal to arrive at a detector. The number of signals or images observed by a detector thus is reduced, in inverse proportion to optical thickness.
All this is solely a corollary of the analysis of radiative transfer in the preceding sections. We accordingly have to live with uncertainties that arise from simply the complex interactions of several heat flow components and from the statistical rules of radiation propagation in non-transparent objects.
6.5 A Practical Consequence for Superconductor Stability
Among other measures to improve stability, standard multi-filamentary conductor architecture applies the distribution of the filaments in a metallic matrix of high thermal conductivity. The discussion in this paper instead has been focused on the radiative properties within the proper superconductor material.
From the results described in the preceding sections, it is concluded that the superconductor material should be developed in a way to strongly promote scattering of radiation (instead of strong absorption/remission processes). Large albedo, Ω → 1, according to Fig. 23a, decreases transit time (compare the blue and red symbols). Though radiation is small in comparison to the solid conduction component, scattering contributions, possibly as intermediate steps in the total transfer process, promote fast distribution of excitations energy within the conductor cross section.
Though radiative equilibrium cannot be obtained under scattering, it is the large signal velocity (or the small transit times) that makes strongly scattering superconductors attractive for improving their stability. At near transition temperature, the small contribution by radiative to total heat transfer, by its optimisation with large albedo, may turn out as the most useful for stability, since temperature close to its critical value is the most critical situation.
It is not clear whether strong scattering might reduce critical current density. This relation should be clarified in future experiments.
7 Summary and Outlook
A substantial difference of extinction coefficients between the superconducting and normal conducting states of the particulate YBaCuO 123, at the phase transition, cannot be confirmed. There is no strict (anti-) correlation between radiation heat transfer, non-transparency and quench.
If a (quasi-) particulate superconductor, like YBaCuO 123 films in a coated conductor, at T< TCrit, is non-transparent to mid-IR radiation, it is non-transparent also in its normal conducting state. The result would be the same for the particulate superconductors BSCCO 2212 and 2223.
Non-transparency of YBaCuO 123 filaments confirms the applicability of the additive approximation for the total thermal conductivity, to calculate solutions of Fourier’s differential equation by analytical or numerical methods.
Optimisation of the scattering contributions to radiative heat transfer decisively can contribute to superconductor stability, in particular near the phase transition, the most critical situation.
Within short time interval (the transit times), there are no uniform equilibrium or non-equilibrium conditions of electron pair density near critical temperature in a non-transparent superconductor. Phase transition accordingly does not occur uniformly (spatial or temporal) in the conductor cross section.
Non-transparency prevents uniformity of events in space and also denies uniformity of their occurrence in time. Because of a large variety of potential transit times in non-transparent objects, time in these objects is not transparent.
These conclusions also show that considering the physical time scale as the fourth component of a common vector space in non-transparent media invariably leads to contradictions: the structure of three spatial and, separately, one time-like components, namely R3 and Z1, in a non-transparent medium is completely different from the usual correlative 4D space-time geometry. There, all time-like space elements, of both R3 and of the fourth component, Z1, are assumed as uncountably infinite. But this is not fulfilled in non-transparent space. One of the central questions discussed in the famous Einstein-Podolsky-Rosen (EPR) paper concerns “completeness of a physical theory”. The theory of radiative transfer in non-transparent objects is not complete. We will later investigate a possibly existing, systematic parallel between the EPR paradox and present understanding of radiative transfer in non-transparent superconductors: Like in quantum-mechanics, a reconstruction cannot be achieved by introduction of later claimed hidden variables (von Neumann), to restore causality and locality from a “fog” of images.
References
Wilson, M.N.: Superconducting magnets. In: Scurlock, R. (ed.) Monographs on Cryogenics. reprinted paperback. Oxford University Press, New York (1989)
Dresner, L.: Stability of superconductors. In: Wolf, S.t. (ed.) Selected Topics in Superconductivity. Plenum, New York (1995)
Flik, M.L., Tien, C.L.: Intrinsic thermal stability of anisotropic thin-film superconductors. ASME Winter Ann. meeting, Chicago (1988)
Reiss, H.: Superconductor stability against quench and its correlation with current propagation and limiting. J. Supercond. Nov. Mag. 28, 2979–2999 (2015)
Reiss, H.: Inhomogeneous temperature fields, current distribution, stability and heat transfer in superconductor 1G multifilaments. J. Supercond. Nov. Mag. 29, 1449–1465 (2016)
Reiss, H.: Finite element simulation of temperature and current distribution in a superconductor, and a cell model for flux flow resistivity—interim results. J. Supercond. Nov. Magn. 29, 1405–1422 (2016)
Reiss, H.: Stability considerations using a microscopic stability model applied to a 2G thin film coated superconductor, J. Supercond. Nov Magn. https://doi.org/10.1007/s10948-017-4245-8 (2017)
Solovyov, M., Pardo, E., Souc, J., Gömöry, F, Skarba, M., Konopka, P., Pekarciková, M, Janovec, J.: Non-uniformity of coated conductor tapes, Supercond. Sci. Technol. 26, 115013 (2013). (9 pp)
Chandrasekhar, S.: Radiative transfer. Dover Publ. Inc, New York (1960)
Hottel, H.C., Sarofim, A.F.: Radiative transfer. McGraw-Hill Book Company, New York (1967)
Sparrow, E.M., Cess, R.D.: Radiation heat transfer. Brooks/Cole Publ. Comp, Belmont (1966)
Reiss, H.: Radiation heat transfer and is impact on stability against quench of a superconductor. J. Supercond. Nov. Magn. 25, 339–350 (2012)
Reiss, H., Troitsky, O Yu: Superconductor stability revisited: impacts from coupled conductive and thermal radiative transfer in the solid. J. Supercond. Nov. Mag. 27, 717–734 (2014)
Rosseland, S.: Astrophysik auf atomtheoretischer Grundlage. In: Born, M., Franck, J. (eds.) Struktur der Materie in Einzeldarstellungen. Verlag von Julius Springer, Berlin (1931)
Glowacki, B.A.: (RE)Ba2Cu3O7 coated conductors for AC and DC applications. In: Narlikar, A.V. (ed.) Frontiers in superconducting materials, pp. 765–832. Springer, Berlin (2005)
Hummel, R.E.: Optische Eigenschaften von Metallen und Legierungen. Springer, Berlin (1971)
Siegel, R., Howell, J.R.: Thermal radiation heat transfer. Int. Stud. Ed., McGraw-Hill Kogakusha, Ltd., Tokyo (1972)
Chen, M.: Optical studies of high temperature superconductors and electronic dielectric materials, PhD Dissertation, Graduate School University of Florida (2005)
Zhang, Z.M., Choi, B.I., Le, T.A., Flik, M.I., Siegel, M.P., Phillips, J.M.: Infrared refractive index of thin YBa2cu3o7 superconducting films. Journal of Heat Transfer, Transacts. ASME 114, 644–652 (1992)
Gao, F.: Temperature dependence of infrared and optical properties of high temperature superconductors, PhD Dissertation, Graduate School University of Florida (1992)
Phelan, P.E., Flik, M.I., Tien, C.L.: Radiative properties of superconducting Y-Ba-Cu-O thin films. Journal of Heat Transfer, Transacts. ASME 113, 487–493 (1991)
Zhang, Z.M., Le, T.A., Flik, M.I., Cravalho, E.G.: Infrared optical constants of the high-Tc superconductor YBa2Cu3O7. Journal of Heat Transfer, Transacts. ASME 116, 253–257 (1994)
Kumar, A.R., Zhang, Z.M., Boychev, V.A., Tanner, D.B., Vale, L.R., Rudman, D.A.: Far-infrared transmittance and reflectance of YBa2,Cu3O7− films on Si substrates. Journal of Heat Transfer Transacts. ASME 121, 844–851 (1999)
Tanner, D.B., Timusk, T. Ginsberg, D.M. (ed.): Optical properties of high-temperature superconductors. World Scientific, Singapore (1992)
Mie, G.: Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 25, 377–445 (1908)
Born, M., Wolf, E.: Principles of optics. 2Nd Rev. Ed., Pergamon (1964)
Kerker, M.: The scattering of light and other electromagnetic radiation. Academic, New York (1969)
van de Hulst, H.C.: Light scattering by small particles. Dover Publications, Inc, New York (1981). republished
Bohren Cr, F., Huffman, D.R.: Absorption and scattering of light by small particles. Wiley, New York (1983)
Mugnai, A., Wiscombe, W.J.: Scattering from nonspherical Chebyshev particles. I: cross sections, single-scattering albedo, asymmetry factor, and backscattered fraction. J. Appl. Optics 25, 1235–1244 (1986)
Percus, J.K., Yevick, G.J.: Analysis of classical statistical mechanics by means of collective coordinates. Phys. Rev. 110, 1–13 (1958)
Reiss, H.: Radiative transfer in nontransparent dispersed media. High Temp.–High Press. 22, 481–522 (1990)
Kaganer, M.G.: Thermal Insulation in Cryogenic Engineering, Translated from Russian by Moscona A. Israel program for scientific translations, Jerusalem (1969)
Huebener, R.P.: Magnetic flux structures in superconductors. In: Springer Series in Solid State Sciences, vol. 6. Springer, Berlin (1979)
Pleines, M.: Untersuchungen zur magnetischen Eindringtiefe in YBa2Cu3O7−-Filmen mit niederenergetischen Myonen, Dissertation (in German), Universität Konstanz. Mathematisch-Naturwissenschaftliche Sektion, Fachbereich Physik (2001)
Buckel, W., Kleiner, R.: Superconductivity, fundamentals and applications, 2nd Ed. (Transl. of the 6th German Ed. by R. Huebener). Wiley-VCH, Weinheim (2004)
Singh, B.P., Kaviany, M.: Independent theory versus direct simulation of radiation heat transfer in packed beds. Int. J. Heat Mass Transf. 34(/11), 2869–2882 (1991)
Reiss, H.: A microscopic model of superconductor stability. J. Supercond. Nov. Magn. 26(3), 593–617 (2013)
Owens, F.J., Poole Jr., C.P.: Electromagnetic absorption in the copper oxide superconductors. In: Wolf, S.t. (ed.) Selected Topics in Superconductivity. Kluwer Academic/Plenum Publ., New York (1999)
Kezuka, H., Masaki, T., Hosokawa, N., Hirata, K., Ishibashi, K.: Refractive index of high-Tc YBCO superconductors. Phys. C 185–189, 999–1000 (1991)
Sandilands, L.J., Reijnders, A.A., Su, A.H., Baydina, V., Xu, Z., Yang, A., Gu, G., Pedersen, T., Borondis, F., Burch, K.S.: Origin of the insulating state in exfoliated high-Tc two-dimensional atomic crystals. Phys. Rev. B 90, 081402–1–081402-5 (2014)
Reiss, H.: Strahlungstransport in Dispersen Nicht-Transparenten Medien, Thesis for Habilitation. University of Wuerzburg, Wuerzburg (1985)
Ebert, H.-P., Arduini-Schuster, M., Fricke, J., Caps, R., Reiss, H.: Infrared-radiation screens with very thin metallised glass fibres. High Temp.–High Press. 23, 143–148 (1991)
Kerker, M., Wang, D.-S., Giles, C.L.: Electromagnetic scattering by magnetic spheres. J. Opt. Soc. Am. 73(/6), 765–767 (1983)
Ku, J.C., Shim, K -H: A comparison of solutions for light scattering and absorption by agglomerated or arbitrarily-shaped particles. J. Quant. Spectrosc. Radiat. Transfer 47(/3), 201–220 (1992)
Rakhmanov, A.L., Yampol’skii, V.A., Fan, J.A., Capasso, F., Nori, F.: Layered superconductors as negative-refractive-index materials. Phys. Rev. B 81, 075101–1–075101-5 (2010)
Mollai, S., Javadzadeh, S.M.H., Shishegar, A.A., Banai, A., Farzaneh, F., Fardmanesh, M.: Analysis of nonlinearities in superconducting microstrip straight bends; FDTD method in comparison with nonlinear circuit modelling, Journal of Superconductivity and Novel Magnetism, doi:https://doi.org/10.1007/s10948-012-2025-z
Fiolhais, M.C.N., Essén, H.: Electromagnetic wave scattering by a superconductor, Europhys. Lett.: http://iopscience.iop.org/0295-5075/97/4/44006/ (arXiv:1202.4793v1 (cond-mat.supr-con), February 21, 2012
Matute, E.A.: On the superconducting sphere in an external field. American Association of Physics Teachers 67(9), 786–788 (1999)
Hund, F.: Zeit als physikalischer Begriff. In: Aichelburg, P. C. (ed.) Zeit im Wandel der Zeit, Friedr. Vieweg & Sohn, pp. 178–192. Braunschweig/Wiesbaden, Germany (1988)
Nickel, G.: Determinism—scenes of the interplay between metaphysics and mathematics. In: Nagel, R., Engel, K. (eds.) One-parameter semigroups for linear evolution equations, pp. 531–554. Springer, Berlin (2000)
Engel, K.J., Nagel, R.: Semigroups Everywhere. In: One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194, pp. 347–496. Springer, New York (2000). https://doi.org/10.1007/0-387-22642-7_6
Klemens, P.G.: Radiative transfer in composites, Proc. 9th Europ. Conf. Thermophys. Prop., Manchester. High Temp.-High Press. 17(1985), 381–385 (1984)
Reiss, H., Troitsky, O.Yu: Radiative transfer and its impact on thermal diffusivity determined in remote sensing. In: Reimer, A. (ed.) Horizons of world physics 276, Chapter 1, pp. 1–67 (2012)
Marzahn, E.: Supraleitende Kabelsysteme, Lecture (in German) given at the 2nd Braunschweiger Supraleiter Seminar Technical University of Braunschweig (Germany). https://www.tu-braunschweig.de/Medien-DB/iot/s-k.pdf (2007)
Eschrig, H., Fink, J., Schultz, L.: 15 Jahre Hochtemperatur Supraleitung. Phys. J. 1(Nr. 1), 45–51 (2002)
Pastor, J.Y., Poza, P., LLorca, J.: Mechanical properties of textured Bi2Sr2CaCu2O8+ high-temperature superconductors. J. Am. Ceram. Soc. 82, 3139–3441 (1999)
Bhattacharya, R.N., Mann, J., Qiao, Y., Zhang, Y., Selvamanickam, V.: Electrodeposited Ag-stabilization layer for high temperature superconducting coated conductors, preprint, Conference paper presented at Materials Science & Technology (MS&t) 2010, Houston, Texas, October 17–21, 2010, prepared under Contract No. DE-AC36-08GO28308, NREL/CP-5900-49702 (2010)
Kautschor, L.O., Joos, C., Born, V.: University of Göttingen, Germany, Dept. Mat. Phys., referenced by Glowacki B A, (RE)Ba2Cu3O7 coated conductors for AC and DC applications. In: Narlikar, A.V. (ed.) Frontiers in Superconducting Materials, pp. 765–832. Springer, Berlin (2005)
Zhang, Z., Wimbush St, C., Kursumovic, A., Suo, H., MacManus-Driscoll, J.L.: Detailed study of the process of biomimetic formation of YBCO platelets from nitrate salts in the presence of the biopolymer dextran and a molten NaCl flux. Cryst. Growth Des. 12, 5635–5642 (2012). (Copyright Am. Chem. Soc.)
Waldmann, O., Steinmeyer, F., Müller, P, Neumeier, J.J., Régi, F.X., Savary, H., Schneck, J.: Temperature and doping dependence of the penetration depth in Bi2Sr2CaCu2O8+. Phys. Rev. B 53, 11825–11830 (1996)
Acknowledgments
Let me express my gratitude to the referees for their helpful comments and to the readers for their patience.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Conductive and radiative thermal resistances (RCond, S and RRad, S, respectively) of grains (schematic), and total resistance (RTotal) of a filament. Grains are indicated by the light grey flat rectangles. Within the solids (index S, thickness z2), the conductive and radiative resistances are switched in parallel. The space between the grains (clearance z1, about 10 nm or less) is empty (index e; within z1, there are only radiative resistances, RRad, e). Total resistance (RTotal) results from switching all grain and clearance resistances in series. The figure helps to identify a weak point when estimating the extinction coefficient from the multi-layer screen concept (Section 4.2) applied to the grains: front and rear side temperatures (TFront and TBack, respectively) in each grain (j, j + 1, j + 2, … , j + N) would be (almost) identical, which is not very clear when considering the finite thermal transport properties of the grain material. Compare the discussion of risks of the conclusions in Section 5.2
Schematic description, like in set theory notation, of dispersed, transparent, translucent and non-transparent media. The figure relates to a fixed wavelength of radiation propagating in these substances. The figure has two hierarchies: first, dispersed media are elements of the thick circle (6); accordingly, all elements outside this circle are non-dispersed (continuous) media like massive solids or liquids without bubbles. Second, elements of transparent, translucent or non-transparent media are elements of the thin circles, and no elements outside these circles exist. Accordingly, elements of non-transparent media are not the complement of the uppermost circle (indexed “transparent”) but are contained only in the lowest circle. The thin circles are ordered with respect to increasing optical thickness (τ) from top to bottom of the figure. A possible population of the seven sets is as follows: (1) metallised or metallic fibres, heavily opacified non-conducting fibres or powders, soot and graphite; (2) metals and liquids (not thin films thereof); (3) glass wool with large fibre diameters compared to the wavelength of incident radiation, low-density powders, aerogels, fog and snow; (4) water and other clear liquids and panes; (5) pure (not opacified) glass fibre boards, powders, particle beds, concrete, sands and dust, with large particle diameters compared with incident wavelength. Region (5) indicates the intermediate region between translucent and non-transparent, both dispersed media. Region (6) collects clouds, powders and fibres with medium optical thickness and (7) the vacuum or dilute gases. The figure is an update of Fig. 2 in [32]
IR and mid-IR photon energy and energy gap (ΔE(T)) of YBaCuO 123 vs. wave number (ω). The energy gap is calculated using the standard BCS relation ΔE(T) = 1.74 ΔE(T= 0) (1 − T/TCrit)0.5, with ΔE(T= 0) = 60 meV. The velocity of light in vacuum is reduced, using the real part of the refractive index of the solid material, to its proper value in the superconductor. The temperature range 90.5 ≤ T< 92 K corresponds to wave numbers of about 312 ≤ ω ≤ 317 (1/cm). Comparison of both curves shows there is no spontaneous phase transition initialized by diffuse, thermal radiation emitted within the material, in this range of wave numbers and radiation temperatures
Rights and permissions
About this article
Cite this article
Reiss, H. Radiative Transfer, Non-transparency, Stability Against Quench in Superconductors and Their Correlations. J Supercond Nov Magn 32, 1529–1569 (2019). https://doi.org/10.1007/s10948-018-4833-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10948-018-4833-2