Stability Considerations Using a Microscopic Stability Model Applied to a 2G Thin Film Coated Superconductor

Abstract

A numerical, finite element simulation of local temperature fields, critical current and transport current distributions is applied to a 2G thin film coated high-temperature superconductor. The focus is on simulation of quenches originating from transport current locally exceeding critical current density. As in previous reports, a statistical treatment of superconductor parameters (critical temperature, current and magnetic field) is applied for this analysis; it shall take into account uncertainties possibly arising from shortcomings in conductor manufacture or during measurements of their properties. The results of the calculations are used as quasi-boundary (driving) conditions for a subsequent transient microscopic numerical stability analysis. Traditionally, stability analysis usually applies analytic stability functions that incorporate conventional, phonon-related timescales, t and disturbances. The question is whether decay of electron pairs and subsequent relaxation of the excited state to a new dynamic equilibrium carrier concentration, the “electron aspect” of the stability problem, under the same disturbances, proceeds on another timescale, t ^′. Is this timescale identical to the traditional (phonon) timescale, t? If not, how large are the differences? The recently reported microscopic stability model, now applied to a thin film conductor, is consulted to find an answer to these questions. A time limit, t _Quench, can be extracted from the simulations, as the time of immediate onset of a quench. This is a new approach in stability considerations since, conventionally, a temperature limit, T < T _Crit, is set as stability criterion. If electrical operation or cooling conditions cannot immediately respond to this challenge, the thin film superconductor, if this time limit is exceeded, will hardly be able to return to zero loss current transport.

1 Survey to the Stability Problem

A superconductor is stable if it does not quench under a disturbance, i.e. perform an undesirable phase transition from superconducting to normal conducting state. Traditionally, disturbances comprise conductor movement, absorption of radiation, fault currents or cooling failure. However, disturbances can also arise in case nominal transport current density exceeds critical current density. Stability models predict under which geometrical, thermal, electrical and magnetic field conditions quenches can be avoided to safely achieve zero loss transport current.

Traditional stability models rely solely on conduction heat transfer using analytical expressions, mostly for diffusion-like thermal transport. Numerical investigations, on the other hand, have been presented only recently (compare [1], with citations to the literature published since 1988); these investigations provide information also on local temperature fields and their impact on magnitude and distribution of critical and transport current and if radiation heat transfer would be taken into account.

Quenching proceeds on timescales, t, in the order of milliseconds or less. The temperature of a superconductor is usually measured with sensors thermally connected to filaments or to thin films by solid/solid or solid/radiative contacts. In the first case (solid/solid contacts), the results reflect the “phonon aspect” of the transient stability problem. The question is whether under increasing temperature initiated by the same disturbance, decay of electron pairs, the inner, “electron aspect” of the disturbance and thus of the stability problem proceeds on another timescale t ^′ and whether this timescale is identical with the traditional (phonon-related) timescale, t. Numerical simulations presented in this paper make an attempt to give an answer to this question, not on the basis of a standard solid/solid contact measurements taken at the superconductor surface but instead by means of a numerical analysis of transient temperature fields in the interior of the conductor.

Experience in previous studies has shown that mismatch between timescales t and t ^′ is expected near the phase transition. Mismatch may have significant impacts not only on superconductor stability or onset or decay of persistent currents: Normal/superconductor phase transition during warm-up or cool-down periods traditionally is considered to occur at exactly the instant when solid temperature, T(x,y,t), the phonon aspect, coincides with critical temperature, T _Crit. However, critical temperature overwhelmingly relies on the electron system of the solid. Critical current density, J _Crit(x,y,t), under the assumption t = t ^′ would become zero exactly at this instant. However, if both timescales would be different, it is not clear that after a disturbance, the electron system of the superconductor has already completed return (relaxation) to a new dynamic equilibrium.

At a very low temperature, the superconducting electron system is largely decoupled from the lattice and of its thermal transport processes. At any temperature, the superconducting electron system reflects its own dynamic response to disturbances or to other specific excitations, by corresponding relaxation times, τ _El. Thermal diffusivity, on the other hand, determines a relaxation time, τ _Ph, for the propagation of thermal (phonon) waves in a solid.

In a recently reported investigation [2], lifetimes of thermally excited electron states were calculated from their relaxation rates using a “sequential” model (it will be explained later why the model was given this name). The model serves to estimate the time τ _El needed to reorganise the electron system to a new dynamic equilibrium. Temperature of the electronic, or of any other system, can be defined only if relaxation is completed.

This model incorporates analogies from (a) an aspect of the nucleon-nucleon, Pion-mediated Yukawa interaction, (b) from the Racah problem (expansion of an anti-symmetric N-particle wave function from a N − 1 parent state) and (c) from the uncertainty principle. This will be explained later, also why it is reasonable to make reference to nuclear physics (specifically, the shell model).

In the present paper, a numerical finite element analysis of transient local temperature fields, T(x,y,t), of critical current and of transport current distributions is applied to a 2G thin film coated conductor; the conductor shall be used in a flat pancake coil. Focus is on simulation of situations close to a quench originating initially from transport current locally exceeding critical current density, a process that subsequently may lead to also Ohmic resistances, with strongly increasing losses.

The transient T(x,y,t) define the conditions under which the sequential model shall be applied; the T(x.y.t) can be considered as quasi-boundary or “driving” conditions for the subsequent microscopic stability analysis.

The paper is organised as follows: Section 2 describes finite element calculations of transient temperature distributions, T(x,y,t), in the coil using a 2G coated YBaCuO conductor. Sections 3 and 4 discuss application of the sequential stability model to the same conductor. The way to extract lifetime, τ _El, of the excited electron system is explained in Section 3. This serves to identify the timescale t ^′; we roughly have t ^′ = t + τ _El. We will calculate to which extent reorganisation of the disturbed electron system can be completed under given variations with time of temperature and transport current.

2 Temperature Evolution in a 2G Coated YBaCuO Conductor Close to Quench

2.1 General Aspects

Standard stability calculations following the Stekly, adiabatic or dynamic stability models derive results under quasi-stationary and, mostly, adiabatic conditions, for a survey see Wilson [3] or Dresner [4]. These and many other textbooks on superconductivity and its applications rely on homogeneous conductor temperature, like [5,6,7,8,9], to mention only a few. There are also countless theoretical and application-oriented papers that neglect temperature distributions in the conductors, compare e.g. [10], where distribution of transport current is considered as resulting solely from materials properties and interfacial resistances. Meanwhile, materials properties and interfacial resistances beyond doubt are of high importance for distribution of transport current; but the impact of temperature distribution, a condition of the same importance, is completely neglected in [10].

Such assumptions, at least in 1G conductors, e.g. those prepared in the powder in tube process, do not reflect reality; this was one of the main results of the summary reported in [1]. Instead, the item “temperature distribution”’ is most important for analysis of current transport processes: Differentiation between flux flow and Ohmic resistances can be made only with respect to temperature distribution in the conductor, which is important in particular when considering the potential of superconductors for current limiting. Flux flow resistivity occurs under the condition that conductor temperature is below its critical value. However, if conductor temperature is not strictly homogeneous, this condition may be fulfilled in only part of the conductor cross section while in other parts current limitation, if any, would be initiated by Ohmic resistances. This situation might give the current limiter a strongly different performance.

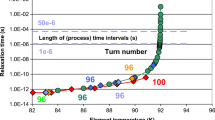
Figure 1 shows the overall simulation scheme of coil and conductor geometry (schematic, not to scale). It consists of (a) a coil with 100 turns of which in the following only turns 96 to 100 will be simulated. The superconductor in each turn consists of a 1 to 2 μm YBaCuO film, with a coating of the superconductor film by an Ag layer of about the same thickness. Thickness of the Ag layers is important for stability of the conductor against quench (and in the simulations, its thickness has been increased to 2 µm in order to expand the time interval during which temperature of the YBaCuO conductors under high load would quickly approach critical temperature). Interfacial resistances (Ag/superconductor and superconductor/buffer layer), each of thickness 40 nm, are indicated in diagram (c) of Fig. 1. This is a new approach for the description of obstacles against current sharing with the Ag coatings. Yet the overall 2G coated conductor architecture and its dimensions as indicated in Fig. 1 are standard (the THEVA conductor design, for example, is very similar, like coated conductors of AMSC, Bruker, Nexans, Sumitomo and others, but we have added interfacial layers into Fig. 1). The conductors are epoxy-impregnated, i.e. encapsulated in protective layers of casting compounds (thermal obstacles, not shown in Fig. 1) that significantly limit heat transfer in x- and y-directions to coolant. Details of the other diagrams will be explained later.

Fig. 1

Overall simulation scheme with coil and conductor geometry (schematic, not to scale). a Coil consisting of 100 turns of which turns 96 to 100 are simulated. b Layers in immediate neighbourhood of the superconductor (SC) thin film (as an example, in turn 99). c Detail showing the simulated, very thin interfacial layers between superconductor film and Ag (metallization) and between superconductor and MgO (buffer layer) in turn 99 (dimension of the roughness is highly exaggerated in this diagram). d Cross section and meshing of the superconductor thin film in one turn; it identifies line numbers 1 to 5 of which element temperatures are given in Fig. 4a, b. Superconductor layer thickness is 2 μm, its width is 6 mm, thickness and width of the Ag elements is the same. Crystallographic c-axis of the YBaCuO-layers is parallel to y-axis of the overall co-ordinate system. Thickness of the interfacial layers is 40 nm; dimensions of the other conductor components are given in Table 1. In SC, Ag and interfacial layers, we have 5 × 200 line divisions for creation of the finite element mesh. Conductor architecture indicated in this figure and dimensions, except for the inclusion of interfacial layers (solely for simulation purposes, diagram c), is standard. Comments received from THEVA are gratefully acknowledged

Trivially, it is to be expected that significant temperature differences will not be observed in thin films, except for possibly extreme load conditions, but there may be temperature differences between different (neighbouring) windings (turns) in the coil.

We analyse local electrical, magnetic and thermal properties of a thin film conductor in the present paper with respect to extended disturbances arising from an alternating nominal current of which its magnitude increased from 0.6 to 1 the ratio of critical current.

As before, the analysis is not intended as a design calculation for a pancake coil or for any other application. It concentrates solely on the physical aspects of the conductor itself and its response to strongly nonlinear operation conditions.

We will use thermal and electric/magnetic data of YBa CuO for the simulations. All materials properties (resistivity, thermal conductivity, critical current and critical temperature, critical lower and upper magnetic fields, anisotropies to transport phenomena) and Ohmic resistivity, used as input data to the superconductor simulation, are the same as used in previous reports (additional data needed for the present analysis is shown in Table 1).

Table 1 Additional data needed for the present analysis

The flux flow resistivity to axial current transport is calculated with the cell model very recently introduced in [1]. We have estimated the transport (weak link) properties of thin film YBaCuO material that generate resistance to transport of magnetic flux quanta (flux flow).

The thermal diffusivity, D _T, of YBaCuO is between 4 10⁻⁶ and 2 10⁻⁶ m ²/s, at temperatures of 77 and 120 K, respectively. For a periodic disturbance, in the present case initiated by flux flow and potentially also by Ohmic resistive losses and when taking a mean value of D _T, with the penetration depth δ(ω) = C (2 D _T/ ω)^1/2 of a thermal wave (Whitaker [11], p. 159), C a constant (taking for simplicity the C = 4.6 for a flat, semi-infinite sample), and ω = 50 Hz, we have δ(ω) ≈ 1600 μm, which is larger by orders of magnitude under sole conduction heat transfer than thickness of a thin film 2G conductor. Local temperature, T(x,y,t), of all volume elements in the superconductor thus will very quickly respond to any disturbance that propagates by thermal diffusivity. Temperature distributions within single YBaCuO layers in each turn, as long as losses are small, thus are homogeneous also because these layers (plus Ag and MgO) are encapsulated between components of smaller thermal conductivity (interfaces, solder, Hastelloy).

This expectation (homogeneous superconductor temperature) will later be confirmed; compare Fig. 4a, b; discussion thus can be concentrated on the temperature of the centroid (the centre of the conductor cross section) in the simulated turns. In order to keep the model as simple as possible, we will again not integrate radiative transport though the analysis deals with thin films.

Inductive and hysteresis losses as before have been estimated following traditional models from standard electro-technical literature. Again, inductive and hysteresis losses are small against their flux flow and Ohmic resistance counterparts.

A new concept introduced in [12] is to consider critical current density, critical temperature, upper critical magnetic field and the weak-link problem connected to flux flow (transport of magnetic flux quanta) as random variables: We neither expect 1G nor 2G superconductors as ideally structured and perfectly homogeneous materials. Instead, under realistic conditions, only part of a 2G thin film conductor is epitaxially grown; there is a large variety of possible misorientation of grains and grain boundaries with respect to current flow and magnetic field. There will be fluctuations also of chemical composition (impurities) and pores and cracks and many other obstacles to current transport, like superconductor/Ag and superconductor/buffer (solid/solid) interfacial layers.

Accounting for all imperfections neither can be realised by analytical nor by numerical modelling. A possible way-out of the problem is to treat the most important critical parameters (T _Crit, J _Crit, etc) as only statistically determined quantities, with random fluctuations around mean values; the method thus integrates all imperfections into a single quantity, and it can be specified separately for each temperature and magnetic field and for any position in the YBaCuO layers.

For this purpose, we have applied statistical variations like those reported in the Appendix to [12]; a schematic illustration of the method is provided in Fig. 2 of the present paper. In this model, critical current density and the other critical parameters of the superconductor and its weak-link resistivity against flux flow are different in each element while the traditional, analytic functional dependency on field and temperature, respectively, of all these parameters is that of the traditional treatment (but even this dependency might be different in each of the elements).

Fig. 2

This 3D diagram illustrates the region of existence of superconductivity (schematic, not to scale). The literature conventionally applies uniquely, i.e. sharply defined curves (dashed blue in this diagram) of T _Crit(B), J _Crit(B) and J _Crit(T) that connect conventional critical superconductivity parameters (open blue circles), see standard volumes on superconductivity; the dependence of T _Crit on B, J _Crit on B and J _Crit on T then is described by analytical (polynomial) expressions. In the present diagram, we instead assume statistical fluctuations (small black dots) of T _Crit(B), J _Crit(B) and J _Crit(T) against their conventional counterparts, in order to account for uncertainties that might arise from shortages in industrial, mass manufacture processes. In the present numerical simulations, the fluctuations are different for each of the 5000 superconductor elements, which means analytical expressions for their description are no longer possible. The thick black solid circles and the random distributions T _Crit(B), J _Crit(B) and J _Crit(T) (red curves, shown for only one single element jj) may significantly be shifted against the corresponding conventional critical values (open blue circles and dashed blue curves). But the shifts are exaggerated in this diagram

The 3D diagram in Fig. 2 indicates the region of existence of superconductivity (schematic, not to scale). The literature conventionally applies uniquely (sharply) defined curves (dashed blue in Fig. 2) of T _Crit(B), J _Crit(B) and J _Crit(T) that connect conventional critical superconductivity parameters (open blue circles). In the present diagram, we instead assume the statistical fluctuations (small black dots in Fig. 2) of T _Crit(B), J _Crit(B) and J _Crit(T) against their conventional counterparts, in order to account for potential uncertainties. The fluctuations are different for each of the (in total 5000) superconductor elements in the simulated five turns. The thick black solid circles and the random distributions T _Crit(B), J _Crit(B) and J _Crit(T) (red curves, shown for only one single element of the whole 5000), accordingly, are shifted against the corresponding conventional (traditional) critical values (open blue circles and dashed blue curves); the shifts are exaggerated in this diagram. Each of the superconductor elements thus provides its own 3D existence diagram (the red solid curves) to the calculations because temperature of each element and its exposure to an external magnetic field might be different.

Strictly speaking, no reliable quantitative information is available for variations of J _Crit of 2G thin film coated superconductors that would arise from materials imperfections or from experimental (measurement) uncertainties. As a worst case limit, we could refer to experimental reports obtained with 1G conductors [13]; these amount to almost 20%, but with 2G thin film conductors, the variations should be much smaller. The variations observed with 1G conductors also included experimental errors, but the electric field strength criteria meanwhile have been improved to below 0.1 µV/cm. Therefore, we have used a variation of ±1% as a standard in the calculations, and with ±0.1 and 10% variations for sensitivity tests of the results only.

2.2 Calculation Scheme

The overall numerical procedure, with the integrated finite element analysis, has been described in our previous papers (compare the references listed in [1] for details). The finite element simulation solely serves for solution of Fourier’s differential equation.

As before, a standard finite element (FE) program (Ansys 16) is applied; mapped meshing is used for creation of the large number of 2D plane elements (this means we assume uniform materials properties and solutions in the z (tangential)-direction of conductor (circumferential direction of the coil windings); compare Fig. 1, diagrams a–d). Shell elements cannot be used for simulation of the thin films because they, by definition, assume homogeneous temperature of the simulated object (an alternative, several layers of shell elements, would complicate meshing, not speed up the simulations, and plane elements provide more flexibility).

There are numerous reports on contact resistance measurements between high-temperature superconductors and Ag, compare e.g. [14], and between superconductors and other metals. However, applicability of the results to the present case is doubtful, since these investigations are concentrated on ideal flat structures, between pairs of identical or different materials, not on a pile of thin films where during deposition irregularities arising possibly in one surface might be transmitted from one thin film to the next.

Instead, interfacial layers and their electrical and thermal resistances have been assigned between superconductor (SC) and Ag, and between SC and buffer (MgO) layers, in all turns. As a new approach, each of these layers (basically a rough surface structure) is simulated as a thin materials solid layer (Fig. 1, diagram c), not as plane (2D) objects and, accordingly, will be meshed like the superconductor and the other solid conductor components. Compared with the application of locally unspecified surface resistances, the present method has the advantage that the resulting solid electrical resistances can be calculated as local quantities, for all contact pairs of superconductor/Ag elements that face each other and that are firmly bonded.

The interfacial layers shall account for possibly existing, isolated, point-like or extended solid/solid contacts, for uncontrolled variations of superconductor layer thickness, for only partial coverage of the superconductor film by Ag, or for voids close to superconductor surface that are filled with Ag during deposition. Compare the Appendix. All contaminations during preparation of the coatings and inter-diffusion between YBaCuO/Ag and YBaCuO/MgO will alter materials properties very close to a surface/surface solid contact.

With surface roughness, R, each in the order d _R = 10 nm, of polished Hastelloy and of MgO − and superconductor (SC) surfaces, thickness d _IFL of the interfacial SC/Ag and SC/MgO layers was estimated as twice the pair (d _R,SC + d _R,Ag) or (d _R,SC + d _R,MgO), i.e. d _IFL ≈ 40 nm.

When simulating thin films, large lateral size/thickness aspect ratios, r, are inevitable, in the present case r = 30/0.4 of superconductor and Ag elements, and r = 30 μm/8 nm of the interfacial layers. However, several tests performed with increasing r have confirmed that these ratios still are applicable, without introducing significant uncertainties in the transient temperature fields.

The total number of all (super- and normal-conducting) elements including insulations, buffer layers, solders and epoxy impregnations in the cross section of the upper five turns, is 65,000. The large number is intended to calculate the field T(x,y,t) in all materials as detailed as possible because all materials properties and their internal temperature fields are responsible for temperature distribution in the superconductor and in the interfacial layers.

We use the same data for boiling heat transfer as in our previous reports. At the solid/liquid interfaces to the coolant, temperature rise and oscillations of T(x,y,t) against constant coolant temperature again are small (quasi-thermal insulation against coolant is provided by epoxy impregnation of the conductors). No data were available for heat transfer to boiling nitrogen from polymer surfaces. Instead, stationary boiling heat transfer to nitrogen, on smooth metallic surfaces, has been applied provisionally; within the simulated periods, this lack does not cause significant errors.

Flux flow resistances are non-zero only if the magnetic field in the elements exceeds its lower temperature-dependent critical field, if the field is below its upper critical value, if element temperature is below critical temperature and, trivially, if transport current density exceeds critical current density. The local magnetic fields in the coil and at the elements of each of its turns are roughly estimated as made in [2], and again the Meissner effect is considered separately in each of the 5000 superconductor elements.

Transient distribution of transport current then follows from application of Kirchhoff’s laws. The results as before serve for re-calculation of all resistances that in turn create new current distributions, new transient losses and new temperature fields, and these are transferred to the next finite element calculation, with a finite time step, Δt, to obtain new resistances, current distributions, losses and temperatures, and so on.

The new current distributions obtained after a step Δt not necessarily would be the same as obtained in previous time steps; instead, the distribution may fluctuate, and the transport current percolate, through the superconductor and Ag cross sections. At the end of each time step, it has to be checked whether summation over all re-calculated local currents yields the same total current, to fulfill conservation of electrical charge including the Ag coating in case there is current sharing.

2.3 Convergence of the Results

A problem well-known in finite element analysis is to obtain convergence if the cross sections involve components of strongly different geometry like aggregates of thin films (thickness a few micrometer or even nanometers) and mechanically protecting layers (millimeter or centimeter), or if materials with strongly different thermal properties contribute to the total conductor cross section (ceramic superconductors, metals like Ag, Cu and Hastelloy, and polymers used as casting compounds and electrical insulations); all this has to be considered in the present case, see Table 1. Appropriate selection of integration time steps, ∂ t, to reduce computation time as far as possible, but without loss of accuracy, thus becomes difficult: At T = 107 K, the thermal diffusivity, D _T, of Ag coating, of interfacial layers and superconductor material are 2.365 10⁻⁴, 5.605 10⁻⁷ and 2.574 10⁻⁶ m ²/s; thickness dy of the corresponding elements is 0.4 μm, 8 nm and 0.4 μm, respectively. This calls for integration time steps ∂ t of below 4.23 10⁻¹¹, 7.136 10⁻¹² and 3.89 10⁻⁹ s (the estimates do not contain any radiation contribution to heat flow; they at least in the interfacial layers and probably also in the superconductors would further reduce the allowed ∂ t). Clearly, with respect to a limitation of computation time, the Ag and interfacial layers, not the superconductor, impose the most critical problems.

Within periods Δt of 50 μs and below, the ∂ t were settled to 10⁻¹⁶ ≤ ∂ t ≤ 4 10⁻⁹ s (the lower limit, 10⁻¹⁶ s, can reasonably be taken only during initial integrations). The upper limit, 4 10⁻⁹ s, guarantees that the approximate relation dy ≈ 3.6(D _T t)^1/2 will be observed in all conductor components other than Ag and interfacial layers where ∂ t = 4 10⁻⁹ s probably is too large. But this becomes critical only if one considers heat flow specifically in y-direction: Heat flow, however, is 2D, with element size in x-direction of 30 μm so that this ∂ t would be sufficiently small. On the other hand, the relation dy = 3.6 (D _T t) ^1/2 results from divergence of solely conductive heat flow, not of heat sources or sinks other than conductive; heat sources will appear in the interfacial layers only if there is current sharing. All this calls for convergence tests to be performed. With the limit ∂ t ≤ 4 10⁻⁹ s, a very large number of integration sub-steps, in each of the periods Δt, have to be expected.

The solution scheme applied sparse matrix direct solvers (requests large memory space; alternatives like JCG or ICG iterative solvers were tested but convergence is not guaranteed). As explained in [15], Fig. 4, the calculations yield a series of quasi-stationary solutions that are obtained at the end of the Δt. The Δt are large in comparison to characteristic diffusion times of electrical and magnetic fields, and they are large also against the time needed to establish a new dynamic equilibrium charge distribution except, and this will become important, for conditions very close to the quench; compare Section 3.

Convergence can be promoted by appropriate selection of tolerance criteria by which the program Ansys accepts solutions in each integration sub-step, ∂ t. For a representative temperature, say 100 K, the tolerance criterion in the present calculations was settled to between 10⁻¹² and 10⁻⁸. Even then (or with still smaller tolerances), convergence was hard to achieve when thermal load was very high; this regularly happens after transport exceeds critical current density and finally induces Ohmic resistances: The more one approaches the voltage maximum at t = 5 ms, the more will transport current density exceed the randomly defined critical current density distribution so that the number of elements in which losses are generated increases with time (compare Fig. 3). Increments (lengths of load steps, Δt) accordingly have to be chosen carefully not to ”capture” in one load step too many elements in which transport current already exceeds critical current density.

Fig. 3

Overall simulation scheme of transport current vs. process time, t (process time denotes the simulated time intervals); the figure is schematic, not to scale, and addresses only one of the 5000 superconductor elements, jj. The thick black horizontal line indicates the mean value of critical current, I _Crit, while the light-blue area describes upper and lower limits of statistical variations ± d I _Crit of I _Crit in the element jj; these variations may arise separately in each of the finite elements (the elements are not shown). As soon as the solid red curve I _Transp of transport current intersects the line I _Crit of any of the elements (as an example, at position A), flux flow losses are observed beginning at the corresponding time, t _A, in this element provided its actual temperature is below its own critical temperature (that again is subject to its own statistical variations d T _Crit). In the simulations, the statistical variations d I _Crit correspond to 0.1, 1 and 10% variation of critical current density, J _Crit. Only if there were no variations of I _Crit (strictly speaking: of critical current density, J _Crit), flux flow losses would not occur before the curve I _Transp hits or exceeds I _Crit at point B

If divergence occurred, temperature run-away (temperature below or above the interval 77 ≤ T ≤ 600 K) was observed always outside the superconductor thin film cross section. Divergence of superconductor temperature not necessarily relies on solely too high a load onto the superconductor elements but could follow from numerical instability related to poor local meshing, or to strong mismatch of materials properties between neighbouring elements, or in case of current sharing, from large heat losses in the Ag layers.

A typical observation of complete divergence is nodal temperature above 600 K or below coolant temperature (77 K).

The upper temperature limit (600 K) is arbitrary but the idea is that YBaCuO certainly loses its superconductor (chemical) materials and thus also its zero loss current transport properties if this limit is exceeded. Nodal temperature of the corresponding superconductor element then was fixed to 600 K in the next time steps. The element in total thus was assigned a large (Ohmic) resistance, which means, it was turned into a quasi-electrically insulating material, and the corresponding current transport channel through this element therefore was closed further on. Selection of this limit, as long as it is strongly above room temperature, according to experience has little or no impacts on the instant when breakdown of transport current occurs.

The same limit, 600 K, then is applied also at the nodes of all normal or non-conducting elements (Ag layer, buffer, insulations, etc). Again, this limit is arbitrary but prevents too large temperature variations in the total conductor cross section that would induce strong conduction or contact heat flow from non-conductor to superconductor elements; in this case, it might no longer be possible to identify an increased superconductor temperature as the result of losses induced by current flow in definitely these elements.

However, if nodal temperature was below 77 K, regardless whether the upper temperature limit was exceeded or not, at any position within the superconductor cross section, the solution was not accepted for the analysis in Section 4.

Computational efforts to cover all these items were enormous: On a standard 4-core PC and under Windows 7, a simulation period of only 5 ms took more than 24 h computation time, even when using the selected ∂ t = 4 10⁻⁹ s in only those periods where strong losses were expected; this was at about t = 4.3 ms after start (t = 0) of the simulations.

Like in previous studies, stagnation temperature, T(∞), was calculated before start of the simulations, in order to check the output of the finite element program against the analytical solution. For this purpose, we used temperature independent and isotropic values of thermal conductivity, λ, and specific heat, c _p. Coincidence between both solutions was found, usually at a time t = 10 ⁴ s after start of an arbitrary disturbance, at all internal positions of conductor cross section; the maximum temperature deviation in this test was below 10⁻²%. But in all following (proper) calculations, λ and c _p are treated as temperature-dependent and local (no longer isotropic) quantities.

2.4 Coil and Conductor Geometry

Coil geometry, cross section of the in total 100 and in the simulated upper five turns, details of conductor geometry and its composition are shown in Fig. 1a–d (materials properties are listed in Table 1).

Finite element 2D and 3D calculations reported in [16, 17] are not doubled by the present paper: The authors in [16] simulate electromagnetic behaviour of a coil at constant temperature, which certainly is only a very rough approximation. In [17], a 2D coupled electromagnetic-thermal model, in an overall H formulation of Maxwell’s equation, is applied to a stack of thin film coated conductors. The model takes into account temperature-dependent thermal and electrical properties, like in the present paper, but it does not take into account buffer layers, and thermal contact between tapes is assumed as perfect. These assumptions are questionable, and the entire (fine, well-formulated) model could be improved by a numerical analysis of local transient temperature and transport current distribution and by local materials properties. In the present simulations, exactly this has been realised, by a microscopic description of transient temperature fields, resistive states of the conductors, local current transport and materials properties, all items considered within cross sections of the conductors.

2.5 Results Obtained for the Temperature Fields

Figure 4a, b shows temperature distribution at t = 5 and 10 ms, under the condition that the ratio, I _Transp/ I _Crit, of transport to critical current is limited to 0.95 and the statistical variation, d _JCrit, of J _Crit is within only 1%. Transport current thus cannot exceed the value I _Crit −dI _Crit so that no current transport losses in the superconductor can be created; compare the scheme in Fig. 3. Obviously, temperature is very homogeneous in the thin 2G coated conductor films, as was to be expected, and also almost identical in neighbouring turns.

Fig. 4

a Superconductor element temperature in the coil, calculated at (process) time t = 5 ms, in lines 1 to 5 of each of the simulated upper five turns, vs. horizontal position (overall axial direction of the coil), x. Open diamonds and solid circles indicate results obtained for turns 96 (innermost of the simulated) and 100 (uppermost turn of the coil), respectively. Turns and element line numbers within each turn are explained in Fig. 1, diagram d. The centroid of the conductor is located in line 3 at position x = 6 mm. Results are calculated for the ratio I _Transp/ I _Crit = 0.95 of transport to critical current (where there are no losses from flux flow or Ohmic resistances) and using the data listed in Table 1. Statistical distributions of superconductor materials properties have been assumed in all of the superconductor elements. With the given ratio I _Transp/ I _Crit, temperature distribution within the conductor, in all turns, is very homogeneous: Calculated variations are in the order of only 10⁻⁸ K. The situation changes strongly when I _Transp/ I _Crit → 1, see next figures. The slight temperature decrease near x = 3 and 9 mm reflects heat transfer to the coolant. By the anisotropy factor X = 10, thermal diffusivity parallel to the x-axis is much larger than in radial (y-) directions where heat transfer additionally is partly suppressed by intermediate electrical insulation and interfacial layers. All curves are calculated with an electrical resistivity ratio ρ _NC,e/ ρ _NC = 10 ³ of the superconductor materials component in the interfacial layers; compare text for explanation of the cell model. b Superconductor element temperature, calculated as before (Fig. 4a), but at t = 10 ms, in lines 1 to 5 of the simulated upper five turns of the coil, vs. horizontal (overall axial) position, x. The ratio I _Transp/ I _Crit again is 0.95 of transport to critical current. Open diamonds and solid circles indicate results obtained for turns 96 (innermost) and 100 (uppermost turn of the coil), respectively. Curves 1 to 5 are still very close to coincidence

The situation changes significantly when the ratio I _Transp/ I _Crit approaches 1 (Figs. 5a–c and 6). In Fig. 5a, b, turns 96 (the innermost of the simulated) and 100 (the outermost turn of the coil), nodal and element temperatures, respectively, are plotted against time. Simulations were stopped at t > 4.3 ms because of serious convergence problems that could not be compensated even by more stringent tolerance restrictions. However, the obtained results are sufficient to understand what happens as soon as transport current approaches its maximum: When in Fig. 3 time, t, exceeds t _A, flux flow losses are generated in at least 1 of the 5000 superconductor elements, at exactly this element position. The losses will increase locally and, if this happens in a sufficiently large number of elements, lead to the quench of conductor and coil.

Fig. 5

a Superconductor nodal temperature of the centroid (of conductor cross section) in turn 96, vs. time, t (we have four nodes in each of the plane finite elements). The centroid is the central element of the conductor. Same calculation as in Fig. 4a, b but now with the ratio I _Transp/ I _Crit = 1 (and the asymmetry factor X = 5). A first quench of the centroid is observed beginning at t = 4.1 and again at t = 4.25 ms. The observed cool-down of nodal temperature beginning at t = 4.15 ms results from heat transfer and, since nodal temperature was increased to above 120 K, from breakdown of transport current (in the whole conductor) that switched off thermal (flux flow and Ohmic resistive) losses. The observed small temperature deviations among the four nodes within each of the 2D plane element indicate almost homogeneous element (centroid) temperature even when at t = 4.25 ms it increases very strongly. b Superconductor element (centroid) temperature (arithmetic mean of nodal temperature) in turns 96 (black and coloured symbols) and 100 (open diamonds), vs. (process) time, t. Same calculation as in Fig. 5a, with the ratio I _Transp/ I _Crit = 1 but with different asymmetry factors, X = D _ab/ D _c, of thermal diffusivity in crystallographic ab-plane and c-axis direction of the superconductor. In comparison to Fig. 5a (temperature differences within a specific element, i.e. the centroid), this figure shows temperature differences between same elements (the centroids) of different turns. When keeping X = 10 constant, the figure also illustrates the impact of thickness and of thermal diffusivity of the interfacial layers (IFL) on superconductor temperature: Black open circles refer to d _IFL = 40 nm (standard) and λ = 100 W/(m K), as a rough estimate made for the SC/Ag interfacial composite; red symbols denote d _IFL = 1 μm and λ = 1 W/(m K), as an extreme, hardly realistic case, and the light-green symbols are obtained with the same (increased) IFL thickness and 100 W/(m K), respectively. The red solid circles thus illustrate that the interfacial layers might thermally insulate the superconductor thin films, and superconductor temperature accordingly increases. c Nodal temperature calculated at time t = 4.2 ms. White dashed lines are part of the mesh (the inner block comprises turns 96 to 100; the narrowly spaced double white lines indicate electrical insulation between turns, and the outer double lines reflect a reinforcement of the casting compound). Superconductor temperature, in turn, 96 has already increased to a maximum of about 94 K, while in turn 97 to 100 temperatures are still close to coolant temperature. The symbols “MX” and “MN” denote maximum and minimum temperature within the total conductor cross section. In this figure, the asymmetry factor is X = 10

Fig. 6

Total transport current (I _Transp, open and solid diamonds) through the (whole) conductor and total critical current (I _Crit, solid circles), vs. time, t (the simulated time intervals). Results are calculated for different ratios I _Transp/ I _Crit using the same materials properties as before (Table 1). With I _Transp/ I _Crit = 1 (solid light-green diamonds), note the sudden decrease of I _Transp at t = 4.1 ms to almost zero and the simultaneous decay of I _Crit. At this instant, the temperature of (almost all) elements of turn 96 (not only of the centroid) under flux flow losses increases to exceed element critical temperature. Phase transition in each of these elements is responsible for large element resistances, all in parallel, and for large total resistance of the coil. With only a 0.1 or 1% statistical variation of J _Crit, there is still no breakdown of superconductivity even if the ratio I _Transp/ I _Crit is increased to 0.95. This is no longer fulfilled if higher percentages like the 10% in Fig. 7 would arise that might possibly result from tolerances or shortages in industrial conductor mass production

Figure 6 shows total transport current I _Transp (open and solid diamonds) through the coil and total critical current I _Crit (solid circles) in the centroid of turn 96, all vs. process time. Process time is the time used in the simulations, with stepwise increase by intervals Δt. Results are calculated for different (increasing) ratios I _Transp/ I _Crit using the same materials properties as before and the statistical variation of J _Crit again within 1%. With finally I _Transp/ I _Crit = 1 (solid light-green diamonds), we note the sudden decrease of I _Transp through the coil at t = 4.1 ms to almost zero and the simultaneous decay of I _Crit (with I _Transp/ I _Crit = 1, this would be observed under any of the statistical variations, not only with the 1% uncertainty). At this instant, the temperature of possibly a large number of elements (not necessarily the temperature of just the centroid element) of turn 96 under flux flow losses increases to exceed element critical temperature. Phase transition in each of these elements then is responsible for large element resistances, all in parallel, and for a large total resistance of the coil that under constant voltage leads to strong limitation of transport current.

As Fig. 6 shows, still within the statistical variation of 1%, there is no breakdown of superconductivity even if the ratio I _Transp/ I _Crit is increased from 0.6 to 0.95. This is no longer fulfilled if higher percentages, like the 10% in Fig. 7, are considered. Such strong variations of critical current have been observed in 1G conductors.

Fig. 7

Total transport current (solid diamonds) through the conductor, and total critical current (solid circles), vs. (process) time, t. Results are calculated for the ratio I _Transp/ I _Crit = 1 of transport to critical current using the same materials properties as before (Table 1) but now for different statistical variations of critical current density, J _Crit. These variations lead to different onset times of the sudden decrease of I _Transp (solid diamonds) to almost zero, as is obvious from the 10% variation of J _Crit that leads to a reduction of J _Crit (red solid circle) at already t = 4 ms, about 0.5 ms earlier than with a variation of 1 or 0.1%. Simultaneously, element temperature of turn 96 increases strongly to exceed element critical temperature with corresponding increase of total resistance of the coil and transport current breakdown (solid red line)

We have studied the impact on transport current limitation under a quench also for statistical variations of critical temperature (by ± 0.5 and 1 K), upper critical magnetic field (by ± 5 and 10 T) and the variation of the anisotropy parameter of thermal diffusivity, D _ab/ D _c = 5, 10 (standard) and 20, but these variations had no significant impacts on the onset of transport current breakdown.

In the following section, we will apply the calculated transient temperature fields, T(x,y,t), obtained close to a quench, to an analysis of relaxation of excited electron states to a new dynamic equilibrium. The results shall indicate whether the said difference between timescales t and t’ can be quantified also in the 2G coated conductor, if they exist at all.

3 Relaxation of Excited Electron States

3.1 Definition of the Wave Functions

The sequential model described in [2] now is adapted to the 2G coated conductor. Consider first relaxation of an arbitrary excited electron state:

Summation over the inverse of average lifetimes, τ _i, of an i th excited electron state, at a given constant temperature (T > 0), with the summation index, i, taken over all 1 ≤ i ≤ N _Exc (with N _Exc the number of thermal electron excitations), describes a relaxation rate (negative of the corresponding generation rate, G _Rel), of this state at a time t, per unit superconductor volume, V, as follows:

$$ G_{\text{Rel}} \left[ {T(t)} \right] = (1/V) \sum {\left\{ {\left[ {1/\tau_{\mathrm{i},\text{Rel}}} \right.\left[ {T(t)} \right]} \right\}} $$

(1)

Dimension of G _Rel[ T(t)] is [1/(m ³ s)].

The dynamic equilibrium between electron pairs and their excitations exists if relaxation of excited electron states to electron pairs, at temperature below critical temperature, on the statistical average compensates decay, and vice versa. Equation (1) essentially is identical to (3) in [18]; only a dependence on time of temperature, T(t), has been added. At constant temperature and for large time, t, the relaxation rate G _Rel[ T(t)] finally becomes constant and is equal to a corresponding excitation (decay) rate, G _Dec[ T(t)] so that the difference between both rates is zero (decay and relaxation of electron states originating from thermal fluctuations will not be not considered). At increasing temperature, in particular if it approaches critical temperature, the rate G _Rel[ T(t)] finally approaches zero.

Equation (1) can be written also in terms of relaxation by decay widths, Γ,

$$ G_{\text{Rel}} \left[ {T(t)} \right] = (1/V) \sum {\left\{ {{\Gamma}_{i,\text{Rel}} \left[ {T(t)} \right]} \right\}} /\left( {\mathrm{h}/2\pi} \right) $$

(2)

of statistically or of thermally excited states, with the usual definition, Γ _i = (h/2 π)/ τ _i , and the summation index 1 ≤ i ≤ N _Exc of the excited electron states (h denotes the Planck constant).

Thermal equilibrium is destroyed if, at a time t ₀, temperature is suddenly increased to T ₁ = T + ΔT, still with T ₁ < T _Crit; this is the case in the present simulations: The finite element calculations in the preceding sections yield temperature evolution, T(x,y,t) with increasing time under flux flow or Ohmic disturbances.

Under dynamic equilibrium, a total wave function, ψ(t ₀), or a set of individual wave functions, φ _i (t ₀), of which ψ(t ₀) is composed, describes the superconducting quantum state at an original time t ₀. A thermal disturbance, and the corresponding temperature increase, requires the original wave function to be rearranged to a new total wave function, ψ(t ₁), either at the end of a single disturbance (like sudden absorption of radiation) or, as in the present case, until the next variation (increase of temperature) is experienced. For relaxation of the excited state, the wave function, ψ(t ₁), of this state has to be re-arranged (relaxed) to a final wave function ψ(t ₂). Time t ₂ indicates completion of relaxation, and the difference, t ₂ – t ₁, accordingly is the lifetime, τ _El, of the disturbed (excited) electron state.

The question then is whether relaxation will be completed before the local heat source changes again (or whether τ _El is smaller than the corresponding time constant, τ _Ph, of the thermal transport processes). In other words, the question is whether the difference t ₂ − t ₁ is smaller than the length of the said process time steps, Δt, in the preceding finite element calculations.

For relaxation of ψ(t ₁) to the new total wave function ψ(t ₂), emphasis is on the whole set of the φ _i(t), not only of part of them, by which ψ(t ₂) has to be expanded. The situation is an analogue to calculation of “coefficients of fractional parentage” in atomic and nuclear physics, see e.g. [19], p. 333–338: If the anti-symmetric, total wave function of a nuclear state incorporating N of nucleons shall be formulated, it can formally be expressed by appropriate coupling of an anti-symmetric wave-function of (N − 1) nucleons with a one-particle wave-function. This yields a product:

$$ \psi \left( {N-1} \right),\,i,\alpha )x\phi_{i} (j) $$

(3)

with i and j indicating angular momenta; the symbol α summarises other quantum states to identify a number of N − 1 and one-particle configurations, respectively. The wave function of the N particle state still has to be anti-symmetrised. For this purpose, the wave function shall be expanded as a product of anti-symmetric wave functions of N − 1 single particle states. Addition of the one-particle state then requires re-arrangement of all previous N − 1 states to correctly obtain the new wave function, ψ(t ₂). The new wave function has to fulfil the Pauli exclusion principle, and the expansion coefficients (in the nuclear shell model) are the well-known Racah coefficients.

Re-arrangement of the total wave function cannot proceed instantaneously but requires a time interval, the total lifetime τ = (t ₂ − t ₁) > 0, of the disturbed system, before it has completed its return to a new dynamic equilibrium. The new anti-symmetric wave function, Ψ, is of the type

$$ {\Psi} = C \!\sum (-1)^{\mathrm{P}} P[\varphi (1,2) \varphi (3,4) \varphi (5,6)\textellipsis \varphi (N-1) \varphi (N)] $$

(4)

with P indicating permutations of the anti-symmetric pair wave functions φ(i,j). Regardless whether Ψ describes a ground state, like in (4), or an excited or a relaxed state, calculation of Ψ always involves a sum of individual permutations of the pair wave functions, φ(i,j). In the present case, each permutation is associated with a single relaxation step. Calculation of t ₂ − t ₁ thus involves a sum of individual contributions over single time steps, each corresponding to a single permutation in (4). The (total) relaxation time, t ₂ − t ₁, contains an enormous number of contributions and of their summations (Section 3.4) since the number of particles to be rearranged is very large.

3.2 Relaxation in Time and Space of Excited Electron States

We consider relaxation of the excited electron state under two different points of view: relaxation in (1) time and (2) in space.

Assume that a local disturbance (a temperature increase) occurs at a particular position x ^′ in the superconductor thin film and at a time, t ₀ (bold symbols denote vector quantities). At t ₁ > t ₀, we accordingly have at this position an increased concentration, c(x, t), of excited electron states over the previous equilibrium value.

The picture “relaxation in space and in time” then follows from the variation of the concentration c(x, t),

$$ dc(\textit{\textbf{x}},t)/\textit{dt} = (\partial c(\textit{\textbf{x}},t)/\partial x) (\partial x/\partial t)+\partial c/\partial t $$

(5)

which identifies the contributions “relaxation in space” = (∂ c(x, t)/ ∂ x) (∂ x/ ∂ t) and “relaxation in time” = ∂ c(x, t)/ ∂ t.

Because of propagation of a thermal wave in a superconductor solid or thin film,

(1) Relaxation in space means that the increased concentration, c(x ^′,t ₁ > t ₀), from any arbitrary position, x ^′, of excited states is distributed by a transport process to positions x ≠x ^′; a particular simple transport mechanism is diffusion.

(2) Relaxation in time means that the disturbed total wave function, ψ(x, t > t ₀), that describes all electron states, returns to equilibrium shape by relaxation processes, with the stagnation result ψ(x, t ₂).

Contributions from both items (1) and (2) have to be summed up to the lifetime, τ = τ _El, of the disturbed system.

Experience [2] has shown that contributions from relaxation in time to (5) is much larger than contributions from relaxation in space (modelling of the diffusion process); the latter contribution thus will be neglected in the following (a quantitative discussion of this item in a 1G conductor can be found in the Appendix to [2]).

Instead of using perturbation theory or time-dependent Ginzburg-Landau theory, we again use for item (2) an aspect of the Yukawa model of nucleon-nucleon interaction: A “time of flight” concept with a mediating Boson is considered as an analogue that can be used (of course with some caution) to describe binding of two electrons to a (Cooper) pair in a superconductor. The relaxation in time from practical reasons is divided into two sub-contributions:

(2a) Contributions Γ _{i j} by two arbitrary particles i and j in a superconductor unit volume that determine an “intrinsic lifetime” of the non-equilibrium state in this volume; it is the exchange of phonons that mediate binding interaction between single particles and that have to travel a non-zero distance between the particles concerned.

(2b) Contributions Γ_Rel = (h/2 π)/ τ resulting from the uncertainty principle, for the proper condensation (or relaxation) event, once the particles i and j are correlated (identified) in step (2a); this step generates one pair by relaxation of 2, then correlated, particles i and j.

For relaxation to one electron pair, each of the individual decay widths, Γ _{i j} , and Γ_Rel, contributes by about 10⁻¹² and 10⁻¹⁴ s, respectively, to individual life times τ _{i j} , for an energy gap of some tens of millielectronvolt. While these are very small contributions to total τ, there is a very large number of individual Γ _{i j} , and Γ_Rel, and correspondingly, τ _{i j} , that have to be taken into account so that the total lifetime, τ, of the total disturbed state may become quite large (this depends strongly on temperature).

Because of the Pauli exclusion principle (and again in view of the Racah-problem), calculation of total lifetime, τ, from the two contributions (2a) and (2b) has to proceed in a step-wise manner, with many, successively performed summations (Section 3.4); therefore, the model has been called the “sequential model”.

3.3 Transfer of the Model from Excited Nuclear to Electron States

The two contributions (2a) and (2b) to item (2) will now be estimated to find the individual lifetimes, τ _{i j} . We start with the contribution (2a):

For this approach, averages of the lifetime must be taken over a (virtual) volume V _C at all positions, x, within the thin film superconductor. Determination of the size of V _C is one of the critical points of the analysis because the number of electrons contained in V _C is very large and so is the number of permutations of the pair wave functions to be performed.

To determine V _C, assuming a spherical volume, we need its radius, r _C. A first, direct but very rough estimate for the ground state can be performed using the inter-particle distances, d = (V/ N)^1/3, with N the number of particles filling a sample volume, V. With the inverse of the electron density in high-temperature superconductors (ρ _El = 6 10 ²⁷/m ³), this yields a mean distance, d _m, between any two electrons of about 0.55 nm, or when taking only that part of the electrons that condense to electron pairs, a fraction of (1/10) of the total number, the mean distance increases to about 1.2 nm. This is about the coherence length of an electron pair in the ab-plane of high-temperature superconductors. This distance is small against the thickness (400 nm) of the superconductor elements in the preceding calculations.

A similar result is obtained from consideration of the Coulomb interaction within an again spherical cloud of volume, V _C, of the large number of electrons. The radius, r _C, of V _C shall be given by the condition that the Coulomb potential energy between two arbitrarily selected electrons i and j, E _C, is minimised and below the binding energy, 2 ΔE, of a single electron pair. The Coulomb energy amounts to

$$ E_{\mathrm{C}}(r_{\mathrm{C}})=\chi e_{i} e_{j}/(4\pi \varepsilon_{0} r_{\mathrm{C}}) \le 2 {\Delta} E(T) $$

(6)

with e _i and e _j denoting electron charge and ε ₀ the dielectric constant.

In metals, the effective Coulomb force is modified by screening. In the solid, the electrostatic (repulsive) Coulomb potential consists of (a) the repulsive interaction (interpreted as a mean field) and (b) the (attractive) positive ion charges in the solid. The two contributions are superimposed. In the simplest form, this can provisionally be simulated using the screening factor, χ, in (6) that essentially modifies the dielectric constant.

As explained [2], almost all electrons, N _El(t ₀) = (½) (ρ _El V _C)/10 contained within the volume V _C, in a rough approximation do not belong to S = 0, L = 0 but to S = 0, L = 2 spin and angular momentum states. Crystal imperfections and impurities could lead to false, s-wave-like charge distributions; this will be neglected by simply assuming perfect crystalline order, clearly outside the interfacial layers to Ag and MgO, and very clean materials in the same thin YBaCuO films.

Positions x _i , x _j of particles i and j, in one dimension, at time, t ≥ t ₁, are predicted in the following using random variables RND _i and RND _j , with 0 ≤ RND _i,j ≤ 1 applied to the r _C which yields the random distance d(t) = x _i (t) −x _j t) of particles before their condensation to electron pairs. Selection of a lower limit of d(t) does not have significant influence on the final results (the coherence length of YBaCuO in c-axis direction, was assumed for this limit).

As an alternative, results could be obtained also using the Thomas-Fermi potential, as was done in [2], with E _TF = E _C(r _C) exp(–r/ r _TF), with E _C(r _C) from (6), without the factor χ, and r _TF the scattering length. Literature values of r _TF are in the order of 0.5 nm, again very small against dimensions of the superconductor elements.

The volume V _C, i.e. the number of all electrons i,j contained therein, located at random positions x _i ,x _j , will be used for summations over all potential interactions (Section 3.4), and the distances, x _i −x _j , for an estimate of contributions, from a time of flight concept, to relaxation times.

The second information needed to calculate total lifetime τ of the excited electron system concerns the Boson that mediates correlation and binding of two electrons to a pair. As an initial approach, we consider an analogue to nucleon-nucleon interactions:

Nuclear forces (compare again [19]), are short-range saturation forces. In the Yukawa-model, the Pion (π), a Boson with spin zero, needs a time interval (in a rough picture a time of flight) of about Δt _π = 4.7 10⁻²⁴ s, much smaller than lifetime of charged Pions (about 10⁻⁸ s), to mediate the binding energy between two nucleons. This time interval is estimated from the uncertainty principle using ΔE = m _π c ², with m _π the rest mass of the Pion and c the velocity of light. It is not clear that its mass necessarily would be the rest mass of a free solid particle, but the range of the Pion-mediated nuclear binding force (the “uncertainty of the nucleon radius”), d = Δt _π c, is about 1.4 10⁻¹⁵ m, a value surprisingly close to the radius of the nucleon.

In the Deuteron, the only stable bound, two-particle nucleon system, we have a central binding force (plus a small electrical quadrupole moment) and a comparatively small binding energy so that the inter-particle distance between proton and neutron even exceeds the range of the nucleon/nucleon interaction force. This is in a surprising analogy to binding of electrons in the BCS-model: It is sufficient that there is a (negative) binding energy that even may be arbitrarily small.

There are of course differences between the three cases (nucleon-nucleon interaction, deuteron and electron pair): (a) In the deuteron, proton and neutron couple to a spin triplet (³ S ₁) state (parallel spins), and it is a free particle; (b) while the exchange Boson in the nucleon-nucleon interaction interacts between two solid particles, it does so only in the interior of a nucleus (we do not consider p-p or p-n scattering reactions); (c) in a superconductor, however, the exchange is between electrons, not between solid particles, with lattice vibrations that provide virtual Bosons to mediate exchange of energy and momentum.

But the other aspects of electron pair formation, (i) two particle interaction, (ii) a Boson (the phonon ω) as the (virtual) exchange particle and (iii) weakly bound, two-particle states, get electron pair formation in superconductors (strictly speaking, a method to estimate its duration with time), though only from formal aspects, at least marginally similar to its nucleon/nucleon analogue. An alternative comparison could be made with the two-electron system in the ⁴He atom, but this comparison formally suffers from the central potential that the electrons in superconductors do not experience.

Formation of both a nucleonic bound state and of an electron bound state (the electron pair) in this model then would proceed within a time interval (the time of flight, or lifetime, Δt _π or Δt _{i j} , of particular excitations, (i,j), respectively) that the corresponding exchange Boson (π or ω, respectively) needs to mediate the binding interaction. Instead of binding interaction, we may also say “correlate the corresponding single particles before their relaxation”. This is not a “recombination” of two previously separated electrons because any pair wave function, φ(i’,j’), of the relaxed state might not be identical with any original pair (i,j); it is not necessary that the candidates (i’,j’) would equal the (i,j).

The interval Δt _π accordingly is the lifetime of two uncoupled (but correlated) nucleons considered as virtually disturbed states before they “condense” to a bound two-particle state in a nucleus. In the same way, Δt _{i j} is the lifetime of two uncoupled (uncorrelated) electrons, the time interval that is needed for relaxation of the two electrons to a pair. When considering all Δt _{i j} of all electrons i and j in the volume V _C, their summation (Section 3.4), for re-arrangement of the total wave function at the new dynamic equilibrium state, delivers the needed time t ₂.

In both cases, Yukawa model of two nucleons, or electron pair, dividing the distance d(t) = x _i −x _j , by the velocity of the corresponding exchange Boson, v _Boson, gives a measure for the “lifetime of the interaction” and, if appropriately summed up over all particles in the volume V _C, the intrinsic part of the “lifetime of the disturbance”, τ = τ _El; this is to be identified with the term ∂ c(x, t)/ ∂ t in (5). The emphasis is on ”appropriately summed up lifetimes”: By (3), relaxations are not allowed to run in parallel.

Also the estimate of the contribution Γ_Rel is made according to an analogue from numerous examples reported in atomic, molecular and nuclear physics: Relaxation of excited states is made by application of the uncertainty principle:

$$ {\Delta} t_{\mathrm{1EP}} = (h/2\pi)/{\Delta} E_{\mathrm{1EP}} $$

(7)

with the binding energy (the energy gap), ΔE _1EP. The time interval, Δt _1EP, holds for decay of one electron pair (1 EP) to two excited electrons as well as for the present purpose, i.e. its reverse, namely relaxation of two excited electrons to one electron pair, with the condition that the (i’,j’) of the original pair not necessarily are identical with any (i,j) of the relaxed pair. The same applies to an arbitrary large number of electron pairs formed from particles contained in the unit volume V _C. With provisionally ΔE = 60 meV (at very low temperature), the contribution Δt _1EP amounts to about 10⁻¹⁴ s.

3.4 The Sequential Model

Finally, calculation of total lifetime, τ, requires contributions Δt _{i j} and Δt _1EP to be weighted by the number of allowed open relaxation channels. Weighing has to take into account the Pauli exclusion principle: As mentioned, after each relaxation step of two single electrons to a pair (i,j), the new wave function has to be defined (re-formulated) appropriately before the next re-arranging step may follow. This next step is allowed only if the Pauli principle is observed; this is the analogue to calculation of the coefficients of fractional parentage, Equation (3). Formation of the total wave function, ψ(t), thus cannot be completed before each permutation, P[ φ(1,2) φ(3,4) φ(5,6)… φ(N − 1) φ(N), of the (pair) wave functions, φ(i,j), of in total N particles contributing to the total sum, is taken into account (compare Equation (5a,b) in [2], for more explanations).

The maximum number N _Cor of possible correlations (between two potential candidates suitable for building one pair) therefore is to be determined from a total of N _Exc particles by the following:

$$ N_{\text{cor}} = N_{\text{Exc}}(t)!/[(N_{\text{Exc}}(t) - 2)!\ 2!] $$

(8)

The total time for mediating the exchange energy between all potential candidates i and j, each correlated to one individual electron pair (i,j) then, is obtained by summation over all N _Cor open correlation steps. Each contribution to Δt _{i j} (t), the time needed to re-arrange the total wave function, is given by summation over individual ratios (time needed for one correlation attempt), d(t)/ v _ω , with particle-particle distances, d(t), and v _ω the velocity of the mediating Boson. Again note that the excited electron system, during the re-arranging procedure, will not take just the very first particles “at hand” from an arbitrary sequence of all potential combinations!

Only when by this sequential procedure each of the two electrons i and j properly are identified (by the conditions s _i = 1/2, s _j = −1/2, l _i = 1, l _j = 1, and p _i = −p _j, namely at positions x _i (t), x _j (t) within V _C), the time interval Δt _1EP from (7) is added to Δt _{i j} (t) to yield ${\Delta } t_{ij}^{\text {Rel}}(t)={\Delta } t_{ij}(t)+{\Delta } t_{\mathrm {1EP}}$. The time interval ${\Delta } t_{ij}^{\text {rel}}(t)$ incorporates (i) (numerical) correlation and (ii) (physical) relaxation (index “rel”, i.e. condensation) of two electrons to one pair.

After formation of a number N _EP of electron pairs, we have N _Exc(t) = N _Exc(t ₁) − 2N _EP as the number of excitations to be used in (8) for the next selection of potential electron pairs, now from the reduced number N _Exc(t). This process is repeated until all N _El candidates still available in V _C are coupled to pairs, which means we have for the total time interval, Δt ^Total, needed to accomplish re-arrangement of the total wave function, a second summation:

$$ {\Delta} t^{\text{Total} }= \sum {\Delta} t_{ij}^{\text{Rel}}(t) $$

(9)

with the summation index running over 2 ≤ Δk ≤ N _Exc(t) in (9) using Δk = 2. It is clear that this procedure to calculate lifetime strongly differs from a particle picture (as for example applied in current injection experiments [17]); for completeness, the latter would have to include particle motions.

Computation time required to calculate the sum in (8) and (9) is enormous: For YBaCuO, at T = 90.5 K, we have N _El(t ₁) and N _cor in V _C in the order of 10 ⁴ and 10 ⁸, respectively, which means summations over a number of terms in the order of 10 ¹² contributions would be the consequence. A possible simplification of this problem was made in [2] (instead of calculation of d(t) from random positions x _i , x _j , mean values, d _m, of the inter-particle distance, d(t), were applied), but in the present simulations, summations were made using real, randomly defined particle positions and their distances, d(t).

When in YBaCuO, temperature T → T _Crit (92 K), all d(t) or d _m diverge, due to the dependence of ΔE on temperature, T, and thus of the radius r _C of the volume V _C. This result, divergence of d(t) and d _m, is indeed the familiar one: All electron pairs finally decay into single, uncorrelated electrons when (local) thin film superconductor temperature very closely approaches its critical temperature, separately in each element.

Summarizing the contributions from diffusion (relaxation in space) and sequential model (relaxation in time), we have for the total lifetime near the phase transition, in a good approximation, τ ≈ τ _El = Δt ^Total.

Total conversion rates, from N _Exc(t > t ₁) excited electrons located in the volume V _C to finally N _Exc(t)/2 electron pairs, by application of τ ≈ Δt ^total read

$$\begin{array}{@{}rcl@{}} G_{\text{Rel}}(t) &=& \textit{dN}_{\text{Exc}}/\textit{dt}\\ &=& N_{\text{Exc}}(t)/\tau \end{array} $$

(10)

For temperature clearly below T _Crit, the total volume of the thin film superconductor contains a very large number of single spherical cells, V _C, with the G _Rel in each cell being identical: The relaxation rates, G _Rel, calculated in (10)per unit cell volume yield also the relaxation rates of the whole thin film because relaxation will most probably, apart from differences resulting from variations of the temperature field, proceed in parallel in each cell (but in each cell, the summations as mentioned have to observe (3)). This means relaxation proceeds in parallel in just one of the finite elements of the thin film (element size is 400 nm × 30 μm, a cross section very large (but of homogenous temperature) compared to cross the section V _C, with a radius r _C in the order of 1 nm.

Relaxation times, τ = τ _El, that result from application of (9) are reported in Section 4 of the present paper. As is to be expected, the curves approach very large values when temperature T → T _Crit. In the extreme case, [ T _Crit − T(t)] → 0, and if temperature T in each interval Δt would be kept constant, it would take the superconductor indefinitely long time to allow relaxation to pairs of all of the increasingly large number of excitations.

But temperature T(x,y,t) within Δt is not constant (because losses increase steadily) so that the whole summation procedure has to be restarted at every new temperature variation. Since temperature increases, and with increasing temperature still more electrons would have to relax to pairs, the calculated relaxation times of the simulated quasi-stationary states thus are lower limits. They approach the real (transient) relaxation times the better the shorter the time intervals Δt (the load steps) and the integration time intervals (the ∂ t). At temperature levels not very close to T _Crit, the increase, ΔT, of element temperature in Fig. 5b between t = 4.1 and 4.15 ms (process time) amounts to about 60 K (blue diamonds and light-green triangles). In one integration time step, ∂ t = 4 10⁻⁹ s, this yields a corresponding increase ∂ T during this period of about 5 mK. Assuming T = 85 K, the difference ∂ T at this temperature level causes a difference between corresponding relaxation times (Fig. 8) of only 1.63 10⁻¹⁷ s. The difference between calculated quasi-stationary and transient relaxation times during integration accordingly is very small.

Fig. 8

Relaxation time (the time needed to obtain dynamic equilibrium in the centroids of turns 96 (light-green, lilac, orange and blue diamonds, respectively) and 100 (red diamonds), after a thermal disturbance originating from transport current density locally exceeding critical current density (the corresponding flux flow losses increase local conductor temperature and finally lead to a quench). The light-green, lilac, orange and blue diamonds refer to element temperature calcu- lated in the finite element simulation; dark-green circles are calculated for an arbitrary sequence of element temperatures. Differences of the calculated relaxation times originate solely from the random distances between two electrons in the volume V _C. As soon as element temperature exceeds 91.925 K, coupling of all electrons in this thin film superconductor to a new dynamic equilibrium can no longer be completed within the integration times (1 or 50 μs, indicated as length of process time intervals (lilac horizontal dashed lines) in this figure)

Then, can the relaxation procedures be completed within any of the intervals Δt? An answer to this question shall be investigated in the next section.

4 Application of the S equential M odel to the YBaCuO C oated C onductor

4.1 Relaxation Times and Rates

Relaxation time for constant element temperature, T, in the centroids of turn 96, after a thermal disturbance, is shown in Fig. 8 (light-green, lilac, orange and blue diamonds, respectively), and in turn 100 by the red symbols. Differences of the calculated relaxation times the between all symbols solely originate from the random distances between two electrons in the volume V _C.

As soon as element temperature exceeds 91.925 K, relaxation to a new dynamic equilibrium no longer can be completed within the given time intervals. The temperature 91.925 K results from the intersection of the three curves in Fig. 8 with the ordinate (integration time axis) at 1 or 50 μs (horizontal dashed lines). The intersection is observed at a time t _Quench. This time can be interpreted as a “time of no return”. After this time, in this thin film superconductor, a quench will inevitably proceed if in an application no immediate actions would be taken by experimentalists or automatically with conventional safety switches (and if no alterations of cooling conditions are possible). This is a new approach in stability considerations since it defines a time limit, while conventionally a temperature limit, T < T _Crit, is set as stability criterion.

Figure 9 shows relaxation time in the centroids of turns 96 and 100; this figure applies the same data as in Fig. 8 but the results are plotted vs. process time (instead of being plotted vs. temperature). In Fig. 9, temperature is close to the quench but still below T _Crit. The strong increase with time of the relaxation time in turn 96 is the consequence of (i) its more or less thermally insulated position within the coil (it is, contrary to the outermost turn, encapsulated between neighbouring turns) and thus (ii) its much higher losses (lower J _Crit but constant J _Transp) that it experiences near the quench.

Fig. 9

Relaxation time in the centroids of turns 96 and 100; this figure applies the same data as in Fig. 8 but the results, instead of being plotted vs. temperature, are in this figure plotted vs. (process) time (the simulated time intervals). Centroid temperature still is below T _Crit. The strong increase with time of the results in turn 96 is the consequence of much higher losses that the centroid experiences in this turn in comparison to turn 100, near the quench

The more the centroid temperature approaches T _Crit, the more electrons become uncoupled and the more time is needed for relaxation of the strongly increasing number of excited states. As a consequence, the relaxation rates are expected to decrease at element temperatures near T _Crit.

This is confirmed in Fig. 10 that shows relaxation rates (per unit volume) of thermally excited electron states in the centroids of turns 96 and 100 vs. (process) time (again the simulated time intervals). The much stronger decrease of relaxation rate in turn 96 originates from the strong increase, dT/dt, of centroid temperature, T; compare Fig. 5b.

Fig. 10

Relaxation rates (per unit volume) of thermally excited electron states in the centroids of turns 96 and 100, vs. (process) time, t. The much stronger decrease of relaxation rate in turn 96 originates from the strong increase, dT/dt, of centroid temperature, T, compare Fig. 5b. The more the centroid temperature approaches T _Crit, the more electrons become uncoupled and the longer periods is needed for relaxation of the strongly increasing number of excited states, in accordance with the increasing time needed for completion of relaxation shown in Fig. 9

4.2 Difference Between the Two Timescales

The strong increase of relaxation time near T _Crit in Fig. 8 suggests that like in the previous study ([2], Figs. 2a, b, 12a, b, and 13a, b), we again observe a temporal mismatch between timescales t (the phonon timescale) and t ^′ (the electron timescale). The scale t ^′, and thus the difference between both timescales, is not a constant but may be different in different regions of the superconductor. As long as temperature distribution within the superconductor remains homogeneous (only small losses), there will be no significant variations of t ^′ with position. Below 4.3 ms, this is fulfilled in the simulations (compare Figs. 4a, b and 5a). The difference between the two timescales will now be determined.

The difference t – t ^′ between both timescales, if it exists, is given by the period t _Crit – t _Quench, with t _Crit and t _Quench the times when the superconductor reaches temperatures T _Quench (the onset of the quench at T = 91.925 K) and T _Crit, respectively. During t _Crit – t _Quench, safe operation of superconductor equipment using this thin film conductor becomes questionable.

Progress of relaxation is shown in Fig. 11, i.e. the residual number, N _Res, of potential, still open, coupling interactions (subsequent sequential relaxation steps) within an integration time interval. Below T _Crit, the number 1 − N _Res accordingly is the number of relaxation processes that still have to be completed before the next temperature increase is simulated; the data in Fig. 11 refer to the interval Δt = 1 μs. When the number N _Res finally becomes zero, the number 1 − N _Res = 1 indicates that relaxation processes no longer can be realised; this is the normal conducting state.

Fig. 11

Residual number of potential (open) coupling interactions (“channels”, relaxation of electrons to pairs) within a given integration time interval (here 1 μs) during a quench. The figure shows the relative extent to which coupling can be completed before, after 1 μs, the next temperature increase is observed, to obtain a new dynamic equilibrium. As soon as element temperature exceeds the limit T _Quench = 91.925 K, all coupling channels become closed, and the electron system remains in a local, highly disturbed, dynamic non-equilibrium state (the curve is valid for any of the YBaCuO conductor elements, which means an electron temperature of this state cannot be defined). The difference between times t _Quench and t _Crit, at which the curve reaches temperatures T _Quench and T _Crit (light-green and red dashed lines), defines the length of a dead time interval (definite assignments of superconductor temperature not possible within this interval

Compared with [2], Eq. (15), the difference t − t ^′ in the present paper no longer relies on t − t ^′ = (d τ _El/dT) (dT/dt) Δt, with the first and second factors (derivative of τ _El with respect to temperature and derivative of superconductor temperature field, T(x,y,t) with real time). Instead the mismatch between scales t and t ^′ is calculated directly from the difference between time t _Quench and t _Crit:

From Fig. 11 and from the temperature evolution, T(x,y,t), of the centroids in turns 96 and 100 (Fig. 5b), the mismatch is extracted as 4.717 10⁻¹⁰ s and 3.702 10⁻⁸ s, respectively. The difference between in both turns results from the very fast increase of centroid temperature in turn 96, in comparison to turn 100. Mismatch in the thin film YBaCuO superconductor thus is very small, in accordance with the result found in [2], Fig. 12b, for a YBaCuO filament (approximately 4 10⁻¹⁰ s). In addition, it is contrary to the enormous mismatch found in a NbTi filament in the order of seconds! (Compare [2], Fig. 12a).

In a strict thermodynamic view, electron temperature, T _El, of whatever magnitude, or the temperature of any other energetic state of a many-particle system, cannot be identified if this state is not in its thermodynamic equilibrium. This means, as soon as element temperature exceeds the limit T _Quench, the electron system remains in a local, highly disturbed, non-equilibrium state. Temperature of this state, within the interval T _Quench < T < T _Crit or, correspondingly, within t _Quench < t < t _Crit, then cannot uniquely be identified.

Accordingly, there are open questions: Since there should be a bijective (one to one) correspondence between temperature and time, T(x,y,t), at any fixed position (x,y) within the conductor cross section, are we sure, again on a strict thermodynamic ground, that a timescale t’ in this time interval really does exist? Moreover, since critical temperature, T = T _Crit, should correspond to t’ = t _Crit that both obviously are interval limits, does this imply that even critical temperature might become meaningless? Or do we simply have to replace equalities T = T _Crit at t’ = t _Crit by T → T _Crit at t’ → t _Crit? (note that the equality sign is replaced by an arrow). If we approach T _Crit from temperatures below or from above? This requires more investigation.

5 Summary and Open Questions

We have simulated the evolution of transient temperature fields in the upper windings of a flat pancake coil. While temperature within the windings initially is very homogeneous, important temperature differences between neighbouring turns come up if transport current increases to values near critical current. We have again included statistical variations of the most important superconductor parameters (T _Crit, J _Crit, B _Crit, ratio of anisotropy); the applied statistical variations against a mean value of J _Crit are between 0.1 and 10%. If transport current is limited below the ratio I _Transp/ I _Crit = 0.95, there will be no quench provided there are no other disturbances that locally might increase conductor temperature. However, if the 2G coated YBaCuO conductor quenches, which with a statistical variation of 1% of J _Crit happens for ratios I _Transp/ I _Crit exceeding 0.95, the quench will be observed first in the inner turns of the magnetic coil.

Current transport through the inner superconductor windings then is limited immediately to the then given (residual) critical current. Current sharing with the Ag-layer might be observed. The outermost windings remain in superconducting state.

The calculated transient temperature evolution has served as input data to a sequential model to estimate the time needed for relaxation of the disturbed electron system to a new dynamic equilibrium (the time needed for completion of relaxation from excited states). A time limit, t _Quench, has been identified beyond which completion of relaxation is no longer possible. Only a limited number of electron pairs then remain available for current transport, which may cause safety problems in superconductor applications. This time limit accordingly appears to be the real onset of the quench. This is a new approach in stability considerations: Conventionally, a temperature limit, T < T _Crit, not a time limit, is set as stability criterion.

From the preceding analysis, it has to be expected that temporal mismatch occurs between timescales, t and t ^′, of which the scale t ^′ is not a constant but a local quantity that may be different in different regions of the superconductor cross section. The effect apparently is very small in the simulated thin film YBaCuO conductor but, as a previous analysis has shown, could be strong in NbTi at temperatures near conductor phase transition. The question is whether at times exceeding the limit t _Quench, temperature of the superconductor, strictly speaking, of its electronic states, can be indicated at all. This in addition might raise the principal question whether even the critical temperature is a uniquely defined quantity.

Appendix

For current sharing, transport current, if it exceeds critical current, has to overcome electrical (resistive) obstacles between superconductor and Ag. These obstacles are characterised by measurable electrical surface resistances; they usually are reported as per unit surface, with little or no spatial (x,z) resolution.

The surface roughness of the superconductor is very small provided it is deposited on almost perfectly smooth substrates and buffer layers; roughness of polished substrates (Ni alloys) and buffer layers like MgO of between 1 and 5 nm are reported in the literature, and the achieved critical current densities accordingly are very large. However, it is not clear that Ag after deposition will always completely cover the superconductor surface.

By analogy, heat flow from superconductor to the buffer layer is limited by obstacles, now between two hard materials.

All obstacles in the present simulations have been collected in one entity, namely, by modeling the interfacial layers as thin films. The problem shall be solved using solid 2D elements, not ideal 2D surface contact resistances. In the finite element mesh, electrical and thermal interconnection between neighbouring layers and their elements are handled by glueing neighbouring nodes. Compared with application of (locally unspecified) surface resistances, the present method has the advantage that the resulting solid electrical resistances can be calculated as local quantities, for all contact pairs (elements) that face each other and are firmly bonded.

The electrical resistance of the interfacial layers between superconductor and Ag is estimated again by application of the Russell cell model (compare [2] for explanations and citation to the original literature): Porosity of the interfacial layers (percentages of YBaCuO and Ag) is approximated roughly as 0.5, with open cell structure. During deposition, Ag penetrates into voids in the superconductor surface; thus the superconductor material (core) at right the solid/solid surface contacts can be imagined as embedded in a matrix (shell) of highly conducting Ag (this is the general idea of a cell model).

For application of the Russell shell model, the resistances of both components, superconductor material and Ag, have to be known. No information is available whether the YBaCuO materials component within the interfacial layers would safely remain in superconducting state, even if temperature in the layers is below nominal T _Crit. Inter-diffusion between YBaCuO/Ag and YBaCuO/MgO and other chemical disturbances might induce suppression of T _Crit, a result that yet could be critical for the present simulations. This is because we deal with situations very close to a quench.

The normal conduction electrical resistivity, ρ _NC,e, of the superconductor component in a highly complicated interfacial layer is certainly larger than the normal conduction resistivity, ρ _NC, of an epitaxially grown, c-axis oriented, thin film superconductor. Electric resistivity of the thin interfacial layers therefore is simulated using, for its superconductor component, the normal conduction value while for the Ag component the resistivity of highly clean Ag is applied.

Because of the high conductivity Ag, onset of a quench and breakdown of transport current through the superconductor does not decisively depend on interfacial layer thickness, d _IFL; this thickness at the most has indirect impacts on onset of transport current breakdown. This expectation is confirmed in Fig. 5b (compare the open black circles with the other curves).

Instead of application of the Russell shell model to also thermal resistances of the interfacial layers, we use in the standard expression R _Th = d/(λ A) variations of thermal conductivity, λ, and of cross section, A, for conduction heat flow, with constant layer thickness, d. Contrary to ρ _NC,e, no data for the thermal resistivity, ρ _NC,Th, are available that would correspond to its electrical counterpart of the same materials structures and composition (superconductor embedded in Ag) and at the same local contact positions. Therefore, we cannot apply the Russel cell model, but sensitivity tests using an effective thermal conductivity, λ, can be performed: Ratios d/ λ = 4 10⁻¹⁰ [m ² K/W] (standard) and 10⁻⁸ or 10⁻⁶ (for sensitivity tests) are applied in the calculations. Results are again shown in Fig. 5b.