Radiation Heat Transfer and Its Impact on Stability Against Quench of a Superconductor

Abstract

Stability functions are an important analytical/numerical tool for appropriate design of conductor geometry and dimensions to prevent conductor losses under a transport current. While standard stability calculations following the Stekly, adiabatic, or dynamic stability models apply purely solid thermal conduction mechanism and derive results under (quasi) stationary conditions, the present paper investigates if, and to which extent, also radiation heat transfer, in addition to solid conduction, can exert impacts on conductor stability. Further, the full transient conductor temperature evolution after a disturbance is calculated. The analysis applies an interplay between Monte Carlo radiative transfer calculations, to describe absorption of heat pulses and their distribution in the conductor, and a rigorous finite element method to calculate the resulting temperature field and stability functions. The results show that radiative heat transfer cannot be neglected in particular if periodic disturbances have to be considered that can arise, e.g., in a flux flow fault current limiter.

1 Survey

A superconductor is stable if it does not quench, i.e., perform an undesirable phase transition from superconducting to normal conducting state. A quench results from disturbances like conductor movement and corresponding transformation of mechanical into thermal energy, from absorption of radiation, fault currents or from momentary cooling failure. Disturbances frequently are transient, but there are also permanent disturbances like hysteretic losses. Stability has been investigated in the literature by stability models, like the simple Stekly or the more advanced adiabatic, dynamic, and intrinsic stability criteria; for a survey on these analytical stability models see, e.g., Wilson [1] or Dresner [2]. Numerical investigations of the stability problem were presented, e.g., by Flik and Tien [3] and Reiss [4].

Stability models predict under which conditions a transport current will propagate without losses through the conductor. For this purpose, all stability models correlate disturbances with corresponding temperature evolution of the superconductor, which in turn determines evolution of critical current density. Temperature and critical current thus depend on (a) magnitude and duration of a disturbance, (b) heat capacity of the solid, (c) heat transfer within the conductor, (d) conductor geometry, and (e) heat transfer to a coolant or to another conductor environment like electrical insulations or matrix materials in multifilament conductors. If conditions (a) to (c) and (e) are fixed, and the conductor, e.g., is of cylindrical cross section, the stability models allow prediction of the maximum conductor radius up to which zero loss transport current can be expected.

All traditional stability models rely on solely conductive heat transfer in the solids. The impact of radiation has not been included so far into stability calculations. This is the aim of the present paper: An investigation to which extent also internal radiative transfer, in addition to classical conductive heat transfer, could modify predictions of conductor stability. As will be shown, impacts from radiation can be substantial.

2 Overall Description of the Stability Calculation

The following numerical procedure relies on a recent investigation (Reiss and Troitsky [5]) how to obtain thermal diffusivity of transparent or semitransparent thin films when they are exposed to a short laser pulse impinging on their surface. This approach is quite different from the traditional method to obtain thermal diffusivity by the laser flash method (Parker and Jenkins [6], and a large variety of its modifications). Results reported in [5] for thin films show that radiation heat transfer may require significant corrections to standard methods for determination of thin film thermal diffusivity, in particular if periodic disturbances are considered (similar impacts must be expected form radiation when investigating stability of superconductors, simply because both rely on internal heat transfer and temperature evolution). Details of the numerical method will not be repeated here, just a short description is presented in the following, as far as it is applicable to the present stability problem.

3 Step 1: Monte Carlo Method

A Monte Carlo model is applied to determine spacial distribution and magnitude of a large number of internal heat sources, Q _int(x,y,t), that in the sample arise from absorption of radiation bundles. The bundles initially are emitted from part of the sample surface (the original disturbance) and later from interior positions. Distribution of the Q _int(x,y,t) depends on extinction properties of the sample material and the angle of emission. Magnitude of the Q _int(x,y,t) depends on the albedo of the material, which determines remission of residual heat pulses after each absorption event, and from the phase function of scattering. All items to determine the Q _int(x,y,t) are treated as random variables.

The Monte Carlo calculation solves the radiative transfer problem that constitutes the integral part of combined conduction plus radiation heat transfer.

4 Step 2: Finite Element Model

In the investigation of thin film diffusivity [5], total length, Δt _P , of the disturbance (a laser pulse) was 8×10⁻⁹ s. During Δt _P , all absorption, remission, and scattering events proceed by velocity of light. But propagation of a thermal wave, by conduction only, is much slower, by many orders of magnitude. The Q _int(x,y,t) accordingly can be considered as initial conditions to the subsequent thermal conduction problem. Thermalization of all heat sources, i.e., the original disturbance at target surface and the Q _int(x,y,t), was calculated in [5] by a rigorous finite element model using a standard finite element (FE) program, with solid thermal conductivity and specific heat taken as temperature dependent quantities, under quasiadiabatic conditions or under heat exchange with environment (escape of radiation from the sample volume prevents the problem to be strictly adiabatic). A radiative conductivity was added to the solid conductivity if optical thickness (total or spectral) permits this approximation, or the Rosseland mean is applied, to account for spectral variations of the extinction coefficient.

The finite element calculation step solves the differential part of the combined conduction plus radiation heat transfer problem (Fourier’s differential equation that contains no integral, i.e., radiative contributions).

5 Application to the Stability Problem

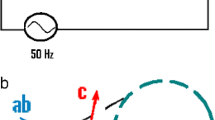
Basically, the same numerical procedures are applied to the present stability problem. Figure 1 schematically shows a section of a cylindrical conductor sample, a superconductor wire of 200 μm radius and of arbitrary length. A target spot (thick horizontal line at y=0) indicates location of an original disturbance. Radius of the target spot is r _Target=40 μm. Without loss of generality, the disturbance is modeled as a surface source (a disturbance of finite volume could be designed as well). Because of symmetry, only the region y≥0 (shaded) is modeled. Bundles (thick solid lines) are emitted from the target spot and from volume elements that are generated by rotating area elements k(i,j) around the vertical symmetry axis (x=0, dashed-dotted line).

Fig. 1

Section (shaded) of a superconductor wire schematically showing area elements k(i,j), cylindrical co-ordinate systems, (x,y) and (i,j), and radiation bundles (thick solid lines). The wire extends in y-direction; length of the wire is arbitrary. Because of symmetry around the target spot (the disturbance; thick horizontal line at y=0), only the region y≥0 (shaded) is modeled. Bundles are emitted from the target spot and from volume elements 1≤k≤1000 that are generated by rotating the area elements k(i,j) around the symmetry axis (dashed–dotted vertical line). Because of their finite mean free path, bundles after emission are multiply absorbed/remitted and/or scattered in the volume elements. With radii r _Target and r _Wire of target spot (40 μm) and sample (200 μm), respectively, dimensions of the shaded area are large in comparison to the radiative mean free path; see text. Full and open circles denote final absorption or scattering of the bundle, respectively. Scattering angle is denoted by θ. Bundles may escape from the sample (index Escape) after a series of absorption/remission or scattering interactions. In case bundles escape from the shaded section into positions x≤r _Wire, y<0, they contribute to temperature evolution at the lower positions of the wire (symmetric to the shaded region), and vice versa

It is sufficient to concentrate the investigations to a conductor length L=4 mm (the shaded region in Fig. 1); the optical thickness then is large enough to treat the radiation problem as a diffusion process, see below. Bundles may escape from the shaded region (index Escape) after a series of absorption/remission or scattering interactions. In case some bundles escape into positions x≤r _Wire, y<0, they contribute to temperature evolution at lower positions (symmetric to the shaded region) of the wire, and vice versa.

6 Data Input to Steps 1 and 2

The analysis is applied to YBaCuO, a high temperature superconductor with critical temperature T _Crit=92 K; it is assumed in the following the sample is a polycrystalline material.

At the axial position (plane) y=0, a single heat pulse of in total 0.2 mJ shall be distributed over the target radius, as a thermal disturbance again of Δt _P =8 ns duration; because of symmetry with respect to y=0, the shaded region experiences a heat pulse of half this value. The length Δt _P , the same as applied in [5], was chosen first to strictly avoid any superposition of the initial heat pulse with propagation of bundles and with solid conduction heat transfer, second to make results (temperature evolution, radiation heat transfer) of both analyses (thin film, stability of a superconductor) comparable.

We will for the moment assume temperature independent values of solid thermal conductivity, λ _S , and specific heat, c _p , of the superconductor YBaCuO. With the density, ρ, of this solid, we calculate energy balance and temperature evolution starting with an initial temperature, T(t=0)=77 K. This procedure simply serves to check whether meshing and time steps appropriately are chosen for the strongly non-linear FE calculation. As a result, the stagnation temperature, T(∞)=77.199 K, is exactly (within a difference of the order 10⁻⁷ K) reproduced by the FE-model, at a time t=10⁴ s after start of the disturbance, at all internal positions of the conductor volume. Isotropic conductivity and specific heat, mapped meshing and time steps of at least 10⁻¹² s were used in this initial calculation. No radiative heat transfer is included in this preliminary step (here, the problem is strictly adiabatic).

But in all following calculations, λ _S and c _p are treated as temperature dependent quantities; these data are the same as used in [7] (see references cited therein) where time dependence of levitation under the Meissner–Ochsenfeld–Effekt was modeled. This data set will in the following be referred to as a standard input (or “standard model”), as it reflects present, standard procedures to consider stability of superconductors, under solely solid conduction heat transfer. The solid thermal conductivity, λ _S , in the following calculations also takes into account anisotropy of conductive heat transfer in YBaCuO, in directions parallel or perpendicular to the crystallographic ab-plane of this material (like in [7], an anisotropy factor of 10 has been applied in the calculations).

Extinction coefficients, E [m⁻¹], needed for the Monte Carlo and FE calculations, define the mean free path, l _m =1/E, of infrared photons (bundles) that are emitted from the target surface and from all positions within the sample. The l _m determines location of the radiative volume sources, Q _int(x,y,t). After each absorption event along the path of the bundle, the magnitude of the Q _int(x,y,t) decreases until the bundle energy is completely extinguished. The total number of bundles is 5×10⁴ which in Figs. 3 and 4b in [5] proved to be sufficiently large to justify a diffusion model approach to the radiative transfer problem.

Extinction coefficients, E, depend on temperature and on wavelength, Λ, in particular with respect to location of the energy gap of a superconductor. While this in principle requires spectral values of E to be used in the Monte Carlo calculations, we will instead apply mean values of E taken in an interval between Λ _max(T) and Λ _min(T), respectively. This approach is justified as follows:

Figure 2a shows Λ _max(T) and Λ _min(T) of the black body thermal wavelength spectrum in dependence of sample temperature, T. Maximum nodal temperature at central front position (x=0,y=0) does not exceed 550 K; see later (Fig. 3). Accordingly, wavelengths Λ<Λ _max(T) are located almost entirely below the wavelength, Λ(2ΔE)=155 μm, that corresponds to the energy gap, ΔE, of the superconductor. A value ΔE=4 meV has been assumed for YBaCuO. Radiation from the tail of the black body spectrum is sufficient for pair breaking only if T>350 K. At lower temperatures, for all Λ>Λ _max(T), the fraction that does not contribute to pair breaking, in relation to the total emissive power of the black body spectrum, is below 6% (Fig. 2b). The corresponding extinction coefficients accordingly can be neglected from the Monte Carlo calculations, in a good approximation.

Fig. 2

(a) Maximum and minimum wavelengths, Λ _max(T) and Λ _min(T), of the black body spectrum (solid diamonds) that is emitted from the target spot after absorption of a heat pulse, Q=0.2 mJ within 8×10⁻⁹ s, in dependence of temperature, T. The thick horizontal line denotes wavelength, Λ(2ΔE)=155 μm, corresponding to an energy gap, ΔE=4 meV, of the superconductor. Radiation from the tail of the black body spectrum is sufficient for pair breaking only if T>350 K. Solid circles, plotted for orientation only, denote the wavelength Λ _i,max(T) at which black body radiation intensity, i(Λ), has its maximum (Wien’s displacement law). (b) Fraction (per cent) of total black body intensity emitted at wavelengths greater than Λ(2ΔE)=155 μm, in dependence of temperature

Fig. 3

(Color online) Nodal temperature at central front position (x=0, y=0) when the wire (its shaded region, Fig. 1) is exposed to a thermal disturbance (a single heat pulse) of Q=0.1 mJ deposited during 8 ns in the target plane (0≤x≤r _Target, y=0). Temperature evolution is calculated by the finite element model following a Monte Carlo simulation of absorption/emission and scattering events in the wire. Data are given either for solely solid thermal conduction (solid black circles) or for conduction plus radiation heat transfer under different values of the extinction coefficient, E (solid diamonds), respectively

In terms of wave numbers, v, it is then sufficient to find a mean value of the extinction coefficient in the interval between v(2ΔE) and v(Λ _min), i.e., 65<v≤3666 [cm⁻¹], respectively, in the superconducting state for investigation whether a quench can be avoided, in the normal conducting state to find out how quickly sample temperature returns to values below T _Crit. In both temperature regimes, the extinction coefficient enters the Monte Carlo calculations (the integral aspect) by stepwise reducing the total bundle energy (absorption) and by redirection of the bundles (scattering) while in the finite element calculations (the gradient aspect of the combined radiation and conduction problem), the extinction coefficient enters the calculations via a radiative conductivity λ _Rad (compare standard volumes on radiative transfer or Eq. 25a,b in [5]). The optical thickness, τ=EL, of the sample must be large, otherwise the approach λ _Total=λ _S +λ _Rad is not valid. With sample thickness L=4 mm, this is safely fulfilled with all E≥10⁴ m⁻¹.

Estimate of the extinction coefficients is described in the Appendix. Fortunately, mean values of E, and thus the numerical analysis is little sensitive to spectral values of E at wavelengths near Λ _max (Fig. 2a) because spectral intensity of the black body radiation at wavelengths close to this value is already very small.

Accordingly, extinction coefficient and also albedo, Ω, are assumed as independent of wave length (gray materials), with Ω=0.5 to account for scattering contributions to radiation extinction in a polycrystalline YBaCuO material. To account for anisotropic (forward) scattering, an anisotropy factor, m _S =6, has been applied; this factor (compare [5], Eq. 22) defines the scattering phase function (a value m _S =2 would indicate almost isotropic scattering).

7 Temperature Evolution After the Disturbance

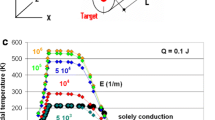
As a result, Fig. 3 shows calculated nodal temperature evolution, T(x,y,t), at the central position of the target spot (x=0,y=0) for the thermal disturbance Q=0.1 mJ released from the target spot to the shaded region in Fig. 1. Results are presented for extinction coefficients 5×10³≤E≤10⁶ m⁻¹ (the reason for practical limitation of the series to finally E=10⁶ m⁻¹ is explained below).

First, the higher the extinction coefficient, the higher the temperature at this position. This finding is in analogy to the results obtained in [5] for materials like Graphite, SiC, or ZrO₂. The absorption coefficient, A=(1−Ω)E, focuses distribution of remitted radiation (bundles) the more closely to the sample surface (x=0) the larger the extinction coefficient, E, and the larger the anisotropy factor, m _S , for constant albedo. Spatial distribution of the heat sources Q _int(x,y,t) obtained for increasing E is described in Figs. 3 and 4a–c in [5]. For the focusing effect exerted by the factor m _S compare the distribution of the Q _int(x,y,t) in Fig. 25 in [5]. Scattered radiation does not contribute to the temperature evolution. That T(x=0,y=0,t) for E≥10⁴ m⁻¹ is larger than obtained with the “standard model” (solely solid thermal conduction) thus can be explained by forward scattering.

Fig. 4

(Color online) Element temperature, T _El (x,y,t) at the time t=0.1 ms after start of the disturbance (Q=0.1 mJ deposited in the target plane of the shaded region in Fig. 1 during 8 ns). Results are given for different axial and radial distances from the coordinate origin (x=0, y=0 in Fig. 1). Black solid circles refer to solely conduction, solid diamonds to conduction plus radiation heat transfer using E=10⁴ m⁻¹

Second, all curves shown in Fig. 3 (and also temperatures at other positions) converge

• (a) to the same stagnation temperature: Contrary to the standard method (solely solid conduction), some radiation is lost simply because of the finite values of E and by multiple scattering that allows some bundles to leave the sample volume, e.g. to positions outside its radius or in forward or backward axial directions. The T(∞) for small E accordingly must be below the value T(∞)_St achieved with the standard method (77.199 K) but increase with E (the larger E, the smaller the losses if albedo, Ω, is constant). This is confirmed by the present results: T(∞) increases from 77.143 to T(∞)_St if E is increased from 5×10³ to 10⁶ m⁻¹, which in turn indicates the losses are small,

• (b) to the same T(x,y,t) at the position (x=0,y=0) for t≥10⁻⁸ s, i.e., after end of the heat pulse. This means it is sufficient to stop the series of calculations with increasing extinction at E=10⁶ m⁻¹.

Element temperature, T _El(x,y,t), the average taken over element nodal temperatures, T(x,y,t), is shown in Fig. 4, at the time t=0.1 ms after start of the disturbance (Q=0.1 mJ deposited in the target plane during 8 ns). Results are given for different axial and radial distances from the coordinate origin (x=0,y=0 in Fig. 1). For solely conduction, we observe almost constant T _El(x,y,t) within radial distances from origin of 0≤x≤20 μm because the disturbance is uniformly distributed over the target spot. Instead, from the strongly anisotropic forward scattering phase function, the results obtained from conduction plus radiation heat transfer are the more focused to small radial distances the smaller the axial distance from the disturbance.

Different temperature profiles must lead to different predictions of superconductor stability. This follows immediately from the temperature dependence of critical current density, J _Crit. This dependence provides a single-valued mapping of the temperature field, T _El(x,y,t) to the field J _Crit(x,y,t), if there is no magnetic field.

The temperature dependence of J _Crit(T) can be modeled as

$$ J_{\mathrm{Crit}}(T) = J_{\mathrm{Crit}}(T=0) \biggl[1 - \frac{T}{T_{\mathrm{Crit}}}\biggr]^{n}$$

(1)

The theoretical Ginzburg–Landau value of the exponent n in (1) is 3/2. From experimental investigations of high temperature superconductors, however, the exponent neither is independent on the method of preparation (thin films, substrate and its microstructure, 1G and 2G wires) nor is it identical for all temperature regions below T _Crit (quantum creep, flux line core pinning or thermally activated depinning regimes; see the results reported by Djupmyr [8]). Values of the exponent n for thin films are between 1≤n≤3 (Djupmyr [8] or Janus and Kus [9]), a value n=2 was found for intergranular critical current in ceramic Bi-2223 samples prepared in a solid-state reaction (Garcia-Fornaris et al. [10]) as well as in Bi-2223 single crystals (Chu and McHenry [11]), and n=2 was also obtained in a 2G YBaCuO-wire (Youssef et al. [12]).

Accordingly, the value n=2 should be applicable for the present purpose. Assuming J _Crit(x,y,t=0)=J _Crit(T=77)=10⁵ A/cm² of YBaCuO in zero magnetic field, this fixes J _Crit(T=0).

At positions close to the origin, J _Crit will be zero in both cases (T>T _Crit at these positions), but the larger the distance from the origin (and the larger time, t), the larger J _Crit, in strict correspondence to the transient temperature field T(x,y,t) This is reflected in the stability function, Φ(t).

8 Results of the Stability Function

The stability function applies the ratio J _Crit(x, y, t)/J _Crit(x, y, t=0) of transient critical current densities to critical current density at t=0,

$$ 0 \leq \varPhi(t) = 1 - \biggl(\frac{1}{A}\biggr) \int \frac{J_{\mathrm{Crit}}(x,y,t)}{J_{\mathrm{Crit}}(x,y,t=0)}\, dA \leq 1$$

(2)

with the integral taken over the conductor cross section, A, at an axial position, y. The ratio J _Crit(x,y,t)/J _Crit(x,y,t=0) gets Φ(t) close to zero if J _Crit(x,y,t) is close to J _Crit(x,y,t=0), in other words, if the temperature field is not seriously disturbed from its initial values. In this case, almost the whole conductor cross section remains open, with high critical current density, to zero loss transport current flow. However, if T _El(x,y,t) becomes close to T _Crit, J _Crit(x,y,t) is very small at these positions, and Φ(t)→1; zero loss current transport current flow then is hardly possible (in a sufficiently strong magnetic field, flux flow resistance will come up).

In order to determine whether a particular conductor cross section meets the stability criterion expressed by (2), the stability function Φ(t) has to be determined for all axial positions (planes) y, or as suggested in [3], as a worst case assumption, the maximum of Φ(t) has to be considered, to safely design the conductor cross section for zero loss current transport (its radius or, for a rectangular conductor cross section, its aspect ratio).

Figure 5a shows Φ(t) for pure solid conduction (black solid circles) or conduction plus radiation heat flow (solid diamonds), at axial distance (plane) y=100 μm from the origin, in dependence of time, for solely solid conduction or conduction plus radiation using different extinction coefficients. Because it is a rather small thermal disturbance, magnitude of the Φ(t) curves is below 0.3.

Fig. 5

(Color online) (a) Stability function, Φ(t), calculated from element temperature evolutions, T(x,y,t), when the wire (shaded region in Fig. 1) is exposed to a thermal disturbance of Q=0.1 mJ deposited in the target plane (y=0) during 8 ns. Results are given at the plane y=100 μm (or distance from the disturbance, a target of 40 μm radius positioned in the plane y=0). The stability function is calculated using (2). A critical current density, J _Crit=10⁵ A/cm² at T=77 K is applied. (b) Zero loss DC transport current, at the corresponding critical current density, J _Crit(x,y,t), through the plane (distance to the disturbance) y=100 μm. Data are calculated from the stability functions given in Fig. 5a

Zero loss DC transport current, I _Transp, is given by

$$ I_{\mathrm{Transp}}(t) = J_{\mathrm{Crit}}(x,y,77~\mathrm{K}) \bigl[1 - \varPhi(t)\bigr]$$

(3)

for all times, t≥0. Deviations from the undisturbed zero loss transport current (Fig. 5b) in the plane y=0 observed at t=5 ms yet become significant: For the standard input, the reduction of zero loss I _Transp at this position is from (undisturbed, t=0) 126 to 88 A (black solid circles) while the dip is from 126 to 97 A if also radiation and E=10⁶ m⁻¹ is taken into account (yellow solid diamonds), a difference by about 10%. This is larger than fluctuations in J _Crit that can be tolerated for safe superconductor performance (fluctuations of this order have been observed in 1G wires and are assigned to conductor inhomogeneity).

But the results shown in Fig. 5a, b constitute the worst case to be expected from the single pulse: At deeper axial conductor positions, on the planes y=300 and 500 μm where the disturbance almost has decayed, deviations of zero loss transport current (Fig. 6a, b) from the undisturbed value are significantly smaller (from 126 to 106 or to 103 A, for solely conduction and conduction plus radiation, under E=10⁶ m⁻¹, respectively).

Fig. 6

(Color online) (a) Stability function, Φ(t), as before calculated from element temperature evolutions, T(x,y,t), using (2). Same input data and calculation as in Fig. 5a but at the planes y=300 (solid symbols) and 500 μm (open symbols). (b) Zero loss DC transport current, at the corresponding critical current density, J _Crit(x,y,t). Same input data and calculation as in Fig. 5b but through the planes y=300 (solid symbols) and 500 μm (open symbols)

From the small stability functions shown in Figs. 5a and 6a, a first impression is that hot spots hardly will arise in the conductor as long as transport current will be limited to the above reported values. However, the stability function, an integral view taken over the whole conductor cross section, does not reflect local high temperatures observed near conductor central front position (Figs. 3 and 4): Nodal T(x=0,y=0,t) and element temperature quickly exceeds critical temperature if after a disturbance radiation significantly contributes to internal heat transfer. It will be shown in the following that radiation may have even more serious impacts on conductor stability in case of periodic disturbances.

9 Results Obtained for a Periodic Disturbance

The target spot of the cylindrical sample (Fig. 1) now is exposed to an intensity-modulated energy pulse Q(t) under a frequency of ω=10⁵ 1/s. For the source, we assume

$$ Q(t) = Q_{0} \sin(2\pi \omega t) + Q_{0}~[\mathrm{J}]$$

(4)

with a very small Q ₀=2×10⁻⁹ J; half of this value is experienced by the shaded region in Fig. 1. The small Q ₀ was taken in order to keep temperature evolution during a simulated time interval of 0.1 ms small, to continue calculations with the same temperature dependent values of conductivity and specific heat of YBaCuO as before (the impact of radiation on internal heat transfer and stability can be demonstrated also with such a small source, as will be seen in the following figures).

The large frequency was chosen to clearly separate between penetration depth of the thermal wave, δ(ω), and the mean free path of the incoming radiation, l _m =1/E. The diffusivity, D _T , of YBaCuO at T=80 K amounts to about 4×10⁻⁶ m²/s. Using for the moment an extinction coefficient E=5×10³ m⁻¹ constant (the comparatively small value is taken just to explain the principle), we have from δ(ω)=C(2D _T /ω)^1/2, with C a constant (C=4.6 for a flat, semiinfinite sample)

Penetration depth of the thermal wave, and thus variations of the stability function in relation to its undisturbed value (Φ=0 at t=0) thus would be restricted to a thin layer of only about 40 μm below the periodically heated surface if there is only solid conduction. But generation of volume power sources, by absorption of radiation emitted from the target spot, is expected, on a statistical average, at least up to a depth of 200 μm. Accordingly, periodic variations of Φ should be observed, at least within this depth.

Penetration of a periodic thermal disturbance applied to the surface of a semiinfinite, solely solid conducting sample (y=0) shows two characteristic items:

• (i) exponential damping of the temperature amplitude, T(x,y,t) by a factor exp[−y(ω/2D _T )^1/2],

• (ii) a phase shift, χ=y(ω/2D _T )^1/2 that increases with depth, y.

Assuming the same predictions approximately apply also to a sample of finite thickness, we will check it by means of the nodal temperature evolution for the center of the target spot (x=0,y=0), again for standard (purely conductive) and conductive plus radiative conditions, respectively. To reduce computer time, we have in the following restricted the calculated periods of time to in total 10 full oscillations (thus total simulated time t=10⁻⁴ s). A stationary state cannot be reached neither within this nor within any other period because we have neglected all possible surface heat sinks (radiative or convective losses to the conductor environment, with the exception that few bundles may escape from the conductor volume). But the simulated period of time of 10⁻⁴ s is long enough to demonstrate the enormous differences that arise between the standard assumption (solely conduction) and the conductive plus radiative case.

Figure 7 (nodal temperature evolution at central front positions) demonstrates that items (i) and (ii) of the above allow to clearly distinguish between the pure conductive and the conductive plus radiative case also with large extinction coefficients:

• (i) While a temperature oscillation at central front position (x=0,y=0), under solely conduction (solid black circles) still can be identified, it will heavily be damped to a tiny temperature amplitude at the depth y=500 μm (see later, Fig. 10). Any significant variation of the temperature field would be made obvious by the behavior of the corresponding stability function and of the zero loss DC transport current. The phase shift, under solely conduction, at this deep position is so large that it exceeds the simulated time interval.

• (ii) Under conduction plus radiation, the temperature amplitude (solid diamonds in Fig. 7) can become much stronger if E increases, and the oscillation of the temperature field and, correspondingly, of the phase function (see below), is clearly maintained, as is to be expected from the distribution of the volume power sources, Q _int(x,y,t), that almost instantaneously reflect the periodic variation of the radiative energy source located at the plane y=0.

  Fig. 7

  

  (Color online) Nodal temperature, T(x,y,t), at central front position (x=0, y=0), under periodic thermal load, compare (4). Data are given for solely solid thermal conduction (black solid circles) and conduction plus radiation (solid diamonds), respectively

Figures 8a, b and 9a, b show stability functions and zero loss DC transport currents at different axial distances (planes) from the origin. Both quantities are much smaller than those that were obtained with the single pulse, because of two reasons: (a) the very small amplitudes of the periodic disturbance, in relation to the amount of the single pulse, (b) the short simulated time interval. At y=100 μm (Fig. 8a), pure solid conduction dominates among the different stability functions, and the reduction of zero loss transport current (Fig. 8b) through this plane remains small, from 126 to 120 A for solely solid conduction, or from 126 to 122 A for conduction plus radiation, at the end of the simulated period of time. At y=300 and 500 μm (Fig. 9a, b), the deviations between the two cases become almost negligible.

Fig. 8

(Color online) (a) Stability function, Φ(t), calculated from element temperature evolutions, T(x,y,t), under periodic thermal load. Results are given at the plane y=100 μm using (2). A critical current density, J _Crit=10⁵ A/cm² at T=77 K is assumed in the calculation of Φ(t). (b) Zero loss DC transport current, at the corresponding critical current density, J _Crit(x,y,t), under periodic thermal load, through the plane y=100 μm

Fig. 9

(Color online) (a) Stability function, Φ(t), calculated from element temperature evolutions, T(x,y,t), using (2), under periodic thermal load. Same input data and calculation as in Fig. 8a but at the planes y=300 (solid symbols) and 500 μm (open symbols) that are large in comparison to the penetration depth of the periodic thermal wave (about 40 μm at a frequency of 10⁵1/s). (b) Zero loss DC transport current, at the corresponding critical current density, J _Crit(x,y,t), under periodic thermal load. Same input data and calculation as in Fig. 8b but at the planes y=300 (solid symbols) and 500 μm (open symbols)

Fig. 10

Zero loss DC transport current through the plane y=500 μm, which is of at least one order of magnitude larger than the penetration depth of the thermal wave, at the frequency 10⁵ 1/s. The figure serves to confirm that variations of the transport current with time are negligible, which means variations of stability function and temperature field must be negligible as well, if considering solely solid thermal conduction (black open circles). Also, a phase difference also can no longer be identified from the black open circles, on this time scale. The opposite result (periodically fluctuating, finite amplitude, even at this distance from the disturbance) is observed for the case conduction plus radiation heat transfer (open diamonds), because of the comparatively large radiation mean free path of the bundles, l _m =100 μm resulting from E=10⁴ m⁻¹

Does this imply propagation of a transport current will not be disturbed seriously by a single or a periodic thermal disturbance? By no means, by two reasons: First, it is clear from Figs. 3 and 7 that superconductor temperature very quickly exceeds critical temperature, and the temperature rise will continue if the period of time of the periodic disturbance would be extended. Second, the stability functions do not reflect run-off of local conductor temperature under conductive plus radiation heat transfer. They cannot exclude conductor damage if strongly forward scattered radiation would significantly contribute to thermalization of a disturbance.

Such a situation can arise in a superconducting, flux flow fault current limiter that protects electrical installations in an AC grid. Here, of course, the frequency of any period disturbance is much smaller so that the penetration depth of the thermal waves, if a period disturbance would exist, is much larger. But the essential point is not coupled to the thermal wave propagating under solid conduction only. It is the radiative aspect that has to be considered: In such a current limiter, flux flow resistance will periodically rise to a maximum, during the period where fault current, J _Fault, exceeds critical current density, J _Crit, and decrease to zero when this condition is no longer fulfilled; then the conductor line again is open to the fault current if it still exists. In the usual design of a fault current limiter, the superconductor volume is large enough to compensate conductor flux flow resistance losses by its increased thermal capacity so that the conductor shall not enter the Ohmic resistance region. But there may be resistances other than by flux flow, e.g., contact resistances between conductor length sections that would initialize periodic losses during those periods where J _Fault<J _Crit. Generation of hot spots and corresponding losses then can arise not only at the exact location of the contact resistance. A means to avoid this situation is by installation of a conventional switch that positioned in line to the fault current limiter interrupts the conductor line before hot spots would be generated. But the question is how safely a conventional switch that like the stability function takes an integral view of the temperature field can resolve periodically fluctuating local disturbances.

10 Summary and Conclusions

We have studied the impact of radiation heat transfer on temperature evolution and predictions of the stability function for zero loss DC transport current in a high temperature superconductor. The numerical analysis is based on a complicated interplay of Monte Carlo simulations of radiation bundles emitted from a target surface (the disturbance) and absorbed within the conductor volume and a rigorous finite element analysis to calculate the resulting temperature profiles in a thin superconductor wire. The calculations are performed either for the standard, purely conductive case, or for conduction plus radiation heat transfer under different constant extinction coefficients, in an absorbing and anisotropically scattering, poly-crystalline material. It follows from the analysis that small stability functions cannot safely exclude local conductor damage if radiation would significantly contribute to thermalization of a disturbance in a conductor. This becomes even more serious if periodic disturbances are considered. Long-living, periodic disturbances like in a flux flow current limiter, under conduction plus radiation heat transfer, not only could lead to local conductor damage but they also might quickly close all open channels for zero loss current transport.

Appendix

If not available from transmission measurements, extinction coefficients for the superconducting and normal conducting states can be estimated from literature values of spectroscopic measurements of reflectivity and corresponding Kramers–Kronig analysis. From the large variety of reflectivity measurements with high temperature superconductors reported in the literature, we in the following apply results from Kamarás et al. [13] and Chen for YBaCuO [14]. First, Kamarás et al. [13] showed that the mid-infrared absorption is a direct electronic absorption, with an onset at 140 cm⁻¹ in YBa₂Cu₃O_7−δ . The authors find that absorption across the gap is weak because the investigated high-T _c materials was in the clean limit, and this weak absorption is masked by the mid-infrared absorption. Chen [14] then applied a two component mode for the dielectric function. Figures 3.13 and 3.17 in this reference exactly cover the region of wave numbers to be considered in the present paper. From the complex optical conductivity for optimally doped YBaCuO, σ=σ ₁+iσ ₂, a mean value of the extinction coefficient, E=4πk/Λ, in the order of 10⁷ m⁻¹ in the superconducting state at a mean Λ=50 μm has been estimated on basis of the usual relations n ²−k ²=ε ₁ and 2nk=ε ₂=2σ/ω, with k the imaginary part of the index of refraction, ε _1,2 the real and imaginary part of the dielectric constant, and ω the frequency. In the normal conducting state, the spectral response of the optical conductivity, in particular at small wave numbers, is clearly different. Both real and imaginary parts of the optical conductivity are definitely smaller than in the superconducting state (the imaginary part by at least an order of magnitude). This means also the extinction coefficient is reduced, to a mean value of about E=5×10⁶ m⁻¹ taken over the same interval of wave numbers. Also, note that the analysis in [14] was applied to thin film samples prepared by pulsed laser ablation from a stoichiometric YBaCuO-target onto SrTiO₃ substrates. For the wire modeled in the present paper, we instead expect a polycrystalline material with smaller extinction coefficient than the values obtained from the optical conductivity reported in [14] (the absorption coefficient, A, is definitely smaller, but there will be some scattering contributions, S=ΩE, to the total extinction coefficient).

Accordingly, Monte Carlo calculations were performed for the series 5×10³≤E≤10⁶ m⁻¹. If the series would be continued up to E=10⁷ m⁻¹, the mean free path, l _m , of the bundles between two interactions becomes very small, l _m =0.1 μm, and the optical thickness, τ, of the sample in y-direction accordingly very large, τ=4×10⁴. Such a large number of absorption/remission and scattering events would very strongly increase computation time in the Monte Carlo analysis to unacceptably long periods of time (this extends to the order of days on a PC under Windows XP using a 3.8 GHz processor and 4GB work space).