Fixed-time synchronization of competitive neural networks with proportional delays and impulsive effect

Abstract

This paper investigates the fixed-time synchronization problems for competitive neural networks with proportional delays and impulsive effect. The concerned network involves two coupling terms, i.e., long-term memory and short-term memory, which leads to the difficulty to the dynamics analysis. Based on Lyapunov functionals, the differential inequalities and for the objective of making the settling time independent of initial condition, a novel criterion guaranteeing the fixed-time synchronization of addressed system is derived. Finally, two examples and their simulations are given to demonstrate the effectiveness of the obtained results.

1 Introduction

In recent years, various neural networks (NNs) such as cellular neural networks, Hopfield neural networks, bidirectional associative memory neural networks, and competitive neural networks have been extensively studied in both theory and application, and they have been successfully applied to signal processing, pattern recognition, associative memory, optimization problems, [1,2,3,4] and multiscale modeling [5,6,7,8]. For example, the authors in [5] present an artificial NNs-based multiscale method for coupling continuum and molecular simulations. In [6], the authors investigated the development of a neural network approach in conjunction with molecular dynamics simulations.

One of the popular NNs is competitive neural networks (CompNNs) which is introduced by Cohen and Grossberg [9] in 1983. Recently, Meyer-Bäse [10] proposed in 1996 the so-called CompNNs with different time scales. So, CompNNs with different time scales are extensions of Hopfield neural networks [11, 12], Grossberg’s shunting network [13] and Amaris model for primitive neuronal competition [14], which model the dynamics of cortical cognitive maps with unsupervised synaptic modifications. In the model of CompNNs, there are two types of state variable: that of the (STM: short-term memory) describing the fast neural activity and that (LTM: long-term memory) describing the slow unsupervised synaptic modifications.

Recently, the study of the dynamics of delayed CompNNs has been widely studied due to their important theoretical significance. On the other hand, much attention has been devoted to analyzing the synchronization of CompNNs, for example, Lou and Cui [15] studied the exponential synchronization of CompNNs by using the Lyapunov functional method and linear matrix inequality techniques. In [16] the authors introduced an adaptive feedback controller to show the complete synchronization of CompNNs with different time scales and stochastic perturbations by using the Salle-type invariance principle. By using stochastic analysis approaches and designing adaptive feedback controller, Gan et al. [17] investigated the exponential synchronization of stochastic CompNNs with different time scales, mixed time-varying delays.

In addition, time delays particularly time-varying delay can be encountered in the implementations of NNs, and the existence of time delays occurs in the response and communication time of neurons. So, it is very important to introduce the dynamics of artificial neural networks with delay [18]. Note that the delays are used in NNs models, coefficients are often constant, and delays are bounded. Contrary to the distributed delay [19,20,21] are the bounded time-varying delay [22,23,24,25,26,27,28] and the constant time delay [29]. The proportional delay $\tau (t)=(1-q)t$ (pantograph delay factor q is a constant and satisfies $0<q<1$) is time-varying, less conservative, unbounded and more widely applied in real world [30].

On the other hand, in view of the importance of the control for delayed NNs, finite-time synchronization requires the master and the slave system remain completely identical after some finite time, which is called the “settling time” [31, 32]. The problem of finite-time synchronization of CompNNs is studied in [33, 34]. In [33], the authors investigated the finite-time synchronization of CompNNs with mixed delays and non-identical perturbations by using Lyapunov–Krasovskii functionals. Note that the settling time in [33] is dependent on the initial values of the coupled CompNNs.

In [34], the authors studied the finite-time synchronization of delayed CompNNs with discontinuous neuron activations by using the theory of differential inclusions, inequality techniques, nonsmooth analysis and a generalized finite-time convergence theorem and the settling time is dependent on the initial conditions. So, in practical applications, the initial conditions of the NNs must be given in advance, which limits practical applications since the knowledge of initial conditions may be difficult to adjust or even impossible to estimate [35]. To avoid this problem, we define a new concept known by the name “fixed-time stability” which was studied in [35, 36]. Fixed-time synchronization means that the system is globally finite-time synchronized and the settling time is bounded for any initial states, that is to say that the convergence settling time is independent of the initial conditions.

Motivated by the above discussions, in this paper, we study the fixed-time synchronization of CompNNs with proportional delays and impulsive effect by using Lyapunov functionals and inequality technique. Based on the fixed-time convergence theory, we establish some new and useful sufficient conditions on the fixed-time synchronization of the addressed system. The proposed controller in this paper can be used to practically secure communication with chaotic nodes, i.e., sender and receiver. The main contributions of this paper are listed as follows: (1) Sufficient conditions are obtained to guarantee that the CompNNs with proportional delays can be synchronized in fixed time; (2) the settling time of the synchronization is bounded for any initial states; (3) from the viewpoint of time delay, CompNNs with proportional delays are different from delayed CompNNs models in [33, 34], so those results in [33, 34] cannot be directly applied to the system given in this paper; (4) it is shown theoretically and numerically that the designed feedback controllers are effective. The rest of the paper is organized as follows. In Sect. 2 we will present the model of CompNNs with proportional delays. In Sect. 3 we will introduce some necessary definitions and lemmas, which will be used in the paper. In Sect. 4 some sufficient conditions are derived ensuring the fixed-time synchronization results. In Sect. 5 an example and their simulations are given to illustrate the effectiveness of our theoretical results. In Sect. 7 we give a brief conclusion.

2 Model description, notations and hypotheses

For convenience, let ${\mathbb {R}}$ denote the set of real numbers. ${\mathbb {R}}^{n}$ denotes the set of all n-dimensional real vectors (real numbers).

For any $\{x_i\}=(x_1,x_2,\ldots ,x_n)\in {\mathbb {R}}^{n}$, $\Vert x\Vert$ is the square norm defined by $\Vert x\Vert =\big ( \sum\nolimits_{j=1}^{n}x^2_i\big )^\frac{1}{2}$. For a bounded and continuous function h(t), let $h^+$, $h^-$ be defined as

$$\begin{aligned} h^+=\displaystyle \sup _{t\in {\mathbb {R}}}h(t),\quad h^-=\displaystyle \inf _{t\in {\mathbb {R}}}h(t) \end{aligned}$$

Consider the following competitive neural networks with proportional delays:

$$\begin{aligned} &{{\text{ STM }}}{:}\;\varepsilon x'_i(t)=-a_i(t)x_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)f_j(x_j(t))\\ &\qquad\qquad\qquad+\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)f_j(x_j(\theta _jt))\\ &\qquad\qquad\qquad +\,B_i(t)\displaystyle \sum _{j=1}^{n}y_jm_{ij}(t)+I_i(t),\\ &{{\text{ LTM }}}{:}\;m'_{ij}(t)=-{\tilde{e}}_i(t)m_{ij}(t)+y_jf_i(x_i(t))+J_i(t)\\ &{\text{ STM} }{:}\;\varDelta x_i\setminus _{t=t_k}=x_i(t_k)-x_i(t_k^-)=-p_ix_i(t_k)\\& {{\text{ LTM }}}{:}\;\varDelta m_{ij}\setminus _{t=t_k}=m_{ij}(t_k)-m_{ij}(t_k^-)=-q_im_{ij}(t_k)\end{aligned}$$

(1)

where $n\ge 2$, $t\ge t_0$ $i,j=1,2\ldots ,n$, $x_i(.)$ is the neuron current activity level; $m_{ij}(.)$ is the synaptic efficiency; $a_i(.)$, ${\widetilde{e}}_i(.)>0$ are the time variable of the neuron; $b_{ij}(.)$ and $c_{ij}(.)$ represent the connection weight and the synaptic weight of delayed feedback between the $i{{\text {th}}}$ neuron and the $j{{\text {th}}}$ neuron, respectively; $y_j$ is the constant external stimulus; $f_j(x_j(.))$ is the output of neurons; $I_i(t)$, $J_i(t)$ denote the external inputs on the ith neuron at time t; $B_i(.)>0$ is the strength of the external stimulus; $\theta _j$ are proportional delay factors and satisfy $0<\theta _j<1$ and $\theta _jt=t-(1-\theta _j)t$, in which $(1-\theta _j)$ correspond to the time delays required in processing and transmitting a signal from the $j{\text {th}}$ cell to the $i{\text {th}}$ neuron, and $(1-\theta _j)t\rightarrow +\infty$ as $t\rightarrow +\infty$; $\varepsilon$ is a fast time scale decided by STM and $\varepsilon >0$, $x_i(t^+_k)=\lim _{t\rightarrow t^+}x_i(t)$, $m_{ij}(t^+_k)=\lim _{t\rightarrow t^+}m_{ij}(t)$, $x_i(t^-_k)=\lim _{t\rightarrow t^-}x_i(t)$, $m_{ij}(t^-_k)=\lim _{t\rightarrow t^-}m_{ij}(t)$. For simplicity, it is assumed that $x_i(t^-_k)=x_i(t_k)$ and $m_{ij}(t^-_k)=m_{ij}(t^k)$, which means $y_i(t)$ and $Z_i(t)$ are left continuous at each $t_k$. The moments of impulse satisfy $t_1<t_2<\cdots<t_k<\cdots$ and $\lim _{k\rightarrow +\infty }t_k=+\infty$. In this paper, taking $\varepsilon =1$ for convenience. After settling $S_i(t)= \sum\nolimits_{j=1}^{n}y_jm_{ij}(t)=m_i(t)^Ty$, where $y=(y_1,\ldots ,y_n)^T$, $m_i(t)=(m_{i1}(t),\ldots ,m_{in}(t))^T$ then (1) can be written as

$$\begin{aligned} &{\text{ STM }}{:}\;x'_i(t)=-a_i(t)x_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)f_j(x_j(t))\\ &\qquad\qquad\quad\, +\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)f_j(x_j(\theta _jt))\\ &\qquad\qquad\quad\,+\,B_i(t)S_i(t)+I_i(t)\\& {\text{ LTM }}{:}\;S'_{i}(t)=-{\tilde{e}}_i(t)S_i(t)+|y|^2f_i(x_i(t))+J_i(t)\\ &{\text{ STM }}{:}\;\varDelta x_i\setminus _{t=t_k}=x_i(t_k)-x_i(t_k^-)=-p_ix_i(t_k)\\& {\text{ LTM }}{:}\;\varDelta S_{i}\setminus _{t=t_k}=S_{i}(t_k)-S_{i}(t_k^-)=-q_iS_i(t_k) \end{aligned}$$

(2)

where $i,j=1,2\ldots ,n$, $|y|^2=y^2_1+y^2_2+\cdots +y^2_n$ is a constant without loss of generality, the input stimulus y is assumed to be a normalized vector with unit magnitude $|y|^2=1$, then (2) are simplified as

$$\begin{aligned} &{\text{ STM }}{:}\; x'_i(t)=-a_i(t)x_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)f_j(x_j(t))\\&\qquad\qquad\quad\, +\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)f_j(x_j(\theta _jt))\\ &\qquad\qquad\quad\, +\,B_i(t)S_i(t)+I_i(t)\\& {\text{ LTM }}{:}\;S'_{i}(t)=-{\tilde{e}}_i(t)S_i(t)+f_i(x_i(t))+J_i(t)\\& {\text{ STM }}{:}\;\varDelta x_i\setminus _{t=t_k}=x_i(t_k)-x_i(t_k^-)=-p_ix_i(t_k)\\& {\text{ LTM }}{:}\;\varDelta S_{i}\setminus _{t=t_k}=S_{i}(t_k)-S_{i}(t_k^-)=-q_iS_i(t_k) \end{aligned}$$

(3)

The initial conditions of system (3) are given by

$$\begin{aligned} x_i(s)&=\varphi _i(s),\;s\in [-\rho _it_0,t_0], S_i(s)=\phi _i(s),\;s\in [-\rho _it_0,t_0], \end{aligned}$$

(4)

where $\rho _i= \max\nolimits_{1\le j\le n}\{p_{j}\}$, $\varphi _i(s),\;\phi _i(s)\in C([-\rho _it_0,t_0],{\mathbb {R}}^n)$ with $C([-\rho _it_0,t_0],{\mathbb {R}}^n)$ denotes the Banach space of all continuous functions mapping $[-\rho _it_0,t_0]$ into ${\mathbb {R}}^n$.

To derive the main results, we assume that the following conditions hold:

${\mathbf (H1)}$:

The activation functions $f_j$ satisfy the Lipschitz condition, i.e., there exist constant $L^f_j>0$, such that $|f_j(x)-f_j(y)|\le L^f_j|x-y|$, $x,y\in {\mathbb {R}}$, for $j=1,2,\ldots ,n$.

In this work, we will make drive-response chaotic neural networks with delays achieve synchronization in fixed-time by designing some effective controllers. The corresponding response system of (3) can be rewritten in the following form of an impulsive differential equation:

$$\begin{aligned} &{\text{ STM }}{:}\; y'_i(t)=-a_i(t)y_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)f_j(y_j(t))\\& \qquad\qquad\qquad\,+\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)f_j(y_j(\theta _jt))\\ &\qquad\qquad\qquad\, +\,B_i(t)Z_i(t)+I_i(t)+R_i(t)\\& {\text{ LTM }}{:}\;Z'_{i}(t)=-{\tilde{e}}_i(t)Z_i(t)+f_i(y_i(t))+J_i(t)+Q_i(t)\\& {\text{ STM }}{:}\;\varDelta y_i\setminus _{t=t^+_k}=y_i(t^+_k)-y_i(t_k^-)=-p_iy_i(t_k)\\& {\text{ LTM }}{:}\;\varDelta Z_{i}\setminus _{t=t^+_k}=Z_{i}(t^+_k)-Z_{i}(t_k^-)=-q_iZ_i(t_k) \end{aligned}$$

(5)

where $y_i=(y_1,y_2,\ldots ,y_n)^T$, $Z_i=(Z_1,Z_2,\ldots ,Z_n)^T$ are the response state scalar of the $i{\text {th}}$ node, $R_i=(R_1,R_2,\ldots ,R_n)^T$ and $Q_i=(Q_1,Q_2,\ldots ,Q_n)^T$ donates the controller that will be appropriately designed for fixed-time synchronization objective, $i=1,2,\ldots ,n$.

Define error states $e_i(t)=y_i(t)-x_i(t)$ and $\varepsilon _i(t)=Z_i(t)-S_i(t)$, we can derive the following error system

$$\begin{aligned} &{\text{ STM }}{:}\; e'_i(t)=-a_i(t)e_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)F_j(e_j(t))\\ &\qquad\qquad\quad\, +\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)F_j(e_j(\theta _jt))\\ &\qquad\qquad\quad\,+\,B_i(t)\varepsilon_i(t)+R_i(t)\\ &{\text{ LTM }}{:}\;\varepsilon'_{i}(t)=-{\tilde{e}}_i(t)\varepsilon_i(t)+F_i(e_i(t))+Q_i(t)\\& {\text{ STM }}{:}\;\varDelta e_i\setminus _{t=t_k}=e_i(t_k)-e_i(t_k^-)=-p_ie_i(t_k)\\& {\text{ LTM }}{:}\;\varDelta \varepsilon_{i}\setminus _{t=t_k}=\varepsilon_{i}(t_k)-\varepsilon_{i}(t_k^-)=-q_i\varepsilon_i(t_k) \end{aligned}$$

(6)

where $F_j(e_j(t))=f_j(y_j(t))-f_j(x_j(t))$ and $F_j(e_j(p_{j}t))=f_j(y_j(p_{j}t))-f_j(x_j(p_{j}t))$.

Remark 1

Based on Assumption ${\mathbf (H1) }$, we conclude that $F_j(.)$ satisfies: $|F(e_j(t))|\le L^f_j|e_j(t)|$.

3 Definitions and lemmas

In this section, we introduce some definitions and state some preliminary results

Definition 1

Let $V: {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}_+$, then V is said to belong to class ${\mathcal {V}}$ if

• (1) V is continuous on each of the sets $(t_k,t_{k+1}]\times {\mathbb {R}}^{2n}$ for $z\in {\mathbb {R}}^{2n}$, $k\in {\mathbb {N}}$ and $V(t,z)=\lim\nolimits_{t,z}\rightarrow (t^+_k,c)V(t^+_k,c)$ exists.

• (2) V is locally Lipschitzian in z.

Definition 2

The competitive neural network is said to be fixed-time synchronization if for any initial condition, there exists a settling-time function $T(z_0)$ such that: $\lim\nolimits_{t\rightarrow T(z_0)}\Vert e(t)\Vert =0$, $\lim\nolimits_{t\rightarrow T(z_0)}\Vert \varepsilon (t)\Vert =0$, and $e(t)=0$, $\varepsilon (t)=0$, where the settling-time function is bounded, i.e., there exist constant $T_{\max }> 0$ such that $T(z_0)\le T_{\max },\;\;\forall z_0\in {\mathbb {R}}^{2n}$.

Lemma 1

[35] Let $x=(x_1,x_2,\ldots ,x_n)\ge 0$, $0<p\le 1$, $q>1$ the following two inequalities hold: $\sum \nolimits _{i=1}^{n}x^p_i\ge \bigg (\sum \nolimits _{i=1}^{n}x_i\bigg )^p$, $\sum \nolimits _{i=1}^{n}x^q_i\ge n^{1-q}\bigg (\sum \nolimits _{i=1}^{n}x_i\bigg )^q$.

Lemma 2

[37] Let $V(x(t))\in {\mathcal {V}}$ be positive definite and radially unbounded function. Assume that the following conditions are satisfied :

$$\begin{aligned} {\dot{V}}(x(t))\le & -\alpha V^p(x(t))-\beta V^q(x(t)),\;t\ne t_k, \; t\in {\mathbb {R}}_+ \end{aligned}$$

(7)

$$\begin{aligned} V(x(t^+_k))\le & V(t_k), \end{aligned}$$

(8)

where $\alpha ,\;\beta >0$, $0<p\le 1$, $q>1$, then the system (6) is globally fixed-time stable and the settling time bounded by

$$\begin{aligned} T\le T_{\max }:=\frac{1}{\alpha (1-p)}+\frac{1}{\beta (q-1)}. \end{aligned}$$

4 Main results

In this section, we will address the controller design problem for fixed time for competitive neural networks with proportional delay and impulsive perturbation.

4.1 Fixed-time synchronization with delay-dependent feedback controller

In this section, we will derive some criteria to guarantee the fixed-time synchronization between drive system (3) and response system (5). First, a delayed feedback controller is defined as follows:

$$\begin{aligned} R_i(t)&=-\lambda _{1}e_i(t)-\lambda _{2}sign(e_i(t))|e_i(t)|^\alpha -\lambda _{3}sign(e_i(t))|e_i(t)|^\beta \\ &\quad -\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)F_j(e_j(p_{j}t))\\ Q_i(t)&=-\rho _{1}\varepsilon_i(t)-\rho _{2}sign(\varepsilon_i(t))|\varepsilon_i(t)|^\alpha -\rho _{3}sign(\varepsilon_i(t))|\varepsilon_i(t)|^\beta \end{aligned}$$

(9)

where $0<\alpha <1$, $\beta >1,$ $\lambda _{p},\;\rho _{p}$, $p=1,2,3$ are the parameters to be designed later.

Theorem 1

Under Assumption (H1),the drive-response systems (3) and (5) will achieve fixed-time synchronization under controller (9) if the following conditions hold

$$\begin{aligned} \lambda _1&\ge -a^-_i+\frac{1}{2}L^f_i+\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ij}|^+L^f_j+\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ji}|^+L^f_i+\frac{1}{2}|B_i|^+,\\ \rho _1&\ge -{\tilde{e}}^-_i+\frac{1}{2}L^f_i+\frac{1}{2}|B_i|^+,\\ \lambda _{2}&>0,\;\lambda _{3}>0,\;\rho _{2}>0,\;\rho _{3}>0,\\ &\quad\displaystyle \max \left\{\max _{1\le i\le n}\{(1-p_i)^2,(1-q_i)^2\}\right\}<1 \end{aligned}$$

(10)

moreover, the finite time $t_1$for synchronization satisfies

$$\begin{aligned} t_1\le & \frac{1}{\min \big \{\lambda _2,\rho _2\big \}2^{\frac{\alpha +1}{2}}(1-\alpha )}\nonumber \\&+\,\frac{1}{\min \big \{\lambda _3,\rho _3\big \}2^{\frac{\beta +1}{2}}n^{\frac{1-\beta }{2}}(\beta -1)}. \end{aligned}$$

(11)

Proof

Consider the following Lyapunov function:

$$\begin{aligned} V(t)=\frac{1}{2}\displaystyle \sum _{i=1}^{n}e_i^2(t)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}\varepsilon_i^2(t) \end{aligned}$$

(12)

Calculating the derivative ${\dot{V}}(t)$ along the solution of system (6), we have

$$\begin{aligned} {\dot{V}}(t)= & \displaystyle \sum _{i=1}^{n}e_i(t){\dot{e}}_i(t)+\displaystyle \sum _{i=1}^{n}\varepsilon_i(t)\dot{\varepsilon}_i(t)\nonumber \\= & \displaystyle \sum _{i=1}^{n}e_i(t)\bigg [-a_i(t)e_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)F_j(e_j(t))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)F_j(e_j(\theta _jt))+B_i(t)\varepsilon_i(t)+R_i(t)\bigg ]\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\varepsilon_i(t)\bigg [-e_i(t)\varepsilon_i(t)+F_i(e_i(t))+Q_i(t)\bigg ]\nonumber \\\le & \displaystyle \sum _{i=1}^{n}\bigg [-a_i(t)e^2_i(t)+\displaystyle \sum _{j=1}^{n}e_i(t)b_{ij}(t)F_j(e_j(t))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}e_i(t)c_{ij}(t)F_j(e_j(\theta _jt))+e_i(t)B_i(t)\varepsilon_i(t)\nonumber \\&-\,\lambda _{1}e^2_i(t)-\lambda _{2}|e_i(t)|^{\alpha +1}-\lambda _{3}|e_i(t)|^{\beta +1}\nonumber \\&-\,\displaystyle \sum _{j=1}^{n}e_i(t)c_{ij}(t)F_j(e_j(p_{j}t))\bigg ]\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-{\tilde{e}}_i(t)\varepsilon^2_i(t)+\varepsilon_i(t)F_i(e_i(t))-\rho _{1}\varepsilon^2_i(t)\nonumber \\&-\,\rho _{2}|\varepsilon_i(t)|^{\alpha +1}-\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]\nonumber \\\le & \displaystyle \sum _{i=1}^{n}\bigg [-a^-_ie^2_i(t)+\displaystyle \sum _{j=1}^{n}|b_{ij}(t)|L^f_j|e_i(t)||e_j(t)|\nonumber \\&+\,|e_i(t)||B_i(t)||\varepsilon_i(t)|-\lambda _{1}e^2_i(t)-\lambda _{2}|e_i(t)|^{\alpha +1}\nonumber \\&-\,\lambda _{3}|e_i(t)|^{\beta +1}\bigg ]+\displaystyle \sum _{i=1}^{n}\bigg [-{\tilde{e}}^-_i\varepsilon^2_i(t)+L^f_i|\varepsilon_i(t)||e_i(t)|\nonumber \\&-\,\rho _{1}\varepsilon^2_i(t)-\rho _{2}|\varepsilon_i(t)|^{\alpha +1}-\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]\nonumber \\\le & \displaystyle \sum _{i=1}^{n}\bigg [-a^-_ie^2_i(t)+\displaystyle \sum _{j=1}^{n}|b_{ij}|^+L^f_j\frac{1}{2}(e^2_i(t)+e^2_j(t))\nonumber \\&+\,|B_i|^+\frac{1}{2}(e^2_i(t)+\varepsilon^2_i(t))-\lambda _{1}e^2_i(t)-\lambda _{2}|e_i(t)|^{\alpha +1}\nonumber \\&-\lambda _{3}|e_i(t)|^{\beta +1}\bigg ]+\displaystyle \sum _{i=1}^{n}\bigg [-{\tilde{e}}^-_i\varepsilon^2_i(t)+L^f_j\frac{1}{2}\big (\varepsilon^2_i(t)\nonumber \\&+\,e^2_i(t)\big )-\rho _{1}\varepsilon^2_i(t)-\rho _{2}|\varepsilon_i(t)|^{\alpha +1}-\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]\nonumber \\\le & \displaystyle \sum _{i=1}^{n}\bigg [-a^-_i-\lambda _1+\frac{1}{2}L^f_i+\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ij}|^+L^f_j\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ji}|^+L^f_i+\frac{1}{2}|B_i|^+\bigg ]e^2_i(t)\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-{\tilde{e}}^-_i-\rho _1+\frac{1}{2}L^f_i+\frac{1}{2}|B_i|^+\bigg ]\varepsilon^2_i(t)\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-\lambda _{2}|e_i(t)|^{\alpha +1}-\lambda _{3}|e_i(t)|^{\beta +1}\nonumber \\&-\,\rho _{2}|\varepsilon_i(t)|^{\alpha +1}-\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]. \end{aligned}$$

(13)

By using (10), and Lemma 1, we have

$$\begin{aligned} D^+V(t)\le & -\min \big \{\lambda _2,\rho _2\big \}\displaystyle \sum _{i=1}^{n}\bigg \{|e_i(t)|^{\alpha +1}+|\varepsilon_i(t)|^{\alpha +1}\bigg \}\nonumber \\&-\,\min \big \{\lambda _3,\rho _3\big \}\displaystyle \sum _{i=1}^{n}\bigg \{|e_i(t)|^{\beta +1}+|\varepsilon_i(t)|^{\beta +1}\bigg \}\nonumber \\\le & -\min \big \{\lambda _2,\rho _2\big \}\displaystyle \sum _{i=1}^{n}\bigg \{|e_i(t)|^{2}+|\varepsilon_i(t)|^{2}\bigg \}^{\frac{\alpha +1}{2}}\nonumber \\&-\,\min \big \{\lambda _3,\rho _3\big \}\displaystyle \sum _{i=1}^{n}\bigg \{|e_i(t)|^{2}+|\varepsilon_i(t)|^{2}\bigg \}^{\frac{\beta +1}{2}}\nonumber \\\le & -\min \big \{\lambda _2,\rho _2\big \}2^{\frac{\alpha +1}{2}}V(t)^{\frac{\alpha +1}{2}}\nonumber \\&-\,\min \big \{\lambda _3,\rho _3\big \}2^{\frac{\beta +1}{2}}n^{\frac{1-\beta }{2}}V(t)^{\frac{\beta +1}{2}}. \end{aligned}$$

(14)

When $t = t_k$, it can be obtained from (12) that

$$\begin{aligned} V(t^+_k)= & \frac{1}{2}\displaystyle \sum _{i=1}^{n}e_i^2(t^+_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}\varepsilon_i^2(t^+_k)\nonumber \\= & \frac{1}{2}\displaystyle \sum _{i=1}^{n}(1-p_i)^2e_i^2(t_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}(1-q_i)^2\varepsilon_i^2(t_k)\nonumber \\\le & \displaystyle \max \{(1-p_i)^2,(1-q_i)^2\}\nonumber \\&\times \bigg (\frac{1}{2}\displaystyle \sum _{i=1}^{n}e_i^2(t_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}\varepsilon_i^2(t_k)\bigg )\nonumber \\\le & \displaystyle \max \{\max _{1\le i\le n}\{(1-p_i)^2,(1-q_i)^2\}\}V(t_k)\nonumber \\\le & V(t_k) \end{aligned}$$

(15)

Thus, by Lemma 2, the error system (6) will converge to zero within $t_1$, that is, the master–slave systems (3) and (5) achieve the fixed-time synchronization and the settling time is given as $t_1$. $\square$

Remark 2

Note that, in Theorem 1, by designing a special fixed-time controller, we achieved the fixed-time synchronization between two chaotic competitive neural networks. On the other hand, the used control (9) is somehow expensive and not easily applicable. Below, we will modify the controller (9) to improve the applicability of our results.

${\mathbf (H2)}$ :

The activation functions $f_j$ are bounded, i.e., there exist constant $M_j>0$, such that $|f_j(.)|\le M_j$, for $j=1,2,\ldots ,n$.

4.2 Fixed-time synchronization with delay-independent feedback controller

Let the following delay-independent feedback controller :

$$\begin{aligned} R_i(t)&=-\lambda _{1}e_i(t)-\lambda _{2}sign(e_i(t))|e_i(t)|^\alpha \\ &\quad -\,\lambda _{3}sign(e_i(t))|e_i(t)|^\beta -\lambda _3 sign(e_i(t))\\ Q_i(t)&=-\rho _{1}\varepsilon_i(t)-\rho _{2}sign(\varepsilon_i(t))|\varepsilon_i(t)|^\alpha \\ &\quad -\rho _{3}sign(\varepsilon_i(t))|\varepsilon_i(t)|^\beta \end{aligned}$$

(16)

Theorem 2

Under the assumptions (H1)–(H2), the drive-response systems (3) and (5) will achieve fixed-time synchronization under controller (16), if (10) is satisfied and

$$\begin{aligned} \lambda _3\ge 2\displaystyle \sum _{j=1}^{n}|c_{ij}|^+M_j \end{aligned}$$

(17)

moreover, the settling time $t_1$ for synchronization is the same as defined in Theorem 1.

Proof

Using the same Lyapunov function that defined in (12) and calculating the derivative ${\dot{V}}(t)$ along the solution of system (6) we have

$$\begin{aligned} {\dot{V}}(t)= & \displaystyle \sum _{i=1}^{n}e_i(t)\bigg [-a_i(t)e_i(t)+\displaystyle \sum _{j=1}^{n}b_{ij}(t)F_j(e_j(t))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}c_{ij}(t)F_j(e_j(\theta _jt))+B_i(t)\varepsilon_i(t)+R_i(t)\bigg ]\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\varepsilon_i(t)\bigg [-{\tilde{e}}_i(t)\varepsilon_i(t)+F_i(e_i(t))+Q_i(t)\bigg ]\nonumber \\\le & \displaystyle \sum _{i=1}^{n}\bigg [-a_i(t)e^2_i(t)+\displaystyle \sum _{j=1}^{n}e_i(t)b_{ij}(t)F_j(e_j(t))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}e_i(t)c_{ij}(t)F_j(e_j(\theta _jt))+e_i(t)B_i(t)\varepsilon_i(t)\nonumber \\&-\,\lambda _{1}e^2_i(t)-\lambda _{2}|e_i(t)|^{\alpha +1}-\lambda _{3}|e_i(t)|^{\beta +1}-\lambda _3|e_i(t)|\bigg ]\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-{\widetilde{e}}_i(t)\varepsilon^2_i(t)+\varepsilon_i(t)F_i(e_i(t))-\rho _{1}\varepsilon^2_i(t)-\rho _{2}|\varepsilon_i(t)|^{\alpha +1}\nonumber \\&-\,\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]\nonumber \\ \end{aligned}$$

(18)

Using the same discussion method as in Theorem 1, one can get that

$$\begin{aligned} {\dot{V}}(t)\le & \displaystyle \sum _{i=1}^{n}\bigg [-a^-_i-\lambda _1+\frac{1}{2}L^f_i+\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ij}|^+L^f_j+\displaystyle \sum _{j=1}^{n}\frac{1}{2}|b_{ji}|^+L^f_i\nonumber \\&+\,\frac{1}{2}|B_i|^+\bigg ]e^2_i(t)\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-{\tilde{e}}^-_i-\rho _1+\frac{1}{2}L^f_i+\frac{1}{2}|B_i|^+\bigg ]\varepsilon^2_i(t)\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-\lambda _3+2\displaystyle \sum _{j=1}^{n}|c_{ij}|^+M_j\bigg ]|e_i(t)|\nonumber \\&+\,\displaystyle \sum _{i=1}^{n}\bigg [-\lambda _{2}|e_i(t)|^{\alpha +1}-\lambda _{3}|e_i(t)|^{\beta +1}-\rho _{2}|\varepsilon_i(t)|^{\alpha +1}\nonumber \\&-\,\rho _{3}|\varepsilon_i(t)|^{\beta +1}\bigg ]. \end{aligned}$$

(19)

from condition of Theorem 2 and Lemma 1, we get

$$\begin{aligned} D^+V(t)\le & -\min \big \{\lambda _2,\rho _2\big \}2^{\frac{\alpha +1}{2}}V(t)^{\frac{\alpha +1}{2}}\nonumber \\&-\,\min \big \{\lambda _3,\rho _3\big \}2^{\frac{\beta +1}{2}}n^{\frac{1-\beta }{2}}V(t)^{\frac{\beta +1}{2}}. \end{aligned}$$

(20)

When $t = t_k$, it can be obtained from (12) that

$$\begin{aligned} V(t^+_k)&= \frac{1}{2}\displaystyle \sum _{i=1}^{n}e_i^2(t^+_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}\varepsilon_i^2(t^+_k)\nonumber \\&= \frac{1}{2}\displaystyle \sum _{i=1}^{n}(1-p_i)^2e_i^2(t_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}(1-q_i)^2\varepsilon_i^2(t_k)\nonumber \\ &\le \displaystyle \max \{(1-p_i)^2,(1-q_i)^2\}\\ &\quad\times\bigg (\frac{1}{2}\displaystyle \sum _{i=1}^{n}e_i^2(t_k)+\frac{1}{2}\displaystyle \sum _{i=1}^{n}\varepsilon_i^2(t_k)\bigg )\nonumber \\ &\le \displaystyle \max \left\{\max _{1\le i\le n}\{(1-p_i)^2,(1-q_i)^2\}\right\}V(t_k)\nonumber \\ &\le V(t_k) \end{aligned}$$

(21)

Thus, by Lemma 2, the error system (6) will converge to zero within $t_1$, that is, the master–slave systems (3) and (5) achieve the fixed-time synchronization and the settling time is given as $t_1$. $\square$

Remark 3

Note that, the competitive neural networks models studied in [33, 34] are considered with constant coefficients. In this paper, we study the model with time-varying coefficients and without impulse. In addition, our models include models in [33, 34] as special cases when $p_i=q_i=0$, $a_i(t)=a_i$, $e_i(t)=e_i$, $B_i(t)=B_i$, $b_{ij}(t)=b_{ij}$, $c_{ij}(t)=c_{ij}$, $I_i(t)=I_i$ and $J_i(t)=0$. So, our results have been shown to be the generalization of existing results reported recently in the literature.

Remark 4

In the designed control inputs used in this works, discontinuous terms $sgn(e_i(t))$ and $sgn(\varepsilon_i(t))$ will result in undesirable chattering phenomenon which is undesirable in practice. In real applications, in order to attenuate the unfavorable chattering, the discontinuous terms $sgn(e_i(t))$ and $sgn(\varepsilon_i(t))$ are approximated by $\frac{e_i(t)}{e_i(t)+\kappa }$ and $\frac{\varepsilon_i(t)}{\varepsilon_i(t)+\overline{\kappa }}$, respectively, where $\kappa >0$ and $\overline{\kappa }>0$ are sufficiently small.

5 Numerical example

In this section, numerical example is given to show the effectiveness of the obtained theoretical analysis. Consider the following competitive neural networks with proportional delays as follows:

$$\begin{aligned} & {\text{ STM }}{:}\; x'_i(t)=-a_i(t)x_i(t)+\displaystyle \sum _{j=1}^{2}b_{ij}(t)f_j(x_j(t))\\&\quad\qquad\qquad\, +\,\displaystyle \sum _{j=1}^{2}c_{ij}(t)f_j(x_j(\theta _jt))\\ &\quad\qquad\qquad\, +\,B_i(t)S_i(t)+I_i(t)\\ &{\text{ LTM }}{:}\;S'_{i}(t)=-e_i(t)S_i(t)+f_i(x_i(t))+J_i(t)\\ &{\text{ STM }}{:}\;\varDelta x_i\setminus _{t=t_k}=x_i(t_k)-x_i(t_k^-)=-p_ix_i(t_k)\\ &{\text{ LTM }}{:}\;\varDelta S_{i}\setminus _{t=t_k}=S_{i}(t_k)-S_{i}(t_k^-)=-q_iS_i(t_k) \end{aligned}$$

(22)

and the slave system described as

$$\begin{aligned} &{\text{ STM }}{:}\; y'_i(t)=-a_i(t)y_i(t)+\displaystyle \sum _{j=1}^{2}b_{ij}(t)f_j(y_j(t))\\& \qquad\quad\qquad\, +\,\displaystyle \sum _{j=1}^{2}c_{ij}(t)f_j(y_j(\theta _jt))\\&\qquad\qquad\quad\, +\,B_i(t)Z_i(t)+R_i(t)\\& {\text{ LTM }}{:}\;Z'_{i}(t)=-e_i(t)Z_i(t)+f_i(y_i(t))+Q_i(t)\\& {\text{ STM }}{:}\;\varDelta y_i\setminus _{t=t^+_k}=y_i(t^+_k)-y_i(t_k^-)=-p_iy_i(t_k)\\& {\text{ LTM }}{:}\;\varDelta Z_{i}\setminus _{t=t^+_k}=Z_{i}(t^+_k)-Z_{i}(t_k^-)=-q_iZ_i(t_k) \end{aligned}$$

(23)

for $i=1,2$, where $a_i(t)=3+0.1\sin (t)$, $e_i(t)=2+1.5\cos (t),$ $I_1(t)=\sin (0.9t),$ $I_2(t)=\cos (0.9t),$ $J_1(t)=\sin (0.8t),$ $J_1(t)=\cos (0.8t),$ $\theta _j=0.5$, $p_i=q_i=0.8,$ the activation function is described by $f_i(x)=\tanh (x)$ and

$$\begin{aligned} (b_{ij}(t))= & \left( \begin{array}{cc} 1.5+0.1\sin (t) &\quad 2+0.1\cos (t)\\ 2.5+0.1\cos (t) &\quad 1+0.1\sin (t)\\ \end{array} \right) \\ (c_{ij}(t))= & \left( \begin{array}{cc} 2.5+0.1\cos (t) &\quad 2+0.1\cos (t)\\ 1.5+0.1\sin (t) &\quad 1.9+0.1\sin (t) \\ \end{array} \right) \\ (B_{i}(t))= & \left( \begin{array}{cc} 0.3|\sin (\sqrt{3}t)| &\quad 0\\ 0 &\quad 0.3|\sin (\sqrt{3}t)| \\ \end{array} \right) \end{aligned}$$

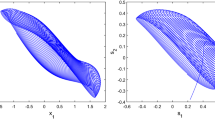
Figure 1 presents the chaotic trajectory of (22) with initial value $x(0)=(0.5,-0.5)^T$, $S(0)=(0.25,-0.25)^T$.

Fig. 1

Trajectories of x(t) and S(t) of (22)

According to the conditions presented in Theorem 1, choose $\lambda _1=1.5200\ge -a^-_1+\frac{1}{2}L^f_1+ \sum\nolimits_{j=1}^{2}\frac{1}{2}|b_{1j}|^+L^f_j + \sum\nolimits_{j=1}^{2}\frac{1}{2}|b_{j1}|^+L^f_1+\frac{1}{2}|B_1|^+=1.5200,\;\; \lambda _1=1.5200\ge -a^-_2+\frac{1}{2}L^f_2+ \sum\nolimits_{j=1}^{2}\frac{1}{2}|b_{2j}|^+L^f_j + \sum\nolimits_{j=1}^{2}\frac{1}{2}|b_{j2}|^+L^f_2+\frac{1}{2}|B_2|^+=1.0200,\;\; \rho _1=0.1500\ge -{\tilde{e}}^-_1+\frac{1}{2}L^f_1+\frac{1}{2}|B_1|^+=0.1500,\;\; \rho _1=0.1500\ge -{\tilde{e}}^-_2+\frac{1}{2}L^f_2+\frac{1}{2}|B_2|^+=0.1500,\;\; \lambda _2=1.2>0,\; \lambda _3=1.1>0,\; \rho _2=1.1>0,\;\rho _3=1.2>0,\; \alpha =0.5,\;\beta =2.$ Thus, the control inputs of the slave system are formulated as

$$\begin{aligned} R_1(t)&=-1.52e_1(t)-0.2sign(e_1(t))|e_1(t)|^{0.5}\\ &\quad-\,0.1sign(e_1(t))|e_1(t)|^2\\ &\quad-\,\displaystyle \sum _{j=1}^{2}c_{1j}(t)F_j(e_j(0.5t))\\ R_2(t)&=-1.52e_2(t)-0.2sign(e_2(t))|e_2(t)|^{0.5}\\ &\quad-\,0.1sign(e_2(t))|e_2(t)|^2\\ &\quad-\,\displaystyle \sum _{j=1}^{2}c_{2j}(t)F_j(e_j(0.5t))\\ Q_1(t&)=-0.15\varepsilon_1(t)-0.1sign(\varepsilon _1(t))|\varepsilon _1(t)|^{0.5}\\ &\quad-\,0.2sign(\varepsilon _1(t))|\varepsilon _1(t)|^2\\ Q_2(t)&=-0.15\varepsilon _2(t)-0.1sign(\varepsilon _2(t))|\varepsilon _2(t)|^{0.5}\\ &\quad-\,0.2sign(\varepsilon _2(t))|\varepsilon _2(t)|^2 \end{aligned}$$

• Under controller (9) the state trajectories of master/salve system are illustrated in Figs. 2, 3, 4 and 5.

• Under controller (9) and the initial conditions $e_1(0)=-6$, $e_2(0)=6$, $\varepsilon _1(0)=-4$, $\varepsilon _2(0)=4$, the evolution of the synchronization errors is described in Fig. 6.

• The settling time for synchronization is estimated by 1.5766.

Fig. 2

Time evolution of variables $x_1(t)$ and $y_1(t)$ of drive neural network (22) and corresponding response system (23)

Fig. 3

Time evolution of variables $x_2(t)$ and $y_2(t)$ of drive neural network (22) and corresponding response system (23)

Fig. 4

Time evolution of variables $S_1(t)$ and $Z_1(t)$ of drive neural network (22) and corresponding response system (23)

Fig. 5

Time evolution of variables $S_2(t)$ and $Z_2(t)$ of drive neural network (22) and corresponding response system (23)

Fig. 6

Synchronization errors $e_1(t)$, $e_2(t)$, $\varepsilon _1(t)$ and $\varepsilon _2(t)$ under controller (9)

Remark 5

In Theorems 1–2, some auxiliary parameters $\lambda _1$, $\lambda _2$, $\lambda _3$, $\rho _1,$ $\rho _2,$ and $\rho _3,$ are introduced to cut down the conservatism of (10) and (11).

In practice, these parameters can be properly selected to improve the feasibility and generality of the obtained results. In addition, by choosing suitable values of these parameters, the above conditions can be always satisfied for different values of the system’s coefficients. On the other hand, when the coefficients of the system are given, the values of these parameters can be adjusted to reduce the values of the control coefficients. In general, the values of the auxiliary parameters are randomly given first (e.g., $\lambda _1=\lambda _2=\lambda _3=\rho _1=\rho _2=\rho _3=1$), and then adjusted appropriately according to the actual situation. As for whether an effective algorithm can be used to select these auxiliary parameters, it is still a valuable research issue.

6 Discussion and comparisons

A laterally inhibited NNs with a deterministic signal Hebbian learning law, which can model the dynamics of cortical cognitive maps with unsupervised synaptic modifications, were recently proposed and its global asymptotic stability was studied in Meyer-Bäse et al. [10, 38]. In this model, there are two types of state variables, the short-term memory variables (STM) describing the fast neural activity and the long-term memory (LTM) variables describing the slow unsupervised synaptic modifications. Thus, there are two time scales in these neural networks, in which one corresponds to the fast changes of the neural network states and another corresponds to the slow changes of the synapses by external stimuli.

Recently, many authors studied the synchronization of competitive neural networks like exponential synchronization [39], adaptive lag synchronization [40], general decay lag synchronization [41] and finite-time synchronization [42]. In practical execution, the fixed-time synchronization is more realistic and valuable. To the best of our knowledge, no such result has been proved on finite-time synchronization between impulsive competitive neural networks with time delays. Comparing with previous published results, this paper reports the optimality in settling time of synchronization. In addition, the proportional delays and impulsive effect are considered for fixed-time synchronization of delayed competitive neural networks. Thus, they can implement the abundance of flexibility and freedom in practical applications for system.

On the other hand, the fixed-time synchronization of impulsive competitive neural networks has not been seen; hence the obtained Theorems 1 and Theorem 2 are substantially new and the explored criteria can be easily expanded to the impulsive effects of study on the fixed-time synchronization of the other kinds of neural networks such as BAM neural networks, Cohen–Grossberg neural networks, and Cohen–Grossberg BAM neural networks.

7 Conclusion and future works

This paper focuses on the fixed-time synchronization problem for a class of competitive neural networks with proportional delays. Using Lyapunov functionals and analytical techniques, we obtain some sufficient conditions for the fixed-time synchronization of the master and slave of addressed systems. To the best of our knowledge, this is the first paper to study the fixed-time synchronization for CompNNs with proportional delays. Finally, an illustrated example with their simulations is given to demonstrate the effectiveness of the theoretical results.

In the present paper, we demonstrate that two different chaotic nonlinear competitive neural networks with proportional delays can be synchronized in fixed-time. In [43] the authors investigated the finite-time synchronization of neural networks with discrete and distributed delays by using periodically intermittent memory feedback control, in addition an application to secure communication is given. Therefore, studying the application of fixed-time synchronization in secure communication will be our future research interest.

$$\begin{aligned} &{{\mathrm {STM}}{:}\, e_{i}^{\prime }(t)=-a_{i}(t) e_{i}(t)+\sum _{j=1}^{n} b_{i j}(t) F_{j}\left( e_{j}(t)\right) } \\ &\qquad\qquad\qquad\,+\,\sum _{j=1}^{n} c_{i j}(t) F_{j}\left( e_{j}\left( \theta _{j} t\right) \right) \\ &\qquad\qquad\qquad\,+\,B_{i}(t) \varepsilon _{i}(t)+R_{i}(t) \\ &{\mathrm {LTM}}{:}\, \varepsilon _{i}^{\prime }(t)=-{\tilde{e}}_{i}(t) \varepsilon _{i}(t)+F_{i}\left( e_{i}(t)\right) +Q_{i}(t) \\ &{\mathrm {STM}}{:}\,\left. \varDelta e_{i}\right| _{t=t_{k}}=e_{i}\left( t_{k}\right) -e_{i}\left( t_{k}^{-}\right) =-p_{i} e_{i}\left( t_{k}\right) \\ &{\mathrm {LTM}}{:}\,\left. \varDelta \varepsilon _{i}\right| _{t=t_{k}}=\varepsilon _{i}\left( t_{k}\right) -\varepsilon _{i}\left( t_{k}^{-}\right) =-q_{i} \varepsilon _{i}\left( t_{k}\right) .\end{aligned}$$

(24)