Pseudo Almost Periodic Solution of Recurrent Neural Networks with D Operator on Time Scales

Abstract

This paper is concerned with a class of neutral type recurrent neural networks with time-varying delays, distributed delay and D operator on time–space scales which unify the continuous-time and the discrete-time recurrent neural networks under the same framework. Some sufficient conditions are given for the existence and the global exponential stability of the pseudo almost periodic solution by using inequality analysis techniques on time scales, fixed point theorem and the theory of calculus on time scales. An example is given to show the effectiveness of the derived results via computer simulations.

1 Introduction

During the last few decades, artificial neural network (NNs) is utilized to simulate the structure and function of a biological neural network [1]. Recently, investigations of artificial NNs have been a prevailing research topic due to their great applications and potentials in various fields, such as such as multilayer neural networks for pattern recognition [2], memristor-based echo state network for time-series forecast [1], and concatenated generative adversarial neural networks to generate videos [3].

Especially, the recurrent NNs are powerful and popular artificial NNs have been widely applied in many fields owing to the pioneering work of Hopfield [4]. In [4], Hopfield consider a class of recurrent artificial neural networks, which can be described as following:

$$\begin{aligned} C_i{\dot{x}}_i= & {} -\frac{x_i}{R_i}+\displaystyle \sum _{j=1}^{n}t_{ij}f_j(x_j)+J_i \end{aligned}$$

(1)

where $i = 1,2,\dots ,n;$$x_i(t)$ denotes the potential of the ith neuron at time t; $C_i$ are a positive constants and $R_i$ are the neuron amplifier input capacitances and resistances, respectively; $t_{ij}$ is the synaptic interconnection strength; $J_i$ is the constant input from outside of the network; $f_j(x_j)$ is the activation function. In terms of electrical circuits $f_j(x_j)$ represents the output characteristic of an amplifier with negligible respond time. For more detailed structure of neural networks (1), the readers are referred to [4]. Denote $e_i=\frac{1}{R_iC_i}$, $b_{ij}=\frac{t_{ij}}{C_i}$ and $I_i=\frac{J_i}{C_i}$. Then the above neural networks (1) are simplified as

$$\begin{aligned} {\dot{x}}_i= & {} -e_ix_i+\displaystyle \sum _{j=1}^{n}b_{ij}f_j(x_j)+I_i. \end{aligned}$$

(2)

This model has been paid much considerable attention due to its wide applications in various areas such as electrical engineering, mechanics, control, parallel computation, automatic and so on [5,6,7,8,9,10,11,12].

In addition, the existence of time delay especially time-varying delay makes the dynamic behaviors become more complex and may cause divergence, oscillation, instability, chaos or other poor performance in NNs, which are usually harmful to the applications of NNs [13, 14]. Therefore, the stability analysis for delayed NNs has become an important research topic and attracted many researchers much attention in the literature [15,16,17,18,19]. For example, Aouiti et al. [19] studied the following recurrent NNs with time-varying coefficients and mixed delays:

$$\begin{aligned} {\dot{x}}_i(t)= & {} a_i(t)x_i(t)+\displaystyle \sum _{j=1}^{n}c_{ij}(t)f_j(x_j(t))+\displaystyle \sum _{j=1}^{n}d_{ij}(t)g_j(x_j(t-\tau (t)))\\&+\,\displaystyle \sum _{j=1}^{n}p_{ij}(t)\int _{-\infty }^{t}K_{ij}(t-s)h_j(x_j(s))ds+J_i(t),\;i=1,2,\dots ,n. \end{aligned}$$

On the other hand, neutral-type phenomenon always exists in the study of population dynamics and automatic control etc [20]. Hence, the dynamic behaviors for different classes of recurrent NNs with neutral type delays were investigated in [5, 20,21,22,23]. It should be mentioned that all neutral type recurrent NNs models considered in the above references can be classified into two types:

• (i) Non-operator-based neutral functional differential equations (NOBNFDEs) [24, 25].

• (ii) D-operator-based neutral functional differential equations (DOBNFDEs) [26,27,28,29,30].

As well known, based on the theory of functional differential equations, DOBNFDEs may have more real significance than NOBNFDEs ones in many practical applications of NNs dynamics [27]. According to the complex neural reactions, neutral type recurrent NNs with D-operator may be described by the following neutral functional differential equations [28,29,30]:

$$\begin{aligned}{}[x_i(t)-q_i(t)x_i(t-r_i(t))]'= & {} -c_i(t)x_i(t)+\displaystyle \sum _{j=1}^{n}a_{ij}(t)F_j(x_j(t))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}b_{ij}(t)G_j(x_j(t-\tau _{ij}(t)))\nonumber \\&+\,\displaystyle \sum _{j=1}^{n}d_{ij}(t)\displaystyle \int _{0}^{+\infty }{\tilde{G}}_j(x_j(t-u))du+I_i(t). \end{aligned}$$

(3)

and criteria ensuring the existence of periodic solutions for system (3) are established in [28].

In addition, the theory of time–space scales, which was first introduced by Hilger [31] in order to unify discrete-time and continuous-time calculus. The books on the subject of time–space scale, by Bohner and Peterson [32], Agarwal [33], organize and recapping much of time–space scale calculus. The theory of time–space scale have been successfully applied in some mathematical models of real processes such as in population dynamics, physics, economics, biotechnology and so on. Since then, many works have investigated the dynamics of NNs on time scales [34,35,36,37, 39, 40, 42]. In [34], the authors studied the global exponential stability of the equilibrium point for a class of delayed bidirectional associative memory (BAM) neural network on the time–space scale. The work of [35] studied the pseudo almost periodic solutions for the following neutral type high-order Hopfield NNs with time-varying delays and leakage delays on time–space scales:

$$\begin{aligned} x^\nabla _i(t)= & {} - c_i(t-\delta (t))+\displaystyle \sum _{j=1}^{n}a_{ij}(t)f_j(x_j(t))+\displaystyle \sum _{j=1}^{n}b_{ij}(t)g_j(x_j(t-\tau _{ij}(t)))\\&+\,\displaystyle \sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}h_j(x^\nabla _j(s))\nabla s+\displaystyle \sum _{j=1}^{n}\displaystyle \sum _{l=1}^{n}T_{ijl}k_j(x_j(t-\xi _{ijl}(t)))k_l(x_l(t-\zeta _{ijl}(t)))\\&+\,I_i(t). \end{aligned}$$

The concept of pseudo almost periodicity (PAP), which is the central subject of our work, was introduced and studied by Zhang [38]. It is well known that PAP solutions, which are more general and complicated than periodic and almost periodic solutions [6, 24, 35, 42]. In [42] the authors studied the and global exponential stability of pseudo almost periodic solution for the following neutral delay BAM neural networks with time-varying delay in leakage terms:

$$\begin{aligned} x^\varDelta _i(t)= & {} - c_i(t-\tau _i(t))+\displaystyle \sum _{j=1}^{n}a_{ij}(t)f_j(x^\varDelta _j(t-\tau _{ij}(t)))\\&+\,\displaystyle \sum _{j=1}^{n}\displaystyle \sum _{l=1}^{n}b_{ijl}g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t)))+I_i(t). \end{aligned}$$

Inspired by the above discussions, in this paper, we propose a class of neutral type recurrent NNs with time-varying delays, distributed delay and D-operator on time–space scales:

$$\begin{aligned}{}[x_i(t)-p_i(t)x_i(t-r_i(t))]^\nabla= & {} - a_{i}(t) x_{i}(t)+ \sum \limits _{j=1}^{n} c_{ij}(t) f_{j} (x_{j}(t)) \nonumber \\&+\, \sum \limits _{j=1}^{n} b_{ij}(t) g_{j}(x_{j}(t-\tau (t)))\nonumber \\&+\, \sum \limits _{j=1}^{n} d_{ij}(t)\int _{-\infty }^{t} N_{ij}(t-s) h_{j}(x_{j}(s))\nabla s \nonumber \\&+\, I_{i}(t),\; t\in {\mathbb {T}}. \end{aligned}$$

(4)

where $i,j=1,2\dots ,n$; n donate the number of neurons in layers; ${\mathbb {T}}$ represent the translation invariant time scale, $x_i(t)$ denotes the activations of the $i\mathrm{th}$ neuron at time t; $a_i(.)>0$ are the rate with the $i\mathrm{th}$ neuron will reset its potential to the resting state in isolation when they are disconnected from the network and the external inputs at time t; $c_{ij}(t)$ , $b_{ij}(t)$$d_{ij}(t)$ and $p_i(t)$ are the elements of feedback template and feed forward template at time t; $f_j$, $g_j$ and $h_j$ are the activation functions; $\tau (t),$$r_i(t)$ are transmission delays at time t and satisfy $t-\tau (t)\in {\mathbb {T}},$$t-r_i(t)\in {\mathbb {T}}$ for $t\in {\mathbb {T}}$; $N_{ij}(t)$ are the delay kernel at time t; $I_i(t)$ denotes the input of the $i\mathrm{th}$ neuron at time t.

We should point out that:

$$\begin{aligned} \left\{ \begin{array}{ll} x^\nabla (t)=\frac{dx(t)}{dt},&{}\quad \text{ if } \; {\mathbb {T}}={\mathbb {R}}, \\ x^\nabla (k)=\nabla x(k)= x(k+1)- x(k),&{}\quad \text{ if } \; {\mathbb {T}}={\mathbb {Z}},\; k\in {\mathbb {Z}}. \end{array}\right. \end{aligned}$$

For each interval J of ${\mathbb {R}}$, we denote by $J_{{\mathbb {T}}}= J \bigcap {\mathbb {T}}$.

The initial conditions associated with system (4) are of the form:

$$\begin{aligned} x_i(s)=\varphi _i(s),\; s\in (-\infty ,0]_{{\mathbb {T}}},\; 1\le i\le n, \end{aligned}$$

where $\varphi (.)$ denotes a real-value bounded right-dense continuous function defined on $(-\infty ,0]_{{\mathbb {T}}}.$

Throughout this paper, for $i,j = 1,2,\dots ,n$, it will be assumed that $a_i,$$r_i$ are almost periodic on ${\mathbb {T}}$ and $c_{ij},$$b_{ij}$, $d_{ij}$, $p_i,$ and $I_{i},$ are pseudo almost periodic functions on ${\mathbb {T}},$ and let the positive constants $c^+_{ij}$,$b^+_{ij}$, $d^+_{ij}$, $p^+_{i},$$r^+_{i},$$I^+_{i}$ such that

$$\begin{aligned} c^+_{ij}= & {} \sup _{t \in {\mathbb {T}}}\mid c_{ij}(t) \mid ,\quad b^+_{ij} = \sup _{t \in {\mathbb {T}}}\mid b_{ij}(t) \mid ,\quad d^+_{ij} = \sup _{t \in {\mathbb {T}}}\mid d_{ijl}(t) \mid , \\ p^+_{i}= & {} \sup _{t \in {\mathbb {T}}} |p_{i}(t)|,\quad r^+_{i} = \sup _{t \in {\mathbb {T}}} |r_{i}(t)|,\quad I^+_{i} = \sup _{t \in {\mathbb {T}}}\mid I_{i}(t) \mid . \end{aligned}$$

We also assume that the following conditions $\mathbf (H_{1})$–$\mathbf (H_{4})$ hold.

$\mathbf (H_1)$ :

Functions $f_j,\;g_j,\;h_j\in \mathrm {C}({\mathbb {R}},{\mathbb {R}})$ and for each $j = \{1,2,\dots ,n\}$, there exist nonnegative constants $L^{f}_{j},$$L^{g}_{j}$ and $L^{h}_{j}$ such that

$$\begin{aligned} f_{j}(0)= & {} 0,\quad \mid f_{j}(u)- f_{j}(v)\mid \le L^{f}_{j} \mid u-v \mid , \\ g_{j}(0)= & {} 0,\quad \mid g_{j}(u)- g_{j}(v)\mid \le L^{g}_{j} \mid u-v \mid , \end{aligned}$$

and

$$\begin{aligned} h_{j}(0)= 0,\quad \mid h_{j}(u)- h_{j}(v)\mid \le L^{h}_{j} \mid u-v \mid . \end{aligned}$$

$\mathbf (H_2)$ :

For $i,j, \in \{1,2,\dots ,n\}$, the delay kernel $N_{ij} :[0, \infty )_{{\mathbb {T}}} \longrightarrow [0, \infty )$ is continuous, and there exist nonnegative constants $N^{+}_{ij}$ such that

$$\begin{aligned} N^{+}_{ij}= \int _{0}^{\infty }N_{ij}(s) \nabla s. \end{aligned}$$

$\mathbf (H_3)$ :

For all $1\le i \le n$, $a_i\in \mathrm {C}({\mathbb {T}},{\mathbb {R}})$ with $a_i\in \mathfrak {R}_v^+$, and $a_i^->0,$ where $\mathfrak {R}_v^+$ denotes the set of positively regressive functions from ${\mathbb {T}}$ to ${\mathbb {R}}$.

$\mathbf (H_4)$ :

Assume that

$$\begin{aligned} r=p_i^+ + \frac{1}{a_i^-} \bigg (a_i^+p_i^++ \sum _{j=1}^{n} (c_{ij}^+ L_{j}^{f} + b^+_{ij} L_{j}^{g}+d_{ij}N_{ij}^+ L_{j}^{h} )\bigg )<1. \end{aligned}$$

Remark 1

If ${\mathbb {T}}={\mathbb {R}}$, then (4) reduces to the following from

$$\begin{aligned}{}[x_i(t)-p_i(t)x_i(t-r_i(t))]'= & {} - a_{i}(t) x_{i}(t)+ \sum \limits _{j=1}^{n} c_{ij}(t) f_{j} (x_{j}(t)) + \sum \limits _{j=1}^{n} b_{ij}(t) g_{j}(x_{j}(t-\tau (t))) \nonumber \\&+\, \sum \limits _{j=1}^{n} d_{ij}(t)\int _{-\infty }^{t} N_{ij}(t-s) h_{j}(x_{j}(s))d s+ I_{i}(t), \; t\in {\mathbb {R}}. \end{aligned}$$

(5)

if ${\mathbb {T}}={\mathbb {Z}}$, then (4) reduces to the following from

$$\begin{aligned}&[x_i(k+1)-p_i(k+1)x_i(k+1-r_i(k+1))]-[x_i(k)-p_i(k)x_i(t-r_i(k))]\nonumber \\&\quad = - a_{i}(k) x_{i}(k)+ \sum \limits _{j=1}^{n} c_{ij}(k) f_{j} (x_{j}(k)) + \sum \limits _{j=1}^{n} b_{ij}(k) g_{j}(x_{k}(t-\tau (t))) \nonumber \\&\qquad + \sum \limits _{j=1}^{n} d_{ij}(k)\int _{-\infty }^{k} N_{ij}(k-s) h_{j}(x_{j}(k))d s +I_{i}(k), \; k\in {\mathbb {Z}}. \end{aligned}$$

(6)

Remark 2

To the best of our knowledge, this is the first time to study the PAP solutions of system (4). Since it is a $\nabla$-dynamic system on time–space scales, the results obtained in [35, 42] concerning the $\nabla$-dynamic systems cannot be directly applied to the system (4). Besides, since it studies the almost periodic problem, although paper [39, 40] deals with $\nabla$-dynamic systems on time–space scales, its results also cannot be directly applied to the system (4).

The organization of the rest of this paper is as follows. In Sect. 2, we will introduce some necessary notations, definitions and fundamental properties of the space $PAP({\mathbb {T}},{\mathbb {R}})$ and make some preparations for later sections. In Sects. 3 and 4, based on the results obtained in the previous sections, Banach’s fixed-point theorem and $\nabla$-differential inequalities on time scales, we present some sufficient conditions that guarantee the existence and global exponential stability of pseudo almost periodic solutions to (4). In Sect. 5, we present examples to illustrate the feasibility and effectiveness of our results obtained in Sects. 3 and 4. Finally, conclusions and open problem are drawn in Sect. 6.

2 Preliminary Results

In this section, we shall first recall some basic definitions and prove some lemmas.

For convenience, we denote by ${\mathbb {R}}^n\big ({\mathbb {R}}= {\mathbb {R}}^1\big )$ the set of all n-dimensional real vectors (real numbers). For any $x = (x_1, x_2,\dots ,x_n)^T\in {\mathbb {R}}^n,$ we let $\{x_i\} = (x_1, x_2,\dots ,x_n)^T,$ |x| denote the absolute-value vector given by $|x| = \{|x_i|\},$ and define $\Vert x\Vert = \max \nolimits _{1\le i\le n} |x_i|.$ Let $\mathrm {BC}({\mathbb {T}},{\mathbb {R}}^n)$ denotes the set of bounded and continued functions from ${\mathbb {T}}$ to ${\mathbb {R}}^n.$ Note that $\big (\mathrm {BC}({\mathbb {T}},{\mathbb {R}}^n),\Vert .\Vert _{\infty }\big )$ is a Banach space where $\Vert .\Vert _{\infty }$ denotes the sup norm

$$\begin{aligned} \Vert f\Vert _{\infty }:= \sup \limits _{t\in {\mathbb {T}}}\Vert f(t)\Vert . \end{aligned}$$

Definition 1

[41] Let ${\mathbb {T}}$ be a nonempty closed subset (time scale) of ${\mathbb {R}}$. The forward and backward jump operators $\sigma ,\;\rho : {\mathbb {T}}\rightarrow {\mathbb {T}}$ and the graininess $\mu : {\mathbb {T}}\rightarrow {\mathbb {R}}^+$ are defined, respectively, by

$$\begin{aligned} \sigma (t)=\inf \{s\in {\mathbb {T}}:s>t\},\quad \rho (t)=\sup \{s\in {\mathbb {T}}:s<t\},\quad \mu (t)=\sigma (t)-t. \end{aligned}$$

Definition 2

[41] A point $t\in {\mathbb {T}}$ is called $\left\{ \begin{array}{ll} \text{ left-dense } &{}\quad \mathrm{if} \,t>\inf {\mathbb {T}} \text{ and } \rho (t)=t,\\ \text{ left-scattered } &{} \quad \mathrm{if}\, \rho (t)<t,\\ \text{ right-dense }&{}\quad \mathrm{if}\, t<\sup {\mathbb {T}} \text{ and } \sigma (t)=t,\\ \text{ right-scattered }&{}\quad \mathrm{if}\,\sigma (t)>t. \end{array} \right.$

If ${\mathbb {T}}$ has a left-scattered maximum m, then ${\mathbb {T}}^k={\mathbb {T}}{\setminus }\{m\}$; otherwise ${\mathbb {T}}^k={\mathbb {T}}$.

If ${\mathbb {T}}$ has a right-scattered minimum m, then ${\mathbb {T}}_k={\mathbb {T}}{\setminus }\{m\}$; otherwise ${\mathbb {T}}_k={\mathbb {T}}$.

Definition 3

[41] A function $f:{\mathbb {T}}\rightarrow {\mathbb {R}}$ is rd-continuous provided it is continuous at each right-dense point in ${\mathbb {T}}$ and has a left-sided limit at each left-dense point in ${\mathbb {T}}$.

The set of rd-continuous functions $f:{\mathbb {T}}\rightarrow {\mathbb {R}}$ will be denoted by $\mathrm {C}_{rd}({\mathbb {T}},{\mathbb {R}}).$

Lemma 1

[41] Assume that $p,q:{\mathbb {T}}\rightarrow {\mathbb {R}}$ are two regressive functions, then

$\mathrm{(a)}$ :

$e_0(t,s)\equiv 1$ and $e_p(t,t)\equiv 1,$

$\mathrm{(b)}$ :

$e_p(t,s)=\frac{1}{e_p(s,t)}=e_{\ominus _{p}}(t,s),$

$\mathrm{(c)}$ :

$e_p(t,s)e_p(s,r)=e_p(t,r),$

$\mathrm{(d)}$ :

$(e_p(t,s))^\nabla =p(t)e_p(t,s).$

Lemma 2

[41] Let f, g be $\nabla$-differentiable function on ${\mathbb {T}},$ then

$\mathrm{(a)}$ :

$(v_1f+v_2g)^\nabla =v_1f^\nabla +v_2g^\nabla ,$    for any constant $v_1,v_2,$

$\mathrm{(b)}$ :

$(fg)^\nabla (t)=f^\nabla (t)g(t)+f(\sigma (t))g^\nabla (t)=f(t)g^\nabla (t)+f^\nabla (t)g(\sigma (t)).$

Lemma 3

[41] Assume that $p(t)\ge 0,$ for $t\ge s$, then $e_p(t,s)\ge 1.$

Definition 4

[41] A function $p:{\mathbb {T}}\rightarrow {\mathbb {R}}$ is called $\nu$-regressive if $1-\nu (t)p(t)\ne 0$ for all $t\in {\mathbb {T}}_k$. If $p\in {\mathscr {R}}_\nu$ then we define the nabla exponential function by

$$\begin{aligned} e_p(t,s)=exp\bigg (\displaystyle \int _{s}^{t}{\hat{\xi }}_{\nu (\tau )}(p(\tau ))\nabla \tau \bigg ),\;\text{ for } \text{ all } t,\;s\in {\mathbb {T}}, \end{aligned}$$

where $\mu$-cylinder transformation is as in

$$\begin{aligned} {\hat{\xi }}_h(z):=\left\{ \begin{array}{ll} -\frac{1}{h}\log (1+zh) &{}\quad \text{ if } h\ne 0\\ -z &{}\quad \text{ if } h=0. \end{array} \right. \end{aligned}$$

Definition 5

[41] Let $\rho :{\mathbb {T}}\rightarrow {\mathbb {R}}$ is called $\mu$-regressive provided $1+\mu (t)\rho (t)\ne 0$ for all $t\in {\mathbb {T}}^k;$$\rho :{\mathbb {T}}\rightarrow {\mathbb {R}}$ is called positively regressive provided $1+\mu (t)\rho (t)>0$ for all $t \in {\mathbb {T}}^k.$ The set of all regressive and rd-continuous functions $\rho : {\mathbb {T}}\rightarrow {\mathbb {R}}$ will be denoted by ${\mathscr {R}}={\mathscr {R}}({\mathbb {T}},{\mathbb {R}}),$ and The set of all regressive and rd-continuous functions $\rho : {\mathbb {T}}\rightarrow {\mathbb {R}}$ will be denoted by ${\mathscr {R}}^+={\mathscr {R}}^+({\mathbb {T}},{\mathbb {R}}).$

Lemma 4

[41] Suppose that $p\in {\mathscr {R}}^+$, then

• (i) $e_p(t,s)>0,$ for all $t,\; s \in {\mathbb {T}},$

• (ii) if $p(t)\le q(t)$ for all $t\ge s,$$t,\; s \in {\mathbb {T}}$, then $e_p(t,s)\le e_q(t,s),$ for all $t\ge s.$

Lemma 5

[41] If $p \in {\mathscr {R}}$ and $a,b,c \in {\mathbb {T}},$ then

$$\begin{aligned}{}[e_p(c,.)]^\nabla =-p[e_p(c,.)]^\sigma \end{aligned}$$

and

$$\begin{aligned} \int _{a}^{b}p(t)e_p(c,\sigma (t))\nabla t=e_p(c,a)-e_q(c,b). \end{aligned}$$

Definition 6

[41] Let $p,q:{\mathbb {T}}\rightarrow {\mathbb {R}}$ are two regressive functions, define

• (1) $(p\oplus _\nu q)(t)=p(t)+q(t)-\nu p(t)q(t),$

• (2) $\ominus _\nu p(t)=-\frac{p(t)}{1-\nu p(t)},$

• (3) $p\ominus _\nu q=p\oplus _\nu (\ominus _\nu q).$

Lemma 6

[41] Let $a\in {\mathbb {T}}^k, b \in {\mathbb {T}}$ and assume that $f:{\mathbb {T}}\times {\mathbb {T}}^k\rightarrow {\mathbb {R}}$ is continuous at (t, t) where $t\in {\mathbb {T}}^k$ with $t>a.$ Also assume that $f^\nabla (t,.)$ is rd-continuous on $[a, \sigma (t)].$ Suppose that for each $\varepsilon >0,$ there exists a neighborhood U of $\tau \in [a ,\sigma (t)]$ such that

$$\begin{aligned} |[f(\sigma (t),\tau )-f(s,\tau )]-f^\nabla (t,\tau )[\sigma (t)-s]|< & {} \varepsilon |\sigma (t)-s|, \forall s \in U \end{aligned}$$

where $f^\nabla$ denotes the derivative of f with respect to the first variable. Then

$$\begin{aligned} g(t):=\int _{a}^{t}f(t,\tau )\nabla \tau&\text{ implies }&g^\nabla (t):= \int _{a}^{t}f^\nabla (t,\tau )\nabla \tau +f(\sigma (t),t), \\ h(t):=\int _{t}^{b}f(t,\tau )\nabla \tau&\text{ implies }&h^\nabla (t):= \int _{t}^{b}f^\nabla (t,\tau )\nabla \tau -f(\sigma (t),t). \\ \end{aligned}$$

In the following, we recall some definitions, notations and basic results of almost periodicity and pseudo almost periodicity on time scales. For more details, we refer the reader to [42]

In this paper, we restrict our discussion on almost periodic time scales.

Definition 7

[42] Let ${\mathbb {T}}$ be an almost periodic time scale. A function $f (t) : {\mathbb {T}} \rightarrow {\mathbb {R}}^n$ is said to be almost periodic on ${\mathbb {T}}$, if for any $\varepsilon > 0,$ the set

$$\begin{aligned} E(\varepsilon , f ) = \bigg \{\tau \in \varPi : | f (t + \tau ) - f (t)| < \varepsilon , \; \forall t \in {\mathbb {T}}\bigg \} \end{aligned}$$

is relatively dense, that is, for any $\varepsilon > 0,$ there exists a constant $l(\varepsilon ) > 0$ such that each interval of length $l(\varepsilon )$ contains at least one $\tau \in E(\varepsilon , f )$ such that

$$\begin{aligned} | f (t + \tau ) - f (t)| < \varepsilon ,\; \forall t \in {\mathbb {T}}. \end{aligned}$$

The set $E(\varepsilon , f )$ is called the $\varepsilon$-translation set of f(t),  $\tau$ is called the $\varepsilon$-translation number of f(t),  and $l(\varepsilon )$ is called the inclusion of $E(\varepsilon , f ).$

In the following, we introduce some notations

$$\begin{aligned} \begin{array} {lll} \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)&{}=&{}\big \{ f\in \mathrm {C}({\mathbb {T}},{\mathbb {R}}^n) : f \text{ is } \text{ almost } \text{ periodic } \big \},\\ \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n)&{}=&{}\bigg \{ f\in \mathrm {BC}({\mathbb {T}},{\mathbb {R}}^n) : \text{ f } \text{ is } \nabla {\mathrm {-}}\text{ measurable } \text{ such } \text{ that } \\ &{}&{}\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\displaystyle \int _{t_0-r}^{t_0+r} |f(s)| \nabla s =0,\; \text{ where } t_0\in {\mathbb {T}}, r\in \varPi \bigg \}. \end{array} \end{aligned}$$

Definition 8

[42] Let ${\mathbb {T}}$ be an almost periodic time scale. A function $f \in \mathrm {C}({\mathbb {T}},{\mathbb {R}}^n)$ is said to be pseudo almost periodic, if $f = g + \phi , \text{ where } g \in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n) \text{ and } \phi \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$ We denote by $\mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n)$ the set of all such functions.

3 Existence of Pseudo Almost Periodic Solution

In this section, we establish some results for the existence and the uniqueness of the pseudo almost-periodic solution of (4).

Lemma 7

[42] If $\varphi , \psi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}})$, then $\varphi + \psi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}})$.

Lemma 8

[42] If $\varphi , \psi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}})$, then $\varphi \times \psi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}})$.

Lemma 9

If $f\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),$ satisfies the Lipschitcz condition, $\theta \in \mathrm {C^1} ({\mathbb {T}},\varPi )$ is almost periodic, $\theta (t)\ge 0$ and $1-\theta ^{\nabla }(t)>0,$ then $f(t-\theta (t))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n).$

Proof

From Definition 8, we have $f=h+\varphi ,$ where $h\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n),$ and $\varphi \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$ Clearly, $h(t-\theta (t))\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n).$

Letting $\beta =\sup \nolimits _{t\in {\mathbb {T}}}\frac{1}{1-\theta ^{\nabla }(t)}$ and $s=t-\theta (t)$ give us

$$\begin{aligned} 0\le \frac{1}{2r}\int _{t_0-r}^{t_0+r} |\varphi (t-\theta (t))|\nabla t\le & {} \frac{1}{2r}\int _{t_0-r-\theta (t_0-r)}^{t_0+r-\theta (t_0+r)} |\varphi (s)| \sup \limits _{t\in {\mathbb {T}}}\frac{1}{1-\theta ^{\nabla }(t)} \nabla s\\\le & {} \beta \frac{1}{2r}\int _{t_0-(r+\theta (t_0-r))}^{t_0+r-\theta (r)} |\varphi (s)| \nabla s\\\le & {} \beta \frac{r+\theta ^+}{r} \frac{1}{2(r+\theta ^+)} \int _{t_0-(r+\theta ^+)}^{t_0+(r+\theta ^+)} |\varphi (s)|\nabla s\\ \end{aligned}$$

which, together with the fact that $\lim \nolimits _{r\rightarrow +\infty }\frac{1}{2(r+\theta ^+)}\int _{t_0-(r+\theta ^+)}^{t_0+(r+\theta ^+)} |\varphi (s)|\nabla s=0,$ implies that $\lim \nolimits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} |\varphi (t-\theta (t))|\nabla t=0,$ and $\varphi (t-\theta (t))\in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$$\square$

Lemma 10

For $i, \;j =1,\dots ,n,$ if $\varphi (.) \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),$ then

$$\begin{aligned} \displaystyle \int _{0}^{+\infty } N_{ij}(s) | \varphi (t-s)| \nabla s \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n). \end{aligned}$$

Proof

Obviously, one can obtain

$$\begin{aligned} \frac{1}{2r} \int _{t_0-r}^{t_0+r}\bigg (\int _{0}^{+\infty } N_{ij}(s) | \varphi (t-s)| \nabla s\bigg )\nabla t= & {} \int _{0}^{+\infty } N_{ij}(s) \bigg ( \frac{1}{2r} \int _{t_0-r}^{t_0+r} | \varphi (t-s)| \nabla t\bigg ) \nabla s. \end{aligned}$$

Let $M^{\varphi }=\sup \nolimits _{\theta \in {\mathbb {T}}} |\varphi (\theta )|,$ and we get

$$\begin{aligned} \int _{0}^{+\infty } N_{ij}(s) \bigg ( \frac{1}{2r} \int _{t_0-r}^{t_0+r} | \varphi (t-s)| \nabla t\bigg ) \nabla s\le & {} \int _{0}^{+\infty } N_{ij}(s) \nabla s M^{\varphi }= N_{ij}^+ M^{\varphi }. \end{aligned}$$

For any sequence $\{r_m\}_{m=1}^{+\infty }$ satisfying

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty }r_m =+ \infty ,\quad r_m>0, \quad m=1,2,\dots , \end{aligned}$$

we denote

$$\begin{aligned} f_m(s)=N_{ij}(s) \frac{1}{2r_m} \int _{t_0-r_m}^{t_0+r_m} | \varphi (t-s)| \nabla t,\quad m=1,2,\dots , \end{aligned}$$

Then

$$\begin{aligned} \lim \limits _{m\rightarrow +\infty } f_m(s)=0, \end{aligned}$$

and

$$\begin{aligned} |f_m(s)|\le M^{\varphi } N_{ij}^+,\quad \forall s\in [0, +\infty )_{{\mathbb {T}}},\; m=1,2,\dots . \end{aligned}$$

According to the Lebesgue dominated convergence theorem, we have

$$\begin{aligned} \lim \limits _{m\rightarrow +\infty } \int _{0}^{+\infty } N_{ij}(s) \bigg ( \frac{1}{2r_m} \int _{t_0-r_m}^{t_0+r_m} | \varphi (t-s)| \nabla t\bigg ) \nabla s =0, \end{aligned}$$

which entails that

$$\begin{aligned}&\lim \limits _{r \rightarrow +\infty }\frac{1}{2r} \int _{t_0-r}^{t_0+r}\bigg (\int _{0}^{+\infty } N_{ij}(s) | \varphi (t-s)| \nabla s\bigg )\nabla t\\&\quad = \lim \limits _{r \rightarrow +\infty } \int _{0}^{+\infty } N_{ij}(s) \bigg ( \frac{1}{2r} \int _{t_0-r}^{t_0+r} | \varphi (t-s)| \nabla t\bigg ) \nabla s =0. \end{aligned}$$

Thus

$$\begin{aligned} \int _{0}^{+\infty } N_{ij}(s) | \varphi (t-s)| \nabla s \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n). \end{aligned}$$

$\square$

Lemma 11

For $i, \;j =1,\dots ,n,$ if $x_j(.)\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),$ then

$$\begin{aligned} d_{ij}(t)\int _{0}^{+\infty } N_{ij}(s) h_{j} (x_{j}(t-s)) \nabla s \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n). \end{aligned}$$

Proof

From Definition 8, we have $x_j(t)=\psi _j(t)+\varphi _j(t),$ where $\psi _j\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)$ and $\varphi _j\in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$ Since $d_{ij}(.)\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),$ then $d_{ij}(t)=d_{ij}^\psi (t)+d_{ij}^\varphi (t),$ where $d_{ij}^\psi \in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)$, $d_{ij}^\varphi \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$ Therefore,

$$\begin{aligned} d_{ij}(t)\int _{0}^{\infty } N_{ij}(s) h_{j}(x_{j}(t-s)) \nabla s= & {} d_{ij}^\psi (t) \int _{0}^{\infty } N_{ij}(s) h_{j} (\psi _{j}(t-s)) \nabla s \\&+ d_{ij}^\varphi (t)\int _{0}^{\infty } N_{ij}(s) h_{j} (\psi _{j}(t-s)) \nabla s\\&+ d_{ij}(t)\int _{0}^{\infty } N_{ij}(s) \bigg [h_{j}\big (\varphi _{j}(t-s)+ \psi _j(t-s)\big )\\&- h_j(\psi _j(t-s))\bigg ] \nabla s \end{aligned}$$

In view of $\mathbf {(H_1)}$, the definition of $\mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)$ and Lemma 10, we can deduce that

$$\begin{aligned} d_{ij}^\psi (t) \int _{0}^{\infty } N_{ij}(s) h_{j} (\psi _{j}(t-s)) \nabla s \in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n), \end{aligned}$$

(7)

and

$$\begin{aligned} \int _{0}^{\infty } N_{ij}(s)| \varphi _{j}(t-s)| \nabla s \in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n), \quad i,\;j=1,2\dots ,n. \end{aligned}$$

(8)

Hence

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} \bigg |d_{ij}^\varphi (t)\int _{0}^{+\infty } N_{ij}(s) h_{j} (\psi _{j}(t-s)) \nabla s\nonumber \\&+ d_{ij}(t)\int _{0}^{+\infty } N_{ij}(s) \bigg [h_{j}\big (\varphi _{j}(t-s)+ \psi _j(t-s)\big )-h_j(\psi _j(t-s))\bigg ] \nabla s \bigg | \nabla t \nonumber \\\le & {} \sup \limits _{t\in {\mathbb {T}}}\bigg |\int _{0}^{+\infty } N_{ij}(s) h_{j} (\psi _{j}(t-s))\nabla s\bigg | \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r}|d_{ij}^\varphi (t)|\nabla t\nonumber \\&+ d^+_{ij} L_j^h \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} \bigg (\int _{0}^{+\infty } N_{ij}(s)| \varphi _{j}(t-s)| \nabla s\bigg ) \nabla t=0, \end{aligned}$$

(9)

which, together with (7) and (9), implies that

$$\begin{aligned} d_{ij}(t)\int _{0}^{\infty } N_{ij}(s) h_{j} (x_{j}(t-s)) \nabla s \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),\quad i,\;j=1,2,\dots ,n. \end{aligned}$$

$\square$

Lemma 12

For $i, \;j =1,\dots ,n,$ if $x_j(.)\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),$ then

$$\begin{aligned} b_{ij}(t) g_{j} (x_{j}(t-\tau (t)))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),\quad c_{ij}(t) f_{j} (x_{j}(t))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n). \end{aligned}$$

Proof

By Lemma 9 we have $x_{j}(t-\tau (t))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n).$ Furthermore, let

$$\begin{aligned} x_{j}(t-\tau (t))=x_j^1(t)+x_j^2(t), \end{aligned}$$

where $x_j^1\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)$, $x_j^2\in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n).$ Since $b_{ij}\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),\quad i,\;j=1,\dots ,n,$ then

$$\begin{aligned} b_{ij}(t)=b_{ij}^1(t)+b_{ij}^2(t), \end{aligned}$$

where $b_{ij}^1\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n)$, $b_{ij}^2\in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}}^n),$$i,\;j=1,\dots ,n.$ Then, for all $t\in {\mathbb {T}}$, we get

$$\begin{aligned} b_{ij}(t) g_{j} (x_{j}(t-\tau (t)))= & {} \big [b_{ij}^1(t)+b_{ij}^2(t)\big ] g_{j} \big (x_{j}^1(t)+x_j^2(t)\big )\\= & {} b_{ij}^1(t)g_j(x_j^1(t))+b_{ij}^2(t)g_j(x_j^1(t))\\&+ b_{ij}(t)\big [g_j(x_j^1(t)+x_j^2(t))-g_j(x_j^1(t))\big ]. \end{aligned}$$

Clearly,

$$\begin{aligned} b_{ij}^1(t)g_j(x_j^1(t))\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}^n),\quad i,\;j=1,\dots ,n. \end{aligned}$$

(10)

Now, we choose constants $\alpha _j$ and $\eta _j$ such that $\alpha _j=\sup \nolimits _{t\in {\mathbb {T}}}|g_j(x_j^1(t))|,\quad \eta _j=\sup \nolimits _{t\in {\mathbb {T}}}|L_j^g b_{ij}(t)|.$ Consequently,

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} \bigg |b_{ij}^2(t)g_j(x_j^1(t))+b_{ij}(t)\big [g_j(x_j^1(t)+x_j^2(t))-g_j(x_j^1(t))\big ]\bigg | \nabla t\\\le & {} \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} |b_{ij}^2(t)||g_j(x_j^1(t))| \nabla t+ \lim \limits _{z\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} |L_j^g b_{ij}(t)||x_j^2(t)|\nabla t\\\le & {} \alpha _j \lim \limits _{r\rightarrow +\infty }\frac{1}{2r} \int _{t_0-r}^{t_0+r}|b_{ij}^2(t)| \nabla t+ \eta _j \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_0-r}^{t_0+r} |x_j^2(t)|\nabla t=0. \end{aligned}$$

It follows from (10) that $b_{ij}(t) g_{j} (x_{j}(t-\tau (t)))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n).$ Similarly,

$$\begin{aligned} c_{ij}(t) f_{j} (x_{j}(t))\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}^n),\quad i,\;j=1,\dots ,n. \end{aligned}$$

$\square$

Lemma 13

Define a nonlinear operator $\varGamma$ by setting

$$\begin{aligned} (\varGamma _\varphi )(t)= & {} \int _{-\infty }^t e_{-a_i}\left( t,\sigma (s)\right) F_i(s)\nabla s,\;i=1,2,\dots ,n, \end{aligned}$$

where

$$\begin{aligned} F_i(s)= & {} - a_i(s)p_i(s)\varphi _i(s-r_i(s))+\sum \limits _{j=1}^{n} c_{ij}(s) f_{j} ( \varphi _{j}(s))+ \sum \limits _{j=1}^n b_{ij}(s) f_j(\varphi _j(s-\tau (s)))\\&+\,\sum \limits _{j=1}^{n} d_{ij}(s)\int ^{\infty }_{0} N_{ij}(s-u) h_{j}(\varphi _{j}(u))\nabla u+I_i(s),\; \varphi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}). \end{aligned}$$

Then $\varGamma _\varphi \in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}).$

Proof

According to $\mathbf {(H1)}$ and $\mathbf {(H4)},$ it is easily to see that $\varGamma \in \mathrm {BC}({\mathbb {T}},{\mathbb {R}}^n).$ From Lemmas 7, 8, 9, 10, 11, 12 we obtain that there are $H_i\in \mathrm {AP}({\mathbb {T}},{\mathbb {R}})$ and $\varPhi _i\in \mathrm {PAP_0}({\mathbb {T}},{\mathbb {R}})$ such that

$$\begin{aligned} F_i(t)=H_i(t)+\varPhi _i(t)\in \mathrm {PAP}({\mathbb {T}},{\mathbb {R}}),\; i\in \{1,2,\dots ,n\} \end{aligned}$$

Noting that $M[a_i]>0,$ using the theory of exponential dichotomy in [42] , we get that

$$\begin{aligned} \int _{-\infty }^t e_{-a_i}(t,\sigma (s))H_i(s)\nabla s \in \mathrm {AP}({\mathbb {T}},{\mathbb {R}}) \end{aligned}$$

(11)

satisfies $y_i^\nabla (t)=-a_i(t)y_i(t)+H_i(t),\; i\;\in \{1,2,\dots ,n\}.$

Arguing as in the verification of Lemma 11 , one can show

$$\begin{aligned} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{t_0-r}^{t_0+r} \int _0^{+\infty } e_{-a^-_i}(u,0) |\varPhi _i(t-u)|\nabla u\nabla t =0,\; i\in \{1,2,\dots ,n\}. \end{aligned}$$

Then

$$\begin{aligned} 0\le & {} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{t_0-r}^{t_0+r} \int ^t_{-\infty } e_{-a_i}(t,\sigma (s)) |\varPhi _j(s)|\nabla s\nabla t\\\le & {} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{t_0-r}^{t_0+r} \int ^t_{-\infty } e_{-a^-_i}(t,\sigma (s)) |\varPhi _j(s)|\nabla s\nabla t\\\le & {} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{t_0-r}^{t_0+r} \int ^{+\infty }_0 e_{-a^-_i}(u,0) |\varPhi _j(t-u)|\nabla u\nabla t=0 \end{aligned}$$

and

$$\begin{aligned} \int _{-\infty }^t e_{-a_i(t,\sigma (s))}\varPhi _j(s)ds\in \mathrm {PAP_0}({\mathbb {R}},{\mathbb {R}}), \; i,\;j\in \{1,2\dots ,n\}. \end{aligned}$$

Combining with (11), it leads to

$$\begin{aligned} (\varGamma _\varphi )(t)= & {} \int _{-\infty }^t e_{-a_i}\left( t,\sigma (s)\right) H_j(s)\nabla s\\&+\,\int _{-\infty }^t e_{-a_i}\left( t,\sigma (s)\right) \varPhi _j(s)\nabla s\in \mathrm {PAP}({\mathbb {R}},{\mathbb {R}}) ,\;i=1,2,\dots ,n, \end{aligned}$$

Theorem 1

Let $\mathbf (H_1)$–$\mathbf (H_4)$ hold. Then, system (10) has a pseudo almost periodic solution in

$$\begin{aligned} B=\left\{ \varphi \in \mathrm {PAP}({\mathbb {R}},{\mathbb {R}}^n), \Vert \varphi -\varphi _0\Vert _{\infty }\le \frac{r \beta }{(1-r)} \right\} , \end{aligned}$$

where

$$\begin{aligned} \varphi _{0}(t) = \left( \begin{array}{c} \int _{-\infty }^{t} e_{-a_{1}}(t,\sigma (s)) I_{1}(s)ds \\ \vdots \\ \int _{-\infty }^{t} e_{-a_{n}}(t,\sigma (s) I_{n}(s)ds \end{array} \right) . \end{aligned}$$

Proof

Let

$$\begin{aligned} Y_i(t)=x_i(t)-p_i(t)x_i(t-r_i(t)),\; 1\le i\le n. \end{aligned}$$

We obtain from (4) that

$$\begin{aligned} Y_i^{\nabla }(t)= & {} [x_i(t)-p_i(t)x_i(t-r_i(t))]^\nabla \nonumber \\= & {} - a_{i}(t) Y_{i}(t)-a_i(t)p_i(t)x_i(t-r_i(t))+ \sum \limits _{j=1}^{n} c_{ij}(t) f_{j} ( x_{j}(t))\nonumber \\&+\, \sum \limits _{j=1}^{n} b_{ij}(t) g_{j}(x_{j}(t-\tau (t))) + \sum \limits _{j=1}^{n} d_{ij}(t)\int _{-\infty }^{t} N_{ij}(t-s) h_{j}(x_{j}(s))\nabla s\nonumber \\&+\,I_{i}(t),\; 1 \le i\le n,\; t\in {\mathbb {T}}. \end{aligned}$$

(12)

Define an operator as follows:

$$\begin{aligned} \varPhi : B \rightarrow B, (\varphi _1,\dots ,\varphi _n)^T\rightarrow \left( (\varPhi _\varphi )_1,\dots ,(\varPhi _\varphi )_n\right) ^T, \end{aligned}$$

where

$$\begin{aligned} (\varPhi _\varphi )_i(t)=p_i(t)x_i(t-r_i(t))+(\varGamma _\varphi )_i(t),\; \forall \varphi \in B. \end{aligned}$$

One has

$$\begin{aligned} \parallel \varphi _{0} \parallel _{\infty }= & {} \sup _{t \in {\mathbb {R}}} \max _{ 1 \le i\le n} \bigg \{\big | \int _{-\infty }^{t} e_{-a_{i} } (t,\sigma (s)) I_{i}(s)ds \big | \bigg \}\\\le & {} \max _{ 1 \le i\le n} \bigg \{\frac{I^+_{i}}{a_{i}^-}\bigg \} = \beta \end{aligned}$$

after

$$\begin{aligned} \parallel \varphi \parallel _{\infty }\le & {} \parallel \varphi - \varphi _{0} \parallel _{\infty } + \parallel \varphi _{0} \parallel _{\infty }\\\le & {} \parallel \varphi - \varphi _{0} \parallel _{\infty } + \beta . \end{aligned}$$

Set $B= \{ \varphi \in \mathrm {PAP}({\mathbb {R}},{\mathbb {R}}^{n}),\parallel \varphi - \varphi _{0} \parallel _{\infty } \le \frac{r\beta }{(1-r)} \}$. Clearly, B is a closed convex subset of $\mathrm {PAP}({\mathbb {R}},{\mathbb {R}}^{n})$ and, therefore, for any $\varphi \in B$ by using the estimate just obtained, we see that

$$\begin{aligned} | \varPhi _{\varphi } (t)- \varphi _{0}(t) |= & {} \bigg | p_i(t)\varphi _i(t-r_i(t))+\int _{-\infty }^{t} e_{-a_{i}}(t,\sigma (s)) \bigg (-a_i(s)p_i(s)\varphi _i(s-r_i(s))\\&+\,\sum _{j=1}^{n} c_{ij}(s) f_{j} (\varphi _{j}(s))+\sum _{j=1}^{n} b_{ij}(s) g_{j}(\varphi _{j}(s-\tau (t)))\\&+\,\sum _{j=1}^{n} d_{ij}(s) \int _{-\infty }^{s} N_{ij}(s-m) h_{j}(\varphi _{j}(m))\nabla m \bigg )\nabla s\bigg |\\\le & {} p_i^+|\varphi _i(t-r_i(t))|+\int _{-\infty }^{t} e_{-a_{i}^-}(t,\sigma (s)) \bigg ( a_i^+p_i^+|\varphi _i(t-r_i(t))|\\&+\, \sum _{j=1}^{n} c_{ij}^+ L_j^f |\varphi _{j}(s)|\\&+\,\sum _{j=1}^{n} b_{ij}^+ L_j^g|\varphi _{j}(s-\tau (t))|+\sum _{j=1}^{n} d_{ij}^+ L_j^h \int _{-\infty }^{s} N_{ij}(s-m) |\varphi _{j}(m))| \nabla m \nabla s \\\le & {} p_i^+ \parallel \varphi \parallel _{\infty }+ \int _{-\infty }^{t} e_{-a_{i}^-}(t,\sigma (s)) \nabla s\bigg (a_i^+p_i^++ \sum _{j=1}^{n} (c_{ij}^+ L_{j}^{f} \\&+ b^+_{ij} L_{j}^{g}+d_{ij}N_{ij}^+ L_{j}^{h} ) \bigg ) \parallel \varphi \parallel _{\infty } \\\le & {} p_i^+ \parallel \varphi \parallel _{\infty }+ \frac{1}{a_i^-} \bigg (a_i^+p_i^++ \sum _{j=1}^{n} (c_{ij}^+ L_{j}^{f} + b^+_{ij} L_{j}^{g}+d_{ij}N_{ij}^+ L_{j}^{h} ) \bigg ) \parallel \varphi \parallel _{\infty } \\= & {} \bigg (p_i^+ + \frac{1}{a_i^-} \bigg (a_i^+p_i^++ \sum _{j=1}^{n} (c_{ij}^+ L_{j}^{f} + b^+_{ij} L_{j}^{g}+d_{ij}N_{ij}^+ L_{j}^{h} ) \bigg ) \bigg ) \parallel \varphi \parallel _{\infty } \\= & {} \parallel \varphi \parallel _{\infty } r \le \frac{r \beta }{(1-r)} \end{aligned}$$

which implies that $\varPhi _\varphi \in B.$ Next, we show that $\varPhi : B \rightarrow B$ is contraction operator. In view of $\mathbf {(H_1)},$ for any $\varphi ,\; \psi \in B$, we have

$$\begin{aligned} | \varPhi _{\varphi } (t)- \varPhi _{\psi } (t)|= & {} \bigg |p_i(t)\big (\varphi _i(t-r_i(t))-\psi _i(t-r_i(t))\big )\\&+\, \int _{-\infty }^{t} e_{-a_{i}}(t,\sigma (s)) \bigg [ -a_i(s)p_i(s)\big (\varphi _i(s-r_i(s))-\psi _i(s-r_i(s))\big )\\&+\, \sum _{j=1}^{n} c_{ij}(s)( f_{j} (\varphi _{j}(s)) - f_{j} (\psi _{j}(s))\\&+\, \sum _{j=1}^{n} b_{ij}(s) ( g_{j}(\varphi _{j}(s-\tau (s)))-g_{j}(\psi _{j}(s-\tau (s))))\\&+\, \sum _{j=1}^{n} d_{ij}(s)\int _{-\infty }^{s} N_{ij}(s-m) ( h_{j}(\varphi _{j}(m))- h_{j}(\psi _{j}(m)))\nabla m \big )\bigg ]\nabla s \bigg | \\\le & {} p_i^+\big |\varphi _i(t-r_i(t))-\psi _i(t-r_i(t))\big |\\&+\, \int _{-\infty }^{t} e_{-a_{i}}(t,\sigma (s)) \bigg [a_i^+ p_i^+ \big |\varphi _i(s-r_i(s))-\psi _i(s-r_i(s))\big |\\&+\, \sum _{j=1}^{n} c_{ij}^+ L_j^f \big |\varphi _{j}(s) - \psi _{j}(s)\big | + \sum _{j=1}^{n} b_{ij}^+L_j^g \big |\varphi _{j}(s-\tau (s))-\psi _{j}(s-\tau (s)))\big |\\&+\, \sum _{j=1}^{n} d_{ij}^+ L_j^h \int _{-\infty }^{s} N_{ij}(s-m) \big |\varphi _{j}(m)- \psi _{j}(m))\big |\nabla m \bigg ]\nabla s \\\le & {} p_i^++ \int _{-\infty }^{t} e_{-a_{i}^-}(t,\sigma (s)) \nabla s \bigg (a_i^+ p_i^+ + \sum _{j=1}^{n} \big (c_{ij}^+ L_j^f \\&+ b_{ij}^+L_j^g + d_{ij}^+ L_j^hN_{ij}^+ \big ) \bigg ) \parallel \varphi -\psi \parallel _{\infty } \\\le & {} p_i^++ \frac{1}{a_i^-} \bigg (a_i^+ p_i^+ + \sum _{j=1}^{n} \big (c_{ij}^+ L_j^f + b_{ij}^+L_j^g + d_{ij}^+ L_j^hN_{ij}^+ \big ) \bigg ) \parallel \varphi -\psi \parallel _{\infty } \\< & {} r \parallel \varphi -\psi \parallel _{\infty }, \end{aligned}$$

because $r<1$, which prove that $\varPhi$ is a contraction mapping. Then, by virtue of the Banach fixed point theorem, $\varPhi$ has a unique fixed point which corresponds to the solution of (4) in $B\subset \mathrm {PAP}({\mathbb {R}},{\mathbb {R}}^{n})$. $\square$

4 Exponential Stability of Pseudo Almost Periodic Solution

In this section, we establish some results for the global exponential stability of the unique $\mathrm {PAP}$ solutions of (4).

Theorem 2

Assume that $\mathbf (H_1)$–$\mathbf (H_4)$ hold, then the unique system $\mathrm {PAP}$ solution of system (4) is globally exponentially stable.

Proof

From Theorem 1, we see that system (4) has a unique $\mathrm {PAP}$ solution

$$\begin{aligned} x^*(t)=(x^*_1(t),\dots ,x^*_n(t))^T, \end{aligned}$$

with initial value $\varphi ^*(s)=(\varphi ^*_1(s),\dots ,\varphi ^*_n(t))^T$. Suppose that $x(t)=(x_1(t),\dots ,x_n(t))^T$ is an arbitrary solution of system (4) with initial value $\varphi (s)=(\varphi _1(s),\dots ,\varphi _n(t))^T$ and

$$\begin{aligned} w_i(t)=x_i(t)-x^*_i(t),\;W_i(t)=w_i(t)-p_i(t)w_i(t-r_i(t)),\;i=1,\dots ,n. \end{aligned}$$

Then

$$\begin{aligned} W_i^\nabla (t)= & {} [w_i(t)-p_i(t)w_i(t-r_i(t))]^\nabla \nonumber \\= & {} - a_{i}(t)W_{i}(t)-a_i(t)p_i(t)w_i(t-r_i(t))+ \sum \limits _{j=1}^{n} c_{ij}(t)\big (f_{j}(x_{j}(t))-f_{j}(x^*_{j}(t))\big )\nonumber \\&+\,\sum \limits _{j=1}^{n}b_{ij}(t)\bigg (g_{j}(x_{j}(t-\tau (t)))-g_{j}(x^*_{j}(t-\tau (t)))\bigg )\nonumber \\&+\, \sum \limits _{j=1}^{n} d_{ij}(t)\int _{-\infty }^{t} N_{ij}(t-s) \big (h_{j}(x_{j}(s))-h_{j}(x^*_{j}(s))\big )\nabla s,\;i=1,2\dots ,n. \end{aligned}$$

From $\mathbf {(H_4)}$, there exists a constant $\lambda \in \{0,\min _{1\le i\le n}\{a^-_i\}\}$ such that $1-p^+_iexp(\lambda r^+_i)>0,$ and

$$\begin{aligned}&\displaystyle \max _{1\le i\le n}\bigg \{\frac{1}{(1-p^+_i\exp (\lambda r^+_i))(a^-_i-\lambda )}\bigg (\exp (\lambda r^+_i)a^+_ip^+_i+\displaystyle \sum _{j=1}^{n}c^+_{ij}L^f_j+\displaystyle \sum _{j=1}^{n}b^+_{ij}L^g_j\exp (\lambda \tau ^+)\\&\quad +\displaystyle \sum _{j=1}^{n}d^+_{ij}L^h_j\int _0^{+\infty }N_{ij}(u) \exp (\lambda u)\nabla u\bigg )\bigg \}<1. \end{aligned}$$

Denote

$$\begin{aligned} \Vert \varphi \Vert _0=\displaystyle \sup _{t\in (-\infty ,0]_{\mathbb {T}}}\max _{1\le i\le n}|(\varphi _i(t)-x^*_i(t))-p_i(t)(\varphi _i(t-r_i(t))-x^*_i(t-r_i(t)))| \end{aligned}$$

and

$$\begin{aligned} \Vert W(t)\Vert =\displaystyle \max _{1\le i\le n}|W_i(t)|. \end{aligned}$$

Let $\varepsilon >0$ and $M>1$. It’s easy to see that

$$\begin{aligned} \Vert W(0)\Vert <(\Vert \varphi \Vert _0+\varepsilon ), \end{aligned}$$

(13)

and

$$\begin{aligned} \Vert W(t)\Vert<(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t,t_0)<M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t,t_0),\;\;\forall t\in (-\infty ,0]_{\mathbb {T}}. \end{aligned}$$

(14)

We claim that

$$\begin{aligned} \Vert W(t)\Vert <M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t,t_0),\;\;\forall t\in (0,+\infty )_{\mathbb {T}}. \end{aligned}$$

(15)

Contrarily, there exist a $t_1\in (t_0,+\infty )_{\mathbb {T}}$ and some $i\in \{1,\dots ,n\}$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} |W_i(t_1)|=\Vert W(t_1)\Vert \ge M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0),\\ \Vert W(t)\Vert \le M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0),\;\;t\in (t_0,t_1]_{\mathbb {T}}. \end{array}\right. \end{aligned}$$

(16)

Therefore, there must exist a constant $\omega > 1$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} |W_i(t_1)|=\Vert W(t_1)\Vert =\omega M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0),\\ \Vert W(t)\Vert \le \omega M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0),\;\;t\in (t_0,t_1]_{\mathbb {T}}. \end{array}\right. \end{aligned}$$

(17)

On the other hand,

$$\begin{aligned} e_{\lambda }(t_2,t_0)|w_i(t_2)|\le & {} e_\lambda (t_2,t_0)|w_i(t_2)-p_i(t_2)w_i(t_2-r_i(t_2))|+e_\lambda (t_2,t_0)|p_i(t_2)w_i(t_2-r_i(t_2))|\nonumber \\\le & {} e_\lambda (t_2,t_0)|w_i(t_2)|+p^+_i\exp (\lambda r^+_i)e_{\lambda }(t_2-r_i(t_2),t_0)|w_i(t_2-r_i(t_2))|\nonumber \\\le & {} \omega M(\Vert \varphi \Vert _0+\varepsilon )+p^+_i\exp (\lambda r^+_i)\displaystyle \sup _{s\le t}e_\lambda (s,t_0)|w_i(t)|, \end{aligned}$$

(18)

for all $t_2\le t$, $t <t_1$, which implies that

$$\begin{aligned} e_\lambda (t,t_0)|w_i(t)|\le \displaystyle \sup _{s\le t}e_\lambda (s,t_0)|w_i(s)|\le \frac{\omega M(\Vert \varphi \Vert _0+\varepsilon )}{1-p^+_iexp(\lambda r^+_i)}. \end{aligned}$$

(19)

Integrating, for all $s\in [t_0,t]_{\mathbb {T}}$

$$\begin{aligned}&e_{-a_i}(t_0,\sigma (s))(W^\nabla _i(s)+a_i(s)W_i(s))=e_{-a_i}(t_0,\sigma (s))\bigg [-a_i(s)p_i(s)w_i(s-r_i(s))\nonumber \\&\quad +\sum \limits _{j=1}^{n} c_{ij}(s)\big (f_{j}(x_{j}(s))-f_{j}(x^*_{j}(s))\big )\nonumber \\&\quad +\sum \limits _{j=1}^{n}b_{ij}(s)\bigg (g_{j}(x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s)))\bigg )\nonumber \\&\quad +\sum \limits _{j=1}^{n} d_{ij}(s)\int _{-\infty }^{s} N_{ij}(s-u) \big (h_{j}(x_{j}(u))-h_{j}(x^*_{j}(u))\big )\nabla u\bigg ],\quad \end{aligned}$$

(20)

we get

$$\begin{aligned} W_i(t)= & {} W_i(t_0)e_{-a_i}(t,t_0)+\displaystyle \int _{t_0}^{t}e_{-a_i(t,r(s))}\bigg [-a_i(s)p_i(s)w_i(s-r_i(s))\nonumber \\&+\,\sum \limits _{j=1}^{n} c_{ij}(s)\big (f_{j}(x_{j}(s))-f_{j}(x^*_{j}(s))\big )\nonumber \\&+\,\sum \limits _{j=1}^{n}b_{ij}(s)\bigg (g_{j}(x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s)))\bigg )\nonumber \\&+\,\sum \limits _{j=1}^{n} d_{ij}(s)\int _{-\infty }^{s} N_{ij}(s-u) \big (h_{j}(x_{j}(u))-h_{j}(x^*_{j}(u))\big )\nabla u\bigg ]\nabla s,\;\;s\in [t_0,t]_{\mathbb {T}},\nonumber \\ \end{aligned}$$

(21)

Thus, $M > 1$, (13), (14), (17) and (19) imply that

$$\begin{aligned} |W_i(t_1)|= & {} \bigg |W_i(t_0)e_{-a_i}(t,t_0)+\displaystyle \int _{t_0}^{t_1}e_{-a_i(t_1,\sigma (s))}\bigg [-a_i(s)p_i(s)w_i(s-r_i(s))\nonumber \\&+\,\sum \limits _{j=1}^{n} c_{ij}(s)\big (f_{j}(x_{j}(s))-f_{j}(x^*_{j}(s))\big )\nonumber \\&+\,\sum \limits _{j=1}^{n}b_{ij}(s)\bigg (g_{j}(x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s)))\bigg )\nonumber \\&+\,\sum \limits _{j=1}^{n} d_{ij}(s)\int _{-\infty }^{s} N_{ij}(s-u) \big (h_{j}(x_{j}(u))-h_{j}(x^*_{j}(u))\big )\nabla u\bigg ]\nabla s\bigg |\nonumber \\\le & {} |W_i(t_0)|e_{-a_i}(t,t_0)+\displaystyle \int _{t_0}^{t_1}e_{-a_i(t_1,\sigma (s))}\bigg |-a_i(s)p_i(s)w_i(s-r_i(s))\nonumber \\&+\,\sum \limits _{j=1}^{n} c_{ij}(s)\big (f_{j}(x_{j}(s))-f_{j}(x^*_{j}(s))\big )\nonumber \\&+\,\sum \limits _{j=1}^{n}b_{ij}(s)\bigg (g_{j}(x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s)))\bigg )\nonumber \\&+\,\sum \limits _{j=1}^{n} d_{ij}(s)\int _{-\infty }^{s} N_{ij}(s-u) \big (h_{j}(x_{j}(u))-h_{j}(x^*_{j}(u))\big )\nabla u\bigg |\nabla s\nonumber \\\le & {} |W_i(t_0)|e_{-a_i}(t,t_0)+\displaystyle \int _{t_0}^{t_1}e_{-a_i(t_1,\sigma (s))}\bigg (a^+_ip^+_i|w_i(s-r_i(s))|\nonumber \\&+\,\sum \limits _{j=1}^{n} c^+_{ij}L^f_j|x_{j}(s))-x^*_{j}(s)|\nonumber \\&+\,\sum \limits _{j=1}^{n}b^+_{ij}L^g_j|x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s))|\nonumber \\&+\,\sum \limits _{j=1}^{n}d^+_{ij}\int _{-\infty }^{s}N_{ij}(s-u)L^h_j|x_{j}(u)-x^*_{j}(u)|\nabla u\bigg |\nabla s\nonumber \\\le & {} M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0)e_{-a_i\oplus \lambda }(t_1,t_0)+\displaystyle \int _{t_0}^{t_1}e_{-a_i(t_1,\sigma (s))}\bigg (a^+_ip^+_i|w_i(s-r_i(s))|\nonumber \\&+\,\sum \limits _{j=1}^{n} c^+_{ij}L^f_j|x_{j}(s))-x^*_{j}(s)|+\sum \limits _{j=1}^{n}b^+_{ij}L^g_j|x_{j}(s-\tau (s)))-g_{j}(x^*_{j}(s-\tau (s))|\nonumber \\&+\,\sum \limits _{j=1}^{n}d^+_{ij}\int _{-\infty }^{s}N_{ij}(s-u)L^h_j|x_{j}(u)-x^*_{j}(u)|\nabla u\bigg |\nabla s\nonumber \\\le & {} M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0)e_{-a_i\oplus \lambda }(t_1,t_0)\nonumber \\&+\,\displaystyle \int _{t_0}^{t_1}e_{-a_i\oplus \lambda }(t_1,\sigma (s))\bigg (\frac{exp(\lambda r^+_i)}{1-p^+_iexp(\lambda r^+_i)}a^+_ip^+_i\nonumber \\&+\,\sum \limits _{j=1}^{n} c^+_{ij}L^f_j\frac{1}{1-p^+_i\exp (\lambda r^+_i)}+\sum \limits _{j=1}^{n}b^+_{ij}L^g_j\frac{\exp (\lambda \tau ^+)}{1-p^+_i\exp (\lambda r^+_i)}\nonumber \\&+\,\sum \limits _{j=1}^{n}d^+_{ij}N^+_{ij}L^h_j\frac{\exp (\lambda u)}{1-p^+_i\exp (\lambda r^+_i)}\bigg )\nabla s\omega M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0)\nonumber \\\le & {} \omega M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0)\bigg (\left( \frac{1}{\omega M}-1\right) e_{-a^-_i\oplus \lambda }(t_1,t_0)+1\bigg )\nonumber \\< & {} \omega M(\Vert \varphi \Vert _0+\varepsilon )e_{\ominus \lambda }(t_1,t_0), \end{aligned}$$

(22)

which contradicts the first equation of (16). Therefore, (15) holds. Letting $\varepsilon \longrightarrow +\infty$, we have

$$\begin{aligned} \Vert W(t)\Vert \le M\Vert \varphi \Vert _0e_{\ominus \lambda }(t,t_0),\;\;\forall t\in (t_0,+\infty )_{\mathbb {T}}. \end{aligned}$$

(23)

Therefore, the unique $\mathrm {PAP}$ solution of system (4) is globally exponentially stable and the uniqueness follows from the stability. The proof is complete. $\square$

Remark 3

Note that from the conditions of Theorems 1 and 2, it is easy to see that both the continuous time case and the discrete time case of recurrent neural networks (4) have the same pseudo-almost periodic.

Remark 4

Theorems 1 and 2 are new even for the both cases of differential equations $({\mathbb {T}} = {\mathbb {R}})$ and difference equations $({\mathbb {T}} = {\mathbb {R}})$.

Remark 5

Because neutral-type recurrent NNs with D operator is a class of DOBNFDEs, the stability of its PAP solutions is not easy to be established. Here, the map construction (4) and the variable substitution $Y_i(t)=y_i(t)-p_i(t)y_i(t-r_i(t))$ play a key role in the  proof of Theorem 1, which can be used to analyze the PAP solution problem for other DOBNFDEs.

Remark 6

Set

$$\begin{aligned} C_0({\mathbb {R}}^+,{\mathbb {R}})=\{f\in BC({\mathbb {R}}^+,{\mathbb {R}}),\lim \limits _{t\rightarrow +\infty } |f(t)|=0\} \end{aligned}$$

and

$$\begin{aligned} P_w({\mathbb {R}}^+,{\mathbb {R}})=\{f\in BC({\mathbb {R}}^+,{\mathbb {R}}), f \text{ is } w{\mathrm {-}}\text{ periodic }\}. \end{aligned}$$

A function $f\in BC({\mathbb {R}}^+,{\mathbb {R}})$ is said to be asymptotically w-periodic if it can be expressed as $f=g+h$ where $g\in P_w({\mathbb {R}}^+,{\mathbb {R}})$ and $h\in C_0({\mathbb {R}}^+,{\mathbb {R}}).$ The collection of such functions will be denoted by $AP_w({\mathbb {R}}^+,{\mathbb {R}}).$ The study of the existence of periodic solutions to differential equations is one of the most important topics in the qualitative theory, due both to its mathematical interest and its applications in many scientific fields, such as mathematical biology, control theory, physics, etc. However, some phenomena in the real world are not periodic, but approximately periodic or asymptotically periodic. As a result, in the past several decades many authors proposed and developed several extensions of the concept of periodicity, such as almost periodicity, almost automorphy, pseudo almost periodicity, pseudo almost automorphy. Then, the space of pseudo almost-periodic functions contains strictly the space of almost-periodic functions, of asymptotical periodicity functions, and of periodic functions, the criteria obtained in this paper extend or improve the results given in [43, 44].

5 Numerical Simulations

In this section, we give an example to illustrate the feasibility and effectiveness of our results. Consider the following delayed recurrent NNs with D operator:

$$\begin{aligned}{}[x_i(t)-p_i(t)x_i(t-r_i(t))]^\nabla= & {} - a_{i}(t) x_{i}(t)+ \sum \limits _{j=1}^{2} c_{ij}(t) f_{j} (x_{j}(t))\nonumber \\&+\, \sum \limits _{j=1}^{2} b_{ij}(t) g_{j}(x_{j}(t-\tau (t)))\nonumber \\&+\, \sum \limits _{j=1}^{2} d_{ij}(t)\int _{-\infty }^{t} N_{ij}(t-s) h_{j}(x_{j}(s))\nabla s \nonumber \\&+\, I_{i}(t),\; 1 \le i\le 2,\; t\in {\mathbb {T}}. \end{aligned}$$

(24)

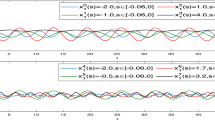
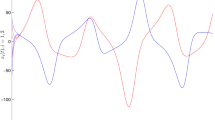
where $f_i(u)=g_i(u)=h_i(u)=\frac{1}{5}\sin (u)$, $p_1(t)=0.1\sin (t)$, $p_2(t)=\frac{1}{15}\cos (t)$, $a_1(t)=0.9+0.1\sin (t)$, $a_2(t)=0.8+0.1\cos (t)$, $c_{11}(t)=0.4+0.1\sin (t)$, $c_{12}(t)=0.3+0.1\cos (t)$, $c_{21}(t)=0.5+0.1\cos (t)$, $c_{22}(t)=0.2+0.1\sin (t)$, $b_{11}(t)=0.2-0.1\cos (t)$, $b_{12}(t)=0.3+0.1\sin (t)$, $b_{21}(t)=0.6-0.1\cos (t)$, $b_{22}(t)=0.5-0.1\sin (t)$, $d_{11}(t)=0.2+0.1\sin (t)$, $d_{12}(t)=0.4+0.1\cos (t)$, $d_{21}(t)=0.2+0.1\cos (t)$, $d_{22}(t)=0.6+0.1\sin (t)$, $r_1(t)=|\cos (t)|$, $r_2(t)=|\sin (t)|$, $\tau (t)=2|cos(t)|$, $N_{ij}=e^{-t}$, $I_1(t)=0.3+0.2\sin (\sqrt{3}t)$, $I_2(t)=0.4+0.1\cos (\sqrt{3}t)$.

By simple calculation, we get

$L^f_i=L^g_i=L^h_i=\frac{1}{5}$, $p^+_1=0.1$, $p^+_2=\frac{1}{15}$, $a^+_1=1$, $a^+_2=0.9$, $a^-_1=0.9$, $a^-_2=0.8$, $c^+_{11}=0.5$, $c^+_{12}=0.4$, $c^+_{21}=0.6$, $c^+_{22}=0.3$, $b^+_{11}=0.3$, $b^+_{12}=0.4$, $b^+_{21}=0.7$, $b^+_{22}=0.6$, $d^+_{11}=0.3$, $d^+_{12}=0.5$, $d^+_{21}=0.3$, $d^+_{22}=0.7$, $r^+1_1=r^+_2=1$, $\tau ^+=2$,

and

$$\begin{aligned} r= & {} \displaystyle \max _{i=1,2}\bigg \{p^+_i+\frac{1}{a^-_i}\bigg (a^+_ip^+_i+\displaystyle \sum _{j=1}^{n}(c^+_{ij}L^f_j+b^+_{ij}L^g_j+d^+_{ij}L^h_j)\bigg )\bigg \}\\= & {} \max \{0.7444,0.9417\}<1. \end{aligned}$$

So condition $\mathbf {(H_4)}$ is satisfied. Therefore, according to Theorems 1 and 2, system (4) has a unique $\mathrm {PAP}$ solution that is globally exponentially stable (see Figs. 1, 2, 3, 4).

Fig. 1

The trajectories of $x_1$ and $x_2$ for $t\in [0, 90]$ (continuous case ${\mathbb {T}}= {\mathbb {R}}$)

Fig. 2

The orbits of $x1-x2$ of (continuous case ${\mathbb {T}}= {\mathbb {R}}$)

Fig. 3

The trajectories of $x_1$ and $x_2$ for $t\in [0, 100]$ (continuous case ${\mathbb {T}}= {\mathbb {Z}}$)

Fig. 4

The orbits of $x_1-x_2$ (continuous case $\mathbb {T }= {\mathbb {Z}}$)

Remark 7

In numerical example, the problem of global exponential stability of PAP solutions of neutral type recurrent NNs (4) with parameters (24) and D operator on time–space scale has not been studied before. One can see that all results obtained in [35, 39, 40, 42] are invalid for system (24).

6 Conclusion and Open Problem

In this paper, we have studied the a class of neutral type recurrent neural networks with time-varying delays, distributed delay and D operator on time–space scales. By using the Banach’s fixed point theorem and the theory of calculus on time scales, we obtain some sufficient conditions for the existence, the uniqueness and the global exponential stability of PAP solutions for system (4). It is the first time that a class of neutral-type recurrent NNs with time-varying delays, distributed delay and D operator on time–space scales is presented. Finally, we formulate some open problems.

Problem 1

We would like to extend our results to more general recurrent NNs with D operator on time–space scales, such as fuzzy recurrent NNs models:

$$\begin{aligned}&[x_i(t)-p_i(t)x_i(t-q_i(t))]^\nabla \\&\quad =-c_{i}(t) x_{i}(t)+ \sum \limits _{j=1}^{n} a_{ij}(t) f_{j} (x_{j}(t))+\sum \limits _{j=1}^{n} b_{ij}(t) g_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&\qquad +\sum \limits _{j=1}^{n} d_{ij}(t)\int _{-\infty }^{t}k_{ij}(t-s) h_{j}(x_{j}(s))\nabla s +\displaystyle \sum _{j=1}^{n}e_{ij}(t)\nu _j(t)+\bigwedge _{j=1}^{n}T_{ij}(t)\nu _j(t)\\&\qquad +\bigwedge _{j=1}^{n}\alpha _{ij}(t)f_j(x_j(t-\tau _{ij}(t))) +\bigvee _{j=1}^{n}\beta _{ij}(t)f_j(x_j(t-\tau _{ij}(t)))+\bigvee _{j=1}^{n}S_{ij}(t)\nu _j(t)\\&\qquad + I_{i}(t),\; 1 \le i\le n,\; t\in {\mathbb {T}}. \end{aligned}$$

where $e_{ij}(.)$ is feed-forward template; $\alpha _{ij}(.)$, $\beta _{ij}(.)$, $T_{ij}(.)$ and $S_{ij}(.)$ donate elements of the fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feed-forward MIN template and fuzzy feed-forward MAX template, respectively; $\displaystyle \bigvee$ denote the fuzzy AND operation and $\displaystyle \bigwedge$ is the fuzzy OR operation; $\nu (.)$ denote the input of the $i\mathrm{th}$ neuron. The corresponding results will appear in the near future.

Problem 2

It is well known that when discussing dynamic behavior of neutral type recurrent neural networks with time-varying delays, distributed delay and D operator on time–space scales, the assumption $\mathbf {(H_1)}$ is very important in the proof process. However, in the existing literatures (see [28,29,30]), almost all results on the stability of pseudo almost periodic solution for neutral type recurrent NNs with D operator are obtained under global Lipschitz neuron activations. When neuron activation functions do not satisfy global Lipschitz conditions, people want to know whether the neutral type recurrent NNs is stable. In practical engineering applications, people also need to present new neural networks. Therefore, developing a new class of neutral type recurrent NNs without global Lipschitz neuron activation functions and giving the conditions of the stability of new neutral type recurrent NNs are very interesting and valuable. Therefore, studying the existence and the global exponential stability of the pseudo almost periodic solution of recurrent NNs on time scale and without $\mathbf {(H_1)}$ will be our future research interest.

Problem 3

It is known that complex numbers are of great significance to fundamental theory and practical applications in engineering such as communication, electromagnetic, quantum mechanics, and so on. At present many research around the stability analysis of complex-valued neural networks such that the stability in Lagrange sense investigated in [45], some sufficient conditions are established in [46] that ensure the boundedness and stability for a general class of complex-valued neural networks with variable coefficients and proportional delays and in [47] the authors investigated the boundedness and robust stability for a class of delayed complex-valued neural networks with interval parameter uncertainties. However, the approach used in the above mentioned work cannot be extended to solve the problem studied in our paper. Thus, the existence and the global exponential stability of the pseudo almost periodic solution of neutral type recurrent neural networks with time-varying delays, distributed delay and D operator on time–space scales will be a real problem to be studied in the near future work.