1 Introduction

During the past decades, the research of neural networks has reached an unprecedented upsurge because of the extensive application of neural networks in a wide range of territories, such as pattern recognition, signal processing and associative memory [1,2,3,4,5]. In particular, CNNs attract a myriad of scholar’s interest [6,7,8]. We understand that lateral inhibitory neural networks with deterministic Hebbian learning laws can simulate the dynamics of the cognitive map of the cerebral cortex without being supervised synaptic modification. Subsequently, Cohen and Grossberg [9] proposed the CNNs model to simulate cell inhibition in neurobiology. Meyer-Bäse [10] put forward the CNNs with different indices at the same time. CNNs are unsupervised learning neural networks, which can simulate biological neural network system to conduct information processing by means of excitability, coordination, inhibition and competition between neurons. The input node and output node of the neural networks are completely connected, which have the characteristics of simple structure, fast operation speed and simple learning algorithm.

In competitive neural networks, when one neuron is excited, it will inhibit other neurons through its branches, which can cause competition between neurons. When more than one neuron is suppressed, the most excited neurons get rid of the inhibition of other neurons to emerge as the winner of the competition. Competitive neural networks have two state models: one state describes the dynamical behavior of neural network state changes, which is frequent and neural network is active, and the corresponding memory model is called short-term memory (STM). Another type of state variable describes the dynamical behavior of cell synaptic changes caused by external stimulation, such changes are relatively slow, and the corresponding memory model is called long-term memory (LTM). Competitive neural networks have a substantial of applications in different industries, and these applications mainly depend on their dynamical behavior, such as stability, multi-stability, synchronization and so on [11,12,13,14,15]. In [11], the author proved the existence and uniqueness of the equilibrium point in the CNNs which consider the influence of time scale parameters by using the Lipschitz method.

Activation function is an indispensable factor in the research of neural networks which have different dynamical behaviors for different activation functions. In a great deal of literatures, the main activation functions used are monotonically increasing and piecewise linear functions. In [16], another kind of non-monotonic piecewise linear activation functions which are called GWTAFs were introduced. It was proved that GWTAFs of neural networks have more equilibrium points. In [17], GWTAFs can prevent the system from falling into the crisis of local minimum and effectively improve the performance of network optimization. So, neural networks with GWTAFs have great preponderance in network optimization and storage capacity, it is necessary to research the neural networks with GWTAFs.

Synchronization represents that the state of coupled system tends to be consistent. In [18], researchers studied the competitive neural networks model of nonsmooth function and proved the existence and uniqueness of system equilibrium point based on nonsmooth analysis technology, and obtained the condition of network exponential stability. In [19], authors researched the memristor-based recurrent network model and obtained the sufficient conditions of exponential synchronization. Until now, many results have been derived for asymptotic synchronization [20,21,22,23,24,25,26]. In these papers, the synchronization time tends to infinity. In the actual situation, due to the restriction of time and resource, the asymptotic synchronization can not be well applied in practice. So many researchers shifted their attention to another kind of synchronization, namely, finite-time synchronization. It means that the system can achieve synchronization in a finite time [27,28,29,30,31,32,33]. Recently, in [34], in order to save communication resources, a novel quantized controller was designed to study the finite-time cluster synchronization of cellular neural networks. However, one disadvantage of finite-time synchronization is that its settling time depends on the initial conditions of the system. It is inconvenient in many application fields, for example, in a great deal of engineering territories, it’s difficult to get the initial conditions. In order to settle this problem, Polyakov [35] came up with fixed-time synchronization, and the settling time is a constant with upper bound irrelevant to initial value. On account of this feature, fixed-time synchronization has been widely used in signal communication [36,37,38,39,40,41]. Recently, in [42], the fixed-time synchronization of quaternion-valued memristive neural networks were studied, it has more complex dynamic behavior than traditional neural networks. Till now, there are no results about fixed-time synchronization of competitive neural networks with GWTAFs. Inspired by the above reasons, we study the problem of fixed-time synchronization of CNNs with Gaussian-wavelet-type activation functions. The main contributions are summarized in the following three aspects:

  1. (1)

    By designing some feedback controllers, simple synchronization conditions are obtained;

  2. (2)

    According to the correlative structure of competitive neural networks, the fixed-time synchronization of CNNs is gained by means of Lyapunov stability theory and inequality technique;

  3. (3)

    We first study the fixed-time synchronization problem of CNNs with GWTAFs, which have great preponderance in network optimization and storage capacity than general activation functions.

The following is the main structure of this article. The model and concepts are described in part 2. Fixed-time synchronization with different controllers is discussed in part 3. In part 4, numerical simulation shows the validity of the conclusion. The conclusion is described in part 5.

Notations \(\dot{x}(t)\) is the derivative of x(t). Any given vector \(x=(x_1, x_2, \dots , x_m)^T \in {\mathbb {R}}^m\), it’s norm can be defined as \(\Vert x\Vert =\max _{1\le k\le m} \{|x_k|\}\). Let the \(C((-\infty ,0],{\mathbb {R}}^m)\) is a continuous mapping from \((-\infty , 0]\) to \({\mathbb {R}}^m\) in Banach space, where norm is defined as \(\Vert \phi \Vert =\max _{1\le k\le m} \{sup_{s\in (-\infty , 0]}\phi _k(s)\}\), and \(\phi (s)=(\phi _1(s), \dots , \phi _m(s))^T \in {\mathbb {R}}^m\).

2 Preliminaries and model description

The equations for CNNs with GWTAFs and discrete delays are considered as the master system:

$$\begin{aligned} \left\{ \begin{aligned} {\textit{STM}{:}} \,\,\dot{x}_k(t)&=\sum \limits _{d=1}^{m}D_{kd}f_d(x_d(t))+\sum \limits _{d=1}^{m}D_{kd}^{\tau }f_d(x_d(t-\tau _d(t)))\\&\quad -\mu _kx_k(t)+B_k\sum \limits _{d=1}^{i}h_{kd}(t)\omega _d+I_k,\\ {\textit{LTM}{:}}\,\, \dot{h}_{kd}(t)&=-\alpha _k h_{kd}(t)+\omega _d\beta _k f_k(x_k(t)),\\&\quad k=1, 2, \dots , m , d= 1, 2, \dots , i, \end{aligned}\right. \end{aligned}$$
(1)

where m and i represent the number of the STM states and constant external stimulus, respectively. \(x_k (t)\) denotes state vector of neuron current, and \(h_{kd}(t)\) is synaptic transfer efficiency; \(\omega _d\) is the constant external stimulus; \(B_k\) is the strength of the external stimulus; \(D_{kd}\) and \(D_{kd}^{\tau }\) represent the connection weight and connection weight with feedback delay; \(I_k\) is the constant input; \(\mu _k>0,\alpha _k\ge 0\), \( \beta _k\ge 0\) are constants, and \(\tau _d(t)\) is discrete delay, which satisfies \(0\le \tau _d (t)\le \upsilon \), where \(\upsilon =\max _{1\le d\le m} \{sup_{t\in \mathbb {R}} \tau _d(t)\}\). \(f_d(\cdot )\) represent the GWTAFs, the following is the specific expression (Fig. 1):

$$\begin{aligned} f_d(t)=\left\{ \begin{array}{ll} u_d , &{}\quad -\infty<t<a_d,\\ \lambda _{1,d}t+\phi _{1,d}, &{}\quad a_d\le t \le b_d,\\ \lambda _{2,d}t+\phi _{2,d},&{}\quad b_d<t<c_d,\\ \lambda _{3,d}t+\phi _{3,d},&{}\quad c_d \le t \le d_d,\\ U_d ,&{}\quad d_d<t<+\infty , \end{array}\right. \end{aligned}$$
(2)

where \(a_d, b_d, c_d, d_d, u_d, \lambda _{1,d}, \lambda _{2,d}, \lambda _{3,d}, \phi _{1,d}, \phi _{2,d}, \phi _{3,d}, U_d\) are constants with \(-\infty<a_d<b_d<c_d<d_d<\infty , \lambda _{1,d},\lambda _{3,d}>0, \lambda _{2,d}<0, u_d=f_d(c_d), U_d=f_d(b_d), d= 1, 2, \dots ,m\).

Fig. 1
figure 1

Gaussian-wavelet-type activation function (2)

Full size image

Let \(S_k(t)=\sum _{d=1}^{i}h_{kd}(t) \omega _d=\omega ^{T} h_k(t)\), where \(\omega =(\omega _1, \omega _2, \dots , \omega _i)^{T}, h_k(t)=(h_{k1}(t), h_{k2}(t), \dots , h_{ki}(t))^T.\) Suppose input stimulus \(\omega \) can be normalized \(|\omega |^2=\omega _1^2+\cdots +\omega _i^2=1\).

It is obvious that the activation function \(f_d(t)\) in (2) satisfies Lipschitz condition, and the Lipschitz constant is \(\gamma _d=max\{|\omega _{1d}|, |\omega _{2d}|,|\omega _{3d}|\},d= 1, 2, \dots ,m\). The simplified equation is as below:

$$\begin{aligned} \left\{ \begin{aligned} {\textit{STM}{:}}\,\, \dot{x}_k(t)&=\sum \limits _{d=1}^{m}D_{kd}f_d(x_d(t))+\sum \limits _{d=1}^{m}D_{kd}^{\tau }f_d(x_d(t-\tau _d(t)))\\&\quad -\mu _kx_k(t)+B_kS_k(t)+I_k,\\ {\textit{LTM}{:}}\,\,\dot{S}_k(t)&=-\,\alpha _k S_k (t)+\beta _k f_k(x_k (t)), k=1,2,\dots ,m. \end{aligned}\right. \end{aligned}$$
(3)

Suppose system (1) meets initial conditions:

$$\begin{aligned} x_k(t)= & {} \varphi _k^x (t)=C([-\upsilon ,0],\mathbb {R}^m), \\ S_k(t)= & {} \varphi _k^s (t)=C([-\upsilon ,0],\mathbb {R}^m),\quad k= 1, 2, \dots , m. \end{aligned}$$

Design the slave system as

$$\begin{aligned} \left\{ \begin{aligned} {\textit{STM}{:}}\,\,\dot{y}_k (t)&=\sum \limits _{d=1}^{m} D_{kd}f_d (y_d (t))+\sum \limits _{d=1}^{m} D_{kd}^{\tau } f_d(y_d(t-\tau _d(t)))\\&\quad -\,\mu _k y_k(t)+B_k R_k (t)+I_k+\zeta _k(t),\\ {LTM{:}}\,\,\dot{R}_k(t)&=-\,\alpha _k R_k(t)+\beta _k f_k(y_k(t))+\nu _k(t),\quad k=1,2,\dots ,m, \end{aligned}\right. \end{aligned}$$
(4)

where \(\zeta _k(t), \nu _k(t) \) are controllers. The corresponding initial values of the system (4) meet the conditions:

$$\begin{aligned} y_k(t)= & {} \phi _k^y(t)=C([-\upsilon ,0],\mathbb {R}^m), \\ R_k(t)= & {} \phi _k^R(t)=C([-\upsilon ,0],\mathbb {R}^m),\quad k= 1, \dots , m. \end{aligned}$$

The errors are defined as \(e_k(t)=y_k(t)-x_k(t), z_k(t)=R_k(t)-S_k(t)\). The error systems can be obtained by subtracting system (4) from system (3) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}_k(t)=-\,\mu _k e_k(t)+Q_k(t)+B_k z_k(t)+\zeta _k(t),\\ \dot{z}_k(t)=-\,\alpha _k z_k(t)+\beta _k f_k(e_k(t))+v_k(t),\quad k=1,2,\dots ,m, \end{array}\right. } \end{aligned}$$
(5)

where \(Q_k(t)=\sum \nolimits _{d=1}^{m}\{D_{kd}(f_d(y_d(t))-f_d(x_d(t)))+D_{kd}^{\tau }(f_d(y_d(t-\tau _d(t)))-f_d(x_d(t-\tau _d(t))))\}\), and \(f_k(e_k(t))=f_k(y_k(t))-f_k(x_k(t))\).

In order to prove the theoretical results, the following assumption is indispensable.

Assumption 1

Let \(D_k^{*}>0\) and \(D_k^{*}\ge \max \{D_{kd},D_{kd}^{\tau }\}, k= 1,2,\dots ,m,d=1,2,\dots ,i.\)

Lemma 1

By Assumption 1 we can get \( |Q_k(t)| \le \pi _k\), where \(\pi _k=\sum \nolimits _{d=1}^{m} 4U_dD_k^{*}\), \(U_d\) is maximum of the activation function \(f_d(t)\).

Proof

Based on the Assumption 1, \(D_k^{*}\ge \max \{D_{kd},D_{kd}^{\tau }\}, k= 1, 2, \dots , m, d= 1, 2, \dots , i, Q_k(t)=\sum \nolimits _{d=1}^{m}\{D_{kd}(f_d(y_d(t))-f_d(x_d(t)))+D_{kd}^{\tau }(f_d(y_d(t-\tau _d (t)))-f_d(x_d(t-\tau _d(t))))\}\), so \(|Q_k(t)|\le \sum \nolimits _{d=1}^{m} D_k^{*}\{ |(f_d(y_d(t))-f_d(x_d(t)))|+|(f_d(y_d(t-\tau _d(t)))-f_d(x_d(t-\tau _d(t))))|\}\). \(U_d\) is the maximum value of the activation functions, so we conclude that \(|Q_k(t)| \le \sum \nolimits _{d=1}^{m} 4U_dD_k^{*}\). \(\square \)

Lemma 2

[32] If \(a_1, a_2, \dots , a_m \ge 0, 0<p\le 1, q>1,\) we can get the result

$$\begin{aligned} \sum \limits _{k=1}^{m} a_k^p\ge \left( \sum \limits _{k=1}^m a_k\right) ^p,\quad \sum \limits _{k=1}^m a_k^q\ge m^{1-q}\left( \sum \limits _{k=1}^{m} a_k\right) ^q. \end{aligned}$$

Definition 1

[40] Let \(L(t)=(e_1(t), e_2(t), \dots , e_m(t), z_1(t), z_2(t), \dots , z_m(t))^T\). If there is a constant \(t^{*} (L(0))> 0\), which satisfies \(\lim \nolimits _{t\rightarrow t^{*} (L(0)) }\Vert L(t)\Vert =0\) and \(\Vert L(t)\Vert \equiv 0\) for \(\forall t>t^{*} (L(0))\), thus master-slave systems (3)–(4) realize finite-time synchronization, where \(t^{*} (L(0))\) is the settling time.

Definition 2

[36] If master–slave systems (3)–(4) meet the following two conditions, fixed-time synchronization can be achieved.

  1. (a)

    Master–slave systems obtain finite-time synchronization;

  2. (b)

    For any initial synchronization error L(0), there is a constant \(T_{max} >0\), which satisfies \(t^{*} (L(0))\le T_{max}\).

Lemma 3

[35] Suppose that \(V(\cdot ) : \mathbb {R}^n \rightarrow \mathbb {R}_{+} \cup \{0\}\) is a continuous radically unbounded function and satisfies the conditions:

  1. (1)

    \(V(x) = 0 \Leftrightarrow x=0\);

  2. (2)

    Any solution L(t) of error system (5) satisfies

    $$\begin{aligned} {\dot{V}}(L(t))\le -aV^p(L(t)-bV^q(L(t)) \end{aligned}$$

    for some \(a, b>0, 0\le p\le 1\) and \( q>1\). So the error system (5) reach fixed-time stability, where \(T_{max}=\frac{1}{a(1-p)}+\frac{1}{b(q-1)}\).

Lemma 4

[41] Let \(V(\cdot ) : \mathbb {R}^n \rightarrow \mathbb {R}_{+} \cup \{0\}\) is a continuous radically unbounded function and meets the next two conditions:

  1. (1)

    \(V(x)=0\Leftrightarrow x=0\);

  2. (2)

    Any solution L(t) of error system (5) meets

    $$\begin{aligned} {\dot{V}}(L(t))\le -aV^p(L(t))-bV^q(L(t)), \end{aligned}$$

    for some \(a, b>0, p=1-\frac{1}{2u}\) and \(q=1+\frac{1}{2u}\), where \(u>1.\) So the error system (5) can achieve fixed-time stability, where \(T_{max}=\frac{\pi u}{\sqrt{ab}}.\)

3 Main results

In order to make the master–slave systems realize fixed-time synchronization, design the corresponding feedback controller as

$$\begin{aligned} \left\{ \begin{aligned} \nu _k(t)&=-j_{1k} sign(z_k(t))-c_{1k}z_k(t)-l_{1k} sign(z_k(t))|z_k(t)|^p,\\ \zeta _k(t)&=-j_{2k}sign(e_k(t))-c_{2k}e_k(t)-l_{2k}sign(e_k(t))|e_k(t)|^p,\\&\quad k=1, 2, \dots , m, \end{aligned}\right. \end{aligned}$$
(6)

where \(j_{2k} ,c_{1k}\), and \(c_{2k}\) need satisfy some conditions, \(j_{1k}, l_{1k}\) and \(l_{2k}\) are positive constants, and \(p>1\).

Theorem 1

Suppose the Assumption 1 is satisfied, if \(j_{2k},c_{1k}\) and \(c_{2k}\) satisfy

$$\begin{aligned} \left\{ \begin{aligned} j_{2k}&>\pi _k ,\\ c_{1k}&>-\alpha _k+\frac{|\beta _k\gamma _k |}{2}+\frac{|B_k|}{2},\\ c_{2k}&>-\mu _k+\frac{|\beta _k \gamma _k|}{2}+\frac{|B_k|}{2},\quad k=1, 2, \dots , m. \end{aligned}\right. \end{aligned}$$
(7)

System (3) and system (4) get fixed-time synchronization under controller (6), in addition,

$$\begin{aligned} T_{max}=\frac{2}{\iota } +\frac{1}{\kappa (p-1)}, \end{aligned}$$

where

$$\begin{aligned} \iota= & {} \sqrt{2}min\left\{ \min _k\{j_{1k}\},\min \limits _k\{j_{2k}-\pi _k\}\right\} , \nonumber \\ \kappa= & {} m^{\frac{1-p}{2}}\min \left\{ \min \limits _k\{l_{1k}\},\min \limits _k\{l_{2k}\}\right\} . \end{aligned}$$
(8)

Proof

Construct the function:

$$\begin{aligned} V(t)=V_1(t)+V_2(t), \end{aligned}$$
(9)

where

$$\begin{aligned} V_1(t)=\frac{1}{2} \sum _{k=1}^{m} (z_k(t))^2,V_2(t)=\frac{1}{2} \sum _{k=1}^{m}(e_k(t))^2. \end{aligned}$$
(10)

According to Lipschitz condition, we can get the \(f_k(e_k(t))\le \gamma _ke_k(t).\)

Then computing the derivative of \(V_1(t)\),

$$\begin{aligned} {\dot{V}}_1(t)&=\sum _{k=1}^{m} z_k(t)\dot{z}_k(t) \nonumber \\&=\sum _{k=1}^{m} z_k(t)[-\alpha _k z_k(t)+\beta _k f_k(e_k(t))+\nu _k(t)] \nonumber \\&=-\sum _{k=1}^{m}\alpha _k z_k^2(t)+\sum _{k=1}^m\beta _k f_k(e_k(t))z_k(t)+\sum _{k=1}^m z_k(t)\nu _k(t) \nonumber \\&\le -\sum _{k=1}^{m}\alpha _k z_k^2(t)+\sum _{k=1}^m\beta _k\gamma _ke_k(t)z_k(t)+\sum _{k=1}^m z_k(t)\nu _k(t) \nonumber \\&\le -\sum _{k=1}^m \alpha _k z_k^2(t)+\sum _{k=1}^{m} \frac{|\beta _k\gamma _k |}{2} e_k^2(t)+\sum _{k=1}^m \frac{|\beta _k\gamma _k |}{2} z_k^2(t) \nonumber \\&\quad -\sum _{k=1}^m j_{1k}|z_k(t)|-\sum _{k=1}^m c_{1k}z_k^2(t)-\sum _{k=1}^m l_{1k}|z_k(t)|^{p+1}. \end{aligned}$$
(11)

Calculating the derivative of \(V_2(t)\) by Lemma 1,

$$\begin{aligned} {\dot{V}}_2(t)&=\sum _{k=1}^m e_k(t)\dot{e}_k(t) \nonumber \\&=\sum _{k=1}^m e_k(t)[-\mu _k e_k(t)+Q_k(t)+B_k z_k(t)+\zeta _k(t)] \nonumber \\&=-\sum _{k=1}^m \mu _k e_k^2(t)+\sum _{k=1}^m e_k(t) Q_k(t) +\sum _{k=1}^{m} B_kz_k(t)e_k(t)+\sum _{k=1}^m e_k(t)\zeta _k(t) \nonumber \\&\le -\sum _{k=1}^{m} \mu _k e_k^2(t)+\sum _{k=1}^m \pi _k|e_k(t)|+\sum _{k=1}^m \frac{|B_k|}{2}e_k^2(t)+\sum _{k=1}^m \frac{|B_k|}{2} z_k^2(t) \nonumber \\&\quad -\sum _{k=1}^m j_{2k}|e_k(t)|-\sum _{k=1}^{m}c_{2k}e_k^2(t)-\sum _{k=1}^{m} l_{2k}|e_k(t)|^{p+1}. \end{aligned}$$
(12)

Therefore,

$$\begin{aligned} {\dot{V}}(t)&={\dot{V}}_1(t)+{\dot{V}}_2(t) \nonumber \\&\le \sum _{k=1}^m \left[ -\alpha _k- c_{1k}+\frac{|\beta _k\gamma _k| }{2}+\frac{|B_k|}{2}\right] z_k^2(t)-\sum _{k=1}^{m} j_{1k}|z_k(t)| \nonumber \\&\quad +\sum _{k=1}^m \left[ -\mu _k-c_{2k}+\frac{|\beta _k\gamma _k| }{2}+\frac{|B_k|}{2}\right] e_k^2(t)-\sum _{k=1}^m [j_{2k}-\pi _k]|e_k(t)| \nonumber \\&\quad -\sum _{k=1}^{m}l_{1k}|z_k(t)|^{p+1}-\sum _{k=1}^m l_{2k}|e_k(t)|^{p+1}. \end{aligned}$$
(13)

Combining (7) with (13), followed by the corresponding result,

$$\begin{aligned} {\dot{V}}(t)&\le -\min _k\{j_{1k}\}\sum _{k=1}^m|z_k(t)|-\min _k\{j_{2k}-\pi _k\}\sum _{k=1}^m|e_k(t)| \nonumber \\&\quad -\min _k\{l_{1k}\}\sum _{k=1}^m |z_k(t)|^{p+1}-\min _k\{l_{2k}\}\sum _{k=1}^m|e_{k}(t)|^{p+1} \nonumber \\&\le -\sqrt{2}\min _k\{j_{1k}\}(V_1(t))^{\frac{1}{2}} -\sqrt{2}\min _k\{j_{2k}-\pi _k\}(V_2(t))^{\frac{1}{2}} \nonumber \\&\quad -m^{\frac{1-p}{2}}2^{\frac{p+1}{2}}\min _k\{l_{1k}\}(V_1(t))^{\frac{p+1}{2}}\nonumber \\&\quad -m^{\frac{1-p}{2}}2^{\frac{p+1}{2}}\min _k\{l_{2k}\}(V_2(t))^{\frac{p+1}{2}}. \end{aligned}$$
(14)

According to Lemma 2,

$$\begin{aligned} {\dot{V}}(t)&\le -\,\iota \left[ (V_1(t))^{\frac{1}{2}}+(V_2(t))^{\frac{1}{2}}\right] -\kappa \cdot 2^{\frac{p+1}{2}}\left[ (V_1(t))^{\frac{p+1}{2}}+(V_2(t))^{\frac{p+1}{2}}\right] \nonumber \\&\le -\,\iota \left[ V_1(t)+V_2(t)\right] ^{\frac{1}{2}}-\kappa \cdot 2^{\frac{p+1}{2}}\cdot 2^{\frac{1-p}{2}}[V_1(t)+V_2(t)]^{\frac{p+1}{2}} \nonumber \\&=-\,\iota \cdot (V(t))^{\frac{1}{2}}-2\kappa \cdot (V(t))^{\frac{p+1}{2}}, \end{aligned}$$
(15)

where

$$\begin{aligned} \iota&=\sqrt{2}\min \left\{ \min _k\{j_{1k}\}, \min _k\{j_{2k}- \pi _k\}\right\} ,\\ \kappa&=m^{\frac{1-p}{2}}\min \left\{ \min _k\{l_{1k}\},\min _k\{l_{2k}\}\right\} . \end{aligned}$$

The conditions in Lemma 3 are satisfied, so system (5) can obtain fixed-time synchronization, where

$$\begin{aligned} T_{max}=\frac{1}{\iota (1-\frac{1}{2})}+\frac{1}{2\kappa (\frac{p+1}{2}-1)}=\frac{2}{\iota }+\frac{1}{\kappa (p-1)}. \end{aligned}$$
(16)

The proof is complete. \(\square \)

Then let’s think about another controller:

$$\begin{aligned} \left\{ \begin{aligned} \nu _k(t)=&-c_{1k}z_k(t)-h_{1k}sign(z_k(t))|z_k(t)|^q \\&-l_{1k}sign(z_k(t))|z_k(t)|^p,\\ \zeta _k(t)=&-j_{2k}sign(e_k(t))-c_{2k}e_k(t)-h_{2k}sign(e_k(t))|e_k(t)|^q \\&-l_{2k}sign(e_k(t))|e_k(t)|^p,\quad k=1, 2, \dots , m, \end{aligned}\right. \end{aligned}$$
(17)

where \(j_{2k}, c_{1k},\) and \(c_{2k}\) needs satisfy some conditions, \(h_{1k}, h_{2k}, l_{1k}\) and \(l_{2k}\) are some non-negative constants, and \( 0<q<1, p>1\).

Theorem 2

If Assumption 1 is satisfied and \(j_{2k}\), \(c_{1k},\)\(c_{2k}\) satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{aligned} j_{2k}&>\pi _k,\\ c_{1k}&>-\alpha _k+\frac{|\beta _k\gamma _k| }{2}+\frac{|B_k|}{2}, \\ c_{2k}&> -\mu _k+\frac{|\beta _k\gamma _k|}{2}+\frac{|B_k|}{2},\quad k=1,2,\dots ,m. \end{aligned}\right. \end{aligned}$$
(18)

System (3) and system (4) under controller (17) get fixed-time synchronization, moreover,

$$\begin{aligned} T_{max}=\frac{2}{h(1-q)}+\frac{1}{l(p-1)}, \end{aligned}$$

where \(h=2^{\frac{q+1}{2}}\min \{\min \nolimits _k\{h_{1k}\},\min \nolimits _k \{h_{2k}\}\}\), \( l= m^{\frac{1-p}{2}}\min \{\min \nolimits _k\{l_{1k}\},\min \nolimits _k\{l_{2k}\}\}\).

Proof

Considering a similar functional

$$\begin{aligned} V(t)=V_1(t)+V_2(t), \end{aligned}$$
(19)

where

$$\begin{aligned} V_1(t)=\frac{1}{2} \sum _{k=1}^{m} (z_k(t))^2,V_2(t)=\frac{1}{2} \sum _{k=1}^{m}(e_k(t))^2. \end{aligned}$$
(20)

In the same way, we can get

$$\begin{aligned} {\dot{V}}(t)&\le -\sum _{k=1}^m h_{1k}|z_k(t)|^{q+1}-\sum _{k=1}^{m} h_{2k}|e_k(t)|^{q+1} \nonumber \\&\quad -\sum _{k=1}^{m}l_{1k}|z_k(t)|^{p+1}-\sum _{k=1}^m l_{2k}|e_k(t)|^{p+1} \nonumber \\&\le -\min _k\{h_{1k}\}\sum _{k=1}^m |z_k(t)|^{q+1}-\min _k\{h_{2k}\}\sum _{k=1}^m|e_k(t)|^{q+1} \nonumber \\&\quad -\min _k\{l_{1k}\}\sum _{k=1}^{m}|z_k(t)|^{p+1}-\min _k\{l_{2k}\}\sum _{k=1}^{m}|e_k(t)|^{p+1} \nonumber \\&\le -2^{\frac{q+1}{2}}\min _k\{h_{1k}\}(V_1(t))^{\frac{q+1}{2}}-2^{\frac{q+1}{2}}\min _k\{h_{2k}\}(V_2(t))^{\frac{q+1}{2}} \nonumber \\&\quad -m^{\frac{1-p}{2}}2^{\frac{p+1}{2}}\min _k\{l_{1k}\}(V_1(t))^{\frac{p+1}{2}}\nonumber \\&\quad -m^{\frac{1-p}{2}}2^{\frac{p+1}{2}}\min _k\{l_{2k}\}(V_2(t))^{\frac{p+1}{2}}. \end{aligned}$$
(21)

Then through Lemma 2

$$\begin{aligned} {\dot{V}}(t)&\le -h\left[ (V_1(t))^{\frac{q+1}{2}}+(V_2(t))^{\frac{q+1}{2}}\right] -l\cdot 2^{\frac{p+1}{2}}\left[ (V_1(t))^{\frac{p+1}{2}}+(V_2(t))^{\frac{p+1}{2}}\right] \nonumber \\&\le -h\left[ V_1(t)+V_2(t)\right] ^{\frac{q+1}{2}}-l\cdot 2^{\frac{p+1}{2}}\cdot 2^{\frac{1-p}{2}}\left[ V_1(t)+V_2(t)\right] ^{\frac{p+1}{2}} \nonumber \\&=-h(V(t))^{\frac{q+1}{2}}-2l(V(t))^{\frac{p+1}{2}}, \end{aligned}$$
(22)

where \(h= 2^{\frac{q+1}{2}}min\{min_k\{h_{1k}\},min_k \{h_{2k}\}\}\), \( l= m^{\frac{1-p}{2}}min\{min_k\{l_{1k}\},min_k\{l_{2k}\}\}\). Based on Lemma 3, The error system (5) gets fixed-time stability. In addition,

$$\begin{aligned} T_{max}&=\frac{1}{h\left( 1-\frac{q+1}{2}\right) }+\frac{1}{2l\left( \frac{p+1}{2}-1\right) } \nonumber \\&=\frac{2}{h(1-q)}+\frac{1}{l(p-1)}. \end{aligned}$$
(23)

This completes the proof.\(\square \)

Corollary 1

Assume the conditions given in Theorem 2 are always true. If p and q in controller (17) satisfy the following expressions:

$$\begin{aligned} q=1-\frac{1}{u},\quad p=1 +\frac{1}{u}, \end{aligned}$$

where \(u>1\), then \(\frac{q+1}{2}=1-\frac{1}{2u},\frac{p+1}{2}=1+\frac{1}{2u}\). According to the Lemma 4, the error system (5) gets fixed-time stability. Moreover, \(T_{max}\) can be calculated

$$\begin{aligned} T_{max}=\frac{\pi u}{\sqrt{2hl}}, \end{aligned}$$

where

$$\begin{aligned} h= & {} 2^{\frac{q+1}{2}}min\{min_k\{h_{1k}\},min_k \{h_{2k}\}\},\\ l= & {} m^{\frac{1-p}{2}}min\{min_k\{l_{1k}\},min_k\{l_{2k}\}\}. \end{aligned}$$

Remark 1

In controllers (6) and (17), \(sign(e_k(t))\) and \(sign(z_k(t))\) are discontinuous functions, for this reason, it is difficult to be used in engineering. So we use the continuous functions \(\frac{e_k(t)}{e_k(t)+\phi }\), \(\frac{z_k(t)}{z_k(t)+\varphi }\) to replace them, where \(\phi >0\), \(\varphi >0 \).

4 Numerical simulation

Example 1

Consider the CNNs with GWTAFs and discrete delays model (24) with the following parameters: \( m = 2, \mu _1=0, \mu _2=2,\alpha _1=\alpha _2=1,\beta _1=\beta _2=1,B_1=B_2=1,D_{11}=0.25,D_{12}=-0.4,D_{11}^\tau =-1.5,D_{12}^\tau =-0.1,D_{21}=-1.9,\)\(D_{22}=0.5,D_{21}^\tau =-0.2,D_{22}^\tau =-2.3,I_1=sin(t),I_2=cos(t), \tau _1(t)=\tau _2(t)=2\),

$$\begin{aligned} f_1(t)=f_2(t)={\left\{ \begin{array}{ll} 1,&{} -\infty<t<0,\\ 2t+1,&{} 0\le t \le 1,\\ -t+4,&{} 1< t<10,\\ 4.5t-51,&{} 10 \le t \le 12,\\ 3,&{} 12< t<\infty . \end{array}\right. } \end{aligned}$$
(24)

The initial values of the system (1) meet the following conditions

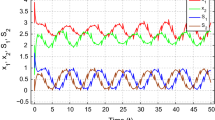
$$\begin{aligned} x_1(t)=-4, x_2(t)=6, S_1(t)=-3.3, S_2(t)=9, t\in [-2,0]. \end{aligned}$$

The initial values of corresponding slave system (4) are \(y_1(t)=2, y_2(t)=1, R_1(t)=1.5, R_2(t)=2, t\in [-2,0]\). The output of systems (3) and (4) without controllers is showed in Fig. 2.

Choosing \(j_{11} = j_{12}= 1, c_{11} = 7.5, c_{12} = 3.5, l_{11} = l_{12} = 0.25, j_{21} = 4.5, j_{22} = 10.7, c_{21} = 1, c_{22} = 0.5, l_{21} = l_{22} = 0.25, q= 1.5\) as parameters of controller (6). System (3) and system (4) under the controller (6) get fixed-time synchronization, and \(T_{max}\approx 10.93\). In Fig. 3, the error system converges to 0 within \(T_{max}\). So Theorem 1 is valid.

Fig. 2
figure 2

State trajectories of error system without control

Full size image
Fig. 3
figure 3

State trajectories of error system under the controller (6)

Full size image

Example 2

Consider the same model in the example 1, \(m = 2, \mu _1=0,\mu _2=2, D_{11}=0.25, D_{12}=-0.14, D_{11}^\tau =-1.5, D_{12}^\tau =-0.1, D_{21}=-1.9, D_{22}=0.5, D_{21}^\tau =-0.2, D_{22}^\tau =-2.3, B_1=B_2=1, \alpha _1=\alpha _2=1,\)\( \beta _1=\beta _2=1, I_1(t)=sin(t), I_2(t)=cos(t).\)\(f_1(t)\) and \(f_2(t)\) have the same expression in (24), \(\tau _1=\tau _2=2\). The initial conditions of systems (3)–(4) are \(x_1(t)=-3, x_2(t)=3, S_1(t)=-2.1, S_2(t)=6, t\in [-2,0]\), \(y_1(t)=4, y_2(t)=1.5, R_1(t)=3.5, R_2(t)=2.2, t\in [-2,0].\)

Selecting the parameters in controller (17) as follows: \(c_{11}=0.5,c_{12}=3.5,h_{11}=h_{12}=0.5,l_{11}=l_{12}=0.25,j_{21}=4.5,j_{22}=10.7,c_{21}=1,c_{22}=3.5,h_{21}=h_{22}=0.5,l_{21}=l_{22}=0.25,p=1.5,q=0.5.\) It is observed from Fig. 4 that the master and slave systems (3)–(4) without controllers eventually diverge. In Fig. 5, we see that the master-slave systems with controller (17) realize synchronization, and \(T_{max}\approx 11.9.\)

Fig. 4
figure 4

State trajectories of error system without control

Full size image
Fig. 5
figure 5

State trajectories of error system under the controller (17)

Full size image

5 Conclusion

In this article, the problem of fixed-time synchronization for CNNs with GWTAFs and discrete delays has been researched. Simple synchronization conditions are obtained by designing some uncomplicated feedback controllers. The neural networks with GWTAFs can optimize the neural network effectively and have more storage capacity. The settling time of fixed-time synchronization is irrelevant to the initial values of the system. Finally, the theoretical results which we derived are attested to be indeed feasible by two numerical examples. Further research is mainly on fixed-time synchronization of QVNNs with event-triggered control.