1 Introduction

Competitive neural networks (CNNs), as the generalization of the classical Hopfield neural networks (HNNs) and Cohen–Grossberg neural networks (CGNNs), was first introduced by Meyer-Baese to model the dynamics of cortical cognitive maps with unsupervised synaptic modifications. CNNs different from the traditional neural networks (NNs) with first-order interactions due to consideration of long-term memory and short-term memory variables [1,2,3]. In implementation of NNs, owing to the finite switching speed of neurons and amplifiers, time delays are inevitable in the signal transmission among the neurons, which will affect the stability of the neural system and may lead to some complex dynamic behaviors such as instability, chaos, oscillation or other performance of the NNs. Therefore, the dynamic analysis of NNs, especially CNNs with delays received much more attention [4,5,6,7].

Since it was first proposed by Pecora and Carrol to synchronize two identical systems with two different initial values [8], synchronization has been comprehensively studied over the past few decades due to their potential applications in a wide variety of areas, ranging from secure communications to pattern recognition, even to modeling the human brain’s activity [9,10,11,12,13]. In the meantime, a large number of synchronization problems have been introduced and studied, such as complete synchronization [8], lag synchronization [14,15,16], impulsive synchronization [17], projective synchronization [18], function projective synchronization [19]. Among them, lag synchronization have received much more attention due to its amazing applications in practice. For example, in the communication of telephone system, the voice one hears on the receiver side at time \(t+\delta \) is the voice from the transmitter side at time t. Hence, it is reasonable to require the states of response system to synchronize the states of drive system at a constant time lag [20]. Compared with other types of synchronization such as complete synchronization or projective synchronization, lag synchronization means that the drive and response systems could be synchronized with a propagation delay. Because the lag synchronization can clearly indicate the fragile nature of neuron systems, it has attracted the concerns of many researchers in various fields and some excellent results have been reported in this research area [20,21,22,23,24,25].

In [20], the exponential lag synchronization for CGNNs with discrete time-delays and distributed delays was investigated via using the intermittent control strategy. By using the analysis method, Lyapunov functional theory and inequality technique, the lag synchronization problem of fuzzy cellular networks (FCNs) with delays was studied in [22]. In [23], an intermittent control scheme was used to investigate the lag synchronization for a type of fractional-order memristive neural networks (FMNNs) with switching jumps. In [24], the authors studied the problem of global exponential lag synchronization of a class of switched NNs with time-varying delays. Very recently, the exponential lag synchronization for a class of neural networks with mixed delays including discrete and distributed delays was concerned by adaptive intermittent control in [25].

When studying the synchronization of chaotic systems, it is a very important topic to find estimate of the convergent rate of synchronization [26]. However, in some special cases, the convergence rate of the synchronization can not be shown or it is not easy to estimate. For example, consider the differential equation \( {\dot{y}}(x)=-\frac{1}{2}y^{3}, \ x\ge 0\). Even though we know that this equation is asymptotically stable, we can not able to estimate the convergent rat of the solution of it. This motivate us to define a new type of convergence rate, such as convergence with general decay. Recently, authors in [27] investigated the general decay synchronization (GDS) of NNs with discontinuous activation functions by nonlinear feedback controller. In [28], the author investigated the GDS of a class of NNs with general neuron activation functions and time-varying delays by constructing suitable Lyapunov functional and using useful inequality techniques. The problem of GDS for memristor-based CGNNs with mixed time-delays and discontinuous activations was considered in [29]. However, to the best of our knowledge, there are few or even no results on general decay lag synchronization (GDLS) of CNNs with constant delays.

Inspired by the above discussions, the aim of the paper is to study the GDLS problem for a class of CNNs with constant delays. By designing a type of nonlinear feedback controller, some simple sufficient criteria ensuring the GDLS of addressed CNNs are obtained by designing a novel nonlinear feedback controller and employing some inequality techniques. Finally, one numerical example is provided to demonstrate the feasibility of the established theoretical results. The results of this paper generalize the classical polynomial synchronization and exponential synchronization via introducing more general convergent rate.

The rest of the paper is organized as follows. In Sect. 1, some useful assumptions, definitions, and lemmas are introduced. In Sect. 2, a class of CNNs model is introduced, and some relative definitions are given. In Sect. 3, we investigated the GDLS of the addressed competitive neural networks with constant delays via designing a novel nonlinear feedback controller. In Sect. 4, two numerical examples and their Matlab simulations are presented. Final section ends up with some general conclusions.

2 Preliminaries

The CNNs with delays in this paper are modeled as follows:

$$\begin{aligned} STM:\ {\dot{x}}_i(t)=&-c_ix_i(t)+\sum _{j=1}^{n}a_{ij}f_j(x_j(t)) +\sum _{j=1}^{n}b_{ij}f_j(x_j(t-\tau _{ij})) \nonumber \\&+B_{i}\sum _{j=1}^{n} m_{ij}(t)h_j + I_{i},\nonumber \\ LTM: {\dot{m}}_{ij}(t)=&-d_im_{ij}(t)+h_jE_if_i(x_i(t)), \end{aligned}$$
(1)

where \(i, j \in {\mathcal {J}}\triangleq \{1,2,\ldots ,n\}\) and \(n\ge 2\); \(x_i(t)\) is the neuron current activity level; \(f_j(\cdot )\) is the output of neurons; \(c_i\) represents the time constant of the neuron; \(m_{ij}(t)\) is the synaptic efficiency; \(h_j\) is the constant external stimulus; \(a_{ij},\ b_{ij}\) represent, respectively, the connection weight and the synaptic weight of delayed feedback between the ith and jth neurons; \(B_i\) is the strength of the external stimulus; \(I_i\) denotes the external inputs on the ith neuron at time t; \(d_i>0\) and \(E_i\) denote disposable scaling constants; \(\tau _{ij}>0\) represents constant delay of the jth unit from the ith unit.

In the paper, without loss of generality, we assume that the input stimulus H can be normalized with unit magnitude \(|H|^2 = 1\), where \(H = (h_1, h_2, \ldots , h_n)^T\). By setting \(S_i =\sum _{j=1}^{n}m_{ij}(t)h_j = H^T m_i(t)\), where \(m_i = (m_{i1}, m_{i2}, \ldots , m_{in})^T\) and summing up the LTM over j, then the drive system (1) can be modified as follows

$$\begin{aligned} STM: {\dot{x}}_i(t)=&-c_ix_i(t)+\sum _{j=1}^{n}a_{ij}f_j(x_j(t)) +\sum _{j=1}^{n}b_{ij}f_j(x_j(t-\tau _{ij}))+B_{i}S_i(t) + I_{i},\nonumber \\ LTM: {\dot{S}}_i(t)=&-d_iS_i(t)+E_if_i(x_i(t)), \end{aligned}$$
(2)

For a positive integer k, let \(R^k \) be a k-dimentional vector space, then the initial values of system (2) are given as

$$\begin{aligned} \begin{aligned} x_i(\theta )&=\varphi ^x_{i}(\theta ), \quad \theta \in [-\tau ,0],\\ S_i(\theta )&=\varphi ^S_{i}(\theta ), \quad \theta \in [-\tau ,0], \end{aligned} \end{aligned}$$

where \(\tau =\max _{i,j\in {\mathcal {J}} } \{ \tau _{ij}\},\ \varphi ^x= \big (\varphi ^x_{1}(\theta ),\varphi ^x_{2}(\theta ), \ldots ,\varphi ^x_{n}(\theta )\big )^T \in C([-\tau ,0],R^n)\), \(\varphi ^S=\big (\varphi ^S_{1} (\theta ),\varphi ^S_{2}(\theta ),\ldots \), \(\varphi ^S_{n}(\theta )\big )^T \in C([-\tau ,0],R^n)\). Here, \(C([\theta _1,\theta _2],R^k)\) for \(\theta _1<\theta _2\ ( \theta _1,\theta _2\in R\)) denotes the Banach space of all continuous functions mapping from \([\theta _1,\theta _2]\) to \(R^k\) with a appropriate norm.

Throughout the paper, we assume that the neuron activation functions \(f_j(v)\) satisfy the following assumptions

\({\mathbf {A}}_1\): For any \(j\in {\mathcal {J}}\), there exist constants \(L_j\) such that,

$$\begin{aligned} \begin{aligned}&|f_j(v_1)-f_j(v_2)|\le L_{j} |v_1-v_2|,\ \ \forall \ v_1,v_2\in R. \end{aligned} \end{aligned}$$

In the paper, the system (2) is assumed to be drive system, and its response system is given by

$$\begin{aligned} STM:{\dot{y}}_i(t)=&-c_iy_i(t)+\sum _{j=1}^{n}a_{ij}f_j(y_j(t)) +\sum _{j=1}^{n}b_{ij}f_j(y_j(t-\tau _{ij})) \nonumber \\&+B_iW_i(t)+I_i+u_i(t),\nonumber \\ LTM:{\dot{W}}_i(t)=&-d_iW_i(t)+E_if_i(y_i(t))+{\tilde{u}}_i(t), \end{aligned}$$
(3)

where \(c_i,\ d_i,\ a_{ij}, \ b_{ij},\ B_i,\ E_i\) are given system (2), \(u_i(t)\) and \({\tilde{u}}_i(t)\) are controllers to be designed.

The initial values of system (3) are given by

$$\begin{aligned} \begin{aligned} y_i(\theta )&=\phi ^y_{i}(\theta ), \quad \theta \in [-{\tau },0], \\ W_i(\theta )&=\phi ^W_{j}(\theta ), \quad \theta \in [-{\tau },0], \end{aligned} \end{aligned}$$

where \(\phi ^y=(\phi ^y_{1}(\theta ),\phi ^y_{2}(\theta ), \ldots ,\phi ^y_{n}(\theta ))^T \in C([-\tau ,0],R^n)\), \(\phi ^W=(\phi ^W_{1}(\theta ),\phi ^W_{2}(\theta ), \ldots ,\phi ^W_{n}(\theta ))^T \in C([-\tau ,0],R^n)\).

Let \(e_{i}(t)=y_i(t)-x_i(t-\sigma )\) and \(z_{i}(t)=W_i(t)-S_i(t-\sigma )\), then the corresponding error system between drive system (2) and response system (3) can be written as

$$\begin{aligned} STM:{\dot{e}}_i(t)=&-c_ie_i(t)+\sum _{j=1}^{n}a_{ij}g_j(e_j(t)) +\sum _{j=1}^{n}b_{ij}g_j(e_j(t-\tau _{ij}))+B_iz_i(t)+u_i(t), \nonumber \\ LTM:{\dot{z}}_i(t)=&-d_iz_i(t)+E_ig_i(e_i(t))+{\tilde{u}}_i(t), \end{aligned}$$
(4)

where \(g_j(e_j(t))=f_j(y_j(t))-f_j(x_j(t-\sigma ))\) and \(g_j(e_j(t-\tau _{ij}))= f_j(y_j(t-\tau _{ij})) -f_j(x_j(t-\tau _{ij}-\sigma ))\).

In order to define the initial condition of error system (4), we supplement the initial condition of \(x_i(t)\) and \(S_i(t)\) as following

$$\begin{aligned} \displaystyle x_i(\theta )= & {} {\bar{\varphi }}^x_i(\theta )= \left\{ \begin{aligned} \displaystyle&\varphi ^x_i(\theta ), \qquad \ -\tau \le \theta \le 0, \\ \displaystyle&\varphi ^x_i(-\tau ), \quad \ -\tau -\sigma \le \theta \le -\tau , \end{aligned}\right. \\ \displaystyle S_i(\theta )= & {} {\bar{\varphi }}^S_i(\theta )= \left\{ \begin{aligned} \displaystyle&\varphi ^S_i(\theta ), \qquad \ -\tau \le \theta \le 0,\\ \displaystyle&\varphi ^S_i(-\tau ), \quad \ -\tau -\sigma \le \theta \le -\tau , \end{aligned}\right. \end{aligned}$$

then the initial condition of system (4) can be given by \(e_i(\theta )=\phi ^y_i(\theta )-{\bar{\varphi }}^x_i(\theta -\sigma ),\ z_i(\theta )=\phi ^W_i(\theta )-{\bar{\varphi }}^S_i(\theta -\sigma )\) for \(-\tau \le \theta \le 0\) and \( i\in {\mathcal {J}}\).

Now, similar to the [28, 30], we introduce the definitions of \(\psi \)-type function and GDS as follows.

Definition 1

[28, 30]. Let \(R^+ \triangleq [0,+\infty )\), then a function \(\psi :R^{+}\rightarrow [1,+\infty )\) is said to be \(\psi \)-type function if it satisfies the following four conditions:

  1. (1)

    It is differentiable and nondecreasing;

  2. (2)

    \(\psi (0)=1\) and \(\psi (+\infty )=+\infty \);

  3. (3)

    \({\tilde{\psi }}(t)={\dot{\psi }}(t)/\psi (t)\) is nonincreasing and \(\psi ^*=\sup _{t\ge 0}{\tilde{\psi }}(t)<+\infty \);

  4. (4)

    For any \(t,\ s \ge 0,\ \psi (t+s)\le \psi (t) \psi (s)\).

For example, the functions \(\psi (t)=e^{\alpha t}\) and \(\psi (t)=(1+t)^\alpha \) for any \(\alpha > 0\) satisfy the above four conditions, thus can be seen as \(\psi \)-type functions.

Definition 2

[26, 29]. The drive-response systems (2) and (3) are said to be general decay synchronized if there exist a scalar \(\varepsilon >0\) such that

$$\begin{aligned} \lim \sup \limits _{t\rightarrow +\infty } \frac{\log \big (\Vert e(t)\Vert +\Vert z(t)\Vert \big )}{\log \psi (t)}\le -\varepsilon , \end{aligned}$$

where \( e(t)=(e_1(t),e_2(t),\ldots ,e_m(t))^T,\ z(t)=(z_1(t),z_2(t),\ldots ,z_n(t))^T\), \(\varepsilon >0\) can be seen the convergence rate as synchronization error approaches zero.

\({\mathbf {A}}_2\): There exist a function \(\varrho (t)\in C(R,R^+)\) and a scaler \(\varepsilon >0\) such that

$$\begin{aligned} {\tilde{\psi }}(t)\le 1,\quad \sup \limits _{t\in [0,+\infty )}\int _{0}^{t}\psi ^{\varepsilon } (s)\varrho (s)ds<+\infty , \quad \text {for any}\ t\ge 0, \end{aligned}$$
(5)

where the functions \(\psi (t), {\tilde{\psi }}(t)\) are defined in the Definition 1.

Following lemma plays a vital role in our later study.

Lemma 1

[31]. Suppose that assumption \({\mathbf {A}}_2\) hold, and synchronization errors e(t) and z(t) between the drive-response systems (2) and (3) satisfied the differential equations \( {\dot{e}}(t)={F}(t,e(t),z(t)) \) and \( {\dot{z}}(t)={G}(t,e(t),z(t)) \), respectively, where the functions F(t, e(t), z(t)) and G(t, e(t), z(t)) are locally bounded. If there exist a Lyapunov functional \(V(t,e(t), z(t)):R^+\times R^n\times R^n \rightarrow R^+\), and positive constants \(\lambda _1, \lambda _2\) such that for any \((t,e(t),z(t))\in R^+\times R^n\times R^n \),

$$\begin{aligned} \lambda _1\left( \Vert e(t)\Vert ^2+\Vert z(t)\Vert ^2\right)\le & {} V(t,e(t),z(t)), \end{aligned}$$
(6)
$$\begin{aligned} \frac{d V(t,e(t),z(t))}{dt}\bigg |_{(4)}\le & {} -\varepsilon V(t,e(t),z(t)) +\lambda _2 \varrho (t), \end{aligned}$$
(7)

where \(\varepsilon \) and \(\varrho (t)\) are defined in \({\mathbf {A}}_2\). Then the drive-response systems (2) and (3) will realize GDS in the sense of Definition 2, and the convergence rate of GDS is \(\varepsilon \).

Proof

The proof of Lemma 1 is similar to Proof of Lemma 1 given in [31], so we have omitted in here. \(\square \)

3 Main Results

In this section, we will derive some sufficient criteria for the GDS of drive-response systems (2) and (3). First letting \(\omega _{ij}\) be any numbers greater that zero, \(\mu _{ij}=\frac{L_j|b_{ij}|}{2}\), and designing the controllers \(u_i(t) \) and \(\ {\tilde{u}}_i(t)\) of response system (3) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_i(t)=- \frac{\eta _i\Vert e(t)\Vert ^2e_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}},\\ {\tilde{u}}_i(t)= -\frac{\xi _i\Vert z(t)\Vert ^2z_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}}, \end{array}\right. } \end{aligned}$$
(8)

where \(\eta _i\) for \(i\in {\mathcal {J}}\) and \(\xi _i\) for \(i\in {\mathcal {J}}\) are positive control gains satisfying

$$\begin{aligned} \displaystyle {\left\{ \begin{array}{ll} -c_i-\eta _i+\frac{L_i|E_i|}{2}+ \frac{|B_i|}{2}+ \frac{1}{2}\sum \limits _{j=1}^n \left( {|a_{ij}|L_j+|a_{ji}|L_i+|b_{ij}|L_{j}}+2\mu _{ji}+2\tau _{ji} \omega _{ji} \right)<0,\\ -d_i -\xi _i+ \frac{L_i|E_i|}{2} +\frac{|B_i|}{2}<0. \end{array}\right. } \end{aligned}$$
(9)

Then by using the nonlinear feedback controller (8), the following theorem can be obtained.

Theorem 1

Suppose \(\mathbf {A_1}\)–\(\mathbf {A_2}\) hold, then the response network (3) can achieve GDS with the derive network (2) under the nonlinear feedback controller (8) if, the control gains \(\eta _i\) and \(\xi _i\) satisfy the inequality (9).

Proof

Construct the following Lyapunov–Krasovskii type functional:

$$\begin{aligned} \begin{aligned} \displaystyle V(t)=&\sum _{i=1}^{n}\frac{1}{2} {e}^2_{i}(t) + \sum _{i=1}^{n}\frac{1}{2}z^2_{i}(t) +\sum _{i=1}^{n} \sum _{j=1}^{n}\int _{t-\tau _{ij}}^{t}\mu _{ij}e^2_{j}(s)ds \\&\displaystyle +\sum _{i=1}^{n} \sum _{j=1}^{n}\int _{-\tau _{ij}}^{0}\int _{t+s}^{t} \omega _{ij} e^2_{j}(\varsigma )d\varsigma ds, \end{aligned} \end{aligned}$$
(10)

where \(\mu _{ij}=\frac{L_j|b_{ij}|}{2}\) and \(\omega _{ij}\) be any numbers greater that zero. Then, there exist positive scalars \(\kappa> 1,\ \gamma > 1 \) such that

$$\begin{aligned} \begin{aligned} \displaystyle \frac{1 }{2}\sum _{i=1}^n e^2_i(t)+\frac{1 }{2}\sum _{i=1}^n z^2_i(t) \le&V(t) \le \displaystyle \kappa \sum _{i=1}^ne^2_i(t) +\gamma \sum _{i=1}^nz^2_i(t) \\&+\frac{\kappa }{\alpha }\sum _{i=1}^n\sum _{j=1}^{n} \omega _{ij} \int _{t-\tau _{ij}}^{t} e^2_j(s) ds, \end{aligned} \end{aligned}$$
(11)

where \(\alpha =\min _{i\in {\mathcal {J}}}\{\alpha _i \}, \ \beta =\min _{i\in {\mathcal {J}}}\{\beta _i \} \) with

$$\begin{aligned} \alpha _i&\triangleq c_i+\eta _i-\frac{L_i|E_i|}{2}- \frac{|B_i|}{2} - \frac{1}{2}\sum _{j=1}^n \bigg ({|a_{ij}|L_j+|a_{ji}|L_i+|b_{ij}|L_{j}}+2\mu _{ji}+2\tau _{ji} \omega _{ji} \bigg )>0,\\ \beta _i&\triangleq d_i +\xi _i- \frac{L_i|E_i|}{2} -\frac{|B_i|}{2}>0. \end{aligned}$$

Now, calculating the time derivative of V(t), we get

$$\begin{aligned} \displaystyle {\dot{V}}(t) =&\displaystyle \sum _{i=1}^n \left\{ e_{i}(t)\left[ -c_ie_{i}(t)+\sum _{j=1}^{n}a_{ij}g_j(e_{j}(t)) +\sum _{j=1}^{n}b_{ij}g_j\left( e_{j}(t-\tau _{ij})\right) +B_iz_i(t) \right. \right. \\&\left. \displaystyle -\frac{\eta _i\Vert e(t)\Vert ^2e_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) }\right] + \sum _{j=1}^{n} {\mu }_{ij}\left( e^2_{j}(t) - e^2_{j}(t-\tau _{ij})\right) \\ {}&\left. + \sum _{j=1}^{n} \omega _{ij}\left( \tau _{ij}e^2_{j}(t) - \int _{t-\tau _{ij}}^{t} e^2_{j}(s) ds\right) \right\} \\&\displaystyle + \sum _{i=1}^n \left\{ z_{i}(t)\left[ -d_iz_{i}(t)+E_ig_i(e_i(t)) -\frac{\xi _i\Vert z(t)\Vert ^2z_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }\right] \right\} . \end{aligned}$$

In view of the assumption \(\mathbf {A_1}\) and inequality \(2ab\le a^2+b^2\) for any \(a> 0,b> 0\), one has

$$\begin{aligned} \sum _{i=1}^{n}\sum _{j=1}^{n}a_{ij}e_{i}(t)g_j(e_{j}(t)) \le \sum _{i=1}^{n}\sum _{j=1}^{n}|a_{ij}||e_{i}(t)||g_j(e_{j}(t))| \le \sum _{i=1}^{n}\sum _{j=1}^{n}\frac{L_j}{2}|a_{ij}|\Big ( e^2_{i}(t)+e^2_{j}(t)\Big ). \end{aligned}$$

Similarly, we have

$$\begin{aligned} \sum _{j=1}^{n}\sum _{i=1}^{n}b_{ij}e_{i}(t)g_j(e_{j}(t-\tau _{ij}))&\le \sum _{j=1}^{n}\sum _{i=1}^{n}\frac{L_{j} }{2}|b_{ij}|\Big ( e^2_{i}(t)+ e^2_{j}(t-\tau _{ij}) \Big ),\\ \sum _{i=1}^{n}B_{i}e_{i}(t)z_{i}(t)&\le \sum _{i=1}^{n}\frac{|B_{i}| }{2}\Big ( e^2_{i}(t)+z^2_{i}(t) \Big ), \\ \sum _{i=1}^{n}E_{i}z_{i}(t)g_i(e_{i}(t)&\le \sum _{i=1}^{n}\frac{L_{i}|E_{i}|}{2} \Big ( z^2_{i}(t)+e^2_{i}(t) \Big ). \end{aligned}$$

Introducing above four inequalities to the derivative of V(t), we have

$$\begin{aligned} \displaystyle {\dot{V}}(t) \le&\displaystyle \sum _{i=1}^n\left[ -c_i+ \frac{|B_i|}{2} +\frac{L_i|E_i|}{2} + \frac{1}{2}\sum _{j=1}^n \bigg ({|a_{ij}|L_j+|a_{ji}|L_i+|b_{ij}|L_{j}}+2\mu _{ji}+2\tau _{ji} \omega _{ji} \bigg )\right] e^2_{i}(t)\\&-\sum _{i=1}^n\frac{\eta _i\Vert e(t)\Vert ^2e^2_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) } -\sum _{i=1}^n\sum _{j=1}^{n} \omega _{ij} \int _{t-\tau _{ij}}^{t} e^2_{j}(s) ds +\sum _{i=1}^n\left[ -d_i + \frac{L_i|E_i|}{2} +\frac{|B_i|}{2} \right] z^2_{i}(t)\\&-\sum _{i=1}^n\frac{\eta _i\Vert z(t)\Vert ^2z_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) } \\ \le&\displaystyle \sum _{i=1}^n\left[ -c_i-\eta _i+\frac{L_i|E_i|}{2}+ \frac{|B_i|}{2} + \frac{1}{2}\sum _{j=1}^n \bigg ({|a_{ij}|L_j+|a_{ji}|L_i+|b_{ij}|L_{j}}+2\mu _{ij}+2\tau _{ij} \omega _{ij} \bigg )\right] e^2_{i}(t) \\&\displaystyle +\bigg [\sum _{i=1}^n\eta _ie^2_{i}(t)-\sum _{i=1}^n \frac{\eta _{i}\Vert e(t)\Vert ^2e^2_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) }\bigg ] -\sum _{i=1}^n\sum _{j=1}^{n} \omega _{ij} \int _{t-\tau _{ij}}^{t} e^2_{i}(s) ds \\&+\displaystyle \sum _{i=1}^n\left[ -d_i -\xi _i+ \frac{L_i|E_i|}{2} +\frac{|B_i|}{2} \right] z^2_{i}(t)+\bigg [\sum _{i=1}^n \xi _iz^2_{i}(t)-\sum _{i=1}^n\frac{\xi _i\Vert z(t)\Vert ^2z^2_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }\bigg ] \\ \le&\displaystyle -\sum _{i=1}^n \alpha _i e^2_{i}(t)+ \max _{i\in {\mathcal {J}}}\{\eta _i\} \frac{\Vert e(t)\Vert ^2\varrho (t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) } -\sum _{i=1}^n\sum _{j=1}^{n} \omega _{ij} \int _{t-\tau _{ij}}^{t} e^2_{j}(s)ds\\&-\sum _{i=1}^n \beta _i z^2_{i}(t)+ \max _{i\in {\mathcal {J}}}\{\xi _i\} \frac{\Vert z(t)\Vert ^2\varrho (t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }. \end{aligned}$$

Also by letting \({\eta }=\max _{i\in {\mathcal {J}}}\{\eta _i\}>0, \ {\xi }=\max _{i\in {\mathcal {J}}}\{\xi _i\}>0\) and using the inequality \(0 \le ab/(a + b) \le a \) for any \(a> 0,b> 0\), we have

$$\begin{aligned} {\dot{V}}(t) \le&-\sum _{i=1}^n \alpha _i e^2_{i}(t) + {\eta }\varrho (t)-\sum _{i=1}^n\beta _{i} z^2_{i}(t) + {\xi }\varrho (t) -\sum _{i=1}^n \sum _{j=1}^n \omega _{ij} \int _{t-\tau _{ij}}^{t}e^2_{j}(s) ds. \end{aligned}$$
(12)

Now taking a small enough \(\delta \) such that \(\delta \kappa \le \alpha ,\ \delta \gamma \le \beta \), then from the inequalities (11) and (12), we get

$$\begin{aligned} \displaystyle \frac{dV(t)}{dt}+ \delta V(t) \le&\displaystyle -\sum _{i=1}^n \alpha _i e^2_{i}(t) + {\eta }\varrho (t) -\sum _{i=1}^n \sum _{j=1}^n \omega _{ij} \int _{t-\tau _{ij}}^{t} e^2_{j}(s) ds \\&-\sum _{j=1}^n\beta _{j} z^2_{j}(t) + {\xi }\varrho (t) \\&+\delta \left[ \kappa \sum _{i=1}^ne^2_i(t) +\frac{\kappa }{\alpha } \sum _{i=1}^n\sum _{j=1}^{n} \chi _{ij} \int _{t-\tau _{ij}}^{t} e^2_i(s) ds +\gamma \sum _{j=1}^nz^2_j(t)\right] \\ \le&\displaystyle (\delta \kappa - \alpha )\sum _{i=1}^n e^2_{i}(t) +\sum _{i=1}^n \sum _{j=1}^n \left( \frac{\delta \kappa }{\alpha }-1 \right) \int _{t-\tau _{ij}}^{t} \mu _{ij}e^2_{j}(s) ds +{\eta }\varrho (t)\\&\displaystyle +(\delta \gamma -\beta )\sum _{i=1}^n z^2_{i}(t) +\xi \varrho (t) \\ \le&\displaystyle (\eta +\xi )\varrho (t), \end{aligned}$$

which means that

$$\begin{aligned} \displaystyle \frac{dV(t))}{dt}+ \delta V(t)\le (\eta +\xi )\varrho (t). \end{aligned}$$
(13)

Thus, from Lemma 1, the drive-response systems (2) and (3) achieved GDLS under the nonlinear feedback controller (8). The convergence rate of e(t) and z(t) approaching zero is \(\delta \). The proof is completed. \(\square \)

When there is no delay in system (2), then it is degenerated to

$$\begin{aligned} STM: {\dot{x}}_i(t)=&-c_ix_i(t)+\sum _{j=1}^{n}a_{ij}f_j(x_j(t)) +B_{i}S_i(t) + I_{i},\nonumber \\ LTM: {\dot{S}}_i(t)=&-d_iS_i(t)+E_if_i(x_i(t)). \end{aligned}$$
(14)

Accordingly, the corresponding response system becomes to the following form

$$\begin{aligned} STM:{\dot{y}}_i(t)=&-c_iy_i(t)+\sum _{j=1}^{n}a_{ij}f_j(y_j(t)) +B_iW_i(t)+I_i+u_i(t),\nonumber \\ LTM:{\dot{W}}_i(t)=&-d_iW_i(t)+E_if_i(y_i(t))+{\tilde{u}}_i(t), \end{aligned}$$
(15)

where \(u_i(t)\) and \({\tilde{u}}_i(t)\) are nonlinear controllers.

In this case, for GDS of drive-response systems (14) and (15), we have a following corollary from Theorem 1.

Corollary 1

Suppose assumptions \(\mathbf {A_1}\)–\(\mathbf {A_2}\) hold, then the response network (15) can achieve GDS with the drive network (14) under the following nonlinear feedback controller

$$\begin{aligned} \begin{aligned}&u_i(t)=- \frac{{\bar{\eta }}_i\Vert e(t)\Vert ^2e_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}},\\&{\tilde{u}}_i(t)= -\frac{{\bar{\xi }}_i\Vert z(t)\Vert ^2z_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}}, \end{aligned} \end{aligned}$$
(16)

where \({\bar{\eta }}_i\) for \(i\in {\mathcal {J}}\) and \({\bar{\xi }}_i\) for \(i\in {\mathcal {J}}\) are positive control gains satisfying

$$\begin{aligned} \displaystyle \left\{ \begin{aligned} \displaystyle&{\bar{\alpha }}_i \triangleq c_i+{\bar{\eta }}_i -\frac{L_i|E_i|}{2} - \frac{1}{2}\sum _{j=1}^n \bigg ({|a_{ij}|L_j+|a_{ji}|L_i}\bigg )>0,\\ \displaystyle&{\bar{\beta }}_i\triangleq d_i+{\bar{\xi }}_i -\frac{L_i|E_i|}{2}-\frac{|B_i|}{2}>0. \end{aligned}\right. \end{aligned}$$
(17)

Remark 1

Even though there are some previously published results on the exponential or asymptotically lag synchronization for CNNs with or without time delays [2, 6, 7], there are still no any results on GDLS for CNNs. As we mentioned earlier in the paper, GDS enable us to estimate to convergence rate of synchronization error via defining a more general convergence rate. In this paper, we firstly studied the GDLS of CNNs with constant delay by introducing a novel nonlinear controller and using some inequality techniques. It it not difficult to see that the results obtained in [2, 6, 7, 20,21,22] can be seen the special cases of our results when the general decay function chosen as \(\psi (t) = e^{\alpha t} \) and \(\psi (t) = (1 + t)^\alpha \) for any \(\alpha > 0\). From this point, our results are more general and have better applicability.

4 Numerical Simulations

In this section, two numerical examples are presented to validate the feasibility of the established results in the paper.

Example 1

For \(n=2\), consider the following delayed CNNs system

$$\begin{aligned} STM: {\dot{x}}_i(t)=&-c_ix_i(t)+\sum _{j=1}^{2}a_{ij}f_j(x_j(t)) +\sum _{j=1}^{2}b_{ij}f_j(x_j(t-\tau _{ij}))+B_{i}S_i(t) + I_{i},\nonumber \\ LTM: {\dot{S}}_i(t)=&-d_iS_i(t)+E_if_i(x_i(t)), \end{aligned}$$
(18)

where \(f_1(u)=f_2(u)=\tanh (u)\). The parameters of system (18) are chosen that \(c_1=c_2=0.8,\ d_1=0.4,\ d_2=0.3,\ a_{11}=1, \ a_{12}=1, \ a_{21}=-\,3, \ a_{22}=-\,3,\ \ b_{11}=-\,1.5, \ b_{12}=2, \ b_{21}=3, \ b_{22}=3.5,\ E_{1}=E_{2}=1, \ B_{1}=B_{2}=1,\ \tau _{ij}= 1\) and \(I_i=0\) for \(i=1,2\).

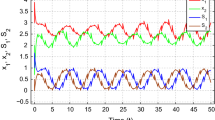
The Matlab simulation of drive system (18) under the initial conditions \(x_1(\theta )=0.2,\ x_2(\theta )=0.6,\ S_1(\theta )=-\,0.1\) and \( S_2(\theta )=0.2\) for \(\theta \in [-\,1,0]\) is shown in Fig. 1, we can see that drive system (18) has a chaotic attractor.

Fig. 1
figure 1

The transient behavior of drive system (18)

Full size image
Fig. 2
figure 2

The evaluation of synchronization errors \({e}_i\)

Full size image
Fig. 3
figure 3

The evaluation of synchronization error \({z}_i\)

Full size image

The corresponding response system is given by

$$\begin{aligned} STM:{\dot{y}}_i(t)=&-c_iy_i(t)+\sum _{j=1}^{2}a_{ij}f_j(y_j(t)) +\sum _{j=1}^{2}b_{ij}f_j(y_j(t-\tau _{ij})) +B_iW_i(t)+I_i+u_i(t),\nonumber \\ LTM:{\dot{W}}_i(t)=&-d_iW_i(t)+E_if_i(y_i(t))+{\tilde{u}}_i(t), \end{aligned}$$
(19)

where \(c_i,\ a_{ij},\ b_{ij},\ f_j,\ \tau _{ij}\) and \(I_i\) are the same as in system (18), and the nonlinear feedback controller \(u_i(t)\) is designed as follows

$$\begin{aligned} \begin{aligned}&u_i(t)=- \frac{\eta _i\Vert e(t)\Vert ^2e_{i}(t)}{\left( \Vert e(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}},\\&{\tilde{u}}_i(t)= -\frac{\xi _i\Vert z(t)\Vert ^2z_{i}(t)}{\left( \Vert z(t)\Vert ^2+\varrho (t)\right) }, \quad i\in {\mathcal {J}}, \end{aligned} \end{aligned}$$
(20)

where \(e_{i}(t)=y_i(t)-x_i(t-\sigma )\) and \(z_{i}(t)=W_i(t)-S_i(t-\sigma )\) for \(i=1,2.\)

Fig. 4
figure 4

Synchronization curves of \(x_i\) and \(y_i\)

Full size image
Fig. 5
figure 5

Synchronization curves of \(S_i\) and \(W_i\)

Full size image

Choosing the time lag \(\sigma =2\), then it is not difficult to estimate that \( {L}_1=L_2=1\) and \(\tau _{ij}=1\). Thus, the assumption \(\mathbf {{A}_1}\) is satisfied. Letting \(\varrho (t)=e^{-0.1 t},\ \psi (t) = e^{ t}\) and choosing \(\eta _1=7.2,\ \eta _2=8.4,\ \xi _1=0.7\) and \( \xi _2=0.8\), then the assumption \(\mathbf {A_2}\) and inequality (9) can also be satisfied. Therefore, according to the Theorem 1, the drive-response systems (18) and (19) can be achieved GDLS under the controller (20). The time evolution of synchronization errors between drive-response systems (18) and (19) are showmen in Figs. 2 and 3, where the initial values of response system (19) are chosen as \(y_1(\theta )=0.460,\ y_2(\theta )=0.310,\ W_1(\theta )= 0.281\) and \(W_2(\theta )=-0.086\) for \(\theta \in [-1,0]\). The synchronization curves between systems (18) and (19) are demonstrated in Figs. 4 and 5.

5 Conclusion

In this work, we studied the GDLS problem for a type of chaotic CNNs with constant delays. By employing useful analysis technique and introducing a Lyapunov-Krasovskii functional, we proposed novel nonlinear feedback control strategies to guarantee the GDLS of considered drive-response systems. Finally, one numerical example and its Matlab simulations are provide to demonstrate the feasibility of the established theoretical results. The results of this can be seen improvement and extension of the previous synchronization studies on CNNs since the GDLS includes the classical polynomial synchronization and exponential synchronization as its special cases.