1 Introduction

Two-time-scale competitive neural networks (CNNs), proposed by Meyer-Baese in [1], have two state variables with different time scales named short-term memory (STM) and long-term memory (LTM), respectively. The former describes rapid neural activity, while the latter describes slow unsupervised changes in synapses caused by external stimuli [2]. Compared with the general single-time-scale neural networks such as Hopfield neural networks and cellular neural networks, CNNs possess stronger ability of modeling the cortical congnitive maps benefiting from the competitive learning law for the changes in synapses [3]. Therefore, CNNs have shown significant application value in the areas of signal processing, neural computation, pattern recognition, optimization, control and attracted the attention of scholars from the fields of mathematics, physics and engineering applications [4,5,6,7,8]. The state equation of the ith neuron in an n-neuron CNNs is expressed as follows:

$$\begin{aligned} {\mathrm{STM}}:\,\,\varepsilon \dot{x}_i(t)&=-a_ix_i(t)+\sum \limits _{j=1}^n\omega _{ij}f_j(x_j(t))\nonumber \\&\quad +b_i\sum \limits _{k=1}^{n_p}m_{ik}(t)q_k \end{aligned}$$
(1a)
$$\begin{aligned} {\mathrm{LTM}}:\,\,\dot{m}_{ik}(t)&=-m_{ik}(t)+q_kf_i(x_i(t)) \end{aligned}$$
(1b)

where \(x_i(t)\in R\) denotes the neuron current activity level, \(m_{ik}(t)\in R\) denotes the synaptic efficiency, \(f_j(\cdot )\) is the activation function, the neuron output is expressed as \(f_j(x_j(t))\), \(a_i>0\) represents time constant of the ith neuron, \(\omega _{ij}\) denotes the connection weight between the ith and jth neurons, \(q_k\in R\) represents the constant external stimulus, the external stimulus strength is expressed as \(b_i\), \(\varepsilon >0\) denotes the time scale parameter of STM state, n is the number of neurons, \(n_p\) is the number of the external stimulus, \(\Sigma \) is the summation operator, \(i,j=1,\dots ,n\), \(k=1,\dots ,n_p\).

During the circuit implementation process of neural networks (NNs), there inevitably exist time delays owing to the transmission lags of signals and finite switching speed of electronic components [2]. Under certain network connection parameters and time delays, NNs usually exhibit complex behaviors such as instability, periodic oscillation, branching and chaotic attractors [9]. Pecora and Carroll first proposed the drive-response idea in [10], which enabled the synchronization of two identical chaotic NNs under different initial values, thus stirring up a research boom on network synchronization. Recently, due to the application potential of artificial NNs synchronization in image encryption, signal encryption and other communication fields [3], the synchronization problem of CNNs has also attracted widespread attention [11,12,13,14,15]. The earliest synchronization results of CNNs can be found in [9] where theoretical criteria was presented to ensure exponential synchronization of two CNNs based on Lyapunov–Krasovskii functionals (LKFs), linear matrix inequalities (LMIs) and Newton–Leibniz formula (NLF). Subsequently, Gu et al. considered the synchronization problem of CNNs with time delays and stochastic perturbation, and designed an adaptive synchronization controller based on the LaSalle-type invariance principle, LKF and LMIs [11]. Adaptive feedback controllers were further designed considering the hybrid perturbations [12] and mixed time delays [13]. For the delayed CNNs with unknown parameters, a parameter identification method was introduced and a robust adaptive controller was designed to ensure synchronization [14]. Based on LKFs, free-weighting matrix method, NLF, invariance principle of stochastic differential equation as well as LMIs, exponential synchronization control for stochastic CNNs was considered in [15]. To deal with the time delay terms, delay partitioning method was utilized and the synchronization condition dependent on time delays was deduced [16]. Considering the time-varying delays [17] and constant time delays [18], exponential synchronization criterion and decay lag synchronization criterion were respectively derived for CNNs based on LKF and algebraic inequality techniques (AITs). In order to synchronize two CNNs within a setting time, finite time synchronization [4, 19] and fixed time synchronization [20, 21] were studied based on LKFs and AITs. In addition, some researchers proposed fractional-order CNNs [22, 23] and memristive CNNs [24,25,26] and obtained synchronization criteria based on LKFs, LMIs and AITs.

Summarizing the above-mentioned literature on CNNs synchronization control, it can be found that most of them are based on relatively fixed methods such as LKFs, AITs and LMIs, except that the complexity of the CNNs models is constantly increased, for example, discontinuous activation functions [4, 19], external disturbances [12, 13], multiple mixed time delays [4, 17, 19], fractional-order systems [22, 23], memristive systems [24,25,26] and so on. Such controller design methods require the calculation of multiple algebraic or matrix inequalities. Moreover, due to the existence of adaptive adjustment parameters [11,12,13,14, 18, 19] or sign functions [4, 20, 21] in the controllers, it is difficult to implement nonlinear feedback controllers in practical applications.

Optimal control is an important branch of the control theory, and its goal is to achieve system stability and optimization of indicators such as tracking and energy consumption [27]. For general coupled NNs, some results about \(H_{\infty }\) control [28, 29], guaranteed cost control [30] as well as optimal control [31,32,33,34] have been obtained to achieve synchronization. The designed controllers can effectively suppress external disturbance [28, 29], or make the synchronization rate as fast as possible [31], or minimize the index of integral square error and control energy [32,33,34]. As far as the authors’ knowledge, no researchers have explored the synchronization control of CNNs from the perspective of optimal solution. Therefore, the optimal synchronization control of CNNs is still an open problem.

However, dealing with nonlinear optimal control problem is difficult mainly because it is not easy to solve the Hamilton–Jacobi–Bellman (HJB) partial differential equation numerically. In the past several decades, inverse optimal control has been developed as an alternative method to solve the nonlinear optimal control problem in the fields of aerospace industry [35], robotics [36] and so on without solving the complex HJB equation [37]. The main idea of inverse optimal control is to construct a stabilizing feedback controller first, then use this controller in the optimization of a meaningful performance functional which is dependent on state variables and control input [38]. In the inverse optimality techniques, the existence of control Lyapunov function (CLF) is vital [39]. If the CLF is known, it can act as the Bellman function to derive the explicit form of stabilizing controller, so as to avoiding solving the HJB equation [40].

In this paper, based on the drive-response idea and inverse optimality techniques, an optimal controller design method is proposed to synchronize two CNNs with constant time delays and minimize a meaningful performance functional. The main contributions are listed below.

  1. (1)

    By means of the drive-response idea and inverse optimality techniques, the optimal synchronization control of two CNNs is solved by considering the inverse optimal control of the error system.

  2. (2)

    By making full use of the coupling relationship between fast and slow dynamics of the error system, a novel CLF is constructed, which is significant to reveal the effect of time scale parameter on synchronization behavior.

  3. (3)

    A state feedback inverse optimal controller design method is proposed, which can synchronize two CNNs and minimize a meaningful performance functional while avoiding solving HJB equation. More importantly, the designed controller is linear and easy to implement.

The structure of this paper is arranged as follows. Section 2 presents the problem formulation and preliminaries. The main results are stated in Sect. 3. The superiority of our method is illustrated by an example in Sect. 4. A conclusion is made in Sect. 5.

2 Problem formulation and preliminaries

Let

$$\begin{aligned} S_i(t)=\sum \limits _{k=1}^{n_p}m_{ik}(t)q_k=q^{\mathrm{T}}m_i(t) \end{aligned}$$
(2)

where the superscript T represents matrix transpose, \(q=[q_1,\dots ,q_{n_p}]^{\mathrm{T}}\), \(\Vert q\Vert ^2=q_1^2+\cdots +q_{n_p}^2\), \(m_i(t)=[m_{i1},\dots , m_{in_p}]^{\mathrm{T}}\). The input stimulus q is a constant vector and can be normalized with unit magnitude without loss of generality [2], that is, \(\Vert q\Vert ^2=1\). Substituting (2) into (1) and taking the constant time delays into consideration, Eq. (1) can be formulated as

$$\begin{aligned} {\mathrm{STM}}:\,\,\varepsilon \dot{x}_i(t)&=-a_ix_i(t)+\sum \limits _{j=1}^n\omega _{ij}f_j(x_j(t))\nonumber \\&\quad +\sum \limits _{j=1}^n\omega _{ij}^{\prime}f_j(x_j(t-\tau ))+b_iS_{i}(t) \end{aligned}$$
(3a)
$$\begin{aligned} {\mathrm{LTM}}:\,\,\dot{S}_{i}(t)&=-S_{i}(t)+f_i(x_i(t)) \end{aligned}$$
(3b)

where \(\omega _{ij}^{\prime}\) represents the interconnection weight of delayed feedback, \(\tau >0\) denotes the constant time delay and the meanings of other variables can refer to Eq. (1).

Assumption 1

The activation function \(f_i(x_i(t))\) is continuous and satisfies

$$\begin{aligned} \begin{array}{l} 0\le \frac{f_i(\mu )-f_i(\nu )}{\mu -\nu }\le \delta _i,\\ \end{array} \end{aligned}$$
(4)

for any \(\mu \ne \nu \), \(\nu \in R\), and \(\delta _i>0\), \(i=1,\dots ,n\). Let \(\Delta ={\mathrm{diag}}(\delta _1,\dots ,\delta _n)\).

Remark 1

The activation function \(f_i(x_i(t))\) can be selected as the sigmoid function, hyperbolic tangent function, or other differentiable function satisfying Assumption 1.

Following the drive-response idea in [10], the CNNs (3) is regarded as drive system. A compact form of (3) is expressed as follows:

$$\begin{aligned} {\mathrm{STM}}:\,\,\varepsilon \dot{x}(t)&=-Ax(t)+Wf(x(t))\nonumber \\&\quad +W^{\prime}f(x(t-\tau ))+BS(t) \end{aligned}$$
(5a)
$$\begin{aligned} {\mathrm{LTM}}:\,\,\dot{S}(t)&=-S(t)+f(x(t)) \end{aligned}$$
(5b)

where \(A={\mathrm{diag}}(a_1,\dots ,a_n)\), \(x(t)=[x_1(t),\dots , x_n(t)]^{\mathrm{T}}\), \(W^{\prime}=[W_1^{\prime},\dots ,W_n^{\prime}]\), \(W_i^{\prime}=[\omega _{1i}^{\prime},\dots ,\omega _{ni}^{\prime}]^{\mathrm{T}}\), \(x(t-\tau )=[x_1(t-\tau ),\dots , x_n(t-\tau )]^{\mathrm{T}}\), \(W=[W_1,\dots ,W_n]\), \(W_i=[\omega _{1i},\dots ,\omega _{ni}]^{\mathrm{T}}\), \(f(x(t))=[f_1(x_1(t)),\dots ,f_n(x_n(t))]^{\mathrm{T}}\),

\(f(x(t-\tau ))=[f_1(x_1(t-\tau )),\dots , f_n(x_n(t-\tau ))]^{\mathrm{T}}\), \(B={\mathrm{diag}}(b_1,\dots , b_n)\), \(S(t)=[S_1(t),\dots ,S_n(t)]^{\mathrm{T}}\), \(i=1,\dots ,n\).

The initial values of drive system (5) are given as

$$\begin{aligned} x(t) = {\phi ^x}(t) \in C\left( {\left[ { - \tau ,0} \right] ,{R^n}} \right) \nonumber \\ S(t) = {\phi ^S}(t) \in C\left( {\left[ { - \tau ,0} \right] ,{R^n}} \right) \end{aligned}$$

where \(C\left( {\left[ { -\tau ,0} \right] ,{R^n}} \right) \) represents the Banach space of all continuous functions from \(\left[ { - \tau ,0} \right] \) to \({R^n}\).

The response CNNs corresponding to (5) is in the following form:

$$\begin{aligned} {\mathrm{STM}}:\,\,\varepsilon \dot{y}(t)&=-Ay(t)+Wf(y(t))\nonumber \\&\quad +W^{\prime}f(y(t-\tau ))+BT(t)+u(t) \end{aligned}$$
(6a)
$$\begin{aligned} {\mathrm{LTM}}:\,\,\dot{T}(t)&=-T(t)+f(y(t)) \end{aligned}$$
(6b)

where \(u(t)=[u_1(t)\dots ,u_n(t)]^{\mathrm{T}}\) and the initial values are given as

$$\begin{aligned} y(t)&= {\varphi ^y}(t) \in C\left( {\left[ { -\tau ,0} \right] ,{R^n}} \right) \\ T(t)&= {\varphi ^{T}}(t) \in C\left( {\left[ { -\tau ,0} \right] ,{R^n}} \right) \end{aligned}$$

Let \(z(t)=y(t)-x(t)\), \(P(t)=T(t)-S(t)\). According to [10], subtract (5) from (6), and we derive the following error system:

$$\begin{aligned} {\mathrm{LTM}}:\,\,\dot{P}(t)&=-P(t)+{\mathbb {F}}(z(t)) \end{aligned}$$
(7a)
$$\begin{aligned} {\mathrm{STM}}:\,\,\varepsilon \dot{z}(t)&=-Az(t)+W{\mathbb {F}}(z(t))\nonumber \\&\quad +W^{\prime}{\mathbb {F}}(z(t-\tau ))+BP(t)+u(t) \end{aligned}$$
(7b)

where \({\mathbb {F}}(z(t)) = f(y(t)) - f(x(t))\), \({\mathbb {F}}(z(t - \tau )) = f(y(t - \tau )) - f(x(t - \tau ))\).

Definition 1

[16] Drive-response systems (5), (6) are in synchronization if

$$\begin{aligned} {\mathop {\lim }\limits _{t \rightarrow + \infty }} {\left\| {z(t)} \right\| ^2}&= {\left\| {y(t) - x(t)} \right\| ^2} = 0\nonumber \\ {\mathop {\lim }\limits _{t \rightarrow + \infty }} {\left\| {P(t)} \right\| ^2}&= {\left\| {T(t) - S(t)} \right\| ^2} = 0 \end{aligned}$$

Definition 1 implies that if the error system (7) is asymptotically stable, then the drive-response CNNs (5), (6) can achieve synchronization.

Let \(\eta (t) = \left[ {\begin{array}{l} {P(t)}\\ {z(t)} \end{array}} \right] \), then the system (7) is rearranged as

$$\begin{aligned} {\dot{\eta }} = F(\eta ) + G(\eta )u \end{aligned}$$
(8)

where

$$\begin{aligned} F(\eta (t))&= \left[ {\begin{array}{ll} { - {I_{n \times n}}}&{}\quad 0\\ {{\varepsilon ^{ - 1}}B}&{}\quad { - {\varepsilon ^{ - 1}}A} \end{array}} \right] \left[ {\begin{array}{l} {P(t)}\\ {z(t)} \end{array}} \right] + \left[ {\begin{array}{l} {{I_{n \times n}}}\\ {{\varepsilon ^{ - 1}}W} \end{array}} \right] {\mathbb {F}}(z(t)) \nonumber \\&\quad + \left[ {\begin{array}{l} 0\\ {{\varepsilon ^{ - 1}}{W^{\prime}}} \end{array}} \right] {\mathbb {F}}(z(t - \tau ))\\ G(\eta )&= \left[ {\begin{array}{l} 0\\ {{\varepsilon ^{ - 1}}{I_{n \times n}}} \end{array}} \right] \end{aligned}$$

According to [27, 34], the optimal synchronization control for the CNNs (5), (6) can be defined as follows.

Definition 2

For the error system (8), if a positive optimal value function \(V(\eta )\) can be found to satisfy the HJB equation below

$$\begin{aligned}&\frac{{\partial {V}}}{{\partial t}} + {\left( {\frac{{\partial {V}}}{{\partial \eta }}} \right) ^{\mathrm{T}}}F(\eta ) + Q(\eta ) \nonumber \\&\quad - \frac{1}{4} {\left( {\frac{{\partial {V}}}{{\partial \eta }}} \right) ^{\mathrm{T}}}G(\eta ){R^{ - 1}} (\eta )G(\eta )^{\mathrm{T}}\frac{{\partial {V}}}{{\partial \eta }} = 0 \end{aligned}$$
(9)

then

$$\begin{aligned} u^*(\eta )=-\frac{1}{2}R^{-1}(\eta )G(\eta )^{\mathrm{T}}\frac{{\partial {V}}}{{\partial \eta }} \end{aligned}$$
(10)

is obtained as the optimal control stabilizing the error system (8) and minimizing the performance functional below

$$\begin{aligned}&J(u)\nonumber \\&\quad ={\mathop {\lim }\limits _{t \rightarrow +\infty }} \left( {V(\eta (t))+\int _0^t\left( Q(\eta (s)) +u^{\mathrm{T}}R(\eta (s))u\right) {\mathrm{d}}s}\right) \end{aligned}$$
(11)

where \(Q(\eta ) \ge 0\), \(R(\eta ) > 0\) for all \(\eta \).

However, for given \(Q(\eta )\) and \(R(\eta )\), the optimal synchronization controller (10) is hard to solve because it is a tedious task to obtain the solution to the HJB equation (9).

Inverse optimal control has been developed as an alternative method to solve the nonlinear optimal control problem without solving the complex HJB equation [38]. To this end, the optimal synchronization control problem can be solved based on the inverse optimality techniques, and the problem to be solved is described as follows.

Problem 1

For the error system (8), construct a stable feedback controller u first, then find a meaningful performance functional of the form (11) so that the controller u and the state trajectory are optimal with respect to it.

3 Main results

An inverse optimal synchronization control method for the error system (8) is presented in this section. First, a CLF is constructed considering the fast–slow dynamics coupling of the error system. Then, based on the CLF, a state feedback inverse optimal controller design method is proposed to synchronize two CNNs and minimize a meaningful performance functional.

For system (8), construct the following CLF

$$\begin{aligned} V&= \frac{1}{2}{P(t)^{\mathrm{T}}}P(t) + \frac{1}{2}\varepsilon {z(t)^{\mathrm{T}}}z(t) \nonumber \\&\quad + \int _{t - \tau }^t {{{({W^{\prime}}{\mathbb {F}}(z(s)))}^{\mathrm{T}}}} {W^{\prime}}{\mathbb {F}}(z(s)){\mathrm{d}}s \end{aligned}$$
(12)

Taking the time derivation of V along the error system (8), we have

$$\begin{aligned} \dot{V}&= P{(t)^{\mathrm{T}}}\left( { - P(t) + {\mathbb {F}}\left( {z(t)} \right) } \right) + z(t)^{\mathrm{T}}\left( -Az(t) \right. \nonumber \\&\quad + W{\mathbb {F}}\left( z(t) \right) \left. + W^{\prime}{\mathbb {F}}\left( z(t - \tau )\right) + BP(t) + u(t) \right) \nonumber \\&\quad + \left( W^{\prime}{\mathbb {F}}(z(t))\right) ^{\mathrm{T}}W^{\prime}{\mathbb {F}}(z(t)) \nonumber \\&\quad - \left( W^{\prime}{\mathbb {F}}(z(t - \tau )\right) ^{\mathrm{T}} W^{\prime}{\mathbb {F}}(z(t - \tau )) \end{aligned}$$
(13)

According to Young’s inequality, we have

$$\begin{aligned} z{(t)^{\mathrm{T}}}BP(t)&\le \frac{1}{2}P{(t)^{\mathrm{T}}}P(t) + \frac{1}{2}{\left\| B \right\| ^2}z{(t)^{\mathrm{T}}}z(t) \end{aligned}$$
(14)
$$\begin{aligned} {P(t)^{\text{T}}}{\mathbb {F}}(z(t))&\le \frac{1}{2}P{(t)^{\mathrm{T}}}P(t) + \frac{1}{2}{\left\| {{\mathbb {F}}(z(t))} \right\| ^2} \end{aligned}$$
(15)
$$\begin{aligned} {z(t)^{\mathrm{T}}}W{\mathbb {F}}(z(t))&\le \frac{1}{2}{z(t)^{\mathrm{T}}}z(t) + \frac{1}{2}{\left\| W \right\| ^2}{\left\| {{\mathbb {F}}(z(t))} \right\| ^2} \end{aligned}$$
(16)

It follows from Assumption 1 that

$$\begin{aligned} \left| {{{\mathbb {F}}_i}({z_i})} \right| = \left| {{f_i}({y_i}) - {f_i}({x_i})} \right| \le {\delta _i}\left| {{y_i} - {x_i}} \right| = {\delta _i}\left| {{z_i}} \right| \end{aligned}$$

Then, we obtain

$$\begin{aligned} {\left\| {{\mathbb {F}}(z(t))} \right\| ^2} \le {\delta ^2}z{(t)^{\mathrm{T}}}z(t) \end{aligned}$$
(17)

where \(\delta = \max \{ {\delta _i}\} \), \(i=1,\dots ,n\).

It follows from (15) and (17) that

$$\begin{aligned} {P(t)^{\text{T}}}{\mathbb {F}}(z(t)) \le \frac{1}{2}P{(t)^{\mathrm{T}}}P(t) + \frac{1}{2} {\delta ^2}z{(t)^{\mathrm{T}}}z(t) \end{aligned}$$
(18)

From (16) and (17), we have

$$\begin{aligned} {z(t)^{\mathrm{T}}}WF(z(t)) \le \frac{1}{2}{z(t)^{\mathrm{T}}}z(t) + \frac{1}{2}{\left\| W \right\| ^2}{\delta ^2}z{(t)^{\mathrm{T}}}z(t) \end{aligned}$$
(19)

In addition, it holds that

$$\begin{aligned} - z{(t)^{\mathrm{T}}}Az(t) \le - az{(t)^{\mathrm{T}}}z(t) \end{aligned}$$
(20)

where \(a = \min \{ {a_i}\}\), \(i=1,\dots ,n\).

Combined with (14), (18)–(20), Eq. (13) can be further derived as follows:

$$\begin{aligned} \dot{V}&\le - P{(t)^{\mathrm{T}}}P(t) + \frac{1}{2}P{(t)^{\mathrm{T}}}P(t) + \frac{1}{2}{\delta ^2}z{(t)^{\mathrm{T}}}z(t)\nonumber \\&\quad - az(t)^{\mathrm{T}}z(t) + \frac{1}{2}z{(t)^{\mathrm{T}}}z(t) + \frac{1}{2}{\left\| W \right\| ^2}{\delta ^2}z{(t)^{\mathrm{T}}}z(t)\nonumber \\&\quad + \frac{1}{2}z{(t)^{\mathrm{T}}}z(t) + \frac{1}{2}{\left\| {{W^{\prime}}} \right\| ^2}{\mathbb {F}}{\left( {z(t - \tau )} \right) ^{\text{T}}} {\mathbb {F}}\left( {z(t - \tau )} \right) \nonumber \\&\quad + \frac{1}{2}{\left\| B \right\| ^2}z{(t)^{\mathrm{T}}}z(t) + \frac{1}{2}P{(t)^{\mathrm{T}}}P(t)\nonumber \\&\quad + {\left\| {{W^{\prime}}} \right\| ^2}{\delta ^2}z{(t)^{\mathrm{T}}}z(t) - {\left\| {{W^{\prime}}} \right\| ^2} {\mathbb {F}}{\left( {z(t - \tau )} \right) ^{\text{T}}}{\mathbb {F}}\left( {z(t - \tau )} \right) \nonumber \\&\quad + {z(t)^{\mathrm{T}}}u\nonumber \\&\le - az{(t)^{\mathrm{T}}}z(t) \nonumber \\&\quad + z{(t)^{\mathrm{T}}}{\frac{{\left( 2 + {{\left\| B \right\| }^2} + {\delta ^2} + {{\left\| W \right\| }^2}{\delta ^2} + {{\left\| {{W^{\prime}}} \right\| }^2}{\delta ^2}\right) }}{2}}z(t)\nonumber \\&\quad + {z(t)^{\mathrm{T}}}u- \frac{1}{2}{\left\| {{W^{\prime}}} \right\| ^2}{\mathbb {F}}{\left( {z(t - \tau )} \right) ^{\text{T}}} {\mathbb {F}}\left( {z(t - \tau )} \right) \end{aligned}$$

For simplicity, define

$$\begin{aligned} {\mathcal {K}}\triangleq 2+ {{\left\| B \right\| }^2}+ {\delta ^2}+ {{\left\| W \right\| }^2}{\delta ^2} + {{\left\| {{W^{\prime}}} \right\| }^2}{\delta ^2} \end{aligned}$$
(21)

Then, we have

$$\begin{aligned} \dot{V}&\le - az{(t)^{\mathrm{T}}}z(t) + z{(t)^{\mathrm{T}}}{\frac{{\mathcal {K}}}{2}}z(t) + {z(t)^{\mathrm{T}}}u \end{aligned}$$
(22)

Selecting a feedback controller formulated as

$$\begin{aligned} u = - {\mathcal {K}}z(t) \end{aligned}$$
(23)

and substituting it into (22) yield

$$\begin{aligned} \dot{V} \le - az{(t)^{\mathrm{T}}}z(t) - z{(t)^{\mathrm{T}}}{\frac{{\mathcal {K}}}{2}}z(t)< 0 \end{aligned}$$
(24)

Thus, according to the Lyapunov stability theory, the error system (8) is asymptotically stable under the controller (23). In view of Definition 1, the state trajectories of response CNNs (6) asymptotically approach that of the drive CNNs (5), which means that the synchronization of two CNNs is achieved, that is, \(\lim \nolimits _{t \rightarrow + \infty }y(t) = \lim \nolimits _{t \rightarrow + \infty }x(t)\), \({\lim \nolimits _{t \rightarrow \infty }}T(t) = {\lim \nolimits _{t \rightarrow \infty }}S(t)\).

Remark 2

The control Lyapunov function V is appropriately selected to take the time scale parameter into account, that is, V is dependent on \(\varepsilon \). In this way, the ill-conditioned numerical issues widely existed in the analysis and design process of two-time-scale systems is circumvented.

In the inverse optimality techniques, the CLF can be taken as a solution to the HJB equation corresponding to a meaningful performance functional [39]. Thus, the CLF defined by Eq. (12) can be considered as the optimal value function for HJB equation (9). Substituting it into (9), we can obtain the following equation:

$$\begin{aligned}&{\left( {{W^{\prime}}{\mathbb {F}}(z(t))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t)) - {\left( {{W^{\prime}}{\mathbb {F}}(z(t - \tau ))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t - \tau ))\nonumber \\&\qquad + \left[ {\begin{array}{*{20}{c}} {P{{(t)}^{\mathrm{T}}}}&{\varepsilon z{{(t)}^{\mathrm{T}}}} \end{array}} \right] \Big ( {\left[ {\begin{array}{*{20}{c}} { - {I_{n \times n}}}&{}0\\ {{\varepsilon ^{ - 1}}B}&{}{ - {\varepsilon ^{ - 1}}A} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {P(t)}\\ {z(t)} \end{array}} \right] } \nonumber \\&\qquad + \left[ {\begin{array}{*{20}{c}} {{I_{n \times n}}}\\ {{\varepsilon ^{ - 1}}W} \end{array}} \right] {\mathbb {F}}\left( {z(t)} \right) + \left[ {\begin{array}{*{20}{c}} 0\\ {{\varepsilon ^{ - 1}}{W^{\prime}}} \end{array}} \right] {\mathbb {F}}\left( {z(t - \tau )} \right) \Big )+ Q(\eta ) \nonumber \\&\qquad - \frac{1}{4}\left[ {\begin{array}{*{20}{c}} {P{{(t)}^{\mathrm{T}}}}&{\varepsilon z{{(t)}^{\mathrm{T}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} 0\\ {{\varepsilon ^{ - 1}}{I_{n \times n}}} \end{array}} \right] {R^{ - 1}}(\eta )\nonumber \\&\qquad \times \left[ {\begin{array}{*{20}{c}} 0&{{\varepsilon ^{ - 1}}{I_{n \times n}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {P(t)}\\ {\varepsilon z(t)} \end{array}} \right] \nonumber \\&\quad = 0 \end{aligned}$$
(25)

Referring to the form of stabilizing controller (23), we define a modified synchronization controller

$$\begin{aligned} u(t)&= -k \frac{{\mathcal {K}}}{2} z(t)=\left[ {\begin{array}{*{20}{c}} 0&{ - k\frac{{\mathcal {K}}}{2}} \end{array}} \right] \eta (t) \end{aligned}$$
(26)

where \(k>2\) is a constant.

Selecting the function \(R(\eta )\) as

$$\begin{aligned} R\left( {\eta (t)} \right) = k^{ - 1}{{\mathcal {K}}}^{-1} \end{aligned}$$
(27)

and according to (25), we have

$$\begin{aligned} Q(\eta (t))&= {\left( {{W^{\prime}}{\mathbb {F}}(z(t-\tau ))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t-\tau ))\nonumber \\&\quad - {\left( {{W^{\prime}}{\mathbb {F}}(z(t))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t)) + P{(t)^{\mathrm{T}}}P(t) \nonumber \\&\quad - z{(t)^{\mathrm{T}}}BP(t) + z{(t)^{\mathrm{T}}}Az(t) - P(t)^{\text{T}}{\mathbb {F}}\left( {z(t)} \right) \nonumber \\&\quad - z{(t)^{\mathrm{T}}}W{\mathbb {F}}\left( {z(t)} \right) - z{(t)^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}\left( {z(t - \tau )} \right) \nonumber \\&\quad + \frac{k}{4}z{(t)^{\mathrm{T}}}{\mathcal {K}}z(t) \end{aligned}$$
(28)

Thus, based on Eq. (27), an optimal synchronization controller of the error system (8) can be formulated as

$$\begin{aligned} u = {u^ * } = - \frac{1}{2}R{\left( {\eta (t)} \right) ^{ - 1}}\left[ {\begin{array}{*{20}{c}} 0&{{I_{n \times n}}} \end{array}} \right] \eta (t) \end{aligned}$$
(29)

Theorem 1

For the error system (8), there exist a positive definite function \(Q(\eta (t))\) (given by Eq. (28)) and a positive function \(R(\eta (t))\) (given by Eq. (27)) such that the state feedback controller (29) is able to make the system (8) globally asymptotically stable at the equilibrium point, that is, systems (5) and (6) can achieve synchronization, and to minimize the following meaningful performance functional

$$\begin{aligned} J(u) ={\lim \limits _{t \rightarrow \infty }}\left( {V(\eta (t)) + \int _0^t {\left( {Q(\eta (s)) + {u^{\mathrm{T}}}R\left( {\eta (s)} \right) u} \right) } {\mathrm{d}}s} \right) \end{aligned}$$
(30)

Proof

Select the Lyapunov candidate function V as shown in (12). Substituting the controller (29) into (12) and taking the derivative of V with respect to t, we derive that

$$\begin{aligned} \dot{V}&= P{(t)^{\mathrm{T}}}\left( { - P(t) + {\mathbb {F}}\left( {z(t)} \right) } \right) \nonumber \\&\quad +z(t)^{\mathrm{T}}\Big ( { - Az(t) + W{\mathbb {F}}\left( {z(t)} \right) + {W^{\prime}}{\mathbb {F}}\left( {z(t - \tau )} \right) + BP(t)}\nonumber \\&\quad { - k\frac{{\mathcal {K}}}{2}z(t)}\Big )+{\left( {{W^{\prime}}{\mathbb {F}}(z(t))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t)) \nonumber \\&\quad - {\left( {{W^{\prime}}{\mathbb {F}}(z(t - \tau ))} \right) ^{\mathrm{T}}}{W^{\prime}}{\mathbb {F}}(z(t - \tau )) \end{aligned}$$

Utilizing Eqs. (12)–(20), we have

$$\begin{aligned} \dot{V}&\le - az{(t)^{\mathrm{T}}}z(t)- (k - 1)z(t)^{\mathrm{T}}{\frac{{\mathcal {K}}}{2}}z(t)< 0 \end{aligned}$$
(31)

Thus, under the controller (29), the system (8) is asymptotically stable, \({\lim \nolimits _{t \rightarrow \infty }}e(t) = 0\), \({\lim \nolimits _{t \rightarrow \infty }}Z(t) = 0\), which means the response CNNs (6) is synchronized with the drive CNNs (5).

Substituting (14), (18)–(20) into (28), it yields

$$\begin{aligned} Q(\eta (t))&\ge az(t)^{\mathrm{T}}z(t)+\frac{1}{2}{\left( {{W^{\prime}}{\mathbb {F}}(z(t-\tau ))} \right) ^{\mathrm{T}}}{W^{\prime}} {\mathbb {F}}(z(t-\tau ))\nonumber \\&\quad + \frac{{k - 2}}{4}{\mathcal {K}}z(t)^{\mathrm{T}}z(t)\nonumber \\&\ge az(t)^{\mathrm{T}}z(t) + \frac{{k - 2}}{4}{\mathcal {K}}z(t)^{\mathrm{T}}z(t)\nonumber \\&\ge 0 \end{aligned}$$

Hence, \(Q(\eta (t))\) is positive definite. Obviously, Eq. (27) means \(R(\eta (t))>0\).

Substituting (27) and (28) into \(\dot{V}\) yields

$$\begin{aligned} \dot{V} =- Q(\eta (t))-{u^{\mathrm{T}}}R(\eta (t))u + {(u-{u^ * })^{\mathrm{T}}}R(\eta (t))(u-{u^ * }) \end{aligned}$$

then we can derive that

$$\begin{aligned} J(u)&= {\lim \limits _{t \rightarrow +\infty }}\left( {V(\eta (t))+\int _0^t{\left( {Q(\eta (s)) +{u^{\mathrm{T}}}R(\eta (s))u} \right) }{\mathrm{d}}s}\right) \nonumber \\&={\lim \limits _{t \rightarrow +\infty }}\Big ( V(\eta (0)) + \int _0^t \big ( \dot{V} + Q(\eta (s))\nonumber \\&\quad + {u^{\mathrm{T}}}R(\eta (s))u \big ){\mathrm{d}}s \Big )\nonumber \\&=V(\eta (0)) + {\lim \limits _{t \rightarrow +\infty }}\int _0^t{{{(u-{u^*})}^{\mathrm{T}}}R(\eta (t))(u-{u^*})} {\mathrm{d}}s \end{aligned}$$
(32)

From (32), we can conclude that \(u=u^*\) is the optimal control to minimize the meaningful performance functional (given by (30)) and

$$\begin{aligned} \mathop {\min }\limits _{{u^ * }} J(u) = V(\eta (0)) \end{aligned}$$
(33)

This completes the proof. □

The complete design process of inverse optimal synchronization controller is summarized as follows.

figure a

Remark 3

Inverse optimal control can be considered as an alternative method to solve nonlinear optimal control problem [37]. The aim of inverse optimal control is to avoid solving HJB equation which is inescapable in nonlinear optimal control. The main idea is to design a stabilizing feedback controller based on the knowledge of CLF first, then find a meaningful performance functional with respect to which the controller and state trajectories are optimal. Note that the performance functional in inverse optimal control is posteriorly determined and it is different from nonlinear optimal control where the performance functional is given in advance.

Remark 4

The controller (29) (or equivalently (26)) is irrelevant to \(\varepsilon \), that is, as long as the network parameters B, W, \(W^{\prime}\) and \(\delta \) are unchanged, the same controller is capable of guaranteeing the optimal synchronization of the drive-response CNNs with respect to (30) in case of different \(\varepsilon \), which implies that the robustness of the system can be enhanced under the designed controller. Besides, the only parameter to be designed in the controller (29) is k and it is required to satisfy \(k>2\). The larger k is, the faster the synchronization rate of the STM state of the error system is, because the controller is a state feedback controller with respect to z.

Remark 5

When \(\varepsilon =1\), the model (1) can be reduced to single-time-scale networks such as Hopfield neural networks and Grossberg’s shunting networks [21]. Therefore, the method proposed in this paper can be generalized to solve the inverse optimal synchronization control of these systems. However, if the time delays are time-varying, the associated HJB equation for the optimal synchronization control will become more complicated and new CLF needs to be designed. Hence, the proposed method cannot be directly extended to the inverse optimal synchronization control of CNNs with time-varying delays. Further research will be carried out in the future.

Remark 6

This work is inspired by [34]. The network model studied in [34] only contains first-order interaction, while the influence of synaptic changes on neuron activity is not considered. In this paper, the optimal synchronization problem of CNNs containing both LTM variables and STM variables is investigated, and the obtained results are more general.

Remark 7

Most of the existing results on CNNs synchronization are based on AITs or LMIs [4, 13, 17]. This paper presents a simple stabilizing controller design method by means of inverse optimality techniques without calculating any LMIs or algebraic inequalities. Nonlinear feedback controllers are designed in [12, 14, 18] to achieve synchronization for CNNs. As a contrast, the controller designed by our method is linear and easy to implement in practical applications.

4 Simulation example

The applicability of the proposed inverse optimal synchronization control method is illustrated by the simulation on drive-response CNNs (5), (6) with the following parameters: \(\varepsilon = 0.25\), \(A = \left[ {\begin{array}{ll} {0.12}&{}\quad 0\\ 0&{}\quad {0.1} \end{array}} \right] \), \(W = \left[ {\begin{array}{ll} {0.3}&{}\quad { - 0.03}\\ {0.8}&{}\quad {0.5} \end{array}} \right] \), \({W^{\prime}} = \left[ {\begin{array}{ll} { - 0.14}&{}\quad {0.01}\\ {0.03}&{}\quad { - 0.8} \end{array}} \right] \), \(B = \left[ {\begin{array}{ll} {0.05}&{}\quad 0\\ 0&{}\quad {0.15} \end{array}} \right] \), \(\tau = 1\). The activation functions are hyperbolic function \(f_i(x_i)={\mathrm{tanh}}(x_i)\), \(i=1,2\), \(n=2\). The initial values are selected as \(x(t) = {\left[ {\begin{array}{ll} {0.4}&\quad {0.6} \end{array}} \right] ^{\mathrm{T}}}\), \(S(t) = {\left[ {\begin{array}{ll} {0.1}&\quad {0.6} \end{array}} \right] ^{\mathrm{T}}}\), \(y(t) = {\left[ {\begin{array}{ll} { - 1}&\quad { - 0.5} \end{array}} \right] ^{\mathrm{T}}}\), \(T(t) = {\left[ {\begin{array}{ll} {0.5}&\quad {1.5} \end{array}} \right] ^{\mathrm{T}}}\), \(\forall t \in [ - 1,0]\).

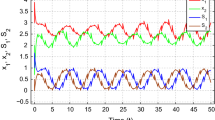
When no control is applied, the STM and LTM state trajectories of drive-response CNNs are shown in Figs. 1 and 2. We can see that two CNNs are not synchronous without control.

Fig. 1
figure 1

STM state trajectories of drive-response CNNs without control

Full size image
Fig. 2
figure 2

LTM state trajectories of drive-response CNNs without control

Full size image

Using Algorithm 1, select \(k=2.5\) and it can be calculated from (27) that \(R(\eta ) = {0.0867}\). Then, two controllers are designed as

$$\begin{aligned} u_1=-5.7658z_1(t) \end{aligned}$$
(34a)
$$\begin{aligned} u_2=-5.7658z_2(t) \end{aligned}$$
(34b)

Under the controllers (34a), (34b), the state trajectories of drive-response systems are shown in Figs. 3 and 4, which show that the designed controllers can eliminate the deviations of network states in a short time so that two CNNs can achieve synchronization.

Fig. 3
figure 3

STM state trajectories of drive-response CNNs with control

Full size image
Fig. 4
figure 4

LTM state trajectories of drive-response CNNs with control

Full size image

Choosing different initial values, we conduct the simulation respectively under the controllers (34a), (34b). Figure 5 shows the state trajectories of error systems with different initial values. It can be seen that the controllers can make the drive-response CNNs synchronize in case of different initial values. It is worth noting that the minimum values of cost functional are different under different initial values, which can be calculated from Eq. (33) as 1.4891, 0.8182, 1.5176, respectively.

Fig. 5
figure 5

State trajectories of error systems with the same control in case of different initial values: a \(x(t) = \left[ 0.4\ 0.6 \right] ^{\mathrm{T}}\), \(S(t) = \left[ 0.1\ 0.6\right] ^{\mathrm{T}}\), \(y(t) = \left[ - 1\ - 0.5\right] ^{\mathrm{T}}\), \(T(t) = \left[ 0.5\ 1.5\right] ^{\mathrm{T}}\), \(\forall t \in [ - 1,0]\). b \(x(t) = \left[ -0.5\ -0.8 \right] ^{\mathrm{T}}\), \(S(t) = \left[ 0.5\ -0.5\right] ^{\mathrm{T}}\), \(y(t) = \left[ 1\ -2\right] ^{\mathrm{T}}\), \(T(t) = \left[ 1\ -1\right] ^{\mathrm{T}}\), \(\forall t \in [ - 1,0]\). c \(x(t) = \left[ 1\ -0.3 \right] ^{\mathrm{T}}\), \(S(t) = \left[ 0.5\ 0.5\right] ^{\mathrm{T}}\), \(y(t) = \left[ -2\ -1\right] ^{\mathrm{T}}\), \(T(t) = \left[ 1\ 0.8\right] ^{\mathrm{T}}\), \(\forall t \in [ - 1,0]\)

Full size image
Fig. 6
figure 6

State trajectories of error systems with the same control in case of different \(\varepsilon \)

Full size image
Fig. 7
figure 7

STM state trajectories of error systems in case of different k

Full size image
Fig. 8
figure 8

STM state trajectories of error systems obtained by our method and the method in [18] when \(\varepsilon =1\)

Full size image
Fig. 9
figure 9

LTM state trajectories of the error systems obtained by our method and the method in [18] when \(\varepsilon =1\)

Full size image

To illustrate Remark 4, when \(\varepsilon =0.25, 1\), we conduct simulation respectively under the same controllers (34a), (34b) and obtain the state trajectories of the corresponding error systems. As implied in Fig. 6, the same controllers can make the corresponding error systems asymptotically stable, that is, the drive-response CNNs can be synchronized in case of different \(\varepsilon \). To show the effect of k on the system performance, we conduct simulation when \(k=2.5, 10\) and the STM state trajectories of error systems are shown in Fig. 7. We can see that the larger k is, the faster the synchronization rate of the STM state of the error system is.

General decay lag synchronization of drive-response CNNs was studied in [18] where the time scale parameter \(\varepsilon \) is set as \(\varepsilon =1\). To make a comparison, when \(\varepsilon =1\), we conduct simulation using our method and the method in [18], respectively. According to [18], four nonlinear controllers need to be designed

$$\begin{aligned}&u_{1c}=\frac{-2\Vert z(t)\Vert ^2z_1(t)}{\Vert z(t)\Vert ^2+e^{-0.1t}} \end{aligned}$$
(35a)
$$\begin{aligned}&u_{2c}=\frac{-3\Vert z(t)\Vert ^2z_2(t)}{\Vert z(t)\Vert ^2+e^{-0.1t}} \end{aligned}$$
(35b)
$$\begin{aligned}&\tilde{u}_{1c}=\frac{-0.5\Vert P(t)\Vert ^2P_1(t)}{\Vert P(t)\Vert ^2+e^{-0.1t}} \end{aligned}$$
(35c)
$$\begin{aligned}&\tilde{u}_{2c}=\frac{-0.5\Vert P(t)\Vert ^2P_2(t)}{\Vert P(t)\Vert ^2+e^{-0.1t}} \end{aligned}$$
(35d)

where the subscript c is added to distinguish them from the controllers designed in this paper. As a contrast, in our method, only two simple linear state feedback controllers (34a), (34b) need to be designed. State trajectories of the error system obtained by our method and the method in [18] are shown in Figs. 8 and 9. Using our method, STM state of the error system approaches 0 within 2 s, while the method in [18] needs about 50 s. LTM state of error system approaches 0 in about 5 s by our method, while it needs 30 s by the method in [18]. Therefore, the synchronization rate of our method is significantly faster than that of [18].

5 Conclusion

In this paper, by means of drive-response idea and inverse optimality techniques, a novel inverse optimal synchronization controller has been presented to make the drive-response CNNs achieve synchronization and to minimize a meaningful performance functional without solving the HJB equation. The designed controller is linear and easy to implement in practice. The simulation example has shown the feasibility and superiority of the obtained theoretical results.