1 Introduction

A key issue in the various engineering fields is that the prediction of the properties, behavior, and performance of different systems is an important aspect [1,2,3,4,5,6,7,8,9,10,11,12]. It is well knowen that the compositionally structures have a intresting thermo-electro-mechanical property and this matter is being an esential fact to get the attention of all engineering fields of reaserches for having efficient productions with the aid of composite structure, especially carbon-based nanofillers reinforced structure [13,14,15,16,17,18,19,20,21,22,23]. In addition to whatwas mentioned owing to the wide applications of wave propagation analysis in structural health monitoring, most recently, an interesting field of research has been started in scholar which is called wave propagation response [24,25,26,27,28,29].

Based on the mentioned issue, Gao et al. [30] could report a mathematical framework to analyze the propagated wave in a GPLs reinforced porous FG plate via a well-known mixture method. Their results indicate that porosity and GPLs weight fraction are two important parameters in the field of structural health monitoring via wave propagation method. Ebrahimi et al. [31] were able to provide results on the characteristics of propagated waves in a compositionally nonlocal plate in which the structure located in a high-temperature environment. Also, they consider the shear deformation in each element of the structure; they found that without doubt the nonlocal effect has a bold role on the characteristics of propagated waves. Safaei et al. [32] tried to report characteristics of the propagated waves in a CNTs reinforced FG thermoelastic plate via the high-order ready plat theory and Mori–Tanaka method. Their important achievement was that the thermal stress and adding small amount of CNTs can make a remarkable effect on the wave velocity in the structure. Also, Many researches [22, 33,34,35,36,37,38,39,40,41,42,43] published the results of their investigation on the static and dynamic responses of the composite structures. By considering the mentioned necessities and in the field of wave propagation in composite beams and plates, Ebrahime et al. [44] could present a paper to investigate the wave propagation of the sandwich plate in which the structure is embedded in a nonlinear foundation. Also, they considered a magnetic environment in their model and used the classical theory for doing their computational formulation. Based on their results, the magnetic layer will play the most important role on the wave response of the sandwich plate [45]. presented a comprehensive formulation on the wave dispersion of a high-speed rotating 2D-FG nanobeam. They used nonlocal theory for consideration of the couple stress in the nanomechanics effect on the wave response of the structure. they could solve their complex formulation via an analytical method and they reported that the rotating speed is the most effective parameter. By employing the new version couple stress theory, Global matrix, and Legendre orthogonal polynomial methods, and, Liu et al. [46] had a try for reporting the characteristics of the propagated wave in a micro FG plate. They reported that by controlling the couple stress, we will have the grater phase velocity in the aspect of wave propagation. Ebrahimi et al. [47] succeeded in publishing a paper in which a computational framework is developed for investigation wave behavior in a thermally affected nonlocal beam which is made by FG materials. One of their assumptions was that the nanobeam is under high-speed rotation and is located in a thermal environment. They presented a lot of results, but the most significant one was that changing the rotating speed can provide some novel results on the wave propagation in the nanostructure. In a novel work, Barati [48] showed the behavior of propagated wave in the porous nanobeam with attention to the nonlocality via strain–stress gradient theory. Also, some researchers tried to predict the static and dynamic properties of different structures and materials via neural network solution [49,50,51,52,53,54,55].

In the scope of investigation of the wave dispertion in the smart structure, Li et al. [56] succeeded in publishing an article in which they examined the wave propagation of a smart plate via a semi-analytical method. They modeled a GPLs-reinforced plate which is covered with a piezoelectric actuator. They used the Reissner–Mindlin plate theory and Hamilton’s principle for developing their computational approach and did the formulation. The application of their result is that GPLs in a matrix can play a positive role in structural health monitoring and improve wave propagation in the structures, especially smart structures. Ebrahimi et al. [57] developed a mathematical model for literature in which wave dispersion of a smart sandwich nanoplate by considering the nanosize effect via nonlocal strain gradient theory and the sandwich structure is made of ceramic face sheets and magnetostrictive core. Abad et al. [58] published an article in which they presented a formulation about the wave propagation problem of a somewhat sandwich thick plate. They smarted the plate by patching a piezoelectric layer on the top face of the structure and they considered Maxwell's assumptions in their computational approach. Habibi et al. [59] studied the wave response in a nanoshell with a GPLs reinforced compositionally core and patched piezoelectric face sheet. When they compared their result with molecular simulation can see that the nonlocality should be considered via NSGT. As a practical outcome they reported that the thickness of the smart layer will have more effect on the characteristics propagated waves in the nanoshell. Also, many studies reported the application of applied soft computing method for prediction of the behavior of complex system [60,61,62,63,64,65,66,67].

Based on the previous reaserch on the property of propagated waves in the cylandrical shell, Bakhtiari et al. [68] provided some results on the wave propagation of the FG shell in which fluid flow through the shell is considered. Ebrahimi et al. [69] studied the wave response in a high speed rotating nanoshell with a GPLs reinforced compositionally core and patched piezoelectric face sheet. They claimed that if the rotating should be controlled for improving the phase velocity of the nanoshell. The dispersion behavior of the wave in the MHC reinforced shell is investigated by Ebrahimi et al. [70]. They used the lowest order shear deformation theory and eigenvalue problem for providing their formulation and results. They found out the impact of nanosize reinforcements is more effective than the macro-size reinforcements for improving the phase velocity of the compositionally shell. Karami et al. [71] developed a mathematical model for literature in which wave dispersion in an imperfect nanoshell via NSG and HSD theories is analyzed. They provided some evidences that sensitivity of the prospected waves to the nonlocal effects, temperature, and humidity in the porous material should be considered. In addition, Stability of the complex structure is investigated in Refs [72, 73].

According to the summary of the presented paper in the literature, the analysis of the wave propagation behavior of a sandwich structure with a soft core and multi-hybrid nanocomposite (MHC) face sheets is carried out as a novel reaserch in the framework of the higher-order shear deformation theory (HSDT). In order to take into account, the viscoelastic influence, the Kelvin–Voight model is presented. In this paper, the constituent material of the core is made of an epoxy matrix which is reinforced by both macro- and nano-size reinforcements, namely carbon fiber (CF) and carbon nanotube (CNT). The effective material properties like Young's modulus or density are derived utilizing a micromechanical scheme incorporated with the Halpin–Tsai model. Then, on the basis of an energy-based Hamiltonian approach, the equations of motion are derived. The detailed parametric study is conducted, focusing on the combined effects of the viscoelastic foundation, CNT' weight fraction, core to total thickness ratio, small radius to total thickness ratio, and carbon fiber angle on the wave propagation behavior of sandwich structure.

2 Mathematical modeling

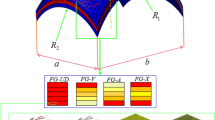
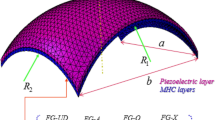
Figure 1 shows a sandwich doubly curved panel in a viscoelastic medium. The effective thickness (hb + hc + ht) and the shell curvatures of the doubly curved panel are presented by heff, R1, and R2R, respectively. Besides, hb hc, and hp are the thickness of the multi-hybrid nanocomposite reinforcement at the top layer, the core layer, and the multi-hybrid nanocomposite reinforcement at the bottom layer, respectively.

Fig. 1
figure 1

A schematic of a sandwich doubly curved panel

Full size image

2.1 MHC Reinforcement

The procedure of homogenization is made of two main steps based upon the Halpin–Tsai model together with a micromechanical theory. The first stage is engaged with computing the effective characteristics of the composite reinforced with carbon fibers [74] as following [75]:

$$ E_{11} = V_{F} E_{11}^{F} + V_{NCM} E^{NCM} $$
(1)
$$ \frac{1}{{E_{22} }} = \frac{{V_{f} }}{{E_{22}^{F} }} + \frac{{V_{NCM} }}{{E^{NCM} }} - V_{F} V_{NCM} \times \frac{{(\nu^{F} )^{2} \frac{{E^{NCM} }}{{E_{22}^{F} }} + (\nu^{NCM} )^{2} \frac{{E_{22}^{F} }}{{E^{M} }} - 2\nu^{F} \nu^{NCM} }}{{V_{F} E_{22}^{F} + V_{NCM} E^{NCM} }} $$
(2)
$$ \frac{1}{{G_{12} }} = \frac{{V_{NCM} }}{{G^{NCM} }} + \frac{{V_{F} }}{{G_{12}^{F} }} $$
(3)
$$ \rho = V_{F} \rho^{F} + V_{NCM} \rho^{NCM} $$
(4)
$$ \nu_{12} = V_{F} \nu^{F} + V_{NCM} \nu^{NCM} $$
(5)

where elasticity modulus, mass density, Poisson’s ratio, and shear modulus are symbolled via, and \(\nu\). the superscripts of the matrix and fiber are NCM and F, respectively. Add the carbon fiber volume fraction ( \(V_{F}\)) to the nanocomposite matrix volume fraction ( \(V_{NCM}\)) is one.

$$ V_{F} + V_{NCM} = 1 $$
(6)

The second step is organized to obtain the effective characteristics of the nanocomposite matrix reinforced with CNTs with the aid of the extended Halpin–Tsai micromechanics as follows:

$$ E^{j} = \frac{5}{8}\left( {\frac{{1 + 2\beta_{dd} V_{CNT} }}{{1 - \beta_{dd} V_{CNT} }}} \right)E^{M} + \frac{3}{8}\left( {\frac{{\beta_{dl} V_{CNT} (2l^{CNT} /d^{CNT} ) + 1}}{{1 - \beta_{dl} V_{CNT} }}} \right) $$
(7)

where \(\beta_{dd}\) and \(\beta_{dl}\) would be computed as the following expression:

$$ \begin{gathered} \beta_{dl} = {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} \mathord{\left/ {\vphantom {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} {(E_{11}^{CNT} /E^{M} ) + (l^{CNT} /2t^{CNT} )}}} \right. \kern-\nulldelimiterspace} {(E_{11}^{CNT} /E^{M} ) + (l^{CNT} /2t^{CNT} )}} \hfill \\ \beta_{dd} = {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} \mathord{\left/ {\vphantom {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} {(E_{11}^{CNT} /E^{M} ) + (d^{CNT} /2t^{CNT} )}}} \right. \kern-\nulldelimiterspace} {(E_{11}^{CNT} /E^{M} ) + (d^{CNT} /2t^{CNT} )}} \hfill \\ \end{gathered} $$
(8)

where volume fraction, thickness, length, elasticity modulus, weight fraction, and diameter of CNTs are \(V_{CNT}\), \(t^{CNT}\), \(l^{CNT}\), \(E^{CNT}\),\(W_{CNT}\), and \(d^{CNT}\). Also, the volume fraction of the matrix and elasticity modulus of the matrix are \(V_{M}\) and \(E^{M}\). So, The CNT volume fraction can be formulated as below:

$$ V_{CNT}^{ * } = \frac{{W_{CNT} }}{{W_{CNT} + \left( {\frac{{\rho^{CNT} }}{{\rho^{M} }}} \right)\left( {1 - W_{CNT} } \right)}} $$
(9)

Also, the effective volume fraction of CNTs can be formulated as follows:

$$ \begin{gathered} V_{CNT} = V_{CNT}^{*} \frac{{\left| {\xi_{j} } \right|}}{h}{\text{ FG } - \text{ X}} \hfill \\ V_{CNT} = V_{CNT}^{*} \left( {1 + \frac{{2\xi_{j} }}{h}} \right){\text{ FG } - \text{ V}} \hfill \\ V_{CNT} = V_{CNT}^{*} \left( {1 - \frac{{2\xi_{j} }}{h}} \right){\text{ FG } - \text{ A}} \hfill \\ V_{CNT} = V_{CNT}^{*} {\text{ FG } - \text{ UD}} \hfill \\ \end{gathered} $$
(10)

where \(\xi_{j} = \left( {\frac{1}{2} + \frac{1}{{2N_{t} }} - \frac{j}{{N_{t} }}} \right)h{\text{ j = 1,2,}}...{,}N_{t}\). Furthermore, the sum of \(V_{M}\) and \(V_{CNT}\) as the two constituents of the nanocomposite matrix is equal to 1.

$$ V_{CNT} + V_{M} = 1 $$
(11)

Also, Poisson’s ratio, mass density, and shear modulus will be calculated as follows:

$$ \rho^{j} = V_{CNT} \rho^{CNT} + V_{M} \rho^{M} $$
(12)
$$ \nu^{j} = \nu^{M} $$
(13)
$$ G^{j} = \frac{{E^{j} }}{{2\left( {1 + \nu^{j} } \right)}} $$
(14)

2.2 Kinematic relations

The displacement fields of the core can be given by [27, 76,77,78,79,80,81]:

$$ \begin{gathered} u^{c} (x,y,z,t) = u_{0}^{c} (x,y,t) + z_{c} \phi_{x}^{c} (x,y,t) - c_{1} z_{c}^{3} \left[ {\phi_{x}^{c} (x,y,t) + \frac{{\partial w_{0}^{c} (x,y,t)}}{\partial x}} \right] \hfill \\ v^{c} (x,y,z,t) = v_{0}^{c} (x,y,t) + z_{c} \phi_{y}^{c} (x,y,t) - c_{1} z_{c}^{3} \left[ {\phi_{y}^{c} (x,y,t) + \frac{{\partial w_{0}^{c} (x,y,t)}}{\partial y}} \right] \hfill \\ w^{c} (x,y,z,t) = w_{0}^{c} (x,y,t) \hfill \\ \end{gathered} $$
(15)

The strain components can be given by

$$ \left\{ \begin{gathered} \varepsilon _{{xx}}^{c} \hfill \\ \varepsilon _{{yy}}^{c} \hfill \\ \gamma _{{xy}}^{c} \hfill \\ \gamma _{{xz}}^{c} \hfill \\ \gamma _{{yz}}^{c} \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} \frac{{\partial u_{0}^{c} }}{{\partial x}} + z_{c} \frac{{\partial \phi _{x}^{c} }}{{\partial x}} - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi _{x}^{c} }}{{\partial x}} + \frac{{\partial ^{2} w_{0}^{c} }}{{\partial x^{2} }}} \right) + \frac{{w_{0}^{c} }}{{R_{1} }} \hfill \\ \frac{{\partial v_{0}^{c} }}{{\partial y}} + z_{c} \frac{{\partial \phi _{x}^{c} }}{{\partial y}} - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi _{y}^{c} }}{{\partial y}} + \frac{{\partial ^{2} w_{0}^{c} }}{{\partial y^{2} }}} \right) + \frac{{w_{0}^{c} }}{{R_{2} }} \hfill \\ \frac{{\partial u_{0}^{c} }}{{\partial y}} + \frac{{\partial v_{0}^{c} }}{{\partial x}} + z_{c} \left( {\frac{{\partial \phi _{x}^{c} }}{{\partial y}} + \frac{{\partial \phi _{y}^{c} }}{{\partial x}}} \right) - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi _{x}^{c} }}{{\partial y}} + \frac{{\partial \phi _{y}^{c} }}{{\partial x}} + 2\frac{{\partial ^{2} w_{0}^{c} }}{{\partial x\partial y}}} \right) \hfill \\ (1 - 3z_{c}^{2} c_{1} )\left( {\phi _{x}^{c} + \frac{{\partial w_{0}^{c} }}{{\partial x}}} \right) \hfill \\ (1 - 3z_{c}^{2} c_{1} )\left( {\phi _{y}^{c} + \frac{{\partial w_{0}^{c} }}{{\partial y}}} \right) \hfill \\ \end{gathered} \right] $$
(16)

Also, the strain–stress equations of the metal structure can be given as [24, 77, 82,83,84,85,86,87,88,89,90,91,92] follows:

$$\left[ \begin{gathered} \sigma _{{xx}}^{c} \hfill \\ \sigma _{{yy}}^{c} \hfill \\ \sigma _{{xy}}^{c} \hfill \\ \sigma _{{xz}}^{c} \hfill \\ \sigma _{{yz}}^{c} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Q_{{11}} } & {Q_{{12}} } & 0 & 0 & 0 \\ {Q_{{21}} } & {Q_{{22}} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{{66}} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{{55}} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{{44}} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon _{{xx}}^{c} \hfill \\ \varepsilon _{{yy}}^{c} \hfill \\ \varepsilon _{{xy}}^{c} \hfill \\ \varepsilon _{{xz}}^{c} \hfill \\ \varepsilon _{{yz}}^{c} \hfill \\ \end{gathered} \right],$$
(17)

in which [80, 93,94,95,96,97,98,99]

$$ Q_{11} = Q_{22} = \frac{{E_{c} }}{{1 - \nu_{c}^{2} }},\,\,\,Q_{12} = Q_{21} = \frac{{E_{c} \nu_{c} }}{{1 - \nu_{c}^{2} }},\,\,\,\,\,\,\,Q_{44} = Q_{55} = Q_{66} = \frac{{E_{c} }}{{2(1 + \nu_{c} )}} $$

In Eq. (17) \(E_{c}\), and \(\nu_{c}\) are Young’s modulus and poison ratio of the metal, respectively.

2.3 Face sheets

In the present structural model for the sandwich panel, the HSDT is adopted for the face sheets. Hence, the displacement components of the top and bottom face sheets (j = t, b) are represented as follows:

$$\begin{gathered} u^{j} (x,y,z,t) = u_{0}^{j} (x,y,t) + z_{j} \phi _{x}^{j} (x,y,t) - c_{1} z_{j}^{3} \left[ {\phi _{x}^{j} (x,y,t) + \frac{{\partial w_{0}^{j} (x,y,t)}}{{\partial x}}} \right] \hfill \\ v^{j} (x,y,z,t) = v_{0}^{j} (x,y,t) + z\phi _{y}^{j} (x,y,t) - c_{1} z_{j}^{3} \left[ {\phi _{y}^{j} (x,y,t) + \frac{{\partial w_{0}^{j} (x,y,t)}}{{\partial y}}} \right] \hfill \\ w^{j} (x,y,z,t) = w_{0}^{j} (x,y,t) \hfill \\ \end{gathered}$$
(18)

The strain components can be given by [78, 83, 100,101,102,103,104,105,106,107,108,109]:

$$\left\{ \begin{gathered} \varepsilon _{{xx}}^{j} \hfill \\ \varepsilon _{{yy}}^{j} \hfill \\ \gamma _{{xy}}^{j} \hfill \\ \gamma _{{xz}}^{j} \hfill \\ \gamma _{{yz}}^{j} \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} \frac{{\partial u_{0}^{j} }}{{\partial x}} + z_{j} \frac{{\partial \phi _{x}^{j} }}{{\partial x}} - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi _{x}^{j} }}{{\partial x}} + \frac{{\partial ^{2} w_{0}^{j} }}{{\partial x^{2} }}} \right) + \frac{{w_{0}^{j} }}{{R_{1} }} \hfill \\ \frac{{\partial v_{0}^{j} }}{{\partial y}} + z_{j} \frac{{\partial \phi _{x}^{j} }}{{\partial y}} - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi _{y}^{j} }}{{\partial y}} + \frac{{\partial ^{2} w_{0}^{j} }}{{\partial y^{2} }}} \right) + \frac{{w_{0}^{j} }}{{R_{2} }} \hfill \\ \frac{{\partial u_{0}^{j} }}{{\partial y}} + \frac{{\partial v_{0}^{j} }}{{\partial x}} + z_{j} \left( {\frac{{\partial \phi _{x}^{j} }}{{\partial y}} + \frac{{\partial \phi _{y}^{j} }}{{\partial x}}} \right) - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi _{x}^{j} }}{{\partial y}} + \frac{{\partial \phi _{y}^{j} }}{{\partial x}} + 2\frac{{\partial ^{2} w_{0}^{j} }}{{\partial x\partial y}}} \right) \hfill \\ (1 - 3z_{j}^{2} c_{1} )\left( {\phi _{x}^{j} + \frac{{\partial w_{0}^{j} }}{{\partial x}}} \right) \hfill \\ (1 - 3z_{j}^{2} c_{1} )\left( {\phi _{y}^{j} +\frac{{\partial w_{0}^{j} }}{{\partial y}}} \right) \hfill \\ \end{gathered} \right]$$
(19)

Also, the strain–stress equations of the metal structure can be given as [110,111,112,113,114]:

$$\left[ \begin{gathered} \sigma _{{xx}} \hfill \\ \sigma _{{yy}} \hfill \\ \sigma _{{xy}} \hfill \\ \sigma _{{xz}} \hfill \\ \sigma _{{yz}} \hfill \\ \end{gathered} \right]^{j} = \left[ {\begin{array}{*{20}c} {\hat{\bar{Q}}^{j} _{{11}} } & {\hat{\bar{Q}}^{j} _{{12}} } & 0 & 0 & {\hat{\bar{Q}}^{j} _{{16}} } \\ {\hat{\bar{Q}}^{j} _{{21}} } & {\hat{\bar{Q}}^{j} _{{22}} } & 0 & 0 & {\hat{\bar{Q}}^{j} _{{26}} } \\ 0 & 0 & {\hat{\bar{Q}}^{j} _{{44}} } & {\hat{\bar{Q}}^{j} _{{45}} } & 0 \\ 0 & 0 & {\hat{\bar{Q}}^{j} _{{45}} } & {\hat{\bar{Q}}^{j} _{{55}} } & 0 \\ {\hat{\bar{Q}}^{j} _{{16}} } & {\hat{\bar{Q}}^{j} _{{26}} } & 0 & 0 & {\hat{\bar{Q}}^{j} _{{66}} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon _{{xx}} \hfill \\ \varepsilon _{{yy}} \hfill \\ \varepsilon _{{xy}} \hfill \\ \varepsilon _{{xz}} \hfill \\ \varepsilon _{{yz}} \hfill \\ \end{gathered} \right]^{j} ,$$
(20)

where [115]

$$\hat{\bar{Q}}^{j} _{{11}} = \cos ^{4} \theta _{f} \tilde{Q}^{j} _{{11}} + 2\sin ^{2} \theta _{f} \cos ^{2} \theta _{f} \,\left( {\tilde{Q}^{j} _{{12}} + 2\tilde{Q}^{j} _{{66}} } \right) + \sin ^{4} \theta _{f} \tilde{Q}^{j} _{{22}}$$
(21-a)
$$\hat{\bar{Q}}^{{}} _{{12}} = \sin ^{2} \theta _{f} \cos ^{2} \theta _{f} \left( {\tilde{Q}^{{}} _{{11}} + \tilde{Q}^{{}} _{{22}} - 4\tilde{Q}^{{}} _{{66}} } \right)\, + \left( {\sin ^{4} \theta _{f} + \cos ^{4} \theta _{f} } \right)\tilde{Q}^{{}} _{{12}}$$
(21-b)
$$\hat{\bar{Q}}^{{}} _{{16}} = \cos ^{3} \theta _{f} \sin \theta _{f} \left( {2\tilde{Q}^{{}} _{{11}} - 2\tilde{Q}^{{}} _{{12}} - \tilde{Q}^{{}} _{{66}} } \right) + \cos \theta _{f} \sin ^{3} \theta _{f} \left( {\tilde{Q}^{{}} _{{66}} + 2\tilde{Q}^{{}} _{{12}} - 2\tilde{Q}^{{}} _{{22}} } \right)$$
(21-c)
$$\hat{\bar{Q}}^{{}} _{{22}} = \sin ^{4} \theta _{f} \tilde{Q}^{{}} _{{11}} + 2\sin ^{2} \theta _{f} \cos ^{2} \theta _{f} \tilde{Q}^{{}} _{{12}} + \cos ^{ 4} \theta _{f} \tilde{Q}^{{}} _{{22}} + 2\sin ^{2} \theta _{f} \cos ^{2} \theta _{f} \left( {\tilde{Q}^{{}} _{{12}} + 2\tilde{Q}^{{}} _{{66}} } \right)$$
(21-d)
$$\hat{\bar{Q}}^{{}} _{{26}} = \cos ^{3} \theta _{f} \sin \theta _{f} \,\left( {2\tilde{Q}^{{}} _{{12}} - 2\tilde{Q}^{{}} _{{22}} + \tilde{Q}^{{}} _{{66}} } \right) + \cos \ theta _{f} \sin ^{3} \theta _{f} \left( {2\tilde{Q}^{{}} _{{11}} - 2\tilde{Q}^{{}} _{{12}} - \tilde{Q}^{{}} _{{66}} } \right)$$
(21-e)
$$\hat{\bar{Q}}^{{}} _{{44}} = \cos ^{2} \theta _{f} \tilde{Q}^{{}} _{{44}} + \sin ^{2} \theta _{f} \tilde{Q}^{{}} _{{55}} \hat{\bar{Q}}^{{}} _{{44}} = \cos ^{2} \theta _{f} \tilde{Q}^{{}} _{{44}} + \sin ^{2} \theta _{f} \tilde{Q}^{{}} _{{55}}$$
(21-f)
$$\hat{\bar{Q}}^{{}} _{{45}} = \cos \theta _{f} \sin \theta _{f} \left( {\tilde{Q}^{{}} _{{55}} - \tilde{Q}^{{}} _{{44}} } \right)$$
(21-g)
$$\hat{\bar{Q}}^{{}} _{{55}} = \cos ^{2} \theta _{f} \tilde{Q}^{{}} _{{55}} + \sin ^{2} \theta _{f} \tilde{Q}^{{}} _{{44}}$$
(21-h)
$$\hat{\bar{Q}}^{{}} _{{66}} = \tilde{Q}^{{}} _{{66}} \left( {\cos ^{2} \theta _{f} - \sin ^{2} \theta _{f} } \right)^{2} \, + 4\sin ^{2} \theta _{f} \cos ^{2} \theta _{f} \left( {\tilde{Q}^{{}} _{{11}} + \tilde{Q}^{{}} _{{22}} - 2\tilde{Q}^{{}} _{{12}} } \right)$$
(21-i)

The terms involved in Eq. (21) would be obtained as follows:

$$Q^{j} _{{11}} = Q^{j} _{{22}} = \frac{{E^{j} }}{{1 - (\nu ^{j} )^{2} }},\,\,\,Q^{j} _{{12}} = Q^{j} _{{21}} = \frac{{E^{j} \nu ^{j} }}{{1 - (\nu ^{j} )^{2} }},\,\,\,\,\,\,\,Q^{j} _{{44}} = Q^{j} _{{55}} = Q^{j} _{{66}} = \frac{{E^{j} }}{{2(1 + \nu ^{j} )}}$$

2.4 Extended Hamilton’s principle

For obtaining the governing equation and associated boundary conditions, we can apply Extended Hamilton’s principle as follows [44, 70, 116, 117]:

$$\int\limits_{{t_{1} }}^{{t_{2} }} {(\delta U - \delta W)dt = 0}$$
(22)

The components of strain energy can be expressed as follows [24, 77, 90, 117,118,119,120,121,122]:

$$\begin{gathered} \delta U = \frac{1}{2}\left(\iiint\limits_{V} {\sigma ^{c} _{{mn}} \delta \varepsilon ^{c} _{{mn}} dV^{c} } + \iiint\limits_{V} {\sigma ^{j} _{{mn}} \delta \varepsilon ^{j} _{{mn}} dV^{j} }\right) = \hfill \\ = \iint\limits_{A} {\left[ \begin{gathered} N^{c} _{{xx}} \left(\frac{{\partial \delta u_{0}^{c} }}{{\partial x}} - \frac{{\delta w_{0}^{c} }}{{R_{1} }}\right) + M^{c} _{{xx}} \frac{{\partial \delta \phi u_{x}^{c} }}{{\partial x}} - P^{c} _{{xx}} c_{1} \left( {\frac{{\partial \delta \phi _{x}^{c} }}{{\partial x}} + \frac{{\partial ^{2} \delta w_{0}^{c} }}{{\partial x^{2} }}} \right) \hfill \\ + N^{c} _{{yy}} \left(\frac{{\partial \delta v_{0}^{c} }}{{\partial y}} - \frac{{\delta w_{0}^{c} }}{{R_{2} }}\right) + M^{c} _{{yy}} \frac{{\partial \delta \phi _{x}^{c} }}{{\partial y}} - P^{c} _{{yy}} c_{1} \left( {\frac{{\partial \delta \phi _{y}^{c} }}{{\partial y}} + \frac{{\partial ^{2} \delta w_{0}^{c} }}{{\partial y^{2} }}} \right) \hfill \\ + N^{c} _{{xy}} \frac{{\partial \delta u_{0}^{c} }}{{\partial y}} + N^{c} _{{xy}} \frac{{\partial \delta v_{0}^{c} }}{{\partial x}} + M^{c} _{{xy}} \left( {\frac{{\partial \delta \phi _{x}^{c} }}{{\partial y}} + \frac{{\partial \delta \phi _{y}^{c} }}{{\partial x}}} \right) \hfill \\ - P^{c} _{{xy}} c_{1} \left( {\frac{{\partial \delta \phi _{x}^{c} }}{{\partial y}} + \frac{{\partial \delta \phi _{y}^{c} }}{{\partial x}} + 2\frac{{\partial ^{2} \delta w_{0}^{c} }}{{\partial x\partial y}}} \right) \hfill \\ + (Q^{c} _{{xz}} - 3S^{c} _{{xz}} c_{1} )\left( {\delta \phi _{x}^{c} + \frac{{\partial \delta w_{0}^{c} }}{{\partial x}}} \right) + (Q^{c} _{{yz}} - 3S^{c} _{{yz}} c_{1} )\left( {\delta \phi _{y}^{c} + \frac{{\partial \delta w_{0}^{c} }}{{\partial y}}} \right) \hfill \\ \end{gathered} \right]\,}(1 + \frac{{z^{c} }}{{R_{1} }})(1 + \frac{{z^{c} }}{{R_{2} }})dA^{c} + \hfill \\ \iint\limits_{A} {\left[ \begin{gathered} N^{j} _{{xx}} \left(\frac{{\partial \delta u_{0}^{j} }}{{\partial x}} - \frac{{\delta w_{0}^{j} }}{{R_{1} }}\right) + M^{j} _{{xx}} \frac{{\partial \delta \phi _{x}^{j} }}{{\partial x}} - P^{j} _{{xx}} c_{1} \left( {\frac{{\partial \delta \phi _{x}^{j} }}{{\partial x}} + \frac{{\partial ^{2} \delta w_{0}^{j} }}{{\partial x^{2} }}} \right) \hfill \\ + N^{j} _{{yy}} \left(\frac{{\partial \delta v_{0}^{j} }}{{\partial y}} - \frac{{\delta w_{0}^{j} }}{{R_{2} }}\right) + M^{j} _{{yy}} \frac{{\partial \delta \phi _{x}^{j} }}{{\partial y}} - P^{j} _{{yy}} c_{1} \left( {\frac{{\partial \delta \phi _{y}^{j} }}{{\partial y}} + \frac{{\partial ^{2} \delta w_{0}^{j} }}{{\partial y^{2} }}} \right) \hfill \\ + N^{j} _{{xy}} \frac{{\partial \delta u_{0}^{j} }}{{\partial y}} + N^{j} _{{xy}} \frac{{\partial \delta v_{0}^{j} }}{{\partial x}} + M^{j} _{{xy}} \left( {\frac{{\partial \delta \phi _{x}^{j} }}{{\partial y}} + \frac{{\partial \delta \phi _{y}^{j} }}{{\partial x}}} \right) \hfill \\ - P^{j} _{{xy}} c_{1} \left( {\frac{{\partial \delta \phi _{x}^{j} }}{{\partial y}} + \frac{{\partial \delta \phi _{y}^{j} }}{{\partial x}} + 2\frac{{\partial ^{2} \delta w_{0} }}{{\partial x\partial y}}} \right) \hfill \\ + (Q^{j} _{{xz}} - 3S^{j} _{{xz}} c_{1} )\left( {\delta \phi _{x}^{j} + \frac{{\partial \delta w_{0}^{j} }}{{\partial x}}} \right) + (Q^{j} _{{yz}} - 3S^{j} _{{yz}} c_{1} )\left( {\delta \phi _{y}^{j} + \frac{{\partial \delta w_{0}^{j} }}{{\partial y}}} \right) \hfill \\ \end{gathered} \right]\,}(1 + \frac{{z^{j} }}{{R_{1} }})(1 + \frac{{z^{j} }}{{R_{2} }})dA^{j} \hfill \\ \end{gathered}$$
(23-a)

in which

$$\begin{gathered} \left\{ {N^{\lambda } _{{xx}} ,N^{\lambda } _{{yy}} ,N^{\lambda } _{{xy}} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma ^{\lambda } _{{xx}} ,\sigma ^{\lambda } _{{yy}} ,\sigma ^{\lambda } _{{xy}} } \right\}} dz_{\lambda } \hfill \\ \left\{ {M^{\lambda } _{{xx}} ,M^{\lambda } _{{yy}} ,M^{\lambda } _{{xy}} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma ^{\lambda } _{{xx}} ,\sigma ^{\lambda } _{{yy}} ,\sigma ^{\lambda } _{{xy}} } \right\}} z_{\lambda } dz_{\lambda } \hfill \\ \left\{ {P^{\lambda } _{{xx}} ,P^{\lambda } _{{yy}} ,P^{\lambda } _{{xy}} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma ^{\lambda } _{{xx}} ,\sigma ^{\lambda } _{{yy}} ,\sigma ^{\lambda } _{{xy}} } \right\}} z_{{_{\lambda } }}^{3} dz_{\lambda } \hfill \\ \left\{ {Q^{\lambda } _{{xz}} ,Q^{\lambda } _{{yz}} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma ^{\lambda } _{{xz}} ,\sigma ^{\lambda } _{{xy}} } \right\}} dz_{\lambda } , \hfill \\ \left\{ {S^{\lambda } _{{xz}} ,S^{\lambda } _{{yz}} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma ^{\lambda } _{{xz}} ,\sigma ^{\lambda } _{{xy}} } \right\}z_{{_{\lambda } }}^{2} } dz_{\lambda } \hfill \\ \end{gathered}$$
(23-b)

where \(\lambda = b,\,t,\,c\). Also, the kinetic energy [123] of each layer of the structure can be defined as follows:

$$ \begin{gathered} \delta K = \int\limits_{{Z^{j} }} {\iint\limits_{{A^{j} }} {\rho^{j} \left\{ {(\frac{{\partial u^{j} }}{\partial t}\frac{{\partial \delta u^{j} }}{\partial t}) + \frac{{\partial v^{j} }}{\partial t}\frac{{\partial \delta v^{j} }}{\partial t} + \frac{{\partial w^{j} }}{\partial t}\frac{{\partial \delta w^{j} }}{\partial t}} \right\}}} (1 + \frac{{z^{j} }}{{R_{1} }})(1 + \frac{{z^{j} }}{{R_{2} }})dA^{j} \hfill \\ + \int\limits_{{Z^{c} }} {\iint\limits_{{A^{c} }} {\rho^{c} \left\{ {(\frac{{\partial u^{c} }}{\partial t}\frac{{\partial \delta u^{c} }}{\partial t}) + \frac{{\partial v^{c} }}{\partial t}\frac{{\partial \delta v^{c} }}{\partial t} + \frac{{\partial w^{c} }}{\partial t}\frac{{\partial \delta w^{c} }}{\partial t}} \right\}}} (1 + \frac{{z^{c} }}{{R_{1} }})(1 + \frac{{z^{c} }}{{R_{2} }})dA^{c} \hfill \\ \end{gathered} $$
(24)

According to the Kelvin–Voight viscoelastic model for the MHC layer, the first variation of the viscoelastic model can be expressed as the following equation:

$$\delta W^{c} = \iint\limits_{A} {K_{w} (2w^{c} \delta w^{c} - w^{b} \delta w^{b} - w^{t} \delta w^{t} )}dA^{c} + C_{d} (2\dot{w}^{c} \delta \dot{w}^{c} - \dot{w}^{b} \delta \dot{w}^{b} - \dot{w}^{t} \delta \dot{w}^{t} )dA^{c}$$
(25-a)

Also, for piezoelectric layer, we have

$$\delta W^{j} = \iint\limits_{{A^{j} }} {K_{w} (2w^{j} \delta w^{j} - w^{c} \delta w^{c} )}dA^{j} + C_{d} (2\dot{w}^{j} \delta \dot{w}^{j} - \dot{w}^{c} \delta \dot{w}^{c} )dA^{j}$$
(25-b)

According to Eq. (25), \(K_{w}\) and \(C_{d}\) are elastic and dmping factor of the foundation.

Finally, the motion equations are derived as follows:

$$ \begin{gathered} \delta u_{0}^{c} :\frac{{\partial N^{c} _{{xx}} }}{{\partial x}} + \frac{{\partial N^{c} _{{xy}} }}{{\partial y}} = I_{0}^{c} \frac{{\partial ^{2} u_{0}^{c} }}{{\partial t^{2} }} + I_{1}^{c} \frac{{\partial ^{2} \phi _{x}^{c} }}{{\partial t^{2} }} - I_{3}^{c} c_{1} \left( {\frac{{\partial ^{2} \phi _{x}^{c} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{c} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta v_{0}^{c} :\frac{{\partial N^{c} _{{yy}} }}{{\partial y}} + \frac{{\partial N^{c} _{{xy}} }}{{\partial x}} = I_{0}^{c} \frac{{\partial ^{2} v_{0}^{c} }}{{\partial t^{2} }} + I_{1}^{c} \frac{{\partial ^{2} \phi _{y}^{c} }}{{\partial t^{2} }} - I_{3}^{c} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right), \hfill \\ \delta w_{0}^{c} :c_{1} \frac{{\partial ^{2} P^{c} _{{xx}} }}{{\partial x^{2} }} + c_{1} \frac{{\partial ^{2} P^{c} _{{yy}} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial ^{2} P^{c} _{{xy}} }}{{\partial x\partial y}} + \frac{{\partial Q^{c} _{{xz}} }}{{\partial x}} - 3c_{1} \frac{{\partial S^{c} _{{xz}} }}{{\partial x}} + \frac{{\partial Q^{c} _{{yz}} }}{{\partial y}} - 3c_{1} \frac{{\partial S^{c} _{{yz}} }}{{\partial y}} \hfill \\ + \frac{{N^{c} _{{xx}} }}{{R_{1} }} + \frac{{N^{c} _{{yy}} }}{{R_{2} }} - K_{w} (2w^{c} \delta w^{c} - w^{b} \delta w^{b} - w^{t} \delta w^{t} ) - C_{d} (2\dot{w}^{c} \delta \dot{w}^{c} - \dot{w}^{b} \delta \dot{w}^{b} - \dot{w}^{t} \delta \dot{w}^{t} ) \hfill \\ = c_{1} I_{3}^{c} \frac{{\partial ^{3} u_{0} }}{{\partial x\partial t^{2} }} + \left( {I_{0}^{c} \frac{{\partial ^{2} w_{0}^{c} }}{{\partial t^{2} }}} \right) + c_{1} I_{3}^{c} \frac{{\partial ^{3} v_{y}^{c} }}{{\partial y\partial t^{2} }} + c_{1} I_{3}^{c} \frac{{\partial ^{3} \phi _{y}^{c} }}{{\partial y\partial t^{2} }} - I_{6}^{c} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{y}^{c} }}{{\partial y\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{c} }}{{\partial t^{2} \partial y^{2} }}} \right) \hfill \\ + c_{1} I_{4}^{c} \frac{{\partial ^{3} \phi _{x}^{c} }}{{\partial x\partial t^{2} }} - I_{6}^{c} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{x}^{c} }}{{\partial x\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{c} }}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ \delta \phi _{x}^{c} :\frac{{\partial M^{c} _{{xx}} }}{{\partial x}} - c_{1} \frac{{\partial P^{c} _{{xx}} }}{{\partial x}} + \frac{{\partial M^{c} _{{xy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{c} _{{xy}} }}{{\partial y}} - Q^{c} _{{xz}} + 3c_{1} S^{c} _{{xz}} = \hfill \\ + I_{1}^{c} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} + I_{2}^{c} \frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }} - I_{4}^{c} c_{1} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w}}{{\partial t^{2} \partial x}}} \right) \hfill \\ - c_{1} I_{3}^{c} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} - c_{1} I_{4}^{c} \frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }} + I_{6}^{c} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{x}^{c} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{c} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ \delta \phi _{y}^{c} :\frac{{\partial M^{c} _{{yy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{c} _{{yy}} }}{{\partial y}} + \frac{{\partial M^{c} _{{xy}} }}{{\partial x}} - c_{1} \frac{{\partial P^{c} _{{xy}} }}{{\partial x}} - Q^{c} _{{yz}} + 3c_{1} S^{c} _{{yz}} = \hfill \\ I_{1}^{c} \frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }} + I_{2}^{c} \frac{{\partial ^{2} \phi _{y} }}{{\partial t^{2} }} - I_{4}^{c} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ - c_{1} I_{3}^{c} \frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }} - c_{1} I_{4}^{c} \frac{{\partial ^{2} \phi _{y} }}{{\partial t^{2} }} + I_{6}^{c} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ \end{gathered} $$
(26)

Also, the motion equations for the nanocomposite face sheets are as follows:

$$ \begin{gathered} \delta u_{0}^{j} :\frac{{\partial N^{j} _{{xx}} }}{{\partial x}} + \frac{{\partial N^{j} _{{xy}} }}{{\partial y}} = I_{0}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta v_{0}^{j} :\frac{{\partial N^{j} _{{yy}} }}{{\partial y}} + \frac{{\partial N^{j} _{{xy}} }}{{\partial x}} = I_{0}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right), \hfill \\ \delta w_{0}^{j} :c_{1} \frac{{\partial ^{2} P^{j} _{{xx}} }}{{\partial x^{2} }} + c_{1} \frac{{\partial ^{2} P^{j} _{{yy}} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial ^{2} P^{j} _{{xy}} }}{{\partial x\partial y}} + \frac{{\partial Q^{j} _{{xz}} }}{{\partial x}} - 3c_{1} \frac{{\partial S^{j} _{{xz}} }}{{\partial x}} + \frac{{\partial Q^{j} _{{yz}} }}{{\partial y}} - 3c_{1} \frac{{\partial S^{j} _{{yz}} }}{{\partial y}} \hfill \\ + \frac{{N^{j} _{{xx}} }}{{R_{1} }} + \frac{{N^{j} _{{yy}} }}{{R_{2} }} - K_{w} (2w^{j} - w^{c} ) - C_{d} (2\dot{w}^{j} - \dot{w}^{c} ) = c_{1} I_{3}^{j} \frac{{\partial ^{3} u_{0}^{j} }}{{\partial x\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial ^{3} \phi _{x}^{j} }}{{\partial x\partial t^{2} }} + \left( {I_{0}^{j} \frac{{\partial ^{2} w_{0}^{j} }}{{\partial t^{2} }}} \right) \hfill \\ + c_{1} I_{3}^{j} \frac{{\partial ^{3} v_{0}^{j} }}{{\partial y\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial ^{3} \phi _{y}^{j} }}{{\partial y\partial t^{2} }} - I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{y}^{j} }}{{\partial y\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{j} }}{{\partial t^{2} \partial y^{2} }}} \right) - I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{x}^{j} }}{{\partial x\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{j} }}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ \delta \phi _{x}^{j} :\frac{{\partial M^{j} _{{xx}} }}{{\partial x}} - c_{1} \frac{{\partial P^{j} _{{xx}} }}{{\partial x}} + \frac{{\partial M^{j} _{{xy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{j} _{{xy}} }}{{\partial y}} - Q^{j} _{{xz}} + 3c_{1} S^{j} _{{xz}} = \hfill \\ + I_{1}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ - c_{1} I_{3}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ \delta \phi _{y}^{j} :\frac{{\partial M^{j} _{{yy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{j} _{{yy}} }}{{\partial y}} + \frac{{\partial M^{j} _{{xy}} }}{{\partial x}} - c_{1} \frac{{\partial P^{j} _{{xy}} }}{{\partial x}} - Q^{j} _{{yz}} + 3c_{1} S^{j} _{{yz}} = \hfill \\ I_{1}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ - c_{1} I_{3}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right)\delta u_{0}^{j} :\frac{{\partial N^{j} _{{xx}} }}{{\partial x}} + \frac{{\partial N^{j} _{{xy}} }}{{\partial y}} = I_{0}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta v_{0}^{j} :\frac{{\partial N^{j} _{{yy}} }}{{\partial y}} + \frac{{\partial N^{j} _{{xy}} }}{{\partial x}} = I_{0}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right), \hfill \\ \delta w_{0}^{j} :c_{1} \frac{{\partial ^{2} P^{j} _{{xx}} }}{{\partial x^{2} }} + c_{1} \frac{{\partial ^{2} P^{j} _{{yy}} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial ^{2} P^{j} _{{xy}} }}{{\partial x\partial y}} + \frac{{\partial Q^{j} _{{xz}} }}{{\partial x}} - 3c_{1} \frac{{\partial S^{j} _{{xz}} }}{{\partial x}} + \frac{{\partial Q^{j} _{{yz}} }}{{\partial y}} - 3c_{1} \frac{{\partial S^{j} _{{yz}} }}{{\partial y}} \hfill \\ + \frac{{N^{j} _{{xx}} }}{{R_{1} }} + \frac{{N^{j} _{{yy}} }}{{R_{2} }} - K_{w} (2w^{j} - w^{c} ) - C_{d} (2\dot{w}^{j} - \dot{w}^{c} ) = c_{1} I_{3}^{j} \frac{{\partial ^{3} u_{0}^{j} }}{{\partial x\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial ^{3} \phi _{x}^{j} }}{{\partial x\partial t^{2} }} + \left( {I_{0}^{j} \frac{{\partial ^{2} w_{0}^{j} }}{{\partial t^{2} }}} \right) \hfill \\ + c_{1} I_{3}^{j} \frac{{\partial ^{3} v_{0}^{j} }}{{\partial y\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial ^{3} \phi _{y}^{j} }}{{\partial y\partial t^{2} }} - I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{y}^{j} }}{{\partial y\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{j} }}{{\partial t^{2} \partial y^{2} }}} \right) - I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{3} \phi _{x}^{j} }}{{\partial x\partial t^{2} }} + \frac{{\partial ^{4} w_{0}^{j} }}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ \delta \phi _{x}^{j} :\frac{{\partial M^{j} _{{xx}} }}{{\partial x}} - c_{1} \frac{{\partial P^{j} _{{xx}} }}{{\partial x}} + \frac{{\partial M^{j} _{{xy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{j} _{{xy}} }}{{\partial y}} - Q^{j} _{{xz}} + 3c_{1} S^{j} _{{xz}} = \hfill \\ + I_{1}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ - c_{1} I_{3}^{j} \frac{{\partial ^{2} u_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4}^{j} \frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ \delta \phi _{y}^{j} :\frac{{\partial M^{j} _{{yy}} }}{{\partial y}} - c_{1} \frac{{\partial P^{j} _{{yy}} }}{{\partial y}} + \frac{{\partial M^{j} _{{xy}} }}{{\partial x}} - c_{1} \frac{{\partial P^{j} _{{xy}} }}{{\partial x}} - Q^{j} _{{yz}} + 3c_{1} S^{j} _{{yz}} = \hfill \\ I_{1}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ - c_{1} I_{3}^{j} \frac{{\partial ^{2} v_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4}^{j} \frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + I_{6}^{j} c_{1} ^{2} \left( {\frac{{\partial ^{2} \phi _{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial ^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ \end{gathered} $$
(27)

where

$$\left\{ {I_{0}^{j} ,I_{1}^{j} ,I_{2}^{j} ,I_{3}^{j} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left\{ {1,z,z^{2} ,z^{3} } \right\}(1 + \frac{z}{{R_{1} }})(1 + \frac{z}{{R_{2} }})dz}$$
(28)

2.5 Solution procedure

Displacement fields for investigation the wave propagation analysis of the structure are defined as follows [117]:

$$\left\{ \begin{gathered} u_{0}^{c} \hfill \\ v_{0}^{c} \hfill \\ w_{0}^{c} \hfill \\ \phi _{x}^{c} \hfill \\ \phi _{y}^{c} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} U_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ V_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ W_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi _{x}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi _{y}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \end{gathered} \right\},\,\,\left\{ \begin{gathered} u_{0}^{j} \hfill \\ v_{0}^{j} \hfill \\ w_{0}^{j} \hfill \\ \phi _{x}^{j} \hfill \\ \phi _{y}^{j} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} U_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ V_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ W_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi _{x}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi _{y}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \end{gathered} \right\}, $$
(29)

where s and n are wave numbers along with the directions of x and y, respectively; also \(\omega\) is called frequency. With replacing Eq. (29) into governing equations we get:

$$ (\left[ K \right] - \omega^{2} [M])\left\{ d \right\} = \left\{ 0 \right\} $$
(30)

where

$$ \left\{ d \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} } & {v_{0} } \\ \end{array} } & {w_{0} } & {\psi_{{x_{0} }} } & {\psi_{{\theta_{0} }} } \\ \end{array} } \right\} $$
(31)

Also, the phase velocity of wave dispersion can be calculated by Eq. (32):

$$ c = \frac{\omega }{s} $$
(32)

In Eq. (32),\(c\) and s are called phase velocity and wavenumber of a laminated nanocomposite cylindrical shell, respectively. These parameters are propagation speeds of the particles in a sandwich panel.

2.6 Validation

The obtained results for the perfect panel are compared with the results of Refs. [124, 125]. These results are listed in Table 1. From this table, it can be seen that the present results have a good agreement with the obtained results in the literature. Note that, the dimensionless form of the frequency can be calculated using the following relation:

$$\Omega = \Omega {\frac{a^2}{h}}{\sqrt{\frac{\rho_M}{E_M}}} $$
(33)
Table 1 Comparison of the first dimensionless natural frequency of simply supported CNT reinforced composite square perfect panel (a/h = 10)
Full size table

For more verification, the fundamental frequencies of the FML moderately thick plates resting on partial elastic foundations are calculated by eigenvalue problem. In Table 2, non-dimensional fundamental frequencies of the symmetrically laminated cross-ply plate \(({0}^{^\circ },{90}^{^\circ },9{0}^{^\circ },{0}^{^\circ })\) are shown as compared for different E1/E2.

Table 2 Non-dimensional fundamental frequency of simply supported cross-ply laminated square plate with G12/E2 = 0.6, G13/E2 = 0.6, G23/E2 = 0.5, a = b = 1, \(\upsilon \)=0.25
Full size table

3 Results

In this part, a comprehensive investigation is carried out to demonstrate the effects of various parameters on the phase velocity response of a multi-hybrid nanocomposite doubly curved panel. The geometrical and material characteristics of constituent materials would be presented in Table 3. Also, the material properties of aluminum properties can be given as follows:\(E = 3.51\,GPa,\,\,\,\,\rho = 1200kg/m^{3} ,\,\,\,\,\,\nu = 0.34\).

Table 3 Material properties of the multiscale hybrid nanocomposite annular plate [33]
Full size table

Figure 2 is presented for investigating the influence of the damping factor of the foundation on the characteristic of the elastic propagating wave. Figure 2 shows that as well as increasing the phase velocity of the FML panel by increasing the wavenumber, this influence will be much more effective by increasing the damping factor. Also, at the grater wave number, we cannot find any change in the wave behavior of the sandwich panel due to increasing the damping factor. As the most impressive result, by improving the elastic foundation the ineffective range of the wavenumber will be limited in which there is not any effect from \({C}_{d}\) of the foundation on the phase velocity. Initially, as the wave number increases, the phase velocity of the panel increases, exponentially, while the relation between phase velocity and wave number is linear at the grater wave number. Last but not the least, as \({C}_{d}\) increase, the phase velocity improves. In Fig. 3 the phase velocity of the hybrid nanocomposite doubly curved panel versus wave number is presented with attention to the effect of elastic parameter \({(K}_{w})\) of the foundation. Base on Fig. 3 can conclude that when the elastic parameter of the foundation is considered zero, as the wave number increases, the phase velocity improves, logarithmic while this relation will be complex by considering \({K}_{w}>0\). For each \({K}_{w}\), at first, the phase velocity of the panel is constant by increasing the wavenumber, and at the medium values of the wavenumber, the phase velocity will be falling, so after a minimum value the relation changes to be increasing. Another important result from Fig. 3 is that the impact of \({K}_{w}\) on the wave response of the structure is considerable for 0.1 \(<{K}_{w}e4<\) 0.8, and this effect from the elastic foundation on the phase velocity could be negligible at the initial and grate value of the wavenumber. Figure 4 is presented for investigating the influence of elastic factor of the foundation and core to total thickness (\({h}_{c}/h\)) on the characteristic of the propagate elastic wave. As stated by Fig. 4 the impact of \({K}_{w}\) on the phase velocity is more obvious and considerable if the \({h}_{c}/h\) is between 0.5 to 0.8. in other words, the phase velocity can improve due to increasing the \({K}_{w}\) and this enhancement will be more considerable for 0.5 \(\le {h}_{c}/h\le \) 0.8. In addition, it is true that when the thickness of the core is small the phase velocity is falling down owing to increasing the \({h}_{c}/h\), but if we consider the thicker core, we can find a direct relation between \({h}_{c}/h\) and phase velocity Figs 5, 6, 7 and 8.

Fig. 2
figure 2

The phase velocity versus wavenumber for four value of \({C}_{d}\)

Full size image
Fig. 3
figure 3

The effect of the elastic parameter of the foundation on the characteristic of the propagated wave in the FML panel

Full size image
Fig. 4
figure 4

The phase velocity versus \({h}_{c}/h\) with having attention to the impact of \({K}_{w}\)

Full size image
Fig. 5
figure 5

The phase velocity versus \({h}_{c}/h\) with having attention to the impact of \({C}_{d}\)

Full size image
Fig. 6
figure 6

The phase velocity versus \({K}_{w}\) with having attention to the impact of wavenumber

Full size image
Fig. 7
figure 7

The phase velocity versus \(\theta /\pi \) with having attention to the impact of \({h}_{c}/h\)

Full size image
Fig. 8
figure 8

The phase velocity versus \(\theta /\pi \) with having attention to the impact of \({C}_{d}\)

Full size image

With close attention to the provided diagrams in Fig. 9 we can see that as well as an improvement on the phase velocity of the structure due to increasing\({K}_{w}\), the mentioned impact is more remarkable when the carbon fibers in the matrix are distributed vertically. In addition, if the fibers are vertical, there is not any change in the phase velocity due to any change in\(\theta /\pi \). The main point of Fig. 9 is that the wave response of the MHC reinforced panel is more dependent on the carbon fiber angle and the impact of the elastic factor of the foundation on the phase velocity is more effective when the fiber angle is vertical. Reported data in Fig. 10 are shown to have a deep presentation about the effects of the carbon fiber angle (\(\theta /\pi \))and CNT weight fraction (\({W}_{CNT}\)) on the wave responses of the sandwich structure. The most general result in Fig. 10 is that for each\({W}_{CNT}\), when the fiber angle is less than\(\pi /2\), the phase velocity is decreasing and this trend will be reverse for the fiber angle more than\(\pi /2\). The most interesting result in

Fig. 10 is that when the fiber angle is 0.4 \(\le \theta /\pi \le \) 0.6, adding more CNTs cannot provide any change on the phase velocity of the structure. As another explanation, if the fibers are distributed in the matrix vertically, changing \({W}_{CNT}\) cannot play any role on the wave response of the sandwich panel and as the fibers become horizontal, the effect of the \({W}_{CNT}\) on the phase velocity becomes more dramatic. Provided diagrams in Fig. 11 are shown to have a comparative study about the effects of elastic and damping factors (\({K}_{w}\) and\({C}_{d}\)) of the foundation on the wave responses of the doubly carved smart panel. The most principal result from Fig. 11 is that in the \({(K}_{w}\), \({C}_{d})\) plane, there is a region as the same as a trapezium in which there are no effects from elastic and damping factors of the foundation on the wave response of the sandwich smart panel and this area will be small by increasing the value of wavenumber. The last and impressive outcome is that the effect of \({C}_{d}\) on the phase velocity is greater than the impact of \({K}_{w}\) on the wave propagation of the panel. The reported 3D diagram in Fig. 12 is shown in order to have a comparative study about the effects of the wavenumber and fiber angle on the wave responses of the doubly carved panel. The most principal and evident result in Fig. 12 is that as the wave number increases, the changes in phase velocity of the sandwich panel which is caused by increasing the fibers angel becomes much more dramatic. In the simpler words, the effects of fiber angle on the phase velocity of the FML panel is highly dependent on the wavenumber.

Fig. 9
figure 9

The phase velocity versus \(\theta /\pi \) with having attention to the impact of the elastic factor of the foundation

Full size image
Fig. 10
figure 10

The phase velocity versus \(\theta /\pi \) with having attention to the impact of the elastic factor of the foundation

Full size image
Fig. 11
figure 11

The impacts of \({K}_{w}\) and \({C}_{d}\) on the wave response of the sandwich smart panel

Full size image
Fig. 12
figure 12

The phase velocity of the panel with respect to the impact of wavenumber and fiber angie

Full size image

4 Conclusion

The analysis of the wave propagation behavior of a sandwich structure with a soft core and multi-hybrid nanocomposite (MHC) face sheets is carried out as a novel reaserch in the framework of the higher-order shear deformation theory (HSDT). In order to take into account the viscoelastic influence, the Kelvin-Voight model is presented. In this paper, the constituent material of the core is made of an epoxy matrix which is reinforced by both macro- and nano-size reinforcements, namely carbon fiber (CF) and carbon nanotube (CNT). The effective material properties like Young's modulus or density are derived utilizing a micromechanical scheme incorporated with the Halpin–Tsai model. Then, on the basis of an energy-based Hamiltonian approach, the equations of motion are derived. Finally, the most bolded results of this paper are as follow:

As well as increasing the phase velocity of the FML panel by increasing the wavenumber, this influence will be much more effective by increasing the damping factor;

By improving the elastic foundation the ineffective range of the wavenumber will be limited in which there is not any effect from \({C}_{d}\) of the foundation on the phase velocity;

\({K}_{w}\)=8e12 is a critical value for the viscoelastic foundation that the relation between wavenumber and phase velocity will change from direct to indirect;

When the orientation of the carbon fiber in the matrix is being close to the vertical axis, the effect of \({C}_{d}\) on the phase velocity of the sandwich panel will be evident and this impact is a positive point for increasing the wave propagation response of the panel;

In a specific range of \(\theta /\pi \), the damping factor of the foundation has an ineffective role on the phase velocity of the panel and the range will be small by boosting the \({C}_{d}\);

If the fibers are distributed in the matrix vertically, changing \({W}_{CNT}\) cannot play any role on the wave response of the sandwich panel and as the fibers become horizontal, the effect of the \({W}_{CNT}\) on the phase velocity becomes more dramatic;

The effects of fiber angel on the phase velocity of the FML panel is hardly dependent on the wavenumber.