1 Introduction

Regarding the new progressions in science and technology, GNPs have engrossed significant attention. Some applications of GNP reinforcement are shown in Ref. [1]. Suna et al. [2] as an experimental study, compared the fracture behavior of functionally graded cemented carbide reinforced with and without the GNPs. In addition, they represented microstructure of the nanocomposites. Figure 1 shows the GNP layered in the matrix of the nanocomposites. They in this paper reported an attractive result that role of GNPs in the nanocomposites is the crack stopper (Fig. 2).

Fig. 1
figure 1

The GNP layered in the matrix of the nanocomposites

Full size image
Fig. 2
figure 2

Role of GNPs as the crack stopper in the nanocomposites

Full size image

Nieto et al. [3] presented the effect of GNP value fraction on grain size and mechanical property of the GNP-reinforced tantalum composite. Their result showed the SEM micrographs of the tantalum/GNP composites (Fig. 3). The grain size of tantalum/GNP composites with different value fractions of GNP is shown in Fig. 4. It should be noted that the results of Fig. 4 are obtained from micrographs similar to Fig. 3.

Fig.. 3
figure 3

SEM micrographs of the pure tantalum and tantalum/GNP composites. a Pure tantalum, b 1 wt% GNP, c 3 wt% GNP, d 5 wt% GNP [3]

Full size image
Fig. 4
figure 4

The grain size of tantalum/GNP composites with different value fraction of GNP [3]

Full size image

According to Figs. 3 and 4, by increasing value fraction of GNP into nanocomposite, it is a reason for production finer grain. It is worth to mention that grain refinement has an important role on the mechanical properties. Rafiee et al. [4] compared the mechanical properties of epoxy nanocomposites refined with 1% value fraction of single-walled carbon nanotubes (SWNT), multiwalled carbon nanotube (DWNT) and GNP with each other. Their results show that Young’s modulus, ultimate tensile strength, fracture toughness, fracture energy and fatigue resistance of the GNPs are more than other materials (Fig. 5). So that GNP materials can be replaced instead of SWNTs and MWNTs in many applications.

Fig. 5
figure 5

Ultimate tensile strength and Young modulus for the baseline epoxy and GNP/epoxy, MWNT/epoxy, and SWNT/epoxy nanocomposites [4]

Full size image

Researches proved that subjoining even a very meager amount of graphene into primary polymer matrix can desperately improve its mechanical, thermal and electrical properties [5,6,7,8,9]. It is worse to mention that nanostructures reinforced with GNP are more applicable in engineering design, so focus on dynamic modeling of the nanostructure with GNP reinforcement is useful and important. Furthermore, polymer matrix reinforced by various types of nanofillers is one of the most efficient and easily extruded nanocomposite materials with a wide range of applications such as field effect transistors, electromechanical actuators, biosensors and chemical sensors, solar cells, photoconductor and superconductor devices. For this reason, the investigation of their mechanical characteristics is a great interest for engineering design and manufacturing. In the field reinforcement structures, Habibi et al. [10,11,12,13,14] with the aid of some methods improved the mechanical property of macro-structures. Dong et al. [15] presented an analytical study on linear and nonlinear vibration characteristics and dynamic responses of spinning FG graphene-reinforced thin cylindrical shells with various boundary conditions and subjected to a static axial load. Dong et al. [16] investigated the buckling behavior of FG graphene-reinforced porous nanocomposite cylindrical shells with spinning motion and subjected to a combined action of external axial compressive force and radial pressure. Dong et al. [17] concerned with free vibration characteristics of the functionally graded graphene-reinforced porous nanocomposite cylindrical shell with spinning motion. In their result section, detailed parametric studies on natural frequencies and critical spinning speeds of the GPL-reinforced porous nanocomposite cylindrical shell are carried out, especially, effect of initial hoop tension on vibration characteristics of the spinning cylindrical shell is numerically discussed. Jang et al. [18] presented the postbuckling and buckling behaviors of FG multilayer nanocomposite beams reinforced with graphene platelets (GNPs). They investigated that GNPs have a remarkable reinforcing effect on the buckling and postbuckling of nanocomposite beams. In another work, Feg et al. [19] found out nonlinear bending behavior of a novel class of multilayer polymer composite beams reinforced with graphene platelets (GNPs). They studied that beam with a higher value fraction of GNPs and symmetric distribution in such a way is less sensitive to the nonlinear deformation.

None of the above researches have taken size effects into account in wave propagation analysis of structures. Continuum mechanics theories including classical theory [20, 21] and size-dependent theories are used to model micro/nanostructures. As classical theory does not consider submicron discontinuities of structure, so it cannot capture size-dependent effects when scale turns to micro or nano. Size-dependent theories including nonlocal [22,23,24,25,26,27,28,29,30], strain gradient [31, 32] and couple stress [33,34,35,36,37,38] theories are better choices and present more accurate outputs in these cases. It should be noted that mentioned theories consist of size-dependent parameters which their exact values must be determined by experimental data or numerical simulations [39,40,41]. For simple structures such as graphene sheets or carbon nanotubes, production of material for experiment or simulation is a straightforward process, but for composite structures, the process becomes complicated and encourages the researchers to approximate the models through mathematics and theories. Gul and Aydogdu [42] employed some length scale-dependent theories for investigation of wave propagation in double-walled carbon nanotubes. As a comparative research, they compared doublet mechanics results with classical elasticity, strain gradient theory, nonlocal theory and lattice dynamics. Experimental wave frequencies and doublet mechanics theory of graphite have good agreement with each other, so they showed that doublet mechanics theory has higher accuracy.

Ard and Aydogdu [43] studied torsional wave propagation for a multiwalled carbon nanotubes in the framework of Eringen’s nonlocal elasticity theory. They considered effect of van der Waals interaction and reported that the interaction has an important role in torsional wave propagation. In another work, Islam et al. [44] represented size effects on torsional wave propagation of circular nanostructure, such as nanoshafts, nanorods and nanotubes. They demonstrated the significance of considering the integral nonlocal model and nanoscale relations in dispersion characteristics of circular nanostructures. Aydogdu [45] employed nonlocal elasticity theory for studying longitudinal wave propagation in multiwalled carbon with including van der Waals force effect in the axial direction. In the result of this paper, the effects of various parameters on wave propagation were examined in detail. In recent years, incorporating the local and nonlocal curvatures in constitutive relations, NSGT has emerged. Based on this theory, the stress of submicron-scale structures appears in both nonlocal stress and pure strain gradient stress fields. Lim et al. [46] used thermodynamic framework to derive NSGT equations, so that the higher-order nonlocal parameters and the nonlocal gradient length coefficients were considered.

Applications of NSGT in vibration analysis of nanostructures [47,48,49] have attracted many researcher’s attentions. Zeighampour et al. [50] investigated wave propagation in double-walled carbon nanotube surrounded by Winkler foundation using the nonlocal strain gradient theory. In their results, nonlocal strain gradient theory and classical theory were compared in terms of the influences of nonlocal and material length scale parameters, wave number, fluid velocity and stiffness of elastic foundation on phase velocity. In another work [51], they modeled a composite cylindrical micro/nanoshells and studied the variation of phase velocity versus material length scale parameters and nonlocal constant. According to that paper, an increase in material length scale increases the phase velocity while nonlocal parameter acts vice versa. Zeighampour et al. [52] conducted a wave propagation study on a thin cylindrical nanoshell surrounded by visco-Pasternak foundation based on nonlocal strain gradient theory. The viscoelastic properties were modeled by Kelvin–Voigt theory. They indicated that the structure has a better stability condition using strain gradient theory in comparison with classical theory. In the field of the wave propagation behavior of a structure coupled with piezoelectric actuators, Lat. Am et al. [53] studied wave propagation of the two-layer piezoelectric composite structure. As a parametric study, they in this work showed the effects of volume fraction, thickness and elastic constant on the wave dispersion of the structure. Arani et al. [54] investigated wave dispersion of the FG carbon nanotube-reinforced piezoelectric composite. They in this work included the visco-Pasternak in their mathematical modeling. The structure was subjected to magnetic and electric fields. Their results showed that external voltage has a significant effect on the wave desperation behavior. Zhou [55] modeled the piezoelectric cylindrical shells and investigated surface effect on wave dispersion of the nanostructure. Their results presented that at the higher mode surface effect has a significant effect on the wave propagation of the structure. Bishe et al. [56] presented wave propagation in smart laminated composite cylindrical shells reinforced with carbon nanotubes in hygrothermal environments. They investigated the effects of temperature/moisture variation, CNT volume fraction and orientation, piezoelectricity, shell geometry, stacking sequence and material properties of the host substrate laminated composite shell at different axial and circumferential wave numbers and the results of their work showed that the temperature/moisture variation influences moderately on the dispersion solutions of smart laminated CNT-reinforced composite shells. Bishe et al. [57] focused on the wave propagation in piezoelectric cylindrical composite shells reinforced with angled and randomly oriented CNTs. Bishe et al. [58] studied and analyzed wave propagation in a piezoelectric cylindrical composite shell reinforced with CNTs by using the Mori–Tanaka micromechanical model and considering the transverse shear effects and rotary inertia via the first-order shear deformation shell theory. Bishe et al. [59] investigated wave behavior in a piezoelectric coupled laminated fiber-reinforced composite cylindrical shell by considering the transverse shear effects and rotary inertia. In the results of their work presented a comparison of dispersion solutions from different shell theories with different axial and circumferential wave numbers and piezoelectric layer thickness is provided to illustrate the transverse shear and rotary inertia effects on wave behavior of a laminated fiber-reinforced composite shell. Guo et al. [60] analyzed the effects of FG interlayers on the wave propagation in covered piezoelectric/piezomagnetic cylinders. They in this work showed that high-order modes are more sensitive to the gradient interlayers, while the low-order modes are more sensitive to the electromagnetic surface conditions. The wave propagation of the porous FG plates with the aid of some shear deformation theories was analyzed by Yahia et al. [61]. As an application, they showed that their results are useful for ultrasonic inspection. Also, they presented the effect of porosity on the wave propagation behavior of the structure. The present study investigates the wave propagation piezoelectric behavior of a GPLRC cylindrical nanoshell coupled with PIAC based on NSGT with considering the calibrated values of nonlocal constant and material length scale parameter for the first time. In this regard, influence of wave number, critical applied voltage and GNP distribution pattern on phase velocity are investigated using mentioned continuum mechanics theory.

2 Mathematical modeling

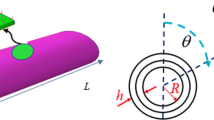
In Fig. 6, a GNPRC cylindrical nanoshell coupled with PIAC is modeled. The thickness, length and the middle surface radius of the cylindrical shell are \(h_{\text{eff}} \left( {h + h_{\text{p}} } \right)\), \(L\) and \(R\), respectively. In addition, the nanostructure is subjected to the electric potential (\(V\)) and z-axis is the poling direction. The cylindrical nanoshell is made of a new composite material.

Fig. 6
figure 6

Geometry of GNPRC cylindrical nanoshell coupled with PIAC

Full size image

2.1 Nonlocal strain gradient theory

According to the nonlocal strain gradient theory, the general constitutive equation can be expressed as follows [62]:

$$(1 - \mu^{2} \nabla^{2} )t_{ij} = C_{ijck} (1 - l^{2} \nabla^{2} )\varepsilon_{ck}$$
(1)

where \(\nabla^{2} = \partial^{2} /\partial x^{2} + \partial^{2} /\partial (\theta R)^{2}\), \(t_{ij}\), \(\varepsilon_{ck}\) and \(C_{ijck}\) are the components of nonlocal strain gradient stress tensor, strain tensor and elasticity tensor, respectively. Nonlocal strain gradient stress tensor is explained in the following form:

$$t_{ij} = \sigma_{ij} - \nabla \sigma_{ij}^{\left( 1 \right)}$$
(2)

where \(\sigma_{ij}\) and \(\begin{aligned} \sigma_{ij}^{\left( 1 \right)} \hfill \\ \hfill \\ \end{aligned}\) are classical and size-dependent stresses, respectively. The \(\mu\) and \(l\) parameters denote the influence of noninvariant stress field and higher-order strain gradient stress field. The calibrated values of mentioned size-dependent parameters are determined through experimental studies. These parameters are considered to be constant and stable for the proposed model. The strain tensor is written as:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)$$
(3)

2.2 Constitutive equations for nanocomposite core and piezoelectric layers

The matrix of nanostructure is composed of GNPRC materials. The volume fraction functions of these materials have been represented by

$${\text{Pattern1:}}\quad V_{\text{GPL}} (k) = V_{\text{GPL}}^{*}$$
(4)
$${\text{Pattern2:}}\quad V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} \left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}}$$
(5)
$${\text{Pattern3:}}\,\,\,\,\,\,V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} \left[ {1 - \left( {\left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}} } \right)} \right]$$
(6)
$${\text{Pattern4:}}\,\,\,\,\,\,\,\,V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} (2k - 1)/N_{\text{L}}$$
(7)

where k is number of layers of the microstructure, \(N_{\text{L}}\) is the total number of layers and \(V_{\text{GPL}}^{*}\) is the total volume fraction of GNPs. The relation between \(V_{\text{GPL}}^{*}\) and their weight fraction \(g_{\text{GPL}}^{{}}\) can be expressed by:

$$V_{\text{GPL}}^{*} = \frac{{g_{\text{GPL}} }}{{g_{\text{GPL}} + (\rho_{\text{GPL}} /\rho_{\text{m}} )(1 - g_{\text{GPL}} )}}$$
(8)

in which \(\rho_{\text{GPL}}\) and \(\rho_{\text{m}}\) are the mass densities of GNP and the polymer matrix. Based on Halpin–Tsai model, the elastic modulus of composites reinforced with randomly GNP approximated by [63]:

$$\begin{aligned} & E = \frac{3}{8}E_{\text{L}} + \frac{5}{8}E_{\text{T}} , \\ & E_{\text{L}} = \frac{{1 + \xi_{\text{L}} n_{\text{L}} V_{\text{GPL}} }}{{1 - n_{\text{L}} V_{\text{GPL}} }}E_{\text{m}} ,\quad E_{\text{T}} = \frac{{1 + \xi_{\text{T}} n_{\text{T}} V_{\text{GPL}} }}{{1 - n_{\text{T}} V_{\text{GPL}} }}E_{\text{m}} \\ \end{aligned}$$
(9)

where \(E\) is effective modulus of composites reinforced with GNPs and \(E_{\text{L}}\) and \(E_{\text{T}}\) are the longitudinal and transverse moduli for a unidirectional lamina. In Eq. (9), the GNP geometry factors (\(\xi_{\text{L}}\) and \(\xi_{\text{T}}\)) and other parameters are given by:

$$\begin{aligned} & \xi_{\text{L}} = 2({\mathbb{Z}}_{\text{GPL}} /h_{\text{GPL}} ),\quad \xi_{\text{T}} = 2(b_{\text{GPL}} /h_{\text{GPL}} ), \\ & n_{\text{L}} = \frac{{(E_{\text{GPL}} /E_{\text{m}} ) - 1}}{{(E_{\text{GPL}} /E_{\text{m}} ) + \xi_{\text{L}} }},\quad n_{\text{T}} = \frac{{(E_{\text{GPL}} /E_{\text{m}} ) - 1}}{{(E_{\text{GPL}} /E_{\text{m}} ) + \xi_{\text{T}} }} \\ \end{aligned}$$
(10)

where \({\mathbb{Z}}_{\text{GPL}} ,h_{\text{GPL}} ,b_{\text{GPL}}\) are the average length, thickness and width of the GPLs. By using the rule of mixture, mass density \(\rho_{c}\) and Poisson’s ratio \(v_{c}\) of the GPL/polymer nanocomposite are expressed as:

$$\begin{aligned} & \bar{E} = E_{\text{GPL}} V_{\text{GPL}} + E_{\text{M}} V_{\text{M}} , \\ & \bar{\rho } = \rho_{\text{GPL}} V_{\text{GPL}} + \rho_{\text{M}} V_{\text{M}} , \\ & \bar{\nu } = \nu_{\text{GPL}} V_{\text{GPL}} + \nu_{\text{M}} V_{\text{M}} , \\ & \bar{\alpha } = \alpha_{\text{GPL}} V_{\text{GPL}} + \alpha_{\text{M}} V_{\text{M}} . \\ \end{aligned}$$
(11)

The mechanical properties of the GPLR cylindrical shell can be obtained by [63]. In addition, the stress–strain relation of the composite core can be expressed as follows:

$$\left[ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{zz} \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{xz} \hfill \\ \sigma_{\theta z} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & {\bar{Q}_{13} } & 0 & 0 & 0 \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & {\bar{Q}_{23} } & 0 & 0 & 0 \\ {\bar{Q}_{13} } & {\bar{Q}_{23} } & {\bar{Q}_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\bar{Q}_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\bar{Q}_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {\bar{Q}_{66} } \\ \end{array} } \right]\left[ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{zz} \hfill \\ \varepsilon_{x\theta } \hfill \\ \varepsilon_{xz} \hfill \\ \varepsilon_{\theta z} \hfill \\ \end{aligned} \right]$$
(12)

where the stiffness coefficients (\(Q_{ij}\)) are obtained in Ref. [64].

2.3 Piezoelectric layers

The relationships between the stress and strain for the piezoelectric layers are written as follows:

$$\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{\theta z} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & 0 & 0 & 0 \\ {c_{12} } & {c_{22} } & 0 & 0 & 0 \\ 0 & 0 & {c_{66} } & 0 & 0 \\ 0 & 0 & 0 & {c_{55} } & 0 \\ 0 & 0 & 0 & 0 & {c_{44} } \\ \end{array} } \right].\left[ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{x\theta } \hfill \\ \varepsilon_{\theta z} \hfill \\ \varepsilon_{xz} \hfill \\ \end{aligned} \right] - \left[ {\begin{array}{*{20}c} 0 & 0 & {e_{31} } \\ 0 & 0 & {e_{32} } \\ 0 & 0 & 0 \\ 0 & {e_{24} } & 0 \\ {e_{25} } & 0 & 0 \\ \end{array} } \right]\left\{ \begin{aligned} E_{x} \hfill \\ E_{\theta } \hfill \\ E_{z} \hfill \\ \end{aligned} \right\}$$
(13)
$$\left\{ \begin{aligned} D_{x} \hfill \\ D_{\theta } \hfill \\ D_{z} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {e_{15} } \\ 0 & 0 & 0 & {e_{24} } & 0 \\ {e_{31} } & {e_{32} } & 0 & 0 & 0 \\ \end{array} } \right].\left[ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{x\theta } \hfill \\ \varepsilon_{\theta z} \hfill \\ \varepsilon_{xz} \hfill \\ \end{aligned} \right] + \left[ {\begin{array}{*{20}c} {s_{11} } & 0 & 0 \\ 0 & {s_{22} } & 0 \\ 0 & 0 & {s_{33} } \\ \end{array} } \right]\left\{ \begin{aligned} E_{x} \hfill \\ E_{\theta } \hfill \\ E_{z} \hfill \\ \end{aligned} \right\}$$
(14)

where \(c_{ijkl} ,e_{mij} ,d_{in} ,p_{i} ,\beta_{ij}\) and \(s_{im}\) are the elasticity matrix, piezoelectric constants, pyroelectric constants, thermal moduli and dielectric constants, respectively. \(D_{i}\) and \(E_{m}\) are electric displacement and electric fields strength of the piezoelectric cylindrical shell, respectively. The electric and magnetic field strength, i.e., \(E_{x} ,E_{\theta } ,E_{z}\) which are used in Eqs. (13) and (14) could be expressed as follows:

$$\begin{aligned} & E_{x} = - \frac{{\partial \tilde{\Phi }}}{\partial x} \\ & E_{\theta } = - \frac{1}{R + z}\frac{{\partial \tilde{\Phi }}}{\partial \theta } \\ & E_{z} = - \frac{{\partial \tilde{\Phi }}}{\partial z}. \\ \end{aligned}$$
(15)

Ghadiri et al. [64] investigated that the potential of electric could be assumed as:

$$\tilde{\Phi }(x,\theta ,z,t) = - \cos (\beta z)\phi (x,\theta ,t) + \frac{{2z\phi_{0} }}{h}$$
(16)

in which \(\beta = \pi /h\), \(\tilde{\Psi }\,\) and \(\tilde{\Phi }\) are the initial external electric and magnetic potential, respectively.

2.4 Displacement field of the cylindrical shell

Based on the first shear deformation theory, the displacement field of the cylindrical shell is as below:

$$\begin{aligned} & U(x,\theta ,z,t) = u(x,\theta ,t) + z\psi_{x} (x,\theta ,t) \\ & V(x,\theta ,z,t) = v(x,\theta ,t) + z\psi_{\theta } (x,\theta ,t) \\ & W(x,\theta ,z,t) = w(x,\theta ,t) \\ \end{aligned}$$
(17)

Here, \(U(x,\theta ,z,t)\), \(V(x,\theta ,z,t)\) and \(W(x,\theta ,z,t)\) indicate displacements of the neutral surface along \(x,\,\theta\) and \(z\) directions, respectively, and \(\psi_{x}\), \(\psi_{\theta }\) show rotations of a cross section around \(\theta\) and \(x\)-direction. Substituting Eq. (17) into Eq. (3), the components of the strain tensor are extracted as follows:

$$\begin{aligned} & \varepsilon_{xx} = \frac{\partial u}{\partial x} + z\frac{{\partial \psi_{x} }}{\partial x} \\ & \varepsilon_{\theta \theta } = \frac{1}{R}\frac{\partial v}{\partial \theta } + \frac{z}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{w}{R} \\ & \varepsilon_{xz} = \frac{1}{2}\left( {\psi_{x} + \frac{\partial w}{\partial x}} \right) \\ & \varepsilon_{x\theta } = \frac{1}{2}\left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + \frac{z}{2}\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right) \\ & \varepsilon_{\theta z} = \frac{1}{2}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right) \\ \end{aligned}$$
(18)

2.5 Derivation of governing equations and boundary conditions

According to the FSDT and nonlocal strain gradient theory, the governing equations and corresponding boundary conditions of the cylindrical shell can be extracted using the Hamilton principle as follows:

$$\int_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta \Pi_{\text{s}} + \delta \Pi_{\text{w}} )} {\text{ d}}t = 0$$
(19)

where K is the kinetic energy, \(\Pi_{\text{s}}\) is strain energy and \(\Pi_{\text{w}}\) is the work done corresponding to external applied forces which are, respectively, expressed as:

2.6 External work

The external work on the GNPRC cylindrical nanoshell with piezoelectric layers is due to external electrical load. So that the first variation of the work done corresponding to the external electric applied force:

$$\Pi_{\text{w}} = \iint\limits_{A} {\left[ {(N_{1}^{P} )w_{,x} \delta w_{,x} + (N_{2}^{P} )v_{,x} \delta v_{,x} } \right]}R{\text{d}}x{\text{d}}\theta$$
(20)

where \(N_{i}^{p}\) is external electric loads. The electric loads could be obtained as follows [64]:

$$N_{1}^{P} = N_{2}^{P} = - 2\left( {e_{31} - \frac{{c_{13} e_{33} }}{{c_{33} }}} \right)\phi_{0}$$
(21)

2.7 Kinetic energy

$$T = \frac{1}{2}\int\limits_{Z} {\iint\limits_{A} {\rho \left\{ {\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} } \right\}}} R\,{\text{d}}z\,{\text{d}}x\,{\text{d}}\theta$$
(22)

2.8 Strain energy

According to nonlocal strain gradient theory, the strain energy is defined as follows [65]:

$$\Pi_{\text{s}} = \frac{1}{2}\iiint\limits_{{V_{\text{core}} }} {\left( {\sigma_{ij} \varepsilon_{ij} + \sigma_{ij}^{\left( 1 \right)} \nabla \varepsilon_{ij} } \right){\text{d}}V_{\text{core}} } + \iiint\limits_{{V_{\text{piezolayer}} }} {(D_{x} \delta E_{x} + D_{\theta } \delta E_{\theta } + D_{z} \delta E_{z} ){\text{d}}V_{\text{piezolayer}} }$$
(23)

By substituting Eqs. (13), (14) and (18) into Eq. (23), the variation of strain energy can be explained as:

$$\begin{aligned} \delta \Pi_{\text{s}} & = \iint\limits_{A} {\left\{ {\begin{array}{*{20}l} {N_{xx} \frac{\partial }{\partial x}\delta u + M_{xx} \frac{\partial }{\partial x}\delta \psi_{x} + N_{\theta \theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta v + \frac{1}{R}\delta w} \right)} \hfill \\ {\quad + \frac{1}{R}M_{\theta \theta } \frac{\partial }{\partial \theta }\delta \psi_{\theta } + Q_{xz} \left( {\delta \psi_{x} + \frac{\partial }{\partial x}\delta w} \right) + N_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta u + \frac{\partial }{\partial x}\delta v} \right)} \hfill \\ {\quad + M_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{x} + \frac{\partial }{\partial x}\delta \psi_{\theta } } \right) + Q_{z\theta } \left( {\delta \psi_{\theta } + \frac{1}{R}\frac{\partial }{\partial \theta }\delta w - \frac{1}{R}\delta v} \right)} \hfill \\ \end{array} } \right\}}R{\text{d}}x{\text{d}}\theta \\ & \quad + \int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - h_{p} /2}}^{{h_{p} /2}} {\left[ {\begin{array}{*{20}l} { - D_{x} \left\{ {\cos (\beta z)\frac{\partial }{\partial x}\delta \phi } \right\}} \hfill \\ {\quad - D_{\theta } \left( {\frac{1}{R + z}} \right)\left\{ {\cos (\beta z)\frac{\partial }{\partial \theta }\delta \phi } \right\}} \hfill \\ {\quad + D_{z} (\beta \sin (\beta z)\phi )} \hfill \\ \end{array} } \right]} } } R{\text{d}}x{\text{d}}z{\text{d}}\theta \\ \end{aligned}$$
(24)

where the force and momentum resultants are:

$$\begin{aligned} & \left\{ {N_{xx} ,N_{\theta \theta } ,N_{x\theta } } \right\} = \int\limits_{{ - h_{ff} /2}}^{{h_{\text{eff}} /2}} {\left\{ {t_{xx} ,t_{\theta \theta } ,t_{x\theta } } \right\}} {\text{ d}}z \\ & \left\{ {M_{xx} ,M_{\theta \theta } ,M_{x\theta } } \right\} = \int\limits_{{ - h_{ff} /2}}^{{h_{ff} /2}} {\left\{ {t_{xx} ,t_{\theta \theta } ,t_{x\theta } } \right\}} \, z{\text{d}}z \\ & \left\{ {Q_{xz} ,Q_{\theta z} } \right\} = \int\limits_{{ - h_{ff} /2}}^{{h_{ff} /2}} {k_{s} \left\{ {t_{xz} ,t_{\theta z} } \right\}} {\text{ d}}z,\quad k_{\text{s}} = 5/6 \\ \end{aligned}$$
(25)

Governing equations for a cylindrical shell based on the FSDT and nonlocal strain gradient theory are derived by substituting Eqs. (20), (23) and (24) into Eq. (19) and integrating by parts.

$$\,\delta u:N_{xx,x} + \frac{{N_{x\theta ,\theta } }}{R} + X_{31} \phi_{,x} = \left( {I_{0} u_{{,t^{2} }} + I_{1} \psi_{{x,t^{2} }} } \right)$$
(26)
$$\delta v:N_{x\theta ,x} + \frac{{N_{\theta \theta ,\theta } }}{R} + \frac{{Q_{z\theta } }}{R} + \frac{{X_{61} }}{R}\phi_{,\theta } - \frac{{k_{s} X_{24} }}{R}\phi_{,\theta } - N_{1}^{P} v_{{,x^{2} }} = \left( {I_{0} v_{{,t^{2} }} + I_{1} \psi_{{\theta ,t^{2} }} } \right)$$
(27)
$$\delta w:Q_{xz,x} + \frac{{Q_{z\theta ,\theta } }}{R} - \frac{{N_{\theta \theta } }}{R} - \frac{{k_{s} X_{24} }}{R}\phi_{{,\theta^{2} }} - k_{s} X_{15} \phi_{{,x^{2} }} - N_{1}^{P} w_{{,x^{2} }} - \frac{{(Y_{xx,\theta x} - Y_{\theta \theta ,x\theta } )}}{2R} = I_{0} w_{{,t^{2} }}$$
(28)
$$\delta \psi_{x} :M_{xx,x} + \frac{{M_{\theta \theta ,\theta } }}{R} - Q_{xz} + X_{32} \phi_{,x} + k_{s} X_{12} \phi_{,x} = \left( {I_{1} u_{{,t^{2} }} + I_{2} \psi_{{x,t^{2} }} } \right)$$
(29)
$$\delta \psi_{\theta } :\frac{{M_{\theta \theta ,\theta } }}{R} + M_{x\theta ,x} - Q_{z\theta } + \frac{{X_{62} }}{R}\phi_{,\theta } + k_{s} X_{13} \phi_{,\theta } = \left( {I_{1} v_{{,t^{2} }} + I_{2} \psi_{{\theta ,t^{2} }} } \right)$$
(30)
$$\delta \phi :\,\,\,\,\int_{ - h/2}^{h/2} {\left\{ {D_{x,x} \cos (\beta z) + D_{\theta ,\theta } \frac{\cos (\beta z)}{R + z} + D_{z} \beta \sin (\beta z)} \right\}{\text{d}}z} = 0$$
(31)

Also, the parameters used in Eq. (31) are expressed as:

$$\begin{aligned} & \int_{{ - h_{p} /2}}^{{h_{p} /2}} {D_{x} \cos (\beta z)} = X_{11} \phi_{,x} + X_{12} (\psi_{x} + w_{,x} ), \\ & \int_{{ - h_{p} /2}}^{{h_{p} /2}} {D_{\theta } \frac{\cos (\beta z)}{R + z}} = X_{22} \phi_{,\theta } + X_{13} \left( {\psi_{\theta } + \frac{1}{R}w_{,\theta } - \frac{v}{R}} \right), \\ & \int_{{ - h_{p} /2}}^{{h_{p} /2}} {D_{z} \beta \sin (\beta z)} = - X_{33} \phi + X_{31} u_{,x} + X_{32} \psi_{x,x} + X_{61} \left( {\frac{1}{R}v_{,\theta } + \frac{w}{R}} \right) + X_{62} \left( {\frac{{\psi_{\theta ,\theta } }}{R}} \right). \\ \end{aligned}$$
(32)

where

$$\begin{aligned} & X_{11} = \int_{ - h/2}^{h/2} {\left\{ {s_{11e} } \right\}(\cos (} \beta z))^{2} {\text{d}}z,\quad X_{22} = \int_{ - h/2}^{h/2} {\left\{ {s_{22e} } \right\}\left( {\frac{\cos (\beta z)}{R + z}} \right)}^{2} {\text{d}}z, \\ & X_{13} = \int_{ - h/2}^{h/2} {\frac{\cos (\beta z)}{R + z}} \,e_{24e} {\text{d}}z,\quad X_{33} = \int_{ - h/2}^{h/2} {\left\{ {s_{33e} } \right\}\left( {\beta \sin (\beta z)} \right)^{2} } {\text{d}}z, \\ & \left\{ {X_{31} ,X_{32} } \right\} = \int_{ - h/2}^{h/2} {\left\{ {1,z} \right\}\beta \sin (\beta z)} \,e_{31e} {\text{d}}z,\quad \left\{ {X_{61} ,X_{62} } \right\} = \int_{ - h/2}^{h/2} {\left\{ {1,z} \right\}\beta \sin (\beta z)} \,e_{32e} {\text{d}}z. \\ \end{aligned}$$
(33)

In addition, associated boundary conditions are as below:

$$\begin{aligned} & \delta u_{0} = 0\quad {\text{or}}\quad N_{xx}^{{}} {\text{d}}\theta + \frac{{N_{x\theta } }}{R}{\text{d}}x = 0 \\ & \delta v_{0} = 0\quad {\text{or}}\quad N_{x\theta }^{{}} {\text{d}}\theta + \frac{{N_{\theta \theta }^{{}} }}{R}{\text{d}}x = 0 \\ & \delta w_{0} = 0\quad {\text{or}}\quad Q_{xz}^{{}} {\text{d}}\theta + \frac{{Q_{\theta z} }}{R}{\text{d}}x = 0 \\ & \delta u_{1} = 0\quad {\text{or}}\quad M_{xx}^{{}} {\text{d}}\theta + \frac{{M_{x\theta } }}{R}{\text{d}}x = 0 \\ & \delta v_{1} = 0\quad {\text{or}}\quad M_{x\theta }^{{}} {\text{d}}\theta + \frac{{M_{\theta \theta } }}{R}{\text{d}}x = 0 \\ \end{aligned}$$
(34)

3 Solution procedure

Displacement fields for investigation the wave propagation analysis of the structure defined as follow:

$$\left\{ \begin{aligned} U(x,\theta ,z,t) \hfill \\ V(x,\theta ,z,t) \hfill \\ W(x,\theta ,z,t) \hfill \\ \psi_{x} (x,\theta ,z,t) \hfill \\ \psi_{\theta } (x,\theta ,z,t) \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} u_{0} \exp (mx + n\theta - \omega t)i \hfill \\ v_{0} \exp (mx + n\theta - \omega t)i \hfill \\ w_{0} \exp (mx + n\theta - \omega t)i \hfill \\ \psi_{{x_{0} }} \exp (mx + n\theta - \omega t)i \hfill \\ \psi_{{\theta_{0} }} \exp (mx + n\theta - \omega t)i \hfill \\ \end{aligned} \right\}$$
(35)

where \(u_{0} ,v_{0} ,w_{0} ,\psi_{{x_{0} }}\) and \(\psi_{{\theta_{0} }}\) are wave amplitude parameters. \(m\) and \(n\) are wave number along the directions of \(x\) and \(\theta\), respectively, also \(\omega\) is called frequency. With replacing Eq. (35) into Eqs. (26–31) achieve to:

$$(\left[ K \right] - \omega^{2} [M])\left\{ d \right\} = \left\{ 0 \right\}$$
(36)

where K and M are the stiffness and mass matrixes, respectively. Also,

$$\left\{ d \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} } & {v_{0} } \\ \end{array} } & {w_{0} } & {\psi_{{x_{0} }} } & {\psi_{{\theta_{0} }} } \\ \end{array} } \right\}$$
(37)

In addition, the phase velocity of wave dispersion can be calculated by Eq. (30):

$$c = \frac{\omega }{m}$$
(38)

In Eq. (38), \(c\) and \(m\) are called phase velocity and wave number of a laminated nanocomposite cylindrical shell. These parameters are propagation speeds of the particles in a laminated nanocomposite cylindrical shell. With considering \(\mu = 0\), the phase velocity of classical continuum theory is computed.

3.1 Parametric study

Results section are presented by two sections, the first section studies the verifications of the results with those available in the literature. The second section presents the influence of GPL distribution pattern, applied voltage and GPL weight function on phase velocity of the GPLRC cylindrical nanoshell coupled with PIAC. The material properties of the GPLRC nanoshell are summarized in Table 1.

Table 1 Material properties of the epoxy and GPL [66]
Full size table

In addition, the material properties of the piezoelectric layer are given in Table 2.

Table 2 Material properties of piezoelectric layer which is composed of BiTiO3–CoFeO4 [40]
Full size table

As discussed in introduction section, a reliable approach to assess the validity of results estimated by various size-dependent theories is to compare them with those of molecular dynamics simulation. In this regard, Fig. 7 displays the variation of phase velocity versus phase number, estimated by different continuum theories of the present study and MD simulation of Ref. [48] for (15, 15) single-walled carbon nanotube. According to this figure from k = 0 to about s = 0.5 (1/m), with increasing the wave number all theories show a similar increase in phase velocity. Afterward, classic theory estimates the phase velocity remains constant, while Eringen and strain gradient theories estimate a steady decrease and increase in phase velocity, respectively. The best consistency with MD simulation is resulted by choosing the appropriate size-dependent parameters (\(\mu = 0.55\;{\text{nm}}, \, l = 0.35\;{\text{nm}}\)) of nonlocal strain gradient theory which shows a gentle decrease in phase velocity. Another validation is presented in Fig. 8 indicating the effect of radius on phase velocity for a SWCNT with \(R/h = 12, \, \mu = 0.55\;{\text{nm}}, \, l = 0.35\;{\text{nm}}, \, E = 0.83\;{\text{GPa;}}\, = 2270; = 0.317; \, n = 1\). As illustrated, results of the present study are of accurate agreement with those of Ref [67] especially in smaller radiuses of SWCNT.

Fig. 7
figure 7

The comparison of phase velocity obtained by current study and MD simulation [50] for different wave numbers and continuum theories

Full size image
Fig. 8
figure 8

Comparison of phase velocity of isotropic homogeneous nanoshells, with different parameters

Full size image

As a parametric study in this section of the current article, effects of different PIAC thickness, pattern of GNP, mode numbers and applied voltage on the phase velocity of the nanostructure are studied in Table 3. It is observed that all patterns of GNP reinforcement in comparison with pure epoxy show the higher values of phase velocity in a cylindrical nanoshell. This is because, by adding GNP reinforcement in the structure, the stability increases. Also, it can be found from this result that, effect of applied voltage on the phase velocity of the nanostructures is inverse. It can be seen from the table that for all values of PIAC thickness and mode number the phase velocities of the nanostructures with GPL distribution pattern 3 are higher than in comparison with other patterns. This result shows an increase in the stability of nanostructures with GPL distribution pattern 3. In other words, O-GPLRC gives larger value of the phase velocity than other patterns. The reason for this issue is in the mathematical function which is presented in the previous section. Besides, it is clearly seen from Table 3 that PIAC thickness and pattern of GNP have direct effects on the phase velocity. Also, by increasing the mode number from first to second, the phase velocity increases but changing from second to third, this behavior is inverse.

Table 3 The effect of different PIAC thickness, pattern of GNP and mode numbers on phase velocity (km/s) of GNPRC nanoshell with s = 1(1/nm), gGPL = 1%, R = 1 nm, h = R/10
Full size table

Figures 9 and 10 present the effects of PIAC thickness and applied voltage on phase velocity of a GNPRC nanoshell covered by PIAC with \(R = 4\;{\text{nm}}, \, h = R/10, = 0.055\;{\text{nm}},l = 0.03\;{\text{nm}}\) and \(g_{\text{GPL}} = 1\%\). According to Figs. 9 and 10, from one of these graphs (for a specific value of PIAC thickness and applied voltage), it can be found that first by increasing wave number the phase velocity increases. After a maximum value of the phase velocity, by increasing the wave number, the phase velocity decreases until the phase velocity reaches a minimum value.

Fig. 9
figure 9

Effect of external applied voltage and wave number on the phase velocity of the GNPRC nanoshell coupled with PIAC with hp= h/15

Full size image
Fig. 10
figure 10

Effect of external applied voltage and wave number on the phase velocity of the GNPRC nanoshell coupled with PIAC with hp= h/100

Full size image

After the minimum value, phase velocity is improved with increasing the wave number. Figures 8 and 9 demonstrate that, by decreasing the PIAC thickness, the minimum and maximum values of the phase velocity shift to left. For a better comprehensive, by decreasing the PIAC thickness, extremum values of phase velocity are seen in the lower values of the wave number. As an important result, by decreasing the PIAC thickness, the phase velocity decreases in the all range of the wave number. In addition, by increasing the applied voltage, the phase velocity decreases in the all range of the wave number. As a comparison report, the PIAC thickness and applied voltage have direct and inverse effects on the phase velocity of the nanostructure, respectively. Furthermore, as a new report of literature, comparison of the effects of PIAC thickness and applied voltage on the phase velocity can be found from these figures which show that by decreasing the effect of PIAC thickness the effect of applied voltage on the phase velocity become more significant. In another word, these figures show that, by increasing the PIAC thickness, the graphs of Fig. 9 are closely than the graphs of Fig. 10. As a useful suggestion of this research is that for designing of a nanostructure coupled with PIAC should be attention to the PIAC thickness and applied voltage, simultaneously. It is worth to mention that increasing the PIAC thickness and applied voltage has negative and positive effects on the stability of the nanostructure, respectively.

Figures 11 and 12 present the phase velocity of GNPRC nanoshell (pattern 2, \(1\% {\text{ GNP}}, \, R = 4\;{\text{nm}}\) and h = R/10) covered by PIAC and pure epoxy (R = 4 nm and h = R/10) for different values of PIAC thickness and applied voltage. These figures explain that, for high value of applied voltage, by increasing this parameter the phase velocity of those nanostructures decreases with an extremely rate. As described in the previous section, Figs. 9 and 10 represent that, by increasing the PIAC thickness, the phase velocity of both nanoshells increases in the all ranges of the applied voltage. Besides, by comparing these figures, the phase velocity of the GNPRC nanoshells is more than pure epoxy nanoshells. As a significant suggestion from this result, it can be found that, by adding GNP in the pure epoxy matrix the dynamic behaviors (phase velocity) of the structure improves. It is worth to mention that, for pure epoxy nanoshells coupled with PIAC, changes of phase velocity with increasing applied voltage is nonlinear, especially for high values of PIAC thickness, while this behavior for GNPRC nanoshells actuated with piezoelectric is linear in every value of PIAC thickness. This result is a reaffirm that, GPL in the epoxy matrix can prevent from nonlinear changes and transform the nonlinear to linear changes.

Fig. 11
figure 11

Effect of PIAC thickness and external applied voltage on the phase velocity of the pure epoxy cylindrical nanoshell coupled with PIAC

Full size image
Fig. 12
figure 12

Effect of PIAC thickness and external applied voltage on the phase velocity of the GPLRC cylindrical nanoshell coupled with PIAC

Full size image

Figures 13, 14, 15 and 16 present the effects of different GPL percentages, PIAC thickness and applied voltage on phase velocity of a GNPRC nanoshell covered by PIAC with R = 4 nm, h = R/10, \(\mu\) = 0.055 nm, l = 0.03 nm and pattern 2. All of these figures show that, with enhancement the nanostructures (GNPRC nanoshell actuated by piezoelectric layer) by increasing the GPL%, the phase velocity of the nanostructures can be improved for all ranges of applied voltage and all values of the PIAC thickness. This result demonstrates another advantage of GNP. For low value of the GNP% and different PIAC thickness, changing of phase velocity with increasing applied voltage is in nonlinear form but by increasing the GNP% this nonlinear behavior can be similar to the linear. An amazing result is that, in the lower values of applied voltage in comparison with higher ones, the effect of PIAC thickness decreases. Another important result is that, by increasing GPL%, the effects of PIAC thickness on the phase velocity decreases.

Fig. 13
figure 13

Effect of PIAC thickness and external applied voltage on the phase velocity of the GPLRC cylindrical nanoshell with gGPL = 1%

Full size image
Fig. 14
figure 14

Effect of PIAC thickness and external applied voltage on the phase velocity of the GPLRC cylindrical nanoshell with gGPL = 1.6%

Full size image
Fig. 15
figure 15

Effect of PIAC thickness and external applied voltage on the phase velocity of the GPLRC cylindrical nanoshell with gGPL = 1.8%

Full size image
Fig. 16
figure 16

Effect of PIAC thickness and external applied voltage on the phase velocity of t he GPLRC cylindrical nanoshell with gGPL = 2%

Full size image

4 Conclusion

This article studies the wave propagation electrical characteristics of a size-dependent GNPRC cylindrical nanoshell coupled with PIAC using NSGT. The governing equations of nanostructure have been evolved using Hamilton’s principle and solved with assistance of the analytical method. For the first time in the current study, wave propagation-electrically characteristics of a GNPRC cylindrical shell coupled with PIAC based on an exact size-dependent continuum theory is examined. Finally, influence of wave number, critical voltage, PIAC thickness and different GNP distribution patterns on phase velocity are investigated using mentioned continuum mechanics theory. In this work, the following main results can be achieved:

  1. 1.

    The results show that, by decreasing the PIAC thickness, extremum values of the phase velocity occur in the lower values of the wave number.

  2. 2.

    It is observed that, by increasing GPL%, the effects of PIAC thickness on the phase velocity decrease.

  3. 3.

    The PIAC thickness and applied voltage have direct and inverse effects on the phase velocity of the nanostructure, respectively.

  4. 4.

    The results demonstrate that, by adding GNP in the pure epoxy matrix, the phase velocity of the nanostructure improves.

  5. 5.

    Another important result is that, by increasing GPL%, the effects of PIAC thickness on the phase velocity decrease.