Fuzzy-Stochastic Advance Payment Inventory Model Having No Shortage and with Uniform Demand Using ABC Algorithm

Abstract

Advance payment is an important issue in inventory models. We, see that the policy of advance payments is of common practice in the today’s market environment. In this paper, an inventory model with advance payment for a single item has been developed. In this model the lead time is taken to be stochastic and also there is no shortage. The crisp model has been developed with these characteristics first. Then the corresponding fuzzy model is formulated. In the fuzzy model, several inventory parameters involved, are taken as parabolic-flat fuzzy numbers. So, finally, the model becomes a fuzzy-stochastic model due to the reason that the lead time is stochastic. The very effective graded mean integration representation method has been used to convert the fuzzy numbers into the crisp numbers. Then the crispified fuzzy-stochastic model has been solved using ABC algorithm. Finally, some numerical examples are presented to illustrate the model and the solution methodology. The effects of change of different inventory parameters have been studied and are presented both in tabular form and graphically.

Introduction

In this present business and market scenario, the practice of advance payment is observed as common practice. It is seen that a wholesaler of some commodities asks for some payment in part or in full during the placement of the supply order of the commodities from the retailer or smaller vendor. It is also noticed that, the wholesaler allows certain percentage of discount on the total purchase cost for that particular order. Sometimes, this discount rate is fixed and sometimes it depends on the amount of advance payment. Further, there are situations in which if a retailer gives an extra advance payment, he may get some price discount during the final payment. On the other hand, the retailer losses the interest on the amount of money paid as advance payment for a period of time from the placing of the order till the supply of the same. Thus, we see that the advance payment is a real life phenomena and the decision regarding the amount of advance payment to be made has a crucial impact on the total profit and inventory decisions.

Though, the advance payment is an important part of total profit in the inventory model, where advance payment is allowed, a few researchers have studied its impact on inventory modeling. It has been observed that, some of the researchers have attempted to describe the effect of advance payment on the total profit and inventory decisions. The effect of advance payment in inventory management both in precise and imprecise environments have been discussed by few researchers. In the existing literature, several inventory models are available in precise environment and only a few discussions are available in the uncertain environment. In the precise environment the inventory parameters (like, ordering cost, selling cost, purchase cost, holding cost, advertisement cost, interest, etc.) controlling the inventory are taken to be fixed/precise.

However, in real life situations these parameters should be imprecise numbers instead of fixed real numbers, because the inventory cost and/or interest might fluctuate due to various reasons. In the imprecise environment, the approaches like, stochastic, fuzzy, fuzzy-stochastic, interval or combination of these may be used. In the stochastic approach, the parameters are assumed to be random variables with known probability distributions. In the fuzzy approach, the parameters, the constraints and the goals are taken to be fuzzy numbers with known membership functions. Parameters are taken to be interval numbers in case of interval approach. In the combined approach, some of the parameters are taken in one form and the rest are taken in the other form.

Till date, only a few researchers have presented different types of inventory problems involving advance payment. Maiti et al. [1] have presented the inventory models with advance payment with the fixed parameters. In this area, the works of Zhang et al. [2], Maiti et al. [3], Gupta et al. [4], Priyan et al. [5], Dinagar and Kannan [6], Dutta and Kumar [7] are worth mentioning. Zhang et al. [2] presented the situation when the buyer is offered a price discount for the advance payment made by him, even not required by the seller, which can be found in bricks and tiles factories. Maiti et al. [3] developed an inventory model with stochastic lead time and price dependent demand incorporating advance payment. Gupta et al. [4] has contributed an application of genetic algorithm in solving an inventory model with advance payment and interval valued inventory costs. Priyan et al. [5] developed EOQ models that focused on advance payment with fuzzy parameters.

A perishable inventory model with stochastic lead-time has been presented by Kalpakam and Sapan [8]. Also, it is assumed that both in the deterministic and probabilistic models, the payment is made just after receiving the ordered materials. It is seen that the supplier gives a credit period for a retailer for stimulating the demand to increase the market share or to decrease inventories of certain items. The EOQ model with permissible delay in payments has been studied by Goyal [9]. The discounted cash flow in the inventory model under trade credit has been studied by Chung [10]. Aggarwal and Jaggi [11] and Hwang and Shinn [12] have studied the deterministic inventory model with constant deterioration rate. Shah and Shah [13] presented a probabilistic inventory model in which delay in payments is allowed. Jamal et al. [14] extended the inventory model in which shortages are involved. Dutta and Kumar [7] have presented a fuzzy inventory model without shortages using trapezoidal fuzzy number.

Sarkar and Saren [15] have presented an inventory model in which partial trade-credit policy is considered along with exponential deterioration. Roy chowdhury et al. [16] have presented an optimal inventory replenishment model for perishable items where demand is time quadratic and also with partially backlogged along with shortages in all cycles. An EOQ model under the condition of permissible delay in payment in which the demand rate is continuous function of time and holding cost is exponentially increased function along with shortages for the completely backlogged cycles have been developed by Rajan and Uthayakumar [17]. Cardenas-Barron et al. [18] have extensively discussed and produced the EOQ model. Tripathi et al. [19] have established an inventory model with exponential time-dependent deterioration for cases with and without shortages. De and Mahata [20] have introduced the fuzzy back-order model with cloudy fuzzy demand. Mishra [21] presented the inventory model with price dependent demand and Weibull deterioration in precise environment. The price sensitive demand for optimal order policy has been discussed by Tripathi [22]. Tripathi and Chaudhury [23] further studied the model with inflation, Weibull deterioration and trade credits. An EOQ model for spoilage products has been considered by Tripathi [24]. The fuzzy impreciseness is considered for imperfect production and repair model with time dependent demand by Jain et al. [25]. The model of permissible delay in payment has been done for deteriorating item in which retailer’s joint ordering, pricing and preservation technology investment policies are utilized in [26]. The two warehouse model has been developed for deterioration, capacity constraints and back ordering under financial consideration [27]. Recently, Das and Roy [28] have nicely developed the imprecise EOQ model for non-instantaneous deteriorating items in interval environment. Also an model with imperfect production and risk is presented by Patra [29]. The advance cash credit payments is considered in the model developed for perishable items [30]. Mishra et al. [21, 31] discussed a model under demand which is dependent on both of price and stock. A good attempt has been seen in the work of Teng et al. [32] in which they have presented a model with lot size expiration and advance payments.

In this paper, we are the first to introduce the fuzzy-stochastic approach in the inventory modeling. In this work, we have considered an inventory modeling in the fuzzy-stochastic environment, where the lead time is taken to be a random variable whose distribution is normal. The inventory control parameters like, purchasing cost, ordering cost, selling price, holding cost, etc. are taken as fuzzy numbers with parabolic-flat membership function. Thus the model extended to a fuzzy-stochastic model and hence the model becomes more realistic in terms of the uncertainty prevailing in the real life situations.

Here, we have presented inventory model with no shortages and with uniform demand both in crisp and fuzzy-stochastic environments. The very effective defuzzification method, the graded mean integration technique to transform the fuzzy-stochastic model into defuzzified stochastic model is used. After that, we have implemented the artificial bee colony algorithm (ABC algorithm) for the said inventory model to find the optimum profit and optimal order quantity.

The whole paper is organized in several sections. The necessary assumptions and useful notations are described in “Assumption and Notations” section. Some elementary definitions relating fuzzy numbers are given in “Some Definitions” section. In “Mathematical Formulation” section, the mathematical formulation of the model in different environments are presented. “Optimization Technique” section covers the optimization technique using ABC algorithm for solving these models. The numerical examples along with the result analysis are given in “Numerical Examples and Result Analysis” section and final conclusion and future prospect of our work is drawn in “Conclusion” section.

Assumption and Notations

Assumptions:

To develop the fuzzy-stochastic inventory model in this work the following assumptions are considered

(i):

advance payment is allowed

(ii):

no shortages are occurring in the model.

(iii):

the lead time is taken to be stochastic having normal distribution

(iv):

the demand rate is constant

(v):

the fuzzy parameters are considered to be parabolic-flat fuzzy numbers

(vi):

time horizon is finite

(vii):

finite number of replenishments

Notations:

$T_{L}$ :

Lead time which is a random variable with distribution $N(m,{\sigma }^2)$

$t_{l}$ :

Real variable corresponding to r.v. $T_{L}$

$f(T_{L})$ :

Density function of $T_{L}$

$F(T_{L})$ :

Distribution function of $T_{L}$

m :

Mean of $T_{L}$ when it follows normal distribution

$\sigma$ :

Standard deviation of $T_{L}$

$T_{H}$ :

Time horizon

n :

Number of replenishment to be made during the prescribed time horizon $T_{H}$

Q :

Order quantity

$Q_{r}$ :

Reorder level

q :

Inventory level at time t

$T_{c}$ :

Cycle length

$O_{cost}$ :

Ordering cost per order

$\widetilde{O}_{cost}$ :

Fuzzy ordering cost per order

$P_{dgw}$($\widetilde{O}_{cost}$):

Defuzzified ordering cost per order

$P_{cost}$ :

Unit purchase cost

$\widetilde{P}_{cost}$ :

Fuzzy unit purchase cost

$P_{dgw}(\widetilde{P}_{cost})$ :

Defuzzified unit purchase cost

$H_{cost}$ :

Holding cost per unit time per unit item

$\widetilde{H}_{cost}$ :

Fuzzy holding cost per unit time per unit item

$P_{dgw}$($\widetilde{H}_{cost}$):

Defuzzified holding cost per unit time per unit item

$S_{price}$ :

Unit selling price

$\widetilde{S}_{price}$ :

Fuzzy unit selling price

$P_{dgw}$($\widetilde{S}_{price}$):

Defuzzified unit selling price

D :

Constant demand rate

$\widetilde{D}$ :

Fuzzy constant demand rate

$P_{dgw}(\widetilde{D})$ :

Defuzzified constant demand rate

$A_{P}$ :

Advance payment of purchasing quantities

$\widetilde{A}_{P}$ :

Fuzzy advance payment of purchasing quantities

$P_{dgw}$($\widetilde{A}_{P}$):

Defuzzified advance payment of purchasing quantities

$L_{p}$ :

Interest on loan from bank

$I_{PD}$ :

Percentage of discount on unit purchase cost

$\widetilde{I}_{PD}$ :

Fuzzy percentage of discount on unit purchase cost

$P_{dgw}(\widetilde{I}_{PD})$ :

Defuzzified percentage of discount on unit purchase cost

$I_{PA}$ :

Percentage of $A_{P}$ with respect to total purchase cost per cycle

$\widetilde{I}_{PA}$ :

Fuzzy percentage of $A_{P}$ with respect to total purchase cost per cycle

$P_{dgw}(\widetilde{I}_{PA})$ :

Defuzzified percentage of $A_{P}$ with respect to total purchase cost per cycle

$I_{PI}$ :

The prevailing interest rate

$\widetilde{I}_{PI}$ :

Fuzzy prevailing interest rate

$P_{dgw}(\widetilde{I}_{PI})$ :

Defuzzified prevailing interest rate

Z :

Total profit over the planning horizon $T_{H}$

$\widetilde{Z}$ :

Total fuzzy profit over the planning horizon $T_{H}$

$P_{dgw}(\widetilde{Z})$ :

Total defuzzified profit over the planning horizon $T_{H}$

$Z^{*}$ :

Optimum profit

$\widetilde{Z}^{*}$ :

Fuzzy optimum profit

$P_{dgw}(\widetilde{Z}^{*})$ :

Defuzzified optimum profit

$Q^*$ :

Optimum order quantity

$\widetilde{Q}^*$ :

Fuzzy optimum order quantity

$P_{dgw}(\widetilde{Q}^*)$ :

Defuzzified optimum order quantity

Some Definitions

Definition 1

A fuzzy set ${\tilde{A}}$ in a universe of discourse X is defined as the set of pairs: $\tilde{A}=\{(x,\mu _{\tilde{A}}(x)): x\in X\}$, where $\mu _{\tilde{A}}:X\rightarrow [0,\,1]$ is a mapping called the membership function or grade of membership of $x \in \tilde{A}$.

Definition 2

The $\alpha -cut$ of $\tilde{A}$ is defined by $A_{\alpha }=\{x:\mu _{\tilde{A}}(x)=\alpha ,\alpha \ge 0\}$.

Definition 3

A fuzzy set $\tilde{A}$ is called convex if and only if for all $x_{1}, x_{2}\in X, \mu _{\tilde{A}}(\lambda x_{1}+(1-\lambda )x_{2})\ge min\{\mu _{\tilde{A}}(x_{1}),\mu _{\tilde{A}}(x_{2})\}$, where $\lambda \in [0,\,1]$.

Definition 4

A fuzzy set $\tilde{A}$ is called a normal fuzzy set if there exists at least one $x\in X$ such that $\mu _{\tilde{A}}(x)=1$.

Definition 5

A fuzzy number is a fuzzy subset of the real line which is both normal and convex. For a fuzzy number $\tilde{A}$, its membership function can be denoted by

$$\begin{aligned} \mu _{\widetilde{A}}(x)= \left\{ \begin{array}{l@{\qquad }l} L(x), &{} \text{ if } x<m \\ 1, &{} \text{ if } m\le {x}\le {n} \\ R(x), &{} \text{ if } x>n. \\ \end{array} \right. \end{aligned}$$

where L(x) and R(x) are the left and right shape functions respectively.

Definition 6

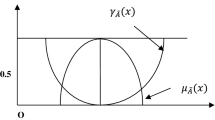
The parabolic-flat fuzzy number (PfFN) denoted by $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ is defined by its continuous membership function (Fig. 1) as;

$$\begin{aligned} \mu _{\widetilde{A}}(x)= \left\{ \begin{array}{l@{\qquad }l} 1-{\frac{(a_{2}-x)^2}{(a_{2}-a_{1})^2}} &{} \text{ if } a_{1}\le {x}\le {a_{2}} \\ {1} &{} \text{ if } a_{2}\le {x}\le {a_{3}} \\ 1-{\frac{(x-a_{3})^2}{(a_{4}-a_{3})^2}} &{} \text{ if } a_{3}\le {x}\le {a_{4}} \\ 0 &{} \text{ otherwise. } \\ \end{array} \right. \end{aligned}$$

Definition 7

(Arithmetic operations) The arithmetic operations between parabolic-flat fuzzy numbers are given below. Let us consider $\tilde{A_{1}}=(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{A_{2}}=(b_{1},b_{2},b_{3},b_{4})$ be two parabolic-flat fuzzy numbers. Then, the addition of $\tilde{A_{1}}$ and $\tilde{A_{2}}$ is defined as

$$\begin{aligned} \tilde{A_{1}}\oplus \tilde{A_{2}}=(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3},a_{4}+b_{4}) \end{aligned}$$

The subtraction of $\tilde{A_{2}}$ from $\tilde{A_{1}}$ is given by

$$\begin{aligned} \tilde{A_{1}}\ominus \tilde{A_{2}}=(a_{1}-b_{4},a_{2}-b_{3},a_{3}-b_{2},a_{4}-b_{1}) \end{aligned}$$

The multiplication of $\tilde{A_{1}}$ and $\tilde{A_{2}}$ is given by

$$\begin{aligned} \tilde{A_{1}}\otimes \tilde{A_{2}}=(a_{1}\otimes {b_{1}},a_{2}\otimes {b_{2}},a_{3}\otimes {b_{3}},a_{4}\otimes {b_{4}}) \end{aligned}$$

The division of $\tilde{A_{1}}$ by $\tilde{A_{2}}$ is defined as

$$\begin{aligned} \tilde{A_{1}}(\div )\tilde{A_{2}}=\left( \frac{a_{1}}{b_{4}},\frac{a_{2}}{b_{3}},\frac{a_{3}}{b_{2}},\frac{a_{4}}{b_{1}}\right) ,\, \,\hbox { where }b_{i}\ne 0,i=1,2,3,4 \end{aligned}$$

If $k\ne 0$ is a scalar and $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ then $k\tilde{A}$ is defined as

$$\begin{aligned} k\tilde{A}= \left\{ \begin{array}{cc} (ka_{1},ka_{2},ka_{3},ka_{4}), &{} \text{ if } k>0 \\ (ka_{4},ka_{3},ka_{2},ka_{1}) &{} \text{ if } k<0. \\ \end{array} \right. \end{aligned}$$

Definition 8

(Graded mean integration representation method for defuzzification) For the generalized fuzzy number $\widetilde{A}$ with membership function $\mu _{\widetilde{A}}$, according to Chen and Hsieh [33], Mahato and Bhunia [34], the Graded Mean Integral Value $P_{dgw}(\widetilde{A})$ of $\widetilde{A}$ is given by

$$\begin{aligned} P_{dgw}(\widetilde{A})= & {} \frac{\int _{0}^{1}[x(1-w)L^{-1}(x)+wR^{-1}(x)]dx}{\int _{0}^{1}xdx} \\= & {} 2\int _{0}^{1}[x(1-w)L^{-1}(x)+wR^{-1}(x)]dx \end{aligned}$$

where the pre-assigned parameter $w\,\in$ [0,1] refers to the degree of optimism. Here, $w=1$ represents an optimistic point of view, $w=0$ represents a pessimistic point of view and $w=0.5$ indicates a moderately optimistic decision maker’s point of view.

For parabolic-flat fuzzy number, we have

$$\begin{aligned} L^{-1}(x)=a_{2}-(a_{2}-a_{1})\sqrt{(1-x)},\, R^{-1}(x)=a_{3}+(a_{4}-a_{3})\sqrt{(1-x)} \end{aligned}$$

Now, the Graded Mean Integral Value (GMIV) of $\widetilde{A}$

$$\begin{aligned}= & {} 2\int _{0}^{1}[x(1-w)(a_{2}-(a_{2}-a_{1})\sqrt{(1-x)})+w(a_{3}+(a_{4}-a_{3})\sqrt{(1-x)})]dx \\= & {} \frac{(1-w)}{15}(8a_{1}+7a_{2})+\frac{w}{15}(7a_{3}+8a_{4}) \end{aligned}$$

Taking $w=0.5$, we get

$$\begin{aligned} P_{dgw}(\widetilde{A})=\frac{1}{30}(8a_{1}+7a_{2}+7a_{3}+8a_{4}) \end{aligned}$$

Mathematical Formulation

We have considered an inventory model in which the business starts with an inventory level of Q units of the item under consideration. Let $t_{j} (j=1,2,\ldots ,n-1)$ denotes the time of reorder at the starting of the jth cycle. The new order is given only when the inventory level reaches to the reorder level $Q_{r}$. After receiving the items, they are kept in store and the demand of the customers is fulfilled accordingly. In the inventory system at most one order will remain outstanding at any time because, it is assumed that installation stock will always exceeds the reorder level after the arrival of an order. The order for the (j+1)th renewable cycle is placed as soon as the stock level reaches to the reorder level $Q_{r}$ at $t=t_{j+1}$. Thus, there are n ordering points at $t=0, t=t_{j} (j=1,2,\ldots ,n-1)$ in the time horizon $[0, T_{H}]$. The lead time $T_{L}$ between the placement and receipt of an order is a random variable and is taken to follow normal distribution. The inventory system is presented in Fig. 2.

Crisp-Stochastic Model

The differential equation of the inventory system is given by

$$\begin{aligned} \frac{dq(t)}{dt} = -D, \end{aligned}$$

with the initial conditions,

$$\begin{aligned} q(0)=Q=DT_{c},\, t_{1}=\frac{Q-Q_{r}}{D},\, q(t_{j})=Q_{r}, j=1, 2, \ldots ., n \end{aligned}$$

Total holding cost

$$\begin{aligned} H_{Tot}= & {} H_{cost}\left( \int _{0}^{t_{1}}q dt+\sum _{j=1}^{n-1}{\int _{t_{j}}^{t_{j}+T_{L}}}q dt+\sum _{j=1}^{n-1}{\int _{t_{j}+T_{L}}^{t_{j+1}}}qdt+\int _{t_{n}}^{T_{H}}q dt\right) \nonumber \\= & {} H_{cost}(\int _{Q}^{Q_{r}}-\frac{q dq}{D}+(n-1){\int _{Q_{r}}^{Q_{r}-DT_{L}}}-\frac{qdq}{D}\nonumber \\&+(n-1){\int _{Q+Q_{r}-DT_{L}}^{Q_{r}}}-\frac{qdq}{D}+\int _{Q_{r}}^{0}-\frac{qdq}{D})\nonumber \\= & {} \frac{H_{cost}}{2D}[nQ^2+2(n-1)Q(Q_{r}-DT_{L})] \end{aligned}$$

(1)

where $Q=\frac{DT_{H}}{n}$ and $A_{p}=I_{PA}(1-I_{PD})QP_{cost}$

$$\begin{aligned} E(H_{Tot})= & {} \frac{H_{cost}}{2D}\int _{0}^{\infty }[nQ^2+2(n-1)Q(Q_{r}-DT_{L})]f(T_{L})dT_{L} \\= & {} \frac{H_{cost}}{2D}\left[ \int _{0}^{\infty }\left\{ nQ^2+2(n-1)QQ_{r}\right\} \right. \\&\left. f(T_{L})dT_{L}-\int _{0}^{\infty }\{2(n-1)QDT_{L}\}f(T_{L})dT_{L}\right] \\= & {} \frac{H_{cost}}{2D}[(nQ^2+2(n-1)QQ_{r})I_{1}-2(n-1)QDI_{2}] \end{aligned}$$

where $I_{1}=\int _{0}^{\infty }f(T_{L})dT_{L}$ and $I_{2}=\int _{0}^{\infty }T_{L}f(T_{L})dT_{L}$

The total profit over the planning horizon $T_{H}\,Z ={<}\hbox {Sales revenue}{>}-{<}\hbox {Purchase cost}>-{<}\hbox {Expected interest}{>}- {<}\hbox {Ordering cost}{>}-{<}\hbox {Expected holding cost}{>}$

$$\begin{aligned}= & {} nS_{price}Q-nQP_{cost}(1-I_{PD})-(n-1)E(L_{p})-nO_{cost}\nonumber \\&- \frac{H_{cost}}{2D}[(nQ^2+2(n-1)QQ_{r})I_{1}-2(n-1)QDI_{2}]\nonumber \\= & {} nS_{price}Q-nQP_{cost}(1-I_{PD})-(n-1)I_{PA}(1-I_{PD})QP_{cost}I_{PI}I_{2}-nO_{cost}\nonumber \\&-\frac{H_{cost}}{2D}[(nQ^2+2(n-1)QQ_{r})I_{1}-2(n-1)QDI_{2}] \end{aligned}$$

(2)

where the interest is $L_{p}=A_{P}T_{L}I_{PI}=I_{PA}(1-I_{PD})QP_{cost}T_{L}I_{PI}$ and the expected interest,

$$\begin{aligned} E(L_{p})= & {} \int _{0}^{\infty }A_{p}T_{L}I_{PI}f(T_{L})dT_{L} \\= & {} I_{PA}(1-I_{PD})QP_{cost}I_{PI} \end{aligned}$$

To find optimum order quantity, let us take

$$\begin{aligned}&\frac{dZ}{dQ}=0 \\&\quad \Rightarrow nS_{price}-nP_{cost}(1-I_{PD})-(n-1)I_{PI}I_{2}(1-I_{PD})P_{cost}I_{PA} \\&\quad -\frac{H_{cost}}{2D}[(2nQ+2(n-1)Q_{r})I_{1}-2(n-1)DI_{2}]=0 \end{aligned}$$

Also, $\frac{d^2Z}{dQ^2}= \frac{-H_{cost}}{D}nI_{1}<0$,

Therefore, the optimum order quantity is obtained as

$$\begin{aligned} Q^{*}= & {} \frac{D}{nI_{1}H_{cost}}[nS_{price}-nP_{cost}(1-I_{PD}) \nonumber \\&+(n-1)P_{cost}(1-I_{PD})I_{PI}I_{2}I_{PA}]+\frac{(n-1)}{nI_{1}}(DI_{2}-Q_{r}I_{1}) \end{aligned}$$

(3)

Total optimum profit

$$\begin{aligned} Z^{*}= & {} nS_{price}Q^{*}-nQ^{*}P_{cost}(1-I_{PD})-(n-1)I_{PA}(1-I_{PD})Q^{*}P_{cost}I_{PI}I_{2}\nonumber \\&-nO_{cost} -\frac{H_{cost}}{2D}[(nQ^{*2}+2(n-1)Q^{*}Q_{r})I_{1}-2(n-1)Q^{*}DI_{2}] \end{aligned}$$

(4)

Fuzzy-Stochastic Model

The differential equation of the inventory system is given by

$$\begin{aligned} \frac{d\widetilde{q}(t)}{dt}=-\widetilde{D}, \end{aligned}$$

with the initial conditions,

$$\begin{aligned} \widetilde{q}(0)=\widetilde{Q}=\widetilde{D}T_{c}, \widetilde{t}_{1}=\frac{\widetilde{Q}-\widetilde{Q}_{r}}{\widetilde{D}}, \widetilde{q}(t_{j})=Q_{r},\, j=1, 2, \ldots ., n \end{aligned}$$

Total fuzzy-stochastic holding cost is

$$\begin{aligned} \widetilde{H}_{Tot}= & {} \frac{\widetilde{H}_{cost}}{2\widetilde{D}} [n\widetilde{Q}^2\oplus 2(n-1)\widetilde{Q}\otimes (Q_{r}\ominus \widetilde{D}T_{L})] \end{aligned}$$

(5)

where

$$\begin{aligned} \widetilde{Q}=\frac{\widetilde{D}T_{H}}{n} \end{aligned}$$

and

$$\begin{aligned} \widetilde{A}_{p}=\widetilde{I}_{PA}\otimes (1-\widetilde{I}_{PD})\otimes \widetilde{Q}\otimes \widetilde{P}_{cost} \end{aligned}$$

Total fuzzy-stochastic profit over the planning horizon $T_{H}$

$$\begin{aligned} \widetilde{Z}= & {} n\widetilde{S}_{price}\otimes \widetilde{Q}\ominus n\widetilde{Q}\otimes \widetilde{P}_{cost}\otimes (1-\widetilde{I}_{PD})\ominus (n-1)\widetilde{I}_{PA}\otimes (1-\widetilde{I}_{PD})\otimes \nonumber \\&\widetilde{Q}\otimes \widetilde{P}_{cost}\otimes \widetilde{I}_{PI}I_{2}\ominus n\widetilde{O}_{cost}\nonumber \\&\ominus \frac{\widetilde{H}_{cost}}{2\widetilde{D}}[(n\widetilde{Q}^2\oplus 2(n-1)\widetilde{Q} Q_{r})I_{1}\ominus 2(n-1)\widetilde{Q}\otimes \widetilde{D}I_{2}] \end{aligned}$$

(6)

The fuzzy-stochastic optimum order quantity

$$\begin{aligned} \widetilde{Q}^{*}= & {} \frac{\widetilde{D}}{nI_{1}\widetilde{H}_{cost}}[n\widetilde{S}_{price}-n\widetilde{P}_{cost}\otimes (1-\widetilde{I}_{PD}) \nonumber \\&\oplus (n-1)\widetilde{P}_{cost}\otimes (1-\widetilde{I}_{PD})\otimes \widetilde{I}_{PI}I_{2}\otimes \widetilde{I}_{PA}]+\frac{(n-1)}{nI_{1}}(\widetilde{D}I_{2}-Q_{r}I_{1}) \end{aligned}$$

(7)

Total fuzzy-stochastic optimum profit

$$\begin{aligned} \widetilde{Z^{*}}= & {} n\widetilde{S}_{price}\otimes \widetilde{Q}^{*}\ominus n\widetilde{Q}^{*}\otimes \widetilde{P}_{cost}\otimes (1-\widetilde{I}_{PD})\ominus (n-1) \widetilde{A}_{p}\otimes \widetilde{I}_{PI}I_{2}\ominus n\widetilde{O}_{cost}\nonumber \\&\ominus \frac{\widetilde{H}_{cost}}{2\widetilde{D}} [(n\widetilde{Q}^{*2}\oplus 2(n-1)\widetilde{Q}^{*}Q_{r})I_{1}\ominus 2(n-1)\widetilde{Q}^{*}\otimes \widetilde{D}I_{2}] \end{aligned}$$

(8)

Defuzzified-Stochastic Model

The differential equation of the inventory system is given by

$$\begin{aligned} \frac{dP_{dgw}(\widetilde{q})(t)}{dt} = -P_{dgw}(\widetilde{D}), \end{aligned}$$

with the initial conditions,

$$\begin{aligned} P_{dgw}(\widetilde{q}(0))=P_{dgw}(\widetilde{Q})=P_{dgw}(\widetilde{D})T_{c},\, t_{1}=\frac{P_{dgw}(\widetilde{Q})-Q_{r}}{P_{dgw}(\widetilde{D})} \end{aligned}$$

Total defuzzified-stochastic holding cost is

$$\begin{aligned} P_{dgw}(\widetilde{H}_{Tot})= & {} \frac{P_{dgw}(\widetilde{H}_{cost})}{2P_{dgw}(\widetilde{D})} [nP_{dgw}(\widetilde{Q^2})+2(n-1)P_{dgw}(\widetilde{Q})(Q_{r}-P_{dgw}(\widetilde{D})T_{L})] \end{aligned}$$

(9)

where

$$\begin{aligned} P_{dgw}(\widetilde{Q})=\frac{P_{dgw}(\widetilde{D})T_{H}}{n} \end{aligned}$$

and

$$\begin{aligned} P_{dgw}(\widetilde{A}_{p})=P_{dgw}(\widetilde{I}_{PA})(1-P_{dgw}(\widetilde{I}_{PD}))P_{dgw}(\widetilde{Q})P_{dgw}(\widetilde{P}_{cost}) \end{aligned}$$

The total defuzzified profit over the planning horizon $T_{H}$

$$\begin{aligned} P_{dgw}(\widetilde{Z})= & {} nP_{dgw}(\widetilde{S}_{price})P_{dgw}(\widetilde{Q})-nP_{dgw}(\widetilde{Q})P_{dgw}(\widetilde{P}_{cost})(1-P_{dgw}(\widetilde{I}_{PD})) \nonumber \\&-(n-1)P_{dgw}(\widetilde{I}_{PA})(1-P_{dgw}(\widetilde{I}_{PD}))P_{dgw}(\widetilde{Q})P_{dgw}(\widetilde{P}_{cost})P_{dgw}(\widetilde{I}_{PI})I_{2}\nonumber \\&-nP_{dgw}(\widetilde{O}_{cost})-\frac{P_{dgw}(\widetilde{H}_{cost})}{2P_{dgw}(\widetilde{D})}\nonumber \\&[(nP_{dgw}(\widetilde{Q}^2)+2(n-1)P_{dgw}(\widetilde{Q})Q_{r})I_{1} \nonumber \\&-2(n-1)P_{dgw}(\widetilde{Q})P_{dgw}(\widetilde{D})I_{2}] \end{aligned}$$

(10)

Total defuzzified-stochastic optimum order quantity

$$\begin{aligned} P_{dgw}(\widetilde{Q}^{*})= & {} \frac{P_{dgw}(\widetilde{D})}{nI_{1}P_{dgw}(\widetilde{H}_{cost})}[nP_{dgw}(\widetilde{S}_{price})- nP_{dgw}(\widetilde{P}_{cost})(1-P_{dgw}(\widetilde{I}_{PD})) \nonumber \\&+(n-1)P_{dgw}(\widetilde{P}_{cost})(1-P_{dgw}(\widetilde{I}_{PD}))P_{dgw}(\widetilde{I}_{PI}I_{2}P_{dgw}(\widetilde{I}_{PA})] \nonumber \\&+ \frac{(n-1)}{nI_{1}}(P_{dgw}(\widetilde{D})I_{2}-Q_{r}I_{1}) \end{aligned}$$

(11)

Total defuzzified-stochastic optimum profit

$$\begin{aligned} P_{dgw}(\widetilde{Z^{*}})= & {} nP_{dgw}(\widetilde{S}_{price})P_{dgw}(\widetilde{Q}^{*})-nP_{dgw}(\widetilde{Q}^{*}) P_{dgw}(\widetilde{P}_{cost})(1-P_{dgw}(\widetilde{I}_{PD})) \nonumber \\&- (n-1)P_{dgw}(\widetilde{A}_{p})P_{dgw}(\widetilde{I}_{PI})I_{2}-nP_{dgw}(\widetilde{O}_{cost})- \frac{P_{dgw}(\widetilde{H}_{cost})}{2P_{dgw}(\widetilde{D})} \nonumber \\&[(nP_{dgw}(\widetilde{Q}^{*2})+2(n-1)P_{dgw}(\widetilde{Q}^{*})P_{dgw}(\widetilde{Q}_{r}))I_{1} \nonumber \\&-2(n-1)P_{dgw}(\widetilde{Q}^{*})P_{dgw}(\widetilde{D})I_{2}] \end{aligned}$$

(12)

Optimization Technique

The artificial bee colony (ABC) algorithm is a swarm based meta-heuristic algorithm which was introduced by Karaboga [35, 36] in 2005 for optimizing numerical problems. It was influenced by the intelligent foraging behavior of honey bees.

ABC algorithm can be used for unconstrained as well as constrained optimization problems [37].

In ABC algorithm, the colony of artificial bees contains three groups of bees

(i)

Employed bees: Employed bees are those bees which are associated with specific food source. For every food source there is only one employed bee. In other words, The number of employed bees is equal to the number of solutions. The number of employed bees search the environment randomly to find a food source , i.e., the ABC creates a randomly distributed initial population of $P_{s}$ solutions, where $P_{s}$ denote the size of population.

(ii)

Onlooker bees: Onlooker bees are those bees which are watching the dance of employed bees within the hive to choose a food source.

(iii)

Scout bees: Scout bees are those bees which are searching for food sources randomly. The employed bee whose food source has been exhausted becomes a scout bee.

The general scheme of ABC algorithm is as follows:

(i)

Initialization phase: At the 1st step, the bees search the environment randomly to find a food source i.e., the ABC creates a randomly distributed initial population of $P_{s}$ solutions. Each solution $x_{i}$ is a m-dimensional vector (i.e., $x_{i}=x_{i,1}, x_{i,2},\ldots x_{i,m}$), which are to be optimized so as to maximize equation (13) might be used for initialization purposes [38].

$$\begin{aligned} X_{i,j}=X^{min}_{i} + rand (0,1)(X^{max}_{i} -X^{min}_{j} ) \end{aligned}$$

(13)

where $i= 1, 2,\ldots , P_{s}, j= 1, 2,\ldots , m$; $X^{min}_{j}$ = Lower bound of the food source position in dimension j; $X^{max}_{i}$= Upper bound of the food source position in dimension i.

(ii)

Employed bees phase: Employed bees search for more profitable new food sources within the neighborhood of the food source in their memory using the following expression (14) [38]

$$\begin{aligned} V_{i,j}=X_{i,j} + \phi _{ij}(X_{i,j} -X_{k,j}) \end{aligned}$$

(14)

where $k= 1, 2,\ldots , P_{s}, j= 1, 2,\ldots , m$; k and j are randomly generated and k must be different from i; $\phi _{ij}$ is a random number between $[-1,1]$.

(iii)

Onlooker bees phase: employed bees share their food-source information with onlooker bees in the nearby hive. Then the onlooker bees choose a food source depending on the probability value calculated by the Eq. (15)

$$\begin{aligned} p_{i} = \frac{0.9*f_{i}}{f_{best}}+0.1 \end{aligned}$$

(15)

where, $f_{i}$ denote the fitness value of solution $X_{i}$.

The fitness value of the solution is calculated for maximization problems using the following formula

$$\begin{aligned} f_{i}= \left\{ \begin{array}{l@{\qquad }l} 1+|f(x_{i})|, &{}\quad \text{ if } f(x_{i})<0 \\ \dfrac{1}{1+f(x_{i})}, &{}\quad \text{ if } f(x_{i})\ge 0, \\ \end{array} \right. \end{aligned}$$

(16)

where $f(X_{i}$) denotes the objective function values of the decision vector $X_{i}$. After choosing the food source $X_{i}$ probabilistically, onlooker bee randomly chooses a neighborhood source $V_{i}$ and determine its fitness value by using the Eq. (16). Then in the onlooker bee phase, a greedy selection is applied between $X_{i}$ and $V_{i}$.

(iv)

Scout bees phase: The employed bees whose solution can’t be improved continuously through predetermined number of trials is called ’limit’ or ’abandonment criteria’, become scouts and their solutions are abandoned. Then the scout bees go for a new food source using the Eq. (17) (Xiang and An [38]).

$$\begin{aligned} X_{i,j}=X^{min}_{j} + rand (0,1)(X^{max}_{j} -X^{min}_{j} ) \end{aligned}$$

(17)

where $j=1,2,\ldots ,\,m$.

(v)

Termination criteria: Memorize the best solution achieved so far until requirements are met, i.e., the number of iterations becomes equal to maximum cycle number (MCN).

In this work, the ABC algorithm is developed using C-programming language.

The computational procedure of ABC algorithm is given below:

• Step-1: Initialize the population size $P_{s}$ and the solutions $X_{i,j}$ using Eq. (13); where $i= 1, 2,\ldots , P_{s}, j= 1, 2,\ldots , m, m$ being the dimension size.

• Step-2: Evaluate the fitness value of the ith solution using Eq. (16).

• Step-3: Set iteration $= 1$

• Step-4: Compute new solution $V_{i}$ for the employed bees by using (13) and then evaluate them as $V_{i,j}=X_{i,j} + \phi _{ij}(X_{i,j}-X_{k,j})$, where $i, k= 1, 2, \ldots , P_{s}, j= 1, 2,\ldots , m$ k and j are randomly generated and k must be different from i, $\phi _{ij}$ is a random number between [-1,1].

• Step-5: Apply the greedy selection process for the employed bees.

• Step-6: If the solution is not better, then assign trial$=1$ ; otherwise, trial$=0$.

• Step-7: Compute the probability of being selected for the food source by Eq. (14) where $f_{i}$ is the objective function value for $i= 1, 2,\ldots , P_{s}$.

• Step-8: Produce the new solutions for the onlooker bees from the ith solution, which is selected depending on $p_{i}$, then evaluate them.

• Step-9: Employ the greedy selection on the onlooker bees.

• Step-10: Determine the abandoned solution for the scout, if it exists, and replace it with a new solution obtained randomly using (13).

• Step-11: Store the best solution obtained so far.

• Step-12: If iteration$<MCN$, set iteration$=$iteration+1 and go to step-4.

• Step-13: Print the best solution.

• Step-14: Stop.

Numerical Examples and Result Analysis

We have considered the inventory model with advance payments, without shortage with constant demand. The lead time is taken to be stochastic having normal distribution. The example has been considered in two environments -

(i) The crisp environment in which all the controlling parameters are taken as crisp numbers and the lead time is stochastic. The input values of the parameters are given in Table 1.

(ii) The fuzzy-stochastic environment in which some of the controlling parameters $(P_{cost}, O_{cost}, S_{price}, H_{cost}, D, I_{PD}, I_{PI}, I_{PA})$ are taken as parabolic-flat fuzzy numbers with stochastic lead time. The input data along with their defuzzified values in this case are given in Table 2.

In this work, the parameters have been taken as parabolic-flat fuzzy numbers. Thus, the precise model has been converted to the fuzzy model with parabolic-flat membership function. After deducing the fuzzy model, the graded mean integration representation method for defuzzification is applied to defuzzify the fuzzy parameters. The defuzzified model with uniform demand is solved using ABC algorithm coded in C programming language. The optimality for optimal order quantity and corresponding profit have been deduced and shown in the table and in figure.

Table 1 Crisp input data (with $m=0.5, \sigma =0.4, n=5, I_{1}=0.8967, I_{2}=0.5229$)

Table 2 Fuzzy input data

Table 3 Optimum order quantity and optimum profit

Table 4 Sensitivity analysis w.r.t. n

Table 5 Sensitivity analysis w.r.t. D and $Q_{r}$ (decreasing)

Table 6 Sensitivity analysis w.r.t. D and $Q_{r}$ (increasing)

In the fuzzy-stochastic environment, the problem of the crisp model has been converted to the corresponding fuzzy-stochastic model and is given by the Eqs. (5)–(6).

Also the optimal order quantity and optimal profit of the both crisp and fuzzy-stochastic environment, have been calculated and are presented in Table 3.

The sensitivity analysis of the profits have been carried out with respect to the number of replenishment (n), reorder level $(Q_{r}),$ demand rate (D) and are presented in the Tables 4, 5 and 6.

Fig. 1

Parabolic-flat fuzzy number

Fig. 2

Instantaneous state of inventory system

Fig. 3

Sensitivity analysis of $Q^{*}$ w.r.t. n

Fig. 4

Sensitivity analysis of $Z^{*}$ w.r.t. n

Fig. 5

Sensitivity analysis of $Q^{*}$ w.r.t. D

Fig. 6

Sensitivity analysis of $Z^{*}$ w.r.t. D

Fig. 7

Sensitivity analysis of $Q^{*}$ w.r.t. $Q_{r}$

Fig. 8

Sensitivity analysis of $Z^{*}$ w.r.t. $Q_{r}$

From Fig. 3, it is observed that the the optimum order quantity is decreasing while number of replenishments is varied from 5 to 60.

It is clear from Fig. 4 that optimum profit is strictly increasing as the number of replenishments is increased.

The sensitivities of $Q^{*}$ and $Z^{*}$ with respect to the demand rate are shown in Table 5 (decreasing case) and Table 6 (increasing case) and these are also shown in Figs. 5 and 6, from where we easily find that both of $Q^{*}$ and $Z^{*}$ are strictly increasing with D increasing.

Also, from Tables 5 and 6 we can see the behaviors of $Q^{*}$ and $Z^{*}$ with respect to reorder level $Q_{r}$ and from Figs. 7 and 8 it is observed that both of the optimum order quantity and optimum profit are decreasing functions of $Q_{r}$.

Conclusions

In this paper, we have considered the effect of advance payment in an inventory model without shortage in fuzzy environment along with stochastic lead time. Here, we have considered the demand as constant. Also, in both the crisp-stochastic and fuzzy-stochastic models we have found the profits, the optimum order quantities and the optimum profits. In the fuzzy model, we have taken the parabolic-flat fuzzy numbers to represent the inventory parameters. We have used the graded mean integration representation method of defuzzification to defuzzify the fuzzy-stochastic model and then the defuzzified-stochastic model has been solved using ABC algorithm which is coded in C programming language.

We have described the model in fuzzy-stochastic environment to make it more realistic and have explained with numerical data along with the effects of different parameters on the profit. There is a lot of scope to consider the other inventory models in different environments like, stochastic, interval, fuzzy (with membership function other than parabolic-flat fuzzy number). One may use some evolutionary algorithms or programming softwares like, MATLAB, Mathematica, etc. to solve the inventory models.