Introduction

In the traditional inventory models, it is usually assumed that retailer must pay to the supplier for the ordered items as soon as the items are received. In practice, however, the supplier is willing to offer the retailer a certain credit period with-out interest to promote market competition. In this connection we may mention a three parameter distribution for describing deterioration depending on time. Deterioration cannot be avoided in business scenarios. Rau et al. [20] presented an integrated model to determine economic ordering policies of deteriorating items in a supply chain management system.

The problem of deteriorating inventory has received considerable attention in recent years. Deterioration is defined as change, damage, decay, spoilage, obsolescence and loss of utility or loss of marginal value of a commodity that results in decreasing usefulness from the original one. Products such as vegetables, medicine, blood, gasoline and radioactive chemicals have finite shelf life, and start to deteriorate once they are produced. Most researches in deteriorating inventory assumed constant rate of deteriorating inventory assumed constant rate of deteriorating. However, the Weibull distribution is used to represent the product in stock deteriorates with time.

Besides, the assumption of constant demand is not always applicable to real situations. For instance, it is usually observed in the supermarket that display of the consumer goods in large quantities attracts more customers and generates higher demand. In the last several years, many researchers have given considerable attention to the situation where the demand rate is dependent on the level of the on-hand inventory. Gupta and Vrat [9] were first to develop models for stock-dependent consumption rate. Later, Baker and Urban [2] also established an economic order quantity model for a power-form inventory-level-dependent demand pattern. Mandal and Phaujdar [14] then developed an economic production quantity model for deteriorating items with constant production rate and linearly stock-dependent demand. Other researches related to this area such as Pal et al. [16], Padmanabhan and Vrat [15], Giri et al. [8], Ray and Chaudhuri [21], Datta et al. [5], Ray et al. [22] and so on.

Furthermore, when the shortages occur, some customers are willing to wait for backorder and others would turn to buy from other sellers. Many researchers such as Park [19], Hollier and Mak [10] and Wee [36] considered the constant partial backlogging rates during the shortage period in their inventory models. In some inventory systems, such as fashionable commodities, the length of the waiting time for the next replenishment would determine whether the backlogging will be accepted or not. Therefore, the backlogging rate is variable and dependent on the waiting time for the next replenishment. Chang and Dye [3] investigated an EOQ model allowing shortage and partial backlogging. It assumed that the backlogging rate is variable and dependent on the length of the waiting time for the next replenishment. Recently, many researchers have modified inventory policies by considering the “time-proportional partial backlogging rate” such as Abad [1], Papachristos and Skouri [17], Chang et al. [4], Papachristos and Skouri [18], etc.

Recently, Ghiami and Williams [6] established a production inventory model in which a Manufacture in delivering a deteriorating products to retailers. Taleizadeh and Nematollahi [27] investigated the effects of time value of money and inflation on the optimal ordering policy in an inventory control systems. Sicilia et al. [25] studied deterministic inventory systems for items with a constant deteriorating rate. Taleizadeh et al. [26] developed a vendor managed inventory model for a two level supply chains comprised of one vendor and several non-competing retailers in which both the raw materials and the finished products have different deteriorations rates. Wee et al. [37] established a VMI strategy for green electronic products. Lee and Kim [13] have established the optimal policy considering both deteriorating and defective items is an integrated productions distributions model for a single-vendor single-buyer supply chains. Wu et al. [38] have built and EOQ model for the retailer to obtain its optimal credit period and cycle time in a supplier-retailer buyer supply chains in which (i) the retailer receives an up-stream trade credits to the buyer (ii) deteriorating items not only deteriorate continuously but also have their expiration dates and (iii) downstream credit period increases not only demand but also opportunity cost and default risk. Wang et al. [35] proposed an economic order quantity model for seller by incorporating the following relevant facts: (i) deteriorating products not only deteriorate continuously but also have their maximum lifetime and (ii) credit period increases not only demand but also default risk. Some related citations in this direction are by Khanra et al. [12], Sarkar et al. [24], RoyChowdhury et al. [23] and Ghosh et al. [7].

For fitting in with realistic circumstances, the problem of determining the optimal replenishment policy for non-instantaneous Weibull deteriorating items with constant demand is considered in this study. In the model, shortages are allowed; the backlogging rate is variable and dependent on the waiting time for the next replenishment. The necessary and sufficient conditions of the existence and uniqueness of the optimal solution are shown. As the special cases, the results for the models with instantaneous or non-instantaneous deterioration rate and with or without shortages are derived. Further, we analytically identify the best circumstance among these special cases based on the minimum total relevant cost per unit time. Sensitivity analysis of the optimal solution with respect to major parameters is carried out. Finally, four numerical examples are presented to demonstrate the developed model and the solution procedure.

In the past most recent studies in the inventory model have considered the influence of inventory model. In this paper we considered the weibull distribution deterioration instead of constant deterioration. Some of the related articles under inflation are Taleizadeh and Nematollahi [27] developed an inventory control problem for deteriorating items with back-ordering and financial considerations. Hou [11] studies an inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting. Tyan Lo et al. [34] developed integrated production-inventory model with imperfect production processes and Weibull distribution deterioration under inflation. Yang [39] discussed two-warehouse inventory models for deteriorating items with shortages under inflation. Gilding (2014) discussed Inflation and the optimal inventory replenishment schedule within a finite planning horizon. Other related articles in this direction are Taleizadeh et al. [28,29,30], Taleizadeh [31], Taleizadeh [32], Tal et al. [33] etc. This was due to belief that inflation have considered the would not influence the inventory police to any significant degree. This belief is unrealistic since the resource of an enterprise in highly correlated to the return on investment. The concept of the inflation should be considered especially for long-term investment and forecasting.

Notation and Assumption

q(t):

: Inventory level at time t

Q :

: Stock level at the beginning of each cycle after fulfilling backorders

\(Q^{*}\) :

: Optimal order quantity

H :

: length of planning horizon

K :

: Constant rate of inflation ($/$/unit time)

C(t):

: Unit purchase cost for an item bought at time t, i.e. \(C(t) = C_{0} e^{K t}\) where \(C_{0}\) is the unit purchase cost at time zero

h :

: Holding cost ($/unit/year) excluding interest charges

\(C_{0}\) :

: Unit purchase Cost

\(C_{2}\) :

: Shortage cost ($/unit/time)

\(C_{3}\) :

: The ordering cost/cycle

\(i_{e}\) :

: Interest earned ($/time)

\(i_{p}\) :

: Interest charged ($/time)

M :

: Permissible delay in settling the accounts

T :

: Length of a cycle

\(T_{1}^{*}\) :

: Optimal Cycle length for Case-I

\(T^{*}_{2}\) :

: Optimal Cycle length for Case-II

TCU :

: The average total inventory cost per unit time

\(TCU_{1}\) :

: The average total inventory cost per unit time for T \(\ge \) M    (Case-I)

\( TCU_{1}^{*}\) :

: The optimal inventory cost per unit time for T \(\ge \) M    (Case-I)

\( TCU_{2}\) :

: The average total inventory cost per unit time for T \(\le \) M    (Case-II)

\( TCU_{2}^{*}\) :

: The optimal inventory cost per unit time for T \(\ge \) M    (Case-II)

In additions the following assumptions are made

  1. (i)

    The inventory system involves only one item.

  2. (ii)

    The rate of replenishment in instantaneous.

  3. (iii)

    The deterioration rate is a two parameter Weibull distribution: \(\theta (t)=\alpha \beta t^{\beta -1}, \quad \alpha , \beta >0, \, t\ge 0\). Where \(\upalpha \) is the shape parameter, \(\upbeta \) is the scale parameter and \(\theta (t)\) is a non-negative real number and \(\upbeta \ne 1\).

  4. (iv)

    The demand rate is D which is constant.

The Mathematical Model

During the time [0,T] the instantaneous inventory level at time t will satisfy the following equations

$$\begin{aligned} \frac{dq}{dt}+\alpha \beta t^{\beta -1}q= -D.\qquad 0 \le \hbox {t} \le \hbox {T} \end{aligned}$$
(1)

with the boundary condition

$$\begin{aligned} q(T) = 0. \end{aligned}$$
(2)

On solving equation (1) and using boundary condition in (2):

$$\begin{aligned} q(t)=D(1-\alpha t^{\beta })\left[ {\left( T+\frac{\alpha T^{\beta +1}}{\beta +1}\right) -\left( t+\alpha \frac{t^{\beta +1}}{\beta +1}\right) }\right] \end{aligned}$$
(3)

Now we find optimal order quantity, using equation (3):

$$\begin{aligned} Q = q(0)=D\left[ {\left( T+\frac{\alpha T^{\beta +1}}{\beta +1}\right) } \right] \end{aligned}$$
(4)

Case (I) (M < T)

The total cost is sum of at ordering, holding, deterioration cost with interest payable minus the interest earned. We evaluate all the cost separately and grouped together.

$$\begin{aligned} \hbox {Total Cost}= & {} \hbox {Ordering Cost} + \hbox {Holding cost} + \hbox {Deterioration Cost} + \hbox {Interest payable} \\&- \hbox {Interest earned}. \end{aligned}$$

The total holding cost HC during [0, T] is

$$\begin{aligned} \hbox {HC}= & {} \hbox {h} \sum _{n=0}^{m-1} {C(nT).\int \limits _0^T {q(t) dt}}\nonumber \\= & {} \hbox {h}\,\hbox {C}_{0}\quad \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \int \limits _{0}^{T} {D(1-\alpha t^{\beta }) \left[ {\left( {T +\frac{\alpha T^{\beta +1}}{\beta +1}} \right) -\left( {t+\frac{\alpha t^{\beta +1}}{\beta +1}} \right) } \right] } \end{aligned}$$
(5)

We assume that the length of planning horizon \(H = n T\), where n is an integer for the number of replenishments to be made during period H, and T is an interval of time between replenishment.

$$\begin{aligned}= & {} \hbox {h}\,\hbox {C}_{0} \left( {\frac{e^{KH}-1}{e^{KT}-1}}\right) .D. \left[ {\frac{T^{2}}{2}-\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)^{2}}-\frac{\alpha T^{\beta +2}}{(\beta +1)(\beta +2)}}\right. \nonumber \\&+\left. {\frac{\alpha T^{\beta +2}}{(\beta +2)} +\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)(2\beta +2)}} \right] \end{aligned}$$
(6)

The interest earned \(\hbox {IE}_{1}\) during time [0,T] is

$$\begin{aligned} \hbox {IE}_{1}=\hbox {i}_{\mathrm{e}}\sum _{n=0}^{m-1}{C(nT)\int \limits _{0}^{T} {t.D\;dt\quad }}=D. i_e .C_0 \frac{T^{2}}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \end{aligned}$$
(7)

The interest payable \(\hbox {IP}_{1}\) per cycle for the inventory not being sold during due date M:

$$\begin{aligned} \hbox {IP}_{1}= & {} i_{p} .\sum \limits _{{n = 0}}^{{m - 1}} {C(nT)\int \limits _{M}^{T} {q(t)dt}}= i_{p} .\,C_{0} .\left( {\frac{{e^{{KH}} - 1}}{{e^{{KT}}-1}}} \right) .\int _{M}^{T} D(1 -\alpha t^{\beta })\nonumber \\&\times \left[ {\left( T+\alpha \frac{{T^{{\beta +1}}}}{{\beta +1}}\right) -\left( t + \alpha \frac{{t^{{\beta +1}}}}{{\beta +1}}\right) } \right] \,dt\nonumber \\= & {} i_{p} .C_{0} .\,D.\left( {\frac{{e^{{KH}} - 1}}{{e^{{KT}} - 1}}} \right) .\left[ \left( T + \frac{{\alpha T^{{\beta + 1}} }}{{\beta + 1}}\right) \left( T - \frac{{\alpha T^{{\beta + 1}} }}{{\beta + 1}} - M + \frac{{\alpha \,M^{{\beta + 1}} }}{{\beta + 1}} \right) \right. \nonumber \\&\left. - \left( {\frac{{T^{2} }}{2} + \frac{{\alpha T^{{\beta + 2}} }}{{(\beta + 1)(\beta + 2)}}}- \frac{{\alpha T^{{\beta + 2}} }}{{(\beta + 2)}} - \alpha ^{2} \frac{{T^{{2\beta + 2}} }}{{(\beta + 1)(2\beta + 2)}} \right) \right. \nonumber \\&\left. + \left( \frac{{M^{2} }}{2}+ \alpha \frac{{M^{{\beta + 2}} }}{{(\beta + 1)(\beta + 2)}} - \frac{{\alpha M^{{\beta + 2}} }}{{(\beta + 2)}} - \frac{{\alpha ^{2} M^{{2\beta + 2}} }}{{(\beta + 1)(2\beta + 2)}} \right) \right] \end{aligned}$$
(8)

The number of deteriorated items during [0, T] is

$$\begin{aligned} = q(0)-\int \limits _{0}^{T} {D\;dt} =D\left( T+\frac{\alpha T^{\beta +1}}{\beta +1}\right) -DT=\alpha .D\left( {\frac{T^{\beta +1}}{\beta +1}}\right) \end{aligned}$$
(9)

The total variable cost, \(TVC_{1}\), is define as

$$\begin{aligned} TVC_{1}= C_{3}+ HC + IP_{1}+ DC- IE_{1} \end{aligned}$$

From Eq. (2)–(7), we obtain \(TVC_{1}\) as

$$\begin{aligned} TVC_{1}= & {} \hbox {C}_{3}+ \hbox {h}\,\hbox {C}_{0} \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) D \left[ {\frac{T^{2}}{2}-\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)^{2}}-\frac{\alpha T^{\beta +2}}{(\beta +1)(\beta +2)}}\right. \nonumber \\&-\left. {\frac{\alpha T^{\beta +2}}{(\beta +2)}-\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)(2\beta +2)}} \right] \nonumber \\&+i_p .C_0 . D.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) .\left[ {\left( {T+\frac{\alpha T^{\beta +1}}{\beta +1}} \right) \left( {T-\frac{\alpha T^{\beta +1}}{\beta +1}-M+\frac{\alpha M^{\beta +1}}{\beta +1}} \right) } \right. \nonumber \\&-\left( {\frac{T^{2}}{2}+\frac{\alpha T^{\beta +2}}{(\beta +1)(\beta +2)}} -\frac{\alpha T^{\beta +2}}{(\beta +2)} - \alpha ^{2}\frac{T^{2\beta +2}}{(\beta +1)(2\beta +2)} \right) \nonumber \\&\left. +\left( {\frac{M^{2}}{2}+\alpha \frac{M^{\beta +2}}{(\beta +1)(\beta +2)}-\frac{\alpha M^{\beta +2}}{(\beta +2)}-\frac{\alpha ^{2}M^{2\beta +2}}{(\beta +1)(2\beta +2)}} \right) \right] \nonumber \\&+ \alpha .D\left( {\frac{T^{\beta +1}}{\beta +1}} \right) - D. i_e .C_0 \frac{T^{2}}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \end{aligned}$$
(10)

The total variable cost per unit time \(\hbox {TCU}_{1}\), during the cycle time [0,T] is

$$\begin{aligned} TCU_{1}= & {} \frac{{TVC}_{{1}}}{T}=\frac{\hbox {C}_{{3}} +\hbox {HC}+\hbox {IP}_{{1}}+\hbox {DC}-\hbox {IE}_{{1}}}{T}\nonumber \\ TCU_1= & {} \frac{1}{T}\left[ C_3 +h C_0 \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \right. \nonumber \\&\times \, D \left\{ {\frac{T^{2}}{2}-\frac{\alpha ^{2} T^{ 2\beta +2}}{(\beta +1)^{2}}-\frac{\alpha T^{\beta +2}}{(\beta +1)(\beta +2)}-\frac{\alpha T^{\beta +2}}{(\beta +2)}-\frac{\alpha ^{ 2} T^{2\beta +2}}{(\beta +1)\quad (2\beta +2)}} \right\} \nonumber \\&+\,i_p \;C_0 \;D\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \left\{ \left( {T+\frac{\alpha T^{\beta +1}}{\beta +1}} \right) \;\left( {T-\frac{\alpha T^{\beta +1}}{\beta +1}-M+\frac{\alpha M^{\beta +1}}{\beta +1}} \right) \right. \nonumber \\&-\,\left( {\frac{T^{2}}{2}+\frac{\alpha T^{ \beta +2}}{(\beta +1)\;(\beta +2)}} {-\frac{\alpha T^{\beta +2}}{(\beta +2)}-\frac{\alpha ^{2}T\;^{2\beta +2}}{(\beta +1) (2\beta +2)}} \right) \nonumber \\&+\,\left. \left( {\frac{M^{2}}{2}+\frac{\alpha M^{ \beta +2}}{(\beta +1)(\beta +2)}-\frac{\alpha M^{\beta +2}}{(\beta +2)}-\frac{\alpha ^{2}M\;^{2\beta +2}}{(\beta +1)\quad (2\beta +2)}} \right) \right\} \nonumber \\&+\,\alpha .D \left( {\frac{T^{ \beta +1}}{\beta +1}} \right) \left. {-D. i_e .C_0 \frac{T^{2}}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) } \right] \end{aligned}$$
(11)

Case (II) (M > T)

Now as per results the ordering cost \(\hbox {C}_{3}\), the deterioration cost DC, the holding cost during the cycle period (0,T) are the same as in case I. So now interest earned per cycle is

$$\begin{aligned} \hbox {IE}_{2}= & {} i_e .C_0 .\frac{e^{KH}-1}{e^{KT}-1}\left\{ {\int \limits _{0}^{T} {D.\;t\;dt+(M-T)\int \limits _{0}^{T} {D\;dt}}}\right\} \nonumber \\= & {} \frac{i_e .C_0 .D.T}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \;(2M-T) \end{aligned}$$
(12)

The total variable cost, \(\hbox {TCV}_{2}\) is defined as

$$\begin{aligned} \hbox {TVC}_{{2}}= & {} \hbox {C}_{{3}} + \hbox {HC} +\hbox {DC}- \hbox {IE}_{{2}}\nonumber \\= & {} \hbox {C}_{3}+ \hbox {h}\,\hbox {C}_{0} \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) .\;D \;\left[ {\frac{T^{2}}{2}-\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)^{2}}-\frac{\alpha T^{\beta +2}}{(\beta +1)\;(\beta +2)}}\right. \nonumber \\&+\left. \frac{\alpha T^{\beta +2}}{(\beta +2)}+\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)\;(2\beta +2)} \right] + \alpha .D\;\left( {\frac{T^{\beta +1}}{\beta +1}} \right) \nonumber \\&-\frac{i_e .C_0 .D.T}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \;(2M-T) \end{aligned}$$
(13)

The total variable cost per unit time \(\hbox {TCU}_{2}\) (0, T) is

$$\begin{aligned} \hbox {TCU}_{{2}}= & {} \frac{TVC_2}{T}=\frac{\hbox {C}_{{3}}+\hbox {HC}+\hbox {DC}-\hbox {IE}_{{2}}}{T}\nonumber \\ \hbox {TCU}_{2}= & {} \frac{1}{T}\;\left[ C_3 +h C_0 \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) . D \left\{ \frac{T^{2}}{2}-\frac{\alpha ^{2}T^{2\beta +2}}{(\beta +1)^{2}}-\frac{\alpha \;T^{\beta +2}}{(\beta +1)\;(\beta +2)}\right. \right. \nonumber \\&+\left. \frac{\alpha \;T^{\beta +2}}{(\beta +2)}+\frac{\alpha ^{2}\;T^{2\beta +2}}{(\beta +1)\;(2\beta +2)} \right\} \nonumber \\&\left. +\,{\alpha .D\;\left( {\frac{T^{\beta +1}}{\beta +1}} \right) -\frac{i_e .C_0 .D.T}{2}.\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \;(2M-T)} \right] \end{aligned}$$
(14)

Now

$$\begin{aligned} \hbox {TCU}=\left\{ \begin{array}{l@{\quad }l} \hbox {TCU}_{{1}},&{} \hbox {T} \le \hbox {M}\\ \hbox {TCU}_{{2}}, &{}\hbox {T} > \hbox {M}\\ \end{array}\right. \end{aligned}$$
(15)

Optimal Slution

For optimal solution we differentiate Eqs. (10) and (13) with respect to T.

$$\begin{aligned}&\frac{dTCU_1 }{dT} = -\frac{C_3 }{T^{2}} +D \;\alpha \;\beta \; \frac{T ^{(\beta -1)}}{(\beta +1)}+D\; C_0 \;\left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \nonumber \\&\quad \times \left[ {h\left\{ {\frac{1}{2}-\frac{\alpha ^{2}\; (2\beta +1) \;T^{ 2\beta }}{(\beta +1)^{2}}-\frac{\alpha \; (\beta +1)\; T ^{\beta }}{(\beta +1) \;(\beta +2)}+\frac{\alpha \;(\beta +1) \;T^{ \beta }}{(\beta +2)}+\frac{\alpha ^{2} \;(2\beta +1)\; T^{ 2\beta }}{( \beta +1 ) \;( 2\beta +2 )}} \right\} } \right. \nonumber \\&\quad +\,i_p \;\left\{ \left( {1+\frac{\alpha \; T ^{\beta }}{(\beta +1)}} \right) \;\left( {1-\frac{\alpha \; (\beta +1)\; T^{ \beta }}{( \beta +1 )}} \right) \right. \nonumber \\&\quad \left. +\left( {T-\frac{\alpha \;T^{(\beta +1)}}{( \beta +1 )}-M+\frac{\alpha \;M\;^{(\beta +1)}}{( \beta +1 )}} \right) \;\;\left( {\frac{\alpha \beta T\;^{(\beta -1)}}{( \beta +1 )}} \right) \right. -\left( {\frac{1}{2}-\;\frac{\alpha (\beta +1) \;T ^{\beta }}{( \beta +2 )}\;} \right. \nonumber \\&\quad +\;\frac{\alpha \; (\beta +1) \;T^{\beta }}{(\beta +1)\;(\beta +2)}\left. \left. {-\frac{\alpha ^{2}\; (2 \beta +1) \;T ^{2 \beta }}{(\beta +1)\;(2 \beta +2)}} \right) \right. \nonumber \\&\quad \left. - \frac{1}{T^{2}}\;\left( {\frac{M^{2}}{2}-\frac{\alpha M\;^{(\beta +2)}}{(\beta +2)}+\frac{\alpha M^{(\beta +2)}}{(\beta +1)\;(\beta +2)}-\frac{\alpha ^{2}M\;^{(2 \beta +2)}}{(\beta +1)\;(2\beta +2)}} \right) \right\} \left. {\;-\;\frac{1}{2}\;i_e } \right] \nonumber \\&\quad - D. C_0 \left( {\frac{K e^{KT}(e^{KH}-1)}{(e^{KT}-1)^{2}}} \right) \nonumber \\&\quad \times \left[ {h\left\{ {\frac{T}{2}-\frac{\alpha ^{2}T^{(2\beta +1)}}{(\beta +1)^{2}}-\frac{\alpha T^{(\beta +1)}}{(\beta +1) (\beta +2)}+\frac{\alpha T^{(\beta +1)}}{(\beta +2)}+\frac{\alpha ^{2}T^{(2\beta +1)}}{(\beta +1) (2\beta +2)}} \right\} } \right. \nonumber \\&\quad +\,i_p \left\{ {\left( {1+\frac{\alpha T^{\beta }}{(\beta +1)}} \right) } \right. \left( {T-\frac{\alpha T^{(\beta +1)}}{(\beta +1)}-M+\frac{\alpha M^{(\beta +1)}}{(\beta +1)}} \right) \nonumber \\&\quad -\left( {\frac{T}{2}-\frac{\alpha T^{(\beta +1)}}{(\beta +2)}+\frac{\alpha T^{(\beta +1)}}{(\beta +1)(\beta +2)}} \right. \nonumber \\&\quad \times \left. {\left. {-\frac{\alpha ^{2}T^{(2\beta +1)}}{(\beta +1)(2\beta +2)}} \right) +\frac{1}{T}\left( {\frac{M^{2}}{2}-\frac{\alpha M^{(\beta +2)}}{(\beta +2)}+\frac{\alpha M^{(\beta +2)}}{(\beta +1)(\beta +2)}-\frac{\alpha ^{2}M^{(2\beta +2)}}{(\beta +1)(2\beta +2)}} \right) } \right\} \nonumber \\&\quad \left. {-\frac{T}{2}\;i_e } \right] \end{aligned}$$
(16)
$$\begin{aligned} \frac{dTCU_2}{dT}= & {} -\;\frac{C_3 }{T^{2}}+\frac{\alpha D \beta T^{(\beta -1)}}{(\beta +1)}+\;C_0 \;D \left( {\frac{e^{KH}-1}{e^{KT}-1}} \right) \nonumber \\&\times \left[ {\left\{ {h\;\left( {\frac{1}{2}-\frac{\alpha ^{2}\;(2\beta +1)\;T^{2\beta }}{(\beta +1)^{2}}-\frac{\alpha \;(\beta +1) T^{\beta }}{(\beta +1) (\beta +2)}} \right. } \right. } \right. \nonumber \\&+\frac{\alpha (\beta +1) T^{\beta }}{(\beta +2)}\left. {+\frac{\alpha ^{2} (2\beta +1) T^{2\beta }}{(\beta +1) (2\beta +2)}} \right) -\left. {\frac{i_e }{2}} \right\} \nonumber \\&-\frac{Ke^{KT}}{(e^{KT}-1)}\;\left\{ {h\;\left( {\frac{T}{2}-\frac{\alpha ^{2}\;\;T^{(2\beta +1)}}{(\beta +1)^{2}}-\frac{\alpha \; T^{(\beta +1)}}{(\beta +1) (\beta +2)}} \right. } \right. \nonumber \\&+\frac{\alpha T^{(\beta +1)}}{(\beta +2)}\left. {+\frac{\alpha ^{2} T^{(2\beta +1)}}{(\beta +1) (2\beta +2)}} \right) \;\left. {\left. {-\frac{i_e }{2} (2M-T)} \right\} }\right] \end{aligned}$$
(17)

The necessary condition for finding optimal (minimum) solution of total inventory cost is

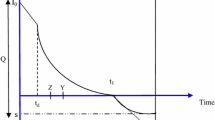
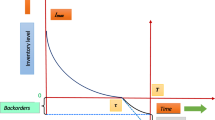
$$\begin{aligned} \frac{dTCU_1 }{dT}=0,\;\mathrm{and}\;\frac{dTCU_2 }{dT}=0. \end{aligned}$$
(18)

It is difficult to find second order derivative for sufficient condition of optimality. We can show it by the graph. The graph of two cases (I & II) is given below:

Case-I (M \({\varvec{<}}\) T)

Fig. 1
figure 1

TCU versus T

Full size image

Case-II (M \({\varvec{>}}\) T)

Fig. 2
figure 2

TCU versus T

Full size image

Above Figs. 1 and 2 for case-I and II are convex, which proves that the optimal total cost with respect to time is minimum. That is, second derivative of \(\frac{d^{2}TCU_1 }{dT^{2}}\;and\;\frac{d^{2}TCU_2 }{dT^{2}}\) are positive.

Numerical Examples

In this paper we discussed the ordering polices in deferent conditions for which we define two cases Case (I) (M < T) (Payment before depletion) and Case (II) (M > T) (Payment after depletion).

Numerical Example-1 on Case-I (M < T)

Let’s take the parameter values \(D=10,000, \alpha = 0.5, \beta = 1.5, M = 0.1, {C}_{0}= 0.5, i_{e} = 0.01, i_{p}= 0.30, K = 0.3, H = 5, h = 10.00, C_{3}= 5.0, C_{2} = 0.8\), in their appropriate units. Substituting these parameter values in the first equation of (18) we get \(T=T_{1}^{*}{} \mathbf{= 0.122438}\,\mathbf{year,}\) the corresponding value of optimal order quantity \({{\varvec{Q}}}_{{{\varvec{1}}}}= {{\varvec{Q}}}_{{{\varvec{1}}}}^{*}\mathbf{= 1234.87}\,\mathbf{units}\,\mathbf{and }\,{{\varvec{TCU}}}_{{{\varvec{1}}}}=\mathbf{TCU}_{{{\varvec{1}}}}^{*} = \$\,\mathbf{51784.3}.\)

Numerical Example-2 on Case-II (M > T)

The following inventory parametric values are used for Case-II, \(D = 1000, \alpha = 0.8, \beta = 1.2, {{\varvec{M}}}{} \mathbf{= 0.7}, C_{0}= 0.5, i_{e}=0.16, i_{p} =0.30, K = 0.3, H = 4, h= 10.00, C_{3}= 5.0, C_{2}=0.8\), in their appropriate units. Substituting these parameter values in the second equation of (18) we get \({{\varvec{T}}}_{{{\varvec{2}}}}={{\varvec{T}}}_{{{\varvec{2}}}}^{*}=\mathbf{0.581251}\,\mathbf{year,}\) the corresponding value of optimal order quantity \({{\varvec{Q}}}_{{{\varvec{2}}}}={{\varvec{Q}}}_{{{\varvec{2}}}}^{*}=\mathbf{691.473}\, \mathbf{units}\) and \({{\varvec{TCU}}}_{{{\varvec{2}}}}={{\varvec{TCU}}}_{{{\varvec{2}}}}^{*}=\mathbf{7282.95.}\)

Sensitivity Analysis

Any business transactions uncertainty may occur. Sensitivity analysis may play important role for decision makers. In this section we study the variation of order quantity, total inventory cost with the variation of several key parameters.

  1. (i)

    Case-1

Variation of D keeping all parameters same as numerical example (1)

D

T

Q

\(TCU_{1}\)

10100

0.122436

1247.2

52294.6

10200

0.122433

1259.52

52801.3

10300

0.122431

1271.84

53311.4

10400

0.122429

1284.17

53821.3

10500

0.122427

1296.50

54331.1

Variation of \(C_{0}\) (keeping all parameters same as numerical example (1)

\(C_{0}\)

T

Q

\(TCU_{1}\)

0.55

0.122485

1235.37

51948.1

0.60

0.122524

1235.75

52083.9

0.65

0.122557

1236.09

52198.7

0.70

0.122585

1236.37

52296.0

0.75

0.122610

1236.63

52382.9

Variation of \(\alpha \) (keeping all parameters same as numerical example (1)

\(\alpha \)

T

Q

\(TCU_{1}\)

0.505

0.120926

1219.53

41587.2

0.510

0.119487

1204.94

31175.7

0.515

0.118116

1191.04

20551.9

0.520

0.116807

1177.77

9711.48

0.525

0.115555

1165.08

\(-\)1348.37

Variation of \(\beta \) (keeping all parameters same as numerical example (1)

\(\beta \)

T

Q

\(TCU_{1}\)

1.0

0.708136

7865.33

168941

1.1

0.540321

5791.26

174199

1.2

0.398229

4157.82

188018

1.3

0.280667

2923.64

196089

1.4

0.184170

1877.62

166393

Variation of K (keeping all parameters same as numerical example (1)

K

T

Q

\(TCU_{1}\)

0.4

0.133285

1345.82

115994

0.5

0.145984

1476.13

216504

0.6

0.159987

1620.35

368626

0.7

0.174611

1771.59

595503

0.8

0.189352

1924.72

933457

  1. (ii)

    Case-II

Variation of D keeping all parameters same as numerical example (2)

D

T

Q

\(TCU_{2}\)

1100

0.581235

760.595

8042.54

1200

0.581222

760.575

8772.7

1300

0.58121

898.839

9502.95

1400

0.5812

967.961

10233.2

1500

0.581192

1037.98

10963.5

Variation of \(C_{0}\) (keeping all parameters same as numerical example (2)

\(C_{0}\)

T

Q

\(TCU_{2}\)

0.35

0.581896

692.387

8502.18

0.40

0.582381

693.075

9692.15

0.45

0.582758

693.609

10882.1

0.50

0.583061

694.039

12072.0

0.55

0.583308

694.39

12074.4

Variation of \(\alpha \) (keeping all parameters same as numerical example (2)

\(\alpha \)

T

Q

\(TCU_{2}\)

0.7

0.638117

756.545

7184.1

0.9

0.535673

639.282

7430.54

1.0

0.498185

596.323

7541.84

1.5

0.378252

458.565

8036.27

2.0

0.312089

382.238

8475.04

Variation of \(\beta \) (keeping all parameters same as numerical example (2)

\(\beta \)

T

Q

\(TCU_{2}\)

1.3

0.591145

694.96

7343.59

1.4

0.60113

699.396

7371.26

1.5

0.611054

704.454

7395.72

1.6

0.620819

709.908

7417.40

1.7

0.630361

715.596

7436.66

Variation of K (keeping all parameters same as numerical example (2)

K

T

Q

\(TCU_{2}\)

0.4

0.588615

659.454

9030.34

0.6

0.603498

679.277

14294.4

1.2

0.651265

744.348

70164.7

1.5

0.678551

782.543

168536.0

1.9

0.721293

843.932

569736.0

From the above table the following inferences can be made:

  • Increase in demand rate D results the values of cycle time T decreases, the value of order quantity Q increases but the total inventory cost TCU increases in both cases.

  • Increase purchase cost \(C_{0}\), results the values of cycle time T decreases, the value of Order quantity Q increases and total inventory cost TCU increases in both cases.

  • Increase of parameter \(\upalpha \), results the values of cycle time T decreases, the value of order quantity Q decreases and total inventory cost TCU decreases in cases-I.

  • Increase of parameter \(\upalpha \) results the values of cycle time T decreases, the value of order quantity Q decreases and total inventory cost TCU increases in cases-II.

  • Increase of parameter \(\upbeta \) results the values of cycle time T decreases, the value of order quantity Q decreases and total inventory cost TCU decreases both cases.

  • Increase in inflation rate K, results the values of cycle time T increases, the value of Order quantity Q increases and total inventory cost TCU increases in both cases.

Conclusion

Any type of business depends on future planning and future planning in uncertain. Probability is a measure of uncertainty. It is beneficial for both vendor and buyer. Deterioration plays an important role for fresh products like bread, green vegetable etc. In this paper we have discussed inventory models for Weibull distribution detracting items under constant demand rate by considering two different cases. Second order approximation has been used for closed form numerical results. From the managerial point of view the following results are obtained:

  • Total cost increases if the demand rate increases in both cases

  • Total cost increases if the purchase cost increases in both cases

  • Total cost decreases if the parameter \(\upbeta \) increases in both cases

  • Total cost increases if the inflation rate increases in both cases

The research work presented in this study generalized in different manners. We may generalize our research work by considering demand rate as stock level. We could also extend the model by adding advertisement cost and freight cost and others.