A Two-Warehouse Inventory Model for Deteriorating Items with Capacity Constraints and Back-Ordering Under Financial Considerations

Abstract

This paper investigated two warehouse inventory model for a single deteriorating items under the assumption of shortages and partial backlogging under payments delay and the effect of inflation and time value for money is also incorporated. Again, two warehouse capacity (owned and rented) have been considered over the finite horizon planning under which back-ordering is assumed. When the order quantity becomes higher than the storage capacity in own warehouse then the system involves two warehouse model. In this model, excess inventory are stored in rented warehouses which are assumed to charge higher unit holding costs than owned warehouses. Moreover, in rented warehouse item deteriorates with higher rates than in owned warehouse. At first own warehouse are filled out by its storage capacity and the rests are kept in rented warehouse. So, at first, the items in RW decreases due to demand and deterioration until it reaches to the level zero while on the other hand a portion on the inventory on OW is depleted due to deterioration only. Then, the inventory on OW decreases due to demand and deterioration until it reaches to the level zero. Finally, shortages start and backlogging rate is negative exponential of function waiting time. Here, the demand is used as exponential function of time and backlogging rate varies negative exponential function of waiting time. The total cost function is carried out under the effect of JIT setup cost. Two numerical examples are illustrated for the developed model and sensitivity analysis has been carried out to identify behaviour of model parameters.

Introduction

For last twenty years, many researchers have been attracted by the effect of permissible delay in payments on optimal inventory management. From an economic point of view, such type of credit policies can be applied to get larger orders since this credit policies results as an alternative solution of price discounts. In that case the main problem is to decide the place where the items should get stock. Many researcher have worked considering the effect of permissible delay in payments for a single warehouse with unlimited capacity. But in a more practical sense, any warehouse has limited capacity. Hartely [1] developed an inventory model involving two different warehouses, one of which is owned (OW) while the other is rented (RW). The items are stored first in OW which has a fixed capacity W and the only excess units are stored in RW which has higher holding cost than in OW. Goswami and Chaudhuri [2] designed two-level storage model including both with and without shortages in which demand was considered as linear increasing function of time. But in this model deterioration was not taken into account. Sarma [3] first developed a two-warehouse model for deteriorating items with an infinite replenishment rate and shortages. Other notable papers in this direction are by Pakkala and Achary [4], Zhou and Yang [5], Lee [6], Yang [7]. Some most recent research works in this direction are by Jaggi et al. [8], Tiwari et al. [9], Sett et al. [10].

Again many researchers have been working on the effect of permissible delays in payments on inventory management during last two decades. Shah [11] considered an inventory model for exponentially decaying inventory under permissible delay in payment. Aggarwal and Jaggi [12] developed economic order policies for deteriorating items under the effect of permissible delay in payments. Then Jamal et al. [13] generalized the model of Aggarwal and Jaggi considering shortages. Sarkar [14] developed an EOQ model with time varying deterioration rate in which the effect of delay in payments were also taken into account. Other numerous papers related to delay in payments are Chung and Liao [15, 16], Shinn and Hwang [17], Huang and Liao [18], Liao [19, 20], Chen et al. [21].

Again, in real world problem, deterioration of many items which is defined as the decay, damage of stored items can not be neglected and as a result of which it decreases usefulness of the items. Ghare and Schrader [22] were the pioneers to establish an inventory model for deteriorating items. Covert and Philip [23] extended Ghare and Schrader’s constant deterioration rate to a two parameter weibull distribution. Cheng et. al. [24] developed an inventory control model for deteriorating items in which trapezoidal type demand and partial backlogging were assumed. Chung and Lin [25] studied trade credit issue in a supply chain model proposed to determine the order quantity of a deteriorating item. Some other related article in this direction are Cardenas-Barron [26], Widyadana [27], Chung et. al. [28]. Recently many researcher have worked on various types of deterioration like probabilistic deterioration, variable deterioration, deterioration on seasonal product and some most recent works in this directions are by Sarkar and Sarkar [29], Sarkar and Sarkar [30], Sarkar et al. [31], sarkar [32], Sarkar et al. [33], Sarkar et al. [34], Wu et al. [35], Sarkar et al. [36], Shah and Cardenas-Barron [37].

Furthermore, both inflation and time value of money have main effect on financial markets. Ray and Chaudhuri [38] developed a finite-horizon EOQ model with back ordering and varying demand rate whereas the effects of inflation and time value of money were taken into consideration. Chen [39] considered the situation in which the demand rate is time-proportional and shortages are fully back ordered. Other articles in this direction come from Bose et.al. [40], Sarkar et al. [41], Roy and Chaudhuri [42], Sana [43], Roy and Chaudhuri [44]. Further more many researcher have considered credit policy in their article and some of which are by Ouyang et al. [45], Wu et al. [46], Chun et al. [47].

Yang [48] developed two-warehouse inventory management problem for perishable products with constant demand rate and back ordering shortages under inflation. Hou [49] developed an EOQ model over finite planning horizon for perishable products with stock-dependent demand rate and full back ordering under inflation and time value of money. Cardenas-Barron et. al. [50] also developed an EOQ model in honor of Ford Whitman Harris where as Liao and Huang [51] developed a two-warehouse deterministic inventory model for deteriorating items considering delay in payments and capacity constraints. But in this model partial backlogging and time value of money were not taken into consideration. Some recent works relating imperfect production, variable back order, inspection, trade credits and time dependent back-logging are by Sarkar and Saren [52], Sarkar [53], Sarkar et al. [54], Tripathi and Chaudhary [55], Das et al. [56], Sarkar et al. [57].

Liao and Huang [51] evaluated a two-warehouse deterministic inventory model for deteriorating items considering delay in payments and capacity constraints. But in this model shortages, partial backlogging and time value of money were not taken into account. In this article we extended Liao and Huang [51] model by developing a two-warehouse inventory model for deteriorating items with the consideration of shortages and partial backlogging under delay in payments and the effect of inflation and time value of money.

Notation and Assumptions

Based on the data of Liao and Huang [49] model, this paper is developed with the following Notation and Assumptions.

Notation

• $C_{0}$: JIT setup cost per replenishment

• D: demand rate per unit time

• W: storage capacity of OW

• T: length of each replenishment cycle

• s: selling price per unit

• c: purchasing cost per unit

• $I_{R}(t)$: on hand inventory at time t in rented warehouse

• $I_{O}(t)$: on hand inventory at time t in own warehouse

• $h_{0}$: holding cost per unit time in OW

• $h_{r}$: holding cost per unit time RW with $h_{r} \ge h_{0}$

• $\alpha$: deterioration rate in OW, where $0<\alpha <1$

• $\beta$: deterioration rate in RW, where $0<\beta <1$ and $\beta >\alpha$

• $t_{w}$: time at which the inventory level reaches zero in RW

• M: credit period set by the supplier

• $I_{0}$: capital opportunity cost (as a percentage)

• $I_{e}$: earned interest rate (as a percentage)

• $I_{c}$: payable interest rate (as a percentage)

• H: length of planning horizon

• i: constant inflation rate

• r: discount rate, representing the time value of money

• R: r − i, representing the net constant discount rate of inflation

• $t_{j}$: time at which the inventory level in jth replenishment cycle drops to zero

• $T_{j}$: total time that is elapsed up to and including the jth replenishment cycle where $T_{0}=0$, $T_{1}=T$ and $T_{N}=H$

• $c_{s}$: shortage cost per unit time

• $I_{m}$: maximum inventory level at the beginning of each replenishment cycle

• $I_{s}$: maximum shortage quantity at the end of each replenishment cycle

• F: fraction of replenishment cycle where the net stock is positive (a decision variable)

• N: number of replenishment during the planning horizon, $N = \frac{H}{T}$

• Q: order quantity of the item.

Assumptions

• (a) The planning horizon in this model is finite.

• (b) The demand rate is a exponential increasing function of time $D(t)= ae^{bt}$, a,$b>$0. The deterioration rates are constant.

• (c) The owned warehouse (OW) has a fixed capacity of W units.

• (d) The rented warehouse (RW) has unlimited capacity.

• (e) The items in OW are consumed only after consuming the items kept in RW.

• (f) In shortage period [$t_{1}$,T] the demand $De^{-\delta (T-t)}$ at any time t is satisfied whereas the remaining part of the demand $D(1-e^{-\delta (T-t)})$ remains unsatisfied, where $\delta$ is a positive constant and (T − t) is the waiting time until the next replenishment begins at time T. So the backlogging rate is $De^{-\delta (T-t)}$ which varies as negative exponential function of waiting time.

• (g) Single deteriorating type of product has been considered.

• (h) The inventory level at the end of the planning horizon will be zero.

• (i) The cost factors are deterministic, but will be inflated under constant inflation rate.

• (j) The number of replenishment are restricted to integer one.

• (k) The inventory costs (including holding cost and deterioration cost) in RW are higher than those in OW. That is $h_{r}+\beta c >h_{0}+\alpha c$.

• (l) The last order is only being placed to satisfy the shortage of last period.

Mathematical Formulation

The problem which we have discussed here is how retailers know whether or not to rent RW to hold the items. If the order quantity $Q\le W$ then it is not necessary to rent the warehouse. But if $Q>W$ then W units are stored in OW and the remainder is dispatched in RW. Here we shall denote $t_{a}=\frac{1}{\alpha +b} log(1+\frac{(\alpha +b)W}{a})$ (see “Appendix A”). The inequality $Q>W$ holds if and only if $t_{a}<t_{1}$ and then the situation of two warehouse inventory system will arise.

Development of Two-Warehouse Model ($t_{a}<t_{1}$)

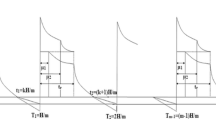
If $Q>W$, the the system involves two warehouse model. At first W units are stored in OW and the rests are kept in RW. So, during the time interval (0,$t_{w}$) the items in RW decreases due to demand and deterioration until it reaches to the level zero. Again on the other hand a portion on the inventory on OW is depleted due to deterioration only. Then, during ($t_{w},t_{1}$) the inventory on OW decreases due to demand and deterioration. After $t=t_{1}$ shortages start and backlogging rate is negative exponential function of waiting time. The pictorial representation of the above inventory system can be represented by Fig. 1.

Fig. 1

Pictorial representation of the inventory cycle

This bahaviour can be represented by following four differential equations:

$$\begin{aligned}&\frac{dI_{R}(t)}{dt}+ \beta I_{R}(t)= -ae^{bt},\quad 0\le t\le t_{w} \end{aligned}$$

(1)

$$\begin{aligned}&\frac{dI_{0}(t)}{dt}= - \alpha I_{0}(t),\quad 0\le t\le t_{w} \end{aligned}$$

(2)

$$\begin{aligned}&\frac{dI(t)}{dt}+ \alpha I(t)= -ae^{bt},\quad t_{w}\le t\le t_{1} \end{aligned}$$

(3)

$$\begin{aligned}&\frac{dI(t)}{dt}= -ae^{bt}e^{-\delta (T-t)},\quad t_{1}\le t\le T \end{aligned}$$

(4)

with initial and boundary condition

$$\begin{aligned} I_{R}(t_{w})=0=I(t_{1}),\quad I_{0}(0)=W , \end{aligned}$$

(5)

The solution of the differential equations (1)–(4) subject to the condition (5) are given by

$$\begin{aligned}&I_{R}(t)=\frac{a}{\beta + b}(e^{\beta (t_{w}-t)+bt_{w}}-e^{bt}),\quad 0\le t\le t_{w} \end{aligned}$$

(6)

$$\begin{aligned}&I_{0}(t)=We^{-\alpha t},\quad 0\le t\le t_{w} \end{aligned}$$

(7)

$$\begin{aligned}&I(t)=\frac{a}{\alpha + b}(e^{\alpha (t_{1}-t)+bt_{1}}-e^{bt}),\quad t_{w}\le t\le t_{1} \end{aligned}$$

(8)

$$\begin{aligned}&I_{R}(t)=\frac{ae^{-\delta T}}{b + \delta }(e^{(b+\delta )t_{1}}-e^{ (b+\delta )t}),\quad t_{1}\le t\le T \end{aligned}$$

(9)

The maximum inventory at the beginning of each cycle

$$\begin{aligned} I_{m}= & {} I_{R}(0)+I_{0}(0)\nonumber \\= & {} \frac{a}{\beta +b}(e^{(\beta +b)t_{w}}-1)+W \end{aligned}$$

(10)

The maximum shortage at the end of each cycle

$$\begin{aligned} I_{s}= & {} -I(T)\nonumber \\= & {} \frac{a}{\delta +b}(e^{bT}-e^{\delta (t_{1}-T)+bt_{1}}) \end{aligned}$$

(11)

JIT Setup Cost

Since the number of replenishment or period is N, so the JIT setup cost over the planning horizon under consideration of inflation and time value of money is

$$\begin{aligned} C_{SET}= & {} \sum _{j=0}^{N}C_{0} \frac{a(e^{bT}-1)}{bI_{m}}e^{-JRT}\nonumber \\= & {} C_{0} \frac{a(e^{bT}-1)}{bI_{m}} \left( \frac{e^{-\frac{N+1}{N}RH}-1}{e^{-\frac{RH}{N}}-1}\right) \end{aligned}$$

(12)

Holding Cost

Holding cost in RW

$$\begin{aligned} C_{RW}= & {} h_{r}\int _{0}^{t_{w}}I_{R}(t)dt\nonumber \\= & {} \frac{ah_{r}}{\beta +b}\left\{ \frac{1}{b}(1-e^{bt_{w}})+ \frac{1}{\beta }(e^{(\beta +b)t_{w}}-e^{bt_{w}})\right\} \end{aligned}$$

(13)

Holding cost in OW

$$\begin{aligned} C_{OW}= & {} h_{0}\left\{ \int _{0}^{t_{w}}I_{0}(t)dt + \int _{t_{w}}^{t_{1}}I_{0}(t)dt\right\} \nonumber \\= & {} \frac{h_{0}W}{\alpha }(1-e^{-\alpha t_{w}})+ \frac{h_{0}a}{\alpha +b}\left\{ \frac{1}{\alpha }(e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{1}})+ \frac{1}{b}(e^{bt_{w}}-e^{bt_{1}})\right\} \qquad \end{aligned}$$

(14)

Total holding cost

$$\begin{aligned} C_{TOT}= & {} C_{RW}+C_{OW}\nonumber \\= & {} \frac{ah_{r}}{b \beta (\beta +b)}\left\{ \beta (1-e^{bt_{w}})+b (e^{(\beta +b)t_{w}}-e^{bt_{w}})\right\} +\frac{h_{0}}{b \alpha (\alpha +b)} \left\{ b(\alpha +b)W\right. \nonumber \\&\left. (1-e^{-\alpha t_{w}})+ ab(e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{1}})+ a \alpha (e^{bt_{w}}-e^{bt_{1}})\right\} \end{aligned}$$

(15)

Total holding cost over planning horizon under inflation and time value of money consideration is

$$\begin{aligned} C_{HOL}= & {} \sum _{J=0}^{N-1}\left[ \frac{ah_{r}}{b \beta (\beta +b)}\{ \beta (1-e^{bt_{w}})+b (e^{(\beta +b)t_{w}}-e^{bt_{w}})\}+\frac{h_{0}}{b \alpha (\alpha +b)} \{b(\alpha +b)\right. W\nonumber \\&\left. (1-e^{-\alpha t_{w}})+ ab(e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{1}})+ a \alpha (e^{bt_{w}}-e^{bt_{1}})\}\right] e^{-JRT}\nonumber \\= & {} \left[ \frac{ah_{r}}{b \beta (\beta +b)}\{ \beta (1-e^{bt_{w}})+b (e^{(\beta +b)t_{w}}-e^{bt_{w}})\}+\frac{h_{0}}{b \alpha (\alpha +b)} \{b(\alpha +b)W\right. \nonumber \\&\left. (1-e^{-\alpha t_{w}})+ ab(e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{1}})+ a \alpha (e^{bt_{w}}-e^{bt_{1}})\}\right] \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(16)

Now $T=\frac{H}{N}$ and $t_{1}=\frac{FH}{N}$ yields to:

$$\begin{aligned} C_{HOL}= & {} \left[ \frac{ah_{r}}{b \beta (\beta +b)}\left\{ \beta (1-e^{bt_{w}})+b (e^{(\beta +b)t_{w}}-e^{bt_{w}})\right\} +\frac{h_{0}}{b \alpha (\alpha +b)}\right. \nonumber \\&\times \left\{ b(\alpha +b)W(1-e^{-\alpha t_{w}})+ ab\left( e^{\alpha \left( \frac{FH}{N}-t_{w}\right) +b\frac{FH}{N}}-e^{b\frac{FH}{N}}\right) \right. \nonumber \\&\left. \left. +\, a \alpha \left( e^{bt_{w}}-e^{b\frac{FH}{N}}\right) \right\} \right] \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(17)

Shortage Cost

Average shortage S should be determined at first.

$$\begin{aligned} S= & {} \frac{1}{2} \int _{t_{1}}^{T}\frac{a}{\delta +b}\left( e^{bT}-e^{\delta (t_{1}-T)+bt_{1}}\right) dt \end{aligned}$$

(18)

$T=\frac{H}{N}$ and $t_{1}=\frac{FH}{N}$ yields to:

$$\begin{aligned} S= & {} \frac{a}{2(\delta +b)}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}- \frac{H}{N}\right) +b \frac{FH}{N}}\right) \left( \frac{H}{N}-\frac{FH}{N}\right) \end{aligned}$$

(19)

Total shortage cost over planning horizon under time value of money and inflation is

$$\begin{aligned} C_{SHO}= & {} \sum _{J=0}^{N-1}c_{s}e^{-JRT}S\nonumber \\= & {} \frac{ac_{s}}{2(\delta +b)}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}- \frac{H}{N}\right) + b \frac{FH}{N}}\right) \left( \frac{H}{N}-\frac{FH}{N}\right) \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(20)

Purchasing Cost

The purchasing cost of jth cycle $C_{pj}$ is being calculated at first. $T=\frac{H}{N}$ and $t_{1}=\frac{FH}{N}$ yields to:

$$\begin{aligned} C_{pj}= & {} \left\{ \frac{ca}{\beta +b}(e^{(\beta +b)t_{w}}-1)+ cW\right\} +\left\{ \frac{ca}{\delta +b}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) + b\frac{FH}{N}}\right) e^{\frac{-RH}{N}}\right\} \qquad \quad \end{aligned}$$

(21)

Total purchasing cost over the planning horizon under inflation and time value of money is

$$\begin{aligned} C_{PUR}= & {} \sum _{J=0}^{N-1}C_{pj}e^{-JRT}\nonumber \\= & {} \left\{ \frac{ca}{\beta +b}(e^{(\beta +b)t_{w}}-1)+ cW\right\} \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \nonumber \\&+\left\{ \frac{ca}{\delta +b}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) + b\frac{FH}{N}}\right) e^{\frac{-RH}{N}}\right\} \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(22)

Interest Earned and Charged ($M<t_{w}<t_{1}$)

Since $M<t_{w}<t_{1}$, the retailer sells the items and continues to accumulate sales revenue and earns interest with rate $I_{e}$ during time 0 to M. Again, the retailer starts paying interest for the items in stock after time M with rate $I_{p}$.

Interest earned:

As the items are sold, so the sales revenue is used to earn interest. At the beginning of the time interval, the back ordered quantity which is $I_{s}$, should be replenished first and the maximum accumulated sold until M is equal to $\int _{0}^{M}Dtdt$. $T=\frac{H}{N}$ and $t_{1}=\frac{FH}{N}$ yields to:

$$\begin{aligned} IE= & {} I_{e}s\left[ I_{s}M+\int _{0}^{M}D t dt\right] \nonumber \\= & {} I_{e}s\left[ \frac{a}{\delta + b}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) +b\frac{F H}{N}}\right) M+ \frac{a}{b^{2}}\left( M be^{bM}-e^{bM}+1\right) \right] \end{aligned}$$

(23)

Total interest earned over the planning horizon under inflation and time value of money is

$$\begin{aligned} TIE= & {} \sum _{J=0}^{N-1}IE e^{-JRT}\nonumber \\= & {} I_{e}s\left[ \frac{a}{\delta + b}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) +b\frac{F H}{N}}\right) M+ \frac{a}{b^{2}}\left( M be^{bM}-e^{bM}+1\right) \right] \nonumber \\&\quad \times \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(24)

Interest charged

Interest payable is

$$\begin{aligned} IC= & {} I_{c}c\int _{M}^{t_{1}}I(t)dt\nonumber \\= & {} I_{c}c\left\{ \int _{M}^{t_{w}}I_{R}(t)dt+\int _{M}^{t_{w}}I_{0}(t)dt+\int _{t_{w}}^{t_{1}}I(t)dt\right\} \nonumber \\= & {} I_{c}c\left[ \frac{a}{(\beta + b)\beta b}\left\{ b\left( e^{\beta (t_{w}-M)+bt_{w}}-e^{bt_{w}}\right) + \beta \left( e^{bM}-e^{bt_{w}}\right) \right\} +\frac{W}{\alpha }\left( e^{-\alpha M}\right. \right. \nonumber \\&\left. \left. -e^{-\alpha t_{w}}\right) +\frac{a}{(\alpha + b)\alpha b}\left\{ b\left( e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{1}}\right) + \alpha \left( e^{bt_{w}}-e^{bt_{1}}\right) \right\} \right] \end{aligned}$$

(25)

Total interest payable over the planning horizon under inflation and time value money is (putting $T=\frac{H}{N}$ and $t_{1}=\frac{FH}{N}$)

$$\begin{aligned} TIC= & {} \sum _{J=0}^{N-1}IC e^{-JRT}\nonumber \\= & {} I_{c}c\left[ \frac{a}{(\beta + b)\beta b}\left\{ b\left( e^{\beta (t_{w}-M)+bt_{w}}-e^{bt_{w}}\right) + \beta \left( e^{bM}-e^{bt_{w}}\right) \right\} \right. \nonumber \\&+\frac{W}{\alpha }\left( e^{-\alpha M}-e^{-\alpha t_{w}}\right) +\frac{a}{(\alpha + b)\alpha b}\left\{ b\left( e^{\alpha \left( \frac{FH}{N}-t_{w}\right) +b\frac{FH}{N}}\right. \right. \nonumber \\&\left. \left. \left. -\,e^{b\frac{FH}{N}}\right) + \alpha \left( e^{bt_{w}}-e^{b\frac{FH}{N}}\right) \right\} \right] \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(26)

So the total cost function is

$$\begin{aligned} TC(F)= & {} C_{SET}+C_{HOL}+C_{SHO}+C_{PUR}+TIC-TIE\nonumber \\= & {} C_{0} \frac{a(e^{b\frac{H}{N}}-1)}{bI_{m}}\left( \frac{e^{-\frac{N+1}{N}RH}-1}{e^{-\frac{RH}{N}}-1}\right) +\left[ \frac{ah_{r}}{b \beta (\beta +b)}\left\{ \beta (1-e^{bt_{w}})+b \left( e^{(\beta +b)t_{w}}\right. \right. \right. \nonumber \\&\left. \left. -\,e^{bt_{w}}\right) \right\} +\frac{h_{0}}{b \alpha (\alpha +b)}\left\{ b(\alpha +b)W(1-e^{-\alpha t_{w}})+ ab\left( e^{\alpha \left( \frac{FH}{N}-t_{w}\right) +b\frac{FH}{N}}\right. \right. \nonumber \\&\left. \left. -\,e^{b\frac{FH}{N}}\right) + a \alpha \left( e^{bt_{w}}-e^{b\frac{FH}{N}}\right) \right\} +\frac{ac_{s}}{2(\delta +b)}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}- \frac{H}{N}\right) +\frac{bFH}{N}}\right) \nonumber \\&\left( \frac{H}{N}-\frac{FH}{N}\right) + \left\{ \frac{ca}{\beta +b}\left( e^{(\beta +b)t_{w}}-1\right) + cW\right\} +\left\{ \frac{ca}{\delta +b}\left( e^{\frac{bH}{N}}\right. \right. \nonumber \\&\left. \left. -\,e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) + b\frac{FH}{N}}\right) e^{\frac{-RH}{N}}\right\} +I_{c}c\left[ \frac{a}{(\beta + b)\beta b}\left\{ b\left( e^{\beta (t_{w}-M)+bt_{w}}-e^{bt_{w}}\right) + \beta \right. \right. \nonumber \\&\left. (e^{bM}-e^{bt_{w}})\right\} +\frac{W}{\alpha }\left( e^{-\alpha M}-e^{-\alpha t_{w}}\right) +\frac{a}{(\alpha + b)\alpha b}\left\{ b\left( e^{\alpha \left( \frac{FH}{N}-t_{w}\right) +b\frac{FH}{N}}\right. \right. \nonumber \\&\left. \left. \left. -\,e^{b\frac{FH}{N}}\right) + \alpha \left( e^{bt_{w}-e^{b\frac{FH}{N}}}\right) \right\} \right] -I_{e}s\left\{ \frac{a}{\delta + b}\left( e^{\frac{bH}{N}}-e^{\delta \left( \frac{FH}{N}-\frac{H}{N}\right) +b\frac{F H}{N}}\right) M\right. \nonumber \\&\left. \left. + \frac{a}{b^{2}}\left( M be^{bM}-e^{bM}+1\right) \right\} \right] \left[ \frac{e^{-RH}-1}{e^{\frac{-RH}{N}}-1}\right] \end{aligned}$$

(27)

Notably, the values of $I_{0}(t_{w})$ and $I({t_{w}})$ should coincide and thus

$I_{0}(t_{w})= W e^{- \alpha t_{w}}= \frac{a}{\alpha + b}(e^{\alpha (t_{1}-t_{w})+bt_{1}}-e^{bt_{w}})$

Therefore we get

$t_{w}= \frac{1}{b}log\frac{ae^{(\alpha +b)t_{1}}-(\alpha +b)W}{a}$

Since, the total cost function is very large in volume and too much complex to differentiate by hand, so we solved it numerically by Mathematica Software. So the sufficient condition for $\frac{\partial ^{2} TC(F)}{\partial F^{2}}> 0$ must be satisfied.

Numerical Example

To illustrate the proposed model, we consider the two examples given below.

Example 1

Let us take the parameter values in the inventory system as $h_{0}$ = $0.2, $h_{r}$ = $0.5, $c_{s}$ = $0.3, c = $5, $C_{0}$ = $50, W = 30, $\alpha$ = 0.02, $\beta$ = 0.8, $R= 0.5$, H = 3, N = 7, $\delta$ = 0.9, $I_{c}$= $0.1, $I_{e}$= $0.06, M = $\frac{1}{12}$, a = 300, b = 2, s = $5 in appropriate units. The optimal solution is $TC(F^{*})=4045.14$, $F^{*}= 0.438$ (Fig. 2).

Fig. 2

Total cost function TC versus F of Example 1

$T=\frac{H}{N}=\frac{3}{7}$, $T_{w}=0.115$, $t_{a}=0.091$, $I_{m}=70.783$, $I_{b}=122.533$, $t_{1}=F^{*}T=0.188$.

In this case, some other numerical examples have been prepared based on changing $\alpha$, $\beta$, R, M with different values of N and taking one parameter at a time and keeping the remaining parameters at their original levels. The result of this numerical analysis are shown in Table 1.

Table 1 Some numerical examples on the data set of Example 1

Example 2

Let us take the parameter values in the inventory system as $h_{0}$ = $0.2, $h_{r}$ = $0.5, $c_{s}$ = $0.3, c = $5, $C_{0}$ = $150, W = 30, $\alpha$ = 0.02, $\beta$ = 0.8, $R= 0.3$, H = 5, N = 9, $\delta$ = 0.9, $I_{c}$= $0.1, $I_{e}$= $0.08, M = $\frac{1}{15}$, a = 200, b = 2, s = $7 in appropriate units. The optimal solution is $TC(F^{*})$=6357.7, $F^{*}= 0.638$ (Figs. 3, 4, 5).

Fig. 3

Total cost function TC versus F of Example 2

Fig. 4

Showing some best results of Example 1

Fig. 5

Showing some best results of Example 2

$T=\frac{H}{N}=\frac{5}{9}$, $T_{w}=0.278$, $t_{a}=0.131$, $I_{m}=114.08$, $I_{b}=92.57$, $t_{1}=F^{*}T=0.354$.

In this case, some other numerical examples have been prepared based on changing $\alpha$, $\beta$, R, M with different values of N and taking one parameter at a time and keeping the remaining parameters at their original levels. The result of this numerical analysis are shown in Table 2.

Table 2 Some numerical examples on the data set of Example 2

Table 3 Sensitivity analysis of Examples 1 and 2

Sensitivity Analysis

Using the numerical Examples 1 and 2 the sensitivity of the decision variable $F^{*}$ and the total cost function $TC(F^{*})$ to changes in each of the 12 parameters $h_{o}$, $h_{r}$, $\alpha$, $\beta$, $C_{0}$, R, $c_{s}$, $\delta$, $I_{c}$,$I_{e}$, a, b is examined in Table 3. The sensitivity analysis is performed by changing each of the parameters by − 50, − 20, + 20 and + 50 %, taking one parameter at a time and keeping the remaining parameters unchanged. It is observed that parameters $C_{0}$, R, a and b are highly sensitive and the parameters $h_{o}$, $h_{r}$, $\alpha$, $\beta$, $c_{s}$, $\delta$, $I_{c}$, $I_{e}$ are slightly sensitive on total cost $TC(F^{*})$. Again, the total cost function $TC(F^{*})$ increases or decreases as the parameters $h_{o}$, $h_{r}$, $\alpha$, $\beta$, $C_{0}$, $c_{s}$, $I_{c}$, a, b increases or decreases whereas the other parameters have reverse effect on total cost function.

Conclusions

Practically, we see that credit policies is an attractive feature in inventory management in order to purchase more items than in a rented warehouse capacity. Thus our research work deals with the optimal replenishment cycle for a two warehouse inventory model where delay in payment is permissible. Some realistic features like effect of inflation and time value of money, different deterioration rate in OW and RW, shortages and partial backlogging are investigated. Also, holding cost in RW has been assumed higher than in OW. The present value of total cost during planning horizon under exponential increasing demand in this inventory system has been developed. Finally, the proposed model has been illustrated through several numerical examples and sensitivity analysis.

• 1. We could extend this model considering time-price or quadratic price dependent demand or stochastically fluctuating demand pattern.

• 2. We could extend this model again by considering fuzzy, fuzzy-stochastic environment and other asMonday, February 5, 2018 at 11:22 amsumption.

Appendix A

From Eq. (3) we obtain order quantity $Q=I(0)=\frac{a}{\alpha + b}(e^{(\alpha + b)t_{1}}-1)$ and if the order quantity $Q\le W$ then it is unnecessary to rent any warehouse. Thus $\frac{a}{\alpha + b}(e^{(\alpha + b)t_{1}}-1)\le W$ implies $t_{1} \le \frac{1}{\alpha + b}log(1+\frac{(\alpha + b)W }{a})$. For simplicity, let $t_{a}=\frac{1}{\alpha + b}log(1+\frac{(\alpha + b)W }{a})$. The inequality $Q\le W$ holds if and only if $t_{a}\ge t_{1}$. Therefore, the inequality $Q>W$ holds if and only if $t_{a}< t_{1}$ which implies that there are W units of items stored in OW and the remainder are despatched in RW.