1 Introduction

Due to the fact that high-order Hopfield neural networks (HHNNs) have stronger approximation property, faster convergence rate, greater storage capacity, and higher fault tolerance than lower-order ones, numerous works have intensively analyzed HHNNs in recent years. In particular, there have been many results on the problem of the existence and stability of equilibrium points, periodic solutions and almost periodic solutions of HHNNs in the literatures. We refer the reader to [1–9] and the references cited therein. In [1], the problem about global exponential stability properties of high-order Hopfield-type neural networks was studied applying Lyapunov functions; in [2], the authors derived some sufficient conditions for the global asymptotic stability of equilibrium points of HHNNs with constant time delays in terms of linear matrix inequality.

It is natural and important that, when describe and model the dynamics for a complex neural reaction [10], some information about the derivative of the past state should be included. Many works investigated the dynamical behaviors of neutral type neural networks. For example, stabilities, periodic solutions, almost periodic solutions and pseudo almost periodic solutions for different classes of neutral type neural networks were studied in [11–16].

It is well known that time delays inevitably exist in biological and artificial neural networks because of the finite switching speed of neurons and amplifiers [17–19], which can also affect the stability of the systems and may lead to some complex dynamical behaviors such as oscillation, chaos and instability. In [20] the mixed time-varying delays were taken into account when modeling realistic neural networks. Moreover, the leakage delay as a type of time delay in the leakage term of the systems and as a considerable factor affecting dynamics for the worse in the systems, is being introduced to the problem studying stability for neural networks. Such time delay in the leakage term is difficult to handle, however, it has great impact to the dynamical behavior [21–27]. It is significant to discuss neural networks with time delays in the leakage term.

In history, both continuous-time and discrete-time neural networks are important in various applications. In Hilger’s Ph.D. dissertation [28], the theory of time scales was initiated, which can unify the continuous and discrete systems. Since then, many works have studied the dynamics of neural networks on time scales [15, 29–31]. In [30], for a class of neutral type HHNNs with delays in leakage terms on time scales, some sufficient conditions for the existence and global exponential stability of almost automorphic solutions were obtained; in [31], for competitive neural networks with delays in the leakage terms on time scales, the existence and global exponential stability of anti-periodic solutions were investigated.

The concept of pseudo almost periodicity, which is the central subject of this paper, was introduced by Zhang [32]. Dads et al. in [33] pointed out that it would be of great interest to study the dynamics of pseudo almost periodic systems with time delays. Pseudo almost periodic solutions, which are more general and complicated than periodic and almost periodic solutions, in the context of differential equations were studied in [16, 34–49]. The work of [48] studied the existence and the global exponential stability of positive pseudo almost periodic solutions. In [49], using the exponential dichotomy theory and the contraction mapping fixed point theorem, the existence and uniqueness of pseudo almost periodic solutions of the shunting inhibitory cellular neural networks with time-varying delays in the leakage terms were discussed. However, few papers are available for the existence of pseudo almost periodic solutions for discrete time neural networks with or without delays.

Li and Wang [50] proposed recently the concept of pseudo almost periodic functions on time scales. There are few works on the existence and stability of pseudo almost periodic solutions for neural networks of neutral type with mixed time-varying delays and leakage delays on time scales, which have importance in theories and applications, and is a challenging problem.

In this paper, we propose a neutral type high-order Hopfield neural network with mixed time-varying delays and leakage delays on time scales:

$$\begin{aligned} x_{i}^{\nabla }(t)& = -c_{i}(t)x_{i}(t-\delta _{i}(t))+\sum _{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t))\nonumber \\&\quad+\sum _{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau _{ij}(t))) \\ & \quad +\sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}h_{j}(x_{j}^{\nabla }(s))\nabla s\nonumber \\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(t)k_{j}(x_{j}(t-\xi _{ijl}(t)))k_{l}(x_{l}(t-\zeta _{ijl}(t))) \\ & \quad +I_{i}(t),\,\,t\in \mathbb {T}, \end{aligned}$$
(1)

where \(\mathbb {T}\) is an almost periodic time scale, \(i=1,2,\ldots ,n\), n corresponding to the number of units in a neural network; \(x_{i}(t)\) is the activation of the ith neuron at time t; \(c_{i}(t)>0\) represents the rate at which the ith unit resets its potential to the resting state in isolation when disconnected from the network and external inputs at time t; \(a_{ij}(t)\), \(b_{ij}(t)\) and \(d_{ij}(t)\) are the delayed strengths of connectivity, neutral delayed strengths of connectivity between cell i and j at time t, respectively; \(T_{ijl}(t)\) denotes the second-order connection weight of the neural network; \(f_{j}\), \(g_{j}\), \(h_{j}\) and \(k_{j}\) are called the activation functions in the system; \(I_{i}(t)\) is an external input to the ith unit at time t; \(\delta _{i}\) denotes the leakage delay satisfying \(t-\delta _{i}(t)\in \mathbb {T}\); \(\tau _{ij}\), \(\sigma _{ij}\), \(\xi _{ijl}\) and \(\zeta _{ijl}\) are transmission delays satisfying \(t-\tau _{ij}(t)\in \mathbb {T}\) , \(t-\sigma _{ij}(t)\in \mathbb {T}\), \(t-\xi _{ijl}(t)\in \mathbb {T}\), \(t-\zeta _{ijl}(t)\in \mathbb {T}\) with \(t\in \mathbb {T}\).

Let \([a,b]_{\mathbb {T}}=\{t|t\in [a,b]\cap \mathbb {T}\}\). We also need the following notations:

$$\begin{aligned}&c_{i}^{+}=\sup \limits _{t\in \mathbb {T}}|c_{i}(t)|,\,\,\,c_{i}^{-}=\inf \limits _{t\in \mathbb {T}}|c_{i}(t)|,\,\,\, \delta _{i}^{+}=\sup \limits _{t\in \mathbb {T}}|\delta _{i}(t)|,\,\,\,\tau _{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\tau _{ij}(t)|,\\&\sigma _{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\sigma _{ij}(t)|,\,\,\, \xi _{ijl}^{+}=\sup \limits _{t\in \mathbb {T}}|\xi _{ijl}(t)|,\,\,\, \zeta _{ijl}^{+}=\sup \limits _{t\in \mathbb {T}}|\zeta _{ijl}(t)|,\,\,\,a_{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|a_{ij}(t)|,\\&b_{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|b_{ij}(t)|,\,\,\,d_{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|d_{ij}(t)|,\,\,\, T_{ijl}^{+}=\sup \limits _{t\in \mathbb {T}}|T_{ijl}(t)|, \,\,i,j,l=1,2,\ldots ,n. \end{aligned}$$

The initial condition of the system (1) is of the form

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s),\,\, x_{i}^{\nabla }(s)=\varphi _{i}^{\nabla }(s),\,\,\,s\in [-\theta ,0]_{\mathbb {T}}, \end{aligned}$$
(2)

where \(\theta =\max \{\delta ,\tau ,\sigma ,\xi ,\zeta \}\), \(\delta =\max \nolimits _{1\le i\le n}\{\delta _{i}^{+}\}\), \(\tau =\max \nolimits _{1\le i,j\le n}\{\tau _{ij}^{+}\}\), \(\sigma =\max \nolimits _{1\le i,j\le n}\{\sigma _{ij}^{+}\}\), \(\xi =\max \nolimits _{1\le i,j,l\le n}\{\xi _{ijl}^{+}\}\), \(\zeta =\max \nolimits _{1\le i,j,l\le n}\{\zeta _{ijl}^{+}\}\), \(i,j,l=1,2,\ldots ,n\). \(\varphi _{k}(\cdot )\) is a real-valued bounded \(\nabla \)-differentiable function defined on \([-\theta ,0]_{\mathbb {T}}\).

We organize the paper as follows. In Sect. 2, we introduce some definitions, as preparations for later sections. We also extend the almost periodic theory on time scales with the delta derivative to that with the nabla derivative. We present some sufficient conditions for the existence of pseudo almost periodic solutions of (1) in Sect. 3, applying some Banach’s fixed point theorem and the theory of calculus on time scales. In Sect. 4, we prove that the pseudo almost periodic solution obtained in the previous section is globally exponentially stable. In Sect. 5, we demonstrate the feasibility of our results by an example. We make a conclusion in Sect. 6.

Remark 1.1

This is the first time to study the pseudo almost periodic solutions of system (1). Since it is a \(\nabla \)-dynamic system on time scales, the results obtained in [15, 29, 30, 50, 53, 54] concerning the \(\triangle \)-dynamic systems cannot be directly applied to (1). Besides, since it studies almost periodic problem, although paper [56] deals with \(\nabla \)-dynamic systems on time scales, its results also cannot be directly applied to (1).

2 Preliminaries

In this section, we shall first recall some fundamental definitions and lemmas. Also, we extend the pseudo almost periodic theory on time scales with the delta derivative to that with the nabla derivative.

A time scale \(\mathbb {T}\) is an arbitrary nonempty closed subset of the real number set \(\mathbb {R}\) with the topology and ordering inherited from \(\mathbb {R}\). The forward jump operator \(\sigma :\mathbb {T}\rightarrow \mathbb {T}\) is defined by \(\sigma (t)=\inf \big \{s\in \mathbb {T},s>t\big \}\) for all \(t\in \mathbb {T}\), while the backward jump operator \(\rho :\mathbb {T}\rightarrow \mathbb {T}\) is defined by \(\rho (t)=\sup \big \{s\in \mathbb {T},s<t\big \}\) for all \(t\in \mathbb {T}\).

A point \(t\in \mathbb {T}\) is called left-dense if \(t>\inf \mathbb {T}\) and \(\rho (t)=t\), left-scattered if \(\rho (t)<t\), right-dense if \(t<\sup \mathbb {T}\) and \(\sigma (t)=t\), and right-scattered if \(\sigma (t)>t\). If \(\mathbb {T}\) has a left-scattered maximum m, then \(\mathbb {T}^k=\mathbb {T}\setminus \{m\}\); otherwise \(\mathbb {T}^k=\mathbb {T}\). If \(\mathbb {T}\) has a right-scattered minimum m, then \(\mathbb {T}_k=\mathbb {T}\setminus \{m\}\); otherwise \(\mathbb {T}_k=\mathbb {T}\). Finally, the backwards graininess function \(\nu : \mathbb {T}_{k}\rightarrow [0,\infty )\) is defined by \(\nu (t)=t-\rho (t)\).

A function \(f:\mathbb {T}\rightarrow \mathbb {R}\) is ld-continuous provided it is continuous at left-dense point in \(\mathbb {T}\) and its right-side limits exist at right-dense points in \(\mathbb {T}\).

Definition 2.1

[51, 52] Let \(f:\mathbb {T} \rightarrow \mathbb {R}\) be a function and \(t\in \mathbb {T}_{k}\). Then we define \(f^{\nabla }(t)\) to be the number (provided its exists) with the property that given any \(\varepsilon >0\), there is a neighborhood U of t (i.e, \(U=(t-\delta ,t+\delta )\cap \mathbb {T}\) for some \(\delta>\)0) such that

$$\begin{aligned} |f(\rho (t))-f(s)-f^{\nabla }(t)(\rho (t)-s)|\le \varepsilon |\rho (t)-s| \end{aligned}$$

for all \(s\in U\), we call \(f^{\nabla }(t)\) the nabla derivative of f at t.

Let \(f:\mathbb {T} \rightarrow \mathbb {R}\) be ld-continuous. If \(F^{\nabla }(t)=f(t)\), then we define the nabla integral by \(\int _a^{b}f(t)\nabla t=F(b)-F(a)\).

A function \(p:\mathbb {T}\rightarrow \mathbb {R}\) is called \(\nu \)-regressive if \(1-\nu (t)p(t)\ne 0\) for all \(t\in \mathbb {T}_k\). The set of all \(\nu \)-regressive and left-dense continuous functions \(p:\mathbb {T}\rightarrow \mathbb {R}\) will be denoted by \(\mathcal {R}_{\nu }=\mathcal {R}_{\nu }(\mathbb {T})=\mathcal {R}_{\nu }(\mathbb {T},\mathbb {R})\). We define the set \(\mathcal {R}_{\nu }^{+}=\mathcal {R}_{\nu }^{+}(\mathbb {T},\mathbb {R})=\{p\in \mathcal {R}_{\nu }:1-\nu (t)p(t)>0,\,\,\forall t\in \mathbb {T}\}\).

If \(p\in \mathcal {R}_{\nu }\), then we define the nabla exponential function by

$$\begin{aligned} \hat{e}_{p}(t,s)=\exp \bigg (\int _{s}^{t}\hat{\xi }_{\nu (\tau )}\big (p(\tau )\big )\nabla \tau \bigg ),\quad \mathrm {for}\,\,t,s\in \mathbb {T} \end{aligned}$$

with the \(\nu \)-cylinder transformation

$$\begin{aligned} \hat{\xi }_h(z)=\bigg \{\begin{array}{ll} -\frac{\mathrm {log}(1-hz)}{h} &\mathrm{if}\,h\ne 0,\\ z &\mathrm{if}\,h=0.\\ \end{array} \end{aligned}$$

Let \(p,q\in \mathcal {R}_{\nu }\), then we define a circle plus addition by \((p \oplus _{\nu } q)(t)= p(t)+q(t)-\nu (t) p(t)q(t)\), for all \(t\in \mathbb {T}_{k}\). For \(p\in \mathcal {R}_{\nu }\), define a circle minus p by \(\ominus _{\nu } p=-\frac{p}{1-\nu p}\).

Lemma 2.2

[51, 52] Let \(p,q\in \mathcal {R}_{\nu }\), and \(s,t,r\in \mathbb {T}\). Then

  1. (i)

    \(\hat{e}_{0}(t,s)\equiv 1\) and \(\hat{e}_{p}(t,t)\equiv 1\);

  2. (ii)

    \(\hat{e}_{p}(\rho (t),s)=(1-\nu (t)p(t))\hat{e}_{p}(t,s)\);

  3. (iii)

    \(\hat{e}_{p}(t,s)=\frac{1}{\hat{e}_{p}(s,t)}=\hat{e}_{\ominus _{\nu } p}(s,t)\);

  4. (iv)

    \(\hat{e}_{p}(t,s)\hat{e}_{p}(s,r)=\hat{e}_{p}(t,r)\);

  5. (v)

    \((\hat{e}_{p}(t,s))^{\nabla }=p(t)\hat{e}_{p}(t,s)\).

Lemma 2.3

[51, 52] Let f, g be nabla differentiable functions on \(\mathbb {T}\), then

  1. (i)

    \((v_{1}f+v_{2}g)^{\nabla }=v_{1}f^{\nabla }+v_{2}g^{\nabla }\), for any constants \(v_{1},v_{2}\);

  2. (ii)

    \((fg)^{\nabla }(t)=f^{\nabla }(t)g(t)+f(\rho (t))g^{\nabla }(t)=f(t)g^{\nabla }(t)+f^{\nabla }(t)g(\rho (t))\);

  3. (iii)

    If f and \(f^{\nabla }\) are continuous, then \((\int _{a}^{t}f(t,s)\nabla s)^{\nabla }=f(\rho (t),t)+\int _{a}^{t}f(t,s)\nabla s.\)

Lemma 2.4

[51, 52] Assume \(p\in \mathcal {R}_{\nu }\) and \(t_{0}\in \mathbb {T}\). If \(1-\nu (t)p(t)>0\) for \(t\in \mathbb {T}\), then \(\hat{e}_{p}(t,t_{0})>0\) for all \(t\in \mathbb {T}\).

Lemma 2.5

Suppose that f(t) is an ld-continuous function and c(t) is a positive ld-continuous function which satisfies that \(c(t)\in \mathcal {R}_{\nu }^{+}\). Let

$$\begin{aligned} g(t)=\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s, \end{aligned}$$

where \(t_{0}\in \mathbb {T}\), then

$$\begin{aligned} g^{\nabla }(t)=f(t)-c(t)\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s. \end{aligned}$$

Proof

$$\begin{aligned} g^{\nabla }(t)& = \bigg (\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s\bigg )^{\nabla }\\& = \bigg (\hat{e}_{-c}(t,t_{0})\int _{t_{0}}^{t}\hat{e}_{-c}(t_{0},\rho (s))f(s)\nabla s\bigg )^{\nabla }\\& = \hat{e}_{-c}(\rho (t),t_{0})\hat{e}_{-c}(t_{0},\rho (t))f(t)-c(t)\hat{e}_{-c}(t,t_{0})\int _{t_{0}}^{t}\hat{e}_{-c}(t_{0},\rho (s))f(s)\nabla s\\& = f(t)-c(t)\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s. \end{aligned}$$

The proof is complete. \(\square \)

Definition 2.6

[53, 54] A time scale \(\mathbb {T}\) is called an almost periodic time scale if

$$\begin{aligned} \Pi :=\{\tau \in \mathbb {R}:t\pm \tau \in \mathbb {T}, \forall t\in \mathbb {T}\}\ne \{0\}. \end{aligned}$$

Definition 2.7

Let \(\mathbb {T}\) be an almost periodic time scale. A function \(f \in C(\mathbb {T},\mathbb {R}^{n})\) is called an almost periodic on \(\mathbb {T}\), if for any \(\varepsilon>\)0, the set

$$\begin{aligned} E(\varepsilon ,f)=\{{\tau \in \Pi :|f(t+\tau )-f(t)|<\varepsilon ,\forall t\in \mathbb {T}}\} \end{aligned}$$

is relatively dense; that is, for any given \(\varepsilon >0\), there exists a constant \(l(\varepsilon )>0\) such that each interval of length \(l(\varepsilon )\) contains at least one \(\tau =\tau (\varepsilon )\in E(\varepsilon ,f)\) such that

$$\begin{aligned} |f(t+\tau )-f(t)|<\varepsilon ,\,\, \forall t\in \mathbb {T}. \end{aligned}$$

The set \(E(\varepsilon ,f)\) is called the \(\varepsilon \)-translation set of f(t), \(\tau \) is called the \(\varepsilon \)-translation number of f(t) and \(l(\varepsilon )\) is called the contain interval length of \(E(\varepsilon ,f)\).

Let \(AP(\mathbb {T})=\{f\in C(\mathbb {T},\mathbb {R}^{n})\): f is almost periodic} and \(BC(\mathbb {T},\mathbb {R}^{n})\) denote the space of all bounded continuous functions from \(\mathbb {T}\) to \(\mathbb {R}^{n}\). Define the class of functions \(PAP_{0}(\mathbb {T})\) as follows:

$$\begin{aligned} PAP_{0}(\mathbb {T})& = \bigg \{f\in BC(\mathbb {T},\mathbb {R}^{n}):f\,\,is\,\,\nabla -measurable\,\,such\,\, that\\&\quad\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|f(s)|\nabla s=0,\,\,where\,\,t_{0}\in \mathbb {T}, r\in \Pi \bigg \}. \end{aligned}$$

Similar to Definition 4.1 in [50], we give

Definition 2.8

A function \(f\in C(\mathbb {T},\mathbb {R}^{n})\) is called pseudo almost periodic if \(f=g+\phi \), where \(g\in AP(\mathbb {T})\) and \(\phi \in PAP_{0}(\mathbb {T})\). Denote by \(PAP(\mathbb {T})\), the set of pseudo almost periodic functions.

By Definition 2.8, one can easily show that

Lemma 2.9

If \(f,g\in PAP(\mathbb {T})\), then \(f+g,fg\in PAP(\mathbb {T})\); if \(f\in PAP(\mathbb {T}),\, g\in AP(\mathbb {T})\), then \(fg\in PAP(\mathbb {T})\).

Lemma 2.10

If \(f\in C(\mathbb {R},\mathbb {R})\) satisfies the Lipschitcz condition, \(\varphi \in PAP(\mathbb {T})\), \(\theta \in C^1(\mathbb {T},\Pi )\) and \(\eta :=\inf \nolimits _{t\in \mathbb {T}}(1-\theta ^{\nabla }(t))>0\), then \(f(\varphi (t-\theta (t)))\in PAP(\mathbb {T})\).

Proof

From Definition 2.8, we have \(\varphi =\varphi _{1}+\varphi _{2}\), where \(\varphi _{1}\in AP(\mathbb {T})\) and \(\varphi _{2}\in PAP_{0}(\mathbb {T})\). Set

$$\begin{aligned} E(t)& = f(\varphi (t-\theta (t)))=f(\varphi _{1}(t-\theta (t)))+[f(\varphi _{1}(t-\theta (t))+\varphi _{2}(t-\theta (t)))-f(\varphi _{1}(t-\theta (t)))]\\:& = E_{1}(t)+E_{2}(t). \end{aligned}$$

Firstly, it follows from Theorem 2.11 in [53] that \(E_{1}\in AP(\mathbb {T})\). Next, we show that \(E_{2}\in PAP_{0}(\mathbb {T})\). Since

$$\begin{aligned}&\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|E_{2}(s)|\nabla s\\& \quad = \lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|f(\varphi _{1}(s-\theta (s))+\varphi _{2}(s-\theta (s))) -f(\varphi _{1}(s-\theta (s)))|\nabla s\\ & \quad \le \lim \limits _{r\rightarrow +\infty }\frac{L}{2r}\int _{t_{0}-r}^{t_{0}+r}|\varphi _{2}(s-\theta (s))|\nabla s \end{aligned}$$

and

$$\begin{aligned} 0\le & \frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|\varphi _{2}(s-\theta (s))|\nabla s\\& \quad= \frac{1}{2r}\int _{t_{0}-r-\theta (t_{0}-r)}^{t_{0}+r-\theta (t_{0}+r)}\frac{1}{1-\theta ^{\nabla }(s)}|\varphi _{2}(u)|\nabla u\\&\quad \le \frac{1}{\eta }\frac{r+\theta ^{+}}{r}\frac{1}{2(r+\theta ^{+})}\int _{t_{0}-(r+\theta ^{+})}^{t_{0}+r+\theta ^{+}}|\varphi _{2}(u)|\nabla u=0, \end{aligned}$$

\(E_{2}\in PAP_{0}(\mathbb {T})\). Thus \(E\in PAP(\mathbb {T})\). The proof is complete. \(\square \)

Similar to Definition 2.12 in [53], we give

Definition 2.11

Let A(t) be an \(n\times n\) matrix-valued function on \(\mathbb {T}\). Then the linear system

$$\begin{aligned} x^{\nabla }(t)=A(t)x(t),\quad t\in \mathbb {T} \end{aligned}$$
(3)

is said to admit an exponential dichotomy on \(\mathbb {T}\) if there exist positive constant \(K, \alpha \), projection P and the fundamental solution matrix X(t) of (3), satisfying

$$\begin{aligned} \Vert X(t)PX^{-1}(s)\Vert _{0} \le K\hat{e}_{\ominus _{\nu } \alpha }(t,s),\quad s, t \in \mathbb {T}, t \ge s,\\ \Vert X(t)(I-P)X^{-1}(s)\Vert _{0} \le K\hat{e}_{\ominus _{\nu } \alpha }(s,t),\quad s, t \in \mathbb {T}, t \le s, \end{aligned}$$

where \(\Vert \cdot \Vert _{0}\) is a matrix norm on \(\mathbb {T}\) (say, for example, if \(A=(a_{ij})_{n\times m}\), then we can take \(\Vert A\Vert _{0}=(\sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{m}|a_{ij}|^{2})^{\frac{1}{2}})\).

Consider the following pseudo almost periodic system:

$$\begin{aligned} x^{\nabla }(t)=A(t)x(t)+f(t),\,\, t \in \mathbb {T}, \end{aligned}$$
(4)

where A(t) is an almost periodic matrix function, f(t) is a pseudo almost periodic vector function. Similar to the proof of Theorem 5.2 in [50], we can get the following lemma.

Lemma 2.12

Suppose that A(t) is almost periodic, (3) admits an exponential dichotomy and function \(f\in PAP(\mathbb {T})\). Then (4) has a unique bounded solution \(x\in PAP(\mathbb {T})\) that can be expressed as follows:

$$\begin{aligned} x(t)=\int _{-\infty }^{t}X(t)PX^{-1}(\rho (s))f(s)\nabla s-\int _t^{+\infty }X(t)(I-P)X^{-1}(\rho (s))f(s)\nabla s, \end{aligned}$$

where X(t) is the fundamental solution matrix of (3).

Similar to the proof of Lemma 2.15 in [53], we have

Lemma 2.13

Let \(c_{i}:\mathbb {T}\rightarrow \mathbb {R}^{+}\) be a bounded ld-continuous function, \(c_{i}\in \mathcal {R}_{\nu }^{+}\) and \(\min \nolimits _{1\le i\le n}\{\inf \nolimits _{t\in \mathbb {T}}c_i(t)\}>0\). Then the linear system

$$\begin{aligned} x^{\nabla }(t)=\mathrm {diag}(-c_{1}(t),-c_{2}(t),\ldots ,-c_{n}(t))x(t) \end{aligned}$$

admits an exponential dichotomy on \(\mathbb {T}\).

3 Existence of pseudo almost periodic solutions

In this section, we will state and prove the sufficient conditions for the existence of pseudo almost periodic solutions of (1).

Let

$$\begin{aligned} \mathbb {B}=\big \{\varphi (t)=(\varphi _{1}(t),\varphi _{2}(t),\ldots ,\varphi _{n}(t))^{T}: \varphi _{i}(t),\varphi ^{\nabla }_{i}(t)\in PAP(\mathbb {T}),\quad i=1,2,\ldots ,n\big \} \end{aligned}$$

with the norm \(\Vert \varphi \Vert _{\mathbb {B}}=\sup \nolimits _{t\in \mathbb {T}}\Vert \varphi (t)\Vert \), where \(\Vert \varphi (t)\Vert =\max \nolimits _{1\le i\le n}\{|\varphi _{i}(t)|,|\varphi ^{\nabla }_{i}(t)|\}\), then \(\mathbb {B}\) is a Banach space.

Throughout the rest of this paper, we assume that the following conditions hold:

  • \((H_{1})\) \(c_{i}\in C(\mathbb {T},\mathbb {R}^{+})\) with \(c_{i}\in \mathcal {R}_{\nu }^{+}\) and \(c_i^->0\), where \(\mathcal {R}_{\nu }^{+}\) denotes the set of positively regressive functions from \(\mathbb {T}\) to \(\mathbb {R}\), \(i=1,2,\ldots ,n\);

  • \((H_{2})\) \(a_{ij},b_{ij},d_{ij},T_{ijl}\in AP(\mathbb {T})\), \(\delta _{i}\in C(\mathbb {T},\Pi ), \tau _{ij}, \sigma _{ij}, \xi _{ijl}, \zeta _{ijl}\in C^1(\mathbb {T},\Pi ),\inf \nolimits _{t\in \mathbb {T}}(1-\tau _{ij}^{\nabla }(t))>0, \inf \nolimits _{t\in \mathbb {T}}(1-\sigma _{ij}^{\nabla }(t))>0,\inf \nolimits _{t\in \mathbb {T}}(1-\xi _{ijl}^{\nabla }(t))>0,\inf \nolimits _{t\in \mathbb {T}}(1-\zeta _{ijl}^{\nabla }(t))>0\) and \(I_{i}\in PAP(\mathbb {T}), i,j,l=1,2,\ldots ,n\);

  • \((H_{3})\) Functions \(f_{j},g_{j},h_{j},k_{j}\in C(\mathbb {R},\mathbb {R})\) and there exist positive constants \(L_{j}^{f},L_{j}^{g},L_{j}^{h},L_{j}^{k}\) such that

    $$\begin{aligned} |f_{j}(u)-f_{j}(v)|\le L_{j}^{f}|u-v|, |g_{j}(u)-g_{j}(v)|\le L_{j}^{g}|u-v|, \end{aligned}$$
    $$\begin{aligned} |h_{j}(u)-h_{j}(v)|\le L_{j}^{h}|u-v|, |k_{j}(u)-k_{j}(v)|\le L_{j}^{k}|u-v|, \end{aligned}$$

    where \(u,v\in \mathbb {R}\) and \(f_{j}(0)=g_{j}(0)=h_{j}(0)=k_{j}(0)=0\),   \(j=1,2,\ldots ,n\).

Theorem 3.1

Let \((H_1)\)–\((H_{3})\) hold. Suppose that

  • \((H_{4})\) there exists a positive constant r such that

    $$\begin{aligned} \max \limits _{1\le i\le n}\bigg \{\frac{\rho _{i}}{c_{i}^{-}}+\frac{I_{i}^{+}}{c_{i}^{-}},\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}\rho _{i} +\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}I_{i}^{+}\bigg \}\le r, \end{aligned}$$
    $$\begin{aligned} \max \limits _{1\le i\le n}\bigg \{\frac{\varrho _i}{c_i^-},\frac{(c_i^++c_i^-)\varrho _i}{c_i^-}\bigg \}< 1, \end{aligned}$$

    where

    $$\begin{aligned} \rho _{i}& = \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\\&\quad +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}r\bigg )r,\\ \varrho _{i}& = c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}) r,\,\,\,\,i=1,2,\ldots ,n. \end{aligned}$$

Then system (1) has at least one pseudo almost periodic solution in the region \(\mathbb {E}=\{\varphi \in \mathbb {B}: \Vert \varphi \Vert _{\mathbb {B}}\le r\}\).

Proof

Rewrite (1) in the form

$$\begin{aligned} x_{i}^{\nabla }(t)& = -c_{i}(t)x_{i}(t)+c_{i}(t)\int _{t-\delta _{i}(t)}^{t}x_{i}^{\nabla } (s) \nabla s+\sum _{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t))\\&\quad +\sum _{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau _{ij}(t))) +\sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}h_{j}(x_{j}^{\nabla }(s))\nabla s\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(t)k_{j}(x_{j}(t-\xi _{ijl}(t)))k_{l}(x_{l}(t-\zeta _{ijl}(t)))+I_{i}(t),\,\,\,t\in \mathbb {T},\,\,\, i=1,2,\ldots ,n. \end{aligned}$$

For any \(\varphi \in \mathbb {B}\), we consider the following system

$$\begin{aligned} x_{i}^{\nabla }(t)=-c_{i}(t)x_{i}(t)+F_{i}(t,\varphi )+I_{i}(t),\,\,\, t\in \mathbb {T},\quad i=1,2,\ldots ,n, \end{aligned}$$
(5)

where

$$\begin{aligned} F_{i}(t,\varphi )& = c_{i}(t)\int _{t-\delta _{i}(t)}^{t}\varphi _{i}^{\nabla } (s) \nabla s+\sum _{j=1}^{n}a_{ij}(t)f_{j}(\varphi _{j}(t))\\&\quad+\sum _{j=1}^{n}b_{ij}(t)g_{j}(\varphi _{j}(t-\tau _{ij}(t))) +\sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}h_{j}(\varphi _{j}^{\nabla }(s))\nabla s\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(t)k_{j}(\varphi _{j}(t-\xi _{ijl}(t)))k_{l}(\varphi _{l}(t-\zeta _{ijl}(t))). \end{aligned}$$

Since \(\min \nolimits _{1\le i\le n}\big \{\inf \nolimits _{t\in \mathbb {T}}c_{i}(t)\big \}>0\), it follows from Lemma 2.13 that the linear system

$$\begin{aligned} x_{i}^{\nabla }(t)=-c_{i}(t)x_{i}(t),\,\, i=1,2,\ldots ,n \end{aligned}$$
(6)

admits an exponential dichotomy on \(\mathbb {T}\). Thus, by Lemma 2.12, we know that system (5) has exactly one pseudo almost periodic solution which can be expressed as follows:

$$\begin{aligned} x_\varphi =(x_{\varphi _1},x_{\varphi _2},\ldots ,x_{\varphi _n})^{T}, \end{aligned}$$

where

$$\begin{aligned} x_{\varphi _{i}}(t)=\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) \big (F_{i}(s,\varphi )+I_{i}(s)\big )\nabla s,\,\, i=1,2,\ldots ,n. \end{aligned}$$

Define an operator

$$\begin{aligned} \Phi :\mathbb {E}\rightarrow & \mathbb {E}\\ (\varphi _{1},\varphi _{2},\ldots ,\varphi _{n})^{T}\rightarrow & (x_{\varphi _1},x_{\varphi _2},\ldots ,x_{\varphi _n})^{T}. \end{aligned}$$

We will show that \(\Phi \) is a contraction.

First, we show that for any \(\varphi \in \mathbb {E}\), we have \(\Phi \varphi \in \mathbb {E}\). Note that

$$\begin{aligned} |F_{i}(s,\varphi )|& = \bigg |c_{i}(s)\int _{s-\delta _{i}(s)}^{s}\varphi _{i}^{\nabla } (u) \nabla u+\sum _{j=1}^{n}a_{ij}(s)f_{j}(\varphi _{j}(s))\\&\quad+\sum _{j=1}^{n}b_{ij}(s)g_{j}(\varphi _{j}(s-\tau _{ij}(s))) +\sum _{j=1}^{n}d_{ij}(s)\int _{s-\sigma _{ij}(s)}^{s}h_{j}(\varphi _{j}^{\nabla }(u))\nabla u\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(s)k_{j}(\varphi _{j}(s-\xi _{ijl}(s)))k_{l}(\varphi _{l}(s-\zeta _{ijl}(s)))\bigg |\\ &\le c_{i}^{+}\bigg |\int _{s-\delta _{i}(s)}^{s}\varphi _{i}^{\nabla }(u) \nabla u\bigg |+\sum _{j=1}^{n}a_{ij}^{+}\big |f_{j}(\varphi _{j}(s))\big |\\&\quad+\sum _{j=1}^{n}b_{ij}^{+}\big |g_{j}(\varphi _{j}(s-\tau _{ij}(s)))\big | +\sum _{j=1}^{n}d_{ij}^{+}\bigg |\int _{s-\sigma _{ij}(s)}^{s}h_{j}(\varphi _{j}^{\nabla }(u))\nabla u\bigg |\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big |k_{j}(\varphi _{j}(s-\xi _{ijl}(s))) k_{l}(\varphi _{l}(s-\zeta _{ijl}(s)))\big |\\& \le c_{i}^{+}\delta _{i}^{+}|\varphi _{i}^{\nabla }(s)|+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f}\big |\varphi _{j}(s)\big | +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}\big |\varphi _{j}(s-\tau _{ij}(s))\big |\\&\quad+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\big |\varphi _{j}^{\nabla }(s)\big | +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}\big |\varphi _{j}(s-\xi _{ijl}(s))\big |\big |\varphi _{l}(s-\zeta _{ijl}(s))\big |\\ &\le \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h} +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}\Vert \varphi \Vert _{\mathbb {B}}\bigg )\Vert \varphi \Vert _{\mathbb {B}}\\& \le \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h} +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}r\bigg )r\\& = \rho _{i},\,\,i=1,2,\ldots ,n. \end{aligned}$$

Therefore, by \((H_4)\), we can get

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}|x_{\varphi _{i}}(t)|& = \sup \limits _{t\in \mathbb {T}}\bigg |\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) \big (F_{i}(s,\varphi )+I_{i}(s)\big )\nabla s\bigg |\\\le & \sup \limits _{t\in \mathbb {T}}\int _{-\infty }^{t}\hat{e}_{-c_{i}^{-}}(t,\rho (s)) \big |F_{i}(s,\varphi )\big |\nabla s+\frac{I_{i}^{+}}{c_{i}^{-}}\\\le & \frac{\rho _{i}}{c_{i}^{-}} +\frac{I_{i}^{+}}{c_{i}^{-}}\le r,\,\,\,\,i=1,2,\ldots ,n. \end{aligned}$$

On the other hand, for \(i=1,2,\ldots ,n\), by \((H_4)\), we have

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}|x_{\varphi _{i}}^{\nabla }(t)|& = \sup \limits _{t\in \mathbb {T}}\bigg | F_{i}(t,\varphi )+I_{i}(t)-c_{i}(t)\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) \big (F_{i}(s,\varphi )+I_{i}(s)\big )\nabla s \bigg |\\\le & \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h} +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}r\bigg )r+I_{i}^{+}\\&+c_{i}^{+}\int _{-\infty }^{t}\hat{e}_{-c_{i}^{-}}(t,\rho (s)) \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}L_{j}^{k}L_{l}^{k}r\bigg )r\nabla s+\frac{I_{i}^{+}}{c_{i}^{-}}\\\le & \frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}\rho _{i} +\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}I_{i}^{+} \le r. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \Vert \Phi (\varphi )\Vert _{\mathbb {B}}=\max \limits _{1\le i\le n}\bigg \{\sup \limits _{t\in \mathbb {T}}|x_{\varphi _{i}}(t)|, \sup \limits _{t\in \mathbb {T}}|x_{\varphi _{i}}^{\nabla }(t)|\bigg \}\le r, \end{aligned}$$

which implies that \(\Phi \varphi \in \mathbb {E}\). Therefore, the mapping \(\Phi \) is a self-mapping from \(\mathbb {E}\) to \(\mathbb {E}\). Next, we shall prove that \(\Phi \) is a contraction mapping. For any \(\varphi ,\psi \in \mathbb {E}\), we denote

$$\begin{aligned} H_{i}(s,\varphi ,\psi )& = c_{i}(s)\int _{s-\delta _{i}(s)}^{s}[\varphi _{i}^{\nabla }(u)-\psi _{i}^{\nabla }(u) ] \nabla u +\sum _{j=1}^{n}a_{ij}(s)\big [f_{j}(\varphi _{j}(s))-f_{j}(\psi _{j}(s))\big ]\\&\quad+\sum _{j=1}^{n}b_{ij}(s)\big [g_{j}(\varphi _{j}(s-\tau _{ij}(s)))-g_{j}(\psi _{j}(s-\tau _{ij}(s)))\big ]\\&\quad+\sum _{j=1}^{n}d_{ij}(s)\int _{s-\sigma _{ij}(s)}^{s}\big [h_{j}(\varphi _{j}^{\nabla }(u))-h_{j}(\psi _{j}^{\nabla }(u))\big ]\nabla u\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(s)\big [k_{j}(\varphi _{j}(s-\xi _{ijl}(s)))k_{l}(\varphi _{l}(s-\zeta _{ijl}(s)))\\&\quad-k_{j}(\psi _{j}(s-\xi _{ijl}(s)))k_{l}(\psi _{l}(s-\zeta _{ijl}(s)))\big ], i=1,2,\ldots ,n. \end{aligned}$$

Thus, for \(i=1,2,\ldots ,n\), we have

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}\big |x_{\varphi _{i}}(t)-x_{\psi _{i}}(t)\big |& = \sup \limits _{t\in \mathbb {T}}\bigg |\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) H_{i}(s,\varphi ,\psi )\nabla s\bigg |\\&\le \sup \limits _{t\in \mathbb {T}}\int _{-\infty }^{t}\hat{e}_{-c_{i}^{-}}(t,\rho (s)) \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}\\&\quad+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h} +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k})r\bigg )\nabla s\Vert \varphi -\psi \Vert _{\mathbb {B}}\\&\le \frac{\varrho _i}{c_{i}^{-}}\Vert \varphi -\psi \Vert _{\mathbb {B}},\\ \quad \sup \limits _{t\in \mathbb {T}}\big |(x_{\varphi _{i}}(t)-x_{\psi _{i}}(t))^{\nabla }\big |& = \sup \limits _{t\in \mathbb {T}}\bigg |\bigg (\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) H_{i}(s,\varphi ,\psi )\nabla s\bigg )^{\nabla }\bigg |\\& = \sup \limits _{t\in \mathbb {T}}\bigg |H_{i}(t,\varphi ,\psi )-c_{i}(t)\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s)) H_{i}(s,\varphi ,\psi )\nabla s\bigg |\\ &\le |H_{i}(t,\varphi ,\psi )|+c_{i}^{+}\sup \limits _{t\in \mathbb {T}}\bigg |\int _{-\infty }^{t}\hat{e}_{-c_{i}^{-}}(t,\rho (s)) H_{i}(s,\varphi ,\psi )\nabla s\bigg |\\ & \le \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k})r\bigg )\Vert \varphi -\psi \Vert _{\mathbb {B}}\\&\quad+\frac{c_{i}^{+}}{c_{i}^{-}}\bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{+}\sigma _{ij}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k})r\bigg )\Vert \varphi -\psi \Vert _{\mathbb {B}}\\& = \frac{(c_{i}^{+}+c_{i}^{-})\varrho _i}{c_{i}^{-}}\Vert \varphi -\psi \Vert _{\mathbb {B}}. \end{aligned}$$

By \((H_{4})\), we have

$$\begin{aligned} \Vert \Phi (\varphi )-\Phi (\psi )\Vert _{\mathbb {B}}<\Vert \varphi -\psi \Vert _{\mathbb {B}}. \end{aligned}$$

Hence, we obtain that \(\Phi \) is a contraction mapping. By the fixed point theorem of Banach space [55], it follows that \(\Phi \) has a fixed point in \(\mathbb {E}\); that is, system (1) has a unique pseudo almost periodic solution. This completes the proof of Theorem 3.1. \(\square \)

4 Global exponential stability of pseudo almost periodic solution

In this section, we will study the exponential stability of pseudo almost periodic solutions of (1).

Definition 4.1

The pseudo almost periodic solution \(x^{*}(t)=(x_{1}^{*}(t),x_{2}^{*}(t),\ldots ,x_{n}^{*}(t))^{T}\) of system (1) with initial value \(\varphi ^{*}(t)=(\varphi _{1}^{*}(t),\varphi _{2}^{*}(t),\ldots ,\varphi _{n}^{*}(t))^{T}\) is said to be globally exponentially stable if there exist a positive constant \(\lambda \) with \(\ominus _{\nu }\lambda \in \mathcal {R}^+_\nu \) and \(M>1\) such that every solution \(x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^{T}\) of system (1) with initial value \(\varphi (t)=(\varphi _{1}(t),\varphi _{2}(t),\ldots ,\varphi _{n}(t))^{T}\) satisfies

$$\begin{aligned} \Vert x(t)-x^{*}(t)\Vert \le Me_{\ominus _{\nu }\lambda }(t,t_0)\Vert \psi \Vert ,\,\,\,\,\forall t\in (0,+\infty )_{\mathbb {T}}, \end{aligned}$$

where \(\Vert \psi \Vert =\sup \nolimits _{t\in [-\theta ,0]_{\mathbb {T}}}\max \nolimits _{1\le i\le n}\{|\varphi _{i}(t)-\varphi _{i}^{*}(t)|,|\varphi _{i}^\nabla (t)-({\varphi _{i}^{*}})^\nabla (t)|\}\), \(t_{0}=\max \{[-\theta ,0]_{\mathbb {T}}\}\).

Theorem 4.2

Assume that \((H_1)\)–\((H_4)\) hold, then system (1) has a unique almost periodic solution that is globally exponentially stable.

Proof

From Theorem 3.1, we see that system (1) has at least one pseudo almost periodic solution \(x^{*}(t)=(x_{1}^{*}(t),x_{2}^{*}(t),\ldots ,x_{n}^{*}(t))^{T}\) with initial value \(\varphi ^{*}(t)=(\varphi _{1}^{*}(t),\varphi _{2}^{*}(t),\ldots ,\varphi _{n}^{*}(t))^{T}\). Suppose that \(x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^{T}\) is an arbitrary solution of (1) with initial value \(\varphi (t)=(\varphi _{1}(t),\varphi _{2}(t),\ldots ,\varphi _{n}(t))^{T}\). Then it follows from system (1) that

$$\begin{aligned} z_{i}^{\nabla }(t)& = -c_{i}(t)z_{i}(t-\delta _{i}(t))+\sum _{j=1}^{n}a_{ij}(t)\big [f_{j}(x_{j}(t))-f_{j}(x^{*}_{j}(t))\big ] +\sum _{j=1}^{n}b_{ij}(t)\big [g_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&-g_{j}(x^{*}_{j}(t-\tau _{ij}(t)))\big ] +\sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}\big [h_{j}(x_{j}^{\nabla }(s))-h_{j}((x^{*}_{j})^{\nabla }(s))\big ]\nabla s\nonumber \\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(t)\big [k_{j}(x_{j}(t-\xi _{ijl}(t)))k_{l}(x_{l}(t-\zeta _{ijl}(t)))\nonumber \\&-k_{j}(x^{*}_{j}(t-\xi _{ijl}(t)))k_{l}(x^{*}_{l}(t-\zeta _{ijl}(t)))\big ], \end{aligned}$$
(7)

where \(z_{i}(t)=x_{i}(t)-x^{*}_{i}(t), i=1,2,\ldots ,n\).

The initial condition of (7) is

$$\begin{aligned} \psi _{i}(s)=\varphi _{i}(s)-\varphi _{i}^{*}(s),\,\,\,\,\, \psi ^{\nabla }_{i}(s)=\varphi ^{\nabla }_{i}(s)-(\varphi _{i}^{*})^{\nabla }(s), \end{aligned}$$

where \(s\in [-\theta ,0]_{\mathbb {T}}\), \(i=1,2,\ldots ,n\).

Rewrite (7) in the form

$$\begin{aligned} z_{i}^{\nabla }(t)+c_{i}(t)z_{i}(t)& = c_{i}(t)\int _{t-\delta _{i}(t)}^{t}z_{i}^{\nabla }(s) \nabla s+\sum _{j=1}^{n}a_{ij}(t)\big [f_{j}(x_{j}(t))-f_{j}(x^{*}_{j}(t))\big ]\nonumber \\&+\sum _{j=1}^{n}b_{ij}(t)\big [g_{j}(x_{j}(t-\tau _{ij}(t))) -g_{j}(x^{*}_{j}(t-\tau _{ij}(t)))\big ]\nonumber \\&+\sum _{j=1}^{n}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}\big [h_{j}(x_{j}^{\nabla }(s))-h_{j}((x^{*}_{j})^{\nabla }(s))\big ]\nabla s\nonumber \\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(t)\big [k_{j}(x_{j}(t-\xi _{ijl}(t)))k_{l}(x_{l}(t-\zeta _{ijl}(t)))\nonumber \\&-k_{j}(x^{*}_{j}(t-\xi _{ijl}(t)))k_{l}(x^{*}_{l}(t-\zeta _{ijl}(t)))\big ],\,\,i=1,2,\ldots ,n. \end{aligned}$$
(8)

Multiplying the both sides of (8) by \(\hat{e}_{-c_{i}}(t_0,\rho (s))\) and integrating over \([t_{0},t]_{\mathbb {T}}\), where \(t_{0}\in [-\theta ,0]_{\mathbb {T}}\), by Lemma 2.5, we get

$$\begin{aligned} z_{i}(t)& = z_{i}(t_{0})\hat{e}_{-c_{i}}(t,t_{0}) +\int _{t_{0}}^{t}\hat{e}_{-c_{i}}(t,\rho (s))\bigg (c_{i}(s)\int _{s-\delta _{i}(s)}^{s}z_{i}^{\nabla }(u) \nabla u\nonumber \\&\quad+\sum _{j=1}^{n}a_{ij}(s)\big [f_{j}(x_{j}(s))-f_{j}(x^{*}_{j}(s))\big ] +\sum _{j=1}^{n}b_{ij}(s)\big [g_{j}(x_{j}(s-\tau _{ij}(s)))\nonumber \\&\quad-g_{j}(x^{*}_{j}(s-\tau _{ij}(s)))\big ] +\sum _{j=1}^{n}d_{ij}(s)\int _{s-\sigma _{ij}(s)}^{s}\big [h_{j}(x_{j}^{\nabla }(u))-h_{j}((x^{*}_{j})^{\nabla }(u))\big ]\nabla u\nonumber \\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}(s)\big [k_{j}(x_{j}(s-\xi _{ijl}(s)))k_{l}(x_{l}(s-\zeta _{ijl}(s)))\nonumber \\&\quad-k_{j}(x^{*}_{j}(s-\xi _{ijl}(s)))k_{l}(x^{*}_{l}(s-\zeta _{ijl}(s)))\big ]\bigg )\nabla s,\,\,\,i=1,2,\ldots ,n. \end{aligned}$$
(9)

Let \(S_{i}\) and \(R_{i}\) be defined as follows:

$$\begin{aligned} S_{i}(\beta )& = c_{i}^{-}-\beta -\exp (\beta \sup \limits _{s\in \mathbb {T}}\nu (s)) \bigg (c_{i}^{+}\delta _{i}^{+}\exp (\beta \delta _{i}^{+})+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}\exp (\beta \tau _{ij}^{+})\\&+\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\sigma _{ij}^{+}\exp (\beta \sigma _{ij}^{+}) +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^+{\big (L_{j}^{k}L_{l}^{k}\exp (\beta \xi _{ijl}^{+}) +}L_{l}^{k}L_{j}^{k}\exp (\beta \zeta _{ijl}^{+})\big )r\bigg ) \end{aligned}$$

and

$$\begin{aligned} R_{i}(\beta )& = c_{i}^{-}-\beta -\big (c_{i}^{+}\exp (\beta \sup \limits _{s\in \mathbb {T}}\nu (s))+c_{i}^{-}-\beta \big ) \bigg (c_{i}^{+}\delta _{i}^{+}\exp (\beta \delta _{i}^{+})\\&+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g}\exp (\beta \tau _{ij}^{+}) +\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\sigma _{ij}^{+}\exp (\beta \sigma _{ij}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}\exp (\beta \xi _{ijl}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\beta \zeta _{ijl}^{+})\big )r\bigg ),\,\,i=1,2,\ldots ,n. \end{aligned}$$

By \((H_{4})\), we get

$$\begin{aligned} S_{i}(0)& = c_{i}^{-}-\bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g} +\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}\big )r\bigg )> 0 \end{aligned}$$

and

$$\begin{aligned} R_{i}(0)& = c_{i}^{-}-(c_{i}^{+}+c_{i}^{-})\bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g} +\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}\big )r\bigg )> 0, \,\,i=1,2,\ldots ,n. \end{aligned}$$

Since \(S_{i}\) and \(R_{i}\) are continuous on \([0,+\infty )\) and \(S_{i}(\beta ), R_{i}(\beta ) \rightarrow -\infty \), as \(\beta \rightarrow +\infty \), there exists \(\zeta _{i},\gamma _{i} > 0\) such that \(S_{i}(\zeta _{i})=R_{i}(\gamma _{i})=0\) and \(S_{i}(\beta )> 0\) for \(\beta \in (0,\zeta _{i})\), \(R_{i}(\beta )> 0\) for \(\beta \in (0,\gamma _{i})\). Take \(a=\min \nolimits _{1\le i\le n}\big \{\zeta _{i}, \gamma _{i}\big \}\), we have \(S_{i}(a)\ge 0\), \(R_{i}(a)\ge 0\). So, we can choose a positive constant \(0< \lambda < \min \big \{a,\min \nolimits _{1\le i \le n}\{c_{i}^{-}\}\big \}\) such that

$$\begin{aligned} S_{i}(\lambda )>0,\,\,\, R_{i}(\lambda )>0, \quad i=1,2,\ldots ,n, \end{aligned}$$

which implies that

$$\begin{aligned}&\frac{c_{i}^{+}\exp (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s))}{c_{i}^{-}-\lambda } \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g} +\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}\big )r\bigg )< 1 \end{aligned}$$

and

$$\begin{aligned}&\bigg (1+\frac{c_{i}^{+}\exp (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s))}{c_{i}^{-}-\lambda }\bigg ) \bigg (c_{i}^{+}\delta _{i}^{+}+\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum _{j=1}^{n}b_{ij}^{+}L_{j}^{g} +\sum _{j=1}^{n}d_{ij}^{+}L_{j}^{h}\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}\big )r\bigg )< 1,\,\,i=1,2,\ldots ,n. \end{aligned}$$

Let

$$\begin{aligned} M=\max \limits _{1\le i \le n}\bigg \{\frac{c_{i}^{-}}{c_{i}^{+}\delta _{i}^{+}+\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum \limits _{j=1}^{n}b_{ij}^{+}L_{j}^{g} +\sum \limits _{j=1}^{n}d_{ij}^{+}L_{j}^{h} +\sum \limits _{j=1}^{n}\sum \limits _{l=1}^{n}T_{ijl}^{+}\big (L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k}\big )r}\bigg \}, \end{aligned}$$

then by \((H_{4})\) we have \(M>1\).

Hence, it is obvious that

$$\begin{aligned} \Vert z(t)\Vert \le M\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}}, \quad \forall t\in [-\theta ,t_{0}]_{\mathbb {T}}, \end{aligned}$$

where \(\ominus _{\nu }\lambda \in \mathcal {R}^{+}_\nu \). We claim that

$$\begin{aligned} \Vert z(t)\Vert \le M\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}}, \quad \forall t\in (t_{0},+\infty )_{\mathbb {T}}. \end{aligned}$$
(10)

To prove (10), we show that for any \(P>1\), the following inequality holds:

$$\begin{aligned} \Vert z(t)\Vert < PM\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}}, \quad \forall t\in (t_{0},+\infty )_{\mathbb {T}}, \end{aligned}$$
(11)

which implies that, for \(i=1,2,\ldots ,n\), we have

$$\begin{aligned} |z_{i}(t)|< PM\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}}, \quad \forall t\in (t_{0},+\infty )_{\mathbb {T}} \end{aligned}$$

and

$$\begin{aligned} |z^{\nabla }_{i}(t)|< PM\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}}, \quad \forall t\in (t_{0},+\infty )_{\mathbb {T}}. \end{aligned}$$

If (11) is not true, then there must be some \(t_{1}\in (t_{0},+\infty )_{\mathbb {T}}\) and some \(i_1, i_2\in \{1,2,\ldots ,n\}\) such that

$$\begin{aligned} \Vert z(t_1)\Vert =\max \{|z_{i_{1}}(t_{1})|,|z_{i_{2}}^{\nabla }(t_1)|\} \ge P M\hat{e}_{\ominus _{\nu }\lambda }(t_1,t_0)\Vert \psi \Vert _{\mathbb {B}} \end{aligned}$$

and

$$\begin{aligned} \Vert z(t)\Vert \le PM\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}},\quad t\in (t_{0},t_{1}]_{\mathbb {T}},\,\,t_{0}\in [-\theta ,0]_{\mathbb {T}}. \end{aligned}$$

Therefore, there must exist a constant \(c\ge 1\) such that

$$\begin{aligned} \Vert z(t_{1})\Vert =\max \{|z_{i_1}(t_1)|,|z_{i_2}^{\nabla }(t_1)|\}=cP M \hat{e}_{\ominus _{\nu }\lambda }(t_1,t_0)\Vert \psi \Vert _{\mathbb {B}} \end{aligned}$$
(12)

and

$$\begin{aligned} \Vert z(t)\Vert \le cP M \hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})\Vert \psi \Vert _{\mathbb {B}},\quad t\in (t_{0},t_{1}]_{\mathbb {T}},\,\,t_{0}\in [-\theta ,0]_{\mathbb {T}}. \end{aligned}$$

In view of (9), we have

$$\begin{aligned}&|z_{i_{1}}(t_{1})| \\& = \bigg |z_{i_{1}}(t_{0})e_{-c_{i_{1}}}(t_{1},t_{0})+\int _{t_{0}}^{t_{1}}e_{-c_{i_{1}}}(t_{1},\rho (s))\bigg ( c_{i_{1}}(s)\int _{s-\delta _{i_{1}}(s)}^{s}z_{i_{1}}^{\nabla }(u) \nabla u\\&\quad +\sum _{j=1}^{n}a_{i_{1}j}(s)\big [f_{j}(x_{j}(s))-f_{j}(x^{*}_{j}(s))\big ] +\sum _{j=1}^{n}b_{i_{1}j}(s)\big [g_{j}(x_{j}(s-\tau _{i_{1}j}(s)))\\&\quad -g_{j}(x^{*}_{j}(s-\tau _{i_{1}j}(s)))\big ] +\sum _{j=1}^{n}d_{i_{1}j}(s)\int _{s-\sigma _{i_{1}j}(s)}^{s}\big [h_{j}(x_{j}^{\nabla }(u))-h_{j}((x^{*}_{j})^{\nabla }(u))\big ]\nabla u\\&\quad +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}(s)\big [k_{j}(x_{j}(s-\xi _{i_{1}jl}(s)))k_{l}(x_{l}(s-\zeta _{i_{1}jl}(s)))\\&\quad -k_{j}(x^{*}_{j}(s-\xi _{i_{1}jl}(s)))k_{l}(x^{*}_{l}(s-\zeta _{i_{1}jl}(s)))\big ]\bigg )\nabla s\bigg |\\& \le \hat{e}_{-c_{i_{1}}}(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} +cPM\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i_{1}}}(t_{1},\rho (s)) \hat{e}_{\lambda }(t_{1},\rho (s))\\&\quad \times \bigg (c_{i_{1}}^{+}\int _{s-\delta _{i_{1}}(s)}^{s}\hat{e}_{\lambda }(\rho (s),u) \nabla u+\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}\hat{e}_{\lambda }(\rho (s),s) +\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\hat{e}_{\lambda }(\rho (s),s-\tau _{i_{1}j}(s))\\&\quad+\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\int _{s-\sigma _{i_{1}j}(s)}^{s}\hat{e}_{\lambda }(\rho (s),u)\nabla u+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\hat{e}_{\lambda }(\rho (s),s-\xi _{i_{1}jl}(s))\\&\quad+L_{l}^{k}L_{j}^{k}\hat{e}_{\lambda }(\rho (s),s-\zeta _{i_{1}jl}(s))\big )r\bigg )\nabla s \end{aligned}$$
$$\begin{aligned}\le & \hat{e}_{-c_{i_{1}}}(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} +cPM\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\int _{t_{0}}^{t_{1}} \hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},\rho (s))\\&\times \bigg (c_{i_{1}}^{+}\delta _{i_{1}}^{+}\hat{e}_{\lambda }(\rho (s),s-\delta _{i_{1}}(s)) +\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}\hat{e}_{\lambda }(\rho (s),s) +\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\hat{e}_{\lambda }(\rho (s),s-\tau _{i_{1}j}(s))\\&+\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\hat{e}_{\lambda }(\rho (s),s-\sigma _{i_{1}j}(s)) +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\hat{e}_{\lambda }(\rho (s),s-\xi _{i_{1}jl}(s))\\&+L_{l}^{k}L_{j}^{k}\hat{e}_{\lambda }(\rho (s),s-\zeta _{i_{1}jl}(s))\big )r\bigg )\nabla s\\\le & \hat{e}_{-c_{i_{1}}}(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} +cPM\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},\rho (s))\\&\times \bigg (c_{i_{1}}^{+}\delta _{i_{1}}^{+}\exp \big [\lambda (\delta _{i_{1}}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s))\big ] +\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}\exp \big (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)\big )\\&+\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\exp \big [\lambda (\tau _{i_{1}j}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s))\big ] +\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\exp \big [\lambda (\sigma _{i_{1}j}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s))\big ]\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+} \big (L_{j}^{k}L_{l}^{k}\exp \big [\lambda (\xi _{i_{1}j}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s))\big ] +L_{l}^{k}L_{j}^{k}\exp \big [\lambda (\zeta _{i_{1}j}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s))\big ]\big )r\bigg )\nabla s\\& = cPM \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\bigg \{\frac{1}{p M}\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},t_{0})+\exp \big (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)\big )\\&\times \bigg (c_{i_{1}}^{+}\delta _{i_{1}}^{+}\exp (\lambda \delta _{i_{1}}^{+}) +\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_{1}j}^{+})\\&+\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\exp (\lambda \sigma _{i_{1}j}^{+}) +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+} \big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_{1}j}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_{1}j}^{+})\big )r\bigg )\\&\times \int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},\rho (s))\bigg \}\nabla s \end{aligned}$$
$$\begin{aligned}\le & cPM \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\bigg \{\frac{1}{p M}\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},t_{0})+\exp \big (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)\big )\\&\times \bigg (c_{i_{1}}^{+}\delta _{i_{1}}^{+}\exp (\lambda \delta _{i_{1}}^{+}) +\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_{1}j}^{+})\\&+\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\exp (\lambda \sigma _{i_{1}j}^{+}) +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+} \big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_{1}j}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_{1}j}^{+})\big )r\bigg )\\&\times \frac{1-\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},t_{0})}{c_{i_{1}}^{-}-\lambda }\bigg \}\\\le & cPM \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\bigg \{ \bigg [\frac{1}{M}-\frac{\exp \big (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)\big )}{c_{i_{1}}^{-}-\lambda }\bigg ( c_{i_{1}}^{+}\delta _{i_{1}}^{+}\exp (\lambda \delta _{i_{1}}^{+})\\&+\sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_{1}j}^{+}) +\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\exp (\lambda \sigma _{i_{1}j}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+} \big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_{1}j}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_{1}j}^{+})\big )r\bigg )\bigg ]\hat{e}_{-c_{i_{1}}\oplus _{\nu }\lambda }(t_{1},t_{0})\\&+\frac{\exp \big (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)\big )}{c_{i_{1}}^{-}-\lambda } \bigg (c_{i_{1}}^{+}\delta _{i_{1}}^{+}\exp (\lambda \delta _{i_{1}}^{+})+ \sum _{j=1}^{n}a_{i_{1}j}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{i_{1}j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_{1}j}^{+})\\&+\sum _{j=1}^{n}d_{i_{1}j}^{+}L_{j}^{h}\sigma _{i_{1}j}^{+}\exp (\lambda \sigma _{i_{1}j}^{+}) +\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{1}jl}^{+} \big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_{1}j}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_{1}j}^{+})\big )r\bigg ) \bigg \}\\\le & cPM \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \end{aligned}$$

and

$$\begin{aligned} |z_{i_{2}}^{\nabla }(t_{1})|\le & c_{i_2}^{+} \hat{e}_{-c_{i_2}}(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}+cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \bigg (c_{i_2}^{+}\int _{t_{1}-\delta _{i_2}(t_{1})}^{t_{1}}\hat{e}_{\lambda }(t_{1},u) \nabla u\\&+\sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}\hat{e}_{\lambda }(t_1,t_1) +\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\hat{e}_{\lambda }(t_1,t_1-\tau _{i_2j}(t_1))\\&+\sum _{j=1}^{n}d_{i_{2}j}^{+}L_{j}^{h}\int _{t_1-\sigma _{i_{2}j}(t_1)}^{t_1}\hat{e}_{\lambda }(\rho (u),u)\nabla u\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\hat{e}_{\lambda }(t_1,t_1-\xi _{i_2jl}(t_1))+ L_{l}^{k}L_{j}^{k}\hat{e}_{\lambda }(t_1,t_1-\zeta _{i_2jl}(t_1))\big )r \bigg )\\&+ c_{i_2}^{+}cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}\int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i_2}}(t_{1}, \rho (s))\hat{e}_{\lambda }(t_{1},\rho (s))\\&\times \bigg \{ c_{i_2}^{+}\int _{s-\eta _{i_2}(s)}^{s}\hat{e}_{\lambda }(\rho (u),u) \nabla u +\sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}\hat{e}_{\lambda }(\rho (s),s)\\&+\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\hat{e}_{\lambda }(\rho (s),s-\tau _{i_2j}(s)) +\sum _{j=1}^{n}d_{i_{2}j}^{+}L_{j}^{h}\int _{s-\sigma _{i_{2}j}(s)}^{s}\hat{e}_{\lambda }(\rho (u),u)\nabla u\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\hat{e}_{\lambda }(s,t_1-\xi _{i_2jl}(s))+ L_{l}^{k}L_{j}^{k}\hat{e}_{\lambda }(s,t_1-\zeta _{i_2jl}(s))\big )r\bigg \} \nabla s\\\le & c_{i_2}^{+} e_{-c_{i_2}}(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}+cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \bigg (c_{i_2}^{+}\delta _{i_2}^{+}\exp (\lambda \delta _{i_2}^{+}) +\sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}\\&+\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_2j}^{+}) +\sum _{j=1}^{n}d_{i_2j}^{+}L_{j}^{h}\sigma _{i_{2}j}^{+}\exp (\lambda \sigma _{i_2j}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_2jl}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_2jl}^{+})\big )r\bigg )\\&\times \bigg (1+c_{i_2}^{+}\exp (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s)) \int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i_2}\oplus \lambda }(t_{1},\rho (s)) \nabla s\bigg )\\\le & cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \bigg \{\frac{c_{i_2}^{+}}{M}\hat{e}_{-(c_{i_2}^{-}-\lambda )}(t_{1},t_{0}) +\bigg (c_{i_2}^{+}\delta _{i_2}^{+}\exp (\lambda \delta _{i_2}^{+}) +\sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}\\&+\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_2j}^{+}) +\sum _{j=1}^{n}d_{i_2j}^{+}L_{j}^{h}\sigma _{i_{2}j}^{+}\exp (\lambda \sigma _{i_2j}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_2jl}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_2jl}^{+})\big )r\bigg )\\&\times \bigg (1+c_{i_2}^{+}\exp (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s))\frac{1}{-(c_{i_2}^{-}-\lambda )} \big (\hat{e}_{-(c_{i_2}^{-}-\lambda )}(t_{1},t_{0})-1\big )\bigg ) \bigg \} \end{aligned}$$
$$\begin{aligned}\le & cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}} \bigg \{\bigg [\frac{1}{M}-\frac{\exp (\lambda \sup \limits _{s\in \mathbb {T}}\nu (s))}{c_{i_2}^{-}-\lambda } \bigg (c_{i_2}^{+}\delta _{i_2}^{+}\exp (\lambda \delta _{i_2}^{+}) \sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}\\&+\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_2j}^{+}) +\sum _{j=1}^{n}d_{i_2j}^{+}L_{j}^{h}\sigma _{i_{2}j}^{+}\exp (\lambda \sigma _{i_2j}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_2jl}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_2jl}^{+})\big )r\bigg )\bigg ]c_{i_2}^{+}\hat{e}_{-(c_{i_2}^{-}-\lambda )}(t_{1},t_{0})\\&+\bigg (1+\frac{c_{i_2}^{+}\exp (\lambda \sup \limits _{s\in \mathbb {T}}\mu (s))}{c_{i_2}^{-}-\lambda }\bigg ) \bigg (c_{i_2}^{+}\delta _{i_2}^{+}\exp (\lambda \delta _{i_2}^{+})\\&+\sum _{j=1}^{n}a_{i_2j}^{+}L_{j}^{f}+\sum _{j=1}^{n}b_{i_2j}^{+}L_{j}^{g}\exp (\lambda \tau _{i_2j}^{+}) +\sum _{j=1}^{n}d_{i_2j}^{+}L_{j}^{h}\sigma _{i_{2}j}^{+}\exp (\lambda \sigma _{i_2j}^{+})\\&+\sum _{j=1}^{n}\sum _{l=1}^{n}T_{i_{2}jl}^{+}\big (L_{j}^{k}L_{l}^{k}\exp (\lambda \xi _{i_2jl}^{+}) +L_{l}^{k}L_{j}^{k}\exp (\lambda \zeta _{i_2jl}^{+})\big )r\bigg )\bigg \}\\< & cP M\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}. \end{aligned}$$

The above two inequalities imply that

$$\begin{aligned} \Vert z(t_{1})\Vert <cPM \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0})\Vert \psi \Vert _{\mathbb {B}}, \end{aligned}$$

which contradicts (12), and so (11) holds. Letting \(P\rightarrow 1\), then (10) holds. Hence, the pseudo almost periodic solution of system (1) is globally exponentially stable. The proof is complete. \(\square \)

5 An example

In this section, we give an example to illustrate the feasibility and effectiveness of our results obtained in Sects. 3 and 4.

Example 5.1

Let \(n=2\). Consider the following neural network system on time scale \(\mathbb {T}\):

$$\begin{aligned} x_{i}^{\nabla }(t)& = -c_{i}(t)x_{i}(t-\delta _{i}(t))+\sum _{j=1}^{2}a_{ij}(t)f_{j}(x_{j}(t))\nonumber \\&\quad+\sum _{j=1}^{2}b_{ij}(t)g_{j}(x_{j}(t-\tau _{ij}(t))) +\sum _{j=1}^{2}d_{ij}(t)\int _{t-\sigma _{ij}(t)}^{t}h_{j}(x_{j}^{\nabla }(s))\nabla s\nonumber \\&\quad+\sum _{j=1}^{2}\sum _{l=1}^{2}T_{ijl}(t)k_{j}(x_{j}(t-\xi _{ijl}(t)))k_{l}(x_{l}(t-\zeta _{ijl}(t))) +I_{i}(t), \end{aligned}$$
(13)

where \(i=1,2\), \(t\in \mathbb {T}\) and the coefficients are follows:

$$\begin{aligned}&f_{1}(x)=\frac{\cos ^{4}x+1}{16},\,\,f_{2}(x)=\frac{\cos ^{3}x+1}{12},\,\,g_{1}(x)=\frac{2\sin ^{3}x+3}{24},\,\,g_{2}(x)=\frac{\sin ^{3}x+7}{12},\\&h_{1}(x)=\frac{\sin ^{4}x+2}{16},\,\,h_{2}(x)=\frac{5-3\cos ^{2}x}{24},\,\,k_{1}(x)=\frac{\cos ^{3}x+7}{12},\,\,k_{2}(x)=\frac{7-2\sin ^{2}x}{16},\\&c_{1}(t)=0.5+0.1|\sin t|,\,\,c_{2}(t)=0.7-0.1|\cos t|,\,\,I_{1}(t)=0.2\sin t,\,\,I_{2}(t)=0.15\cos t,\\&a_{11}(t)=0.1|\sin (\sqrt{2}t)|,\,\,a_{12}(t)=0.2|\cos (\sqrt{3}t)|,\,\,a_{21}(t)=0.1|\cos t|,\,\,a_{22}(t)=0.2|\sin t|,\\&b_{11}(t)=0.2|\cos (\sqrt{2} t)|,\,\,b_{12}(t)=0.15|\sin t|,\,\,b_{21}(t)=0.1|\cos t|,\,\,b_{22}(t)=0.25|\sin (\sqrt{3} t)|,\\&d_{11}(t)=0.15\sin ^{2}t,\,\,d_{12}(t)=0.2\cos ^{2}t,\,\,d_{21}(t)=0.1|\cos (\sqrt{3} t)|,\,\,d_{22}(t)=0.15\cos ^{4}t,\\&T_{111}(t)=T_{211}(t)=0.015|\cos t|,\,\,T_{112}(t)=T_{212}(t)=0.01|\sin t|,\\&T_{121}(t)=T_{221}(t)=0.02\sin ^{2} t,\,\,T_{122}(t)=T_{222}(t)=0.015|\cos t|,\\&\delta _{1}(t)=0.02|\cos ( 2\pi t)|,\,\,\delta _{2}(t)=0.03\sin |( 2\pi t)|,\,\,\tau _{ij}(t)=0.1\sin ^{2}(4\pi t),\\&\sigma _{ij}(t)=0.4\sin ^{2}( \pi t),\,\,\xi _{ijl}(t)=\zeta _{ijl}(t)=0.3\sin ^{2}(2\pi t),\,i,j,l=1,2. \end{aligned}$$

By a simple calculation, we have \(L_{1}^{f}=L_{2}^{f}=L_{1}^{g}=L_{2}^{g}=L_{1}^{h}=L_{2}^{h}=L_{1}^{k}=L_{2}^{k}=\frac{1}{4}\),

$$\begin{aligned} \rho _{1}& = \big (c_{1}^{+}\delta _{1}^{+}+\sum _{j=1}^{2}a_{1j}^{+}L_{j}^{f} +\sum _{j=1}^{2}b_{1j}^{+}L_{j}^{g}+\sum _{j=1}^{2}d_{1j}^{+}\sigma _{1j}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{2}\sum _{l=1}^{2}T_{1jl}^{+}L_{j}^{k}L_{l}^{k}r\big )r=0.2095r+0.00375r^{2},\\ \rho _{2}& = \big (c_{2}^{+}\delta _{2}^{+}+\sum _{j=1}^{2}a_{2j}^{+}L_{j}^{f} +\sum _{j=1}^{2}b_{2j}^{+}L_{j}^{g}+\sum _{j=1}^{2}d_{2j}^{+}\sigma _{2j}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{2}\sum _{l=1}^{2}T_{2jl}^{+}L_{j}^{k}L_{l}^{k}r\big )r=0.2085r+0.00375r^{2},\\ \varrho _{1}& = c_{1}^{+}\delta _{1}^{+}+\sum _{j=1}^{2}a_{1j}^{+}L_{j}^{f} +\sum _{j=1}^{2}b_{1j}^{+}L_{j}^{g}+\sum _{j=1}^{2}d_{1j}^{+}\sigma _{1j}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{2}\sum _{l=1}^{2}T_{1jl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k})r=0.2095r+0.0075r^{2},\\ \varrho _{2}& = c_{2}^{+}\delta _{2}^{+}+\sum _{j=1}^{2}a_{2j}^{+}L_{j}^{f} +\sum _{j=1}^{2}b_{2j}^{+}L_{j}^{g}+\sum _{j=1}^{2}d_{2j}^{+}\sigma _{2j}^{+}L_{j}^{h}\\&\quad+\sum _{j=1}^{2}\sum _{l=1}^{2}T_{2jl}^{+}(L_{j}^{k}L_{l}^{k}+L_{l}^{k}L_{j}^{k})r=0.2085r+0.0075r^{2}, \end{aligned}$$

and we let \(r=1\), then we obtain

$$\begin{aligned} \max \limits _{1\le i\le 2}\bigg \{\frac{\rho _{i}}{c_{i}^{-}}+\frac{I_{i}^{+}}{c_{i}^{-}},\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}\rho _{i} +\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}I_{i}^{+} \bigg \}=\max \{0.8265,0.60375,0.90915,0.784875\}<1= r, \end{aligned}$$

and

$$\begin{aligned}&\max \limits _{1\le i\le 2}\bigg \{\frac{\varrho _{i}}{c_{i}^{-}},\frac{c_{i}^{+}+c_{i}^{-}}{c_{i}^{-}}\varrho _{i} \bigg \}=\max \{0.434,0.36,0.4774,0.468\}<1. \end{aligned}$$
Fig. 1
figure 1

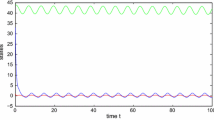
\(\mathbb {T}=\mathbb {R}.\) Numerical solution \(x_1(t)\) and \(x_2(t)\) of system (7) for \((\varphi _1(t),\varphi _2(t))=(1.3,0.8).\)

Full size image
Fig. 2
figure 2

\(\mathbb {T}=\mathbb {Z}.\) Numerical solution \(x_1(n)\) and \(x_2(n)\) of system (7) for \((\varphi _1(n),\varphi _2(n))=(1.7,1.3).\)

Full size image

Therefore, for \(1-\nu (t)c_{i}(t)>0\), \(i=1,2\), all the conditions of Theorem 4.2 are satisfied, hence, we know that system (13) has a unique pseudo almost periodic solution that is globally exponentially stable. Especially, whether \(\mathbb {T}=\mathbb {R}\) or \(\mathbb {T}=\mathbb {Z}\), all the conditions of Theorem 4.2 are satisfied. Therefore, system (13) has a unique pseudo almost periodic solution that is globally exponentially stable when \(\mathbb {T}=\mathbb {R}\) or \(\mathbb {T}=\mathbb {Z}\). This is, the continuous-time neural network and its discrete-time analogue have the same dynamical behaviors for the pseudo almost periodicity (see Figs. 1, 2).

Remark 5.2

All the results obtained in [16, 33–49, 56] cannot be applied to obtain that system (13) has a unique pseudo almost periodic solution.

6 Conclusion

In this paper, we proposed a class of neutral type high-order Hopfield neural networks with mixed time-varying delays and leakage delays on time scales. Based on the exponential dichotomy of linear dynamic equations on time scales, Banach’s fixed point theorem and the theory of calculus on time scales, we obtained the existence and global exponential stability of pseudo almost periodic solutions for this class of neural networks that effectively unified the continuous-time and discrete-time neural network cases. The results of this paper are essentially new. Our methods used in this paper can be used to study the pseudo almost periodic problem for other types’ neural networks. For example, fuzzy neural networks that are very important in implementation and applications (see [57–63]).