The Existence and the Stability of Weighted Pseudo Almost Periodic Solution of High-Order Hopfield Neural Network

Abstract

In this paper, by employing fixed point theorem and differential inequality techniques, some sufficient conditions are given for the existence and the global exponential stability of the unique weighted pseudo almost-periodic solution of high-order Hopfield neural networks with delays. An illustrative example is also given at the end of this paper to show the effectiveness of our results.

1 Introduction

High order Hopfield neural networks (HOHNNs) have attracted many attentions in recent years due to the fact that they have stronger approximation property, faster convergence rate, greater storage capacity, and higher fault tolerance than lower-order neural networks. In particular, there have been extensive results on the problem of the existence and stability of equilibrium points, periodic solutions, and almost periodic solution of HOHNNs in the literature. We refer the reader to [1–5] and the references therein.

As is well known, both in biological and man-made neural networks, delays are inevitable, due to various reasons. For instance, time delays can be caused by the finite switching speed of amplifier circuits in neural networks. Time delays in the neural networks make the dynamic behaviors become more complex, and may destabilize the stable equilibria [2–5]. Thus, it is very important to study the dynamics of neural networks delay.

In this paper, we are mainly concerned with the existence of weighted pseudo almost periodic solutions to the following models for HOHNNs with delays:

$$\begin{aligned} x'_{i}(t)&\,= - c_{i} x_{i}(t)+ \sum _{j=1}^{n} d_{ij}(t) g_{j} (x_{j}(t))+ \sum _{j=1}^{n} a_{ij}(t) g_{j} (x_{j}(t-\tau )) \nonumber \\&\quad + \sum _{j=1}^{n} \sum _{l=1}^{n} b_{ijl}(t) g_{j}(x_{j}(t-\sigma )) g_{l}(x_{l}(t-\nu )) \nonumber \\&\quad + I_{i}(t), \, \, i=1,\dots ,n. \end{aligned}$$

(1)

where n corresponds to the number of units in a neural network, $x_{i}(t)$ corresponds to the state vector of the ith unit at the time t, $c_{i}> 0$ represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t, $d_{ij}(t), a_{ij}(t)$ and $b_{ijl}(t)$ are connection weights of the neural network, $\tau \ge 0, \sigma \ge 0$ and $\nu \ge 0$ correspond to the transmission delays, $I_{i}(t)$ denote the external inputs at time t, and $g_{j}$ is the activation function of signal transmission.

For instance, we make the following assumptions:

• (H1) For all $1\le i,j,l \le n$, the functions $t\longmapsto d_{ij}(t), \, t\longmapsto a_{ij}(t),\, t\longmapsto b_{ijl}(t), \, t\longmapsto I_{i}(t)$ are weighted pseudo almost-periodic functions.

• (H2) Let $\rho : \mathbb {R}\longmapsto (0,+\infty )$, $\rho \in \mathbb {U}_{\infty }$ is continuous and assume

  $$\begin{aligned} \sup \limits _{s \in \mathbb {R}} [\frac{\rho (s+\delta )}{\rho (s)}]<\infty \hbox { and } \sup \limits _{T >0}[\frac{\mu (T+\delta ,\rho )}{\mu (T,\rho )}]<\infty ,\hbox { for each } \delta \in \mathbb {R} \end{aligned}$$

• (H3) For each $j = \{1,2,\dots ,n\}$, there exist nonnegative constants $L^{g}_{j}$ and $M^{g}_{j}$ such that for all $u,v \in \mathbb {R}$

  $$\mid g_{j}(u)- g_{j}(v)\mid \le L^{g}_{j} \mid u-v \mid ,\, \, \mid g_{j}(u)\mid \le M^{g}_{j}. $$

  Furthermore, we suppose that for all $1\le j \le n$, $g_{j}(0)= 0$.

Throughout this paper, we will use the following concepts and notations. $BC(\mathbb {R},\mathbb {R}^{n})$ denotes the set of bounded continued functions from $\mathbb {R}$ to $\mathbb {R}^{n}$. Note that $(BC(\mathbb {R},\mathbb {R}^{n}),\parallel . \parallel _{\infty })$ is a Banach space where $\parallel . \parallel _{\infty }$ denotes the sup norm

$$\parallel f \parallel _{\infty }= \max _{1 \le i \le n} \sup _{t \in \mathbb {R}} \mid f_{i}(t) \mid . $$

Furthermore, $C(\mathbb {R},\mathbb {R}^{n})$ denotes the class of continuous functions from $\mathbb {R}$ into $\mathbb {R}^{n}$. Let $(\mathbb {R}^{n},\parallel . \parallel _{\infty })$ be Banach space. Let $\mathbb {U}$ denotes the collection of functions (weights) $\rho : \mathbb {R}\longmapsto (o,\infty )$ which are locally integrable over $\mathbb {R}$ such that $\rho >0$ almost everywhere. From now on, if $\rho \in \mathbb {U}$ and for $T > 0$, we then set

$$\mu (T,\rho )= \int _{-T}^{T} \rho (x)dx.$$

As in the particular case when $\rho (x)=1$ for each $x\in \mathbb {R}$, we are exclusively interested in those weights $\rho$, for which $\lim \limits _{T\longrightarrow \infty } \mu (T,\rho )= \infty$.

Let $\mathbb {U}_{\infty }:= \{ \rho \in \mathbb {U} : \lim \limits _{T\longrightarrow \infty } \mu (T,\rho )= \infty \}$

and $\mathbb {U}_{B}:= \{ \rho \in \mathbb {U}_{\infty }: \rho \hbox { is bounded with } \inf \limits _{x\in \mathbb {R}} \rho (x)> 0 \}.$

Obviously, $\mathbb {U}_{B}\subset \mathbb {U}_{\infty }\subset \mathbb {U}$, with strict inclusions.

Definition 1

[3]. A function $f \in C(\mathbb {R},\mathbb {R}^{n})$ is called (Bohr) almost periodic if for each $\varepsilon > 0$ there exists $L(\varepsilon )>0$ such that every interval of length $L(\varepsilon )>0$ contains a number $\tau$ with the property that $\parallel f(t+\tau )-f(t) \parallel _{\infty } < \varepsilon$, for each $t\in \mathbb {R}$. The number $\tau$ above is called an $\varepsilon$-translation number of f, and the collection of all such functions will be denoted as $AP(\mathbb {R},\mathbb {R}^{n})$.

To introduce those weighted pseudo-almost periodic functions, we need to define the weighted ergodic space $PAP_{0}(\mathbb {R},\mathbb {R}^{n},\rho )$. Weighted pseudo-almost periodic functions will then appear as perturbations of almost periodic functions by elements of $PAP_{0}(\mathbb {R},\mathbb {R}^{n},\rho )$.

Let $\rho \in \mathbb {U}_{\infty }$. Define

$$PAP_{0}(\mathbb {R},\mathbb {R}^{n},\rho ):= \{f \in BC(\mathbb {R},\mathbb {R}^{n}): \lim _{T\longrightarrow \infty } \frac{1}{\mu (T,\rho )} \int ^{T}_{-T} \parallel f(\sigma )\parallel \rho (\sigma )d\sigma = 0 \}.$$

Definition 2

[3]. Let $\rho \in \mathbb {U}_{\infty }$. A function $f \in BC(\mathbb {R},\mathbb {R}^{n})$ is called weighted pseudo-almost periodic (or $\rho$-pseudo almost periodic) if it can be expressed as $f= g+\phi$, where $g \in AP(\mathbb {R},\mathbb {R}^{n})$ and $\phi \in PAP_{0}(\mathbb {R},\mathbb {R}^{n},\rho )$. The collection of such functions will be denoted by $PAP(\mathbb {R},\mathbb {R}^{n},\rho )$.

The initial conditions associated with (1) are of the form

$$x_{i}(s) = \varphi _{i}(s), \, \, \, s \in (-\theta ,0], i=1,2,\dots ,n,$$

The rest of this paper is organized as follow. In Sect. 2, the existence of weighted pseudo almost-periodic solutions of (1) are discussed. In Sect. 3, a numerical example is given to illustrate the effectiveness of our results. Finally, we draw conclusion in Sect. 4.

2 The Existence and the Global Exponential Stability of Weighted Pseudo Almost Periodic Solution

In this section, we establish some results for the existence of the weighted pseudo almost-periodic solution of (1). For convenience, we introduce the following notations, for $i,j,l = 1,2,\dots ,n$, it will be assumed that $d_{ij}, I_{i}, a_{ij},$ $b_{ijl}: \mathbb {R} \longrightarrow \mathbb {R}$, and there exist constants $\overline{d}_{ij}, \overline{I}_{i}, \overline{a}_{ij}$ and $\overline{b}_{ijl}$ such that

$$\sup _{t \in \mathbb {R}}(\mid d_{ij}(t) \mid ) = \overline{d}_{ij}, \, \, \sup _{t \in \mathbb {R}}(\mid I_{i}(t) \mid )= \overline{I}_{i},$$

$$ \sup _{t \in \mathbb {R}}(\mid a_{ij}(t) \mid ) = \overline{a}_{ij}, \, \, \sup _{t \in \mathbb {R}}(\mid b_{ijl}(t) \mid ) = \overline{b}_{ijl}. $$

Lemma 1

Suppose that assumptions (H2) hold. If $\varphi (.) \in PAP(\mathbb {R},\mathbb {R}^{n},\rho )$, then $\varphi (.-h) \in PAP(\mathbb {R},\mathbb {R}^{n},\rho )$.

Lemma 2

If $\varphi , \psi \in PAP(\mathbb {R},\mathbb {R},\rho )$, then $\varphi \times \psi \in PAP(\mathbb {R},\mathbb {R},\rho )$.

Lemma 3

Suppose that assumptions (H1)–(H3) hold and for all $1 \le i \le n$

$$(H4): \, \, \sup _{T>0} \bigg \{ \int _{-T}^{T} e^{-c_{i} (T+t)} \rho (t) dt \bigg \} < \infty . $$

Define the nonlinear operator $\varGamma$ as follows, for each $\varphi =(\varphi _{1},\ldots ,\varphi _{n}) \in PAP(\mathbb {R},\mathbb {R}^{n},\rho ),$ $(\varGamma _{\varphi })(t):= x_{\varphi }(t)$ where

$$ x_{\varphi }(t)= (\int _{-\infty }^{t} e^{-(t-s)c_{1}} F_{1}(s)ds,\ldots ,\int _{-\infty }^{t} e^{-(t-s)c_{n}} F_{n}(s)ds )^{T}$$

and

$$\begin{aligned} F_{i}(s)&= \sum _{j=1}^{n} d_{ij}(s) g_{j} (\varphi _{j}(s))+ \sum _{j=1}^{n} a_{ij}(s) g_{j} (\varphi _{j}(s-\tau ))\\&\quad + \sum _{j=1}^{n} \sum _{l=1}^{n} b_{ijl}(s) g_{j}(\varphi _{j}(s-\sigma )) g_{l}(\varphi _{l}(s-\nu )) + I_{i}(s), \end{aligned}$$

then $\varGamma$ maps $PAP(\mathbb {R},\mathbb {R}^{n},\rho )$ into itself.

Theorem 1

Suppose that assumptions (H1)–(H4) hold and (H5): there exist nonnegative constants L, p and q such that

$$L = \max _{1 \le i \le n} \{ \frac{\overline{I}_{i}}{c_{i}} \}, p= \max _{1 \le i \le n} \{ c^{-1}_{i} [\sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j}+ \sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}+\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl} L^{g}_{j} M^{g}_{l} ] \} < 1, $$

$$ q = \max _{1 \le i \le n} \{ c^{-1}_{i} [\sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j}+ \sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}+\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl} (L^{g}_{j} M^{g}_{l}+ M^{g}_{j} L^{g}_{l} ) ] \} < 1. $$

Then the delayed HOHNNs of (1) has a unique weighted pseudo almost periodic solution in the region $\mathbb {B}= \{ \varphi \in PAP(\mathbb {R},\mathbb {R}^{n},\rho ),\parallel \varphi - \varphi _{0} \parallel _{\infty } \le \frac{p L}{(1-p)} \},$ where

$$ \varphi _{0}(t)= (\int _{-\infty }^{t} e^{-(t-s)c_{1}} I_{1}(s)ds,\ldots ,\int _{-\infty }^{t} e^{-(t-s)c_{n}} I_{n}(s)ds )^{T}.$$

Proof

One has

$$\begin{aligned} \parallel \varphi _{0} \parallel _{\infty }= & {} \sup _{t \in \mathbb {R}} \max _{ 1 \le i\le n} (\mid \int _{-\infty }^{t} e^{-(t-s)c_{i}} I_{i}(s)ds \mid )\\\le & {} \max _{ 1 \le i\le n} (\frac{\overline{I}_{i}}{c_{i}}) = L. \end{aligned}$$

After

$$\begin{aligned} \parallel \varphi \parallel _{\infty }\le & {} \parallel \varphi - \varphi _{0} \parallel _{\infty } + \parallel \varphi _{0} \parallel _{\infty } \\\le & {} \parallel \varphi - \varphi _{0} \parallel _{\infty } + L. \end{aligned}$$

Set $\mathbb {B}=\mathbb {B}(\varphi _{0},p)= \{ \varphi \in PAP(\mathbb {R},\mathbb {R}^{n},\rho ),\parallel \varphi - \varphi _{0} \parallel _{\infty } \le \frac{pL}{(1-p)} \}$. Clearly, $\mathbb {B}$ is a closed convex subset of $PAP(\mathbb {R},\mathbb {R}^{n},\rho )$ and, therefore, for any $\varphi \in \mathbb {B}$ by using the estimate just obtained, we see that

$$\begin{aligned}&\parallel \varGamma _{\varphi } - \varphi _{0} \parallel _{\infty }\\= & {} \max _{1 \le i \le n} \sup _{t \in \mathbb {R}} \{ \mid \int _{-\infty }^{t} e^{-(t-s)c_{i}} [\sum _{j=1}^{n} d_{ij}(s)g_{j} (\varphi _{j}(s))+\sum _{j=1}^{n} a_{ij}(s)g_{j} (\varphi _{j}(s-\tau )) \\+ & {} \sum _{j=1}^{n} \sum _{l=1}^{n} b_{ijl}(s) g_{j}(\varphi _{j}(s-\sigma )) g_{l}(\varphi _{l}(s-\nu )) ]ds \mid \}\\\le & {} \max _{1 \le i \le n} \sup _{t \in \mathbb {R}} \{ \int _{-\infty }^{t} e^{- c_{i} (t-s)} [\sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j} \parallel \varphi \parallel _{\infty } +\sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j} \parallel \varphi \parallel _{\infty } \\+ & {} \sum _{j=1}^{n}\sum _{l=1}^{n} \overline{b}_{ijl} L^{g}_{j} M^{g}_{l} \parallel \varphi \parallel _{\infty }] ds \}\\\le & {} \max _{1 \le i \le n} \{c^{-1}_{i} [ \sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j}+\sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j} +\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl} L^{g}_{j} M^{g}_{l} ] \} \parallel \varphi \parallel _{\infty } \\= & {} p \parallel \varphi \parallel _{\infty } \le \frac{pL}{1-p}, \end{aligned}$$

where $p = \max \limits _{1 \le i \le n}\{c^{-1}_{i} [\sum \limits _{j=1}^{n} \overline{d}_{ij} L^{g}_{j} +\sum \limits _{j=1}^{n} \overline{a}_{ij} L^{g}_{j} +\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n} \overline{b}_{ijl} L^{g}_{j} M^{g}_{l} ] \} <1$, it implies that $(\varGamma _{\varphi })(t) \in \mathbb {B}$. So, the mapping $\varGamma$ is a self-mapping from $\mathbb {B}$ to $\mathbb {B}$.

Next, we prove that the mapping $\varGamma$ is a contraction mapping of the $\mathbb {B}$. In fact, in view of (H3), for $\forall \phi ,\psi \in \mathbb {B}$, we have

$$\begin{aligned}&\mid (\varGamma _{\phi }-\varGamma _{\psi } )_{i}(t)\mid \\= & {} \mid \int _{-\infty }^{t} e^{-(t-s)c_{i}} [ \sum _{j=1}^{n} d_{ij}(s) (g_{j} (\phi _{j}(s))- g_{j} (\psi _{j}(s))) +\sum _{j=1}^{n} a_{ij}(s) (g_{j} (\phi _{j}(s-\tau ))-g_{j} (\psi _{j}(s-\tau ))) \\+ & {} \sum _{j=1}^{n} \sum _{l=1}^{n} b_{ijl}(s) ( g_{j}(\phi _{j}(s-\sigma )) g_{l}(\phi _{l}(s-\nu ))- g_{j}(\psi _{j}(s-\sigma )) g_{l}(\psi _{l}(s-\nu )))]ds \mid \\\le & {} \int _{-\infty }^{t} e^{-(t-s)c_{i}} [ \sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j}\sup _{t \in \mathbb {R}} \mid \phi _{j}(t)-\psi _{j}(t) \mid +\sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}\sup _{t \in \mathbb {R}} \mid \phi _{j}(t)-\psi _{j}(t) \mid \\+ & {} \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl}\mid g_{j}(\phi _{j}(s-\sigma )) g_{l}(\phi _{l}(s-\nu )) - g_{j}(\psi _{j}(s-\sigma )) g_{l}(\phi _{l}(s-\nu )) \\+ & {} g_{j}(\psi _{j}(s-\sigma )) g_{l}(\phi _{l}(s-\nu )) - g_{j}(\psi _{j}(s-\sigma )) g_{l}(\psi _{l}(s-\nu )) \mid ] ds \\\le & {} \int _{-\infty }^{t} e^{-(t-s)c_{i}} [ \sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j}\sup _{t \in \mathbb {R}} \mid \phi _{j}(t)-\psi _{j}(t) \mid +\sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}\sup _{t \in \mathbb {R}} \mid \phi _{j}(t)-\psi _{j}(t) \mid \\+ & {} \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl} (L^{g}_{j} M^{g}_{l}+ M^{g}_{j} L^{g}_{l}) \parallel \phi - \psi \parallel _{\infty }] ds \\\le & {} c^{-1}_{i} [\sum _{j=1}^{n} \overline{d}_{ij} L^{g}_{j} +\sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}+ \sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl} (L^{g}_{j} M^{g}_{l}+ M^{g}_{j} L^{g}_{l}) ] \parallel \phi - \psi \parallel _{\infty }, \end{aligned}$$

where $i = 1, 2,\dots ,n,$ it follows that

$$\begin{aligned} \parallel \varGamma _{\phi }-\varGamma _{\psi } \parallel _{\infty }\le & {} \max _{1 \le i \le n} \{ c^{-1}_{i} [ \sum _{j=1}^{n} \overline{a}_{ij} L^{g}_{j}+\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b}_{ijl}\\\times & {} (L^{g}_{j} M^{g}_{l}+ M^{g}_{j} L^{g}_{l} ) ] \} \parallel \phi - \psi \parallel _{\infty }. \end{aligned}$$

Notice that $q= \max \limits _{1 \le i \le n} \{ c^{-1}_{i} [ \sum \limits _{j=1}^{n} \overline{d_{ij}} L^{g}_{j}+ \sum \limits _{j=1}^{n} \overline{a_{ij}} L^{g}_{j}+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n} \overline{b}_{ijl} (L^{g}_{j} M^{g}_{l}+ M^{g}_{j} L^{g}_{l} ) ] \} < 1$, it is clear that the mapping $\varGamma$ is a contraction. Therefore the mapping $\varGamma$ possesses a unique fixed point $z^{*} \in \mathbb {B}, Tz^{*} = z^{*}$. So $z^{*}$ is a weighted pseudo almost-periodic solution of system (1) in the region $\mathbb {B}$. The proof of Theorem 1 is now complete.

Theorem 2

If the conditions (H1)–(H5) hold, then system (1) has a unique weighted pseudo almost periodic solution z(t) which is globally exponentially stable.

Proof

It follows from Theorem 1 that system (1) has at least one weighted pseudo almost periodic solution $z(t)=(z_{1}(t),\ldots ,z_{n}(t))^{T} \in \mathbb {B}$ with initial value $u(t)=(u_{1}(t),\ldots ,u_{n}(t))^{T}$. Let $x(t)=(x_{1}(t),\ldots ,x_{n}(t))^{T}$ be an arbitrary solution of system (1) with initial value $\varphi ^{*}(t) =(\varphi _{1}^{*}(t),\ldots ,\varphi _{n}^{*}(t))^{T}$.

Let $y_{i}(t)=x_{i}(t)-z_{i}(t)$, $\varphi _{i}(t)=\varphi _{i}^{*}(t)-u_{i}(t)$ $i=1 \ldots n$, then

$$\begin{aligned} y'_{i}(t)&= - c_{i}(t) y_{i}(t)+ \sum _{j=1}^{n} d_{ij}(t) (g_{j} (y_{j}(t-u)+ z_{j}(t-u))-g_{j} (z_{j}(t-u))) \nonumber \\&\quad +\sum _{j=1}^{n} a_{ij}(t) (g_{j} (y_{j}(t-\tau )+ z_{j}(t-\tau ))-g_{j} (z_{j}(t-\tau ))) \nonumber \\&\quad + \sum _{j=1}^{n} \sum _{l=1}^{n} b_{ijl}(t) ( g_{j} (y_{j}(t-\sigma )+ z_{j}(t-\sigma ))g_{l} (y_{l}(t-\nu )\nonumber \\&\quad + z_{l}(t-\nu )) - g_{j}(z_{j}(t-\sigma ))g_{l}(z_{l}(t-\nu )) ), \, \, i=1,\ldots ,n. \end{aligned}$$

(2)

Let $F_{i}$ be defined by

$$F_{i}(w)= c_{i}-w- \sum _{j=1}^{n} \overline{d_{ij}} L^{g}_{j}- \sum _{j=1}^{n} \overline{a_{ij}} L^{g}_{j} e^{w \tau } -\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b_{ijl}} ( L^{g}_{j} e^{w \sigma } M^{g}_{l} + M^{g}_{j} L^{g}_{l} e^{w \nu } ),$$

where $i=1,\ldots ,n$, $w\in [0,+\infty [$ and by (H5), we obtain that

$$F_{i}(0)= c_{i}- \sum _{j=1}^{n} \overline{d_{ij}} L^{g}_{j}-\sum _{j=1}^{n} \overline{a_{ij}} L^{g}_{j} -\sum _{j=1}^{n} \sum _{l=1}^{n} \overline{b_{ijl}} ( L^{g}_{j} M^{g}_{l} + M^{g}_{j} L^{g}_{l} ) > 0. $$

Since $F_{i}(.)$ is continuous on $[0,\infty [$ and $F_{i}(w) \longrightarrow - \infty ; w\longmapsto +\infty$, there exist $\varepsilon _{i}^{*} > 0$ such that $F_{i}(\varepsilon _{i}^{*}) = 0$ and $F_{i}(\varepsilon _{i}) > 0$ for $\varepsilon _{i} \in (0,\varepsilon _{i}^{*})$.

By choosing $\eta = \min \{ \varepsilon _{1}^{*},\ldots ,\varepsilon _{n}^{*} \}$, we obtain that the weighted pseudo almost periodic solution of system (1) is globally exponentially stable. The globally exponential stability implies that the pseudo almost periodic solution is unique. We complete the proof.

3 Application

In order to illustrate some feature of our main results, we will apply the model for $n=2$:

$$\begin{aligned} x'_{i}(t)&= - c_{i} x_{i}(t)+ \sum _{j=1}^{2} d_{ij}(t) g_{j} (x_{j}(t))+ \sum _{j=1}^{2} a_{ij}(t) g_{j} (x_{j}(t-\tau )) \nonumber \\&\quad + \sum _{j=1}^{2} \sum _{l=1}^{2} b_{ijl}(t) g_{j}(x_{j}(t-\sigma )) g_{l}(x_{l}(t-\nu )) + I_{i}(t), \, \, 1\le i \le 2, \end{aligned}$$

(3)

where $c_{1}= c_{2} = 2, g_{1}(t) = g_{2}(t) = \sin t, \tau = \sigma = \nu = 1, \rho (t)= e^{t}$

Fig. 1.

Example 1.

$$(d_{ij}(t))_{1 \le i,j \le 2} = \left( \begin{array}{cc} 0.2 \sin t + 0.1 e^{-t} &{} 0.1 \cos t \\ 0.1 \sin \sqrt{2}t + 0.1 e^{-t} &{} 0.2 \cos \sqrt{2}t + 0.1 e^{-t} \\ \end{array} \right) $$

$$ (a_{ij}(t))_{1 \le i,j \le 2} = \left( \begin{array}{cc} 0.1 \cos t + 0.1 e^{-t} &{} 0.2 \sin t \\ 0.4 \cos t + 0.1 e^{-t} &{} 0.1 \sin t + 0.1 e^{-t} \\ \end{array} \right) , (I_{i}(t))_{1 \le i \le 2} = \left( \begin{array}{c} 0.8 \cos \sqrt{5}t \\ 0.5 \sin t + 0.1 e^{-t}\\ \end{array} \right) $$

$$(b_{1jl}(t))_{1 \le j,l \le 2} = \left( \begin{array}{cc} 0 &{} 0.3 \sin \sqrt{3}t + 0.1 e^{-t} \\ 0 &{} 0 \\ \end{array} \right) , (b_{2jl}(t))_{1 \le j,l \le 2} = \left( \begin{array}{cc} 0 &{} 0.2 \cos \sqrt{5}t + 0.1 e^{-t} \\ 0 &{} 0 \\ \end{array} \right) $$

Then $L = 0.4, p= 0.75< 1, q = 0.9 < 1$ and $\sup \limits _{T>0} \{ \int _{-T}^{T} e^{-c_{i} (T+t)} \rho (t) dt \} < \infty$.

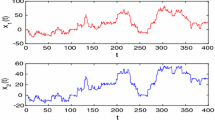
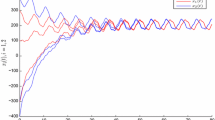
Consequently, it is not difficult to verify that this example satisfies Theorem 1, then model (1) has a unique weighted pseudo almost periodic solution in the considered region. Figure 1 shows the oscillations of the solution of Eq. (1).

4 Conclusion

In nature there is no phenomenon that is purely periodic, and this gives the idea to consider the almost-periodic oscillation, the pseudo almost-periodic and weighted pseudo almost-periodic situations. So, in this paper, some sufficient conditions are presented ensuring the existence and uniqueness of weighted pseudo almost-periodic solutions of HOHNNs with delays (1). Finally, an illustrative example is given to demonstrate the effectiveness of the obtained results.