1 Introduction

It is well known that studies on neural dynamic systems not only involve a discussion of stability properties [1–3], but also involve many dynamic behaviors such as periodic oscillatory behavior [4, 5], almost periodic oscillatory properties [6–10], chaos and bifurcation [11]. In the past four decades, people have paid much attention to the problem on almost periodic solutions and pseudo almost periodic solutions for cellular neural networks (CNNs) with leakage delays because of its successful applications in variety of areas such as signal processing, pattern recognition, chemical processes, nuclear reactors, biological systems, static image processing, associative memories, optimization problems and so on (see [12–16] and the references cited therein).

We note that many of the above works concerning almost periodic solutions only considered the case of time delays, including time-varying delays and distributed delays. Moreover, since the complexity of problems in reality, models describing these problems should reflect effects of such fluctuation factors. Hence, it is significantly important in theory and application to study CNNs with complex deviating arguments, which has a wider meaning than CNNs with other delays. Recently, sufficient conditions for the existence of periodic solutions of continuous-time CNNs and discrete-time CNNs with complex deviating arguments have been obtained in [17, 18]. However, to the best of our knowledge, there is no result on the existence of almost periodic solutions and pseudo almost periodic solutions of CNNs with complex deviating arguments.

Motivated by the above discussions, in this paper, we will consider the existence of pseudo almost periodic solutions for the following CNNs with leakage delays and complex deviating arguments:

$$\begin{aligned} x_{i}^{\prime}(t) & = - c_{i} (t)x_{i} (t - \eta_{i} (t)) + \sum\limits_{{j = 1}}^{n} {a_{{ij}} } (t)f_{j} (x_{j} (t))\quad \\ & \quad + \sum\limits_{{j = 1}}^{n} {b_{{ij}} } (t)g_{j} (x_{j} (x_{j} (t))) + I_{i} (t),\quad i = 1,2, \ldots ,n, \\ \end{aligned}$$
(1.1)

where n corresponds to the number of units in a neural network, \(x_{i}(t)\) corresponds to the state vector of the ith unit at the time \(t, c_{i}(t)>0\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time \(t, a_{ij}(t)\) and \(b_{ij}(t)\) are the connection weights at the time \(t, \eta_{i}(t)\ge 0\) denotes the leakage delay, and \(I_{i}(t)\) denotes the external inputs at time t, \(f_{j}\) and \(g_{j}\) are activation functions of signal transmission, \(i,j\in J=\{1, 2, \ldots , n\}\). From the basic theory on state-dependent delay-differential equations in [19], CNNs (1.1) is a special type of state-dependent delay-differential equations. Here \(x_{j}(x_{j}(t))=x_{j}(t-\tau_{j}(t))\), and \(\tau_{j}(t )=t-x_{j}(t)\) is the state deviating argument, which is said to be complex deviating argument.

For convenience, we denote by \({\mathbb{R}}^{n}({\mathbb{R}}={\mathbb{R}}^{1})\)) the set of all n-dimensional real vectors (real numbers). Let \(\{x_{i} \}=(x_{1} , \ x_{2} , \ldots , x_{n}) .\) For any \(\{x_{i} \} \in {\mathbb {R}}^{n}\), we let \(\left| x \right|\) denote the absolute-value vector given by \(\left| x \right| = \left\{ {\left| {x_{i} } \right|} \right\}\) and define \(\left\| x \right\| = \mathop {\max }\limits_{{i \in J}} \left| {x_{i} } \right|\). A matrix or vector \(A\ge 0\) means that all entries of A are greater than or equal to zero. \(A>0\) can be defined similarly. For matrices or vectors \(A_{1}\) and \(A_{2}\), \(A_{1}\ge A_{2}\) (resp. \(A_{1}> A_{2}\)) means that \(A_{1}- A_{2}\ge 0\) (resp. \(A_{1}- A_{2}>0). BC({\mathbb {R}},{\mathbb {R}}^{n})\) denotes the set of bounded and continuous functions from \({\mathbb {R}}\,\hbox {to}\,{\mathbb {R}}^{n}\), and \(BUC({\mathbb {R}},{\mathbb {R}}^{n})\) denotes the set of bounded and uniformly continuous functions from \({\mathbb {R}}\) to \({\mathbb {R}}^{n}\). Note that \((BC({\mathbb{R}},{\mathbb{R}^{n}}),\left\| \cdot \right\|_{\infty })\) is a Banach space, where \(\left\| \cdot \right\|_{\infty }\) denotes the supremum norm \(\left| f \right|_{\infty } : = \mathop {\sup }\limits_{{t \in {\mathbb{R}}}} \left| {f(t)} \right|\). For \(h\in BC({\mathbb {R}},{\mathbb {R}})\), let \(h^+\) and \(h^-\) be defined as

$$h^{+} = \mathop {\sup }\limits_{{t \in {\mathbb{R}}}} \left| {h(t)} \right|,\quad h^{-} = \mathop {\inf }\limits_{{t \in {\mathbb{R}}}} \left| {h(t)} \right|.$$

2 Preliminaries

In this section, we shall first recall some basic definitions, lemmas which are used in what follows.

Definition 2.1

(see [20, 21]). Let \(u(t)\in BC({\mathbb {R}},{\mathbb {R}}^{n}). u(t)\) is said to be almost periodic on \({\mathbb {R}}\) if, for any \(\varepsilon >0\), the set \(T(u,\varepsilon ) = \left\{ {\delta :\left\| {u(t + \delta ) - u(t)} \right\| < \varepsilon \quad {\text{for}}\;{\text{all}}\;t \in {\mathbb{R}}} \right\}\) is relatively dense, i.e., for any \(\varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\) with the property that, for any interval with length \(l(\varepsilon )\), there exists a number \(\delta =\delta (\varepsilon )\) in this interval such that \(\left\| {u(t + \delta ) - u(t)} \right\| < \varepsilon ,{\mkern 1mu} {\text{for all}} {\mkern 1mu} \, t \in {\mathbb{R}}.\) We denote by \(AP({\mathbb {R}},{\mathbb {R}}^{n})\) the set of the almost periodic functions from \({\mathbb{R}}\) to \(\mathbb {R}^{n}\). Besides, the concept of pseudo almost periodicity was introduced by C. Zhang in the early nineties. It is a natural generalization of the classical almost periodicity. Precisely, define the class of functions \(PAP_{0}({\mathbb {R}},{\mathbb{R}}^{n})\) as follows:

$$\left\{ {f \in BC(\mathbb{R},\mathbb{R}^{n} )\left| {\mathop {\lim }\limits_{{T \to + \infty }} \frac{1}{{2T}}\int_{{ - T}}^{T} | f(t)} \right|{\text{d}}t = {\mathbf{0}}} \right\}.$$

A function \(f \in BC({\mathbb{R}},{\mathbb{R}}^{n} )\) is called pseudo almost periodic if it can be expressed as

$$f = h + \varphi ,$$

where \(h\in {AP({\mathbb{R}}, {\mathbb{R}}^{n})}\) and \(\varphi \in {PAP_{0}({\mathbb{R}},{\mathbb{R}}^{n})}\). The collection of such functions will be denoted by \(PAP({\mathbb{R}},{\mathbb{R}}^{n})\). The functions h and \(\varphi\) in above definition are, respectively, called the almost periodic component and the ergodic perturbation of the pseudo almost periodic function f. The decomposition given in definition above is unique. Observe that \((PAP({\mathbb{R}},{\mathbb{R}}^{n} ),\left\| . \right\|_{\infty } )\) is a Banach space and \(AP({\mathbb{R}},{\mathbb{R}}^{n})\) is a proper subspace of \(PAP({\mathbb{R}},{\mathbb{R}}^{n})\) since the function \(\phi (t) = {\text{cos}}\pi t + {\text{cos}}t + {\text{e}}^{{-t^{4} \sin ^{2} t}}\) is pseudo almost periodic, but not almost periodic [15].

For \(i,j \in J,\) it will be assumed that \(c_{i} :{\mathbb{R}} \to (0, + \infty )\) is an almost periodic function, \(\eta_{i }: {\mathbb {R}}\rightarrow [0, \ +\infty )\), \(I_{i}, \ a_{ij}, \ b_{ij}, \ :\mathbb {R}\rightarrow {\mathbb {R}}\) are pseudo almost periodic on \({\mathbb{R}}\).

We also make the following assumption which will be used later.

\((A_1)\) For each \(j\in J\), there exist nonnegative constants \(L^{f}_{j}\) and \(L^{g}_{j}\) such that

$$g_{j} (0) = f_{j} (0) = 0,\;\left| {f_{j} (u) - f_{j} (v)} \right| \le L_{j}^{f} \left| {u - v} \right|,\left| {g_{j} (u) - g_{j} (v)} \right| \le L_{j}^{g} \left| {u - v} \right|,\quad {\text{for}}\;{\text{all}}\;u,\;v \in R.$$

Lemma 2.1

(see [15], Lemma 4 and Remark 5). Let \({\mathbf{Z}} = \{ f\left| {f,f^{\prime } \in PAP({\mathbb{R}},{\mathbb{R}}^{n} )} \right.\}\) be equipped with the induced norm defined by

$$\left\| f \right\|_{{\mathbf{Z}}} = \max \left\{ {\left\| f \right\|_{\infty } ,\left\| {f^{\prime } } \right\|_{\infty } } \right\} = \max \left\{ {\mathop {\sup }\limits_{{t \in {\mathbb{R}}}} \left\| {f(t)} \right\|,\mathop {\sup }\limits_{{t \in {\mathbb{R}}}} \left\| {f^{\prime } (t)} \right\|} \right\}.$$

Then, \({\mathbf{Z}}\) is a Banach space.

Let \(L>0, \ l>0\) and \(0<\theta <1\) be three constants such that

$$B^{L} = \{ \varphi |\varphi \in PAP(\mathbb{R},\mathbb{R}^{n} ),\;\{ \left| {\varphi_{i} (t_{1} ) - \varphi_{i} (t_{2} )} \right|\}\le \{ L|t_{1} - t_{2} |\} ,\quad {\text{for all}}\;t_{1} ,t_{2} \in{\mathbb{R}}\} ,$$

and

$$B^{*} = \left\{ {\varphi \left| {\left\| {\varphi - \varphi_{0} } \right\|_{{\mathbf{Z}}} \le \frac{{\theta l}}{{1 - \theta }},\;\varphi \in {\mathbf{Z}} ,} \right.} \right\}$$

where

$$\varphi_{0} = \left\{ {\int_{{ - \infty }}^{t} {{\text{e}}^{{ - \int_{s}^{t} {c_{i} } (w)dw}} } I_{i} (s){\text{d}}s} \right\},\;\left\{ {\max \left\{ {\frac{{I_{i}^{ + } }}{{c_{i}^{ - } }},\;\left( {1 + \frac{{c_{i}^{ + } }}{{c_{i}^{ - } }}} \right)I_{i}^{ + } } \right\}} \right\} \le \{ l\} .$$

Then, we get

Lemma 2.2

\(B^{L}\) is a closed subset of \(PAP({\mathbb{R}},{\mathbb{R}}^{n})\).

Proof

Suppose that \(\{x_p\}_{p=1}^{+\infty }\subseteq B^{L}\) satisfies

$$\mathop {\lim }\limits_{{p \to + \infty }} \left\| {x_{p} - \varphi } \right\|_{\infty } = 0.$$
(2.1)

Obviously, \(\varphi \in PAP({\mathbb{R}},{\mathbb{R}}^{n})\). We next show that

$$\{ \left| {\varphi_{i} (t_{1} ) - \varphi_{i} (t_{2} )} \right|\} \le \{ L\left| {t_{1} - t_{2} } \right|\} ,\quad {\text{for}}\;{\text{all}}\;t_{1} ,t_{2} \in{\mathbb{R}}.$$
(2.2)

Let \(t_{1}, t_{2}\in {\mathbb{R}}\), for any \(\varepsilon >0\), from (2.1), we can choose \(p>0\) such that

$$\left\| {x_{p} - \varphi } \right\|_{\infty } < \frac{\varepsilon }{2}.$$
(2.3)

Since \(x_{p}\in B^{L}\), we obtain

$$\left| {x_{p} (t_{1} ) - x_{p} (t_{2} )} \right| \le \{ L\left| {t_{1} - t_{2} } \right|\} ,$$

which, together with (2.3), implies that

$$\begin{aligned} |\varphi (t_{1})-\varphi (t_{2})|&\le |\varphi (t_{1})-x_{p}(t_{1})|+|x_{p}(t_{1})-x_{p}(t_{2})|+|x_{p}(t_{2})-\varphi (t_{2})|\nonumber \\&< \{\varepsilon +L| t_{1} - t_{2} | \}. \end{aligned}$$
(2.4)

Letting \(\varepsilon \rightarrow 0\), (2.4) provides that (2.2) is true. Hence, \(B^L\) is a closed subset of \(PAP({\mathbb{R}},{\mathbb{R}}^{n})\). This completes the proof of Lemma 2.2. \(\square\)

Definition 2.2

(see [20, 21]). Let \(x\in {\mathbb{R}}^{n}\) and \(Q(t)\) be an \(n\times n\) continuous matrix defined on \({\mathbb{R}}\). The linear system

$$x^{\prime } (t) = Q(t)x(t)$$
(2.5)

is said to admit an exponential dichotomy on \({\mathbb{R}}\) if there exist positive constants \(k, \alpha\), projection \(P\) and the fundamental solution matrix \(X(t)\) of (2.5) satisfying

$$\begin{aligned}&\Vert X(t)PX^{-1}(s)\Vert \le ke^{-\alpha (t-s)}\quad \hbox {for}\; t\ge s,\\&\Vert X(t)(I-P)X^{-1}(s)\Vert \le ke^{-\alpha (s-t)}\quad \hbox {for}\; t\le s. \end{aligned}$$

Lemma 2.3

(see [20, 21]). Assume that \(Q(t)\) is an almost periodic matrix function and \(g (t) \in PAP({\mathbb{R}},{\mathbb{R}}^{n})\). If the linear system (2.5) admits an exponential dichotomy, then pseudo almost periodic system

$$\begin{aligned} x^{\prime}(t)=Q(t)x(t)+g(t) \end{aligned}$$
(2.6)

has a unique pseudo almost periodic solution \(x(t)\), and

$$\begin{aligned} x(t)=\int_{-\infty }^{t}X(t)PX^{-1}(s)g(s)\hbox{d}s-\int ^{+\infty }_{t} X(t)(I-P)X^{-1}(s)g(s)\hbox{d}s. \end{aligned}$$
(2.7)

Lemma 2.4

(see [20–22]). Let \(c_{i}(t)\) be an almost periodic function on \({\mathbb{R}}\) and

$$\begin{aligned} M[c_{i}]=\lim \limits_{T\rightarrow +\infty }\frac{1}{T}\int_{t}^{t+T} c_{i}(s)ds>0, \quad i=1, 2, \ldots , n. \end{aligned}$$

Then, the linear system

$$\begin{aligned} x^{\prime}(t)= \text{ diag } (-c_{1}(t), -c_{2}(t), \cdots , -c_{n}(t))x(t) \end{aligned}$$

admits an exponential dichotomy on \({\mathbb{R}}\).

3 Existence and uniqueness of pseudo almost periodic solutions

In this section, we establish sufficient conditions on the existence and uniqueness of pseudo almost periodic solutions of (1.1).

Theorem 3.1

Let \((A_{1})\) hold. Suppose that there exist constants \(\alpha_{i}>0\) and \(L>0,\) such that

$$\begin{aligned} 0<\theta&= \max \limits_{i\in J}\left\{ \left( 1+\frac{c_{i }^{+}}{c_{i }^{-}}\right) \left[ c_{i } ^{+}\eta_{i }^{+} +\sum ^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})\right] , \frac{1}{c_{i }^{-}} \left[ c_{i } ^{+}\eta_{i }^{+} +\sum ^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})\right] \right\} <1,\end{aligned}$$
(3.1)
$$\begin{aligned}&\left\{ \left[ c_{i} ^{+} + c_{i}^{+} \eta_{i} ^{+} + \sum_{j=1}^{n}a_{ij} ^{+}(L^{f}_{j} + b_{ij}^{+} L^{g}_{j})\right] \frac{l}{1-\theta } + I_{i} ^{+}\right\} \le \{L\}, \end{aligned}$$
(3.2)

and

$$\begin{aligned} -c_{i} ^{-}+ c_{i}^{+}\eta_{i}^{+}+ \sum ^n_{j=1} a_{ij}^{+} L^{f}_{j} + \sum ^n_{j=1} b_{ij}^{+} L^{g}_{j}(1+L) \le - \alpha_{i},\ c_{i}^{-}- \alpha_{i}+c_{i}^{+}\left( 1-\frac{\alpha_{i}}{c_{i}^{+}}\right) <1, \ i\in J. \end{aligned}$$
(3.3)

Then, there exists a unique pseudo almost periodic solution of equation (1.1) in the region \({\mathbf{B}}= B^{L}\bigcap B^{*}\).

Proof

It follows from Lemma 2.1 and Lemma 2.2 that \({\mathbf{B}}\) is a closed subset of \({\mathbf{Z}}\). Let \(\varphi \in \mathbf{B}\). Obviously, the boundedness of \(\varphi^{\prime}\) and \((A_{1})\) imply that \(f_{j}, \ g_{j}\) and \(\varphi_{i }\) are uniformly continuous functions on \({\mathbb{R}}\) for \(i, j\in J\). Set \(\widetilde{f}(t,z)=\varphi_{i }(t-z) (i \in J)\). By Theorem 5.3 in [20, p. 58], and Definition 5.7 in [20, p. 59], we can obtain that \(\widetilde{f}\in PAP({\mathbb{R}}\times \Omega )\) and \(\widetilde{f}\) is continuous in \(z\in K\) and uniformly in \(t\in {\mathbb {R}}\) for all compact subset \(K\) of \(\Omega \subset {\mathbb{R}}\). This, together with \(\eta_{i }\in PAP({\mathbb{R}},{\mathbb{R}})\) and Theorem 5.11 in [20, p. 60], implies that

$$\begin{aligned} \varphi_{i }(t-\eta_{i }(t))\in PAP({\mathbb{R}},{\mathbb{R}}), \quad \ i \in J. \end{aligned}$$

From Corollary 5.4 in [r20, p. 58], we have

$$\begin{aligned} f_{j}( \varphi_{ j}(t)), \ g_{j}( \varphi_{ j}( \varphi_{ j}(t) ))\in PAP({\mathbb{R}},{\mathbb{R}}), \quad \ j\in J, \end{aligned}$$
(3.4)

which, together with the fact that \(\varphi_{i }(t-\eta_{i }(t))\in PAP({\mathbb{R}},{\mathbb{R}})\), implies

$$\begin{aligned} c_{i }(t)\int_{t-\eta_{i }(t)}^{t}\varphi_{i }^{\prime}(s)\hbox{d}s=c_{i }(t)\varphi_{i }(t)-c_{i }(t)\varphi_{i }(t-\eta_{i }(t))\in PAP({\mathbb{R}},{\mathbb{R}}) , \quad \ i \in J, \end{aligned}$$
(3.5)

and

$$\begin{aligned} \sum_{j=1}^{n}a_{ij}(t)f_{j}( \varphi_{j}(t)) + \sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t))) + I_{i}(t)\in PAP({\mathbb{R}},{\mathbb{R}}), \ i \in J. \end{aligned}$$
(3.6)

For any \(\varphi \in {\mathbf{B}}\), we consider the pseudo almost periodic solution \(x^{\varphi }(t)\) of nonlinear pseudo almost periodic differential equations:

$$\begin{aligned} x_{i}^{\prime}(t)&= -c_{i}(t)x_{i}(t )+c_{i}(t)\int_{t-\eta_{i}(t)}^{t}\varphi_{i}^{\prime}(s)ds+ \sum_{j=1}^{n}a_{ij}(t)f_{j}( \varphi_{j}(t))\nonumber \\ & \quad \quad +\,\sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t) )) + I_{i}(t), \ i\in J. \end{aligned}$$
(3.7)

Then, notice that \(M[c_{i}]>0, \ i=1, \ 2, \ \ldots , n\), it follows from Lemma 2.4 that the linear system

$$\begin{aligned} x_{i}^{\prime}(t)=-c_{i}(t)x_{i}(t), i\in J, \end{aligned}$$
(3.8)

admits an exponential dichotomy on \({\mathbb{R}}\). Thus, by Lemma 2.3, we obtain that the system (3.7) has exactly one pseudo almost periodic solution:

$$\begin{aligned} x^{\varphi }(t)&= \{x^{\varphi }_{i}(t)\}\nonumber \\&= \left\{ \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}\left[ c_{i}(s) \int_{s-\eta_{i}(s)}^{s}\varphi_{i}^{\prime}(u)\hbox{d}u+ \sum ^n_{j=1}a_{ij}(s)f_{j}( \varphi_{j}(s))\right. \right. \nonumber \\ & \quad \quad \left. \left. +\, \sum_{j=1}^{n}b_{ij}(s) g_{j}( \varphi_{j}( \varphi_{j}(s)))+ I_{i}(s)\right]\hbox{d}s\right\} . \end{aligned}$$
(3.9)

Let

$$\begin{aligned} F_{i}(t)&= c_{i}(t)\int_{t-\eta_{i}(t)}^{t} \varphi_{i}^{\prime}(u)\hbox{d}u + \sum ^n_{j=1}a_{ij}(t) f_{j}( \varphi_{j}(t))\\& \quad + \sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t))) + I_i(t), \ i\in J. \end{aligned}$$

Then, \(\{F_{i}\}\in PAP({\mathbb{R}},{\mathbb{R}}^{n})\), and

$$\begin{aligned} x_{i}^{\prime}(t)=-c_{i}(t)x_{i}(t)+F_{i}(t), \ i\in J, \end{aligned}$$

has exactly one pseudo almost periodic solution

$$\begin{aligned} \left\{ \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}F_{i}(s)ds\right\} \in PAP({\mathbb{R}},{\mathbb{R}}^{n}). \end{aligned}$$
(3.10)

From (3.5), (3.6) and (3.10), we get

$$\begin{aligned} (x^{\varphi }(t))^{\prime}&= \left\{ \left[ c_{i}(t)\int_{t-\eta_{i}(t)}^{t} \varphi_{i}^{\prime}(u)\hbox{d}u + \sum ^n_{j=1}a_{ij}(t) f_{j}( \varphi_{j}(t))\right. \right. \nonumber \\ & \quad \quad \left. + \, \sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t))) + I_i(t)\right] \nonumber \\ & \quad \quad - \, c_{i}(t)\int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}[c_{i}(s)\int_{s-\eta_{i}(s)}^{s} \varphi_{i}^{\prime}(u) \hbox{d}u\nonumber \\ & \quad \quad \left. + \, \sum ^n_{j=1}a_{ij}(s) f_{j}( \varphi_{j}(s)) + \sum_{j=1}^{n}b_{ij}(s) g_{j}( \varphi_{j}( \varphi_{j}(s))) + I_i(s)]\hbox{d}s\right\} \nonumber \\ &= \{ F_{i}(t) -c_{i}(t)\int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}F_{i}(s)\hbox{d}s\}\in PAP(\mathbb {R},{\mathbb{R}}^{n}). \end{aligned}$$
(3.11)

Now, we define a mapping \(T:{\mathbf{B}} \rightarrow PAP({\mathbb{R}},{\mathbb{R}}^{n})\) by setting

$$\begin{aligned} (T\varphi )(t)=x^{\varphi }(t), \quad \forall\, \varphi \in {\mathbf{B}}. \end{aligned}$$

First we show that for any \(\varphi \in {\mathbf{B}} , \ T \varphi =x^{\varphi } \in {\mathbf{B}}\).

Note that

$$\begin{aligned} \Vert \varphi_{0}\Vert_{\infty }&= \max \limits_{i\in J}\left\{ \sup \limits_{t\in {\mathbb{R}}}|\int ^t_{-\infty }{\rm e}^{-\int ^t_{s}c_{i}(w)dw}I_{i}(s)ds |\right\} \le \max \limits_{i\in J}\left\{ \frac{I_{i}^{+}}{c_{i}^{-}}\right\} \le l,\\ \Vert \varphi_{0} ^{\prime}\Vert_{\infty }&= \max \limits_{i\in J}\left\{ \sup \limits_{t\in {\mathbb{R}}}|-c_{i}(t)\varphi_{0} (t) +I_{i}(t) |\right\} \le \max \limits_{i\in J}\left\{ (1+\frac{c_{i}^{+}}{c_{i}^{-}})I_{i}^{+}\right\} \le l. \end{aligned}$$

We get

$$\begin{aligned} ||\varphi ||_{\mathbf{Z}}\le ||\varphi -\varphi_{0}||_{\mathbf{Z}} +||\varphi_{0}||_{\mathbf{Z}}\le \frac{\theta l}{1-\theta }+l=\frac{l}{1-\theta } . \end{aligned}$$
(3.12)

\(\square\)

According to \((A_{1})\), (3.1), (3.2), (3.3) and (3.12), we obtain

$$\begin{aligned} |(T\varphi )(t)- \varphi_{0}(t)|&= \left\{ \left| \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}[c_{i}(s)\int_{s-\eta_{i}(s)}^{s}\varphi_{i}^{\prime}(u)\hbox{d}u+ \sum^n_{j=1}a_{ij}(s)f_{j}( \varphi_{j}(s))\right. \right. \\ & \quad \quad \left. \left. + \, \sum_{j=1}^{n}b_{ij}(s) g_{j}( \varphi_{j}( \varphi_{j}(s)))]\hbox{d}s\right| \right\} \\ & \, \le \left\{ \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t} c_{i }^{-} \hbox{d}u}[c_{i } ^{+}\eta_{i }^{+} +\sum ^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})]ds\Vert \varphi \Vert_{\mathbf{Z}} \right\} \\ & \, \le \left\{ \frac{1}{c_{i }^{-}} \left[ c_{i } ^{+}\eta_{i }^{+} +\sum ^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})\right] \frac{l}{1-\theta }\right\} \\ & \, \le \left\{ \frac{\theta l}{1-\theta }\right\}, \quad \forall t \in {\mathbb{R}}, \end{aligned}$$

and

$$\begin{aligned} |((T\varphi )(t)- \varphi_{0}(t))'|&= \left\{ \left| \left[ c_{i}(t)\int_{t-\eta_{i}(t)}^{t} \varphi_{i}'(u) {\rm d}u + \sum ^n_{j=1}a_{ij}(t) f_{j}( \varphi_{j}(t)) + \sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t))) \right] \right. \right. \\ & \quad \quad - \, c_{i}(t)\int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)du}\left[ c_{i}(s)\int_{s-\eta_{i}(s)}^{s} \varphi_{i}'(u) {\rm d}u + \sum ^n_{j=1}a_{ij}(s) f_{j}( \varphi_{j}(s))\right. \\ & \quad \quad \left. \left. \left. + \, \sum_{j=1}^{n}b_{ij}(s) g_{j}( \varphi_{j}( \varphi_{j}(s))) \right] {\rm d}s\right| \right\} \\ & \,\le \left\{ \left( 1+\frac{c_{i }^{+}}{c_{i }^{-}}\right) \left[ c_{i } ^{+}\eta_{i }^{+} +\sum ^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})\right] \frac{l}{1-\theta }\right\} \\ & \,\le \left\{ \frac{\theta l}{1-\theta }\right\} , \quad \forall t \in {\mathbb {R}}. \end{aligned}$$

It follows that

$$\begin{aligned} ||T\varphi -\varphi_{0}||_{\infty }&\le \frac{\theta l}{1-\theta },||(T\varphi -\varphi_{0})'||_{\infty }\le \frac{\theta l}{1-\theta },\nonumber \\ ||T\varphi ||_{\infty }&\le ||T\varphi -\varphi_{0}||_{\infty }+||\varphi_{0}||_{\infty }\le \frac{\theta l}{1-\theta }+l=\frac{l}{1-\theta },\\ |((T\varphi ) (t))'|&= \left\{ \left| -c_{i}(t)((T \varphi ) (t))_{i}+ c_{i}(t)\int_{t-\eta_{i}(t)}^{t}\varphi_{i}'(s){\rm d}s+ \sum_{j=1}^{n}a_{ij}(t)f_{j}( \varphi_{j}(t))\right. \right. \nonumber \\ & \quad \quad \left. \left. + \, \sum_{j=1}^{n}b_{ij}(t) g_{j}( \varphi_{j}( \varphi_{j}(t))) + I_{i}(t)\right| \right\} \nonumber \\ & \le \left\{ \left[ c_{i} ^{+} + c_{i}^{+} \eta_{i} ^{+} + \sum_{j=1}^{n}a_{ij} ^{+}(L^{f}_{j} + b_{ij}^{+} L^{g}_{j} )\right] \frac{l}{1-\theta } + I_{i} ^{+}\right\} \le \{L\}, \quad \forall t \in {\mathbb {R}},\nonumber \end{aligned}$$
(3.13)

and

$$\left| {(T\varphi )(t_{1} ) - (T\varphi )(t_{2} )} \right| = \left\{ {\left| {(((T\varphi )(t))_{i} )^{\prime } |_{{t = t_{1} + \Delta (t_{2} - t_{1} )}} (t_{1} - t_{2} )} \right|} \right\} \le \{ L|t_{1} - t_{2} |\} ,$$
(3.14)

where \(\text{for}\,\text{all} \ t_{1}, t_{2}\in {\mathbb{R}}, \ \Delta \in (0, \ 1)\), and \(t_{1}+\Delta (t_{2}-t_{1})\) is the mean point in Lagrange’s mean value theorem. Thus, (3.13) and (3.14) yield \(T\varphi \in {\mathbf{B}}\). So, the mapping \(T\) is a self-mapping from \({\mathbf{B}}\) to \({\mathbf{B}}\) .

We next prove that the mapping \(T\) is a contraction mapping of the \(\mathbf{B}\). In fact, in view of \((A_{1})\), (3.1), (3.2), (3.9) and (3.11) , for \(\varphi , \psi \in {\mathbf{B}}\), we have

$$\begin{aligned} |(T\varphi )(t) -(T\psi )(t)|&= \{|((T\varphi )(t) -(T\psi )(t))_{i}|\}\nonumber \\ &= \left\{ \left| \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}\left[ c_{i}(s) \int_{s-\eta_{i}(s)}^{s}(\varphi_{i}^{\prime}(u)-\psi_{i}^{\prime}(u))\hbox{d}u\right. \right. \right. \nonumber \\ & \quad \quad + \, \sum ^n_{j=1}a_{ij}(s)(f_{j}( \varphi_{j}(s))-f_{j} (\psi_{j}(s)))\nonumber \\ & \quad \quad\left. \left. \left. + \, \sum_{j=1}^{n}b_{ij}(s) (g_{j}( \varphi_{j}(\varphi_{j}(s))) -g_{j}( \psi_{j}(\psi_{j}(s)))) \right]\hbox{d}s\right| \right\} \nonumber \\ & \le \left\{ \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}\left[ c_{i}(s) \int_{s-\eta_{i}(s)}^{s}|\varphi_{i}^{\prime}(u)-\psi_{i}^{\prime}(u)|\hbox{d}u\right. \right. \nonumber \\ & \quad \quad \left. \left. + \, \sum ^n_{j=1} a_{ij} ^{+} L^{f}_{j} |\varphi_{j}(s) - \psi_{j}(s)| + \sum_{j=1}^{n} b_{ij}^{+} L^{g}_{j} |\varphi_{j}(\varphi_{j}(s)) - \psi_{j}(\psi_{j}(s))|\right]\hbox{d}s \right\} \nonumber \\ & \le \left\{ \int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}\left[ c_{i}(s) \int_{s-\eta_{i}(s)}^{s}\left| \varphi_{i}^{\prime}(u)-\psi_{i}^{\prime}(u)|\hbox{d}u +\sum ^n_{j=1} a_{ij} ^{+} L^{f}_{j} |\varphi_{j}(s) - \psi_{j}(s)\right| \right. \right. \nonumber \\ & \quad \quad \left. \left. + \, \sum_{j=1}^{n} b_{ij}^{+} L^{g}_{j} (|\varphi_{j}(\varphi_{j}(s)) - \psi_{j}(\varphi_{j}(s) )|+|\psi_{j}(\varphi_{j}(s)) -\psi_{j}(\psi_{j}(s))|)\right]\hbox{d}s \right\} \nonumber \\ & \le \left\{ \int ^t_{-\infty }{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u} \left[ c_{i}^{+}\eta_{i}^{+}+ \sum ^n_{j=1} a_{ij}^{+}L^{f}_{j} + \sum ^n_{j=1} b_{ij}^{+} L^{g}_{j}(1+L)\right]\hbox{d}s \Vert \varphi (t) -\psi (t)\Vert_{\mathbf{Z}}\right\} \nonumber \\ & \le \left\{ \int ^t_{-\infty }{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}(c_{i}(s)-\alpha_{i })\hbox{d}s\right\} \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}\nonumber \\ & \, \le \left\{ \int ^t_{-\infty }{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}d\left( -\int_{s}^{t}c_{i}(u)\hbox{d}u\right) -\alpha_{i}\int ^t_{-\infty }{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}\hbox{d}s \right\} \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}\nonumber \\ & \,\le \left\{ 1 -\alpha_{i}\int ^t_{-\infty }{\rm e}^{-\int_{s}^{t} c_{i}^{+} \hbox{d}u}\hbox{d}s \right\} \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}\nonumber \\ & \,\le \left\{ 1-\frac{\alpha_{i}}{ c_{i}^{+}}\right\} \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}} , \end{aligned}$$
(3.15)

and

$$\begin{aligned} |((T\varphi )(t))^{\prime} -((T\psi )(t)) ^{\prime} |&= \{|(((T\varphi )(t))^{\prime} -((T\psi )(t)) ^{\prime})_{i}|\} \nonumber \\&= \left\{ \left| \left[ c_{i}(t)\int_{t-\eta_{i}(t)}^{t}(\varphi_{i}^{\prime}(u)-\psi_{i}^{\prime}(u))\hbox{d}u+ \sum ^n_{j=1}a_{ij}(t)(f_{j}(\ \varphi_{j}(t))-f_{j}( \psi_{j}(t)))\right. \right. \right. \nonumber \\ & \quad \quad \left. + \, \sum_{j=1}^{n}b_{ij}(t) (g_{j}( \varphi_{j}(\varphi_{j}(t)))-g_{j}( \psi_{j}(\psi_{j}(t) ))) \right] \nonumber \\ & \quad \quad - \, c_{i}(t)\int_{-\infty }^{t}{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u}[c_{i}(s) \int_{s-\eta_{i}(s)}^{s}(\varphi_{i}^{\prime}(u)-\psi_{i}^{\prime}(u))\hbox{d}u\nonumber \\ & \quad \quad + \, \sum ^n_{j=1}a_{ij}(s)(f_{j}( \varphi_{j}(s))-f_{j}( \psi_{j}(s )))\nonumber \\ & \quad \quad \left. \left. + \, \sum_{j=1}^{n}b_{ij}(s) (g_{j}( \varphi_{j}(\varphi_{j}(s)))-g_{j}( \psi_{j}( \psi_{j}(s)))) ]ds\right| \right\} \nonumber \\ & \, \le \left\{ \left[ c_{i} ^{+}\eta_{i}^{+}+ \sum ^n_{j=1} a_{ij}^{+}L^{f}_{j} +\sum ^n_{j=1} b_{ij}^{+} L^{g}_{j}(1+L) \right] \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}\right. \nonumber \\ & \quad \quad \left. + \, c_{i}^{+}\int ^t_{-\infty }{\rm e}^{-\int_{s}^{t}c_{i}(u)\hbox{d}u} [c_{i}^{+}\eta_{i}^{+}+ \sum ^n_{j=1} a_{ij}^{+}L^{f}_{j} + \sum ^n_{j=1} b_{ij}^{+} L^{g}_{j}(1+L) ]\hbox{d}s\Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}\right\} \nonumber \\ & \le \left\{c_{i} ^{-}-\alpha_{i}+c_{i}^{+}\left(1-\frac{\alpha_{i}}{c_{i}^{+}}\right)\right\} \Vert \varphi (t)-\psi (t)\Vert_{\mathbf{Z}}. \end{aligned}$$
(3.16)

From (3.3), we have \(0<1-\frac{\alpha_{i}}{c_{i}^{+}}<1,\) and

$$\begin{aligned} K=\max \left\{ \max \limits_{1 \le i \le n}\left\{ 1-\frac{\alpha_{i}}{c_{i}^{+}}\right\} , \ \ \max \limits_{1 \le i \le n}\left\{ c_{i}^{-}- \alpha_{i}+c_{i}^{+}(1-\frac{\alpha_{i}}{c_{i}^{+}})\right\} \right\} <1, \end{aligned}$$

which, together with (3.15) and (3.16), give us that \(\Vert T \varphi -T \psi \Vert_{\mathbf{Z}} \le K\Vert \varphi -\psi \Vert_{\mathbf{Z}},\) and the mapping \(T:{\mathbf{B}} \longrightarrow {\mathbf{B}}\) is a contraction mapping. Therefore, the mapping \(T\) possesses a unique fixed point

$$\begin{aligned} x^{* }=(x_{1}^{* }(t), x_{2}^{* }(t), \cdots , x_{n}^{* }(t))^{T}\in \mathbf{B}, \ Tx^{* }=x^{* }. \end{aligned}$$

By (3.7), \(x^{*}\) satisfies (1.1). So (1.1) has a unique continuously differentiable pseudo almost periodic solution \(x^{* }\). The proof of Theorem 3.1 is now completed.

4 Example

Example 4.1

Consider the following CNNs with leakage delays and complex deviating arguments:

$$\begin{aligned} \left\{ \begin{array}{lll} x_{1}^{\prime}(t)& = - \, \left(\frac{1}{8}|\cos t +\cos \sqrt{2} t|+\frac{1}{4}\right) x_{1}\left(t-\frac{ |\cos t|}{10}\right)\\ & \quad \quad + \, \frac{ |\cos t| }{20} \sin (x_{2}(x_{2}(t)))+\frac{1}{16}{\rm e}^{-t^{4}\sin ^{2} t},\\ x_{2}^{\prime}(t)& = -\left(\frac{1}{8}|\cos t +\cos \sqrt{3} t|+\frac{1}{4}\right) x_{2}\left(t- \frac{|\sin t|}{10}\right)\\ & \quad \quad + \, \frac{ |\cos \sqrt{3} t| }{20} \sin (x_{1}(x_{1}(t)))+ \frac{1}{16}{\rm e}^{-t^{4}|\sin t|}. \end{array} \right. \end{aligned}$$
(4.1)

Notice that

$$\begin{aligned} g_{1}(x)&= g_{2}(x)=\sin x, \ f_{1}(x)=f_{2}(x)=0, \ \ L_{j}^{g}=1, \ L_{j}^{f}=0, \ l=\max \limits_{i=1,2}\frac{I_{i}^{+}}{c_{i} ^{-}}=\frac{1}{4},\\ c_{1}(t)&= \frac{1}{8}|\cos t +\cos \sqrt{2} t|+ \frac{1}{4} , \ c_{2}(t)=\frac{1}{8}|\cos t +\cos \sqrt{3} t|+\frac{1}{4}, \ b_{11} ^{+}= b_{22} ^{+}=0,a_{ij}^{+}=0,\\ \ \eta_{i} ^{+}&= \frac{1}{10}, \ b_{12} ^{+}= b_{21} ^{+}=\frac{1}{20}, \ \ c_{i} ^{+}= \frac{1}{2}, \ c_{i} ^{-}=\frac{1}{4}, \quad i,\,j=1, 2. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \theta&= \max \limits _{i\in \{1,2\}}\left\{ \left(1+\frac{c_{i }^{+}}{c_{i }^{-}}\right) \left[c_{i } ^{+}\eta _{i }^{+} +\sum^n_{j=1}(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j})\right] , \frac{1}{c_{i }^{-}} \left[ c_{i } ^{+}\eta _{i }^{+} +\sum ^n_{j=1}\left(a_{ij}^{+}L^{f}_{j} +b_{ij} ^{+} L^{g}_{j}\right)\right] \right\} \\&= \max \limits _{i\in \{1,2\}}\left\{ (1+2) \left( \frac{1}{20} + \frac{1}{20}\right) , \ 4\left( \frac{1}{20} + \frac{1}{20}\right) \right\} =0.4<1,\\ & \left\{ \left[ c_{i} ^{+} + c_{i}^{+} \eta _{i} ^{+} + \sum _{j=1}^{n}a_{ij} ^{+}\left(L^{f}_{j} + b_{ij}^{+} L^{g}_{j}\right)\right] \frac{l}{1-\theta } + I_{i} ^{+}\right\} = \left\{ \frac{5}{16}\right\} ,\\ & \quad \quad - \, c_{i} ^{-}+ c_{i} ^{+}\eta _{i}^{+}+ \sum ^n_{j=1} a_{ij}^{+} L^{f}_{j} + \sum ^n_{j=1} b_{ij}^{+} L^{g}_{j}(1+L)=- \frac{43}{320} , \end{aligned}$$

and

$$\begin{aligned} c_{i}^{-}- \alpha _{i}+c_{i}^{+}\left(1-\frac{\alpha _{i}}{c_{i}^{+}}\right)=\frac{77}{160}<1, \end{aligned}$$

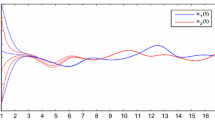
where \(\alpha_{i}=\frac{43}{320}, L=\frac{5}{16}, i=1,2\). It is straightforward to check that all the conditions needed in Theorem 3.1 are satisfied. Therefore, by Theorem 3.1, system (4.1) has exactly one pseudo almost periodic solution \(x^{*}(t)\) in the region \(\mathbf{B}= B^{L}\bigcap B^{*}\).

Remark 4.1

For all we know, there is no research on the existence of pseudo almost periodic solutions to CNNs with complex deviating arguments. We also mention that all results in the references [12–16] and [17, 18] cannot be applied to imply the existence of pseudo almost periodic solutions of (4.1). Here, we employ a novel proof to establish some criteria to guarantee the existence of pseudo almost periodic solutions for CNNs with leakage delays and complex deviating arguments. This implies that the result of this paper is essentially new.

5 Conclusion

In this paper, a class of cellular neural networks systems with leakage delays and complex deviating arguments has been studied. Under some appropriate conditions, the existence of pseudo almost periodic solutions for this model has been established by using the exponential dichotomy theory, contraction mapping fixed point theorem and inequality analysis technique. Our results can be applied for some practical problems concerning cellular neural networks. Moreover, an example is given to illustrate the effectiveness of our new results. In the real world, fuzzy theory is considered as a more suitable method for the sake of taking vagueness into consideration (see [23, 24]). Whether or not our results and method in this paper are available for the existence of pseudo almost periodic solutions of the fuzzy cellular neural networks models in [23, 24], it is an interesting problem and we leave it as our work in the future.