Pseudo Almost Periodic Solutions for CNNs with Continuously Distributed Leakage Delays

Abstract

In this paper, based on the exponential dichotomy theory, contraction mapping fixed point theorem and inequality analysis technique, we obtain some sufficient conditions ensuring the existence and global exponential stability of pseudo almost periodic solutions for a new generalized cellular neural network model with continuously distributed leakage delays. Our results complement with some recent ones. Moreover, an illustrative example and its numerical simulation are given to demonstrate the effectiveness of the obtained results.

1 Introduction

In the last three decades, the dynamical behaviors of delayed cellular neural networks (DCNNs) have received much attention due to their potential applications in associated memory, parallel computing,pattern recognition, signal processing and optimization problems (see [1–5]). In particular, a neural network usually has a spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths, it is desired to model them by introducing continuously distributed delays over a certain duration of time (see [6–8]). Recently, a typical time delay called Leakage (or “forgetting”) delay may exist in the negative feedback terms of the neural network system, and these terms are variously known as forgetting or leakage terms (see[9–13]). Consequently, the dynamic behaviors of cellular neural networks with continuously distributed leakage delays have been extensively and intensively studied. We refer the reader to [14–18] and the references cited therein.

On the other hand, the variation of the environment plays an important role in the dynamics of DCNNs. As pointed out in [19, 20], periodically varying environment and almost periodically varying environment are foundations for the theory of nature selection. Compared with periodic effects, almost periodic effects are more frequent, and many phenomena exhibit great regularity with being pseudo almost periodic which allow complex repetitive phenomena to be represented as an almost-periodic process plus an ergodic component. Therefore, many researchers have focused their attention on the study of existence and stability of almost periodic solutions and pseudo almost periodic solutions for DCNNs (see [21–25] and the references cited therein). Most recently, Zhang [26] considered the following CNNs with continuously distributed delays in leakage terms:

$$\begin{aligned} x'_{i}(t)&= -c_{i}(t) \int _0^\infty {h_i }(s) x_i (t - s)ds + \sum _{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&+\, \sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(x_{j}(t-u))du+I_{i}(t), \quad i=1, 2, \ldots , n, \end{aligned}$$

(1.1)

in which $n$ corresponds to the number of units in a neural network, $x_{i}(t)$ corresponds to the state vector of the $i$th unit at the time $t,\, c_{i}(t)>0$ represents the rate with which the $i$th unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time $t$. $a_{ij}(t)$ and $b_{ij}(t)$ are the connection weights at the time $t,\, h_{i}(s)\ge 0,\, K_{ij}(u)$ and $\tau _{ij}(t)\ge 0$ denote the leakage delay kernel, transmission delay kernel and transmission delay, respectively, and $I_{i}(t)$ denotes the external inputs at time $t$. $f_{j}$ and $g_{j}$ are activation functions of signal transmission, $i,j=1, 2, \ldots , n$.

By using Lyapunov functional method and differential inequality techniques, in [26], it has been established some sufficient conditions to guarantee that all solutions of (1.1) converge exponentially to the almost periodic solution. Moreover, it is well known that the global exponential exponential convergence behavior of solutions plays a key role in characterizing the behavior of dynamical system since the exponential convergent rate can be unveiled (see [27–30]). However, to the best of our knowledge, few authors have considered the exponential convergence on the pseudo almost periodic solution for (1.1). Motivated by the above discussions, in this paper, we shall establish the existence and uniqueness of pseudo almost periodic solution of (1.1) by using the exponential dichotomy theory and contraction mapping fixed point theorem. Meanwhile, we also shall give the conditions to guarantee that all solutions and their derivatives of solutions for (1.1) converge exponentially to the pseudo almost periodic solution and its derivative, respectively.

The initial conditions associated with system (1.1) are of the form

(1.2)

where $\varphi _{i}(\cdot )$ and $\varphi _{i}'(\cdot )$ are real-valued bounded continuous functions defined on $(-\infty , 0]$.

In the following part of this paper, given a bounded continuous function $g$ defined on $\mathbb {R}$, let $g^+$ and $g^-$ be defined as

For convenience, we denote by $\mathbb {R}^{n}(\mathbb {R}=\mathbb {R}^{1})$ the set of all $n-$dimensional real vectors (real numbers). We will use $x=(x_{1}, \ x_{2}, \, \ldots , x_{n})^{T}\in \mathbb {R}^{n}$ to denote a column vector, in which the symbol $(^{T})$ denotes the transpose of a vector. We let $|x|$ denote the absolute-value vector given by $|x|=(|x_{1}|, \, |x_{2}|,\ldots , |x_{n}|)^{T}$, and define $\ \Vert x\Vert =\max \limits _{1\le i\le n}|x_{i}|$. A matrix or vector $A\ge 0$ means that all entries of $A$ are greater than or equal to zero. $A>0$ can be defined similarly. For matrices or vectors $A$ and $B,\, A\ge B$ (resp. $A>B$) means that $A-B\ge 0$ (resp. $A-B>0$).

The paper is organized as follows. Section 2 includes some lemmas and definitions, which can be used to check the existence of pseudo almost periodic solutions of (1.1). In Sect. 3, we present some new sufficient conditions for the existence and uniqueness of the continuously differentiable pseudo almost periodic solution of (1.1). In Sect. 4, we establish sufficient conditions on the global exponential stability of pseudo almost periodic solutions of (1.1). At last, an example and its numerical simulation are given to illustrate the effectiveness of the obtained results.

2 Preliminary Results

In this section, we shall first recall some basic definitions, lemmas which are used in what follows.

In this paper, $BC(\mathbb {R},\mathbb {R}^{n})$ denotes the set of bounded continued functions from $\mathbb {R}$ to $\mathbb {R}^{n}$. Note that $(BC(\mathbb {R},\mathbb {R}^{n}), \Vert \cdot \Vert _{\infty })$ is a Banach space where $\Vert \cdot \Vert _{\infty }$ denotes the sup norm $\Vert f\Vert _{\infty } := \sup \limits _{ t\in \mathbb {R}} \Vert f (t)\Vert$.

Definition 2.1

(see [19, 20]) Let $u(t)\in BC(\mathbb {R},\mathbb {R}^{n})$. $u(t)$ is said to be almost periodic on $\mathbb {R}$ if, for any $\varepsilon >0$, the set $T(u,\varepsilon )= \{\delta :\Vert u(t+\delta )-u(t)\Vert <\varepsilon \; \hbox {for all } \; t\in \mathbb {R}\}$ is relatively dense, i.e., for any $\varepsilon >0$, it is possible to find a real number $l=l(\varepsilon )>0,$ for any interval with length $l(\varepsilon )$, there exists a number $\delta =\delta (\varepsilon )$ in this interval such that $\Vert u(t+\delta )-u(t)\Vert <\varepsilon , \, \hbox {for all }\, t\in \mathbb {R}.$

We denote by $AP(\mathbb {R},\mathbb {R}^{n})$ the set of the almost periodic functions from $\mathbb {R}$ to $\mathbb {R}^{n}$. Besides, the concept of pseudo almost periodicity (pap) was introduced by Zhang in the early nineties. It is a natural generalization of the classical almost periodicity. Precisely, define the class of functions $PAP_{0}(\mathbb {R},\mathbb {R}^{n})$ as follows:

$$\begin{aligned} \left\{ f\in BC(\mathbb {R},\mathbb {R}^{n})|\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{-r}^{r}|f(t)|dt=0\right\} . \end{aligned}$$

A function $f\in {BC(\mathbb {R},\mathbb {R}^{n})}$ is called pseudo almost periodic if it can be expressed as

$$\begin{aligned} f=h+\varphi , \end{aligned}$$

where $h\in {AP(\mathbb {R},\mathbb {R}^{n})}$ and $\varphi \in {PAP_{0}(\mathbb {R},\mathbb {R}^{n})}.$ The collection of such functions will be denoted by $PAP(\mathbb {R},\mathbb {R}^{n}).$ The functions $h$ and $\varphi$ in above definition are respectively called the almost periodic component and the ergodic perturbation of the pseudo almost periodic function $f$. The decomposition given in definition above is unique. Observe that $(PAP(\mathbb {R},\mathbb {R}^{n}),\Vert .\Vert _{\infty })$ is a Banach space and $AP(\mathbb {R},\mathbb {R}^{n})$ is a proper subspace of $PAP(\mathbb {R},\mathbb {R}^{n})$ since the function $\phi (t)=\cos \pi t+\cos t+e^{-t^{4}\sin ^{2 }t}$ is pseudo almost periodic function but not almost periodic. It should be mentioned that pseudo almost periodic functions possess many interesting properties; we shall need only a few of them and for the proofs we shall refer to [19].

Lemma 2.1

(see [19, p. 57]) If $f\in PAP(\mathbb {R},\mathbb {R})$ and $g$ is its almost periodic component, then we have

$$\begin{aligned} g(\mathbb {R})\subset \overline{f(\mathbb {R})}. \end{aligned}$$

Therefore $\Vert f\Vert _{\infty }\ge \Vert g\Vert _{\infty }\ge \inf \limits _{x\in \mathbb {R}}|g(x)|\ge \inf \limits _{x\in \mathbb {R}}|f(x)|$.

Lemma 2.2

(see [19, p. 140]) Suppose that both functions $f$ and its derivative $f'$ are in $PAP(\mathbb {R},\mathbb {R})$. That is, $f=g+\varphi$ and $f'=\alpha +\beta$, where $g,\alpha \in AP(\mathbb {R},\mathbb {R})$ and $\varphi ,\beta \in PAP_{0}(\mathbb {R},\mathbb {R})$. Then the functions $g$ and $\varphi$ are continuous differentiable so that

$$\begin{aligned} g'=\alpha , \quad \varphi '=\beta . \end{aligned}$$

Lemma 2.3

Let $B^{*}=\{f|f,f'\in PAP(\mathbb {R},\mathbb {R}) \}$ equipped with the induced norm defined by $\Vert f\Vert _{B^{*}}=\max \{\Vert f\Vert _{\infty }, \Vert f'\Vert _{\infty }\}=\max \{\sup \limits _{t\in \mathbb {R}}|f(t)|, \sup \limits _{t\in \mathbb {R}}|f'(t)|\}$, then $B^{*}$ is a Banach space.

Proof

Suppose that $\{f_p\}_{p=1}^{+\infty }$ is a Cauchy sequence in $B^{*}$, then for any $\varepsilon >0$, there exists $~N(\varepsilon )>0$ such that

$$\begin{aligned} \Vert f_p-f_q\Vert _{B^{*}}= \max \{\sup \limits _{t\in R}|f_p(t)-f_q(t)|, \ \ \sup \limits _{t\in R}|f_p'(t)-f_q'(t)|\}<\varepsilon , \ \forall p,q\ge N(\varepsilon ). \end{aligned}$$

(2.1)

By the definition of pseudo almost periodic function, let

$$\begin{aligned} f_p=g_p+\varphi _p, \, \hbox {where} \, g_p\in AP(\mathbb {R},\mathbb {R}), \,\varphi _p\in PAP_0 (\mathbb {R},\mathbb {R}) \, \hbox {and} \, p=1,2,\cdots . \end{aligned}$$

From Lemma 2.2, we obtain

$$\begin{aligned} f'_p=g'_p+\varphi '_p, \, \hbox {where} \, g'_p\in AP(\mathbb {R},\mathbb {R}), \, \varphi '_p\in PAP_0 (\mathbb {R},\mathbb {R}) \, \hbox {and} \, p=1,2,\cdots . \end{aligned}$$

On combining (2.1) with Lemma 2.1, we deduce that, $\{g_p\}_{p=1}^{+\infty },\{g_p'\}_{p=1}^{+\infty }\subset AP(\mathbb {R},\mathbb {R})$ are Cauchy sequence, so that $\{\varphi _p\}_{p=1}^{+\infty }, \{\varphi _p'\}_{p=1}^{+\infty }\subset PAP_0(\mathbb {R},\mathbb {R})$ are also Cauchy sequence.

Firstly, we show that there exists $g\in AP(\mathbb {R},\mathbb {R})$ such that $g_p$ uniformly converges to $g$, as $p\rightarrow +\infty$.

Note that $\{g_p\}$ is Cauchy sequence in $AP(\mathbb {R},\mathbb {R})$. $\forall ~ \varepsilon >0$, $\exists ~N(\varepsilon )$, such that $\forall ~ p,q\ge N(\varepsilon )$

$$\begin{aligned} |g_p(t)-g_q(t)|<\varepsilon , \quad \hbox {for all } t\in \mathbb {R}. \end{aligned}$$

(2.2)

So for fixed $t\in \mathbb {R}$, it is easy to see $\{g_p(t)\}_{p=1}^{+\infty }$ is Cauchy number sequence. Thus, the limits of $g_p(t)$ exists as $p\rightarrow +\infty$ and let $g(t)=\lim \limits _{p\rightarrow +\infty }g_p(t)$. In (2.2), let $q\rightarrow +\infty$, we have

$$\begin{aligned} |g(t)-g_p(t)|\le \varepsilon , \quad \hbox {for all}\, t\in \mathbb {R}, \, p\ge N(\varepsilon ). \end{aligned}$$

(2.3)

Thus, $g_p$ uniformly converges to $g$, as $p\rightarrow +\infty$. Moreover, from the theorem 1.9 [20, p. 5], we obtain $g\in AP(\mathbb {R},\mathbb {R})$. Similarly, we also obtain that there exist $g ^{*}\in AP (\mathbb {R},\mathbb {R})$ and $\varphi ,\varphi ^{*}\in BC(\mathbb {R},\mathbb {R})$, such that

$$\begin{aligned} |g^{*}(t)\!-\!g'_p(t)|\le \varepsilon , \ |\varphi (t)\!-\!\varphi _p(t)|\le \varepsilon , \ |\varphi ^{*}(t)-\varphi '_p(t)|\le \varepsilon , \quad \hbox {for all}\quad t\in \mathbb {R}, \, p\ge N(\varepsilon ),\nonumber \\ \end{aligned}$$

(2.4)

which imply that

$$\begin{aligned} g_p' \Rightarrow g^{*}, \, \varphi _p \Rightarrow \varphi , \, \varphi _p' \Rightarrow \varphi ^{*}, \end{aligned}$$

where $p\rightarrow +\infty$ and $``\Rightarrow ''$ means uniform convergence.

Next, we claim that $\varphi ,\varphi ^{*}\in PAP_0(R)$. Together with (2.4) and the facts that

$$\begin{aligned}&\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}| \varphi _p(s)|ds=0, ~~\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}| \varphi _p'(s)|ds=0, p=1,\ n 2,\ldots ,\\&\frac{1}{2r}\int ^r_{-r}| \varphi (s)|ds\le \frac{1}{2r}\int ^r_{-r}| \varphi (s)-\varphi _p(s)|ds +\frac{1}{2r}\int ^r_{-r}| \varphi _p(s)|ds, \ r>0,\ p=1,2,\ldots , \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2r}\int ^r_{-r}| \varphi ^{*}(s)|ds\le \frac{1}{2r}\int ^r_{-r}| \varphi ^{*} (s)-\varphi _p'(s)|ds +\frac{1}{2r}\int ^r_{-r}| \varphi '_p(s)|ds, \ r>0,\ p=1,2,\ldots , \end{aligned}$$

we have

$$\begin{aligned} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}| \varphi (s)|ds=0, ~~\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}| \varphi ^{*}(s)|ds=0. \end{aligned}$$

Hence $\varphi ,\varphi ^{*}\in PAP_0(R)$. Let $f=g+\varphi$, $f^{*}=g^{*}+\varphi ^{*}$, then $f=g+\varphi \in PAP(R)$, $f^{*}=g^{*}+\varphi ^{*}\in PAP(R)$ and $f_p \Rightarrow f$, $f_p' \Rightarrow f^{*}$ as $p\rightarrow +\infty$.

Finally, we reveal $f' = f^{*}$. For $t,\Delta t\in R$, it follows that

$$\begin{aligned} f_p(t+\Delta t)-f_p(t)=\int _t^{t+\Delta t} f_p'(s)ds \end{aligned}$$

(2.5)

In view of the uniform convergence of $f_p$ and $f_p'$, let $p\rightarrow +\infty$ for (2.5), we get

$$\begin{aligned} f(t+\Delta t)-f(t)=\int _t^{t+\Delta t} f^{*}(s)ds, \end{aligned}$$

which implies that

$$\begin{aligned} f^{*}(t)=\lim \limits _{\Delta t\rightarrow 0}\frac{\int \limits _t^{t+\Delta t} f^{*}(s)ds}{\Delta t}=\lim \limits _{\Delta t\rightarrow 0}\frac{f(t+\Delta t)-f(t)}{\Delta t} =f'(t). \end{aligned}$$

(2.6)

In summary, in view of (2.3), (2.4) and (2.6), we obtain that the Cauch sequence $\{f_p\}_{p=1}^{+\infty }\subset B^{*}$ satisfies

$$\begin{aligned} \Vert f_p-f\Vert _{B^{*}}\longrightarrow 0 (p\rightarrow +\infty ), \end{aligned}$$

and $f\in B^{*}$. This yields that $B^{*}$ is a Banach space. The proof is completed.$\square$

Remark 2.1

Let $B=\{f|f,f'\in PAP(\mathbb {R},\mathbb {R}^{n}) \}$ equipped with the induced norm defined by $\Vert f\Vert _{B}=\max \{\Vert f\Vert _{\infty }, \Vert f'\Vert _{\infty }\}=\max \{\sup \limits _{t\in \mathbb {R}}\Vert f(t)\Vert , \sup \limits _{t\in \mathbb {R}}\Vert f'(t)\Vert \}$. It follows from Lemma 2.3 that $B$ is a Banach space.

Definition 2.2

(see [19, 20]) Let $x\in \mathbb {R}^{n}$ and $Q(t)$ be a $n\times n$ continuous matrix defined on $\mathbb {R}$. The linear system

$$\begin{aligned} \begin{array}{rcl} x'(t)=Q(t)x(t) \end{array} \end{aligned}$$

(2.7)

is said to admit an exponential dichotomy on $\mathbb {R}$ if there exist positive constants $k, \alpha$, projection $P$ and the fundamental solution matrix $X(t)$ of (2.7) satisfying

$$\begin{aligned} \begin{array}{rcl} &{}&{}\Vert X(t)PX^{-1}(s)\Vert \le ke^{-\alpha (t-s)}\quad \hbox {for}\,\, t\ge s,\\ &{}&{}\Vert X(t)(I-P)X^{-1}(s)\Vert \le ke^{-\alpha (s-t)}\quad \hbox {for}\,\, t\le s. \end{array} \end{aligned}$$

Lemma 2.4

(see [19]) Assume that $Q(t)$ is an almost periodic matrix function and $g (t) \in PAP(\mathbb {R},\mathbb {R}^{n})$. If the linear system (2.7) admits an exponential dichotomy, then pseudo almost periodic system

$$\begin{aligned} \begin{array}{rcl} x'(t)=Q(t)x(t)+g(t) \end{array} \end{aligned}$$

(2.8)

has a unique pseudo almost periodic solution $x(t)$, and

$$\begin{aligned} x(t)=\int _{-\infty }^{t}X(t)PX^{-1}(s)g(s)ds-\int ^{+\infty }_{t}X(t)(I-P)X^{-1}(s)g(s)ds. \end{aligned}$$

(2.9)

Lemma 2.5

(see [19, 20]) Let $c_{i}(t)$ be an almost periodic function on $\mathbb {R}$ and

$$\begin{aligned} M[c_{i}]=\lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}c_{i}(s)ds>0, \quad i=1, 2, \ldots , n. \end{aligned}$$

Then the linear system

$$\begin{aligned} x'(t)= \text{ diag } (-c_{1}(t), -c_{2}(t), \ldots , -c_{n}(t))x(t) \end{aligned}$$

admits an exponential dichotomy on $R$.

3 Existence and Uniqueness of Pseudo Almost Periodic Solutions

In this section, we establish sufficient conditions on the existence of pseudo almost periodic solutions of (1.1).

For $i, j=1, \ 2,\ldots , n,$ it will be assumed that $h_{i} :\mathbb {R}\rightarrow [0, \ +\infty )$ is a continuous function with $0 <\int _0^\infty {h_i }(v) dv <+\infty$ and $\int _0^\infty v{h_i }(v)e^{\kappa v} dv <+\infty$ for a certain positive constant $\kappa ,\, c_{i} :\mathbb {R}\rightarrow (0, \ +\infty )$ is an almost periodic function, $\tau _{ij}:\mathbb {R}\rightarrow [0, \ +\infty )$ and $I_{i}, \ a_{ij}, \ b_{ij} :\mathbb {R}\rightarrow \mathbb {R}$ are uniformly continuous pseudo almost periodic functions. We also make the following assumptions which will be used later.

$(A_1)$ :

for each $j\in \{1,2, \ \ldots , n \}$, there exist nonnegative constants $L ^{f}_{j}$ and $L^{g}_{j}$ such that

$$\begin{aligned} |f_{j}(u )-f_{j}(v )|\le L ^{f}_{j}|u -v |, |g_{j}(u )-g_{j}(v )| \le L^{g}_{j}|u -v |, \quad \hbox {for all} \quad u, \ v \in \mathbb {R}. \end{aligned}$$

$(A_{2})$ :

for $i, j\in \{1,2, \ldots , n \}$, the delay kernels $K_{ij}:[0, \infty )\rightarrow \mathbb {R}$ are continuous, $|K_{ij}(t)|e^{\kappa t}$ are integrable on $[0, \infty )$.

$(A_{3})$ :

for each $i\in \{1, \ 2,\ldots , n \}$, there exist constants $\alpha _{i}>0$ and $\xi _{i}>0,$ such that

$$\begin{aligned}&-\,c_{i} ^{-}\int _0^\infty {h_i }(v) dv +c_{i} ^{+} \int _0^\infty v{h_i }(v) dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} \\&\quad +\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)| du L^{g}_{j}\xi _{j} \le - \alpha _{i}, \end{aligned}$$

and

$$\begin{aligned} c_{i}^{-}\int _0^\infty {h_i }(v) dv- \alpha _{i}+c_{i}^{+}\int _0^\infty {h_i }(v) dv(1-\frac{\alpha _{i}}{c_{i}^{-}\int _0^\infty {h_i }(v) dv})<1. \end{aligned}$$

Lemma 3.1

Assume that assumptions $(A_{1})$ and $(A_{2})$ hold. Then, for $\varphi (\cdot )\in PAP(\mathbb {R},\mathbb {R} )$, the function $\int _{0}^{\infty }K_{ij}(u) g_{j}(\varphi (t-u))du$ belongs to $PAP(\mathbb {R},\mathbb {R} )$, where $i,j=1, 2, \ldots , n.$

Proof

Let $\varphi \in PAP(\mathbb {R},\mathbb {R} )$. Obviously, $(A_{1})$ implies that $g_{j}$ is a uniformly continuous function on $\mathbb {R}$. By using Corollary 5.4 in [19, p. 58], we immediately obtain the following,

$$\begin{aligned} g_{j}(\varphi (t ))=\chi _{ j1}(t)+\chi _{ j2}(t)\in PAP(\mathbb {R},\mathbb {R} ), \end{aligned}$$

where $\chi _{ j1}\in AP(\mathbb {R},\mathbb {R} ), \chi _{ j2}\in PAP_{0}(\mathbb {R},\mathbb {R} ),\, j=1, 2, \ldots , n.$ Then, for any $\varepsilon >0,$ it is possible to find a real number $l=l( \varepsilon ))>0,$ for any interval with length $l$, there exists a number $\tau =\tau (\varepsilon )$ in this interval such that

$$\begin{aligned} |\chi _{ j1}(t+\tau )-\chi _{ j1}(t)|< \frac{\varepsilon }{1+\int _{0}^{\infty }|K_{ij}(u)|du},~~\forall {t\in {\mathbb {R}}},\quad i, j=1, 2, \ldots , n, \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}| \chi _{ j2}(v)|dv=0, \quad j=1, 2, \ldots , n. \end{aligned}$$

It follows that

$$\begin{aligned}&\big |\int _{0}^{\infty }K_{ij}(u) \chi _{ j1}(t+\tau -u) du-\int _{0}^{\infty }K_{ij}(u) \chi _{ j1}(t -u)du\big |\\&\quad \le \int _{0}^{\infty }|K_{ij}(u)||\chi _{ j1}(t+\tau -u)-\chi _{ j1}(t -u)|du\\&\quad < \int _{0}^{\infty }|K_{ij}(u)|du\frac{\varepsilon }{1+\int _{0}^{\infty }|K_{ij}(u)|du}<\varepsilon ,~~\forall {t\in {\mathbb {R}}}, \quad i,j=1, 2, \ldots , n, \end{aligned}$$

and

$$\begin{aligned}&\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}\big |\int _{0}^{\infty }K_{ij}(u) \chi _{ j2}( v-u) du \big |dv\\&\quad \le \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int ^r_{-r}\int _{0}^{\infty }\big |K_{ij}(u)|| \chi _{ j2}(v-u) \big |du dv\\&\quad =\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{0}^{\infty }\big |K_{ij}(u)|\int ^r_{-r}| \chi _{ j2}(v-u) \big |dvdu \\&\quad =\lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{0}^{\infty }\big |K_{ij}(u)|\int ^{r-u}_{-r-u}| \chi _{ j2}(z) \big |dzdu\\&\quad \le \lim \limits _{r\rightarrow +\infty } \frac{1}{2r}\int _{0}^{\infty }\big |K_{ij}(u)|\int ^{r+u}_{-r-u}| \chi _{ j2}(z) \big |dzdu\\&\quad \le \lim \limits _{r\rightarrow +\infty } \int _{0}^{\infty }\big |K_{ij}(u)|(1+\frac{ 1}{ r}u)\frac{1}{2(r+u)}\int ^{r+u}_{-r-u}| \chi _{ j2}(z) \big |dzdu\\&\quad \le \lim \limits _{r\rightarrow +\infty } \int _{0}^{\infty }\big |K_{ij}(u)| e^{\frac{ 1}{ r}u} \frac{1}{2(r+u)}\int ^{r+u}_{-r-u}| \chi _{ j2}(z) \big |dzdu\\&\quad \le \lim \limits _{r\rightarrow +\infty } \int _{0}^{\infty }\big |K_{ij}(u)|e^{\kappa u}\frac{1}{2(r+u)}\int ^{r+u}_{-r-u}| \chi _{ j2}(z)\big |dzdu= 0,\quad \text{ where }\, r>\frac{1}{\kappa },\\&\qquad i, j=1, 2, \ldots , n. \end{aligned}$$

Thus,

$$\begin{aligned} \int _{0}^{\infty }K_{ij}(u) \chi _{ j1}(t -u) du \in AP (\mathbb {R},\mathbb {R} ) \ \text{ and } \ \int _{0}^{\infty }K_{ij}(u) \chi _{ j2}( t-u) du\in PAP_{0}(\mathbb {R},\mathbb {R} ), \end{aligned}$$

which yield

$$\begin{aligned} \int _{0}^{\infty }K_{ij}(u) g_{j}(\varphi (t\!-\!u))du&= \int _{0}^{\infty }K_{ij}(u) \chi _{ j1}(t \!-\!u) du\!+\, \int _{0}^{\infty }K_{ij}(u) \chi _{ j2}( t\!-\!u) du\!\in \! PAP (\mathbb {R},\mathbb {R} ), \\&i, j=1, 2, \ldots , n. \end{aligned}$$

The proof of Lemma 3.1 is completed.$\square$

Theorem 3.1

Let $(A_{1}),\, (A_{2})$ and $(A_{3})$ hold. Then, there exists a unique continuously differentiable pseudo almost periodic solution of system (1.1).

Proof

Set

$$\begin{aligned} \bar{x}_{i}(t)=\xi ^{-1}_{i}x_{i}(t), \end{aligned}$$

then we can transform (1.1) into the following system

$$\begin{aligned} \bar{x}_{i}'(t)&= -\,c_{i}(t) \int _0^\infty {h_i }(s) \bar{x}_i (t - s)ds+ \xi ^{-1}_{i}\sum _{j=1}^{n}a_{ij}(t)f_{j}(\xi _{j}\bar{x}_{j}(t-\tau _{ij}(t)))\\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\bar{x}_{j}(t-u))du +\xi ^{-1}_{i}I_{i}(t)\\&= -\,c_{i}(t) \int _0^\infty {h_i }(s) ds\bar{x}_i (t )+ c_{i}(t) \int _0^\infty {h_i }(s) \int _{t -s }^{t}\bar{x}'_i (u)duds\\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}a_{ij}(t)f_{j}(\xi _{j}\bar{x}_{j}(t-\tau _{ij}(t)))\\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\bar{x}_{j}(t-u))du +\xi ^{-1}_{i}I_{i}(t), \quad i=1, 2,\ldots , n. \end{aligned}$$

Let $\varphi \in B$. Obviously, the boundedness of $\varphi '$ and $(A_{1})$ imply that $f_{j}$ and $\varphi _{j}$ are uniformly continuous functions on $\mathbb {R}$ for $j=1, 2, \ldots , n$. Set $f(t,z)=\varphi _{j}(t-z) (j\in \{1, 2, \ldots , n \}).$ By Theorem 5.3 in [19, p. 58] and Definition 5.7 in [19, p. 59], we can obtain that $f\in PAP(\mathbb {R}\times \Omega )$ and $f$ is continuous in $z\in K$ and uniformly in $t\in \mathbb {R}$ for all compact subset $K$ of $\Omega$. This, together with $\tau _{ij}\in PAP(\mathbb {R},\mathbb {R})$ and Theorem 5.11 in [19, p. 60], implies that

$$\begin{aligned} \varphi _{j}(t-\tau _{ij}(t))\in PAP(\mathbb {R},\mathbb {R}), \quad i,j=1, \ 2, \ldots , n. \end{aligned}$$

Again from Corollary 5.4 in [19, p. 58], we have

$$\begin{aligned} f_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t)))\in PAP(\mathbb {R},\mathbb {R}), \quad i,j=1,2, \ldots , n. \end{aligned}$$

(3.1)

In view of $\int _0^\infty {h_i }(v) dv <+\infty$ and $\int _0^\infty v{h_i }(v) dv <+\infty$, by using a similar argument as in proof of Lemma 3.1, we can show

$$\begin{aligned} \int _0^\infty {h_i }(s) \int _{t -s }^{t}\varphi '_i (u)duds =\int _0^\infty {h_i }(s) ds\varphi _i(t )-\int _0^\infty {h_i }(s) \varphi _i(t -s )ds\in PAP(\mathbb {R},\mathbb {R}),\nonumber \\ \end{aligned}$$

(3.2)

for all $i =1,2,\ldots , n.$

By combining (3.1), (3.2) with Lemma 3.1, we obtain

$$\begin{aligned}&c_{i}(t) \int _0^\infty {h_i }(s) \int _{t -s }^{t}\varphi '_i (u)duds + \xi ^{-1}_{i}\sum _{j=1}^{n}a_{ij}(t)f_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t)))\\&\quad +\,\, \xi ^{-1}_{i}\sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\varphi _{j}(t\!-\!u))du \!\!+\,\,\xi ^{-1}_{i}I_{i}(t)\!\in \! PAP(\mathbb {R},\mathbb {R}), \quad i\!=\!1, 2,\ldots , n. \end{aligned}$$

For any $\varphi \in B$, we consider the pseudo almost periodic solution $x^{\varphi }(t)$ of the pseudo almost periodic differential equations

$$\begin{aligned} \bar{x}_{i}'(t)&= -\,c_{i}(t) \int _0^\infty {h_i }(s) ds\bar{x}_i (t )+ c_{i}(t) \int _0^\infty {h_i }(s) \int _{t -s }^{t}\varphi '_i (u)duds\nonumber \\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}a_{ij}(t)f_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t)))\nonumber \\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\varphi _{j}(t-u))du +\xi ^{-1}_{i}I_{i}(t), \quad i=1,2,\ldots , n.\nonumber \\ \end{aligned}$$

(3.3)

Then, notice that $M[c_{i}(t)\int _0^\infty {h_i }(s) ds]>0, \; i=1, \ 2,\ldots , n$, it follows from Lemma 2.5 that the linear system

$$\begin{aligned} \bar{x}_{i}'(t)=-c_{i}(t)\int _0^\infty {h_i }(s) ds\bar{x}_{i}(t), \quad i=1,2,\ldots , n, \end{aligned}$$

(3.4)

admits an exponential dichotomy on $\mathbb {R}$. Thus, by Lemma 2.4, we obtain that the system (3.3) has exactly one pseudo almost periodic solution:

$$\begin{aligned} x^{\varphi }(t)&= (x^{\varphi }_{1}(t), \ x^{\varphi }_{2}(t),\ldots ,x^{\varphi }_{n}(t))^{T}\nonumber \\&= (\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu}[c_{1}(s) \int _0^\infty {h_1 }(v) \int _{s -v }^{s}\varphi '_1 (u)dudv \nonumber \\&+\,\xi ^{-1}_{1}\sum ^n_{j=1}a_{1j}(s)f_{j}(\xi _{j}\varphi _{j}(s-\tau _{1j}(s)))\nonumber \\&+\, \xi ^{-1}_{1}\sum _{j=1}^{n}b_{1j}(s) \int _{0}^{\infty }K_{1j}(u) g_{j}(\xi _{j}\varphi _{j}(s-u))du+\xi ^{-1}_{1}I_{1}(s)]ds\cdots ,\nonumber \\&\times \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n}(v) dvdu}[c_{n}(s) \int _0^\infty {h_n }(v) \int _{s -v }^{s}\varphi '_n (u)dudv \nonumber \\&+\, \xi ^{-1}_{n}\sum ^n_{j=1}a_{nj}(s)f_{j}(\xi _{j}\varphi _{j}(s-\tau _{nj}(s)))\nonumber \\&+\, \xi ^{-1}_{n}\sum _{j=1}^{n}b_{nj}(s) \int _{0}^{\infty }K_{nj}(u) g_{j}(\xi _{j}\varphi _{j}(s-u))du+\xi ^{-1}_{n}I_{n}(s)]ds)^{T}. \end{aligned}$$

(3.5)

In view of the uniform continuity of coefficients and delays, from $(A_{1}),\, (A_{2})$ and the Corollary 5.6 in [19, p. 59], we get

$$\begin{aligned} (x_{i}^{\varphi }(t))'&= \Bigg [c_{i}(t) \int _0^\infty {h_i }(v) \int _{t -v }^{t} \varphi _{i}'(u) dudv + \xi ^{-1}_{i}\sum ^n_{j=1}a_{ij}(t) f_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t))) \\&+\, \xi ^{-1}_{i}\sum _{j=1}^{n}b_{ij}(t) \int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\varphi _{j}(t-u)) du+\xi ^{-1}_{i}I_i(t) \Bigg ]\\&-\,c_{i}(t)\int _0^\infty {h_i }(v) dv\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{i}(u)\int _0^\infty {h_i }(v) dvdu}\Bigg [c_{i}(s) \int _0^\infty {h_i }(v) \int _{s -v }^{s} \varphi _{i}'(u) dudv \\&+\,\xi ^{-1}_{i}\sum ^n_{j=1}a_{ij}(s) f_{j}(\xi _{j}\varphi _{j}(s\!-\!\tau _{ij}(s))) \!+\! \xi ^{-1}_{i}\sum _{j\!=\!1}^{n}b_{ij}(s)\!\int _{0}^{\infty }K_{ij}(u) g_{j}(\xi _{j}\!\varphi _{j}(s\!-\!u)) du\\&+\,\xi ^{-1}_{i}I_i(s) \Bigg ]ds, \end{aligned}$$

is a pseudo almost periodic function, where $i= 1,2,\ldots ,n$.

Now, we define a mapping $T:B \rightarrow B$ by setting

$$\begin{aligned} T(\varphi )(t)=x^{\varphi }(t), \quad \forall \varphi \in B. \end{aligned}$$

We next prove that the mapping $T$ is a contraction mapping of the $B$. In fact, in view of (3.5), $(A_{1})$ and $(A_{3})$, for $\varphi , \psi \in B$, we have $\ |T(\varphi (t))-T(\psi (t))|$

$$\begin{aligned}&= (|(T(\varphi (t))-T(\psi (t)))_{1}|,\ldots ,|(T(\varphi (t))-T (\psi (t)))_{n}|)^{T} \\&= \Bigg (|\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu}[c_{1}(s) \int _0^\infty {h_1 }(v) \int _{s -v }^{s}(\varphi _{1}'(u)-\psi _{1}'(u))dudv \\&+\,\xi ^{-1}_{1}\sum ^n_{j=1}a_{1j}(s)(f_{j}(\xi _{j}\varphi _{j}(s-\tau _{1j}(s)))-f_{j}(\xi _{j}\psi _{j}(s-\tau _{1j}(s))))\\&+\, \xi ^{-1}_{1}\sum _{j=1}^{n}b_{1j}(s)\int _{0}^{\infty }K_{1j}(u) (g_{j}(\xi _{j}\varphi _{j}(s-u))-g_{j}(\xi _{j}\psi _{j}(s-u)))du ]ds|,\cdots ,\\&\times |\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu}[c_{n}(s) \int _0^\infty {h_n }(v) \int _{s -v }^{s}(\varphi _{n}'(u)-\psi _{n}'(u))dudv \\&+\, \xi ^{-1}_{n}\sum ^n_{j=1}a_{nj}(s)(f_{j}(\xi _{j}\varphi _{j}(s-\tau _{nj}(s)))-f_{j}(\xi _{j}\psi _{j}(s-\tau _{nj}(s))))\\&+\, \xi ^{-1}_{n}\sum _{j=1}^{n}b_{nj}(s) \int _{0}^{\infty }K_{nj}(u) (g_{j}(\xi _{j}\varphi _{j}(s-u))-g_{j}(\xi _{j}\psi _{j}(s-u)))du ]ds|\Bigg )^{T}\\&\le \Bigg ( \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu}[c_{1}(s) \int _0^\infty {h_1 }(v) \int _{s -v }^{s}|\varphi _{1}'(u)-\psi _{1}'(u)|dudv \\&+\,\xi ^{-1}_{1}\sum ^n_{j=1}|a_{1j}(s)|L^{f}_{j} \xi _{j}|\varphi _{j}(s-\tau _{1j}(s)) - \psi _{j}(s-\tau _{1j}(s))| \\&+\, \xi ^{-1}_{1}\sum _{j=1}^{n}|b_{1j}(s)| \int _{0}^{\infty }|K_{1j}(u)| L^{g}_{j} \xi _{j}|\varphi _{j}(s-u) - \psi _{j}(s-u)|du ]ds,\cdots ,\\&\times \,\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu}[c_{n}(s) \int _0^\infty {h_n }(v) \int _{s -v }^{s}|\varphi _{n}'(u)-\psi _{n}'(u)|dudv\\&+\, \xi ^{-1}_{n}\sum ^n_{j=1}|a_{nj}(s)|L^{f}_{j} \xi _{j}|\varphi _{j}(s-\tau _{nj}(s)) - \psi _{j}(s-\tau _{nj}(s))| \\&+\, \xi ^{-1}_{n}\sum _{j=1}^{n}|b_{nj}(s)| \int _{0}^{\infty }|K_{nj}(u)| L^{g}_{j} \xi _{j}|\varphi _{j}(s-u) - \psi _{j}(s-u)|du ]ds\Bigg )^{T}\\&\le \Bigg (\int ^t_{-\infty }e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu} [c_{1} ^{+}\int _0^\infty v {h_1 }(v) dv+\xi ^{-1}_{1}\sum ^n_{j=1}( a_{1j}^{+} L^{f}_{j} \\&+\, b_{1j}^{+}\int _{0}^{\infty }|K_{1j}(u)|du L^{g}_{j} )\xi _{j} ] ds \Vert \varphi (t)-\psi (t)\Vert _{B},\ldots ,\\&\int ^t_{-\infty }e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu} [c_{n} ^{+}\int _0^\infty v {h_n }(v) dv+\xi ^{-1}_{n}\sum ^n_{j=1}( a_{nj}^{+} L^{f}_{j} \\&+\, b_{nj}^{+}\int _{0}^{\infty }|K_{nj}(u)|du L^{g}_{j} )\xi _{j} ] ds\Vert \varphi (t)-\psi (t)\Vert _{B}\Bigg )^{T} \end{aligned}$$

$$\begin{aligned}&\le \Bigg (\int ^t_{-\infty }e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu} (c_{1}(s)\int _0^\infty {h_1 }(v) dv-\alpha _{1}) ds,\ldots , \nonumber \\&\ \int ^t_{-\infty }e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu} (c_{n}(s)\int _0^\infty {h_n }(v) dv-\alpha _{n})ds\Bigg )^{T}\Vert \varphi (t)-\psi (t)\Vert _{B}\nonumber \\&\le \Bigg (\int ^t_{-\infty }e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu} d\bigg (-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu\bigg )\nonumber \\&-\,\alpha _{1}\int ^t_{-\infty }e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu} ds,\ldots ,\nonumber \\&\int ^t_{-\infty }e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu} d\bigg (-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu\bigg )\nonumber \\&-\,\alpha _{n}\int ^t_{-\infty }e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu} ds \Bigg )^{T}\Vert \varphi (t)-\psi (t)\Vert _{B}\nonumber \\&\le \Bigg (1 -\alpha _{1}\int ^t_{-\infty }e^{-\int _{s}^{t} c _{1}^{+}\int _0^\infty {h_1 }(v) dv du} ds,\ldots , \nonumber \\&1 -\alpha _{n}\int ^t_{-\infty }e^{-\int _{s}^{t} c _{n}^{+} \int _0^\infty {h_n }(v) dv du} ds\Bigg )^{T}\Vert \varphi (t)-\psi (t)\Vert _{B}\nonumber \\&\le \Big ( 1-\frac{\alpha _{1}}{ c _{1}^{+}\int _0^\infty {h_1 }(v) dv},\ldots , \ 1-\frac{\alpha _{n}}{ c _{n}^{+}\int _0^\infty {h_n }(v) dv}\Big )^{T}\Vert \varphi (t)-\psi (t)\Vert _{B}, \end{aligned}$$

(3.6)

and $\ |T'(\varphi (t))-T'(\psi (t))|$

$$\begin{aligned}&= (|(T'(\varphi (t))-T'(\psi (t)))_{1}|,\ldots , \ |(T'(\varphi (t))-T' (\psi (t)))_{n}|)^{T} \\&= (|[c_{1}(t) \int _0^\infty {h_1 }(v) \int _{t -v }^{t}(\varphi _{1}'(u)-\psi _{1}'(u))dudv\\&+\, \xi ^{-1}_{1}\sum ^n_{j=1}a_{1j}(t)(f_{j}(\xi _{j}\varphi _{j}(t-\tau _{1j}(t)))-f_{j}(\xi _{j}\psi _{j}(t-\tau _{1j}(t))))\\&+\, \xi ^{-1}_{1}\sum _{j=1}^{n}b_{1j}(t) \int _{0}^{\infty }K_{1j}(u) (g_{j}(\xi _{j}\varphi _{j}(t-u))-g_{j}(\xi _{j}\psi _{j}(t-u)))du ]\\&-\,c_{1}(t)\int _0^\infty {h_1 }(v) dv\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu}[c_{1}(s) \int _0^\infty {h_1 }(v) \int _{s -v }^{s}(\varphi _{1}'(u)-\psi _{1}'(u))dudv \\&+\,\xi ^{-1}_{1}\sum ^n_{j=1}a_{1j}(s)(f_{j}(\xi _{j}\varphi _{j}(s-\tau _{1j}(s)))-f_{j}(\xi _{j}\psi _{j}(s-\tau _{1j}(s))))\\&+\, \xi ^{-1}_{1}\sum _{j=1}^{n}b_{1j}(s) \int _{0}^{\infty }K_{1j}(u) (g_{j}(\xi _{j}\varphi _{j}(s-u))-g_{j}(\xi _{j}\psi _{j}(s-u)))du ]ds|,\ldots ,\\&|[c_{n}(t) \int _0^\infty {h_n }(v) \int _{t -v }^{t}(\varphi _{n}'(u)-\psi _{n}'(u))dudv\\&+\, \xi ^{-1}_{n}\sum ^n_{j=1}a_{nj}(t)(f_{j}(\xi _{j}\varphi _{j}(t-\tau _{nj}(t)))-f_{j}(\xi _{j}\psi _{j}(t-\tau _{nj}(t))))\\&+\, \xi ^{-1}_{n}\sum _{j=1}^{n}b_{nj}(t) \int _{0}^{\infty }K_{nj}(u) (g_{j}(\xi _{j}\varphi _{j}(t-u))-g_{j}(\xi _{j}\psi _{j}(t-u)))du ]\\&-\,\, c_{n}(t)\int _0^\infty {h_n }(v) dv\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu}[c_{n}(s) \int _0^\infty {h_n }(v) \int _{s -v }^{s}(\varphi _{n}'(u)-\psi _{n}'(u))dudv \\&+\, \xi ^{-1}_{n}\sum ^n_{j=1}a_{nj}(s)(f_{j}(\xi _{j}\varphi _{j}(s-\tau _{nj}(s)))-f_{j}(\xi _{j}\psi _{j}(s-\tau _{nj}(s))))\\&+\, \xi ^{-1}_{n}\sum _{j=1}^{n}b_{nj}(s) \int _{0}^{\infty }K_{nj}(u) (g_{j}(\xi _{j}\varphi _{j}(s-u))-g_{j}(\xi _{j}\psi _{j}(s-u)))du ]ds|)^{T}\\&\le ([c_{1}^{+}\int _0^\infty v{h_1 }(v) dv+\xi ^{-1}_{1}\sum ^n_{j=1}( a_{1j}^{+} L^{f}_{j} \\&+\, b_{1j}^{+}\int _{0}^{\infty }|K_{1j}(u)|du L^{g}_{j} )\xi _{j} ] \Vert \varphi (t)-\psi (t)\Vert _{B}\\&+\,c_{1}^{+}\int _0^\infty {h_1 }(v) dv\int ^t_{-\infty }e^{-\int _{s}^{t}c_{1}(u)\int _0^\infty {h_1 }(v) dvdu} [c_{1}^{+}\int _0^\infty v{h_1 }(v) dv+\xi ^{-1}_{1}\sum ^n_{j=1}( a_{1j}^{+} L^{f}_{j} \end{aligned}$$

$$\begin{aligned}&+\, b_{1j}^{+}\int _{0}^{\infty }|K_{1j}(u)|du L^{g}_{j} )\xi _{j} ] \Vert \varphi (t)-\psi (t)\Vert _{B},\ldots ,\nonumber \\&[c_{n}^{+}\int _0^\infty v{h_n }(v) dv+\xi ^{-1}_{n}\sum ^n_{j=1}( a_{nj} ^{+} L^{f}_{j} \nonumber \\&+\, b_{nj}^{+}\int _{0}^{\infty }|K_{1j}(u)|du L^{g}_{j} )\xi _{j} ] \Vert \varphi (t)-\psi (t)\Vert _{B}\nonumber \\&+\,c_{n}^{+}\int _0^\infty {h_n }(v) dv\int ^t_{-\infty }e^{-\int _{s}^{t}c_{n}(u)\int _0^\infty {h_n }(v) dvdu} [c_{n}^{+}\int _0^\infty v{h_n }(v) dv+\xi ^{-1}_{n}\sum ^n_{j=1}( a_{nj}^{+} L^{f}_{j} \nonumber \\&+\, b_{nj}^{+}\int _{0}^{\infty }|K_{nj}(u)|du L^{g}_{j} )\xi _{j} ] \Vert \varphi (t)-\psi (t)\Vert _{B})^{T} \nonumber \\&\le (c_{1}^{-}\int _0^\infty {h_1 }(v) dv- \alpha _{1}+c_{1}^{+}\int _0^\infty {h_1 }(v) dv(1-\frac{\alpha _{1}}{c_{1}^{+}\int _0^\infty {h_1 }(v) dv}),\ldots ,\nonumber \\&\ c_{n}^{-}\int _0^\infty {h_n }(v) dv\!-\! \alpha _{n}\!+\!c_{n}^{+}\int _0^\infty {h_n }(v) dv(1\!-\!\frac{\alpha _{n}}{c_{n}^{+}\int _0^\infty {h_n }(v) dv}))^{T}\Vert \varphi (t)\!-\!\psi (t)\Vert _{B}.\qquad \end{aligned}$$

(3.7)

From $(A_{3})$, we have

$$\begin{aligned} 0<1-\frac{\alpha _{i}}{c_{i}^{+}\int _0^\infty {h_i }(v) dv}<1, \end{aligned}$$

and

$$\begin{aligned} K&= \max \left\{ \max \limits _{1 \le i \le n}\left\{ 1-\frac{\alpha _{i}}{c_{i}^{+}\int _0^\infty {h_i }(v) dv}\right\} ,\right. \\&\left. \max \limits _{1 \le i \le n}\left\{ c_{i}^{-}\int _0^\infty {h_i}(v) dv- \alpha _{i}+c_{i}^{+}\int _0^\infty {h_i }(v) dv(1-\frac{\alpha _{i}}{c_{i}^{+}\int _0^\infty {h_i }(v) dv})\right\} \right\} < 1, \end{aligned}$$

which, together with (3.6) and (3.7), yield

$$\begin{aligned} \Vert T (\varphi (t))-T (\psi (t))\Vert _{B} \le K\Vert \varphi (t)-\psi (t)\Vert _{B}, \end{aligned}$$

which implies that the mapping $T:B \longrightarrow B$ is a contraction mapping. Therefore, the mapping $T$ possesses a unique fixed point

$$\begin{aligned} x^{**}=(x_{1}^{**}(t), x_{2}^{**}(t), \ldots , x_{n}^{**}(t))^{T}\in B, \ Tx^{**}=x^{**}. \end{aligned}$$

By (3.3) and (3.5), $x^{** }$ satisfies (3.3). So (1.1) has a unique continuously differentiable almost periodic solution $x^{* }=(\xi _{1}x_{1}^{**}(t), \xi _{2}x_{2}^{**}(t), \ldots , \xi _{n}x_{n}^{**}(t))^{T}$. The proof of Theorem 3.1 is now completed.$\square$

4 Global Exponential Stability of the Pseudo Almost Periodic Solution

In this section, we will discuss the global exponential stability of the pseudo almost periodic solution of system (1.1).

Definition 4.1

Let $x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\ldots ,x^{*}_{n}(t))^{T}$ be the pseudo almost periodic solution of system (1.1). If there exist constants $\alpha >0$ and $M>1$ such that for every solution $x(t)=(x_{1}(t), x_{2}(t),\ldots ,x_{n}(t))^{T}$ of system (1.1) with any initial value $\varphi (t)=(\varphi _{1}(t), \varphi _{2}(t),\ldots ,\varphi _{n}(t))^{T}$ satisfying $( 1.2),$

$$\begin{aligned}&\Vert x (t)-x^{*}(t)\Vert _{1}=\max \limits _{i=1, 2,\cdots , \ n}\{\max \{|x_{i}(t)-x^{*}_{i}(t)|, |x'_{i}(t)-x^{*} _{i} \ '(t)|\}\}\le M \Vert \varphi -x^{*}\Vert _{0}e^{-\alpha t},\\&\quad \forall t>0, \end{aligned}$$

where $\Vert \varphi -x^{*}\Vert _{0}=\max \{\sup \limits _{t\le 0 }\max \limits _{1\le i\le n }|\varphi _{i} (t) -x^{*}_{i}(t)|, \ \sup \limits _{t\le 0}\max \limits _{1\le i\le n }|\varphi _{i}' (t)-x^{*} _{i} \ '(t) | \}$. Then $x^{*}(t)$ is said to be globally exponentially stable.

Theorem 4.2

Suppose that all conditions in Theorem (3.1) are satisfied. Moreover, assume that

$$\begin{aligned}&(1+\frac{c_{i} ^{+}\int \limits _0^\infty {h_i }(v) dv }{c_{i} ^{-}\int _0^\infty {h_i }(v) dv })\left[ c_{i} ^{+} \int _0^\infty v{h_i }(v) dv +\xi _{i}^{-1}\sum ^n_{j=1} a_{ij} ^{+} L^{f}_{j}\xi _{j}\right. \nonumber \\&\quad \left. +\,\xi _{i}^{-1}\sum ^n_{j=1} a^{+}_{ij}L^{f}_{j} \xi _{j} + \xi ^{-1}_{i} \sum \limits _{j=1}^{n}b^{+}_{ij} \int \nolimits _{0}^{\infty }|K_{ij}(u)| du L^{g}_{j}\xi _{j}\right] < 1;\,\, i=1; 2; \cdots ;n.\qquad \qquad \end{aligned}$$

(4.1)

Then system (1.1) has at least one pseudo almost periodic solution $x^{*}(t)$. Moreover, $x^{*}(t)$ is globally exponentially stable.

Proof

By Theorem 3.1, (1.1) has a unique continuously differentiable pseudo almost periodic solution $x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\ldots ,x^{*}_{n}(t))^{T}$. Suppose that $x(t)=(x_{1}(t), x_{2}(t),\ldots ,x_{n}(t))^{T}$ is an arbitrary solution of (1.1) associated with initial value $\varphi (t)=(\varphi _{1}(t), \varphi _{2}(t),\ldots ,\varphi _{n}(t))^{T}$ satisfying (1.2).

Let

$$\begin{aligned} y (t)&= (y_{1}(t), y_{2}(t),\ldots ,y_{n}(t))^{T}\\&= (\xi _{1}^{-1}(x_{1}(t)-x^{*}_{1}(t)), \xi _2^{-1}(x_{2}(t)-x^{*}_{2}(t)), \ldots , \xi _n^{-1}(x_{n}(t)-x^{*}_{n}(t)))^{T}. \end{aligned}$$

Then

$$\begin{aligned} y_{i}'(t)&= -\,c_{i}(t)\int _0^\infty {h_i }(s) y_i (t \!-\! s)ds\!+\!\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) (f_{j}( x_{j}(t\!-\!\tau _{ij}(t))) -f_{j}(x^{*}_{j}(t-\tau _{ij}(t))))\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij}(t)\int _{0}^{\infty }K_{ij}(u) (g_{j}(x_{j}(t-u)) -g_{j}(x^{*}_{j}(t-u)))du\nonumber \\&= -\,c_{i}(t) \int _0^\infty {h_i }(s) dsy_i (t )+ c_{i}(t) \int _0^\infty {h_i }(s) \int _{t -s }^{t}y'_i (u)duds\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) (f_{j}(x_{j}(t-\tau _{ij}(t))) -f_{j}(x^{*}_{j}(t-\tau _{ij}(t))))\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij}(t)\int _{0}^{\infty }K_{ij}(u) (g_{j}( x_{j}(t-u)) -g_{j}(x^{*}_{j}(t-u)))du, \end{aligned}$$

(4.2)

where $i=1, 2,\ldots , n.$

Define continuous functions $\Gamma _{i}(\omega )$ and $\Pi _{i}(\omega )$ by setting

$$\begin{aligned} \Gamma _{i}(\omega )&= -\,c_{i} ^{-}\int _0^\infty {h_i }(v) dv +\omega +c_{i} ^{+} \int _0^\infty v{h_i }(v)e^{ \omega v } dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} e^{ \omega \tau _{ij} ^{+} }\\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)|e^{ \omega u} du L^{g}_{j}\xi _{j}, \end{aligned}$$

and

$$\begin{aligned} \Pi _{i}(\omega )&= \left( 1+\frac{c_{i} ^{+}\int _0^\infty {h_i }(v) dv }{c_{i} ^{-}\int _0^\infty {h_i }(v) dv-\omega }\right) \left[ c_{i} ^{+} \int _0^\infty v{h_i }(v)e^{ \omega v } dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} e^{ \omega \tau _{ij} ^{+} }\right. \\&\left. +\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)|e^{ \omega u} du L^{g}_{j}\xi _{j}\right] , \end{aligned}$$

$\text{ where } \ t>0, \omega \in [0, \ \kappa ], \; i=1,2,\ldots , n.$ Then, from $(A_{3})$ and (4.1), we have

$$\begin{aligned} \Gamma _{i}(0)&= -\,c_{i} ^{-}\int _0^\infty {h_i }(v) dv +c_{i} ^{+} \int _0^\infty v{h_i }(v) dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)| du L^{g}_{j}\xi _{j}\le -\alpha _{i}<0, \quad i=1,2,\ldots , n, \end{aligned}$$

and

$$\begin{aligned} \Pi _{i}(0)&= \left( 1+\frac{c_{i} ^{+}\int _0^\infty {h_i }(v) dv }{c_{i} ^{-}\int _0^\infty {h_i }(v) dv }\right) \Bigg (c_{i} ^{+} \int _0^\infty v{h_i }(v) dv \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} a_{ij} ^{+}L^{f}_{j}\xi _{j} +\xi _{i}^{-1}\sum ^n_{j=1} b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)| du L^{g}_{j}\xi _{j}\Bigg )<1, \quad i=1, \ 2,\ldots , n, \end{aligned}$$

which, together with the continuity of $\Gamma _{i} (\omega )$ and $\Pi _{i} (\omega )$, implies that we can choose a constants $\lambda \in (0, \ \min \{\kappa , \min \limits _{i=1, 2,\cdots , n}c_{i} ^{-}\})$ such that

$$\begin{aligned} \Gamma _{i}(\lambda )&= -\,c_{i} ^{-}\int _0^\infty {h_i }(v) dv +\lambda +c_{i} ^{+} \int _0^\infty v{h_i }(v)e^{ \lambda v } dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} e^{ \lambda \tau _{ij} ^{+} }\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)|e^{ \lambda u} du L^{g}_{j}\xi _{j}\nonumber \\&= \Bigg (c_{i} ^{-}\int _0^\infty {h_i }(v) dv -\lambda \Bigg )\Bigg (\frac{\beta _{i}}{c_{i} ^{-}\int _0^\infty {h_i }(v) dv -\lambda }-1\Bigg )<0, \end{aligned}$$

(4.3)

and

$$\begin{aligned} \Pi _{i}(\lambda )&= \left( 1+\frac{c_{i} ^{+}\int \limits _0^\infty {h_i }(v) dv }{c_{i} ^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda } \right) \left[ c_{i} ^{+} \int _0^\infty v{h_i }(v)e^{ \lambda v } dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} e^{ \lambda \tau _{ij} ^{+} }\right. \nonumber \\&\left. +\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)|e^{ \lambda u} du L^{g}_{j}\xi _{j}\right] \nonumber \\&= \left( 1+\frac{c_{i} ^{+}\int \limits _0^\infty {h_i }(v) dv}{c_{i} ^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda }\right) \beta _{i}<1, \end{aligned}$$

(4.4)

where

$$\begin{aligned} \beta _{i} = c_{i} ^{+} \int _0^\infty v{h_i }(v)e^{ \lambda v } dv +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij} ^{+} L^{f}_{j}\xi _{j} e^{ \lambda \tau _{ij} ^{+} } +\xi _{i}^{-1}\sum ^n_{j=1}b_{ij} ^{+}\int \limits _{0}^{\infty }|K_{ij}(u)|e^{ \lambda u} du L^{g}_{j}\xi _{j}, \end{aligned}$$

and $i=1, 2,\ldots , n.$

Let

$$\begin{aligned} \Vert \varphi -x^{*}\Vert _{\xi }=\max \{\sup \limits _{t\le 0 }\max \limits _{1\le i\le n }\xi _{i}^{-1}|\varphi _{i} (t) -x^{*}_{i}(t)|, \ \sup \limits _{t\le 0}\max \limits _{1\le i\le n }\xi _{i}^{-1}|\varphi _{i}' (t)-x^{*} _{i} \ '(t) | \}\quad \end{aligned}$$

(4.5)

and $M$ be a constant such that

$$\begin{aligned} M>\frac{c_{i} ^{-}\int \limits _0^\infty {h_i }(v) dv -\lambda }{\beta _{i}}>1, \quad \hbox {for all} \quad i = 1, 2,\ldots , n, \end{aligned}$$

(4.6)

which, together with (4.3), yields

$$\begin{aligned} \frac{1}{M}-\frac{\beta _{i}}{c_{i}^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda }<0,\quad \frac{\beta _{i}}{c_{i}^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda }<1, \quad \hbox {for all}\quad i = 1, 2,\ldots , n, \end{aligned}$$

(4.7)

Consequently, for any $\varepsilon >0$, it is obvious that

$$\begin{aligned} \Vert y(t)\Vert _{1}< (\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda t}<M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda t} \text{ for } \text{ all }\, t \in (- \infty , \ 0]. \end{aligned}$$

In the following, we will show

$$\begin{aligned} \Vert y(t)\Vert _{1}<M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda t} \text{ for } \text{ all }\, t > 0. \end{aligned}$$

(4.8)

Otherwise, there must exist $i \in \{ 1, 2,\ldots , n \}$ and $\theta >0$ such that

$$\begin{aligned} \left\{ \begin{array}{rcl} \Vert y(\theta )\Vert _{1}&{}=&{} \max \{ |y_{i}(\theta ) |, |y'_{i}(\theta ) |\} = M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda \theta },\\ \Vert y(t)\Vert _{1}&{}<&{}M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda t} \hbox {for all}\, t \in (- \infty , \ \theta ). \end{array} \right. \end{aligned}$$

(4.9)

Note that

$$\begin{aligned}&y_{i}'(s)+ c_{i}(s) \int _0^\infty {h_i }(v) dv y_i (s ) \nonumber \\&\quad = c_{i}(s) \int _0^\infty {h_i }(v) \int _{s -v}^{s}y'_i (u)dudv \nonumber \\&\quad +\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) (f_{j}(x_{j}(s-\tau _{ij}(s))) -f_{j}(x^{*}_{j}(s-\tau _{ij}(s))))\nonumber \\&\quad +\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij}(s)\int _{0}^{\infty }K_{ij}(u) (g_{j}( x_{j}(s-u)) -g_{j}(x^{*}_{j}(s-u)))du,\ \ s\in [0, t], \ t\in [0, \theta ].\nonumber \\ \end{aligned}$$

(4.10)

Multiplying both sides of (4.10) by $e ^{ \int _{0}^{s}c_{i}(u) \int _0^\infty {h_i }(v) dvdu}$, and integrating on $[0, t]$, we get

$$\begin{aligned} y_{i} (t)&= y_{i} (0) e ^{-\int _{0}^{t}c_{i}(u) \int _0^\infty {h_i }(v) dvdu}\nonumber \\&+\, \int _{0}^{t}e ^{ -\int _{s}^{t}c_{i}(u) \int _0^\infty {h_i }(v) dvdu}[c_{i}(s) \int _0^\infty {h_i }(v) \int _{s -v }^{s}y'_i (u)dudv\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) (f_{j}(x_{j}(s-\tau _{ij}(s))) -f_{j}(x^{*}_{j}(s-\tau _{ij}(s))))\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij}(s)\int _{0}^{\infty }K_{ij}(u) (g_{j}( x_{j}(s-u)) -g_{j}(x^{*}_{j}(s-u)))du]ds, \ t\in [0, \theta ]. \end{aligned}$$

Thus, with the help of (4.9), we have

$$\begin{aligned} |y_{i} (\theta )|&= \bigg | y_{i} (0) e ^{-\int _{0}^{\theta }c_{i}(u)\int _0^\infty {h_i }(v) dv du}\nonumber \\&+\, \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }c_{i}(u)\int _0^\infty {h_i }(v) dv du}[c_{i}(s) \int _0^\infty {h_i }(v) \int _{s -v}^{s}y'_i (u)dudv\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) (f_{j}(x_{j}(s-\tau _{ij}(s))) -f_{j}(x^{*}_{j}(s-\tau _{ij}(s))))\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}b_{ij}(s)\int _{0}^{\infty }K_{ij}(u) (g_{j}( x_{j}(t-u)) -g_{j}(x^{*}_{j}(s-u)))du]ds \bigg |\nonumber \\&\le (\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-c_{i}^{-}\int _0^\infty {h_i }(v) dv \theta }\nonumber \\&+\, \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }c_{i}(u)\int _0^\infty {h_i }(v) dv du}[c_{i} ^{+} \int _0^\infty v{h_i }(v) e^{ \lambda v}dv M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda s }\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(s)| L^{f}_{j}\xi _{j}|y_{j}(s-\tau _{ij}(s))|\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|b_{ij}(s)|\int _{0}^{\infty }K_{ij}(u) L^{g}_{j}\xi _{j}|y_{j} (s-u)|du]ds\nonumber \\&\le (\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-c_{i}^{-}\int _0^\infty {h_i }(v) dv \theta }\nonumber \\&+\, \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }c_{i}(u)\int _0^\infty {h_i }(v) dv du}[c_{i} ^{+} \int _0^\infty v{h_i }(v) e^{ \lambda v}dv M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda s }\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(s)| L^{f}_{j}\xi _{j}M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda (s-\tau _{ij}(s))}\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|b_{ij}(s)|\int _{0}^{\infty }|K_{ij}(u)| L^{g}_{j}\xi _{j}M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda (s-u)}du]ds\nonumber \\&\le (\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-c_{i}^{-} \int _0^\infty {h_i }(v) dv\theta }\nonumber \\&+\, \int _{0}^{\theta }e ^{-\int _{s}^{\theta }c_{i}(u)\int _0^\infty {h_i }(v) dv du}[c_{i} ^{+} \int _0^\infty v{h_i }(v) e^{ \lambda v}dv e^{-\lambda s }\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} a_{ij}^{+} L^{f}_{j}\xi _{j} e^{ \lambda \tau _{ij} ^{+}}e^{- \lambda s}\nonumber \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} b_{ij}^{+}\int _{0}^{\infty }K_{ij}(u) L^{g}_{j}\xi _{j}e^{ \lambda u}du e^{- \lambda s}]ds M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )\nonumber \\&\le (\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-c_{i}^{-} \int _0^\infty {h_i }(v) dv\theta }\nonumber \\&+\, e ^{-c_{i}^{-} \int _0^\infty {h_i }(v) dv\theta }\int _{0}^{\theta }e ^{(c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda ) s} ds\beta _{i} M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )\nonumber \\&\le M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-\lambda \theta }\left[ \frac{e ^{(\lambda -c_{i}^{-}\int _0^\infty {h_i }(v) dv )\theta }}{M}\right. \nonumber \\&\left. +\, \frac{\beta _{i}}{c_{i}^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda }(1-e ^{(\lambda -c_{i}^{-}\int _0^\infty {h_i }(v) dv )\theta })\right] \nonumber \\&= M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-\lambda \theta }\nonumber \\&\times \left[ \left( \frac{1}{M}-\frac{\beta _{i}}{c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda }\right) e ^{(\lambda -c_{i}^{-}\int \limits _0^\infty {h_i }(v) dv )\theta }+ \frac{\beta _{i}}{c_{i}^{-}\int \limits _0^\infty {h_i }(v) dv-\lambda }\right] \!,\nonumber \\ \end{aligned}$$

(4.11)

which, together with (4.7) and (4.9), implies that

$$\begin{aligned} |y_{i}(\theta ) |< M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-\lambda \theta }, \end{aligned}$$

and

$$\begin{aligned} \Vert y(\theta )\Vert _{1} = \max \{ |y_{i}(\theta ) |, |y'_{i}(\theta ) |\} =|y'_{i}(\theta ) |= M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda \theta }. \end{aligned}$$

(4.12)

From (4.4) and (4.7), (4.10) and (4.11) yield

$$\begin{aligned} |y_{i}'(\theta )|&\le c_{i}(\theta ) \int _0^\infty {h_i }(v) dv |y_i (\theta ) | + c_{i}(\theta ) \int _0^\infty {h_i }(v) \int _{\theta -v}^{\theta }|y'_i (u)|dudv\\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(\theta )| |f_{j}(x_{j}(\theta -\tau _{ij}(\theta ))) -f_{j}(x^{*}_{j}(\theta -\tau _{ij}(\theta )))|\\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|b_{ij}(\theta )||\int _{0}^{\infty }K_{ij}(u) (g_{j}( x_{j}(\theta -u)) -g_{j}(x^{*}_{j}(\theta -u)))du|\\&\le c_{i} ^{+} \int _0^\infty {h_i }(v) dv |y_{i} (\theta )|+ c_{i}^{+} \int _0^\infty v{h_i }(v)e^{ \lambda v } dv M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda \theta } \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} a_{ij}^{+} L^{f}_{j}\xi _{j}|y_{j}(\theta -\tau _{ij}(\theta ))|\\&+\,\xi _{i}^{-1}\sum ^n_{j=1} b_{ij}^{+}\int _{0}^{\infty }|K_{ij}(u)| L^{g}_{j}\xi _{j} |y_{j}(\theta -u)|du\\&\le \bigg \{c_{i} ^{+}\int _0^\infty {h_i }(v) dv \left[ \left( \frac{1}{M}-\frac{\beta _{i}}{c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda }\right) e ^{(\lambda -c_{i}^{-}\int _0^\infty {h_i }(v) dv )\theta }\right. \\&\left. +\,\, \frac{\beta _{i}}{c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda }\right] \\&+\, c_{i}^{+} \int _0^\infty v{h_i }(v)e^{ \lambda v } dv +\xi _{i}^{-1}\sum ^n_{j=1} a_{ij}^{+} L^{f}_{j}\xi _{j} e^{ \lambda \tau _{ij} ^{+} }\\&+\,\xi _{i}^{-1}\sum ^n_{j=1} b_{ij}^{+}\int _{0}^{\infty }|K_{ij}(u)|e^{ \lambda u} du L^{g}_{j}\xi _{j}\bigg \}M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon )e^{-\lambda \theta }\\&\le M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-\lambda \theta }\Bigg [c_{i}^{+}\int _0^\infty {h_i }(v)dv\\&\times \left( \frac{1}{M}-\frac{\beta _{i}}{c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda }\right) e ^{(\lambda -c_{i}^{-} \int _0^\infty {h_i }(v) dv)\theta }\\&+\,\, \beta _{i}\left( \frac{c_{i}^{+}\int _0^\infty {h_i }(v) dv}{c_{i}^{-}\int _0^\infty {h_i }(v) dv-\lambda }+1\right) \Bigg ]\\&< M(\Vert \varphi -x^{*}\Vert _{\xi }+\varepsilon ) e ^{-\lambda \theta }, \end{aligned}$$

which contradicts (4.12). Hence, (4.8) holds. Letting $\varepsilon \longrightarrow 0^{+}$, we have from (4.8) that

$$\begin{aligned} \Vert y(t)\Vert _{1}\le M\Vert \varphi -x^{*}\Vert _{\xi }e^{-\lambda t} \text{ for } \text{ all } t > 0, \end{aligned}$$

which implies

$$\begin{aligned} \Vert x (t)-x^{*}(t)\Vert _{1} \le M \Vert \varphi -x^{*}\Vert _{0}e^{-\lambda t} \hbox {for all} t > 0. \end{aligned}$$

This completes the proof.$\square$

5 An Example

In this section, we give an example to demonstrate the results obtained in previous sections.

Example 1

Consider the following CNNs with continuously distributed leakage delays:

$$\begin{aligned} \left\{ \begin{array}{rcl} x_{1}'(t)&{} = &{}- \frac{1}{11.2}\int _{0}^{\infty }e^{-4s^{2}}x_{1}(t-s)ds +\frac{\sin t}{4000}f_{1}(x_{1}(t-2\sin ^{2}t))\\ &{}&{}+\,\frac{\sin t}{36000} f_{2}(x_{2}(t-\sin ^{4}t))+\frac{\sin t}{4000}\int _{0}^{\infty }|\sin u |e^{-u} g_{1}( x_{1}(t-u))du \\ &{}&{}+\,\frac{\sin t}{36000}\int _{0}^{\infty }|\cos u |e^{-u} g_{2}( x_{2}(t-u))du+I_{1}(t), \\ x_{2}'(t)&{} = &{} -\frac{1}{16.3}\int _{0}^{\infty }e^{-16s^{2}}x_{2}(t-s)ds +\frac{1}{1000(1+t^2)}f_{1}(x_{1}(t-\cos ^{2}t)) \\ &{}&{}+\,\frac{\cos t}{4000}f_{2}(x_{2}(t-2\cos ^{4}t)) +\frac{1}{1000(1+t^2)}\int _{0}^{\infty }|\cos u |e^{-u}g_{1}(x_{1}(t-u))du\\ &{}&{}+\,\frac{\cos t}{4000} \int _{0}^{\infty }|\sin u |e^{-u} g_{2}(x_{2}(t-u))du+I_{2}(t), \end{array} \right. \end{aligned}$$

(5.1)

where $f_{1}(x)\!=\!f_{2}(x)\!=\!g_{1}(x)\!=\!g_{2}(x)\!=\! |x|,\,I_{1}(t)\!=\!I_{2}(t)\!=\!\frac{1}{1000}\left( 4\!+\!\sin t\!+\!\sin \sqrt{2}t\!+\!\frac{1}{ 1+t^{2} }\right)$.

Obviously,

$$\begin{aligned}&c_{1}(t)=\frac{1}{11.2}, c_{2}(t)=\frac{1}{16.3},\ h_{1}(s)=e^{-4s^{2}}, h_{2}(s)=e^{-16s^{2}},\\&a_{11}(t) = b_{11}(t) =\frac{\sin t}{4000}, a_{12}(t) = b_{12} (t)= \frac{\sin t}{36000}, \\&a_{21}(t) = b_{21}(t) =\frac{1}{1000(1+t^2)}, \ a_{22}(t) = b_{22}(t) =\frac{\cos t}{4000}, \\&L^{f} _{i}=L^{g} _{i} =1, \int _{0}^{\infty }|K_{ij}(s)|ds \le 1,\quad i,j=1,2. \end{aligned}$$

Let $\xi _{1}= \xi _{2}=1$. Then,

$$\begin{aligned}&-\,c_{1} ^{-}\int _0^\infty {h_1 }(v) dv +c_{1} ^{+} \int _0^\infty v{h_1 }(v) dv +\xi _{1}^{-1}\sum ^2_{j=1} a_{1j} ^{+} \xi _{j} +\xi _{1}^{-1}\sum ^2_{j=1} b_{1j} ^{+}\int _{0}^{\infty }|K_{1j}(u)| du L^{g}_{j}\xi _{j}\\&\le -\,\frac{1}{11.2}\times \frac{\sqrt{\pi }}{2}+\frac{1}{11.2}\times \frac{1}{8}+\frac{1}{4000}+\frac{1}{36000}+\frac{1}{4000}+\frac{1}{36000}\\&\approx -\,0.0674\\&< -\,0.067,\\&-\,c_{2} ^{-}\int _0^\infty {h_2 }(v) dv +c_{2} ^{+} \int _0^\infty v{h_2 }(v) dv +\xi _{2}^{-1}\sum ^2_{j=1} a_{2j} ^{+} \xi _{j} +\xi _{2}^{-1}\sum ^2_{j=1} b_{2j} ^{+}\int _{0}^{\infty }|K_{1j}(u)| du L^{g}_{j}\xi _{j}\\&\le -\,\frac{1}{16.3}\times \frac{\sqrt{\pi }}{4}+\frac{1}{16.3}\times \frac{1}{32}+\frac{1}{1000}+\frac{1}{4000}+\frac{1}{1000}+\frac{1}{4000}\\&\approx -\,0.0228\\&< -\,0.022,\\&1-\,\frac{\alpha _{1}}{c_{1}^{+}\int _0^\infty {h_1 }(v) dv }\approx 0.1533, \ 1-\frac{\alpha _{2}}{c_{2}^{+}\int _0^\infty {h_2 }(v) dv }\approx 0.1907,\\&c_{1}^{-}\int _0^\infty {h_1 }(v) dv - \alpha _{1}+c_{1}^{+}\int _0^\infty {h_1 }(v) dv (1-\frac{\alpha _{1}}{c_{1}^{+}\int _0^\infty {h_1 }(v) dv })\approx 0.0243,\\&c_{2}^{-}\int _0^\infty {h_2 }(v) dv - \alpha _{2}+c_{2}^{+}\int _0^\infty {h_2 }(v) dv (1-\frac{\alpha _{2}}{c_{2}^{+}\int _0^\infty {h_2 }(v) dv })\approx 0.0104, \end{aligned}$$

and

$$\begin{aligned}&\left( 1+\frac{c_{i} ^{+}\int _0^\infty {h_i }(v) dv }{c_{i} ^{-}\int _0^\infty {h_i }(v) dv}\right) \\&\quad \left( c_{i} ^{+} \int _0^\infty v{h_i }(v) dv +\,\xi _{i}^{-1}\sum ^n_{j=1} a_{ij} ^{+}L^{f}_{j}\xi _{j} +\xi _{i}^{-1}\sum ^n_{j=1} b_{ij} ^{+}\int _{0}^{\infty }|K_{ij}(u)| du L^{g}_{j}\xi _{j}\right) \\&\quad < 0.05, \quad i=1,2. \end{aligned}$$

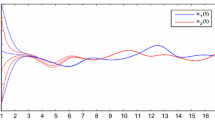
Hence, from Theorem (4.2), system (5.1) has exactly one pseudo almost periodic solution $x^{*}(t)$. Moreover, all solutions and their derivatives of solutions for (5.1) with initial conditions (1.2) converge exponentially to $x^{*}(t)$ and $x^{*} \ '(t)$, respectively. The exponential convergent rate is about $0.001$. The fact is verified by the numerical simulation in Fig. 1.

Fig. 1

Numerical solution $x(t)=(x_1(t),x_2(t))^T$ of system (5.1) for initial value $\varphi (t)\equiv (0.1,0.3)^T$

Remark 5.1

To the best of our knowledge, there is no research on the globally exponential convergence of the pseudo almost periodic solution of DCNNs with continuously distributed leakage delays. We also mention that all results in the reference [26] cannot be applied to imply that all solutions and their derivatives of solutions for (5.1) with initial conditions (1.4) converge exponentially to $x^{*}(t)$ and $x^{*} \ '(t)$, respectively. Here we employ a novel proof to establish some criteria to guarantee the existence and exponential stability of pseudo almost periodic solutions for DCNNs with continuously distributed leakage delays. This implies that the results of this paper are essentially new.