Existence and Global Exponential Stability of Almost Periodic Solution for High-Order BAM Neural Networks with Delays on Time Scales

Abstract

In this paper, by using a fixed point theorem and by constructing a suitable Lyapunov functional, we study the existence and global exponential stability of almost periodic solution for high-order bidirectional associative memory neural networks with delays on time scales. An examples shows the feasibility of our main results.

1 Introduction

It is well known that high-order neural networks have been extensively applied in psychophysics, speech, perception, robotics, adaptive pattern recognition, vision, and image processing. This is due to the fact that high-order neural networks have stronger approximation property, faster convergence rate, greater storage capacity, and higher fault tolerance than lower-order neural networks. Many interesting results on the existence and stability of periodic and almost periodic solutions of high-order neural networks have been achieved in recent years. For details, we refer to [1–11] and references therein.

As we know, both continuous and discrete systems are very important in implementation and applications. But it is troublesome to study the existence and stability of almost periodic solutions for continuous and discrete systems, respectively. Therefore, it is meaningful to study that on time scales which can unify the continuous and discrete situations. Recently, several types of neural networks on time scales have been presented and studied, see, for e.g. [7, 12–16], which can unify the continuous and discrete situations. To the best of our knowledge, there is no work on the existence and exponential stability of the almost periodic solutions of high-order bidirectional associative memory (BAM) neutral networks on time scales. Moreover, it is known that the existence and stability of the almost periodic solution play a key role in characterizing the behavior of dynamical system (see [17–19]). Thus, it is worth while to continue to investigate the existence and stability of almost periodic solution to high-order BAM neutral networks on time scales.

Motivated by the above, in this paper, we consider the following high-order BAM neutral networks with time-varying delays on time scales:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{i}^{\Delta }(t)=-a_{i}(t)x_{i}(t)+\sum \limits ^{m}_{j=1}b_{ij}(t)g_{j}\left( y_{j}\left( t-\tau _{j}(t)\right) \right) \\ \quad \quad \quad \qquad +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t)p_{j}\left( y_{j}\left( t-\tau _{j}(t)\right) \right) q_{l}\left( y_{l}\left( t-\tau _{l}(t)\right) \right) +I_{i}(t),\\ y_{j}^{\Delta }(t)=-d_{j}(t)y_{j}(t)+\sum \limits ^{n}_{i=1}c_{ji}(t)f_{i}\left( x_{i}\left( t-\omega _{i}(t)\right) \right) \\ \quad \quad \quad \qquad +\sum \limits ^{n}_{i=1}\sum \limits ^{n}_{l=1}s_{jil}(t)v_{i}\left( x_{i}\left( t-\omega _{i}(t)\right) \right) w_{l}\left( x_{l}\left( t-\omega _{l}(t)\right) \right) +J_{j}(t), \end{array}\right. \end{aligned}$$

(1.1)

where $i=1,\,2,\ldots ,n,\,j=1,\,2,\ldots ,m,\,t>0,\,x_{i}(t)$ and $y_{j}(t)$ denote the potential (or voltage) of the cell $i$ and $j$ at time $t,\,a_{i}(t)$ and $d_{j }(t)$ denote the rate with which the cell $i$ and $j$ reset their potential to the resting state when isolate from the other cells and inputs, time delay $\tau (t)$ and $\omega (t)$ are non-negative, they correspond to finite speed of axonal signal transmission, $b_{ij},\,c_{ji},\,e_{ijl}$ and $s_{jil}$ are the first- and second-order connection weights of the neural network, respectively, $I_{i}$ and $J_{j}$ denote the $i$th and the $j$th component of an external input source that introduce from outside the network to the cell $i$ and $j,$ respectively.

The system (1.1) is supplemented with initial values given by

$$\begin{aligned} x_{i}(s)=\phi _{i}(s), \quad y_{j}(s)= \psi _{j}(s), \quad \theta =\max \{\tau ^{\prime },\,\omega ^{\prime }\}, \end{aligned}$$

where $\phi _{i} \in C([-\omega ^{\prime },\,0]_{\mathbb{T }},\,\mathbb{R }),\, \psi _{j} \in C([-\tau ^{\prime },\,0]_{\mathbb{T }},\,\mathbb{R }),\, i,\,j\!=1,\,2,\ldots ,m,\,\tau ^{\prime }\!=\max \nolimits _{1\le j \le m}\sup \nolimits _{t\in \mathbb{T }}\{\tau _j(t)\},\, \omega ^{\prime }=\max \nolimits _{1\le i \le m}\sup \nolimits _{t\in \mathbb{T }}\{\omega _i(t)\},$ and denote $\varphi (t)=(\phi _{1}(t),\ldots , \phi _{m}(t),\,\psi _{1}(t),\ldots ,\psi _{m}(t)),\,s\in [-\theta ,\,0]_{\mathbb{T }}.$

For the sake of convenience, we introduce the following notations:

$$\begin{aligned} \Vert z\Vert&= \max \limits _{1\le i \le n}|x_{i}|+\max \limits _{1\le j \le m}|y_{j}|\quad \text{ for }\quad z=(x_{1},\,x_{2},\ldots ,x_{m},\,y_{1},\,y_{2},\ldots ,y_{m})^{T}\in R^{2m},\\ {\overline{a_{i}}}&= \sup \limits _{t\in \mathbb{T }}|a_{i}(t)|, \quad {\overline{d_{j}}}=\sup \limits _{t\in \mathbb{T }}|d_{j}(t)|,\quad {\overline{I_{i}}}=\sup \limits _{t\in \mathbb{T }}|I_{i}(t)|,\quad {\overline{J_{j}}}=\sup \limits _{t\in \mathbb{T }}|J_{j}(t)|,\\ {\overline{b_{ij}}}&= \sup \limits _{t\in \mathbb{T }}|b_{ij}(t)|,\quad {\overline{c_{ji}}}=\sup \limits _{t\in \mathbb{T }}|c_{ji}(t)|,\quad {\overline{e_{ijl}}}=\sup \limits _{t\in \mathbb{T }}|e_{ijl}(t)|,\\ {\overline{s_{jil}}}&= \sup \limits _{t\in \mathbb{T }}|s_{jil}(t)|,\quad {\underline{a_{i}}}=\inf \limits _{t\in \mathbb{T }}|a_{i}(t)|,\quad {\underline{d_{j}}}=\inf \limits _{t\in \mathbb{T }}|d_{j}(t)|,\quad i,\,j,\,l=1,\,2,\ldots ,m, \end{aligned}$$

and make the following assumptions:

• (H1) $a_{i},\,d_{j},\,b_{ij},\,c_{ji},\,e_{ijl},\,s_{jil},\,I_{i},\, J_{j},\,t-\tau _{j}(t),\,t-\omega _{i}(t)\in AP(\mathbb{T }),\,-a_{i},\, -d_{j} \in \mathcal{R }^{+}$ and ${\underline{ a_{i}}}>0,\, {\underline{ d_{j}}}>0,$ for $i,\,j,\,l=1,\,2,\ldots ,m.$

• (H2) There exist positive constants $G_{j},\,P_{j},\,Q_{l},\,F_{i},$ $V_{i},\, W_{l},$ such that $|g_{j}(x)|\!\le \! G_{j}, |p_{j}(x)| \le P_{j},\,|q_{l}(x)|\le Q_{l},\,|f_{i}(x)|\le F_{i},\,|v_{i}(x)|\le V_{i},\,|w_{l}(x)|\le W_{l},\, i,\,j,\,l=1,\,2,\ldots ,m,\,x\in \mathbb{R }.$

• (H3) Functions $g_{j}(u),\,p_{j}(u),\,q_{l}(u),\,f_{i}(u),\,v_{i}(u),\,w_{l}(u)\,(i,\,j,\,l=1,\,2,\ldots ,m)$ satisfy the Lipschitz condition, that is, there exist constants $G_{j}^{\prime },\,P_{j}^{\prime },\,Q_{l}^{\prime },\,F_{i}^{\prime },\,V_{i}^{\prime },\,W_{l}^{\prime }>0\,(i,\,j,\,l=1,\,2,\ldots ,m)$ such that

  $$\begin{aligned}&|g_{j}\left( u_{1}\right) -g_{j}\left( u_{2}\right) |\le G_{j}^{\prime }|u_{1}- u_{2}|,\quad |p_{j}\left( u_{1}\right) -p_{j}\left( u_{2}\right) | \le P_{j}^{\prime }|u_{1}- u_{2}|,\\&|q_{l}\left( u_{1}\right) -q_{l}\left( u_{2}\right) |\le Q_{l}^{\prime }|u_{1}- u_{2}|,\quad |f_{i}\left( u_{1}\right) -f_{i}\left( u_{2}\right) | \le F_{i}^{\prime }|u_{1}- u_{2}|,\\&|v_{i}\left( u_{1}\right) -v_{i}(u_{2})| \le V_{i}^{\prime }|u_{1}- u_{2}|,\quad |w_{l}\left( u_{1}\right) -w_{l}\left( u_{2}\right) | \le W_{l}^{\prime }|u_{1}-u_{2}|. \end{aligned}$$

The organization of this paper is as follows. In Sect. 2, necessary preliminaries are presented. In Sect. 3, a set of sufficient conditions are derived for the existence of almost periodic solutions. In Sect. 4, by constructing a suitable Lyapunov function, some sufficient conditions are obtained for the global exponential stability of system (1.1). We give an example in Sect. 5.

2 Preliminaries

In this section, we shall first recall some basic definitions and results about almost periodic dynamic equations on time scales. Throughout this paper, $\mathbb{E }^{m}$ denotes $\mathbb{R }^{m}$ or $\mathbb{C }^{m}.$

Let $\mathbb{T }$ be a non-empty closed subset (time scale) of $\mathbb{R }.$ The forward and backward jump operators $\sigma ,\,\rho :\,\mathbb{T } \rightarrow \mathbb{T }$ and the graininess $\mu :\,\mathbb{T }\rightarrow \mathbb{R }^{+}$ are defined, respectively, by

$$\begin{aligned} \sigma (t)=\inf \{s\in \mathbb{T }:\,s>t\},\quad \rho (t)=\sup \{s\in \mathbb{T }:\,s<t\},\quad \mu (t)=\sigma (t)-t. \end{aligned}$$

A point $t\in \mathbb{T }$ is called left-dense if $t>\inf \mathbb{T }$ and $\rho (t)=t,$ left-scattered if $\rho (t)<t,$ right-dense if $t<\sup \mathbb{T }$ and $\sigma (t)=t,$ and right-scattered if $\sigma (t)>t.$ If $\mathbb{T }$ has a left-scattered maximum $m,$ then $\mathbb{T }^{k}=\mathbb{T }\setminus \{m\};$ otherwise $\mathbb{T }^{k}=\mathbb{T }.$ If $\mathbb{T }$ has a right-scattered minimum $m,$ then $\mathbb{T }_{k}=\mathbb{T }\setminus \{m\},$ otherwise $\mathbb{T }_{k}=\mathbb{T }.$

A function $f:\,\mathbb{T }\rightarrow \mathbb{R }$ is right-dense continuous provided it is continuous at right-dense point in $\mathbb{T }$ and its left-side limits exist at left-dense points in $\mathbb{T }.$ If $f$ is continuous at each right-dense point and each left-dense point, then $f$ is said to be a continuous function on $\mathbb{T }.$

For $y:\,\mathbb{T } \rightarrow \mathbb{R }$ and $t\in \mathbb{T }^{k},$ we define the delta derivative of $y(t),\,y^{\Delta }(t),$ to be the number (if it exists) with the property that for a given $\varepsilon >0,$ there exists a neighborhood $U$ of $t$ such that

$$\begin{aligned} \left| [y(\sigma (t))-y(s)]-y^{\Delta }(t)[\sigma (t)-s]\right| <\varepsilon |\sigma (t)-s|, \end{aligned}$$

for all $s\in U.$

Let $y$ be right-dense continuous, if $Y^{\Delta }(t)=y(t),$ then we define the delta integral by

$$\begin{aligned} \int \limits _{a}^{t}y(s)\Delta s=Y(s)-Y(a). \end{aligned}$$

A function $p:\,\mathbb{T }\rightarrow \mathbb{R }$ is called regressive provided $1+\mu (t)p(t)\ne 0$ for all $t\in \mathbb{T }^{k}.$ The set of all regressive and rd-continuous functions $p:\,\mathbb{T }\rightarrow \mathbb{R }$ will be denoted by $\mathcal{R }=\mathcal{R }(\mathbb{T })=\mathcal{R }(\mathbb{T },\,\mathbb{R }).$ We define the set $\mathcal{R }^{+}=\mathcal{R }^{+}(\mathbb{T },\,\mathbb{R })=\{p\in \mathcal{R }:\,1+\mu (t)p(t)>0,\,\forall t\in \mathbb{T }\}.$

If $r$ is a regressive function, then the generalized exponential function $e_{r}$ is defined by

$$\begin{aligned} e_{r}(t,\,s)=\exp \left\{ \int \limits _{s}^{t}\xi _{\mu (\tau )}(r(\tau ))\Delta \tau \right\} , \end{aligned}$$

for all $s,\,t\in \mathbb{T },$ with the cylinder transformation

$$\begin{aligned} \xi _h(z)=\left\{ \begin{array}{l@{\quad }l} \frac{\text{ Log } (1+hz)}{h}, &{}\text{ if } h\ne 0,\\ z,&{}\text{ if } h=0. \end{array} \right. \end{aligned}$$

Definition 2.1

([20, 21]) Let $p,\,q:\,\mathbb T \rightarrow \mathbb{R }$ be two regressive functions, define

$$\begin{aligned} p\oplus q=p+q+\mu pq,\quad \ominus p=-\frac{p}{1+\mu p},\quad p\ominus q=p\oplus (\ominus q). \end{aligned}$$

Lemma 2.1

([20, 21]) Assume that $p,\,q:\,\mathbb{T }\rightarrow \mathbb{R }$ are two regressive functions, then

• (i) $e_{0}(t,\,s)\equiv 1,$ and $e_{p}(t,\,t)\equiv 1;$

• (ii) $e_{p}(\sigma (t),\,s)=(1+\mu (t)p(t))e_{p}(t,\,s);$

• (iii) $e_{p}(t,\,s)=\frac{1}{e_{p}(s,\,t)}=e_{\ominus p}(s,\,t);$

• (iv) $e_{p}(t,\,s)e_{p}(s,\,r)=e_{p}(t,\,r);$

• (v) $(e_{\ominus p}(t,\,s))^{\Delta }=(\ominus p)(t)e_{\ominus p}(t,\,s);$

• (vi) If $a,\,b,\,c\in \mathbb{T },$ then $\int ^{b}_{a}p(t)e_{p}(c,\,\sigma (t))\Delta t=e_{p}(c,\,a)-e_{p}(c,\,b).$

Definition 2.2

([22]) A time scale $\mathbb{T }$ is called an almost periodic time scale if

$$\begin{aligned} \Pi :=\,\{\tau \in \mathbb{R }:\,t+\tau \in \mathbb{T },\,\forall \, t\in \mathbb{T }\}\ne \{0\}. \end{aligned}$$

Definition 2.3

([22]) Let $\mathbb{T }$ be an almost periodic time scale. A function $f\in C(\mathbb{T },\,\mathbb{E }^{m})$ is called almost periodic if the $\varepsilon$-translation set of $f$

$$\begin{aligned} E\{\varepsilon ,\,f\}=\{\tau \in \Pi :\, |f(t+\tau )-f(t)|<\varepsilon ,\mathrm{for\ all}\,t\in \mathbb{T }\}, \end{aligned}$$

is relatively dense in $\mathbb{T }$ for all $\varepsilon >0;$ that is, for any given $\varepsilon >0,$ there exists an constant $l(\varepsilon )>0$ such that each interval of length contains at least one $\tau =\tau (\varepsilon )\in E\{\varepsilon ,\,f\}$ satisfying

$$\begin{aligned} |f(t+\tau )-f(t)|<\varepsilon ,\quad \mathrm{for\;all}\, t\in \mathbb{T }. \end{aligned}$$

$\tau$ is called $\varepsilon$-translation number of $f,$ and $l(\varepsilon )$ is called contain interval length of $E\{\varepsilon ,\,f\}.$

Lemma 2.2

([22]) Let $f\in C(\mathbb{T },\,\mathbb{E }^{m})$ be an almost periodic function, then $f(t)$ is bounded on $\mathbb{T }.$

Theorem 2.1

([22]) If $f,\,g\in C(\mathbb{T },\,\mathbb{E }^{m})$ are almost periodic, then $f+g,\,fg$ are almost periodic.

Theorem 2.2

([22]) If $f(t)\in C(\mathbb{T },\,\mathbb{E }^{m})$ is almost periodic, F(t, x) is almost periodic if and only if $F(t)$ is bounded on $\mathbb{T },$ where $F(t)=\int ^{t}_{0}f(s)\Delta (s).$

Theorem 2.3

([22]) If $f(t)$ is almost periodic, $F(\cdot )$ is uniformly continuous on the value field of $f(t),$ then $F \circ f$ is almost periodic.

Definition 2.4

([22]) Let $z\in \mathbb{E }^{m},$ and $A(t)$ be an $m \times m$ rd-continuous matrix on $\mathbb{T },$ the linear system

$$\begin{aligned} z^{\Delta }(t)= A(t)z(t),\quad t\in \mathbb{T }, \end{aligned}$$

(2.1)

is said to admit an exponential dichotomy on $\mathbb{T }$ if there exist positive constant $k,\,\alpha ,$ projection $P,$ and the fundamental solution matrix $Z(t)$ of (2.1), satisfying

$$\begin{aligned}&|Z(t) P Z^{-1}(\sigma (s))|\le k e_{\ominus \alpha }(t,\,\sigma (s)), \quad \quad \quad \quad s,t \in \mathbb{T },\quad t\ge \sigma (s),\\&|Z(t) (I-P) Z^{-1}(\sigma (s))|\le k e_{\ominus \alpha }(\sigma (s),\,t),\quad s,\,t \in \mathbb{T },\quad t\le \sigma (s), \end{aligned}$$

where $|\cdot |$ is a matrix norm on $\mathbb{T }$ (say, e.g., if $B=(b_{ij})_{m \times m},$ then we can take $|B|=(\sum \nolimits ^{m}_{i=1}\sum \nolimits ^{m}_{j=1}|b_{ij}|^{2})^{\frac{1}{2}}).$

Consider the following almost periodic system

$$\begin{aligned} z^{\Delta }(t)= A(t)z(t)+f(t),\quad t\in \mathbb{T }, \end{aligned}$$

(2.2)

where $A(t)$ is an almost periodic matrix function, $f(t)$ is an almost periodic vector function.

Lemma 2.3

([22]) Let $A(t)$ be an almost periodic matrix function and $f(t)$ be an almost periodic vector function. If (2.1) admits exponential dichotomy, then system (2.2) has a unique almost periodic solution $z(t)$ as follows:

$$\begin{aligned} z(t)=\int \limits _{-\infty }^{t}Z(t) P Z^{-1}(\sigma (s))f(s)\Delta (s)-\int \limits _{t}^{+\infty }Z(t) (I-P) Z^{-1}(\sigma (s))f(s)\Delta (s), \end{aligned}$$

where Z(t) is the fundamental solution matrix of (2.1).

Lemma 2.4

([16]) Let $c_{i}(t)$ be an almost periodic function on $\mathbb{T },$ where $c_{i}(t)>0,\,-c_{i}(t)\in \mathcal{R }^{+},\, \forall \,t \in \mathbb T$ and

$$\begin{aligned} \min \limits _{1\le i \le n}\left\{ \inf \limits _{t \in \mathbb{T }} c_{i}(t)\right\} ={\tilde{m}}>0, \end{aligned}$$

then the linear system

$$\begin{aligned} z^{\Delta }(t)=\text{ diag }\left( -c_{1}(t),\,-c_{2}(t),\ldots ,-c_{m}(t)\right) z(t), \end{aligned}$$

admits an exponential dichotomy on $\mathbb{T }.$

Definition 2.5

The almost periodic solution $x^*=(x_1^*,\,x_2^*,\ldots , x_m^*,\,y_1^*,\,y_2^*,\ldots ,y_m^*)^T$ of system (1.1) is said to be globally exponentially stable, if there exist constants $\lambda$ and $M=M(\lambda )\ge 1,$ for any solution $x(t)=(x_1(t),\,x_2(t), \ldots , x_m(t),\,y_{1}(t), y_{2}(t),\ldots ,y_{m}(t))^T$ of system (1.1) with the initial value $\varphi (t)\!=\!(\phi _1(t), \phi _2(t),\!\ldots \!,\phi _m(t), \psi _1(t), \psi _2(t), \!\ldots ,\psi _m(t))^T,$ where $(\phi _1(t), \phi _2(t),\!\ldots ,\phi _m(t))\in C([-\omega ^{\prime },\, 0]_\mathbb{T },\,\mathbb{R }^m)$ and $(\varphi _1(t),\,\varphi _2(t), \ldots ,\varphi _m(t))\in C([-\tau ^{\prime },\,0]_\mathbb{T },\, \mathbb{R }^m),$ such that

$$\begin{aligned} \sum _{i=1}^m|x_i(t)\!-\!x_i^*(t)|\!+\!\sum _{j=1}^m|y_{j}(t)\!-\!y_{j}^*(t)|\!\le \! M(\lambda )e_{\ominus \lambda }(t,\, 0)\left( \sum _{i=1}^{m}\Vert x_i\!-\!x^*\Vert \!+\!\sum _{j=1}^{m}\Vert y_i\!-\!y^*\Vert \right) , \end{aligned}$$

where

$$\begin{aligned} \Vert x_i-x^*\Vert&= \sum _{i=1}^n \max _{s\in [-\omega ^{\prime }, 0]_\mathbb{T }}|\phi _i(s)-x_i^*(s)|,\quad s\in [-\omega ^{\prime },\, 0]_\mathbb{T },\\ \Vert y_j-y^*\Vert&= \sum _{j=1}^m \max _{s\in [-\tau ^{\prime },\, 0]_\mathbb{T }}|\psi _j(s)-y_j^*(s)|,\quad s\in [-{\tau }^{\prime },\, 0]_\mathbb{T }. \end{aligned}$$

3 Existence of Almost Periodic Solutions

Set $S^{2m}\!=\!\{z| z\!=\!(\phi _{1},\, \phi _{2},\ldots ,\phi _{m},\,\psi _{1},\,\psi _{2},\ldots ,\psi _{m})^{T},\,\phi _{i},\,\psi _{j}\in AP(\mathbb{T }),\,i,\,j\!=\!1,\,2, \ldots ,m\}.$ For any $z\in S^{2m},$ we define induced module $\Vert z\Vert =\sup \nolimits _{t\in \mathbb{T }}\Vert z(t)\Vert =\sup \nolimits _{t\in \mathbb{T }}\max \nolimits _{1\le i \le m}|\phi _{i}(t)|+\sup \nolimits _{t\in \mathbb{T }}\max \nolimits _{1\le j \le m}|\psi _{j}(t)|,$ then $S^{2m}$ is an Banach space.

Theorem 3.1

Assume that $(H1)$–$(H3)$ hold, and suppose that

• (H4)
  $$\begin{aligned} \rho&\triangleq \max \limits _{1 \le i \le m}\frac{\sum \nolimits ^{m}_{j=1}{\overline{b_{ij}}}G_{j}^{\prime }+\sum \nolimits ^{m}_{j=1}\sum \nolimits ^{m}_{l=1}{\overline{e_{ijl}}} (P_{j}Q_{l}^{\prime }+Q_{l}P_{j}^{\prime })}{\underline{a_{i}}}\\&+\max \limits _{1 \le j \le m}\frac{\sum \nolimits ^{m}_{i=1} {\overline{c_{ji}}}F_{i}^{\prime }+\sum \nolimits ^{m}_{i=1} \sum \nolimits ^{m}_{l=1}{\overline{s_{jil}}} (V_{i}W_{l}^{\prime }+W_{l}V_{i}^{\prime })}{\underline{d_{j}}} < 1. \end{aligned}$$

Then (1.1) has a unique almost periodic solution.

Proof

For any given $z=(\phi _{1},\,\phi _{2},\ldots ,\phi _{m},\,\psi _{1},\,\psi _{2},\ldots ,\psi _{m})^{T}\in S^{2m},$ we consider the following almost periodic system:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{i}^{\Delta }(t)=-a_{i}(t)x_{i}(t)+\sum \limits ^{m}_{j=1}b_{ij}(t)g_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) \\ \quad \quad \quad \qquad +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t)p_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) q_{l} \left( \psi _{l}\left( t-\tau _{l}(t)\right) \right) +I_{i}(t),\\ y_{j}^{\Delta }(t)=-d_{j}(t)y_{j}(t)+\sum \limits ^{m}_{i=1}c_{ji}(t)f_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) \\ \quad \quad \qquad \quad +\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}s_{jil}(t)v_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) w_{l} \left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) +J_{j}(t), \end{array}\right. \end{aligned}$$

since $\min \nolimits _{1 \le i \le n}\{\inf \nolimits _{t\in \mathbb{T }} a_{i}(t)\}> 0,\,\min \nolimits _{1 \le j \le m}\{\inf \nolimits _{t\in \mathbb{T }} d_{j}(t)\}>0,\,i,\,j=1,\,2,\ldots ,m,\,t\in \mathbb{T },$ it follows from Lemma 2.4 that the linear system

$$\begin{aligned} \left\{ \begin{array}{ll} x_{i}^{\Delta }(t)=-a_{i}(t)x_{i}(t),\quad \;\; i=1,\,2,\ldots ,m,\\ y_{j}^{\Delta }(t)=-d_{j}(t)y_{j}(t),\quad j=1,\,2,\ldots ,m, \end{array}\right. \end{aligned}$$

admits an exponential dichotomy on $\mathbb{T }.$ Thus, by Lemmas 2.3 and 2.4, we obtain that system (1.1) has a bounded solution:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{\psi i}(t) \!=\!\displaystyle \int \limits _{-\infty }^{t} e_{-a_{i}}(t,\,\sigma (s))\times \bigg (\sum \limits ^{m}_{j=1}b_{ij}(t)g_{j}\left( \psi _{j}\left( t\!-\!\tau _{j}(t)\right) \right) \\ \quad \quad \;\qquad +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t)p_{j}\left( \psi _{j}\left( t\!-\!\tau _{j}(t)\right) \right) q_{l} \left( \psi _{l}\left( t\!-\!\tau _{l}(t)\right) \right) \!+\!I_{i}(t)\bigg ) \Delta s,\quad i\!=\!1,\,2,\ldots ,m,\\ y_{\phi j}(t) \!=\!\displaystyle \int \limits _{-\infty }^{t} e_{-d_{j}}(t,\,\sigma (s))\times \bigg (\sum \limits ^{m}_{i=1}c_{ji}(t)f_{i}\left( \phi _{i}\left( t\!-\!\omega _{i}(t)\right) \right) \\ \quad \quad \qquad \;+\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}s_{jil}(t)v_{i}\left( \phi _{i}\left( t\!-\!\omega _{i}(t)\right) \right) w_{l}\left( \phi _{l}\left( t\!-\!\omega _{l}(t)\right) \right) \!+\!J_{j}(t) \bigg )\Delta s,\quad j\!=\!1,\,2,\ldots ,m, \end{array}\right. \end{aligned}$$

and it follows from Theorems 2.1–2.3 and $e_{-a_{i}}(t,\,\sigma (s)),\, e_{-d_{j}}(t,\,\sigma (s))$ being almost periodic that $(x_{\psi },\,y_{\phi })$ is also almost periodic.

Denote

$$\begin{aligned}&\max \limits _{1\le i \le m}\left\{ \frac{\sum \nolimits ^{m}_{j=1}{\overline{b_{ij}}}G_{j}+ \sum \nolimits ^{m}_{j=1}\sum \nolimits ^{m}_{l=1} {\overline{e_{ijl}}}P_{j}Q_{l}}{\underline{a_{i}}} \right\} +\max \limits _{1\le i \le m}\bigg \{\frac{{\overline{I_{i}}}}{\underline{a_{i}}}\bigg \} \nonumber \\&\quad +\max \limits _{1\le j \le m}\left\{ \frac{\sum \nolimits ^{m}_{i=1}{\overline{c_{ji}}}F_{i}+ \sum \nolimits ^{m}_{i=1}\sum \nolimits ^{m}_{l=1} {\overline{s_{jil}}}V_{i}W_{l}}{\underline{d_{j}}} \right\} + \max \limits _{1\le j \le m}\bigg \{ \frac{{\overline{J_{j}}}}{{\underline{d_{j}}}}\bigg \} \triangleq L. \end{aligned}$$

Now we define a mapping $T:\,S^{2m}\rightarrow S^{2m},\, Tz=T(\phi ,\,\psi )^{T}(t)=(x_{\psi i}(t), y_{\phi j}(t))_{i,j=1,2,\ldots ,m}^{T},\;\forall z\in S^{2m}.$ Set

$$\begin{aligned} B^{*}=\left\{ z|z=\left( \phi _{1},\,\phi _{2},\ldots ,\phi _{m},\,\psi _{1},\,\psi _{2},\ldots ,\psi _{m}\right) ^{T}\in S^{2m},\,\Vert z\Vert \le L\right\} . \end{aligned}$$

Next, let us check that $Tz \in B^{*}.$ For any given $z\in B^{*},$ it suffices to prove that $\Vert T(z)\Vert \le L.$ Noting that

$$\begin{aligned} \Vert T(z)\Vert&= \sup \limits _{t\in \mathbb{T }}\max \limits _{1\le i \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-a_{i}}(t,\,\sigma (s))\bigg ( \sum \limits ^{m}_{j=1}b_{ij}(t)g_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) \\&+\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t) p_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) q_{l}\left( \psi _{l}\left( t-\tau _{l}(t)\right) \right) +I_{i}(t)\bigg )\Delta s\bigg |\bigg \}\\&+\,\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le j \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-d_{j}}(t,\,\sigma (s))\bigg ( \sum \limits ^{m}_{i=1}c_{ji}(t)f_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) \\&+\,\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}s_{jil}(t) v_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) w_{l}\left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) +J_{j}(t)\bigg )\Delta s\bigg |\bigg \}\\&\le \sup \limits _{t\in \mathbb{T }}\max \limits _{1\le i \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-\underline{a_{i}}}(t,\,\sigma (s))\bigg ( \sum \limits ^{m}_{j=1}\overline{b_{ij}}g_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) \\&+\,\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}\overline{e_{ijl}} p_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) q_{l}\left( \psi _{l}\left( t-\tau _{l}(t)\right) \right) \bigg )\Delta s\bigg |\bigg \}+\max _{1 \le i \le n}\bigg \{\frac{\overline{I_{i}}}{\underline{a_{i}}}\bigg \}\\&+\,\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le j \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-\underline{d_{j}}}(t,\,\sigma (s))\bigg (\sum \limits ^{m}_{i=1}\overline{c_{ji}}f_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) \\&+\,\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}\overline{s_{jil}} v_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) w_{l}\left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) \bigg )\Delta s\bigg |\bigg \}+\max _{1 \le j \le m}\bigg \{\frac{\overline{J_{j}}}{\underline{d_{j}}}\bigg \}\\&\le \max \limits _{1\le i \le m}\left\{ \frac{\sum \limits ^{m}_{j=1}\overline{b_{ij}}G_{j}+\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}\overline{e_{ijl}}P_{j}Q_{l}}{\underline{a_{i}}} \right\} +\max \limits _{1\le i \le m}\bigg \{\frac{\overline{I_{i}}}{\underline{a_{i}}}\bigg \} \nonumber \\&+\max \limits _{1\le j \le m}\left\{ \frac{\sum \limits ^{m}_{i=1}\overline{c_{ji}}F_{i}+\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}\overline{s_{jil}}V_{i}W_{l}}{{\underline{d_{j}}}} \right\} +\max \limits _{1\le j \le m}\bigg \{\frac{{\overline{J_{j}}}}{{\underline{d_{j}}}}\bigg \} = L, \end{aligned}$$

which shows that $Tz \in B^{*}.$ So $T$ is a self-mapping from $B^{*}$ to $B^{*}.$ Next, we shall prove that $T$ is a contraction of $B^{*}.$ For any $z_{1}=(\xi _{1},\,\xi _{2},\ldots ,\xi _{m},\,\eta _{1},\,\eta _{2},\ldots ,\eta _{m})^{T},\,z_{2}=(\phi _{1},\,\phi _{2},\ldots ,\phi _{m},\,\psi _{1},\,\psi _{2},\ldots ,\psi _{m})^{T},$ and $z_{1},\,z_{2} \in B^{*},$

$$\begin{aligned}&\Vert T\left( z_{1}\right) -T\left( z_{2}\right) \Vert =\sup \limits _{t \in \mathbb{T }}\Vert T\left( z_{1}\right) (t)-T\left( z_{2}\right) (t)\Vert \nonumber \\&\quad =\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le i \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-a_{i}}(t,\,\sigma (s))\bigg ( \sum \limits ^{m}_{j=1}b_{ij}(t)\left( g_{j}\left( \eta _{j}\left( t-\tau _{j}(t)\right) \right) -g_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) \right) \nonumber \\&\qquad +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t) \left( p_{j}\left( \eta _{j}\left( t-\tau _{j}(t)\right) \right) q_{l}\left( \eta _{l}\left( t-\tau _{l}(t)\right) \right) \right. \\&\qquad \left. -p_{j}\left( \psi _{j}\left( t-\tau _{j}(t)\right) \right) q_{l}\left( \psi _{l}\left( t-\tau _{l}(t)\right) \right) \right) \bigg )\Delta s\bigg |\bigg \}\nonumber \\&\qquad +\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le j \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-d_{j}}(t,\,\sigma (s))\bigg (\sum \limits ^{m}_{i=1}c_{ji}(t)\left( f_{i}\left( \xi _{i}\left( t-\omega _{i}(t)\right) \right) \right. \\&\qquad \left. -f_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) \right) \nonumber \\&\qquad +\,\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}s_{jil}(t) \left( v_{i}\left( \xi _{i}\left( t-\omega _{i}(t)\right) \right) w_{l}\left( \xi _{l}\left( t-\omega _{l}(t)\right) \right) \right. \\&\qquad \left. -\,v_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) w_{l}\left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) \right) \bigg ) \Delta s\bigg |\bigg \}\nonumber \\&\quad \le \sup \limits _{t\in \mathbb{T }}\max \limits _{1\le i \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-a_{i}}(t,\,\sigma (s))\bigg (\sum \limits ^{m}_{j=1}b_{ij}(t)\left( g_{j}\left( \eta _{j}\left( t\!-\!\tau _{j}(t)\right) \right) -g_{j}\left( \psi _{j}\left( t\!-\!\tau _{j}(t)\right) \right) \right) \nonumber \\&\qquad +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}e_{ijl}(t)\left( p_{j} \left( \eta _{j}\left( t\!-\!\tau _{j}(t)\right) \right) |q_{l}\left( \eta _{l}\left( t\!-\!\tau _{l}(t)\right) \right) \!-\!q_{l} \left( \psi _{l}\left( t\!-\!\tau _{l}(t)\right) \right) \right) |\nonumber \\&\qquad +\,q_{l}\left( \psi _{l}\left( t-\tau _{l}(t)\right) \right) |p_{j}\left( \eta _{j}\left( t-\tau _{j}(t)\right) \right) -p_{j}\left( \psi _{j}\left( t\!-\!\tau _{j}(t)\right) \right) |\bigg )\Delta s\bigg |\bigg \}\nonumber \\&\qquad +\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le j \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-d_{j}}(t,\,\sigma (s)) \bigg (\sum \limits ^{m}_{i=1}c_{ji}(t)\left( f_{i}\left( \xi _{i}\left( t\!-\!\omega _{i}(t)\right) \right) \!-\!f_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) \right) \nonumber \\&\qquad +\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}s_{jil}(t) \left( v_{i}\left( \xi _{i}\left( t-\omega _{i}(t)\right) \right) \right) |w_{l}\left( \xi _{l}\left( t-\omega _{l}(t)\right) \right) -w_{l}\left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) |\nonumber \\&\qquad +\, w_{l}\left( \phi _{l}\left( t-\omega _{l}(t)\right) \right) |v_{i}\left( \xi _{i}\left( t-\omega _{i}(t)\right) \right) -v_{i}\left( \phi _{i}\left( t-\omega _{i}(t)\right) \right) |\bigg )\Delta s\bigg |\bigg \}\\&\quad \le \sup \limits _{t\in \mathbb{T }}\max \limits _{1\le i \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-\underline{a_{i}}}(t,\,\sigma (s))\bigg (\sum \limits ^{m}_{j=1}\overline{b_{ij}}G_{j}^{\prime }\Vert z_{1}-z_{2}\Vert +\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}\overline{e_{ijl}} (P_{j}Q_{l}^{\prime }\Vert z_{1}-z_{2}\Vert \nonumber \\&\qquad +Q_{l}P_{j}^{\prime }\Vert z_{1}-z_{2}\Vert )\bigg )\Delta s \bigg |\bigg \}+\sup \limits _{t\in \mathbb{T }}\max \limits _{1\le j \le m}\bigg \{\bigg |\int \limits _{-\infty }^{t}e_{-\underline{d_{j}}}(t,\,\sigma (s))\bigg (\sum \limits ^{m}_{i=1}\overline{ c_{ji}}F_{i}^{\prime }\Vert z_{1}-z_{2}\Vert \nonumber \\&\qquad +\sum \limits ^{m}_{i=1}\sum \limits ^{m}_{l=1}\overline{s_{ijl}}(V_{i}W_{l}^{\prime }\Vert z_{1}-z_{2}\Vert +W_{l}V_{i}^{\prime }\Vert z_{1}-z_{2}\Vert )\bigg )\Delta s \bigg |\bigg \}\nonumber \\&\quad =\left\{ \max \limits _{1 \le i \le m}\frac{\sum ^{m}_{j=1}\overline{b_{ij}}G_{j}^{\prime }+\sum ^{m}_{j=1}\sum ^{m}_{l=1}\overline{e_{ijl}} \left( P_{j}Q_{l}^{\prime }+Q_{l}P_{j}^{\prime }\right) }{\underline{a_{i}}}\right. \\&\quad \left. +\max \limits _{1 \le j \le m}\frac{\sum ^{m}_{i=1}\overline{c_{ji}}F_{i}^{\prime }+\sum ^{m}_{i=1}\sum ^{m}_{l=1}\overline{s_{jil}} \left( V_{j}W_{l}^{\prime }+W_{l}V_{i}^{\prime }\right) }{\underline{d_{j}}}\right\} \times \Vert z_{1}-z_{2}\Vert = \rho \Vert z_{1}-z_{2}\Vert . \end{aligned}$$

Because $\rho <1,$ so $T$ is a contraction of $B^{*}.$ By the fixed point theorem of Banach space, $T$ has a unique fixed point $z \in B^{*}$ such that $Tz=z.$ Therefore, system (1.1) has a unique almost periodic solution $z\in B^{*}.$ The proof is complete. $\square$

4 Global Exponential Stability of the Almost Periodic Solution

Suppose that $z^{*}(t)=(x_{1}^{*}(t),\ldots ,x_{m}^{*}(t),\,y_{1}^{*}(t),\ldots ,y_{m}^{*}(t))^{T}$ is an almost periodic solution of system (1.1) with the initial value $z^{*}(s)=(x_{1}^{*}(s),\ldots ,x_{m}^{*}(s),\,y_{1}^{*}(s),\ldots ,y_{m}^{*}(s))^{T},\, s\in [-\theta ,\,0]_{\mathbb{T }}.$ In this section, we will construct some Lyapunov functionals to study the global exponential stability of the almost periodic solution. Denote $\mathbb{T }_{0}^{+}:=\,[0,\,+\infty )_\mathbb{T }.$

Theorem 4.1

Suppose that the system (1.1) satisfies $(H1)$–$(H3),\, 0\in \mathbb{T }$ and $\tau _{j}(t)\equiv \tau _{j},\,\omega _{i}(t)\equiv \omega _{i}$ are constants for $i,\,j=1,\,2,\ldots ,m,$ if there exist constants $\lambda _{i},\,\xi _{j}$ and $p>0$ such that

$$\begin{aligned} T_{i}\left( \lambda _{i},\,p\right)&= \lambda _{i}\bigg [p+\bigg (\overline{a_{i}}^{2}\mu (t)-2\underline{a_{i}}+\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\nonumber \\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]\nonumber \\&+\sum \limits _{j=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu \left( t+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\nonumber \\&+\,\mu \left( t+\omega _{i}\right) \left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\nonumber \\&\times \left( 1+p\mu \left( t+\omega _{i}\right) \right) e_{p}\left( t+\omega _{i},\,t\right) \!<\!0, \end{aligned}$$

(4.1)

for all $i\,j=1,\,2,\ldots ,m,\,t\in \mathbb{T }_{0}^{+};$

$$\begin{aligned} H_{j}\left( \xi _{j},\,p\right) \!&= \!\xi _{j}\bigg [p\!+\!\bigg (\overline{d_{j}}^{2}\mu (t)\!-\!2\underline{d_{j}}+\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\nonumber \\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]\nonumber \\&+\sum \limits _{i=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu \left( t+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\nonumber \\&+\,\mu \left( t\!+\!\tau _{j}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\nonumber \\&\times \left( 1\!+\!p\mu \left( t\!+\!\tau _{j}\right) \right) e_{p}\left( t\!+\!\tau _{j},\,t\right) \!<\!0, \end{aligned}$$

(4.2)

for all $i,\,j=1,\,2,\ldots ,m,\,t\in \mathbb{T }_{0}^{+},$ then the almost periodic solution of system (1.1) is globally exponentially stable.

Proof

According to Theorem 3.1, we know that (1.1) has an almost periodic solution

$$\begin{aligned} x^*(t)=\big (x_1^*(t),\,x_2^*(t),\ldots ,x_m^*(t),\,y_{1}^*(t),\,y_2^*(t),\ldots ,y_m^*(t)\big )^{T}. \end{aligned}$$

Suppose that

$$\begin{aligned} x(t)=\big (x_1(t),\,x_2(t),\ldots ,x_m(t),\,y_1(t),\,y_2(t),\ldots ,y_m(t)\big )^{T} \end{aligned}$$

is an arbitrary solution of (1.1). Then it follows from system (1.1) that

$$\begin{aligned} k_{i}^{\Delta }(s)\!+\!a_{i}(s)k_{i}(s)\!&= \!\sum \limits _{j=1}^{m}b_{ij}(t)\big [g_{j}\left( z_{j}\left( t\!-\!\tau _{j}\right) \!+\!y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \!-\!g_{j}\left( y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \big ]\nonumber \\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big [\left[ p_{j}\left( z_{j}\left( t\!-\!\tau _{j}\right) \!+\!y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \!-\!p_{j}\left( y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \right] \nonumber \\&\times \, q_{l}\left( z_{l}\left( t\!-\!\tau _{l}\right) \!+\!y_{l}^*\left( t\!-\!\tau _{l}\right) \right) \big ]\nonumber \\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big [\left[ q_{l}\left( z_{l}\left( t\!-\!\tau _{l}\right) \!+\!y_{l}^*\left( t\!-\!\tau _{l}\right) \right) -q_{l}\left( y_{l}^*\left( t\!-\!\tau _{l}\right) \right) \right] \nonumber \\&\times p_{j}\left( y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \big ], \end{aligned}$$

(4.3)

where $x_{i}(t)-x_{i}^*(t)=k_{i}(t),\,i=1,\,2,\ldots ,m,$ the initial condition of (4.3) is

$$\begin{aligned} \alpha _i(s)=\phi _i(s)-x_i^*(s),\quad s\in [-\omega ^{\prime },\,0]_{\mathbb{T }},\quad i=1,\,2,\ldots ,m. \end{aligned}$$

Similarly, we also have

$$\begin{aligned} z_{j}^{\Delta }(s)\!+\!d_{j}(s)z_{j}(s)\!&= \!\sum \limits _{i=1}^{n}c_{ji}(t)\big [f_{i}\left( k_{i}\left( t\!-\!\omega _{i}\right) \!+\!x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \!-\!f_{i}\left( x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \big ]\nonumber \\&+\,\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{n}s_{jil}(t)\big [\left[ v_{i}\left( k_{i}\left( t\!-\!\omega _{i}\right) \!+\!x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \!-\!v_{i}\left( x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \right] \nonumber \\&\quad \times \, w_{l}\left( k_{l}\left( t\!-\!\omega _{l}\right) \!+\!x_{l}^*\left( t\!-\!\omega _{l}\right) \right) \big ]\nonumber \\&+\,\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{n}s_{jil}(t)\big [\left[ w_{l}\left( k_{l}\left( t\!-\!\omega _{l}\right) \!+\!x_{l}^*\left( t\!-\!\omega _{l}\right) \right) \!-\!w_{l}\left( x_{l}^*\left( t\!-\!\omega _{l}\right) \right) \right] \nonumber \\&\quad \times \, v_{i}\left( x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \big ], \end{aligned}$$

(4.4)

where $y_{j}(t)-y_{j}^*(t)=z_{j}(t),\,j=1,\,2,\ldots ,m,$ the initial condition of (4.4) is

$$\begin{aligned} \beta _j(s)=\psi _j(s)-y_j^*(s),\quad s\in [-\tau ^{\prime },\,0]_{\mathbb{T }},\quad j=1,\,2,\ldots ,m. \end{aligned}$$

Now, we construct the Lyapunov functional $F(t)$ as follows:

$$\begin{aligned} F(t)\!&= \!F_1(t)\!+\!F_2(t)\!+\!F_3(t)\!+\!F_4(t),\\ F_1(t)&= \sum \limits _{i=1}^{m}\lambda _{i}k_{i}^{2}(t)e_{p}(t,\,0),\\ F_2(t)&= \sum \limits _{i=1}^{m}\xi _{j}z_{j}^{2}(t)e_{p}(t,\,0),\\ F_3(t)&= \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\int \limits _{t\!-\!\tau _{j}}^{t}\bigg [\left( 1\!+\!\overline{a_{i}}\mu \left( s\!+\!\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\mu \left( s\!+\!\tau _{j}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1\!+\!p\mu \left( s\!+\!\tau _{j}\right) \right) z_{j}^{2}(s)e_{p}\left( s\!+\!\tau _{j},\,0\right) \Delta s,\\ F_4(t)&= \sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\int \limits _{t-\omega _{i}}^{t}\bigg [\left( 1\!+\!\overline{d_{j}}\mu \left( s\!+\!\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu \left( s\!+\!\omega _{i}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1\!+\!p\mu \left( s\!+\!\omega _{i}\right) \right) k_{i}^{2}(s)e_{p}\left( s\!+\!\omega _{i},\,0\right) \Delta s. \end{aligned}$$

Calculating $\Delta$-derivative $F^{\Delta }(t)$ of $F(t)$ along the solution of (4.3), (4.4), we have

$$\begin{aligned} F_1^{\Delta }(t)&= \sum \limits _{i=1}^{m}\lambda _{i}\left[ \left( k_i^{2}(t)\right) ^{\Delta }e_{p}(\sigma (t),\,0)+k_{i}^{2}(t)e_{p}^{\Delta }(t,\,0)\right] \\&= \sum \limits _{i=1}^{m}\lambda _{i}\left[ \left( k_{i}(t)+k_{i}(\sigma (t))\right) k_{i}^{\Delta }(t)e_{p}(\sigma (t),\,0)+k_{i}^{2}(t)pe_{p}(t,\,0)\right] \\&= \sum \limits _{i=1}^{m}\lambda _{i}\left[ \left( k_i(t)+\mu (t)k_{i}^{\Delta }(t)+k_{i}(t)\right) k_{i}^{\Delta }(t)e_{p}(\sigma (t),\,0)+k_{i}^{2}(t)pe_{p}(t,\,0)\right] \\&= \sum \limits _{i=1}^{m}\lambda _{i}\left[ \left( 2k_{i}(t)k_{i}^{\Delta }(t)+\mu (t)\left( k_{i}^{\Delta }(t)\right) ^{2}\right) e_{p}(\sigma (t),\,0)+k_{i}^{2}(t)pe_{p}(t,\,0)\right] \\&= \sum \limits _{i=1}^{m}\lambda _{i}\bigg [\bigg (2k_{i}(t)\bigg (-a_{i}(t)k_{i}(t)+\sum \limits _{j=1}^{m}b_{ij}(t)\big (g_{j}\left( z_{j}\left( t-\tau _{j}\right) +y_{j}^*\left( t-\tau _{j}\right) \right) \\&-g_{j}\left( y_{j}^*\left( t-\tau _{j}\right) \right) \big )+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big ([p_{j}(z_{j}(t-\tau _{j})+y_{j}^*(t-\tau _{j}))\\&-p_{j}(y_{j}^*(t-\tau _{j}))]\times q_{l}(z_{l}(t-\tau _{l}) +y_{l}^*(t-\tau _{l}))\big )\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big (\left[ q_{l}\left( z_{l}\left( t-\tau _{l}\right) +y_{l}^*\left( t-\tau _{l}\right) \right) -q_{l}\left( y_{l}^*\left( t-\tau _{l}\right) \right) \right] \\&\times p_{j}\left( y_{j}^*\left( t-\tau _{j}\right) \right) \big )\bigg )\\&+\,\mu (t)\bigg (\!-\!a_{i}(t)k_{i}(t)\!+\!\sum \limits _{j=1}^{m}b_{ij}(t)\big (g_{j}\left( z_{j}\left( t-\tau _{j}\right) \!+\!y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \!-\!g_{j}\left( y_{j}^*\left( t\!-\!\tau _{j}\right) \right) \big )\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big (\left[ p_{j}\left( z_{j}\left( t-\tau _{j}\right) +y_{j}^*\left( t-\tau _{j}\right) \right) -p_{j}\left( y_{j}^*\left( t-\tau _{j}\right) \right) \right] \\&\times \, q_{l}\left( z_{l}\left( t-\tau _{l}\right) +y_{l}^*\left( t-\tau _{l}\right) \right) \big )+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}e_{ijl}(t)\big ([q_{l}\left( z_{l}\left( t-\tau _{l}\right) +y_{l}^*\left( t-\tau _{l}\right) \right) \\&-\,q_{l}\left( y_{l}^*\left( t-\tau _{l}\right) \right) ]\times p_{j}\left( y_{j}^*\left( t-\tau _{j}\right) \right) \big )\bigg )^{2}\bigg )e_{p}(\sigma (t),\,0)+k_{i}^{2}(t)pe_{p}(t,\,0)\bigg ] \end{aligned}$$

$$\begin{aligned}&\le \sum \limits _{i=1}^{m}\bigg [\lambda _{i}e_{p}(\sigma (t),\,0)\bigg (-2{\underline{a_{i}}}k_{i}^{2}(t)+2\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }|z_{j}\left( t-\tau _{j}\right) ||k_{i}(t)|\\&+2\sum \limits _{j=1}^{m}\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}^{\prime }Q_{l}|z_{j}\left( t-\tau _{j}\right) ||k_{i}(t)|+2\sum \limits _{j=1}^{m}\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}^{\prime }P_{j}|z_{l}\left( t-\tau _{l}\right) ||k_{i}(t)|\\&+\,\mu (t)\bigg (\overline{a_{i}}^{2}k_{i}^{2}(t)\!+\!2\overline{a_{i}}|k_{i}(t)|\!\bigg (\!\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }|z_{j}\left( t\!-\!\tau _{j}\right) \!|\!+\!\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }|z_{j}\left( t\!-\!\tau _{j}\right) \!|\\\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }|z_{l}\left( t\!-\!\tau _{l}\right) |\bigg )+\left( m^{2}\!+\!m\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}|z_{j}\left( t\!-\!\tau _{j}\right) |^{2}\\\\&+\,\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}|z_{j}\left( t\!-\!\tau _{j}\right) |^{2}\!+\!\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}|z_{l}\left( t\!-\!\tau _{l}\right) |^{2}\bigg )\bigg )\bigg )\\\\&+\,\lambda _{i}k_{i}^{2}(t)pe_{p}(t,\,0)\bigg ]\\&\le \sum \limits _{i=1}^{m}\bigg [\lambda _{i}k_{i}^{2}(t)pe_{p}(t,\,0)+\lambda _{i}e_{p}(\sigma (t),\,0)\bigg (\left( \overline{a_{i}}^{2}\mu (t)-2{\underline{a_i}}\right) k_{i}^{2}(t)\\\\&+\,\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }\left( z_{j}^{2}\left( t-\tau _{j}\right) +k_{i}^{2}(t)\right) \\\\&+\,\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\left( z_{j}^{2}\left( t-\tau _{j}\right) +k_{i}^{2}(t)\right) \end{aligned}$$

$$\begin{aligned}&+\,\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\left( z_{l}^{2}\left( t-\tau _{l}\right) +k_{i}^{2}(t)\right) \bigg )\\&+\mu (t)\left( m^{2}+m\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}|z_{j}\left( t-\tau _{j}\right) |^{2}\\&+\,\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}|z_{j}\left( t\!-\!\tau _{j}\right) |^{2}\!+\!\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}|z_{l}\left( t\!-\!\tau _{l}\right) |^{2}\bigg )\bigg )\bigg ]\\\\&= \sum \limits _{i=1}^{m}\lambda _{i}\bigg [p+\bigg (\overline{a_{i}}^{2}\mu (t)-2{\underline{a_i}}+\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)k_{i}^{2}(t)\\&+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \,(1+p\mu (t))z_{j}^{2}(t-\tau _{j})e_{p}(t,\,0).\\\\ F_2^{\Delta }(t)&= \sum \limits _{j=1}^{m}\xi _{j}\left[ \left( z_j^{2}(t)\right) ^{\Delta }e_{p}(\sigma (t),\,0)+z_{j}^{2}(t)e_{p}^{\Delta }(t,\,0)\right] \\\\&= \sum \limits _{j=1}^{m}\xi _{j}\left[ \left( z_{j}(t)+z_{j}(\sigma (t))\right) z_{j}^{\Delta }(t)e_{p}(\sigma (t),\,0)+z_{j}^{2}(t)pe_{p}(t,\,0)\right] \end{aligned}$$

$$\begin{aligned}&= \sum \limits _{j=1}^{m}\xi _{j}\left[ \left( z_j(t)+\mu (t)z_{j}^{\Delta }(t)+z_{j}(t)\right) z_{j}^{\Delta }(t)e_{p}(\sigma (t),\,0)+z_{j}^{2}(t)pe_{p}(t,\,0)\right] \\&= \sum \limits _{j=1}^{m}\xi _{j}\left[ \left( 2z_{j}(t)z_{j}^{\Delta }(t)+\mu (t)\left( z_{j}^{\Delta }(t)\right) ^{2}\right) e_{p}(\sigma (t),\,0)+z_{j}^{2}(t)pe_{p}(t,\,0)\right] \\&= \sum \limits _{j=1}^{m}\xi _{j}\bigg [\bigg (2z_{j}(t)\bigg ({-}d_{j}(t)z_{j}(t)+\sum \limits _{i=1}^{m}c_{ji}(t)\big (f_{i}(k_{i}\left( t-\omega _{i}\right) +x_{i}^*\left( t-\omega _{i}\right) ) \nonumber \\&-f_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \big ) +\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}s_{jil}(t)\big (\left[ v_{i}\left( k_{i}\left( t-\omega _{i}\right) +x_{i}^*\left( t-\omega _{i}\right) \right) \right. \nonumber \\&\left. -v_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \right] \times w_{l}\left( x_{l}\left( t-\omega _{l}\right) +x_{l}^*\left( t-\omega _{l}\right) \right) \big )\nonumber \\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}s_{jil}(t)\big (\left[ w_{l}\left( k_{l}\left( t-\omega _{l}\right) +x_{l}^*\left( t-\omega _{l}\right) \right) -w_{l}\left( x_{l}^*\left( t-\omega _{l}\right) \right) \right] \nonumber \\&\times v_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \big )\bigg )\\&+\,\mu (t)\bigg (\!-\!d_{j}(t)z_{j}(t)\!+\!\sum \limits _{i=1}^{m}c_{ji}(t)\big (f_{i}\left( k_{i}\left( t\!-\!\omega _{i}\right) \!+\!x_{i}^*\left( t\!-\!\omega _{i}\right) \right) \!-\!f_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \big ) \end{aligned}$$

$$\begin{aligned}&+\,\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}s_{jil}(t)\big (\left[ v_{i}\left( k_{i}\left( t-\omega _{i}\right) +x_{i}^*\left( t-\omega _{i}\right) \right) -v_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \right] \\&\times w_{l}\left( k_{l}\left( t-\omega _{l}\right) +x_{l}^*\left( t-\omega _{l}\right) \right) \big )\nonumber \\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}s_{jil}(t)\big (\left[ w_{l}\left( k_{l}\left( t-\omega _{l}\right) +x_{l}^*\left( t-\omega _{l}\right) \right) -w_{l}\left( x_{l}^*\left( t-\omega _{l}\right) \right) \right] \nonumber \\&\times v_{i}\left( x_{i}^*\left( t-\omega _{i}\right) \right) \big )\bigg )^{2}\bigg )e_{p}(\sigma (t),\,0)+z_{j}^{2}(t)pe_{p}(t,\,0)\bigg ]\\&\le \sum \limits _{j=1}^{m}\bigg [\xi _{j}e_{p}(\sigma (t),\,0)\bigg (-\!2{\underline{d_{\!j}}}z_{j}^{2}(t)+2\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }|k_{i}\left( t-\omega _{i}\right) ||z_{j}(t)|\\&+\,2\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}^{\prime }W_{l}|k_{i}\left( t-\omega _{i}\right) ||z_{j}(t)|+2\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}^{\prime }V_{i}|k_{l}\left( t-\omega _{l}\right) ||z_{j}(t)|\\&+\,\mu (t)\bigg (\overline{d_{j}}^{2}z_{j}^{2}(t)\!+\!2\overline{d_{j}}|z_{j}(t)|\bigg (\!\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }|k_{i}\left( t\!-\!\omega _{i}\right) |\!+\!\!\sum \limits _{i=1}^{m}\!\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }|k_{i}\left( t\!-\!\omega _{i}\right) \!|\\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }|k_{l}\left( t-\omega _{l}\right) |\bigg )+\left( m^{2}+m\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}|k_{i}\left( t-\omega _{i}\right) |^{2} \end{aligned}$$

$$\begin{aligned}&\!+\!\sum \limits _{i=1}^{m}\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( \!V_{i}^{\prime }\right) ^{2}|k_{i}\left( t\!-\!\omega _{i}\right) |^{2}+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}|k_{l}\left( t\!-\!\omega _{l}\right) |^{2}\bigg )\bigg )\bigg )\\&+\,\xi _{j}z_{j}^{2}(t)pe_{p}(t,\,0)\bigg ]\\\\&\le \sum \limits _{j=1}^{m}\bigg [\xi _{j}z_{j}^{2}(t)pe_{p}(t,\,0)+\xi _{j}e_{p}(\sigma (t),\,0)\bigg (\left( \overline{d_{j}}^{2}\mu (t)-2{\underline{d_{\!j}}}\right) z_{j}^{2}(t)\\&+\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }\left( k_{i}^{2}\left( t-\omega _{i}\right) +z_{j}^{2}(t)\right) \\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\left( k_{i}^{2}\left( t-\omega _{i}\right) +z_{j}^{2}(t)\right) \\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\left( k_{l}^{2}\left( t-\omega _{l}\right) +z_{j}^{2}(t)\right) \bigg )\\&+\mu (t)\left( m^{2}+m\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}|k_{i}\left( t-\omega _{i}\right) |^{2} \end{aligned}$$

$$\begin{aligned}&\!+\!\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}|k_{i}\left( t\!-\!\omega _{i}\right) |^{2}\!+\!\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}|k_{l}\left( t-\omega _{l}\right) |^{2}\bigg )\bigg )\bigg ]\\\\&= \sum \limits _{j=1}^{m}\xi _{j}\bigg [p+\bigg (\overline{d_{j}}^{2}\mu (t)-2{\underline{d_{\!j}}}+\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)z_{j}^{2}(t)\\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))k_{i}^{2}\left( t-\omega _{i}\right) e_{p}(t,\,0).\\ F_3^{\Delta }(t)&= \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu \left( t+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg ) \end{aligned}$$

$$\begin{aligned}&\!+\,\mu \left( t\!+\!\tau _{j}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\tau _{j}\right) \right) z_{j}^{2}(t)e_{p}\left( t+\tau _{j},\,0\right) \\&-\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \, (1+p\mu (t))z_{j}^{2}\left( t-\tau _{j}\right) e_{p}(t,\,0)\Delta s.\\ F_4^{\Delta }(t)&= \sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu \left( t+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg ) \end{aligned}$$

$$\begin{aligned}&+\,\mu \left( t\!+\!\omega _{i}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\omega _{i}\right) \right) k_{i}^{2}(t)e_{p}\left( t+\omega _{i},\,0\right) \\&-\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))k_{i}^{2}\left( t-\omega _{i}\right) e_{p}(t,\,0). \end{aligned}$$

Hence,

$$\begin{aligned} F^{\Delta }(t)&= F_1^{\Delta }(t)+F_2^{\Delta }(t)+F_3^{\Delta }(t)+F_4^{\Delta }(t)\\&\le \sum \limits _{i=1}^{m}\lambda _{i}\bigg [p+\bigg (\overline{a_{i}}^{2}\mu (t)-2\underline{a_{i}}+\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)k_{i}^{2}(t)\\&+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\mu (t)\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))z_{j}^{2}\left( t-\tau _{j}\right) e_{p}(t,\,0)\\&+\sum \limits _{j=1}^{m}\xi _{j}\bigg [p+\bigg (\overline{d_{j}}^{2}\mu (t)-2\underline{d_{j}}+\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)z_{j}^{2}(t)\\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))k_{i}^{2}\left( t-\omega _{i}\right) e_{p}(t,\,0)\\&+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu \left( t+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\mu \left( t+\tau _{j}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\tau _{j}\right) \right) z_{j}^{2}(t)e_{p}\left( t+\tau _{j},\,0\right) \\&-\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))z_{j}^{2}\left( t-\tau _{j}\right) e_{p}(t,\,0)\\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu \left( t+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu \left( t+\omega _{i}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\omega _{i}\right) \right) k_{i}^{2}(t)e_{p}\left( t+\omega _{i},\,0\right) \\&-\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu (t)\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\mu (t))k_{i}^{2}\left( t-\omega _{i}\right) e_{p}(t,\,0)\\&= \sum \limits _{i=1}^{m}\lambda _{i}\bigg [p+\bigg (\overline{a_{i}}^{2}\mu (t)-2\underline{a_{i}}+\left( 1+\overline{a_{i}}\mu (t)\right) \bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)k_{i}^{2}(t)\\&+\sum \limits _{j=1}^{m}\xi _{j}\bigg [p+\bigg (\overline{d_{j}}^{2}\mu (t)-2\underline{d_{j}}+\left( 1+\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]e_{p}(t,\,0)z_{j}^{2}(t)\\&+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu \left( t+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\mu \left( t\!+\!\tau _{j}\right) \!\left( \!m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( \!G_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\tau _{j}\right) \right) z_{j}^{2}(t)e_{p}\left( t+\tau _{j},\,0\right) \\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu \left( t+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\mu \left( t\!+\!\omega _{i}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\omega _{i}\right) \right) k_{i}^{2}(t)e_{p}\left( t+\omega _{i},\,0\right) \\&= \sum \limits _{i=1}^{m}e_{p}(t,\,0)\bigg \{\lambda _{i}\bigg [p\!+\!\bigg (\overline{a_{i}}^{2}\mu (t)\!-\!2\underline{a_{i}}\!+\!\left( 1\!+\!\overline{a_{i}}\mu (t)\right) \!\bigg (\sum \limits _{j=1}^{m}\overline{b_{ij}}G_{j}^{\prime }\!+\!\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }\\&+\sum \limits _{j=1}^{m}\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]\\&+\sum \limits _{j=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\mu \left( t+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu \left( t\!+\!\omega _{i}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\omega _{i}\right) \right) e_{p}\left( t+\omega _{i},\,t\right) \bigg \}k_{i}^{2}(t)\\&\!+\!\sum \limits _{j=1}^{m}e_{p}(t,\,0)\bigg \{\!\xi \!_{j}\bigg [p\!+\!\bigg (\!\overline{d_{j}}^{2}\mu (t)\!-\!2\underline{d_{j}}\!+\!\left( 1\!+\!\overline{d_{j}}\mu (t)\right) \bigg (\sum \limits _{i=1}^{m}\overline{c_{ji}}F_{i}^{\prime }\!+\!\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }\\&+\sum \limits _{i=1}^{m}\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\bigg )(1+p\mu (t))\bigg ]\\&+\sum \limits _{i=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\mu \left( t+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\mu \left( t+\tau _{j}\right) \left( m^{2}\!+\!m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}\!+\!\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( t+\tau _{j}\right) \right) e_{p}\left( t+\tau _{j},\,t\right) \bigg \}z_{j}^{2}(t). \end{aligned}$$

By using (4.1), (4.2), we can conclude that $F^{\Delta }(t)\le 0,$ for $t\in \mathbb{T }_{0}^{+},$ which implies that $F(t)\le F(0),$ for $t\in \mathbb{T }_{0}^{+}.$

$$\begin{aligned} F(0)&= F_1(0)+F_2(0)+F_3(0)+F_4(0)\\&= \sum \limits _{i=1}^{m}\lambda _{i}k_{i}^{2}(0)e_{p}(0,\,0)+\sum \limits _{i=1}^{m}\xi _{j}z_{j}^{2}(0)e_{p}(0,\,0)\\&+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\int \limits _{-\tau _{j}}^{0}\bigg [\left( 1+\overline{a_{i}}\mu \left( s+\tau _{j}\right) \right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\mu \left( s+\tau _{j}\right) \left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( s+\tau _{j}\right) \right) z_{j}^{2}(s)e_{p}\left( s+\tau _{j},\,0\right) \Delta s\\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\int \limits _{-\omega _{i}}^{0}\bigg [\left( 1+\overline{d_{j}}\mu \left( s+\omega _{i}\right) \right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\mu \left( s+\omega _{i}\right) \left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times \left( 1+p\mu \left( s+\omega _{i}\right) \right) k_{i}^{2}(s)e_{p}\left( s+\omega _{i},\,0\right) \Delta s\\&\le \sum \limits _{i=1}^{m}\bigg \{\lambda _{i}+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\int \limits _{-\omega _{i}}^{0}\bigg [\left( 1+\overline{d_{j}}\bar{\mu }\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\\&+\,\bar{\mu }\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\bar{\mu })e_{p}\left( s+\omega _{i},\,0\right) \Delta s\bigg \}\sup \limits _{-\omega ^{\prime }\le s\le 0}k_{i}^{2}(s)\\&+\sum \limits _{j=1}^{m}\bigg \{\xi _{j}+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\int \limits _{-\tau _{j}}^{0}\bigg [\left( 1+\overline{a_{i}}\bar{\mu }\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\\&+\,\bar{\mu }\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\\&\times (1+p\bar{\mu })e_{p}\left( s+\tau _{j},\,0\right) \Delta s\bigg \}\sup \limits _{-\tau ^{\prime }\le s\le 0}z_{j}^{2}(s) \end{aligned}$$

$$\begin{aligned}&\le \max \limits _{1\le i\le m}\bigg \{\lambda _{i}+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m}\xi _{j}\bigg [\left( 1+\overline{d_{j}}\bar{\mu }\right) \bigg (\overline{c_{ji}}F_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}W_{l}V_{i}^{\prime }+\sum \limits _{l=1}^{m}\overline{s_{jil}}V_{i}W_{l}^{\prime }\bigg )\nonumber \\&+\,\bar{\mu }\left( m^{2}+m\right) \bigg (\overline{c_{ji}}^{2}\left( F_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}W_{l}^{2}\left( V_{i}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{s_{jil}}^{2}V_{i}^{2}\left( W_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\nonumber \\&\times (1+p\bar{\mu })\omega ^{\prime }e_{p}(\omega ^{\prime },\,0)\bigg \}\sum \limits _{i=1}^{m}\sup \limits _{-\omega ^{\prime }\le s\le 0}k_{i}^{2}(s)\nonumber \\&+\max \limits _{1\le j\le m}\bigg \{\xi _{j}+\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{m}\lambda _{i}\bigg [\left( 1+\overline{a_{i}}\bar{\mu }\right) \bigg (\overline{b_{ij}}G_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}Q_{l}P_{j}^{\prime }+\sum \limits _{l=1}^{m}\overline{e_{ijl}}P_{j}Q_{l}^{\prime }\bigg )\nonumber \\&+\,\bar{\mu }\left( m^{2}+m\right) \bigg (\overline{b_{ij}}^{2}\left( G_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}Q_{l}^{2}\left( P_{j}^{\prime }\right) ^{2}+\sum \limits _{l=1}^{m}\overline{e_{ijl}}^{2}P_{j}^{2}\left( Q_{l}^{\prime }\right) ^{2}\bigg )\bigg ]\nonumber \\&\times (1+p\bar{\mu })\tau ^{\prime }e_{p}(\tau ^{\prime },\,0)\bigg \}\sum \limits _{j=1}^{m}\sup \limits _{-\tau ^{\prime }\le s\le 0}z_{j}^{2}(s), \end{aligned}$$

(4.5)

where $\mu (t)\le \bar{\mu }:=\,\sup \nolimits _{t\in \mathbb{T }}\mu (t).$ Observe that

$$\begin{aligned} F(t)\ge \min \limits _{1\le i\le m}\sum \limits _{i=1}^{m}k_{i}(t)e_{p}(t,\,0)+\min \limits _{1\le j\le m}\xi _{j}\sum \limits _{j=1}^{m}z_{j}^{2}(t)e_{p}(t,\,0). \end{aligned}$$

(4.6)

Then it follows from (4.5) and (4.6) that

$$\begin{aligned} \sum \limits _{i=1}^{m}k_{i}^{2}(t)+\sum \limits _{j=1}^{m}z_{j}^{2}(t)\le \frac{M}{e_{p}(t,\,0)}\bigg [\sum \limits _{i=1}^{m}\sup \limits _{-\omega ^{\prime }\le s\le 0}k_{i}^{2}(s)+\sum \limits _{j=1}^{m}\sup \limits _{-\tau ^{\prime }\le s\le 0}z_{j}^{2}(s)\bigg ] \end{aligned}$$

for $t\in \mathbb{T }_{0}^{+},$ where $M\ge 1$ is a constant. The proof is complete. $\square$

5 Numerical Example and Simulations

Consider the following BAM neural network on an almost periodic time scale $\mathbb{T }:$

$$\begin{aligned} \left\{ \begin{array}{ll} x_{i}^{\Delta }(t)=-a_{i}(t)x_{i}(t)+\sum \limits ^{2}_{j=1}b_{ij}(t)g_{j}\left( y_{j}\left( t-\tau _{j}(t)\right) \right) \\ \quad \quad \!\!\! \!+\!\sum \limits ^{2}_{j=1}\sum \limits ^{2}_{l=1}e_{ijl}(t)p_{j}\left( y_{j}\left( t\!-\!\tau _{j}(t)\right) \right) q_{l}\left( y_{l}\left( t\!-\!\tau _{l}(t)\right) \right) \!+\!I_{i}(t),\quad i,\,j,\,l=1,\,2,\quad t\!>\!0,\\ y_{j}^{\Delta }(t)=-d_{j}(t)y_{j}(t)+\sum \limits ^{2}_{i=1}c_{ji}(t)f_{i}\left( x_{i}\left( t-\omega _{i}(t)\right) \right) \\ \quad \!+\!\sum \limits ^{2}_{i=1}\!\sum \limits ^{2}_{l=1}s_{jil}(t)v_{i}\left( x_{i}\left( t\!-\!\omega _{i}(t)\right) \right) w_{l}\left( x_{l}\left( t\!-\!\omega _{l}(t)\right) \right) \!+\!J_{j}(t),\quad i,\,j,\,l\!=\!1,\,2,\quad t\!>\!0, \end{array}\right. \end{aligned}$$

(5.1)

where

$$\begin{aligned} g_{1}\left( y_{1}\right)&= p_{1}\left( y_{1}\right) =q_{1}\left( y_{1}\right) =\sin \frac{\sqrt{2}}{2}y_{1},\, g_{2}\left( y_{2}\right) =p_{2}\left( y_{2}\right) =q_{2}\left( y_{2}\right) =\cos \frac{\sqrt{2}}{2}y_{2},\\ f_{1}\left( x_{1}\right)&= v_{1}\left( x_{1}\right) =w_{1}\left( x_{1}\right) =\frac{1}{4}\sin \frac{1}{3}x_{1},\, f_{2}\left( x_{2}\right) =v_{2}\left( x_{2}\right) =w_{2}\left( x_{2}\right) =\frac{1}{3}\cos \frac{2}{3}x_{2}, \end{aligned}$$

obviously, $g_{i}(y_{i}),\,p_{i}(y_{i}),\,q_{i}(y_{i}),\,f_{i}(x_{i}),\,v_{i}(x_{i}),\,w_{i}(x_{i})(i=1,\,2)$ satisfy $(H2)$ and $(H3),$ and

$$\begin{aligned} G_{i}= P_{i} =Q_{i}= F_{i}= V_{i}=W_{i} =G_{i}^{\prime } = P_{i}^{\prime }= Q_{i}^{\prime } =F_{i}^{\prime }=V_{i}^{\prime }=W_{i}^{\prime } =1, \quad i=1,\,2. \end{aligned}$$

Take $\mathbb{T }$ is an arbitrary time scale and satisfies $-a_{i},\,-d_{j}\in \mathcal R ^{+},$ then one can take

$$\begin{aligned}&a_{1}(t)=0.5+0.3\sin 2t,\quad a_{2}(t)=0.4+0.2\sin t,\quad b_{11}(t)=0.004+0.004\cos t, \\&b_{12}(t)=0.003\!+\!0.003\cos 3t,\,\, b_{21}(t)\!=\!0.006\!+\!0.006\cos 6t,\,\, b_{22}(t)\!=\!0.001\!+\!0.001\cos \frac{t}{2} ,\\&e_{111}(t)=e_{222}(t)=0.002+0.002\sin 2t,\quad e_{112}(t)=e_{212}(t)= 0.0025+0.0025\cos \frac{t}{4},\\&e_{121}(t)=e_{221}(t)\!=\!0.0045+0.0045\cos \sqrt{3}t,\quad e_{122}(t)\!=\!e_{211}(t)\!=\!0.0015\!+\!0.0015\sin \sqrt{2}t,\\&I_{1}(t)=0.0025\sin \frac{3}{4}t,\,\, I_{2}(t)\!=\!0.001\cos \frac{t}{5},\,\, d_{1}(t)\!=\!0.5\!+\!0.2\cos \frac{t}{2},\,\, d_{2}(t)\!=\!0.4\!+\!0.1\sin \frac{3}{4}t,\\&c_{11}(t)=0.003\!+\!0.002\cos \frac{t}{2}, \,\, c_{12}(t)\!=\!0.002\!+\!0.003\sin \frac{t}{5},\,\, c_{21}(t)\!=\!0.003\!+\!0.004\cos \sqrt{2}t,\\&c_{22}(t)=0.004+0.003\sin \sqrt{3}t,\,\, s_{111}(t)=s_{222}(t)=0.001+0.002\sin \frac{4}{3}t,\\&s_{112}(t)=s_{212}(t)= 0.002+0.001\cos \frac{2}{5}t,\,\, s_{121}(t)=s_{221}(t)=0.003+0.002\sin \frac{3}{5}t,\\&s_{122}(t)=s_{211}(t)\!=\!0.002+0.004\cos \frac{4}{5}t,\quad J_{1}(t)\!=\!0.001\cos \sqrt{3}t,\quad J_{2}(t)=0.002\sin \sqrt{5}t. \end{aligned}$$

We get that (H1) is satisfied, and

$$\begin{aligned}&\overline{a_{1}}\!=\!0.8,\quad \underline{a_{1}}\!=\!0.2,\quad \overline{a_{2}}=0.6,\quad \underline{a_{2}}\!=\!0.2,\quad \overline{b_{11}}\!=\!0.008,\quad \overline{b_{12}}=0.006,\quad \overline{b_{21}}=0.012,\\&\overline{b_{22}}=0.002,\quad \overline{e_{111}}=\overline{e_{222}}=0.004,\quad \overline{e_{112}}=\overline{e_{212}}=0.005,\quad \overline{e_{121}}=\overline{e_{221}}=0.009,\\&\overline{e_{122}}=\overline{e_{211}}=0.003,\quad \overline{I_{1}}=0.0025,\quad \overline{I_{2}}=0.001,\quad \overline{J_{1}}=0.001,\quad \overline{J_{2}}=0.002,\quad \overline{d_{1}}=0.7,\\&\underline{d_{1}}\!=\!0.3,\quad \overline{d_{2}}\!=\!0.5,\quad \underline{d_{2}}\!=\!0.3,\quad \overline{c_{11}}\!=\!0.005,\quad \overline{c_{12}}\!=\!0.005,\quad \overline{c_{21}}\,{=}\,0.007,\quad \overline{c_{22}}\,{=}\,0.007,\\&\tau _{1}=\tau _{2}=\omega _{1}=\omega _{2}=0.001,\quad \overline{s_{111}}=\overline{s_{222}}=0.003,\quad \overline{s_{112}}=\overline{s_{212}}=0.003,\quad \\&\overline{s_{121}}=\overline{s_{221}}=0.005,\quad \overline{s_{122}}=\overline{s_{211}}=0.006, \end{aligned}$$

so, we have

$$\begin{aligned} \rho&= \max \limits _{1 \le i \le 2}\frac{\sum \nolimits ^{2}_{j=1}\overline{b_{ij}}G_{j}^{\prime }+\sum \nolimits ^{2}_{j=1}\sum \nolimits ^{2}_{l=1}\overline{e_{ijl}} (P_{j}Q_{l}^{\prime }+Q_{l}P_{j}^{\prime })}{\underline{a_{i}}}\\&+\max \limits _{1 \le j \le 2}\frac{\sum \nolimits ^{2}_{i=1}\overline{c_{ji}}F_{i}^{\prime }+\sum \nolimits ^{2}_{i=1}\sum \nolimits ^{2}_{l=1}\overline{s_{jil}} (V_{i}W_{l}^{\prime }+W_{l}V_{i}^{\prime })}{\underline{d_{j}}} =0.44 <1, \end{aligned}$$

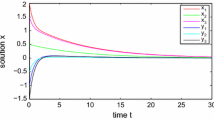
and taking $\lambda _{1}=1,\,\lambda _{2}=1,\,\xi _{1}=1,\,\xi _{2}=1,\,p=0.001,$ then $T_{1}(\lambda _{1},\,p)=T_{1}(1,\,0.001)\approx -0.3010<0,\,T_{2}(\lambda _{2},\,p)=T_{2}(1,\,0.01)\approx -0.2930<0,\,H_{1}(\xi _{1},\,p)=H_{1}(1,\,0.001)\approx -0.5070<0,\,H_{2}(\xi _{2},\,p)=H_{2}(1,\,0.001)\approx -0.3010<0.$ Hence, conditions in Theorems 3.1 and 4.1 are all satisfied. Therefore, we know that system (5.1) has an almost periodic solution, which is globally exponentially stable on this time scale (see Fig. 1).

Fig. 1

Transient responses of states $x_1,\,x_2,\,y_1,\,y_2$ in example

6 Conclusion

On the existence and stability of almost periodic solutions for high-order discrete time BAM neural networks with time-varying delays, to the best of our knowledge, the aspect results have not yet appeared in the related literature. Since both continuous and discrete systems are very important in implementations and applications, while it is troublesome to study the existence and stability of almost periodic solutions for continuous system and discrete systems, respectively, it is meaningful to study that on time scales which can unify the continuous and discrete situations. In this paper, sufficient conditions are derived to guarantee the global exponential stability and existence of almost periodic solutions for high-order BAM neural networks with delays on time scales.