Introduction

Natural rock masses consist of intact rock blocks separated by discontinuities. Therefore, the mechanical properties of intact rock, the geotechnical properties of discontinuities, and the rock mass structure are the most important parameters affecting the engineering deformation properties of rock masses. It is also known that weathering significantly affects these engineering properties of rocks (Ceryan 2015). One of the most important intact rock properties affecting the engineering behavior of rock mass is the elastic modulus (\({E}_{\text{s}}\)) just as uniaxial compressive strength (UCS), and Poisson ratio (\(\nu\)). Therefore, \({E}_{\text{s}}\) of intact rock is generally used as an input in both numerical models and in empirical relationships to evaluate the engineering behavior of rock masses (Kayabasi et al. 2003; Sonmez et al. 2006; Hoek and Diederichs 2006; Bidgoli et al. 2013; Zhang 2017; Saedi et al. 2019; Alemdag et al. 2016).

UCS tests, standardized by the International Society for Rock Mechanics (ISRM), are utilized to measure the \({E}_{\text{s}}\) and UCS of rock materials directly. The tests require well-prepared rock specimens that cannot always be extracted from weak, thinly bedded, stratified, highly fractured, highly weathered, high-porosity, clay-containing, coarse-grained, and block-in-matrix rocks. Furthermore, the tests are expensive, complicated, time-consuming, and require sophisticated and expensive instruments (Gokceoglu and Zorlu 2004; Xia et al. 2014; Ko et al. 2016), making it difficult to evaluate \({E}_{\text{s}}\) using standard laboratory tests. To overcome these difficulties for directly measuring \({E}_{\text{s}}\), regression models have been developed (Nefeslioglu 2013; Ozkat et al. 2017a,b; Aboutaleb et al. 2018; Mashayekhi et al. 2020). The independent variables (i.e., the inputs) used in these models, are commonly the physical properties of rock samples that can be measured easily and cheaply. These simple and non-destructive index properties include the elastic wave velocity (Kurtuluş et al. 2010; Brotons et al. 2016), porosity, effective porosity, void ratio, unit weight, density, and water saturation (Tugrul 2004; Yilmaz and Yuksek 2008; Erguler and Ulusay 2009; Marques et al. 2010; Wang et al. 2014; Kim et al. 2017). Other inputs derived from the index tests are the slake durability index (Yagiz et al. 2012; Ceryan 2014; Ghasemi et al. 2018), weathering indices (Ceryan 2015, 2016), texture coefficient, and mineral content; especially determining quartz, plagioclase, and clay content (Shakoor and Bonelli 1991; Singh and Verma 2012; Pan et al. 2013; Diamantis et al. 2014; Heap et al. 2014; Undul and Florian 2015; Ajalloeian et al. 2017). Simple mechanical test results, including the Schmidt hammer rebound hardness, the point loading index, tensile strength, the blocked punch index, and the cylindrical punch index are also employed in regression models (Dinçer et al. 2004; Karakus et al. 2005; Yilmaz and Yuksek 2009; Khandelwal and Singh 2011; Singh and Verma 2012; Singh et al. 2012; Alikarami et al. 2013; Armaghani et al. 2015; Saedi et al. 2018; Mahdiabadi and Khanlari 2019).

Conventional regression methods, such as simple linear regression and multi-linear regression methods, are widely used in the literature to estimate \({E}_{\text{s}}\). In general, the equations obtained with conventional regression methods are recommended only for specific rock types (Fener et al. 2005; Beiki et al. 2013). If new data are substantially different from the original data, the form of the obtained equations needs to be updated. Moreover, in some cases, the prediction results are inadequate (Sonmez et al. 2006; Yilmaz and Yuksek 2009; Beiki et al. 2013; Rezaei et al. 2014). Considering these difficulties in the prediction of \({E}_{\text{s}}\) using conventional regression methods, many researchers have employed soft computing methods (Table 1).

Table 1 Soft computing models proposed to estimate the modulus of elasticity of rock materials
Full size table

The main purpose of this study is to examine the applicability and capability of Support Vector Regression (SVR), Gaussian Process Regression (GPR), and Artificial Neural Network (ANN) models in the \({E}_{\text{s}}\) prediction of magmatic rocks with different degrees of weathering. The inputs, porosity (n), P-wave velocity (\({V}_{p}\)), and slake durability index (\({I}_{d}\)) used in the proposed models were determined by the best subset regression method, and the performances of these models were evaluated with the maximum determination coefficient (R2), Root Mean Square Error (RMSE), normalized RMSE (NRMSE), Mean Absolute Error (MAE), normalized MAE (NMAE), Mean Squared Error (MSE), Nash–Sutcliffe coefficient (NS), Variance Account Factor (VAF), Performance Index (PI), Regression Error Characteristic Curve (REC), and Taylor diagrams.

The remainder of the paper is organized as follows: “Materials and experimental details” describes the materials and experimental procedures; “Problem formulation” defines the inputs and output and explains the proposed regression models. The results and discussions are introduced in “Results” and “Discussion”, respectively. The conclusions are presented in “Conclusion”.

Materials and experimental details

The sample blocks in the present study were gathered from three different formation/lithodemes exposed in the Eastern Pontides, NE Turkey. They mainly consisted of (1) Late Cretaceous volcanic rocks, (2) volcano-sedimentary rock aged Eosen, and (3) granitic rocks (Fig. 1).

Fig. 1
figure 1

Geology map of Eastern Pontides, NE Turkey, and location of the study area (Guven 1993; Hippolyte et al. 2017)

Full size image

The tests for Schmidt hardness, specific gravity, slake durability, P-wave velocity, and UCS were conducted according to standards defined by ISRM (2007). The core samples used in these tests were extracted from block samples that had different degrees of weathering (Fig. 2). The index properties and modulus of elasticity of the samples used in this study are presented in Table 2.

Fig. 2
figure 2

Core samples investigated

Full size image
Table 2 Lithology, index properties, and the modulus of elasticity (Es) of the samples
Full size table

The N-type rebound hammer was used in the Schmidt hammer test to determine the hardness value (SHH). The \({\text{SHH}} \times \gamma\) term (Deere and Miller 1966; Aufmuth 1974) was obtained by multiplying the measured hardness values (SHH) by unit weight (\(\gamma\)). The grain density \(\left({\rho }_{\text{s}}\right)\) was determined by employing the specific gravity test, and the dry density was obtained experimentally. Subsequently, the porosity value (\(n\)) was calculated using Eq. (1).

$$n = 1 - \frac{{\rho _{d} }}{{\rho _{{\text{s}}} }}$$
(1)

The samples were subjected to a four-cycle slake durability test to determine the slake durability index (Gokceoglu et al. 2000). This test was performed three times for each sample. The ultrasonic pulse velocity (UPV) test was conducted using the Portable Ultrasonic Non-destructive Digital Indicating Tester (PUNDIT®) without applying any pressure to the samples. The equipment generates an ultrasonic pulse with a frequency of 400 kHz and measures the transit time from the transmitter transducer through the sample to the receiving transducers. The time of ultrasonic pulses was read with an accuracy of 0.1 ms. The P-wave velocity of the rock samples without pores and fissures (\({V}_{\text{m}}\)) was calculated using Eq. (2) (Barton 2007), and the P-durability index (\(V_{{{\text{id}}}}\)) is defined in Eq. (3) (Ceryan 2016)

$$\frac{1}{{V_{p} }} = \frac{\phi }{{V_{{{\text{fl}}}} }} + \frac{{1 - \phi }}{{V_{{\text{m}}} }}$$
(2)
$$V_{{{\text{id}}}} = 0.01\;V_{{\text{m}}} I_{d}$$
(3)

where \(V_{{{\text{fl}}}}\) is the velocity in the fluid, \(\phi\) is the ratio of the path length in the fluid to the total path length (the porosity), and \({I}_{d}\) is the slake durability index.

To determine \({E}_{\text{s}}\), representing the sample stiffness against a uniaxial load, initially, the stress–strain curve for axial deformations was obtained for UCS. Then, \({E}_{\text{s}}\) was defined as the slope of a line tangent to the stress–strain curve at a fixed percentage of the ultimate strength, 50%, for the test sample (Table 2).

Problem formulation

Methodology

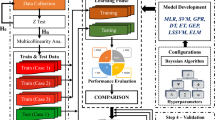
The methodology for predicting the elastic modulus (\({E}_{\text{s}}\)) is illustrated in Fig. 3. The flow chart consists of three main steps, which are (1) selection of inputs, (2) model development, and (3) model performance evaluation. In Step 1, the best subset regression approach was employed to determine inputs from the experimental study. The dataset was divided into two parts for the training (75% of the original data) and test (25% of the original data) sets of the regression models. In Step 2, the proposed regression models, namely, SVR, GPR, and ANN were developed using the training dataset. In Step 3, the developed regression models were validated using the test dataset. The statistical key performance indicators (KPIs), namely RMSE, NRMSE, R2, MAE, NMAE, NS, VAF, AOC, Taylor diagram, the performance index with RMSE (PIRMSE), and the performance index with MAE (PIMAE), were applied in this step to evaluate the performances of the models.

Fig. 3
figure 3

The methodology of the present study for predicting the elastic modulus

Full size image

Selection of inputs

The accuracy of the regression models largely depends on the type of function being used, as well as the quality and quantity of observed data. If there are more inputs than there should be, selecting a suitable set of inputs is necessary to reduce the noise resulting from unnecessary input data. Using suitable inputs, the interpretability of the model can be improved and the predictive ability increases (Omoruyi et al. 2019).

The input selection methods for the regression model can be collected under three main categories: (1) filter method (for example, Pearson’s Correlation, Akaike information criterion, Bayesian information criterion, linear discriminant analysis, principal component analysis, analysis of variance, and chi-square), (2) embedded methods (for example, least angle and shrinkage selection operator and ridge regression), and (3) wrapper methods (for example, forward selection, backward elimination, recursive future elimination, stepwise method, best subset regression) (Huang et al. 2010; Desboulets 2018; Haque et al. 2018; Park and Klabjan 2020).

Here, the best subset regression approach was employed to determine the inputs. First, all possible regression models derived from all possible combinations of the inputs were defined. Then, the best model was determined according to KPIs, including Mean Square Error (MSE), RMSE, R2, adjusted determination coefficient (adjR2), and Mallow’s \({C}_{p}\) (Mallows and Sloane 1973), given in Eqs. (4)–(8).

$${\text{MSE}} = \frac{1}{{n - p}}\mathop \sum \limits_{{i = 1}}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2}$$
(4)
$${\text{RMSE}} = \sqrt {{\text{MSE}}}$$
(5)
$$R^{2} = 1 - \frac{{{\text{MSE}}_{i} }}{{\sigma ^{2} }}$$
(6)
$${\text{Adj}}R^{2} = 1 - \frac{{n - 1}}{{n - i - 1}}\left( {1 - R^{2} } \right)$$
(7)
$$C_{p} = \left( {n - p} \right)\frac{{{\text{MSE}}_{i} }}{{{\text{MSE}}_{F} }} - \left( {n - 2i - 1} \right)$$
(8)

where \({y}_{i}\) and \({\widehat{y}}_{i}\) are the measured and predicted values, respectively. \({\text{MSE}}_{i}\) is the mean of residual squares in the model with \(i\) parameters, \({\text{MSE}}_{F}\) is the mean of residual squares in the full model with \(p\) parameters, \({\sigma }^{2}\) is the variance of the dependent variable, \(n\) is the number of data, \(i\) is the number of inputs in the model, and \(p\) is the number of parameters in the aforementioned model.

R2 increases with an increasing number of inputs, and therefore, it does not indicate the correct regression model. Instead, adjR2 is generally considered to be a more accurate goodness-of-fit measure than R2 because it applies a penalty score to the model when considering more inputs. The RSME is frequently used as a measure of the differences between the predicted and measured values. The performance of the model improves as the RMSE value decreases. The goal of Mallow’s \({C}_{p}\) is to achieve a balanced number of inputs in the model. It compares the precision and bias of the full model generated using all inputs to the models generated using a subset of inputs. The full model always yields a Mallow’s \({C}_{p}\) value equal to the number of parameters in the regression model (\(p\)), so the full model based on \({C}_{p}\) should not be selected. Furthermore, a Mallow’s \({C}_{p}\) value below the p value represents sampling errors. If several models have Mallow’s \({C}_{p}\) near the p value, the model with the smallest value of the difference between the Mallow’s \({C}_{p}\) and the p value can be chosen as the best model.

The index properties, measured experimentally in this study, are: (1) Schmidt hammer hardness (SHH), (2) \({\text{SHH}} \times \gamma\) index, (3) slake durability index (\({I}_{d}\)), (4) porosity (\(n\)), (5) P-wave velocity (\({V}_{p}\)), (6) P-velocity in the solid part of the samples (\({V}_{\text{m}}\)), and (7) P-durability index (\(V_{{{\text{id}}}}\)). These properties are also, the most frequently used inputs in the \({E}_{\text{s}}\) prediction. The \({V}_{p}\) and \({I}_{d}\) values were measured experimentally, and the \({V}_{\text{m}}\) and \(V_{{{\text{id}}}}\) values were calculated empirically from Eqs. (2) and (3). Therefore, the prediction models, namely, SVR, GPR, and ANN should be created by selecting only one of the \({V}_{\text{m}}\), \(V_{{{\text{id}}}}\), and \({V}_{p}\) values. Similarly, \(V_{{{\text{id}}}}\) and \({I}_{d}\) cannot be used as inputs for the same prediction model at the same time. According to these defined conditions, the seven inputs were divided into three groups as follows: (1) \(n\), \({V}_{p}\), \({I}_{d}\), SHH, and \({\text{SHH}} \times \gamma\), (2) \(n\), \(V_{{{\text{id}}}}\), SHH, and \({\text{SHH}} \times \gamma\), and (3) \(n\), \({V}_{\text{m}}\), SHH, and \({\text{SHH}} \times \gamma\). Then, the best subset regression analysis was performed for each group to determine the inputs for the prediction models.

According to the results of the best subset regression analysis, the highest R2 and adjR2 values, as well as the lowest RSME value, for the linear regression model using the inputs in the second and third groups were 0.611, 0.575, and 4.930 MPa, respectively. However, the R2, adjR2, and RSME values for the linear regression model using the inputs of the first group were 0.774, 0.753, and 3.7635 MPa, respectively. Considering these values, the inputs in the first group, namely, \(n\), \({V}_{p}\), \({I}_{d}\), SHH, and \({\text{SHH}} \times \gamma\) were selected to determine the optimum inputs that would be employed during the development of the prediction models.

Table 3 presents the results of the best subset regression analysis performed for different combinations of inputs from the first group and illustrates the two best-fitting models for each combination. The differences between Mallow’s \({C}_{p}\) and p value (the number of parameters in the full model) obtained for the 1st, 2nd, and 4th rows are larger than others. Although the smallest values of the differences between Mallow’s \({C}_{p}\) and the number of the parameters in the full model are obtained in the 7th and 9th rows, the input parameters in the 7th and 9th rows cannot be used because both SHH, and \({\text{SHH}} \times \gamma\) are used together in the regressions (Table 3). SHH, and \({\text{SHH}} \times \gamma\) are not independent of each other as \({\text{SHH}} \times \gamma\) is a function of R. The performance of the regression model in the 3rd row is slightly better than that of the model in the 8th row. In addition, while there are two inputs in the 3rd row, there are four inputs in the 8th row. Although the Mallow’s Cp value obtained in the 3rd row is smaller than that in the 5th row, the R2, adjR2, RSME, and Mallow’s \({C}_{p}\) − p values in the 5th row are better than those in the 3rd row (Table 3).

Table 3 Best subset regression; Es versus \(n\), \({V}_{p}\), \({I}_{d}\), SHH and \({\text{SHH}} \times \gamma\)
Full size table

As a result of the best subset regression analysis, the regression in which porosity (\(n\)), P-wave velocity (\({V}_{p}\)) and slake durability index (\({I}_{d}\)) are used together yields the best performance. Thus, \(n\), \({V}_{p}\), and \({I}_{d}\) were employed as inputs for the regression models developed for the modulus of elasticity of the investigated samples.

Figure 4 illustrates the resulting histograms, cumulative distribution functions (CDFs), and additional statistical information, namely the number of data (N), maximum and minimum values, mean and standard deviations of both inputs (porosity, p-wave velocity, and slake durability index) and output (elastic modulus).

Fig. 4
figure 4

Histograms and statistical summaries of porosity, p-wave velocity, slake durability index, and elastic modulus in the dataset

Full size image

Most, if not all, machine learning algorithms, such as regression models, rely on selected training and test sets. These are often selected based on simple random sampling with prescribed ratios while considering that the training set should be larger than the test set. The experimental results (i.e. original dataset) are arbitrarily divided into two datasets that are the training dataset, which contains 75% of the original data, and the test dataset, which contains 25% of the original data. The training dataset was employed to fit the machine learning models, and the test dataset was used to evaluate the machine learning model fit based on the defined KPIs.

Regression model development

This study aims to develop reliable predictive models to determine the elastic modulus of magmatic rocks using porosity (\(n\)), P-wave velocity (\({V}_{p}\)) and Slake durability index (\({I}_{d}\)); and then, to compare the developed models utilizing the KPIs, the Performance Index, the REC curves, and Taylor diagram. Let us gather three inputs that are Porosity \(\left(n\right)\) (i.e. x1), P-wave velocity \(\left({V}_{p}\right)\) (i.e. x2), and the Slake durability index \(\left({I}_{d}\right)\) (i.e. x3) in Eq. (9), where \(i\) and \(j\) are the index of experiments and inputs; whereas, \({N}_{i}\) and \({N}_{j}\) are the numbers of experiments and inputs, respectively.

$${\mathbf{X}} = \left\{ {{\mathbf{x}}_{{\mathbf{i}}} } \right\} = \left\{ {x_{{i,j}} } \right\}~~~\forall i = 1, \ldots ,Ni~~,~~\forall j = 1, \ldots ,Nj$$
(9)

Similarly, let us gather the dependent variable Es (i.e. y1) in a set given in Eq. (10).

$${\mathbf{Y}} = \left\{ {y_{i} } \right\}~~~\forall i = 1, \ldots ,Ni~~$$
(10)

In general, the regression models \(\left( {f\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{\beta }}} \right)} \right)\), between independent variables (inputs) and the dependent variables (targets/outputs), can be represented as follows:

$$\begin{gathered} \hat{y}_{i} = f\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{\beta }}} \right) + \epsilon _{i} \hfill \\ {\mathbf{\beta }} = \left\{ {\beta _{0} ,\beta _{1} , \ldots ,\beta _{j} , \ldots ,\beta _{{Nj}} } \right\} \hfill \\ {\mathbf{x}}_{{\mathbf{i}}} = \left\{ {x_{{i,1}} ,x_{{i,2}} , \ldots ,x_{{i,j}} , \ldots ,x_{{i,Nj}} } \right\} \hfill \\ \end{gathered}$$
(11)

where (\(\boldsymbol{\beta }\)) is the set of unknown parameters, and (\(\epsilon\)) is the error term. One of the aims of this research is to develop regression models that most closely fits the experimental results, and then evaluate and compare the performance of the developed regression models using defined KPIs. The background of the SVR, GPR, and ANN models are briefly explained in the following subsections.

Support vector regression

SVR model derived from statistical learning theory (Vapnik 1995) is used the sigmoid kernel function which is equivalent to a two-layer perceptron neural network. SVRs are alternative training methods for polynomial, radial basis function, and multilayer perceptron classifiers in which the weights of the network are found by solving a quadratic programming problem with linear constraints, rather than by solving a non-convex, unconstrained minimization problem as in standard ANN training (Huang et al. 2010).

The goal in linear regression is to minimize the error term between the actual and the predicted values of the dependent variables; whereas, the goal in SVR is to make sure that the errors do not exceed the threshold value (i.e. \(\varepsilon\)) (Suykens and Vandewalle 1999). Suppose that the empirical risk (ER) value is minimized, as follows:

$${\text{ER}} = \frac{1}{N}\sum\limits_{{i = 1}}^{{Ni}} | y_{i} - \hat{y}_{i} |$$
(12)

where \(|y_{i} - \hat{y}_{i} |\) is \(\varepsilon\)-insensitive loss function written as:

$$\left| {y_{i} - \hat{y}_{i} } \right| = \left\{ {\begin{array}{ll} 0 & {{\text{if}}\;\left| {y_{i} - \hat{y}_{i} } \right| < \varepsilon } \\ {\left| {y_{i} - f\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{\beta }}} \right) - \varepsilon } \right| - \varepsilon } & {{\text{otherwise~~~~~~~~}}} \\ \end{array} } \right.$$
(13)

The proposed solution to this minimization problem is presented in Eq. (14).

$$\begin{gathered} \begin{array}{*{20}c} {{\text{minimize}}} & {\frac{1}{2}{\mathbf{\beta }}^{T} {\mathbf{\beta }} + C\sum\limits_{{i = 1}}^{{Ni}} {\left( {\xi _{i} + \xi _{i}^{*} } \right)} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{\text{subjec to}}} & {\begin{array}{*{20}c} {y_{i} - f({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{\beta }}) - \varepsilon \le \varepsilon + \xi _{i} } \\ {f({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{\beta }}) + \varepsilon - y_{i} \le \varepsilon + \xi _{i}^{*} } \\ {\xi _{i} ,\xi _{i}^{*} \ge 0} \\ \end{array} } \\ \end{array} \hfill \\ \end{gathered}$$
(14)

where \(\xi _{i} ,\xi _{i}^{*}\) are positive and negative slack variables from the threshold value \((\varepsilon )\), respectively, and \(C\) is the meta-parameter which controls the trade between the model complexity (i.e. flatness) and the deviations from the \((\varepsilon )\). If C is too large, the target only minimizes the empirical risk without considering model complexity in the optimization formulation. Additionally, the value of \((\varepsilon )\) influences the number of support vectors used for constructing the regression function. The bigger the value \((\varepsilon )\), the fewer support vectors are selected.

Gaussian process regression

GPR is a non-parametric kernel-based probabilistic regression model. Despite GPR is a powerful modeling tool, this method has been addressed in solving very few problems related to rock mechanics (Momeni et al. 2020; Kumar et al. 2013, 2014; Huang et al. 2017). The basic idea behind GPR is to predict the value of a function at a given point by computing a weighted average of the known values of the function in the neighborhood of the point. It combines a global model and local deviations (Rasmussen 2004; Hong et al. 2014). Now consider that the unseen observation, where the prediction will happen, \({\mathbf{x}}_{*} = \{ x_{{*,j}} \} ~~~\forall j = 1, \cdots ,Nj\). The GPR model is of the form (Eq. 15)

$$\hat{y}({\mathbf{x}}_{*} ) = f({\mathbf{x}}_{*} ,\beta ) + Z({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} )$$
(15)

where \(f({\mathbf{x}}_{*} ,{\mathbf{\beta }})\) is the unknown polynomial function, and \(Z({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} )\) is the realization of a stochastic process with mean zero and nonzero covariance, which is given in Eq. (16).

$${\text{cov}}\left( {Z\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} } \right)} \right) = \sigma ^{2} {\mathbf{R}}\left( {R\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} } \right)} \right)$$
(16)

where \({\mathbf{R}}\) is the correlation matrix, and \(R({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} )\) is the correlation function between two observations (i.e. \({\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}}\)). When the Gaussian correlation function is employed, the correlation function is expressed as:

$$R\left( {{\mathbf{x}}_{{\mathbf{i}}} ,{\mathbf{x}}_{{\mathbf{k}}} } \right) = \exp \left[ {\sum\limits_{{j = 1}}^{{Nj}} {\theta _{j} } \left( {x_{{i,j}} - x_{{k,j}} } \right)} \right]\quad \forall i,k = 1, \ldots ,Ni$$
(17)

where \(\theta _{j}\) is the unknown correlation parameter to be determined, and \({N}_{j}\) is the number of inputs.

$$f\left( {{\mathbf{x}}_{*} ,\beta } \right) = \widehat{{\mathbf{\beta }}} + {\mathbf{r}}^{{\mathbf{T}}} \left( {{\mathbf{x}}_{*} } \right){\mathbf{R}}^{{ - 1}} \left( {{\mathbf{y}} - {\mathbf{f}}\widehat{\beta }} \right)$$
(18)

where \({\mathbf{y}}\) is the column vector of length \({N}_{i}\) that contains the responses of the experimental data and \({\mathbf{f}}\) is a column vector of length \({N}_{i}\) that is filled with ones when \({\mathbf{f}}({\mathbf{x}})\) is taken as a constant. \({\mathbf{r}}^{{\mathbf{T}}} ({\mathbf{x}}_{*} )\) is the correlation vector between the unseen observation \(x_{*}\) and the whole seen observation (i.e.\({\mathbf{X}} = \{ {\mathbf{x}}_{{\mathbf{i}}} \} \quad \forall i = 1, \cdots ,Ni\)), which is defined as:

$${\mathbf{r}}^{{\mathbf{T}}} ({\mathbf{x}}_{*} ) = \left[ {R\left( {{\mathbf{x}}_{*} ,{\mathbf{x}}_{{\mathbf{1}}} } \right), \ldots ,R\left( {{\mathbf{x}}_{*} ,{\mathbf{x}}_{{\mathbf{i}}} } \right), \ldots ,R\left( {{\mathbf{x}}_{*} ,{\mathbf{x}}_{{{\mathbf{Ni}}}} } \right)} \right]^{T}$$
(19)

The parameter \(\widehat{\beta }\) is calculated in Eq. (20).

$$\hat{\beta } = \left( {{\mathbf{f}}^{{\mathbf{T}}} {\mathbf{R}}^{{ - {\mathbf{1}}}} {\mathbf{f}}} \right)^{{ - {\mathbf{1}}}} {\mathbf{f}}^{{\mathbf{T}}} {\mathbf{R}}^{{ - {\mathbf{1}}}} {\mathbf{y}}$$
(20)

The estimated variance is calculated as:

$$\hat{\sigma }^{2} = \frac{{({\mathbf{y}} - {\mathbf{f}}\beta )^{T} {\mathbf{R}}^{{ - 1}} ({\mathbf{y}} - {\mathbf{f}}\beta )}}{{N_{i} }}$$
(21)

The unknown parameters \(\theta _{j}\) in Eq. (21) obtained employing the maximum likelihood approached defined as:

$${\text{max}}~\phi \left( {\theta _{j} } \right) = - \frac{{N_{i} \ln \left( {\hat{\sigma }^{2} } \right) + \ln (|{\mathbf{R}}|)}}{2}$$
(22)

Artificial neural network

ANN model is an alternative fitting method to map a relation between inputs and outputs. A neuron, which is the building blocks of ANN, is composed of the input layer, one or more hidden layers, and the output layer. Every neuron has connections, which are called weights, with every neuron in both the previous and the following layer. Moreover, each neuron has a bias that makes it work or not work depending on the level of the input signal (Agatonovic-Kustrin and Beresford 2000; Bektas et al. 2019a). The inter-connectivity between neurons is generally done either feed-forward (FFNN) and recurrent (RNN) architectures. In the presented work, a feed-forward hierarchical topology is used, and the neuron’s output z can be expressed in Eq. (23).

$$z_{j} = \sum\limits_{{j = 1}}^{n} {w_{j} } x_{j} + \beta$$
(23)

where xj is the input, wj is the weight of the neuron, β is the bias value, and n is the number of the elements in inputs. The relationship between the output and the inputs is formulated as:

$$y_{j} = f_{h} \left( {z_{j} } \right)$$
(24)

where \({f}_{h}\) is activation function which is generally linear and sigmoid. In the presented work, the sigmoid activation function was employed as defined in Eq. (25) (Ham and Kostanic 2000; Bektas et al. 2019b)

$$f_{h} = \frac{1}{{1 + e^{{ - x}} }}$$
(25)

The general network structure for a two-layer feedforward with a sigmoid transfer function (fh) in the hidden layer and a linear transfer function (fo) in the output is written in Eq. (26).

$$y_{j} = f_{0} \left( {b + \sum\limits_{{h = 1}}^{{n_{h} }} {w_{h} \cdot f_{h} \left( {b_{h} + \sum\limits_{{i = 1}}^{n} {w_{{ih}} \cdot x_{{t - i}} } } \right)} } \right)$$
(26)

Depending on the techniques used to train the feed-forward neural network models, different back-propagation algorithms have been developed. In this study, the Levenberg–Marquardt back-propagation algorithm was used for training. In the back-propagation phase, the performance index E(W) to be minimized was defined as the sum of the squared errors between the target and network output as defined in Eq. (27).

$$E(W) = e^{T} e$$
(27)

where W consists of all weights in the network, and e is the error vector comprising the errors for all the training examples. When training with the Levenberg–Marquardt algorithm, the changing weights ΔW can be computed as follows:

$$\Delta W_{k} = - \left[ {J_{k}^{T} J_{k} + \mu _{k} I} \right]^{{ - 1}} J_{k}^{T} e_{k}$$
(28)

Then, the update of the weights can be adjusted according to Eq. (29)

$$W_{{k + 1}} = W_{k} + \Delta W_{k}$$
(29)

where J is the Jacobian matrix, I is the identity matrix, and µ is the Marquardt parameter to be updated using the decay rate β depending on the outcome. In particular, µ is multiplied by the decay rate β (0 < β < 1) when E(W) decreases, while µ is divided by β when E(W) increases in a new k-step. After the construction of the overall network, weights and biases parameters are iteratively adjusted to meet the predefined error criteria. Iteration by iteration the weights and the biases are updated proportionally to the mean squared error between the calculated output and the desired targets.

Criteria for the performance evaluation and data normalization

To justify the accuracies of the SVR, GPR, and ANN models, the following KPIs, namely, MSE, RMSE, R2, adjR2, MAE, the Nash–Sutcliffe coefficient (NS) to evaluate the capability of the model at simulating output data from the mean statistics, the variance account factor (VAF) to represent the ratio of the error variance to the measured data variance, and the Performance Index (PI), were computed for each model. MSE, RMSE, R2, and adjR2 were calculated using Eqs. (4)–(8). MAE, NS, and VAF were calculated using Eqs. (30)–(32), where \({y}_{i}\) and \({\widehat{y}}_{i}\) are the measured and predicted values. Here, the PI index is calculated separately according to both the normalized RMSE and normalized MAE values written in Eqs. (33) and (34). The NRMSE and NMAE values were obtained by dividing the RMSE and MAE values by the standard deviation of the Es values measured.

$${\text{MAE}} = \frac{1}{{N_{i} }}\sum\limits_{{t = 1}}^{{N_{i} }} {\left| {y_{t} - \hat{y}_{t} } \right|}$$
(30)
$${\text{NS}} = 1 - \frac{{\sum\limits_{{t = 1}}^{{N_{i} }} {\left( {y_{t} - \hat{y}_{t} } \right)^{2} } }}{{\sum\limits_{{t = 1}}^{{N_{i} }} {\left( {y_{t} - \bar{y}_{t} } \right)^{2} } }}$$
(31)
$${\text{VAF}}_{i} = \left( {1 - \frac{{{\text{var}}\left( {y_{i} - \hat{y}_{i} } \right)}}{{{\text{var}}\left( {y_{i} } \right)}}} \right) \cdot 100\%$$
(32)
$${\text{PI}}_{{{\text{RMSE}}}} = {\text{adj}}R^{2} + 0.01\;{\text{VAF}} - {\text{NRMSE}}$$
(33)
$${\text{PI}}_{{{\text{RMAE}}}} = {\text{adj}}R^{2} + 0.01\;{\text{VAF}} - {\text{NMAE}}$$
(34)

The Taylor diagram is also used to assess the performance of the regression models (Taylor 2001). It is a two-dimensional plot showing four statistical quantities: (1) the standard variation of observed data (\({\sigma }_{o}\)), (2) the standard variation of predicted data (\({\sigma }_{p}\)), (3) the correlation coefficient (R), and (4) the centered RMSE, which is the key to constructing the Taylor diagram, is defined Eq. (35).

$${\text{RMSE}}_{{{\text{centered}}}} = \sigma _{o}^{2} + \sigma _{p}^{2} - 2\sigma _{o} \sigma _{p} R$$
(35)

The standard deviation shown in Fig. 5 is denoted by the radial distance from the origin. When the standard deviation of the predicted value (\({\sigma }_{p}\)) is closer to the standard deviation of the observed (\({\sigma }_{o}\)), the performance of the model is higher. R is represented by the azimuthal angle (Fig. 5). The centered RMSE is related to the distance between the observed (OBS) and developed model (MDL), assessed in units identical to those of the standard deviation. While the performance of the model increases with increasing R, it decreases with increasing centered RMSE value.

Fig. 5
figure 5

reproduced from Taylor 2001)

Drawing of Taylor Diagram (

Full size image

Another graphical assessment of the performance of the models was conducted with the REC, which is a generalization of receiver operating characteristic (ROC) curves for regression (Bi and Bennett 2003). The REC curves plot the error tolerance on the x-axis versus the percentage of points predicted within the tolerance on the y-axis. The resulting curve estimates the cumulative distribution function of the error. The area over the REC curve (AOC) provides an approximation of the expected error. The AOC reveals additional information that can be used to assess the model. The smaller AOC, the better the model will perform (Bi and Bennett 2003).

The experimental results differ in scale. Therefore, an adjustment was made before employing the suggested methods to prevent the models from being dominated by variables with large values. Z-score normalization is widely used in this field, and its formulation is defined in Eq. (36).

$$\begin{gathered} {\mathbf{x}}_{{\mathbf{i}}}^{{{\mathbf{norm}}}} = \frac{{x_{{i,j}} - {\mathbf{\bar{x}}}_{{\mathbf{i}}} }}{{\sqrt {\frac{1}{{Nj}}\sum\limits_{{j = 1}}^{{Nj}} {\left( {x_{{i.j}} - {\mathbf{\bar{x}}}_{{\mathbf{i}}} } \right)^{2} } } }}\quad \forall j = 1, \ldots ,Nj \hfill \\ {\mathbf{X}}^{{{\mathbf{norm}}}} = {\mathbf{x}}_{{\mathbf{i}}}^{{{\mathbf{norm}}}} \quad \forall i = 1, \ldots ,Ni \hfill \\ \end{gathered}$$
(36)

Results

Application and prediction

In this study, the SVR, GPR, and ANN models developed for the prediction of \({E}_{\text{s}}\) were implemented in the MATLAB 2019a software environment. Considering the results of best subset regression, porosity (\(n\)), P-wave velocity (\({V}_{p}\)) and slake durability index (\({I}_{d}\)) were taken into account as input parameters in the models. The experimental results, that is, the original dataset, were randomly divided into two datasets, which were (1) the training dataset that contained 75% of the original data and (2) the test dataset that contained 25% of the original data.

In supervised machine learning, the covariance function (kernel function) expresses the statistical relationship between two data points (\({x}_{i}\), \({x}_{j}\)). The kernel function (k(\({x}_{i}\), \({x}_{j}\))), which is specified by hyperparameters (\(\theta\)), can be defined in various forms, such as Gaussian, exponential Gaussian, rational quadratic, Matern 5/2, and radial basis function. In this study, the MATLAB hyper-parameter optimization method was employed to obtain the optimum hyper-parameters for each regression model. For the SVR model, the Gaussian function was selected as the kernel and its hyper-parameters were optimized by the kernel scale method. The kernel scale, input means (µ), input standard deviation (σ), and bias terms (β) were found to be 6.9, (4.9, 3.5, 90.73), (3.14, 0.46, 8.68), and 19.44, respectively. For the GPR model, the exponential Gaussian function was chosen as the kernel and its hyper-parameters were optimized by the sigma method. The characteristic length scale, input standard deviation, and bias term were computed as 9.29, 10.03, and 18.75, respectively. The Levenberg–Marquardt back-propagation approach was used to train a feedforward neural network using supervised learning. The constructed neural network was composed of one input layer with three neurons, two hidden layers with ten neurons in the 1st hidden layer and six neurons in the 2nd hidden layer, and an output layer with one neuron. The tansig function was a suitable function for smooth prediction in the ANN model and was thus used as a kernel function. The ANN model constructed was run for 300 iterations, and the best ANN model was selected according to the lowest MSE. Thirty-nine training epochs were used, and the 29th epoch was found to be the best, with an MSE of 1.678.

A comparison of the estimated values with the measured true values is shown in Figs. 6 and 7. Figure 6 indicates that the Es values obtained from the ANN and GPR models are located closer to the measured values, compared to the values obtained for the SVR model. When considering the outputs of the regression line drawn according to the measured and predicted \({E}_{\text{s}}\) values, and the line (1:1 line) where the measured and predicted values are equal (Fig. 7), the ANN and GPR model outputs are more successful than the other models.

Fig. 6
figure 6

Comparison of the estimated and measured \({E}_{\text{s}}\) values

Full size image
Fig. 7
figure 7

Scatter plots for the SVR, GPR, and ANN models developed showing the training and test periods

Full size image

Response surface

The training dataset was used to develop the regression models. The unseen values required for response surface plots were estimated using the developed models. The impacts of P-wave velocity and slake durability index with a constant porosity on \({E}_{\text{s}}\) are depicted in Figs. 8, 9 and 10. According to all the regression models developed, \({E}_{\text{s}}\) tends to increase with decreasing porosity, and with increasing P-wave velocity, and slake durability index. When the \(n\) value is kept constant, the \({E}_{\text{s}}\) value increases as the \({V}_{p}\) value increases. However, the change of \({E}_{\text{s}}\) with \({I}_{d}\) is not very clear. Moreover, when considering the plotted response surfaces, the SVR model shows linear behaviors, and the GPR model indicates quasi-linear behaviors, but the ANN model demonstrates completely nonlinear behaviors. Owing to the calculation algorithms of the SVR model, the response surfaces exhibit more linear behaviors compared to the GPR and ANN models. As shown in Fig. 9, the \({E}_{\text{s}}\) value reaches its maximum at the maximum \({V}_{p}\) value, regardless of the \({I}_{d}\) value. This is because \({V}_{p}\) plays an important role in estimating the \({E}_{\text{s}}\) value in the ANN model. The response surfaces of the training and test data illustrate the same trends for each regression model.

Fig. 8
figure 8

Surface and contour plots for the SVR model showing the effect of \({I}_{d}\) and \({V}_{p}\) for selected \(n\) values on \({E}_{\text{s}}\); a training dataset and b test dataset

Full size image
Fig. 9
figure 9

Surface and contour plots for the GPR model showing the effect of \({I}_{d}\) and \({V}_{p}\) for selected \(n\) values on \({E}_{\text{s}}\); a training dataset and b test dataset

Full size image
Fig. 10
figure 10

Surface and contour plots for the ANN model showing the effect of \({I}_{d}\) and \({V}_{p}\) for selected \(n\) values on \({E}_{\text{s}}\); a training dataset and b test dataset

Full size image

Performance evaluation

In the training and test periods, the performance of the ANN model is very close to that of the GPR model, but there is a significant difference between the ANN and SVR models. This is also true for the SVR and GPR models (Table 4, Figs. 11 and 12).

Table 4 Performance evaluation of the developed models using the defined KPIs
Full size table
Fig. 11
figure 11

Performance evaluation by Taylor diagram of the models developed

Full size image
Fig. 12
figure 12

ROC curves of the models developed

Full size image

During the training period, the RMSE, NRMSE, MAE, NMAE R2, NS, and VAF values for the SVR model were 3.244 GPa, 0.459, 2.558 GPa, 0.362, 0.787, 0.782, and 78.26%, respectively (Table 4). When considering the RMSE, the standard deviation of the \({E}_{\text{s}}\) values estimated, and R values in the Taylor diagram, the performance of the SVR model is significantly worse than the performances of the ANN and GPR models (Fig. 11). The AOC value of the SVR model is 2.521 MPa (Fig. 12). The PIRMSE and PIMAE values obtained for the SVR model are 1.101 and 1.198, respectively (Table 4). From the performance indicators obtained for the SVR model, it can be concluded that the learning ability of the SVR model is insufficient.

During the training period, the RMSE, NRMSE, R2, NS, and VAF values of the GPR model were 2.066 GPa, 0.292, 0.912, 0.908, and 91.17%, respectively, while the values for the ANN model were 2.486 GPa, 0.352, 0.870, 0.872, and 87.24%, respectively (Table 4). Additionally, the AOC, MAE, and NMAE values of the ANN model were 1.6846 GPa, 1.493 GPa, and 0.211, respectively, and were 2.377 GPa, 1.532, and 0.217, respectively, for the GPR model (Table 4 and Fig. 12). The standard deviation of the measured \({E}_{\text{s}}\) was 7.0707 GPa, that of the predicted \({E}_{\text{s}}\) GPa using the ANN model was 7.0673 GPa, and that of the predicted \({E}_{\text{s}}\) using the GPR model was 6.3447. Therefore, the variability of the \({E}_{\text{s}}\) values measured and that estimated by the ANN model are similar. The ANN model is more successful in terms of proximity to the measured Es (Fig. 11). In addition, the best result for approaching the maximum and minimum values of \({E}_{\text{s}}\) is obtained with the ANN model. However, as shown in the Taylor diagram (Fig. 11), the GPR model is more successful in terms of the RMSE and R values, than the ANN model. In terms of the PIRMSE and PIMAE values, the GPR model performed better than the ANN model. While the PIRMSE and PIMAE values of the GPR model are 1.5251 and 1.6006, and those of the ANN model are 1.3844 and 1.5249, respectively.

For the test period, the RMSE, MAE, NRMSE, NMAE, R2, NS, VAF, and AOC values of the SVR model are 5.662 GPa, 5.196 GPa, 0.619, 0.568, 0.695, 0.615, 62.7%, and 4.198 GPa, respectively (Table 4 and Fig. 12). The PIRMSE and PIMAE values obtained with the SVR model for the test data are 0.6519 and 0.7029, respectively. When considering the values of the key performance indices, the PIRMSE, and PIMAE, the SVR model is not successful in predicting the \({E}_{\text{s}}\) of the samples investigated.

For the test data, the ANN and GPR models are better than the SVR model in terms of R, RMSE, proximity to the standard deviation of the measured \({E}_{\text{s}}\), and AOC values (Figs. 11 and 12).

The performance of the GPR model for the test data for R2, RMSE, NRMSE, NS, and VAF is higher than that of the ANN model (Table 4). In the test period, the R2, RMSE, NRMSE, NS, and VAF values obtained for the GPR model are 3.365 GPa, 0.368, 0.898, 0.864, and 86.5%, respectively, and those for the ANN model are 3.767 GPa, 0.412, 0.859, 0.835, and 83.4%, respectively (Table 4). When considering only the MAE, NMAE, and AOC values, the success of the ANN model in predicting \({E}_{\text{s}}\) is higher than that of the GPR method. For the test period, the MAE, NMAE, and AOC values for the ANN model are 2.337 GPa, 0.255, and 1.3822 GPa, respectively, while those for the GPR model are 3.043 GPa, 0.332, and 1.5598 GPa, respectively (Table 4 and Fig. 12).

As illustrated in the Taylor diagram for the test data, the slope of the line connecting the point representing the GPR model with the origin is lower than the point representing the ANN model (Fig. 11). This indicates that the GPR model has a higher R value and a lower RMSE value than the ANN model in the test period. However, the point representing the ANN model is closer to the circle passing through the OBS (observed value) than the point representing the GPR model (Fig. 11). In the test period, the standard deviation of the measured \({E}_{\text{s}}\) is 9.0517 GPa, while the standard deviations of \({E}_{\text{s}}\) predicted using the ANN and GPR models are 7.637 GPa and 7.157 GPa, respectively. Therefore, for the test data, as for the training data, the variability of the measured \({E}_{\text{s}}\) values and the variability of \({E}_{\text{s}}\) values estimated by the ANN model are significantly closer to each other than that of the GPR model (Fig. 11). In the test period, the PIRMSE and PIMAE values obtained for the ANN model are 1.2567, and 1.4139, respectively, while those obtained for the GPR model are 1.3779 and 1.4142, respectively. When considering that PIRMSE and PIMAE were formed by more than one KPI, the GPR model performed better than the ANN model.

Discussion

To compare the performance of the models developed in this study to the prediction models given in the literature, the studies aimed to predict \({E}_{\text{s}}\) of magmatic, and metamorphic rocks and include the prediction models based on ANN, SVR, and GPR models. As shown in Table 1, the properties of intact rock commonly used in the prediction models suggested for \({E}_{\text{s}}\) of magmatic and metamorphic rocks are the Schmidt hammer hardness (SHH), shore hardness (SH), UCS, tensile strength (TS), point load index (PLI), and block punch index (BPI). Although the measurement of SHH is rapid and easily executed, simple, and portable, it has limitations, such as the anisotropy and heterogeneity of the rocks, a very small test conduction area, and surface roughness (Yilmaz 2009). UCS, TS, and BPI tests have two main limitations and problems, which are (1) a standard sample cannot always be obtained and (2) the tests cannot be repeatable. The BPI test is only valid for very thin small discs, and an irregular failure causes the need for a substantial amount of rock specimens (Yilmaz 2009). These limitations and problems related to the UCS, TS, and BPI are more concerning for weathered rocks. The disadvantages of PLI that do not need a standard sample are as follows: (1) tests are applied in very small areas, (2) invalid test results frequently occur, (3) the specimen may move during loading, and (4) micro-fissures may cross the conical platens (Yilmaz 2009). In addition, the force measurement accuracy in PLI may not be sufficient for the testing of weathered rock samples, and in these samples, there may be penetrating conical platens in the sample. The main shortcoming of the SH test is that the measurements are obtained from a random mineral, and anisotropy and/or heterogeneity of the rocks. Taking into account the limitations and problems, it can be acknowledged that there may be difficulties in using the results of such hardness and strength tests as inputs in the regression models.

The performances of the soft computing models to estimate the \({E}_{\text{s}}\) of magmatic and metamorphic rock samples reported in Khandelwal and Singh (2011), Saedi et al. (2018), Tian et al. (2019), Armaghani et al. (2020), and Acar and Kaya (2020) are higher than those of the GPR model proposed in this study when comparing their R2 values (Table 1). However, these prediction models use one or more of the SHH, SH, UCS, TS, PLI, and BPI as inputs. Other prediction models developed for the \({E}_{\text{s}}\) of magmatic and metamorphic rock samples reported by Sonmez et al. (2006), Manouchehrian et al. (2013), Armaghani et al. (2016), Atici (2016), and Behzadafshar et al. (2019) also used hardness and strength properties as inputs, even though they had limitations and problems (Table 1). Furthermore, the performances of the regression models were not better than those of the GPR and ANN models developed in this study.

Kumar et al. (2013) adopted a relevance vector machine (RVM), GPR, and minimax probability machine regression (MPMR) for the prediction of UCS and \({E}_{\text{s}}\) of travertine samples. The GPR model in their study had a higher R2 value than the GPR and ANN models developed in this study, but UCS and PLI were used as inputs in their study. The ANFIS models used by Armaghani et al. (2015) and Singh et al. (2017) performed better than the GPR models developed in this study but here, the GPR models were developed with different magmatic rock types with different degrees of weathering, while the ANFIS models were developed with only one rock type (Table 1). The input parameters of the LS-SVM models for predicting the \({E}_{\text{s}}\) of weathered rock samples given in Ceryan (2016) are the effective porosity and the P-durability index. The P-durability index is based on the slake durability index and P-wave velocity. Although the LS-SVM model successfully predicted \({E}_{\text{s}}\), it had a lower R2 value than the GPR and ANN models developed in this study. In addition, the P-durability index could not be selected as a suitable input parameter while selecting input parameters using the best subset regression analysis applied in this study. Behnia et al. (2017) developed a gene expression programming (GEP) model to predict the \({E}_{\text{s}}\) and UCS of different rocks. The model used quartz content, porosity, and density as input parameters and performed successfully, with an R2 value of 0.927. It can be concluded that using the GEP model to predict the \({E}_{\text{s}}\) of weathered magmatic and metamorphic rock is useful.

When selecting inputs used in the suggested models in this study, the following factors were taken into account: (1) inputs are able to characterize these intrinsic characteristics and the state of weathering, (2) their measurements can be performed easily and rapidly in practical and economic terms, and (3) they provide high performance to the prediction models in which they are used. The simple and non-destructive properties (\(n\), \({V}_{p}\), \({V}_{\text{m}}\), \(V_{{{\text{id}}}}\), \({I}_{d}\), SHH, and \({\text{SHH}} \times \gamma\)) were obtained experimentally for use in the \({E}_{s}\) estimation of the studied samples. As indicated in Table 1, these properties are the most frequently used inputs in prediction models. However, not all of them have been used in the same prediction models because of the practical and technical difficulties discussed here. For this, the best subset regression approach was employed to determine the inputs. As a result, porosity (\(n\)), P-wave velocity (\({V}_{p}\)), and the slake durability index (\({I}_{d}\)) were employed as inputs for the proposed SVR, GPR, and ANN models.

There are good relationships between the elastic wave velocity and the chemical and mineralogical composition of rocks (Ceryan 2015). This is also valid for weathered rock because the fresh mineral content decreases, while micro-fracture voids increase with weathering. Therefore, \({V}_{p}\) decreases with increasing weathering (Ceryan et al. 2008a; Wyering et al. 2014; Momeni et al. 2017; de Vilder et al. 2019), and it is possible to characterize weathered magmatic and metamorphic rock material properties by \({V}_{p}\) measurements (Ceryan et al. 2008b). Furthermore, it was also proposed that a non-destructive measurement of \({V}_{p}\) offers an alternative input for \({E}_{\text{s}}\) estimation with relative ease and at a low operational cost (Yasar and Erdogan 2004). The pore characteristics and fundamental microstructural parameters are important physical properties that govern the physical attributes of rocks, for example, strength, deformability, and hydraulic conductivity (Tugrul 2004). There are difficulties in determining pore size distribution, pore geometry, pore infilling, and pore connectivity, and therefore, porosity and effective porosity are commonly used to define the pores of rock materials (Ceryan 2014, 2015). The total porosity and the number of connected pores generally characterize the weathering state and these properties increase with weathering (Ceryan et al. 2008a). For these reasons, porosity or effective porosity is commonly used for estimating the \({E}_{\text{s}}\) of rock materials (Table 1). The slake durability test is an inexpensive and easy test to conduct and requires very little sample preparation. Therefore, it is a good index for representing weathering processes (Lee and De Freitas 1989; Cargill and Shakoor 1990; Ceryan et al. 2008b; Sharma et al. 2008; Ceryan 2015). The slake durability index can be used inexpensively and easily to estimate the deformation modulus of weathered or soft rocks (Table 1). When the result of considering the best subset regression analysis performed, and the characterization of the weathering process in magmatic and metamorphic rocks, it is apparent that using porosity, slake durability index, and P-wave velocity as inputs in prediction models developed for rock materials is a practical and economical approach.

In all regression models, the combination of \({V}_{p}\) and \({I}_{d}\) can estimate the behavior of \({E}_{\text{s}}\) referred to response surfaces illustrated in Figs. 7, 8, 9 and 10. Furthermore, the maximum \({E}_{\text{s}}\) value is obtained at higher \({V}_{p}\) and \({I}_{d}\) values and lower \(n\) values as expected.

When the \(n\) value is kept constant, the \({E}_{\text{s}}\) value enhances as the \({V}_{p}\) value increases. On the other hand, the increase in the \({E}_{\text{s}}\) value is very subtle only increasing with the \({I}_{d}\) value when other inputs are held constant. For example, considering the same data point [\({V}_{p}\): 4.16 km/s, \({I}_{d}\): 99.5%] the \({E}_{\text{s}}\) values are around 27 GPa with \(n\): 2.52% for SVR, and GPR; whereas the \({E}_{\text{s}}\) value is around 21 GPa with \(n\): 11.057% for SVR, and GPR. Moreover, the estimated \({E}_{\text{s}}\) value at the given data point for lower porosity value was around 27 GPa, but it decreased to around 12 GPa with the increase of the porosity value. As a result, ANN is more sensitive chances in \({V}_{p}\) and \(n\). On the other hand, the SVR and GPR models are more sensitive chances in \({V}_{p}\). As seen in the response surfaces, while the output values of the models are most sensitive to the change of \({V}_{p}\), they are least sensitive to the change of \({I}_{d}\). The sensitivity of the output of the models in chances of the input parameters is related to the results of weathering processes on the rock material, as is related to the characteristics of soft computing techniques. Due to that the weathering product content, which having lower \({V}_{p}\) than fresh minerals, and micro-fracture voids increase with weathering, the decreasing of \({V}_{p}\) with weathering is more regularly and faster than \({I}_{d}\) and \(n\).

KPIs, namely VAF, RMSE, MAE, and R2, can be separately used to examine model accuracy, but none are superior and therefore, the PI, which combines these KPIs, was suggested (Yagiz et al. 2012). Successively, adjR2 was employed in computing the PI value instead of R2 because it is a statistic with systematic error based on the number of independent variables in the equation, sample size, and the coefficient of variation (Ceryan 2014). However, the PI value given in Ceryan (2014) depends on the RMSE. The RMSE and MAE metrics, can range from 0 to ∞ and are indifferent to the direction of errors. The errors are squared before they are averaged, and therefore, the RMSE gives a relatively high weight to large errors. Owing to this characteristic of RMSE, it usually determines model performance differences better than other indices (Chai and Draxler and 2014). However, RMSE has important disadvantages because it is a function of three characteristics of a set of errors, rather than of one (the average error). RMSE varies with the variability within the distribution of error magnitudes, and the square root of the sample number, as well as with the average error magnitude (MAE) (Willmott and Matsuura 2005). Without the benefit of other information, for example, MAE, it is impossible to discern the extent to which RMSE reflects the central tendency (average error) or the variability within the distribution of squared errors (Mielke and Berry 2001; Willmott and Matsuura 2005; Willmott et al. 2009). Given the definition of MAE, it is clear that MAE, unlike RMSE, is an unambiguous measure of average error magnitude (Willmott and Matsuura 2005). However, the MAE might be affected by a large number of average error values without adequately reflecting some large errors (Chai and Draxler 2014). For these reasons, using the KPI, which considers both the errors themselves and the squares of the errors, would be more accurate. With this in mind, a new PI, PIMAE, has been proposed using normalized MAE instead of normalized RMSE. Both PIRMSE and PIMAE were used in this study. When the values of these performance indices are less than 1, the prediction model fails, and the success of the model is higher as the value approaches 2. A prediction model is more successful if it has a larger PIRMSE and PIMAE value than the other model. If the PIRMSE is large and the PIMAE is small, other performance criteria should also be considered.

In this study, the REC diagram is drawn using the absolute value of errors (as in MAE). In contrast, RMSE is used in the Taylor diagram and does not provide the differences between the measured and obtained values directly. To overcome this deficiency, the REC curve was used to evaluate the performance of the models developed in this study.

Based on performance evaluation according to Performance Indexes, Taylor, and REC diagrams, it is clear that the SVR model developed in this study is the worst model for estimating the \({E}_{\text{s}}\) of the investigated samples. In the training and test periods, the GPR model performs better than the ANN model in terms of the R and centered RMSE components of the Taylor diagram, while the variability (standard deviation) of \({E}_{\text{s}}\) values obtained with the ANN model is closer to the variability of the observed \({E}_{\text{s}}\) values. The AOC value obtained according to the absolute values of the errors (as in the MAE) is lower for the ANN model. However, the GPR model has a better performance than the ANN model in terms of PIRMSE and PIMAE values.

The SVR, GPR, and ANN models can approximate almost all types of non-linear functions, including quadratic functions. The soft computing models use a “black box” approach and have some difficulties in sharing the methodology with other researchers (Suykens and Vandewalle 1999; Agatonovic-Kustrin and Beresford 2000; Rasmussen 2004; Desai et al. 2008; Ahmadi and Rodehutscord 2017; Ozkat et al. 2017c). The SVR and GPR models are based on the same probabilistic regressive model, while ANN is not a probabilistic model. The GPR and SVR models developed here assume a Gaussian data distribution, but the ANN model does not assume any data distribution. The ANN and GPR models do not have a sparse solution. They use all sample/feature information to perform the prediction. The SVR model has the noteworthy advantage of frequently yielding sparse solutions. It minimizes reconstruction errors through convex optimization, ensuring that the optimal estimate is found, but it is not a unique solution. In the ANN model, the optimization is not always convex, and therefore, the solution is not always a global minimum (Suykens and Vandewalle 1999; Agatonovic-Kustrin and Beresford 2000; Rasmussen 2004; Khandelwal and Singh 2009; Kumar et al. 2013; Samui et al. 2019).

Parametric approaches distill knowledge about the training data into a set of numbers. They require a large amount of data, especially for architectures with many layers because of the vast number of weights and connections in ANN models. In contrast, Gaussian processes are non-parametric methods. A Gaussian processes kernel allows for the specification of a prior control on the function space, which can be extremely useful, especially when there are scant data (Bijl et al. 2017). However, as Gaussian processes are non-parametric, they need to take all the training data into account each time they make a prediction. This means that the computational cost of predictions increases with the number of training samples (Agatonovic-Kustrin and Beresford 2000; Rasmussen 2004; Bijl et al. 2017).

The originality and limitations of this study are as follows:

The best subset regression approach was employed to determine the inputs in the proposed prediction model developed. As a result of this analysis, the most suitable parameters were found to be porosity (\(n\)), P-wave velocity (\({V}_{p}\)), and the slake durability index (\({I}_{d}\)). They are frequently used inputs in prediction models (Table 1) and are commonly used to define the state of weathering and in predicting the UCS and \({E}_{\text{s}}\) of weathered magmatic and metamorphic rocks (Ceryan 2018). The measurements of \({V}_{p}\) and \(n\) are non-destructive, repeatable, easy, and economical. The slake durability test is an inexpensive and easy test to conduct and requires very little sample preparation.

The ANN and GPR models developed in this study successfully predicted the \({E}_{\text{s}}\) of the samples investigated. Although there are many ANN models to predict the \({E}_{\text{s}}\) of rock materials, the number of GPR methods is quite low (Table 1). Moreover, according to the literature, there are very few soft computing models developed to assess the \({E}_{\text{s}}\) of magmatic rock material with different degrees of weathering (Table 1). This study provides data and approaches to overcome this deficiency.

This study demonstrates that it is more useful to use together criteria based on the square of errors (e.g., RMSE and Taylor diagram) and criteria based on the absolute value of errors (i.e., MAE and REC have drawn depending on the absolute value of errors). In this study, the new Performance Index, PIMAE, which takes MAE into account, was created and it was stated that it would be beneficial to use together with this performance index and the Performance index based on RMSE. The ANN and GPR models given in this study have been developed to estimate the Es of magmatic and metamorphic rock samples with different degrees of weathering. These models can be applied to magmatic and metamorphic rock samples containing at least three different degrees of weathering.

Conclusion

This study from NE Turkey, examined the applicability and capability of the SVR, GPR, and ANN models in \({E}_{\text{s}}\) prediction of magmatic rocks with different degrees of weathering. The selection of the inputs for use in the models was performed using the best subset regression approach. As a result of these analyses, porosity, P-wave velocity, and the slake durability index that are used commonly in defining the weathering state and in predicting the \({E}_{\text{s}}\) of weathered rocks, were selected as inputs for the prediction models developed in this study. Here, the weathering effect on the engineering behaviors of rock material is considered, and it is shown that using porosity, slake-durability index, and P-wave velocity together is a very powerful tool for estimating the elastic modulus of weathered magmatic and metamorphic rocks.

Given the difficulties of RMSE and MAE in expressing the error alone, it is useful to use both the index based on the absolute value of errors and the index based on the square value of error in evaluating the performance of the prediction models. For this, a new PI, PIMAE, is proposed here, using normalized MAE instead of normalized RMSE.

According to the computed KPIs, Taylor diagram, and REC curves, it is concluded that the SVR model is insufficient for predicting the elastic modulus of the weathered magmatic rock samples. In the test period, the R2, RMSE, and AOC values obtained for the SVR model were 0695, 5.662 GPa, and 4.198 GPa, respectively. In addition, the PIRMSE and PIMAE obtained for the SVR model developed were lower than 1.0, being 0.6519 and 0.7028, respectively.

During the training and test periods, the results of the performance analysis of the ANN and GPR models using KPIs, the Taylor diagram, and the REC curves were excellent. In both the training and test periods, when the performance metrics were considered one by one, in the criteria based on the absolute value of error, for example, MAE, NMAE, and AOC, and when approaching extreme measured values and standard deviation of \({E}_{\text{s}}\) value, the ANN model was more successful than the GPR model. The MAE, NMAE, and AOC values of the ANN model for the test data were 2.337 GPa, 0.255, and 1.3822 GPa, respectively, while those of the GPR model were 0.043, 0.332, and 1.5598 GPa, respectively. Conversely, in terms of R2, RMSE, NRMSE, NS, and VAF, the GPR model performed better than the ANN model. In the test period, the R2 value obtained for the GPR model was 0.898, while that for the ANN model was 0.859. For PIRMSE and PIMAE, which were created by combining multiple KPIs, the performance of the GPR model was better than that of the ANN model. The PIRMSE and PIMAE values of the GPR model for the test data were 1.3779 and 1.4142, respectively, while those for the ANN model were 1.2567 and 1.4139, respectively. In the Taylor diagram, the GPR model performed better than the ANN model. Moreover, because of the probabilistic and non-parametric nature of the GPR system, it can be easily simulated and projected.

The performance of the GPR model is slightly better than that of the ANN model, although both the models are successful in predicting the \({E}_{\text{s}}\) of the magmatic rock samples with different degrees of weathering. It would be useful to develop GPR and ANN models with porosity, P-wave velocity, and the slake durability index to predict the \({E}_{\text{s}}\) and UCS of other weathered rock samples, including samples with at least three different degrees of weathering.